| Issue |
A&A
Volume 544, August 2012
|
|
|---|---|---|
| Article Number | A148 | |
| Number of page(s) | 8 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201219400 | |
| Published online | 23 August 2012 | |
Electron acceleration during three-dimensional relaxation of an electron beam-return current plasma system in a magnetic field
1 Astronomical Institute of the Academy of Sciences of the Czech Republic, 25165 Ondřejov, Czech Republic
e-mail: karlicky@asu.cas.cz
2 SUPA, School of Physics & Astronomy, University of Glasgow, G12 8QQ, UK
Received: 12 April 2012
Accepted: 10 July 2012
Aims. We investigate the effects of acceleration during non-linear electron-beam relaxation in magnetized plasma in the case of electron transport in solar flares.
Methods. The evolution of electron distribution functions is computed using a three-dimensional particle-in-cell electromagnetic code. Analytical estimations under simplified assumptions are made to provide comparisons.
Results. We show that, during the non-linear evolution of the beam-plasma system, the accelerated electron population appears. We found that, although the electron beam loses its energy efficiently to the thermal plasma, a noticeable part of the electron population is accelerated. For model cases with initially monoenergetic beams in uniform plasma, we found that the amount of energy in the accelerated electrons above the injected beam-electron energy varies depending the plasma conditions and could be around 10–30% of the initial beam energy.
Conclusions. This type of acceleration could be important for the interpretation of non-thermal electron populations in solar flares. Its neglect could lead to the over-estimation of accelerated electron numbers. The results emphasize that collective plasma effects should not be treated simply as an additional energy-loss mechanism, when hard X-ray emission in solar flares is interpreted, notably in the case of RHESSI data.
Key words: Sun: flares / Sun: particle emission / Sun: X-rays, gamma rays
© ESO, 2012
1. Introduction
Solar flare X-ray observations provide often unique insights into the processes of electron acceleration and transport. Recent observations of solar flares, notably with RHESSI (Lin et al. 2002) have emphasized the high efficiency of electron acceleration in solar flares (for a recent review of electron properties, see Kontar et al. 2011; and for the corresponding implications for particle transport in solar flares, Karlický 1997; and Holman et al. 2011).
The high efficiency of electron acceleration results in high electron fluxes or concentrations of deka-keV electrons in solar flares, and the subsequent importance of collective effects to particle transport in the solar atmosphere. The presence of large number of energetic electrons in coronal loops could trigger a number of instabilities and generate plasma waves, which in turn affect the transport of energetic particles from the acceleration region down to the chromosphere. It has been shown that accounting for these collective effects could affect the interpretation of hard X-ray spectra and lead to additional observational consequences that are essential to the study of solar flares. For example, the inclusion of Langmuir wave generation in the treatment of spatially localized electron beams (Hannah et al. 2009) prevents the formation of a pronounced low-energy cut-off that appears in purely collisional models (e.g. Brown 1971; Brown et al. 2002). Weibel instability (Weibel 1959) can quickly increase the velocities in the direction perpendicular to the beam propagation and affect the observed X-ray anisotropy (Karlický & Bárta 2009; Karlický & Kašparová 2009). The presence of Langmuir waves in a flaring loop could also result in plasma emission (e.g. Vlahos & Papadopoulos 1979; Emslie & Smith 1984; Hamilton & Petrosian 1987), providing additional constraints on non-thermal electron populations in solar flares.
In laboratory plasma experiments, collision-less effects involving various instabilities have been demonstrated to play a key role in electron transport. In experiments to study the beam-plasma interaction, the appearance of electrons with energies exceeding that of the injected beam energy was noted in early studies (e.g. Berezin et al. 1964; Fainberg 1968; Kovalenko 1983). These above-the-injected energy electrons are normally connected to either the presence of plasma inhomogeneities (Vedenov et al. 1967; Ryutov 1969; Nishikawa & Ryutov 1976; Escande 1979) or the nonlinear effects of wave-particle interactions (Breizman & Ryutov 1975; Timofeev & Terekhov 2010). Furthermore, the influence of plasma inhomogeneities or wave-wave interactions on beam-plasma instability in the solar context has been studied extensively in connection to the theory of solar radio-type III bursts (e.g. Muschietti et al. 1985; Tyshetskiy et al. 2007; Kontar & Reid 2009; Tsiklauri 2010; Reid & Kontar 2010; Ziebell et al. 2011). The processes governing non-thermal electron evolution in solar flares span a computationally prohibitive range of timescales from the inverse plasma period 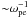 to observational timescales of thousands of seconds. Therefore, modeling efforts in solar flare physics have focused either on relatively long observational timescales by either ignoring short-timescales or addressing the micro-physics on scales smaller than the observational scales (e.g. Bret 2009; Bingham et al. 2001; Eliasson et al. 2006; Hewett et al. 1991; Lee et al. 2008; Messmer 2002; Rose et al. 2002; Sakai et al. 2006; Saito & Sakai 2004).
to observational timescales of thousands of seconds. Therefore, modeling efforts in solar flare physics have focused either on relatively long observational timescales by either ignoring short-timescales or addressing the micro-physics on scales smaller than the observational scales (e.g. Bret 2009; Bingham et al. 2001; Eliasson et al. 2006; Hewett et al. 1991; Lee et al. 2008; Messmer 2002; Rose et al. 2002; Sakai et al. 2006; Saito & Sakai 2004).
Kontar et al. (2012) showed that the k-spectrum evolution of beam-generated Langmuir waves in collisional plasma could result in substantial energy gain by high energy electrons or the effective acceleration of electrons of the same beam above 20 keV for solar flare conditions. Thus, if collisional relaxation is assumed, the number of energetic electrons inferred from X-ray spectra could be overestimated and may lead to an apparently large number of accelerated electrons. However, the treatment of Kontar et al. (2012) is a one-dimensional analysis based on weak turbulence theory. They showed that a positive density gradient, externally excited density fluctuations, and the three-wave interaction involving ion-sound mode could lead to an effective acceleration of beam electrons. However, the role of the guiding magnetic field as well as three-dimensional (3D) aspects of beam-plasma interaction have not yet been addressed.
This paper investigates the non-linear evolution of non-thermal electron beams in a plasma. Using the particle-in-cell (PIC) model developed in Karlický (2009) and Karlický & Kašparová (2009), we investigate the effects of the acceleration of electrons in the beam during a non-linear stage of beam-plasma instability for various values of the guiding magnetic field. We show that about ≃ 10 − 30% of electrons are accelerated to the energies greater than the energies at which they were injected. The presence of a guiding field increases the number of electrons accelerated during a beam-plasma interaction. The results show the appearance of accelerated electrons and highlight that collective effects can lead to not only additional energy losses for lower energy electrons but the acceleration of some electrons above the initial energy of electrons. As the hard X-ray spectra in solar flares is normally due to deka-keV electrons, this acceleration effect should be taken into account when the number of accelerated electrons is estimated. In this paper, we compared these results with analytical estimates.
 |
Fig. 1 The electron velocity distributions for model E at four different times: at the initial state a), at ωpet = 40 b), at ωpet = 140 c), and ωpet = 200 d). Crosses correspond to f(vz), dotted and dashed lines display f(vx) and f(vy), respectively. Note that f(vx) and f(vy) overlap. The vertical line in the part a) at v/c = 0.666 denotes the monoenergetic electron beam. |
 |
Fig. 2 The Langmuir wave energy for model E in the k-space at four different times: ωpet = 40 a), ωpet = 60 b), ωpet = 140 c), and ωpet = 200 d) (solid lines). For comparison in each panel, the initial Langmuir wave energy is added (dashed line). |
 |
Fig. 3 The electron energy distributions for model E at four different times: ωpet = 40 a), ωpet = 60 b), ωpet = 140 c), and ωpet = 200 d) (solid lines). For comparison in each panel, the initial electron-plasma distribution together with the initial monoenergetic beam are added (dashed lines). |
 |
Fig. 4 The electron energy distributions (solid lines) at ωpet = 200 as a function of the magnetic field in models A-F with ωce/ωpe = 0.0, 0.1, 0.5, 0.7, 1.0, and 1.3, respectively. For comparison in each panel we plot the initial electron plasma distribution together with the initial monoenergetic beam (dashed lines). |
2. Simulation model
It is commonly accepted that electrons in solar flares are accelerated at low corona heights by primary energy-release processes. They propagate along the magnetic field lines as electron beams downwards to loop footpoints, where they generate hard X-ray emission. The rapid variations (of timescales ~45 ms) in this hard X-ray emission observed in some events indicate that the acceleration as well as the electron beam flux can may themselves rapidly varying (e.g. Kiplinger et al. 1983; Aschwanden et al. 1995). This means that the effect of fast propagation needs to be considered in the evolution of these electron beams. Assuming that the electrons have a power-law distribution in the acceleration region. Owing to the propagation, fast electrons could then overtake slower ones at some distance from the acceleration site (e.g. Hannah et al. 2009), forming an unstable distribution that can be approximated by the mono-energetic beam.
For our study, we used a 3D (three spatial and three velocity components) relativistic electromagnetic PIC code (Karlický 2009). The system sizes are Lx = 45Δ, Ly = 45Δ, and Lz = 600Δ, where Δ is the grid size.
We initiated a spatially homogeneous electron-proton plasma with the proton-electron mass ratio mp/me = 16 (models A-H in Table 1). This ratio was chosen to shorten the computational times and keep the proton skin-depth shorter than the dimensions of the numerical box. Nevertheless, the ratio was still sufficient to clearly separate the dynamics of electrons and protons. The electron thermal velocity was vTe = 0.06 c, where c is the speed of light. In all models, 160 electrons and 160 protons per cube grid were used. The electron plasma frequency was ωpe = 0.05(Δt)-1 (Δt = 1 is the time step) and the electron Debye length was λD = vTe/ωpe = 0.6Δ. The electron and proton skin-depths were λce = c/ωpe = 10Δ and λcp = c/ωpp = 40Δ (where ωpp is the proton plasma frequency), respectively.
We then included a mono-energetic beam that was homogeneous throughout the numerical box. To keep the total current zero in these models in their initial states, we introduced an initial return current by shifting the background plasma electrons in the velocity space according to the relation vd = −vbnb/ne, where vb is the velocity of the electron beam, and nb and ne are the beam and background plasma densities; for an example of this type of initialization, see Niemiec et al. (2008). In principle, it is possible to start from a zero initial return current. However, owing to inductive effects included in the used 3-D electromagnetic code, the current starts to oscillate at the electron plasma frequency with the amplitude of the stabilizing return current. Therefore in these simulations, we recommend starting from an already stabilized return current (Nishikawa 2008). Although these current oscillations can influence the studied acceleration, for simplification, we did not take this effect into account. We similarly neglected any effects of the return-current formation (electrostatic ones) on the front of the propagating beams.
Model parameters and the fraction (FR) of the beam energy in the electrons with energies greater than the initial-beam electron energy.
The beam velocity was chosen to be vb/c = 0.666 in the z direction. The ratio of the beam to the plasma densities was chosen to show the details of the acceleration process nb/ne = 1/8, which is a rather high value (however still realistic). The lower values of nb/ne = 1/40, see Table 1, for comparison, were used in models G and H.
To investigate the influence of the magnetic field in the models, we consider several values of the background magnetic field, so that the ratio of the electron-cyclotron to electron-plasma frequencies (ωce/ωpe) is 0.0, 0.1, 0.5, 0.7, 1.0, and 1.3 (see Table 1). In all models, the periodic boundary conditions were used.
3. Results of numerical simulations
Using the above described model, we performed eight runs (A-H) using the parameters given in Table 1. As an example (see Fig. 1), a time evolution of the electron velocity distribution for model E is shown at four different times: the initial state (a), ωpet = 40 (b), ωpet = 140 (c), and ωpet = 200 (d). Crosses correspond to f(vz), and dotted and dashed lines display f(vx) and f(vy), respectively. The vertical line in the initial state at v/c = 0.666 denotes the mono-energetic electron beam. As can be seen here, a plateau forms in the velocity space between the velocity of the initial beam and that of the background plasma electrons. It is produced by the so-called quasi-linear relaxation, in which the electron beam generates the Langmuir waves (see Fig. 2). The Langmuir waves were initially generated at the k-wave vector corresponding to the resonance condition for the beam-plasma instability, i.e. at ω = kzvb (see the peak in the Langmuir wave energy-spectrum in Fig. 2a), where ω is the frequency of the Langmuir waves and vb is the electron beam velocity (Mikhailovskii 1975). These Langmuir waves then decay and merge mainly in accordance with the three wave interactions (for details, see e.g. Bárta & Karlický 2000) and evolve in the k-vector space (see the enhanced Langmuir wave spectrum in Figs. 2b − d). The Langmuir waves, on the other hand, scatter the beam electrons and heat the background plasma. During this process, the plateau in the electron distribution function f(vz) is formed (see detailed discussion of the quasi-linear relaxation in the following section). However, during this process some beam electrons, owing to an interaction with the Langmuir waves, obtain an energy that is higher than the electron energy in the initial beam. This is shown in Fig. 3, where a time evolution of the electron energy distributions for model E at four different times is presented: at (a) ωpet = 40 (b) ωpet = 60, (c) ωpet = 140, and (d) ωpet = 200. For comparison, we show in each panel in this figure the initial electron-plasma distribution together with the initial mono-energetic beam (dashed lines). Here, it can clearly be seen that some electrons have the energies higher than those of the initial beam.
Although in the initial state, we started from a uniform background plasma, very soon (owing to the dense beam) strong density fluctuations appeared (see Fig. 5). During the evolution, their characteristic lengths became longer (compare Figs. 5a and 5b). In the early stages of evolution, the associated electric field densities are not correlated with the density fluctuations. On the other hand, in the later stages of evolution, e.g., at ωpet = 190 it can be seen that the electric fields (Langmuir waves) start to be trapped in density depressions (see e.g. the electric field densities at z, equal to 300Δ and 430Δ respectively).
To investigate the energetics of the accelerated electrons, we computed their energy (expressed in fraction of the initial beam energy) above some selected energy levels. The time evolution of these fractions for the energies higher than E/mc2 = 0.25 and E/mc2 = 0.3, for model E are shown in Fig. 6. The initial energy of the beam electron was E/mc2 = 0.22178. In this figure, for comparison the time evolution of the maximum energy of the electron (E/mc2) is plotted. The fractions firstly increase in time, owing to the some time taken for acceleration of these electrons to the selected energy levels. The fractions then slowly decrease to some saturation level, in agreement with the saturation of the quasi-linear relaxation process. The fractions generally decrease with the increase in the energy interval between the beam energy and selected energy level. We also computed the fractions of these accelerated electrons for the energy levels just above the beam energy. For all computational models (A-H) at the time ωpet = 200, these fractions are summarized as percentages in the last column of Table 1. These fractions increase as the magnetic field increase, e.g. from FR = 10% for ωce/ωpe = 0 (model A) to FR = 29% for ωce/ωpe = 1 (model E). For even greater values of ωce/ωpe, the fractions start to decrease (see FR = 27% for ωce/ωpe = 1.3 in model F). Similar results were found for models G and H, where we considered a beam density lower than in models A-F (see Table 1). As shown and analyzed in the papers of Karlický & Bárta (2009) and Karlický & Kašparová (2009) for the models with weak magnetic fields (models A-B), the Weibel instability is significant and strongly influences the resulting electron distribution function. On the other hand, the strong magnetic field (e.g. model E) reduces the role of the Weibel instability (see also the discussion and Fig. 8).
As an illustration, we present in Fig. 4 the electron energy distributions at ωpet = 200 for all runs, i.e. for ωce/ωpe = 0.0, 0.1, 0.5, 0.7, 1.0, and 1.3, respectively (models A-F, Table 1). The number of electrons accelerated above the initial electron-beam energy (expressed by the vertical dashed line) corresponds to the fractions FR in Table 1.
4. Quasi-linear relaxation – analytical estimates
While the analytical treatment of a 3D non-linear beam-plasma system is impossible, the efficiency of acceleration can be estimated in the quasi-linear limit. In this limit, the evolution of energetic electrons is described by two coupled kinetic equations (Vedenov & Velikhov 1963; Vedenov et al. 1967; Tsytovich 1995). For a weakly magnetized plasma, when the field is strong enough to provide one-dimensional electron dynamics, the electron beam evolution can be described using standard quasi-linear theory 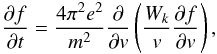 (1)
(1)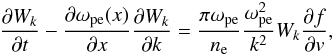 (2)where f(v,t) is the electron distribution function, Wk is the spectral energy density of the Langmuir waves, ωpe is an electron plasma density, and e and m are the electron charge and mass. The equations describe the resonance (ωpe = kv) interaction of the electron beam with the surrounding plasma via the generation of plasma waves and include plasma inhomogeneity effects (see, e.g. Vedenov et al. 1967; Ryutov 1969; Kontar & Pécseli 2002).
(2)where f(v,t) is the electron distribution function, Wk is the spectral energy density of the Langmuir waves, ωpe is an electron plasma density, and e and m are the electron charge and mass. The equations describe the resonance (ωpe = kv) interaction of the electron beam with the surrounding plasma via the generation of plasma waves and include plasma inhomogeneity effects (see, e.g. Vedenov et al. 1967; Ryutov 1969; Kontar & Pécseli 2002).
When the plasma is uniform 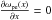 , the stationary solution for the initially unstable beam distribution f(v,t = 0) = g0(v), v < vb of the coupled quasi-linear equations is well-known (Vedenov & Velikhov 1963). The electron distribution function has the form of a plateau
, the stationary solution for the initially unstable beam distribution f(v,t = 0) = g0(v), v < vb of the coupled quasi-linear equations is well-known (Vedenov & Velikhov 1963). The electron distribution function has the form of a plateau 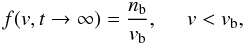 (3)and the spectral energy density of plasma waves Wk can be found from Eqs. (1), (2) using Eq. (3)
(3)and the spectral energy density of plasma waves Wk can be found from Eqs. (1), (2) using Eq. (3) 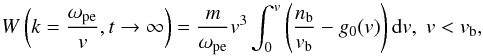 (4)thus the spectral energy density becomes
(4)thus the spectral energy density becomes 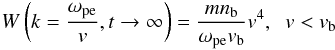 (5)for g0(v) = nbδ(v − vb) and takes the form
(5)for g0(v) = nbδ(v − vb) and takes the form 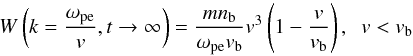 (6)for
(6)for 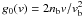 , v < vb, (see Kontar 2001, for details). The total energy density of plasma waves from Eq. (5) is
, v < vb, (see Kontar 2001, for details). The total energy density of plasma waves from Eq. (5) is 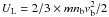 and
and 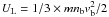 for the second case given by Eq. (6).
for the second case given by Eq. (6).
However, when the plasma has a positive density gradient 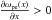 , which corresponds to electrons propagating into the region of higher density (as in the standard flare scenario), the Langmuir waves slowly evolve towards larger phase velocities or smaller wavenumbers k. As Langmuir wave packets propagate within the plasma, the total energy of the wave packet ω(k,x) must be constant (Vedenov et al. 1967), which requires that the wavenumber change be negative for a positive plasma-density gradient, such that
, which corresponds to electrons propagating into the region of higher density (as in the standard flare scenario), the Langmuir waves slowly evolve towards larger phase velocities or smaller wavenumbers k. As Langmuir wave packets propagate within the plasma, the total energy of the wave packet ω(k,x) must be constant (Vedenov et al. 1967), which requires that the wavenumber change be negative for a positive plasma-density gradient, such that 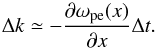 (7)Therefore, the motion of Langmuir wave over the time range Δt results in a decrease in the wavenumber from k to
(7)Therefore, the motion of Langmuir wave over the time range Δt results in a decrease in the wavenumber from k to 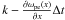 . The waves shifted to higher v (smaller k) can be effectively re-absorbed by the beam, which leads to an acceleration of the electrons and the formation of an extended plateau above v > vb. Using the conservation of energy, and assuming that all Langmuir waves are re-absorbed by the beam owing to the plasma inhomogeneity, W(k = ω/v,t → ∞) = 0, one finds that for the energy
. The waves shifted to higher v (smaller k) can be effectively re-absorbed by the beam, which leads to an acceleration of the electrons and the formation of an extended plateau above v > vb. Using the conservation of energy, and assuming that all Langmuir waves are re-absorbed by the beam owing to the plasma inhomogeneity, W(k = ω/v,t → ∞) = 0, one finds that for the energy 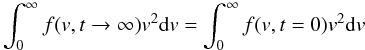 (8)the electron distribution has electrons with velocity v > vb
(8)the electron distribution has electrons with velocity v > vb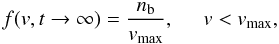 (9)where the new maximum velocity is from Eq. (8)
(9)where the new maximum velocity is from Eq. (8) 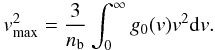 (10)Numerical solutions of Eqs. (1) and (2) (see Kontar 2001, for details) show that the value of the density gradient mostly affects the rate of the extended plateau formation and that the final state of the initially unstable distribution
(10)Numerical solutions of Eqs. (1) and (2) (see Kontar 2001, for details) show that the value of the density gradient mostly affects the rate of the extended plateau formation and that the final state of the initially unstable distribution 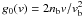 , v < vb, gives
, v < vb, gives 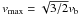 . In the case of g0(v) = nbδ(v − vb), one finds that
. In the case of g0(v) = nbδ(v − vb), one finds that 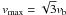 .
.
 |
Fig. 5 Normalized plasma density (solid line) and the electric field density (dashed line) in the z-direction along the line with x = y = 22Δ for model E at two times: ωpet = 60 a) and ωpet = 190 b). The electric field density is expressed in arbitrary units, but the electric field density at b) is multiplied by a factor of 50. |
 |
Fig. 6 Fractions of the beam energy in electrons with energies greater than E/mc2 = 0.25 (dashed line) and greater than E/mc2 = 0.3 (dotted line), for model E. The initial energy of the beam electron is E/mc2 = 0.22. For comparison, we plot the time evolution of the maximum energy of the electron (solid line). |
 |
Fig. 7 The X-ray spectrum for model E at ωpet = 200 (solid line) and the initial state (dashed line). |
In the case of non-linear interactions and various density fluctuations, the energy exchange between the electrons and plasma waves becomes more complicated. Kontar et al. (2012) used numerical simulations to estimate the role of these effects. Here, assuming that small-scale density fluctuations in the plasma generated during the beam-plasma instability are random with zero mean, the evolution of Langmuir waves in plasma can be approximated as a symmetric diffusion in k-space (see Eq. (14) in Kontar et al. 2012). This leads to equal numbers of plasma waves spreading towards smaller and larger the phase velocities. The former waves will be Landau-absorbed by the thermal plasma, while the latter will be absorbed by the beam resulting in electron acceleration in the tail of distribution. Therefore, for the Langmuir wave spectrum flattened in k-space, (see Fig. 2), these simplistic arguments suggest that only half of the Langmuir wave energy given by Eqs. (5) and (6) will be reabsorbed back. The maximum velocity then becomes 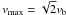 and the energy of the electrons with v > vb becomes
and the energy of the electrons with v > vb becomes 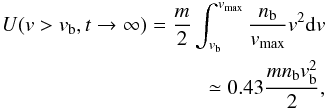 (11)for g0(v) = nbδ(v − vb). We note that these estimates are rather close to the numbers inferred from the 3D PIC simulations presented in Table 1. It is worth noting that the collisional relaxation of the electron power-law spectrum, which is initially stable was considered by Kontar et al. (2012), while in this paper we treat a “classical” case of beam-plasma instability.
(11)for g0(v) = nbδ(v − vb). We note that these estimates are rather close to the numbers inferred from the 3D PIC simulations presented in Table 1. It is worth noting that the collisional relaxation of the electron power-law spectrum, which is initially stable was considered by Kontar et al. (2012), while in this paper we treat a “classical” case of beam-plasma instability.
5. Discussion and conclusions
We have performed a number of 3D PIC simulations of the beam-plasma instability with monoenergetic beams and have shown that during relaxation a population of electrons with velocities exceeding those of the injected electrons appears. The energy of these electrons is around 10–30% of the initial beam energy.
Using PIC simulations, it is difficult to predict the long-term time evolution of these processes in solar flares. However, as shown in Fig. 7 this effect is indicated by the high-energy limit of the X-ray spectrum, namely that the accelerated high-energy electrons shift the X-ray spectrum to higher energies. This result together with the radio diagnostics can be used for an estimation of these acceleration processes. For example, if we take the dm-spikes as a radio signature of the acceleration process in solar flares (Guedel et al. 1991), then the advanced theory of these bursts can be used to estimate the electron distribution function at the acceleration site. Comparing this function with that determined from the hard X-ray spectrum at the flare footpoints, the acceleration efficiency can then be estimated.
We have found that the increasing magnetic field strength leads to a larger fraction of accelerated electrons. Therefore, we decided to compare the electron distribution functions of the cases with and without a magnetic field (in models A and E, Fig. 8). As presented and analyzed in Karlický & Bárta (2009) and Karlický & Kašparová (2009), the main difference in both cases is caused by the Weibel instability. In model E, the Weibel instability is reduced, while in model A (without the magnetic field) the Weibel instability transfers the beam energy to a heating of mainly perpendicular components of the background plasma. Thus, in the case without the magnetic field, not only the bump-on-tail instability but also the Weibel instability operates and less energy (than in model E) is transferred to the Langmuir waves, leading to a weaker acceleration.
 |
Fig. 8 Comparison of the electron distribution functions in model A (without the magnetic field) and model E (ωce/ωpe = 1.0). Crosses correspond to f(vz) and dashed lines display overlapping f(vx) and f(vy). |
We considered two values of the ratio of the beam to background plasma densities nb/ne = 1/8 and 1/40, which imply that the return-current electron speeds are vd = 0.083 c and vd = 0.016 c (where c is the speed of light), respectively. This corresponds to two regimes of the return-current electron speed either greater or lower than the thermal plasma velocity, which is in our model vTe = 0.06 c. In both cases, the percentage of the energy in accelerated electrons is similar. The case where nb/ne = 1/8, i.e. the case with the drift speed greater than the initial thermal velocity, should be unstable for the Buneman instability. However, the time of evolution considered in the present study is shorter than the time required to develop such an instability. For much longer term evolutions of similar systems in this regime computed with a 1-D Vlasov code, the formation of weak double layers was found and proposed as an explanation of broken power-law X-ray spectra in solar flares by Lee et al. (2008) (see also Karlický 2012).
We note that the size of our numerical box (45Δ × 45Δ × 600Δ) is limited by the memory and speed limits of our computer. The limited number of spatial grids limits a number of grids in the k-vector space. This limitation can influence the wave-wave and wave-particle interactions in this acceleration process. This is especially important in the linear regime of these interactions, which would correspond here to the cases with low density beams. However, in the present study we considered very dense beams (nb/ne = 1/8 and 1/40), which generate strong density fluctuations ensuring that these interactions are far from linear regimes (We note that in the interpretation of the hard X-ray emission the dense electron beams are often required). We made additional tests for model E. We used the same parameters as in model E, but we varied the size of the numerical system. We obtained similar results. For the system size (20Δ × 20Δ × 1500Δ) at the time ωpet = 200, the fraction FR is 26% and for the size (10Δ × 10Δ × 3000Δ) at the same time the fraction FR = 25%; compare with the fraction FR = 29% for model E in Table 1. Nevertheless, to make these results more precise we plan to repeat these computations in larger numerical boxes on a more powerful computer.
Comparing the numerical and analytical treatment, we propose that for this type of acceleration the density fluctuations and non-linear wave-wave interactions are essential. While in a strictly uniform plasma this acceleration is impossible (see the analytical estimations), in real conditions with sufficiently dense electron beams some beam electrons are accelerated to energies greater than the initial ones via non-linear wave interactions and density fluctuations.
In solar flares, high non-thermal electron fluxes are often required to explain the observed X-ray emission, which provide the suitable conditions for fast beam-plasma instability. As we have shown, the beam-plasma instability generates the Langmuir wave turbulence. The acceleration of electrons occurs owing to the k-space evolution of Langmuir waves, in which not only the Langmuir waves with phase velocities smaller than the initial beam velocity are generated (as in the case of beam relaxation in uniform plasma) but also those with higher phase velocities. The process of electron acceleration is fast, and occurs on a timescale much shorter than the electron transport time from an acceleration site to the dense chromospheric region. We therefore expect that during these processes the tail of the distribution extends towards higher energies. The number of high-energy electrons above some energy level increases and thus influences the hard X-ray spectrum. However, the total number of beam electrons is conserved and the process only redistributes the beam energy. These results emphasize that the transport of electrons should not be treated using a single particle description, and that the collective effects produce not only energy loss, but an effective acceleration of electrons. The analysis of a hard X-ray spectrum assuming only collisional losses could therefore infer that a larger number of electrons than actually is initially accelerated owing to the additional in-flight acceleration.
Acknowledgments
The authors thank the anonymous referee for comments that improved the paper. All computations were performed on the parallel computer OCAS (Ondřejov Cluster for Astrophysical Simulations, see http://wave.asu.cas.cz/ocas). This research was supported by the grant P209/12/0103 (GA CR). Financial support by the STFC rolling grant (E.P.K.), the Leverhulme Trust (E.P.K.), and the European Commission through the HESPE (FP7-SPACE-2010-263086) (E.P.K.) and “Radiosun” (PEOPLE-2011-IRSES-295272) Networks (M.K., E.P.K.) is gratefully acknowledged.
References
- Aschwanden, M. J., Benz, A. O., Dennis, B. R., & Schwartz, R. A. 1995, ApJ, 455, 347 [NASA ADS] [CrossRef] [Google Scholar]
- Bárta, M., & Karlický, M. 2000, A&A, 353, 757 [NASA ADS] [Google Scholar]
- Berezin, A. K., Berezina, G. P., Bolotin, L. I., & Fainberg, Y. B. 1964, J. Nucl. Energy, 6, 173 [NASA ADS] [CrossRef] [Google Scholar]
- Bingham, R., Dawson, J. M., & Shapiro, V. D. 2001, J. Plasma Phys., 68, 161 [Google Scholar]
- Bret, A. 2009, ApJ, 699, 990 [NASA ADS] [CrossRef] [Google Scholar]
- Breizman, B. N., & Ryutov, D. D. 1975, Sov. J. Exp. Theoret. Phys. Lett., 21, 192 [NASA ADS] [Google Scholar]
- Brown, J. C. 1971, Sol. Phys., 18, 489 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, J. C., Aschwanden, M. J., & Kontar, E. P. 2002, Sol. Phys., 210, 373 [NASA ADS] [CrossRef] [Google Scholar]
- Eliasson, B., Shukla, P. K., & Dieckmann, M. E. 2006, New J. Phys., 8, 55 [NASA ADS] [CrossRef] [Google Scholar]
- Emslie, A. G., & Smith, D. F. 1984, ApJ, 279, 882 [NASA ADS] [CrossRef] [Google Scholar]
- Escande, D. F. 1979, Phys. Fluids, 22, 321 [NASA ADS] [CrossRef] [Google Scholar]
- Fainberg, Y. B. 1968, Czechoslovak J. Phys., 18, 652 [Google Scholar]
- Guedel, M., Benz, A. O., & Aschwanden, M. J. 1991, A&A, 251, 285 [NASA ADS] [Google Scholar]
- Hamilton, R. J., & Petrosian, V. 1987, ApJ, 321, 721 [NASA ADS] [CrossRef] [Google Scholar]
- Hannah, I. G., Kontar, E. P., & Sirenko, O. K. 2009, ApJ, 707, L45 [NASA ADS] [CrossRef] [Google Scholar]
- Hewett, D. W., Francis, G. E., & Max, C. E. 1991, Adv. Space Res., 11, 193 [NASA ADS] [CrossRef] [Google Scholar]
- Holman, G. D., Aschwanden, M. J., Aurass, H., et al. 2011, Space Sci. Rev., 159, 107 [NASA ADS] [CrossRef] [Google Scholar]
- Karlický, M. 1997, Space Sci. Rev., 81, 143 [NASA ADS] [CrossRef] [Google Scholar]
- Karlický, M. 2009, ApJ, 690, 189 [NASA ADS] [CrossRef] [Google Scholar]
- Karlický, M., & Bárta, M. 2009, Nonlinear Process. Geophys., 16, 525 [Google Scholar]
- Karlický, M., & Kašparová, J. 2009, A&A, 506, 1437 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kiplinger, A. L., Dennis, B. R., Frost, K. J., Orwig, L. E., & Emslie, A. G. 1983, ApJ, 265, L99 [NASA ADS] [CrossRef] [Google Scholar]
- Kontar, E. P. 2001, A&A, 375, 629 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kontar, E. P., & Pécseli, H. L. 2002, Phys. Rev. E, 65, 066408 [NASA ADS] [CrossRef] [Google Scholar]
- Kontar, E. P., & Reid, H. A. S. 2009, ApJ, 695, L140 [NASA ADS] [CrossRef] [Google Scholar]
- Kontar, E. P., Brown, J. C., Emslie, A. G., et al. 2011, Space Sci. Rev., 159, 301 [NASA ADS] [CrossRef] [Google Scholar]
- Kontar, E. P., Ratcliffe, H., & Bian, N. H. 2012, A&A, 539, A43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kovalenko, V. P. 1983, Sov. Phys. Uspekhi, 26, 116 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, K. W., Büchner, J., & Elkina, N. 2008, A&A, 478, 889 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lin, R. P., Dennis, B. R., Hurford, G. J., et al. 2002, Sol. Phys., 210, 3 [Google Scholar]
- Messmer, P. 2002, A&A, 382, 301 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mikhailovskii, A. B. 1975, Moscow Atomizdat, 1 [Google Scholar]
- Muschietti, L., Goldman, M. V., & Newman, D. 1985, Sol. Phys., 96, 181 [NASA ADS] [CrossRef] [Google Scholar]
- Niemiec, J., Pohl, M., Stroman, T., & Nishikawa, K. 2008, ApJ, 684, 1174 [NASA ADS] [CrossRef] [Google Scholar]
- Nishikawa, K. 2008, priv. comm. [Google Scholar]
- Nishikawa, K., & Ryutov, D. D. 1976, J. Phys. Soc. Japan, 41, 1757 [NASA ADS] [CrossRef] [Google Scholar]
- Reid, H. A. S., & Kontar, E. P. 2010, ApJ, 721, 864 [NASA ADS] [CrossRef] [Google Scholar]
- Rose, D. V., Guillory, J. U., & Beall, J. H. 2002, Phys. Plasmas, 9, 1000 [NASA ADS] [CrossRef] [Google Scholar]
- Ryutov, D. D. 1969, Sov. J. Exp. Theoret. Phys., 30, 131 [NASA ADS] [Google Scholar]
- Saito, S., & Sakai, J.-I. 2004, Phys. Plasmas, 11, 5547 [NASA ADS] [CrossRef] [Google Scholar]
- Sakai, J. I., Nagasugi, Y., Saito, S., & Kaufmann, P. 2006, A&A, 457, 313 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Timofeev, I. V., & Terekhov, A. V. 2010, Phys. Plasmas, 17, 083111 [NASA ADS] [CrossRef] [Google Scholar]
- Tsiklauri, D. 2010, Sol. Phys., 267, 393 [NASA ADS] [CrossRef] [Google Scholar]
- Tsytovich, V. N. 1995, Lectures on Non-linear Plasma Kinetics, eds. V. N. Tsytovich, & D. ter Haar [Google Scholar]
- Tyshetskiy, Y., Roberts, J. A., Robinson, P. A., Cairns, I. H., & Li, B. 2007, Phys. Plasmas, 14, 122111 [NASA ADS] [CrossRef] [Google Scholar]
- Vedenov, A. A., Gordeev, A. V., & Rudakov, L. I. 1967, Plasma Phys., 9, 719 [NASA ADS] [CrossRef] [Google Scholar]
- Vedenov, A. A., & Velikhov, E. P. 1963, Sov. J. Exp. Theoret. Phys., 16, 682 [Google Scholar]
- Vlahos, L., & Papadopoulos, K. 1979, ApJ, 233, 717 [NASA ADS] [CrossRef] [Google Scholar]
- Weibel, E. S. 1959, Phys. Rev. Lett., 2, 83 [NASA ADS] [CrossRef] [Google Scholar]
- Ziebell, L. F., Yoon, P. H., Pavan, J., & Gaelzer, R. 2011, ApJ, 727, 16 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Model parameters and the fraction (FR) of the beam energy in the electrons with energies greater than the initial-beam electron energy.
All Figures
 |
Fig. 1 The electron velocity distributions for model E at four different times: at the initial state a), at ωpet = 40 b), at ωpet = 140 c), and ωpet = 200 d). Crosses correspond to f(vz), dotted and dashed lines display f(vx) and f(vy), respectively. Note that f(vx) and f(vy) overlap. The vertical line in the part a) at v/c = 0.666 denotes the monoenergetic electron beam. |
| In the text | |
 |
Fig. 2 The Langmuir wave energy for model E in the k-space at four different times: ωpet = 40 a), ωpet = 60 b), ωpet = 140 c), and ωpet = 200 d) (solid lines). For comparison in each panel, the initial Langmuir wave energy is added (dashed line). |
| In the text | |
 |
Fig. 3 The electron energy distributions for model E at four different times: ωpet = 40 a), ωpet = 60 b), ωpet = 140 c), and ωpet = 200 d) (solid lines). For comparison in each panel, the initial electron-plasma distribution together with the initial monoenergetic beam are added (dashed lines). |
| In the text | |
 |
Fig. 4 The electron energy distributions (solid lines) at ωpet = 200 as a function of the magnetic field in models A-F with ωce/ωpe = 0.0, 0.1, 0.5, 0.7, 1.0, and 1.3, respectively. For comparison in each panel we plot the initial electron plasma distribution together with the initial monoenergetic beam (dashed lines). |
| In the text | |
 |
Fig. 5 Normalized plasma density (solid line) and the electric field density (dashed line) in the z-direction along the line with x = y = 22Δ for model E at two times: ωpet = 60 a) and ωpet = 190 b). The electric field density is expressed in arbitrary units, but the electric field density at b) is multiplied by a factor of 50. |
| In the text | |
 |
Fig. 6 Fractions of the beam energy in electrons with energies greater than E/mc2 = 0.25 (dashed line) and greater than E/mc2 = 0.3 (dotted line), for model E. The initial energy of the beam electron is E/mc2 = 0.22. For comparison, we plot the time evolution of the maximum energy of the electron (solid line). |
| In the text | |
 |
Fig. 7 The X-ray spectrum for model E at ωpet = 200 (solid line) and the initial state (dashed line). |
| In the text | |
 |
Fig. 8 Comparison of the electron distribution functions in model A (without the magnetic field) and model E (ωce/ωpe = 1.0). Crosses correspond to f(vz) and dashed lines display overlapping f(vx) and f(vy). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


