| Issue |
A&A
Volume 544, August 2012
|
|
|---|---|---|
| Article Number | A51 | |
| Number of page(s) | 11 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201116645 | |
| Published online | 25 July 2012 | |
Time delay between images of the lensed quasar UM673⋆,⋆⋆
1 Department of Physics, National Taiwan University, No. 1, Sec. 4, Roosevelt Rd., 106 Taipei, Taiwan
e-mail: ekaterina@phys.ntu.edu.tw; chiuehth@phys.ntu.edu.tw
2 Graduate Institute of Astronomy, National Central University, Jhongli City, Taoyuan County 320, Taiwan
e-mail: wchen@astro.ncu.edu.tw
3 Sternberg Astronomical Institute (SAI), Moscow M.V. Lomonosov State University, Universitetskii pr. 13, 119992 Moscow, Russia
e-mail: artamon@sai.msu.ru; oknyan@sai.msu.ru
4 Ulugh Beg Astronomical Institute of the Uzbek Academy of Sciences, Astronomicheskaya 33, 100052 Tashkent, Uzbekistan
e-mail: nurit2006@yahoo.com
5 Institute of Radio Astronomy, Krasnoznamennaya 4, 61002 Kharkov, Ukraine
6 Institut d’Astrophysique et de Géophysique, Université de Liège, Allée du 6 Août 17, Sart Tilman, B5c, 4000 Liège, Belgium
Received: 4 February 2011
Accepted: 11 June 2012
Aims. We study brightness variations in the double lensed quasar UM673 (Q0142-100) with the aim of measuring the time delay between its two images.
Methods. We combined our previously published observational data of UM673 obtained during the 2003–2005 seasons at the Maidanak Observatory with archival and recently observed Maidanak and CTIO UM673 data. We analyzed the V, R and I-band light curves of the A and B images of UM673, which cover ten observational seasons from August 2001 to November 2010. We also analyzed the time evolution of the difference in magnitudes (flux ratio) between images A and B of UM673 over more than ten years.
Results. We find that the quasar exhibits both short-term (with an amplitude of ~0.1 mag in the R band) and long-term (with an amplitude of ~0.3 mag) variability on timescales of about several months and several years, respectively. These brightness variations are used to constrain the time delay between the images of UM673. From a cross-correlation analysis of the A and B quasar light curves and an error analysis we measure a mean time delay of 89 days with an rms error of 11 days. Given the input time delay of 88 days, the most probable value of the delay that can be recovered from light curves with the same statistical properties as the observed R-band light curves of UM673, is 95-16+5-29+14 days (68% and 95% confidence intervals). Analysis of the V − I color variations and the V, R and I-band magnitude differences of the quasar images does not show clear evidence for microlensing variations between 1998 and 2010.
Key words: gravitational lensing: strong / methods: data analysis / quasars: individual: UM673
Figures 2 and 3 are available in electronic form at http://www.aanda.org
Photometry is only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/544/A51
© ESO, 2012
1. Introduction
Multiple images of lensed quasars show changes in their brightness over time. There are two main reasons for these brightness variations. One is that the quasar itself, as a variable source, changes in brightness with time. Brightness variations of the quasar are observed in the light curves of all quasar images, but they are not synchronized. Changes in brightness in one image follow or lead the brightness changes in others with certain time lags (time delays). The time delay between these brightness variations in any two images of the quasar is a combination of delays that arise from geometrical differences between the light paths (and thus light travel times) for each quasar image and the difference in the gravitational potential between quasar images. The geometrical term is related to the Hubble constant through the angular diameter distances (see Schneider et al. 1992). This relation gives us a method for estimating the Hubble constant independently of the distance ladder (Refsdal 1964). The gravitational potential term is determined by the mass distribution in a lens. Thus the mass distribution of lensing galaxies can be studied using the time delays as one of the observational constraints (see, e.g., Kochanek 2002).
The passage of individual stars in the lensing galaxy near the light paths of quasar images can also cause variations in image brightness known as microlensing (Chang & Refsdal 1979). These brightness variations in each of the quasar images are not correlated. The probability for microlensing depends on the density of stars at image positions. Normally we would expect both the microlensing and the quasar’s intrinsic variations to be present in the light curves of the quasar images. Accurate measurement of the time delay between a pair of images permits variations caused by microlensing to be separated from the variations intrinsic to the quasar (see Paraficz et al. 2006). However, time delay measurement itself is often not a simple and straightforward task. Successful measurement of the delay requires a combination of several conditions, such as changes in the brightness of the quasar during observations, good sampling and observational time spans, and minimal contamination of the quasar’s intrinsic variations by variations caused by microlensing.
In this study we analyze brightness variations in images of the lensed system UM673 (Q0142-100) discovered by MacAlpine & Feldman (1982). The system consists of a distant quasar at redshift zq = 2.719 (Surdej et al. 1987; 1988) gravitationally lensed by an elliptical galaxy at redshift zl = 0.49 (Surdej et al. 1988; Smette et al. 1992; Eigenbrod et al. 2007) into A and B images with an image separation of 2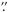 2.
2.
UM673 has been extensively observed since its discovery (Daulie et al. 1993; Sinachopoulos et al. 2001). However, earlier studies measured only relative or integral photometry of the two images of UM673, and therefore the detected brightness variations could be explained by either intrinsic quasar variability or microlensing.
The first V- and i-band light curves for each of the A and B images of UM673 were presented in Nakos et al. (2005). The observations showed both quasar components to be variable on timescales ranging from several months to years. During the first season of observations, Nakos et al. (2005) detected a short-term event lasting for 120 days in the A and B images. It had an amplitude of about 0.08 mag in the V band. The overall brightness changes detected in one year of observations were 0.14 and 0.08 mag in the V- and Gunn i-band, respectively. Nakos et al. (2005) did not find the time delay between the quasar images. After shifting the light curve of image B relative to that of image A, these authors found that the observed brightness changes of the UM673 images did not match. Therefore, the authors concluded that either the time delay between the images was longer than 150 days (150 days was the duration between two consecutive V-band observations of UM673 in the 1999 and 2001 seasons) or the brightness variations were contaminated by microlensing. Their analysis of the V − i color indices of images A and B showed that the part of the variations in the brighter A image might be connected to microlensing by the stars in the lensing galaxy. It was found that image A became bluer as its brightness increased, as expected during microlensing (Wambsganss & Paczinski 1991). The brightness and color variations in image B were puzzling and could not be interpreted unambiguously. Analysis of the UM673 A&B emission line-to-continuum ratios from September 2002 showed that they were the same in both images, indicating the absence of microlensing in the system (Wisotski et al. 2004).
We have been conducting monitoring observations of several gravitationally lensed systems with the aims of measuring lensing time delays, and studied microlensing variability (see Koptelova et al. 2005; 2006; 2007; Ullán et al. 2006; Goicoechea et al. 2006; 2008; Shalyapin et al. 2008; 2009). UM673 is one of our targets. In our first paper (Koptelova et al. 2010; Paper I) we presented an analysis of observations of the UM673 system obtained with the 1.5-m telescope of the Maidanak Observatory (see also Koptelova et al. 2008). Observations were conducted in the V, R and I bands in the 2003, 2004 and 2005 observational seasons. The two UM673 components brightened during the first season of observations and then gradually faded until the end of 2005. We interpreted the similar photometric behavior (brightening and fading) of the A and B images as variability intrinsic to the quasar. With this assumption, the cross-correlation analysis led to a time delay between images A and B of about 150 days (image A is leading).
Unfortunately, the data presented in Paper I did not allow for a detailed interpretation of the observed brightness variations. In the current work we present new photometry and a time delay analysis of the longer light curves obtained between August 2001 and November 2010. The details of the monitoring program and the observational data are presented in Sects. 2 and 3, respectively. Based on new observations and analysis of the observed brightness variations we revise the time delay measurement between the UM673 images. The analysis of the brightness variations in the lensed system UM673 and the time delay measurements are presented in Sects. 4 and 5. A discussion is given in Sect. 6.
2. Observations
We used monitoring observations of UM673 obtained during different observational seasons at two sites. The majority of the observational data were collected during the quasar monitoring program carried out by the Maidanak GLQ collaboration (see Dudinov et al. 2000). The data were obtained with the 1.5-m AZT-22 telescope of the Maidanak Observatory (Central Asia, Uzbekistan) during the 1998–2010 observational seasons in the Bessel V, R and I bands. A considerable part of these observations, the 2003–2005 data, have been presented in Koptelova et al. (2008) and Paper I. The V, R and I-band observations of the lensed system were also made between July 28, 2008 and January 18, 2010 using the 1.3-m SMARTS telescope at CTIO, Chile. These observations were part of the ToO observations carried out by National Central University, Taiwan. UM673 was usually observed from August until December, or sometimes January, when it was well visible at both sites. A summary of the observational data acquired between 1998 and 2010 is given in Table 1.
The Maidanak data were obtained with different CCD cameras installed at the 1.5-m telescope. During the 1998 observational season images were obtained with the TI 800 × 800 Pitt and Pictor-416 CCD cameras with pixel scales of 0.13 and 0.16 arcsec pixel-1, respectively. The 1999 image frames were obtained with the ST-7 760 × 510 pixel CCD provided by the Maidanak Foundation (see Dudinov et al. 2000). The field of view (FOV) of the frames taken with these three CCD cameras was small so these image frames did not include any bright stars in the vicinity of UM673, which would have been useful for performing differential photometry of the UM673 A and B quasar components. Between August 2001 and August 2006 image frames were obtained with the 2000 × 800 pixel SITe-005 CCD camera manufactured in the laboratory of Copenhagen University. The images taken in long-focus and short-focus modes have pixel scales of 0.135 and 0.268 arcsec pixel-1, respectively. The most recent observational data were obtained with a new 4096 × 4096 SNUCAM camera provided by Seoul University. The images taken with this CCD camera have a pixel scale of 0.266 arcsec pixel-1 and FOV of 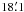 ×
× 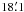 . Characteristics and performance of SNUCAM on the 1.5-m telescope are discussed in detail in Im et al. (2010). The 1.3-m SMARTS telescope obtained images using the dual-channel optical/near-infrared CCD camera ANDICAM, which has a FOV of 6
. Characteristics and performance of SNUCAM on the 1.5-m telescope are discussed in detail in Im et al. (2010). The 1.3-m SMARTS telescope obtained images using the dual-channel optical/near-infrared CCD camera ANDICAM, which has a FOV of 6 3 × 6
3 × 6 3 (0.369 arcsec pixel-1). On every observational night images were taken in a series of 2–8 frames in the V, R and I bands.
3 (0.369 arcsec pixel-1). On every observational night images were taken in a series of 2–8 frames in the V, R and I bands.
3. UM673 A and B light curves
The V, R and I-band photometry of UM673 from August 2001 to November 2010 is now discussed. In the current work we revisit photometry of UM673 of the 2003–2005 observational seasons presented in Koptelova et al. (2008) and Paper I (magnitudes of the A and B images of UM673 for this period are given in Table 2 of Koptelova et al. 2008), and perform photometry of the 2001 and 2006–2010 data. The photometry method we used is the point spread function (PSF) fitting method, which has been described in Paper I. In the current analysis we improved the accuracy of the photometry in the following ways. First, we found that the performance of the PSF fitting method is poor when applied to individual frames of UM673. The fainter image of UM673 has a low signal-to-noise ratio, especially in the new 2006–2010 data when the quasar was faint. For example, the signal-to-noise ratio of the A and B components of UM673 in the 2006 R-band data is estimated to be about 200 and 70, respectively. The low performance of the method results in a high level of statistical and correlated errors. We found that these errors are more severe for the 2006–2010 data and significantly affect the time delay analysis of the 2006–2010 light curves, producing spurious peaks at short time lags. To minimize the errors, we applied the PSF fitting method to the combined frames of UM673. The combined frames are the sum of two or three individual frames with similar seeing taken on the same observational night. Usually we summed three sequential frames from the same night series. For some small fraction of nights when the quasar was observed only twice, we summed two frames of UM673. This allowed us to enhance the signal-to-noise ratio of the quasar components by a factor of 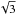 or
or 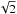 . Second, in the current analysis we chose several isolated stars around UM673 to construct the PSF model. The shape of the PSF can vary over the image plane as a result of optical aberrations in the telescope-camera system. The aberrations distort the PSF shape from the center outward. We estimate that this effect is more severe for the new 2006–2010 Maidanak data taken with the large area 4096 × 4096 pixel SNUCAM CCD. UM673 is usually not in the center of the SNUCAM frames. In this case, the PSF constructed from several nearby stars is a better representation of the PSF shape at the location of UM673 on image frames. The PSF was constructed using the bright star northeast of UM673, labeled as star 1 (see Fig. 1 in Paper I), and stars 1 and 3 from the catalog of secondary standard stars in the vicinity of 14 lensed quasars (see Nakos et al. 2003). In this way, the photometric analysis was applied to the whole data set. The measured fluxes were calibrated relative to star 1 introduced in Paper I. The magnitudes of star 1 in the V, R and I bands are mV = 14.653 ± 0.008, mR = 14.278 ± 0.008 and mI = 13.954 ± 0.009 mag, respectively.
. Second, in the current analysis we chose several isolated stars around UM673 to construct the PSF model. The shape of the PSF can vary over the image plane as a result of optical aberrations in the telescope-camera system. The aberrations distort the PSF shape from the center outward. We estimate that this effect is more severe for the new 2006–2010 Maidanak data taken with the large area 4096 × 4096 pixel SNUCAM CCD. UM673 is usually not in the center of the SNUCAM frames. In this case, the PSF constructed from several nearby stars is a better representation of the PSF shape at the location of UM673 on image frames. The PSF was constructed using the bright star northeast of UM673, labeled as star 1 (see Fig. 1 in Paper I), and stars 1 and 3 from the catalog of secondary standard stars in the vicinity of 14 lensed quasars (see Nakos et al. 2003). In this way, the photometric analysis was applied to the whole data set. The measured fluxes were calibrated relative to star 1 introduced in Paper I. The magnitudes of star 1 in the V, R and I bands are mV = 14.653 ± 0.008, mR = 14.278 ± 0.008 and mI = 13.954 ± 0.009 mag, respectively.
There might be a contribution of the lensing galaxy to the flux of the closest image B. It is estimated to be negligible in the V band (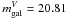 mag, Lehár et al. 2000). The galaxy contribution in the R and I-band fluxes of image B is measured to be 0.069 and 0.126 mag, respectively (see Koptelova et al. 2008).
mag, Lehár et al. 2000). The galaxy contribution in the R and I-band fluxes of image B is measured to be 0.069 and 0.126 mag, respectively (see Koptelova et al. 2008).
The resulting Maidanak and CTIO R-band light curves of the A and B quasar images are shown in Fig. 1. The filled and open circles indicate the Maidanak data points for images A and B, respectively. The triangles and stars indicate the CTIO data points obtained during the 2008–2010 seasons for images A and B, respectively. The V and I-band light curves are presented in Figs. 2 and 3. Transmission properties of the CTIO filters are slightly different from the Bessel filters used in the Maidanak observations1. For the Maidanak data, the measured magnitude differences between star 3 and bright star 1 are 2.850, 2.878 and 2.892 mag in the V, R and I bands, respectively. The corresponding differences for the CTIO data are 2.916, 2.942 and 2.977 mag in the V, R and I bands, respectively. The CTIO light curves are matched to the Maidanak light curves taking into account these differences in the relative magnitudes of stars 1 and 3 in the different bands. The photometric errors of individual measurements were estimated as standard deviations of the mean values of several measurements made on each observational night. The mean standard errors of the photometry in the R band are estimated to be 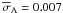 and
and 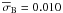 mag for images A and B, respectively. Figure 1 also shows the light curves for reference stars 2 and 3 in the FOV of UM673. Stars are labeled as in our first paper (see Fig. 1 in Paper I). The fluxes of these two stars were measured relative to calibration star 1. From our data, the R-band magnitude of star 2 is mR = 16.246 ± 0.008 mag. Photometry of other nearby stars in the field of UM673, including star 3 (mR = 17.196 ± 0.014), was presented in Nakos et al. (2003). The FOV of the image frames taken with the 1.3-m SMARTS telescope is smaller and does not include star 2 or some other bright stars seen in the Maidanak images. Therefore, for the CTIO data we plot the relative photometry of star 3 and bright star 1 (indicated by the open rhomboids in Fig. 1).
mag for images A and B, respectively. Figure 1 also shows the light curves for reference stars 2 and 3 in the FOV of UM673. Stars are labeled as in our first paper (see Fig. 1 in Paper I). The fluxes of these two stars were measured relative to calibration star 1. From our data, the R-band magnitude of star 2 is mR = 16.246 ± 0.008 mag. Photometry of other nearby stars in the field of UM673, including star 3 (mR = 17.196 ± 0.014), was presented in Nakos et al. (2003). The FOV of the image frames taken with the 1.3-m SMARTS telescope is smaller and does not include star 2 or some other bright stars seen in the Maidanak images. Therefore, for the CTIO data we plot the relative photometry of star 3 and bright star 1 (indicated by the open rhomboids in Fig. 1).
 |
Fig. 1 R-band light curves of the A and B images of UM673 from August 2001 to November 2010. For better representation, the light curve of image B is shifted by − 1.87 mag. The light curves of reference stars 2 and 3 are shown at the bottom. (This figure is available in color in electronic form.) |
As can be seen in Fig. 1, the global brightness changes of both components of UM673 are similar over the course of our observations. Along with long-term brightness changes, which take years, we can detect short-term brightness variations on timescales of several months. These variations on different timescales probably have different origins. The global long-term behavior of the light curves with the strongest brightness changes (more than 0.3 mag in the R band) might be connected with the formation and evolution of the quasar accretion disk (e.g., Lyuty 2006; Arévalo et al. 2009). In these long-term brightness variations we can distinguish the global maximum and minimum observed in both light curves in 2004 and in 2009, respectively. The short-term brightness variations might be caused by reprocessing of the X-ray flares by the accretion disk (see Krolik et al. 1991). Short-term brightness variations of the UM673 images on timescales of several months have been previously detected by Nakos et al. (2005). Between January 2 and 18, 2010 we detect a short high-amplitude variability event in image B of UM673. The amplitude of this event is several times higher than is usually observed on similar timescales within observational seasons. If this brightness variation is a result of the quasar variability, then similar variation has to be seen first in image A. However, we detect no similar event in the image A light curves during the same observational season. Although there is no other variation like the image B event in the A and B light curves, it might not be unique for the lensed system. Analysis of the flux ratios between images A and B in 1998 shows another evidence for short-term variations of comparable amplitude. This event is discussed below in Sect. 5. In the next section, we perform a cross-correlation analysis of the A and B light curves to measure the time delay between the quasar images.
4. Intrinsic quasar variability and time delay analysis
The previous estimate of the time delay between the A and B images of UM673 was made based on slow long-term brightness changes observed between the 2003–2005 seasons. Analysis of the better-sampled R-band light curves gave a time delay and conservative errors of 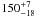
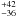 days (68% and 95% confidence intervals) (see Paper I). The estimated delay of 150 days is comparable to one season of observations of the lensed system at the Maidanak Observatory. The light curves of the A and B quasar images shifted by this delay did not overlap. This made it difficult to verify the previously obtained result.
days (68% and 95% confidence intervals) (see Paper I). The estimated delay of 150 days is comparable to one season of observations of the lensed system at the Maidanak Observatory. The light curves of the A and B quasar images shifted by this delay did not overlap. This made it difficult to verify the previously obtained result.
As can be seen in Figs. 1–3, both images of UM673 also show noticeable short-term brightness changes within observational seasons. These short-term brightness variations were not carefully considered in Paper I under the assumption that brightness variations of the quasar are not significant on short timescales. There are also more features in the global behavior of the light curves than in the previously analyzed data. The quasar seems to reach the minimum of its brightness in 2009 and starts to gradually brighten again. In our current time delay analysis we consider these long-term high-amplitude brightness variations with the maximum in 2004 and minimum in 2009. We also take into account the short-term variations in brightness within each observational season.
The time delay was measured with the modified cross-correlation function (MCCF) method (see Oknyanskij 1993). The method, its application and the test performance for the analysis of time series containing large annual gaps have been described in Paper I. Here, we briefly outline the approach. In the MCCF method, each data point from the B light curve, B(ti), forms a pair with an interpolated point from the A light curve, A(ti + τ) at time ti + τ, where τ is the time lag. The pairs of data points for which 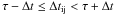 (where Δtij = | tj − ti | is the time shift between the ti point of the A light curve and the tj point of the B light curve) are then used to calculate the cross-correlation function. The interpolation interval
(where Δtij = | tj − ti | is the time shift between the ti point of the A light curve and the tj point of the B light curve) are then used to calculate the cross-correlation function. The interpolation interval 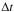 is usually chosen as a compromise between the desire to decrease the interpolation errors and to find a sufficient number of data pairs to reliably calculate the correlation coefficient for a given time lag.
is usually chosen as a compromise between the desire to decrease the interpolation errors and to find a sufficient number of data pairs to reliably calculate the correlation coefficient for a given time lag.
For the analysis of the light curves presented in Paper I the value of 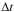 was adopted to be 90 days. This was the lowest value of
was adopted to be 90 days. This was the lowest value of 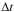 that one could choose because of the large annual gaps in the light curves of UM673. For this value of
that one could choose because of the large annual gaps in the light curves of UM673. For this value of 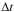 the MCCF method is insensitive to brightness variations shorter than 90 days. Therefore the short-term variations of the quasar that are comparable to, or sometimes shorter than, the interpolation interval of 90 days, are ignored by the method. In addition, interpolation errors produced for high values of
the MCCF method is insensitive to brightness variations shorter than 90 days. Therefore the short-term variations of the quasar that are comparable to, or sometimes shorter than, the interpolation interval of 90 days, are ignored by the method. In addition, interpolation errors produced for high values of 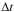 can lead to an erroneous time delay estimate.
can lead to an erroneous time delay estimate.
We used two interpolation intervals, Δtmax and Δtmin to account for the short-term variations in brightness and minimize the interpolation errors. The interpolation interval Δtmax = 90 days is the same interval as was adopted for calculations of the CCF in Paper I. The interpolation interval Δtmin was introduced to take into account the short-term brightness variations of UM673. It was used to calculate the cross-correlation function for those data pairs, for which both data points in the pair (the real point from the B light curve and the interpolated one from the A light curve) are within the same observational season. When the data points do not lie within the same season of observations, Δtmax was used instead of Δtmin. This approach was applied to calculate the cross-correlation function between the time-shifted interpolated A light curve and the discrete B light curve. The time lag τ ranges from − 500 to 500 days with a step of 1 day. A value of 10 days chosen for Δtmin is comparable to average sampling of the light curves within one observational season. The origin of the high-amplitude rapid brightness variation observed in image B in January 2010 is unclear. It can be either intrinsic to the quasar, with the counterpart in image A that was missed, or unique for image B. To avoid the influence of the data points corresponding to this event on the correlation between the A and B light curves, these data were excluded from the time delay analysis.
 |
Fig. 4 CCFs calculated between the R-band light curves of images A and B with the data points corresponding to the high-amplitude event in image B excluded (shown by a thick black line); and the data points corresponding to the high-amplitude event in image B included (shown by a thin black line). The CCF calculated between the R-band light curves corresponding to the 2003–2005 period is shown by a thick gray line. |
 |
Fig. 5 CCFs calculated between the V (thick black line) and I-band (thin black line) light curves of the A and B images. The thick gray line shows the V-band CCF calculated for a value of Δtmax = 110 days. |
The resulting CCFs for the R, V and I-band data are shown in Figs. 4 and 5. The CCF calculated between the better-sampled R-band light curves (shown by a thick black line in Fig. 4) reaches its maximum at a delay of 88 days with a correlation coefficient of 0.981. For comparison, we plot the CCF calculated between the R-band light curves including the data points corresponding to the high-amplitude event in image B (shown by a thin black line in Fig. 4). As can be seen, this CCF also reaches its maximum at a delay of about 88 days but with lower correlation coefficients. It is not as smooth as the first CCF and has secondary peaks at short delays. We interpret these short-delay peaks to have originated from the high-amplitude event in image B. The gray thick line in Fig. 4 shows the CCF calculated between the segments of the R-band light curves that include only the data points collected between 2003 and 2005. These are the same observational data that have been used to measure the time delay between the images of UM673 in Paper I. The corresponding CCF has a different shape and reaches its maximum at a very different delay of 142 days. The most probable reason for the disagreement in the results is that the single parabola-shape long-term brightness variation observed between 2003 and 2005 cannot reliably constrain the delay. The broad peak of this CCF falls in the range of time delays for which the A and B light curves do not overlap. We found that to measure a delay that is longer than, or comparable to, observational seasons, it is important to analyze more features in the global behavior of the light curves and not only one single event. Altogether, the long-term brightness changes provide a better constraint on the time delay in UM673.
As can be seen in Fig. 5, the shapes of the V and I-band CCFs are different from the shape of the R-band CCF (especially for the I-band light curves). The CCF calculated between the V-band light curves reaches its maximum at a delay of 79 days. The V-band CCF has several secondary peaks near the main peak. The secondary peaks at longer delays disappear with the increase of the interpolation interval. This is demonstrated with the CCF calculated for a value of Δtmax = 110 days (shown by a thick gray line in Fig. 5). Therefore, we conclude that these secondary peaks are most probably artifacts caused by errors in the calculation of the V-band CCF at longer time lags. For long time lags the number of data pairs contributing to the calculation of correlation coefficients is small, leading to low accuracy of the CCF. The other features of the V-band CCF corresponding to the more prominent central peak remain unchanged. The I-band CCF reaches its maximum at a very different time lag of about 20 days, although it also has secondary peaks at longer delays. Apparently, the poorly sampled I-band light curves with smaller amplitudes of the brightness changes cannot accurately constrain delays longer than the duration of the observational seasons in the I band. As a result, the MCCF method cannot find sufficient data pairs to reliably calculate the CCF at delays longer than 20 days. This leads to a decrease of the I-band CCF at longer delays.
Thus, cross-correlation analysis shows that the V and R-band CCFs give consistent time delays, despite being slightly different. Because the R-band light curves are better sampled and the R-band time delay corresponds to a higher value of the correlation coefficient than the V-band delay, we consider the R-band value of the delay as a more robust measurement.
The main difficulty in the time delay analysis of the UM673 light curves is the presence of the large annual gaps. The duration of the observational seasons, which varies from 50 to 190 days, is much shorter than the duration of the gaps. In the MCCF method, the fluxes of reference image A in the gaps are estimated using linear interpolation. Uncertainties in the interpolated fluxes may lead to a biased measurement of the delay when it is longer than the duration of the observational seasons. In Paper I we showed that the MCCF method performs well and does not introduce significant bias into a recovered delay when the time delay is shorter than 150 days (in other words, when the delay is shorter than, or comparable to, the time span of one observational season). Therefore, we do not expect the large bias in the measured delay of 88 days due to interpolation. When observational data are regularly sampled and there is a good overlap between time-shifted light curves, interpolation can be avoided as in the method proposed by Pelt et al. (1994). In this method, the time delay is estimated by minimizing the dispersion spectrum of the combined A and time-delay-shifted B light curves. In the method, only pairs of data points within some interval, called the decorrelation length, contribute to the calculation of the dispersion spectrum. The dispersion spectra calculated for two values of the decorrelation length, 60 and 90 days, are shown in Fig. 6 by gray and black lines, respectively. We found only a tentative minimum in the global behavior of the dispersion spectra corresponding to a range of delays from 70 to 110 days. The shape of the minimum is not well constrained at longer delays, between 120 and 250 days. This region corresponds to the delays for which the A and B light curves do not overlap. Therefore, the method cannot be used to measure delays from this range. The minimum between 70 and 110 days consists of several secondary minima corresponding to different delays. We averaged the dispersion function in this range of time delays to estimate the location of its global minimum. The delay corresponding to the global minimum is 86 days in both cases, for values of the decorrelation timescale of 60 and 90 days. This estimate of the delay agrees with the time delay measured using the MCCF method. We found that in comparison with the dispersion function method, the MCCF method gives a more definite measurement of the delay.
 |
Fig. 6 Dispersion spectra calculated for the combined A and B light curves for decorrelation lengths of 60 (gray line) and 90 (black line) days. |
 |
Fig. 7 R-band light curves of image A (filled circles and triangles) and image B shifted by a time delay of 88 days with a magnitude offset of − 2.12 mag (open circles and stars). (This figure is available in color in electronic form.) |
The light curves of the UM673 images corrected for a time delay of 88 days and a magnitude offset of 2.12 mag are shown in Fig. 7. For ease of presentation the errorbars in the A and B light curves are not shown. We found a good match in the global behavior of both light curves. There is also an overlap of about two months between the light curves for most of the observational seasons.
Uncertainties in time delay measurement due to photometric errors and systematic sampling effects were investigated with the Monte Carlo simulations. We performed simulations of 1000 artificial light curves using Timmer & Koenig’s algorithm (1995) (these simulations are discussed in detail in Paper I). The distribution of the time delays recovered from cross-correlation analysis of the Monte Carlo simulated R-band light curves of images A and B, shifted by the input time delay of 88 days, is shown in Fig. 8. For this distribution we found a mean time delay of 89 (marked by a dotted line in Fig. 8) and an rms error of 11 days. On the other hand, the most probable value of the delay that can be measured from light curves with similar statistical properties and variability pattern as the observed R-band light curves is 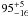
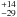 days (68% and 95% confidence intervals).
days (68% and 95% confidence intervals).
5. Color variations and evolution of flux ratio
In this section we analyze the color variations and flux ratio of the UM673 images over more than ten years. The V − I color light curves of the A and B images of UM673 between August 2001 and November 2010 are shown in Fig. 9. The color variations in both images of UM673 are expected to be similar but separated by the time delay. In Fig. 9 the image B light curve is shifted by a time delay of 88 days and corrected for the V − I color difference between images A and B of about 0.326 mag. The combined light curve represents the V − I color light curve of the quasar in the period from 2001 to 2010. As can be seen in Figs. 7 and 9, the color variations are well correlated with the brightness variations of the quasar. Similar to the brightness changes, the color curve also shows the global maximum and minimum in 2004 and 2009, respectively. From the brightness and color variations of the quasar one can see that the image B light curve recorded the brightest state of the quasar. The quasar was bluer than on average at the maximum of the brightness, and it was redder than on average at the minimum of the brightness. The light curves show an overall change in the V − I color index of about 0.3 mag, and an overall change in the brightness of more than 0.4 mag in the V band. The correlation between color and brightness variations of the quasar agrees with numerous observations that showed that quasars are generally bluer when brighter (see, e.g., Trèvese et al. 2001; Wilhite et al. 2005).
 |
Fig. 8 Distribution of peaks of the CCF obtained for 1000 Monte Carlo realizations of the R-band light curves. The peak of the distribution is marked by a solid gray line. The dotted line corresponds to the mean value of the delay. |
We also analyzed the archive Maidanak image frames of UM673 taken in the V, R and I bands in November 1998. These image frames have a small FOV and do not contain any bright stars except for the lensed system UM673. Analysis of these data gives only the relative magnitudes of images A and B of UM673 in the V, R and I bands. We used these measurements of the relative fluxes to estimate the difference between the V − I color indices of the quasar images in 1998, calculated as 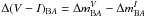 . The measured color difference Δ(V − I)BA for November 1998 is 0.373 ± 0.014 mag. We found that this value closely agrees with the mean color difference between the UM673 images measured based on the 2001–2010 data. Therefore, the color difference between the quasar images remained roughly constant over more than ten years. This can be considered as evidence that there were no noticeable microlensing variations in the images of UM673.
. The measured color difference Δ(V − I)BA for November 1998 is 0.373 ± 0.014 mag. We found that this value closely agrees with the mean color difference between the UM673 images measured based on the 2001–2010 data. Therefore, the color difference between the quasar images remained roughly constant over more than ten years. This can be considered as evidence that there were no noticeable microlensing variations in the images of UM673.
In addition, we analyzed the differences in magnitude (flux ratios) between images A and B in the V, R and I bands at different epochs. The relation between the magnitude difference and flux ratio is given by Δm(B − A) = 2.512 ∗ lg(FA/FB). For the analysis we used the following data: images of UM673 taken with the EMMI camera of the ESO New Technology Telescope in 19982; images obtained with FORS1 at the ESO Very Large Telescope in 20003, 20044 and 20065; archive Maidanak data collected during the 1998 and 1999 seasons and more recently, between 2001 and 2010 (see Table 1). Note that the ESO data used in the analysis were obtained in the same Bessel system of filters as the Maidanak data. Figure 10 shows the flux ratios between images A and B over 12 years. The flux ratios measured using the ESO images for the V, R and I-band data are marked by open stars, open triangles and open squares, respectively. The Maidanak flux ratios for the V, R and I-band data are indicated by open circles, filled circles and stars, respectively. The R-band Maidanak flux ratio measured between 2003 and 2010 was corrected for a time delay of 88 days. The rest of the data were poorly sampled or taken only at a single epoch and therefore time-delay corrected flux ratios cannot be calculated. The Maidanak-CTIO flux ratios that were not corrected for the time delay were estimated as average flux ratios for each observational season. The ESO flux ratios were measured based on single-epoch observations. Errors in the flux ratio were estimated as follows. From the A and B light curves, the rms amplitudes of the quasar variability for each season of observations are in the range of 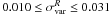 mag in the R band. To account for possible changes in the quasar brightness on timescales of 88 days we added
mag in the R band. To account for possible changes in the quasar brightness on timescales of 88 days we added 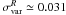 in quadrature to the weighted average errors measured for each season of observations (see also Shalyapin et al. 2009).
in quadrature to the weighted average errors measured for each season of observations (see also Shalyapin et al. 2009).
 |
Fig. 9 V − I color curves of images A (filled circles and triangles) and B (open circles and stars) of UM673. The color curve of image B is shifted by a time delay of 88 days and a magnitude offset of −0.326 mag. The dotted line traces the average color of the quasar. (This figure is available in color in electronic form.) |
 |
Fig. 10 V, R and I-band magnitude differences between images A and B of UM673 for the 1998–2010 period. The measurements based on the ESO archive data are indicated by open stars, open triangles and open squares for the V, R and I bands, respectively. The Maidanak-CTIO magnitude differences are shown by open circles, filled circles and stars. The mean V, R and I-band magnitude differences are shown by dotted lines. |
We estimate that the flux ratios were ΔmV = 2.19, ΔmR = 2.11 and ΔmI = 2.03 mag for the ESO VLT observations in July, 2000. They roughly agree with the Maidanak V, R and I-band flux ratios of the quasar images in 1998 and 1999. The magnitude differences for the earlier HST/WFPC2 data obtained in 1994 (see Keeton et al. 1998) are ΔmF555W = 2.24, ΔmF675W = 2.29 and ΔmF814W = 2.09 mag (where the F555W, F675W and F814W HST/WFPC2 bands roughly match the standard Johnson-Cousins V, R and I bands, see, e.g., Holtzman et al. 1995). The Maidanak V, R, I-band flux ratios measured based on the multi-epoch data collected between 1998 and 2010 are ΔmV = 2.19 ± 0.04, ΔmR = 2.12 ± 0.04 and ΔmI = 1.99 ± 0.04 mag. These values of the flux ratio also roughly agree with the NIR K and L′-band flux ratios measured by Fadely & Keeton (2011) based on single-epoch observations (ΔmK = 2.24 and ΔmL′ = 2.19 mag, respectively).
As can be seen in Fig. 10, the V, R and I-band flux ratios were stable at different epochs. This can be seen better from the R-band flux ratio measurements corrected for the time delay. The stability of the flux ratio in the different bands indicates the absence of microlensing variations in the system. Small deviations of the flux ratio, not corrected for the time delay, from its multi-epoch mean value can be explained by the variations intrinsic to the quasar.
Apparently, the quasar can exhibit high-amplitude variations over short timescales. From the analysis of the archive Maidanak data we found evidence for rapid brightness variations in the system between November 13 and December 23, 1998. The V, R, and I-band relative fluxes of the A and B images changed significantly over a very short time. In particular, the weighted average magnitude differences of the UM673 images between November 13 and November 26, 1998 were ΔmV = 2.21 ± 0.04, ΔmR = 2.07 ± 0.04 and ΔmI = 1.99 ± 0.04 mag. However, in the next month (between December 8 and December 23, 1998) the weighted average magnitude differences were already ΔmV = 2.53 ± 0.04, ΔmR = 2.27 ± 0.04 and ΔmI = 2.05 ± 0.04 mag. These measurements are shown by gray symbols in Fig. 10. The increase in magnitude difference Δm(B − A) (of about 0.3 mag in the V band) might indicate significant brightening of image A or simultaneous fading of image B and brightening of image A in December 1998. The R-band magnitude difference measured from data obtained in September 1999 showed that it returned to the value of November 1998: ΔmR = 2.03 ± 0.04 mag. The magnitude difference calculated for this event shows a clear dependence on wavelength. The change of the V-band flux ratio is more prominent than that of the I-band flux ratio. Nakos et al. (2005) published photometric results for nearly the same epoch of observations. During the time interval covered by the observations, the A and B light curves of UM673 showed rapid short-term variations in both images (see Figs. 3 and 4 in Nakos et al. 2005). These rapid variations could alter the single-epoch flux ratio during a very short time.
The high-amplitude brightness variation observed in image B in January 2010 does not have its counterpart in image A. Taking into account the time delay of 88 days, it should be seen in the A light curve at the beginning of October 2009. Because we do not detect the same brightness variation in image A, it is most probably not connected with the intrinsic quasar variations. The amplitude of the brightness changes during this event is higher in the V band (about 0.39 mag) than in the I band (about 0.31 mag), as expected for microlensing variations (see Wambsganss & Paczynski 1991). However, microlensing by the stars in the lensing galaxy would take a much longer time. We conclude that an independent confirmation of this event might be needed to find an explanation for its origin.
6. Discussion
We presented the V, R and I-band light curves of images A and B of the lensed quasar UM673. The light curves cover ten observational seasons, from August 2001 to November 2010. We found that both images of UM673 show brightness variations on short (several months) and long (several years) timescales in all three bands. Using cross-correlation analysis of the better-sampled R-band light curves we estimated a mean time delay between images A and B (image A is leading) of 89 days with an rms error of 11 days. From the Monte Carlo simulations, the most probable value of the delay that can be measured from light curves with similar statistical properties and variability pattern as the observed R-band light curves is 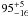
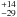 days (68 and 95% confidence intervals). These measurements are based on observations of a much longer time span than in Paper I. The time delay of about 150 days measured in Paper I was constrained based on the long-term parabola-shape brightness variation observed between 2003 and 2005. We found that this single event does not allow for the correct determination of the time delay. For the revised time delay of 89 days, the global behavior of the A and B light curves matches well. This demonstrates that the observed brightness variations are mainly caused by variations intrinsic to the quasar. Analysis of the brightness and color changes does not show evidence for microlensing in the UM673 images. The bluer-when-brighter behavior of image A detected in the earlier observations of Nakos et al. (2005) is most probably caused by quasar variability and not by microlensing.
days (68 and 95% confidence intervals). These measurements are based on observations of a much longer time span than in Paper I. The time delay of about 150 days measured in Paper I was constrained based on the long-term parabola-shape brightness variation observed between 2003 and 2005. We found that this single event does not allow for the correct determination of the time delay. For the revised time delay of 89 days, the global behavior of the A and B light curves matches well. This demonstrates that the observed brightness variations are mainly caused by variations intrinsic to the quasar. Analysis of the brightness and color changes does not show evidence for microlensing in the UM673 images. The bluer-when-brighter behavior of image A detected in the earlier observations of Nakos et al. (2005) is most probably caused by quasar variability and not by microlensing.
We found that the magnitude difference between the quasar images corrected for the time delay does not evolve with time. Therefore, the flux of the UM673 images is not altered by microlensing, which would otherwise cause changes in the flux ratio with time. The measured mean flux ratios FA/FB are 7.6, 7.1 and 6.3 in the V, R and I bands, respectively. The estimated V-band mean flux ratio agrees well with the value of Wisotzki et al. (2004). In Wisotzki et al. (2004) the spectrum of image B was rescaled by a factor of 7.78 to match the C IV emission line of image A. Therefore, the estimated emission-line flux ratio between the images was found to be 7.78 at 5780 Å, which roughly corresponds to the effective wavelengths of the V filter. Since there is no microlensing, the difference in the flux ratio in the V, R and I bands is most probably caused by the dust extinction in the lensing galaxy (Yonehara et al. 2008).
The measured time delay can be used to estimate the Hubble parameter and constrain the mass model of the lensing galaxy. There have been several lens models that predict different time delays between the UM673 images. The predicted time delay for the lens with elliptical symmetry and H0 = 75 km s-1 Mpc-1 is about 7 weeks (Surdej et al. 1988). Lehár et al. (2000) fitted a set of four standard lens models (SIE, constant M/L models, and those with external shear). The SIE and constant M/L models predict time delays of hΔt = 80 and hΔt = 121 days, respectively. The SIE and constant M/L models with external shear predict time delays of hΔt = 84 ÷ 87 and hΔt = 115 days, respectively. Given that Δt = 89 days, the SIE and M/L models yield estimates of the Hubble constant 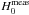 of 90 and 136 km s-1 Mpc-1, respectively. The SIE and M/L models with shear yield values of
of 90 and 136 km s-1 Mpc-1, respectively. The SIE and M/L models with shear yield values of 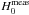 of 94 and 129 km s-1 Mpc-1, respectively. These estimates of the Hubble constant are higher than the Hubble key project result of 72 ± 8 km s-1 Mpc-1 (Freedman et al. 2001) or improved result of 74.2 ± 3.6 km s-1Mpc-1 (Riess et al. 2009). This might be due to an additional convergence to the lensing potential from nearby objects or objects on the line of sight to the quasar (see, e.g., Keeton et al. 2000).
of 94 and 129 km s-1 Mpc-1, respectively. These estimates of the Hubble constant are higher than the Hubble key project result of 72 ± 8 km s-1 Mpc-1 (Freedman et al. 2001) or improved result of 74.2 ± 3.6 km s-1Mpc-1 (Riess et al. 2009). This might be due to an additional convergence to the lensing potential from nearby objects or objects on the line of sight to the quasar (see, e.g., Keeton et al. 2000).
Lehár et al. (2000) estimated the total shear γT and convergence kT produced by nearby galaxies in the FOV of ten double lensed quasars observed with the Hubble Space Telescope (HST), including UM673. The total convergence from five galaxies within 20′′of UM673 was estimated to be 0.138 (see Table 4 of Lehár et al. 2000). In the calculations Lehár et al. assumed that each galaxy has an SIS mass distribution, and their M/L ratios and redshifts are the same as for the lensing galaxy. Because of the assumptions made, the derived value of kT can only be considered as approximate. For the SIS model, the Hubble parameter corrected for the field convergence of 0.138 as 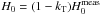 , is 78 ± 10 km s-1 Mpc-1. This value roughly agrees within the errors with the Hubble key project value. The result can be improved even more when detail measurements of kT in the field of UM673 are available.
, is 78 ± 10 km s-1 Mpc-1. This value roughly agrees within the errors with the Hubble key project value. The result can be improved even more when detail measurements of kT in the field of UM673 are available.
An additional contribution to the total convergence produced by the objects on the line of sight to the quasar should also be investigated. Recently, Cooke et al. (2010) reported the discovery of a previously unrecognized DLA system at z = 1.63 in the spectrum of image A of UM673. They also found a weak Lyα emission line in the spectrum of image B at the same redshift as the DLA that indicates a star formation rate of 0.2 solar mass per year. The discovery provides evidence for an additional mass, a galaxy that gives rise to the DLA system toward the UM673 quasar.
The accuracy of the Hubble constant from the time delay in UM673 can be improved in the future by analyzing the external convergence produced by the objects in the FOV of UM673 and reducing the error in the time delay measurement. The latter requires coordinated observations of UM673 at different sites over the time interval that can provide better overlap between time-delay-corrected light curves of the quasar images than the Maidanak-CTIO data do. UM673 might exhibit rapid brightness variations of more than 0.1 mag on timescales from one to several months. Observations of these rapid brightness variations during coordinated monitoring of the system can help to reduce the uncertainty in the time delay down to several per cent.
Online material
 |
Fig. 2 V-band light curves of the A and B images of UM673 from August 2001 to November 2010. The light curve of image B is shifted by − 1.95 mag. |
 |
Fig. 3 I-band light curves of the A and B images of UM673 from August 2001 to November 2010. The light curve of image B is shifted by − 1.62 mag. |
Transmission curves of the CTIO filters in comparison with the Bessel filters can be found at http://www.ctio.noao.edu/telescopes/50/1-3m.html
Acknowledgments
We thank the referee for many useful comments and help in improving the content of this paper. We would like to thank Vyacheslav Shalyapin for helpful discussions. This research project was supported by the National Taiwan University grant No. 10R40044 and by the Taiwan National Science Councils grant No. NSC99-2811-M-002-051. We also gratefully acknowledge the support of the Russian Foundation for Basic Research (RFBR, grant No. 09-02-00244a) for travel of the SAI team to the Maidanak Observatory. Observations carried out by the UBAI team in 2003–2005 were supported by the German Research Foundation (DFG) grant 436 USB 113/5/0-1. The research was also supported by a grant for young scientists from the President of the Russian Federation (No. MK-2637.2006.2), and the Deutscher Akademischer Austausch Dienst (DAAD) grant No. A/05/56557. T.Ak. gratefully acknowledges the Research Fellowship grant awarded him by the Belgian Federal Science Policy Office (BELSPO). This research has made use of the ESO Science Archive data taken with the NTT and VLT telescopes.
References
- Arévalo, P., Uttley, P., Lira, P., et al. 2009, MNRAS, 397, 2004 [NASA ADS] [CrossRef] [Google Scholar]
- Chang, K., & Refsdal, S. 1979, Nature, 282, 561 [Google Scholar]
- Cooke, R., Pettini, M., Steidel, C. C., et al. 2010, MNRAS, 409, 679 [NASA ADS] [CrossRef] [Google Scholar]
- Daulie, G., Hainaut, O., Hutsemékers, D., et al. 1993, Gravitational Lenses in the Universe, in Proc. 31st Liege International Astrophysical Colloquium, eds. J. Surdej, D. Fraipont-Caro, E. Gosset, S. Refsdal, & M. Remy, Université de Liège, Institut d’Astrophysique, Liège, 181 [Google Scholar]
- Dudinov, V., Bliokh, P., Paczynski, B., et al. 2000, Kin. & Phys. Cel. Bodies, 3, 170 [Google Scholar]
- Eigenbrod, A., Courbin, F., & Meylan, G. 2007, A&A, 465, 51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fadely, R., & Keeton, C. R. 2011, AJ, 141, 101 [NASA ADS] [CrossRef] [Google Scholar]
- Freedman, W. L., Madore, B. F., Gibson, B. K., et al. 2001, ApJ, 553, 47 [NASA ADS] [CrossRef] [Google Scholar]
- Goicoechea, L. J., Ullàn, A., Ovaldsen, J. E., et al. 2006, in Highlights of Spanish Astrophysics IV, eds. F. Figueras, J. M. Girart, M. Hernanz, & C. Jordi (Dordrecht: Springer), CD-ROM [arXiv:astro-ph/0609647] [Google Scholar]
- Goicoechea, L. J., Shalyapin, V. N., Koptelova, E., et al. 2008, New A, 13, 182 [Google Scholar]
- Holtzman, J. A., Burrows, C. J., Casertano, S., et al. 1995, PASP, 107, 1065 [NASA ADS] [CrossRef] [Google Scholar]
- Im, M., Ko, J., Cho, Y., et al. 2010, JKAS, 43, 75 [NASA ADS] [CrossRef] [Google Scholar]
- Krolik, J. H., Horne, K., Kallman, T. R., et al. 1991, ApJ, 371, 541 [NASA ADS] [CrossRef] [Google Scholar]
- Keeton, C. R., Kochanek, C. S., & Falco, E. E. 1998, ApJ, 509, 561 [NASA ADS] [CrossRef] [Google Scholar]
- Keeton, C. R., Christlein, D., & Zabludoff, A. I. 2000, ApJ, 545, 129 [NASA ADS] [CrossRef] [Google Scholar]
- Kochanek, C. S. 2002, ApJ, 578, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Koptelova, E., Shimanovskaya, E., & Artamonov, B. 2005, MNRAS, 356, 323 [NASA ADS] [CrossRef] [Google Scholar]
- Koptelova, E. A., Oknyanskij, V. L., & Shimanovskaya, E. V. 2006, A&A, 452, 37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Koptelova, E. A., Artamonov, B. P., Shimanovskaya, E. V., et al. 2007, Astron. Rep., 51, 797 [Google Scholar]
- Koptelova, E., Artamonov, B. P., Bruevich, V. V., Burkhonov, O. A., & Sergeev, A. V. 2008, Astron. Rep., 52, 270 [NASA ADS] [CrossRef] [Google Scholar]
- Koptelova, E., Oknyanskij, V. L., Artamonov, B. P., & Burkhonov, O. 2010, MNRAS, 401, 2805 (Paper I) [NASA ADS] [CrossRef] [Google Scholar]
- Lehár, J., Falco, E. E., Kochanek, C. S., et al. 2000, ApJ, 536, 584 [NASA ADS] [CrossRef] [Google Scholar]
- Lyuty, V. M. 2006, in AGN Variability from X-Rays to Radio Waves, eds. C. M. Gaskell, I. M. McHardy, B. M. Peterson, & S. G. Sergeev, ASP Conf. Ser. (San Francisco: ASP), 360, 3 [Google Scholar]
- MacAlpine, G. M., & Feldman, F. R. 1982, ApJ, 261, 412 [NASA ADS] [CrossRef] [Google Scholar]
- Nakos, Th., Ofek, E. O., Boumis, P., et al. 2003, A&A, 402, 1157 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nakos, Th., Courbin, F., Poels, J., et al. 2005, A&A, 441, 443 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Oknyanskij, V. L. 1993, Pis’ma Astron. Zh., 19, 1021 [Google Scholar]
- Paraficz, D., Hjorth, J., Burud, I., Jakobsson, P., & Elíasdóttir, Á. 2006, A&A, 455, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pelt, J., Hoff, W., Kayser, R., Refsdal, S., & Schramm, T. 1994, A&A, 286, 775 [NASA ADS] [Google Scholar]
- Refsdal, S. 1964, MNRAS, 128, 307 [NASA ADS] [CrossRef] [Google Scholar]
- Riess, A. G., Macri, L., Casertano, S., et al. 2009, ApJ, 699, 539 [NASA ADS] [CrossRef] [Google Scholar]
- Schneider, P., Ehlers, J., & Falco, E. E. 1992, Gravitational Lenses (Berlin: Springer) [Google Scholar]
- Sinachopoulos, D., Nakos, Th., Boumis, P., et al. 2001, ApJ, 122, 1692 [Google Scholar]
- Shalyapin, V. N., Goicoechea, L. J., Koptelova, E., Ullàn, A., & Gil-Merino, R. 2008, A&A, 492, 401 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shalyapin, V. N., Goicoechea, L. J., Koptelova, E., et al. 2009, MNRAS, 397, 1982 [NASA ADS] [CrossRef] [Google Scholar]
- Smette, A., Surdej, J., Shaver, P. A., et al. 1992, ApJ, 389, 39 [NASA ADS] [CrossRef] [Google Scholar]
- Surdej, J., Magain, P., Swings, J.-P., et al. 1987, Nature, 329, 695 [Google Scholar]
- Surdej, J., Magain, P., Swings, J.-P., et al. 1988, A&A, 198, 49 [NASA ADS] [Google Scholar]
- Timmer, J., & König, M. 1995, A&A, 300, 707 [NASA ADS] [Google Scholar]
- Trèvese, D., Kron, R. G., & Bunone, A. 2001, ApJ, 551, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Ullán, A., Goicoechea, L. J., Zheleznyak, A. P., et al. 2006, A&A, 452, 25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wambsganss, J., & Paczinski B. 1991, ApJ, 102, 864 [CrossRef] [Google Scholar]
- Wilhite, B. C., Van den Berk, D. E., Kron, R. G., et al. 2005, ApJ, 633, 638 [NASA ADS] [CrossRef] [Google Scholar]
- Wisotzki, L., Becker, T., Christensen, L., et al. 2004, Astron. Nachr., 325, 135 [NASA ADS] [CrossRef] [Google Scholar]
- Yonehara, A., Hirashita, H., & Richter, P. 2008, A&A, 478, 95 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 R-band light curves of the A and B images of UM673 from August 2001 to November 2010. For better representation, the light curve of image B is shifted by − 1.87 mag. The light curves of reference stars 2 and 3 are shown at the bottom. (This figure is available in color in electronic form.) |
| In the text | |
 |
Fig. 4 CCFs calculated between the R-band light curves of images A and B with the data points corresponding to the high-amplitude event in image B excluded (shown by a thick black line); and the data points corresponding to the high-amplitude event in image B included (shown by a thin black line). The CCF calculated between the R-band light curves corresponding to the 2003–2005 period is shown by a thick gray line. |
| In the text | |
 |
Fig. 5 CCFs calculated between the V (thick black line) and I-band (thin black line) light curves of the A and B images. The thick gray line shows the V-band CCF calculated for a value of Δtmax = 110 days. |
| In the text | |
 |
Fig. 6 Dispersion spectra calculated for the combined A and B light curves for decorrelation lengths of 60 (gray line) and 90 (black line) days. |
| In the text | |
 |
Fig. 7 R-band light curves of image A (filled circles and triangles) and image B shifted by a time delay of 88 days with a magnitude offset of − 2.12 mag (open circles and stars). (This figure is available in color in electronic form.) |
| In the text | |
 |
Fig. 8 Distribution of peaks of the CCF obtained for 1000 Monte Carlo realizations of the R-band light curves. The peak of the distribution is marked by a solid gray line. The dotted line corresponds to the mean value of the delay. |
| In the text | |
 |
Fig. 9 V − I color curves of images A (filled circles and triangles) and B (open circles and stars) of UM673. The color curve of image B is shifted by a time delay of 88 days and a magnitude offset of −0.326 mag. The dotted line traces the average color of the quasar. (This figure is available in color in electronic form.) |
| In the text | |
 |
Fig. 10 V, R and I-band magnitude differences between images A and B of UM673 for the 1998–2010 period. The measurements based on the ESO archive data are indicated by open stars, open triangles and open squares for the V, R and I bands, respectively. The Maidanak-CTIO magnitude differences are shown by open circles, filled circles and stars. The mean V, R and I-band magnitude differences are shown by dotted lines. |
| In the text | |
 |
Fig. 2 V-band light curves of the A and B images of UM673 from August 2001 to November 2010. The light curve of image B is shifted by − 1.95 mag. |
| In the text | |
 |
Fig. 3 I-band light curves of the A and B images of UM673 from August 2001 to November 2010. The light curve of image B is shifted by − 1.62 mag. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


