| Issue |
A&A
Volume 543, July 2012
|
|
|---|---|---|
| Article Number | A67 | |
| Number of page(s) | 5 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201219176 | |
| Published online | 27 June 2012 | |
Research Note
The internal structure of neutron stars and white dwarfs, and the Jacobi virial equation⋆
Instituto de Astrofísica de Andalucía, CSIC, Apartado 3004, 18080 Granada, Spain
e-mail: claret@iaa.es
Received: 6 March 2012
Accepted: 29 May 2012
Aims. The internal structure constants kj and the radius of gyration are useful tools for investigating the apsidal motion and tidal evolution of close binaries and planetary systems. These parameters are available for various evolutionary phases but they are scarce for the late stages of stellar evolution. To cover this gap, we present here the calculations of the apsidal-motion constants, the fractional radius of gyration, and the gravitational potential energy for two grids of cooling evolutionary sequences of white dwarfs and for neutron star models.
Methods. The cooling sequences of white dwarfs were computed with LPCODE. An additional alternative to the white dwarf models was also adopted with the MESA code which allows non-stop calculations from the pre main-sequence (PMS) up to the white dwarf cooling sequences. Neutron star models were acquired from the NSCool/TOV subroutines. The apsidal-motion constants, the moment of inertia, and the gravitational potential energy were computed with a fourth-order Runge-Kutta method.
Results. The parameters are made available for four cooling sequences of white dwarfs (DA and DB types): 0.52, 0.57, 0.837 and 1.0 M⊙ and for neutron star models covering a mass range from 1.0 up to 2.183 M⊙, in 0.1 mass step. We show that, contrary to previously established opinion, the product of the form-factors β and α, which are related to the moment of inertia, and gravitational potential energy, is not constant during some evolutionary phases. Regardless of the final products of stellar evolution (white dwarfs, neutron stars and perhaps black holes), we found that they recover the initial value of product αβ at the pre main-sequence phase (≈0.4). These results may have important consequences for the investigation of the Jacobi virial equation.
Key words: binaries: eclipsing / stars: interiors / stars: evolution / stars: rotation / white dwarfs / stars: neutron
Tables A.1–A.9 and additional data are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/543/A67
© ESO, 2012
1. Introduction
Close binary stars are an excellent tool for investigating the proximity effects such as tidal and rotation distortions, limb-darkening, mutual irradiation, etc., which are responsible for differences between binary and single star evolution. One can use those changes to obtain additional information on stellar and physical parameters including the internal density concentration. Rotational and tidal distortions can be described as a function of the internal structure of the stars (Kopal 1978) and in eccentric systems, they produce a motion of line of apses that can be accurately monitored trough observations of minima time. The apsidal motion strongly depends on relative radii (as r-5), stellar masses, rotational velocities, orbital eccentricity, and internal structure constants of the stars. Observational data need to be of very high quality to compare them with theoretical predictions because of the functional dependences involved. Recent updates of theory-observation comparison can be found in Claret & Giménez (2010) and for relativistic systems in Claret (1997) and Wolf et al. (2010).
On the other hand, the observed levels of circularisation and synchronisation also provide important information about the internal physical structure and evolutionary status of the component stars in a binary system. To compare these levels with the theoretical ones, we need to compute the moment of inertia and the theoretical apsidal motion constants from evolutionary models. These parameters are used to integrate the differential equations that govern the evolution of the orbital elements (Hut 1981; Eggleton & Kiseleva-Eggleton 2002). The parameters needed for studying the apsidal motion and tidal evolution are available for various masses and chemical compositions but only for certain evolutionary stages such as the main-sequence (MS) and the red giant branch. Recently, we covered part of this gap with the publication of calculations for the pre-main sequence (PMS) phase (see Claret 2012). However, for compact objects – such as white dwarfs (WD) and neutron stars (NS) – the calculations are very scarce or even lacking. In this research note, we present the calculations of the apsidal-motion constants, of the fractional radius of gyration, and of the gravitational potential energy for two grids of cooling evolutionary sequences of WD, and for NS with masses between 1.0 and 2.183 M⊙. These calculations can be used to investigate the apsidal motion and the tidal evolution of compact objects. In addition, several non-stop evolution sequences, from the PMS to the cooling sequence of white dwarfs, were also computed with the aim to shed some light on the investigation of the Jacobi virial equation.
2. The stellar models
2.1. White dwarf models
The white dwarf models used in this paper were computed with LPCODE (Althaus et al. 2001a,b). The models were generated by evolving progenitors from the ZAMS (zero age main sequence) through the core hydrogen-burning phase, the helium-burning, and the thermally pulsing asymptotic giant branch phase to the white dwarf stage (Renedo et al. 2010). The code takes into account an updated input physics such as a detailed network for thermonuclear reactions, OPAL radiative opacities, full-spectrum turbulence theory of convection, detailed equations of state, and neutrino emission rates. The evolution of the chemical abundance distribution caused by gravitational settling and chemical and thermal diffusion of nuclear species are also considered. We refer the interested reader to Renedo et al. (2010) for more details on the input physics. Four cooling sequences for white dwarfs were computed for DA and DB types: 0.52, 0.57, 0.837, and 1.0 M⊙.
A second and interesting alternative to white dwarf cooling models is computing it with MESA code (Paxton et al. 2011, version 3290). This code allows non-stop calculations from the PMS to white dwarfs cooling sequences. We add some subroutines to compute the apsidal-motion constants, the radius of gyration, and the gravitational potential energy. These models are, as we will see in the next sections, important for investigating the behaviour of the moment of inertia and gravitational potential energy, which are related with Jacobi dynamics.
2.2. Neutron star models
The neutron star models were computed with the spherically symmetric neutron star cooling code NSCool/TOV (Page & Reddy 2006; Page et al. 2006). The four differential equations – in the general relativistic framework – for the internal structure of neutron stars (mass, gravitational energy, hydrostatic equilibrium, and baryon number) were solved by a fourth order Runge-Kutta method. We used 14 models with masses ranging from 1.0 up to 2.183 M⊙ in 0.1 mass step. The models were computed with the equation of state provided by Akmal et al. (1998).
3. Apsidal-motion constants, radius of gyration, and gravitational potential energy
The theoretical internal structure constants (apsidal-motion constants) kj are derived by integrating the differential equations of Radau: 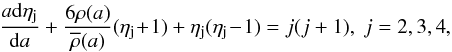 (1)where
(1)where 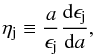 (2)and a is the mean radius of the configuration, ϵj is the deviation from sphericity, ρ(a) is the mass density at the distance a from the centre, and
(2)and a is the mean radius of the configuration, ϵj is the deviation from sphericity, ρ(a) is the mass density at the distance a from the centre, and 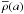 is the mean mass density within a sphere of radius a. The kj are then computed following
is the mean mass density within a sphere of radius a. The kj are then computed following 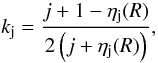 (3)where R refers to the values of ηj at the star’s surface.
(3)where R refers to the values of ηj at the star’s surface.
 |
Fig. 1 Apsidal-motion constant k2 for white dwarf models. Continuous lines represent DA models while dashed ones denote DB models. The numbers indicate the model mass in solar units and the arrow indicates the direction of the evolution. |
The fractional radius of gyration β is obtained for each stellar configuration through the following equation (Newtonian limit): 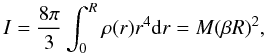 (4)where I is the moment of inertia. The amount of work necessary to bring the entire spherical star in from infinity (the gravitational potential energy), is
(4)where I is the moment of inertia. The amount of work necessary to bring the entire spherical star in from infinity (the gravitational potential energy), is 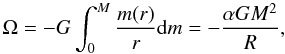 (5)where the form-factors β and α describe the moment of inertia and the gravitational potential energy, respectively. The form-factor α is a measure of the mass concentration for a given configuration. Equations (1), (4), and (5) were integrated through a fourth-order Runge-Kutta method.
(5)where the form-factors β and α describe the moment of inertia and the gravitational potential energy, respectively. The form-factor α is a measure of the mass concentration for a given configuration. Equations (1), (4), and (5) were integrated through a fourth-order Runge-Kutta method.
The internal structure constants for white dwarfs are shown in Fig. 1. The DA models are represented by continuous lines and the DB are denoted by dashed ones. These cooling sequences show some interesting properties. The models evolve from more concentrated configurations to less mass centrally condensed ones. The differences in mass concentration are not large between DA and DB models, though they increase for less massive models. The final point of each cooling sequence, concerning log k2, corresponds approximately to an effective polytropic model with n = 1.5–2.0 while the corresponding n for the beginning of the cooling sequences varies from 3.7 (for a 0.52 M⊙ model) to 2.8 for a 1.0 M⊙ model. Note, however, that polytropic models do not represent real stars well; the indexes n were used here to serve as guidelines only. The product of the form-factors α and β is almost constant (around 0.4) and it is independent of the evolutionary phase or of the mass of the WD model.
The apsidal-motion constant k2 of neutron stars is nearly a linear function of the mass of the model; the less massive models are more mass concentrated. In Fig. 2 we show the apsidal-motion constant log k2, the radius of gyration, and the form-factor α for models with masses between 1.0 and 2.183 M⊙. Concerning mass concentration, neutron stars behave like configurations with an effective polytropic index lower than 1. The constancy of the product αβ can be also inferred by inspecting Fig. 2.
4. Some considerations on the Jacobi virial theorem
The virial theorem is a useful but almost forgotten method to investigate stellar astrophysics. It can be applied to many dynamical systems, including rotation, magnetic fields, etc. Often, we must solve the associated force equations to describe a given configuration. These equations are obtained from the formalism by Lagrange, Hamilton, or from the Boltzmann equation. These vectorial equations are frequently very complicated to solve in a closed form. The virial theorem reduces the complexity of a dynamical problem since it basically deals with scalar variables. However, the price to be paid is that some information is lost in the process. In return, this simplification also allows us to solve problems more complicated that, using the three above formalisms, would be almost impossible to treat. Thus, the balance of using a virial equation is positive. In a nutshell, the virial theorem can be seen as the relation between the average potential and the kinetic energies of a given system in steady or quasi-steady state. A very good review on the virial theorem and its applications can be found in Collins (2003).
 |
Fig. 2 Internal structure constants for neutron star models as a function of mass. Continuous line represents log k2, dashed line denotes (–α) and dotted-dashed line represents (–β). |
Next, we used the results from Eqs. (1), (4) and (5) to investigate the dynamical behaviour of stellar models in the light of the Jacobi virial theorem. One of the innovations arising from the introduction of this theorem will be that the usual diagrams (HR and its variants) will be replaced by dynamic ones, showing the relationship between the changes in the radius and the changes in the form-factors α and β.
The product αβ is approximately constant during the PMS (Claret 2012), early stages of the main-sequence (Claret 2004), and also for the white dwarf and neutron star models, as we have seen here. This is an important input into the study of the Jacobi virial equation and also into some other investigations of the stellar dynamics, structure, and evolution. That equation can be written as 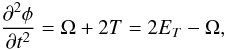 (6)where the Jacobi function is given by
(6)where the Jacobi function is given by 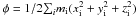 , T is the kinetic energy and ET is the total energy of a given configuration. For spherical configurations, we have φ = 3/4I ≡ 3/4M(Rβ)2. A common version of the virial theorem is obtained when we assume a convenient average time of Eq. (6). For steady systems we obtain
, T is the kinetic energy and ET is the total energy of a given configuration. For spherical configurations, we have φ = 3/4I ≡ 3/4M(Rβ)2. A common version of the virial theorem is obtained when we assume a convenient average time of Eq. (6). For steady systems we obtain 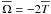 . The Jacobi function and Eq. (5) provide a relationship between the moment of inertia and the gravitational potential energy that can be expressed by the constancy of the product αβ:
. The Jacobi function and Eq. (5) provide a relationship between the moment of inertia and the gravitational potential energy that can be expressed by the constancy of the product αβ: 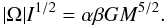 (7)For conservative systems, for example, the Jacobi virial equation can be transformed into a differential equation with only one unknown function (Ferronsky et al. 1978)
(7)For conservative systems, for example, the Jacobi virial equation can be transformed into a differential equation with only one unknown function (Ferronsky et al. 1978) 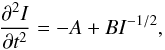 (8)where A = 8/3 | ET | and B = 4/3αβGM5/2. However, the key question is whether the assumption (constancy of αβ) is valid for all evolutionary stages and not only for PMS, early MS, WD, and NS. To check this possibility, we investigated in more detail how this product evolves with time, using a 1.3 M⊙ model evolving from the PMS up to the WD stage (Fig. 3). We confirm that during the PMS and during the earlier stages of the MS the product is almost constant, as can be verified by inspecting such a figure. However, as the models evolve out of the MS, the product αβ increases much during the later phases before the WD stage; about 4 orders of magnitude. The changes in αβ may be related to the presence/absence of nuclear reactions, mass loss, different equations of state and/or with chemical inhomogeneities. To check whether the results shown in Fig. 3 depend on the mass of the progenitor, we calculated several models with initial masses ranging from 0.6 to 1.8 M⊙. Obviously, the morphology of these tracks on the Herzsprung-Russel (HR) diagram are distinct but the behaviour of αβ is very similar to that shown in Fig. 3, including the invariance of such a product at PMS and WD stages. The difference is that the maximum value of αβ is slightly high for more massive models. We also changed the initial chemical composition, but the overall result does not depend on this input. It is also interesting to point out that the evolution of αβ shown in Fig. 3 contradicts the results by Ferronsky et al. (1978), who found that this product is constant and independent of the mass of the configuration and of the radial mass distribution. They argued that the constancy of the product αβ establishes a direct link with the Jacobi equation. However, these authors used simple laws of mass distribution to evaluate the product αβ that covers only a branch of the HR diagram. Nevertheless, as we have shown, the product αβ is not constant for all evolutionary phases and therefore, the resolution of Jacobi’s equation is not straightforward, as previously thought.
(8)where A = 8/3 | ET | and B = 4/3αβGM5/2. However, the key question is whether the assumption (constancy of αβ) is valid for all evolutionary stages and not only for PMS, early MS, WD, and NS. To check this possibility, we investigated in more detail how this product evolves with time, using a 1.3 M⊙ model evolving from the PMS up to the WD stage (Fig. 3). We confirm that during the PMS and during the earlier stages of the MS the product is almost constant, as can be verified by inspecting such a figure. However, as the models evolve out of the MS, the product αβ increases much during the later phases before the WD stage; about 4 orders of magnitude. The changes in αβ may be related to the presence/absence of nuclear reactions, mass loss, different equations of state and/or with chemical inhomogeneities. To check whether the results shown in Fig. 3 depend on the mass of the progenitor, we calculated several models with initial masses ranging from 0.6 to 1.8 M⊙. Obviously, the morphology of these tracks on the Herzsprung-Russel (HR) diagram are distinct but the behaviour of αβ is very similar to that shown in Fig. 3, including the invariance of such a product at PMS and WD stages. The difference is that the maximum value of αβ is slightly high for more massive models. We also changed the initial chemical composition, but the overall result does not depend on this input. It is also interesting to point out that the evolution of αβ shown in Fig. 3 contradicts the results by Ferronsky et al. (1978), who found that this product is constant and independent of the mass of the configuration and of the radial mass distribution. They argued that the constancy of the product αβ establishes a direct link with the Jacobi equation. However, these authors used simple laws of mass distribution to evaluate the product αβ that covers only a branch of the HR diagram. Nevertheless, as we have shown, the product αβ is not constant for all evolutionary phases and therefore, the resolution of Jacobi’s equation is not straightforward, as previously thought.
 |
Fig. 3 Evolution of the product αβ of a 1.3 M⊙ initial mass model from the PMS to the white dwarf stage. Symbols for the evolutionary phases: PMS (continuous line), main-sequence and thermally pulsing asymptotic giant branch (asterisks), “blue loops” (dashed line) and cooling sequence of white dwarfs (dots). The position of neutron stars is indicated by an open star. The corresponding HR diagram is shown in the left upper corner of the figure. |
 |
Fig. 4 Evolution of the product αβ and the apsidal-motion constant log k2 for two selected models with initial masses 0.6 (left) and 1.8 (right) M⊙. Same symbols as in Fig. 3. |
Regardless of the final products of stellar evolution (white dwarfs, neutron stars, and perhaps black holes), we have found that they recover the initial value of the product αβ at the PMS stage (≈0.4). This means that after the MS evolution – when the product achieves a high value – some physical processes, such as changes of nuclear reactions, of equations of state, in the chemical/density profiles, etc. drastically affect the structure of the model, recovering the value 0.4.
A confirmation of these characteristics can be verified using, for example, the evolution of the apsidal-motion constant log k2 and the product αβ shown in Fig. 4 for models with different initial masses. Indeed, during the PMS phase, the apsidal-motion constant behaves like a configuration with an effective polytropic index 1.5–2.0. As the model evolves, the mass concentration increases with the corresponding decrease of log k2. For later phases, specially during giant phases, the mass concentration increases again, but in a much more drastic way with log k2 reaching values of almost –8.0, which corresponds to an effective polytropic index near 5.0. When the cooling sequences of white dwarfs is reached, the initial value of log k2 is gradually restored to the PMS values. The simultaneous restoration of the product αβ and the log k2 in the final stages of the WD phase to the values of the PMS seems to be a general property of the models, regardless of the initial mass and chemical composition. Figure 4 shows that the evolution of αβ and log k2 occurs according to a closed curve that looks like the diagrams of classical thermodynamics.
The effects of the General Relativity (GR) on the moment of inertia and gravitational potential energy are not important for PMS/MS stars or for white dwarfs. However, for neutron stars significant changes are expected due to their compactness. To evaluate these effects, we calculated IGR and ΩGR (for the approximation of the moment of inertia we refer to Ravenhall & Pethick 1994): ![\begin{eqnarray} &&J_{\rm GR} = \frac{8\pi}{3}\!\int_{0}^{R} \Lambda(r)r^4\left[\rho (r) + P(r)/c^2\right] {\rm d}r ,~\, I_{\rm GR} \approx \frac{J_{\rm GR}}{\left(1 + {2GJ_{\rm GR}\over{R^3c^2}}\right)} \\ &&\Omega_{\rm GR} = -4\pi\int_{0}^{R} {r^2\rho\left[\Lambda^{1/2}(r) - 1\right]{\rm d}r} , \end{eqnarray}](/articles/aa/full_html/2012/07/aa19176-12/aa19176-12-eq41.png) \arraycolsep1.75ptwhere P(r) is the pressure, c is the speed of light and the auxiliary function Λ(r) can be written as
\arraycolsep1.75ptwhere P(r) is the pressure, c is the speed of light and the auxiliary function Λ(r) can be written as ![\hbox{$\left[1 - {2 G m(r)\over{r c^2}}\right]^{-1}$}](/articles/aa/full_html/2012/07/aa19176-12/aa19176-12-eq45.png) . The respective values of αGR and βGR are listed in Table A.9, together with the corresponding Newtonian ones. The “fossil” product αβ is also restored ( ≈ 0.4) for neutron stars in the Newtonian approximation (Eqs. (4) and (5), Fig. 2, and Table A.9). When we adopt the GR formalisms for NS, this product is no longer constant and increases with mass. However, it can still be written in terms of [αβ]Newt: [αβ]GR ≈ [αβ]NewtΛ0.9(R), where the auxiliary function Λ(R) is evaluated at the surface of the neutrons stars and is constant for each model. Therefore, in General Relativity, the restored “fossil” quantity is [αβ]GR/Λ0.9(R) ≈ 0.4. In the Newtonian limit (PMS/MS and white dwarfs) we have [αβ]GR/Λ0.9(R) → [αβ]Newt. Other equations of state (Shen et al. 2011) were used to test the above relationship between [αβ]GR and [αβ]Newt, including strange stars with masses 1.4 and 1.8 M⊙. Although the resulting mass-radius relations are clearly different from that obtained by adopting the equation of state by Akmal et al. (1998), the “fossil” product [αβ]GR/Λ0.9(R) ≈ 0.4 is preserved. These results and others reported here may have important consequences on the investigation of the Jacobi virial equation and will be studied in the future.
. The respective values of αGR and βGR are listed in Table A.9, together with the corresponding Newtonian ones. The “fossil” product αβ is also restored ( ≈ 0.4) for neutron stars in the Newtonian approximation (Eqs. (4) and (5), Fig. 2, and Table A.9). When we adopt the GR formalisms for NS, this product is no longer constant and increases with mass. However, it can still be written in terms of [αβ]Newt: [αβ]GR ≈ [αβ]NewtΛ0.9(R), where the auxiliary function Λ(R) is evaluated at the surface of the neutrons stars and is constant for each model. Therefore, in General Relativity, the restored “fossil” quantity is [αβ]GR/Λ0.9(R) ≈ 0.4. In the Newtonian limit (PMS/MS and white dwarfs) we have [αβ]GR/Λ0.9(R) → [αβ]Newt. Other equations of state (Shen et al. 2011) were used to test the above relationship between [αβ]GR and [αβ]Newt, including strange stars with masses 1.4 and 1.8 M⊙. Although the resulting mass-radius relations are clearly different from that obtained by adopting the equation of state by Akmal et al. (1998), the “fossil” product [αβ]GR/Λ0.9(R) ≈ 0.4 is preserved. These results and others reported here may have important consequences on the investigation of the Jacobi virial equation and will be studied in the future.
List of available models.
The calculations for α and β were carried out for spherical configurations. For ellipsoidal symmetry, these parameters can be computed as a function of the spherical structure and a correction factor dependent on the geometry of the perturbation. This topic will be the subject of a future study.
The organisation of Tables A.1–A.8 (10 columns) is the following: the age (in years), the mass (solar units), log L (in solar units), log Teff, log g(cgs), log k2, log k3, log k4, α, and β. Table A.9 contains the data for the neutron star models: mass (solar units), radius (cm), log g (cgs), log k2, log k3, log k4, α, β, αGR and βGR.
Acknowledgments
I would like to thank L. Althaus and D. Page for useful discussions concerning the modelling of white dwarfs and neutron stars. B. Paxton and A. Dotter are particularly acknowledged for their help during the implementation of MESA. I would also like to thank M. Benacquista, B. Rufino and V. Costa for their comments. The Spanish MEC (AYA2009-10394, AYA2009-14000-C03-01) is gratefully acknowledged for its support during the development of this work. This research has made use of the SIMBAD database, operated at the CDS, Strasbourg, France, and of NASA’s Astrophysics Data System Abstract Service.
References
- Akmal, A., Pandharipande, V. R., & Ravenhall, D. G. 1998, Phys. Rev. C, 58, 1804 [NASA ADS] [CrossRef] [Google Scholar]
- Althaus, L. G., Serenelli, A. M., & Benvenuto, O. G. 2001a, MNRAS, 323, 471 [NASA ADS] [CrossRef] [Google Scholar]
- Althaus, L. G., Serenelli, A. M., & Benvenuto, O. G. 2001b, MNRAS, 324, 617 [NASA ADS] [CrossRef] [Google Scholar]
- Claret, A. 1997, A&A, 327, 11 [NASA ADS] [Google Scholar]
- Claret, A. 2004, A&A, 424, 919 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Claret, A. 2012, A&A, 541, A113 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Claret, A., & Giménez, A. 2010, A&A, 519, A57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Collins II, G. W. 2003, The Virial Theorem in Stellar Astrophysics, Web Edition [Google Scholar]
- Eggleton, P. P., & Kiseleva-Eggleton, L. 2002, ApJ, 575, 461 [NASA ADS] [CrossRef] [Google Scholar]
- Ferronski, V. I., Denisik, S. A., & Ferrosnki, S. V. 1978, Celest. Mech., 18, 113 [NASA ADS] [CrossRef] [Google Scholar]
- Hut, P. 1981, A&A, 99, 126 [NASA ADS] [Google Scholar]
- Kopal, Z. 1978, Dynamics of Close Binary Systems (Dordrecht, Holland: Reidel) [Google Scholar]
- Page, D., & Reddy, S. 2006, Annu. Rev. Nucl. & Part. Sci., 56, 327 [Google Scholar]
- Page, D., Geppert, U., & Weber, F. 2006, Nucl. Phys. A, 777, 497 [NASA ADS] [CrossRef] [Google Scholar]
- Paxton, B., Bildsten, L., Dotter, A., et al. 2011, ApJS, 192, 3 [Google Scholar]
- Ravenhall, D. G., & Pethick, C. J. 1994, ApJ, 424, 846 [NASA ADS] [CrossRef] [Google Scholar]
- Renedo, I., Althaus, L. G., Miller Bertolami, M. M., et al. 2010, ApJ, 717, 183 [NASA ADS] [CrossRef] [Google Scholar]
- Shen, H., Toki, H., Oyamatsu, K., & Sumiyoshi, K. 2011, ApJS, 197, 20 [Google Scholar]
- Wolf, M., Claret, A., Kotkova, H., et al. 2010, A&A, 509, A18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Apsidal-motion constant k2 for white dwarf models. Continuous lines represent DA models while dashed ones denote DB models. The numbers indicate the model mass in solar units and the arrow indicates the direction of the evolution. |
| In the text | |
 |
Fig. 2 Internal structure constants for neutron star models as a function of mass. Continuous line represents log k2, dashed line denotes (–α) and dotted-dashed line represents (–β). |
| In the text | |
 |
Fig. 3 Evolution of the product αβ of a 1.3 M⊙ initial mass model from the PMS to the white dwarf stage. Symbols for the evolutionary phases: PMS (continuous line), main-sequence and thermally pulsing asymptotic giant branch (asterisks), “blue loops” (dashed line) and cooling sequence of white dwarfs (dots). The position of neutron stars is indicated by an open star. The corresponding HR diagram is shown in the left upper corner of the figure. |
| In the text | |
 |
Fig. 4 Evolution of the product αβ and the apsidal-motion constant log k2 for two selected models with initial masses 0.6 (left) and 1.8 (right) M⊙. Same symbols as in Fig. 3. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


