| Issue |
A&A
Volume 543, July 2012
|
|
|---|---|---|
| Article Number | A47 | |
| Number of page(s) | 5 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201218997 | |
| Published online | 25 June 2012 | |
Research Note
Isolated and non-isolated dwarfs in terms of modified Newtonian dynamics
1 Sterrenkundig Observatorium, Universiteit Gent, Krijgslaan 281-S9, 9000 Gent, Belgium
e-mail: gianfranco.gentile@ugent.be
2 Astrophysics, Cosmology & Gravity Centre, University of Cape Town, Private Bag X3, Rondebosch, 7700, South Africa
3 Observatoire Astronomique, Université de Strasbourg, CNRS UMR 7550, 67000 Strasbourg, France
4 AIfA, Universtät Bonn, 53121 Bonn, Germany
5 International Centre for Radio Astronomy Research (ICRAR), Univ. of Western Australia, 35 Stirling Highway, Perth, WA 6009, Australia
6 ARC Centre of Excellence for All-sky Astrophysics (CAASTRO), 44-70 Rosehill Street, Redfern NSW 2016, Sydney, Australia
7 ASTRON, the Netherlands Institute for Radio Astronomy, Postbus 2, 7990 AA, Dwingeloo, The Netherlands
Received: 9 February 2012
Accepted: 4 May 2012
Within the framework of modified Newtonian dynamics (MOND), we investigate the kinematics of two dwarf spiral galaxies belonging to very different environments, namely KK 246 in the Local Void and Holmberg II in the M 81 group. A mass model of the rotation curve of KK 246 is presented for the first time, and we show that its observed kinematics are consistent with MOND. We re-derive the outer rotation curve of Holmberg II, by modelling its HI data cube, and find that its inclination should be closer to face-on than previously derived. This implies that Holmberg II has a higher rotation velocity in its outer parts, which, although not very precisely constrained, is consistent with the MOND prediction.
Key words: galaxies: kinematics and dynamics / dark matter / galaxies: dwarf / gravitation
© ESO, 2012
1. Introduction
One of the biggest challenges facing the current Lambda cold dark matter (ΛCMD) model of cosmology is the observational appearance of an acceleration constant a0 ~ 10-10 m s-2 ~  in many apparently unrelated scaling relations between dark matter and baryons in galaxies (see, e.g., McGaugh 2004; Donato et al. 2009; Gentile et al. 2009; Famaey & McGaugh 2012). These scaling relations, including the baryonic Tully-Fisher relation, the Freeman limit for stable pure disks, the universality of dark and baryonic surface densities within the halo core radius, and more generally the mass discrepancy-acceleration relation, might all require a large amount of fine-tuning for collisionless dark matter models. Surprisingly, these relations can all be summarised by the empirical formula of Milgrom (1983), which the modified Newtonian dynamics (MOND) paradigm is based on, linking the true gravitational attraction g to the Newtonian gravitational field gN (calculated from the observed distribution of visible matter) by g = (gNa0)1/2 in the limit of gN ≪ a0. The success of this formula would mean that the observed gravitational field in galaxies mimicks a universal force law generated by the baryons alone. In the case of inert, collisionless, and dissipationless dark matter, Milgrom’s law would probably precisely emerge only after an unreasonable amount of fine-tuning in the expected feedback from the baryons. The relation between the distribution of baryons and dark matter should indeed depend on the various different histories of formation, intrinsic evolution, and interaction with the environment of the various different galaxies, whereas Milgrom’s law provides a successful, unique, environment-independent, and history-independent relation. This is the strongest argument to consider MOND as a serious alternative to the current cosmological model.
in many apparently unrelated scaling relations between dark matter and baryons in galaxies (see, e.g., McGaugh 2004; Donato et al. 2009; Gentile et al. 2009; Famaey & McGaugh 2012). These scaling relations, including the baryonic Tully-Fisher relation, the Freeman limit for stable pure disks, the universality of dark and baryonic surface densities within the halo core radius, and more generally the mass discrepancy-acceleration relation, might all require a large amount of fine-tuning for collisionless dark matter models. Surprisingly, these relations can all be summarised by the empirical formula of Milgrom (1983), which the modified Newtonian dynamics (MOND) paradigm is based on, linking the true gravitational attraction g to the Newtonian gravitational field gN (calculated from the observed distribution of visible matter) by g = (gNa0)1/2 in the limit of gN ≪ a0. The success of this formula would mean that the observed gravitational field in galaxies mimicks a universal force law generated by the baryons alone. In the case of inert, collisionless, and dissipationless dark matter, Milgrom’s law would probably precisely emerge only after an unreasonable amount of fine-tuning in the expected feedback from the baryons. The relation between the distribution of baryons and dark matter should indeed depend on the various different histories of formation, intrinsic evolution, and interaction with the environment of the various different galaxies, whereas Milgrom’s law provides a successful, unique, environment-independent, and history-independent relation. This is the strongest argument to consider MOND as a serious alternative to the current cosmological model.
It is thus a fundamental prediction of MOND (and, if verified, a challenge to ΛCDM) that all galaxies should obey Milgrom’s law1 independently of their history and environment, regardless of whether they reside in large voids or dense groups. For instance, KK 246 and Holmberg II are two dwarf irregular galaxies in very different environments: KK 246 is a very isolated galaxy in the Local Void (Tully et al. 2008), while Holmberg II belongs to the M 81 group of galaxies (e.g. Karachentsev 2005; Walter et al. 2007). If MOND is correct, they should both conform to Milgrom’s law. However, the recently determined rotation curve of Holmberg II (Oh et al. 2011) seems a priori inconsistent with MOND, because Milgrom’s law severely overpredicts the observed rotation curve. The isolated galaxy KK 246, on the other hand, has a maximum velocity consistent with MOND, despite having a very high mass discrepancy: its dynamical-to-baryonic mass ratio is ≈ 15. We note that despite its many successes in terms of global scaling relations and dozens of individual galaxy rotation curves, a few galaxies indeed remain challenging for MOND (for instance NGC 3198, see Gentile et al. 2011), but none as much as the published rotation curve of Holmberg II.
Here, we re-analyse in detail the MOND rotation curves of these two galaxies. The previous analyses of KK 246 are not as detailed as the one presented here, because the whole set of data necessary to perform a mass decomposition based on the rotation curve was unavailable. On the other hand, we investigate the inclination angle of Holmberg II in detail, building model data cubes and comparing them to the observed ones, thereby showing that the previously derived inclination angle was too high, at least in the outer parts (as could also be qualitatively inferred from the axis ratio in the total HI map).
 |
Fig. 1 All the panels are based on the rotation curve of KK 246 from Kreckel et al. (2011), corrected for beam-smearing (see text for details). Panel a): asymmetric-drift corrected (full circles) and uncorrected (open circles) rotation curves of KK 246, assuming a distance of 7.8 Mpc. Panels b) − d): MOND fits of the rotation curve with distances of 9.3 Mpc (the best-fit value, which is only weakly constrained), 7.8 Mpc (Karachentsev et al. 2006), and 6.4 Mpc (Tully et al. 2008), respectively. The best-fit stellar M/L ratios (in the H-band) are 0.22, 0.98, and 1.32, respectively. The dotted line represents the Newtonian stellar contribution to the rotation curve, the dashed line is the Newtonian gas disk contribution, and the solid line is the total MOND fit. |
2. KK 246
KK 246 is a very isolated galaxy in the Local Void (Tully et al. 2008); its distance was estimated to be 7.8 ± 0.6 Mpc by Karachentsev et al. (2006) using the tip of the red giant branch (TRGB) method. However, Tully et al. (2008) claimed that, because of the reddening estimate they used, Karachentsev et al.’s might have been too high. This new reddening value brings the distance down by almost 20%, to 6.4 Mpc. We assumed a distance of 7.8 Mpc, but we also assumed an uncertainty on the distance of 20%, to include intrinsic uncertainties in the TRGB method and reddening uncertainties.
Atomic hydrogen HI data of KK 246 were presented by Kreckel et al. (2011), who analysed Very Large Array (VLA) and Expanded Very Large Array (EVLA) data. Amongst other results, they derived a rotation curve and a neutral hydrogen surface density profile. The rotation curve was derived based on tilted-ring modelling of the intensity-weighted velocity field, which is probably not the optimal way to derive the rotation curve because the velocity field is quite poorly resolved. In addition, the uncertainties in the published rotation curve are likely to be unrealistically small, as they range between 0.19 km s-1 and 0.75 km s-1. Following Sicking (1997), to account for the correlation of the data, the formal uncertainties in the tilted-ring fit were multiplied by a factor 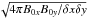 ~ 12, where B0x and B0y describe the size of the Gaussian beam,
~ 12, where B0x and B0y describe the size of the Gaussian beam, 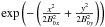 , and δx and δy are the pixel size.
, and δx and δy are the pixel size.
Since the velocity field is poorly resolved and the rotation curve was derived from the intensity-weighted mean velocity field, the innermost parts of the rotation curve are likely to be underestimated due to beam-smearing, as also qualitatively visible in the channel maps and position-velocity diagram published by Kreckel et al. (2011). We estimated the beam-smearing correction to the Kreckel et al. rotation curve by making use of the similarity between KK 246 and NGC 3741 in terms of the inclination angle and the inner rotation curve shape and amplitude. For the latter galaxy, Begum et al. (2005) derived various rotation curves by making tilted-ring models of the intensity-weighted mean velocity fields at different angular resolutions. The velocity difference between the rotation curve at the highest angular resolution and the rotation curve at the resolution comparable to the Kreckel et al. (2011) observations gave us an estimate of the beam-smearing correction, which we found to decrease from ~7 km s-1 for the innermost point to ~3 km s-1 at a radius of 90 arcsec. Keeping in mind that this is only a rough estimate, we performed the rest of the analysis on the rotation curve corrected for beam-smearing.
In small dwarf spiral galaxies such as KK 246, the rotation velocity is only a factor of a few times larger than the gas velocity dispersion. This means that the observed rotation velocity Vrot has to be corrected for pressure support (asymmetric drift). Following Bureau & Carignan (2002), we derived the corrected rotation velocity Vcor using 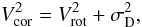 (1)where σD is the asymmetric drift correction, derived from
(1)where σD is the asymmetric drift correction, derived from 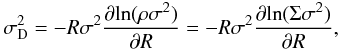 (2)assuming a constant scale-height. Here σ is the velocity dispersion, Σ is the surface density (from Kreckel et al. 2011), and ρ is the volume density.
(2)assuming a constant scale-height. Here σ is the velocity dispersion, Σ is the surface density (from Kreckel et al. 2011), and ρ is the volume density.
The derivative in Eq. (2) can have large fluctuations, thus following Oh et al. (2011) we fitted the product Σσ2 with the function 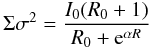 (3)where I0, R0, and α are parameters, and we assumed a constant σ of 8 km s-1. We found that the maximum correction is about 3 km s-1, as shown in Fig. 1.
(3)where I0, R0, and α are parameters, and we assumed a constant σ of 8 km s-1. We found that the maximum correction is about 3 km s-1, as shown in Fig. 1.
To make mass models based on the rotation curve, photometric data were also needed to model the contribution of the stellar disk. We used the data of Kirby et al. (2008), who presented deep H-band images of a sample of nearby galaxies (including KK 246), and the corresponding surface brightness profiles.
The asymmetric-drift corrected rotation curve Vcor was decomposed into its stellar and gaseous components, Vstars and Vgas respectively. We adopted the “simple” MOND interpolating function (Famaey & Binney 2005), which is known to best match other galaxy rotation curves (Gentile et al. 2011), finding that Vcor becomes: 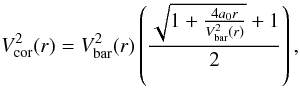 (4)where Vbar is the Newtonian baryonic contribution to the rotation curve
(4)where Vbar is the Newtonian baryonic contribution to the rotation curve 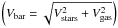 .
.
The scale-height of the gaseous disk is a difficult quantity to determine in non edge-on galaxies: for dwarf galaxies, values ranging roughly from 0.1 kpc to 0.5 kpc have been estimated (Elmegreen et al. 2001; Walter & Brinks 2001). We derived Vgas based on the HI surface density profile (corrected for primordial He) and assumed a thickness of the gaseous disk of 0.3 kpc.
The contribution of the stars, Vstars, was derived from the NIR photometric profile, assuming a sech2 distribution in the vertical direction with a scale-height of z0 = h/5, where h is the exponential scale-length (15.4 arcsec) that we derived from a fit to the photometric profile.
Kirby et al. (2008) gave a total stellar mass, which was based on the H-band absolute luminosity (5.0 × 107 L⊙) and with the assumption of a mass-to-light (M/L) ratio in the H-band of 1.0. On the basis of the B − H colour (3.16) published in Kirby et al., we found a H-band M/L ratio of 0.66, using the model of Bell & de Jong (2001). We considered the uncertainty in the M/L ratio to range from one third of 0.66 up to two times 0.66 (de Jong & Bell 2007; Bershady et al. 2011).
A MOND rotation curve fit to KK 246 is shown in Fig. 1. The distance was left as a free parameter, but it was allowed to span only the 20% uncertainty range we assumed. The best-fit distance is 9.3 Mpc and the best-fit stellar M/L ratio is at the lowest end of the permitted range (0.22). The fit is overall excellent. Because a distance of 9.3 Mpc is only marginally consistent with the distances given in Karachentsev et al. (2006) and Tully et al. (2008), we also show fits where the distance was fixed at 7.8 Mpc and 6.4 Mpc, respectively (Fig. 1), where the fit quality gets increasingly worse. For these smaller distances, the best-fit stellar M/L ratios are 0.98 for a distance of 7.8 Mpc and 1.32 (the highest end of the allowed range) for a distance of 6.4 Mpc.
Alternatively, considerations similar to Angus et al. (2012) could be made: they varied the gaseous scale-height while fitting the rotation curve of DDO 154, and found that increasing the scale-height from 0.3 kpc to 0.7 kpc reduced the χ2 by 30%. The effect of increasing the scale-height of KK 246 would mainly be to reduce the velocity of the MOND prediction at the innermost point.
Had we not applied the beam-smearing correction, but used the original Kreckel et al. (2011) rotation curve, little would have changed: the innermost point would have been slightly overestimated by the fits, the quality of the fits would have been somewhat worse and the stellar M/L ratio of the fit with a distance of 7.8 Mpc would have decreased to 0.40.
 |
Fig. 2 Left: MOND mass model of Holmberg II assuming the rotation curve presented by Oh et al. (2011). The dotted line is the contribution of the stellar disk assuming a M/L ratio in the 3.6 μm band of 0.39, the dashed line is the gas disk contribution, and the black line is the MOND prediction using a distance of 3.4 Mpc (Karachentsev et al. 2002). Right: rotation curve of Holmberg II beyond 210 arcsec. The black points and the solid line are the same as in the left panel, and the dashed line is the MOND prediction using a distance of 3.05 Mpc (Hoessel et al. 1998). The blue errorbars represent the range of outer rotation velocities derived in the present paper and for the blue open circles we assumed a velocity that is at the middle of the allowed range. |
 |
Fig. 3 Total HI map of Holmberg II. The 1.5 × 1020 atoms cm-2 contour is shown for the observations (black), the model data cube based on the parameters derived by Oh et al. (2011) (red), and the parameters derived in the present paper: the two blue lines represent the two extremes of the outer inclination range allowed by the data (20° to 35°). The FWHM beam size is 13.7 × 12.6 arcsec. |
3. Holmberg II
In contrast to the isolated galaxy KK 246, Holmberg II belongs to the M 81 group of galaxies (e.g. Karachentsev 2005; Walter et al. 2007). More precisely, Bureau & Carignan (2002) argue that it belongs to the subgroup dominated by NGC 2403, the second largest galaxy of the M 81 group.
The HI rotation curve of this galaxy, presented by Oh et al. (2011), is based on a tilted-ring fit to the “bulk velocity field”, which is a method for deriving the velocity field by separating random motions from the bulk rotation of a disk galaxy, and isolating only the latter (Oh et al. 2008). Oh et al. (2011) initially allowed all parameters to vary for each ring, to search for the best values of centre, systemic velocity, position angle, and inclination; they then performed a new tilted-ring fit with these parameters fixed to a smooth line going through the best-fit values, to look for the best rotation curve. They found a rotation curve that remains approximately flat (at a value slightly above ~30 km s-1) from 3 kpc to the last measured radius of 10 kpc, even though for the mass models they only considered data out to 7 kpc.
As also discussed by Oh et al. (2011), the inclination is a concern in Holmberg II. In their tilted-ring fit, the ring-to-ring scatter in the best-fit inclination values is quite high, and the outer inclination that they found (relatively low, roughly between 40° and 50°), raises some questions about the derived rotation curve.
We therefore investigated the inclination angle of Holmberg II in some more detail, especially in the outer parts of this galaxy. To this end, we made model data cubes and compared them to the observed ones; in particular, we compared the total HI maps, because they are most sensitive to the choice of inclination angle. We made various models with different inclinations beyond a radius of 210 arcsec (~3.5 kpc when assuming a distance of 3.4 Mpc), because this is where the discrepancy between the Oh et al. (2011) rotation curve and the one predicted by MOND, regardless of the stellar M/L ratio, becomes significant (Fig. 2). To be consistent with Oh et al., we assumed a scale-height of 0.28 kpc.
In Fig. 3, we have compared the outer contours of the observed total HI map with three models. The comparison shows that the parameters derived by Oh et al. (2011) do not match the data well, and that their outer inclination angle is too high. In contrast, a range of outer inclinations between 20° and 35° that are consistent with the one (~25°) based on the baryonic Tully-Fisher relation, provides a closer match to the observed total HI map. We also shifted the position of the centre by ~25 arcsec (about two beam FWHM) towards the NE and we slightly changed the outer position angle to match the outer contours of the total HI map. The better match of the present model is also due to a different position angle around a radius of 6 arcmin, which is likely to be caused by a non-circular component in the velocity that causes a shift between the kinematical and morphological position angles. However, owing to the irregular shape of the total HI emission in the innermost part (and, to a lesser extent, in the outermost parts), an accurate determination of the radial dependence of the morphological position angle is unfeasible.
Correcting the (asymmetric-drift corrected) observed rotation curve for an outer inclination between 20° and 35° gives an outer rotation velocity range between 40 km s-1 and 75 km s-1 (Fig. 2). As errorbars, we considered the squared sum of (1) the original uncertainty given by Oh et al. (2011), corrected for the inclination; and (2) the difference between the velocity using an inclination of 20° and the velocity using an inclination of 35°. This implies that, including these systematic errors in the inclination angle, the outer rotation curve is compatible with both the MOND prediction and the baryonic Tully-Fisher relation. We compared the MOND prediction using two accurate derivations of the distance: 3.05 Mpc by Hoessel et al. (1998) using Cepheids, and 3.4 Mpc by Karachentsev et al. (2002) using the tip of the red giant branch method. Figure 2 shows that with the new inclination angles in the outer part, the rotation curve of Holmberg II is consistent with the MOND prediction using both estimates of the distance. A reliable derivation of the inclination variation over the full range of radii is a very challenging task, because in such a low-inclination dwarf spiral galaxy the shape of the HI emission in both the single channel maps and the total HI map at smaller radii is dominated by shells and holes, thus it goes beyond the goal of the present paper. We note that the errorbars in a rotation curve that includes systematic errors in the inclination are larger than the point-to-point scatter, but reflect the true uncertainty in each velocity point. Additionally, if we assume that there is an extreme flare in the outer parts, increasing the scale-height up to 1 kpc, the inclination range changes to 22° − 39°, and the corresponding velocity range changes to 36 − 68 km s-1, which is still consistent (though marginally) with the MOND prediction.
4. Conclusions
We have investigated the kinematics of two dwarf spiral galaxies within the framework of MOND. These two galaxies are in very different environments: KK 246 is in the Local Void (Tully et al. 2008), whereas Holmberg II is a member of the M 81 group of galaxies (Karachentsev 2005; Walter et al. 2007).
For KK 246, we used the HI rotation curve presented in Kreckel et al. (2011) and the H-band photometry obtained by Kirby et al. (2008). We have found that, although the best-fit distance is slightly large, within its uncertainties and those of the stellar M/L ratio, the observed rotation curve is consistent with the MOND prediction.
The other galaxy, Holmberg II, is at first sight inconsistent with MOND, using the rotation curve of Oh et al. (2011). However, after modelling the HI data cube and comparing the observed and modelled total HI maps, we found that the inclination angle in the outer parts had been overestimated. The inclination angle is indeed closer to face-on than had previously been determined. This results in a rotation curve with a higher amplitude and a larger uncertainty; this new rotation curve is compatible with the MOND prediction. In addition, with the new inclination, Holmberg II now falls on the baryonic Tully-Fisher relation (its baryonic Tully-Fisher velocity is ~65 km s-1). It is clear that the limited resolution of the observations, and the inherent uncertainties in the geometrical parameters of these galaxies limits their application to either the confirmation or falsification of dark matter or alternative theories. Further decreasing systematic uncertainties
in the determination of rotation curves of dwarf galaxies residing in different environments will thus be very useful in the future in testing the MOND paradigm more rigourously in the realm where it is supposed to work best.
Modulo a possible effect of a strong gravitational field environment, known as the external field effect, and with some dependence on the assumed “interpolating function” between the Newtonian regime aN and MONDian regime g = (gNa0)1/2 (see, e.g., Famaey & McGaugh 2012).
Acknowledgments
We thank the referee for useful comments that improved the quality of this paper. G.G. is a postdoctoral researcher of the FWO-Vlaanderen (Belgium). B.F. acknowledges the support of the AvH foundation. Some of SHO research was carried at the “Centre for All-sky Astrophysics”, which is an Australian Research Council Centre of Excellence, funded by grant CE11E0090.
References
- Angus, G. W., van der Heyden, K., Famaey, B., et al. 2012, MNRAS, 421, 2598 [NASA ADS] [CrossRef] [Google Scholar]
- Bell, E. F., & de Jong, R. S. 2001, ApJ, 550, 212 [NASA ADS] [CrossRef] [Google Scholar]
- Begum, A., Chengalur, J. N., & Karachentsev, I. D. 2005, A&A, 433, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bershady, M. A., Martinsson, T. P. K., Verheijen, M. A. W., et al. 2011, ApJ, 739, L47 [NASA ADS] [CrossRef] [Google Scholar]
- Bureau, M., & Carignan, C. 2002, AJ, 123, 1316 [NASA ADS] [CrossRef] [Google Scholar]
- de Jong, R. S., & Bell, E. F. 2007, Island Universes – Structure and Evolution of Disk Galaxies, 107 [Google Scholar]
- Donato, F., Gentile, G., Salucci, P., et al. 2009, MNRAS, 397, 1169 [NASA ADS] [CrossRef] [Google Scholar]
- Elmegreen, B. G., Kim, S., & Staveley-Smith, L. 2001, ApJ, 548, 749 [NASA ADS] [CrossRef] [Google Scholar]
- Famaey, B., & Binney, J. 2005, MNRAS, 363, 603 [NASA ADS] [CrossRef] [Google Scholar]
- Famaey, B., & McGaugh, S. 2012, Liv. Rev. Relativ. [arXiv:1112.3960] [Google Scholar]
- Gentile, G., Famaey, B., Zhao, H., & Salucci, P. 2009, Nature, 461, 627 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Gentile, G., Famaey, B., & de Blok, W. J. G. 2011, A&A, 527, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hoessel, J. G., Saha, A., & Danielson, G. E. 1998, AJ, 115, 573 [NASA ADS] [CrossRef] [Google Scholar]
- Karachentsev, I. D. 2005, AJ, 129, 178 [NASA ADS] [CrossRef] [Google Scholar]
- Karachentsev, I. D., Dolphin, A. E., Geisler, D., et al. 2002, A&A, 383, 125 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Karachentsev, I. D., Dolphin, A., Tully, R. B., et al. 2006, AJ, 131, 1361 [NASA ADS] [CrossRef] [Google Scholar]
- Kirby, E. M., Jerjen, H., Ryder, S. D., & Driver, S. P. 2008, AJ, 136, 1866 [NASA ADS] [CrossRef] [Google Scholar]
- Kreckel, K., Peebles, P. J. E., van Gorkom, J. H., van de Weygaert, R., & van der Hulst, J. M. 2011, AJ, 141, 204 [NASA ADS] [CrossRef] [Google Scholar]
- Kregel, M., van der Kruit, P. C., & de Grijs, R. 2002, MNRAS, 334, 646 [NASA ADS] [CrossRef] [Google Scholar]
- McGaugh, S. S. 2004, ApJ, 609, 652 [NASA ADS] [CrossRef] [Google Scholar]
- Milgrom, M. 1983, ApJ, 270, 365 [NASA ADS] [CrossRef] [Google Scholar]
- Oh, S.-H., de Blok, W. J. G., Walter, F., Brinks, E., & Kennicutt, R. C., Jr. 2008, AJ, 136, 2761 [NASA ADS] [CrossRef] [Google Scholar]
- Oh, S.-H., de Blok, W. J. G., Brinks, E., Walter, F., & Kennicutt, R. C., Jr.. 2011, AJ, 141, 193 [NASA ADS] [CrossRef] [Google Scholar]
- Sicking, F. J. 1997, Ph.D. Thesis, University of Groningen [Google Scholar]
- Tully, R. B., Shaya, E. J., Karachentsev, I. D., et al. 2008, ApJ, 676, 184 [NASA ADS] [CrossRef] [Google Scholar]
- Walter, F., & Brinks, E. 2001, AJ, 121, 3026 [NASA ADS] [CrossRef] [Google Scholar]
- Walter, F., Cannon, J. M., Roussel, H., et al. 2007, ApJ, 661, 102 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1 All the panels are based on the rotation curve of KK 246 from Kreckel et al. (2011), corrected for beam-smearing (see text for details). Panel a): asymmetric-drift corrected (full circles) and uncorrected (open circles) rotation curves of KK 246, assuming a distance of 7.8 Mpc. Panels b) − d): MOND fits of the rotation curve with distances of 9.3 Mpc (the best-fit value, which is only weakly constrained), 7.8 Mpc (Karachentsev et al. 2006), and 6.4 Mpc (Tully et al. 2008), respectively. The best-fit stellar M/L ratios (in the H-band) are 0.22, 0.98, and 1.32, respectively. The dotted line represents the Newtonian stellar contribution to the rotation curve, the dashed line is the Newtonian gas disk contribution, and the solid line is the total MOND fit. |
| In the text | |
 |
Fig. 2 Left: MOND mass model of Holmberg II assuming the rotation curve presented by Oh et al. (2011). The dotted line is the contribution of the stellar disk assuming a M/L ratio in the 3.6 μm band of 0.39, the dashed line is the gas disk contribution, and the black line is the MOND prediction using a distance of 3.4 Mpc (Karachentsev et al. 2002). Right: rotation curve of Holmberg II beyond 210 arcsec. The black points and the solid line are the same as in the left panel, and the dashed line is the MOND prediction using a distance of 3.05 Mpc (Hoessel et al. 1998). The blue errorbars represent the range of outer rotation velocities derived in the present paper and for the blue open circles we assumed a velocity that is at the middle of the allowed range. |
| In the text | |
 |
Fig. 3 Total HI map of Holmberg II. The 1.5 × 1020 atoms cm-2 contour is shown for the observations (black), the model data cube based on the parameters derived by Oh et al. (2011) (red), and the parameters derived in the present paper: the two blue lines represent the two extremes of the outer inclination range allowed by the data (20° to 35°). The FWHM beam size is 13.7 × 12.6 arcsec. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


