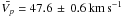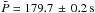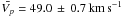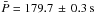© ESO, 2012

1. Introduction

Propagating extreme ultraviolet (EUV) intensity disturbances were discovered in the solar polar plumes (Deforest & Gurman 1998) and coronal loops (Berghmans & Clette 1999) with the Extreme ultraviolet Imaging Telescope (EIT) onboard SOlar and Heliospheric Observatory (SOHO). The follow-up studies (e.g. Ofman et al. 1999; De Moortel et al. 2000, 2002b,a; Robbrecht et al. 2001; King et al. 2003; Marsh et al. 2003; De Moortel 2009) were carried out with or in combination with the Transition Region and Coronal Explorer (TRACE, see Handy et al. 1999), which observed a part of the Sun with a better resolution, 0.5 arcsec/pixel in contrast to the 2.6 arcsec/pixel of SOHO/EIT. The propagating speeds, observed as the apparent speed projected to the image plane perpendicular to the line-of-sight (LOS) of the imagers, were normally found to be lower than the local sound speed (which can be estimated as ≃ $\mathrm{152}\sqrt{\mathit{T}\mathrm{\left[}\mathrm{MK}\mathrm{\right]}}\mathrm{\approx }\mathrm{150}\mathrm{-}\mathrm{260}\hspace{0.17em}\mathrm{km}\hspace{0.17em}{\mathrm{s}}^{-1}$ for the temperature T from 1 MK to 3 MK). A stereoscopic observation with the Extreme Ultraviolet Imager (EUVI, A and B) on Solar TErrestrial RElations Observatory (STEREO) revealed that the phase speed was well consistent with the sound speed inferred from the temperature measure (Marsh et al. 2009). The propagating EUV disturbances are usually interpreted as propagating slow magnetoacoustic waves (Nakariakov et al. 2000; De Moortel 2006; Verwichte et al. 2010). Its wave nature was additionally confirmed by joint observations of intensity (density) and Doppler shift (velocity) oscillations with the EUV Imaging Spectrometer (EIS) on Hinode (Wang et al. 2009a,b; Mariska & Muglach 2010).

The amplitude of propagating EUV disturbances is normally found to be ~1−10% of the background intensity (De Moortel et al. 2002b). The low-amplitude disturbances were found to be satisfactorily modelled in the linear approximation (Nakariakov et al. 2000). The amplitude is observed to damp very quickly, typically within 2.9−23.3 Mm (1−2 visible wave fronts) along the wave path (De Moortel et al. 2002b). Thermal conduction appears to be the dominant damping mechanism (De Moortel & Hood 2003; Ofman & Wang 2002; Klimchuk et al. 2004). The energy flux carried by the EUV propagating disturbances was estimated to be far too insufficient to contribute significantly to coronal heating (Ofman et al. 2000; De Moortel et al. 2002b).

Propagating EUV disturbances are usually quasi-monochromatic with the periods categorised into two classes: the short period (~3−5 min, see De Moortel et al. 2000, 2002b,a; De Moortel 2009; King et al. 2003; Marsh et al. 2003; Wang et al. 2009a) and long period (~10−30 min, see Berghmans & Clette 1999; McIntosh et al. 2008; Marsh et al. 2009; Wang et al. 2009b; Yuan et al. 2011). De Moortel et al. (2002b) found statistically that the 3-min oscillations are more likely to be detected above sunspot regions, while the 5-min oscillations are usually found off the sunspots (e.g. above the plage region). This feature suggests the likely association of the coronal propagating disturbances with chromospheric 3-min oscillations and the photospheric 5-min oscillations, respectively. Chromospheric 3-min oscillations were found to leak from sunspot umbrae to the corona (Shibasaki 2001; Sych et al. 2009; Botha et al. 2011). Photospheric 5-min oscillations in plage regions are apt to be wave-guided to the corona by inclined magnetic field lines (Bel & Leroy 1977), and could be associated with the leakage of global p-modes from the photosphere (De Pontieu et al. 2005). Long-period oscillations are detected often in the corona as well, but the possible source remains poorly understood (see discussions in Yuan et al. 2011).

There are also observations of cases with multiple periods (Mariska & Muglach 2010; Wang et al. 2009b). Wang et al. (2009b) detected two harmonics in 12 and 25 min with EIS/Hinode and found that the detection length (70 − 90 Mm) of the long-period oscillations are much longer than previous TRACE studies (e.g. De Moortel et al. 2002b). This result is in agreement with the period-dependency of the damping length of slow magnetoacoustic wave decaying due to thermal conduction mechanism.

The apparent phase speed was measured at tens to hundreds of km s^-1 (De Moortel et al. 2002b; De Moortel 2009). The spread of the measured speeds is usually attributed to the variation of the angle between the propagating direction and image plane in different cases. Robbrecht et al. (2001) reported that the phase speeds of propagating disturbances measured in TRACE 171 Å (1 MK) are normally lower than those measured in EIT 195 Å (1.6 MK). The temperature-dependence of the phase speed was recently found in polar plumes and the interplume medium with AIA (Krishna Prasad et al. 2011). In some cases, acceleration of the disturbances was detected at larger heights (typically above ~20 Mm, see Banerjee et al. 2011, for a review).

Although joint imaging and spectroscopic investigations revealed that in the coronal propagating disturbances the Doppler shift is in phase with the intensity variations (Wang et al. 2009a,b; Mariska & Muglach 2010) (which is consistent with the slow magnetoacoustic wave theory, see Nakariakov et al. 2000; Tsiklauri & Nakariakov 2001), in recent studies, the observed blue-wing asymmetry in the emission spectral lines at the footpoints of coronal fan structure was interpreted in terms of periodic upflows (e.g. Doschek et al. 2007, 2008; Sakao et al. 2007; Del Zanna 2008; Harra et al. 2008; Hara et al. 2008; De Pontieu & McIntosh 2010; Tian et al. 2011a,b; Martínez-Sykora et al. 2011). A single Gaussian fit to the spectral lines suggest that the flow speed is about ~ 10 km s^-1, much less than the observed apparent speed of propagating disturbances. Tian et al. (2011b) implemented a guided double-Gaussian fit to the spectral lines and found that the emission-line width could be associated with two components. The secondary component contributes a few percent of the total emission, its blueward asymmetry is associated with flows of speed of 50−150 km s^-1. The faint secondary component modulates the peak intensity, line centroid and line width quasi-periodically, therefore propagating disturbances can be observed consistently (De Pontieu & McIntosh 2010; Tian et al. 2011b). A similarity was reported between the spatial distribution of flow speed observed with Hinode/EIS and the temporal distribution of the speed of propagating disturbances observed with SDO/AIA (Tian et al. 2011b). On the other hand, the blue-wing asymmetry was found to be an intrinsic feature of upward propagating slow magnetoacoustic waves (Verwichte et al. 2010).

The typical method for studying coronal propagating disturbances is the so-called time-distance plot. In each image, a cut is taken following the direction of propagation, F(x_i,y_j,t_k), where x_i and y_j are the image pixel coordinates, t_k is the time frame index. The time-distance array C(s_m,t_k), where s_m is the index along the cut, is made by stacking the cuts in order of time. Propagating disturbances of the emission intensity are featured by diagonal ridges in the plot of the time-distance array (a time-distance plot). The visibility of the ridges is normally fairly poor, since EUV disturbances are weak, normally ≲ 10% of the background intensity, and of the same order of magnitude with the data noise. A simple and well-implemented technique, the running difference, can be applied to a time-distance plot to enhance the contrast (visibility) of the propagating disturbances. The running difference is obtained by subtracting from the cut C(s_m,t_k) the value of another cut C(s_m,t_k − l) taken in the lth image ahead of the current one R(s_m,t_k) = C(s_m,t_k) − C(s_m,t_k − l). The slope of the ridges in the running distances relative to the time axis is the apparent (projected) phase speed of the propagating disturbances. Another way to enhance the visibility is to remove the quasi-static background from the image, and normalise the residue with it. The background can be obtained by temporal averaging

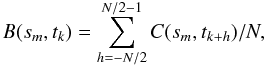$\mathit{B}\mathrm{\left(}{\mathit{s}}_{\mathit{m}}\mathit{,}{\mathit{t}}_{\mathit{k}}\mathrm{\right)}\mathrm{=}\sum _{\mathit{h}\mathrm{=}\mathrm{-}\mathit{N}\mathit{/}\mathrm{2}}^{\mathit{N}\mathit{/}\mathrm{2}\mathrm{-}\mathrm{1}}\mathit{C}\mathrm{\left(}{\mathit{s}}_{\mathit{m}}\mathit{,}{\mathit{t}}_{\mathit{k}\mathrm{+}\mathit{h}}\mathrm{\right)}\mathit{/}\mathit{N,}$where N is the number of time frames. Thus, a time-distance array with background-removal and normalisation is obtained by D(s_m,t_k) = [C(s_m,t_k) − B(s_m,t_k)] /B(s_m,t_k). We refer generally hereafter to the enhanced time-distance plot X(s_m,t_k) as either the time-distance array made by the running difference R(s_m,t_k) or the background-subtracted and normalised array D(s_m,t_k).

Although a number of measurements were made on the phase speed (see De Moortel et al. 2002b,a; De Moortel 2009), no method was designed to quantify and standardise the measurement, to remove human-based bias and to make the measurements consistently comparable. The aim of this paper is to design rigorous methods for measuring the apparent phase speed of propagating disturbances in coronal imaging data, and compare their performance by the analysis of coronal propagating disturbances observed with AIA.

We describe the data pre-processing and the observation dataset in Sect. 2; the image flux error analysis is given in Sect. 3; the methods for phase speed measurement are detailed in Sect. 4; the results are summarised in Sect. 5; the conclusion is made in Sect. 6.

2. Dataset

2.1. Instrument

The Atmospheric Imaging Assembly (AIA, Lemen et al. 2011) onboard the Solar Dynamics Observatory provides continuous observations of the Sun since 2010 March 29. It images the full solar disk with 4k × 4k detectors with a resolution of 0.6 arcsec/pixel. A short cadence time (~12 s) can be sustained during most of its mission. The Sun is imaged in 10 different narrow-band channels, seven of which are in EUV bandpasses: Fe xviii (94 Å), Fe viii, xxi (131 Å), Fe ix (171 Å), Fe xii, xxiv (193 Å), Fe xiv (211 Å), He ii (304 Å), Fe xvi (335 Å). The observed temperature in EUV bands ranges from ~0.6 MK to ~16 MK, and which covers the upper transition region, quiet corona, active-region corona, and flaring regions quite well.

The AIA data are stored in the level 0 format, as the raw telemetric data compressed with the Rice algorithm. The level 1 data are obtained from level 0 (Lemen et al. 2011). In level 1 data, the digital offset of the camera, CCD readout noise and dark current are removed, a flat-field correction is applied, then the permanent bad pixels, much less than 0.1%, are detected and replaced with interpolated values from neighbouring pixels. The spikes due to energetic particles are removed with the algorithm adopted from the TRACE (Handy et al. 1999) program.

We useed level 1.5 data prepared with the subroutine aia_prep.pro (Version 4.11, status 2011-06-14) of SolarSoft. The images were normalised to their exposure time. A small residual roll angle between the four AIA telescopes was removed from the images. The plate scale size of the AIA images was adjusted to exactly 0.6 arcsec/pixel. Boresighting was co-aligned by adjusting the secondary mirror offset on-orbit, and the residual differences were removed by interpolating the images onto a pixel coordinate aligned with the solar centre (Lemen et al. 2011).

2.2. Observations

We used the observation dataset over a very quiescent active region (NOAA 11330) in the 171 Å bandpass at 04:00 − 08:00 UT on 27 Oct. 2011. No flare occurred during the observation time interval that the active region was gradually approaching the centre of the solar disk. The leading eastern part of the active region formed a fan-like feature (see Fig. 1a) that consisted of both closed and open plasma structures. Continuous propagating EUV disturbances were observed following the fan-like feature.

Fig. 1 a) AIA 171 Å image of active region NOAA 11330 observed on 27 Oct. 2011 at 04:30:01 UT is shown with the flux on the logarithmic scale. A cut that was taken to make the time-distance plot is indicated with a black bar. b) The running difference R1 of the time-distance plot started at 04:30:01 UT. R2 is the first half of R1, to the left of the white dashed line. It covers about 10 cycles of the propagating features. Panel c) shows the background-subtracted time-distance plot D1. The first half of D1 on the left of the white dashed line is D2.

A four-hour dataset was downloaded as a cutout data of level 1 and prepared into level 1.5 as described in Sect. 2.1. A typical image is displayed in Fig. 1. The cadence time was very uniform, 12.000 ± 0.006 s, the exposure time was 1.9996052 ± 0.0000038 s, the total number of images in 171 Å was 1200. We truncated the size of the dataset into an array F(x_i,y_j,t_k), a set of 1200 images of 100 × 100 pixels, so that the fan-like structure becomes the only prominent morphological feature in the images. The images were corrected for the solar differential rotation and further co-aligned with the offsets calculated by 2D cross-correlation. The morphology of the images did not change much during the observations, either geometrically (shape) or photometrically (intensity), so the co-alignment reached a fairly good accuracy of sub-pixel.

Propagating EUV disturbances are visible along most of the strands in the fan that extends from the footpoint. We took a cut (41 pixels, ~17.7 Mm) in every image starting from the foot point and following the coronal structure extended from the west to the east (see Fig. 1). The intensity of each pixel in each image was averaged over three pixels in the vertical direction. The running difference was made with R(s_m,t_k) = C(s_m,t_k) − C(s_m,t_k − 9) (T_lag = t_k − t_k − 9 = 9 × 12 = 108 s). The running difference plot is shown in Fig. 1b. The background-subtracted normalised time-distance plot D(s_m,t_k) was obtained by estimating the background with N = 50 smoothing (T_detr = 50 × 12 = 10 min) and is illustrated in Fig. 1c. The propagating EUV disturbances are featured by the repeating diagonal ridges in the time-distance plot (~10 cycles during a 30-min observation). The EUV disturbances are gradually damped with height (or are buried in noise) after ~17.7 Mm along the slit. The gradient of the ridges relative to the time axis is the phase speed of EUV disturbances, projected to the image plane perpendicular to the LOS. The typical observables and physical parameters of the propagating disturbances are summarised in Table 1.

We measured the average apparent speed in the enhanced time-distance plot X(s_m,t_k) with either a full (41 pixels, both the prominent part and relatively noisier part) set of pixels or its lower half (20 pixels, only the prominent part), see Fig. 1b. We prepared the enhanced time-distance plots of two sizes 41 × 150 and 20 × 150 pixels (referred to hereafter as R₁ and R₂, consequently, and R for running difference, either R₁ or R₂; D₁, D₂ and D are their analogues taken from the background-subtracted and normalised time-distance plot). R₂ (D₂) is the first half of R₁ (D₁) between 0 and 8.6 Mm along the slit, see Fig. 1a. The quality of X(s_m,t_k) is quantified by two parameters: the amplitude ratio of the propagating waves and the data noise ⟨A_w⟩/⟨A_n⟩, and the amplitude ratio of the propagating waves and the background intensity ⟨A_w⟩/⟨A_b⟩. The amplitude is defined as the root mean square (rms), 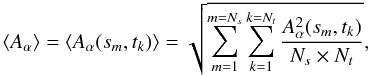$⟨{\mathit{A}}_{\mathit{\alpha }}⟩\mathrm{=}\mathrm{⟨}{\mathit{A}}_{\mathit{\alpha }}\mathrm{\left(}{\mathit{s}}_{\mathit{m}}\mathit{,}{\mathit{t}}_{\mathit{k}}\mathrm{\right)}\mathrm{⟩}\mathrm{=}\sqrt{\sum _{\mathit{m}\mathrm{=}\mathrm{1}}^{\mathit{m}\mathrm{=}{\mathit{N}}_{\mathit{s}}}\sum _{\mathit{k}\mathrm{=}\mathrm{1}}^{\mathit{k}\mathrm{=}{\mathit{N}}_{\mathit{t}}}\frac{{\mathit{A}}_{\mathit{\alpha }}^{\mathrm{2}}\mathrm{\left(}{\mathit{s}}_{\mathit{m}}\mathit{,}{\mathit{t}}_{\mathit{k}}\mathrm{\right)}}{{\mathit{N}}_{\mathit{s}}\mathrm{\times }{\mathit{N}}_{\mathit{t}}}}\mathit{,}$(1)where α is w, n or b for the wave, noise and background amplitude, respectively. s_m and t_k are the indices along the s and t axes, respectively. N_s and N_t are the total numbers of pixels along the axes. N_s = 41 or 20 for R₁ (D₁) and R₂ (D₂), respectively, and N_t = 150 for both of them. The array A_w is defined as A_w(s_m,t_k) = X(s_m,t_k), and A_n(s_m,t_k) = σ(X(s_m,t_k)) is the data noise of X(s_m,t_k) and is discussed in Sect. 3. A_b(s_m,t_k) = B(s_m,t_k) is the background amplitude. The ratios ⟨A_w⟩/⟨A_n⟩ are 3.3 (4.9) and 3.5 (6.9), and ⟨A_w⟩/⟨A_b⟩ are 0.0145 (0.0169) and 0.0145 (0.0207), for R₁ (D₁) and R₂ (D₂), respectively.

3. Flux error analysis

3.1. AIA image noise

Although AIA outperforms TRACE (Handy et al. 1999) in FOV, cadence time and the number of observing channels, it resembles TRACE in most aspects, and many of the calibration and data preparation routines are adopted from the TRACE programme (Sect. 2.1). We followed the study of Aschwanden et al. (2000) on TRACE and analysed the noise in the 171 Å image flux. Data obtained in other EUV/UV channels can be analysed similarly.

In the data calibration, we neglected the uncertainties introduced by preparing the data from level 1 to 1.5, namely the errors accompanying the roll angle rotation and plate scale resizing, because the data processing is irreversible and untraceable (detached from CCD pixels). Therefore the data noise was analysed by assuming the data are of level 1 (connected to the CCD pixels). For a pixel flux value F, we combined the uncertainties generated from all the steps in units of data numbers (DN), accumulated over a fixed exposure time of 2 s, the photon Poisson noise, electronic readout noise, digitisation noise, compression noise, dark current noise, subtraction noise, and the noise due to removal of spikes in the images (Aschwanden et al. 2000): 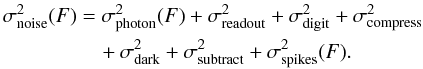$\begin{array}{}\begin{array}{}\end{array}\begin{array}{}\begin{array}{}\end{array}{\mathit{\sigma }}_{\mathrm{noise}}^{\mathrm{2}}\mathrm{\left(}\mathit{F}\mathrm{\right)}\mathrm{=}{\mathit{\sigma }}_{\mathrm{photon}}^{\mathrm{2}}\mathrm{\left(}\mathit{F}\mathrm{\right)}\mathrm{+}{\mathit{\sigma }}_{\mathrm{readout}}^{\mathrm{2}}\mathrm{+}{\mathit{\sigma }}_{\mathrm{digit}}^{\mathrm{2}}\mathrm{+}{\mathit{\sigma }}_{\mathrm{compress}}^{\mathrm{2}}\begin{array}{}\end{array} \mathrm{+}{\mathit{\sigma }}_{\mathrm{dark}}^{\mathrm{2}}\mathrm{+}{\mathit{\sigma }}_{\mathrm{subtract}}^{\mathrm{2}}\mathrm{+}{\mathit{\sigma }}_{\mathrm{spikes}}^{\mathrm{2}}\mathrm{\left(}\mathit{F}\mathrm{\right)}\mathit{.}\end{array}\begin{array}{}\end{array}\end{array}$(2)We first examine the photon statistics. The image flux in units of DN was translated from the charge readout from each pixel through an analog-to-digital converter (ADC). The camera gain (G_λ in   e/DN) is defined as the number of electrons acquired in the detector to generate a unit DN read in the image pixel, it is a telescope (bandpass λ) specific parameter (Boerner et al. 2012, Table 6). The electrons are accumulated in the detector and follow Poisson statistics, thus for a pixel flux F in the image in bandpass λ, FG_λ electrons are detected with an uncertainty of 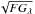$\sqrt{\mathit{F}{\mathit{G}}_{\mathit{\lambda }}}$, so the photon noise in F is $\sqrt{\mathit{F}{\mathit{G}}_{\mathit{\lambda }}}\mathit{/}{\mathit{G}}_{\mathit{\lambda }}\mathrm{=}\sqrt{\mathit{F}\mathit{/}{\mathit{G}}_{\mathit{\lambda }}}$.

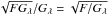The intrinsic trait of CCD is the readout noise that is inevitable in all applications. The readout noise in AIA CCDs is ≈ 20 − 22 e = 1.1 − 1.2 DN. For the 171 Å images, it is constant σ_readout = 1.15 DN (Boerner et al. 2012).

The rounding of the ADC signal into integer introduces a maximum uncertainty of σ_digit = 0.5 DN (Aschwanden et al. 2000).

Fig. 2 Data noise σnoise(F) (+) in Eq. (3) as a function of pixel flux F in AIA 171 Å images. The components caused by the photon noise, compression, despiking and other reasons are plotted with ⋄ , △ , □, respectively.

The AIA images implement the Rice compression algorithm, a lossless compression. A look-up table was used with the bin size proportional to the pixel value (Boerner et al. 2012), thus we assume the noise σ_compress = 0.25σ_photon as suggested in Boerner (2011, priv. comm.). The TRACE images deployed the jpeg data compression algorithm, a lossy compression algorithm. The average noise caused by the compression for the entire image was estimated as σ_compress ≲ 0.1 DN (Aschwanden et al. 2000). The compression noise for TRACE was underestimated.

The noise caused by the dark current is quite low. In the current AIA operation, the seasonal variation has not be corrected yet, and we assumed a half digit noise level σ_dark = 0.5 DN (Boerner 2011, priv. comm.).

Subtracting the dark current, as well as the background variation, in integer DN in the data processing from level 0 to level 1, adds two additional digitisation errors, 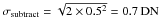${\mathit{\sigma }}_{\mathrm{subtract}}\mathrm{=}\sqrt{\mathrm{2}\mathrm{\times }{\mathrm{0.5}}^{\mathrm{2}}}\mathrm{=}\mathrm{0.7}\hspace{0.17em}\mathrm{DN}$ (Aschwanden et al. 2000).

The despiking algorithm for AIA images was directly adopted from the TRACE programme (Lemen et al. 2011), so the uncertainty analysis is transferable as well. In the deep cleaning algorithm (Aschwanden et al. 2000), if a pixel value is above q_thresh = 1.15 times its local median value (defined by the nearest eight neighbours around the spiky pixel), it would be replaced with the local median, three iterations were applied to the images. A residue of σ_spikes(F) = F(q_thresh − 1) = 0.15F was generated in the spiky pixel and its nearest four neighbours (Aschwanden et al. 2000). In Aschwanden et al. (2000), an uncertainty of σ_spikes(F) = 0.15F was assigned to each pixel empirically. In AIA images, about 10⁴ pixels out of 4k × 4k are normally hit by energetic particles in quiet Sun condition (Boerner 2011, priv. comm.). As an upper limit, therefore we assumed that about 10⁵ pixels (0.6%) are affected, and estimated σ_spike(F) = 0.006 × 0.15F = 0.0009F for the entire image.

Then we summarised the above estimations, the data noise for a signal pixel with the flux value F in the 171 Å images is 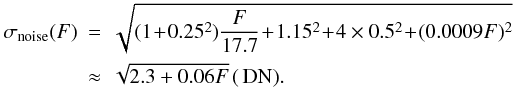$\begin{array}{ccc}{\mathit{\sigma }}_{\mathrm{noise}}\mathrm{\left(}\mathit{F}\mathrm{\right)}& \mathrm{=}& \sqrt{\mathrm{(}\mathrm{1}\mathrm{+}{\mathrm{0.25}}^{\mathrm{2}}\mathrm{)}\frac{\mathit{F}}{\mathrm{17.7}}\mathrm{+}{\mathrm{1.15}}^{\mathrm{2}}\mathrm{+}\mathrm{4}\mathrm{\times }{\mathrm{0.5}}^{\mathrm{2}}\mathrm{+}\mathrm{(}\mathrm{0.0009}\mathit{F}{\mathrm{)}}^{\mathrm{2}}}\\ & \mathrm{\approx }& \sqrt{\mathrm{2.3}\mathrm{+}\mathrm{0.06}\mathit{F}}\hspace{0.17em}\mathrm{\left(}\hspace{0.17em}\mathrm{DN}\mathrm{\right)}\mathit{.}\end{array}$(3)The data noises of different origin in the 171 Å bandpass are plotted in Fig. 2 as a function of the image flux F. The photon noise is comparable to the other noises, caued by readout and dark current extraction and compression, at lower flux value F, and become the dominant noise at the flux value of hundreds and over. The despiking noise is practically negligible, but could become significant during a flare.

3.2. Uncertainties in the enhanced time-distance plot

The time-distance plot was taken by averaging over three pixels across the slit, therefore the data noise as in Eq. (3) should be scaled by a factor of 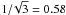$\mathrm{1}\mathit{/}\sqrt{\mathrm{3}}\mathrm{=}\mathrm{0.58}$. The running difference was generated by R(s_m,t_k) = C(s_m,t_k) − C(s_m,t_k − 9). We assumed the images were taken independently, there was no data noise correlation along the time sequence. For a value in the running difference plot, the uncertainty is estimated as 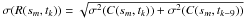$\mathit{\sigma }\mathrm{\left(}\mathit{R}\mathrm{\right(}{\mathit{s}}_{\mathit{m}}\mathit{,}{\mathit{t}}_{\mathit{k}}\mathrm{\left)}\mathrm{\right)}\mathrm{=}\sqrt{{\mathit{\sigma }}^{\mathrm{2}}\mathrm{\left(}\mathit{C}\mathrm{\right(}{\mathit{s}}_{\mathit{m}}\mathit{,}{\mathit{t}}_{\mathit{k}}\mathrm{\left)}\mathrm{\right)}\mathrm{+}{\mathit{\sigma }}^{\mathrm{2}}\mathrm{\left(}\mathit{C}\mathrm{\right(}{\mathit{s}}_{\mathit{m}}\mathit{,}{\mathit{t}}_{\mathit{k}\mathrm{-}\mathrm{9}}\mathrm{\left)}\mathrm{\right)}}$. The noise amplitude in the running difference plot can be estimated with Eq. (1). On average, it is ~ 0.4% of the background intensity and ~ 30% of the amplitude of the propagating disturbances.

The background is constructed by averaging over N = 50 points. The uncertainty in B(s_m,t_k) is 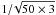$\mathrm{1}\mathit{/}\sqrt{\mathrm{50}\mathrm{\times }\mathrm{3}}$ of a normal flux value, and hence is neglected. Thus σ(D(s_m,t_k)) = σ(C(s_m,t_k))/B(s_m,t_k). It is ~0.3% of the background intensity and ~20% of the disturbance amplitude.

4. The measurement of the apparent phase speed

In the analysed dataset, propagating disturbances are seen at distances of less than ~20 Mm. Also, the apparent propagation speed appears constant at these distances. It is consistent with previous observations of this phenomenon, which showed that any noticeable speed variation can appear at larger heights only (Robbrecht et al. 2001; Gupta et al. 2010). No other periodicities, except 3-min oscillations, are found in the power spectrum of the time signal. We designed three methods for measuring the apparent speed of propagating disturbances, taking the observed fact that the phase speed in the sample does not change either with time or spatial location along the cut. Accordingly, we approximated the propagating disturbances with a propagating harmonic wave function Acos(ωt − kx + φ), with constant parameters A, ω, k and φ, which is the key element in the three methods:

• cross-fitting technique (CFT, Sect. 4.1);

• 2D coupled fitting (DCF, Sect. 4.2);

• best similarity match (BSM, Sect. 4.3).

4.1. Cross-fitting technique

We assumed that the enhanced time-distance plot X(s_m,t_k) is well described by Acos(ωt − kx + φ). At each spatial location (pixel), the variation of the pixel flux X(s_m,∗)¹ is taken as a time series. The errors σ(X(s_m,∗)) are estimated as in Sect. 3.2. The time series is then fitted with A_scos(ω_st + φ_s) + δ_s². Thus, the value of ω_s and its uncertainty³ are obtained for each pixel. This is repeated for every pixel. The weighted mean and its uncertainty are calculated from abundant measurements (see top right panels of Figs. 3a,c,b and d). For each time sample, the spatial pixel flux variation X(∗,t_k) along the direction of propagating disturbances is fitted with A_tcos(k_tx + φ_t) + δ_t to obtain the wave number. By repeating this operation for each pixel, we are able to get a weighted mean of k (see bottom left panels of Figs. 3a,c,b and d). Finally, the parameters ω and k, with their weighted means, are combined to calculate the phase speed (see bottom right panels of Figs. 3a,c,b and d).

Fig. 3 Application of CFT to R1a), R2c), D1b), and D2d). In each panel, top left: the running difference of the time-distance plot, overlaid with the contour (white dashed line) of the model function Acos(ωt − kx + φ) with the best-fitted parameters. Top right: the fitting result of ω as a function of the spatial location. The thick solid line is the weighted mean, the dashed lines indicate its uncertainties. Bottom left: the fitting result of k as a function of time. The thick solid line is the weighted mean, and the dashed lines indicate its uncertainties. Bottom right: the dispersion diagram and the calculation of phase speed Vp and its uncertainties. The fitted parameters are as follows: a) for R1, ω = 0.0347 ± 0.00002 rad/s, k = 0.738 ± 0.002 Mm-1, P = 181.2 ± 0.1 s, Vp = 47.0 ± 0.1 km s-1; c) for R2ω = 0.0350 ± 0.00003 rad/s, k = 0.727 ± 0.005 Mm-1, P = 179.7 ± 0.2 s,Vp = 48.1 ± 0.3 km s-1; b) for D1ω = 0.0349 ± 0.00003 rad/s, k = 0.762 ± 0.00 Mm-1, P = 180.0 ± 0.1 s, Vp = 45.8 ± 0.2 km s-1; d) for D2ω = 0.0349 ± 0.00003 rad/s, k = 0.716 ± 0.006 Mm-1, P = 180.0 ± 0.2 s,Vp = 48.6 ± 0.4 km s-1.

Fig. 4 Application of DCF to R1 a), R2 c), D1 b), and D2 d). In each panel, the running difference of the time-distance plot is overlaid with the contour (white dashed line) of the model function Acos(ωt − kx + φ) with the best-fitted parameters. The best-fitted parameters are: a) for R1, P = 240.7 ± 0.7 s, Vp = 48.8 ± 0.2 km s-1; c) for R2, P = 177.2 ± 0.9 s, Vp = 65.8 ± 0.3 km s-1; b) for D1, P = 198.9 ± 0.7 s, Vp = 44.5 ± 0.2 km s-1; d) for D2, P = 250.5 ± 2.2 s,Vp = 51.4 ± 0.5 km s-1.

We performed the Levenberg-Marquardt least-squares minimisation using the function mpfitfun.pro provided by Markwardt (2009). We applied constraints on the amplitude in the fitting, the A_t,s are bounded between A_w and 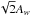$\sqrt{\mathrm{2}}{\mathit{A}}_{\mathit{w}}$, based on the fact that the root mean square of the wave Acos(ωt − kx + φ) is 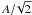$\mathit{A}\mathit{/}\sqrt{\mathrm{2}}$. The results are displayed in Fig. 3 and summarised in Sect. 5.

4.2. 2D coupled fitting

Similarly to CFT, we assumed that the signal is of a harmonic form. Instead of performing independent non-linear fitting in both axes, we performed global 2D fitting with the function Acos(ωt − kx + φ) + δ.

We applied the same non-linear fitting algorithm: the Levenberg-Marquardt least-squares minimisation, using the 2D fitting function mpfit2dfun.pro provided by Markwardt (2009). Similarly to CFT, we constrained the amplitude between A_w and 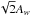$\sqrt{\mathrm{2}}{\mathit{A}}_{\mathit{w}}$. The results are illustrated in Fig. 4 and described in Sect. 5.

4.3. Best similarity match

The enhanced time-distance plot can be regarded as an image with tilted ridges, which can be roughly described by the harmonic propagating function Acos(ωt − kx + φ). We are able to measure the propagating speed and period by shape matching between the enhanced time-distance plot and a model image M(s_m,t_k) = Acos(ωt_k − ks_m + φ). The shape matching is quantified by a similarity measure, which is mostly based on the Minkowski distance 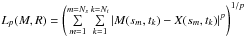${\mathit{L}}_{\mathit{p}}\mathrm{\left(}\mathit{M,R}\mathrm{\right)}\mathrm{=}{\left(\sum _{\mathit{m}\mathrm{=}\mathrm{1}}^{\mathit{m}\mathrm{=}{\mathit{N}}_{\mathit{s}}}\sum _{\mathit{k}\mathrm{=}\mathrm{1}}^{\mathit{k}\mathrm{=}{\mathit{N}}_{\mathit{t}}}{\left|\mathit{M}\mathrm{\left(}{\mathit{s}}_{\mathit{m}}\mathit{,}{\mathit{t}}_{\mathit{k}}\mathrm{\right)}\mathrm{-}\mathit{X}\mathrm{\left(}{\mathit{s}}_{\mathit{m}}\mathit{,}{\mathit{t}}_{\mathit{k}}\mathrm{\right)}\right|}^{\mathit{p}}\right)}^{\mathrm{1}\mathit{/}\mathit{p}}$, where p is a positive number whose values ranges from 1 to ∞ depending on a specific definition. We calculated the Euclidean distance (p = 2) to find the similarity measure. If images M and R match exactly, L_p = 0, otherwise, the best similarity measure is found by minimising L_p.

In our case, let X = X(s_m,t_k) be R₁ (D₁) or R₂ (D₂) (and is referred to as the reference image hereafter), and construct the model image M with the model function of the same size as X. The amplitude of M was scaled by a factor ⟨X⟩/⟨M⟩, where ⟨...⟩ means rms, so that M and X have approximately the same amplitude.

The model image M = M_P,Vp,φ(s_m,t_k) is parametrised by the period P = 2π/ω, apparent phase speed V_p = ω/k and phase φ. We set P ∈ [150,200] s in 1 s step, V_p ∈ [20,120] km s^-1 in 1 km s^-1 step, and φ ∈ [0,2π]  in 5 degree step. For every combination of P, V_p and φ, a model image is constructed and the associated Minkowski distance L_p(R,M_P,Vp,φ) is calculated. By locating 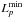${\mathit{L}}_{\mathit{p}}^{\min }$ in the parametric space, we are able to find the best combination of P, V_p and φ, these are the parameters that we need to measure R. We accepted 1% above the 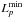${\mathit{L}}_{\mathit{p}}^{\min }$, and took a set of P, V_p and φ, with the means and standard deviations as the observed value and their uncertainties. The application of BSM to R₁ (D₁) and R₂ (D₂) is shown in Fig. 5.

The shape matching can generally be improved by the image regularisation (smoothing). For an image I(x,y), the regularised image can be obtained by its convolution with a normalised Gaussian kernel, I_σx,σy = I(x,y) ∗ G(σ_x,σ_y). In our case, neither R₁ (D₁) nor R₂ (D₂) have enough pixels to perform smoothing without severely subjecting to the edge effect, therefore we only regularised the image with a three-point discrete Gaussian kernel along the time axis. 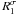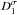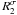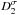The resulting images ${\mathit{R}}_{\mathrm{1}}^{\mathit{\sigma }}$ (${\mathit{D}}_{\mathrm{1}}^{\mathit{\sigma }}$) and ${\mathit{R}}_{\mathrm{2}}^{\mathit{\sigma }}$ (${\mathit{D}}_{\mathrm{2}}^{\mathit{\sigma }}$) are displayed in Fig. 6. The ridge pattern looks clearer than in Fig. 5. The effect of regularisation on the measurement of BSM will be discussed in Sect. 5.

5. Results

We applied CFT to the sample R₁ (Fig. 3a). The fits of ω have a relative error lower than 1% and are distributed in a very narrow band. The weighted mean gives ω = 0.0347 ± 0.00002 rad/s, which corresponds to a period of P = 181.2 ± 0.1 s. Fits to k haves a relative error of ≲ 10%. The weighted mean k = 0.738 ± 0.002 Mm^-1 has a relative error of less than 1%, and the values scatter about ± 50% of the mean. Thus the apparent phase speed is calculated as V_p = 47.0 ± 0.1 km s^-1. The resulting propagating features are overlaid with R₁ as the white dashed line in the top left panel of Fig. 3a. The spacing (P) matches very well, implying good fits to ω, the slope V_p of the dashed lines deviates slightly from the well recognised ridges, while remaining in the acceptable range.

We shortened the spatial length of the sample and applied CFT to R₂. The spatial length of R₂ is a half of R₁, but it includes the most prominent part of the ridges that represents the propagating disturbances. The results are shown in Fig. 3c. The rise of the relative error in k to above 10% is due to the decrease in the number of data points in the spatial direction, therefore the constraint on k is loosed. As seen in Fig. 3c, the best-fitting values of k are distributed in a broader range than those obtained for R₁. The weighted mean of k is about k = 0.727 ± 0.005 Mm^-1. The measure of ω retains a good accuracy (ω = 0.0350 ± 0.00003 rad/s, P = 179.7 ± 0.2 s), which is slightly worsened because of the decrease in the number of samples. The phase speed is calculated as V_p = 48.1 ± 0.3 km s^-1. The spacing remains consistent with the running difference as illustrated in the top left panel of Fig. 3c, the alignment is also very good.

Applying CFT to D₁ and D₂ with a higher signal-to-noise ratio (S/N) gives V_p = 45.8 ± 0.2 km s^-1 and P = 180.0 ± 0.1 s and V_p = 48.6 ± 0.4 km s^-1 and P = 180.0 ± 0.2 s, respectively. Both fits are acceptable, and consistent with those obtained for R₁ and R₂.

The application of DCF to R₁ (D₁) and R₂ (D₂) is displayed in Figs. 4a,b and Figs. 4c,d. The fit values are listed in Table 2. The DCF is very sensitive to the initial guess for the fit parameters. Since 2D fitting is coupled in both axes, the optimised fit can be reached only for one of the parameters. In our case, we optimised the fit of V_p, by changing the initial guess. It can be optimised for P as well. A fully automatic fit is not feasible because of the dependence on the initial guess.

Fig. 5 Application of BSM to R1 a), R2 c), D1 b), and D2 d). In each panel, the running difference of the time-distance plot is overlaid with the contour (white dashed line) of the model function Acos(ωt − kx + φ) with the fitted parameters. The fitted parameters are as follows: a) for R1, P = 180.0 ± 1.8 s, Vp = 47.0 ± 2.6 km s-1; c) for R2, P = 178.0 ± 2.0 s, Vp = 49.0 ± 4.5 km s-1; b) for D1, P = 180.0 ± 1.0 s, Vp = 47.0 ± 1.4 km s-1; d) for D2, P = 178.0 ± 1.0 s,Vp = 49.0 ± 2.8 km s-1.

Fig. 6 Application of BSM to ${\mathit{R}}_{\mathrm{1}}^{\mathit{\sigma }}$ a), ${\mathit{R}}_{\mathrm{2}}^{\mathit{\sigma }}$ c), ${\mathit{D}}_{\mathrm{1}}^{\mathit{\sigma }}$ b), and ${\mathit{D}}_{\mathrm{2}}^{\mathit{\sigma }}$ d). In each panel, the running difference of the time-distance plot is overlaid with the contour (white dashed line) of the model function Acos(ωt − kx + φ) with the best-fitted parameters. The best-fitted parameters are follows: a) for ${\mathit{R}}_{\mathrm{1}}^{\mathit{\sigma }}$, P = 180.0 ± 1.0 s, Vp = 48.0 ± 1.3 km s-1; c) for ${\mathit{R}}_{\mathrm{2}}^{\mathit{\sigma }}$, P = 180.0 ± 1.0 s, Vp = 50.0 ± 2.6 km s-1; b) for ${\mathit{D}}_{\mathrm{1}}^{\mathit{\sigma }}$, P = 180.0 ± 1.0 s, Vp = 48.0 ± 1.3 km s-1; d) for ${\mathit{D}}_{\mathrm{2}}^{\mathit{\sigma }}$, P = 180.0 ± 0.9 s,Vp = 50.0 ± 2.3 km s-1.

The BSM works well for all variants of the sample: R₁ (D₁), R₂ (D₂), and the regularised samples 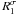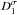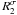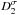${\mathit{R}}_{\mathrm{1}}^{\mathit{\sigma }}$ (${\mathit{D}}_{\mathrm{1}}^{\mathit{\sigma }}$), ${\mathit{R}}_{\mathrm{2}}^{\mathit{\sigma }}$ (${\mathit{D}}_{\mathrm{2}}^{\mathit{\sigma }}$), as illustrated in Figs. 5 and 6. The measurements are summarised in Table 2. The measurement of P and V_p are persistently good in all samples. It appears that BSM is very robust and not sensitive to any pre-processing of the sample.

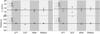Fig. 7 Comparison of the measurements obtained with CFT, DCF, BSM and BSM(σ). Vp and P are plotted in the upper and lower panels, respectively. The solid line is the corresponding average value and the dashed lines enclose the uncertainty of 1σ range in each panel. For R1 (⋄) and R2 (✴), $\overline{{\mathit{V}}_{\mathit{p}}}\mathrm{=}\mathrm{47.6}\hspace{0.17em}\mathrm{\pm }\hspace{0.17em}\mathrm{0.6}\hspace{0.17em}\mathrm{km}\hspace{0.17em}{\mathrm{s}}^{-1}$ and . For D1 (□) and D2 ( × ), $\overline{{\mathit{V}}_{\mathit{p}}}\mathrm{=}\mathrm{49.0}\hspace{0.17em}\mathrm{\pm }\hspace{0.17em}\mathrm{0.7}\hspace{0.17em}\mathrm{km}\hspace{0.17em}{\mathrm{s}}^{-1}$ and .

Fig. 8 a) Measurement of the phase speed and period in R1 as a function of the lag time, and those in D1 as a function of the smoothing time. b) The corresponding measurement in R2 and D2. In a) and b), the upper panel is the measurement of Vp and the bottom one is of P. The measurements obtained with CFT, BSM and BSM (σ) are shown in , ⋄  and □ respectively.

5.1. The effect of lag time

The choice of the lag time (T_lag = l × cadence) determines the quality of the running difference plot. Our choice of l = 9 applied above is just a specific case that appears to be in a good range of selection. To illustrate the effect of the lag time constructing the running-difference data set on the method performance, we plot the measurements of CFT, BSM and BSM(σ) as a function of the lag time in the left columns of Fig. 8a⁴ (R₁) and Fig. 8b⁴ (R₂). The results of DCF are omitted due to its sensitivity to the initial guess. Clearly, for R₁, the measurements of V_p and P are consistently good with the lag time ranging from 12 s to 156 s. However, for the shorter sample R₂, the selection of the lag time is more constrained within 84 s and 132 s, within which the quality of ridges is optimised. This means that for samples with a larger spatial length the choice of the lag time is less limited than for shorter ones.

5.2. The effect of detrending time

For the time-distance plot with the background removal and normalisation, the detrending time (T_detr = N × cadence) affects the results as well. We plot the measurements of CFT, BSM and BSM(σ) as a function of the detrending time in the right columns of Fig. 8a⁴ (D₁) and Fig. 8b⁴ (D₂). For D₁, the measurements are consistently good for all choices of the detrending time. It appears that the detrending time affects the results very little, while for those of D₂, the period P is measured very well with CFT, BSM and BSM (σ) in the whole range. For V_p, the measurements obtained with CFT are systematically lower than those of BSM and BSM(σ). The error bars of the BSM and BSM(σ) measurements are larger than those in D₁.

6. Conclusion

We designed three methods, CFT, DFC and BSM, to measure the average apparent phase speed of propagating EUV disturbances. The applications to R₁ (D₁), R₂ (D₂), 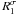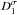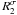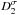${\mathit{R}}_{\mathrm{1}}^{\mathit{\sigma }}$ (${\mathit{D}}_{\mathrm{1}}^{\mathit{\sigma }}$), ${\mathit{R}}_{\mathrm{2}}^{\mathit{\sigma }}$ (${\mathit{D}}_{\mathrm{2}}^{\mathit{\sigma }}$) are summarised in Table 2 and illustrated in Fig. 7. Figure 8 shows the effect of the lag time and detrending time on the measurements.

From the computational aspect, the CPU time consumption descends as BSM, CFT, DCF. Applying these methods to R₁(R₂) in a GNU/linux x86_64 computer, it takes 321(158) s, 4.9(2.5) s and 2.5(0.7) s for BSM, CFT and DCF, respectively. The CPU time consumption for D₁ and D₂ are very similar. In addition, CFT and DCF require estimating the data noise, but provide better accuracy. Also, the DCF is very sensitive to the initial guess for the parameters in the fitting function, therefore it is not suitable for automatic measurements (see, e.g. Sych et al. 2010; Martens et al. 2012). The BSM is more tolerant to the data noise and pre-operations that do not affect the image morphology.

The valid measurements of the apparent phase speed V_p in the analysed event range from 48 to 52 km s^-1, with an average value of 47.6 ± 0.6 km s^-1 and 49.0 ± 0.7 km s^-1 for R₁(R₂) and D₁ (D₂), respectively (see Table 2 and Fig. 7, top panel).

For all three methods, it appears that the measurements made for R₁ and D₁ are on average better than those for R₂ and D₂. Accordingly, spatially-longer cuts, even if the amplitude of the disturbance is continuously declining, are preferable for the analysis. Longer samples are more tolerant to the choice of the lag time and detrending time, while shorter ones restrict the choice. We also showed that the measurements in D₁ (D₂) generally outperform those made in R₁ (R₂), therefore the background-removal method seems to be superior than running difference, at least in our applications.

The measurements of the oscillating period are consistent in all methods and agree well with the measurements based upon spectral methods (e.g. Fourier transform or periodogram). Therefore, the methods described in the paper provide also an alternative tool for the estimation of the period.

The systematic error in the apparent phase speed estimation mainly originates from the traits of the propagating disturbance. In particular, the apparent phase speed may change along the propagating direction because of the geometry, projection or (and) physics, so that the diagonal ridges may be bent. But in the analysed case, the spatial scale of the detection of the propagating disturbances does not reach ~20 Mm, above which a noticeable change of propagating speed was reported (e.g. Robbrecht et al. 2001; Gupta et al. 2010). It may also be a variant of time, so different ridges do not have the same slope. In the analysed data we did not find this effect. Another deviation may originate from the inconsistency with the harmonic wave feature in our assumption. The good agreement in the measurement with the propagating harmonic wave form also implies that the propagating disturbances are slow magnetoacoustic waves rather than recurring upflows. The designed methods are not likely to work on samples taken during transient, e.g. flaring activity.

The amplitude A of the disturbance decreases during its travelling. The methods can be improved by accounting for the spatial variation of the amplitude A = A(s_x). However, this will add an extra dimension to these methods, which means higher complexity. Another way of coping with this feature is to normalise the amplitude in each pixel along the cut to the highest amplitude of the narrowband signal measured at this pixel, before applying the methods.

Moreover, it is known that the amplitude of 3-min oscillations in sunspots is modulated by long-period oscillations (e.g. Sych et al. 2012). Therefore, it is natural to expect the same effect in their coronal counterpart observed in EUV. This effect can be studied with the methods designed in this paper, by applying them to a sliding window in time, imposed on a longer dataset. Likewise, the window can be applied in the spatial domain. This will reveal any possible speed variations in time and at different locations.

The three methods were shown to work well on the AIA data in EUV bandpasses. These methods can also be applied to other imaging data-cubes, obtained with other instruments and in other bands, e.g. UV, visible light and microwave.

Acknowledgments

We would like to acknowledge P. Boerner for the useful advice on AIA flux error analysis. The AIA data were used as courtesy of NASA/SDO and the AIA science teams.

References

All Tables

All Figures

Fig. 1 a) AIA 171 Å image of active region NOAA 11330 observed on 27 Oct. 2011 at 04:30:01 UT is shown with the flux on the logarithmic scale. A cut that was taken to make the time-distance plot is indicated with a black bar. b) The running difference R1 of the time-distance plot started at 04:30:01 UT. R2 is the first half of R1, to the left of the white dashed line. It covers about 10 cycles of the propagating features. Panel c) shows the background-subtracted time-distance plot D1. The first half of D1 on the left of the white dashed line is D2.

In the text

	Fig. 2 Data noise σnoise(F) (+) in Eq. (3) as a function of pixel flux F in AIA 171 Å images. The components caused by the photon noise, compression, despiking and other reasons are plotted with ⋄ , △ , □, respectively.
In the text

Fig. 3 Application of CFT to R1a), R2c), D1b), and D2d). In each panel, top left: the running difference of the time-distance plot, overlaid with the contour (white dashed line) of the model function Acos(ωt − kx + φ) with the best-fitted parameters. Top right: the fitting result of ω as a function of the spatial location. The thick solid line is the weighted mean, the dashed lines indicate its uncertainties. Bottom left: the fitting result of k as a function of time. The thick solid line is the weighted mean, and the dashed lines indicate its uncertainties. Bottom right: the dispersion diagram and the calculation of phase speed Vp and its uncertainties. The fitted parameters are as follows: a) for R1, ω = 0.0347 ± 0.00002 rad/s, k = 0.738 ± 0.002 Mm-1, P = 181.2 ± 0.1 s, Vp = 47.0 ± 0.1 km s-1; c) for R2ω = 0.0350 ± 0.00003 rad/s, k = 0.727 ± 0.005 Mm-1, P = 179.7 ± 0.2 s,Vp = 48.1 ± 0.3 km s-1; b) for D1ω = 0.0349 ± 0.00003 rad/s, k = 0.762 ± 0.00 Mm-1, P = 180.0 ± 0.1 s, Vp = 45.8 ± 0.2 km s-1; d) for D2ω = 0.0349 ± 0.00003 rad/s, k = 0.716 ± 0.006 Mm-1, P = 180.0 ± 0.2 s,Vp = 48.6 ± 0.4 km s-1.

In the text

Fig. 4 Application of DCF to R1 a), R2 c), D1 b), and D2 d). In each panel, the running difference of the time-distance plot is overlaid with the contour (white dashed line) of the model function Acos(ωt − kx + φ) with the best-fitted parameters. The best-fitted parameters are: a) for R1, P = 240.7 ± 0.7 s, Vp = 48.8 ± 0.2 km s-1; c) for R2, P = 177.2 ± 0.9 s, Vp = 65.8 ± 0.3 km s-1; b) for D1, P = 198.9 ± 0.7 s, Vp = 44.5 ± 0.2 km s-1; d) for D2, P = 250.5 ± 2.2 s,Vp = 51.4 ± 0.5 km s-1.

In the text

Fig. 5 Application of BSM to R1 a), R2 c), D1 b), and D2 d). In each panel, the running difference of the time-distance plot is overlaid with the contour (white dashed line) of the model function Acos(ωt − kx + φ) with the fitted parameters. The fitted parameters are as follows: a) for R1, P = 180.0 ± 1.8 s, Vp = 47.0 ± 2.6 km s-1; c) for R2, P = 178.0 ± 2.0 s, Vp = 49.0 ± 4.5 km s-1; b) for D1, P = 180.0 ± 1.0 s, Vp = 47.0 ± 1.4 km s-1; d) for D2, P = 178.0 ± 1.0 s,Vp = 49.0 ± 2.8 km s-1.

In the text

Fig. 6 Application of BSM to ${\mathit{R}}_{\mathrm{1}}^{\mathit{\sigma }}$ a), ${\mathit{R}}_{\mathrm{2}}^{\mathit{\sigma }}$ c), ${\mathit{D}}_{\mathrm{1}}^{\mathit{\sigma }}$ b), and ${\mathit{D}}_{\mathrm{2}}^{\mathit{\sigma }}$ d). In each panel, the running difference of the time-distance plot is overlaid with the contour (white dashed line) of the model function Acos(ωt − kx + φ) with the best-fitted parameters. The best-fitted parameters are follows: a) for ${\mathit{R}}_{\mathrm{1}}^{\mathit{\sigma }}$, P = 180.0 ± 1.0 s, Vp = 48.0 ± 1.3 km s-1; c) for ${\mathit{R}}_{\mathrm{2}}^{\mathit{\sigma }}$, P = 180.0 ± 1.0 s, Vp = 50.0 ± 2.6 km s-1; b) for ${\mathit{D}}_{\mathrm{1}}^{\mathit{\sigma }}$, P = 180.0 ± 1.0 s, Vp = 48.0 ± 1.3 km s-1; d) for ${\mathit{D}}_{\mathrm{2}}^{\mathit{\sigma }}$, P = 180.0 ± 0.9 s,Vp = 50.0 ± 2.3 km s-1.

In the text

Fig. 7 Comparison of the measurements obtained with CFT, DCF, BSM and BSM(σ). Vp and P are plotted in the upper and lower panels, respectively. The solid line is the corresponding average value and the dashed lines enclose the uncertainty of 1σ range in each panel. For R1 (⋄) and R2 (✴), $\overline{{\mathit{V}}_{\mathit{p}}}\mathrm{=}\mathrm{47.6}\hspace{0.17em}\mathrm{\pm }\hspace{0.17em}\mathrm{0.6}\hspace{0.17em}\mathrm{km}\hspace{0.17em}{\mathrm{s}}^{-1}$ and . For D1 (□) and D2 ( × ), $\overline{{\mathit{V}}_{\mathit{p}}}\mathrm{=}\mathrm{49.0}\hspace{0.17em}\mathrm{\pm }\hspace{0.17em}\mathrm{0.7}\hspace{0.17em}\mathrm{km}\hspace{0.17em}{\mathrm{s}}^{-1}$ and .

In the text

	Fig. 8 a) Measurement of the phase speed and period in R1 as a function of the lag time, and those in D1 as a function of the smoothing time. b) The corresponding measurement in R2 and D2. In a) and b), the upper panel is the measurement of Vp and the bottom one is of P. The measurements obtained with CFT, BSM and BSM (σ) are shown in , ⋄  and □ respectively.
In the text