| Issue |
A&A
Volume 543, July 2012
|
|
|---|---|---|
| Article Number | A15 | |
| Number of page(s) | 13 | |
| Section | Astronomical instrumentation | |
| DOI | https://doi.org/10.1051/0004-6361/201218808 | |
| Published online | 21 June 2012 | |
Error characterization of the Gaia astrometric solution
II. Validating the covariance expansion model
Lund Observatory, Lund University, Box 43, 22100 Lund, Sweden
e-mail: Berry.Holl@astro.lu.se; Lennart.Lindegren@astro.lu.se; David.Hobbs@astro.lu.se
Received: 11 January 2012
Accepted: 1 May 2012
Context. To use the data in the future Gaia catalogue it is important to have accurate estimates of the statistical uncertainties and correlations of the errors in the astrometric data given in the catalogue.
Aims. In a previous paper we derived a mathematical model for computing the covariances of the astrometric data based on series expansions and a simplified attitude description. The aim of the present paper is to determine to what extent this model provides an accurate representation of the expected random errors in the astrometric solution for Gaia.
Methods. We simulate the astrometric core solution by making least-squares solutions of the astrometric parameters for one million stars and the attitude parameters for a five-year mission, using nearly one billion simulated elementary observations for a total of 26 million unknowns. Two cases are considered: one in which all stars have the same magnitude, and another with 30% brighter and 70% fainter stars. The resulting astrometric errors are statistically compared with the model predictions.
Results. In all cases considered, and within the statistical uncertainties of the numerical experiments (typically below 0.4%), the theoretically calculated variances and covariances are consistent with the simulations. To achieve this it is however necessary to expand the covariances to at least third or fourth order, and to apply a (theoretically motivated and derived) “fudge factor” in the kinematographic model.
Conclusions. The model provides a feasible method to estimate the covariance of arbitrary astrometric data, accurate enough for most applications, and as such it should be available as part of the user’s interface to the Gaia catalogue. A main assumption in the current model is that the observational errors are uncorrelated (e.g., photon noise), and further studies are needed on how correlated modelling errors, in particular in the attitude, can be taken into account.
Key words: astrometry / catalogs / methods: data analysis / methods: statistical / space vehicles: instruments
© ESO, 2012
1. Introduction
Gaia is the European Space Agency astrometric mission scheduled for launch in 2013. It will observe roughly one billion stars, quasars and other point like objects (hereafter called “sources”), for which the five astrometric parameters (position, parallax and proper motion) will be determined. The Gaia catalogue is expected to become available around 2021. Efficient use of the catalogue data requires that the astrometric errors are reliably characterized, and in particular that the standard uncertainties (or equivalently the variances) are correctly estimated. When combining several astrometric parameters their statistical correlations (or equivalently the covariances) may also be important. Thus, in general we need to know the full variance-covariance matrix (or covariance matrix for brevity) of all the astrometric parameters. Because of the extremely large number of astrometric parameters (~5 × 109), the standard method of estimating the covariance matrix, involving the inversion of an equally large normal matrix, cannot be applied.
In Holl & Lindegren (2012, Paper I) we derived an approximate series expansion model to compute the covariance matrix for arbitrary subsets of the astrometric parameters (or more generally for arbitrary functions of the astrometric parameters), taking into account the statistical correlations introduced by the attitude estimation errors. The aim of the present paper is to test the validity of this model by means of numerical experiments simulating the astrometric core solution for one million sources.
The model formulated in Paper I uses a “kinematographic” attitude model, where the continuous scanning of Gaia is approximated by a “step and stare” motion. This greatly reduces the complexity of computing the attitude contribution to the covariances since each observation is linked to only one attitude parameter instead of many, as in the case of a continuous (spline) representation of the attitude. The covariance model allows us to approximate the covariance matrix U between all the source parameters by means of the series expansion 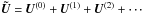 (Eq. (19) of Paper I, hereafter I:19), where the top “ ~ ” indicates the approximation. In practice we are interested in the truncated expansion up to some finite α, denoted by square brackets:
(Eq. (19) of Paper I, hereafter I:19), where the top “ ~ ” indicates the approximation. In practice we are interested in the truncated expansion up to some finite α, denoted by square brackets: ![\begin{equation} \label{eq:Uexp} \vec{\tilde{U}}^{[\alpha]} = \vec{U}^{(0)} + \vec{U}^{(1)} + \cdots + \vec{U}^{(\alpha)}. \end{equation}](/articles/aa/full_html/2012/07/aa18808-12/aa18808-12-eq6.png) (1)As mentioned in Paper I, we more generally want to characterize the joint errors of m different scalar quantities y = (y1, ..., ym) depending on some subset of n astrometric parameters x = (x1, ..., xn). Introducing the m × n Jacobian matrix J with elements Jμν = ∂yμ/∂xν we have
(1)As mentioned in Paper I, we more generally want to characterize the joint errors of m different scalar quantities y = (y1, ..., ym) depending on some subset of n astrometric parameters x = (x1, ..., xn). Introducing the m × n Jacobian matrix J with elements Jμν = ∂yμ/∂xν we have 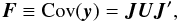 (2)where U = Cov(x) is the covariance matrix of the relevant subset of astrometric parameters. Using Eq. (1) we can approximate Eq. (2) as
(2)where U = Cov(x) is the covariance matrix of the relevant subset of astrometric parameters. Using Eq. (1) we can approximate Eq. (2) as ![\begin{equation} \label{eq:Dexp} \vec{\tilde{F}}^{[\alpha]} = \vec{F}^{(0)} + \vec{F}^{(1)} + \cdots + \vec{F}^{(\alpha)}, \end{equation}](/articles/aa/full_html/2012/07/aa18808-12/aa18808-12-eq16.png) (3)where F(α) = JU(α)J′ for α = 0, 1, ... The algorithm for the practical computation of covariances described in Sect. 5 of Paper I uses this more general formulation. The length of the computations increases by a large factor for each higher-order term.
(3)where F(α) = JU(α)J′ for α = 0, 1, ... The algorithm for the practical computation of covariances described in Sect. 5 of Paper I uses this more general formulation. The length of the computations increases by a large factor for each higher-order term.
The two main issues addressed in this paper concern: (i) the validity of the approximations introduced in Paper I, in particular the kinematographic approximation; and (ii) the minimum α needed for a given relative accuracy of the covariances. They are discussed in Sect. 4, following a brief description of the numerical simulations (Sect. 2) and a discussion of the methodology for the numerical validation (Sect. 3).
2. Numerical simulations
2.1. Simulating astrometric solutions using AGISLab
The covariance model developed in Paper I will be validated through a comparison with numerical results simulating the astrometric solution that is a central part of the Gaia data processing. Ideally, the validation should use the models, algorithms and software developed for the analysis of the real Gaia data, known as AGIS (Astrometric Global Iterative Solution) and comprehensively described in Lindegren et al. (2012). For practical reasons we use a separate software system called AGISLab, which has a subset of the most important functionalities of AGIS, only implemented in a light-weight processing framework more suitable for small-scale experimental runs on small computers. Importantly, AGISLab adds a number of features specifically designed for numerical experiments, in particular on-the-fly generation of simulated input data (“observations”) and the ability to perform scaled-down experiments (involving much fewer parameters than a minimum AGIS run) in a meaningful way using a single scaling parameter S (Holl et al. 2010; Bombrun et al. 2012). The simulations described in this paper use the observation generator in AGISLab to obtain input data with well-defined statistical properties, but do not make use of the down-scaling facility in AGISLab; in other words all observations are generated for nominal values of the CCD size, focal plane geometry, field-of-view size, satellite spin rate, and scanning law, equivalent to S = 1; see, e.g., Table 1 in Lindegren (2010) for a summary of the main mission parameters of Gaia.
Like virtually all Gaia data processing software, AGIS and AGISLab are entirely written in the Java language (O’Mullane et al. 2011) and make extensive use of the common Java toolboxes collected and maintained by the Gaia software development teams. Consistency between AGIS and AGISLab is ensured by the use of common code for many of the central tasks such as the calculation of the observation equations and the updating of source and attitude parameters. In fact, much of this code was first developed and tested in AGISLab before it was introduced in AGIS. Thus we are confident that the present simulation results, obtained with AGISLab, are in all relevant aspects equivalent to the corresponding AGIS output.
2.2. Requirements for the simulations
The structure of the normal equations depends strongly on the number of source and attitude parameters that are included. Ideally we would like to simulate a realistic AGIS solution with the expected 108 primary sources and an attitude model having a spline knot interval in the 5–30 s range as expected for the real mission (due to the CCD observations integration time of ≃ 4.42 s for the majority of the sources, variations on shorter timescales cannot be distinguished). Given available computational resources we are able to use a reasonably realistic attitude knot interval of 30 s but are however restricted to a maximum of 106 sources. Distributing these sources randomly on the sky results in a mean number density of 24.2 deg-2, which translates into an average of 12 sources simultaneously visible in each of the two fields of view.
The three-axis attitude of Gaia is reconstructed, as a function of time, by combining across-scan (AC) measurements of source positions in the skymappers (SM) of the two fields of view with along-scan (AL) measurements in the combined astrometric field (AF). For a 5 yr mission the mean number of field-of-view transits for randomly distributed sources is 88.0 (excluding dead-time), corresponding to 16.7 source transits per 30 s attitude knot interval in the combined fields of view. Because there is typically one AC observation (in the SM) and nine AL observations (in the AF) per transit, this results in 16.7 AC observations and 151 AL observations per knot interval, which is sufficient to ensure a proper attitude determination over the whole mission duration. It is however (almost) necessary that the 1 million sources have a uniform random distribution on the sky, rather than following some more realistic (Galactic) density distribution: otherwise there would not be a sufficient number of observations per attitude knot interval when both fields of view are looking away from the Galactic plane. We have not considered to use a variable knot interval (which to some degree would circumvent the density problem) because it would lead to unrealistically large intervals part of the time.
Although we are only able to simulate 1% of the expected 108 primary sources anticipated for the final astrometric core solution (Lindegren et al. 2012), the resulting 12 sources per field of view sample the scanning-law induced structure between sources on a sufficiently small spatial scale that the resulting connectivity structure is similar to what we would have for a (much) larger number of sources1. Holl et al. (2010) found that the largest correlations between the astrometric parameters of different sources are obtained for pairs that have an angular separation much less than the field of view, with a maximum correlation coefficient inversely proportional to the number of sources in the combined fields of view. Since the present experiments use much fewer primary sources than the final astrometric solution for the Gaia catalogue, the experiments are likely to exaggerate the correlations by a significant factor.
It is no coincidence that the number of field-of-view transits per attitude interval (~16) is similar to the mean number of sources per (combined) field of view (~24). In simple words one must determine the next “field pointing” before the current field moves completely out of view. As a field-of-view transit takes about 43 s, the attitude interval should be of a similar or shorter duration, e.g., the adopted 30 s.
2.3. Simulation experiments
The numerical validation of the covariance model was carried out for the following two cases:
-
Case A:
1 million randomly distributed sources ofa single magnitude (G = 13);
-
Case B:
A random mixture of 0.3 million sources of magnitude G = 13 and 0.7 million sources with G = 15.
The purpose of Case A is to serve as a reference for subsequent experiments: the assumptions are as simple as possible, and it gives the highest astrometric weight per source and per unit time that can be achieved with our imposed restriction of at most 106 primary sources. For the statistical results reported below the choice of magnitude is in fact irrelevant in Case A, since all attitude and astrometric errors scale linearly with the assumed standard deviation of the observational noise (which is σAL = 92 μas per AL observation in the astrometric field), while the computed covariances scale with  . However, at G = 13 the CCD pixel values at the centre of the stellar images are close to saturation (above which gating is used to reduce the integration time), and this σAL therefore represents the expected noise level also for the brighter sources. Moreover, the minimum density of stars brighter than G = 13 is approximately 50 deg-2 (i.e., around the galactic poles), of which probably half could be used as primary sources in a real astrometric solution. With a density of 24.2 deg-2, Case A is therefore not dissimilar to the uniform grid of primary sources having the highest astrometric weight that can be achieved in the actual mission.
. However, at G = 13 the CCD pixel values at the centre of the stellar images are close to saturation (above which gating is used to reduce the integration time), and this σAL therefore represents the expected noise level also for the brighter sources. Moreover, the minimum density of stars brighter than G = 13 is approximately 50 deg-2 (i.e., around the galactic poles), of which probably half could be used as primary sources in a real astrometric solution. With a density of 24.2 deg-2, Case A is therefore not dissimilar to the uniform grid of primary sources having the highest astrometric weight that can be achieved in the actual mission.
The purpose of Case B is to study how the covariance model adapts to different magnitudes. The astrometric results for bright sources are expected to suffer relatively more from the attitude uncertainty than those of faint sources. Ideally, we should simulate the expected magnitude distribution of the primary sources (extending down to G = 20), but that would mean a very small number of bright sources, given our computational restriction of 1 million sources in total. The use of two discrete magnitudes (G = 13 and 15), their separation by 2 magnitudes (giving a factor 2.5 in σAL), and the ratio of the number of sources (3:7) were mainly dictated by the practicalities of the data analysis. Comparing the results for the two cases at the common magnitude G = 13 allows to estimate how the total weight of the primary sources affects the attitude errors.
A mission length of 5 yr was assumed (with no dead-time), which gives on average 880 AL (SM + AF) and 88 AC (SM) observations per source. In each case we generated the full set of ~109 observations with a single realization of the Gaussian observation noise, and performed a least-squares solution for the 5 × 106 astrometric source parameters and 2.1 × 107 attitude parameters (for a spline knot interval of 30 s). Using AGISLab with the conjugate gradients algorithm described in Bombrun et al. (2012) the solution was iterated until convergence (rms updates <0.001 μas) from an initial approximation equal to the true parameter values2. Figure 1 shows the evolution of the rms astrometric errors and updates during the iterations in Case A; the corresponding plot for Case B is very similar.
 |
Fig. 1 Convergence plot for the astrometric solution in Case A. The solid curves show the rms errors of the astrometric parameter (i.e., the rms differences between the calculated and true values) as functions of the iteration number; the dashed curves show the rms of the corresponding source parameter updates. The different astrometric parameters are colour coded (green: α∗, blue: δ, red: ϖ, magenta: μα∗, cyan: μδ). |
2.4. Computing the covariance estimates
The implementation of the covariance model used for this paper follows exactly the description given in Sect. 5 of Paper I. For both Case A and B the number of sources was 1 million, each having 5 astrometric parameters. The kinematographic attitude bin interval (B) was set equal to the attitude spline knot interval of 30 s, resulting in 5.2 × 106 attitude intervals covering the 5 yr mission length. Technical details about the implementation, including memory usage and computing times, are found in Appendix C.
3. Validation methodology
3.1. General considerations
The aim of the validation is to determine to what extent the mathematical model described in Paper I provides an accurate statistical representation of the random errors in the astrometric solution. As discussed in Paper I, a basic assumption for the model is that the input data (observations) are unbiased and uncorrelated, with known standard uncertainties. In the present paper the validation is made under the hypothesis that these assumptions are correct, which may be reasonable if photon noise and CCD readout noise are the only sources of errors. In reality there are many other (although generally less important) error sources, resulting in observations that are to some extent biased and correlated, and whose standard uncertainties are not perfectly known. The characterization of the resulting astrometric errors under these conditions is a problem left for future studies (see Sect. 5); the effects of CCD radiation damage are for example considered by Holl et al. (2012b). Under the given hypothesis, however, the statistical properties of the astrometric errors are completely defined by the corresponding least-squares problem, and the validation can be reduced to a comparison with quantities computed from the rigorous least-squares solution.
As outlined in the Introduction the covariance model most generally provides ![\hbox{$\vec{\tilde{F}}^{[\alpha]}$}](/articles/aa/full_html/2012/07/aa18808-12/aa18808-12-eq44.png) , being an approximation of F using the series expansion with α + 1 terms, for a given Jacobian J. Provided that the number of rows in J, or m = dim(y), is not too large, it would be feasible to compute F rigorously by means of the iterative astrometric solution algorithm. All that is needed (in principle) is to replace the right-hand side of the normal equations with the columns of J′, iterate to obtain the m solution vectors, and left-multiply by J. We have not tried this method, as it is computationally expensive and would not allow us to sample a large set of covariances.
, being an approximation of F using the series expansion with α + 1 terms, for a given Jacobian J. Provided that the number of rows in J, or m = dim(y), is not too large, it would be feasible to compute F rigorously by means of the iterative astrometric solution algorithm. All that is needed (in principle) is to replace the right-hand side of the normal equations with the columns of J′, iterate to obtain the m solution vectors, and left-multiply by J. We have not tried this method, as it is computationally expensive and would not allow us to sample a large set of covariances.
The adopted validation methodology is instead based on numerical simulation experiments. Observational noise with well-defined statistical properties is created, using a good pseudo-random number generator, and the errors in the resulting solutions are analysed in terms of suitable statistics. The simplest and most straightforward way of estimating F would use Monte Carlo simulations: the solution is repeated many (say K) times with different (random) observation noise realizations but otherwise identical conditions (positions and magnitudes of the sources, the scanning law, etc.). If ek is the vector of astrometric errors obtained in the kth such experiment, we can then compute the estimate 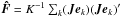 for arbitrary J. As the relative precision of the sample variance for a sample of size K is approximately
for arbitrary J. As the relative precision of the sample variance for a sample of size K is approximately 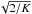 , it follows that a relative precision of 1% would require about 20 000 experiments, which is clearly not feasible time wise.
, it follows that a relative precision of 1% would require about 20 000 experiments, which is clearly not feasible time wise.
However, since each solution contains one million different parallax errors (for example), it would seem possible to obtain very good statistics from just one such solution, and that is indeed the approach taken here. The only problem is to define the relevant statistics for our purpose of validating the covariance model. Given that we have only one error vector e, our task is to define statistics that allow us to combine the results for many sources. This in essence means that we need to combine the individual errors to quantities that all follow the same (expected) distribution. Since J can be set up to extract arbitrary subsets of the astrometric parameters (e.g., the parallaxes for all sources, or for all sources of a given magnitude), the statistics can always be formulated in terms of ![\hbox{$\vec{\tilde{F}}^{[\alpha]}$}](/articles/aa/full_html/2012/07/aa18808-12/aa18808-12-eq44.png) rather than
rather than ![\hbox{$\vec{\tilde{U}}^{[\alpha]}$}](/articles/aa/full_html/2012/07/aa18808-12/aa18808-12-eq55.png) .
.
In the αth approximation ![\hbox{$\vec{\tilde{F}}^{[\alpha]}$}](/articles/aa/full_html/2012/07/aa18808-12/aa18808-12-eq44.png) is the estimated covariance of the transformed errors Je. The statistic
is the estimated covariance of the transformed errors Je. The statistic ![\begin{equation} \label{eq:X2} X^2 = (\vec{J}\vec{e})'\,\left(\vec{\tilde{F}}^{[\alpha]}\right)^{-1}(\vec{J}\vec{e}) \end{equation}](/articles/aa/full_html/2012/07/aa18808-12/aa18808-12-eq57.png) (4)is therefore expected to follow the chi-square distribution with ν = dim(F) degrees of freedom,
(4)is therefore expected to follow the chi-square distribution with ν = dim(F) degrees of freedom, 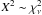 , if
, if ![\hbox{$\vec{\tilde{F}}^{[\alpha]}=\vec{F}$}](/articles/aa/full_html/2012/07/aa18808-12/aa18808-12-eq60.png) . In particular, the expected value of X2 is ν and the variance is 2ν. For our purposes a more convenient statistic is the relative deviation, X2/ν − 1, which should ideally be zero and has an uncertainty of
. In particular, the expected value of X2 is ν and the variance is 2ν. For our purposes a more convenient statistic is the relative deviation, X2/ν − 1, which should ideally be zero and has an uncertainty of 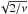 . However, it is not practical to compute this statistic for values of ν that are large enough to obtain a useful precision. Instead, we use the average over a large number (n) of sources:
. However, it is not practical to compute this statistic for values of ν that are large enough to obtain a useful precision. Instead, we use the average over a large number (n) of sources: 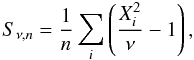 (5)where
(5)where 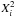 is the chi-square statistic for the transformed errors of the single source i, evaluated using the corresponding submatrix
is the chi-square statistic for the transformed errors of the single source i, evaluated using the corresponding submatrix ![\hbox{$\vec{\tilde{F}}^{[\alpha]}_{ii}$}](/articles/aa/full_html/2012/07/aa18808-12/aa18808-12-eq69.png) , and ν is now the number of transformed errors per source. Assuming that the correlations between the sources are generally small, the uncertainty of Sν,n is ≃
, and ν is now the number of transformed errors per source. Assuming that the correlations between the sources are generally small, the uncertainty of Sν,n is ≃ 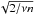 .
.
As previously remarked, the covariance model neglects the across-scan (AC) observations, although they are by necessity used in the simulations and therefore contribute some astrometric weight to the solution. In principle this could result in a slight overestimation of the variances in the model compared with the simulations. The maximum size of this effect can be evaluated by just considering the AC contribution to the total weight. Given that the standard uncertainty of an AC observation (in SM) is about six times larger than the AL observation (in AF), and that there are nine times as many AL observations, the AC observations only contribute about 0.3% of the total weight, and could at most lead to a (negative) bias of 0.003 units in Sν,n. This number is comparable to the uncertainty of the statistics in the numerical experiments, and therefore will not (significantly) affect the analysis.
3.2. Covariances for individual sources
By specifying a trivial Jacobian filled with 0’s and 1’s in the appropriate places, the covariance model can return the estimated covariance matrix ![\hbox{$\vec{\tilde{U}}^{[\alpha]}_{ii}$}](/articles/aa/full_html/2012/07/aa18808-12/aa18808-12-eq72.png) of the five astrometric parameters (α ∗ , δ, ϖ, μα ∗ , μδ) of a single source i. Given the error vectors ei and the estimated covariance matrices for a set of n sources, we define one statistic S5,n and five different statistics S1,n as follows.
of the five astrometric parameters (α ∗ , δ, ϖ, μα ∗ , μδ) of a single source i. Given the error vectors ei and the estimated covariance matrices for a set of n sources, we define one statistic S5,n and five different statistics S1,n as follows.
The statistic S5,n is obtained by averaging 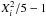 over the n sources, where
over the n sources, where ![\begin{equation} X^2_i=\vec{e}_i'\,\left(\vec{\tilde{U}}^{[\alpha]}_{ii}\right)^{-1}\vec{e}_i \end{equation}](/articles/aa/full_html/2012/07/aa18808-12/aa18808-12-eq77.png) (6)should ideally follow the chi-square distribution with 5 degrees of freedom. S5,n tests the ensemble of 5 × 5 covariance matrices for the sources against the astrometric errors obtained in the solution.
(6)should ideally follow the chi-square distribution with 5 degrees of freedom. S5,n tests the ensemble of 5 × 5 covariance matrices for the sources against the astrometric errors obtained in the solution.
The diagonal elements in ![\hbox{$\vec{\tilde{U}}^{[\alpha]}_{ii}$}](/articles/aa/full_html/2012/07/aa18808-12/aa18808-12-eq72.png) are the estimated variances of the five astrometric parameters. These variances are individually tested by means of the statistics S1,n obtained by averaging
are the estimated variances of the five astrometric parameters. These variances are individually tested by means of the statistics S1,n obtained by averaging 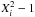 over the sources, where Xi in this case is the individual astrometric error (e.g., in α ∗ ) divided by the estimated uncertainty (square root of the corresponding diagonal element in
over the sources, where Xi in this case is the individual astrometric error (e.g., in α ∗ ) divided by the estimated uncertainty (square root of the corresponding diagonal element in ![\hbox{$\vec{\tilde{U}}^{[\alpha]}_{ii}$}](/articles/aa/full_html/2012/07/aa18808-12/aa18808-12-eq72.png) ). There are thus five separate statistics, denoted S1,n(α ∗ ), S1,n(δ), etc.
). There are thus five separate statistics, denoted S1,n(α ∗ ), S1,n(δ), etc.
It is also possible to devise separate tests for each of the 10 non-redundant off-diagonal elements in the sources covariance matrices, but these statistics are not detailed here.
3.3. Covariances for pairs of sources
With n sources of a particular kind (e.g., in a magnitude bin) there are n(n − 1)/2 possible pairs to consider, which is typically far too many. As we are particularly concerned about the correlations on small angular scales (less than the size of the field of view), we will only compute these statistics for pairs of sources that are neighbours on the sky. More precisely, each source is paired with its nearest neighbour among the remaining unpaired sources, resulting in n/2 unique pairs among n sources.
By appropriate specification of the Jacobian the joint covariance of the astrometric parameters for the pair ij is returned as a 10 × 10 matrix consisting of ![\hbox{$\vec{\tilde{U}}^{[\alpha]}_{ii}$}](/articles/aa/full_html/2012/07/aa18808-12/aa18808-12-eq72.png) ,
, ![\hbox{$\vec{\tilde{U}}^{[\alpha]}_{ij}$}](/articles/aa/full_html/2012/07/aa18808-12/aa18808-12-eq87.png) ,
, ![\hbox{$\vec{\tilde{U}}^{[\alpha]}_{ji}=\vec{\tilde{U}}^{[\alpha]\prime}_{ij}$}](/articles/aa/full_html/2012/07/aa18808-12/aa18808-12-eq88.png) , and
, and ![\hbox{$\vec{\tilde{U}}^{[\alpha]}_{jj}$}](/articles/aa/full_html/2012/07/aa18808-12/aa18808-12-eq89.png) . In analogy with Sect. 3.2 we define S10,n/2 for testing the ensemble of joint covariances for the n/2 different pairs, and 10 separate statistics S1,n/2 for specific combinations of the astrometric parameters (to be detailed below).
. In analogy with Sect. 3.2 we define S10,n/2 for testing the ensemble of joint covariances for the n/2 different pairs, and 10 separate statistics S1,n/2 for specific combinations of the astrometric parameters (to be detailed below).
Given the error vectors ei and ej we have for each pair the statistic ![\begin{equation} \label{eq:Xij} X_{ij}^2 = \begin{bmatrix} ~\vec{e}_{i}~ \\[3pt] ~\vec{e}_{j}~ \\[3pt] \end{bmatrix}^{\,\prime} \begin{bmatrix} ~\vec{\tilde{U}}_{ii}^{[\alpha]} & \vec{\tilde{U}}_{ij}^{[\alpha]}~ \\[3pt] ~\vec{\tilde{U}}_{ji}^{[\alpha]} & \vec{\tilde{U}}_{jj}^{[\alpha]}~ \\[3pt] \end{bmatrix}^{-1} \begin{bmatrix} ~\vec{e}_{i}~ \\[3pt] ~\vec{e}_{j}~ \\[3pt] \end{bmatrix}, \end{equation}](/articles/aa/full_html/2012/07/aa18808-12/aa18808-12-eq93.png) (7)which ideally should follow the chi-square distribution with 10 degrees of freedom. S10,n/2 is obtained by averaging
(7)which ideally should follow the chi-square distribution with 10 degrees of freedom. S10,n/2 is obtained by averaging 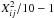 over the n/2 pairs. Note that S10,n/2 has the same uncertainty as the S5,n defined above for single sources, if n is the same.
over the n/2 pairs. Note that S10,n/2 has the same uncertainty as the S5,n defined above for single sources, if n is the same.
Although S10,n/2 correctly tests the overall level of the covariances, it may not be very sensitive to possible spatial correlations, due to the fact that the off-diagonal terms of the inverse matrix in Eq. (7) can have either sign and therefore to some extent will cancel. More powerful statistics, and better insight into the properties of the solution, can be obtained by considering the predicted variances for some very specific combinations of the astrometric parameters of the sources. Two such quantities are the sum and the difference of the parallaxes, Σϖ ≡ ϖi + ϖj and Δϖ = ϖi − ϖj. The former may be used to estimate the distance to a binary or cluster, using the mean parallax, while the second is relevant for example for testing whether the sources are physically connected. In both cases it is important that the variance of the combination is correctly estimated. The example is particularly interesting, since a positive correlation between the parallax errors would be detrimental for the first purpose, but beneficial for the second (the reverse is true for negative correlation). Moreover, the transformation from (ϖi,ϖj) to (Σϖ,Δϖ) is orthogonal and therefore preserves the information in the original data. But whereas the variances of the original data do not depend on the covariance, the variances of the transformed data do.
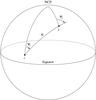 |
Fig. 2 Definition of the angles ψi and ψj for two sources i and j separated by the angle θ. NCP is the North Celestial Pole (δ = + 90°). |
Extending this idea to the positions and proper motions is not so obvious, as their errors are vector quantities in the tangent plane of the celestial sphere. The proposed solution is to decompose the vectorial errors into components that are parallel and normal to the great-circle arc connecting the two sources (Fig. 2). For convenience, we introduce a generic variable ϕ representing “differential position” in much the same way as μ is used to represent “proper motion”. Thus ϕα ∗ = Δαcosδ and ϕδ = Δδ. The corresponding components parallel and normal to the great-circle arc are denoted ϕ || and ϕ ⊥ , and similarly for the proper motion components μ || and μ ⊥ . With ψ denoting the position angle of the great-circle arc from i to j at the respective source, we have: ![\begin{equation} \label{eq:transf1} \left. \begin{array}{ll} \varphi_{||} &\displaystyle = \phantom{-}\varphi_{\alpha*}\sin\psi + \varphi_{\delta}\cos\psi \\[1mm] \varphi_{\perp} &\displaystyle = -\varphi_{\alpha*}\cos\psi + \varphi_{\delta}\sin\psi\\[1mm] \mu_{||} &\displaystyle = \phantom{-}\mu_{\alpha*}\sin\psi + \mu_{\delta}\cos\psi \\[1mm] \mu_{\perp} &\displaystyle = -\mu_{\alpha*}\cos\psi + \mu_{\delta}\sin\psi \end{array} \quad\right\}. \end{equation}](/articles/aa/full_html/2012/07/aa18808-12/aa18808-12-eq113.png) (8)\arraycolsep1.75ptWe can now define an orthogonal transformation from the 10 astrometric parameter errors in ei and ej to the errors in the 10 quantities Σϕ||, Σϕ⊥, Σϖ, Σμ||, Σμ⊥, Δϕ||, Δϕ⊥, Δϖ, Δμ||, and Δμ ⊥ obtained as the sums and differences of the variables in Eq. (8). The Jacobian Jij of this transformation is detailed in Appendix A, which also gives a recipe for computing the trigonometric factors in Eq. (8). We can now define the statistics S1,n/2(Σϕ||), etc., based on the individual transformed errors divided by their estimated standard uncertainties. The latter are obtained from the diagonal elements of the transformed covariance matrix,
(8)\arraycolsep1.75ptWe can now define an orthogonal transformation from the 10 astrometric parameter errors in ei and ej to the errors in the 10 quantities Σϕ||, Σϕ⊥, Σϖ, Σμ||, Σμ⊥, Δϕ||, Δϕ⊥, Δϖ, Δμ||, and Δμ ⊥ obtained as the sums and differences of the variables in Eq. (8). The Jacobian Jij of this transformation is detailed in Appendix A, which also gives a recipe for computing the trigonometric factors in Eq. (8). We can now define the statistics S1,n/2(Σϕ||), etc., based on the individual transformed errors divided by their estimated standard uncertainties. The latter are obtained from the diagonal elements of the transformed covariance matrix, ![\begin{equation} \label{eq:transf2} \vec{\tilde{F}}^{[\alpha]}_{ij} = \vec{J}_{ij} \begin{bmatrix} ~\vec{\tilde{U}}_{ii}^{[\alpha]} & \vec{\tilde{U}}_{ij}^{[\alpha]}~ \\[3pt] ~\vec{\tilde{U}}_{ji}^{[\alpha]} & \vec{\tilde{U}}_{jj}^{[\alpha]}~ \\[3pt] \end{bmatrix} \vec{J}_{ij}', \end{equation}](/articles/aa/full_html/2012/07/aa18808-12/aa18808-12-eq126.png) (9)where Jij is given by Eq. (A.1).
(9)where Jij is given by Eq. (A.1).
It can be noted that some of the transformed errors, viz., Σϖ, Δϕ||, Δϖ, and Δμ||, are invariant to a (small) change in the orientation and spin of celestial reference system, and therefore not affected by the possible issue of the rank-deficient normal matrix discussed in Sect. 3.2 of Paper I. The two remaining differences, Δϕ ⊥ and Δμ ⊥ , are less affected by such a change than the remaining sums as long as the angular separation of the pair (θ in Fig. 2) is small.
 |
Fig. 3 Autocovariance function of the along-scan attitude errors in Case A, as calculated from the actual errors in the simulation (solid line), and as estimated by the kinematographic model including terms to fourth order (dashed line). |
4. Results
4.1. Attitude errors and the kinematographic approximation
In Paper I it was shown that the covariance of the astrometric parameters can be written 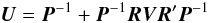 (10)(Eq. (17) in Paper I), where P-1 is the (trivially computed) covariance of the source parameters in the absence of attitude errors, and the second term is the correction due to the attitude errors. The correction term contains V, the covariance of the attitude parameters, and a connection matrix R specifying how the astrometric parameters depend on the attitude parameters. Since the whole point is about estimating this correction term, which clearly scales with the attitude errors, it is natural to start by comparing the empirical V (from the simulation experiments) with its theoretical expectation based on the covariance model of Paper I. This has the advantage that it brings us immediately to consider the kinematographic approximation and its possible improvement by means of the fudge factor ω.
(10)(Eq. (17) in Paper I), where P-1 is the (trivially computed) covariance of the source parameters in the absence of attitude errors, and the second term is the correction due to the attitude errors. The correction term contains V, the covariance of the attitude parameters, and a connection matrix R specifying how the astrometric parameters depend on the attitude parameters. Since the whole point is about estimating this correction term, which clearly scales with the attitude errors, it is natural to start by comparing the empirical V (from the simulation experiments) with its theoretical expectation based on the covariance model of Paper I. This has the advantage that it brings us immediately to consider the kinematographic approximation and its possible improvement by means of the fudge factor ω.
The solid line in Fig. 3 is the autocovariance function C4(τ) of the actual along-scan attitude errors for the third (middle) year of the simulation in Case A, computed according to Eq. (C.1) of Paper I. The subscript 4 indicates that it is based on the attitude model using cubic splines (i.e., of order M = 4). On the horizontal axis the delay τ is expressed in units of the spline knot interval Δt = 30 s. The dashed line is the autocovariance C1(τ) according to the kinematographic model for a bin width of B = 30 s, calculated according to Paper I by adding terms up to and including α = 4 and putting ω = 1.
Comparing Fig. 3 with its theoretical counterpart, Fig. C.1 (bottom) in Paper I, two differences stand out. First, the empirical autocovariance function for the cubic attitude spline in Fig. 3 goes through zero already at the delay τ = 0.74Δt, compared to the theoretical τ = Δt expected from Fig. C.1 (Paper I). A possible explanation of this result is given in Appendix D. Secondly, the variance is correspondingly larger, C4(0) ≃ C1(0)/0.74, making the integrals of the two autocovariance functions roughly equal (which makes sense since the integral is the inverse of the mean rate of the astrometric weight of the observations). In Paper I the correlation length L of the attitude autocovariance function was defined as the value of τ at the first zero crossing; thus we use L = 22.2 s in the following.
The autocovariance functions in Fig. 3 refer to the instantaneous attitude errors e(t) from the simulations or according to theory. As explained in Appendix C of Paper I, the attitude error a(t) obtained by averaging e(t) over the nine consecutive CCD observations in the astrometric field is in fact more relevant for the astrometric errors. In particular, we may estimate the fudge factor ω by comparing the variance of a(t) from the simulations with the variance according to the fourth-order kinematographic approximation. The latter is calculated as ![\begin{equation} \label{eq:omegaSum} \text{Var}\left[ a^{[4]} \right] = \sum_{\alpha=0}^4 \omega^{\alpha+1} \text{Var}\left[ a^{(\alpha)} \right], \end{equation}](/articles/aa/full_html/2012/07/aa18808-12/aa18808-12-eq147.png) (11)where the variances on the right-hand side of the equation are computed as described in Paper I, using ω = 1. Adjusting ω for equality between Var [a] from the simulation and the sum in Eq. (11) gives ω = 1.158.
(11)where the variances on the right-hand side of the equation are computed as described in Paper I, using ω = 1. Adjusting ω for equality between Var [a] from the simulation and the sum in Eq. (11) gives ω = 1.158.
This empirical estimate of ω agrees very well with the theoretical prediction from Eq. (C.5) in Paper I. Using the correlation length L = 22.2 s from Fig. 3, the attitude bin width B = 30 s and the temporal separation of the CCD observations, T = 4.85 s, we obtain ω = 1.164. In the subsequent analysis of the astrometric errors we will consider the two cases ω = 1 and ω = 1.16.
 |
Fig. 4 Distribution of the separation angle θ for the considered 150 000 pairs of sources in Case A and B (G = 13). |
4.2. Astrometric errors
The main results for the astrometric errors are summarised in Tables 1–4 and discussed hereafter. It should be recalled that the tables give the statistic Sν,n defined by Eq. (5), which ideally should be zero. A value of + 0.1, for example, means that the corresponding variance is underestimated by 10%, in the sense that it requires correction by the factor 1.1. The corresponding standard uncertainty is underestimated by ≃ 5%, in that it requires a correction by the factor 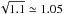 .
.
Although the astrometric errors are of course obtained for all 106 sources in each experiment, the calculation of the theoretical covariances was for practical reasons only done for 300 000 sources at each magnitude (i.e., for 300 000 sources in Case A, and for 300 000 brighter and an equal number of fainter sources in Case B). Figure 4 shows the distribution of the separation angle θ for the 150 000 source pairs considered when computing the source pair statistics in Case A (Table 2) and for the brighter pairs in Case B (Table 4). The distribution is essentially the same for the fainter pairs in Case B. The mean separation is ⟨ θ ⟩ = 0.21°.
4.2.1. Case A (uniform brightness)
Single source statistics in Case A.
Source pair statistics in Case A.
In this case we have the simplest possible configuration of sources (uniform brightness and uniform distribution over the celestial sphere), implying a constant astrometric weight per observation, per source, and per attitude bin. The average number of sources simultaneously visible in the combined field of view is 24 (the actual number at any time is a Poisson random variable with mean value 24, and consequently has a standard deviation of nearly 5). According to Sect. 4.5 in Paper I (see also Holl et al. 2010), we thus expect that the zero-order covariance estimate U [0] underestimates the variances by (at least) 1/25 ≃ 4%, and that the (neglected) correlations between sources with a small angular separation is also of this size.
The single-source statistics S5,n and S1,n for Case A, given in Table 1, show that the underestimation of the variances for α = 0 is in fact slightly worse, or about 5–6% depending on which parameter is considered. The smaller value is obtained for the declination at the mean epoch of observation, δ, and a larger value is obtained for the proper motion in right ascension, μα ∗ . As we shall see, it is a general feature that δ is slightly less and μα ∗ slightly more susceptible to the attitude errors than the other astrometric parameters. This is probably related to the more favourable geometry for the determination of δ implied by the scanning law, also reflected in the generally smaller uncertainties in that parameter (e.g., Eq. (5.5) and Table 3 in Lindegren 2010)3.
In the higher-order approximations (α = 1, 2, ... ) the degree of underestimation gradually decreases but does not disappear for ω = 1 (upper part of Table 1). Using the fudge factor ω = 1.16 estimated from the attitude variance gives much better results and almost correct variances for α = 3. For α = 4 it gives a small overestimation of the variances (negative values in the table), suggesting that a slightly smaller fudge factor should perhaps be preferred. Figure 5 shows that the individual source statistics 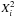 (for ν = 5) follow the expected chi-square distribution for α ≥ 3.
(for ν = 5) follow the expected chi-square distribution for α ≥ 3.
 |
Fig. 5 Distribution of the chi-square values included in the calculation of S5,n for the single sources in Case A. The thick grey curve is the expected chi-square distribution with 5 degrees of freedom; the coloured curves give the experimental distribution for 300 000 sources using successively higher orders of approximation (α) for the estimated covariances. A fudge factor ω = 1.16 was assumed. For the highest order (α = 4) the experimental distribution is indistinguishable from the theoretical one. |
Single source statistics in Case B.
Source pair statistics in Case B.
Table 2 gives the results for the source pair statistics S10,n/2 and S1,n/2. The overall results given by S10,n/2 are almost identical to the S5,n in Table 1. However, a different picture emerges when the results are divided up between the sums (Σ) and differences (Δ) of the errors in a pair. In the zero-order approximation (α = 0) the variances of the sums are strongly underestimated (by 9–10%), while the differences are only slightly underestimated (by about 1%). Compared with the single source statistics in Table 1 the underestimation of the sums Σ is almost doubled, which can be understood as the combined result of underestimating the variance of the parameter for each source (as in Table 1) and neglecting the positive correlation between them; for the differences Δ the two effects almost cancel since the correlation enters with the opposite sign.
Going to higher orders (α = 1, 2, ... ) improves the results. At α = 3 and 4 and using the fudge factor ω = 1.16 the agreement is quite good in all cases considered, when the statistical uncertainties are taken into account. The fact that both the sums Σ and the differences Δ obtain virtually unbiased variances indicates that the correlations at the relevant spatial scales (≃0.2°) are correctly estimated by the model. A more direct validation of this can be made by comparing the sample correlation coefficients from the simulation with the theoretical values. Figure 6 shows such a comparison for the parallaxes; the results for the other astrometric parameters are very similar (cf. Holl et al. 2010). Again, the simulations suggest that, for ω = 1.16, the best agreement is found for α = 3, alternatively that a slightly smaller value of ω should be used.
When comparing the results for the parameters that are invariant to a change in the reference system (e.g., Σϖ) to those that are not (the remaining Σ parameters), we do not find any difference that could be related to the rank deficiency of the normal matrix (Sect. 3.3). We conclude that the rank deficiency is not an issue at the level of errors considered in this study.
4.2.2. Case B (two different magnitudes)
 |
Fig. 6 Comparison of the sample correlation coefficients (circles) of the parallax errors of source pairs in Case A with the average theoretical coefficients (lines) computed for ω = 1.16 in successive approximations (α). The pairs were grouped in samples of equal size depending on θ, and the sample correlation coefficient plotted against the average θ of each group. To reduce the statistical uncertainty of the sample correlation coefficients (indicated by the error bars), many more pairs were used to compute the sample values than the 150 000 pairs for which theoretical values were available. |
The total number of observations in Case B is the same as in Case A, but only 30% of them have the same noise level as before, σAL = 92 μas (for G = 13), while 70% have σAL = 231 μas (for G = 15). The total astrometric weight is therefore about 41% of what we had in Case A, and the attitude variance is expected to be about 2.4 times higher.
The single-source statistics S5,n and S1,n for Case B are given in Table 3. For the brighter sources (G = 13) the underestimation of the variances for α = 0 is now about 14%, or 2.6 times higher than in Case A, in reasonable agreement with the increased attitude variance. For the fainter sources the underestimation is only 2%, or 6.8 times smaller than for the brighter sources, mainly reflecting the weight ratio 6.3 between the observations.
In the higher-order approximations (α = 1, 2, ... ) the degree of underestimation decreases in much the same way as in Case A, if one allows for the different overall levels among the brighter and fainter sources. This is true for both values of the fudge factor ω. It is especially gratifying to note that the same factor ω = 1.16 (or perhaps a slightly smaller value) turns out to be optimal at both magnitudes. Figure 7 shows the distribution of the individual source statistics 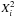 for ν = 5. For α ≥ 3 the empirical distributions follow the theoretical chi-square distribution for both brighter and fainter sources.
for ν = 5. For α ≥ 3 the empirical distributions follow the theoretical chi-square distribution for both brighter and fainter sources.
The source pair statistics in Table 4 show a qualitatively similar behaviour as discussed in Sect. 4.2.1 for Case A, only even more pronounced for the brighter sources (and much less for the fainter). In particular the variances for both the sums and the differences are essentially correctly estimated for α = 4, if ω = 1.16 is used. Figure 8 shows the variation of the correlation coefficient in parallax as a function of the separation angle. As expected, the correlations are much stronger for the brighter pairs (left) than for the fainter ones (right). Similar to Fig. 6 the theoretical curves for α = 3 seem to fit the simulations better than α = 4, while the latter value gives the best match of the variances especially for the bright sources in Tables 3 and 4. The reason for this discrepancy is not completely understood, but we note that the shape of the theoretical autocorrelation curves is affected by the choice of the attitude bin width, B. Since that parameter was not optimized for the present study it is possible that a different combination of B and ω would allow a better matching of the kinematographic model to both the variances and the correlation values (cf. the discussion at the end of Appendix C in Paper I).
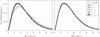 |
Fig. 7 Same as Fig. 5 but for Case B, showing the distributions of the chi-square values included in the calculation of S5,n for the brighter sources (G = 13) to the left and for the fainter sources (G = 15) to the right. |
 |
Fig. 8 Same as Fig. 6 but for Case B, showing the correlation coefficient for the brighter sources (G = 13) to the left and for the fainter sources (G = 15) to the right. |
Case B is somewhat contrived in that weight ratio of a single bright source to the total weight of the sources in the combined field of view is quite high, or about 0.10. This is partly a consequence of practical limitations (e.g., the total number of sources in the simulation), but it also provides a more stringent validation of the covariance model as the higher-order terms become relatively more important. The actual weight ratios obtained in the final astrometric solution for Gaia depends on the number and selection of primary sources and their distribution on the celestial sphere. A typical maximum weight ratio of about 0.01 is estimated by assuming that about 80% of the stars down to G = 16 can be used as primary sources (Hobbs et al. 2010) and by considering the least favourable case when both fields of view are at relatively high galactic latitudes ( ± 53°). In principle we expect that this should reduce the correlations between different sources by (at least) a factor of 10 compared with the present simulations for the brighter sources in Case B. Thus, very good estimates of the variances can probably be obtained already with α = 2 or 3.
5. Conclusions and future work
The aim of this paper was to test the validity of the covariance series expansion and associated assumptions, in particular the kinematographic approximation, using simulated astrometric solutions. As discussed in Sect. 3.1 the validation is made under the hypothesis that the observational errors are unbiased, uncorrelated, and with known standard uncertainties. Based on the numerical experiments reported above we conclude that the covariance model works very well: remaining differences (at the appropriate order and using a suitable fudge factor) are essentially within the statistical uncertainties of our numerical tests. In particular, the following results are noted.
-
1.
The correlation length of the attitude errors is generallysomewhat shorter than the knot interval of the attitude splines,due to the weak constraint on the quaternion length imposed onthe solution. When the reduced correlation length is taken intoaccount, the fudge factor ω, and hence the attitude variance per field-of-view transit, can be accurately predicted by means of the formulae given in Appendix C of Paper I.
-
2.
Using this value of ω, the variances of the astrometric parameters are correctly estimated in all the cases considered (including the mixture of brighter and fainter sources in Case B). In the worst case (the brighter sources in Case B) the variance estimation errors are <2.5% if a second-order expansion is used (α = 2) and <1% for a third-order expansion. In the final Gaia solution, using many more primary sources, the attitude errors should be much smaller resulting in estimation errors that are at least 10 times smaller.
-
3.
Within the statistical uncertainties of the experiments, the model correctly estimates the covariances (or correlations) for pairs of sources separated by ≃ 0.2°, although it would be desirable to improve the statistics by additional Monte Carlo experiments and examine the effect of the attitude bin width B.
The accuracy of the covariance expansion clearly improves if terms of higher order are included (at least up to α = 4). Since the higher orders are computationally expensive, it would be highly interesting if short-cuts could be found by approximation or extrapolation methods. A very simple extrapolation scheme would for example combine a truncated series with a somewhat larger fudge factor. In general the optimal α is a trade-off between accuracy and computational effort, and will depend on many factors including the magnitude distribution of the relevant sources and the nature of the scientific problem addressed. It is therefore not possible to give even an approximate guideline here for the choice of α.
The numerical experiments described in this paper are highly idealised, and future experiments need to address a number of problems resulting from more realistic assumptions, including: (1) a very non-uniform distribution of primary sources on the celestial sphere; (2) a much wider range of magnitudes; (3) attitude modelling errors due to the control system and high-frequency perturbations; (4) radiation damage and other correlated effects on the CCD level; (5) robustness issues, e.g., how the observation downweighting and excess noises (Sect. 5.1.2 in Lindegren et al. 2012) are propagated to the covariance estimates. The present study is therefore a first, but very important step towards a comprehensive modelling of the astrometric errors in the Gaia catalogue.
“Connectivity” here refers to the circumstance that two spatially separated sources may be observed together in the combined field of view, and thus connected by a common stretch of attitude. The angular separation between the connected sources could either be small ( ≲ 0.7°, the size of the field of view) or close to the basic angle of 106.5°. A more general concept is the “distance” d(i,k) between arbitrary sources i and k introduced in Paper I; the sources are directly connected if d(i,k) = 2, indirectly connected via a third star if d(i,k) = 4, etc.
It was demonstrated in Bombrun et al. (2012) that the converged solution does not depend on the initial values; thus starting from the true values does not prejudice the results but saves a number of iterations.
Acknowledgments
B. Holl’s work was supported by the European Marie-Curie research training network ELSA (MRTN-CT-2006-033481). L. Lindegren and D. Hobbs gratefully acknowledge support by the Swedish National Space Board. We thank the referee for comments that helped to improve the paper.
References
- Bombrun, A., Lindegren, L., Hobbs, D. L., et al. 2012, A&A, 538, A77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Butkevich, A. G., & Klioner, S. A. 2008, in IAU Symp. 248, ed. W. J. Jin, I. Platais, & M. A. C. Perryman, 252 [Google Scholar]
- Hobbs, D., Holl, B., Lindegren, L., et al. 2010, in IAU Symp. 261, ed. S. A. Klioner, P. K. Seidelmann, & M. H. Soffel, 315 [Google Scholar]
- Holl, B., & Lindegren, L. 2012, A&A, 543, A14 (Paper I) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Holl, B., Hobbs, D., & Lindegren, L. 2010, in IAU Symp. 261, ed. S. A. Klioner, P. K. Seidelmann, & M. H. Soffel, 320 [Google Scholar]
- Holl, B., Lindegren, L., & Hobbs, D. 2012a, in Workshop on Astrostatistics and Data Mining in Large Astronomical Databases, La Palma, 30 May–3 June 2011, ed. L. Sarro, J. De Ridder, L. Eyer, & W. O’Mullane, in press [Google Scholar]
- Holl, B., Prod’homme, T., Lindegren, L., & Brown, A. 2012b, MNRAS, in press [Google Scholar]
- Lindegren, L. 2010, in IAU Symp. 261, ed. S. A. Klioner, P. K. Seidelmann, & M. H. Soffel, 296 [Google Scholar]
- Lindegren, L., Lammers, U., Hobbs, D., et al. 2012, A&A, 538, A78 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- O’Mullane, W., Luri, X., Parsons, P., et al. 2011, Exp. Astron., 31, 243 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: The trigonometric factors in Eq. (8)
The Jacobian in Eq. (9) is
![\appendix \setcounter{section}{1} \begin{eqnarray} \label{eq:J10} \vec{J}_{ij} = \begin{bmatrix} \phantom{-}s_i & \phantom{-}c_i & \phantom{-}0 & \phantom{-}0 & \phantom{-}0 & \phantom{-}s_j & \phantom{-}c_j & \phantom{-}0 & \phantom{-}0 & \phantom{-}0~\\[3pt] -c_i & \phantom{-}s_i & \phantom{-}0 & \phantom{-}0 & \phantom{-}0 & -c_j & \phantom{-}s_j & \phantom{-}0 & \phantom{-}0 & \phantom{-}0~\\[3pt] \phantom{-}0 & \phantom{-}0 & \phantom{-}1 & \phantom{-}0 & \phantom{-}0 & \phantom{-}0 & \phantom{-}0 & \phantom{-}1 & \phantom{-}0 & \phantom{-}0~\\[3pt] \phantom{-}0 & \phantom{-}0 & \phantom{-}0 & \phantom{-}s_i & \phantom{-}c_i & \phantom{-}0 & \phantom{-}0 & \phantom{-}0 & \phantom{-}s_j & \phantom{-}c_j~\\[3pt] \phantom{-}0 & \phantom{-}0 & \phantom{-}0 & -c_i & \phantom{-}s_i & \phantom{-}0 & \phantom{-}0 & \phantom{-}0 & -c_j & \phantom{-}s_j~\\[3pt] \phantom{-}s_i & \phantom{-}c_i & \phantom{-}0 & \phantom{-}0 & \phantom{-}0 & -s_j & -c_j & \phantom{-}0 & \phantom{-}0 & \phantom{-}0~\\[3pt] -c_i & \phantom{-}s_i & \phantom{-}0 & \phantom{-}0 & \phantom{-}0 & \phantom{-}c_j & -s_j & \phantom{-}0 & \phantom{-}0 & \phantom{-}0~\\[3pt] \phantom{-}0 & \phantom{-}0 & \phantom{-}1 & \phantom{-}0 & \phantom{-}0 & \phantom{-}0 & \phantom{-}0 & -1 & \phantom{-}0 & \phantom{-}0~\\[3pt] \phantom{-}0 & \phantom{-}0 & \phantom{-}0 & \phantom{-}s_i & \phantom{-}c_i & \phantom{-}0 & \phantom{-}0 & \phantom{-}0 & -s_j & -c_j~\\[3pt] \phantom{-}0 & \phantom{-}0 & \phantom{-}0 & -c_i & \phantom{-}s_i & \phantom{-}0 & \phantom{-}0 & \phantom{-}0 & \phantom{-}c_j & -s_j~ \end{bmatrix}, \end{eqnarray}](/articles/aa/full_html/2012/07/aa18808-12/aa18808-12-eq187.png) (A.1)where for conciseness we have put ci = cosψi, si = sinψi, etc.
(A.1)where for conciseness we have put ci = cosψi, si = sinψi, etc.
The angles ψi and ψj defined in Fig. 2 can be computed using the equatorial normal triads [pi qi ri] and [pj qj rj] at the two sources (for the definition of the normal triad, see Eq. (5) in Lindegren et al. 2012). With θ denoting the angle between the sources we have ![\appendix \setcounter{section}{1} \begin{equation} \label{eq:calc_cspsi} \left. \begin{aligned} c_i \equiv\cos\psi_i\hspace{0.5pt} &= \phantom{-}\vec{q}_i'\vec{r}_j / \sin\theta \\[4pt] s_i \equiv\sin\psi_i\hspace{2.5pt} &= \phantom{-}\vec{p}_i'\vec{r}_j / \sin\theta \\[4pt] c_j \equiv\cos\psi_j\hspace{0pt} &= -\vec{q}_j'\vec{r}_i / \sin\theta \\[2pt] s_j \equiv\sin\psi_j\hspace{2pt} &= -\vec{p}_j'\vec{r}_i / \sin\theta \end{aligned} \quad\right\}, \end{equation}](/articles/aa/full_html/2012/07/aa18808-12/aa18808-12-eq193.png) (A.2)where
(A.2)where 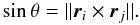 (A.3)If the position angles are needed they can be obtained as ψi = atan2(si,ci) and ψj = atan2(sj,cj), where atan2 is the arctan function without quadrant ambiguity. Similarly, the angular separation of the sources can be obtained as θ = atan2(sinθ, cosθ), where
(A.3)If the position angles are needed they can be obtained as ψi = atan2(si,ci) and ψj = atan2(sj,cj), where atan2 is the arctan function without quadrant ambiguity. Similarly, the angular separation of the sources can be obtained as θ = atan2(sinθ, cosθ), where 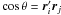 .
.
Appendix B: AGISLab
In this section we describe the software tool, AGISLab, used for the simulations. AGISLab was designed to be a lightweight processing framework to allow small scale realistic experiments, controlled by a scale factor, S, and to help develop new algorithms which would eventually be used in the real mission data processing software. AGISLab contains much of the algorithmic functionality of AGIS but is designed to generate observations on-the-fly as simulated input rather than ingesting raw data (simulated or real) as is done in AGIS. The core algorithms for the source, attitude and global update blocks were developed in AGISLab and are now in a common tool box called AGISTools which allows them to be used also by the AGIS processing framework. There are currently two additional blocks in AGISLab, the calibration and velocity blocks. The calibration block has not been developed much but merely acts as a place holder for future studies if needed. Calibration has largely been developed in AGIS where it is essential for the reduction of real data but has not yet been needed for our simulations. The velocity block has been used to develop algorithms and study the problem of determining the barycentric velocity of Gaia using its own observation data (Butkevich & Klioner 2008). This block has not yet been included in AGIS.
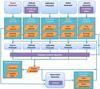 |
Fig. B.1 Overview of AGISLab showing the block structure and information flow. |
AGISLab provides features to generate a set of true parameter values, including a random distribution of sources on the celestial sphere and the true attitude (e.g., following the nominal Gaia scanning law), and hence the observations obtained by adding a Gaussian random number to the computed (“True”) observation times. Similarly, true values for global, calibration and velocity blocks can be generated. AGISLab can also generate starting values for each block’s parameters that deviate from the true values by random and systematic offsets. The starting values for each block are created in dedicated generators and are then used as the “Running” values shown in Fig. B.1. They are updated each iteration with improved estimates. Both the “Running” and “True” parameters for each block are stored in memory via a container and are used to generate errors plots, a feature that is very useful for analysis but will not be available in the real mission. AGISLab generates observations in a scanner based on information held in a satellite container, including for example the CCD geometry and the satellite orbit. Additionally, the scanner must compute the source direction via a simple or a full relativity model. Having generated the observations, AGISLab sets up the least-squares problem in dedicated processors for each block. The least squares problem is then solved using the conjugate gradient algorithm described in Bombrun et al. (2012). The process is iteratively repeated until convergence is achieved. Note that the generation of observations is only needed once at the start and the observation noise is added on-the-fly to avoid storing two sets of data. Finally, AGISLab contains a number of utilities to generate statistics and graphical output.
AGIS aims to make astrometric core solutions with up to some 5 × 108 (primary) sources, based on about 4 × 1011 observations, and is therefore built on a software framework specially designed to handle very efficiently the corresponding large data volumes and systems of equations. It is in practice hardly possible to run AGIS with less than about 106 primary sources, which (just) gives a sufficient number of observations per unit time to do a successful attitude determination. For numerical experiments it is often desirable to use considerably less than 106 sources running in a correspondingly much shorter time, and it is an important feature of AGISLab is that it can run such scaled-down versions of AGIS. Moreover, in order to accumulate statistics of the astrometric errors, the small-scale runs may have to be repeated many times with different noise realisations but otherwise identical conditions, which is easily done in AGISLab since the simulation of the input data is an integrated part of the system.
The scaling in AGISLab uses a single parameter S such that S = 1 leads to an astrometric solution that uses approximately the current Gaia design and a minimum of 106 primary sources, while S = 0.1 would only use 10% as many primary sources, etc. For S < 1 it is necessary to modify the Gaia design used in the simulations in order to preserve certain key quantities such as the mean number of sources in the focal plane at any time, the mean number of field transits of a given source over the mission, and the mean number of observations per degree of freedom of the attitude model. In practice this is done by formally reducing the focal length of the astrometric telescope (in order to get enough sources in the field of view at any time) and the spin rate of the satellite by the factor S1/2, and increasing the time interval between attitude spline knots by the factor S-1 (to get enough observations per attitude spline knot interval). The main considerations are as follows:
-
1.
The total mission length is independent of S. Rationale: the disentanglement of position, parallax and proper motion depends critically on having a mission length of at least a few years (nominally 5 yr). Thus it makes no sense to try to save computations by reducing the mission length.
-
2.
At any time, the expected number of sources in the focal plane, n, should be independent of S (with n ≫ 1). Rationale: Gaia can only make relative measurements among the sources simultaneously visible in the combined field of view. This depends on having a certain minimum number at any time.
-
3.
The mean number m of field transits of a given source over the mission should be independent of S. Rationale: the nominal scanning law is carefully tuned to give at least the minimum number of transits needed to guarantee successful resolution of the astrometric parameters for any source. Reducing m could result in bad solutions for at least some sources.
-
4.
The mean number k of field-of-view transits of primary sources per attitude knot interval should be independent of S. Rationale: successful determination of the attitude spline coefficients requires a certain minimum number of AL and AC observations in each knot interval. Reducing k could result in bad attitude determination in some intervals.
Let L be the mission length, N the total number of primary sources on the sky (assumed to be uniformly distributed in a statistical sense), ΦAL and ΦAC the full width of the field of view in the AL and AC directions, Ω the satellite spin rate, and Δt the mean time interval between attitude knots. Then ![\appendix \setcounter{section}{2} \begin{eqnarray} n &= &\frac{N}{\pi}\,\Phi_{\rm AL}\sin\left({\textstyle\frac{1}{2}}\Phi_{\rm AC}\right), \label{eq01}\\[6pt] m &=& \frac{1}{\pi}\,\Omega L\sin\left({\textstyle\frac{1}{2}}\Phi_{\rm AC}\right), \label{eq02}\\[6pt] k &= &\frac{N}{\pi}\,\Omega\Delta t\sin\left({\textstyle\frac{1}{2}}\Phi_{\rm AC}\right), \label{eq03} \end{eqnarray}](/articles/aa/full_html/2012/07/aa18808-12/aa18808-12-eq211.png) not counting dead-time. For the current Gaia design we have the nominal parameters L0 = 5 yr, ΦAL,0 = 0.708°, ΦAC,0 = 0.691°, and Ω0 = 60′′ s-1. Assuming N0 = 106 and Δt0 = 30 s we get n0 ≃ 24, m0 ≃ 88, and k0 ≃ 17.
not counting dead-time. For the current Gaia design we have the nominal parameters L0 = 5 yr, ΦAL,0 = 0.708°, ΦAC,0 = 0.691°, and Ω0 = 60′′ s-1. Assuming N0 = 106 and Δt0 = 30 s we get n0 ≃ 24, m0 ≃ 88, and k0 ≃ 17.
Now suppose we scale the problem by the factor S (<1), so that the total number of sources is N = SN0. To keep the same n we see from Eq. (B.1) that ΦAL and/or ΦAC must be increased. It is desirable to keep the focal-plane layout fixed by modifying both angles by the same factor, which can be achieved my changing the effective focal length F (nominal value F0 = 35 m). Using the small-angle approximation we find that ΦAL,AC ∝ F-1 and consequently n ∝ NF-2. Choosing F = S1/2F0 therefore makes n independent of S. From Eq. (B.2) we then find that Ω = S1/2Ω0 makes m independent of S, and finally from Eq. (B.3) we find that Δt = S-1Δt0 makes k independent of S. We note that the angle ΩΔt covered by the attitude knot interval scales as S − 1/2, thus preserving the ratio ΩΔt/ΦAL. To summarize: ![\appendix \setcounter{section}{2} \begin{eqnarray} \label{eq05} &&N \propto S^1, \quad F \propto S^{1/2}, \quad \Phi_{\rm AL,AC} \propto S^{-1/2}, \nonumber\\[3pt] &&~~~~~~~~~~~~~~~~~\Omega \propto S^{1/2}, \quad \Delta t \propto S^{-1}, \quad \Omega\Delta t \propto S^{-1/2}. \quad \end{eqnarray}](/articles/aa/full_html/2012/07/aa18808-12/aa18808-12-eq233.png) (B.4)It can be noted that the AC field size is also related to the spin rate and precession rate of the spin axis (
(B.4)It can be noted that the AC field size is also related to the spin rate and precession rate of the spin axis (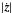 ) by the condition that there should be sufficient overlap between successive scans of the field of view. The prescription for z(t) is independent of the scaling factor, which is then also the case for
) by the condition that there should be sufficient overlap between successive scans of the field of view. The prescription for z(t) is independent of the scaling factor, which is then also the case for 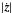 . The change in the z axis in one spin period (2π/Ω) is consequently inversely proportional to Ω and scales as S − 1/2. But ΦAC ∝ S − 1/2, so the relative amount of field overlap is independent of S.
. The change in the z axis in one spin period (2π/Ω) is consequently inversely proportional to Ω and scales as S − 1/2. But ΦAC ∝ S − 1/2, so the relative amount of field overlap is independent of S.
In conclusion, AGISLab is a versatile tool which allows both full scale solutions with at least one million sources and small scale simulations which allow algorithms to be developed and tested easily. Except for the experiments shown in Fig. D.1 the simulations presented in this paper did not use the scaling option (i.e., S = 1 was used), as we wanted to have the maximum degree of realism compatible with the available computing resources. However, the scaling did help greatly with the development and testing of the algorithms, which could be done very efficiently with a much smaller S.
Appendix C: Implementation details on the covariance model
This appendix provides some technical details concerning the implementation of the covariance model used in this paper. The set-up for the present simulations with 1 million sources and 5.2 million attitude bins results in the following amount of data needed by the model:
-
for every source i the inverse Cholesky factor
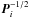 : 15 reals, in total 1.5 × 107 reals;
: 15 reals, in total 1.5 × 107 reals; -
for every source–attitude point combination ip with at least one observation, the 5 × 1 array hip according to Eq. (I:54): 5 reals. For an average of 88 field-of-view transits, each taking on average 1.4 attitude intervals, this gives in total 6.1 × 108 reals;
-
for every attitude point p, the inverse square root of the weight
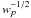 : 1 real, in total 5.2 × 106 reals;
: 1 real, in total 5.2 × 106 reals; -
three arrays defining the structure of the connections. (a) For every source a list of the attitude points at which it was observed, total: 1.2 × 108 integers. (b) For every attitude point a list of the sources observed at that point, total: 1.2 × 108 integers. (c) The array lookup can be done without any searching by creating one additional array pointing to where in the source-ordered arrays a particular attitude point is referenced (or vice versa): 1.2 × 108 integers. From any of the three arrays the other two can be constructed, so only one of them need to be persisted on disk.
Disregarding the matrix structure overhead and using 4 bytes per real or integer, the data size is 4 GigaByte (GB), in practice needing 8 GB when stored uncompressed on disk. Although the data are stored in single precision (4 bytes), all computations are done in double precision (8 bytes).
The model is initialised based on all AL observation made by the AF and SM CCDs. The AC observations are not used in the model as they contribute only marginally to the source parameters (see the discussion in Sect. 2.1 of Paper I), although they are by necessity included in the numerical experiments. Note that the model does not use the observations themselves, only values related to the partial derivatives, weights, and the structure of the equations. The inverse Cholesky factor 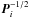 and the array hip are initialised using the partial derivatives with respect to the true astrometric parameters; the difference compared to using the final estimated parameters is negligible since the observation model can be considered linear within the parameter errors. The weights used in
and the array hip are initialised using the partial derivatives with respect to the true astrometric parameters; the difference compared to using the final estimated parameters is negligible since the observation model can be considered linear within the parameter errors. The weights used in 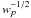 and hip are computed from the true observation uncertainties. As mentioned in Sect. 2.3 their actual values are irrelevant in Case A, and only their relative values matter in Case B. For the real mission the observation uncertainties will be accurately estimated partly based on the residual statistics.
and hip are computed from the true observation uncertainties. As mentioned in Sect. 2.3 their actual values are irrelevant in Case A, and only their relative values matter in Case B. For the real mission the observation uncertainties will be accurately estimated partly based on the residual statistics.
To use the model it must be loaded completely into memory. For any Jacobian mapping to the source or attitude parameters, the model returns an estimate of the covariance matrix, cf. Eq. (3). Because the internal computation sequentially estimates terms of increasing order, a stopping criterion might be used, but in practice terms are estimated up to a pre-defined maximum order. The sequence of successive approximations can be returned without additional computational cost. For most of the tests in this paper a trivial Jacobian is used that results in the covariance matrix for a single source or pair of sources. With a total of N sources (5N astrometric parameters) and P attitude points in the model, and considering the covariance of Q quantities (number of rows in the Jacobian), the model allocates two large arrays that store the intermediate data of G(α) (see Eq. (52) in Paper I): one source matrix of size Q × 5N when α is even, and one attitude matrix of size Q × P when α is odd. For example, requesting the covariance matrix for one source requires Q = 5. For the experiments in this paper both matrices are of size ≃ Q × 40 MegaByte (MB), using double precision reals. Because the recursion alternates between the two matrices, the new version (of order α) may overwrite the old one (of order α − 2) in memory.
When a quantity only combines a small number of sources the source and attitude matrices will start out extremely sparse but will get increasingly more populated towards higher terms. Numerical experiments by Holl et al. (2012a) suggest that for α ≥ 6 all sources are connected, implying that the source and attitude matrices will be completely filled. Because the amount of computations for each next term is proportional to the number of non-zero elements in the source or attitude matrix of the previous term, the computation time will increase steeply with the number of terms evaluated. Computing the next uneven term involves, for each of the Q quantities, the multiplication of the source (matrix) parameter element with hip for all attitude points p observed by the source, and storing the results at the corresponding points in the attitude matrix. The computation of the next even term involves the multiplication of an attitude (matrix) parameter element with 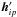 for all sources i observed at this point, and storing the results at the corresponding indices in the source matrix. This procedure can easily be multi-threaded by dividing up the non-zero elements of the initial matrix, as long as the writing to the target matrix is synchronised (e.g., because different sources are observed in the same attitude interval). For this study we used Q = 5 and 10 (for single sources and pairs), meaning that the internal source and attitude matrices needed some 200 and 400 MB, respectively. On our system, with two dual core 2.3 GHz Intel Xeon processors, the multi-threaded runtime for computing the covariance of Q = 10 parameters up to fourth order (α = 4) was about 6 s.
for all sources i observed at this point, and storing the results at the corresponding indices in the source matrix. This procedure can easily be multi-threaded by dividing up the non-zero elements of the initial matrix, as long as the writing to the target matrix is synchronised (e.g., because different sources are observed in the same attitude interval). For this study we used Q = 5 and 10 (for single sources and pairs), meaning that the internal source and attitude matrices needed some 200 and 400 MB, respectively. On our system, with two dual core 2.3 GHz Intel Xeon processors, the multi-threaded runtime for computing the covariance of Q = 10 parameters up to fourth order (α = 4) was about 6 s.
Appendix D: The flexibility of the attitude splines
In Sect. 4.1 it was noted that the autocovariance function of the along-scan attitude errors, shown in Fig. 3, is compressed along the time axis compared with the theoretical function given in Paper I. The correlation length L, defined as the delay at the first zero of the autocovariance function, is found to be shorter than the knot interval Δt, while in Fig. C.1 of Paper I we had L = Δt. The result that L < Δt was at first very surprising to us, but we now understand that it is related to the numerical attitude representation, using splines for each of the four components of the quaternion. This model therefore has four degrees of freedom per knot interval, whereas the physical attitude only has three. In the attitude updating of AGIS (and AGISLab) the solution is rendered unique by means of the regularization parameter λ (see Eq. (81) in Lindegren et al. 2012), which gently pushes the length of the quaternion towards 1. The numerical experiments described in this paper use a very small degree of
regularization, with λ2 = 10-7, resulting in an attitude solution with (almost) maximum flexibility for the given knot interval, and hence the smallest correlation length (it may be significant that we find L/Δt ≃ 3/4, or one degree of freedom per correlation length). Small-scale tests with progressively larger values of λ indeed result in stiffer attitude solutions, as shown by the increasing correlation lengths in Fig. D.1; in the limit of large λ we have L ≃ Δt. Thus the flexibility of the attitude spline depends not only on the knot interval Δt but also on the regularization parameter used in the solution.
 |
Fig. D.1 Autocorrelation functions of the along-scan attitude errors for different values of the attitude regularization parameter λ. These curves were obtained in small-scale simulations of the astrometric solution, using the AGISLab scaling parameter S = 0.012 for about 12 000 sources uniformly distributed over the celestial sphere. |
All Tables
All Figures
 |
Fig. 1 Convergence plot for the astrometric solution in Case A. The solid curves show the rms errors of the astrometric parameter (i.e., the rms differences between the calculated and true values) as functions of the iteration number; the dashed curves show the rms of the corresponding source parameter updates. The different astrometric parameters are colour coded (green: α∗, blue: δ, red: ϖ, magenta: μα∗, cyan: μδ). |
| In the text | |
 |
Fig. 2 Definition of the angles ψi and ψj for two sources i and j separated by the angle θ. NCP is the North Celestial Pole (δ = + 90°). |
| In the text | |
 |
Fig. 3 Autocovariance function of the along-scan attitude errors in Case A, as calculated from the actual errors in the simulation (solid line), and as estimated by the kinematographic model including terms to fourth order (dashed line). |
| In the text | |
 |
Fig. 4 Distribution of the separation angle θ for the considered 150 000 pairs of sources in Case A and B (G = 13). |
| In the text | |
 |
Fig. 5 Distribution of the chi-square values included in the calculation of S5,n for the single sources in Case A. The thick grey curve is the expected chi-square distribution with 5 degrees of freedom; the coloured curves give the experimental distribution for 300 000 sources using successively higher orders of approximation (α) for the estimated covariances. A fudge factor ω = 1.16 was assumed. For the highest order (α = 4) the experimental distribution is indistinguishable from the theoretical one. |
| In the text | |
 |
Fig. 6 Comparison of the sample correlation coefficients (circles) of the parallax errors of source pairs in Case A with the average theoretical coefficients (lines) computed for ω = 1.16 in successive approximations (α). The pairs were grouped in samples of equal size depending on θ, and the sample correlation coefficient plotted against the average θ of each group. To reduce the statistical uncertainty of the sample correlation coefficients (indicated by the error bars), many more pairs were used to compute the sample values than the 150 000 pairs for which theoretical values were available. |
| In the text | |
 |
Fig. 7 Same as Fig. 5 but for Case B, showing the distributions of the chi-square values included in the calculation of S5,n for the brighter sources (G = 13) to the left and for the fainter sources (G = 15) to the right. |
| In the text | |
 |
Fig. 8 Same as Fig. 6 but for Case B, showing the correlation coefficient for the brighter sources (G = 13) to the left and for the fainter sources (G = 15) to the right. |
| In the text | |
 |
Fig. B.1 Overview of AGISLab showing the block structure and information flow. |
| In the text | |
 |
Fig. D.1 Autocorrelation functions of the along-scan attitude errors for different values of the attitude regularization parameter λ. These curves were obtained in small-scale simulations of the astrometric solution, using the AGISLab scaling parameter S = 0.012 for about 12 000 sources uniformly distributed over the celestial sphere. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


