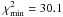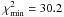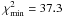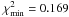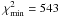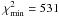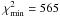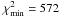| Issue |
A&A
Volume 543, July 2012
|
|
|---|---|---|
| Article Number | A104 | |
| Number of page(s) | 8 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/201117944 | |
| Published online | 04 July 2012 | |
Galaxy cluster angular-size data constraints on dark energy
1 Department of Astronomy, Beijing Normal University, 100875, Beijing, PR China
e-mail: chenyun@mail.bnu.edu.cn
2 Department of Physics, Kansas State University, 116 Cardwell Hall, Manhattan, KS 66506, USA
e-mail: ratra@phys.ksu.edu
Received: 25 August 2011
Accepted: 20 April 2012
We use angular size versus redshift data for galaxy clusters provided by Bonamente and collaborators to place constraints on model parameters of constant and time-evolving dark energy cosmological models. These constraints are compatible with those from other recent data, but are not very restrictive. A joint analysis of the galaxy cluster angular-size data with the more restrictive baryon acoustic oscillation peak length scale and supernova Type Ia apparent-magnitude data, favors a spatially flat cosmological model currently dominated by a time-independent cosmological constant, but does not exclude time-varying dark energy.
Key words: cosmology: miscellaneous / cosmology: theory / dark energy
© ESO, 2012
1. Introduction
A number of lines of observational evidence support a “standard” model of cosmology with an energy budget that is significantly dominated by dark energy. Dark energy is most simply characterized as a negative-pressure substance that powers the observed accelerated cosmological expansion. It can evolve slowly in time and vary weakly in space, although current data are consistent with it being equivalent to Einstein’s cosmological constant. On the other hand, some studies argue that the observed accelerated expansion should instead be viewed as an indication that general relativity does not accurately describe gravitational physics on large cosmological length scales. For relevant reviews, we refer to Frieman (2008), Ratra & Vogeley (2008), Caldwell & Kamionkowski (2009), Sami (2009), Bartelmann (2010), Cai et al. (2010), and Brax (2009). In what follows, we assume that general relativity provides an accurate description of gravitation on cosmological length scales.
There are many dark energy models under discussion. For recent discussions, we cite the studies of Wei (2011), Jamil & Saridakis (2010), Maggiore (2011), Dutta & Scherrer (2010), Shao & Chen (2010), Lepe & Peña (2010), Sloth (2010), Liu (2010), Honorez et al. (2010), and references therein. Perhaps the most economical – and the current “standard” model – is the ΛCDM model (Peebles 1984), where the accelerated cosmological expansion is powered by Einstein’s cosmological constant, Λ, a spatially homogeneous fluid with equation of state parameter ωΛ = pΛ/ρΛ = −1 (with pΛ and ρΛ being the fluid pressure and energy density). In this model, the cosmological energy budget is dominated by ρΛ, with cold dark matter (CDM) being the second largest contributor. The ΛCDM model provides a reasonable fit to most observational constraints, although the “standard” CDM structure formation model might be in some observational trouble (see, e.g., Peebles & Ratra 2003; Perivolaropoulos 2010).
The ΛCDM model has a few apparent puzzles. Prominent among these is that the needed Λ energy density scale is of order an meV, very small compared to the higher (cutoff) value suggested by a perhaps naive application of quantum mechanics. Another puzzle is that we happen to be observing at a time not very different from when the Λ energy density started dominating the cosmological energy budget (this is the “coincidence” puzzle).
If the dark energy density – that responsible for powering the accelerated cosmological expansion – slowly decreased in time (rather than remaining constant like ρΛ), the energy densities of dark energy and nonrelativistic matter (CDM and baryons) would remain comparable for a longer period of time, and so alleviate the coincidence puzzle. In addition, a slowly decreasing dark energy density that is based on more fundamental physics at an energy density scale much higher than an meV, would result in a current dark energy density scale of an meV through gradual decrease over the long lifetime of the Universe. Thus, a slowly decreasing dark energy density could resolve some of the puzzles of the ΛCDM model (Ratra & Peebles 1988).
The XCDM parametrization is often used to describe a slowly decreasing dark energy density. In this parametrization, the dark energy is modeled as a spatially homogeneous (X) fluid with an equation of state parameter wX = pX/ρX, where wX < − 1/3 is an arbitrary constant and pX and ρX are the pressure and energy density of the X-fluid. When wX = −1, the XCDM parametrization reduces to the ΛCDM model, which is a complete and consistent model. For any other value of wX(< − 1/3), the XCDM parametrization is incomplete as it cannot describe spatial inhomogeneities (see, e.g., Ratra 1991). For computational simplicity, we study the XCDM parametrization only in the spatially flat cosmological case.
If the dark energy density evolves in time, physics demands that it also be spatially inhomogeneous. The φCDM model – in which dark energy is modeled as a scalar field φ with a gradually decreasing (in φ) potential-energy density V(φ) – is the simplest complete and consistent model of a slowly decreasing (in time) dark energy density. Here we focus on an inverse power-law potential-energy density V(φ) ∝ φ − α, where α is a nonnegative constant (Peebles & Ratra 1988; Ratra & Peebles 1988). When α = 0, the φCDM model reduces to the corresponding ΛCDM case. Here we only consider the spatially flat φCDM cosmological model.
It has been known for some time that a spatially flat ΛCDM model with a current energy budget dominated by a constant Λ is largely consistent with most observational constraints (see, e.g., Jassal et al. 2010; Wilson et al. 2006; Davis et al. 2007; Allen et al. 2008). Supernovae Type Ia (SNeIa) apparent-magnitude measurements (e.g., Riess et al. 1998; Perlmutter et al. 1999; Shafieloo et al. 2009; Holsclaw et al. 2010), in conjunction with cosmic microwave background (CMB) anisotropy data (e.g., Ratra et al. 1999; Podariu et al. 2001b; Spergel et al. 2003; Komatsu et al. 2009, 2011) combined with low estimates of the cosmological mass density (e.g., Chen & Ratra 2003b), as well as baryon acoustic oscillation (BAO) peak length scale estimates (e.g., Percival et al. 2007; Gaztañaga et al. 2009; Samushia & Ratra 2009b; Wang 2009) strongly suggest that we live in a spatially flat ΛCDM model with nonrelativistic matter contributing a little less than 30% of the current cosmological energy budget, with the remaining slightly more than 70% being contributed by a cosmological constant. These three sets of data carry by far the most weight when determining constraints on models and cosmological parameters.
Future data from space missions will tighten the constraints (see, e.g., Podariu et al. 2001a; Samushia et al. 2011; Wang et al. 2010). However, at present, it is of great importance to consider independent constraints that can be derived from other presently available data sets. While these data do not yet carry as much statistical weight as the SNeIa, CMB, and BAO data, they can potentially reassure us (if they provide constraints consistent with those from the better known data), or if the two sets of constraints are inconsistent this might lead to the discovery of hidden systematic errors or rule out the cosmological model under consideration.
Other data that have been used to constrain cosmological parameters include galaxy cluster gas-mass fraction (e.g., Allen et al. 2008; Samushia & Ratra 2008; Ettori et al. 2009), gamma-ray burst luminosity distance (e.g., Schaefer 2007; Liang & Zhang 2008; Wang 2008; Samushia & Ratra 2010), large-scale structure (e.g., Courtin et al. 2011; Baldi 2011; Basilakos et al. 2010), strong gravitational lensing (e.g., Chae et al. 2002, 2004; Lee & Ng 2007; Yashar et al. 2009), and lookback time (e.g., Capozziello et al. 2004; Simon et al. 2005; Samushia et al. 2010; Dantas et al. 2011) or Hubble parameter (Samushia & Ratra 2006; Samushia et al. 2007; Fernandez-Martinez & Verde 2008; Yang & Zhang 2010) data. While the constraints provided by these data are much less restrictive than those derived from the SNeIa, CMB, and BAO data, both types of data result in largely compatible constraints that generally support a currently accelerating cosmological expansion. This gives us confidence that the broad outlines of the “standard” cosmological model are now in place.
Angular-size data from compact radio sources have also been used to constrain cosmological parameters (see, e.g., Gurvits et al. 1999; Guerra et al. 2000; Lima & Alcaniz 2000; Lima & Alcaniz 2002; Chen & Ratra 2003a; Podariu et al. 2003; Santos & Lima 2008). There are two very recent samples of angular size versus redshift data from galaxy clusters obtained by combining their Sunyaev-Zeldovich effect (SZE) and X-ray surface brightness observations. These are the 25 data points from De Filippis et al. (2005) and the 38 data points from Bonamente et al. (2006). De Filippis et al. (2005) obtained their angular-size data by using an isothermal elliptical model for the galaxy clusters, while Bonamente et al. (2006) derived their data by assuming a non-isothermal spherical model. The sample of De Filippis et al. (2005) was used to constrain H0, result in good agreement with the independent studies of the Hubble Space Telescope key project and the estimates of WMAP (Cunha et al. 2007). The sample of Bonamente et al. (2006) has been previously used to constrain some cosmological parameters and to test the distance duality relationship of metric gravity models (see, e.g., De Bernardis et al. 2006; Holanda et al. 2012a; Lima et al. 2010; Cao & Liang 2011; Liang et al. 2011). In some literature, these two samples have been adopted to test the distance duality relationship, and it turns out that the sample of De Filippis et al. (2005) is more in accordance with no violation of the duality relation (Holanda et al. 2010, 2011, 2012b; Li et al. 2011; Meng et al. 2012).
In this paper, we use the newer and larger sample of galaxy cluster angular size versus redshift data from Bonamante et al. (2006, hereafter B06) to constrain cosmological models that have not been previously considered, and to constrain other cosmological parameters in models that have been previously considered. We show that these constraints are compatible with those derived using other data. We also perform a joint analysis of these angular-size data and SNeIa and BAO measurements and show that including the angular size data in the analysis affects the constraints, although not greatly so as the angular-size data do not yet have sufficient statistical weight.
Our paper is organized as follows. In Sect. 2, we present the basic equations of the three dark energy models we study. Constraints from the B06 angular diameter distances of galaxy clusters are derived in Sect. 3. In Sect. 4, the BAO data and the SNeIa measurements are used to constrain the dark energy models. In Sect. 5, we determine joint constraints on the dark energy parameters from different combinations of the data sets. Finally, we summarize our main conclusions in Sect. 6.
2. Basic equations of the dark energy models
The Friedmann equation of the ΛCDM model with spatial curvature can be written as 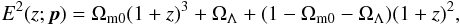 (1)where z is the redshift, E(z) = H(z)/H0 is the dimensionless Hubble parameter where H0 is the Hubble constant, and the model-parameter set is p = (Ωm0,ΩΛ) where Ωm0 is the nonrelativistic (baryonic and cold dark) matter density parameter and ΩΛ that of the cosmological constant. Throughout, the subscript 0 denotes the value of a quantity today. In this paper, the subscripts Λ, X, and φ represent the corresponding quantities of the dark energy component in the ΛCDM, XCDM, and φCDM models.
(1)where z is the redshift, E(z) = H(z)/H0 is the dimensionless Hubble parameter where H0 is the Hubble constant, and the model-parameter set is p = (Ωm0,ΩΛ) where Ωm0 is the nonrelativistic (baryonic and cold dark) matter density parameter and ΩΛ that of the cosmological constant. Throughout, the subscript 0 denotes the value of a quantity today. In this paper, the subscripts Λ, X, and φ represent the corresponding quantities of the dark energy component in the ΛCDM, XCDM, and φCDM models.
In this work, for computational simplicity, the spatial curvature is set to zero in the XCDM and φCDM cases. The Friedmann equation for the XCDM parametrization is then 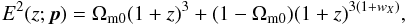 (2)where the model-parameter set is p = (Ωm0,wX).
(2)where the model-parameter set is p = (Ωm0,wX).
In the φCDM model, the inverse power-law potential-energy density of the scalar field adopted in this paper is 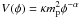 , where mp is the Planck mass, and α and κ are non-negative constants (Peebles & Ratra 1988). In the spatially flat case, the Friedmann equation of the φCDM model is
, where mp is the Planck mass, and α and κ are non-negative constants (Peebles & Ratra 1988). In the spatially flat case, the Friedmann equation of the φCDM model is 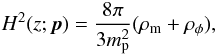 (3)where H(z) = ȧ/a is the Hubble parameter, and a(t) is the cosmological scale factor and an overdot denotes a time derivative. The energy densities of the matter and the scalar field are
(3)where H(z) = ȧ/a is the Hubble parameter, and a(t) is the cosmological scale factor and an overdot denotes a time derivative. The energy densities of the matter and the scalar field are 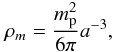 (4)and
(4)and 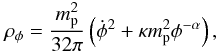 (5)respectively. According to the definition of the dimensionless density parameter, one has
(5)respectively. According to the definition of the dimensionless density parameter, one has 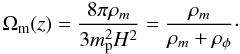 (6)The scalar field φ obeys the differential equation
(6)The scalar field φ obeys the differential equation 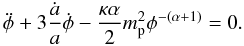 (7)Using Eqs. (3) and (7), as well as the initial conditions described in Peebles & Ratra (1988), one can numerically compute the Hubble parameter H(z). In this case, the model-parameter set is p = (Ωm0,α).
(7)Using Eqs. (3) and (7), as well as the initial conditions described in Peebles & Ratra (1988), one can numerically compute the Hubble parameter H(z). In this case, the model-parameter set is p = (Ωm0,α).
To use observational data to constrain cosmological models, we need various distance expressions. The coordinate distance is ![\begin{equation} \label{eq:r} r = \frac{c}{a_0 H_0 \sqrt{|\Omega_k|}} {\rm sinn}\left[\sqrt{|\Omega_k|} \int_{0}^{z}\frac{{\rm d}z'}{E(z')}\right], \end{equation}](/articles/aa/full_html/2012/07/aa17944-11/aa17944-11-eq39.png) (8)where Ωk is the spatial curvature density parameter and c is the speed of light, and
(8)where Ωk is the spatial curvature density parameter and c is the speed of light, and 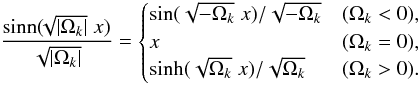 (9)The luminosity distance dL and the angular diameter distance dA are simply related to the coordinate distance as
(9)The luminosity distance dL and the angular diameter distance dA are simply related to the coordinate distance as 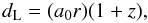 (10)and
(10)and 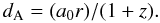 (11)
(11)
3. Constraints from the angular-size data
X-ray observations of the intracluster medium combined with radio observations of the galaxy cluster Sunyaev-Zeldovich effect allow an estimate to be made of the angular diameter distance (ADD) dA of galaxy clusters. Here we use the 38 ADDs of B06 to constrain cosmological parameters. These data can be found in Tables 1 and 2 of B06. For convenience, we re-collect them in Table 1.
Angular diameter distances of galaxy clusters from B06.
There are three sources of uncertainty in the measurement of dA: the cluster modeling error σmod, the statistical error σstat, and the systematic error σsys. The modeling errors are shown in Table 1 and the statistical and systematic errors are presented in Table 3 of B06. In our analysis here, we combine these errors in quadrature. Thus, the total uncertainty σtot satisfies 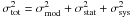 .
.
We constrain cosmological parameters by minimizing 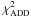
![\begin{equation} \label{eq:chi2ADD} \chi_{\rm ADD}^2 (H_0, \vec{p}) = \sum_{i=1}^{38}\frac{\left[d^{\rm th}_{\rm A} (z_i; H_0, \vec{p})-d_{\rm A}^{\rm obs}(z_i)\right]^2}{\sigma^2_{{\rm tot},i}}\cdot \end{equation}](/articles/aa/full_html/2012/07/aa17944-11/aa17944-11-eq91.png) (12)Here zi is the redshift of the observed galaxy cluster,
(12)Here zi is the redshift of the observed galaxy cluster, 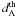 is the predicted value of the ADD in the cosmological model under consideration and
is the predicted value of the ADD in the cosmological model under consideration and 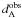 is the measured value. From
is the measured value. From 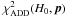 , we compute the likelihood function L(H0,p). We then treat H0 as a nuisance parameter and marginalize over it using a Gaussian prior with H0 = 68 ± 3.5 km s-1 Mpc-1 (Chen et al. 2003) to get a likelihood function L(p) that is a function only of the cosmological parameters of interest. The best-fit parameter values p ∗ are those that maximize the likelihood function and the 1, 2, and 3σ constraint contours are the set of cosmological parameters (centered on p∗) that enclose the 68.27%, 95.45% and 99.73% confidence levels, respectively, of the probability under the likelihood function.
, we compute the likelihood function L(H0,p). We then treat H0 as a nuisance parameter and marginalize over it using a Gaussian prior with H0 = 68 ± 3.5 km s-1 Mpc-1 (Chen et al. 2003) to get a likelihood function L(p) that is a function only of the cosmological parameters of interest. The best-fit parameter values p ∗ are those that maximize the likelihood function and the 1, 2, and 3σ constraint contours are the set of cosmological parameters (centered on p∗) that enclose the 68.27%, 95.45% and 99.73% confidence levels, respectively, of the probability under the likelihood function.
 |
Fig. 1 We display the 1, 2, and 3σ constraint contours for the ΛCDM model from the ADD data. The dashed diagonal line corresponds to spatially flat models and the shaded area in the upper left-hand corner is the region for which there is no big bang. The star marks the best-fit pair (Ωm0,ΩΛ) = (0.19, − 0.62) with |
Two standard-deviation bounds on cosmological parameters.
Figures 1–3 show the constraints from the ADD data on the three dark energy models we consider. Comparing these results to those shown in Figs. 1–3 of Chen & Ratra (2003a), which were derived using the compact radio source angular-size data of Gurvits et al. (1999), and to Figs. 1, 2 of Podariu et al. (2003), derived using the FRIIb radio galaxy angular-size data from Guerra et al. (2000), we see that the B06 galaxy cluster angular-size data provide approximately comparable constraints on cosmological parameters as those derived from the two earlier angular-size data sets. These ADD constraints are comparable to those from gamma-ray burst data (Samushia & Ratra 2010, Figs. 1–3 and 7–9), as well as those from Hubble parameter measurements (Samushia et al. 2007, Figs. 1–3).
 |
Fig. 2 We show the 1, 2, and 3 σ constraint contours for the XCDM parametrization from the ADD data. The dashed horizontal line at ωX = −1 corresponds to spatially flat ΛCDM models. The star marks the best-fit pair (Ωm0,wX) = (0.01, − 0.12) with |
 |
Fig. 3 We perform the 1, 2, and 3 σ constraint contours for the φCDM model from the ADD data. The horizontal axis at α = 0 corresponds to spatially flat ΛCDM models. The star marks the best-fit pair (Ωm0,α) = (0.54,5) with |
Current ADD data constraints are clearly not very restrictive, although it is encouraging that the ADD constraints on these dark energy models do not disfavor the regions of parameter space that are favored by other data. More importantly, we anticipate that ADD data to be acquired in the near future will provide significantly tighter constraints on cosmological parameters.
4. Constraints from BAO and SNeIa data
The BAO peak length scale can be used as a standard ruler to constrain cosmological parameters. Here we use the BAO data of Percival et al. (2010) to constrain the parameters of the ΛCDM and φCDM models and the XCDM parametrization.
 |
Fig. 4 We show the 1, 2, and 3 σ constraint contours for the φCDM model derived from the BAO data. The horizontal axis at α = 0 corresponds to spatially flat ΛCDM models. The star marks the best-fit pair (Ωm0,α) = (0.32,2.01) with |
Percival et al. (2010) measure the position of the BAO peak from the SDSS DR7 and 2dFGRS data, determining rs(zd)/DV(z = 0.275) = 0.1390 ± 0.0037, where rs(zd) is the comoving sound horizon at the baryon drag epoch, and ![\hbox{$D_V(z)\equiv [(1+z)^2 d_{\rm A}^2 cz/H(z)]^{1/3}$}](/articles/aa/full_html/2012/07/aa17944-11/aa17944-11-eq120.png) . By using Ωm0h2 = 0.1326 ± 0.0063 and Ωb0h2 = 0.02273 ± 0.00061 (where Ωb0 is the current value of the baryonic mass density parameter and h is the Hubble constant in units of 100 km s-1 Mpc-1) from WMAP5 (Komatsu et al. 2009), one can get
. By using Ωm0h2 = 0.1326 ± 0.0063 and Ωb0h2 = 0.02273 ± 0.00061 (where Ωb0 is the current value of the baryonic mass density parameter and h is the Hubble constant in units of 100 km s-1 Mpc-1) from WMAP5 (Komatsu et al. 2009), one can get 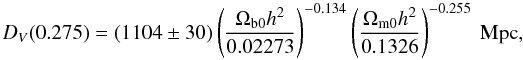 (13)as shown in Eq. (13) of Percival et al. (2010). The error in Ωb0h2 is ignored in this work, as the WMAP5 data constrains Ωb0h2 to within 0.5%.
(13)as shown in Eq. (13) of Percival et al. (2010). The error in Ωb0h2 is ignored in this work, as the WMAP5 data constrains Ωb0h2 to within 0.5%.
 |
Fig. 5 We display the 1, 2, and 3σ constraint contours for the φCDM model from the SNeIa data. The horizontal axis at α = 0 corresponds to spatially flat ΛCDM models. Thin solid lines (best fit at Ωm0 = 0.27 and α = 0.0 with |
Our results for the ΛCDM model and the XCDM parametrization agree very well with the Percival et al. (2010) results shown in their Fig. 5. Our results for the φCDM model are shown in Fig. 4. The BAO data constrains Ωm0 significantly, leaving ΩΛ, wX, and α almost unconstrained (see, e.g., Samushia & Ratra 2009a). The results obtained from the BAO data of Percival et al. (2010) are most directly comparable to those derived from the earlier BAO data of Eisenstein et al. (2005). Comparing to the constraints shown in Figs. 2–4 of Samushia & Ratra (2009a), one sees that the Percival et al. (2010) data lead to slightly more restrictive constraints than the Eisenstein et al. (2005) data.
Type Ia supernovae are standardizable candles that can be used to constrain cosmological parameters. Here we use the Union2 compliation of 557 SNeIa (covering a redshift range 0.015 ≤ z ≤ 1.4) of Amanullah et al. (2010) to constrain parameters of the ΛCDM and φCDM models and the XCDM parametrization.
Cosmological constraints from SNeIa data are obtained by using the distance modulus μ(z). The theoretical (predicted) distance modulus is ![\begin{equation} \label{eq:mu} \mu_{\rm th}(z; \vec{p}, \mu_0 )=5\log_{10} [D_{\rm L}(z; \vec{p})]+\mu_0, \end{equation}](/articles/aa/full_html/2012/07/aa17944-11/aa17944-11-eq138.png) (14)where μ0 = 42.38 − 5log 10h and the Hubble-free luminosity distance is given by
(14)where μ0 = 42.38 − 5log 10h and the Hubble-free luminosity distance is given by 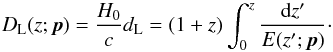 (15)The best-fit values of cosmological model parameters can be determined by minimizing the χ2 function
(15)The best-fit values of cosmological model parameters can be determined by minimizing the χ2 function ![\begin{equation} \label{eq:chi2SN} \chi^2_{SN}(\vec{p},\mu_0)=\sum_{i=1}^{557}\frac{[\mu_{{\rm th},i}(z_i; \vec{p},\mu_0)-\mu_{{\rm obs},i}(z_i)]}{\sigma^2_{\mu_i}}, \end{equation}](/articles/aa/full_html/2012/07/aa17944-11/aa17944-11-eq142.png) (16)where μobs,i(zi) is the distance modulus obtained from observations and σμi is the total uncertainty in the SNeIa data. The zero-point μ0 is treated as a nuisance parameter and marginalized over analytically (Di Pietro & Claeskens 2003; Perivolaropoulos 2005; Nesseris & Perivolaropoulos 2005). The covariance matrix with or without systematic errors can be found on the web1.
(16)where μobs,i(zi) is the distance modulus obtained from observations and σμi is the total uncertainty in the SNeIa data. The zero-point μ0 is treated as a nuisance parameter and marginalized over analytically (Di Pietro & Claeskens 2003; Perivolaropoulos 2005; Nesseris & Perivolaropoulos 2005). The covariance matrix with or without systematic errors can be found on the web1.
 |
Fig. 6 Thick (thin) solid lines are 1, 2, and 3σ constraint contours for the ΛCDM model from a joint analysis of the BAO and SNeIa (with systematic errors) data, with (and without) the ADD data. The cross (“+”) marks the best-fit point determined from the joint sample without the ADD data at Ωm0 = 0.28 and ΩΛ = 0.76 with |
Our results for the ΛCDM model and the XCDM parametrization agree very well with the Amanullah et al. (2010) results shown in their Figs. 10 and 11. The constraints on φCDM model parameters from these data are shown in Fig. 5. Comparing to Fig. 4 of Samushia & Ratra (2009b), we can see that the constraints of the Amanullah et al. (2010) data with systematic errors are approximately comparable to those of the earlier Kowalski et al. (2008) data for 307 SNeIa without consideration of their systematic errors. As for the BAO data, the SNeIa data constraints are also fairly one-dimensional, tightly constraining one combination of the cosmological parameters, while only weakly constraining the “orthogonal” combination.
 |
Fig. 7 Thick (thin) solid lines are 1, 2, and 3σ constraint contours for the XCDM parametrization from a joint analysis of the BAO and SNeIa (with systematic errors) data, with (and without) the ADD data. The cross (“+”) marks the best-fit point determined from the joint sample without the ADD data at Ωm0 = 0.28 and ωX = −1.04 with |
 |
Fig. 8 Thick (thin) solid lines are 1, 2, and 3σ constraint contours for the φCDM model from a joint analysis of the BAO and SNeIa (with systematic errors) data, with (and without) the ADD data. The cross (“ × ”) marks the best-fit point determined from the joint sample without the ADD data at Ωm0 = 0.28 and α = 0 with |
 |
Fig. 9 One-dimensional marginalized distribution probabilities of the cosmological parameters for the LCDM model. Thick (thin) lines are the results from a joint analysis of the BAO and SNeIa (with systematic errors) data, with (and without) the ADD data. |
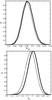 |
Fig. 10 One-dimensional marginalized distribution probabilities of the cosmological parameters for the XCDM parametrization. Thick (thin) lines are the results from a joint analysis of the BAO and SNeIa (with systematic errors) data, with (and without) the ADD data. |
 |
Fig. 11 One-dimensional marginalized distribution probabilities of the cosmological parameters for the φCDM model. Thick (thin) lines are the results of a joint analysis of the BAO and SNeIa (with systematic errors) data, with (and without) the ADD data. |
5. Joint constraints
Figures 6–8 show the constraints provided on the cosmological parameters of both the ΛCDM and φCDM models and the XCDM parametrization by a joint analysis of the BAO and SNeIa data, as well as by a joint analysis of the BAO, SNeIa, and ADD data. With the inclusion of systematic errors in the analysis of the SNeIa data of Amanullah et al. (2010), the new joint BAO and SNeIa constraints (thin solid contours in Figs. 6–8) are similar to the earlier ones shown in Figs. 4–6 of Samushia & Ratra (2010), which made use of the smaller SNeIa data set of Kowalski et al. (2008) that did not include systematic errors.
Figures 9–11 display the one-dimensional marginalized distribution probabilities of the cosmological parameters for the three cosmological models considered in this work, derived from a joint analysis of the BAO and SNeIa data, as well as from a joint analysis of the BAO, SNeIa, and ADD data. The marginalized 2σ intervals of the cosmological parameters are presented in Table 2.
The combination of BAO and SNeIa data gives tight constraints on the cosmological parameters. Adding the currently available galaxy-cluster ADD data to this combination does shift the constraint contours, although the effect is not large. Current ADD data do not have enough statistical weight to significantly affect the combined BAO and SNeIa results. The ADD data have approximately the same weight as currently available gamma-ray burst luminosity measurements (Samushia & Ratra 2010, Figs. 4–6 and 10–12).
The observational data considered here are clearly very consistent with the predictions of a spatially-flat cosmological model with an energy budget dominated by a time-independent cosmological constant. However, the data do not rule out time-evolving dark energy, although they do require that it not vary rapidly.
6. Conclusion
We have shown that the galaxy-cluster angular size versus redshift data of B06 can also be used to constrain dark energy model cosmological parameters. The resulting constraints are compatible with those derived from other sets of current data, thus strengthening support for the current “standard” cosmological model. The ADD constraints are approximately as restrictive as those that follow from currently available gamma-ray burst luminosity data, strong gravitational-lensing measurements, or lookback time (or Hubble parameter) observations. They are, however, much less restrictive than those that follow from a combined analysis of BAO peak length scale and SNeIa apparent-magnitude data.
The spatially flat ΛCDM model, currently dominated by a constant cosmological constant, provides a good fit to the data that we have studied here. However, these data are not inconsistent with a time-evolving dark energy.
We anticipate that angular-size data to be acquired in the near future will provide significantly tighter constraints on cosmological parameters. In conjunction with other observations, these angular-size data will prove very useful in pinning down parameter values of the “standard” cosmological model.
Acknowledgments
Yun Chen thanks Zong-Hong Zhu and Lado Samushia for their generous and helpful advice. Y.C. was supported by the Ministry of Science and Technology national basic science program (project 973) under grant No. 2012CB821804. BR was supported by DOE grant DEFG03-99EP41093.
References
- Allen, S. W., Rapetti, D. A., Schmidt, R. W., et al. 2008, MNRAS, 383, 879 [NASA ADS] [CrossRef] [Google Scholar]
- Amanullah, R., Lidman, C., Rubin, D., et al. 2010, ApJ, 716, 712 [NASA ADS] [CrossRef] [Google Scholar]
- Baldi, M. 2011, MNRAS, 411, 1077 [Google Scholar]
- Bartelmann, M. 2010, Rev. Mod. Phys., 82, 331 [NASA ADS] [CrossRef] [Google Scholar]
- Basilakos, S., Plionis, M., & Solà, J. 2010, Phys. Rev. D, 82, 083512 [NASA ADS] [CrossRef] [Google Scholar]
- Bonamente, M., Chapman, S. C., Ibata, R. A., et al. 2006, ApJ, 647, 25 (B06) [NASA ADS] [CrossRef] [Google Scholar]
- Brax, P. 2009 [arXiv:0912.3610] [Google Scholar]
- Cai, Y.-F., Saridakis, E. N., Setare, M. R., et al. 2010, Phys. Rept., 493, 1 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Caldwell, R. R., & Kamionkowski, M. 2009, Ann. Rev. Nucl. Part. Sci., 59, 397 [NASA ADS] [CrossRef] [Google Scholar]
- Cao, S., & Liang, N. 2011, RA&A, 11, 1199 [Google Scholar]
- Capozziello, S., Cardone, V. F., Funaro, M., et al. 2004, Phys. Rev. D, 70, 123501 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Chae, K.-H., Biggs, A. D., Blandford, R. D., et al. 2002, Phys. Rev. Lett., 89, 151301 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Chae, K.-H., Chen, G., Ratra, B., et al. 2004, ApJ, 607, L71 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, G., & Ratra, B. 2003a, ApJ, 582, 586 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, G., & Ratra, B. 2003b, PASP, 115, 1143 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, G., Gott, J. R., & Ratra, B. 2003, PASP, 115, 1269 [NASA ADS] [CrossRef] [Google Scholar]
- Courtin, J., Rasera, Y., Alimi, J.-M., et al. 2011, MNRAS, 410, 1911 [NASA ADS] [Google Scholar]
- Cunha, J. V., Marassi, L., & Lima, J. A. S. 2007, MNRAS, 379, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Dantas, M. A., Alcaniz, J. S., Mania, D., et al. 2011, Phys. Lett. B, 699, 239 [NASA ADS] [CrossRef] [Google Scholar]
- Davis, T. M., Mörtsell, E., Sollerman, J., et al. 2007, ApJ, 666, 716 [NASA ADS] [CrossRef] [Google Scholar]
- De Bernardis, F., Giusarma, E., & Melchiorri, A. 2006, Int. J. Mod. Phys. D, 15, 759 [NASA ADS] [CrossRef] [Google Scholar]
- De Filippis, E., Sereno, M., Bautz, M. W., et al. 2005, ApJ, 625, 108 [NASA ADS] [CrossRef] [Google Scholar]
- Di Pietro, E., & Claeskens, J.-F. 2003, MNRAS, 341, 1299 [NASA ADS] [CrossRef] [Google Scholar]
- Dutta, S., & Scherrer, R. J. 2010, Phys. Rev. D, 82, 043526 [NASA ADS] [CrossRef] [Google Scholar]
- Eisenstein, D. J., Zehavi, I., Hogg, D. W., et al. 2005, ApJ, 633, 560 [NASA ADS] [CrossRef] [Google Scholar]
- Ettori, S., Morandi, A., Tozzi, P., et al. 2009, A&A, 501, 61 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fernandez-Martinez, E., & Verde, L. 2008, J. Cosmol. Astropart. Phys., 0808, 023 [NASA ADS] [CrossRef] [Google Scholar]
- Frieman, J. A. 2008, AIP Conf. Proc., 1057, 87 [NASA ADS] [CrossRef] [Google Scholar]
- Gaztañaga, E., Cabré, A., & Hui, L. 2009, MNRAS, 399, 1663 [NASA ADS] [CrossRef] [Google Scholar]
- Guerra, E. J., Daly, R. A., & Wan, L. 2000, ApJ, 544, 659 [NASA ADS] [CrossRef] [Google Scholar]
- Gurvits, L. I., Kellermann, K. I., & Frey, S. 1999, A&A, 342, 378 [NASA ADS] [Google Scholar]
- Holanda, R. F. L., Lima, J. A. S., & Ribeiro, M. B. 2010, ApJ, 722, L233 [NASA ADS] [CrossRef] [Google Scholar]
- Holanda, R. F. L., Lima, J. A. S., & Ribeiro, M. B., 2011, A&A, 528, L14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Holanda, R. F. L., Cunha, J. V., & Lima, J. A. S. 2012a, Gen. Relativ. Gravit., 44, 501 [NASA ADS] [CrossRef] [Google Scholar]
- Holanda, R. F. L., Lima, J. A. S., & Ribeiro, M. B. 2012b, A&A, 538, A131 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Holsclaw, T., Alam, U., Sansó, B., et al. 2010, Phys. Rev. Lett., 105, 241302 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Honorez, L. L., Reid, B. A., Mena, O., Verde, L., & Jimenez, R. 2010, J. Cosmol. Astropart. Phys., 1009, 029 [CrossRef] [Google Scholar]
- Jamil, M., & Saridakis, E. N. 2010, J. Cosmol. Astropart. Phys., 1007, 028 [Google Scholar]
- Jassal, H. K., Bagla, J. S., & Padmanabhan, T. 2010, MNRAS, 405, 2639 [NASA ADS] [Google Scholar]
- Komatsu, E., Dunkley, J., Nolta, M. R., et al. 2009, ApJS, 180, 330 [NASA ADS] [CrossRef] [Google Scholar]
- Komatsu, E., Smith, K. M., Dunkley, J., et al. 2011, ApJS, 192, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Kowalski, M., Rubin, D., Aldering, G., et al. 2008, ApJ, 686, 749 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, S., & Ng, K.-W. 2007, Phys. Rev. D, 76, 043518 [NASA ADS] [CrossRef] [Google Scholar]
- Lepe, S., & Peña, F. 2010, Eur. Phys. J. C, 69, 575 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Li, Z., Wu, P., & Yu, H. 2011, ApJ, 729, L14 [NASA ADS] [CrossRef] [Google Scholar]
- Liang, N., & Zhang, L. N. 2008, AIP Conf. Proc., 1065, 367 [NASA ADS] [CrossRef] [Google Scholar]
- Liang, N., Cao, S., Liao, K., & Zhu, Z.-H. 2011 [arXiv:1104.2497] [Google Scholar]
- Lima, J. A. S., & Alcaniz, J. S. 2000, A&A, 357, 393 [NASA ADS] [Google Scholar]
- Lima, J. A. S., & Alcaniz, J. S. 2002, ApJ, 566, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Lima, J. A. S., Holanda, R. F. L., & Cunha, J. V. 2010, AIP Conf. Proc., 1241, 224 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, D.-J. 2010, Phys. Rev. D, 82, 063523 [NASA ADS] [CrossRef] [Google Scholar]
- Maggiore, M. 2011, Phys. Rev. D, 83, 063514 [NASA ADS] [CrossRef] [Google Scholar]
- Meng, X.-L., Zhang, T.-J., & Zhan, H. 2012, ApJ, 745, 98 [NASA ADS] [CrossRef] [Google Scholar]
- Nesseris, S., & Perivolaropoulos, L. 2005, Phys. Rev. D, 72, 123519 [NASA ADS] [CrossRef] [Google Scholar]
- Peebles, P. J. E. 1984, ApJ, 284, 439 [NASA ADS] [CrossRef] [Google Scholar]
- Peebles, P. J. E., & Ratra, B. 1988, ApJ, 325, L17 [Google Scholar]
- Peebles, P. J. E., & Ratra, B. 2003, Rev. Mod. Phys., 75, 559 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Perivolaropoulos, L. 2010, J. Phys. Conf. Ser., 222, 012024 [NASA ADS] [CrossRef] [Google Scholar]
- Percival, W. J., Cole, S., Eisenstein, D. J., et al. 2007, MNRAS, 381, 1053 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Percival, W. J., Reid, B. A., Eisenstein, D. J., et al. 2010, MNRAS, 401, 2148 [NASA ADS] [CrossRef] [Google Scholar]
- Perivolaropoulos, L. 2005, Phys. Rev. D, 71, 063503 [NASA ADS] [CrossRef] [Google Scholar]
- Perlmutter, S., Aldering, G., Goldhaber, G., et al. 1999, ApJ, 517, 565 [NASA ADS] [CrossRef] [Google Scholar]
- Podariu, S., Nugent, P., & Ratra, B. 2001a, ApJ, 553, 39 [NASA ADS] [CrossRef] [Google Scholar]
- Podariu, S., Ohyama, Y., Murayama, T., et al. 2001b, ApJ, 559, 9 [Google Scholar]
- Podariu, S., Daly, R. A., Mory, M. P., & Ratra, B. 2003, ApJ, 584, 577 [NASA ADS] [CrossRef] [Google Scholar]
- Ratra, B., & Peebles, P. J. E. 1988, Phys. Rev. D, 37, 3406 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Ratra, B. 1991, Phys. Rev. D, 43, 3802 [NASA ADS] [CrossRef] [Google Scholar]
- Ratra, B., Stompor, R., Ganga, K., et al. 1999, ApJ, 517, 549 [NASA ADS] [CrossRef] [Google Scholar]
- Ratra, B., & Vogeley, M. S. 2008, PASP, 120, 235 [NASA ADS] [CrossRef] [Google Scholar]
- Riess, A. G., Filippenko, A. V., Challis, P., et al. 1998, AJ, 116, 1009 [NASA ADS] [CrossRef] [Google Scholar]
- Sami, M. 2009, Curr. Sci., 97, 887 [Google Scholar]
- Samushia, L., & Ratra, B. 2006, ApJ, 650, L5 [Google Scholar]
- Samushia, L., & Ratra, B. 2008, ApJ, 680, L1 [Google Scholar]
- Samushia, L., & Ratra, B. 2009a, ApJ, 701, 1373 [Google Scholar]
- Samushia, L., & Ratra, B. 2009b, ApJ, 703, 1904 [Google Scholar]
- Samushia, L., & Ratra, B. 2010, ApJ, 714, 1347 [NASA ADS] [CrossRef] [Google Scholar]
- Samushia, L., Chen, G., & Ratra, B. 2007 [arXiv:0706.1963] [Google Scholar]
- Samushia, L., Dev, A., Jain, D., et al. 2010, Phys. Lett. B, 693, 509 [NASA ADS] [CrossRef] [Google Scholar]
- Samushia, L., Percival, W. J., Guzzo, L., et al. 2011, MNRAS, 410, 1993 [NASA ADS] [Google Scholar]
- Santos, R. C., & Lima, J. A. S. 2008, Phys. Rev. D, 77, 083505 [NASA ADS] [CrossRef] [Google Scholar]
- Schaefer, B. E. 2007, ApJ, 660, 16 [NASA ADS] [CrossRef] [Google Scholar]
- Shafieloo, A., Sahni, V., & Starobinsky, A. A. 2009, Phys. Rev. D, 80, 101301 [Google Scholar]
- Shao, S.-H., & Chen, P. 2010, Phys. Rev. D, 82, 126012 [NASA ADS] [CrossRef] [Google Scholar]
- Simon, J., Verde, L., & Jimenez, R. 2005, Phys. Rev. D, 71, 123001 [Google Scholar]
- Sloth, M. S. 2010, Int. J. Mod. Phys. D, 19, 2259 [NASA ADS] [CrossRef] [Google Scholar]
- Spergel, D. N., Verde, L., Peiris, H. V., et al. 2003, ApJS, 148, 175 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, Y. 2008, Phys. Rev. D, 78, 123532 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, Y. 2010, Mod. Phys. Lett. A, 25, 3093 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, Y., Percival, W., Cimatti, A., et al. 2010, MNRAS, 409, 737 [NASA ADS] [CrossRef] [Google Scholar]
- Wei, H. 2011, Phys. Lett. B, 695, 307 [CrossRef] [Google Scholar]
- Wilson, K. M., Chen, G., & Ratra, B. 2006, Mod. Phys. Lett. A, 21, 2197 [NASA ADS] [CrossRef] [Google Scholar]
- Yang, R.-J., & Zhang, S. N. 2010, MNRAS, 407, 1835 [Google Scholar]
- Yashar, M., Bozek, B., Abrahamse, A., et al. 2009, Phys. Rev. D, 79, 103004 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 We display the 1, 2, and 3σ constraint contours for the ΛCDM model from the ADD data. The dashed diagonal line corresponds to spatially flat models and the shaded area in the upper left-hand corner is the region for which there is no big bang. The star marks the best-fit pair (Ωm0,ΩΛ) = (0.19, − 0.62) with |
| In the text | |
 |
Fig. 2 We show the 1, 2, and 3 σ constraint contours for the XCDM parametrization from the ADD data. The dashed horizontal line at ωX = −1 corresponds to spatially flat ΛCDM models. The star marks the best-fit pair (Ωm0,wX) = (0.01, − 0.12) with |
| In the text | |
 |
Fig. 3 We perform the 1, 2, and 3 σ constraint contours for the φCDM model from the ADD data. The horizontal axis at α = 0 corresponds to spatially flat ΛCDM models. The star marks the best-fit pair (Ωm0,α) = (0.54,5) with |
| In the text | |
 |
Fig. 4 We show the 1, 2, and 3 σ constraint contours for the φCDM model derived from the BAO data. The horizontal axis at α = 0 corresponds to spatially flat ΛCDM models. The star marks the best-fit pair (Ωm0,α) = (0.32,2.01) with |
| In the text | |
 |
Fig. 5 We display the 1, 2, and 3σ constraint contours for the φCDM model from the SNeIa data. The horizontal axis at α = 0 corresponds to spatially flat ΛCDM models. Thin solid lines (best fit at Ωm0 = 0.27 and α = 0.0 with |
| In the text | |
 |
Fig. 6 Thick (thin) solid lines are 1, 2, and 3σ constraint contours for the ΛCDM model from a joint analysis of the BAO and SNeIa (with systematic errors) data, with (and without) the ADD data. The cross (“+”) marks the best-fit point determined from the joint sample without the ADD data at Ωm0 = 0.28 and ΩΛ = 0.76 with |
| In the text | |
 |
Fig. 7 Thick (thin) solid lines are 1, 2, and 3σ constraint contours for the XCDM parametrization from a joint analysis of the BAO and SNeIa (with systematic errors) data, with (and without) the ADD data. The cross (“+”) marks the best-fit point determined from the joint sample without the ADD data at Ωm0 = 0.28 and ωX = −1.04 with |
| In the text | |
 |
Fig. 8 Thick (thin) solid lines are 1, 2, and 3σ constraint contours for the φCDM model from a joint analysis of the BAO and SNeIa (with systematic errors) data, with (and without) the ADD data. The cross (“ × ”) marks the best-fit point determined from the joint sample without the ADD data at Ωm0 = 0.28 and α = 0 with |
| In the text | |
 |
Fig. 9 One-dimensional marginalized distribution probabilities of the cosmological parameters for the LCDM model. Thick (thin) lines are the results from a joint analysis of the BAO and SNeIa (with systematic errors) data, with (and without) the ADD data. |
| In the text | |
 |
Fig. 10 One-dimensional marginalized distribution probabilities of the cosmological parameters for the XCDM parametrization. Thick (thin) lines are the results from a joint analysis of the BAO and SNeIa (with systematic errors) data, with (and without) the ADD data. |
| In the text | |
 |
Fig. 11 One-dimensional marginalized distribution probabilities of the cosmological parameters for the φCDM model. Thick (thin) lines are the results of a joint analysis of the BAO and SNeIa (with systematic errors) data, with (and without) the ADD data. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.