| Issue |
A&A
Volume 542, June 2012
|
|
|---|---|---|
| Article Number | A117 | |
| Number of page(s) | 6 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201219289 | |
| Published online | 15 June 2012 | |
Lithium production in the merging of white dwarf stars
1 Departament de Física i Enginyeria Nuclear, EUETIBUniversitat Politècnica de Catalunya, C/ Comte d’Urgell 187, 08036 Barcelona, Spain
e-mail: richard.longland@upc.edu
2 Institut d’Estudis Espacials de Catalunya (IEEC), Ed. Nexus-201, C/ Gran Capità 2-4, 08034 Barcelona, Spain
3 Departament de Física Aplicada, Universitat Politècnica de Catalunya, C/ Esteve Terrades, 5, 08860 Castelldefels, Spain
4 Facultad de Ciencias Astronómicas y Geofísicas, Universidad Nacional de La Plata, Paseo del Bosque s/n, (1900) La Plata, Argentina
Received: 27 March 2012
Accepted: 10 May 2012
The origin of R Coronae Borealis stars has been elusive for over 200 years. Currently, two theories for their formation have been presented. These are the final flash scenario, in which a dying asymptotic giant branch star throws off its atmosphere to reveal the hydrogen poor, heavily processed material underneath, and the double degenerate scenario, in which two white dwarfs merge to produce a new star with renewed vigour. Some theories predict that the temperatures reached during the latter scenario would destroy any lithium originally present in the white dwarfs. The observed lithium content of some R Coronae Borealis stars, therefore, is often interpreted as an indication that the final flash scenario best describes their formation. In this paper, we show that lithium production can, indeed, occur in the merging of a helium white dwarf with a carbon-oxygen white dwarf if their chemical composition, particularly that of 3He, is fully considered. The production mechanism is described in detail, and the sensitivity of lithium production to the merger environment is investigated. Nucleosynthesis post-processing calculations of smoothed-particle hydrodynamics (SPH) tracer particles are performed to show that any lithium produced in these environments will be concentrated towards the cloud of material surrounding the R CrB star. Measurements of the lithium content of these clouds would, therefore, provide a valuable insight into the formation mechanism of R CrB stars.
Key words: nuclear reactions, nucleosynthesis, abundances / stars: abundances / white dwarfs / stars: evolution / stars: AGB and post-AGB
© ESO, 2012
1. Introduction
Some chemically peculiar stars are deficient in hydrogen, while being enriched in carbon and oxygen. They are known collectively as hydrogen-deficient stars, and can be broken into three sub-groups: hydrogen deficient carbon (HdC), extreme helium (EHe), and R Coronae Borealis (R CrB) stars. Their origin is difficult to explain through standard stellar evolution theory, so alternative scenarios for their formation are needed. One such theory is the final flash (FF) scenario, in which a late helium-shell flash occurs in a post-asymptotic giant branch (AGB) star, hence moving it back towards the AGB part of the Hertzsprung-Russell diagram. The numerical models of Schönberner (1979) first showed that fully developed helium shell flashes at temperatures greater than 100 MK are possible, lending weight to this theory. Indeed, FF objects, such as Sakurai’s object, are known to exist (Duerbeck & Benetti 1996). The other leading theory is known as the double degenerate (DD) scenario, which involves the merging of two white dwarf stars – one with a carbon-oxygen (CO) core, the other, helium (He). Full understanding of these two production mechanisms is yet to be reached, and considerable effort is still needed to explain all of the observational signatures of these stars.
A valid question that arises when considering the DD scenario is as follows: How feasible is it that two white dwarfs with the required compositions and masses merge to form an object resembling an R CrB star? To answer this question, the rate of these events within an observable distance can first be estimated. Roughly two of every three stars are born in binary systems (Nelemans et al. 2001). Of these stars, however, only a fraction are expected to evolve into double white dwarf systems that will merge within one Hubble time. Various estimates for this fraction are available, but as an example, the models of Nelemans et al. (2001) suggest that the birth rate of double white dwarfs in our galaxy is around 0.05 yr-1, of which around 50% will merge within one Hubble time. About 15% of those merging systems will comprise of a carbon-oxygen and a helium white dwarf (where the CO white dwarf was formed first). While direct comparisons of this rate with the population of known hydrogen deficient stars is not trivial, these rates are consistent with the known population of close binary systems (Iben et al. 1997).
The DD scenario is also successful, at least qualitatively, in explaining the bulk of the surface abundances in hydrogen deficient stars (e.g., Jeffery et al. 2011). Recently, models with detailed nuclear networks have shown that nucleosynthesis can occur in the DD scenario, thus explaining the over-abundance of 19F and 18O in R CrB stars (Longland et al. 2011). However, some details such as the enrichment of s-process elements are more difficult to explain. Lithium abundances also pose a problem, with four stars analysed by Asplund et al. (2000) yielding over-abundances in the range of 1.4 to 2.3 dex. It has been hypothesised that lithium can be enriched to these levels successfully in the FF scenario, while being hard to reconcile with high oxygen abundances in the DD scenario (Asplund et al. 2000; Clayton et al. 2011). The authors of those studies therefore interpreted the success of lithium production in the FF scenario as evidence that hydrogen deficient stars are most likely created in the dying stages of AGB stars. However, the formation of lithium in the DD scenario has not been fully explored to date.
The aim of this paper is to show that lithium can, indeed, be produced in the merging of a helium white dwarf with a carbon-oxygen white dwarf. We will begin in Sect. 2 by discussing the evolution of main sequence stars into a white dwarf binary system before explaining the mechanism necessary for lithium enrichment in Sect. 3. A number of numerical tests of this production are presented in Sect. 4 and its sensitivity to the thermodynamic properties of the merging event is discussed. These numerical tests will be compared with a detailed nucleosynthesis study by using Smoothed Particle Hydrodynamics tracer particles in Sect. 5 and we will conclude in Sect. 6.
2. Prior evolution of the binary system
In order to understand the mechanism responsible for producing lithium in the DD scenario, the evolution of the binary system must first be addressed. The most likely system giving rise to the necessary white dwarf pair (one 0.6 M⊙ carbon-oxygen and one 0.4 M⊙ helium white dwarf) is a system containing stars with masses of 5 M⊙ and 1 M⊙, respectively. Following two common envelope episodes, mass is ejected from the system resulting in two white dwarf stars in a close orbit (see Iben & Tutukov 1984; Nelemans et al. 2001, for more information).
Before considering the nucleosynthesis that occurs during the merger, the compositions of the white dwarfs must be understood. It has been pointed out (Saio & Jeffery 2002; Jeffery et al. 2011) that the surface composition of merging white dwarfs is different from their core compositions. This is because during the mass loss phases of the stars, not all unburned material is lost in stellar winds, thus thin, partially burned layers remain on the white dwarf surfaces. Therefore, some buffer regions were defined in those studies to take this material into account. This material is partially processed because it was originally close to the hydrogen burning shell in the progenitor star, so its chemical make-up should be altered from its original composition.
To estimate the chemical abundances in the partially processed layer, let us consider how hydrogen burns in these environments. For the helium white dwarf (originally a 1 M⊙ star), hydrogen should be consumed through the CNO cycle (dominating the energy production) and the pp-chain, which converts four protons into helium while releasing energy in the form of photons and neutrinos. The pp-chain follows three paths depending on the temperature of the environment. The dominant proton-burning paths with respect to ascending temperature are:
-
PPI
p(p,β + )d(p,γ)3He(3He,2p)4He,
-
PPII
p(p,β + )d(p,γ)3He(4He,γ)7Be(e − ,ν)7Li(p,4He)4He,
-
PPIII
p(p,β + )d(p,γ)3He(4He,γ)7Be(p,γ)8B(β + )8Be → 24He.
A series of partial differential equations can be written to describe these chains (see, for example, Iliadis 2007). Of particular interest to us are those governing the evolution of 3He as will become apparent in Sect. 3. By assuming that deuterium quickly reaches its equilibrium abundance in the star, the equation governing 3He evolution can be written as 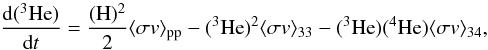 (1)where (H), (3He), and (4He) are the abundances of hydrogen, 3He, and 4He, respectively; ⟨ σv ⟩ pp is the rate of the p(p,β + )d reaction; ⟨ σv ⟩ 33 is the rate of the 3He(3He,2p)4He reaction; and ⟨ σv ⟩ 34 is the reaction rate of 3He(4He,γ)7Be. The equilibrium abundance of 3He, (3He)e, is determined by finding the roots of this quadratic equation when d(3He)/dt = 0, the only physical solution being
(1)where (H), (3He), and (4He) are the abundances of hydrogen, 3He, and 4He, respectively; ⟨ σv ⟩ pp is the rate of the p(p,β + )d reaction; ⟨ σv ⟩ 33 is the rate of the 3He(3He,2p)4He reaction; and ⟨ σv ⟩ 34 is the reaction rate of 3He(4He,γ)7Be. The equilibrium abundance of 3He, (3He)e, is determined by finding the roots of this quadratic equation when d(3He)/dt = 0, the only physical solution being ![\begin{eqnarray} (^3\textrm{He})_{\rm e} &=& \displaystyle \frac{1}{2 \langle \sigma v \rangle_{33}}\Bigg[-(^4\textrm{He})\langle \sigma v \rangle_{34} \nonumber \\ &&+ \sqrt{2(\textrm{H})^2\langle \sigma v \rangle_{\rm pp}\langle \sigma v \rangle_{33}+(^4\textrm{He})^2 \langle \sigma v \rangle_{34}^2}\Bigg]\cdot \label{eq:3he-equil} \end{eqnarray}](/articles/aa/full_html/2012/06/aa19289-12/aa19289-12-eq26.png) (2)Hydrogen shell burning in a red giant branch star with approximately 1 M⊙ occurs at 10–20 MK, thus energy is produced primarily through the CNO cycle. However, the pp-chain is still active in these conditions with a minor contribution to energy production and is essential for the production of 3He, and hence 7Li. Throughout the following discussion, a point in the hydrogen burning shell defined as the position at which H = 0.5 and (4He) = 0.5 is considered1. This point, with an estimated temperature of T = 15 MK, is destined to become part of the hydrogen buffer in both white dwarfs once their envelopes have been lost to stellar winds. By using these values in Eq. (2), 3He mass fractions of (3He)e = 1 × 10-5 are found to be reached in 5 × 105 years, well below the red giant branch lifetime for these stars. Note that the bulk of 3He is produced in the envelope of the star at much larger radii (and lower temperatures) than considered here. At later stages of the star’s evolution, the envelope material is convectively mixed into this region, consequently increasing the 3He content relative to what is produced in the hydrogen-burning shell. In this section, we do not take these time-dependent effects into account, but rather take the conservative approximation that no convective mixing takes place to increase 3He in the partially H-burned shell. These approximations are only made in Sects. 2–4 in order to illustrate the mechanism for producing 7Li in white dwarf mergers. In Sect. 5, these approximations are relaxed to take the full evolutionary history of the white dwarfs into account. In the centre of the hydrogen burning shell in a 1 M⊙ red giant star, one would therefore expect 3He to be overabundant. Later, once the star’s envelope has been eroded during the common envelope stage, this 3He persists in the surface layers of both white dwarfs. The fate of this material becomes essential in understanding lithium production during white dwarf mergers.
(2)Hydrogen shell burning in a red giant branch star with approximately 1 M⊙ occurs at 10–20 MK, thus energy is produced primarily through the CNO cycle. However, the pp-chain is still active in these conditions with a minor contribution to energy production and is essential for the production of 3He, and hence 7Li. Throughout the following discussion, a point in the hydrogen burning shell defined as the position at which H = 0.5 and (4He) = 0.5 is considered1. This point, with an estimated temperature of T = 15 MK, is destined to become part of the hydrogen buffer in both white dwarfs once their envelopes have been lost to stellar winds. By using these values in Eq. (2), 3He mass fractions of (3He)e = 1 × 10-5 are found to be reached in 5 × 105 years, well below the red giant branch lifetime for these stars. Note that the bulk of 3He is produced in the envelope of the star at much larger radii (and lower temperatures) than considered here. At later stages of the star’s evolution, the envelope material is convectively mixed into this region, consequently increasing the 3He content relative to what is produced in the hydrogen-burning shell. In this section, we do not take these time-dependent effects into account, but rather take the conservative approximation that no convective mixing takes place to increase 3He in the partially H-burned shell. These approximations are only made in Sects. 2–4 in order to illustrate the mechanism for producing 7Li in white dwarf mergers. In Sect. 5, these approximations are relaxed to take the full evolutionary history of the white dwarfs into account. In the centre of the hydrogen burning shell in a 1 M⊙ red giant star, one would therefore expect 3He to be overabundant. Later, once the star’s envelope has been eroded during the common envelope stage, this 3He persists in the surface layers of both white dwarfs. The fate of this material becomes essential in understanding lithium production during white dwarf mergers.
3. Merging event
Following the common envelope stages, gravitational wave emission is responsible for further reducing angular momentum in the system until finally, once tidal forces become strong enough, the helium white dwarf is disrupted rapidly (in about 100 s) and is accreted on to the carbon-oxygen white dwarf. This merging episode results in an object that consists of three parts: (i) a dense, central object consisting of the core of the carbon-oxygen white dwarf; (ii) a hot corona in which nucleosynthesis has occurred; and (iii) a thick accretion disk (e.g., Lorén-Aguilar et al. 2010). While the hot corona should contain some material originating in the outer regions of the carbon-oxygen white dwarf, thus explaining the high abundances of carbon and oxygen in hydrogen deficient stars, it consists primarily of material from the helium white dwarf.
As we have shown in Sect. 2, the hydrogen rich buffer of the white dwarfs is expected to be enriched in 3He. This is of particular interest because helium burning conditions are reached during the merger, so the unstable nucleus 7Be can be synthesised, which subsequently captures an electron to produce 7Li. This synthesis depends on rapid heating and cooling of material on timescales that are rare in astrophysical environments (see Sect. 4). The production reaction chain itself is simple: 3He(α,γ)7Be(e − ,ν)7Li. It is complicated somewhat because 7Be can be destroyed by proton capture to produce 8B, which subsequently decays back into two α-particles or undergo further proton capture to produce 9C. Furthermore, at high temperatures, the reverse reaction 8B(γ,p)7Be is particularly important for 7Be production (e.g., Boffin et al. 1993; Hernanz et al. 1996). Nevertheless, at low temperatures, the partial differential equations discussed in Sect. 2 are consulted once again to provide us with the 7Be equilibrium abundance: 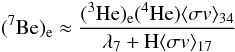 (3)where λ7 is the electron capture rate of 7Be into 7Li and ⟨ σv ⟩ 17 is the rate of the 7Be(p,γ)8B reaction.
(3)where λ7 is the electron capture rate of 7Be into 7Li and ⟨ σv ⟩ 17 is the rate of the 7Be(p,γ)8B reaction.
The behaviour of this equilibrium abundance and its timescale are important in 7Li production. As the stellar temperature rises, so does the (7Be)e abundance, and the time required to reach those equilibrium values decreases dramatically. At a temperature of T = 100 MK, therefore, equilibrium abundances of (7Be)e = 1 × 10-7 are reached in about one second for material originating from the centre of the hydrogen buffer. Therefore, if high temperatures are reached followed by rapid cooling before exhaustion of the 3He reservoir (the timescales involved do not allow for replenishment of 3He), 7Be will freeze-out at highly enriched values. This 7Be is then free to undergo electron capture, producing 7Li with a half-life of about 53 days (Audi et al. 2003), resulting in a stellar environment enriched in 7Li.
We have shown that, in principle, 7Be (and consequently 7Li) can be produced in high concentrations if the environment reaches the required temperatures for the correct time period. The obvious question that arises, therefore, is: how sensitive is this 7Be production to the thermodynamic properties of the merging material?
4. Numerical tests
In the case of a white dwarf merger, the buffer layer of the helium white dwarf is expected to be amongst of the first material to impact the surface of the carbon-oxygen white dwarf, thus reaching high temperatures – typically above 300 MK (Lorén-Aguilar et al. 2010). The energy generated by nuclear burning at these temperatures ejects the processed material back out to larger orbits, cooling it and allowing for any 7Be to decay into 7Li. The assumed temperature density profile for buffer material falling on to the surface of a carbon-oxygen white dwarf therefore consists of three stages: (i) a rapid exponential rise; (ii) a brief stage in which both the temperature and density remain constant; and (iii) an exponential, adiabatic cooling stage.
A small hydrogen burning network is used consisting of nuclei from A = 1 to A = 12 to study the 7Li production sensitivity on the profile parameters. The network contains all reactions pertinent to nucleosynthesis in the pp-chain, including reverse reactions. Rates are adopted from the REACLIB database (Cyburt et al. 2010). In order to approximate the production of 7Li in the merger, the same location in the hydrogen buffer as used in Sect. 3 is considered. This region has 1H and 4He abundances of (H) = (4He) = 0.5 and a 3He abundance of (3He) = 1 × 10-5, as calculated in Sect. 2. All other nuclei have negligible initial abundances.
Sensitivity study variables.
The 7Li production sensitivity is investigated with respect to four profile parameters: (i) rise time, tr, taken to heat the material from T = 1 MK to the maximum temperature, Tmax; (ii) cooling time, tc (i.e., the time taken to cool to T = 1 MK); (iii) amount of time spent at peak temperature, tp; and (iv) maximum temperature Tmax. 7Li production is also sensitive to the initial abundances, depending mostly on the initial concentration of 3He. The parameter ranges adopted are summarised in Table 1. The density is chosen to vary from ρ0 = 1 × 103 g/cm3 to ρmax = 1 × 105 g/cm3, with a cooling tail that follows an adiabatic cooling curve. This behaviour is consistent with the SPH models of Lorén-Aguilar et al. (2010). An equally spaced grid of 20 values are used for each variable, thus nucleosynthesis arising from 160 000 profiles is analysed. A maximum 7Li abundance of (7Li) = 1.4 × 10-5 (corresponding to a factor of 1000 more lithium than is found in our solar system) occurs at temperatures of 350 MK with the fastest rise, cooling, and peak times considered. These extreme values are, however, unrealistic. In reality, rapid heating of the material is expected, but the cooling time is subject to variability depending on the dynamical situation of the merger. We therefore consider the dependence of 7Li production to peak temperature and cooling time assuming a nominal rise and peak times of 1 s. This sensitivity is shown in Fig. 1. A number of interesting features are apparent. First, lithium is produced most efficiently for sharp profiles (i.e., short rise and cooling times). This is because of the freeze-out mechanism discussed in Sect. 3 coupled to the fact that 3He replenishment cannot occur quickly enough to maintain the 3He:7Be equilibrium at peak temperatures. Secondly, the production of lithium as a function of temperature seems to follow a rather complicated pattern that requires some detailed discussion.
 |
Fig. 1 (Colour online) Sensitivity of 7Li production to the cooling time, tc, and maximum temperature, Tmax, of the profile. The contour labels refer to log 10(7Li)/(7Li)⊙ (i.e., zero represents a lithium abundance equal to solar values). These values have been calculated assuming a rise time of tr = 1 s and a peak-time of tp = 1 s. |
By considering Fig. 1, three temperature regions are defined according to how much 7Li is produced: (i) the low temperature region in which 7Li production is independent of fall time; (ii) the medium temperature region of 200 < Tmax < 400 MK, in which the 7Li abundance depends strongly on the profile shape and peaks around Tmax = 300 MK; and (iii) the high temperature region in which very little 7Li is produced.
In the low temperature regime, around Tmax = 100 MK, the rate of the 3He(α,γ)7Be reaction is not high enough to fully destroy 3He during the merger. Therefore, an equilibrium is reached, which is rather insensitive to the dynamics affecting the shape of the profile. The equilibrium 7Be abundance then follows the behaviour discussed in Sect. 3. However, as the temperature rises, the reaction rates increase, thus causing 3He to be partially, and eventually fully destroyed. In this event, 7Be can only be replenished by the photo-disintegration reaction, 8B(γ,p)7Be, whose rate is low around 200 MK, thus explaining the rapid drop in 7Li production from 150 MK to 200 MK.
In the medium temperature regime, 7Be can no longer be produced from 3He, and the equilibrium ratio of 7Be/8B is approximately proportional to the ratio of their reaction rates: λ87/ ⟨ σv ⟩ 78 (where λ87 is the photo-disintegration rate of 8B into 7Be and ⟨ σv ⟩ 78 is the proton capture rate of 7Be(p,γ)8B). Assuming that all of the 3He is converted to 7Be and 8B early in the merging event, and noticing that the reaction rate ratio increases with temperature, it follows that the surviving 7Be should increase with temperature. However, one further effect needs addressing: the destruction of 8B by the 8B(p,γ)9C reaction. This reaction, active above T = 100 MK, erodes the 8B abundance and thus the abundance of 7Be. For this reason, longer profiles (i.e., profiles that take longer to cool) suffer from lower 7Li production.
At high temperatures, above T = 400 MK, another process comes into play: the destruction of 7Be by the 7Be(α,γ)11C reaction. This reaction serves to divert the reaction flow away from 8B, and thus, the equilibrium 7Be/8B cannot be established. The rapid increase of the 7Be(α,γ)11C rate as a function of temperature causes the sharp cut-off in 7Li production shown in Fig. 1. Therefore, in helium rich environments, 7Be is not expected to survive destruction by this mechanism at temperatures above T = 400 MK.
5. Results from hydrodynamic models
5.1. White dwarf models
As shown in the preceding sections, the initial composition of the white dwarfs is critical to understanding lithium production during the merger event. Therefore, the detailed white dwarf models of Althaus et al. (2010) and Renedo et al. (2010) are used to evolve stars from the main sequence to the white dwarf stage. These evolutionary models contain a limited nuclear network of 16 elements: 1H, 2H, 3He, 4He, 7Be, 12C, 13C, 14N, 15N, 16O, 17O, 18O, 19F, 20Ne, and 22Ne. This network is sufficient for following nuclear energy generation during the evolution of the star.
The carbon-oxygen white dwarf model is obtained by evolving 2.5 M⊙ main sequence stars with metallicities of Z = 1.5 × 10-2 and Z = 1 × 10-5 through the thermally pulsing AGB stage and subsequent mass loss period (using the prescription of Vassiliadis & Wood 1993) through the planetary nebula phase to the white dwarf phase. The subsequent cooling of the white dwarf is carefully modelled (see Althaus et al. 2010, for more information) to take into account the effects of, among others, diffusion of material.
The helium white dwarf model is computed similarly to the carbon-oxygen white dwarf. However, since the orbital radius of the two stars decreases during the first common envelope stage (i.e., when the more massive star loses mass in its AGB phase), the common envelope could occur earlier in the stars evolutionary path. A 2.5 M⊙ main sequence star is therefore used. During the stars evolution on the red giant branch, an artificially high mass-loss rate is applied to account for the common envelope stage. As a consequence of this high mass-loss rate, the star loses its envelope before core helium burning commences, and evolves on to the helium white dwarf cooling track.
Following the evolution described above, white dwarf models are obtained that describe the distribution of isotopes in the two stars as a function of radius. These models are then mapped onto our hydrodynamic models in order to follow the evolution of these abundances as the two white dwarfs undergo a merging event.
5.2. Merging system models
The hydrodynamic models used to provide us with input to our nucleosynthesis calculations are the same as those presented in Guerrero et al. (2004), Lorén-Aguilar et al. (2009, 2010), and Longland et al. (2011). A Lagrangian Smoothed Particle Hydrodynamics (SPH) code is used to obtain temperature-density profile input for the post-processing nuclear network. The model used for the calculations presented here is computed for the merging of a 0.4 M⊙ helium white dwarf with a carbon-oxygen white dwarf of mass 0.8 M⊙. While this model does not correspond exactly with the white dwarf masses required to form an R CrB star, their dynamical merging nature should be similar. Additionally, since the envelope of the final system is mostly comprised of material originating in the helium white dwarf, this merging system should reproduce sufficiently the 0.4 + 0.6 M⊙ case. The SPH particle masses were 2.6 × 10-6 M⊙ and 5.3 × 10-6 M⊙ for the two stars, respectively to provide a total of 300 000 particles.
A sample of 10 000 tracer particles is chosen to follow the chemical evolution of material during the merger. Following the merging event, only material that is present in the hot corona and surrounding accretion disk will be visible to any observer. Consequently, only particles that finish their evolution with orbital radii outside the dense central object are chosen as tracers. These particles correspond to those that would form the atmosphere and chromosphere (Clayton 1996) of a hydrogen deficient star. A similar nuclear network as that presented in Sect. 4 (with additional isotopes introduced to account for those in our white dwarf models) is used, which is sufficient to model the synthesis of light elements. Elemental abundances, for comparison with observational data, are then calculated by summing the isotopic abundances obtained from the models.
5.3. Model results
Average lithium abundances, normalised to solar values, as a function of radius in the merger product are shown in Fig. 2. Clearly, lithium enrichment is present in the outer regions of the object with respect to solar abundances. The radii at which this high enrichment are found are, indeed, rather large, and correspond most likely to the accretion disk surrounding the merger product. The reason for this enrichment is that the buffer material, which is destined to produce lithium because of its high concentration of 3He, is amongst the first matter accreted on to the carbon-oxygen white dwarf. Consequently, it will heat up rapidly and is forced out to larger orbital radii. Subsequent accretion of helium rich matter from the destroyed helium white dwarf prevents this material from falling back on to the carbon-oxygen white dwarf’s surface and it remains in the accretion disk following the merging event.
Lithium production is also expected to be independent of metallicity (it depends mainly on the 3He enrichment of the white dwarfs). Indeed, this is the case in the low metallicity models considered (represented by a dashed red line in Fig. 2) where the lithium abundance found in the outer regions of the final object agree very well with those found with our high metallicity models.
 |
Fig. 2 (Colour online) Lithium abundance yield obtained from our SPH models as a function of radius in the post-merger object. The abundances are represented as logarithmic abundances relative to solar values i.e., [Li] = log 10((Li)/(Li)⊙) and (Li) is the mass fraction of lithium. R/R⊙ represents the radius in units of solar radii. The solid black line represents the radial lithium abundance resulting from the merging of solar metallicity stars, while the dashed red line represents that of Z = 1 × 10-5 stars. The single point with error bars represents the range of observed lithium abundances in R CrB stars (see Jeffery et al. 2011, and references therein). |
The distribution of lithium in our models could explain why lithium is only observed in a limited number of R CrB stars. Although no accretion disks have been detected, our SPH models suggest that a rapidly rotating Keplerian disk should be formed subsequent to the merging event (see Lorén-Aguilar et al. 2010, and references therein). This disk could be partially responsible for the observed circumstellar material surrounding R CrB stars. If this is the case, then if an observer were to view the object side-on, the accretion disk could obscure the atmosphere of the star and dominate any spectra obtained. If the star were face-on to the observer, however, radiation from the surface of the star itself will dominate the observers measurements, and hence, lithium abundance measurements would be rather low. Our discovery for the distribution of lithium in the merger product could also be used observationally to distinguish between the FF and DD merger scenarios. If, indeed, the DD scenario was the formation channel for the star, our models indicate that lithium will be present primarily in the cloud of material surrounding the star. The leading theory explaining the characteristic declines of these stars (Clayton 1996) suggests that the dramatic drop in luminosity of the star is caused by a “puff” of carbon-rich material that is being accelerated towards the observer. If the star can be observed early during one of these declines, the surface of the star will be partially eclipsed, a process known as “veiling” (Lambert et al. 1990), hence revealing the diffuse surrounding material for measurement. If lithium is present in high quantities in this material, it could indicate that the DD scenario is, indeed, responsible for the formation of R CrB stars.
6. Conclusions
In this paper, we have investigated the production of lithium in hot mergers of helium and carbon-oxygen white dwarf stars. Both by performing analytical calculations and by post-processing nucleosynthesis of SPH tracer particles, significant lithium production is possible.
In our analytical models, we have shown that this production is strongly dependent on the dynamical properties of the material in the merger and have placed constraints on the conditions required for lithium production. To produce large amounts of lithium the material, which was enriched in 3He in prior evolution, must reach high temperatures rapidly, and then cool rather rapidly also. Lithium production also depends sensitively on the maximum temperature reached by the material through a rather complicated interplay of reactions and their reverse counterparts. Maximum lithium yields are achieved at peak temperatures of around Tmax = 300 MK provided the material undergoes rapid heating and cooling episodes.
Post-processing of tracer particles from SPH models of merging white dwarfs confirms that lithium can, indeed, be produced in the DD scenario, thus satisfying the constraints investigated in our analytical models. By performing these calculations for the merging of a 0.4 M⊙ helium white dwarf with a 0.8 M⊙ carbon-oxygen white dwarf, we have shown that the agreement between our models and the observed lithium surface abundance in hydrogen deficient stars is reassuring. Furthermore, our models predict that lithium should be predominantly produced in the outer regions of the merger product. If measurements are made to identify the location of lithium in R CrB stars, they would provide a vital clue in determining the formation mechanism of these peculiar stars. Further studies should also be performed to investigate the influence of other factors such as the white dwarf masses, compositions, and dynamical properties on the nucleosynthesis of lithium in white dwarf mergers.
It was previously believed that lithium observations in some R CrB stars indicated that they are produced by a powerful final helium flash in a dying AGB star. As we have shown in this paper, lithium can be produced in the merging of two white dwarfs if the conditions meet the criteria laid out here. Lithium cannot, therefore, be used as a strong indicator that the DD formation scenario is invalid for R CrB stars.
Acknowledgments
This work has been partially supported by the Spanish grants AYA2010-15685 and AYA2011-23102, by AGAUR grant SGR1002/2009, by the E.U. FEDER funds, and by the ESF EUROCORES Program EuroGENESIS through the MICINN grant EUI2009-04167.
References
- Althaus, L. G., García-Berro, E., Renedo, I., et al. 2010, ApJ, 719, 612 [NASA ADS] [CrossRef] [Google Scholar]
- Asplund, M., Gustafsson, B., Lambert, D. L., & Rao, N. K. 2000, A&A, 353, 287 [NASA ADS] [Google Scholar]
- Audi, G., Bersillon, O., Blachot, J., & Wapstra, A. H. 2003, Nucl. Phys. A, 729, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Boffin, H. M. J., Paulus, G., Arnould, M., & Mowlavi, N. 1993, A&A, 279, 173 [NASA ADS] [Google Scholar]
- Clayton, G. C. 1996, PASP, 108, 225 [NASA ADS] [CrossRef] [Google Scholar]
- Clayton, G. C., Sugerman, B. E. K., Stanford, S. A., et al. 2011, ApJ, 743, 44 [NASA ADS] [CrossRef] [Google Scholar]
- Cyburt, R. H., Amthor, A. M., Ferguson, R., et al. 2010, ApJS, 189, 240 [NASA ADS] [CrossRef] [Google Scholar]
- Duerbeck, H. W., & Benetti, S. 1996, ApJ, 468, L111 [NASA ADS] [CrossRef] [Google Scholar]
- Guerrero, J., García-Berro, E., & Isern, J. 2004, A&A, 413, 257 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hernanz, M., Jose, J., Coc, A., & Isern, J. 1996, ApJ, 465, L27 [NASA ADS] [CrossRef] [Google Scholar]
- Iben, Jr., I., & Tutukov, A. V. 1984, ApJS, 54, 335 [NASA ADS] [CrossRef] [Google Scholar]
- Iben, Jr., I.,Tutukov, A. V., & Yungelson, L. R. 1997, ApJ, 475, 291 [NASA ADS] [CrossRef] [Google Scholar]
- Iliadis, C. 2007, Nuclear physics of stars (Wiley-VCH) [Google Scholar]
- Jeffery, C. S., Karakas, A. I., & Saio, H. 2011, MNRAS, 414, 3599 [NASA ADS] [CrossRef] [Google Scholar]
- Lambert, D. L., Rao, N. K., & Giridhar, S. 1990, JA&A, 11, 475 [NASA ADS] [Google Scholar]
- Longland, R., Lorén-Aguilar, P., José, J., et al. 2011, ApJ, 737, L34 [NASA ADS] [CrossRef] [Google Scholar]
- Lorén-Aguilar, P., Isern, J., & García-Berro, E. 2009, A&A, 500, 1193 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lorén-Aguilar, P., Isern, J., & García-Berro, E. 2010, MNRAS, 406, 2749 [NASA ADS] [CrossRef] [Google Scholar]
- Nelemans, G., Yungelson, L. R., Portegies Zwart, S. F., & Verbunt, F. 2001, A&A, 365, 491 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Renedo, I., Althaus, L. G., Miller Bertolami, M. M., et al. 2010, ApJ, 717, 183 [NASA ADS] [CrossRef] [Google Scholar]
- Saio, H., & Jeffery, C. S. 2002, MNRAS, 333, 121 [NASA ADS] [CrossRef] [Google Scholar]
- Schönberner, D. 1979, A&A, 79, 108 [NASA ADS] [Google Scholar]
- Vassiliadis, E., & Wood, P. R. 1993, ApJ, 413, 641 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 (Colour online) Sensitivity of 7Li production to the cooling time, tc, and maximum temperature, Tmax, of the profile. The contour labels refer to log 10(7Li)/(7Li)⊙ (i.e., zero represents a lithium abundance equal to solar values). These values have been calculated assuming a rise time of tr = 1 s and a peak-time of tp = 1 s. |
| In the text | |
 |
Fig. 2 (Colour online) Lithium abundance yield obtained from our SPH models as a function of radius in the post-merger object. The abundances are represented as logarithmic abundances relative to solar values i.e., [Li] = log 10((Li)/(Li)⊙) and (Li) is the mass fraction of lithium. R/R⊙ represents the radius in units of solar radii. The solid black line represents the radial lithium abundance resulting from the merging of solar metallicity stars, while the dashed red line represents that of Z = 1 × 10-5 stars. The single point with error bars represents the range of observed lithium abundances in R CrB stars (see Jeffery et al. 2011, and references therein). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


