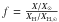| Issue |
A&A
Volume 542, June 2012
|
|
|---|---|---|
| Article Number | A67 | |
| Number of page(s) | 21 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/201219043 | |
| Published online | 08 June 2012 | |
Production and evolution of Li, Be, and B isotopes in the Galaxy
Institut d’Astrophysique de Paris, UMR 7095 CNRS,
Univ. P. & M. Curie, 98bis Bd.
Arago,
75104
Paris,
France
e-mail: prantzos@iap.fr
Received:
15
February
2012
Accepted:
5
April
2012
Context. We reassess the problem of the production and evolution of the light elements Li, Be and B and of their isotopes in the Milky Way in the light of new observational and theoretical developments.
Aims. The main novelty is the introduction of a new scheme for the origin of Galactic cosmic rays (GCR), which for the first time enables a self-consistent calculation of their composition during galactic evolution.
Methods. The scheme accounts for key features of the present-day GCR source composition, it is based on the wind yields of the Geneva models of rotating, mass-losing stars and it is fully coupled to a detailed galactic chemical evolution code.
Results. We find that the adopted GCR source composition accounts naturally for the observations of primary Be and helps understanding why Be follows Fe more closely than O. We find that GCR produce ~70% of the solar 11B/10B isotopic ratio; the remaining 30% of 11B presumably result from ν-nucleosynthesis in massive star explosions. We find that GCR and primordial nucleosynthesis can produce at most ~30% of solar Li. At least half of the solar Li has to originate in low-mass stellar sources (red giants, asymptotic giant branch stars, or novae), but the required average yields of those sources are found to be much higher than obtained in current models of stellar nucleosynthesis. We also present radial profiles of LiBeB elemental and isotopic abundances in the Milky Way disc. We argue that the shape of those profiles – and the late evolution of LiBeB in general – reveals important features of the production of those light elements through primary and secondary processes.
Key words: Galaxy: evolution / nuclear reactions, nucleosynthesis, abundances / stars: abundances / cosmic rays
© ESO, 2012
1. Introduction
The idea that the light and fragile elements Li, Be and B are produced by the interaction of the energetic nuclei of galactic cosmic rays (CGR) with the nuclei of the interstellar medium (ISM) was introduced 40 years ago (Reeves et al. 1970; Meneguzzi et al. 1971, hereafter MAR). In those early works it was shown that taking into account the relevant cross-sections and with plausible assumptions about the GCR properties – source composition, intensity, and spectrum – one may reproduce the abundances of those light elements observed in GCR and in meteorites (=pre-solar) reasonably well. The only exception is Li, which can have only a minor contribution (<20%) from GCR and requires a stellar source. Despite more than 30 years of theoretical and observational work, the stellar source of Li remains elusive at present.
A new impetus was given to the subject by observations of halo stars in the 1990ies showing that Be and B behave as Fe, i.e. as primary elements (Gilmore et al. 1992; Ryan et al. 1992; Duncan et al. 1992), contrary to theoretical expectations. The reason for this “puzzling” behaviour was rapidly inferred by Duncan et al. (1992): GCR must have a metallicity-independent composition to produce primary LiBeB (see also Prantzos 1993). Other ideas (e.g. Prantzos et al. 1993) were only partially successful in that respect (see Reeves 1994 for a summary of the situation in the mid-90ies). Ramaty et al. (1997) showed that a metallicity-independent GCR composition is the only viable alternative for energetic reasons: if in the early Galaxy GCR had a metallic content much lower than today, they would need much more energy than supernovae can provide to always yield primary Be. It was claimed that GCR can aquire a metallicity-independent composition in the environment of superbubbles, powered and enriched by the ejecta of dozens of massive stars and supernovae (Higdon et al. 1997). In the absence of convincing alternatives, the “superbubble paradigm” became the physical explanation for both the origin of GCR (e.g. Parizot et al. 2004) and – by default – for primary Be (despite some criticism, e.g. in Prantzos 2006a).
Independently of the crucial question of the GCR origin, the Be and B observations of the 1990ies made it necessary to link the physics of GCR to detailed models of galactic chemical evolution (Prantzos et al. 1993; Ramaty et al. 1997). In the past few years, important developments occured in both observations and theory, making a reassessment of this vast subject necessary.
From the observational side, large surveys of Be in stars of low metallicities (Primas 2010; Tan et al. 2009; Smiljianic et al. 2009; Boesgaard et al. 2011) considerably improved the statistics of the Be vs. Fe, but also of Be vs. O relationships, providing combined and tighter constraints to models than those previously available. Furthermore, observations of Li isotopic ratios became available, both in low-metallicity halo stars (Asplund et al. 2006; Garcia-Perez et al. 2009) and in the local ISM (Kawanomoto et al. 2009). The former, suggesting a surprisingly high 6Li/7Li ratio in the early Galaxy, stimulated a large body of theoretical work (see Prantzos 2006b, and references therein) but remains controversial (Spite & Spite 2010, and references therein); the latter, combined to the well-known meteoritic ratio of 6Li/7Li, constrains the late evolution of Li isotopes in the local region of the Galaxy.
On the theoretical side, Prantzos (2012) argued that GCR are accelerated mainly by the forward shocks of supernova explosions, propagating through the winds of massive stars and the ISM. By using detailed recent models of nucleosynthesis in massive, mass losing stars, he showed quantitatively that the most prominent feature of the observed GCR composition, namely the high isotopic 22Ne/20Ne ratio (~5 times solar), can be nicely obtained if acceleration occurs in the early Sedov phase of supernova remnants, for shock velocities >1500 km s-1. Furthermore, models of rotating, mass-losing stars were calculated by the Geneva group (Hirschi et al. 2005), showing that the amounts of CNO nuclei released in the stellar winds are almost independent of stellar metallicity (Hirschi 2006). These theoretical results open the way, for the first time, for a self-consistent calculation of the GCR composition (and the resulting LiBeB production from spallation of CNO) throughout the whole Galactic evolution.
The aim of this work is threefold: 1) to evaluate the GCR (spallogenic) production of LiBeB on the basis of the new scheme for the GCR origin; 2) to constrain the yields of the stellar sources of Li by removing the contribution of GCR and primordial nucleosynthesis; 3) to explore the late evolution of the Li and B isotopic ratios, both in the solar neighbourhood and in the Galactic disc and to assess the importance of the secondary component of their production (which reveals itself only at high metallicities). The plan of the paper is as follows:
In Sect. 2 we present an overview of the problem of LiBeB production by GCR. After a short presentation of some basic results (Sect. 2.1), we discuss the problem raised by the observed primary behaviour of Be vs. Fe (Sect. 2.2) and of the implications it has for the composition of GCR. By comparing the various ideas for the origin of GCR we conclude that the only site compatible with all direct observational requirements (which concern the present-day GCR composition) is the one involving shock waves propagating through the winds of massive stars (Sect. 2.3). We argue then, based on recent stellar models (Sect. 2.4), that the circumstellar environment of rotating, mass-losing stars naturally provides a GCR composition across Galactic history that is compatible with the observed evolution of Be.
In Sect. 3.1 we present the model for the chemical evolution of the Milky Way (stellar initial mass function, supernova rates, yields of chemical elements, observational constraints other than those of LiBeB), and the results obtained with this model for the evolution of the key elements C, N and O in the ISM. In Sect. 3.2 we calculate the composition of the GCR as a function of metallicity, by using the results of the chemical evolution model and the new scheme of the GCR origin presented in Sect. 2. In Sect. 3.3 we present in some detail the adopted treatment of the LiBeB production from GCR (spectra, composition, coupling to SN energetics, etc.).
In Sect. 4.1 we discuss the results obtained for Be and the reason for its primary behaviour with respect to Fe rather than O. In Sect. 4.2 we present results for the B isotopes, in particular concerning the contribution of neutrino nucleosynthesis in core-collapse supernovae (CCSN) to 11B production.
The evolution of the Li isotopes is considered in Sect. 5. In Sect. 5.1 we consider the evolution of 7Li and from our models we infer the required yields of the low-mass stellar component of that isotope, after taking into account contributions from primordial nucleosynthesis and GCR. We find that the required 7Li yields are much higher than those calculated in the literature. We discuss the controversial question of high early 6Li in Sect. 5.2 and the implications of the late evolution of 6Li/7Li ratio in Sect. 5.3. In Sect. 6 we discuss the radial profiles of LiBeB and of the corresponding isotopic ratios across the Milky Way disc. Summary and conclusions are presented in Sect. 7.
2. Overview of the subject
2.1. Definitions and basic results
The present-day abundances of LiBeB, produced after ~10 Gyr of cosmic evolution through
spallation of CNO nuclei by GCR, can be obtained in a straightforward way, at least to a
first approximation1. The production rate
(s-1) of the abundance
YL = NL/NH
(per H atom) of LiBeB nuclei in the ISM is given by 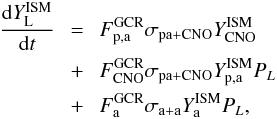 (1)where
F (cm-2 s-1) is the average GCR flux of protons,
alphas or CNO, YISM the abundances (per H atom) of those
nuclei in the ISM, and σ (cm2) is the average (over the
equilibrium energy spectrum of GCR) cross-section for the corresponding spallation
reactions producing LiBeB. The first term of the right-hand side of this equation (fast
protons and alphas hitting CNO nuclei of the ISM) is known as the direct
term, the second one (fast CNO nuclei being fragmented on ISM protons and alphas)
is the reverse term, and the last one involves “spallation-fusion”
α + α reactions, concerning only the Li isotopes.
PL is the probability that nuclide
L (produced at high energy) will be thermalised and remain in the ISM
(see Sect. 3.3 for details). Obviously, the GCR flux term
(1)where
F (cm-2 s-1) is the average GCR flux of protons,
alphas or CNO, YISM the abundances (per H atom) of those
nuclei in the ISM, and σ (cm2) is the average (over the
equilibrium energy spectrum of GCR) cross-section for the corresponding spallation
reactions producing LiBeB. The first term of the right-hand side of this equation (fast
protons and alphas hitting CNO nuclei of the ISM) is known as the direct
term, the second one (fast CNO nuclei being fragmented on ISM protons and alphas)
is the reverse term, and the last one involves “spallation-fusion”
α + α reactions, concerning only the Li isotopes.
PL is the probability that nuclide
L (produced at high energy) will be thermalised and remain in the ISM
(see Sect. 3.3 for details). Obviously, the GCR flux term
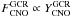 is
proportional to the abundances of CNO nuclei in GCR, a fact of paramount importance for
the evolution of Be and B, as we shall see below.
is
proportional to the abundances of CNO nuclei in GCR, a fact of paramount importance for
the evolution of Be and B, as we shall see below.
In Eq. (1) one may substitute typical values – see MAR – for GCR fluxes
(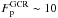 p cm-2 s-1
for protons and scaled values for other GCR nuclei), for the corresponding cross sections
(averaged over the GCR equilibrium spectrum
σp,a + CNO− → Be ~ 10-26
cm2) and for ISM abundances
(YCNO ~ 10-3); integrating for
Δt ~ 10 Gyr, one finds then that
YBe ~ 2 × 10-11, i.e. approximately the
meteoritic Be value (Lodders 2003). Satisfactory results are also obtained for the
abundances of 6Li and 10B. Despite the crude approximations adopted
(constant GCR fluxes and ISM abundances for 10 Gyr, average production cross sections,
secondary production channels ignored), the above calculation correctly reproduces both
the absolute values (within a factor of two) and the relative values (within 10% of the
solar abundances) of 6Li, 9Be and 10B. This constitutes
the strongest, quantitative, argument for the validity of the idea of LiBeB produced by
GCR.
p cm-2 s-1
for protons and scaled values for other GCR nuclei), for the corresponding cross sections
(averaged over the GCR equilibrium spectrum
σp,a + CNO− → Be ~ 10-26
cm2) and for ISM abundances
(YCNO ~ 10-3); integrating for
Δt ~ 10 Gyr, one finds then that
YBe ~ 2 × 10-11, i.e. approximately the
meteoritic Be value (Lodders 2003). Satisfactory results are also obtained for the
abundances of 6Li and 10B. Despite the crude approximations adopted
(constant GCR fluxes and ISM abundances for 10 Gyr, average production cross sections,
secondary production channels ignored), the above calculation correctly reproduces both
the absolute values (within a factor of two) and the relative values (within 10% of the
solar abundances) of 6Li, 9Be and 10B. This constitutes
the strongest, quantitative, argument for the validity of the idea of LiBeB produced by
GCR.
In the original MAR paper, two problems were identified with the GCR production of LiBeB nuclei, compared to the meteoritic composition: they concern the 7Li/6Li ratio, which is ~2 in GCR, but ~12 in meteorites; and the 11B/10B ratio, which is ~2.5 in GCR, but ~4 in meteorites. It was then suggested in MAR that supplementary sources are needed for 7Li and 11B. The idea of an ad hoc low-energy GCR component (a “carrot”), producing mostly 7Li (because of the corresponding large α + α cross sections at low energies) was quantitatively explored in Menneguzzi and Reeves (1975). However, it implied high ionisation rates of the ISM near the acceleration sites and strong γ-ray fluxes – from p-p collisions and subsequent pion decay – which have not been detected (see, however, Indriolo & McCall 2012, for recent observations suggesting higher ionisation rates than found before).
Modern solutions to those problems involve stellar production of ~40% of 11B (through ν-induced spallation of 12C in CCSN, see Sect. 4.2) and of ~60% of 7Li (in the hot envelopes of red giants, AGB stars and/or novae, see Sect. 5.1). In both cases, however, uncertainties in the yields are such that observations are used to constrain the yields of the candidate sources rather than to confirm the validity of the scenario. We shall turn to those questions in the corresponding sections.
2.2. The problem of primary Be
Observations of halo stars in the 90ies revealed a linear relationship between Be/H and
Fe/H (Gilmore et al. 1992; Ryan et al. 1992) as well as between B/H and Fe/H (Duncan et al.
1992). That was unexpected, since Be and B were
thought to be produced as secondaries2. It is clear that the “direct” term in Eq. (1) leads to secondary production of Be and B, since it depends
explicitly on the ever increasing abundances YCNO of the ISM.
The “reverse” term was thought to be symmetric to the direct one, with the GCR fluxes of
CNO nuclei  being
proportional to the ISM abundances of those nuclei. Indeed, according to the “paradigm”
for the GCR composition in the 80ies (Meyer 1985), GCR originate in the coronae of
ordinary, low-mass stars (sharing the composition of the ambient ISM), from where they are
injected in the ISM and are subsequently accelerated by SN shock waves. For both the
direct and the reverse terms, then, the production rate of Be in Eq. (1) is proportional to
being
proportional to the ISM abundances of those nuclei. Indeed, according to the “paradigm”
for the GCR composition in the 80ies (Meyer 1985), GCR originate in the coronae of
ordinary, low-mass stars (sharing the composition of the ambient ISM), from where they are
injected in the ISM and are subsequently accelerated by SN shock waves. For both the
direct and the reverse terms, then, the production rate of Be in Eq. (1) is proportional to
 and leads to Be
production as a secondary. Only the Li isotopes, produced at low metallicities mostly by
α + α reactions – third term in Eq. (1) – were thought
to be produced as primaries (Steigman & Walker 1992), since the abundance of 4He varies little during galactic
evolution. However, Li abundance at low metallicities is totally dominated by primordial
7Li, and the small fraction of 6Li was below detectability levels
in the 90ies.
and leads to Be
production as a secondary. Only the Li isotopes, produced at low metallicities mostly by
α + α reactions – third term in Eq. (1) – were thought
to be produced as primaries (Steigman & Walker 1992), since the abundance of 4He varies little during galactic
evolution. However, Li abundance at low metallicities is totally dominated by primordial
7Li, and the small fraction of 6Li was below detectability levels
in the 90ies.
 |
Fig. 1 Observations of Be vs. Fe (left) and vs. O (right). In all panels, dotted lines indicate slopes of 1 (primary) and 2 (secondary). Data are from Primas (2010, circles), Tan et al. (2009, asterisks), Smiljanic et al. (2009, open squares), and Boesgaard et al. (2011, dots). |
A compilation of recent measurements for Be appears in Fig. 1, as a function of Fe/H and of O/H3. Evidently, Be/H behaves as a primary with respect to Fe in the whole metallicity range (covering three orders of magnitude, from [Fe/H] = −3.4 to [Fe/H] = 0) while the situation with respect to O is more complex: while at low metallicities ([O/H] < −1) the slope of Be/H vs. O/H is 1, at higher metallicities the scatter in the data prevents one from defining a slope; however, a secondary-like behaviour is apparently required to explain the late evolution of Be up to [O/H] = 0. The lower panels of Fig. 1 display those same features more clearly, emphasising the large scatter of Be/Fe or Be/O (about 1 dex) at any metallicity.
The only way to produce primary Be is by assuming that GCR always have the same CNO
content, as suggested in Duncan et al. (1992). In
the first ever work combining a detailed chemical evolution code with the physics of LiBeB
production by GCR, Prantzos et al. (1993) attempted
to enhance the early production of secondary Be by invoking a better confinement of GCR in
the early Galaxy, leading to higher GCR fluxes FGCR; a similar
reasoning was adopted in Fields et al. (2001).
Fields & Olive (1999) explored the possibility of a high O/Fe at low
metallicities, which increases the contribution of the term
 . All those
efforts – and a few others - slightly alleviated the problem, but could not solve it. The
reason for that failure was clearly revealed by the energetics argument
put forward by Ramaty et al. (1997): if SN
are the main source of GCR energy, there is a limit to the amount of light elements
produced per SN, which depends on GCR and ISM composition, but also on the energy imparted
to the GCR particles, i.e. on the magnitude of the term FGCR
in Eq. (1). If the CNO content of
both ISM and GCR becomes too low, there is simply not enough energy in
GCR to keep the Be yields constant.
. All those
efforts – and a few others - slightly alleviated the problem, but could not solve it. The
reason for that failure was clearly revealed by the energetics argument
put forward by Ramaty et al. (1997): if SN
are the main source of GCR energy, there is a limit to the amount of light elements
produced per SN, which depends on GCR and ISM composition, but also on the energy imparted
to the GCR particles, i.e. on the magnitude of the term FGCR
in Eq. (1). If the CNO content of
both ISM and GCR becomes too low, there is simply not enough energy in
GCR to keep the Be yields constant.
 |
Fig. 2 Energy input required from energetic particles accelerated by one CCSN to produce a given mass of Be, such as to have [Be/Fe] = 0 (solar), assuming that a core-collapse SN produces, on average, 0.1 M⊙ of Fe. Solid curve corresponds to the case of a constant composition for GCR, dotted curve corresponds to a time-variable composition, following that of the ISM. In the former case, the required energy is approximately equal to the energy imparted to energetic particles by supernovae, namely ~0.1 of their kinetic energy of ~1.5 × 1051 erg; in the latter case, the energy required to keep [Be/Fe] = 0 becomes much higher than the total kinetic energy of a CCSN for metallicities [Fe/H] ≤ −1.6. |
Anticipating on the content of Sect. 3.3, we display in Fig. 2 the results of such a calculation. If the CNO content of GCR is assumed to be always constant and equal to its present-day value, it takes 10% of the SN kinetic energy, i.e. ~1050 erg per SN, to produce a constant yield of Be yBe ~ 10-7 M⊙; combined with a typical Fe yield of CCSN yFe ~ 0.1 M⊙, this leads to a production ratio [Be/Fe] = 0, as observed. In contrast, if the CNO content of GCR is assumed to decrease at low metallicities, following that of the ISM, then below [Fe/H] = −1.6 it takes more than the total kinetic energy of a CCSN to obtain yBe ~ 10-7 M⊙. The only possibility left to achieve roughly constant LiBeB yields is then to assume that the “reverse” component is primary, i.e. that GCR have a roughly constant metallicity. This has profound implications for our understanding of the GCR origin, as we discuss in the next section. Of course, before the aforementioned Be and B observations, no one would have had the idea to ask about the GCR composition in the early Galaxy.
2.3. The origin of Galactic cosmic rays
For quite some time it was thought that GCR originate from the average ISM, where they are accelerated by the forward shocks of SN explosions (Fig. 3A). However, this can only produce secondary Be.
A roughly constant abundance of C and O in GCR can “naturally” be understood if SN accelerate their own ejecta through their reverse schock (Ramaty et al. 1997, see Fig. 3B). However, the absence of unstable 59Ni (decaying through e− capture within 105 yr) from observed GCR suggests that acceleration occurs >105 yr after the explosion (Wiedenbeck et al. 1999) when SN ejecta are presumably already diluted in the ISM. Furthermore, the reverse shock has only a small fraction of the SN kinetic energy, while observed GCR require a large fraction of it4.
Taking up an idea of Kafatos et al. (1981), Higdon et al. (1998) suggested that GCR are accelerated out of superbubble (SB) material (Fig. 3C), enriched by the ejecta of many SN as to have a large and approximately constant metallicity. In this scenario, it is the forward shocks of SN that accelerate material ejected from other, previously exploded SN. Furthermore, it has been argued that in such an environment GCR could be accelerated to higher energies than in a single SN remnant (Parizot et al. 2004). That scenario has also been invoked to explain the present-day source isotopic composition of GCR (Higdon & Lingenfelter 2003; Binns et al. 2005, 2008). Notice that the main feature of that composition, namely a high 22Ne/20Ne ratio, is explained as being caused by the contribution of winds from Wolf-Rayet (WR) stars (Cassé & Paul 1982), and the SB scenario apparently offers a plausible framework for bringing together contributions from both SN and WR stars.
 |
Fig. 3 Scenarios for the origin of GCR. A) GCR originate from the interstellar medium (ISM) and are accelerated from the forward shock (FS) of SN. B) GCR originate from the interior of supernovae and are accelerated by the reverse shock (RS), propagating inwards. C) GCR originate from superbubble (SB) material, enriched by the metals ejected by supernovae and massive star winds; they are accelerated by the forward shocks of supernovae and stellar winds. D) GCR originate from the wind material of massive rotating stars, always rich in CNO (but not in heavy nuclei) and they are accelerated by the forward shock of the SN explosion. |
In a recent work, Prantzos (2012, hereafter P12) showed both qualitatively – on the basis of a simple nucleosynthesis argument – and quantitatively that superbubbles cannot be the main source of GCR acceleration. Indeed, the main feature of the GCR source composition, namely the high 22Ne/20Ne ratio, cannot be obtained in a superbubble environment: the reason is that massive stars are the only source of both 22Ne and 20Ne in the Universe and a full mixture of their ejecta – such as the one presumably obtained in a superbubble – is expected to have a solar 22Ne/20Ne ratio. This powerful qualititative argument was substantiated in P12 by a detailed calculation of the evolving 22Ne/20Ne ratio in a superbubble, progressively enriched by the winds and the explosions of massive stars: only under unrealistically favourable circumstances and for a short early period is the 22Ne/20Ne ratio in a superbubble comparable to the observed one in GCR sources.
In that same work, P12 showed quantitatively how the GCR source ratio of 22Ne/20Ne can be explained by assuming acceleration by the forward shocks of supernova explosions, running through the winds of massive stars and the ISM (Fig. 3D). As already discussed, the idea of GCR 22Ne/20Ne being due to WR winds has been suggested long ago (Cassé & Paul 1982); however, the appropriate mixture of wind and ISM material was always obtained by hand5 while the connexion between the composition and the acceleration of GCR was left unclear. P12 proposed a “unified” treatment, which brings together all massive stars (both low-mass ones with negligible winds and massive ones with large mass losses, linked by the stellar initial mass function) and which couples in a natural way the acceleration by the forward shock in the circumstellar medium to the (time-dependent) composition of accelerated particles: in the most massive stars, mostly wind material (rich in 22Ne) is accelerated, while in the less massive stars mostly ISM (with solar 22Ne) is accelerated. The main finding of P12 is that acceleration has to occur only in the early Sedov-Taylor phase of the supernova remnant, for shock velocities higher than 1600–2000 km s-1. Indeed, to reproduce the GCR source 22Ne/20Ne ratio, only a few tens of solar masses of circumstellar material must be swept-up by the shock, otherwise the 22Ne/20Ne ratio will be diluted to low values.
In this work we follow the ideas of P12 and assume that during the evolution of the Galaxy, GCR are accelerated mainly by the forward shocks of supernovae, as they sweep up the massive star winds and the ISM. The novel – and most important – feature of this work is that we calculate the evolving composition of GCR (instead of assuming it to be constant, as previous workers in the field) by adopting realistic models of rotating massive stars with mass loss, as we discuss in the next section.
2.4. Wind composition of rotating massive stars
The properties of rotating, massive stars are nicely summarised in the recent review paper of Maeder & Meynet (2011) and are presented in considerable depth in the monograph of Maeder (2008). In particular, rotation has a twofold effect on stellar yields: it increases the size of the nuclearly processed layers (since it mixes material further than convection alone) and reduces the escape velocity in the stellar equator, allowing larger amounts of mass to be ejected into the wind. Both effects enhance the wind yields up to some mass limit; above it, the wind has removed so much mass that less material is left in the star to be processed in subsequent stages of the evolution, thus reducing the corresponding yields with respect to non-rotating models.
 |
Fig. 4 CNO content of the winds of rotating massive stars from the Geneva group. In all panels, yields are for stars of 120 M⊙ (thick dotted), 80 M⊙ (thick dashed), 60 M⊙ (thick solid), 40 M⊙ (thin solid), 25 M⊙ (thin dashed) and 15 M⊙ (thin dotted). The curves connect yields that are provided at three values of the metallicity Z (Z = 10-8, 10-5, 0.02). The thick dots correspond to yields averaged over a Salpeter IMF; average values depend little on metallicity, because they are always dominated by the extremely high yields of the most massive stars. |
To calculate the 22Ne/20Ne ratio in present-day GCR, P12 adopted the models of the Geneva group (Hirschi et al. 2005), calculated for solar metallicity. The initial rotational velocity of those models is vRot = 300 km s-1 on the ZAMS, corresponding to an average velocity of 220 km s-1 on the main sequence, i.e. close to the average observed value. For the purposes of this work, we adopted a set of yields from the same group, extending down to a metallicity of Z = 10-8, i.e. ~5 × 10-6Z⊙ (Fig. 4). In principle, this latter set is not quite homogeneous, since for the two lowest metallicities (Z = 10-8, calculated in Hirschi 2006, and Z = 10-5, calculated in Decressin et al. 2007) initial rotational velocities are υinit = 800 km s-1. As convincingly argued in Hirschi (2006), higher rotational velocities at lower metallicities are a consequence of angular momentum conservation, since less metallic stars are hotter and more compact than their higher metallicity counterparts. This theoretical argument seems to be supported by observations of rotating Be stars in the Magellanic Clouds and the Milky Way (Martayan et al. 2007), although the observational situation is far from settled yet (see Penny & Gies 2009).
An indirect support for considerably higher rotational velocities at low metallicities is provided by the observed evolution of nitrogen. The puzzle of the observed primary behaviour of N vs. Fe was known for a long time. Although intermediate-mass stars were known to be able to provide primary N through hot-bottom burning (e.g. Renzini & Voli 1981), these stars appear relatively late in the evolution of the Galaxy and cannot account for the observations, especially after the VLT data of Spite et al. (2005) became available down to metallicities [Fe/H] ~ –3. In an early attempt using yields of rotating massive stars, Prantzos (2003a) noticed that the then available N yields of the Geneva group, which concerned only rotational velocities of 300 km s-1 across the full metallicity range, are too low to reproduce the observations. In contrast, subsequently calculated yields at Z = 10-8 with velocities of 800 km s-1 (Hirschi 2006) produce much more N at low Z and are indeed able to reproduce the observed evolution of N, as shown in Chiappini et al. (2007). This result should by no means be considered as a proof of the validity of the concept of these high rotational velocities at low Z, but it certainly constitutes an encouraging hint towards that direction and we adopt those same yields in this work.
The main feature of Fig. 4 is that the yields of the rotating massive stars, when averaged over a stellar initial mass function (the one of Salpeter being adopted here) show a remarkable constancy with metallicity: the winds of those stars expel about the same overall amount of C, N and O nuclei at all metallicities. If GCR are accelerated from such material, then they can naturally provide primary Be, as observed. Notice, however, that the actual calculation of the GCR composition from the aforementioned yields is not straightforward; we present it in some detail in Sect. 3.2.
3. Model and ingredients
3.1. Model of galactic chemical evolution
The model adopted here is an updated version of the one presented in Goswami & Prantzos (2000, hereafter GP2000). The set of chemical evolution equations is solved without the instantaneous recycling approximation (IRA), for two galactic systems representing the halo and the local disc, respectively. The halo is formed on a timescale of 1 Gyr with a star formation rate (SFR) proportional to the gas mass and an outflow rate equal to eight times the SFR; the latter ingredient is necessary in order to reproduce the observed halo metallicity distribution (see Prantzos 2003b, and references therein). The local disc is formed with the same prescription as for the SFR, but on a longer timescale of 8 Gyr, allowing one to reproduce the corresponding metallicity distribution; the combination of SFR and infall rates reproduces the present-day local gas fraction of σGas ~ 0.2.
 |
Fig. 5 CNO yields of massive stars of solar initial metallicity adopted in this work: total yields for stars with no mass loss and no rotation in the 11–40 M⊙ range, from WW95 (points); and wind yields of rotating mass-losing stars in the 12–120 M⊙ range, from Hirschi et al. (2005, curves). |
The IMF is taken from Kroupa (2003) and extends from 0.1 M⊙ to 120 M⊙. The adopted yields are from van den Hoek and Gronewegen (1997) for low and intermediate mass stars and taken from Woosley & Weaver (1995, hereafter WW95) for stars in the 11–40 M⊙ range, where stellar winds play a negligible role even at solar metallicity. For stars more massive than 40 M⊙, instead of extrapolating the WW95 yields, we adopted the yields of rotating, mass-losing stars of the Geneva group for H, He, C, N, and O, as described in Sect. 2.4. The adopted massive star yields at solar metallicity appear in Fig. 5. It can be seen that the contribution of the winds to the O yields is negligible, but it becomes substantial for C and N; it becomes dominant for N at low metallicities, because N is produced as secondary in WW95. All the yields are metallicity-dependent and they are properly interpolated in mass and metallicity. This concerns also the yields of 7Li and 11B from massive stars, which are produced by ν-induced nucleosynthesis in WW95 and will be further discussed in Sects. 4.2 and 5.1, respectively. It is assumed that the ejecta of stars of all masses contain no 6Li, Be or 10B, i.e. that those fragile isotopes are astrated with a 100% efficiency. Those nuclides suffer more from astration than deuterium – which receives a continuous contribution from infalling gas of primordial composition – and their astration has to be included in chemical evolution models. Low-mass stars may be net producers of 7Li, at least within some mass range (see discussion in Sect. 5.1). Yields for SNIa are taken from Iwamoto et al. (1999), while the SNIa rate (important for the evolution of Fe) follows the prescription of Greggio (2005) for the single-degenerate scenario.
As described in GP2000, the model reproduces the main features of the local halo and disc well, including the absolute abundances of most elements and isotopes between C and Zn at the Sun’s formation 4.5 Gyr ago. In Fig. 6 it can be seen that it reproduces quite satisfactorily the full evolution of the abundance of all three elements that contribute to LiBeB production, namely C, N and O. In the case of N, the success is due to the adoption of the Geneva yields of rapidly rotating stars at low metallicities (unavailable at the time of GP2000), as already shown by Chiappini et al. (2007). Figure 6 indicates then that the evolution of the direct component of the LiBeB production will be consistently calculated, since the ISM abundances of all CNO elements as a function of metallicity agree with the observations. The only other work on LiBeB presenting the ISM abundances of all three CNO elements is the one of Alibes et al. (2002), where early N was calculated as secondary.
3.2. Composition of GCR
It was realised early on that the elemental composition of GCR at the source (i.e. after accounting for propagation effects) differs significantly from that of the ISM. Volatiles behave differently from refractories: the former display a mass-dependent enrichment with respect to H, which reaches a factor of 10 for the heaviest of them; the latter are all overabundant (w.r.t. H) by a factor of 20, while C and O display intermediate overabundances, by factors of 9 and 5, respectively (e.g. Wiedenbeck et al. 2007, and references therein). Finally, He is slightly underabundant, with (He/H)GCR/(He/H)⊙ = 0.8.
This complex pattern is now thought to result not from ionisation effects (as suggested in Cassé & Goret 1978; and further developped by Meyer 1985) but rather from effects related to elemental condensation temperature (Meyer et al. 1997). Supernova shocks pick up and accelerate gas ions and dust grains simultaneously. The gas ions are accelerated directly to cosmic-ray energies in the shock, which produces an enhancement of ions with higher mass/charge ratios (i.e., heavier elements). On the other hand, refractories are locked in dust grains, which are sputtered by repeated SN shocks and the released ions are easily picked-up and accelerated (see Ellison et al. 1997, for a detailed presentation of the model). This quite elaborate scheme, which builds on earlier ideas by e.g. Bibring & Cesarsky (1981), accounts quantitatively for most of the observed features of GCR source composition.
 |
Fig. 6 Evolution of O/Fe, N/Fe and C/Fe vs. Fe/H. Data sources: Spite et al. (2005, open squares for C, N, O), Lai et al. (2008, X for C, N, O), Primas (2010, filled circles for O), Tan et al. (2009, open triangles for O), Boesgaard et al. (2011, open circles for O), Bensby et al. (2003, filled squares for O), Israelian et al. (2004, filled pentagons for N), Bensby et al. (2006, asterisks for C), Fabbian et al. (2009, filled circles for C). |
 |
Fig. 7 Illustration of the scheme adopted for the acceleration of GCR in Prantzos (2012) and here. At explosion, the star of initial mass M ∗ has a mass MEXP and leaves behind a remnant of mass MREM, i.e. the explosively ejected mass is MEJ, while the mass previously ejected by the wind is MWind = M ∗ –MEXP. Particle acceleration starts at the beginning of the Sedov-Taylor phase, located at mass coordinate A1 = MExp+ MEj, i.e. when the forward shock (FS, arrows), launched at MExp, has swept up a mass MS1=MEj. Acceleration stops at mass coordinate A2, selected in P12 to reproduce – after an average with a Salpeter IMF – the GCR source ratio of 22Ne/20Ne = 5.3 in solar units; in the case of rotating stars adopted here, it corresponds to a shock velocity of 1900 km s-1. The mass sampled by the FS between those two regions is MAcc = A2–A1. For rotating stars with mass M > 30 M⊙, an increasing part of MAcc includes nuclearly processed material (shaded aerea), while for rotating stars with M < 18 M⊙, MAcc contains only material of ISM composition. The yields of Fig. 4 correspond to the mass MWind = M ∗ –MEXP, while the composition of GCR adopted here corresponds to the mass MACC. |
The most conspicuous feature of GCR source composition is undoubtely the high isotopic 22Ne/20Ne ratio, which is 5.3 ± 0.3 times the value of the (22Ne/20Ne)⊙ ratio in the solar wind (Binns et al. 2008). Contrary to the case of the elemental source GCR abundances, which may be affected by various physico-chemical factors (first ionisation potential, condensation temperature, etc.), isotopic ratios can only be affected by nucleosynthetic processes and thus provide crucial information on the origin of cosmic ray particles. P12 showed how this ratio can be explained quantitatively by assuming that the forward shocks of supernovae accelerate circumstellar material of mass-losing stars, which is composed either of nuclearly processed material (rich in 22Ne, in the case of stars with mass M > 40 M⊙) or by pure ISM (with normal 22Ne, in the case of stars with M < 30 M⊙). To obtain the observed GCR source 22Ne/20Ne ratio, P12 found that acceleration had to occur only in the early Sedov-Taylor phase of the supernova for shock velocities higher than ~1900 km s-1 for the rotating stars of the Geneva group6. This value is obtained after all stars between 10 and 120 M⊙ are considered and the corresponding composition is averaged over the IMF.
Figure 7 illustrates the scheme adopted in P12. In that work it was shown that this scheme, although nicely fitting the GCR 22Ne/20Ne ratio, cannot directly reproduce the observed GCR abundancs of CNO elements. The resulting C/O and N/O ratios (expressed in solar units) are higher than the corresponding GCR source ratios by factors of ~2 (see Fig. 6 in P12). The reason is that the winds of massive stars are loaded essentially with products of H-burning (He and N) and early He-burning (C and 22Ne), while O is a product of late He-burning and appears only marginally in the stellar winds. P12 argued that this apparent disagreement can be easily understood in the framework proposed by Meyer et al. (1997) and Ellison et al. (1997): the (mildly) refractory O is more easily picked up and accelerated by the shock than the less refractory C and the volatile N. Its abundance in GCR is then enhanced and the calculated C/O and N/O ratios (shaped by nucleosynthesis and mass loss) have to decrease accordingly, modulated by atomic effects of shock acceleration.
This modulation appears in Fig. 8. The abundances of He, C, N and O (with respect to H and in solar units) appear in the upper panel for both the GCR sources and the accelerated material, according to the model results of P12, which are obtained for the Geneva models at solar metallicity. Clearly, O/H is much higher in GCR sources than in accelerated material and C/H only slightly so, while for volatiles the ratios He/H and N/H are lower in GCR sources than in the model.
 |
Fig. 8 Source abundances in GCR (filled circles) and in the particles accelerated in the
mass MAcc of Fig. 6 (open squares). They are normalised
to the abundance of hydrogen and expressed in the corresponding solar units:
|
The lower panel of Fig. 8 displays the correction factors Rcor required to bring into agreement the model results (fMACC) with the GCR source abundances (fGCR): a large enhancement (Rcor = 4) has to be aplied to O (which is efficiently accelerated as a refractory), a smaller enhancement to the less refractory C and depletion factors (Rcor < 1) to both volatiles He and N. Those corrections, which are justified from the current paradigm of GCR acceleration, bring into agreement the model results with the observed GCR source values of all elements participating in LiBeB production through the reverse component.
Such a GCR source composition, valid for the present-day cosmic rays, has been adopted in some previous works in the subject (e.g. Ramaty et al. 19977). In those works it was assumed that at lower metallicities the same GCR composition applies also (as suggested by the observed linearity of Be vs. Fe) and a theoretical justification for that was invoked, namely the superbubble scenario for GCR acceleration. In this work we dispense with these assumptions, but we actually calculate the GCR source composition as a function of metallicity, by using the wind composition of pre-supernova stars (provided by the Geneva rotating models of Sect. 2.4) and the ISM composition (provided by our model of Sect. 3.1): in each time step we calculate the composition of accelerated particles (as a mixture of ISM and wind compositions, properly weighted by the IMF according to the scheme of Fig. 7) and we apply to it the correction factors of Fig. 8.
The results appear in Fig. 9, displaying the He, C, N, and O abundances of the evolving ISM (top), of the stellar winds (middle) and of the GCR sources (bottom). The latter fits well the observed GCR source composition today by construction (i.e. through the application of the correction factors discussed in the beginning of this subsection).
After calculating in a consistent way the abundances of all key elements that produce LiBeB both in the ISM and in GCR, we proceed with the calculation of spallogenic LiBeB production in the next section.
 |
Fig. 9 Evolution of the chemical composition (normalised to corresponding solar abundances) of He (solid), C (dotted), N (short dashed) and O (long dashed)in: ISM (top), massive star winds (middle) and GCR (bottom); the latter is the one calculated for the accelerated particles of MACC (Fig. 6) corrected to reproduce GCR source abundances today (as in Fig. 7). Dots in lower panel indicate estimated GCR source composition today, from Ellison et al. (1997). |
3.3. Production of LibeB by GCR
The abundances by number 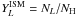 (per hydrogen atom of
the ISM) of the light nuclides L during the evolution of the Galaxy are
calculated by
(per hydrogen atom of
the ISM) of the light nuclides L during the evolution of the Galaxy are
calculated by 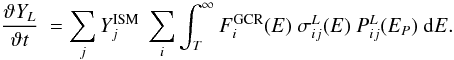 (2)In this expression,
L = 1, ..., 5 for 6Li,7Li, 9Be,
10B and 11B. The indices i and j
run over the range 1, ..., 5 for H, 4He, 12C, 14N, and
16O. The omnidirectional flux of GCR particles
(2)In this expression,
L = 1, ..., 5 for 6Li,7Li, 9Be,
10B and 11B. The indices i and j
run over the range 1, ..., 5 for H, 4He, 12C, 14N, and
16O. The omnidirectional flux of GCR particles
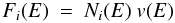 (3)(where
v(E) is the particle velocity as a function of the
energy per nucleon E), is obtained by assuming that the
propagated energy
spectrumNi(E) of
GCR reaches equilibrium, i.e. that the various losses (through escape, ionisation,
spallation etc.) just balance continuous injection from sources with an injection
spectrumQi(E);
the equilibrium solution for primary nuclei, like H, He, C, N, O, as
obtained e.g. in MAR, is
(3)(where
v(E) is the particle velocity as a function of the
energy per nucleon E), is obtained by assuming that the
propagated energy
spectrumNi(E) of
GCR reaches equilibrium, i.e. that the various losses (through escape, ionisation,
spallation etc.) just balance continuous injection from sources with an injection
spectrumQi(E);
the equilibrium solution for primary nuclei, like H, He, C, N, O, as
obtained e.g. in MAR, is ![\begin{equation} N_i(E) \ = \ \frac{1}{b_i(E)} \ \int_E^{\infty} Q_i(E') \ {\rm exp} \left[-\frac{R_i(E')-R_i(E)}{\Lambda} \right] \ {\rm d}E', \end{equation}](/articles/aa/full_html/2012/06/aa19043-12/aa19043-12-eq99.png) (4)where
(4)where
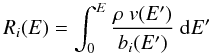 (5)is the
ionisation range, with ρ the ISM mass density and
Λ = ρvτESC is the escape length
from the Galaxy, τESC the corresponding time scale,
and b(E) represents ionisation losses. The functions
b(E) and τ(E) are
determined from basic physics and from the observed properties of the ISM (density,
composition, ionisation stage) and of the CR (abundance ratios of primary to secondary and
of unstable to stable nuclei), see e.g. Strong et al. (2007) and references therein.
(5)is the
ionisation range, with ρ the ISM mass density and
Λ = ρvτESC is the escape length
from the Galaxy, τESC the corresponding time scale,
and b(E) represents ionisation losses. The functions
b(E) and τ(E) are
determined from basic physics and from the observed properties of the ISM (density,
composition, ionisation stage) and of the CR (abundance ratios of primary to secondary and
of unstable to stable nuclei), see e.g. Strong et al. (2007) and references therein.
 |
Fig. 10 Cross sections (mb) for the production of Li, Be and B by spallation of CNO nuclei with protons and alphas, as a function of particle energy per nucleon. Data are from Read & Viola (1984) and Mercer et al. (2001, α + α reactions). In all panels thick dotted curves correspond to production of 11B, thin dotted to 10B, thick solid to 7Li, thin solid to 6Li and dashed to 9Be. In the bottom right panel appear the adopted GCR spectra (arbitrary units): injection Q (dotted) and equilibrium F (solid). |
The cross sections 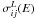 represent the probability of
producing nucleus L through the interaction of nuclei i
and j, and they have a threshold T (Fig. 10).
represent the probability of
producing nucleus L through the interaction of nuclei i
and j, and they have a threshold T (Fig. 10).
The quantities 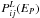 represent the fraction of light
nuclei L that are produced at energy
EP and are incorporated in the ISM. They
are given by
represent the fraction of light
nuclei L that are produced at energy
EP and are incorporated in the ISM. They
are given by ![\begin{equation} P_{ij}^L(E_P) \ = \ {\rm exp}\left[-\frac{R_L(E_P)}{\Lambda}\right] \end{equation}](/articles/aa/full_html/2012/06/aa19043-12/aa19043-12-eq111.png) (6)where
RL(E) is the ionisation
range of nucleus L. The energy
EP is close to zero when a fast proton or
alpha hits a CNO nucleus of the ISM (i.e. the resulting light nucleus is created at rest
and P ~ 1), and
EP = E when fast CNO
nuclei are spallated by ISM protons and alphas (i.e. the resulting light nuclei inherit
the same energy per nucleon). For the fusion reaction
α + α− → 6,7Li
(i = j = 2) the resulting Li nuclei are created with a
velocity about half that of the fast α particles, and
EP = E/4
(see Eq. (6) in MAR).
(6)where
RL(E) is the ionisation
range of nucleus L. The energy
EP is close to zero when a fast proton or
alpha hits a CNO nucleus of the ISM (i.e. the resulting light nucleus is created at rest
and P ~ 1), and
EP = E when fast CNO
nuclei are spallated by ISM protons and alphas (i.e. the resulting light nuclei inherit
the same energy per nucleon). For the fusion reaction
α + α− → 6,7Li
(i = j = 2) the resulting Li nuclei are created with a
velocity about half that of the fast α particles, and
EP = E/4
(see Eq. (6) in MAR).
The CR equilibrium spectrum is known very poorly at low energies, precisely those that
are important for LiBeB production (in view of the relevant production cross sections, see
Fig. 10). The reason is the poorly understood
modulation effects of the solar wind. Instead of using a demodulated spectrum (e.g. Ip
& Axford 1985), in most studies of Li
production, a theoretical injection spectrum is adopted and propagated in the Galaxy to
recover the equilibrium spectrum through Eq. (3). The form of the injection spectrum is
motivated by theories of collisionless shock acceleration (e.g. Ellison & Ramaty
1985) and we adopt here the frequently used
(Prantzos et al. 1993; Fields et al. 1994, 2001; Ramaty et al. 1997, 2000) momentum spectrum of the form
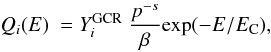 (7)where
β = v/c is the
velocity expressed as a fraction of the light velocity, p the particle
momentum per nucleon, the factor s is usually
2 < s < 3 (in the case
of strong shocks) and we adopte s = 2.3 here and
EC is a cut-off energy that we take here to be
EC = 1 TeV. The resulting injection and equilibrium spectra
(after propagation through a “canonical” path length of Λ = 10 g cm-2 appear in
Fig. 10 (bottom right panel).
(7)where
β = v/c is the
velocity expressed as a fraction of the light velocity, p the particle
momentum per nucleon, the factor s is usually
2 < s < 3 (in the case
of strong shocks) and we adopte s = 2.3 here and
EC is a cut-off energy that we take here to be
EC = 1 TeV. The resulting injection and equilibrium spectra
(after propagation through a “canonical” path length of Λ = 10 g cm-2 appear in
Fig. 10 (bottom right panel).
The total power (energy per unit time) in accelerated particles is
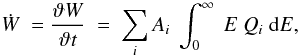 (8)where
multiplication by the mass number Ai accounts
for the fact that energy E is always expressed in units of
energy/nucleon. This power is provided by the main energy source of GCR, namely
supernovae. Theoretical arguments suggest that a fraction
eGCR ~ 0.1 of the kinetic energy
EK ~ 1.5 × 1051 erg of supernovae goes into GCR
acceleration. Thus
(8)where
multiplication by the mass number Ai accounts
for the fact that energy E is always expressed in units of
energy/nucleon. This power is provided by the main energy source of GCR, namely
supernovae. Theoretical arguments suggest that a fraction
eGCR ~ 0.1 of the kinetic energy
EK ~ 1.5 × 1051 erg of supernovae goes into GCR
acceleration. Thus 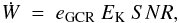 (9)where SNR is the rate
of supernovae (number of SN explosions per unit time) given by the model.
(9)where SNR is the rate
of supernovae (number of SN explosions per unit time) given by the model.
The link between the chemical evolution model and the local production of LiBeB by GCR is
provided by Eqs. (2) to (7) concerning the chemistry
(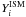 appears in
Eq. (2) and
appears in
Eq. (2) and 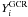 in Eq. (7)) and
through Eqs. (8) and (9) concerning the energetics (since the latter equations allow one
to normalise the injection spectra Q(E)). The
self-consistent calculation of the “coupling term”
in Eq. (7)) and
through Eqs. (8) and (9) concerning the energetics (since the latter equations allow one
to normalise the injection spectra Q(E)). The
self-consistent calculation of the “coupling term” 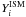 has firstly
been performed in Prantzos et al. (1993) and that
of the energetics in Ramaty et al. (1997) but it is
the first time that the term
has firstly
been performed in Prantzos et al. (1993) and that
of the energetics in Ramaty et al. (1997) but it is
the first time that the term 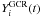 is calculated
on the basis of realistic models (see Sect. 3.2) and not just assumed, as in all
previous studies.
is calculated
on the basis of realistic models (see Sect. 3.2) and not just assumed, as in all
previous studies.
Before proceeding to present the results of our model, we notice that the uncertainties due to the nuclear physics are small. Indeed, the uncertainties in the adopted cross-sections are, in general, smaller than 10% (at least at low energies, where most of the GCR particles reside, see discussion in Mercer et al. 2001). Moreover, Kneller et al. (2003) investigated the key approximations made in the simplified calculation (Eqs. (2) to (6)) from the nuclear physics point of view and found that the introduced errors are negligible. Thus, the overall uncertainties of our calculation will be almost exclusively of astrophysical origin.
4. Evolution of Be and B
This section presents the results for the evolution of Be and B of the chemical evolution model of Sect. 3.1, augmented with the calculation of GCR composition of Sect. 3.2 and the spallogenic production of LiBeB of Sect. 3.3.
4.1. Be evolution
The evolution of Be is presented in the middle and bottom panels of Fig. 11 as a function of Fe/H and O/H, respectively. Evidently, the adopted prescriptions lead to a Be/H evolution that is linear with respect to Fe/H, to a very high accuracy: over four decades in [Fe/H] (from –4 to 0) the differences from linearity are less than 0.1 dex, as can be best seen in the bottom-left panel of Fig. 11. This result is due to two factors:
-
i)
the adopted GCR energetics and Fe yields, which are independent of the metallicity. At all metallicities, it is assumed that core-collapse SN release ~0.07 M⊙ of Fe (the average of WW95 yields) and accelerate GCR with an average energy of 1.5 × 1050 erg;
-
ii)
the combination of the compositions of the evolving ISM and of the winds of rotating massive stars which render the resulting GCR composition approximately metallicity independent (notice that the slow increase of C and O in GCR – see bottom panel of Fig. 9 – plays some role in the late behaviour of LiBeB isotopes, as discussed below).
 |
Fig. 11 Evolution of O/Fe (top), Be/H (middle) and Be/Fe bottom, as a function of Fe (left) and O (right). Dotted lines in middle and bottom panels indicate primary and secondary evolution, respectively. Data sources are as in Fig. 1, but only stars with both O and Be detected are displayed here. |
Notice that, although ingredients (i) and (ii) play a key role in the resulting linearity
of Be/H with Fe/H, the solution they provide is – at least formally – degenerate: the same
result would be obtained if e.g. Fe yields and GCR energies were allowed to vary in
lockstep during galactic evolution (i.e. the present-day values of those quantities could
be reached after starting from values 10 times higher or lower in the early Galaxy). In
that case, the variation in the Be production would be compensated by a similar variation
in the Fe production, leaving the Be/Fe ratio intact8. A similar degeneracy would occur if variation in GCR energetics were
accompanied by a similar variation in GCR composition. In that case, the equality of
Eq. (8) would be preserved with both members varying in the same way, i.e. by assuming a
variation of Ẇ(t) (from Eq. (9)) equal to the variation
of Qi(E,t) (from
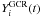 in Eq. (7)). Although the
combined variation of those properties cannot be excluded9, such a precise synchronisation appears improbable and we shall consider here
only our basic scenario, i.e. quasi-constant yields of primary elements and constant SN
energetics.
in Eq. (7)). Although the
combined variation of those properties cannot be excluded9, such a precise synchronisation appears improbable and we shall consider here
only our basic scenario, i.e. quasi-constant yields of primary elements and constant SN
energetics.
In Fig. 11 we also present the evolution of Be vs. O and O vs. Fe, but in contrsast to the case of Fig. 1 we display O vs. Fe observations only for the stars with detected abundances of Be. Clearly, Be correlates better with Fe than with O, both observationally and theoretically. This may appear puzzling at first sight, because Be is produced by spallation of O, not Fe. However, O in the ISM (now seen in halo stars) is produced by metallicity-independent yields of massive stars, while Be in ISM (seen in halo stars) is produced by slowly increasing O of GCR (bottom panel in Fig. 9). The amount of O in GCR increases at late times because their composition results from a mixture of ISM and stellar winds; the latter is quasi-constant in time (hence the flat early Be/Fe ratio), while the former increases steadily and dominates Be production at late times. This enhanced late Be production rate compensates for the late increase in Fe from SNIa and makes Be/Fe roughly constant also at high metallicities. For that reason [Be/O] (bottom right panel in Fig. 11) displays a behaviour that mirrors the one of [O/Fe] (top right panel in Fig. 11). Because of the large scatter in the O data, it is unclear at present whether Be behaves as primary or secondary with respect to oxygen. However, in the stars with the lowest O metallicities detected so far, the behaviour of Be appears to be much closer to that of a primary element.
Despite its success, the simple picture presented here for the evolution of Be cannot be the whole story. It has been known for some time (Nissen & Schuster 1997) that [α/Fe] displays a bi-modal distribution in halo stars, and this was recently confirmed by Nisssen & Schuster (2010) with a precise abundance analysis of 94 stars in the solar neighbourhood. Building on that work, Primas (2010) found systematic differences in the Be abundances among the high [α/Fe] and the low [α/Fe] populations, and her work was substantiated by Tan & Zhao (2011) with high-resolution and high signal/noise ratio VLT spectra: Be abundances in stars with low [α/Fe] ratios are systematically lower (by 0.3 dex) than in stars with higher [α/Fe] ratios, for stars of similar metallicities (in the range [Fe/H] ~ –1.2 to –0.8). This variation cannot be reproduced in the framework of the simple model presented in Fig. 11, which is only meant to reproduce average trends of abundances and abundance ratios.
At this point it should be recalled that according to the current paradigm of galaxy formation, the Milky Way as a whole and its halo in particular were formed not through a monolithic collapse, but from the merging of smaller units with different evolutionary histories. Prantzos (2008) has shown semi-analytically that one key property of the halo, namely, its metallicity distribution, can be satisfactorily reproduced in that framework, assuming that the smaller – and more abundant – units had a lower effective yield (attributed to an easier escape of the supernova ejecta from lower potential wells). It is expected therefore that the different evolutionary histories of the merging units will affect the chemical evolution of the halo, producing e.g. some scatter in abundance ratios (Prantzos 2006c).
We perform here a limited investigation of those ideas for the case of Be, aiming to reproduce the findings of Tan & Zhao (2011). We used oxygen as a proxy for α elements, since they display a similar behaviour for metallicities [Fe/H] < −1.5. The results appear in Fig. 12. It is seen that the “baseline” model (presented in Fig. 11) reproduces the data for the high [α/Fe] sample. Adopting a lower SFR efficiency makes it possible to obtain the observed low [α/Fe] values for the same [Fe/H] (upper panels); the reason is that Fe contribution from SNIa comes at lower metallicities in that case. However, the corresponding low values of Be/O cannot be satisfactorily reproduced, unless it is assumed that the GCR nucleosynthesis was also less efficient than in the standard case; we chose to simulate this effect by adopting a shorter escape length (Λ = 6 g cm-2 instead of 10 g cm-2) and this allows us to obtain lower Be/O values than in the standard case.
 |
Fig. 12 Same as Fig. 11, with two new data sets (thick symbols) for stars with high [α/Fe] (filled squares) and low [α/Fe] (open circles) from Tan & Zhao (2011); all other data of Fig. 11 are displayed as dots. The thin solid curves correspond to the “standard” model presented in Fig. 11, while the thick dotted curves to a model with reduced SF efficiency and the thick dashed curves to a model with reduced SF efficiency and reduced escape length Λ for GCR (see text). |
The expected variety in the physical properties of the merging components of the Galactic halo (size, gas content, potential well, magnetic field) implies a corresponding variety in the properties of the accelerated particles (different confinement times and escape lengths). This implies different efficiencies in the spallogenic production of LiBeB, even if the composition of GCR is assumed to be approximately constant during that period. One should expect then a rather large – albeit difficult to quantify – scatter in the Be/Fe or Be/O abundance ratios at a given metallicity. Incidentally, this argues against the idea of “Be as a chronometer” (see Smilijanic et al. 2009 and references therein): at any given time – or metallicity – the Be/H value is expected to differ among the evolving components that will later merge to form the halo. Be would be a good chronometer only if GCR would have the same properties across the whole galactic system. This excludes the MW halo (made from components differing in their GCR properties), but could be realised in the local disc, which apparently underwent little merging in its late evolution and which is pervaded by a homogeneous GCR “fluid”: a well-defined relationship between Be/H and stellar age would be the expected signature of such a process. However, radial migration of stars in the galactic disc is known to induce scatter in the age-metallicity relation (Sellwood & Binney 2002), bringing in the local volume stars born in different galactocentric radii, with different initial abundances. We calculate the radial profile of Be/H in the MW disc in Sect. 6 and show that a sizeable gradient of Be/H is expected in the ISM, steeper than for oxygen. In that case, radial migration would blur any Be-age relation.
 |
Fig. 13 Left: contributions (percentages) to the production rate of Li, Be and B isotopes, with thick curves indicating the reverse component and thin curves the direct one for C (dotted), N (short-dashed) and O (long-dashed). Right: same thing, with the sums of C+N+O contributions for each component and the contributions of α+α (dotted curves) indicated for the Li isotopes. |
Figure 13 displays the detailed contributions of
the various components to the spallogenic production of Li, Be and B
(i.e. percentages of LiBeB production by GCR alone). In the right panels, it can be seen
that the reverse component always dominates LiBeB production, even at high metallicities;
the direct component contributes at most 25–40% at the highest metallicities. This appears
counterintuitive, because the reverse component produces fast LiBeB nuclei: some of them
are lost from the Galaxy in the leaky-box model adopted here, while all the slow LiBeB
nuclei produced by the direct component are immediately incorporated in the ISM (the
probabilities 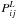 in Eq. (6)
are 1 for the direct component terms but lower than 1 for those of the reverse component).
However, this “advantage” of the direct component is more than compensated for by the
higher C and O abundances of the reverse component: as discussed in Sects. 3.2, the GCR
source abundances of C/H and O/H adopted here, are considerably higher than those of the
ISM. The same is true for the Li isotopes, where the reverse component dominates even at
the lowest metallicities while the α + α component
contributes ~20% at most. Because of the enhanced presence of C and O in the reverse
component and of its primary nature, the situation for Li is different from that
envisioned in Steigman & Walker (1992),
who suggested that α + α reactions would dominate
production of Li isotopes at low metallicities.
in Eq. (6)
are 1 for the direct component terms but lower than 1 for those of the reverse component).
However, this “advantage” of the direct component is more than compensated for by the
higher C and O abundances of the reverse component: as discussed in Sects. 3.2, the GCR
source abundances of C/H and O/H adopted here, are considerably higher than those of the
ISM. The same is true for the Li isotopes, where the reverse component dominates even at
the lowest metallicities while the α + α component
contributes ~20% at most. Because of the enhanced presence of C and O in the reverse
component and of its primary nature, the situation for Li is different from that
envisioned in Steigman & Walker (1992),
who suggested that α + α reactions would dominate
production of Li isotopes at low metallicities.
In the left panels of Fig. 13 appear the separate contributions of C, N, and O to the spallogenic production of LiBeB. As expected, C and O dominate, while N has a negligible contribution (at the 1% level) because of its low abundance. With the adopted GCR composition, O dominates the early production of 6Li and 9Be, while its contribution matches that of C for the other LiBeB isotopes.
4.2. Evolution of B isotopes
From the two boron isotopes, 10B is an almost 100% product of GCR, like the
monoisotopic Be. Indeed, the meteoritic 10B/Be ratio is nicely reproduced by
our calculations (to better than 10%) with the adopted GCR spectra and composition. In
fact, the well-known spallation cross-sections (Fig. 10) are the key ingredient here, because both 9Be and 10B
are produced in about the same amounts by 12C and 16O. On the other
hand, as already mentioned in Sect. 2, a supplementary source of 11B is
required to obtain the meteoritic (11B/10B)⊙ = 4 ratio.
That source may be the ν-process in CCSN, extensively studied in Woosley
et al. (1990): a fraction of the most energetic
among the ~1059 neutrinos of a SN explosion have energies above a few MeV and
are able to spallate 12C nuclei in the C-shell of the stellar envelope,
providing 11B as well as some 7Li in the He layer (see Sect. 5.1).
Soon after the HST observations of the primary behaviour of B (Duncan et al. 1992) it was realised that the
ν-process can provide such primary 11B (Olive et al. 1994). But, if Be is produced as primary by GCR, as
suggested by observations, then more than ~50% of 11B is also produced as
primary by that same process, leaving a rather small role to the
ν-process. That role was subsequently investigated in models with
parametrised neutrino spectra (e.g. Heger et al. 2005; Nakamura et al. 2010). In fact, the
large uncertainties in the ν yields of 11B do not allow one to
perform an accurate evaluation of the B evolution: instead the observed B evolution
(resulting from both GCR and ν-process) has to be used to constrain the
11B yields of CCSN. Thus, Yoshida et al. (2008) argued that the temperature of
νμ,τ− and
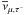 neutrinos inferred from the supernova contribution of 11B in Galactic chemical
evolution models is constrained to the 4.3–6.5 MeV range. Notice that the
ν-yields of 11B depend also on other factors: the available
amount of 12C in the C-shell, which in turn depends – among other things – on
3-α and 12C(α,γ) reaction rates (see Austin
et al. 2011); and the compactness of the exploding
star, which enhances the neutrino flux (see Nakamura et al. 2010, for progenitor stars of type Ic supernova).
neutrinos inferred from the supernova contribution of 11B in Galactic chemical
evolution models is constrained to the 4.3–6.5 MeV range. Notice that the
ν-yields of 11B depend also on other factors: the available
amount of 12C in the C-shell, which in turn depends – among other things – on
3-α and 12C(α,γ) reaction rates (see Austin
et al. 2011); and the compactness of the exploding
star, which enhances the neutrino flux (see Nakamura et al. 2010, for progenitor stars of type Ic supernova).
 |
Fig. 14 From top to bottom: evolution of B/H, B/Fe and B/Be. In the first two panels dotted lines indicate primary and secondary evolution. In the bottom panel, the solid curve corresponds to the total 11B production (GCR + ν-nucleosynthesis) and the dotted curve to 11B produced by GCR alone. Data are from: Primas et al. (1999, filled squares), Garcia-Lopez et al. (1999, filled circles), Cunha et al. (2000, asterisks), and Tan et al. (2010, open squares). |
In Fig. 14 we present the results of our model for the total B (produced by both GCR and ν-process) and we compare them to observations. B clearly behaves as primary with respect to Fe, for the same reasons as Be (see Sect. 4.1). Notice that to fit the meteoritic B abundance, the ν yields of 11B in WW95 had to be divided by a factor of ~5, otherwise B/H and B/Fe would be largely overproduced10. Those yields display some metallicity dependence – yields at Z = Z⊙ are higher than those at Z = 0.1 Z⊙ by a factor of a few – and this is visible in the increase of the B/Be ratio after Z = 0.1 Z⊙; however, the late rise of the secondary component of Be (exclusively produced by GCR) makes that ratio decrease again as the metallicity approaches Z = Z⊙. This behaviour is also found in the 11B/10B ratio (see below).
Notice that the model B/Be ratio is ~24 (i.e. approximately solar) during the whole galactic evolution, while the average observed ratio in halo stars is B/Be ~ 15 and it is compatible with pure GCR production of both elements (dashed curve in the bottom panel of Fig. 14). However, the large error bars of that ratio prevent any conclusions and call for future observations to clarify this important issue.
 |
Fig. 15 Evolution of 11B/10B as a function of metallicity (left) and time (right). Solid curves correspond to the total 11B production (GCR + ν-nucleosynthesis) and dashed curves to 11B produced by GCR alone. The meteoritic (=solar) value (11B/10B)⊙ = 4.02 (Lodders 2003) is indicated at [Fe/H] = 0 and at time t = 7.5 Gyr, whereas the local value (11B/10B)0 = 3.4 ± 0.7 (Lambert et al. 1998) is plotted at t = 12 Gyr. |
Finally, in Fig. 15 we present the results of our calculations for the evolution of the boron isotopic ratio 11B/10B. We compare them to the meteoritic ratio (11B/10B)⊙ = 4.02 (Lodders 2003) and to the one measured in local diffuse intestellar clouds (11B/10B)0 = 3.4 ± 0.7 (Lambert et al. 1998). If the spallogenic production alone is considered (dashed curves in Fig. 15), one sees that 11B/10B remains quasi-constant with metallicity (or time) and decreases only slightly at late times. The reason lies in the evolution of the GCR composition calculated in Fig. 9 (bottom) and in the weight that C and O have in the production of the two boron isotopes (Fig. 13). At the time of solar system formation (t = 7.5 Gyr) we find a value of (11B/10B)GCR = 2.8, slightly higher than the usually quoted value of 2.5; this small difference is attributed to the GCR composition adopted here, particularly enriched in C (which favours production of 11B rather than 10B).
The evolution of the total ratio (11B/10B)GCR+ν (i.e. considering the production of 11B by both GCR and ν-nucleosynthesis) is displayed as solid curves in Fig. 15. The pre-solar (meteoritic) value of (11B/10B )⊙ = 4 is correctly reproduced by construction, since the ν yields of CCSN have been adjusted to that. An interesting feature is the slow decrease of the predicted 11B/10B ratio during the late evolution, for [Fe/H] > −0.6, i.e. later than 4 Gyr. This is a generic feature of the calculation and arises because during this late evolution, the rising secondary (direct) GCR component contributes more to 10B than to 11B (which receives a metallicity-independent 40% contribution from ν-nucleosynthesis); as a result, the 11B/10B ratio declines slowly. Observations (Lambert et al. 1998) find a local 11B/10B ratio lower than, but certainly compatible with, solar, because of large associated uncertainties. In any case, according to the theoretical framework presented in this work, the present-day 11B/10B ratio has to be lower than solar.
5. Evolution of Li isotopes
Among the 92 naturally occuring elements, Li is certainly the one with the richest and most complex history, which is poorly understood at present. The reason is that Li – in particular the isotope 7Li – has three different nucleosynthesis sites: primordial nucleosynthesis, stars, and GCR. Only the contribution of the latter is relatively well known at present, because it is tightly connected to the production of Be (an exclusive product of GCR) through the corresponding spallation cross-sections (Fig. 10).
The primordial component is uncertain at present, because of the as yet unsettled question of the difference between theory and observations: the so-called “Spite plateau” of Li/H in low-metallicity halo stars (Spite & Spite 1982) lies a factor of ~3 below theoretical predictions of standard Big Bang nucleosynthesis (SBBN in the following) corresponding to the cosmic baryon density provided by WMAP results (see Steigman 2010; and Iocco et al. 2009, for recent summaries). To make the situation worse, it appears that below [Fe/H] = −2.5 Li/H decreases with decreasing Fe/H and displays some dispersion (Sbordone et al. 2010), two features that do not characterise halo stars of higher [Fe/H].
Mechanisms for Li destruction involving physics beyond the Standard model have been proposed in the literature (see Jedamzik & Pospelov 2009, and references therein). Astrophysical mechanisms, such as astration of high primordial Li by a pre-galactic Pop. III population of massive stars (Piau et al. 2006) face severe problems of metal overproduction (Prantzos 2006c). Alternatively, primordial Li may have been depleted in the surface layers of halo stars by internal stellar processes (atomic diffusion and mixing and/or rotation); observational arguments for the latter alternative have been provided by Korn et al. (2006), on the basis of parametrised models of Richard et al. (2005), and their results have been confirmed with a substantially larger sample by Lind et al. (2009). In the following we shall adopt the high primordial 7Li value, assuming that its difference with the Spite plateau is caused by as yet unspecified internal stellar processes.
5.1. Evolution of the stellar component of Li
The stellar source of Li is extremely controversial at present11, but it involves generical production by the 4He+3He reaction in various sites: in AGB stars, where the so-called “Cameron-Fowler mechanism” operates in the hot base of their convective envelopes (d’Antona & Ventura 2010, and references therein); in low-mass red giants (RG), through extra deep mixing and the associated “cool-bottom processing” (Sackmann & Boothroyd 1999); in novae, with explosive nucleosynthesis in the He-layer accreted onto the white dwarf (Hernanz et al. 1996); and in core-collapse SN, with the μ and τ neutrinos of the explosion producing 3He through excitation and subsequent de-excitation of the α particles in the He shell (Woosley et al. 1990). The various uncertainties still hampering our understanding of all those sites render the calculated Li yields highly speculative at present. In the case of RGs and AGBs neither the mass range of Li producers, nor the corresponding Li yields or their possible metallicity dependence are known. In the case of CCSN, the temperature of the neutrinosphere – which fixes the energy of spallating neutrinos – is poorly known (see Mueller et al. 2012), while the position of the He-layer – affecting the neutrino flux through the 1/r2 factor – depends a lot on poorly constrained stellar physics. Finally, in the case of novae, neither the Li yields nor the nova rate and its evolution with time are well known.
Models of Li production.
To make things worse, observed Li abundances on the surfaces of low-mass long-lived stars offer no real constraints on the Li evolution, contrary to the case of other elements, because Li is depleted in them by poorly known factors: the Spite plateau most probably does not reflect the true value of Li in the gas from which the stars were formed and the same probably holds for disc stars (see Lambert & Berry 2004, for discussion).
In those conditions, we perform calculations for only a few cases – out of the many possible – to illustrate some, hopefully realistic, aspects of the true Li evolution. For that purpose we adopt Li from four different types of sourcces:
-
1)
SBBN with a high primordial value:log(Li/H)P = −9.4;
-
2)
GCR, as presented in Sect. 3 (but see next section for the possibility of pre-galactic contribution to 7Li);
-
3)
ν-nucleosynthesis in CCSN, with yields provided by WW95. We keep the nominal values of those yields, without applying a reduction by a factor of ~6 (contrary to what was done in the case of 11B yields, where boron overproduction had to be avoided). Although our procedure is not self-consistent, we seek here the maximum possible contribution of the WW95 yields to the Li abundance, to see if they violate any observational constraint (see also Matteucci et al. 1995); results can be easily scaled downwards and even down to zero contribution from CCSN;
-
4)
stellar sources other than CCSN, that is low-mass RGs, AGB stars, and novae. The situation has not evolved much since the extensive discussions in Travaglio et al. (2001) and Romano et al. (2001), which clearly show that the uncertainties in all those Li sources make any quantitative calculation of Li evolution almost meaningless.
Our baseline model (Model A) includes all classes of sources (1), (2), (3), and (4). We find that the first three sources can produce at most ~45% of solar (=meteoritic) Li after 7.5 Gyr of evolution, thus leaving more than half of solar Li to be produced by class (4) sources. In Model A we adopt 2–4 M⊙ AGB stars, their yields (assumed constant with metallicity and stellar mass) being adjusted to have the solar (=meteoritic) Li reproduced. Notice that the death rate of 2–4 M⊙ stars turns out to be approximately proportional to that of SNIa, at least according to the formalism of Greggio (2005) for single-degenerate white dwarfs that is adopted here. In its turn, the evolution of the SNIa rate is as good a guess as can be made at present for the evolution of the unknown nova rate, because both phenomena involve accretion onto white dwarfs in binary systems. Then the absolute rate of nova is obtained by normalising the model value of SNIa rate at t = 12 Gyr by the factor f = Rnova/RSNIa, where Rnova ~ 20–30 yr-1 is the present-day nova rate in the whole Galaxy and RSNIa ~ 4 × 10-3 yr-1 is the present-day SNIa rate (see e.g. Prantzos et al. 2011, and references therein). Thus, we can use Model A to infer average Li yields of either AGBs of 2–4 M⊙ or of typical novae (assuming that each one of those sources is, alternatively, the only stellar source of Li of class 4).
 |
Fig. 16 Evolution of Li (top) according to our Model A (see Table 1) and percentages of its various components (bottom): 7Li from GCR (dot-dashed), 6Li from GCR (dotted), 7Li from ν-nucleosynthesis (NN, dashed) and 7Li from a delayed stellar source (novae and/or AGB stars, long dashed). Solid curves indicate total Li (upper panel) and primordial 7Li (lower panel). Abundance data (upper panel for halo stars are taken from Charbonnel & Primas (2005, filled squares), Sbordone et al. (2010, filled circles), Bonifacio et al. (2007, open circles), Garcia-Perez et al. (2009, open triangles), Asplund et al. (2006, asterisks) and for disc stars from Lambert & Reddy (2004, dots). In the latter case, points with error bars indicate the average values of the six most Li-rich stars in the corresponding metallicity bins. |
In Model B, we drop source (3), because CCSN can produce at most 20% of solar Li and the results of the B evolution suggest a severe downwards revision for the corresponding WW95 yields. We explore then the constraints on the Li yields of stars of either 1–2 M⊙, 2–4 M⊙ or 2–6 M⊙, assuming that each stellar class produces half of the solar Li. The former class of stars corresponds to the low-mass red giants where Li may be produced by “cool-bottom processing” according to Sackmann and Boothroyd (1999). The other two include most of the AGB stars.
The results of Model A appear in Fig. 16. As already discussed, observations provide no constraints on Li/H evolution, because it is assumed that Li in stellar surfaces has been depleted by internal processes from its original value. The first three of the aforementioned Li sources can produce a total of ~47% of the solar Li12. This leaves about 50% of the solar Li to be produced by the low-mass stellar sources. Notice that if the CCSN Li yields of WW95 are reduced by e.g. a factor of 6 (as we did for 11B yields, see Sect. 4.2), the CCSN contribution to the solar Li will be reduced by a similar factor (from 18% to 3%) and the contribution of low-mass sources will grow by that same amount (15%), i.e. it will increase from ~50% to ~65%.
We find that to produce ~50% to ~65% of solar Li, 2–4 M⊙ AGBs have to eject a Li yield of y2−4(Li) ~ 2 × 10-7 M⊙ on average (independent of mass or metallicity). These values are considerably higher than most of the Li yields found for AGB stars by Ventura and d’Antona (as provided in Romano et al. 2001) or by Karakas (2010) for various parametrisations of the AGB envelopes. On the other hand, if novae provide ~50% to ~65% of solar Li, they ought to have a typical Li yield of ynova(Li) ~ 10-9 M⊙. This is considerably higher than values found with hydrodynamical models by Hernanz et al. (1996) for classical CO novae and, taken at face value, it implies that those objects are quite insignificant sources of Li in the Galaxy. This conclusion was also reached in Romano et al. (2001) on the basis of similar arguments.
 |
Fig. 17 Same as the previous figure, but for Model B, with no contribution from CCSN and a different assumption for the stellar Li component (see Table 1 and text). |
Yields of Li (in M⊙) from low-mass sources.
The results of Model B appear in Fig. 17. CCSN are dropped as Li sources, and 1–2 M⊙ stars start enriching the ISM at [Fe/H] ~ −1, i.e. about 1 Gyr after the beginning. To produce the required 70% of solar Li (SBBN and GCR accounting for ~30%), these low-mass stars must produce an average yield of y1−2(Li) ~ 10-7M⊙. Again, these values are much higher than those evaluated for red giants by e.g. Travaglio et al. (2001) or Karakas (2010). Notice that the sharp rise with metallicity of the Li contribution from low-mass stars with metallicity-independent Li yields mimics the behaviour of higher mass stars with metallicity-dependent Li yields (increasing with increasing metallicity). Even in that case, however, the requirement of Table 2 on the average yields remain.
It seems then that the main Li source remains elusive at present: clearly, the firmly established Li sources (SBBN and GCR) can only produce ~30% of the solar Li and the uncertain contribution of ν-nucleosynthesis from CCSN yields at most another ~20%; but the remaining part – the majority of solar Li – can hardly be explained by present-day models of novae, RGs or AGB stars.
The situation may appear more optimistic in the case of novae: 1D hydrodynamical calculations of nucleosynthesis in CO novae find an overproduction factor of ~103 for 7Li (Hernanz et al. 1996) in the ejecta, i.e. a mass fraction of X7 ~ 10-5, and a typical ejecta mass of ~10-5 M⊙; the latter, however, is ~5–10 times lower than observationally inferred ejecta masses, suggesting a problem of 1D nova models at this level. If this “low ejecta mass” problem is fixed, then for the same overproduction factor the 7Li yield will increase to 10-9 M⊙, exactly to the level required by chemical evolution arguments. In that case, our baseline Model A would be, perhaps, not far from reality – provided the nova rate is approximately proportional to the SNIa rate and the SNIa rate follows the Greggio (2005) formalism, as assumed here. However, as Travaglio et al. (2001) correctly point out, in that case novae would overproduce by large factors the minor CNO isotopes (13C, 15N and 17O, see their Table 2); this constitutes a powerful argument against novae as significant 7Li producers and leaves RGs and AGBs as the only viable source. It should be stressed, at this point, that nucleosynthesis in those sites has been calculated with 1D models up to now and that mass loss plays a critical role in the overall evolution and the 7Li yields of those sources. The introduction of 2D or 3D models and a better treatment of mass loss may change our understanding of those complex astrophysical sites considerably and, perhaps, increase their Li yields drastically.
 |
Fig. 18 Evolution of Li/H (top) and of Li/Fe (bottom) in the local disc, as a function of [Fe/H] (left) and of time (right). In all panels, solid curves correspond to Model A and dotted curves to Model B. Data are from Lambert & Reddy (2004) and are provided as a function of metallicity. They are plotted as a function of time (right panels) by applying the model age-metallicity relation. |
In Fig. 18 we plot the late evolution of Li for metallicities higher than [Fe/H] = –1.3 and we compare it with data for the local disc from Lambert & Reddy (2004). In their discussion, Lambert & Reddy (2004) acknowledged the possibility that the upper envelope of their data – represented by the averages of the six most Li-rich stars in each of their [Fe/H] bins – does not reflect the true Li evolution, contrary to views held previously (before the release of WMAP results). After a detailed analysis of the Li abundances as a function of the metallicities and masses of the stars of their sample, Lambert & Reddy (2004) suggest that, at least for [Fe/H] < –0.4, the true Li/H value was probably higher by ~0.5 dex and, therefore, Li/H may have evolved little through the lifetime of the thin disc. Our results support this view, although they are clearly model-dependent: different choices of the rate of the main Li source, or even simply the adoption of metallicity-dependent Li yields (increasing with metallicity) would lead to a model curve closer to the data. Taken at face value, the difference between our model curve and the data may imply a metallicity- (or age-) dependent depletion of Li in stars. However, as Lambert & Reddy (2004) pointed out, other factors, such as mass and rotation may also play a role. Clearly, a lot of work is still required to separate the various factors affecting the evolution of Li inside stars and in the ISM.
Contributions (%) of various sources to solar LiBeB production.
Finally, Table 3 summarises the contributions of the various sources to the solar abundance of each one of the LiBeB isotopes. As already stated, three of those isotopes, namely 6Li, 9Be and 10B, are exclusively produced by GCR (with the possible exception of a pre-galactic production for 6Li, see next section). 11B requires the contribution of ~30% of a non-GCR source, presumably ν-nucleosynthesis. Finally, ~12% of the solar 7Li is due to SBBN (after accounting for all factors affecting its evolution, namely astration and infall) and ~20% to GCR. This leaves ~70% to the stellar source(s); ν-nucleosynthesis can produce at most 20%, but certainly much less, leaving more than half of the solar 7Li to be produced by low mass stars.
5.2. Early 6Li: “high” or “low”?
The report of an “upper envelope” for 6Li/H in low-metallicity halo stars by Asplund et al. (2006) gave a new twist to the LiBeB saga. The reported 6Li/H value at [Fe/H] = –2.7 is much higher – by a factor of fifteen – than expected if GCR are the only source of the observed 6Li/H in that star, assuming that GCR account for the observed evolution of Be (see Fig. 19). Things are even worse if the true primordial Li is the one corresponding to the WMAP+SBBN value (as assumed here), because 6Li is more fragile than 7Li: in that case, the initial 6Li values in halo stars should be at least a factor of 3 higher than evaluated by Asplund et al. (2006), bringing the dicrepancy with the theory to a factor of >40.
Cayrel et al. (2007) argued that asymmetric convective motions in stellar atmospheres could alter the profile of the Li line, mimicking the presence of 6Li. Because of those uncertainties, the reality of high 6Li values in halo stars has not been definitely established yet; the answer will require 3D model atmospheres in the non-LTE regime (see Asplund & Lind 201; Steffen et al. 2010; and Spite & Spite 2010; and references therein). As clearly stated in Asplund & Lind (2010); “it is not yet possible to say that 6Li has definitely been detected, but it is definitely too early to say that 6Li has not been detected”.
The possibility of important pre-galactic production of 6Li by non-standard GCR has drawn considerable attention from theoreticians, who proposed several scenarios:
-
1)
Primordial, non-standard, production during Big Bang nucleosynthesis: the decay/annihilation of some massive particle (e.g. neutralino) releases energetic nucleons/photons that produce 3He or 3H by spallation/photodisintegration of 4He, while subsequent fusion reactions between 4He and 3He or 3H create 6Li (e.g. Kusakabe et al. 2008; Jedamzik & Pospelov 2009 and references therein). Observations of 6Li/H constrain then the masses/cross-sections/densities of the massive particle;
-
2)
Pre-galactic, by fusion reactions of 4He nuclei, accelerated by the energy released by massive stars (Reeves 2005) or by shocks induced during structure formation (Suzuki & Inoue 2002; Rollinde et al. 2005, 2006; Evoli et al. 2008);
-
3)
In situ production by stellar flares, through 3He+4He reactions (Deliyannis & Malaney 1995) involving large amounts of accelerated 3He (Tatischeff & Thibaud 2007).
Prantzos (2006b) showed that the energetics of 6Li production by accelerated particles severely constrain any scenario proposed in category (2) above, including jets accelerated by massive black holes; this holds also for the “stellar flare” scenario (3), the parameters of which have to be pushed to their extreme values to obtain the “upper envelope” of the Asplund et al. (2006) observations. This difficulty is confirmed by Evoli et al. (2008), who calculated pre-galactic 6Li production by α + α reactions with a semi-analytical model for the evolution of the early Milky Way; they found maximum values lower by factors >10 (and plausible values lower by 3 orders of magnitude) than the values reported by Asplund et al. (2006). Acording to the authors “neither the level nor the flatness of the 6Li distribution with [Fe/H] can be reproduced under the most favourable conditions by any model in which 6Li production is tied to a (data constrained) Galactic star formation rate via cosmic ray spallation”. Those results confirm that the putative pre-galactic cosmic rays are unable to produce 6Li at the level suggested by Asplund et al. (2006), unless they are powered by some new energy source, unrelated to star formation and Fe production. Notice also that the problem becomes much worse if it is assumed that the enhanced 6Li abundance is cosmic and not local (see discussion in Prantzos 2006b): in the former case, the total baryonic content of the Universe is polluted to that high level, while in the latter only the material involved in the formation of halo stars is concerned. Taking into account that the mass of the halo is ~1% of the Milky Way and that the baryons in stars or intracluster plasma today constitute only ~10% of the total baryonic content of the Universe (90% being in intergalactic plasma, Fukugita & Peebles 2004), ones sees that the energetic requirements are 1000 times more severe in the former case than in the latter.
 |
Fig. 19 Evolution of total Li (solid curves), 6Li (dashed curves) and 7Li from GCR (dotted curves) in the standard case (low 6Li from SBBN, thick curves) and in the case of high pre-galactic 6Li and 7Li (thin curves). In the latter case, a minimum amount of depletion of 6Li within stars (equal to that of 7Li) has been conservatively assumed. 7Li data for halo stars are as in Fig. 16, while 6Li data are from Asplund et al. (2006, As09, open squares) and Garcia-Perez et al. (2009, GP09, filled circles). |
In Fig. 19 we plot the results of our model for 6Li, assuming it is exclusively produced by standard GCR (thick curve) and a pre-galactic production from some unspecified mechanism (thin curve). In the latter case, it is assumed that the pre-galactic 6Li value exceeds the “Asplund upper envelope” by a factor of three, i.e. by the same factor separating the SBBN+WMAP value from the Spite plateau. This a conservative estimate of 6Li destruction within stellar envelopes, because 6Li is more fragile than 7Li and it should be more depleted than the latter. The total pre-galactic Li (7Li+6Li) produced in that case by cosmic rays is about 17% of the Li produced in SBBN(+WMAP). It seems implausible that such an energetically inefficient process as spallation-fusion reactions can produce almost as much Li as the Big Bang itself. If it turns out that ~5% of Li in halo stars is indeed in the form of 6Li as claimed by Asplund et al. (2006), a solution involving localised processes (rather than affecting the total baryonic content of the Universe), should be favoured, because it is less problematic energetically.
5.3. Evolution of the 6Li/7Li ratio
After the determinations of the 6Li/7Li isotopic ratio in the local ISM in the 1990ies (Lemoine et al. 1993; Meyer et al. 1993), Reeves (1993) and Steigman (1993) assessed the importance of that ratio for our understanding of Li sources and chemical evolution since the formation of the Sun. However, the complexity of the topic (related to the large number of unknowns) made a quantitative – and even a qualitative – assessment impossible13.
In this section we reassess the late evolution of the 6Li/7Li ratio on the basis of our models and motivated by the recent measurements of that ratio in the local ISM by Kawanomoto et al. (2009). While Lemoine et al. (1993) found a 6Li/7Li value equal to the solar one along one line of sight, Meyer et al. (1993) found more than twice that value along two lines of sight. Kawanomoto et al. (2009) found intermediate values along three lines of sight and their 1σ error bars extend between the values found by Lemoine et al. (1993, 1995) and Meyer et al. (1993). In view of those results, it appears that the 6Li/7Li ratio in the local ISM has either remained almost constant or increased in the past 4.5 Gyr.
 |
Fig. 20 Left: evolution of 6Li/7Li ratio as a function of [Fe/H] (left) and of time (right). Data are taken from Asplund et al. (2006, As06), Garcia-Perez et al. (2009, GP09) and Kawanomoto et al. (2009, K09). Solid curves correspond to Model A and dotted curves to Model B, respectively, both starting with standard (low) pre-galactic 6Li; dashed curves correspond to Model A with high pre-galactic 6Li. |
Figure 20 displays the evolution of the 6Li/7Li ratio according to our models compared to data for the early halo (highly uncertain, see discussion in previous section) and in the local ISM. Theoretical predictions for the early evolution obviously depend on the adopted pre-galactic 6Li/7Li ratio. Late evolution depends on the adopted yields of 7Li, since the evolution of 6Li is well determined. A generic feature of our models (i.e. independent of whether the sources are low mass RGs, AGBs or novae) is the slow late rise of 6Li/7Li , which brings the model results up to 6Li/7Li ~ 0.1, i.e. within the 1σ error bars of the measurements. This slow increase is due to the fact that 7Li behaves essentially as a a primary (the dominant stellar component has metallicity-independent yields) while 6Li has a substantial secondary contribution (~30%) from its direct component (thin curve in the right panel of Fig. 9). The increase of 6Li is thus slightly faster than the one of 7Li and this is reflected in the rise of the 6Li/7Li ratio.
Notice, however, that if the 7Li yields of low-mass sources turn out to be increasing with metallicity, the tendency would be inversed and the late 6Li/7Li ratio would be found to decrease (before or after solar system formation). On the other hand, if the current 1σ error bars of the measurements shrink to, say, 0.01 (and the average local 6Li/7Li value is still twice as high as the meteoritic one), then possible alternatives might involve 7Li yields decreasing with metallicity; or localised irradiation of the ISM by GCR, increasing the 6Li/7Li ratio. Much more precise measurements of the local 6Li/7Li ratio are required to definitely conclude on this important question.
6. Radial profiles of LiBeB in the MW disc
Profiles of chemical abundances in galactic discs provide key diagnostics of the evolutionary processes that shaped them because they depend on i) stellar nucleosynthesis, i.e. whether they were made as primaries or secondaries and in short- or long-lived sources, and ii) galactic processes, in particular the ratio between the rates of star formation and infall. For the Milky Way disc, much observational and theoretical work has been made on the profiles of several key elements, such as oxygen, and their evolution (see e.g. the discussion in Chapt. 4 of Stasinska et al. 2012, for oxygen profiles).
The abundances of the light elements Li, Be and B have not been observed in other parts of the Milky Way disc except in the solar neighbourhood, up to now. Still, it is interesting to see what current models of the MW disc evolution predict for the radial profiles of those elements and their isotopes, because future observations may provide additional constraints on models of LiBeB evolution, supplementing those already obtained in the local halo and disc.
We adopt here a considerably updated version of the evolutionary model for the Milky Way disc presented in Boissier & Prantzos (1999), which satisfies all the major observational constraints (radial profiles of gas, stars and SFR, total rates of CCSN and SNIa, luminosities in various wavelength bands, etc.). That model was also used to study in considerable detail the radial profiles of several elements, confronting successfully model predictions to observations (Hou et al. 2000). Among the various improvements brought to the model, which are relevant for this work, are the introduction of the Greggio (2005) SNIa rate; and, in particular, the implementation of the full formalism of LiBeB production (Sect. 3.3) taking into account the evolving composition of GCR (according to Sect. 3.2). The results presented here have been obtained with Model A for Li production (see Sect. 5.1).
The results of the model for O, Li, Be and B are presented in Fig. 21. Oxygen presents a present-day gradient of dlog(O/H)/dR = −0.049 dex/kpc in the range 4–12 kpc, in broad agreement with observations (although there is no general agreement as to the precise value of that gradient and even on the exact shape of the oxygen profile at present). Li displays a similar profile, clearly suggesting its primary nature, since it behaves like oxygen. The reason is, obviously, the fact that in Model A the major Li source is low-mass stars with metallicity-independent yields. Be, on the other hand, displays an interestingly different behaviour, since its final abundance profile is considerably steeper than those of O and Li. The reason is that in the late evolution of Be, the secondary component plays a substantial role (Fig. 13), which becomes even more important in the inner, metal-rich regions of the disc. In the case of B, late evolution involves both the secondary component and the primary one (from ν-nucleosynthesis), making its profile less steep than the one of Be. Thus, detection of the Li, Be and B profiles in the MW disc could provide crucial information on the importance of the secondary component on the production of those elements: for instance, if the Li profile turns out to be much steeper than predicted here, it would imply that the stellar Li source (be it CCSN, RGs or AGbs) has metallicity-dependent yields. Similarly, a Be profile flatter than predicted here would imply that the secondary component plays a much less important role than found here, and this would in turn impact on our assumptions on the GCR composition in the inner disc. Obviously, such conclusions would be drawn only after a proper treatment of various biases, such as depletion of Li in stars by internal processes and in the ISM by fractionation.
 |
Fig. 21 Radial profiles of O/H, Li/H, Be/H and B/H (from top to bottom) at time t = 7.5 Gyr (solar system formation, dotted curves) and at t = 12. Gyr (now, solid curves). Present-day profiles between 4 and 12 kpc are fitted with exponentials (thick segments) and the corresponding slopes appear in the lower left corner of each panel. |
Finally, in Fig. 22 we present the results for the abundance ratios of the Li and B isotopic ratios. Both 6Li/7Li and 10B/11B increase towards the inner disc, for reasons similar to those discussed in the previous section for Be: in each one of the two isotopic ratios, the isotopes in the nominator (6Li and 10B, respectively) have a stronger secondary component than those in the denominator (because the latter also have substantial primary components). It is precisely for this reason that 6Li/7Li and 10B/11B increase slowly in the last few Gyr in the solar neighbourhood (see Figs. 20 and 15, respectively). This secondary component is more pronounced in the higher metallicities of the inner galactic regions, making the corresponding isotopic ratios reach higher values there. This is a robust prediction of the model and any qualitative deviations from it – for example, a flat 11B/10B profile – would have profound implications for our understanding of the synthesis of the corresponding isotopes.
 |
Fig. 22 Radial profiles of 6Li/7Li (top) and 11B/10B (bottom) at time t = 7.5 Gyr (solar system formation, dotted curves) and at t = 12. Gyr (now, solid curves). |
7. Summary
In this work we reassessed the problem of the production and evolution of the light elements Li, Be and B and of their isotopes in the Milky Way in the light of new observational and theoretical developments. The main novelty with respect to the large body of previous theoretical work in the field is the introduction of a new scheme for the origin of Galactic cosmic rays (Sect. 2.3), which for the first time enables a self-consistent calculation of their evolving composition (Sect. 3.2). The scheme, proposed and quantitatively elaborated in Prantzos (2012), accounts for the key feature of the present-day GCR source composition, namely the high 22Ne/20Ne ratio, and is based on the wind yields of the Geneva models of rotating, mass-losing stars (Sect. 2.4). The adopted model of Galactic chemical evolution (Sect. 3.1) satisfies all the major observational constraints in the solar neighbourhood and it is properly coupled to the detailed formalism of LiBeB production (Sect. 3.3) through the energetics of GCRs and of their power sources (CSSN and SNIa).
The GCR source composition is strongly enhanced in CO nuclei, rendering the reverse LiBeB component (fast CNO nuclei hitting protons and alphas of the ISM) dominant at all metallicities. We showed that the GCR composition calculated within the new scheme leads naturally to a primary production of Be, as observed (Sect. 4.1). Although the result is not new, we think that it is now established – both qualitatively and quantitatively – on more solid theoretical foundations than before (i.e. when incorrect arguments about GCR composition originating in superbubbles were used). Moreover, the adopted GCR composition helps understanding why Be follows Fe better than O: the late increase of C and O in GCR (because of the contribution of the accelerated ISM) compensates for the late Fe contribution of SNIa and makes the Be/Fe ratio nearly constant. We interpreted the recent finding of lower Be abundances in stars with lower [α/Fe] ratios (Tan & Zhao 2011) in terms of the inhomogeneous chemical evolution of the halo in the framework of hierarchical galaxy formation. We argued that this implies that Be (or any other element) cannot be used as a “chronometer”, at least for the period of the halo evolution.
We found (Sect. 4.2) that GCR alone can produce a boron isotopic ratio of 11B/10B = 2.8 at solar system formation, i.e. about 70% of the meteoritic one; the remaining 30% of 11B can be provided by ν-nucleosynthesis in CCSN, but the WW95 yields of 11B have to be reduced by a factor of ~6 to obtain that result. We showed that the 11B/10B ratio has to decline slowly in late times, because of the rising importance of the direct component – producing secondary LiBeB –, which contributes more to 10B than to 11B. Current observations are compatible with that trend, but their error bars are too large to allow conclusions.
We showed that the two well-known sources of Li, namely primordial nucleosynthesis and GCR, can provide ~12% and ~18% of solar Li, respectively (assuming a primordial 7Li value obtained through SBBN+WMAP). ν-nucleosynthesis in CCSN can provide another 20% at most, assuming nominal values for the WW95 yields of 7Li; if those yields are reduced by the same factors as those of 11B, then CCSN contribute only ~3% of solar Li (Sect. 5.1). In any case, more than 50% of solar Li require another source, which must involve low stellar mass objects: RGs, AGBs, and/or novae. The 7Li yields of all those sources suffer from large uncertainties, making any quantitative evaluation of their role infeasible at present. Here we inverted the question and estimated the average 7Li yield of each one of those candidate sources, assuming that it is the sole source of 50% of solar Li. It turned out that those yields are higher by substantial factors (~10) than yields proposed in the literature (Table 2): the low-mass source of Li is unknown at present. New models, accounting properly for mass loss and mixing effects in 2D or 3D, may help to improve our understanding of Li production in those sites.
Claims for a high abundance of 6Li in low-metallicity halo stars remain controversial at present. We confirm that standard GCR can produce only 1/15th of the claimed value (Sect. 5.2); if depletion of 6Li by a factor of ~3 is allowed (as is done for Li in the “Spite plateau”), then the discrepancy between theory and observations rises to a factor of >45. Energy requirements put stringent constraints on any sources of pre-galactic 6Li production through spallation-fusion reactions, in particular on astrophysical sources assumed to enrich the total baryonic content of the Universe. If the observations of high early 6Li are confirmed, then only localised astrophysical sources (i.e. within the galactic structures enriched in 6Li) should be considered as viable. Similarly to the case of 11B/10B isotopic ratio, we showed that the 6Li/7Li ratio should slowly increase at late times. Again, observations are compatible with that prediction, but large error bars make it impossible to draw any quantitative conclusion (Sect. 5.3).
Finally, the radial abundance profiles of LiBeB in the MW disc were calculated, through a detailed model that reproduces all the relevant observational constraints (Sect. 6). We found that Li has a present-day profile similar to that of O, i.e. it displays a purely primary behaviour (because low-mass stars, which constitute its major production component, are assumed here to have constant 7Li yields). In contrast, Be is found to display a much steeper profile, because the direct component of its production by GCR is secondary in nature and becomes important in the inner disc. For the same reason, the 6Li/7Li and 10B/11B profiles are found to rise in the inner Galaxy. We argued that future and accurate observations of those isotopic ratios are required to understand the respective roles of the reverse (primary) and direct (secondary) components of LiBeB production, since their importance becomes comparable only at late times.
In summary, this work provides a coherent theoretical framework allowing one to put in perspective the vast body of relevant observational data and to study all aspects of the LiBeB production and evolution in the Galaxy. The identification of the main Li source and the extent of Li depletion in the envelopes of low-mass stars remain, in our opinion, the major open questions in the field, as far as theory is concerned; other important problems are related to the possibility of pre-galactic 6Li production, the extent of ν-nucleosynthesis in CCSN and the GCR properties in the merging units that formed the halo. From the observations point of view, key questions concern: the upper envelope of Li/H across the full metallicity range, from the earliest halo stars to the youngest stars in the solar neighbourhood; the amount of early 6Li and the B/Be ratio in low Z halo stars; the accurate determination of 6Li/7Li and 11B/10B isotopic ratios in the local ISM; and the determination of radial LiBeB abundance profiles across the MW disc.
In galactic chemical evolution, primary elements have a production rate independent of metallicity (they are produced by H and He), while secondary elements have a production rate proportional – explicitly or implicitly – on metallicity (or time, because metallicity increases approximately proportionally to time and thus can be taken as a proxy for it).
It should be emphasized that the scatter displayed in Fig. 1 – and all other figures displaying abundance data from different sources – is partly due to systematic uncertainties in the data analysis (effective temperature scales, oxygen abundance indicators, etc.); the true scatter would be less than suggested by the figure.
Practioners in the field should be cautious with the use of the WW95 yields. It is well known that to fit the α/Fe ratio of halo stars, the WW95 Fe yields should be divided by a factor of two (see e.g. Timmes et al. 1995; or Goswami & Prantzos 2000) and this reduction is adopted here. After considering primary production of Be and B from GCR, the remaining 11B production – to fit the solar 11B/10B – requires reducing the WW95 ν-yields of 11B by a factor of 6. If the reduction of Fe yield is not applied, then the reduction of 11B yields has to be smaller. Furthermore, the WW95 yields at Z⊙ are a few times higher than those at lower metallicities. It is sufficient to apply the reduction factor of 6 only to the solar metallicity yields and not to the others to obtain the correct 11B/10B ratio at solar system formation; for consistency reasons, we applied that correction to all 11B yields here.
Acknowledgments
I am grateful to F. Primas and to G. Meynet, R. Hirschi and T. Decressin for providing data and for enlightening discussions; also to Poul Nissen for drawing my attention to the problem of Be abundances in stars with low and high α/Fe ratios and to an anonymous referee for a constructive report.
References
- Alibés, A., Labay, J., & Canal, R. 2002, ApJ, 571, 326 [NASA ADS] [CrossRef] [Google Scholar]
- Asplund, M., & Lind, K. 2010, IAU Symp., 268, 191 [NASA ADS] [Google Scholar]
- Asplund, M., Lambert, D., Nissen, P., Primas, F., & Smith, V. 2006, ApJ, 644, 229 [NASA ADS] [CrossRef] [Google Scholar]
- Austin, S. M., Heger, A., & Tur, C. 2011, Phys. Rev. Lett., 106, 152501 [NASA ADS] [CrossRef] [Google Scholar]
- Bensby, T., & Feltzing, S. 2006, MNRAS, 367, 1181 [NASA ADS] [CrossRef] [Google Scholar]
- Bensby, T., Feltzing, S., & Lundström, I. 2003, A&A, 410, 527 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bibring, J.-P., & Cesarsky, C. J. 1981, International Cosmic Ray Conference, 2, 289 [Google Scholar]
- Binns, W., Wiedenbeck, M., Arnould, M., et al. 2005, ApJ, 634, 351 [NASA ADS] [CrossRef] [Google Scholar]
- Binns, W., Wiedenbeck, M., Arnould, M., et al. 2008, New Astr. Rev., 52, 427 [Google Scholar]
- Boesgaard, A. M., Rich, J. A., Levesque, E. M., & Bowler, B. P. 2011, ApJ, 743, 140 [NASA ADS] [CrossRef] [Google Scholar]
- Bonifacio, P., Molaro, P., Sivarani, T., et al. 2007, A&A, 462, 851 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boissier, S., & Prantzos, N. 1999, MNRAS, 307, 857 [NASA ADS] [CrossRef] [Google Scholar]
- Casse, M., & Goret, P. 1978, ApJ, 221, 703 [NASA ADS] [CrossRef] [Google Scholar]
- Casse, M., & Paul, J. A. 1982, ApJ, 258, 860 [NASA ADS] [CrossRef] [Google Scholar]
- Cayrel, R., Steffen, M., Chand, H., et al. 2007, A&A, 473, L37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Charbonnel, C., & Primas, F. 2005, A&A, 442, 961 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chiappini, C., Hirschi, R., Meynet, G. et al. 2006, A&A, 449, L27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cunha, K., Smith, V. V., Boesgaard, A. M., & Lambert, D. L. 2000, ApJ, 530, 939 [NASA ADS] [CrossRef] [Google Scholar]
- Decressin, T., Meynet, G., Charbonnel, C., Prantzos, N., & Ekström, S. 2007, A&A, 464, 1029 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Deliyannis, C. P., & Malaney, R. A. 1995, ApJ, 453, 810 [NASA ADS] [CrossRef] [Google Scholar]
- Duncan, D. K., Lambert, D. L., & Lemke, M. 1992, ApJ, 401, 584 [NASA ADS] [CrossRef] [Google Scholar]
- Ellison, D. C., & Ramaty, R. 1985, ApJ, 298, 400 [Google Scholar]
- Ellison, D. C., Drury, L. O., & Meyer, J.-P. 1997, ApJ, 487, 197 [NASA ADS] [CrossRef] [Google Scholar]
- Engelmann, J. J., Ferrando, P., Soutoul, A., Goret, P., & Juliusson, E. 1990, A&A, 233, 96 [NASA ADS] [Google Scholar]
- Evoli, C., Salvadori, S., & Ferrara, A. 2008, MNRAS, 390, L14 [NASA ADS] [Google Scholar]
- Fabbian, D., Nissen, P. E., Asplund, M., Pettini, M., & Akerman, C. 2009, A&A, 500, 1143 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fields, B. D., Olive, K. A., & Schramm, D. N. 1994, ApJ, 435, 185 [NASA ADS] [CrossRef] [Google Scholar]
- Fields, B. D., Olive, K. A., Cassé, M., & Vangioni-Flam, E. 2001, A&A, 370, 623 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fukugita, M., & Peebles, P. J. E. 2004, ApJ, 616, 643 [NASA ADS] [CrossRef] [Google Scholar]
- Garcia Lopez, R. J., Lambert, D. L., Edvardsson, B., et al. 1998, ApJ, 500, 241 [NASA ADS] [CrossRef] [Google Scholar]
- García Pérez, A. E., Aoki, W., Inoue, S., et al. 2009, A&A, 504, 213 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gilmore, G., Gustafsson, B., Edvardsson, B., & Nissen, P. E. 1992, Nature, 357, 379 [NASA ADS] [CrossRef] [Google Scholar]
- Goswami, A., & Prantzos, N. 2000, A&A, 359, 191 [NASA ADS] [Google Scholar]
- Greggio, L. 2005, A&A, 441, 1055 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Heger, A., Kolbe, E., Haxton, W. C., et al. 2005, Phys. Lett. B, 606, 258 [NASA ADS] [CrossRef] [Google Scholar]
- Hernanz, M., Jose, J., Coc, A., & Isern, J. 1996, ApJ, 465, L27 [NASA ADS] [CrossRef] [Google Scholar]
- Higdon, J., Lingenfelter, R., Ramaty, R. 1998, ApJ, 509, L33 [CrossRef] [Google Scholar]
- Higdon, J. C., & Lingenfelter, R. E. 2003, ApJ, 590, 822 [NASA ADS] [CrossRef] [Google Scholar]
- Hirschi, R., Meynet, G., & Maeder, A. 2005, A&A, 433, 1013 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hirschi, R., et al. 2006, Rev. Mod. Astron., 19, 101 [NASA ADS] [CrossRef] [Google Scholar]
- Hou, J. L., Prantzos, N., & Boissier, S. 2000, A&A, 362, 921 [NASA ADS] [Google Scholar]
- Indriolo, N., & McCall, B. J. 2012, ApJ, 745, 91 [NASA ADS] [CrossRef] [Google Scholar]
- Iocco, F., Mangano, G., Miele, G., Pisanti, O., & Serpico, P. D. 2009, Phys. Rep., 472, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Ip, W.-H., & Axford, W. I. 1985, A&A, 149, 7 [NASA ADS] [Google Scholar]
- Israelian, G., Ecuvillon, A., Rebolo, R., et al. 2004, A&A, 421, 649 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Iwamoto, K., Brachwitz, F., Nomoto, K., et al. 1999, ApJS, 125, 439 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Jedamzik, K., & Pospelov, M. 2009, New J. Phys., 11, 105028 [NASA ADS] [CrossRef] [Google Scholar]
- Kafatos, M., Bruhweiler, F., & Sofia, S. 1981, International Cosmic Ray Conference, 2, 222 [NASA ADS] [Google Scholar]
- Karakas, A. I. 2010, MNRAS, 403, 1413 [NASA ADS] [CrossRef] [Google Scholar]
- Kawanomoto, S., Kajino, T., Aoki, W., et al. 2009, ApJ, 701, 1506 [NASA ADS] [CrossRef] [Google Scholar]
- Kneller, J. P., Phillips, J. R., & Walker, T. P. 2003, ApJ, 589, 217 [NASA ADS] [CrossRef] [Google Scholar]
- Korn, A. J., Grundahl, F., Richard, O., et al. 2006, Nature, 442, 657 [Google Scholar]
- Kroupa, P., Tout, C. A., & Gilmore, G. 1993, MNRAS, 262, 545 [NASA ADS] [CrossRef] [Google Scholar]
- Kusakabe, M., Kajino, T., Boyd, R. N., Yoshida, T., & Mathews, G. J. 2008, ApJ, 680, 846 [Google Scholar]
- Lai, D. K., Bolte, M., Johnson, J. A., et al. 2008, ApJ, 681, 1524 [NASA ADS] [CrossRef] [Google Scholar]
- Lambert, D. L., Sheffer, Y., Federman, S. R., et al. 1998, ApJ, 494, 614 [NASA ADS] [CrossRef] [Google Scholar]
- Lemoine, M., Ferlet, R., Vidal-Madjar, A., Emerich, C., & Bertin, P. 1993, A&A, 269, 469 [NASA ADS] [Google Scholar]
- Lemoine, M., Ferlet, R., & Vidal-Madjar, A. 1995, A&A, 298, 879 [NASA ADS] [Google Scholar]
- Lind, K., Primas, F., Charbonnel, C., Grundahl, F., & Asplund, M. 2009, A&A, 503, 545 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
- Lodders, K. 2003, ApJ, 591, 1220 [NASA ADS] [CrossRef] [Google Scholar]
- Maeder, A. 2008, Physics, formation and evolution of rotating stars (Springer) [Google Scholar]
- Maeder, A., & Meynet, G. 2012, Rev. Mod. Phys., 84, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Martayan, C., Frémat, Y., Hubert, A.-M., et al. 2007, A&A, 462, 683 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Matteucci, F., D’Antona, F., & Timmes, F. X. 1995, A&A, 303, 460 [NASA ADS] [Google Scholar]
- Meneguzzi, M., & Reeves, H. 1975, A&A, 40, 91 [NASA ADS] [Google Scholar]
- Meneguzzi, M., Audouze, J., & Reeves, H. 1971, A&A, 15, 337 [NASA ADS] [Google Scholar]
- Mercer, D. J., Austin, S. M., Brown, J. A., et al. 2001, Phys. Rev. C, 63, 065805 [NASA ADS] [CrossRef] [Google Scholar]
- Meyer, D. M., Hawkins, I., & Wright, E. L. 1993, ApJ, 409, L61 [NASA ADS] [CrossRef] [Google Scholar]
- Meyer, J.-P. 1985, ApJS, 57, 173 [NASA ADS] [CrossRef] [Google Scholar]
- Meyer, J.-P., Drury, L. O., & Ellison, D. C. 1997, ApJ, 487, 182 [NASA ADS] [CrossRef] [Google Scholar]
- Mueller, B., Janka, H.-T., & Marek, A. 2012, ApJ, submitted [arXiv:1202.0815] [Google Scholar]
- Nakamura, K., Yoshida, T., Shigeyama, T., & Kajino, T. 2010, ApJ, 718, L137 [NASA ADS] [CrossRef] [Google Scholar]
- Nissen, P. E., & Schuster, W. J. 1997, A&A, 326, 751 [NASA ADS] [Google Scholar]
- Nissen, P. E., & Schuster, W. J. 2010, A&A, 511, L10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Olive, K., Prantzos, N., Scully, S., & Vangioni-Flam, E. 1994, ApJ, 424, 66 [NASA ADS] [CrossRef] [Google Scholar]
- Parizot, E., Marcowith, A., van der Swaluw, E., Bykov, A., & Tatischeff, V. 2004, A&A, 424, 747 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Penny, L. R., & Gies, D. R. 2009, ApJ, 700, 844 [NASA ADS] [CrossRef] [Google Scholar]
- Piau, L., Beers, T., Balsara, D., et al. 2006, ApJ, 653, 300 [NASA ADS] [CrossRef] [Google Scholar]
- Prantzos, N. 1993, in Nuclei in the Cosmos II, ed. F. Kappeler, & K. Wisshak (IOP), 471 [Google Scholar]
- Prantzos, N. 2003a, in CNO in the Universe, ASP Conf. 304, ed. C. Charbonnel et al., 361 [arXiv:astro-ph/0301043] [Google Scholar]
- Prantzos, N. 2003b, A&A, 404, 211 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Prantzos, N. 2006a, in Chemical Abundances and Mixing in Stars in the Milky Way and its Satellites, ESO Symp., ed. S. Randich et al., 351 [arXiv:astro-ph/0411569] [Google Scholar]
- Prantzos, N. 2006b, A&A, 448, 665 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Prantzos, N. 2006c, in Nuclei in the Cosmos IX, CERN, 254 [arXiv:astro-ph/0612633] [Google Scholar]
- Prantzos, N. 2008, A&A, 489, 525 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Prantzos, N. 2010, IAU Symp., 268, 473 [NASA ADS] [Google Scholar]
- Prantzos, N. 2012, A&A, 538, A80 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Prantzos, N., Arnould, M., & Arcoragi, J.-P. 1987, ApJ, 315, 209 [NASA ADS] [CrossRef] [Google Scholar]
- Prantzos, N., Casse, M., & Vangioni-Flam, E. 1993, ApJ, 403, 630 [NASA ADS] [CrossRef] [Google Scholar]
- Prantzos, N., Boehm, C., Bykov, A. M., et al. 2011, Rev. Mod. Phys., 83, 1001 [NASA ADS] [CrossRef] [Google Scholar]
- Primas, F. 2010, IAU Symp., 268, 221 [NASA ADS] [Google Scholar]
- Primas, F., Duncan, D. K., Peterson, R. C., & Thorburn, J. A. 1999, A&A, 343, 545 [NASA ADS] [Google Scholar]
- Ramaty, R., Kozlovsky, B., Lingenfelter, R. E., & Reeves, H. 1997, ApJ, 488, 730 [NASA ADS] [CrossRef] [Google Scholar]
- Ramaty, R., Scully, S. T., Lingenfelter, R. E., & Kozlovsky, B. 2000, ApJ, 534, 747 [NASA ADS] [CrossRef] [Google Scholar]
- Read, S. M., & Viola, V. E., Jr. 1984, Atomic Data and Nuclear Data Tables, 31, 359 [NASA ADS] [CrossRef] [Google Scholar]
- Reeves, H. 1993, A&A, 269, 166 [NASA ADS] [Google Scholar]
- Reeves, H. 1994, Rev. Mod. Phys., 66, 193 [NASA ADS] [CrossRef] [Google Scholar]
- Reeves, H. 2005, EAS Pub. Ser., 17, 15 [CrossRef] [EDP Sciences] [Google Scholar]
- Reeves, H., & Meyer, J.-P. 1978, ApJ, 226, 613 [NASA ADS] [CrossRef] [Google Scholar]
- Reeves, H., Fowler, W., & Hoyle, F. 1970, Nature, 226, 727 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Renzini, A., & Voli, M. 1981, A&A, 94, 175 [NASA ADS] [Google Scholar]
- Richard, O., Michaud, G., & Richer, J. 2005, ApJ, 619, 538 [NASA ADS] [CrossRef] [Google Scholar]
- Rollinde, E., Vangioni, E., & Olive, K. 2005, ApJ, 627, 666 [NASA ADS] [CrossRef] [Google Scholar]
- Rollinde, E., Vangioni, E., & Olive, K. A. 2006, ApJ, 651, 658 [NASA ADS] [CrossRef] [Google Scholar]
- Romano, D., Matteucci, F., Ventura, P., & D’Antona, F. 2001, A&A, 374, 646 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ryan, S. G., Norris, J. E., Bessell, M. S., & Deliyannis, C. 1992, ApJ, 388, 184 [NASA ADS] [CrossRef] [Google Scholar]
- Ryan, S. G., Kajino, T., Beers, T. C., et al. 2001, ApJ, 549, 55 [NASA ADS] [CrossRef] [Google Scholar]
- Sackmann, I.-J., & Boothroyd, A. I. 1999, ApJ, 510, 217 [NASA ADS] [CrossRef] [Google Scholar]
- Sbordone, L., Bonifacio, P., Caffau, E., et al. 2010, A&A, 522, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sellwood, J. A., & Binney, J. J. 2002, MNRAS, 336, 785 [NASA ADS] [CrossRef] [Google Scholar]
- Smiljanic, R., Pasquini, L., Bonifacio, P., et al. 2009, A&A, 499, 103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Spite, F., & Spite, M. 1982, A&A, 115, 357 [NASA ADS] [Google Scholar]
- Spite, M., & Spite, F. 2010, IAU Symp., 268, 201 [NASA ADS] [Google Scholar]
- Spite, M., Cayrel, R., Plez, B., et al. 2005, A&A, 430, 655 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stasinska, G., et al. 2012, Oxygen in the Universe, in press [Google Scholar]
- Steffen, M., Cayrel, R., Bonifacio, P., Ludwig, H.-G., & Caffau, E. 2010, IAU Symp., 268, 215 [NASA ADS] [Google Scholar]
- Steigman, G. 1993, ApJ, 413, L73 [NASA ADS] [CrossRef] [Google Scholar]
- Steigman, G. 2010, IAU Symp., 268, 19 [NASA ADS] [Google Scholar]
- Steigman, G., & Walker, T. P. 1992, ApJ, 385, L13 [NASA ADS] [CrossRef] [Google Scholar]
- Strong, A. W., Moskalenko, I. V., & Ptuskin, V. S. 2007, Ann. Rev. Nucl. Part. Sci., 57, 285 [NASA ADS] [CrossRef] [Google Scholar]
- Suzuki, T. K., & Inoue, S. 2002, ApJ, 573, 168 [NASA ADS] [CrossRef] [Google Scholar]
- Tan, K., & Zhao, G. 2011, ApJ, 738, L33 [NASA ADS] [CrossRef] [Google Scholar]
- Tan, K., Shi, J., & Zhao, G. 2010, ApJ, 713, 458 [NASA ADS] [CrossRef] [Google Scholar]
- Tatischeff, V., & Thibaud, J.-P. 2007, A&A, 469, 265 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Timmes, F. X., Woosley, S. E., & Weaver, T. A. 1995, ApJS, 98, 617 [NASA ADS] [CrossRef] [Google Scholar]
- Travaglio, C., Randich, S., Galli, D., et al. 2001, ApJ, 559, 909 [NASA ADS] [CrossRef] [Google Scholar]
- van Dyk, S. D., Hamuy, M., & Filippenko, A. V. 1996, AJ, 111, 2017 [NASA ADS] [CrossRef] [Google Scholar]
- van den Hoek, L. B., & Groenewegen, M. A. T. 1997, A&AS, 123, 305 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ventura, P., & D’Antona, F. 2010, MNRAS, 402, L72 [NASA ADS] [CrossRef] [Google Scholar]
- Wiedenbeck, M. E., Binns, W. R., Christian, E. R., et al. 1999, ApJ, 523, L6 [Google Scholar]
- Wiedenbeck, M. E., Binns, W. R., Cummings, A. C., et al. 2007, SSRv, 130, 415 [Google Scholar]
- Woosley, S. E., & Weaver, T. A. 1995, ApJS, 101, 181 [NASA ADS] [CrossRef] [Google Scholar]
- Woosley, S. E., Hartmann, D. H., Hoffman, R. D., & Haxton, W. C. 1990, ApJ, 356, 272 [NASA ADS] [CrossRef] [Google Scholar]
- Yoshida, T., Suzuki, T., Chiba, S., et al. 2008, ApJ, 686, 448 [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Observations of Be vs. Fe (left) and vs. O (right). In all panels, dotted lines indicate slopes of 1 (primary) and 2 (secondary). Data are from Primas (2010, circles), Tan et al. (2009, asterisks), Smiljanic et al. (2009, open squares), and Boesgaard et al. (2011, dots). |
| In the text | |
 |
Fig. 2 Energy input required from energetic particles accelerated by one CCSN to produce a given mass of Be, such as to have [Be/Fe] = 0 (solar), assuming that a core-collapse SN produces, on average, 0.1 M⊙ of Fe. Solid curve corresponds to the case of a constant composition for GCR, dotted curve corresponds to a time-variable composition, following that of the ISM. In the former case, the required energy is approximately equal to the energy imparted to energetic particles by supernovae, namely ~0.1 of their kinetic energy of ~1.5 × 1051 erg; in the latter case, the energy required to keep [Be/Fe] = 0 becomes much higher than the total kinetic energy of a CCSN for metallicities [Fe/H] ≤ −1.6. |
| In the text | |
 |
Fig. 3 Scenarios for the origin of GCR. A) GCR originate from the interstellar medium (ISM) and are accelerated from the forward shock (FS) of SN. B) GCR originate from the interior of supernovae and are accelerated by the reverse shock (RS), propagating inwards. C) GCR originate from superbubble (SB) material, enriched by the metals ejected by supernovae and massive star winds; they are accelerated by the forward shocks of supernovae and stellar winds. D) GCR originate from the wind material of massive rotating stars, always rich in CNO (but not in heavy nuclei) and they are accelerated by the forward shock of the SN explosion. |
| In the text | |
 |
Fig. 4 CNO content of the winds of rotating massive stars from the Geneva group. In all panels, yields are for stars of 120 M⊙ (thick dotted), 80 M⊙ (thick dashed), 60 M⊙ (thick solid), 40 M⊙ (thin solid), 25 M⊙ (thin dashed) and 15 M⊙ (thin dotted). The curves connect yields that are provided at three values of the metallicity Z (Z = 10-8, 10-5, 0.02). The thick dots correspond to yields averaged over a Salpeter IMF; average values depend little on metallicity, because they are always dominated by the extremely high yields of the most massive stars. |
| In the text | |
 |
Fig. 5 CNO yields of massive stars of solar initial metallicity adopted in this work: total yields for stars with no mass loss and no rotation in the 11–40 M⊙ range, from WW95 (points); and wind yields of rotating mass-losing stars in the 12–120 M⊙ range, from Hirschi et al. (2005, curves). |
| In the text | |
 |
Fig. 6 Evolution of O/Fe, N/Fe and C/Fe vs. Fe/H. Data sources: Spite et al. (2005, open squares for C, N, O), Lai et al. (2008, X for C, N, O), Primas (2010, filled circles for O), Tan et al. (2009, open triangles for O), Boesgaard et al. (2011, open circles for O), Bensby et al. (2003, filled squares for O), Israelian et al. (2004, filled pentagons for N), Bensby et al. (2006, asterisks for C), Fabbian et al. (2009, filled circles for C). |
| In the text | |
 |
Fig. 7 Illustration of the scheme adopted for the acceleration of GCR in Prantzos (2012) and here. At explosion, the star of initial mass M ∗ has a mass MEXP and leaves behind a remnant of mass MREM, i.e. the explosively ejected mass is MEJ, while the mass previously ejected by the wind is MWind = M ∗ –MEXP. Particle acceleration starts at the beginning of the Sedov-Taylor phase, located at mass coordinate A1 = MExp+ MEj, i.e. when the forward shock (FS, arrows), launched at MExp, has swept up a mass MS1=MEj. Acceleration stops at mass coordinate A2, selected in P12 to reproduce – after an average with a Salpeter IMF – the GCR source ratio of 22Ne/20Ne = 5.3 in solar units; in the case of rotating stars adopted here, it corresponds to a shock velocity of 1900 km s-1. The mass sampled by the FS between those two regions is MAcc = A2–A1. For rotating stars with mass M > 30 M⊙, an increasing part of MAcc includes nuclearly processed material (shaded aerea), while for rotating stars with M < 18 M⊙, MAcc contains only material of ISM composition. The yields of Fig. 4 correspond to the mass MWind = M ∗ –MEXP, while the composition of GCR adopted here corresponds to the mass MACC. |
| In the text | |
 |
Fig. 8 Source abundances in GCR (filled circles) and in the particles accelerated in the
mass MAcc of Fig. 6 (open squares). They are normalised
to the abundance of hydrogen and expressed in the corresponding solar units:
|
| In the text | |
 |
Fig. 9 Evolution of the chemical composition (normalised to corresponding solar abundances) of He (solid), C (dotted), N (short dashed) and O (long dashed)in: ISM (top), massive star winds (middle) and GCR (bottom); the latter is the one calculated for the accelerated particles of MACC (Fig. 6) corrected to reproduce GCR source abundances today (as in Fig. 7). Dots in lower panel indicate estimated GCR source composition today, from Ellison et al. (1997). |
| In the text | |
 |
Fig. 10 Cross sections (mb) for the production of Li, Be and B by spallation of CNO nuclei with protons and alphas, as a function of particle energy per nucleon. Data are from Read & Viola (1984) and Mercer et al. (2001, α + α reactions). In all panels thick dotted curves correspond to production of 11B, thin dotted to 10B, thick solid to 7Li, thin solid to 6Li and dashed to 9Be. In the bottom right panel appear the adopted GCR spectra (arbitrary units): injection Q (dotted) and equilibrium F (solid). |
| In the text | |
 |
Fig. 11 Evolution of O/Fe (top), Be/H (middle) and Be/Fe bottom, as a function of Fe (left) and O (right). Dotted lines in middle and bottom panels indicate primary and secondary evolution, respectively. Data sources are as in Fig. 1, but only stars with both O and Be detected are displayed here. |
| In the text | |
 |
Fig. 12 Same as Fig. 11, with two new data sets (thick symbols) for stars with high [α/Fe] (filled squares) and low [α/Fe] (open circles) from Tan & Zhao (2011); all other data of Fig. 11 are displayed as dots. The thin solid curves correspond to the “standard” model presented in Fig. 11, while the thick dotted curves to a model with reduced SF efficiency and the thick dashed curves to a model with reduced SF efficiency and reduced escape length Λ for GCR (see text). |
| In the text | |
 |
Fig. 13 Left: contributions (percentages) to the production rate of Li, Be and B isotopes, with thick curves indicating the reverse component and thin curves the direct one for C (dotted), N (short-dashed) and O (long-dashed). Right: same thing, with the sums of C+N+O contributions for each component and the contributions of α+α (dotted curves) indicated for the Li isotopes. |
| In the text | |
 |
Fig. 14 From top to bottom: evolution of B/H, B/Fe and B/Be. In the first two panels dotted lines indicate primary and secondary evolution. In the bottom panel, the solid curve corresponds to the total 11B production (GCR + ν-nucleosynthesis) and the dotted curve to 11B produced by GCR alone. Data are from: Primas et al. (1999, filled squares), Garcia-Lopez et al. (1999, filled circles), Cunha et al. (2000, asterisks), and Tan et al. (2010, open squares). |
| In the text | |
 |
Fig. 15 Evolution of 11B/10B as a function of metallicity (left) and time (right). Solid curves correspond to the total 11B production (GCR + ν-nucleosynthesis) and dashed curves to 11B produced by GCR alone. The meteoritic (=solar) value (11B/10B)⊙ = 4.02 (Lodders 2003) is indicated at [Fe/H] = 0 and at time t = 7.5 Gyr, whereas the local value (11B/10B)0 = 3.4 ± 0.7 (Lambert et al. 1998) is plotted at t = 12 Gyr. |
| In the text | |
 |
Fig. 16 Evolution of Li (top) according to our Model A (see Table 1) and percentages of its various components (bottom): 7Li from GCR (dot-dashed), 6Li from GCR (dotted), 7Li from ν-nucleosynthesis (NN, dashed) and 7Li from a delayed stellar source (novae and/or AGB stars, long dashed). Solid curves indicate total Li (upper panel) and primordial 7Li (lower panel). Abundance data (upper panel for halo stars are taken from Charbonnel & Primas (2005, filled squares), Sbordone et al. (2010, filled circles), Bonifacio et al. (2007, open circles), Garcia-Perez et al. (2009, open triangles), Asplund et al. (2006, asterisks) and for disc stars from Lambert & Reddy (2004, dots). In the latter case, points with error bars indicate the average values of the six most Li-rich stars in the corresponding metallicity bins. |
| In the text | |
 |
Fig. 17 Same as the previous figure, but for Model B, with no contribution from CCSN and a different assumption for the stellar Li component (see Table 1 and text). |
| In the text | |
 |
Fig. 18 Evolution of Li/H (top) and of Li/Fe (bottom) in the local disc, as a function of [Fe/H] (left) and of time (right). In all panels, solid curves correspond to Model A and dotted curves to Model B. Data are from Lambert & Reddy (2004) and are provided as a function of metallicity. They are plotted as a function of time (right panels) by applying the model age-metallicity relation. |
| In the text | |
 |
Fig. 19 Evolution of total Li (solid curves), 6Li (dashed curves) and 7Li from GCR (dotted curves) in the standard case (low 6Li from SBBN, thick curves) and in the case of high pre-galactic 6Li and 7Li (thin curves). In the latter case, a minimum amount of depletion of 6Li within stars (equal to that of 7Li) has been conservatively assumed. 7Li data for halo stars are as in Fig. 16, while 6Li data are from Asplund et al. (2006, As09, open squares) and Garcia-Perez et al. (2009, GP09, filled circles). |
| In the text | |
 |
Fig. 20 Left: evolution of 6Li/7Li ratio as a function of [Fe/H] (left) and of time (right). Data are taken from Asplund et al. (2006, As06), Garcia-Perez et al. (2009, GP09) and Kawanomoto et al. (2009, K09). Solid curves correspond to Model A and dotted curves to Model B, respectively, both starting with standard (low) pre-galactic 6Li; dashed curves correspond to Model A with high pre-galactic 6Li. |
| In the text | |
 |
Fig. 21 Radial profiles of O/H, Li/H, Be/H and B/H (from top to bottom) at time t = 7.5 Gyr (solar system formation, dotted curves) and at t = 12. Gyr (now, solid curves). Present-day profiles between 4 and 12 kpc are fitted with exponentials (thick segments) and the corresponding slopes appear in the lower left corner of each panel. |
| In the text | |
 |
Fig. 22 Radial profiles of 6Li/7Li (top) and 11B/10B (bottom) at time t = 7.5 Gyr (solar system formation, dotted curves) and at t = 12. Gyr (now, solid curves). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.