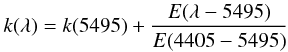| Issue |
A&A
Volume 541, May 2012
|
|
|---|---|---|
| Article Number | A54 | |
| Number of page(s) | 10 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201118712 | |
| Published online | 27 April 2012 | |
Ultraviolet extinction toward a quiescent molecular cloud in the Small Magellanic Cloud
1 Instituto de Astrofísica de Andalucía-CSIC, Glorieta de la Astronomía s/n, 18008 Granada, Spain
e-mail: jmaiz@iaa.es
2 Departamento de Astronomía, Universidad de Chile, Casilla 36-D, Santiago, Chile
e-mail: monica@das.uchile.cl
Received: 22 December 2011
Accepted: 27 January 2012
Context. The mean UV extinction law for the Small Magellanic Cloud (SMC) is usually taken as a template for low-metallicity galaxies. However, its current derivation is based on only five stars, which renders its universality questionable. More targets with measured extinction laws in the SMC are necessary to determine its possible dependence on parameters such as metallicity and star-forming activity.
Aims. We aim to measure the UV extinction law for several stars in the quiescent molecular cloud SMC B1-1.
Methods. We obtained HST/STIS slitless UV spectroscopy of a 25′′ × 25′′ field of view and combined it with ground-based NIR and visible photometry of the stars in the field. The results were processed using the Bayesian photometric package CHORIZOS to derive the visible-NIR extinction values for each star. The unextinguished spectral energy distributions (SEDs) obtained in this way were then used to derive the UV extinction law for the four most extinguished stars. We also recalculated the visible-NIR extinction for the five SMC stars with preexisting UV extinction laws.
Results. The UV extinction law for four SMC B1-1 stars that are situated within several pc of each other differs significantly from star to star. The 2175 Å bump is moderately strong in one, weak in two, and absent in the fourth.
Key words: dust, extinction / Magellanic Clouds / ultraviolet: ISM / stars: early-type
© ESO, 2012
1. Introduction
In the 1980s the International Ultraviolet Explorer (IUE) was extensively used to derive the UV extinction law for a large number of stars in the Milky Way and the Magellanic Clouds. It became clear then that there were considerable variations among sightlines in the three galaxies. Cardelli et al. (1989) used several tens of stars to derive a one-parameter family of extinction laws for the Galaxy. There were even fewer useful targets for the Large Magellanic Cloud (LMC) and still less for the Small Magellanic Cloud (SMC). The often quoted SMC extinction law of Prévot et al. (1984) was based in only three stars (AzV 398, AzV 18/Sk 13, and Sk 191). Sk 191 turned out to be a poor choice since it is actually an unreddened object, which left only two useful objects. The re-analysis of Gordon & Clayton (1998) added two more targets, AzV 214 and AzV 456/Sk 143, and Gordon et al. (2003) completed the current list of SMC stars with a derived UV extinction law with a fifth target, AzV 23/Sk 17.
The characteristic that is most often quoted about the SMC extinction laws is the absence of the 2175 Å wide absorption bump, which in the Fitzpatrick & Massa (1990) parameterization translates into a zero or very small c3 term. However, this is not true of all SMC extinction laws since AzV 456/Sk 143 clearly shows the absorption feature. The different location of AzV 456/Sk 143 in the SMC “wing” compared with that of the other stars in the SMC bar prompted Gordon & Clayton (1998) to compute two different SMC extinction laws, one for the wing and one for the bar, based on one and three1 stars, respectively. The results of Gordon et al. (2003) also suggest another possible difference between the two regions: their measured RV values for the four bar stars are in the typical range of 2.40–3.30 while that of the wing star is, 2.05 ± 0.17. The existence of these detected variations in a small sample is an obvious sign for the need for a better sample to quantify the prevalence of the different extinction laws and to understand the underlying reason for these variations. Another reason why a better sample is needed are the relatively low values of E(B − V) for the five stars, 0-15-0.26 (Gordon et al. 2003), which cause large uncertainties in the measured RV values.
Why should we care about the SMC extinction law? In addition to the importance that it has by itself, because the SMC is our best template for low-metallicity galaxies. Indeed, it was assumed for some time that the absence of the 2175 Å bump in the SMC extinction law was a metallicity effect but the detection of such a feature in Azv 456/Sk 143 seems to invalidate that hypothesis. Several explanations are possible, such as the existence of metallicity gradients in the ISM or the effect of “star-formation activity”, a term that refers to the possible destruction of dust grains by UV radiation or shocks from massive stars. Until we have a better sample, we will likely not be able to decide which explanation is the most plausible one.
We selected as our target SMC B1-1, a cold molecular cloud without signs of star formation that is located at the southern end of the SMC bar. It has a molecular mass of 2.4 × 104 M⊙ (Rubio et al. 2004) as derived from the CO(1–0) emission line and its virial mass was determined using observations made with the Swedish ESO Submilllimeter Telescope (SEST) at La Silla Observatory. Of the stars with existing UV extinction laws, the closest one to SMC B1-1 is AzV 18/Sk 13, located ~ 14′ away.
2. Observations and data description
2.1. STIS data
SMC B1-1 was observed with the Space Telescope Imaging Spectrograph (STIS) onboard the Hubble Space Telescope (HST) on 27 May 2004. We obtained four imaging exposures with STIS/NUV-MAMA, two imaging exposures with STIS/FUV-MAMA, and one slitless spectral exposure with STIS/NUV-MAMA. Both MAMA detectors have no read noise and, in imaging mode, cover a field of 25′′ × 25′′ with 1024 × 1024 pixels. The NUV imaging exposures used two different filters, F25CN270 (centered at 2702 Å, see Fig. 1) and F25CN182 (centered at 1895 Å) with total exposures times of 100 s for each filter. The FUV imaging exposures used a single filter, F25QTZ (centered at 1559 Å) with a total exposure time of 200 s. The slitless spectral exposures, which cover an area slightly bigger than that of the images, were obtained with the NUV objective prism (Fig. 2) with a total exposure time of 916 s. The NUV objective prism has a variable dispersion that goes from ≈5 Å/pixel at 1750 Å to ≈45 Å/pixel at 3000 Å (STScI 2007). Our spectral exposures were obtained in the shadowed part of the orbit and with the F25SRF2 filter to minimize the effect of the geocoronal background.
There are 15 stars that are easily detected in all three UV imaging filters and in the spectral exposures. They have been labeled in Figs. 1 and 2 in order of ascending y coordinate. Note that the stars were not placed on an absolute reference frame, so it is possible that the RA+Dec grid is offset by ~1′′, as is typical with coordinates derived from the header information in HST images.
2.2. NIR imaging
Deep NIR JHKs imaging was obtained with ISAAC at the 8.2 m VLT telescope at Paranal Observatory on 24–25 September 1999 (63.C-0329(A)). We used the short wavelength arm equipped with a 1024 × 1024 1024 pixels Hawaii Rockwell array, with a spatial resolution of 0 148′′/pix and a total field of view of 2
148′′/pix and a total field of view of 2 5 × 2
5 × 2 5.
5.
The observations were made in a series of six frames (NDIT), each individual frame with a 10 s integration time (DIT) in each filter. The individual frames were coadded and a 60 s image was stored. A ten position dither mosaic was made with a separation of 15′′ using the same observing strategy to cover the SMC B1-1 region. In each filter, we interleaved sky frame observations for every 10 min of on-source imaging. These sky frames were chosen in a field with faint stars and no extended emission located 300′′ south of the position of SMC B1-1. The sky field was observed in a similar way as the source frames. The procedure was repeated until we achieved a final integration time of 3600 s in J, H, and Ks.
To produce the final images, each image was dark-corrected, flat-fielded, and sky-subtracted, and then median-averaged and combined using IRAF procedures. The final images were registered with respect to the J image by means of several common stars. The final ISAAC/VLT images cover a 2 5 × 5
5 × 5 0 area and have limiting magnitudes of about J = 21, H = 21, and Ks = 22, respectively.
0 area and have limiting magnitudes of about J = 21, H = 21, and Ks = 22, respectively.
We identified the 15 stars observed in the HST field in the VLT/NIR images and performed aperture photometry using the IRAF/DAOPHOT package. We used the standard stars observed on both nights to calibrate the photometry in Ks (observed the first night) and in H and J (observed the second night). Additionally, we selected several stars from the 2MASS IR images with good photometry (AAA label) and compared their catalog magnitudes with our JHKs photometry. The agreement between our photometry and 2MASS is good to 0.01 mag. The NIR photometry in given in Table 1. Two of the stars (06 and 07) are too close together in the ground-based data to be resolved, so unresolved magnitudes are provided.
ISAAC/VLT NIR photometry.
2.3. Visible photometry
The Johnson-Cousins UBVI photometry of the sources present in the STIS exposures was obtained from Zaritsky et al. (2002) using the VizieR (Ochsenbein et al. 2000) J/AJ/123/855 catalog. 13 of the 15 stars are resolved in the Zaritsky et al. (2002) data while the pair 06+07 appears as a single unresolved source.
 |
Fig. 1 F25CN270 STIS NUV-MAMA image of the SMC B1-1 region. The stars for which photometry was extracted are labeled. |
 |
Fig. 2 STIS NUV-MAMA objective prism exposure of the SMC B1-1 region. See Fig. 1 for orientation and field size. |
3. Processing of the SMC B1-1 data
Our goal in this paper is to obtain the UV extinction law of as many as possible of the stars in the SMC B1-1 region for which we can measure their spectra. The strategy to accomplish that is:
-
1.
measure the effective temperature (Teff) and optical/NIRextinction of the 14 sources that are point-like inthe ground-based photometry;
-
2.
extract the spectra for the 15 point sources in the NUV slitless exposures;
-
3.
select the sources with the highest optical/NIR extinction, since for those objects the UV extinction should be more easily measurable;
-
4.
calculate the extinction law k(λ) for the stars selected in the previous step.
3.1. Effective temperatures and optical color excesses
The traditional mechanism to measure UV extinction laws is known as the pair method (Massa et al. 1983) and requires obtaining spectra of two stars of the same spectral type, one with high extinction and the other one with low extinction. The fluxes of the two stars are corrected for distance effects if necessary, the low-extinction spectral energy distribution is divided by the high-extinction one, and the result is normalized by the extinction difference between the two. The pair method requires the accurate measurement of the spectral type of the extinguished star, which may not be straightforward for dim objects, and the availability of data for a star with the same spectral type, which can lead to errors due to mismatches between stars.
Alternatively, it is possible to measure extinction without referring to a standard star by using a synthetic spectral energy distribution (SED) library and a numerical code that matches the available (spectro-)photometry to a grid with different stellar parameters (e.g. Teff, log g, and Z) and extinction amounts and laws (Maíz Apellániz 2004; Fitzpatrick & Massa 2005). In this way, it is possible to derive the intrinsic or unextinguished SED directly from the data and, hence, calculate the extinction law directly by comparison with the observed spectral fluxes. Here we will follow that approach for the optical/NIR extinction using CHORIZOS (Maíz Apellániz 2004, 2005a), a Bayesian code that allows the fitting of (spectro-)photometric data to an SED grid of up to five dimensions, including parameterized extinction laws2. For the amount of extinction CHORIZOS uses as parameter E(4405−5495) ≡ A(4405) − A(5495), the monochromatic equivalent to E(B − V), because the former depends only on the amount and type of dust while the latter also depends on the spectral type of the source3. In other words, the same amount and type of dust in front of an O star and an M star will produce the same E(4405 − 5495) but different E(B − V), so using E(B − V) as an indicator of the amount of extinction can lead to some counterintuitive results (see e.g. Massey et al. 2005) and should be avoided to characterize an extinction law.
In order to use CHORIZOS to derive the intrinsic SED of the UV-bright objects in SMC B1-1 it is useful to take into account different considerations. First of all, optical-NIR extinction laws have relatively simple functional forms and the Galactic laws can in principle be accurately described using a single-family parameter (Cardelli et al. 1989)4. In this wavelength range the published SMC extinction laws are not too different from the Galactic ones5: for example, the SMC-bar law of Gordon & Clayton (1998) is quite similar to the Cardelli et al. (1989) law with R5495 = 2.8 for λ > 3000 Å (R5495 ≡ A(5495)/E(4405 − 5495) is the monochromatic equivalent to RV). See also Maíz Apellániz et al. (2012, in prep.). In the UV, the extinction morphology is more complicated and, as Fitzpatrick & Massa (2007) have shown, cannot be accurately described by a single-parameter family. Therefore, it makes sense to derive the intrinsic SEDs by excluding the photometric data with the shortest wavelengths because of the likely confusion between intrinsic (e.g. Teff) and extinction-law effects. Consequently, we will use the longest-wavelength UV photometric data (F25CN270) combined with the optical (UBVI) and NIR (JHK) data for that purpose. Second, given the location in the SMC and the observed magnitudes, we expect our stars to be early-to-mid B main-sequence stars with metallicity near log Z = −1.0. Also, given that the optical-NIR colors of non-supergiant B stars are relatively insensitive to gravity and metallicity, it will be appropriate to constrain our synthetic SED grid to main-sequence models with log Z = −1.0 and to use Teff, E(4405 − 5495), and extinction law type as the free parameters in the grid. Note that the best photometric discriminant for the effective temperature of B stars in the optical-NIR range is the Balmer jump and that with our filter selection we have two photometric points to its left (F25CN270 and U) and two points to its right (B and V), which allows us to measure the temperature precisely. Finally, in order to use consistent zero-points for the different photometric systems involved, we will use the Johnson sensitivity curves as determined by Maíz Apellániz (2006) and the zero-point system of Maíz Apellániz (2007).
 |
Fig. 3 Contour plots showing the likelihood in the Teff-E(4405 − 5495) plane for the four stars in the second CHORIZOS run with the highest mean value for E(4405−5495). The contour intervals are linearly spaced with the minimum and maximum at 0.05 and 0.95 times the peak (mode) value, respectively. The star shows the location of the mode (not the mean) and the plots on each axis show the integrated likelihood for that parameter. |
 |
Fig. 4 MULTISPEC and fixed extinction-law CHORIZOS results for the four stars with the highest E(4405 − 5495). The red and blue data points with error bars correspond to the observed UV-optical-NIR photometric magnitudes, with the vertical error bars showing the uncertainties and the horizontal ones the approximate extent of the filters. Only the blue data points points were used for the CHORIZOS fits. The continuous FUV-to-NIR line shows the CHORIZOS mode SED, which assumes a Gordon & Clayton (1998) SMC-bar extinction law throughout the full wavelength range, while the NUV-only histogram shows the MULTISPEC extraction. The green stars show the synthetic photometry that corresponds to the CHORIZOS mode SED. The CHORIZOS values for Teff and E(4405 − 5495) are given for each star. |
Taking into account the considerations in the previous paragraph, we executed an initial CHORIZOS run for each of the 14 point-like visible sources using as input the F25CN270 + UBVI + JHK photometry and as SEDs Kurucz atmospheres with main-sequence gravities and log Z = −1.0 and Cardelli et al. (1989) extinction laws, leaving three free parameters to fit (Teff, E(4405−5495), and R5495). The results of that initial run show that all 14 sources have E(4405 − 5495) lower than 0.60 and only three have values above 0.25. Given the low extinction of the 11 sources with E(4405−5495) < 0.25, their values of R5495 are mostly unconstrained, as expected if the spectral types are not known a priori. For the three more extinguished stars we derive values of R5495 between 2.9 and 3.5 with uncertainties of ≈ 0.3 i.e. similar to those of the average Galactic and SMC extinction laws. This result prompted us to do a second and final CHORIZOS run with the same photometric data and parameters but using a fixed extinction law, the SMC-bar of Gordon & Clayton (1998). The obtained values for Teff and E(4405−5495) in the final CHORIZOS run are similar to those of the first one but with slightly lower error bars. The results of the second run are shown in Table 2 and plotted (for the four stars with the highest mean values of E(4405 − 5495)) in Figs. 3 and 4. As expected, all stars have temperatures consistent with being B stars6. Their extinction-corrected luminosities are all consistent with being main-sequence stars.
3.2. Spectral extraction
To extract the multiple spectra present in the objective prism data (Fig. 2) we used MULTISPEC (Maíz Apellániz 2005b), a software package specifically designed for the extraction of multiple spectra from slitless HST exposures of crowded fields7. MULTISPEC works by fitting multiple spatial profiles for each column in the spectral exposure. We used v2.0 of the code, which allows the use of tabulated spatial profiles and which has been applied by Knigge et al. (2008) to extract UV spectra from STIS/FUV-MAMA G140L exposures of 47 Tuc. For the flux calibration of the data we used Maíz Apellániz & Bohlin (2005) and included time-dependent sensitivity corrections.
The extracted spectra for stars 08, 09, 10, and 11 are shown in Fig. 4 along with the mode CHORIZOS SED, which assumes a Gordon & Clayton (1998) SMC-bar extinction law. The extracted spectra have been binned in wavelength to obtain a uniform signal-to-noise ratio (S/N) in each bin. The observed and model spectra have relatively similar values of fν in their common wavelength range, indicating that the extinction law for those stars cannot be too different from the SMC-bar one of Gordon & Clayton (1998). Note, however, that there are some readily apparent differences: stars 08 and 11 show a weak 2175 Å absorption structure and the measured UV fluxes for stars 09 and 10 are higher than the model ones.
3.3. Source selection
Second-run CHORIZOS results.
 |
Fig. 5 Observed extinction laws (histogram used for the spectral data, points with error bars for the photometric data) and fitted Fitzpatrick & Massa (1990) extinction laws (continuous line) for each of the four stars in Fig. 4. The values of the fitted parameters are given in each case with their random and systematic errors indicated by “r.” and “s.”, respectively. |
As previously mentioned, only three point sources (08, 10, and 12) have E(4405−5495) > 0.25 and a fourth one (09) has a slightly lower value. Those will be the four sources for which we will calculate the UV extinction law because for the rest the relative uncertainties on k(λ) are too large to yield a useful result. Note that previous studies have derived extinction laws for stars with even lower values of E(4405−5495), but that was possible because of the availability of data with higher S/N than we are using here.
3.4. UV extinction-law calculation
Finally, we obtain the UV extinction law k(λ) which, following the usual practice, we normalize as:
and then consider only the second term, which is 0 for λ = 5495 Å and 1 for λ = 4405 Å. We recall that we used monochromatic rather than filter-integrated values for the definition of the extinction law. The mode value of k(λ) − k(5495) is obtained by dividing the extracted spectrum for each star by the unextinguished version of the CHORIZOS-derived mode SED and normalizing the result. A similar procedure can be performed for the filter-integrated quantities derived from the measured F25QTZ and F25CN182. Both spectral and photometric results are shown in Fig. 5. One readily apparent result is that there is a decrease in the intensity of the 2175 Å absorption structure as we follow the stellar sequence 11 → 08 → 09 → 10.
One practical way of characterizing the UV extinction law is by using the six-parameter (c1, c2, c3, c4, x0, γ) Fitzpatrick & Massa (1990) recipe, which gives 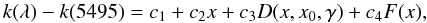 (2)where x = 1/λ (usually expressed in μ-1),
(2)where x = 1/λ (usually expressed in μ-1), 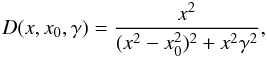 (3)and
(3)and
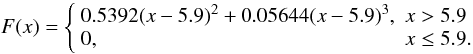 (4)We wrote a χ2-minimization code to fit such a Fitzpatrick & Massa (1990) six-parameter function to the spectral (1700–2900 Å) and photometric (F25QTZ and F25CN182) data for each of the four stars with higher extinction. When doing so, one has to be careful to account not only for random errors arising from the finite S/N of the data but also for systematic ones arising from possible spectral mismatches (in our case, this corresponds to the uncertainty in the Teff and E(4405−5495) values derived by CHORIZOS). The results are shown and plotted in Fig. 5.
(4)We wrote a χ2-minimization code to fit such a Fitzpatrick & Massa (1990) six-parameter function to the spectral (1700–2900 Å) and photometric (F25QTZ and F25CN182) data for each of the four stars with higher extinction. When doing so, one has to be careful to account not only for random errors arising from the finite S/N of the data but also for systematic ones arising from possible spectral mismatches (in our case, this corresponds to the uncertainty in the Teff and E(4405−5495) values derived by CHORIZOS). The results are shown and plotted in Fig. 5.
As previously noted, there is a sequence of intensities of the 2175 Å absorption structure (measured by c3) in the order 11 → 08 → 09 → 10. It should be also pointed out that the values of the parameter that measure the FUV slope (c4) are anomalously high. However, those values are not very significant (their errors are very large) because they are based mostly on a single photometric point (F25QTZ) centered at relatively long FUV wavelengths.
For our calculations we did not perform a prior subtraction of the Galactic contribution to the extinction. As described by Zagury (2007), for the Magellanic Clouds this cannot be done from the data itself unless one assumes a smooth spatial distribution of the Galactic cirri, something that the MIR observations do not support. Therefore, the UV extinction laws derived here are in principle a combination of a Galactic and an SMC components. However, the existence of stars with very low extinction in the vicinity [e.g. star 02 has E(4405 − 5495) = 0.03 ± 0.03] argues in favor of the dominance of the SMC component. An additional point against the importance of a Galactic dust component is the wide range in reddenings in our sample, with values from 0.03 to 0.51 mag. Note that at a distance of e.g. 1 kpc to a hypothetical Galactic cloud, 10′′ correspond to just 10 000 AU. To our knowledge, no Galactic cirrus shows such large variations on such small scales. The low value of E(4405 − 5495) for star 02 also agrees with the foreground reddening of 0.037 measured by Schlegel et al. (1998) and with the more recent work of Subramaniam & Subramanian (2010), who found that most of the SMC has a Galactic foreground extinction lower than AV = 0.1 mag.
CHORIZOS results for the five stars with preexisting UV extinction laws.
4. Looking back at the five SMC stars with preexisting extinction laws
To check that our methods are consistent with previous works, we used CHORIZOS to calculate the values of E(4405 − 5495) and R5495 for the five SMC stars with preexisting extinction laws. For that purpose, we used the Gordon et al. (2003)UBVRI and the 2MASS JHKs photometry for those stars8. In this case we used a newer version of CHORIZOS that allows the stellar parameters to be Teff, luminosity class, and metallicity. By luminosity class, we mean a quantity that runs from 0.0 (hypergiants) to 5.5 (ZAMS) and, for a given Teff and metallicity, yields a luminosity similar to the one derived from spectral classification (with Ia+ translated as 0.0 and Vz as 5.5). The SEDs in this case were TLUSTY (Lanz & Hubeny 2003, 2007). Three parameters were left fixed: Teff (from the spectral type), metallicity (SMC), and the logarithm of the distance (4.782). Three parameters were allowed to vary: Luminosity class, R5495, and E(4405−5495). For AzV 398 we excluded the Ks photometry from the fit after an initial run because the star appears to have an excess in that band compared to the TLUSTY models, likely a wind effect. The Cardelli et al. (1989) extinction laws were used. Results are shown in Table 3. Note that the values there for R5495 and E(4405−5495) are monochromatic quantities while AV is filter-integrated.
The reduced 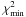 in all cases is quite good, indicating the good quality of the photometry. The (photometry-derived) luminosity classes are all between 1.0 and 2.0, as expected for supergiants. Our results for E(4405−5495) and R5495 differ significantly from the band-integrated ones [E(B − V) and RV, respectively] of Gordon et al. (2003). The differences in E(4405 − 5495) likely arise because we are measuring absolute extinctions while they were measuring extinctions relative to a comparison star. Indeed, our values for E(4405−5495) are higher than their values of E(B − V) by 0.01 to 0.10 mag, as expected under these circumstances. However, we also measure values of R5495 that are systematically higher by ~0.6. That is harder to assign to the inclusion of an additional R5495 = 3.1 component in our values (the one responsible for the additional extinction), since that would pull them toward 3.1 and not increase all of them independently of R5495. The difference may be attributed to the different methodologies and to the fact that our quantities are monochromatic and theirs are band-integrated.
in all cases is quite good, indicating the good quality of the photometry. The (photometry-derived) luminosity classes are all between 1.0 and 2.0, as expected for supergiants. Our results for E(4405−5495) and R5495 differ significantly from the band-integrated ones [E(B − V) and RV, respectively] of Gordon et al. (2003). The differences in E(4405 − 5495) likely arise because we are measuring absolute extinctions while they were measuring extinctions relative to a comparison star. Indeed, our values for E(4405−5495) are higher than their values of E(B − V) by 0.01 to 0.10 mag, as expected under these circumstances. However, we also measure values of R5495 that are systematically higher by ~0.6. That is harder to assign to the inclusion of an additional R5495 = 3.1 component in our values (the one responsible for the additional extinction), since that would pull them toward 3.1 and not increase all of them independently of R5495. The difference may be attributed to the different methodologies and to the fact that our quantities are monochromatic and theirs are band-integrated.
The uncertainties in Table 3 (and in Table 2 as well) are formal (or random) ones. There are also systematic uncertainties caused by the mismatch between the SEDs used and the real ones and due to the problems with the Cardelli et al. (1989) extinction laws (fundamentally, the use of a seventh-degree polynomial as a functional form in the optical range, see Maíz Apellániz et al. 2007; Maíz Apellániz & Sota 2008; Maíz Apellániz et al. 2012, in prep.). However, an analysis of the photometric residuals indicates that the Balmer jump seems to be well fit. Furthermore, these objects have E(4405−5495) < 0.5, so the systematic effects of the Cardelli et al. (1989) extinction laws should be small9. Therefore, we do not expect the systematic uncertainties to be larger than the random ones, especially for R5495.
The weighted mean of the R5495 values for the four SMC bar stars is 3.36 ± 0.07 and the results are consistent with the four real R5495 values being the same (three cases within one sigma, one between one and two sigma). Therefore, the results for those four stars and the three more extinguished stars in SMC B1-1 are consistent with a visible-NIR extinction law not too different from the typical Galactic one, which has R5495 = 3.1−3.2. On the other hand, the result for AzV 456/Sk 143 does indeed seem different, since its R5495 is ~ 5 sigmas lower.
5. Discussion
In this paper we have calculated for the first time the UV extinction law for four stars in SMC B1-1, a quiescent cloud in the Small Magellanic Cloud. For those stars and for the other five stars with previously existing UV extinction laws we have also calculated their E(4405−5495) and R5495 from visible-NIR photometry.
For the four stars in SMC B1-1. all located within a few pc of each other, we found significant variations in the extinction law and values. The latter is simply a manifestation of the small-scale structure in the dust distribution while the former implies a different dust composition. The most clear variations in the UV extinction law are in the strength of the 2175 Å bump, which goes from non-existing (as is the case for the four of the SMC bar stars with preexisting laws) to a case of moderate strength by Galactic standards though still weaker than the previously studied SMC bar star (c3 = 1.76 ± 0.30 for the new target, 2.57 ± 0.22 for the old one). c3 does not appear positively correlated with E(4405−5495) (the most and the least extinguished stars have weak bumps while the two stars with intermediate extinctions represent the extremes in bump strength), which argues against a foreground Galactic cloud as the source of the extinction.
Despite the significant UV variations, the SMC visible-NIR extinction law appears to be more uniform, at least within the current measurement errors. The variations in R5495 have been attributed to different dust grain sizes for a long time (Baade & Minkowski 1937). All observed eight SMC bar stars with well-measured R5495 have values compatible with the typical Galactic one and only the SMC star measured in the wing has a somewhat lower R5495. However, there are no clear cases of high values (R5495 ~ 5), such as those found in some Galactic H ii regions (see e.g. Arias et al. 2006). That is not surprising, given that the Galactic cases with large R5495 are found within the bright areas of their H ii regions and that is not the case for any of the analyzed SMC stars10.
The existence of the 2175 Å bump in stars located in relatively quiescent regions of the SMC argues in favor of its absence being caused by the presence of intense UV radiation fields and stellar winds, which would destroy its carrier (see Clayton et al. 2003; Sofia et al. 2006). Nevertheless, our results also suggest that the final explanation may be more complex. Otherwise, the four stars in SMC B1-1 would show the bump in their extinction laws. Also, since extinction appears to be patchy and associated with local dust clouds, c3 should be correlated with E(4405−5495). Neither of those two effects appear in on our results.
As we have already mentioned, Gordon et al. (2003) added another star, AzV 23/Sk 17, also located in the bar.
MULTISPEC is a public sofware written in IDL that can be downloaded from http://jmaiz.iaa.es
A quite different situation compared to the more extinguished case of Pismis 24-1 case discussed in Maíz Apellániz et al. (2007).
Acknowledgments
This article is based on observations made with the NASA/ESA Hubble Space Telescope (HST) associated with GO program 9718 and obtained at the Space Telescope Science Institute, which is operated by the Association of Universities for Research in Astronomy, Inc., under NASA contract NAS 5-26555. Support for both authors was provided by the Chilean FONDECYT grant number 1080335. J.M.A. also acknowledges support from [a] the Spanish Government Ministerio de Educación y Ciencia through grants AYA2004-08260-C03, AYA2004-05395, AYA2007-64712, AYA2007-64052, and AYA2010-17631 and the Ramón y Cajal Fellowship program, co-financed with FEDER funds, and [b] the Consejería de Educación of the Junta de Andalucía through grants TIC-101 and P08-TIC-4075. M.R. is also supported by the Chilean Center for Astrophysics FONDAP grant number 15010003. The authors would like to thank the referee, Geoff Clayton, for his suggestions in improving the paper, and François Boulanger for his inspiration and support in the early stages of this project.
References
- Arias, J. I., Barbá, R. H., Maíz Apellániz, J., Morrell, N. I., & Rubio, M. 2006, MNRAS, 366, 739 [NASA ADS] [CrossRef] [Google Scholar]
- Baade, W., & Minkowski, R. 1937, ApJ, 86, 123 [NASA ADS] [CrossRef] [Google Scholar]
- Cardelli, J. A., Clayton, G. C., & Mathis, J. S. 1989, ApJ, 345, 245 [NASA ADS] [CrossRef] [Google Scholar]
- Clayton, G. C., Wolff, M. J., Sofia, U. J., Gordon, K. D., & Misselt, K. A. 2003, ApJ, 588, 871 [NASA ADS] [CrossRef] [Google Scholar]
- Fitzpatrick, E. L., & Massa, D. 1990, ApJS, 72, 163 [NASA ADS] [CrossRef] [Google Scholar]
- Fitzpatrick, E. L., & Massa, D. 2005, AJ, 130, 1127 [NASA ADS] [CrossRef] [Google Scholar]
- Fitzpatrick, E. L., & Massa, D. 2007, ApJ, 663, 320 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gordon, K. D., & Clayton, G. C. 1998, ApJ, 500, 816 [NASA ADS] [CrossRef] [Google Scholar]
- Gordon, K. D., Clayton, G. C., Misselt, K. A., Landolt, A. U., & Wolff, M. J. 2003, ApJ, 594, 279 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Knigge, C., Dieball, A., Maíz Apellániz, J., et al. 2008, ApJ, 683, 1006 [NASA ADS] [CrossRef] [Google Scholar]
- Lanz, T., & Hubeny, I. 2003, ApJS, 146, 417 [NASA ADS] [CrossRef] [Google Scholar]
- Lanz, T., & Hubeny, I. 2007, ApJS, 169, 83 [CrossRef] [Google Scholar]
- Maíz Apellániz, J. 2004, PASP, 116, 859 [NASA ADS] [CrossRef] [Google Scholar]
- Maíz Apellániz, J. 2005a, in The Three-Dimensional Universe with Gaia, ed. C. Turon, K. S. O’Flaherty, & M. A. C. Perryman, ESA SP, 576, 449 [Google Scholar]
- Maíz Apellániz, J. 2005b, STIS Instrument Science Report 2005-02 (STScI: Baltimore) [Google Scholar]
- Maíz Apellániz, J. 2006, AJ, 131, 1184 [NASA ADS] [CrossRef] [Google Scholar]
- Maíz Apellániz, J. 2007, in The Future of Photometric, Spectrophotometric and Polarimetric Standardization, ed. C. Sterken, ASP Conf. Ser., 364, 227 [Google Scholar]
- Maíz Apellániz, J., & Bohlin, R. C. 2005, STIS Instrument Science Report 2005-01 (STScI: Baltimore) [Google Scholar]
- Maíz Apellániz, J., & Sota, A. 2008, in Rev. Mex. Astron. Astrofís. Conf. Ser., 33, 44 [Google Scholar]
- Maíz Apellániz, J., Walborn, N. R., Morrell, N. I., Niemelä, V. S., & Nelan, E. P. 2007, ApJ, 660, 1480 [NASA ADS] [CrossRef] [Google Scholar]
- Massa, D., Savage, B. D., & Fitzpatrick, E. L. 1983, ApJ, 266, 662 [NASA ADS] [CrossRef] [Google Scholar]
- Massey, P., Plez, B., Levesque, E. M., et al. 2005, ApJ, 634, 1286 [NASA ADS] [CrossRef] [Google Scholar]
- Ochsenbein, F., Bauer, P., & Marcout, J. 2000, A&AS, 143, 23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Prévot, M. L., Lequeux, J., Maurice, E., Prévot, L., & Rocca-Volmerange, B. 1984, A&A, 132, 389 [NASA ADS] [Google Scholar]
- Rubio, M., Boulanger, F., Rantakyro, F., & Contursi, A. 2004, A&A, 425, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schlegel, D. J., Finkbeiner, D. P., & Davis, M. 1998, ApJ, 500, 525 [NASA ADS] [CrossRef] [Google Scholar]
- Sofia, U. J., Gordon, K. D., Clayton, G. C., et al. 2006, ApJ, 636, 753 [NASA ADS] [CrossRef] [Google Scholar]
- STScI 2007, STIS Instrument Handbook, ed. J. Kim Quijano, S. Hoifeltz, & J. Maíz Apellániz [Google Scholar]
- Subramaniam, A., & Subramanian, S. 2010, Interstellar Matter and Star Formation: A Multi-wavelength Perspective, ed. D. K. Ojha, ASI Conf. Ser., 1, 107 [Google Scholar]
- Zagury, F. 2007, Ap&SS, 312, 113 [NASA ADS] [CrossRef] [Google Scholar]
- Zaritsky, D., Harris, J., Thompson, I. B., Grebel, E. K., & Massey, P. 2002, AJ, 123, 855 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 F25CN270 STIS NUV-MAMA image of the SMC B1-1 region. The stars for which photometry was extracted are labeled. |
| In the text | |
 |
Fig. 2 STIS NUV-MAMA objective prism exposure of the SMC B1-1 region. See Fig. 1 for orientation and field size. |
| In the text | |
 |
Fig. 3 Contour plots showing the likelihood in the Teff-E(4405 − 5495) plane for the four stars in the second CHORIZOS run with the highest mean value for E(4405−5495). The contour intervals are linearly spaced with the minimum and maximum at 0.05 and 0.95 times the peak (mode) value, respectively. The star shows the location of the mode (not the mean) and the plots on each axis show the integrated likelihood for that parameter. |
| In the text | |
 |
Fig. 4 MULTISPEC and fixed extinction-law CHORIZOS results for the four stars with the highest E(4405 − 5495). The red and blue data points with error bars correspond to the observed UV-optical-NIR photometric magnitudes, with the vertical error bars showing the uncertainties and the horizontal ones the approximate extent of the filters. Only the blue data points points were used for the CHORIZOS fits. The continuous FUV-to-NIR line shows the CHORIZOS mode SED, which assumes a Gordon & Clayton (1998) SMC-bar extinction law throughout the full wavelength range, while the NUV-only histogram shows the MULTISPEC extraction. The green stars show the synthetic photometry that corresponds to the CHORIZOS mode SED. The CHORIZOS values for Teff and E(4405 − 5495) are given for each star. |
| In the text | |
 |
Fig. 5 Observed extinction laws (histogram used for the spectral data, points with error bars for the photometric data) and fitted Fitzpatrick & Massa (1990) extinction laws (continuous line) for each of the four stars in Fig. 4. The values of the fitted parameters are given in each case with their random and systematic errors indicated by “r.” and “s.”, respectively. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.