| Issue |
A&A
Volume 541, May 2012
|
|
|---|---|---|
| Article Number | A153 | |
| Number of page(s) | 11 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201118639 | |
| Published online | 22 May 2012 | |
Time-dependent escape of cosmic rays from supernova remnants, and their interaction with dense media
1
DESY
Platanenallee 6,
15738
Zeuthen,
Germany
e-mail: igor.telezhinsky@desy.de
2
Universität Potsdam, Institut für Physik &
Astronomie, Karl-Liebknecht-Strasse
24/25, 14476
Potsdam,
Germany
3
University of Chicago, Department of Astronomy &
Astrophysics, 5640 S Ellis Ave, AAC
010c, Chicago,
IL
60637,
USA
Received: 14 December 2011
Accepted: 22 March 2012
Context. Supernova remnants (SNRs) are thought to be the main source of Galactic cosmic rays (CRs) up to the “knee” in CR spectrum. During the evolution of a SNR, the bulk of the CRs are confined inside the SNR shell. The highest-energy particles leave the system continuously, while the remaining adiabatically cooled particles are released when the SNR has expanded sufficiently and decelerated so that the magnetic field at the shock is no longer able to confine them. Particles escaping from the parent system may interact with nearby molecular clouds, producing γ-rays in the process via pion decay. The soft gamma-ray spectra observed for a number of SNRs interacting with molecular clouds, however, challenge current theories of non-linear particle acceleration that predict harder spectra.
Aims. We study how the spectrum of escaped particles depends on the time-dependent acceleration history in both Type Ia and corecollapse SNRs, as well as on different assumptions about the diffusion coefficient in the vicinity of the SNR.
Methods. We solve the CR transport equation in a test-particle approach combined with numerical simulations of SNR evolution.
Results. We extend our method for calculating the CR acceleration in SNRs to trace the escaped particles in a large volume around SNRs. We calculate the evolution of the spectra of CRs that have escaped from a SNR into a molecular cloud or dense shell for two diffusion models. We find a strong confinement of CRs in a close region around the SNR, and a strong dilution effect for CRs that were able to propagate out as far as a few SNR radii.
Key words: ISM: supernova remnants / ISM: clouds / cosmic rays
© ESO, 2012
1. Introduction
Supernova remnants (SNRs) are now widely considered to be sources of Galactic cosmic rays (CRs). Diffusive shock acceleration (DSA) (Axford et al. 1977; Krymskii 1977; Bell 1978; Blandford & Ostriker 1978) and its non-linear modification (NDSA) (Malkov & O’C Drury 2001) predict a power-law distribution (N(E) ∝ E−s) of relativistic particles with index s = 2 (s < 2 for the high-energy tail in NDSA). Despite recent advances in DSA and NDSA, it is still unclear why we observe soft (s > 2) CR spectra at Earth (Ave et al. 2009) and soft gamma-ray spectra from a number of SNRs: RX J0852.0-4622 (Aharonian et al. 2007), RCW 86 (Aharonian et al. 2009), SN 1006 (Acero et al. 2010), Cas A (Acciari et al. 2010; Abdo et al. 2010a), and Tycho’s SNR (Acciari et al. 2011; Giordano et al. 2012).
Understanding gamma-ray SNR spectra in various situations requires the study of the acceleration of the particles in the system (consisting of one or two shock waves), followed by the escape of these particles, their diffusion into the Galactic medium (Ptuskin et al. 2010; Caprioli et al. 2010), and computation of the γ-ray emission by various processes. In an earlier paper (Telezhinsky et al. 2012), we studied the acceleration of particles at SNR shock fronts. In this paper, we follow up this work by studying the escape of these particles from the system, and their interaction with dense media.
A useful probe of the escape of particles from SNRs may be high-energy gamma-ray emission from molecular clouds located close to an efficiently accelerating SNR, the so-called MC-SNR systems. A number of these have been observed by Cherenkov telescopes (CTs) and Fermi. Most sources, including W28 (Abdo et al. 2010b), W44 (Abdo et al. 2010c), IC 443 (Acciari et al. 2009; Abdo et al. 2010d), G349.7+0.2, CTB 37A, 3C 391, and G8.7-0.1 (Castro & Slane 2010) are located close to dense regions or molecular clouds (MCs), thus one may use them to infer the diffusion parameters in their vicinity. Triggered by these observations, a number of studies (Gabici et al. 2009; Fujita et al. 2009) have attempted to explain the soft gamma-ray emission from MC-SNR systems in terms of escaped CRs. These studies have been based on analytical models (Atoyan et al. 1995; Aharonian & Atoyan 1996) and several assumptions: (i) the SNR evolution is either stationary or Sedov-like; (ii) often that particle acceleration is quasi-instantaneous compared with the CR diffusion time; and (iii) the escaping-particle distribution is a power-law or monoenergetic at a given maximum momentum. The source of CRs is considered to be point-like, i.e., the SNR radius is much smaller than the distance to the MC. Li & Chen (2010), Li & Chen (2011), and Ohira et al. (2011), extended the analytical models to include finite-size sources and finite-size target MCs.
Despite their simplicity, the analytical studies demonstrate that to explain observations, the diffusion coefficient in the SNR vicinity must be roughly two orders of magnitude smaller than the average Galactic value, supporting earlier claims (Wentzel 1974) that the diffusion coefficient might be smaller because of plasma waves that scatter particles. Using a simple model of SNR evolution and Monte Carlo simulations of CR diffusion, Fujita et al. (2010) showed that particles may be trapped around the SNR for a significant period of time. Subsequently, Fujita et al. (2011) confirmed this result using a transport equation to describe particle acceleration at the forward shock (FS), and then a simplified transport equation to follow the propagation of particles with p/m0c ≥ 102.4 from the precursor boundary (set at four Bohm diffusion length-scales) to distances far away from the shock. These findings are consistent with the conclusions of Reville et al. (2009), who argue that beyond some critical value, L, which they call the free-escape boundary, the number density of CRs falls significantly. The position of L is dictated by the level of excited magnetohydrodynamics (MHD) turbulence, which may be significant out to one SNR radius from the FS (Zirakashvili & Ptuskin 2008). The detailed variation of the turbulence amplitudes and the CR diffusion coefficient depends on the micro-physical balance of streaming instabilities and turbulence damping (Yan et al. 2012).
Besides the diffusion coefficient in the SNR vicinity, other important aspects of the study of escaped CRs are their spectral and spatial distributions. These distributions affect the radiative properties of the SNR itself as escaping CRs modify the high-energy part of the CR spectrum, and, if present, the radiative properties of the nearby dense matter consisting of a MC or a dense shell swept up by the winds of a high-mass SN progenitor). Much of the research dealing with stationary and (semi-)analytical solutions cannot recover the spectral and spatial shapes of the CR distribution, but only gives the integrated escaping CR energy flux. Kinetic models provide the shape of the distribution, which depends significantly on the assumed diffusion models. Ellison & Bykov (2011) parametrized the spectral distribution of escaping CRs, and then propagated the escaping CRs in the upstream region of the SNR obtaining spatial distributions. They used a spherically symmetric code for the hydro simulations of the SNR evolution that is identical to the code used in this work, but without the grid expansion that significantly increases the resolution. However, the particle acceleration was treated in a plane-parallel steady-state approximation ignoring dilution effects. Ellison & Bykov (2011) focused on the core-collapse explosion of a massive star in a low density medium surrounded by a dense shell, a case similar to our model for a core-collapse SNR (CC-SNR) in a wind bubble.
In this paper, we investigate how both the spectrum of particles escaped from the SNR into a nearby MC or shell and the particle emission due to interaction with dense matter depends on the acceleration history of young ejecta-dominated Type-Ia and Type-Ic (core-collapse) SNRs, using given different assumptions about CR diffusion in the vicinity of the SNR. For this purpose, we combine a test-particle treatment of CR acceleration with an account of escaping particles. We solve the CR transport equation in a spherically symmetric geometry. Our calculations are based on realistic high-resolution hydrodynamic simulations of SNR evolution. We explore two SN types, focusing on the complexities in the circumstellar environment. In the case of Type-Ia SNRs, we assume that evolution proceeds in a uniform ISM. We also consider a core-collapse SNR arising from a Wolf-Rayet (WR) progenitor, expanding in the wind-blown bubble created by the progenitor star. The SNR shock wave first evolves in the freely expanding wind of the progenitor, and then, beyond the wind-termination shock, in the shocked-wind region. Subsequently, we would expect the shock to impact the dense shell bordering the wind-blown bubble. However, our intention here is to study the interaction of the accelerated particles produced by the SNR with this dense shell, hence we terminated the SNR evolution before the shock-shell impact took place. We considered particle acceleration at both the forward and reverse shock. In addition, in the CC-SNR case we consider particle re-acceleration at secondary shocks formed when the SNR forward shock collides with the termination shock of the wind zone. The spatial domain considered in our particle simulations extends to about 100 times the SNR radius to facilitate the study of particle escape. The “absorbing” boundary located that far from the SNR does not affect the result of our simulations. It is the spatial profile of the diffusion coefficient in the vicinity of the SNR that determines the degree to which particles can escape from the CR precursor. To estimate the observational consequences of CR escape, we consider the interaction of the escaped particles with a target MC close to a Type-Ia SNR, or in the core-collapse case we consider the interaction of CRs with the dense shell. The MC/shell are located well inside the simulation domain, hence we know the cosmic-ray number density at their location at any time. Using two different models of the CR diffusion upstream of the FS, we calculated the evolutions of both the cosmic-ray spectra at the location of the MC/shell and the hadronic gamma-ray emission as the SNR shock approaches the MC/shell. If not stated otherwise, we refer to particles as escaped when they have escaped from the precursor region of the FS and are found at the location of the MC or shell. The respective particle spectra are averaged over the volume of the MC or shell.
2. Method
We describe the hydrodynamics of the expanding SNR by numerical simulations. For the Type-Ia SNR, we use the ejecta-density profile described in Dwarkadas & Chevalier (1998), expanding into a constant-density medium. The simulation itself is described in detail in Telezhinsky et al. (2012). The evolution of core-collapse Type-Ic SNRs is much more complicated. We assume that the formation of a wind-blown bubble is similar to that described by Dwarkadas (2005, 2007). The WR wind is assumed to have a mass-loss rate of 10-5 M⊙ yr-1, and a velocity of 1500 km s-1. The wind termination shock is assumed to be a strong shock that forms at a radius of 7 pc. As the SNR shock expands outwards in radius, it evolves in the freely expanding wind, impacts the wind termination shock, and then evolves into a constant density shocked wind. Finally, although this is not included in the current simulation, the shock will collide with the dense wind-blown shell surrounding the bubble.
We treat CRs as test particles in gas-flow profiles given by the simulations described above. Our method (Telezhinsky et al. 2012) is based on a numerical solution of the CR transport equation in a grid co-moving with the shock wave. To ensure sufficient resolution near the shock, the spatial coordinate is substituted with a new coordinate, x ∗ , for which a uniform grid is used when solving the particle transport equation 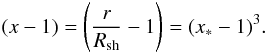 (1)Thus, a rather coarse grid in x ∗ is transformed into a very fine grid in x close to the shock, where the high resolution is needed to properly account for the acceleration of newly injected particles. At the same time, this transformation allows us to significantly extend the grid far into the ISM (x ≫ 1) with only a small extension in x ∗ . The resolution obviously deteriorates with distance from the shock, but the mean free path of the particles in the CSM/ISM is orders of magnitude larger than in the shock vicinity, thus permitting the use of a moderate resolution. The extension of the grid to several dozens of SNR radii, and the spherical geometry, imply that the volume upstream of the shock is much larger than downstream. The co-moving grid obliterates any need to introduce an artificial “absorbing” or “escape” boundary because the particles will never reach it during the simulation time. The number of particles escaping from the SNR shock is defined purely by the diffusion properties of the upstream region. We do not need to define the diffusive flux through some artificial boundary to count the particles escaping through this boundary. In the current approach, owing to the grid extension the total number of injected particles is conserved and distributed over the considered volume according to diffusion. By the end of the simulation, we observe at the boundary of the simulation domain only numerical noise, which indicates that the boundary is reached by an insignificant fraction of particles. Technically, a macroscopic treatment of diffusion does not differentiate between individual particles bouncing back and forth in the shock precursor, thus all particles found upstream of the FS can be assumed to have escaped from the SNR1. Here we are interested in particles found at the location of the MC/shell (sufficiently far away from the shock precursor), and so we refer to these particles as escaped.
(1)Thus, a rather coarse grid in x ∗ is transformed into a very fine grid in x close to the shock, where the high resolution is needed to properly account for the acceleration of newly injected particles. At the same time, this transformation allows us to significantly extend the grid far into the ISM (x ≫ 1) with only a small extension in x ∗ . The resolution obviously deteriorates with distance from the shock, but the mean free path of the particles in the CSM/ISM is orders of magnitude larger than in the shock vicinity, thus permitting the use of a moderate resolution. The extension of the grid to several dozens of SNR radii, and the spherical geometry, imply that the volume upstream of the shock is much larger than downstream. The co-moving grid obliterates any need to introduce an artificial “absorbing” or “escape” boundary because the particles will never reach it during the simulation time. The number of particles escaping from the SNR shock is defined purely by the diffusion properties of the upstream region. We do not need to define the diffusive flux through some artificial boundary to count the particles escaping through this boundary. In the current approach, owing to the grid extension the total number of injected particles is conserved and distributed over the considered volume according to diffusion. By the end of the simulation, we observe at the boundary of the simulation domain only numerical noise, which indicates that the boundary is reached by an insignificant fraction of particles. Technically, a macroscopic treatment of diffusion does not differentiate between individual particles bouncing back and forth in the shock precursor, thus all particles found upstream of the FS can be assumed to have escaped from the SNR1. Here we are interested in particles found at the location of the MC/shell (sufficiently far away from the shock precursor), and so we refer to these particles as escaped.
Since our method is based on the test-particle approximation, it requires that the CR pressure at the shock be less than 10% of the ram pressure. We use a thermal-leakage injection model (Blasi et al. 2005), and adjust the injection so that the CR-pressure limit is not violated. The injection coefficient, a free parameter, is adjusted to be approximately 3 × 10-7 for the Type-Ia SNR, and 5 × 10-6 for CC-SNR.
3. Magnetic field and diffusion
3.1. Magnetic field parametrization
Observations of young SNe, for example SN 1993J (Chandra et al. 2004) or Tycho’s SNR (Acciari et al. 2011), suggest that the magnetic field (MF) required to explain the observed level of emission is orders of magnitude stronger than the average ISM field. We therefore assume that the MF in the shock vicinity is amplified, e.g. by streaming CRs (Bell 2004). Although in general both resonant and non-resonant modes operate, non-resonant amplification probably dominates in the early stages of SNR evolution (Caprioli et al. 2009). The amplified field is then given by 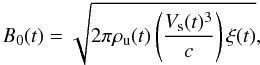 (2)where ρu(t) is the density upstream the shock, Vs(t) is the shock speed, c is the speed of light, and ξ(t) is the ratio of cosmic-ray to ram pressure. In our calculations, ξ(t) ≈ 0.05 with small deviations throughout the simulation.
(2)where ρu(t) is the density upstream the shock, Vs(t) is the shock speed, c is the speed of light, and ξ(t) is the ratio of cosmic-ray to ram pressure. In our calculations, ξ(t) ≈ 0.05 with small deviations throughout the simulation.
We parametrize the MF inside and outside the SNR. The scaling inside follows the time-dependent density distribution 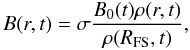 (3)where
(3)where 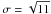 is the compression ratio of the turbulent MF, and is assumed to be isotropic. We assume that the MF falls off exponentially down to the strength of the interstellar field (5 μG) (or circumstellar MF (CMF) in the case of core-collapse SNR), at 0.05 RFS ahead of the FS (Zirakashvili & Aharonian 2010), and likewise down to the very small ejecta field (0.01–0.1 μG) at 0.05 RRS toward the interior of the SNR.
is the compression ratio of the turbulent MF, and is assumed to be isotropic. We assume that the MF falls off exponentially down to the strength of the interstellar field (5 μG) (or circumstellar MF (CMF) in the case of core-collapse SNR), at 0.05 RFS ahead of the FS (Zirakashvili & Aharonian 2010), and likewise down to the very small ejecta field (0.01–0.1 μG) at 0.05 RRS toward the interior of the SNR.
 |
Fig. 1 Time dependence of magnetic-field profiles for Type-Ia (top) and core-collapse (bottom) SNRs. |
To define the magnetic field in the wind zone of the WR star, we assume that the dominant component at large distances is merely the toroidal component of the stellar surface magnetic field, which decreases outwards with radius. Thus, this component is defined as 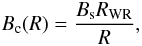 (4)where Bs ≈ 100 G is the MF at the surface of WR star, RWR = 8 R⊙ is the radius of WR star, and R is the distance from the star. Beyond the WR wind zone, in the constant density region, the MF is assumed to be constant and equal to the shock-compressed value at the edge of the WR wind zone. We assume a constant MF in the MC/shell, since it has been found that the MF does not increase if the number density in the cloud, n ≲ 300 cm-3 (Crutcher et al. 2010). The evolution of the MF profiles for two types of SNR is shown in Fig. 1.
(4)where Bs ≈ 100 G is the MF at the surface of WR star, RWR = 8 R⊙ is the radius of WR star, and R is the distance from the star. Beyond the WR wind zone, in the constant density region, the MF is assumed to be constant and equal to the shock-compressed value at the edge of the WR wind zone. We assume a constant MF in the MC/shell, since it has been found that the MF does not increase if the number density in the cloud, n ≲ 300 cm-3 (Crutcher et al. 2010). The evolution of the MF profiles for two types of SNR is shown in Fig. 1.
3.2. Diffusion models
To study the propagation of cosmic rays in the vicinity of SNRs, it is necessary to make assumptions about the efficiency of diffusion close to the SNR shock. We note that the type of particle scattering does not depend on the amplitude of the MF, but rather on the wave-number spectrum of MHD turbulence. In other words, one can have Bohm-type diffusion in the non-amplified MF even significantly far away from the shock. Bohm diffusion is widely assumed to operate close to the shock and inside the SNR, otherwise DSA theories would fail to explain particles with energies up to the “knee”. On the other hand, the average diffusion coefficient in the Galaxy is much larger than Bohmian, and inevitably there must be a transition between the small Bohmian coefficient and the large Galactic coefficient.
Since the transition from Bohm diffusion in the vicinity of the forward shock to Galactic diffusion further away is not clearly understood, we consider two different models of CR diffusion outside the SNR. In model D1, the diffusion coefficient is Bohmian inside the SNR and in the FS upstream region, up to a fiducial boundary, L = 2 RSNR, at which the transition to the Galactic diffusion occurs. We emphasize that the boundary L is not a physical boundary in any sense, and does not denote an “escape” boundary as in our previous work. It is merely a convenient radius at which the transition in diffusion coefficient is assumed to occur. In this model the diffusion coefficient is defined as 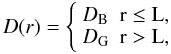 (5)where the Bohm diffusion coefficient is given by
(5)where the Bohm diffusion coefficient is given by 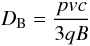 (6)while the Galactic diffusion coefficient is taken to be (Berezinskii et al. 1990)
(6)while the Galactic diffusion coefficient is taken to be (Berezinskii et al. 1990) 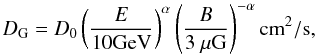 (7)where E is the CR energy and D0 is the normalization. Following a statistical analysis of cosmic-ray propagation models (Trotta et al. 2011), we use D0 = 1029 cm2/s and α = 1/3.
(7)where E is the CR energy and D0 is the normalization. Following a statistical analysis of cosmic-ray propagation models (Trotta et al. 2011), we use D0 = 1029 cm2/s and α = 1/3.
In model D2, we explore a less abrupt transition to Galactic diffusion. We assume that Bohm diffusion is valid both inside the SNR and in the FS upstream region stretching out to 5% of the SNR radius, i.e., up to l = 1.05 RSNR. Between l and L, we introduce an intermediate diffusion coefficient, smaller than the Galactic diffusion coefficient, thus mimicking the presence of MHD waves, which may be invoked by CRs streaming away from the SNR (Yan et al. 2012). We define the diffusion coefficient in D2 model as 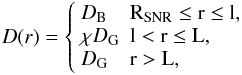 (8)where χ = 0.01. A schematic view of the diffusion models and corresponding boundaries is given in Fig. 2.
(8)where χ = 0.01. A schematic view of the diffusion models and corresponding boundaries is given in Fig. 2.
We do not consider the confinement of particles by the dense shell at the boundary of the WR wind zone in the CC-SNR models as done by Ellison & Bykov (2011). The ion-neutral friction in dense and partially ionized media may suppress plasma instabilities, and thus increase the diffusion coefficient (Ptuskin & Zirakashvili 2005; Drury 2011). Similar arguments would apply to MCs. For instance, Everett & Zweibel (2011) consider the diffusion coefficient in MCs to be 1–500% of the Galactic value. They claim that this variation does not significantly affect their findings, which state that the cosmic-ray density does not increase within clouds. Therefore, we assume that the diffusion coefficient inside the MC/shell is the same as in the surrounding medium. A possible variation of the diffusion coefficient inside the MC/shell and the resulting consequences for our calculations are discussed in Sect. 4.1.
 |
Fig. 2 Schematic view of diffusion models. |
4. Results and discussion
 |
Fig. 3 Results for Type-Ia SNR. Top: the time evolution of volume-integrated CR spectra inside the SNR (denoted “snr”) and the MC (denoted “mc”) for two different diffusion models (“D1”/“D2”) and two different distances from the SNR to MC: 12 pc (“n”) and 16 pc (“f”). Bottom: the corresponding hadronic gamma-ray emission spectra. The thick solid lines represent the Galactic CR background and the corresponding gamma-ray emission from the MC, both of which do not depend on time. The thin solid lines represent the spectra of CRs outside the SNR for the D2 model and the corresponding emission from ambient diffuse gas. |
 |
Fig. 4 Results for core-collapse SNR. Top: the time evolution of volume-integrated CR spectra inside the SNR (denoted “snr”) and at the dense shell (denoted “sh”) for two different diffusion models (“D1”/“D2”) and two different distances from the SNR to the shell: 16 pc (“n”) and 30 pc (“f”). Bottom: the corresponding hadronic gamma-ray emission spectra. The thick solid lines represent the Galactic CR background and the corresponding gamma-ray emission from the dense shell, both of which still do not depend on time. The thin solid lines represent the spectra of CRs outside the SNR for the D2 model and the corresponding emission from ambient diffuse gas. |
We have calculated the confined and escaped cosmic-ray spectra at 400, 1000, and 2000 years after explosion, assuming the diffusion models described above. We have also calculated the corresponding emission from the SNRs and the target material in their vicinity. In calculating the emission, we considered only CR protons, and their radiation via pion decay (Huang et al. 2007).
Given the initial parameters assumed in the simulation, the Type-Ia SNR approaches the Sedov stage after around 1000 years. Beyond this time, we approximate the plasma-flow profiles with a Sedov solution (Cox & Franco 1981). Although hydrodynamically the RS is still present, usage of the Sedov solution is justified since the contribution from the RS to particle and emission spectra is negligible at that time (Telezhinsky et al. 2012). After 2000 years, the FS radius in Type-Ia SNR is about 8 pc. The CC-SNR, on the other hand, by design, expands in a wind of much lower density, followed by a constant-density shocked-wind zone, and therefore remains in the ejecta-dominated stage until the end of the simulation. At the edge of the constant-density zone, we assume the presence of a cold, thin (0.5 pc) dense shell of swept-up material, similar to those known to exist around WR stars (Cappa et al. 2003). After 2000 years, the forward shock of this Type-Ic SNR has expanded out to a radius of about 14 pc.
The spectrum of particles interacting with the MC is a function of its distance from the SNR shock, as well as the diffusion coefficient. We consider two center-to-center distances from the Type-Ia SNR to the MC, 12 pc (the “near” scenario) and 16 pc (the “far” scenario), thus study the effect of a variation in the diffusion coefficient on the particle spectrum as the cloud approaches the SNR. The MC is assumed to have a radius of 4 pc and a mass of Mc ≈ 1500 M⊙, corresponding to a number density nc = 150 cm-3.
For the CC-SNR case, we consider a swept-up shell located at 16 pc (the “near” scenario) or at 30 pc (the “far” scenario). The number density of the shell, ns = 100 cm-3, corresponds to a mass Ms ≈ 1300 M⊙ for the “near” and Ms ≈ 4500 M⊙ for the “far” scenario. We note that the gamma-ray flux simply scales with the gas mass in the MC or the dense shell, and therefore the choice of mass only affects the normalization of the spectra.
4.1. Particle spectra
The time evolution of the spectra of confined and escaped protons are presented in the upper panels of Fig. 3 for Type-Ia SNR and Fig. 4 for CC-SNR, respectively. All spectra are volume-averaged. The Galactic CR background and its gamma-ray emission are shown for comparison.
We note from the figures that the choice of diffusion model influences the cut-off energy in the spectra of the confined particles, as well as the energy of the spectral peak of escaped CRs. Particle acceleration becomes slow when the CR precursor extends to the radius l in the upstream region at which diffusion becomes faster in the D2 model. Thus, the spectra of confined particles cut off at lower energies, and likewise the spectra of escaped CRs have maxima at lower energies, because escape from the SNR is more efficient. In both models of diffusion and both types of SNR, we do not observe any significant contribution of the RS to the population of the CRs found upstream of the FS. This is partly because the reverse-shock contribution diminishes with time, and is largely negligible after about 1000 years. Furthermore, since the MF is assumed to scale with the SNR density in the shocked interaction region, the large MF at the contact discontinuity, and the low maximum energy attained by CRs at the reverse shock do not permit particles accelerated at the RS to diffuse out of the SNR.
 |
Fig. 5 Radial distributions of CRs at the peak energy in the spectra of escaped CRs at the given time (thick lines), compared with the Galactic CR background at the same energies (thin lines) for diffusion models “D1” (left) and “D2” (right). Type-Ia SNRs are shown in the top row and core-collapse SNR in the bottom row. |
 |
Fig. 6 Radial distribution of CRs with energy 20 TeV at different times compared with the Galactic CR background at the same energy (dotted line) for diffusion models “D1” (left) and “D2” (right). Type-Ia SNRs are shown in the top row and core-collapse in the bottom row. |
In Type-Ia SNR, the spectral shapes of escaped particles in the D1 and D2 diffusion models are similar. They have a narrow, parabola-like shape at a certain energy, usually referred to as Emax, that is consistent with the approximations made by Ellison & Bykov (2011). The intensity changes with time depending on the assumed distance to the MC. In the “far” scenario, the MC always stays beyond the L boundary, and the intensity of the CR spectra at the location of the MC rapidly decreases with time on account of dilution. In the “near” scenario, the MC is partially (after 1000 years) or totally (after 2000 years) within L, where the number density of CRs is high. However, the CRs in the D2 model have a shallower gradient than in the D1 model, and so the CR illumination of the MC increases even if the MC is only partially within L (1000 years). In the D1 model, the spectrum is still affected by dilution, and it is only later (after 2000 years), when the MC is totally inside L, that the spectral intensity rises dramatically.
The behavior of escaped particles in the D1 model is similar for both types of SNR. However, the spectral shape of the escaped particles in the D2 model is somewhat different in the CC-SNR case. The spectral peak for the escaped CRs shifts to higher energies with time. Therefore, an asymmetry is seen in their spectra, most visibly so at later times.
We now discuss the consequences of a different diffusion coefficient inside the MC/shell. First, we note that the shell thickness is so small that the shell spectra are virtually unaffected, unless the diffusion coefficient inside is extremely small. Suppose then that the plasma waves are damped so effectively that the diffusion coefficient inside the MC increases significantly (about ten times) with respect to the diffusion coefficient of the surrounding medium. It is obvious that the CRs will quickly attain a uniform distribution inside the MC, and the CR number density at the far side of the MC will be nearly equal to that at the near side. This should affect the CR intensity inside the MC after about 1000 years, when the MC is located at a position corresponding to a strong gradient in the CR distribution (it is partially within boundary L). Estimates show that the CR intensity in this case may increase by a factor of a few. At other times, the differences will be marginal.
The diffusion coefficient inside the MC may also be lower than in the ISM. This may be due to a strong gradient in CRs at the outskirts of the MC, which may trigger plasma instabilities and in turn reduce the CR diffusivity. A reasonable value could be 0.01 DG. We note that this case may affect the D1 model after 1000 years in the same manner as described above, because the diffusion coefficient inside the MC will be larger than within the boundary L. Spectra at other times and for other models should not be affected. The main effect of a reduced diffusion coefficient inside the MC is the longer penetration time and consequently a delay in the illumination of the MC. If one estimates the time needed for a 10-TeV particle to reach the center of the MC, one finds 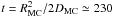 years, where DMC = 0.01 DG. However, the outer 1.5-pc thick shell of the MC would then supply 80% of the flux, and a 10-TeV CR would need only ~30 years to penetrate to this depth. The delay in illumination is therefore negligible compared with the uncertainties in the size and structure of the MC.
years, where DMC = 0.01 DG. However, the outer 1.5-pc thick shell of the MC would then supply 80% of the flux, and a 10-TeV CR would need only ~30 years to penetrate to this depth. The delay in illumination is therefore negligible compared with the uncertainties in the size and structure of the MC.
4.2. Spatial distributions of CRs
 |
Fig. 7 1-TeV Intensity distributions of Type-Ia/MC (top) and CC-SNR/shell (bottom) at the age of 1000 (left) and 2000 (right) years. The log-scaled colormap spans roughly over 2.5 orders of magnitude for each image. |
To study the propagation of escaping particles in the medium around SNRs and understand the significance of their contribution to the local CR level, we plot the radial distributions of particles of given energies for different types of SNR and different diffusion models. Figure 5 presents the radial distributions of protons at the peak energy in the spectra of escaped CRs, which is sometimes referred to as Emax. This energy changes with time, therefore at each time particles of different energy are plotted (thick lines), along with the corresponding Galactic background (thin lines). The evolution of Emax is shown in Fig. 8 and discussed below. We observe significant confinement of cosmic-ray particles close to the shock for all SNRs and diffusion models, even at the highest particle energies. Remarkably, for Type-Ia SNR in both diffusion models the highest-energy CRs still dominate over the background at a few SNR radii, whereas for CC-SNR this happens only in the D2 diffusion model. This may be because in our simulations the Type-Ia SNR propagates into a medium of higher average density, and therefore has a radius roughly twice as small as the CC-SNR, which implies less dilution. The CC-SNR produce a lower CR energy density than Type-Ia SNRs owing to the lower density at the FS, hence lower injection into the acceleration process. Therefore, the intensity of CRs around CC-SNR only marginally exceeds the background. While these results are applicable to Type-Ic SNR, they are not to SNR of Type-IIP. The latter could have even smaller radii than Type-Ia, for instance, as they expand within the high-density red supergiant wind. In future papers, we will discuss the various SNR types in more detail.
We are particularly interested in the spatial distribution of CRs that produce TeV-band gamma-ray emission. We show the time evolution of these distributions for a CR energy of 20 TeV in Fig. 6, including for comparison the Galactic CR background. We note from this figure that in the D1 diffusion model, 20-TeV CRs are trapped very close to the SNR shock (≲1.4 RSNR for Type-Ia SNR and ≲1.2 RSNR for CC-SNR) at all times. Even in the D2 model, in which the diffusion coefficient is very large, at late times the intensity of 20-TeV CRs exceeds the background at a few RSNR only in the case of a Type-Ia SNR. Therefore, the detection of gamma-ray emission from MCs as probe of hadronic acceleration in SNR in the era of Fermi and current CTs is a far more complicated task than previously thought. The object observed is always a composite of the SNR itself, emission from the MC, or a dense shell illuminated by freshly accelerated CRs, and the emission of interactions between upstream CRs and the ambient diluted gas. One may be successful in scenarios in which the MC is located close to the SNR. The distance to the MC should then be generally smaller or comparable to RSNR, otherwise at the location of the MC/shell the background CRs dominate over the CRs from the SNR. This is a direct consequence of both diffusion and dilution, which becomes a serious factor at large distances from the SNR.
4.3. Gamma-ray emission from the SNR-MC/shell
We calculated the gamma-ray emission from the MC/shell illuminated by CRs that had escaped from the SNR. For comparison, we plot their spectra together with the emission spectra from the SNRs themselves (Figs. 3 and 4, lower panels). The gamma-ray emission is only moderately affected by the choice of diffusion model. In the case of the D2 model, we observe higher fluxes at lower energies and also that the spectral peak is shifted to lower energies, thus making the spectra soft in the band above ~10 TeV. The spectra thus reflect the spatial variation in the diffusion coefficient in the vicinity of the SNR. In Type-Ia SNR, the MC is always significantly brighter than expected when illuminated by Galactic CRs. In contrast, the dense shell around a CC-SNR does not experience a significantly enhanced CR illumination until the shock is very close. The emission from the CC-SNR itself is never particularly bright, and so at late times the shell emission strongly dominates. On the other hand, the Type-Ia SNR dominates the intensity distribution of the SNR-MC system in all scenarios and diffusion models, but only at the latest time, and in the “near” scenario the emission levels of SNR and MC become comparable. The intensity of gamma-ray emission from the MC/shell obviously strongly depends on the mass carried by the MC/shell, but the trend described above holds and may permit us to differentiate between Type-Ia and Type-Ic SNRs.
Additionally, for model D2 we constructed the intensity distributions of gamma-ray emission from Type-Ia SNR/MC and CC-SNR/shell systems, along with the background created by the upstream CRs in the vicinity of the SNR (see Fig. 7). Since the number density of CRs confined within boundary L significantly exceeds the number density of CRs beyond L, we consider L as the boundary of the SNR vicinity. One can see how the expanding halo of upstream CRs illuminates the surrounding diluted gas and dense matter. The sharp contrast in brightness between the inner and outer parts of the MC at the age of 1000 years arises from the abrupt transition from intermediate to Galactic diffusion and is in that sense an artifact. Moreover, as noted earlier in Sect. 4.1, if the diffusion coefficient inside the MC were larger than that in the surrounding medium, the CR illumination of the MC after 1000 years would be more uniform so that the far side becomes brighter. However, the image, though idealized, is not unrealistic. The bright outer ring in CC-SNR intensity maps is the swept-up shell illuminated by escaping CRs. The smaller ring at the age of 1000 years corresponds to the contact discontinuity (CD) of the CC-SNR. The FS can almost not be seen owing to the very low density in the wind zone. At the age of 2000 years, the shell strongly dominates, and the shocks are not seen. There is only a marginal hint of emission from the CD region.
4.4. Emax
 |
Fig. 8 Time evolution of Emax, the peak energy in the spectrum of escaped CRs. |
Different authors may define Emax in different ways, e.g., the maximum energy at which particles leave the system, the cut-off energy, or the peak in the spectrum of escaped particles. In practice, these definitions should provide nearly identical values. In some models of CR acceleration, including analytical studies of CR escape, Emax is a free parameter used in lieu of a free-escape boundary.
The time evolution of Emax is a crucial issue. We derive Emax from fitting the spectra of escaped CRs for each SNR type and diffusion models. The results are plotted in Fig. 8, along with the results of Ellison & Bykov (2011) and Gabici et al. (2009). Although we consider MF amplification (MFA), we do not find as rapid a decrease in Emax as predicted by Gabici et al. (2009). Our curves are more compatible with those of Ellison & Bykov (2011), although they did not include MFA. Most analytical studies are based on the Sedov solution, MFA, and the assumption that particles start leaving the system at the beginning of the Sedov stage when the highest energies are reached (e.g. Gabici et al. 2009). When we accurately account for the evolution of a young SNR, in which the shock velocity is not constant and falls with time, and we include the effects of dilution by considering spherically symmetric systems, we find that particles leave the SNR during the “free expansion” stage. In addition, Drury (2011) reminds us that escape is a random process and it is only in a probabilistic sense controlled by the ratio of the diffusion length to SNR radius. Therefore, in our opinion solving one diffusion-advection equation for all CRs, both those trapped inside the SNR and those “escaping”, is the best way to treat the problem. At any instant, one can easily see which particles are inside and which outside the SNR. Defining Emax by the spectrum of CRs that have escaped into the MC/shell and observing the time evolution of Emax, one notices a dramatic difference between our result and that derived with Sedov scaling. Moreover, as shown in Fig. 8, besides the early SNR evolution and SNR type, the evolution of Emax may also depend on the assumed diffusion model. We must note, however, that the trend seen in CC-SNRs for a D2 diffusion model may be an artifact arising from our choice of transition boundary from Bohm to intermediate diffusion coefficient, χDG. In our case, the transition is at 5% of the SNR radius, which given the CC-SNR evolution, is roughly equal to the size of the CR precursor, DB(Emax)/Vs. If the CR precursor extends into a region with a large diffusion coefficient, shock acceleration loses efficiency, thus effectively prescribing the Emax. With time and increasing SNR radius, the physical separation of the forward shock and the transition point in the diffusion model increases, thus permitting particles to reach higher energies.
4.5. General remarks
Ellison & Bykov (2011) provided analytical approximations of the spectra of escaping particles, which were then incorporated into their Monte Carlo cosmic-ray propagation model. Our results on the spectra of escaped CRs are compatible with those of Ellison & Bykov (2011), if the shock is sufficiently far away from the location of interest and the system is still young. At later times, the time evolution of Emax (see Fig. 8) leads to the formation of tails in the spectra of escaped CRs, that are populated by particles that left the remnant early (see the 2000-year plot at Fig. 4).
We noted that for both types of SNR and diffusion models (especially in D1) we find a significantly smaller intensity ratio of escaped CRs to trapped CRs at Emax than Ellison & Bykov (2011), even considering their use of NDSA. This discrepancy possibly arises from the neglect of dilution in their model.
We compared the radial profiles with those presented in the literature. In general, the radial profiles obtained in our D2 models are compatible with those in Fujita et al. (2011) (model C disregarding the growth of Alfvén waves) and with the profiles of Ellison & Bykov (2011) (propagation in pure CSM) out to a radius of RSNR from the shock. These authors, however, did not make any comparisons with the background level as their results are presented in arbitrary units. We were unable to find research that shows the profiles for pure Bohm diffusion out to a full SNR radius from the shock.
4.6. Observational implications
The TeV-band intensity map of the young Type-Ia SNR Tycho observed with VERITAS (Acciari et al. 2011) shows off-center emission, which may correspond to a fluctuation. However, it may also indicate an interaction of escaping CRs with a nearby MC. If this is true, Fig. 3 suggests that in the GeV band emission from the SNR itself should dominate. So, if the TeV-band emission indeed partly originates from an illuminated MC outside the remnant, the component from the SNR itself must have a softer spectrum than suggested by a naive comparison of Fermi and VERITAS data.
Another interesting example is the young TeV-bright CC-SNR RX J1713.7-3946 detected with Fermi (Abdo et al. 2011). Ellison et al. (2012) applied their model to explain its high-energy emission via escaping CRs and found that this scenario is very unlikely. However, Fig. 4 indicates peculiar spectral transitions, in particular for the D2 model, that make multi-component spectra quite conceivable in which most of the GeV-band emission arises from the SNR itself, whereas a substantial fraction of TeV-band emission originates from gas exterior to the remnant. More careful modeling is needed to test the applicability of this scenario to RX J1713.7-3946.
Although our treatment extends only over the first 2000 years of SNR evolution, we note that the rather peculiar spectra of CC-SNRs found in our models have spectral breaks that appear similar to those observed from some older Fermi SNRs (e.g. Castro & Slane 2010; Abdo et al. 2010d). In addition, the observed discrepancy in the locations of the TeV and (sub-)GeV emission in the SNR vicinity can be considered in line with our models. For instance, as seen from the lower panels of Figs. 3 and 4, the emission from the dense matter far away from the SNR may dominate at TeV energies and disappear at low (sub-)GeV energies. At the same time, the emission from the SNR itself would be stronger at GeV and weaker at TeV energies. Altogether, this makes the emission “peak” move over the image with the changing energy of the observations. In some sense, a similar scenario is put forward by the AGILE team (Giuliani et al. 2011) for the regions around SNRs W28 and IC 443, to explain why in the GeV-band the peak-emission error box is separated from the TeV-emission error box observed by VERITAS and MAGIC.
5. Conclusions
We have modified our modeling technique developed in Telezhinsky et al. (2012) to examine the distribution of escaped CRs at distances far from SNRs. Our approach combines a realistic treatment of SNR evolution using hydrodynamic simulations with test-particle calculations of CR acceleration, by solving the transport equation of cosmic rays in a spherically symmetric geometry. Both the reverse and forward shocks are included in these simulations. We also account for the re-acceleration at reflected shocks in core-collapse SNR. Our approach inherently includes the effects of dilution due to the expansion of the system, as well as the finite size of the SNR and any gas target illuminated by escaping CRs. It permits the reconstruction of the spectra of escaped CRs at any given distance from the source.
We have shown that the peak energy and intensity of escaped particles strongly depends on the efficiency of the diffusion in the vicinity of the SNR. If diffusion is Bohmian out to the boundary L = 2 RSNR, CRs are very efficiently confined to the SNR, and only the highest-energy particles are able to diffuse out to some distance from the SNR. Even though CRs at Emax leave the SNR, they are still trapped at distances far less than one SNR radius from the FS. If the diffusion coefficient in the FS upstream region is much larger than Bohmian, but not at the level of average Galactic diffusion, then CRs of lower energy are able to escape from the SNR. Consequently, one observes the broader spectra of escaped CRs with lower Emax and the cut off in the spectra of confined CRs is slower than exponential.
It is possible but difficult to constrain the diffusion coefficient in the vicinity of the SNR using the emission from nearby dense material. The particles cannot generally propagate far from the shock. Thus, to study CR acceleration in SNRs via CR escape into a nearby MC or shell, one needs to find MCs or shells located very close, unless the diffusion coefficient in the immediate environment of the SNR is a significant fraction of the average Galactic one, in which case Emax is lower. We note that in all diffusion models, and especially in the “far” scenarios, one can clearly observe the striking effect of dilution, i.e. the decrease in the CR intensity upstream of the FS, introduced by the spherical geometry of the SNR. Ignoring the spherical geometry of the system is a serious mistake when one models the gamma-ray emission from MCs placed at significant distances from the SNRs.
We find that Type-Ia SNR in our simulation has a higher CR energy density in its vicinity than Type-Ic core-collapse SNR. Therefore, Type-Ia SNR may have brighter pion-decay gamma-ray emission than Type-Ic SNR that is still evolving in the wind zones of its progenitor star. The emission of Type-Ia SNR is normally brighter than the MC emission until the SNR shock is very close to the MC. Only then is the gamma-ray flux from the MC comparable to that from the SNR. The emission from the CC-SNR and the wind-blown shell is initially near the background level. At a later stage, the shell emission can significantly dominate over the SNR emission. Although the exact scenario depends on the MC/shell parameters, most importantly the target mass, the described trend may serve to differentiate between these SNR types.
Finally, we find that the commonly used approximation for the Emax evolution based on Sedov scaling is not reproduced when the evolution of the SNR shocks is computed accurately. Moreover, the Emax behavior critically depends on the diffusion coefficient in the vicinity of the SNR.
Acknowledgments
V.V.D.’s research is supported by NASA through Chandra awards issued by the Chandra X-ray Observatory Center and NASA/Fermi grant NNX10AO44G.
References
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2010a, ApJ, 710, L92 [NASA ADS] [CrossRef] [Google Scholar]
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2010b, ApJ, 718, 348 [Google Scholar]
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2010c, Science, 327, 1103 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2010d, ApJ, 712, 459 [NASA ADS] [CrossRef] [Google Scholar]
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2011, ApJ, 734, 28 [NASA ADS] [CrossRef] [Google Scholar]
- Acciari, V. A., Aliu, E., Arlen, T., et al. 2009, ApJ, 698, L133 [NASA ADS] [CrossRef] [Google Scholar]
- Acciari, V. A., Aliu, E., Arlen, T., et al. 2010, ApJ, 714, 163 [Google Scholar]
- Acciari, V. A., Aliu, E., Arlen, T., et al. 2011, ApJ, 730, L20 [Google Scholar]
- Acero, F., Aharonian, F., Akhperjanian, A. G., et al. 2010, A&A, 516, A62 [Google Scholar]
- Aharonian, F. A., & Atoyan, A. M. 1996, A&A, 309, 917 [NASA ADS] [Google Scholar]
- Aharonian, F., Akhperjanian, A. G., Bazer-Bachi, A. R., et al. 2007, ApJ, 661, 236 [NASA ADS] [CrossRef] [Google Scholar]
- Aharonian, F., Akhperjanian, A. G., de Almeida, U. B., et al. 2009, ApJ, 692, 1500 [NASA ADS] [CrossRef] [Google Scholar]
- Atoyan, A. M., Aharonian, F. A., & Völk, H. J. 1995, Phys. Rev. D, 52, 3265 [NASA ADS] [CrossRef] [Google Scholar]
- Ave, M., Boyle, P. J., Höppner, C., Marshall, J., & Müller, D. 2009, ApJ, 697, 106 [NASA ADS] [CrossRef] [Google Scholar]
- Axford, W. I., Leer, E., & Skadron, G. 1977, in International Cosmic Ray Conference, 11, 132 [Google Scholar]
- Bell, A. R. 1978, MNRAS, 182, 147 [NASA ADS] [CrossRef] [Google Scholar]
- Bell, A. R. 2004, MNRAS, 353, 550 [Google Scholar]
- Berezinskii, V. S., Bulanov, S. V., Dogiel, V. A., & Ptuskin, V. S. 1990, Astrophysics of cosmic rays, ed. V. S. Berezinskii, S. V. Bulanov, V. A. Dogiel, & V. S. Ptuskin [Google Scholar]
- Blandford, R. D., & Ostriker, J. P. 1978, ApJ, 221, L29 [Google Scholar]
- Blasi, P., Gabici, S., & Vannoni, G. 2005, MNRAS, 361, 907 [NASA ADS] [CrossRef] [Google Scholar]
- Cappa, C. E., Arnal, E. M., Cichowolski, S., Goss, W. M., & Pineault, S. 2003, in A Massive Star Odyssey: From Main Sequence to Supernova, ed. K. van der Hucht, A. Herrero, & C. Esteban, IAU Symp., 212, 596 [Google Scholar]
- Caprioli, D., Blasi, P., & Amato, E. 2009, MNRAS, 396, 2065 [NASA ADS] [CrossRef] [Google Scholar]
- Caprioli, D., Amato, E., & Blasi, P. 2010, Astropart. Phys., 33, 160 [NASA ADS] [CrossRef] [Google Scholar]
- Castro, D., & Slane, P. 2010, ApJ, 717, 372 [NASA ADS] [CrossRef] [Google Scholar]
- Chandra, P., Ray, A., & Bhatnagar, S. 2004, ApJ, 604, L97 [NASA ADS] [CrossRef] [Google Scholar]
- Cox, D. P., & Franco, J. 1981, ApJ, 251, 687 [NASA ADS] [CrossRef] [Google Scholar]
- Crutcher, R. M., Wandelt, B., Heiles, C., Falgarone, E., & Troland, T. H. 2010, ApJ, 725, 466 [NASA ADS] [CrossRef] [Google Scholar]
- Drury, L. O. 2011, MNRAS, 415, 1807 [NASA ADS] [CrossRef] [Google Scholar]
- Dwarkadas, V. V. 2005, ApJ, 630, 892 [NASA ADS] [CrossRef] [Google Scholar]
- Dwarkadas, V. V. 2007, ApJ, 667, 226 [NASA ADS] [CrossRef] [Google Scholar]
- Dwarkadas, V. V., & Chevalier, R. A. 1998, ApJ, 497, 807 [NASA ADS] [CrossRef] [Google Scholar]
- Ellison, D. C., & Bykov, A. M. 2011, ApJ, 731, 87 [NASA ADS] [CrossRef] [Google Scholar]
- Ellison, D. C., Slane, P., Patnaude, D. J., & Bykov, A. M. 2012, ApJ, 744, 39 [NASA ADS] [CrossRef] [Google Scholar]
- Everett, J. E., & Zweibel, E. G. 2011, ApJ, 739, 60 [Google Scholar]
- Fujita, Y., Ohira, Y., Tanaka, S. J., & Takahara, F. 2009, ApJ, 707, L179 [NASA ADS] [CrossRef] [Google Scholar]
- Fujita, Y., Ohira, Y., & Takahara, F. 2010, ApJ, 712, L153 [NASA ADS] [CrossRef] [Google Scholar]
- Fujita, Y., Takahara, F., Ohira, Y., & Iwasaki, K. 2011, MNRAS, 415, 3434 [NASA ADS] [CrossRef] [Google Scholar]
- Gabici, S., Aharonian, F. A., & Casanova, S. 2009, MNRAS, 396, 1629 [NASA ADS] [CrossRef] [Google Scholar]
- Giordano, F., Naumann-Godo, M., Ballet, J., et al. 2012, ApJ, 744, L2 [Google Scholar]
- Giuliani, A., Cardillo, M., Tavani, M., & for the AGILE collaboration 2011, ArXiv e-prints [Google Scholar]
- Huang, C., Park, S., Pohl, M., & Daniels, C. D. 2007, Astropart. Phys., 27, 429 [NASA ADS] [CrossRef] [Google Scholar]
- Krymskii, G. F. 1977, Akademiia Nauk SSSR Doklady, 234, 1306 [NASA ADS] [Google Scholar]
- Li, H., & Chen, Y. 2010, MNRAS, 409, L35 [NASA ADS] [CrossRef] [Google Scholar]
- Li, H., & Chen, Y. 2011, ArXiv e-prints [Google Scholar]
- Malkov, M. A., & O’C Drury, L. 2001, Rep. Prog. Phys., 64, 429 [NASA ADS] [CrossRef] [Google Scholar]
- Ohira, Y., Murase, K., & Yamazaki, R. 2011, MNRAS, 410, 1577 [NASA ADS] [Google Scholar]
- Ptuskin, V. S., & Zirakashvili, V. N. 2005, A&A, 429, 755 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [PubMed] [Google Scholar]
- Ptuskin, V., Zirakashvili, V., & Seo, E. 2010, ApJ, 718, 31 [NASA ADS] [CrossRef] [Google Scholar]
- Reville, B., Kirk, J. G., & Duffy, P. 2009, ApJ, 694, 951 [NASA ADS] [CrossRef] [Google Scholar]
- Telezhinsky, I., Dwarkadas, V., & Pohl, M. 2012, Astropart. Phys., 35, 300 [NASA ADS] [CrossRef] [Google Scholar]
- Trotta, R., Jóhannesson, G., Moskalenko, I. V., et al. 2011, ApJ, 729, 106 [NASA ADS] [CrossRef] [Google Scholar]
- Wentzel, D. G. 1974, ARA&A, 12, 71 [NASA ADS] [CrossRef] [Google Scholar]
- Yan, H., Lazarian, A., & Schlickeiser, R. 2012, ApJ, 745, 140 [NASA ADS] [CrossRef] [Google Scholar]
- Zirakashvili, V. N., & Aharonian, F. A. 2010, ApJ, 708, 965 [NASA ADS] [CrossRef] [Google Scholar]
- Zirakashvili, V. N., & Ptuskin, V. S. 2008, ApJ, 678, 939 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1 Time dependence of magnetic-field profiles for Type-Ia (top) and core-collapse (bottom) SNRs. |
| In the text | |
 |
Fig. 2 Schematic view of diffusion models. |
| In the text | |
 |
Fig. 3 Results for Type-Ia SNR. Top: the time evolution of volume-integrated CR spectra inside the SNR (denoted “snr”) and the MC (denoted “mc”) for two different diffusion models (“D1”/“D2”) and two different distances from the SNR to MC: 12 pc (“n”) and 16 pc (“f”). Bottom: the corresponding hadronic gamma-ray emission spectra. The thick solid lines represent the Galactic CR background and the corresponding gamma-ray emission from the MC, both of which do not depend on time. The thin solid lines represent the spectra of CRs outside the SNR for the D2 model and the corresponding emission from ambient diffuse gas. |
| In the text | |
 |
Fig. 4 Results for core-collapse SNR. Top: the time evolution of volume-integrated CR spectra inside the SNR (denoted “snr”) and at the dense shell (denoted “sh”) for two different diffusion models (“D1”/“D2”) and two different distances from the SNR to the shell: 16 pc (“n”) and 30 pc (“f”). Bottom: the corresponding hadronic gamma-ray emission spectra. The thick solid lines represent the Galactic CR background and the corresponding gamma-ray emission from the dense shell, both of which still do not depend on time. The thin solid lines represent the spectra of CRs outside the SNR for the D2 model and the corresponding emission from ambient diffuse gas. |
| In the text | |
 |
Fig. 5 Radial distributions of CRs at the peak energy in the spectra of escaped CRs at the given time (thick lines), compared with the Galactic CR background at the same energies (thin lines) for diffusion models “D1” (left) and “D2” (right). Type-Ia SNRs are shown in the top row and core-collapse SNR in the bottom row. |
| In the text | |
 |
Fig. 6 Radial distribution of CRs with energy 20 TeV at different times compared with the Galactic CR background at the same energy (dotted line) for diffusion models “D1” (left) and “D2” (right). Type-Ia SNRs are shown in the top row and core-collapse in the bottom row. |
| In the text | |
 |
Fig. 7 1-TeV Intensity distributions of Type-Ia/MC (top) and CC-SNR/shell (bottom) at the age of 1000 (left) and 2000 (right) years. The log-scaled colormap spans roughly over 2.5 orders of magnitude for each image. |
| In the text | |
 |
Fig. 8 Time evolution of Emax, the peak energy in the spectrum of escaped CRs. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


