| Issue |
A&A
Volume 541, May 2012
|
|
|---|---|---|
| Article Number | A9 | |
| Number of page(s) | 25 | |
| Section | Stellar atmospheres | |
| DOI | https://doi.org/10.1051/0004-6361/201118598 | |
| Published online | 19 April 2012 | |
Long-term magnetic activity of a sample of M-dwarf stars from the HARPS program
II. Activity and radial velocity ⋆,⋆⋆,⋆⋆⋆
1
Centro de Astrofísica, Universidade do Porto,
Rua das Estrelas,
4150-762
Porto,
Portugal
e-mail: Joao.Silva@astro.up.pt
2 Departamento de Física e Astronomia, Faculdade de Ciências,
Universidade do Porto, Portugal
3
UJF-Grenoble 1 / CNRS-INSU, Institut de Planétologie et
d’Astrophysique de Grenoble (IPAG) UMR 5274, 38041
Grenoble,
France
4
Observatoire de Genève, Université de Genève,
51 Ch. des Maillettes,
1290
Versoix,
Switzerland
Received: 6 December 2011
Accepted: 7 February 2012
Owing to their low mass and luminosity, M dwarfs are ideal targets if one hopes to find low-mass planets similar to Earth using the radial velocity (RV) method. However, stellar magnetic cycles could add noise or even mimic the RV signal of a long-period companion. We extend our previous study of the correlation between activity cycles and long-term RV variations for K dwarfs to the lower-end of the main sequence. Our objective is to detect any correlations between long-term activity variations and the observed RV of a sample of M dwarfs. We use a sample of 27 M-dwarfs with a median observational timespan of 5.9 years. The cross-correlation function (CCF) with its parameters RV, bisector inverse slope (BIS), full width at half maximum (FWHM), and contrast are computed from the HARPS spectrum. The activity index is derived using the Na i D doublet. These parameters are compared with the activity level of the stars to search for correlations. We detect RV variations up to ~5 m s-1 that we can attribute to activity cycle effects. However, only 36% of the stars with long-term activity variability appear to have had their RV affected by magnetic cycles, on the typical timescale of ~6 years. Therefore, we suggest a careful analysis of activity data when searching for extrasolar planets using long-timespan RV data.
Key words: planets and satellites: detection / stars: activity / stars: late-type / techniques: radial velocities / techniques: spectroscopic
Based on observations made with the HARPS instrument on the ESO 3.6-m telescope at La Silla Observatory under programme ID 072.C-0488(E).
Tables with the data used for Figs. A.1–A.27 are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/541/A9
Appendix A is available in electronic form at http://www.aanda.org
© ESO, 2012
1. Introduction
The majority of extrasolar planets discovered so far were either detected or confirmed via the radial velocity (RV) method1. This technique measures the Doppler effect caused by the wobble of the star around the centre of mass of the star-planet system. As an indirect method, it is sensitive to stellar sources of noise such as oscillations, granulation, rotating active regions, and magnetic cycles.
Stellar oscillations and granulation induce RV variations on timescales of up to some hours and these variations can easily be suppressed if an optimized observational strategy is used (Dumusque et al. 2011). However, this is not true in the case of rotationally modulated active regions, for which the observed variations have longer timescales. The effect of rotating active regions on line profiles, hence RV measurements, can easily hide or mimic the signal of orbiting companions (e.g. Saar & Donahue 1997; Santos et al. 2000; Queloz et al. 2001). In some cases, these effects can be diagnosed e.g. by the anti-correlation between instantaneous measurements of RV and the bisector inverse slope (BIS) (Queloz et al. 2001; Boisse et al. 2011), and corrected by either subtracting the anti-correlation slope from the RV measurements (e.g. Melo et al. 2007; Boisse et al. 2009) or fitting an extra Keplerian orbit to the RV data with the period detected in the activity time-series (e.g. Bonfils et al. 2007; Forveille et al. 2009). Queloz et al. (2009) and Boisse et al. (2011) proposed to the fitting of the activity signal with sinusoids of different periods: the rotation one and its harmonics. In contrast, Saar & Fischer (2000) used a different technique to correct the RV induced by long-term activity. These authors used the slope of the SIR–RV correlation to remove the activity influence from the RV signal.
Long-term stellar magnetic cycles can also be a source of noise for precise RV measurements. Kürster et al. (2003) studied the correlation between the RV and the Hα index of the nearby Barnard’s star (Gl 699). They found an anti-correlation between the RV and the activity index with a correlation coefficient of ρ = −0.50. The authors concluded that the activity measured by the hydrogen line produces a blueshift of the photospheric absorption lines.
By using simulations, Meunier et al. (2010) showed that magnetic activity cycles can induce RV variations in the case of the Sun as seen edge-on, with amplitudes that can reach the ~10 m s-1 level. These kinds of variations in a star with a periodic activity cycle might be able to mimic the signal of a long-period extra-solar planet.
In this context, Santos et al. (2010) used a sample of 8 solar-type stars to determine whether a correlation between long-term activity and RV variations exists. The long-term variations were detected in the SMW, Hα, and He i indices and in the BIS, full-width-at-half-maximum (FWHM), and contrast of the cross-correlation function (CCF) but only two stars were found to have correlations with RV stronger than ρ > |0.75|: one positive correlation and one anti-correlation. The authors concluded then that the possible amplitudes of induced RV variations for the early-K dwarfs was low, of the ~1 m s-1 level and similar to the HARPS precision.
Using a larger sample of around 300 stars from the HARPS FGK high precision program, Lovis et al. (2011) studied the correlation between long-term activity variations and the RV in a similar fashion to Santos et al. (2010). They found a correlation between the slope of the RV–activity index (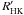 ) correlation, effective temperature (Teff), and metallicity ([Fe/H]). The slope is weaker for late-type dwarfs than for early ones, hence the RVs of later-K dwarfs appear to be less affected by magnetic cycles than the RVs of early-G dwarfs. Therefore, the influence of long-term activity could be corrected if the activity level, effective temperature, and metallicity of the star can be inferred from the slope of the RV–
) correlation, effective temperature (Teff), and metallicity ([Fe/H]). The slope is weaker for late-type dwarfs than for early ones, hence the RVs of later-K dwarfs appear to be less affected by magnetic cycles than the RVs of early-G dwarfs. Therefore, the influence of long-term activity could be corrected if the activity level, effective temperature, and metallicity of the star can be inferred from the slope of the RV–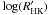 relation.
relation.
Hints of long-term RV variations produced by activity cycles were found by Moutou et al. (2011) in the stars BD-114672 and HIP21934, with periods of 1692 and 1100 days respectively. Ségransan et al. (2012) also found a long-term period of ~500 days in the RV data of HD104067 (K2V). The activity index of this star, hosting a 55-day period Neptune-like planet, was found to have a correlation with the RV residuals (with σRV = 4.6 m s-1) after the planetary signal was removed.
More recently, three exoplanets were discovered in three early-K stars with magnetic cycles by correcting the activity signals in the RV data (Dumusque et al. 2012). The planets were found by fitting simultaneously two Keplerians: one for the planet and one for the magnetic cycle. All the parameters of the Keplerian fitting the cycle, except the amplitude, were fixed to the ones obtained when fitting the activity index only. This proves that (i) the magnetic activity cycles of stars can influence RV and hide the signal of long-period planets, and (ii) a correction of the long-term activity-induced RV is possible and can be used to recover the embedded signal of a planet.
In Gomes da Silva et al. (2011, hereafter Paper I) we compared the long-term activity variations using four activity indices for a sample of M-dwarf stars from the HARPS program. We arrived at the conclusion that the Na i index was the most appropriate of the four available indices (which included the SCaII, Hα, and He i indices) to study the activity of these type of stars. In this paper, we use the Na i index as a proxy of activity to enable us to compare long-term activity to RV and some other relevant CCF parameters using the same sample of stars. This paper therefore extends our first study in Santos et al. (2010) to the case of early-M dwarfs.
This paper is organised as follows: in Sect. 2, we present our sample and observation log and explain our data analysis; in Sect. 3, we describe our selection of a subsample of stars with long-term activity variability; in Sect. 4, we determine which stars have hints of periodic magnetic cycles; in Sect. 5, we compare the long-term activity with RV and the CCF parameters; in Sect. 6, we examine individual stars with strong activity-RV correlation and other interesting cases; and finally in Sect. 7, we draw our conclusions from the present work.
2. Sample and observations
Basic parameters and observational log of the sample.
Our sample was selected from the HARPS M-dwarf planet search program that started in 2003 and ended in 2009 (see Bonfils et al. 2012). We used this sample in Paper I to study four known chromospheric activity indices and to select stars with long-term activity variability. However, we now complement this data set with data taken in 2010 as part of the Bonfils et al. (2012) program extension. We therefore decided to redo the same analysis as in Paper I using the new data to detect any new cases of activity variability that could arise from more data points.
We obtained simultaneous RV, BIS, FWHM, contrast, and the Na i activity indicator. The median RV error of the nightly averaged data was 1.2 m s-1. Although HARPS is capable of more precise measurements (e.g. Mayor et al. 2011), our sample includes dim stars for which it is more difficult to acquire high signal-to-noise ratio (S/N) data and therefore higher-precision RVs. To measure activity2, we used the index based on the Na i D1 and D2 lines in a same way as in Paper I (see also Díaz et al. 2007a). The CCF parameters were used because of their potential as complementary long-term activity proxies (e.g. Santos et al. 2010).
Owing to an instrumental drift detected in the HARPS data that affected the FWHM and contrast of the CCF, these parameters were corrected using the expressions 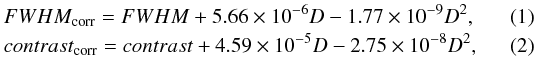 where D is (BJD−2 454 500) days. However, this correction is very small and represents a long-term drift. For example, the FWHM drift is only 0.1% in five years.
where D is (BJD−2 454 500) days. However, this correction is very small and represents a long-term drift. For example, the FWHM drift is only 0.1% in five years.
Since this sample includes some stars very close to the Sun, these stars may undergo significant secular acceleration that could produce a trend in the observed RV. We corrected all stars for this effect using the proper motions and parallaxes that were retrieved from the Hipparcos catalog (ESA 1997). The secular accelerations were calculated following the description in Zechmeister et al. (2009) and the radial-velocities were subsequently corrected (see also Bonfils et al. 2012).
Some of the stars in this sample are known to be planetary hosts, namely Gl 176, Gl 433, Gl 436, Gl 581, Gl 667 C, Gl 674, Gl 832, Gl 849, Gl 876, HIP12961, and HIP85647 (Bonfils et al. 2012). Since we are only interested in variations caused by activity, these planetary signals were subtracted from the observed RVs by fitting Keplerian functions based on the published orbital parameters.
The selection criteria was the same as in our previous paper. We nightly averaged and binned the data into 150-day bins to average out short timescale variability, since we are only concerned with long-term variations. Only bins of more than three nights and stars with at least four bins were selected. The errors used for each bin are the statistical errors in the average, 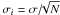 , where σ is the root-mean-square (rms) of the nightly averaged data in each bin, and N is the number of nights included in the bin.
, where σ is the root-mean-square (rms) of the nightly averaged data in each bin, and N is the number of nights included in the bin.
We also decided to select only stars with data for at least three years of observations, which resulted in GJ 361, GJ 2049, and GJ 3218 being discarded from the sample. Our final sample consisted of 27 stars that passed the selection criteria, whose basic parameters are presented in Table 1. These stars have spectral types in the range M0–M5.5 V and have V magnitudes between 7.34 and 11.81, with V − I colours ranging from 1.64 to 3.62 mag. In the same table, we also present the observation log, with information about the number of nights of observation, the time span in days, the average S/N at spectral order 56 (the order of the Na i doublet, ~5893 Å) and the average RV error. The time span of the observations range from 3.3 to 7.2 years (with a median value of 5.9 years). The average errors on RV per star for the nightly averaged data vary between 0.8 and 3.0 m s-1.
Statistics for RV and Na i, and probabilities P(F) of the variability F-tests for activity.
3. Na I index variability
In Paper I, we compared four activity indices, namely SCa II, Hα, Na i, and He i, and arrived at the conclusion that the Na i index is the most suitable for monitoring the long-term activity of M-dwarf stars. We also tested our sample for variability and found that Gl 1, Gl 273, Gl 433, Gl 436, Gl 581, Gl 588, Gl 667 C, Gl 832, Gl 849, Gl 877, Gl 908, and HIP 85647 showed significant (P(F) ≤ 0.05) long-term activity variability in at least two indices. However, we are now using the latest data with new measurements from 2010 (previously we used data covering the years 2003–2009) and consequently other stars might now show statistically significant variability in their long time scale activity that has not been detected before. We therefore decided to repeat the variability F-tests, this time using only the Na i index.
The Na i activity proxy was determined as explained in Paper I, by measuring the flux in the centre of the sodium D1 and D2 lines relative to the flux in two reference bands. This index has not been calibrated to the bolometric flux of the stars, hence depends on the effective temperature of each star (see discussion on Sect. 6.6 of Paper I). As a consequence, this index cannot be used to compare the activity of stars with different effective temperatures. Nevertheless, it can be used to detect activity variability with time for a given star.
In a similar fashion to our analysis in Paper I, we investigated whether the long time scale variations observed in our data were of statistical significance. As previously done in Paper I, we used the F-test with an F-value of 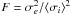 , where σe is the standard deviation and ⟨ σi ⟩ the average of the error in the mean of the binned parameter for each star (see Endl et al. 2002; Zechmeister et al. 2009; Bonfils et al. 2012). This F-test gives the probability that the observed standard deviation can be explained by the random scatter due to the internal errors. Therefore, a low value of P(F) will discriminate against the stars that have experienced significant variability that is not justified by the internal errors. The results of these tests are shown in Table 2. Bold face values indicate probabilities lower than 0.05 (95% significance level). The F-value used to calculate the probabilities was F = σe(Na i)2/ ⟨ σi(Na i) ⟩ 2, where σe stands for the rms of the (binned) data and ⟨ σi ⟩ is the average of the error in the mean. We also show the number of bins Nbins, an indication of whether the star passed the variability tests in Paper I, Sel., the RV rms ⟨ σe(Vr) ⟩ and the average error in the mean ⟨ σi(Vr) ⟩ , and the average value of the Na i index, ⟨ Na i ⟩ .
, where σe is the standard deviation and ⟨ σi ⟩ the average of the error in the mean of the binned parameter for each star (see Endl et al. 2002; Zechmeister et al. 2009; Bonfils et al. 2012). This F-test gives the probability that the observed standard deviation can be explained by the random scatter due to the internal errors. Therefore, a low value of P(F) will discriminate against the stars that have experienced significant variability that is not justified by the internal errors. The results of these tests are shown in Table 2. Bold face values indicate probabilities lower than 0.05 (95% significance level). The F-value used to calculate the probabilities was F = σe(Na i)2/ ⟨ σi(Na i) ⟩ 2, where σe stands for the rms of the (binned) data and ⟨ σi ⟩ is the average of the error in the mean. We also show the number of bins Nbins, an indication of whether the star passed the variability tests in Paper I, Sel., the RV rms ⟨ σe(Vr) ⟩ and the average error in the mean ⟨ σi(Vr) ⟩ , and the average value of the Na i index, ⟨ Na i ⟩ .
Fourteen of the 27 stars displayed long-term activity variability with P(F) ≤ 0.05, representing 52% of the sample. These stars are Gl 273, Gl 433, Gl 436, Gl 526, Gl 581, Gl 588, Gl 667 C, Gl 699, Gl 832, Gl 849, Gl 876, Gl 877, Gl 908, and HIP 85647. These are the same stars that passed the tests in Paper I plus Gl 526, Gl 699, and Gl 876, and less Gl 1. Four more stars, Gl 680, Gl 887, HIP 19394, and HIP 38594, have 0.05 < P(F) ≤ 0.1, which if they are considered increases the percentage of stars with variability to 67%. In Paper I, we found that 17 stars out of 30 showed variability in the Na i index with P(F) ≤ 0.1, representing 57% of the sample. This represents an increase in the number of variable stars by 10% from our previous work which has been achieved by simply adding one more year of observations, thus more of these stars might have shown long-term variability if data of a longer time-span had been considered. We note that Gl 1 passed the variability test on Paper I but not here. This is because in Paper I this star passed the test because of its variability in both the SCa ii and Hα indices, while not showing significant variability in Na i. Since we only used the Na i index and for Gl 1 we did not have more data points in 2010, we found that this star failed to pass the F-test based solely on Na i.
By using a sample of old FGK stars in the solar neighbourhood that had been studied for up to seven years, Lovis et al. (2011) found that 61% have a magnetic activity cycle. Although we cannot confirm the cyclic nature of our detected long-term activity variations, our results are compatible with those of Lovis et al. (2011).
From now on, we consider only these 14 stars for the rest of the study, unless specified.
4. Activity cycle fits
Some stars show clear long-term variation in their activity, that is clearly visible with a general trend (increase or decrease in activity over several observational seasons). These include stars that have not passed the variability F-tests of Sect. 3. There is evidence that the periodic activity cycles of M-dwarf stars can be well-fitted by a sinusoidal function (see Cincunegui et al. 2007; Díaz et al. 2007b; Buccino et al. 2011). Given the usually smaller number of points in our study, fitting other functions (e.g. Keplerian) would not provide tighter constraints since it would increase the number of free-fitting parameters close to the number of data points. We therefore tried to fit a sinusoidal signal to the Na i data to obtain the periods of these cycles (minimum periods in the case of data covering less than one period). The fitted sinusoidal signal was of the form 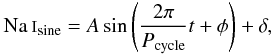 (3)where A is the semi-amplitude in units of Na i, Pcycle the activity cycle period in days, t the observation epoch in days, φ the phase, and δ a constant offset. The quality of the fit was obtained by a p-value, which gives the probability that the data is more accurately fit by a straight line than a sinusoidal signal. This p-value was calculated via an F-value given by
(3)where A is the semi-amplitude in units of Na i, Pcycle the activity cycle period in days, t the observation epoch in days, φ the phase, and δ a constant offset. The quality of the fit was obtained by a p-value, which gives the probability that the data is more accurately fit by a straight line than a sinusoidal signal. This p-value was calculated via an F-value given by 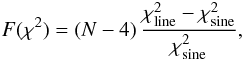 (4)where line and sine identify whether the model used was the linear fit or sinusoidal fit, respectively, and N is the number of data points. The chi-squared function used was
(4)where line and sine identify whether the model used was the linear fit or sinusoidal fit, respectively, and N is the number of data points. The chi-squared function used was ![\begin{eqnarray} \chi^2 = \sum^N_1 \left[ \frac{\ion{Na}{i}_n - \ion{Na}{i}_{n,\,{\rm sine}}}{\sigma_i(\ion{Na}{i})_n} \right]^2,~\mathrm{for}~1 \leq n \leq N, \end{eqnarray}](/articles/aa/full_html/2012/05/aa18598-11/aa18598-11-eq55.png) (5)where Na in are the observed values of the activity index, Na in, sine are the activity values obtained from the fitted sine model, and σi(Na i)n are the internal errors in each individual Na in. Smaller p-values indicate that the data were more tightly fitted by a sinusoid. We note that these fits were carried out without taking into consideration whether the star passed the variability F-tests in Sect. 3. In addition, it was only possible to calculate the probabilities for the stars that have five or more data points, otherwise (N − 4) ≤ 0. Eight stars had their long-term activity successfully fitted by a sinusoidal signal, with P(χ2) ≤ 0.1. These stars are Gl 1, Gl 382, Gl 433, Gl 581, Gl 667 C, Gl 680, Gl 832, and HIP 85647. However, Gl 1, Gl 382, and Gl 680 did not pass the long-term variability F-tests hence were discarded from further discussion. The others are discussed individually in Sect. 6.
(5)where Na in are the observed values of the activity index, Na in, sine are the activity values obtained from the fitted sine model, and σi(Na i)n are the internal errors in each individual Na in. Smaller p-values indicate that the data were more tightly fitted by a sinusoid. We note that these fits were carried out without taking into consideration whether the star passed the variability F-tests in Sect. 3. In addition, it was only possible to calculate the probabilities for the stars that have five or more data points, otherwise (N − 4) ≤ 0. Eight stars had their long-term activity successfully fitted by a sinusoidal signal, with P(χ2) ≤ 0.1. These stars are Gl 1, Gl 382, Gl 433, Gl 581, Gl 667 C, Gl 680, Gl 832, and HIP 85647. However, Gl 1, Gl 382, and Gl 680 did not pass the long-term variability F-tests hence were discarded from further discussion. The others are discussed individually in Sect. 6.
5. RV, activity, and CCF parameters
Figures A.1–A.27 present the time-series of RV data, activity, and the CCF parameters’ BIS, FWHM, and contrast for the 27 stars that passed the selection criteria (prior to the variability F-tests). Small points are nightly averaged data used to calculate the bins, and points with errorbars are the binned data (the errors are explained in Sect. 2). The peak-to-peak variation (Δ) and rms (σ) are also shown. The known planetary companions’ signal were subtracted from the RV time-series.
After removal of secular acceleration, HIP38594 showed a trend in the RV time-series with a slope of −50.83 ± 0.51 m s-1 yr-1. This corresponds to a variation of Δ(Vr) = 307.5 m s-1 across the time span of our data and is probably due to a stellar companion. A Keplerian fit gives an orbit for a companion with a minimum period (only a linear trend is observed in the data) of 4941 ± 1516 days. Since we are only concerned with low-amplitude and long-term variations, we removed this trend.
Other stars appear to have linear trends in RV, such as Gl 205 (with Δ(Vr) = 9 m s-1) and Gl 680 (Δ(Vr) = 15 m s-1), but since these trends have smaller amplitude variations we decided to keep them for the rest of the study (see Sect. 5.2 for more information).
5.1. Activity and RV scatter
 |
Fig. 1 Top: RV scatter versus Na i scatter. Bottom: RV scatter versus relative Na i scatter. |
Table 2 shows the RV rms after the subtraction of the orbits together with the mean and rms of the Na i index for the binned data of the full sample. The scatter in RV, σe(Vr), varies between 0.29 m s-1 for Gl 849 and 5.9 m s-1 for Gl 680. The most active star in the sample is Gl 551 (Proxima Centauri) with an average Na i index of 0.49, while the most inactive star is Gl 699 (Barnard’s star) with an average Na i value of 0.059 (but the largest relative scatter in Na i of ~14%). We note, however, that the average Na i index values depend on stellar colour (see Fig. 6 of Paper I) and should not be used to compare the activity of stars with different colours for which the index is not calibrated for the photospheric contribution and the bolometric flux is not taken into consideration.
Pearson correlation coefficients and their respective FAPs.
The most active star in the sample, Gl 551, also has the largest absolute scatter in Na i index (and 12% relative scatter). However, its RV dispersion is not particularly high, having a standard deviation of σe(Vr) = 1.5 m s-1.
Meunier et al. (2010) simulated the effects of spots, plages, and inhibition of convection in the solar RV during a solar activity cycle with the Sun seen edge-on and observed as a star, by measuring its integrated flux over the whole disk. The authors found that the signal induced by the three effects on the solar RV during the cycle had an rms of σ(Vr) = 2.40 m s-1, with a peak-to-peak variation of 10.6 m s-1.
The median RV rms of 1.5 m s-1 for our sample is smaller than the results of Meunier et al. (2010) and therefore in agreement with the extrapolation towards M dwarfs of Lovis et al. (2011), who found that later-type stars have lower amplitude RV influenced by long-term activity than earlier-type stars. The stronger contribution to RV from magnetic activity cycles is expected to originate from the inhibition of convection (Meunier et al. 2010). Since the cell-convection structure depends strongly on the effective temperature of the stars, the impact of their inhibition should also depend of spectral type. Thus, activity cycles are expected to have a different influence on RV for different types of stars.
Figure 1 shows the rms variation in RV against the rms in Na i index (top panel) and the relative variation in Na i (lower panel). A relation between these parameters is clearly visible: stars with a larger long-term scatter in their activity also have a larger long-term scatter in RV. The minimum long-term relative variation we could detect in the Na i index was around 2%, with the highest scatter reaching around 14%. The star Gl 699 appears to be an outlier, more evidently when we consider the relative activity values. Although this star has an average value of σ(Vr), when compared to the rest of the sample, it has the highest relative activity variation, almost twice that of the star with the second highest relative activity variation.
5.2. Correlation between RV and activity
Table 3 shows the correlation coefficients of the relation between RV and Na i and the respective FAPs. The FAPs were calculated using bootstrapping of the nightly averaged data, in addition to a re-binning and a subsequent determination of the correlation coefficient for each of the 10 000 permutations (see also Paper I). The tendency for positive correlations is clear, with an average correlation coefficient of ⟨ ρ ⟩ = 0.49. Five stars have a significant correlation coefficient (with ≤ 5% false-alarm probability) between activity and RV, which represents 36% of the sample. These stars are Gl 273, Gl 433, Gl 436, Gl 588, and Gl 908 and their coefficients range between 0.82 and 0.91. One more star, Gl 876, has a FAP value lower than 10%, with a correlation coefficient of 0.63. If a FAP lower than 10% is taken as the limit, then we can conclude that for ~43% of the variable stars the RV is induced by long-term activity.
Figure 2 shows the slope of the correlation between RV and Na i index as a function of (V − I) colour. The symbols have three sizes that depend on the correlation coefficient values: large for ρ ≥ 0.75, medium for 0.50 ≤ ρ < 0.75, and small for ρ < 0.50. The data points have three colours based on the FAP values: black for FAP ≤ 0.01, grey for 0.01 < FAP ≤ 0.05, and white for FAP > 0.1. The errorbars are the errors in the slope. We can see in the figure that there is a clear tendency for positive slopes in the correlation RV–Na i. This implies that a positive change in activity will induce a positive change in the apparent stellar velocity.
All the cases of a significant correlation have positive coefficients and the slopes of the correlation range from 85 m s-1 Na i-1 to 338 m s-1 Na i-1. In contrast to the findings of Lovis et al. (2011) for FGK stars, we found no strong relationship between the slopes and stellar colour (a proxy of Teff) for this sample of early-M dwarfs. Furthermore, we found no cases of significant anti-correlations as would be expected from the author’s study. Possible explanations are that the author’s correlation observed in their Fig. 18 (lower panel) reaches a plateau for lower effective temperatures or that the variations induced by long-term activity in the RV of M dwarfs are so small that they are more difficult to observe (some of the observed scatter reaches the same level as the instrument precision). Another possibility could be that still undetected small planets might interfere with the RV data, preventing any clear hypothetical correlation.
 |
Fig. 2 Slope of the correlation between RV and activity against (V − I) colour. Symbol sizes depend on the value of the correlation coefficient between RV and activity: large for ρ ≥ 0.75, medium for 0.50 ≤ ρ < 0.75, and small for ρ < 0.50. The data points have three colours based on the FAP values: black for FAP ≤ 0.01, grey for 0.01 < FAP ≤ 0.05, and white for FAP > 0.1. The errorbars are the errors in the slope. |
5.3. Correlation between activity and the CCF parameters
5.3.1. Na I versus BIS
We found a marginal tendency for negative correlations between Na i and BIS, with ⟨ ρ ⟩ = −0.18. We detected no cases of significant coefficients with a FAP ≤ 5%. Three cases of marginal (5% < FAP ≤ 10%) anti-correlation, Gl 273 with ρ = −0.64, Gl 877 with ρ = −0.74, and Gl 908 with ρ = −0.61 (21% of the sample). Owing to the lack of significant cases of correlation with activity, the line bisector thus does seem not to be a very good long-term activity indicator for early-M dwarfs.
This is different from the trend found between activity and BIS for early-K stars, where the two were found to be positively correlated (e.g. Santos et al. 2010). While the BIS values found here were all negative, Santos et al. (2010) measured positive BIS values in all stars. Although the absolute value of BIS would increase with activity, in the case of the negative values found in this study it means that the increase was a negative increase, hence anti-correlated with activity. We can speculate that the difference in the signal of the BIS values might be attributed to either the bisectors of K and M dwarfs that have inverse shapes, or the use of different cross-correlation masks to obtain the CCF line profiles (see e.g. Dall et al. 2006).
5.3.2. Na I versus FWHM
We found a tendency for positive correlations between our activity indicator and width of the CCF profile, with ⟨ ρ ⟩ = 0.53 (the strongest average correlation coefficient between parameters). We also found, a positive trend for early-K stars (e.g. Santos et al. 2010), hence we conclude that the qualitative behaviour of FWHM with activity is similar for different spectral types, an effect also shown in Lovis et al. (2011). Six stars have strong correlations in the range 0.60–0.93 with FAP ≤ 1%, representing 43% of our 14-star sample. These are Gl 433, Gl 436, Gl 581, Gl 877, Gl 908, and HIP 85647. Two more stars display a marginal correlation, Gl 526 and Gl 849. If we count them, then 57% of our stars have a long-term correlation between activity and FWHM. This means that the use of FWHM should be useful to detect long-term activity-like variations in M-dwarfs and can be used in addition to other activity proxies.
5.3.3. Na I versus contrast
As found by Santos et al. (2010) for earlier-type stars, we measured an apparent anti-correlation, ⟨ ρ ⟩ = −0.30 between the activity level and the contrast of the CCF. However we found only two cases of significant coefficients, Gl 273 with ρ = −0.89 and HIP 85647 with ρ = −0.87. This represents only 14% of the sample, an indication that the depth of the CCF line is not an optimal measure of the activity level of M dwarfs (at least that measured by the Na i/Ca ii lines). Two other cases of marginal correlation, Gl 699 with ρ = −0.79 and Gl 908 with ρ = 0.43 are present.
6. Individual cases
6.1. Stars with significant RV–activity correlation
Gl 273.
This star has the highest slope in the RV–activity relation of the stars with significant correlation. Its slope has a value of 338 m s-1 Na i-1 with the RV having a peak-to-peak variation of Δ = 5 m s-1 and a rms of ~1.5 m s-1. Its RV–activity correlation coefficient is 0.84 with a FAP of 2% (Fig. 3). This star also has a strong anti-correlation between Na i and contrast with ρ = −0.89 (FAP = 0.0074). A moderate anti-correlation is also observed between Na i and BIS (ρ = −0.64, FAP = 0.094). Although we found signs of a correlation between activity and RV we were unable to properly fit a sinusoidal to the Na i time series.
 |
Fig. 3 RV relation with Na i index for Gl 273. Small dots without errorbars are nightly averaged data points and points with errorbars are averaged over 150 days. The dashed line is the best linear fit. The correlation coefficient ρ and the respective FAP are shown. |
Gl 433.
In Paper I, we found that this star reaches a maximum in activity, which is typical of cycle-type long-term activity variations. Figure 4 (middle and bottom panels) shows that the RV time-series, after removal of the planetary signal (Delfosse et al. 2012), follows a similar pattern to the Na i index. The correlation coefficient between the two is ρ = 0.91 with a FAP of 0.0018 (Fig. 4, top panel). The Na i index also shows correlations with CCF parameters of −0.70 and 0.70 for BIS and FWHM, respectively. We can therefore confirm that the activity cycle maximum is inducing the maximum in RV. The slope of the RV–Na i correlation is 328 m s-1 Na i-1 and we measured an overall variation in RV of 3.29 m s-1 (with σe(Vr) = 1.22 m s-1). The amplitude and period of the cycle in both Na i or RV scales could not be inferred because we do not have an entire cycle period in our data. However, a minimum limit for the amplitude and period could be calculated by fitting a sinusoid to the activity time-series. We found that the minimum activity cycle period is 1665 days with a minimum amplitude of 0.004 in Na i (Fig. 4, middle panel). A similar minimum period was also found for the RV signal with a value of 1758 days and an amplitude of 1.45 m s-1 (Fig. 4, bottom panel). This star therefore represents a good example of an RV signal induced by an activity cycle.
 |
Fig. 4 Top: RV relation with Na i index for Gl 433. Middle: sinusoidal fit to the Na i index for Gl 433. Bottom: sinusoidal fit to RV of Gl 433. Small dots without errorbars are nightly averaged and points with errorbars are averaged over 150 days. The dashed lines represent the best linear (top) and sinusoidal (middle, bottom) fits to the data. |
Gl 436.
This star has the smallest slope of the RV–activity correlation with a value of 85 m s-1 Na i-1. From Fig. 5, we can observe a large scatter in the nightly averaged data. Ballard et al. (2010) reported the measurement of short-term noise in photometry that they attributed to stellar spots. Furthermore, Knutson et al. (2011) detected evidence of occulted spots during the transits of Gl 436 b (Butler et al. 2004). It is probable that short-term activity variability is producing the large scatter in Na i and contributing to a reduction in the slope’s value. Nevertheless, the correlation coefficient of the RV–activity relation is ρ = 0.83 with a FAP of 0.9%, providing clues for the influence of long-term activity on the observed RV of the star. A strong correlation coefficient between Na i and FWHM of 0.82 (FAP = 0.7%) was also found. However, we tried to fit a sinusoidal signal to both the RV and Na i time series but obtained no significant results. The activity time series in Fig. A.8 shows a decreasing trend in activity, which might be due to a long-period magnetic cycle, but more data will be needed to firmly prove this.
 |
Fig. 5 RV relation for the Na i index in the case of Gl 436. Small dots without errorbars are nightly averaged data points and points with errorbars are averaged over 150 days. The dashed line is the best linear fit. The correlation coefficient ρ and the respective FAP are shown. |
Gl 588.
With a correlation coefficient of 0.82 (FAP = 3.3%), this star also has a strong long-term relationship between RV and activity (Fig. 6). This correlation has a slope of 181 m s-1 Na i-1. The RV time series (Fig. A.13) has a periodic-like signal with a peak-to-peak variation of 3.6 m s-1, which is similar to the Na i time series apart from a point at BJD ~2 453 560 d. This is a point that includes data for only four nights and might be influenced by short-term activity variability. It is therefore impossible to conclude anything about the periodicity of this stars’ activity cycle.
 |
Fig. 6 RV relation for the Na i index in the case of Gl 588. Small dots without errorbars are nightly averaged data points and points with errorbars are averaged over 150 days. The dashed line is the best linear fit. The correlation coefficient ρ and the respective FAP are shown. |
Gl 908.
This is another good example of a long-term correlation between RV and activity. The correlation coefficient has a value of 0.85 (FAP = 0.4%) and the trend can be observed in both the binned and the nightly averaged data (Fig. 7). The slope of the correlation is 322 m s-1 Na i-1 and we measured an RV peak-to-peak variation of 3.85 m s-1. A strong correlation between Na i and FWHM with ρ = 0.82 (FAP = 0.75%) was also detected. Although we have strong evidence that the RV was induced by long-term activity, we could not fit a sinusoidal signal to both time series with significant p(χ2). This star probably has a magnetic “cycle” with no clear period, i.e., a star with a long-term aperiodic magnetic-activity variability, the variations of which are often classified as var (variable) by (Baliunas et al. 1995).
 |
Fig. 7 RV relation for the Na i index in the case of Gl 908. Small dots without errorbars are nightly averaged data points and points with errorbars are averaged over 150 days. The dashed line is the best linear fit. The correlation coefficient ρ and the respective FAP are shown. |
6.2. Other interesting cases
Gl 176.
This star has what appears to be a long-term periodic signal with P ~ 2043 d in RV (see the time-series plot Fig. A.2). The same trend is not observed in the Na i index and the data for this star did not pass the variability tests. This star has a confirmed planetary companion, Gl 176 b with P = 8.7 d, and a rotationally modulated activity signal with a period of P = 39 d (Forveille et al. 2009). However, none of these signals can explain the ~2000 d variation, which might be due to a yet undiscovered long-period planet.
Gl 581.
This star has the highest probability that its activity data can be fitted by a periodic sinusoidal signal instead of a linear trend. We obtained a signal with a period of P = 3.85 years (P(χ2) = 0.01%) and our timespan for this star is long enough to cover more than one activity cycle period (Fig. 8). Furthermore, Gl 581 also passed the variability tests. To date, four planets are known to orbit the star, and the possibility of two more planets has been discarded (Bonfils et al. 2005; Udry et al. 2007; Mayor et al. 2009; Forveille et al. 2011a). We removed the signal of the four confirmed planets resulting in a long-term RV rms of 0.96 m s-1, which is of the order of the instrument precision. No correlation was found between the long-term RV and activity but the Na i index is correlated with FWHM (ρ = 0.60, FAP = 1.9%). Owing to of the large number of detected planets, we note that their orbits might not have been properly subtracted from the data. We therefore draw no conclusions about the possibility of the activity cycle having influence on the RV signal of this star.
 |
Fig. 8 Sinusoidal fit to the activity time series of Gl 581. |
Gl 667C.
Two planets are known to orbit this star (Delfosse et al. 2012). It is also a member of a triple system and orbits the A + B binary system. This system introduces a trend in RV that was subtracted together with the planetary companions signal. The Na i activity index passed the variability F-test and a sinusoidal function with a period of P = 3.18 years is well-fitted to the activity time series (with P(χ2) = 3.3%, Fig. 9). However, the RV signal is only marginally correlated with activity, having a correlation coefficient of ρ = 0.45 with a FAP of 12%. No correlations between the other parameters are detected.
 |
Fig. 9 Sinusoidal fit to the activity time series of Gl 667 C. |
Gl 699.
Kürster et al. (2003) found an anti-correlation between RV and the Hα index for Bernard’s star with a coefficient of ρ = −0.50. Using a longer timespan for the same star, Zechmeister et al. (2009) detected a similar correlation with ρ = −0.42. We found only a marginal positive correlation with the Na i index (ρ = 0.32, FAP = 0.32). The Na i index of this star is moderately correlated with both FWHM (ρ = 0.55, FAP = 0.15) and contrast (ρ = −0.79, FAP = 0.070).
Gl 832.
This star passed the activity variability tests but we found no correlation with RV after the removal of the planetary companion (Bailey et al. 2009). None of the other parameters are correlated apart from a marginal correlation between activity and FWHM of ρ = 0.57 but with a high FAP of 19%. The activity time series is well-fitted by a sinusoidal function with P(χ2) = 3.2% and a minimum period of 4.73 years (Fig. 10).
 |
Fig. 10 Sinusoidal fit to the activity time series of Gl 832. |
HIP 85647.
After removal of the signal of the planetary companion (Forveille et al. 2011b) of this star and a linear trend caused by a stellar companion, we found no correlation between RV and activity. There are strong correlations between Na i and the CCF parameters FWHM and contrast with ρ = 0.81 (FAP = 3.9%) and ρ = −0.87 (FAP = 1.4%), respectively. We successfully fitted a sinusoidal signal to the activity time series and obtained a period of 2.74 years (with P(χ2) = 3.4%, Fig. 11).
 |
Fig. 11 Sinusoidal fit to the activity time series of HIP 85647. |
7. Conclusions
We have used a sample of 27 M0 to M5.5 dwarfs to study the relationship between long-term activity, RV, and parameters of the CCF given by the HARPS pipeline. As the indicator for activity, level we used the Na i index as suggested in Paper I. We binned the data into 150-day bins to average out high-frequency noise and removed any RV signals induced by known stellar or planetary companions.
A selection of stars with long-term activity variability was carried out by using F-tests. This resulted in a subsample of 14 variable stars, which means that around half of the stars in our sample have significant long-term activity variations.
The activity time series of some stars were closely fitted by sinusoidal functions to infer the activity cycle’s period or minimum period. Five stars could be statistically well-fitted by sinusoids and the inferred periods varied between 2.8 and 4.7 years. We should note, however, that our data covered close to one period or less of the fitted signals and therefore the cyclic nature of the signals cannot be fully established. Even if these stars have cyclic activity variability, the periods obtained by the sinusoidal fitting should be regarded as minimum periods since the timespan is not long enough to cover two periods.
We measured a long-term RV rms in the range 0.30 to 5.9 m s-1 and a relative scatter in the Na i index for the 14-star variable subsample in the range ~2–14%. These two parameters, σ(Vr) and σ(Na i), appear to be correlated. The median RV rms of 1.5 m s-1 that can possibly be induced by activity is lower than the one obtained in the case of the Sun by Meunier et al. (2010) as predicted by extrapolation of the trend in Fig. 18 (lower panel) of Lovis et al. (2011) to the case of late-type stars.
We then searched for correlations between RV, activity, and the CCF parameters BIS, FWHM, and contrast. The main general results we obtained can be summarised as:
-
We found overall evidence of positive correlations between long-term activity and RV variations. No relation between the slope of the correlation and stellar colour was found.
-
Five out of 14 stars with long-term variability have a significant correlation between activity and RV. This amounts to 36% of our subsample. These stars are Gl 273, Gl 433, Gl 436, Gl 588, and Gl 908. The maximum peak-to-peak RV variation we obtained for stars with significant correlation between long-term activity and RV was ~5 m s-1. Only for Gl 433 was the activity closely fitted by a sinusoidal signal, even though the signal spans less than a full period. We determined a minimum period of 4.6 years for the activity cycle of this star, and a similar minimum period of 4.8 years was found for the RV signal. The other stars could have aperiodic activity cycles but more data is needed to confirm this hypothesis.
-
Although we found a general tendency for BIS to be anti-correlated with activity, those correlations were not statistically significant. Only 21% of the stars with long-term variability displayed marginal correlations between activity and BIS. While we found a general trend for anti-correlations between activity and BIS for M dwarfs, Santos et al. (2010) found positive correlations between the SMW activity index and BIS for early-K stars. This is a curious result that should be investigated further.
-
We found that the long-term activity level was in general well-correlated with FWHM, where 43% of the stars with long-term variability had their activity level significantly correlated with FWHM. This is a good indication that the width of the CCF profile can be used to follow long-term activity in M dwarfs, as a complement to activity indices. A similar result was previously found in the case of early-K dwarfs by Santos et al. (2010).
-
When compared with activity, the contrast appeared to follow negative correlations, which in only 14% of the cases was significant. This finding of anti-correlations was also found by Santos et al. (2010) for early-K dwarfs, but since the fraction of significant coefficients is very low, this parameter does not seem to be a strong tool to help us diagnose long-term activity variability.
In light of these results, we advise planet hunters to carefully check for long-term activity variations when analysing long-timespans of RV data since activity cycles could be adding noise to the data or even mimicking the low-amplitude (≤ 5 m s-1) signals of planetary companions.
Online material
Appendix A: Data times series
In the following figures, we present the time series for all the parameters of the sample we used in this work. Black points are nightly averaged data points, red squares with errorbars are the 150-day bins, Δ is the peak-to-peak variation, and σ the standard deviation in the data. The errorbars are the error in the mean 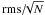 , where N is the number of measurements in each bin.
, where N is the number of measurements in each bin.
 |
Fig. A.1 Time-series of RV, Na i index data, and the BIS, FWHM, and contrast of the CCF line profile for Gl 1. |
 |
Fig. A.2 Time-series of RV, Na i index data, and the BIS, FWHM, and contrast of the CCF line profile for Gl 176. |
 |
Fig. A.3 Time-series of RV, Na i index data, and the BIS, FWHM, and contrast of the CCF line profile for Gl 205. |
 |
Fig. A.4 Time-series of RV, Na i index data, and the BIS, FWHM, and contrast of the CCF line profile for Gl 273. |
 |
Fig. A.5 Time-series of RV, Na i index data, and the BIS, FWHM, and contrast of the CCF line profile for Gl 382. |
 |
Fig. A.6 Time-series of RV, Na i index data, and the BIS, FWHM, and contrast of the CCF line profile for Gl 393. |
 |
Fig. A.7 Time-series of RV, Na i index data, and the BIS, FWHM, and contrast of the CCF line profile for Gl 433. |
 |
Fig. A.8 Time-series of RV, Na i index data, and the BIS, FWHM, and contrast of the CCF line profile for Gl 436. |
 |
Fig. A.9 Time-series of RV, Na i index data, and the BIS, FWHM, and contrast of the CCF line profile for Gl 479. |
 |
Fig. A.10 Time-series of RV, Na i index data, and the BIS, FWHM, and contrast of the CCF line profile for Gl 526. |
 |
Fig. A.11 Time-series of RV, Na i index data, and the BIS, FWHM, and contrast of the CCF line profile for Gl 551. |
 |
Fig. A.12 Time-series of RV, Na i index data, and the BIS, FWHM, and contrast of the CCF line profile for Gl 581. |
 |
Fig. A.13 Time-series of RV, Na i index data, and the BIS, FWHM, and contrast of the CCF line profile for Gl 588. |
 |
Fig. A.14 Time-series of RV, Na i index data, and the BIS, FWHM, and contrast of the CCF line profile for Gl 667C. |
 |
Fig. A.15 Time-series of RV, Na i index data, and the BIS, FWHM, and contrast of the CCF line profile for Gl 674. |
 |
Fig. A.16 Time-series of RV, Na i index data, and the BIS, FWHM, and contrast of the CCF line profile for Gl 680. |
 |
Fig. A.17 Time-series of RV, Na i index data, and the BIS, FWHM, and contrast of the CCF line profile for Gl 699. |
 |
Fig. A.18 Time-series of RV, Na i index data, and the BIS, FWHM, and contrast of the CCF line profile for Gl 832. |
 |
Fig. A.19 Time-series of RV, Na i index data, and the BIS, FWHM, and contrast of the CCF line profile for Gl 849. |
 |
Fig. A.20 Time-series of RV, Na i index data, and the BIS, FWHM, and contrast of the CCF line profile for Gl 876. |
 |
Fig. A.21 Time-series of RV, Na i index data, and the BIS, FWHM, and contrast of the CCF line profile for Gl 877. |
 |
Fig. A.22 Time-series of RV, Na i index data, and the BIS, FWHM, and contrast of the CCF line profile for Gl 887. |
 |
Fig. A.23 Time-series of RV, Na i index data, and the BIS, FWHM, and contrast of the CCF line profile for Gl 908. |
 |
Fig. A.24 Time-series of RV, Na i index data, and the BIS, FWHM, and contrast of the CCF line profile for HIP 12961. |
 |
Fig. A.25 Time-series of RV, Na i index data, and the BIS, FWHM, and contrast of the CCF line profile for HIP 19394. |
 |
Fig. A.26 Time-series of RV, Na i index data, and the BIS, FWHM, and contrast of the CCF line profile for HIP 38594. |
 |
Fig. A.27 Time-series of RV, Na i index data, and the BIS, FWHM, and contrast of the CCF line profile for HIP 85647. |
Acknowledgments
We would like to thank our anonymous referee for the helpful comments and suggestions. This work has been supported by the European Research Council/European Community under the FP7 through a Starting Grant, as well as in the form of a grant reference PTDT/CTE-AST/098528/2008, funded by Fundação para a Ciência e a Tecnologia (FCT), Portugal. J.G.S. would like to thank the financial support given by FCT in the form of a scholarship, namely SFRH/BD/64722/2009. N.C.S. would further like to thank the support from FCT through a Ciência 2007 contract funded by FCT/MCTES (Portugal) and POPH/FSE (EC).
References
- Bailey, J., Butler, R. P., Tinney, C. G., et al. 2009, ApJ, 690, 743 [Google Scholar]
- Baliunas, S. L., Donahue, R. A., Soon, W. H., et al. 1995, ApJ, 438, 269 [NASA ADS] [CrossRef] [Google Scholar]
- Ballard, S., Christiansen, J. L., Charbonneau, D., et al. 2010, ApJ, 716, 1047 [NASA ADS] [CrossRef] [Google Scholar]
- Boisse, I., Moutou, C., Vidal-Madjar, A., et al. 2009, A&A, 495, 959 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boisse, I., Bouchy, F., Hébrard, G., et al. 2011, A&A, 528, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bonfils, X., Forveille, T., Delfosse, X., et al. 2005, A&A, 443, L15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bonfils, X., Mayor, M., Delfosse, X., et al. 2007, A&A, 474, 293 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bonfils, X., Delfosse, X., Udry, S., et al. 2012, A&A, in press [Google Scholar]
- Buccino, A. P., Díaz, R. F., Luoni, M. L., Abrevaya, X. C., & Mauas, P. J. D. 2011, AJ, 141, 34 [NASA ADS] [CrossRef] [Google Scholar]
- Butler, R. P., Vogt, S. S., Marcy, G. W., et al. 2004, ApJ, 617, 580 [NASA ADS] [CrossRef] [Google Scholar]
- Cincunegui, C., Díaz, R. F., & Mauas, P. J. D. 2007, A&A, 461, 1107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dall, T. H., Santos, N. C., Arentoft, T., Bedding, T. R., & Kjeldsen, H. 2006, A&A, 454, 341 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Delfosse, X., Bonfils, X., Forveille, T., et al. 2012, A&A, submitted [arXiv:1202.2467] [Google Scholar]
- Díaz, R. F., Cincunegui, C., & Mauas, P. J. D. 2007a, MNRAS, 378, 1007 [NASA ADS] [CrossRef] [Google Scholar]
- Díaz, R. F., González, J. F., Cincunegui, C., & Mauas, P. J. D. 2007b, A&A, 474, 345 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dumusque, X., Udry, S., Lovis, C., Santos, N. C., & Monteiro, M. J. P. F. G. 2011, A&A, 525, A140 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dumusque, X., Lovis, C., Ségransan, D., et al. 2012, A&A, 535, A55 [Google Scholar]
- Endl, M., Kürster, M., Els, S., et al. 2002, A&A, 392, 671 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- ESA 1997, VizieR Online Data Catalog, 1239, [Google Scholar]
- Forveille, T., Bonfils, X., Delfosse, X., et al. 2009, A&A, 493, 645 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Forveille, T., Bonfils, X., Delfosse, X., et al. 2011a, A&A, submitted [arXiv:1109.2505] [Google Scholar]
- Forveille, T., Bonfils, X., Lo Curto, G., et al. 2011b, A&A, 526, A141 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gomes da Silva, J., Santos, N. C., Bonfils, X., et al. 2011, A&A, 534, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hawley, S. L., Gizis, J. E., & Reid, I. N. 1996, AJ, 112, 2799 [NASA ADS] [CrossRef] [Google Scholar]
- Knutson, H. A., Madhusudhan, N., Cowan, N. B., et al. 2011, ApJ, 735, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Koen, C., Kilkenny, D., van Wyk, F., & Marang, F. 2010, MNRAS, 403, 1949 [Google Scholar]
- Kürster, M., Endl, M., Rouesnel, F., et al. 2003, A&A, 403, 1077 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lovis, C., Dumusque, X., Santos, N. C., et al. 2011, A&A, submitted [arXiv:1107.5325] [Google Scholar]
- Mayor, M., Bonfils, X., Forveille, T., et al. 2009, A&A, 507, 487 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mayor, M., Marmier, M., Lovis, C., et al. 2011, A&A, submitted [arXiv:1109.2497] [Google Scholar]
- Melo, C., Santos, N. C., Gieren, W., et al. 2007, A&A, 467, 721 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Meunier, N., Desort, M., & Lagrange, A.-M. 2010, A&A, 512, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Moutou, C., Mayor, M., Lo Curto, G., et al. 2011, A&A, 527, A63 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Queloz, D., Bouchy, F., Moutou, C., et al. 2009, A&A, 506, 303 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Queloz, D., Henry, G. W., Sivan, J. P., et al. 2001, A&A, 379, 279 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Saar, S. H., & Donahue, R. A. 1997, ApJ, 485, 319 [NASA ADS] [CrossRef] [Google Scholar]
- Saar, S. H., & Fischer, D. 2000, ApJ, 534, L105 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Santos, N. C., Mayor, M., Naef, D., et al. 2000, A&A, 361, 265 [NASA ADS] [Google Scholar]
- Santos, N. C., Gomes da Silva, J., Lovis, C., & Melo, C. 2010, A&A, 511, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ségransan, D., Mayor, M., Udry, S., et al. 2012, A&A, 535, A54 [Google Scholar]
- Udry, S., Bonfils, X., Delfosse, X., et al. 2007, A&A, 469, L43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zechmeister, M., Kürster, M., & Endl, M. 2009, A&A, 505, 859 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
Statistics for RV and Na i, and probabilities P(F) of the variability F-tests for activity.
All Figures
 |
Fig. 1 Top: RV scatter versus Na i scatter. Bottom: RV scatter versus relative Na i scatter. |
| In the text | |
 |
Fig. 2 Slope of the correlation between RV and activity against (V − I) colour. Symbol sizes depend on the value of the correlation coefficient between RV and activity: large for ρ ≥ 0.75, medium for 0.50 ≤ ρ < 0.75, and small for ρ < 0.50. The data points have three colours based on the FAP values: black for FAP ≤ 0.01, grey for 0.01 < FAP ≤ 0.05, and white for FAP > 0.1. The errorbars are the errors in the slope. |
| In the text | |
 |
Fig. 3 RV relation with Na i index for Gl 273. Small dots without errorbars are nightly averaged data points and points with errorbars are averaged over 150 days. The dashed line is the best linear fit. The correlation coefficient ρ and the respective FAP are shown. |
| In the text | |
 |
Fig. 4 Top: RV relation with Na i index for Gl 433. Middle: sinusoidal fit to the Na i index for Gl 433. Bottom: sinusoidal fit to RV of Gl 433. Small dots without errorbars are nightly averaged and points with errorbars are averaged over 150 days. The dashed lines represent the best linear (top) and sinusoidal (middle, bottom) fits to the data. |
| In the text | |
 |
Fig. 5 RV relation for the Na i index in the case of Gl 436. Small dots without errorbars are nightly averaged data points and points with errorbars are averaged over 150 days. The dashed line is the best linear fit. The correlation coefficient ρ and the respective FAP are shown. |
| In the text | |
 |
Fig. 6 RV relation for the Na i index in the case of Gl 588. Small dots without errorbars are nightly averaged data points and points with errorbars are averaged over 150 days. The dashed line is the best linear fit. The correlation coefficient ρ and the respective FAP are shown. |
| In the text | |
 |
Fig. 7 RV relation for the Na i index in the case of Gl 908. Small dots without errorbars are nightly averaged data points and points with errorbars are averaged over 150 days. The dashed line is the best linear fit. The correlation coefficient ρ and the respective FAP are shown. |
| In the text | |
 |
Fig. 8 Sinusoidal fit to the activity time series of Gl 581. |
| In the text | |
 |
Fig. 9 Sinusoidal fit to the activity time series of Gl 667 C. |
| In the text | |
 |
Fig. 10 Sinusoidal fit to the activity time series of Gl 832. |
| In the text | |
 |
Fig. 11 Sinusoidal fit to the activity time series of HIP 85647. |
| In the text | |
 |
Fig. A.1 Time-series of RV, Na i index data, and the BIS, FWHM, and contrast of the CCF line profile for Gl 1. |
| In the text | |
 |
Fig. A.2 Time-series of RV, Na i index data, and the BIS, FWHM, and contrast of the CCF line profile for Gl 176. |
| In the text | |
 |
Fig. A.3 Time-series of RV, Na i index data, and the BIS, FWHM, and contrast of the CCF line profile for Gl 205. |
| In the text | |
 |
Fig. A.4 Time-series of RV, Na i index data, and the BIS, FWHM, and contrast of the CCF line profile for Gl 273. |
| In the text | |
 |
Fig. A.5 Time-series of RV, Na i index data, and the BIS, FWHM, and contrast of the CCF line profile for Gl 382. |
| In the text | |
 |
Fig. A.6 Time-series of RV, Na i index data, and the BIS, FWHM, and contrast of the CCF line profile for Gl 393. |
| In the text | |
 |
Fig. A.7 Time-series of RV, Na i index data, and the BIS, FWHM, and contrast of the CCF line profile for Gl 433. |
| In the text | |
 |
Fig. A.8 Time-series of RV, Na i index data, and the BIS, FWHM, and contrast of the CCF line profile for Gl 436. |
| In the text | |
 |
Fig. A.9 Time-series of RV, Na i index data, and the BIS, FWHM, and contrast of the CCF line profile for Gl 479. |
| In the text | |
 |
Fig. A.10 Time-series of RV, Na i index data, and the BIS, FWHM, and contrast of the CCF line profile for Gl 526. |
| In the text | |
 |
Fig. A.11 Time-series of RV, Na i index data, and the BIS, FWHM, and contrast of the CCF line profile for Gl 551. |
| In the text | |
 |
Fig. A.12 Time-series of RV, Na i index data, and the BIS, FWHM, and contrast of the CCF line profile for Gl 581. |
| In the text | |
 |
Fig. A.13 Time-series of RV, Na i index data, and the BIS, FWHM, and contrast of the CCF line profile for Gl 588. |
| In the text | |
 |
Fig. A.14 Time-series of RV, Na i index data, and the BIS, FWHM, and contrast of the CCF line profile for Gl 667C. |
| In the text | |
 |
Fig. A.15 Time-series of RV, Na i index data, and the BIS, FWHM, and contrast of the CCF line profile for Gl 674. |
| In the text | |
 |
Fig. A.16 Time-series of RV, Na i index data, and the BIS, FWHM, and contrast of the CCF line profile for Gl 680. |
| In the text | |
 |
Fig. A.17 Time-series of RV, Na i index data, and the BIS, FWHM, and contrast of the CCF line profile for Gl 699. |
| In the text | |
 |
Fig. A.18 Time-series of RV, Na i index data, and the BIS, FWHM, and contrast of the CCF line profile for Gl 832. |
| In the text | |
 |
Fig. A.19 Time-series of RV, Na i index data, and the BIS, FWHM, and contrast of the CCF line profile for Gl 849. |
| In the text | |
 |
Fig. A.20 Time-series of RV, Na i index data, and the BIS, FWHM, and contrast of the CCF line profile for Gl 876. |
| In the text | |
 |
Fig. A.21 Time-series of RV, Na i index data, and the BIS, FWHM, and contrast of the CCF line profile for Gl 877. |
| In the text | |
 |
Fig. A.22 Time-series of RV, Na i index data, and the BIS, FWHM, and contrast of the CCF line profile for Gl 887. |
| In the text | |
 |
Fig. A.23 Time-series of RV, Na i index data, and the BIS, FWHM, and contrast of the CCF line profile for Gl 908. |
| In the text | |
 |
Fig. A.24 Time-series of RV, Na i index data, and the BIS, FWHM, and contrast of the CCF line profile for HIP 12961. |
| In the text | |
 |
Fig. A.25 Time-series of RV, Na i index data, and the BIS, FWHM, and contrast of the CCF line profile for HIP 19394. |
| In the text | |
 |
Fig. A.26 Time-series of RV, Na i index data, and the BIS, FWHM, and contrast of the CCF line profile for HIP 38594. |
| In the text | |
 |
Fig. A.27 Time-series of RV, Na i index data, and the BIS, FWHM, and contrast of the CCF line profile for HIP 85647. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


