| Issue |
A&A
Volume 541, May 2012
|
|
|---|---|---|
| Article Number | A161 | |
| Number of page(s) | 13 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/201118549 | |
| Published online | 23 May 2012 | |
Modeling of weak-lensing statistics
I. Power spectrum and bispectrum
1
Institut de Physique Théorique, CEA Saclay,
91191
Gif-sur-Yvette,
France
e-mail: patrick.valageas@cea.fr
2
Department of Physics, Nagoya University,
464-8602
Nagoya,
Japan
3
Institute for the Physics and Mathematics of the Universe,
University of Tokyo, Kashiwa, Chiba
277-8568,
Japan
Received:
30
November
2011
Accepted:
19
April
2012
Aims. We investigate the performance of an analytic model of the 3D matter distribution, which combines perturbation theory with halo models, for weak-lensing statistics.
Methods. We compare our predictions for the weak-lensing convergence power spectrum and bispectrum with numerical simulations and fitting formulas proposed in previous works.
Results. We find that this model provides better agreement with simulations than published fitting formulas. This shows that building on systematic and physically motivated models is a promising approach. Moreover, this makes explicit the link between the weak-lensing statistics and the underlying properties of the 3D matter distribution, as a function of scale ℓ. Thus, we obtain the contributions to the lensing power spectrum and bispectrum that arise from perturbative terms (complete up to one-loop) and nonperturbative terms (e.g., “1-halo” term). Finally, we show that this approach recovers the dependence on cosmology (for realistic scenarios).
Key words: gravitational lensing: weak / large-scale structure of Universe
© ESO, 2012
1. Introduction
Weak gravitational lensing of background galaxies by foreground large-scale structures, the so-called cosmic shear, is one of the best tools to probe the nature of the main components of the Universe, such as dark matter and dark energy. Thus, weak lensing has the highest potential to constrain the properties of dark energy among other cosmological observations, if the systematic errors are well kept under control (Albrecht et al. 2006). To address questions about the nature of dark energy and the properties of gravity on cosmological scales, various surveys are planned, such as the Hyper Suprime-Cam Weak Lensing Survey (Miyazaki et al. 2006)1, the Dark Energy Survey (DES)2, the Large Synoptic Survey Telescope (LSST)3, Euclid (Refregier et al. 2010)4, and the Wide-Field Infrared Survey Telescope (WFIRST)5.
To exploit the full potential of future weak-lensing surveys, it will be important to analyze data with adequate statistical measures and tools. Particularly, one needs to properly take into account the correlations of the observables between different angular scales and redshifts, i.e., their covariance matrices (Cooray & Hu 2001; Takada & Jain 2009; Sato et al. 2009, 2011b). Furthermore, one has to use an appropriate likelihood function with given marginal distributions (Sato et al. 2010, 2011a).
Since most of the useful cosmological information contained in the cosmic shear signal is associated with small angular scales that are affected by nonlinear clustering, we also need to include these nonlinear effects to accurately model the weak-lensing statistics (Takada & Jain 2004; Sato et al. 2009). Most researchers use fitting formulas based on numerical simulations or phenomenological approaches but it would be useful to obtain analytical methods that are more directly related to the cosmological parameters and primordial fluctuations.
In this paper, we examine the performance of the theoretical modeling of the 3D matter density distribution proposed by Valageas & Nishimichi (2011a,b), which is based on a combination of perturbation theories and halo models. We focus on the convergence power spectrum and bispectrum, which are basic statistical measurements in weak lensing studies (see, Hikage et al. 2011, for a recent method of lensing power spectrum measurement). As compared with simple fitting formulas or direct numerical simulations, a significant advantage of our approach is that we can evaluate and compare different contributions that can be measured in weak-lensing surveys. Since different contributions suffer from different theoretical uncertainties, this is useful to estimate the accuracy that can be aimed at in weak-lensing statistics, as a function of scales. Furthermore, we find that our model provides better agreement with numerical simulations than other existent models.
This paper is organized as follows. In Sect. 2 we first present our model for the 3D matter density power spectrum and bispectrum. Next, we recall how this yields the weak lensing convergence power spectrum and bispectrum through the Born approximation. We describe our numerical simulations and the data analysis in Sect. 3. Then, we present detailed comparisons between the simulation results, previous models, and our theoretical predictions, for the convergence power spectrum in Sect. 4, and for the convergence bispectrum in Sect. 5, considering the cases of both equilateral and more general isosceles configurations. We study the relative importance of the different contributions to the power spectrum and bispectrum in Sect. 6, arising from “1-halo”, “2-halo”, or “3-halo” terms. Finally, we check the robustness of our model as we vary the cosmological parameters in Sect. 7 and we conclude in Sect. 8.
2. Analytic models
2.1. 3D matter power spectrum and bispectrum
Our Fourier-space normalizations for the density contrast, its power spectrum and
bispectrum, are 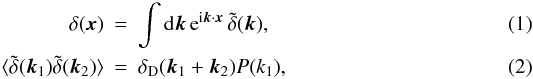 and
and
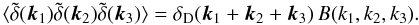 (3)In this section we
recall the model that we use to describe the 3D matter distribution, which is presented in
greater detail in Valageas & Nishimichi
(2011a,b). It combines systematic
perturbation theory, which governs large scales, with a phenomenological halo model, which
governs small scales. This is achieved by writing the 3D matter power spectrum as
(3)In this section we
recall the model that we use to describe the 3D matter distribution, which is presented in
greater detail in Valageas & Nishimichi
(2011a,b). It combines systematic
perturbation theory, which governs large scales, with a phenomenological halo model, which
governs small scales. This is achieved by writing the 3D matter power spectrum as
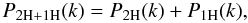 (4)as in the usual halo
model (Cooray & Sheth 2002). The main
improvements with respect to previous works are that the “2-halo” term is obtained from a
perturbative resummation scheme, which is complete up to one-loop order (and includes
partial resummations of diagrams at all higher orders), while the “1-halo” term includes a
“counterterm” associated with mass conservation that ensures its well-behaved asymptote at
low k.
(4)as in the usual halo
model (Cooray & Sheth 2002). The main
improvements with respect to previous works are that the “2-halo” term is obtained from a
perturbative resummation scheme, which is complete up to one-loop order (and includes
partial resummations of diagrams at all higher orders), while the “1-halo” term includes a
“counterterm” associated with mass conservation that ensures its well-behaved asymptote at
low k.
More precisely, the 2-halo contribution is written as 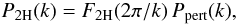 (5)where
F2H(q) is the fraction of pairs, with
initial (i.e. Lagrangian) separation q, that belong to two distinct
halos, and Ppert(k) is the matter power
spectrum obtained by perturbation theory. As discussed in Valageas & Nishimichi (2011a), it is not possible to use standard
perturbation theory (beyond linear order) for
Ppert(k), unless one adds a nonperturbative
ad-hoc cutoff, because this would yield a term that keeps growing at
high k and prevents a good agreement with numerical simulations. A
natural cure to this problem is to use a resummation scheme that remains well-behaved at
high k. As in Valageas &
Nishimichi (2011a), we use the “direct steepest-descent” resummation developed in
Valageas (2007, 2008), going to “one-loop” order. This provides a perturbative term
Ppert(k) that is consistent with standard
perturbation theory up to one-loop order (i.e. up to order
(5)where
F2H(q) is the fraction of pairs, with
initial (i.e. Lagrangian) separation q, that belong to two distinct
halos, and Ppert(k) is the matter power
spectrum obtained by perturbation theory. As discussed in Valageas & Nishimichi (2011a), it is not possible to use standard
perturbation theory (beyond linear order) for
Ppert(k), unless one adds a nonperturbative
ad-hoc cutoff, because this would yield a term that keeps growing at
high k and prevents a good agreement with numerical simulations. A
natural cure to this problem is to use a resummation scheme that remains well-behaved at
high k. As in Valageas &
Nishimichi (2011a), we use the “direct steepest-descent” resummation developed in
Valageas (2007, 2008), going to “one-loop” order. This provides a perturbative term
Ppert(k) that is consistent with standard
perturbation theory up to one-loop order (i.e. up to order
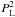 ) while keeping
close to PL at high k (thanks to the partial
resummation of higher orders). The prefactor
F2H(2π/k)
is equal to unity at all orders of perturbation theory, since it also writes as
) while keeping
close to PL at high k (thanks to the partial
resummation of higher orders). The prefactor
F2H(2π/k)
is equal to unity at all orders of perturbation theory, since it also writes as
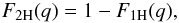 (6)where
F1H is the fraction of pairs of initial
separation q that belong to a single halo, and
F1H = 0 at all orders of perturbation theory (because this
is a nonperturbative quantity that behaves as
(6)where
F1H is the fraction of pairs of initial
separation q that belong to a single halo, and
F1H = 0 at all orders of perturbation theory (because this
is a nonperturbative quantity that behaves as 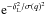 for Gaussian initial conditions).
for Gaussian initial conditions).
Next, the 1-halo contribution is written as 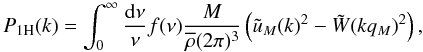 (7)where
f(ν) defines the halo mass function through (Press & Schechter 1974)
(7)where
f(ν) defines the halo mass function through (Press & Schechter 1974) 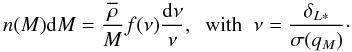 (8)Here,
σ(qM) is the rms linear
density contrast at mass M, or Lagrangian radius
qM, with
(8)Here,
σ(qM) is the rms linear
density contrast at mass M, or Lagrangian radius
qM, with 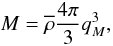 (9)and
(9)and 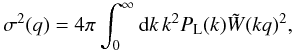 (10)where
(10)where
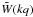 is the Fourier transform of
the top-hat of radius q, defined as
is the Fourier transform of
the top-hat of radius q, defined as 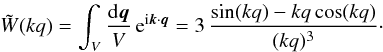 (11)We use the scaling
function f(ν) from Valageas (2009) with the threshold
δL ∗ associated with halos defined by a
nonlinear density contrast of 200. In Eq. (7)
(11)We use the scaling
function f(ν) from Valageas (2009) with the threshold
δL ∗ associated with halos defined by a
nonlinear density contrast of 200. In Eq. (7) 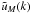 is the Fourier transform of
the density profile ρM(x) of
halos of mass M,
is the Fourier transform of
the density profile ρM(x) of
halos of mass M, 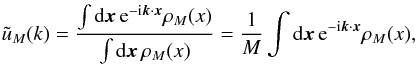 (12)whereas
(12)whereas
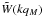 was defined in Eq. (11). We use the usual “NFW” halo profile
(Navarro et al. 1997) with the mass-concentration
relation from Valageas & Nishimichi
(2011a). The counterterm
was defined in Eq. (11). We use the usual “NFW” halo profile
(Navarro et al. 1997) with the mass-concentration
relation from Valageas & Nishimichi
(2011a). The counterterm 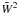 in Eq. (7) ensures that the 1-halo contribution decays
as P1H(k) ∝ k2 at
low k, so that the total power (4) goes to the linear power for CDM cosmologies. This follows from the
conservation of matter and the fact that halo formation corresponds to small-scale
redistribution of matter (Peebles 1974). In fact,
taking also momentum conservation into account would yield an even steeper
k4 tail (Peebles
1974) but the form (7) is sufficient
for practical purposes.
in Eq. (7) ensures that the 1-halo contribution decays
as P1H(k) ∝ k2 at
low k, so that the total power (4) goes to the linear power for CDM cosmologies. This follows from the
conservation of matter and the fact that halo formation corresponds to small-scale
redistribution of matter (Peebles 1974). In fact,
taking also momentum conservation into account would yield an even steeper
k4 tail (Peebles
1974) but the form (7) is sufficient
for practical purposes.
Thus, this framework ensures that the power spectrum (4) is consistent with perturbation theory (up to the order of truncation of the resummation scheme) while going smoothly to the 1-halo power at high k. A more detailed derivation of Eqs. (5) and (7) is given in Valageas & Nishimichi (2011a), through a Lagrangian point of view.
As described in Valageas & Nishimichi
(2011b), the 3D matter bispectrum is obtained in a similar fashion as the sum of
3-halo, 2-halo and 1-halo terms, 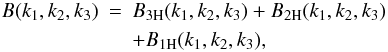 (13)with
(13)with
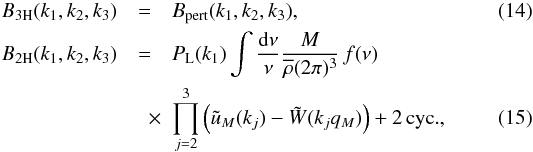 where
“2 cyc.” stands for two terms obtained by circular permutations over
{ k1,k2,k3 } ,
and
where
“2 cyc.” stands for two terms obtained by circular permutations over
{ k1,k2,k3 } ,
and ![\begin{eqnarray} B_{1\rm H}(k_1,k_2,k_3) & = & \int \frac{\dd\nu}{\nu} \, f(\nu) \, \left( \frac{M}{\rhob(2\pi)^3} \right)^{\!2} \nonumber \\[-2mm] \label{B-1H} && \times \prod_{j=1}^3 \left( \tu_M(k_j) - \tW(k_jq_M) \right) . \end{eqnarray}](/articles/aa/full_html/2012/05/aa18549-11/aa18549-11-eq39.png) (16)Again,
the counterterms
(16)Again,
the counterterms 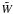 in Eqs. (15) and (16) ensure that the 2-halo and 1-halo
contributions decay on large scales so that the bispectrum goes to the perturbative
prediction Bpert. However, as found in Valageas & Nishimichi (2011b) and contrary to the situation
encountered for the power spectrum, the standard one-loop perturbation theory prediction
for Bpert is well-behaved at high k (i.e. it
is significantly smaller than the 1-halo contribution) and it is more accurate than two
alternative resummations that have been investigated. Therefore, we simply use the
standard one-loop perturbation theory prediction for Bpert.
in Eqs. (15) and (16) ensure that the 2-halo and 1-halo
contributions decay on large scales so that the bispectrum goes to the perturbative
prediction Bpert. However, as found in Valageas & Nishimichi (2011b) and contrary to the situation
encountered for the power spectrum, the standard one-loop perturbation theory prediction
for Bpert is well-behaved at high k (i.e. it
is significantly smaller than the 1-halo contribution) and it is more accurate than two
alternative resummations that have been investigated. Therefore, we simply use the
standard one-loop perturbation theory prediction for Bpert.
While Eq. (13) yields a reasonably good
match to numerical simulations (~10%) over all scales for the bispectrum, Eq. (4) significantly underestimates the power
spectrum on the transition scales (by ~20%) even though it gives a good accuracy on
larger scales (~1%) and smaller scales (~10%). In Valageas & Nishimichi (2011b) we devised a simple geometrical
modification to Eq. (4),
Ptang(k), such that 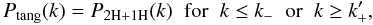 (17)and
(17)and ![\begin{equation} \log\left[ \frac{P_{\rm tang}(k)}{P_{\rm tang}(k_-)}\right] = \frac{\log(k/k_-)}{\log(k_+'/k_-)} \log\left[\frac{P_{\rm tang}(k_+')}{P_{\rm tang}(k_-)}\right] \label{P-tang-2} \end{equation}](/articles/aa/full_html/2012/05/aa18549-11/aa18549-11-eq47.png) (18)for
(18)for
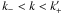 . In other
words, Ptang is identical to
P2H + 1H of Eq. (5) outside of the transition range
. In other
words, Ptang is identical to
P2H + 1H of Eq. (5) outside of the transition range ![\hbox{$[k_-,k_+']$}](/articles/aa/full_html/2012/05/aa18549-11/aa18549-11-eq51.png) , and we interpolate by a
straight line in the plane { log k,log P } over the
interval
, and we interpolate by a
straight line in the plane { log k,log P } over the
interval ![\hbox{$[k_-,k_+']$}](/articles/aa/full_html/2012/05/aa18549-11/aa18549-11-eq51.png) . This partly cures the
underestimate of the power spectrum in this range, while keeping the perturbative and
1-halo behaviors on large and small scales. As explained in Valageas & Nishimichi (2011b), the wavenumbers
k− and
. This partly cures the
underestimate of the power spectrum in this range, while keeping the perturbative and
1-halo behaviors on large and small scales. As explained in Valageas & Nishimichi (2011b), the wavenumbers
k− and 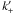 are
determined by the constraint that the reduced equilateral bispectrum,
Qeq(k) = B(k,k,k)/ [3P(k)2] ,
is monotonically increasing. Indeed, it happens that Eq. (4) underestimates the actual power spectrum on transition scales, which
leads to a spurious peak for Qeq(k). Then,
from the shape of this naive prediction for
Qeq(k) we automatically detect the range
are
determined by the constraint that the reduced equilateral bispectrum,
Qeq(k) = B(k,k,k)/ [3P(k)2] ,
is monotonically increasing. Indeed, it happens that Eq. (4) underestimates the actual power spectrum on transition scales, which
leads to a spurious peak for Qeq(k). Then,
from the shape of this naive prediction for
Qeq(k) we automatically detect the range
![\hbox{$[k_-,k_+']$}](/articles/aa/full_html/2012/05/aa18549-11/aa18549-11-eq51.png) where the model is not
sufficienly accurate (because higher-order perturbative contributions come into play or
the decomposition over 2-halo and 1-halo terms is too simple to accurately describe
regions such as outer shells and filamentary branches of collapsing halos that have not
yet relaxed). This typically gives
k− = 0.4 h Mpc-1 and
where the model is not
sufficienly accurate (because higher-order perturbative contributions come into play or
the decomposition over 2-halo and 1-halo terms is too simple to accurately describe
regions such as outer shells and filamentary branches of collapsing halos that have not
yet relaxed). This typically gives
k− = 0.4 h Mpc-1 and
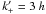 Mpc-1 at
z = 1. The main point here is that the range
Mpc-1 at
z = 1. The main point here is that the range
![\hbox{$[k_-,k_+']$}](/articles/aa/full_html/2012/05/aa18549-11/aa18549-11-eq51.png) is automatically determined
from the shape of P2H + 1H(k) and
B(k,k,k), and it evolves with redshift and with the
initial power. We refer the reader to Valageas &
Nishimichi (2011b) for further details.
is automatically determined
from the shape of P2H + 1H(k) and
B(k,k,k), and it evolves with redshift and with the
initial power. We refer the reader to Valageas &
Nishimichi (2011b) for further details.
Thus, Eqs. (13)–(16) and (17), (18) define the analytic model that we investigate in this paper for the 3D matter bispectrum and power spectrum.
2.2. 2D weak-lensing power spectrum and bispectrum
Using Born’s approximation, the weak-lensing convergence
κ(θ) can be written as the integral of
the density contrast along the line of sight (Bartelmann
& Schneider 2001; Munshi et al.
2008), 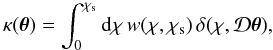 (19)where
χ and
(19)where
χ and 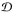 are the radial and angular comoving distances,
are the radial and angular comoving distances, 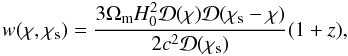 (20)and
zs is the redshift of the source (in this article we only
consider the case where all sources are located at a single redshift, to simplify the
comparisons with numerical simulations and the dependence on the source redshift). Then,
using a flat-sky approximation, which is valid for small angles below a few degrees (Valageas et al. 2011), we define its 2D Fourier
transform through
(20)and
zs is the redshift of the source (in this article we only
consider the case where all sources are located at a single redshift, to simplify the
comparisons with numerical simulations and the dependence on the source redshift). Then,
using a flat-sky approximation, which is valid for small angles below a few degrees (Valageas et al. 2011), we define its 2D Fourier
transform through 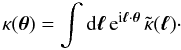 (21)As in 3D, we define the
2D convergence power spectrum and bispectrum as
(21)As in 3D, we define the
2D convergence power spectrum and bispectrum as 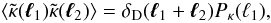 (22)and
(22)and 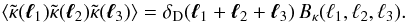 (23)From Eq. (19) one obtains at once, using Limber’s
approximation (Limber 1953; Kaiser 1992; Bartelmann &
Schneider 2001; Munshi et al. 2008),
(23)From Eq. (19) one obtains at once, using Limber’s
approximation (Limber 1953; Kaiser 1992; Bartelmann &
Schneider 2001; Munshi et al. 2008),
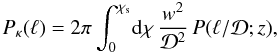 (24)
(24)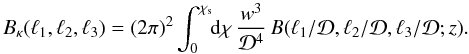 (25)This provides the
weak-lensing convergence power spectrum and bispectrum from our model described in
Sect. 2.1 for the 3D matter density power spectrum
and bispectrum, through a simple integration over the radial coordinate up to the source
plane.
(25)This provides the
weak-lensing convergence power spectrum and bispectrum from our model described in
Sect. 2.1 for the 3D matter density power spectrum
and bispectrum, through a simple integration over the radial coordinate up to the source
plane.
3. Numerical simulations
To obtain accurate predictions of the convergence power spectrum and bispectrum we must perform the ray-tracing simulations through large-volume, high-resolution N-body simulations of structure formation (Jain et al. 2000; Hamana & Mellier 2001; Hilbert et al. 2009; Sato et al. 2009). To perform the N-body simulations, we use a modified version of the Gadget-2 code (Springel 2005). The ray-tracing simulations are constructed from 2 × 200 realizations of N-body simulations with cubic 240 and 480 h-1 Mpc on a side, respectively. We employ 2563 particles for each simulation. For our fiducial cosmology, we adopt the standard ΛCDM cosmology with matter fraction Ωm = 0.238, baryon fraction Ωb = 0.0416, dark energy fraction Ωde = 0.762 with the equation of state parameters w0 = −1 and wa = 0, spectral index ns = 0.958, normalization As = 2.35 × 10-9, and Hubble parameter h = 0.732, which are consistent with the WMAP 3-year results (Spergel et al. 2007). This fiducial cosmology gives for the variance of the density fluctuations in a sphere of radius 8 h-1 Mpc the normalization σ8 = 0.759. We consider source redshifts at either zs = 0.6, 1.0, or 1.5. Using ray-tracing simulations we generate 1000 realizations of 5° × 5° convergence maps for each source redshift.
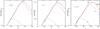 |
Fig. 1 Convergence power spectrum for sources at redshifts zs = 0.6,1, and 1.5. The points are the results from numerical simulations with 3-σ error bars. The low black dashed line “L” is the linear power, the middle blue dot-dashed line “S” is the result from the “halo-fit” of Smith et al. (2003), and the upper red solid line “comb.” is the result from our model, which combines 1-loop perturbation theory with a halo model. The vertical arrow close to the peak shows the scale up to which the simulation result is valid within 5%. |
In addition to the fiducial cosmology case, we performed ray-tracing simulations for several slightly different cosmologies. We vary each of the following cosmological parameters: As, ns, the cold dark matter density Ωch2, Ωde, and w0 by ± 10%, respectively. In varying the parameters, we keep the flatness of the universe and the physical baryon density Ωbh2 to be unchanged. Therefore the three parameters, h, Ωm, and Ωb, are varied simultaneously. For each of these 10 different cosmologies, we obtain 40 realizations of convergence fields for each of the three source redshifts. Details of the methods used for the ray-tracing simulations can be found in Sato et al. (2009). All convergence maps used in this paper are the same as those used in Seo et al. (2012), but for varied cosmologies we use three orthogonal projection axes instead of using only one projection axis to increase the independence.
In Sects. 4–6, we use the maps for the fiducial cosmology while in Sect. 7 we use those for the varied cosmologies to investigate the robustness of our model. In Sect. 7 we show the results for six cases, varying ns, Ωch2, and w0 by ± 10%, which we denote as ns ± , Ωch2 ± , and w0 ± . The exact values for these cosmological parameters are listed in Table A.1 in Appendix A.
The binned convergence power spectrum and bispectrum are measured as follows. We first
apply Fast Fourier Transformation to each of the convergence fields to obtain
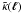 . We then
bin the data into logarithmically-equal bins in ℓ, whose widths are set as
Δlnℓ = 0.3 for the power spectrum, and
Δlnℓ = ln2/2 ≈ 0.35 for the bispectrum, respectively.
The power spectrum and the bispectrum are obtained by simply averaging the products of
modes:
. We then
bin the data into logarithmically-equal bins in ℓ, whose widths are set as
Δlnℓ = 0.3 for the power spectrum, and
Δlnℓ = ln2/2 ≈ 0.35 for the bispectrum, respectively.
The power spectrum and the bispectrum are obtained by simply averaging the products of
modes: ![\begin{eqnarray} \label{Pkappa-Est} \hat{\Pkappa}(\ell)&=&\frac{1}{N_{\ell}}\sum_{|\vell|\in\ell}|\tilde{\kappa}(\vell)|^2, \\ \hat{\Bkappa}(\ell_1,\ell_2,\ell_3)&=&\frac{1}{N_{\ell_1,\ell_2,\ell_3}}\sum_{|\vell_i|\in\ell_i}{\rm Re}\left[\tilde{\kappa}(\vell_1)\tilde{\kappa}(\vell_2)\tilde{\kappa}(\vell_3)\right], \end{eqnarray}](/articles/aa/full_html/2012/05/aa18549-11/aa18549-11-eq111.png) where
Re[...] denotes the real part of a complex number, and the summation runs over modes
ℓ
(ℓi,
i = 1,2,3) which fall into
bin ℓ (ℓi) for the power
(bi-) spectrum. In the above, Nℓ is the number
of modes taken for the summation and is given by
Nℓ ≈ AshellΩs/(2π)2
where Ashell is the area of two-dimensional shell around the
bin ℓ and can be given as
Ashell ≈ 2πℓΔℓ + π(Δℓ)2,
and Ωs is the survey area. Similarly, the factor
Nℓ1,ℓ2,ℓ3,
which appears in the estimator of the bispectrum, denotes the number of triangles
in ℓ space. We then average the measured spectra over 1000 random
realizations to obtain our final estimates of
Pκ and
Bκ. The statistical uncertainty of our
estimates are also estimated from the variance of
where
Re[...] denotes the real part of a complex number, and the summation runs over modes
ℓ
(ℓi,
i = 1,2,3) which fall into
bin ℓ (ℓi) for the power
(bi-) spectrum. In the above, Nℓ is the number
of modes taken for the summation and is given by
Nℓ ≈ AshellΩs/(2π)2
where Ashell is the area of two-dimensional shell around the
bin ℓ and can be given as
Ashell ≈ 2πℓΔℓ + π(Δℓ)2,
and Ωs is the survey area. Similarly, the factor
Nℓ1,ℓ2,ℓ3,
which appears in the estimator of the bispectrum, denotes the number of triangles
in ℓ space. We then average the measured spectra over 1000 random
realizations to obtain our final estimates of
Pκ and
Bκ. The statistical uncertainty of our
estimates are also estimated from the variance of 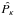 and
and 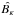 over 1000 realizations. We plot the 3-σ uncertainty as error bars in what
follows.
over 1000 realizations. We plot the 3-σ uncertainty as error bars in what
follows.
4. Convergence power spectrum
We now compare our results for the weak-lensing power spectrum with numerical simulations. In addition, we also consider the predictions obtained from the popular “halo-fit” fitting function for the 3D density power spectrum given in Smith et al. (2003), to estimate the gains that can be reached by using a somewhat more systematic approach.
We show our results for the convergence power spectrum, Pκ(ℓ), in Fig. 1. For reference we also plot the linear power and we can check that both simulations and analytical models recover the linear regime on large scales. The numerical error bars increase on large scales because of the finite size of the simulation box. On small scales the numerical error is dominated by systematic effects, due to the finite resolution, that lead to an underestimate of the small-scale power (as clearly shown by the sharp decline at very high ℓ). For each source redshift we estimated the scale ℓ up to which the simulations have an accuracy of better than 5% by comparing with higher-resolution simulations (with 5123 particles instead of 2563). This scale is shown by the vertical arrow in Fig. 1 and we can check that our model indeed agrees with the numerical simulations up to this multipole.
We recover the well-known fact that on scales that are of interest for cosmological analysis of weak gravitational lensing, 102 < ℓ < 104, nonlinear terms significantly contribute to or dominate the power spectrum (Bartelmann & Schneider 2001; Munshi et al. 2008). The overall shapes of the power spectra obtained from our model, described in Sect. 2, and from the fitting formula from Smith et al. (2003), are very similar. This is expected since the latter “halo-fit” also goes to the linear power on large scales and it is based on numerical simulations for its small-scale behavior, while the halo model that underlies our approach on small scales also agrees with similar simulations (in particular it involves the “NFW” profile and a mass-concentration relation that are derived from simulations). These similar shapes also confirm that the sharp falloff of the power at high ℓ found in the ray-tracing simulations is not physical but due to the finite resolution.
The improvements that can be expected from our approach, as compared with a simpler fitting formula to measures of the 3D power, are that i) on large scales we are consistent with perturbation theory up to one-loop order, and ii) on small scales we directly use a physical halo model (instead of using some formula for the power spectrum with free exponents that are fitted to a set of simulations).
On large scales the error bars of our ray-tracing simulations (and their lack of large-scale power) are too large to clearly see the benefit of the one-loop perturbative terms at low zs. However, the higher accuracy due to these higher-order perturbative contributions can be seen at zs = 1 and zs = 1.5, as will be shown more clearly in Sect. 6.1 below. (The benefit of these terms has already been shown in studies of the 3D matter density power spectrum, especially for the accurate prediction of the baryon acoustic oscillations, e.g. Jeong & Komatsu 2006; Nishimichi et al. 2007, 2009; Crocce & Scoccimarro 2008; Matsubara 2008; Taruya et al. 2009; Sato & Matsubara 2011; Valageas & Nishimichi 2011a,b). In the weak-lensing context, this higher accuracy could also be useful for the analysis of future observations such as the Euclid mission (Refregier et al. 2010).
On small scales, although the agreement of our model with the simulations is not perfect we can see a clear improvement as compared with the fitting formula from Smith et al. (2003). This is not surprising since the latter was derived from a set of older numerical simulations with somewhat different cosmological parameters than the ones we consider in this paper. The underestimate of the power on small scales by this “halo-fit” formula, by about 30% around the peak for zs = 1, was already noticed in Hilbert et al. (2009). The comparison of our model with the 3D power spectrum in Valageas & Nishimichi (2011a,b) was also based on simulations with different cosmological parameters, but through the explicit expression (7) we automatically take into account the dependence on cosmology of the linear growth factor D + (t) of the density fluctuations and of the linear threshold δL∗ associated with the nonlinear density contrast of 200 (Valageas 2009). We mostly neglect the dependence on cosmology of the halo profiles and of their mass-concentration relation. However, even though virialization processes do not reach complete relaxation, that is, a violent relaxation “à la Lynden-Bell” (Lynden-Bell 1967) is not complete in this cosmological context and does not allow the halos to reach a statistical equilibrium that is fully independent of the initial conditions, internal halo properties are almost universal and independent of cosmological parameters up to a good accuracy (for realistic CDM scenarios). Similarly, deviations of the halo mass function from “universality” have been detected but are rather weak (Tinker et al. 2008; More et al. 2011; Bhattacharya et al. 2011). This is especially true for our purpose as we integrate over the full halo mass function (which is normalized to unity) and we take into account the dependence on cosmology of its large-mass cutoff. This explains why our model is able to reach a good agreement with the numerical simulations.
On the intermediate scales, which are sensitive to the interpolation (18), we also obtain a satisfactory match to the numerical simulations. Within this range, around ℓ ~ 300, the “halo-fit” prediction happens to provide a similar, or in a few cases slightly better, agreement with the simulations. These transition scales, where both the one-loop perturbative contribution and the 1-halo term are subdominant as shown in Fig. 4 below, are governed by the interpolation (18). This means that this interpolation is not fully satisfactory and that there remains room for improvement. However, to keep our model as simple as possible and to remain consistent with our previous 3D studies we do not investigate here alternative prescriptions.
We shall check in Sect. 7 below that the overall agreement found in Fig. 1 remains valid as we change the values of the cosmological parameters.
 |
Fig. 2 Convergence bispectrum for sources at redshifts zs = 0.6,1, and 1.5, for equilateral triangles. The points are the results from numerical simulations with 3-σ error bars. The low black dashed line “treeL” is the tree-order bispectrum (28), the green dotted line “treeNL” is the tree-order formula (30), where we use the nonlinear power from the “halo-fit” of Smith et al. (2003), the two yellow dashed lines “F2,NL” (31) include in addition a fitting formula for the kernel F2,NL from Scoccimarro & Couchman (2001) and use either PS(k) (lower curve) or Ptang(k) (upper curve) for the 3D power spectrum, the upper blue dot-dashed line “scal.” is the phenomenological scale transformation (32) from Pan et al. (2007), and the red solid line “comb.” is our combined model (13)–(16). The vertical arrows are at the same scale as in Fig. 1. |
5. Convergence bispectrum
We now compare our results for the weak-lensing bispectrum with numerical simulations. In addition, we also consider the predictions obtained from the following four simple models, which have been used in some previous works.
We first compute the results obtained from the lowest-order (“tree-order”) prediction from
standard perturbation theory for the 3D bispectrum (Bernardeau et al. 2002), 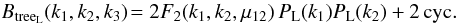 (28)where
μ12 = (k1·k2)/(k1k2)
and
(28)where
μ12 = (k1·k2)/(k1k2)
and 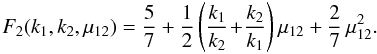 (29)Second, we consider
a “tree-nonlinear” approximation where in Eq. (28) we replace the linear 3D power
PL(k) by the nonlinear power
PS(k) from Smith et al. (2003),
(29)Second, we consider
a “tree-nonlinear” approximation where in Eq. (28) we replace the linear 3D power
PL(k) by the nonlinear power
PS(k) from Smith et al. (2003), 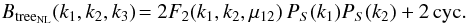 (30)Third, we
consider the fitting formula from Scoccimarro &
Couchman (2001),
(30)Third, we
consider the fitting formula from Scoccimarro &
Couchman (2001), 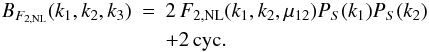 (31)where
the kernel F2,NL is an effective kernel that
interpolates from the large-scale perturbative result (29) to a small-scale ansatz where the angular dependence on
μ12 vanishes. Here we shall use the nonlinear power spectrum
PS(k) from Smith et al. (2003) as well as the nonlinear power
spectrum Ptang(k) of our model, Eqs. (17), (18).
(31)where
the kernel F2,NL is an effective kernel that
interpolates from the large-scale perturbative result (29) to a small-scale ansatz where the angular dependence on
μ12 vanishes. Here we shall use the nonlinear power spectrum
PS(k) from Smith et al. (2003) as well as the nonlinear power
spectrum Ptang(k) of our model, Eqs. (17), (18).
Four, we consider the scale transformation studied in Pan
et al. (2007), following the spirit of the scale transformation introduced in Hamilton et al. (1991) for the two-point correlation
function and next in Peacock & Dodds (1996)
for the power spectrum, 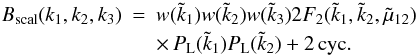 (32)with
for i = 1,2,3,
(32)with
for i = 1,2,3,
![\begin{equation} \tk_i = [1+\Delta^2_S(k_i)]^{-1/3} k_i , \;\;\; w(\tk_i)= \sqrt{P_S(\tk_i)/P_{\rm L}(\tk_i)} . \end{equation}](/articles/aa/full_html/2012/05/aa18549-11/aa18549-11-eq148.png) (33)
(33)
5.1. Equilateral triangles
We first show in Fig. 2 our results for the bispectrum for equilateral configurations. By construction, all curves must converge to the lowest-order perturbative prediction (28) on large scales. We can check that this is indeed the case. As for the lensing power spectrum our simulations are too small to reach this “tree-order” regime but they are consistent with this asymptotic behavior.
Again, we recover the well-known fact that on the scales of interest lowest-order perturbation theory is not sufficient to predict weak-lensing statistics and we must take into account higher-order terms or nonperturbative contributions. Using the nonlinear power within the “tree-level” expression, as in Eq. (30), significantly increases the convergence bispectrum and improves the overall shape but it remains far from the simulation results and cannot be used for practical purposes. Adding a modification to the kernel F2, as in Eq. (31) using the fitting formula from Scoccimarro & Couchman (2001), further improves the predictions and it provides a good match to the simulations on weakly nonlinear scales. However, this simple fitting procedure underestimates the power at high ℓ. This is partly related to the underestimate of the power spectrum on small scales by the “halo-fit” fitting formula of Smith et al. (2003). Indeed, we can see that using in Eq. (31) the nonlinear 3D power spectrum provided by our model, which provides a good match to simulations for both the 3D power (Valageas & Nishimichi 2011b) and the 2D convergence power spectrum (Fig. 1) increases the power at high ℓ. This improves the agreement with the simulations but there remains a significant discrepancy.
The scale transformation (32) fares better on weakly nonlinear scales (at least for this equilateral configuration) but it greatly overestimates the power at high ℓ. The same breakdown was already observed for the 3D bispectrum (Pan et al. 2007; Valageas & Nishimichi 2011b). The best agreement with the numerical simulations is provided by our model (13)–(16). In particular, it is interesting to note the good match on the transition scales, ℓ ~ 103, which a priori are the most difficult to reproduce since they are at the limit of validity of both perturbative approaches (which break down at shell crossing) and halo models (which assume virialized halos). A similarly good agreement was also observed for the 3D bispectrum in Valageas & Nishimichi (2011b).
At high ℓ we again predict more power than is measured in the simulations, but as for the lensing power spectrum this is at least partly due to the lack of small-scale power in the simulations because of the finite resolution. Thus, we again plot in Fig. 2 the vertical arrows that were plotted in Fig. 1. Since the bispectrum typically scales as the square of the power spectrum this should roughly correspond to an accuracy threshold of about 10% for the simulations. We can check that our model agrees with the numerical results up to this multipole.
5.2. Isosceles triangles
We now plot in Fig. 3 the convergence bispectrum for isosceles configurations, where ℓ1 = ℓ2. Instead of the angle ϑ12 between the two sides ℓ1 = ℓ2 we show the dependence on the length of either the two equal sides or of the third side. This avoids putting all “squeezed” triangles in a narrow region around ϑ12 = 0.
As for the equilateral configurations shown in Fig. 2, we can check that the “tree-order” bispectrum (28) is not the dominant contribution on these scales, inserting the nonlinear power spectrum as in (30) is not sufficient, and the scale transformation (32) breaks down too early on nonlinear scales. Thus, the only two reasonable models are the expression (31), which involves fitting formulas for both the nonlinear power spectrum and the kernel F2,NL, and our model (13)–(16).
 |
Fig. 3 Convergence bispectrum Bκ(ℓ1,ℓ2,ℓ3) for isosceles configurations, where ℓ1 = ℓ2. The first two rows show the dependence on the common side ℓ1 = ℓ2, at fixed ℓ3 (in the weakly nonlinear regime in the first row, and in the highly nonlinear regime in the second row), while the third row shows the dependence on the third side ℓ3 at fixed ℓ1 = ℓ2 (around the transition scales). The symbols are the same as in Fig. 2. |
In the first row, where ℓ3 ≃ 107 (the analysis uses the flat-sky approximation hence ℓ is not necessarily an integer), both curves (31) and (13) agree rather well with the numerical simulations, except that for extremely “squeezed” configurations, ℓ1 ≳ 100ℓ3, our model yields a downturn which underestimates the bispectrum whereas the fitting model (31) remains in good agreement with the numerical data. We shall come back to this point in Sect. 6.2.2 below, where we shall find out that this is probably due to an inaccuracy of the 2-halo contribution B2H. On the other hand, using the nonlinear power spectrum Ptang(k) in Eq. (31) increases the power on small scales, as in Fig. 2, which spoils the match to simulations for these extremely “squeezed” configurations.
In the second row, which is farther into the nonlinear regime, we find in agreement with the equilateral case of Fig. 2 that the fitting formula (31) underestimates the bispectrum whereas our model provides a reasonable match to the numerical simulations. More importantly, Eq. (31) does not reproduce the shape of the bispectrum as a function of ℓ1, since it does not capture the falloff that appears for ℓ1 ≳ 10ℓ3, and this is not cured by using a more accurate 3D power spectrum. In contrast, our model (13) correctly predicts this shape as well as the overall amplitude.
In the third row, which corresponds to transition scales in the mildly nonlinear regime, neither model shows a perfect match to the simulations but our prediction fares significantly better and still provides a reasonable agreement.
These results show that it is difficult to reproduce the bispectrum for a wide variety of configurations and scales by using a global ansatz such as (31). Approaches such as the one studied in this paper, which are built on explicit and physical ingredients, are better controlled and offer an easier route to systematic improvement. Indeed, by improving the accuracy of each ingredient (e.g., including higher orders of perturbation theory or more complex halo profiles) one should reach a higher accuracy for the final 3D and 2D statistics for any configuration and scale (although transition regimes may still prove difficult). Moreover, by splitting the problem into several elements it is easier to make progress by improving each contribution in turn.
6. Relative importance of the different contributions
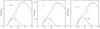 |
Fig. 4 Convergence power spectrum for sources at redshifts zs = 0.6,1, and 1.5. The points are the results from numerical simulations with 3-σ error bars. The low black dashed line “L” is the linear power, the middle black dot-dashed line “1-loop” is the result from the 2-halo contribution (5), where we use a perturbative resummation that is complete up to 1-loop order, the upper blue dashed line “1H” is the result from the 1-halo contribution (5), and the red solid line is the result of our model (17)–(18). |
We have seen in the previous section that our model, based on a combination of perturbation theories and halo models, provides a good match to numerical simulations. This means that such an approach can be useful to obtain predictions for weak-lensing statistics for a variety of cosmologies, which is an important goal for observational and practical purposes.
A second advantage of our approach, as compared with simple fitting formulas (or direct simulations), is that we can easily evaluate and compare the different contributions that eventually add up to the signal that can be measured in weak-lensing surveys. Thus, we can distinguish the various perturbative terms as well as the nonperturbative contributions associated with 1-halo or 2-halo terms.
This is useful to estimate the accuracy that can be aimed at in weak-lensing statistics, as a function of scales, since different contributions suffer from different theoretical uncertainties. For instance, the perturbative contributions are obtained in a systematic and rigorous manner for any cosmology, and the accuracy is only limited by the order of the perturbative expansion, whereas “halo contributions”, which depend on the halo profiles and mass functions, are phenomenological ingredients that involve at some stage input from numerical simulations and do not offer systematic routes to arbitrarily high accuracy.
This also allows us to understand which aspects of the dynamics are probed by weak-lensing statistics, so that depending on one’s goals (e.g., to constrain cosmological parameters or to estimate halo properties themselves) one can focus on the appropriate range of the weak-lensing signals.
6.1. Convergence power spectrum
We plot our results for the convergence power spectrum in Fig. 4, showing the underlying 2-halo and 1-halo contributions in addition to the full model curve that was already shown in Fig. 1. We can see that including the 1-loop perturbative term yields slightly more power on quasi-linear scales and helps to obtain a good match to the simulations. At high ℓ the 2-halo contribution goes back close to the linear power thanks to the partial resummation of higher orders. As recalled in Sect. 2.1, this is a useful improvement over the standard 1-loop perturbation theory because it ensures that at high k for the 3D power, and at high ℓ for the lensing power, the 2-halo term does not give significant contributions. At high ℓ around its peak, the lensing power becomes dominated by the 1-halo term but as for the 3D power there remains a wide intermediate range, about a decade over ℓ. In our model, the 3D power on these transition scales is described by the interpolation (18), which was seen in Valageas & Nishimichi (2011b) to provide a good match to numerical simulations. As expected, Fig. 4 shows that this also provides a good interpolation for the 2D convergence power spectrum. It may be possible to reduce this range on its low-ℓ side by including higher orders of perturbation theory in the 2-halo term, but it is likely that the high-ℓ side receives significant contributions from nonperturbative terms, associated with shell crossing (Valageas 2011), that are not well described either by a simple 1-halo term (e.g., associated with dense filaments or infalling regions close to the virial radius). In any case, Fig. 4 clearly shows how the convergence power spectrum depends on large-scale perturbative density fluctuations or on small scale halo properties, as the multipole ℓ varies.
Future surveys plan to measure the weak lensing power spectrum on these scales, 50 < ℓ < 7000, with an accuracy of about 1% for LSST (LSST Science Collaborations et al. 2009) or even slightly better for Euclid (Laureijs et al. 2011). Our numerical simulations do not allow us to check our model down to this accuracy. However, the comparison between our predictions and the “halo-fit” in Fig. 1 already shows that this is beyond the accuracy of current models and is a very challenging theoretical goal. Our model already provides an accuracy of about 1% on perturbative scales and 10% on the transition and highly nonlinear scales (this is the typical accuracy checked on 3D simulations in Valageas & Nishimichi 2011b). Figure 4 explicitly shows that for 100 < ℓ < 1000 the one-loop correction to the linear power is required to reach this accuracy. Unfortunately, for ℓ > 200 this is not sufficient since higher-order terms or non-perturbative corrections cannot be neglected and the power spectrum is sensitive to the transition scales, described by the interpolation (18). This suggests that for ℓ > 500 a percent accuracy is probably beyond the reach of systematic perturbative approaches, which cannot go beyond shell crossing (Valageas 2011), and requires dedicated numerical simulations.
6.2. Convergence bispectrum
We now study the contributions from various terms to the lensing bispectrum. From Eq. (13) we now have three contributions, associated with the 3-halo, 2-halo and 1-halo terms, the 3-halo contribution being identified with the perturbative contribution.
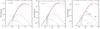 |
Fig. 5 Convergence bispectrum for sources at redshifts zs = 0.6,1, and 1.5, for equilateral triangles. The points are the results from numerical simulations with 3-σ error bars. The low black dashed line “L” is the tree-order bispectrum (28), the “1-loop” dot-dashed black line is the prediction of 1-loop standard perturbation theory, which is identified with our 3-halo term (14), the green dotted line “2H” is the 2-halo contribution (15) and the upper blue dashed line “1H” is the 1-halo contribution (16). |
6.2.1. Equilateral triangles
We plot our results for the convergence bispectrum for equilateral configurations in Fig. 5, showing the various contributions in addition to the full model curve that was already shown in Fig. 2. As recalled in Sect. 2.1, the 3-halo term is identified with the perturbative prediction and in this paper we use standard perturbation theory at one-loop order for this contribution. As for the 3D bispectrum (Valageas & Nishimichi 2011b), and contrary to the power spectrum, this gives a contribution that becomes negligible on small scales, so that it is not necessary to use a resummation scheme or to add a nonperturbative cutoff to ensure a good high-ℓ behavior. On the other hand, contrary to the power spectrum we can see that going to 1-loop order now makes a strong improvement over the tree-order result. This feature was already noticed for the 3D density field (Sefusatti et al. 2010; Valageas & Nishimichi 2011b). In fact, combining this 1-loop perturbative contribution with the 2-halo and 1-halo terms is sufficient to obtain a good match to the simulations, from the quasilinear to the highly nonlinear scales. This suggests that higher orders of perturbation theory do not significantly contribute to the bispectrum and that we already have a reasonably successful model. For these equilateral triangles the 2-halo term is also subdominant on all scales (by a factor ~10 at least). This is a nice property since being a mixed term, which involves both large-scale halo correlations and internal halo structures, it may be more difficult to predict than the 3-halo term (derived from systematic perturbation theories) and the 1-halo term (that only depends on internal halo profiles and mass function). These various features were also observed for the 3D bispectrum (Valageas & Nishimichi 2011b), from which they directly derive through the relation (25).
Again, our numerical simulations do not allow us to reach the percent accuracy aimed at by future surveys (LSST Science Collaborations et al. 2009; Laureijs et al. 2011), and Figs. 2 and 5 show that this is a challenging goal. As noticed above, including 1-loop corrections is clearly important to reach this accuracy. A nice feature is that without introducing any interpolation on transition scales we already have a reasonably good model and that the 2-halo term contributes to about 1% or less on most scales. Then, our model already provides an accuracy of 10% (this is the typical accuracy checked on 3D simulations in Valageas & Nishimichi 2011b) on the scales shown in Fig. 5, and better at low ℓ in the perturbative regime. At high ℓ, ℓ > 104, including the effects of baryons on halo profiles (as compared with dark matter only N-body simulations) is probably necessary to reach percent accuracy, but this is beyond the scope of this paper.
6.2.2. Isosceles triangles
We turn to isosceles configurations in Fig. 6. As for the equilateral case plotted in Fig. 5, the upper row shows that on weakly nonlinear scales the 1-loop contribution makes a significant improvement over the tree-order prediction and allows us to obtain a good match to the numerical simulations. Moreover, we can see that our underestimate of the bispectrum for very “squeezed” triangles, at ℓ1 ≳ 100ℓ3 with ℓ3 ≃ 107, which was already noticed in Fig. 3, corresponds to a change of regime. Indeed, this downturn follows the 1-loop prediction and it occurs at a point where the 2-halo and 1-halo contributions become important. Then, this discrepancy may be understood as a difficulty of our simple model to reproduce the bispectrum in this corner of configuration space because the transition from the 3-halo perturbative regime to the 1-halo highly nonlinear regime is not sufficiently well described (e.g., simple spherical halo models cannot be expected to describe very well intermediate regions such as filaments and outer infalling regions of halos). Alternatively, it may happen that adding higher orders of perturbation theory to the 3-halo contribution improves the agreement with simulations for these isosceles triangles, without contributing much to the equilateral triangles where the agreement is already rather good. Another possibility is that our 2-halo term is not very accurate and gives too small a contribution for these isosceles configurations. This would be a natural and simple cure, because as seen in Fig. 5 this 2-halo term is negligible for equilateral cases. Therefore, it should be possible to “tune” the 2-halo term so as to match the isosceles simulation results of Fig. 6 without damaging the good agreement obtained for the equilateral case in Fig. 5. This would also be a more natural explanation than a problem in the 1-halo term, because the latter should be simpler to model (since by definition it only deals with inner regions of halos) and it provides successful results in regimes where it dominates the bispectrum, as shown by the second row in Fig. 6 and the high-ℓ part of Fig. 5.
 |
Fig. 6 Convergence bispectrum Bκ(ℓ1,ℓ2,ℓ3) for isosceles configurations, as in Fig. 3. The symbols are the same as in Fig. 5. In the first row we show the absolute value of the 1-halo contribution, which becomes negative at ℓ1 ~ 2500. |
Since the problem found in the high-ℓ1 part of the upper row of Fig. 6 corresponds to very “squeezed” triangles, ℓ1 ≳ 100ℓ3, hence to a limited region of the configuration space for the triplet { ℓ1,ℓ2,ℓ3 } , and our goal is to study simple and systematic models (i.e., that do not require fitting internal parameters for each new set of cosmological parameters), we do not investigate in this paper how to improve the model (e.g., through added complexity of the 2-halo term) to better describe this regime.
We can see in the second row, which is fully dominated by the 1-halo contribution, that the curved shape of the bispectrum does not arise from a change of regime and a switch from one contribution to the other as in the first row. This is a genuine effect associated with the behavior of the 1-halo term that is well described by our model. In contrast, as seen in Fig. 3, this shape was not well recovered by the ansatz (31). This shows the benefits of our approach that explicitly combines perturbation theory with a halo model, taking advantage of the good behavior of these two ingredients in the regimes where they dominate.
In the third row, which corresponds to transition scales, we can see a change of regime as the bispectrum is dominated by the 1-loop perturbative contribution at low ℓ3 and by the 1-halo contribution at high ℓ3. In contrast to the first row, the 2-halo contribution does not play a significant role and our model provides a good agreement with the simulations on all scales. This is a nice result since one could have expected transitions to be difficult to reproduce. This again suggests that the mismatch found for extremely “squeezed” triangles in the first row may be due to the 2-halo term. Moreover, this shows that a good modeling of the 3-halo (i.e. perturbative) and 1-halo terms is sufficient to provide accurate predictions for the lensing convergence bispectrum for a wide variety of configurations including some transition regimes. This agrees with the good agreement obtained for equilateral configurations, which are also dominated by the 3-halo and 1-halo terms as seen in Fig. 5.
7. Dependence on cosmology
In this section we investigate the robustness of our model as we vary the cosmological parameters. We consider six alternative cosmologies, where ns, Ωch2, and w0 are modified by ± 10% with respect to the fiducial cosmology used in the previous sections. The values of the associated cosmological parameters are given in Table A.1 in Appendix A. We compare the predictions of our model with numerical simulations for these six alternative cosmologies in Figs. 7 and 8, for the convergence power spectrum and bispectrum at zs = 1. To avoid overcrowding the figures we do not plot the error bars of the numerical simulations. Each pair ns, Ωch2, and w0 gives two curves that are roughly symmetric around the fiducial cosmology result, since we consider small deviations of ± 10%. The deviations are largest for the ns case, which changes the shape of the initial power spectrum as well as the normalization σ8. These six cases roughly cover the range that is allowed by current data and the ns case is already somewhat beyond the observational bounds (Komatsu et al. 2011). Thus, they provide a good check of the robustness of our model for realistic scenarios.
 |
Fig. 7 Convergence power spectrum for sources at redshift zs = 1, for the six cosmologies given in Table A.1. The points are the results from numerical simulations and the lines are the predictions of our model. |
We can see that the dependence of the convergence power spectrum on the cosmological parameters is well recovered by our model. The agreement is somewhat less accurate for the bispectrum, since as for the fiducial cosmology the theoretical predictions give more power on small scales than is measured in the simulations. However, we recover the general trend and obtain a reasonable match up to intermediate scales. We can see that the simulation results for the convergence bispectrum are scattered around the theoretical predictions on large scales because the number of realizations is not large enough to converge. (Here we only use 40 realizations, whereas for the fiducial cosmology we used 1000 realizations.) On small scales the effects of the finite resolution are larger than for the power spectrum and the range of wavenumbers where simulation results are reliable is clearly narrower in Fig. 8 than in Fig. 7 (we clearly see unphysical deviations at low and high ℓ). This explains why the agreement appears worse for the bispectrum as this is partly due to the larger numerical noise.
We obtain similar results for zs = 0.6 and zs = 1.5, as well as for other cosmologies where we vary As or Ωde by ± 10%. This shows that our model and, more generally, models based on combinations of perturbation theory and halo models provide a good modeling of the matter distribution and of weak gravitational lensing effects and capture their dependence on cosmology. In particular, Figs. 7 and 8 show that the accuracy of our model is sufficient to constrain ns, Ωch2, and w0 to better than 10%.
 |
Fig. 8 Convergence bispectrum for sources at redshift zs = 1, for the six cosmologies given in Table A.1. The points are the results from numerical simulations and the lines are the predictions of our model. |
8. Conclusion
The cosmological parameter values for fiducial and six alternative cosmologies.
In this article we have investigated the performance of current theoretical modeling of the 3D matter density distribution with respect to weak-lensing statistics, focusing on Fourier space statistics, specifically the convergence power spectrum and bispectrum. We find that for both quantities a model introduced in previous works (Valageas & Nishimichi 2011a,b) that combines 1-loop perturbation theory with a halo model fares better than some other recipes based on fitting formulae to numerical simulations or more phenomenological approaches. It yields a reasonable agreement with numerical simulations and provides a competitive approach, since it remains difficult and time-consuming to describe a range of scales that spans three orders of magnitude or more by ray-tracing simulations. Even though this particular model may still be improved, these results already show that building on systematic and physically motivated models of the 3D matter distribution is a promising route to predict both 3D and 2D (i.e. projected) statistics.
An advantage of this approach, as compared with numerical simulations or global fitting formulas, is that it provides a clear link between the observed weak-lensing quantities, such as the convergence power spectrum or bispectrum on a given range of multipoles ℓ, and the various ingredients that govern the underlying 3D matter density field. In particular, we can distinguish the scales associated with the perturbative regime from those that probe nonperturbative features described for instance by the 1-halo term. This is useful since the perturbative regime can be predicted by rigorous and systematic approaches (e.g., in this paper we use both standard perturbation theory and a peculiar resummation scheme, up to one-loop order), which offers a well-controlled constraint on the cosmological parameters. The nonperturbative regime relies on a more phenomenological approach, i.e. a halo model, so that the link to cosmological parameters is somewhat weaker. Indeed, the accuracy is lower (because there is no rigorous and systematic framework) and the model involves some intermediate parameters, such as halo profiles, that show a weak dependence on cosmology. Therefore, it can be useful to separate both regimes when deriving constraints on cosmology from observations. Moreover, the explicit link provided by such models allows one to use gravitational lensing effects to probe the halo properties themselves.
We find that going to one-loop order brings a more significant improvement, with respect to lowest-order perturbation theory, for the lensing bispectrum than for the power spectrum. Moreover, while for the bispectrum the combination of the 1-halo and 2-halo terms with the one-loop perturbative contribution (associated with the 3-halo term) provides a reasonable match to simulations, for the power spectrum there remains an intermediate regime that is not well described by the simplest combination. This suggests that higher orders of the perturbative expansion play a greater role for the power spectrum and should be taken into account, or that the matching between the 2-halo and 1-halo contributions need be improved. In our case, we used a simple geometric interpolation for the 3D power spectrum and we find that it also provides good results for the weak lensing power spectrum. These features agree with previous results for the 3D density power spectrum and bispectrum (Sefusatti et al. 2010; Valageas & Nishimichi 2011b).
As in 3D, the 2-halo term does not significantly contribute to the lensing bispectrum for equilateral configurations. It only plays a role for very “squeezed” configurations on weakly nonlinear scales, with a ratio of ~100 or more between the two long sides and the smallest side of the Fourier-space triangle. This is also the regime where we find a discrepancy between our predictions and the simulations. Since both the 3-halo and the 1-halo terms provide good agreement with the simulations for all other regimes, where they dominate, this suggests that this discrepancy arises from a lower accuracy of the 2-halo term. This is not really surprising since this contribution is a priori more intricate, because it combines internal halo properties with larger-scale correlations. Nevertheless, since this regime corresponds to extreme configurations it is not a very serious practical problem.
Overall, we find that our model provides a good agreement with the numerical simulations for a variety of cosmologies and gives a robust framework. It could still be improved in various manners. First, the accuracy of the perturbative contribution may be increased by including higher orders beyond one-loop or by using alternative resummation schemes. Second, the underlying halo model could be refined to include substructures (Sheth 2003; Giocoli et al. 2010), deviations from spherical profiles (Jing & Suto 2002; Smith et al. 2006), or the effect of baryons (Guillet et al. 2010). Next, the model could be generalized to non-Gaussian initial conditions, which should yield distinctive signatures in the bispectrum (Sefusatti et al. 2010). Another interesting generalization would be to include the effects of massive neutrinos. Indeed, it is still difficult to model the damping associated with neutrino free-streaming using numerical simulations and simple fitting formulae, and analytic or semi-analytic prescriptions could be useful (Lesgourgues et al. 2009; Saito et al. 2009; Bird et al. 2012).
In this first study we focused on Fourier-space statistics, the convergence power spectrum and bispectrum, from which other statistics such as real-space correlation functions can be derived. We shall present our results for such real-space statistics in a companion paper (Valageas et al. 2012).
Acknowledgments
M.S. and T.N. are supported by a Grant-in-Aid for the Japan Society for Promotion of Science (JSPS) fellows. This work is supported in part by the French “Programme National de Cosmologie et Galaxies” and the French-Japanese “Programme Hubert Curien/Sakura, projet 25727TL”, the JSPS Core-to-Core Program “International Research Network for Dark Energy”, a Grant-in-Aid for Scientific Research on Priority Areas No. 467 “Probing the Dark Energy through an Extremely Wide and Deep Survey with Subaru Telescope”, a Grant-in-Aid for Nagoya University Global COE Program, “Quest for Fundamental Principles in the Universe: from Particles to the Solar System and the Cosmos”, and World Premier International Research Center Initiative (WPI Initiative), MEXT, Japan. We acknowledge Kobayashi-Maskawa Institute for the Origin of Particles and the Universe, Nagoya University for providing computing resources. Numerical calculations for the present work have been in part carried out under the “Interdisciplinary Computational Science Program” in Center for Computational Sciences, University of Tsukuba, and also on Cray XT4 at Center for Computational Astrophysics, CfCA, of National Astronomical Observatory of Japan.
References
- Albrecht, A., Bernstein, G., Cahn, R., et al. 2006 [arXiv:astro-ph/0609591] [Google Scholar]
- Bartelmann, M., & Schneider, P. 2001, Phys. Rep., 340, 291 [NASA ADS] [CrossRef] [Google Scholar]
- Bernardeau, F., Colombi, S., Gaztañaga, E., & Scoccimarro, R. 2002, Phys. Rep., 367, 1 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
- Bhattacharya, S., Heitmann, K., White, M., et al. 2011, ApJ, 732, 122 [NASA ADS] [CrossRef] [Google Scholar]
- Bird, S., Viel, M., & Haehnelt, M. G. 2012, MNRAS, 420, 2551 [NASA ADS] [CrossRef] [Google Scholar]
- Cooray, A., & Hu, W. 2001, ApJ, 554, 56 [NASA ADS] [CrossRef] [Google Scholar]
- Cooray, A., & Sheth, R. 2002, Phys. Rep., 372, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Crocce, M., & Scoccimarro, R. 2008, Phys. Rev. D, 77, 023533 [NASA ADS] [CrossRef] [Google Scholar]
- Giocoli, C., Bartelmann, M., Sheth, R. K., & Cacciato, M. 2010, MNRAS, 408, 300 [NASA ADS] [CrossRef] [Google Scholar]
- Guillet, T., Teyssier, R., & Colombi, S. 2010, MNRAS, 405, 525 [NASA ADS] [Google Scholar]
- Hamana, T., & Mellier, Y. 2001, MNRAS, 327, 169 [NASA ADS] [CrossRef] [Google Scholar]
- Hamilton, A. J. S., Kumar, P., Lu, E., & Matthews, A. 1991, ApJ, 374, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Hikage, C., Takada, M., Hamana, T., & Spergel, D. 2011, MNRAS, 412, 65 [NASA ADS] [CrossRef] [Google Scholar]
- Hilbert, S., Hartlap, J., White, S. D. M., & Schneider, P. 2009, A&A, 499, 31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jain, B., Seljak, U., & White, S. 2000, ApJ, 530, 547 [NASA ADS] [CrossRef] [Google Scholar]
- Jeong, D., & Komatsu, E. 2006, ApJ, 651, 619 [NASA ADS] [CrossRef] [Google Scholar]
- Jing, Y. P., & Suto, Y. 2002, ApJ, 574, 538 [NASA ADS] [CrossRef] [Google Scholar]
- Kaiser, N. 1992, ApJ, 388, 272 [NASA ADS] [CrossRef] [Google Scholar]
- Komatsu, E., Smith, K. M., Dunkley, J., et al. 2011, ApJS, 192, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Laureijs, R., Amiaux, J., Arduini, S., et al. 2011 [arXiv:1110.3193L] [Google Scholar]
- Lesgourgues, J., Matarrese, S., Pietroni, M., & Riotto, A. 2009, J. Cosmol. Astropart. Phys., 6, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Limber, D. N. 1953, ApJ, 117, 134 [NASA ADS] [CrossRef] [Google Scholar]
- LSST Science Collaborations, Abell, P. A., Allison, J., et al. 2009 [arXiv:0912.0201] [Google Scholar]
- Lynden-Bell, D. 1967, MNRAS, 136, 101 [NASA ADS] [CrossRef] [Google Scholar]
- Matsubara, T. 2008, Phys. Rev. D, 77, 063530 [NASA ADS] [CrossRef] [Google Scholar]
- Miyazaki, S., Komiyama, Y., Nakaya, H., et al. 2006, Proc. SPIE, 6269, 9 [NASA ADS] [Google Scholar]
- More, S., Kravtsov, A. V., Dalal, N., & Gottlöber, S. 2011, ApJS, 195, 4 [NASA ADS] [CrossRef] [Google Scholar]
- Munshi, D., Valageas, P., van Waerbeke, L., & Heavens, A. 2008, Phys. Rep., 462, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Navarro, J. F., Frenk, C. S., & White, S. D. M. 1997, ApJ, 490, 493 [NASA ADS] [CrossRef] [Google Scholar]
- Nishimichi, T., Ohmuro, H., Nakamichi, M., et al. 2007, PASJ, 59, 1049 [NASA ADS] [Google Scholar]
- Nishimichi, T., Shirata, A., Taruya, A., et al. 2009, PASJ, 61, 321 [NASA ADS] [Google Scholar]
- Pan, J., Coles, P., & Szapudi, I. 2007, MNRAS, 382, 1460 [NASA ADS] [Google Scholar]
- Peacock, J. A., & Dodds, S. J. 1996, MNRAS, 280, L19 [NASA ADS] [CrossRef] [Google Scholar]
- Peebles, P. J. E. 1974, A&A, 32, 391 [NASA ADS] [Google Scholar]
- Press, W. H., & Schechter, P. 1974, ApJ, 187, 425 [NASA ADS] [CrossRef] [Google Scholar]
- Refregier, A., Amara, A., Kitching, T. D., et al. 2010 [arXiv:1001.0061] [Google Scholar]
- Saito, S., Takada, M., & Taruya, A. 2009, Phys. Rev. D, 80, 083528 [NASA ADS] [CrossRef] [Google Scholar]
- Sato, M., & Matsubara, T. 2011, Phys. Rev. D, 84, 043501 [NASA ADS] [CrossRef] [Google Scholar]
- Sato, M., Hamana, T., Takahashi, R., et al. 2009, ApJ, 701, 945 [NASA ADS] [CrossRef] [Google Scholar]
- Sato, M., Ichiki, K., & Takeuchi, T. T. 2010, Phys. Rev. Lett., 105, 251301 [NASA ADS] [CrossRef] [Google Scholar]
- Sato, M., Ichiki, K., & Takeuchi, T. T. 2011a, Phys. Rev. D, 83, 023501 [NASA ADS] [CrossRef] [Google Scholar]
- Sato, M., Takada, M., Hamana, T., & Matsubara, T. 2011b, ApJ, 734, 76 [NASA ADS] [CrossRef] [Google Scholar]
- Scoccimarro, R., & Couchman, H. M. P. 2001, MNRAS, 325, 1312 [NASA ADS] [CrossRef] [Google Scholar]
- Sefusatti, E., Crocce, M., & Desjacques, V. 2010, MNRAS, 406, 1014 [NASA ADS] [Google Scholar]
- Seo, H.-J., Sato, M., Takada, M., & Dodelson, S. 2012, ApJ, 748, 57 [NASA ADS] [CrossRef] [Google Scholar]
- Sheth, R. K. 2003, MNRAS, 345, 1200 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, R. E., Peacock, J. A., Jenkins, A., et al. 2003, MNRAS, 341, 1311 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, R. E., Watts, P. I. R., & Sheth, R. K. 2006, MNRAS, 365, 214 [NASA ADS] [CrossRef] [Google Scholar]
- Spergel, D. N., Bean, R., Doré, O., et al. 2007, ApJS, 170, 377 [NASA ADS] [CrossRef] [Google Scholar]
- Springel, V. 2005, MNRAS, 364, 1105 [NASA ADS] [CrossRef] [Google Scholar]
- Takada, M., & Jain, B. 2004, MNRAS, 348, 897 [NASA ADS] [CrossRef] [Google Scholar]
- Takada, M., & Jain, B. 2009, MNRAS, 395, 2065 [NASA ADS] [CrossRef] [Google Scholar]
- Taruya, A., Nishimichi, T., Saito, S., & Hiramatsu, T. 2009, Phys. Rev. D, 80, 123503 [NASA ADS] [CrossRef] [Google Scholar]
- Tinker, J., Kravtsov, A. V., Klypin, A., et al. 2008, ApJ, 688, 709 [NASA ADS] [CrossRef] [Google Scholar]
- Valageas, P. 2007, A&A, 465, 725 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Valageas, P. 2008, A&A, 484, 79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Valageas, P. 2009, A&A, 508, 93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Valageas, P. 2011, A&A, 526, A67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Valageas, P., & Nishimichi, T. 2011a, A&A, 527, A87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Valageas, P., & Nishimichi, T. 2011b, A&A, 532, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Valageas, P., Clerc, N., Pacaud, F., & Pierre, M. 2011, A&A, 536, A95 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Valageas, P., Sato, M., & Nishimichi, T. 2012, A&A, 541, A162 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Appendix A: Six alternative cosmologies
We give in Table A.1 the six alternative sets of
cosmological parameters that we consider in Sect. 7
to test the robustness of our model. The first line is our fiducial cosmology, used in
other sections, while lines two to seven give the cosmological parameters associated with
the six scenarios where ns,
Ωch2, and w0 are
modified by ± 10%. The parameters marked as “–” remain equal to the fiducial values.
Several parameters in Table A.1 may simultaneously
vary because we use the following set of independent parameters:
As, ns,
Ωch2,
Ωbh2, Ωde,
w0, and we assume the Universe is flat. For instance, if we
change Ωch2 keeping other parameters fixed,
h has to be varied from the following equation:
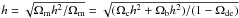 .
Then, Ωc and Ωb have to be varied as well, because of
Ωb = Ωbh2/h2
and the assumption of flat Universe. In the case of varying ns
and w0, σ8 is changed because
other parameters (including As) are fixed.
.
Then, Ωc and Ωb have to be varied as well, because of
Ωb = Ωbh2/h2
and the assumption of flat Universe. In the case of varying ns
and w0, σ8 is changed because
other parameters (including As) are fixed.
All Tables
The cosmological parameter values for fiducial and six alternative cosmologies.
All Figures
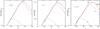 |
Fig. 1 Convergence power spectrum for sources at redshifts zs = 0.6,1, and 1.5. The points are the results from numerical simulations with 3-σ error bars. The low black dashed line “L” is the linear power, the middle blue dot-dashed line “S” is the result from the “halo-fit” of Smith et al. (2003), and the upper red solid line “comb.” is the result from our model, which combines 1-loop perturbation theory with a halo model. The vertical arrow close to the peak shows the scale up to which the simulation result is valid within 5%. |
| In the text | |
 |
Fig. 2 Convergence bispectrum for sources at redshifts zs = 0.6,1, and 1.5, for equilateral triangles. The points are the results from numerical simulations with 3-σ error bars. The low black dashed line “treeL” is the tree-order bispectrum (28), the green dotted line “treeNL” is the tree-order formula (30), where we use the nonlinear power from the “halo-fit” of Smith et al. (2003), the two yellow dashed lines “F2,NL” (31) include in addition a fitting formula for the kernel F2,NL from Scoccimarro & Couchman (2001) and use either PS(k) (lower curve) or Ptang(k) (upper curve) for the 3D power spectrum, the upper blue dot-dashed line “scal.” is the phenomenological scale transformation (32) from Pan et al. (2007), and the red solid line “comb.” is our combined model (13)–(16). The vertical arrows are at the same scale as in Fig. 1. |
| In the text | |
 |
Fig. 3 Convergence bispectrum Bκ(ℓ1,ℓ2,ℓ3) for isosceles configurations, where ℓ1 = ℓ2. The first two rows show the dependence on the common side ℓ1 = ℓ2, at fixed ℓ3 (in the weakly nonlinear regime in the first row, and in the highly nonlinear regime in the second row), while the third row shows the dependence on the third side ℓ3 at fixed ℓ1 = ℓ2 (around the transition scales). The symbols are the same as in Fig. 2. |
| In the text | |
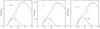 |
Fig. 4 Convergence power spectrum for sources at redshifts zs = 0.6,1, and 1.5. The points are the results from numerical simulations with 3-σ error bars. The low black dashed line “L” is the linear power, the middle black dot-dashed line “1-loop” is the result from the 2-halo contribution (5), where we use a perturbative resummation that is complete up to 1-loop order, the upper blue dashed line “1H” is the result from the 1-halo contribution (5), and the red solid line is the result of our model (17)–(18). |
| In the text | |
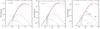 |
Fig. 5 Convergence bispectrum for sources at redshifts zs = 0.6,1, and 1.5, for equilateral triangles. The points are the results from numerical simulations with 3-σ error bars. The low black dashed line “L” is the tree-order bispectrum (28), the “1-loop” dot-dashed black line is the prediction of 1-loop standard perturbation theory, which is identified with our 3-halo term (14), the green dotted line “2H” is the 2-halo contribution (15) and the upper blue dashed line “1H” is the 1-halo contribution (16). |
| In the text | |
 |
Fig. 6 Convergence bispectrum Bκ(ℓ1,ℓ2,ℓ3) for isosceles configurations, as in Fig. 3. The symbols are the same as in Fig. 5. In the first row we show the absolute value of the 1-halo contribution, which becomes negative at ℓ1 ~ 2500. |
| In the text | |
 |
Fig. 7 Convergence power spectrum for sources at redshift zs = 1, for the six cosmologies given in Table A.1. The points are the results from numerical simulations and the lines are the predictions of our model. |
| In the text | |
 |
Fig. 8 Convergence bispectrum for sources at redshift zs = 1, for the six cosmologies given in Table A.1. The points are the results from numerical simulations and the lines are the predictions of our model. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


