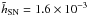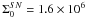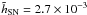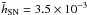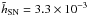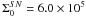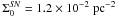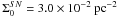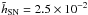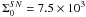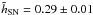| Issue |
A&A
Volume 540, April 2012
|
|
|---|---|---|
| Article Number | L5 | |
| Number of page(s) | 7 | |
| Section | Letters | |
| DOI | https://doi.org/10.1051/0004-6361/201118545 | |
| Published online | 28 March 2012 | |
Evidence of nuclear disks in starburst galaxies from their radial distribution of supernovae⋆
Instituto de Astrofísica de Andalucía – CSIC,
PO Box 3004,
18008
Granada,
Spain
e-mail: herrero@iaa.es
Received:
29
November
2011
Accepted:
12
March
2012
Galaxy–galaxy interactions are expected to be responsible for triggering massive star formation and possibly accretion onto a supermassive black hole, by providing large amounts of dense molecular gas down to the central kiloparsec region. Several scenarios to drive the gas further down to the central ~100 pc, have been proposed, including the formation of a nuclear disk around the black hole, where massive stars would produce supernovae. Here, we probe the radial distribution of supernovae and supernova remnants in the nuclear regions of the starburst galaxies M 82, Arp 299-A, and Arp 220, by using high-angular resolution (≲ 0.′′1) radio observations published in the literature (for M 82 and Arp 220), or obtained by ourselves from the European VLBI Network (Arp 299-A). Our main goal was to characterize the nuclear starbursts in those galaxies and thus test scenarios that propose that nuclear disks of sizes ~100 pc form in the central regions of starburst galaxies. We obtained the radial distribution of supernovae (SNe) in the nuclear starbursts of M 82, Arp 299-A, and Arp 220, and derived scale-length values for the putative nuclear disks powering the bursts in those central regions. The scale lengths for the (exponential) disks range from ~20–30 pc for Arp 299-A and Arp 220, up to ~140 pc for M 82. The radial distribution of SNe for the nuclear disks in Arp 299-A and Arp 220 is also consistent with a power-law surface density profile of exponent γ = 1, as expected from detailed hydrodynamical simulations of nuclear disks. Our results support scenarios where a nuclear disk of size ~100 pc is formed in (U)LIRGs, and sustained by gas pressure, in which case the accretion onto the black hole could be lowered by supernova feedback.
Key words: galaxies: starburst / galaxies: luminosity function, mass function / galaxies: individual: Arp 299-A / supernovae: general / radiation mechanisms: non-thermal / radio continuum: stars
Appendices are available in electronic form at http://www.aanda.org
© ESO, 2012
1. Introduction
The activity in the central regions of luminous and ultra-luminous infrared galaxies (LIRGs, 1011 L⊙ ≤ LIR < 1012 L⊙, and ULIRGs, LIR ≥ 1012 L⊙, respectively) is powered by either accretion onto a supermassive black hole (SMBH), and/or by a burst of activity due to young, massive stars. It has been found that LIRGs and ULIRGs are associated with interacting and merging galaxies, respectively, and the interaction between the galaxies is assumed to provide large amounts of dense molecular gas that eventually reach the central regions of the galaxies, where they are responsible for triggering massive star formation and possibly accretion onto an SMBH (e.g., Di Matteo et al. 2007). While interactions and bars seem to aid the transport of the molecular gas into the kiloparsec region of galaxies (e.g., Simkin et al. 1980), it has been recognized that a major difficulty is in driving the gas from the kiloparsec region down to the central parsec, or parsecs, of (U)LIRGs, where a nuclear starburst and/or an active galactic nucleus (AGN) are expected to exist. Several mechanisms have been proposed to overcome this problem, including tidal torques driven by either stellar bars (Shlosman et al. 1990) or major and minor mergers (Mihos & Hernquist 1994, 1996), gas drag and dynamical friction in a dense nuclear star cluster (Norman & Scoville 1988), or radiation drag (Umemura 2001; Kawakatu & Umemura 2002). However, not all the accumulated gas is expected to be accreted directly onto the putative SMBH, since the removal of the angular momentum of the gas is very inefficient (Umemura 2001). The angular momentum that is not removed will then permit the accreted gas to form a reservoir, namely a nuclear disk in the central ~100 pc around the AGN (e.g., Wada & Norman 2002; Kawakatu & Wada 2008, and references therein). Furthermore, if the gas in the nuclear starburst is dense enough, vigorous star formation is expected to occur, which can be detected via, e.g., high-angular resolution observations of recently exploded supernovae (e.g., in the LIRG Arp 299, Pérez-Torres et al. 2009; or the ULIRG Arp 220, Lonsdale et al. 2006). The nuclear starburst is also expected to affect the growth of the SMBH, since the radiation and/or supernova (SN) feedback caused by starbursts can eventually trigger the mass accretion onto a SMBH (e.g., Umemura et al. 1997; Wada & Norman 2002).
Kawakatu & Wada (2008) proposed an scenario for (U)LIRGs, where a nuclear disk is supported by the turbulent pressure of SNe. In their model, the turbulence due to supernova activity transports the angular momentum toward the central pc-scale region. One of the implications of the model developed by Kawakatu & Wada (2008) is that the BH growth rate depends on the spatial distribution of both young stars and SNe in the nuclear disk. However, the study of this spatial distribution is a challenging observational task for two main reasons. First, the huge column densities present in nuclear starbursts cause enormous extinction toward the central regions of (U)LIRGs at optical and infrared wavelengths, such that essentially no supernova would be detected at those wavelengths in the central few hundred parsecs of a (U)LIRG. Second, the enormous angular resolution needed to discern individual objects at the typical distances to (U)LIRGs (≳ 50 Mpc) requires milliarcsecond angular resolution to resolve individual core-collapse supernovae (CCSNe) and/or supernova remnants (SNRs).
In this paper, we use high-angular radio observations from the literature, as well as data obtained by us, of three starburst galaxies in the local universe (M 82, Arp 299-A, and Arp 220) to analyze the radial distribution of CCSNe/SNRs in their central few hundred parsecs, which may have strong implications for the (co)-evolution of AGN and (nuclear) starbursts in galaxies, in general, and in (U)LIRGs in particular.
2. The radial distribution of SNe in nuclear starbursts
The radial distribution of SNe1 on galactic scales has been thoroughly studied (see, e.g., Bartunov et al. 1992; van den Bergh 1997; Anderson & James 2009; Hakobyan et al. 2009). Optical observations have been very useful for this purpose, as dust extinction plays a minor role in the external regions of most galaxies. However, the dust-enshrouded environments of the nuclear regions in (U)LIRGs, as well as the need for milliarcsecond angular resolution to pinpoint individual SNe, have prevented this kind of studies in the central regions of local (U)LIRGs. Fortunately, both issues – obscuration and (angular) resolution – can be overcome by means of Very Long Baseline Interferometry (VLBI) radio observations of the central regions of (U)LIRGs, since radio is dust-extinction free, and VLBI provides milliarsecond angular resolution.
2.1. Methods
We used VLBI observations to probe the radial distribution of SNe in the nuclear regions
of Arp 299-A (31 objects) and Arp 220 (48 objects), as well as MERLIN, VLA, and VLBI
observations toward M 82 (38 objects). For each galaxy, we fitted the surface density
profile of the SNe to two different disk profiles: (i) an exponential disk,
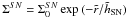 , and (ii) a
disk with a power-law density profile with radius,
, and (ii) a
disk with a power-law density profile with radius, 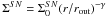 . The
first case (exponential disk) assumes that the SN distribution follows the radial
surface-brightness density in spiral disks (Freeman
1970), while the second one (power-law disk) was used to probe the profiles
predicted by numerical simulations (Wada & Norman
2002). The notation follows the one used in Hakobyan et al. (2009), where
. The
first case (exponential disk) assumes that the SN distribution follows the radial
surface-brightness density in spiral disks (Freeman
1970), while the second one (power-law disk) was used to probe the profiles
predicted by numerical simulations (Wada & Norman
2002). The notation follows the one used in Hakobyan et al. (2009), where 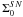 is the
surface density of SN at the center,
is the
surface density of SN at the center, 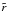 is the normalized radius, and rout is the radius of the
farthest SN analyzed, considered here to be the outer boundary of the putative nuclear
disk. The main parameters that are obtained from those fits are the scale length,
is the normalized radius, and rout is the radius of the
farthest SN analyzed, considered here to be the outer boundary of the putative nuclear
disk. The main parameters that are obtained from those fits are the scale length,
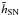 ,
and the index of the power-law profile, γ, of the putative nuclear disks
in the central regions of these galaxies.
,
and the index of the power-law profile, γ, of the putative nuclear disks
in the central regions of these galaxies.
Our approach consisted in model fitting the surface density profile of the radial distribution of SNe, by determining the number of sources in concentric rings around the center of the galaxy. For this purpose, we carried out a similar data analysis to the one described in Hakobyan et al. (2009, hereafter, H09), and we refer the reader to that paper for further details. In particular, we calculated the de-projected distance of each compact source to the center of the galaxy (the AGN, whenever its identification was possible) from the position angle of the galaxy major axis, and the inclination of the galactic disk. We obtained those parameter values from the HyperLeda database. We also followed H09, and measured radial distances in units of R25, i.e., the isophotal radius at which the surface brightness was 25 mag/arcsec2 in the Johnson B filter. We then derived the surface density profile by determining the number of sources in concentric rings around the nucleus, and fitting the data to both an exponential and a power-law disk, as described above.
Since the supernova samples for all our three galaxies are of relatively small size,
resulting in some small size bins, the actual uncertainties in the fits could be larger
than formally obtained from a single fit. To assess the robustness of our fitting
procedure, we performed a series of Monte Carlo (MC) simulations. For each galaxy, we
generated 10 000 mock supernova samples, whose values were uniformly distributed within
the uncertainty of each data point, and fitted them. In this way, we obtained a
distribution of 10 000 different fitting values for the scale-length parameter,
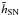 ,
and the power-law index, γ, for each galaxy. This approach allowed us to
obtain more reliable values of those parameters, since no assumption was made about the
Gaussianity of the distributions of both the scale length and power-law index, or of their
errors. We then used the median value of the distribution of our MC values to characterize
,
and the power-law index, γ, for each galaxy. This approach allowed us to
obtain more reliable values of those parameters, since no assumption was made about the
Gaussianity of the distributions of both the scale length and power-law index, or of their
errors. We then used the median value of the distribution of our MC values to characterize
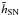 and γ, and set the uncertainty in these parameters at the 90% confidence
level. To test our method, we reanalyzed the sample of H09 for 239 CCSNe within 216 host
galaxies, and obtained a value of
and γ, and set the uncertainty in these parameters at the 90% confidence
level. To test our method, we reanalyzed the sample of H09 for 239 CCSNe within 216 host
galaxies, and obtained a value of 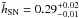 ,
which is in excellent agreement with their estimate2,
and confirms the robustness of our analysis.
,
which is in excellent agreement with their estimate2,
and confirms the robustness of our analysis.
2.2. Results
We outline the results obtained for each individual galaxy. We refer the reader to the Appendices for details on the SN data used in our fitting analysis.
2.2.1. Arp 299-A
Arp 299-A (D = 44.8 Mpc) is one of the two interacting galaxies of the
LIRG Arp 299. The sample of SNe used for our study comes from both observations from the
European VLBI Network (EVN) at 5.0 GHz, presented in Pérez-Torres et al. (2009) and in Bondi et al.
(2012) (see also Appendix A), as well as
from published data obtained with the Very Long Baseline Array (VLBA) at 2.3 and 8.4 GHz
by Ulvestad (2009). The existence and precise
location of the low luminosity AGN in Arp 299-A was reported by Pérez-Torres et al. (2010), hence its position was used to calculate
accurate de-projected distances for all SNe in the nuclear region of Arp 299-A. The
sample has a total of 31 sources. However, although there are sources at distances as
far as 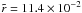 ,
only one source is further than
,
only one source is further than 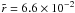 ,
so the latter value of
,
so the latter value of 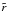 was used as the limiting radius for our study, giving a final number of 30 sources. The
scale length obtained using the non-linear fit is
was used as the limiting radius for our study, giving a final number of 30 sources. The
scale length obtained using the non-linear fit is
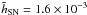 ,
with a standard deviation of 0.5 × 10-3. After performing the MC analysis, we
obtained a final value
,
with a standard deviation of 0.5 × 10-3. After performing the MC analysis, we
obtained a final value 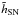 of
of 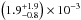 and
and 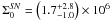 .
.
2.2.2. Arp 220
Arp 220 is a merging system at 77 Mpc, and the closest and most well-studied ULIRG.
High-angular resolution radio observations from its two nuclear regions were first
obtained by Lonsdale et al. (2006) using global
VLBI, who found a total of 49 radio supernovae in both the east (20) and west (29)
nuclei. We used the position of the peak flux density from a delay-rate VLBI map as the
estimated position for the center of each galactic nucleus (Parra et al. 2007). One of the compact sources in the Arp 220 east
nucleus is at a much larger distance than the rest of them, which we did not use in our
fit, thus limiting the normalized radii to 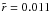 . Therefore, a total of
48 SNe were considered in the fits, which we carried both separately, for each nucleus,
and for the combined data set (Fig. A.3).
Similarly, we performed MC simulations for each of the two nuclei, as well as for the
combined sample In this way, we obtained a scale-length for the east and west nuclei of
. Therefore, a total of
48 SNe were considered in the fits, which we carried both separately, for each nucleus,
and for the combined data set (Fig. A.3).
Similarly, we performed MC simulations for each of the two nuclei, as well as for the
combined sample In this way, we obtained a scale-length for the east and west nuclei of
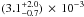 and
and 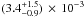 ,
respectively, and a combined scale-length for Arp 220 is
,
respectively, and a combined scale-length for Arp 220 is
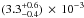 .
To quantify the effect of the uncertain position of the putative AGNs, we shifted them
100 times randomly around our nominal position, given by the peak flux density, by a
maximum value of
σ(RA, Dec) = FWHM/(2 S/N),
where FWHM is the full-width at half maximum, and S/N is the signal-to-noise ratio,
resulting in 4.2 mas for the east nucleus and 1.4 mas for the west one, and then fitted
to the data. The maximum differences obtained were considered as a systematic error,
which we added to our nominal values, such that the combined scale length became
.
To quantify the effect of the uncertain position of the putative AGNs, we shifted them
100 times randomly around our nominal position, given by the peak flux density, by a
maximum value of
σ(RA, Dec) = FWHM/(2 S/N),
where FWHM is the full-width at half maximum, and S/N is the signal-to-noise ratio,
resulting in 4.2 mas for the east nucleus and 1.4 mas for the west one, and then fitted
to the data. The maximum differences obtained were considered as a systematic error,
which we added to our nominal values, such that the combined scale length became
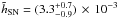 ,
with
,
with 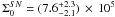 .
.
2.2.3. Combination of Arp 299-A and Arp 220
The normalized radii of Arp 299-A and Arp 220 (both east and west nuclei) are
comparable. We can thus combine every source prior to the analysis to obtain an average
scale-length parameter with smaller errors to help characterize both nuclear starbursts.
The scale length obtained for the combined samples is
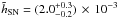 .
The original non-linear fit is shown in Fig. 1 and
our MC analysis results are shown in Fig. 2. After
taking into account systematic errors due to the uncertainty in the precise location of
the AGNs of the Arp 220 east and west nuclei, the final value for the scale length is
.
The original non-linear fit is shown in Fig. 1 and
our MC analysis results are shown in Fig. 2. After
taking into account systematic errors due to the uncertainty in the precise location of
the AGNs of the Arp 220 east and west nuclei, the final value for the scale length is
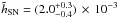 and
and 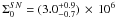 .
.
 |
Fig. 1 Non-linear fit of the surface density profile of the combined sample of SNe from both Arp 299-A and Arp 220. |
 |
Fig. 2 MC histogram of |
2.2.4. M 82
At a distance of 3.2 Mpc, M 82 is the prototypical starburst galaxy, which has been the
target of many observations at high-angular resolution. For our analysis, we combined
sources catalogued as SNe (or SNR) detected by Wills
et al. (1997), Allen & Kronberg
(1998), McDonald et al. (2002), Fenech et al. (2008), and Brunthaler et al. (2009). These comprise observations at several
frequencies with MERLIN, VLA, and VLBA, including a total of 39 sources. Since no AGN
has yet been discovered in M 82, we instead used the radio kinematic center of M 82
(Weliachew et al. 1984) as the position of its
nucleus. The scale length obtained with the MC simulation is
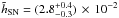 .
Although the radio kinematic center is likely to be very close, if not exactly
coincident, with the putative nucleus of M 82, we nevertheless quantified the effect
that an error in the position chosen as the nucleus of M 82 would have in the fits. In
particular, we shifted our fiducial position for the nucleus by up to 20 parsec in
several directions, and then fitted the data. The maximum differences were considered as
a systematic error, which we added to our nominal value, thus yielding
.
Although the radio kinematic center is likely to be very close, if not exactly
coincident, with the putative nucleus of M 82, we nevertheless quantified the effect
that an error in the position chosen as the nucleus of M 82 would have in the fits. In
particular, we shifted our fiducial position for the nucleus by up to 20 parsec in
several directions, and then fitted the data. The maximum differences were considered as
a systematic error, which we added to our nominal value, thus yielding
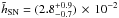 ,
and
,
and 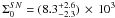 .
.
 |
Fig. 3 Radial distribution of SNe for (nuclear) starbursts and spiral galaxies. The data correspond to the combined Arp 299-A + Arp 220 sample (blue squares), M 82 (green circles), and the H09 sample of spiral galaxies (red diamonds), and the fitted lines are for Arp 299-A + Arp 220 (solid line), M 82 (dotted-dashed line), and H09 (dashed line). For the sake of clarity, only the innermost part of the H09 sample is shown in the plot. |
Scale length parameters for the galaxies discussed in this paper.
3. Discussion and summary
Our main results are summarized in Table 1 and Fig. 3, where we show the scale lengths, index of the power-law SN profile, and the radial distribution of SNe for the three galaxies discussed in this paper, as well as for the sample of spiral galaxies from H09.
We note that the scale lengths for the exponential disk fits to the radial distribution of
SNe in the nuclear regions of the starburst galaxies, are at least an order of magnitude
smaller that those obtained by H09 for the whole disks of spiral galaxies. In particular,
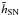 is two orders of magnitude smaller in the case of Arp 299-A and Arp 220. Correspondingly,
the physical sizes inferred for the scale lengths of the nuclear disks (Col. 3 in
Table 1) are much smaller than for galactic disks:
~20–30 pc for Arp 299-A or Arp 220, which is similar to the size derived for the nuclear
starburst of the LIRG NGC 7469 (30–60 pc; Davies et al.
2004b), using CO interferometric observations, and ~160 pc for M 82, which is
also similar to the scale-length of the nuclear disk in the ULIRG/QSO Mrk 231 (Davies et al. 2004a).
is two orders of magnitude smaller in the case of Arp 299-A and Arp 220. Correspondingly,
the physical sizes inferred for the scale lengths of the nuclear disks (Col. 3 in
Table 1) are much smaller than for galactic disks:
~20–30 pc for Arp 299-A or Arp 220, which is similar to the size derived for the nuclear
starburst of the LIRG NGC 7469 (30–60 pc; Davies et al.
2004b), using CO interferometric observations, and ~160 pc for M 82, which is
also similar to the scale-length of the nuclear disk in the ULIRG/QSO Mrk 231 (Davies et al. 2004a).
We show in Fig. 3 the radial distribution of SNe in our three starburst galaxies and, for comparison, also for spiral galaxies (from the H09 sample), along with the fits to these data. We note the clear existence of three different regimes: one characterized by a very steep profile of the surface number density of SNe, which is typical of strong, nuclear starbursts (Arp 299-A+Arp 220); a second, less steep profile, as indicated for the (circum)nuclear starburst in M 82; and a third, flatter profile, which is typical of very large disks, such as those in spiral galaxies (H09 sample). These results suggest that the surface density of SNe, hence of available gas to convert into stars, reaches a maximum in the vicinities of the SMBH in LIRGs and ULIRGs. We also show in Col. 4 of Table 1 the fits to a power-law disk profile, consistent with the fiducial value of γ = 1 used by Wada & Norman (2002) and Kawakatu & Wada (2008) for the nuclear disk, and appears to yield further support to their modeling.
We have modeled for the first time the radial distribution of SNe in the nuclear starbursts of M 82, Arp 299-A, and Arp 220, and derived scale-length values for exponential disks, which are in the range between ~20 pc and ~140 pc. We have also modeled these SNe distributions as power-law disk profiles, and found that they agree with state-of-the art numerical simulations of nuclear disks around SMBHs. We interpret our results as evidence of nuclear disks around the centers, i.e., AGNs, of starburst-dominated galaxies and also support for evolutionary scenarios where a nuclear disk of size ≲ 100 pc is formed in LIRGs and ULIRGs (Kawakatu & Wada 2008). In particular, the scale-length obtained for the LIRG Arp 299-A and the LLAGN nature of its SMBH (Pérez-Torres et al. 2010), suggests that its nuclear disk is likely supported by gas pressure, such that the accretion onto the SMBH is smaller than for a turbulent-supported disk. It is very likely that this is also the case for the ULIRG Arp 220. Future deep VLBI observations of a significantly large sample of (U)LIRGs, which would result in the discovery of new SN factories, will be of much use for deriving statistically significant results on the size of nuclear disks, and thus setting useful constraints on (co)-evolutionary scenarios.
Online material
Appendix A: Arp 299-A and Arp 220
 |
Fig. A.1 Surface density profile of the 30 inner SNe in Arp 299-A. The solid green line is
a non-linear fit to an exponential disk with
|
 |
Fig. A.2 Surface density of SNe vs radii normalized to the furthest source, rout, in Arp 299-A and non-linear fit to a power law with γ = 1.1. |
 |
Fig. A.3 Non-linear fits to the surface density profile of the radial distribution of SNe
in Arp 220. Top left: fit to the 19 inner sources in the eastern
nucleus ( |
 |
Fig. A.4 Surface density profile of the combined sources for the east and west nuclei of
Arp 220, in parsecs. The non-linear fit yields a scale length of
hSN = 23.4 pc, with
|
 |
Fig. A.5 Surface density profile of the combined sources for Arp 299-A and Arp 220, in
parsecs. The non-linear fit yields a scale-length of
hSN = 19.4 pc and
|
 |
Fig. A.6 Non-linear power-law fits of the surface density of SNe vs. radius, normalized to the furthest source, rout, in Arp 220. Top left: east nucleus, with γ = 1.0. Top right: west nucleus, with γ = 0.7. Bottom: combined analysis for the east and west nuclei (48 sources), yielding γ = 0.7. Note that some of the points are in rings where no sources were detected. While their corresponding surface density is zero, their upper limits were used in the fit. |
 |
Fig. A.7 Surface density of SNe vs radii normalized to the furthest source, rout, for the combined sample of SNe from Arp 299-A and the two nuclei of Arp 220. A non-linear fit to a power law with radius yields γ = 0.9. |
Appendix B: M 82
 |
Fig. B.1 Surface density profile for the radial distribution of SNe in M 82 (39 objects).
The solid green line is a non-linear fit to an exponential disk with
|
 |
Fig. B.2 Surface density of SNe vs. radii normalized to the furthest source, rout and non-linear fit to a power law (nuclear) disk for M 82. The poor goodness of the fit does not seem to be consistent with a nuclear disk whose SN surface density follows a power law in the central few hundred pc. |
Appendix C: Nature of the radio sources
The sources used in this paper are classified generically as supernovae (SNe), by which we mean core collapse supernovae (CCSNe) and SNRs. In the case of M 82, the closest of the three galaxies discussed here, we used the source list in McDonald et al. (2002) and Fenech et al. (2008), where the authors already discriminate SNe from HII regions based on their spectral shape, brightness temperature, and observed shell structure. In the cases of the more distant galaxies, Arp 299 and Arp 220, we used available spectral information from the literature, and especially, the brightness temperatures inferred from VLBI observations, which for all of the sources correspond to non-thermal radio emitters (e.g., Pérez-Torres et al. 2009, for Arp 299A; Parra et al. 2007, for Arp 220).
Single or multiple ultra compact HII (UC HII) regions can be ruled out because their ionizing radiation is normally dominated by a single O star, whose maximum free-free thermal radio luminosity is several orders of magnitude below the radio luminosity from any of the objects detected in either Arp 299-A or Arp 220. The expected thermal radio emission from super star clusters (SSCs), which can host up to a few 105 stars, similarly cannot be responsible for the observed emission. At the distances of Arp 299 and Arp 220, the VLBI beam sizes correspond to ~1.5 pc, implying radial sizes of at most about 0.8 pc. Young massive stellar clusters of this size have a mass of at most 5 × 105 M⊙ (e.g. Portegies Zwart et al. 2010). Assuming a Kroupa initial mass function with α = −1.0 between 0.1 and 0.5 M⊙, and α = −2.35 between 0.5 and 100 M⊙, the number of O6 and earlier type stars is 142 (out of a total of 105 stars), hence the maximum attainable thermal radio luminosity would be ~2 × 1025 erg/s/Hz, which is at least an order of magnitude lower than observed in Arp 299-A or Arp 220.
Acknowledgments
We are grateful to Rob Beswick and the anonymous referee for useful suggestions and comments. The authors acknowledge support by the Spanish MICINN through grant AYA2009-13036-CO2-01, partially funded by FEDER funds. This research has also been partially funded by the Autonomic Government of Andalusia under grants P08-TIC-4075 and TIC-126. We acknowledge the usage of the HyperLeda database (http://leda.univ-lyon1.fr/).
References
- Allen, M. L., & Kronberg, P. P. 1998, ApJ, 502, 218 [NASA ADS] [CrossRef] [Google Scholar]
- Anderson, J. P., & James, P. A. 2009, MNRAS, 399, 559 [NASA ADS] [CrossRef] [Google Scholar]
- Bartunov, O. S., Makarova, I. N., & Tsvetkov, D. I. 1992, A&A, 264, 428 [NASA ADS] [Google Scholar]
- Bondi, M., Perez-Torres, M. A., Herrero-Illana, R., & Alberdi, A. 2012, A&A, 539, A134 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brunthaler, A., Menten, K. M., Reid, M. J., et al. 2009, A&A, 499, L17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Davies, R. I., Tacconi, L. J., & Genzel, R. 2004a, ApJ, 613, 781 [NASA ADS] [CrossRef] [Google Scholar]
- Davies, R. I., Tacconi, L. J., & Genzel, R. 2004b, ApJ, 602, 148 [NASA ADS] [CrossRef] [Google Scholar]
- Di Matteo, P., Combes, F., Melchior, A.-L., & Semelin, B. 2007, A&A, 468, 61 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fenech, D. M., Muxlow, T. W. B., Beswick, R. J., Pedlar, A., & Argo, M. K. 2008, MNRAS, 391, 1384 [NASA ADS] [CrossRef] [Google Scholar]
- Freeman, K. C. 1970, ApJ, 160, 811 [NASA ADS] [CrossRef] [Google Scholar]
- Hakobyan, A. A., Mamon, G. A., Petrosian, A. R., Kunth, D., & Turatto, M. 2009, A&A, 508, 1259 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kawakatu, N., & Umemura, M. 2002, MNRAS, 329, 572 [NASA ADS] [CrossRef] [Google Scholar]
- Kawakatu, N., & Wada, K. 2008, ApJ, 681, 73 [NASA ADS] [CrossRef] [Google Scholar]
- Lonsdale, C. J., Diamond, P. J., Thrall, H., Smith, H. E., & Lonsdale, C. J. 2006, ApJ, 647, 185 [NASA ADS] [CrossRef] [Google Scholar]
- McDonald, A. R., Muxlow, T. W. B., Wills, K. A., Pedlar, A., & Beswick, R. J. 2002, MNRAS, 334, 912 [NASA ADS] [CrossRef] [Google Scholar]
- Mihos, J. C., & Hernquist, L. 1994, ApJ, 425, L13 [NASA ADS] [CrossRef] [Google Scholar]
- Mihos, J. C., & Hernquist, L. 1996, ApJ, 464, 641 [NASA ADS] [CrossRef] [Google Scholar]
- Norman, C., & Scoville, N. 1988, ApJ, 332, 124 [NASA ADS] [CrossRef] [Google Scholar]
- Parra, R., Conway, J. E., Diamond, P. J., et al. 2007, ApJ, 659, 314 [NASA ADS] [CrossRef] [Google Scholar]
- Pérez-Torres, M. A., Romero-Cañizales, C., Alberdi, A., & Polatidis, A. 2009, A&A, 507, L17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pérez-Torres, M. A., Alberdi, A., Romero-Cañizales, C., & Bondi, M. 2010, A&A, 519, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Portegies Zwart, S. F., McMillan, S. L. W., & Gieles, M. 2010, ARA&A, 48, 431 [NASA ADS] [CrossRef] [Google Scholar]
- Shlosman, I., Begelman, M. C., & Frank, J. 1990, Nature, 345, 679 [NASA ADS] [CrossRef] [Google Scholar]
- Simkin, S. M., Su, H. J., & Schwarz, M. P. 1980, ApJ, 237, 404 [NASA ADS] [CrossRef] [Google Scholar]
- Ulvestad, J. S. 2009, AJ, 138, 1529 [NASA ADS] [CrossRef] [Google Scholar]
- Umemura, M. 2001, ApJ, 560, L29 [NASA ADS] [CrossRef] [Google Scholar]
- Umemura, M., Fukue, J., & Mineshige, S. 1997, ApJ, 479, L97 [NASA ADS] [CrossRef] [Google Scholar]
- van den Bergh, S. 1997, AJ, 113, 197 [NASA ADS] [CrossRef] [Google Scholar]
- Wada, K., & Norman, C. A. 2002, ApJ, 566, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Weliachew, L., Fomalont, E. B., & Greisen, E. W. 1984, A&A, 137, 335 [NASA ADS] [Google Scholar]
- Wills, K. A., Pedlar, A., Muxlow, T. W. B., & Wilkinson, P. N. 1997, MNRAS, 291, 517 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Non-linear fit of the surface density profile of the combined sample of SNe from both Arp 299-A and Arp 220. |
| In the text | |
 |
Fig. 2 MC histogram of |
| In the text | |
 |
Fig. 3 Radial distribution of SNe for (nuclear) starbursts and spiral galaxies. The data correspond to the combined Arp 299-A + Arp 220 sample (blue squares), M 82 (green circles), and the H09 sample of spiral galaxies (red diamonds), and the fitted lines are for Arp 299-A + Arp 220 (solid line), M 82 (dotted-dashed line), and H09 (dashed line). For the sake of clarity, only the innermost part of the H09 sample is shown in the plot. |
| In the text | |
 |
Fig. A.1 Surface density profile of the 30 inner SNe in Arp 299-A. The solid green line is
a non-linear fit to an exponential disk with
|
| In the text | |
 |
Fig. A.2 Surface density of SNe vs radii normalized to the furthest source, rout, in Arp 299-A and non-linear fit to a power law with γ = 1.1. |
| In the text | |
 |
Fig. A.3 Non-linear fits to the surface density profile of the radial distribution of SNe
in Arp 220. Top left: fit to the 19 inner sources in the eastern
nucleus ( |
| In the text | |
 |
Fig. A.4 Surface density profile of the combined sources for the east and west nuclei of
Arp 220, in parsecs. The non-linear fit yields a scale length of
hSN = 23.4 pc, with
|
| In the text | |
 |
Fig. A.5 Surface density profile of the combined sources for Arp 299-A and Arp 220, in
parsecs. The non-linear fit yields a scale-length of
hSN = 19.4 pc and
|
| In the text | |
 |
Fig. A.6 Non-linear power-law fits of the surface density of SNe vs. radius, normalized to the furthest source, rout, in Arp 220. Top left: east nucleus, with γ = 1.0. Top right: west nucleus, with γ = 0.7. Bottom: combined analysis for the east and west nuclei (48 sources), yielding γ = 0.7. Note that some of the points are in rings where no sources were detected. While their corresponding surface density is zero, their upper limits were used in the fit. |
| In the text | |
 |
Fig. A.7 Surface density of SNe vs radii normalized to the furthest source, rout, for the combined sample of SNe from Arp 299-A and the two nuclei of Arp 220. A non-linear fit to a power law with radius yields γ = 0.9. |
| In the text | |
 |
Fig. B.1 Surface density profile for the radial distribution of SNe in M 82 (39 objects).
The solid green line is a non-linear fit to an exponential disk with
|
| In the text | |
 |
Fig. B.2 Surface density of SNe vs. radii normalized to the furthest source, rout and non-linear fit to a power law (nuclear) disk for M 82. The poor goodness of the fit does not seem to be consistent with a nuclear disk whose SN surface density follows a power law in the central few hundred pc. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.