| Issue |
A&A
Volume 540, April 2012
|
|
|---|---|---|
| Article Number | A52 | |
| Number of page(s) | 17 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201118499 | |
| Published online | 23 March 2012 | |
The dust scaling relations of the Herschel Reference Survey⋆,⋆⋆
1 European Southern Observatory, Karl Schwarzschild Str. 2, 85748 Garching bei München, Germany
e-mail: lcortese@eso.org
2 Laboratoire d’Astrophysique de Marseille, UMR 6110 CNRS, 38 rue F. Joliot-Curie, 13388 Marseille, France
3 INAF – Osservatorio Astrofisico di Arcetri, Largo Enrico Fermi 5, 50125 Firenze, Italy
4 School of Physics and Astronomy, Cardiff University, The Parade, Cardiff, CF24 3AA, UK
5 UK ALMA Regional Centre Node, Jodrell Bank Centre for Astrophysics, School of Physics and Astronomy, University of Manchester, Oxford Road, Manchester M13 9PL, UK
6 Sterrenkundig Observatorium, Universiteit Gent, Krijgslaan 281 S9, 9000 Gent, Belgium
7 Kavli Institute for Astronomy & Astrophysics, Peking University, 100871 Beijing, PR China
8 Institut d’Astrophysique Spatiale (IAS), Batiment 121, Universite Paris-Sud 11 and CNRS, 91405 Orsay, France
9 Visiting Astronomer, Max-Planck-Institut für extraterrestrische Physik, Giessenbachstrasse, Postfach 1312, 85741 Garching bei München, Germany
10 Dark Cosmology Centre, Niels Bohr Institute University of Copenhagen, Juliane Maries Vej 30, 2100 Copenhagen, Denmark
11 Astrophysics Group, Blackett Lab, Imperial College, Prince Consort Road, London SW7 2AZ, UK
12 University of California, Irvine, Department of Physics & Astronomy, 4186 Frederick Reines Hall, Irvine, CA, USA
13 Institute of Astronomy, University of Cambridge, Madingley Road, Cambridge, CB3 0HA, UK
14 Istituto di Fisica dello Spazio Interplanetario, INAF, via Fosso del Cavaliere 100, 00133 Roma, Italy
15 Joint ALMA Office, Alonso de Cordova 3107, Vitacura, Santiago, Chile
16 Departamento de Astronomia, Universidad de Chile, Casilla 36-D, Santiago, Chile
Received: 22 November 2011
Accepted: 10 January 2012
We combine new Herschel/SPIRE sub-millimeter observations with existing multiwavelength data to investigate the dust scaling relations of the Herschel Reference Survey, a magnitude-, volume-limited sample of ~300 nearby galaxies in different environments. We show that the dust-to-stellar mass ratio anti-correlates with stellar mass, stellar mass surface density and NUV − r colour across the whole range of parameters covered by our sample. Moreover, the dust-to-stellar mass ratio decreases significantly when moving from late- to early-type galaxies. These scaling relations are similar to those observed for the Hi gas-fraction, supporting the idea that the cold dust is tightly coupled to the cold atomic gas component in the interstellar medium. We also find a weak increase of the dust-to-Hi mass ratio with stellar mass and colour but no trend is seen with stellar mass surface density. By comparing galaxies in different environments we show that, although these scaling relations are followed by both cluster and field galaxies, Hi-deficient systems have, at fixed stellar mass, stellar mass surface density and morphological type systematically lower dust-to-stellar mass and higher dust-to-Hi mass ratios than Hi-normal/field galaxies. This provides clear evidence that dust is removed from the star-forming disk of cluster galaxies but the effect of the environment is less strong than what is observed in the case of the Hi disk. Such effects naturally arise if the dust disk is less extended than the Hi and follows more closely the distribution of the molecular gas phase, i.e., if the dust-to-atomic gas ratio monotonically decreases with distance from the galactic center.
Key words: dust, extinction / galaxies: evolution / submillimeter: galaxies / galaxies: clusters: individual: Virgo
Herschel is an ESA space observatory with science instruments provided by European-led Principal Investigator consortia and with important participation from NASA.
Appendices are available in electronic form at http://www.aanda.org
© ESO, 2012
1. Introduction
One of the main challenges for extragalactic astronomy is to understand how galaxies evolved from simple clouds of un-enriched gas into the complex eco-systems harboring stars, planets, dust, metals and different gas phases we observe today. Of course, this transformation must be related to the star formation cycle in galaxies. The gas cools, condensing into molecular clouds that collapse forming stars. Heavy elements are formed during nuclear reactions in the stellar cores and then, when the stars die, they are expelled into the interstellar medium (ISM) and either mix with the gas phase or condense forming dust grains. However, we still know very little about the detailed physical processes regulating the star formation cycle in galaxies and how much it is affected by the internal properties of galaxies (e.g., mass, dynamics and morphology) and the environment they inhabit.
In the last decades, wide-area optical surveys of the local Universe and deep investigations of high-redshift systems have allowed an accurate reconstruction of the average star formation history (SFH) of galaxies in different environments across the Hubble time (e.g., Abazajian et al. 2009; Scoville et al. 2007). They have not only revealed that the star formation rate (SFR) density of the Universe had a peak around z ~ 1 and is now rapidly declining (e.g., Lilly et al. 1996; Madau et al. 1998), but they have also shown that the SFH of galaxies is tightly linked to their total mass (i.e., massive systems formed the bulk of their stellar populations earlier than dwarf galaxies; Cowie et al. 1996; Gavazzi et al. 1996), and to the environment (i.e., at the current epoch, galaxies in high density regions are less active than isolated systems; Lewis et al. 2002; Gómez et al. 2003; Boselli & Gavazzi 2006). The next step is to investigate why the conversion of gas into stars is mass and environment dependent and how this impacts on the metal enrichment of the ISM.
A unique role in the star formation cycle of galaxies is played by dust grains. Since dust is formed out of the metals produced during stellar nucleosynthesis, its properties provide us with important clues about the recent star formation activity of galaxies. Moreover, dust is also believed to act as catalyzer for the formation of molecular hydrogen (H2) and prevents its dissociation by the interstellar radiation field, thus helping to regulate the future star formation activity (e.g., Hollenbach & Salpeter 1971). Finally, since dust can also be destroyed, in particular if not embedded into the cold ISM (e.g., Clemens et al. 2010), its presence and abundance can yield important information about the properties of the other components of the ISM in galaxies.
Although dust properties have been studied for several decades (Savage & Mathis 1979), it has become gradually clear that, in order to obtain a proper census of dust in the Universe, it is necessary to incorporate extragalactic investigations of the far-infrared/sub-millimeter (submm) regime. It is in this part of the electromagnetic spectrum that the cold dust component dominating the dust mass budget in galaxies hides. Pioneers in this area have been the IRAS (Neugebauer et al. 1984), ISO (Kessler et al. 1996) and Spitzer (Werner et al. 2004) telescopes and the SCUBA camera (Holland et al. 1999), but now with the launch of Herschel (Pilbratt et al. 2010) are we entering a new era for interstellar dust studies. Thanks to its unprecedented sensitivity in the wavelength range 200 < λ < 600 μm and a much improved spatial resolution at 70 < λ < 160 μm (with respect to Spitzer), Herschel is a unique instrument to unveil the role played by dust in the evolutionary history of galaxies.
The first, natural step in this direction is to quantify how the dust content of galaxies varies with internal galaxy properties such as, stellar mass, colour, surface density, gas content, etc. These scaling relations will provide initial clues on the role played by dust on the star formation cycle and strong constraints for chemical evolution models. For example, it is important to quantify the link between the dust and the cold gas component of the ISM and investigate whether or not they follow similar scaling relations.
The main scaling relation investigated during the pre-Herschel era has been the evolution of the dust-to-gas ratio with stellar mass and metallicity (e.g., Issa et al. 1990; Lisenfeld & Ferrara 1998; Popescu et al. 2002; Draine et al. 2007; Galametz et al. 2011). Several studies have shown an increase of the dust-to-gas ratio as a function of stellar mass, mimicking what has already been observed in the case of the stellar mass vs. gas-phase metallicity relation (Tremonti et al. 2004). Although several investigations have quantified the variation of the total far-infrared-to-optical/near-infrared luminosity (usually interpreted as a proxy for the ratio between obscured SFR and stellar mass) as a function of morphological type (e.g., de Jong et al. 1984; Devereux & Hameed 1997; Bendo et al. 2002; Popescu et al. 2002), surprisingly very little is known about the relation between the dust-to-stellar mass ratio and galaxy properties. Only very recently, da Cunha et al. (2010) have shown that the dust-to-stellar mass strongly correlates with specific SFR (SSFR, i.e., the ratio between the current SFR and the stellar mass), as predicted by chemical evolution models. However, it is still unknown whether or not morphology and stellar mass also regulate the amount of dust present in nearby galaxies.
Even more limited is our knowledge of the role (if any) played by the environment on the dust content of galaxies. Whereas it is now well established that the atomic hydrogen (Hi) content of galaxies depends on the environment they inhabit, it is still debated whether or not the harsh cluster environment can also affect the molecular hydrogen component in the ISM (Boselli et al. 2002; Fumagalli et al. 2009). Thus, since the dust is supposed to be more directly linked to the molecular than to the atomic gas phase, it is not clear if dust is removed from the star-forming disks of cluster galaxies. Before the launch of Herschel, no definitive evidence of dust stripping in cluster galaxies had been found (e.g., Tuffs et al. 2002; Popescu et al. 2002; Contursi et al. 2001; Boselli & Gavazzi 2006).
The situation has considerably improved in the last year, thanks to the Herschel science demonstration phase. Herschel observations have not only allowed us to directly witness dust stripping in clusters of galaxies (Cortese et al. 2010a; Gomez et al. 2010), but they have also clearly demonstrated that the dust disk is significantly reduced in very Hi-deficient cluster galaxies, following remarkably well the observed “truncation” of the Hi disk (Cortese et al. 2010b). Moreover, Walter et al. (2011) have found evidence of dust stripping also in the M 81 triplet. Thus, while it is becoming clear that dust can really be perturbed by the environment, it is still uncertain whether these are just extreme cases or dust stripping is a common evolutionary phase for cluster galaxies.
Dust scaling relations are the necessary step to solve this issue: only after the relation between internal galaxy properties and dust content has been properly quantified, will it be possible to determine the role played by the environment. It is in fact mandatory to compare the properties of galaxies in different environments at fixed stellar mass, morphological type and colour to exclude that our findings are just a result of secondary trends between galaxy structure, star formation activity and environment.
For all these reasons, in this paper we take advantage of Herschel observations of the Herschel Reference Survey (HRS, Boselli et al. 2010b) to quantify how the dust-to-stellar mass and dust-to-Hi mass vary with internal galaxy properties and environment. The HRS is the ideal sample to carry out this analysis in the local Universe. Its selection criteria (magnitude- and volume-limited), size (~300 galaxies), sensitivity to the cold dust component (down to ~104 M⊙ at the distance of the Virgo cluster) and multiwavelength coverage, make this sample ideal to investigate dust properties in the local Universe, thus providing strong constraints for theoretical models and a reference for high-redshift studies.
This paper is organized as follows. In Sect. 2 we describe the Herschel observations and data reduction, the technique used to estimate the dust mass and the ancillary data used to trace the other components of the ISM. In Sects. 3 and 4 we discuss the relation of the dust-to-stellar mass and dust-to-gas mass with galaxy properties and environment while in Sect. 5 we discuss the implications of our results for chemical evolution models and for environmental studies. In appendix we investigate possible biases affecting our dust mass estimates.
2. The data
The HRS consists of a volume-limited sample (i.e., 15 ≤ D ≤ 25 Mpc) including late-type galaxies (Sa and later) with 2MASS (Skrutskie et al. 2006) K-band magnitude KS tot ≤ 12 mag and early-type galaxies (S0a and earlier) with KS tot ≤ 8.7 mag. Additional selection criteria are high galactic latitude (b > + 55°) and low Galactic extinction (AB < 0.2 mag, Schlegel et al. 1998), to minimize Galactic cirrus contamination. The total sample consists of 322 galaxies (260 late- and 62 early-type galaxies1). As extensively discussed in Boselli et al. (2010b), this sample is not only representative of the local Universe but also spans different density regimes (i.e., from isolated systems to the center of the Virgo cluster) and so it is ideal for environmental studies (see also Hughes & Cortese 2009; Cortese & Hughes 2009; Boselli et al. 2009; Cortese et al. 2011). As discussed in Boselli et al. (2010b), we fixed the distances for galaxies belonging to the Virgo cluster (i.e., 23 Mpc for the Virgo B cloud and 17 Mpc for all the other clouds; Gavazzi et al. 1999), while for the rest of the sample distances have been estimated from their recessional velocities assuming a Hubble constant H0 = 70 km s-1 Mpc-1.
2.1. Herschel/SPIRE observations, data reduction and flux extraction
Herschel/SPIRE (Griffin et al. 2010) observations of galaxies in the HRS were originally planned as part of the guaranteed time of the SPIRE and PACS consortia. However, after the selection of the Herschel open time key projects, it emerged that 83 HRS galaxies were also targeted, to a similar depth, by the Herschel Virgo Cluster Survey (HeViCS, Davies et al. 2010), a key program focused on the study of ~60 deg2 in the Virgo cluster using PACS/SPIRE (Griffin et al. 2010; Poglitsch et al. 2010) parallel mode. To reduce as much as possible the duplication of Herschel observations, the local galaxies group of the SPIRE science team (SAG2) and the HeViCS team have agreed to share the data obtained for the galaxies in common between the two programs. Thus, the Herschel/SPIRE data presented in this work have been obtained as part of these two Herschel key projects.
The 239 galaxies outside the HeViCS footprint, plus 4 galaxies in HeViCS targeted by the HRS during the Herschel science demonstration phase, have been observed using the SPIRE scan-map mode with a nominal scan speed of 30′′/s. The size of each map was chosen on the basis of the optical extent of the target. Galaxies with optical diameters smaller than ~3′ were observed using the small scan-map mode providing homogeneous coverage over a circular area of ~5′ diameter. For larger galaxies, the large scan-map mode was used, with each map covering at least an area with diameter 1.5 times the optical diameter of the target. The typical sizes of these maps are 8′ × 8′, 12′ × 12′ and 16′ × 16′. The depth of each map was decided according to the morphological type of the target: 3 and 8 pairs of cross-linked scan-map observations for late- and early-type galaxies, respectively. This resulted into a pixel-by-pixel rms at 250, 350 and 500 μm of ~7, 8, 9 mJy/beam for late-type galaxies and ~6, 6 and 7 mJy/beam for early-type systems. For additional details see Ciesla et al. (in prep.).
The remaining 79 HRS galaxies targeted by the HeViCS survey have been observed by Herschel using the SPIRE/PACS parallel scan-map mode with a fast scan speed of 60′′/s. Eight cross-scans fields of ~ 4 × 4 deg2 each across the Virgo cluster were observed covering a total area of ~60 deg2 (see Davies et al. 2010, 2012 for additional details). The typical pixel-by-pixel rms measured around the HRS galaxies are ~7, 7 and 8 mJy/beam at 250, 350 and 500 μm.
Both datasets were reduced using the same data reduction technique. Extensive details of our data reduction procedure can be found in Smith et al. (in prep.). In the following we briefly summarize the main steps. The SPIRE photometer data were processed up to Level-1 with a script adapted from the official SPIRE pipeline. The main differences with respect to the standard pipeline are that we use a different deglitching method and did not run the default temperature drift correction and the residual baseline subtraction. Instead, we used the BriGAdE method (Smith et al., in prep.) to remove the temperature drift and bring all bolometers to the same level (equivalent to baseline removal). This method provides a better baseline subtraction, in particular when strong temperature variations are present. All scans were then combined into a map using the naive map maker included in the standard pipeline. The pixel sizes of each map are 6, 8 and 12 arcsec and the corresponding full widths at half maximum (FWHM) 18.2′′, 24.5′′, 36.0′′ at 250, 350, 500 μm, respectively.
Total integrated flux densities were obtained as extensively described in Ciesla et al. (in prep.). Briefly, for extended sources2 elliptical apertures with a typical major axis 1.4 times the optical diameter of the galaxies were used. In some cases (e.g., early-type galaxies) the size of the aperture was significantly reduced in order to include all the emission from the galaxy and/or avoid as much as possible contamination from other sources or foreground cirrus emission. Background was estimated using circular annuli around the target (Ciesla et al., in prep.). Errors were estimated following Boselli et al. (2003). For point-like sources (8 out of 322 galaxies at 500 μm), flux densities were extracted directly from the time-line data using the method developed by Bendo et al. (in prep.). This turns out to provide a more reliable flux density estimate than the aperture photometry technique. Errors for point sources come directly from the time-line fitting technique. The typical errors on the flux estimates for all HRS galaxies are ~6%, 8% and 11% at 250, 350, 500 μm, respectively. These do not include the SPIRE calibration error of ~7%. In case of non-detections, upper-limits have been determined assuming a 3σ signal over a circular aperture of radius 0.3, 0.8 and 1.4 the optical radius for E, S0 and spirals, respectively (Ciesla et al., in prep.). In the following, we will work with relative spectral responsivity function (RSRF)-weighted flux density measurements. Since the SPIRE pipeline produces monochromatic flux densities assuming that the source is point-like, we had to apply correction factors to convert monochromatic flux densities into RSRF-weighted flux densities. Thus, we divided monochromatic flux densities obtained from the maps by 1.0113, 1.0087 and 1.0065, at 250, 350 and 500 μm, respectively (see Herschel Space Observatory 20113, and the SPIRE Photometer Cookbook4).
In total, 276 out of the 322 HRS galaxies (~86%) have been detected in all the three SPIRE bands, 38 galaxies are non-detections in all bands, 3 have been detected at 250 μm only and 5 galaxies at 250 and 350 μm only.
2.2. Dust mass estimate
The main aim of this paper is to investigate the relation between dust content and internal and environmental properties of galaxies. Thus, an accurate estimate of dust masses is mandatory. Ideally, the best method to quantify the amount of dust in galaxies would be via spectral energy distribution (SED) fitting of data across the whole ultraviolet to far-infrared/submm regime using up-to-date dust models and energy balance/radiative transfer techniques (e.g., Zubko et al. 2004; Draine & Li 2007; Bianchi 2008; Galliano et al. 2008; da Cunha et al. 2008; Baes et al. 2010; Compiègne et al. 2011) or just assuming simple single/double modified black-body emission (e.g., Dunne et al. 2000; Vlahakis et al. 2005). Unfortunately, no homogeneous dataset for all the HRS galaxies is currently available for λ < 200 μm (see Boselli et al. 2010b), making an accurate SED fitting of only the three SPIRE flux densities unfeasible in the case of detailed dust models and perhaps not ideal even in the case of a single modified black-body emission (Shetty et al. 2009a,b). This is mainly because, with only the SPIRE points, no constraints on the shape of the SED below 250 μm are available and no detailed error analysis can be performed. Thus, in order to avoid introducing systematic biases due to the incomplete coverage of the HRS in the mid- and far-infrared wavelength regime, we derive empirical recipes to estimate dust masses from the three SPIRE flux densities only. This approach is similar to what has been done in the past to determine stellar masses from optical and near-infrared luminosities and colours (e.g., Bell et al. 2003; Zibetti et al. 2009). In recent years, these empirical calibrations have become the ideal tool to roughly quantify the stellar content of galaxies when accurate SED fitting is not possible. Thus, the technique here adopted must not be considered equivalent to a proper SED fitting, but it just provides us with a way to have a first view on the dust properties of the HRS sample.
As a first step, we test the feasibility of this technique by using two different approaches. Firstly, we assume that the dust SED is well approximated by a simple single modified black-body radiation, then we will compare our results with the predictions of the models developed by Draine & Li (2007). A discussion on the possible biases affecting our dust mass estimates is also presented in Appendix A.
2.2.1. Modified black-body
In this case, the dust mass is given by (Hildebrand 1983) 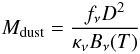 (1)where fν is the flux density emitted at the frequency ν, κν is the dust mass absorption coefficient [in the following we will assume κν = κ350(ν/ν350)β], D is the distance and Bν(T) is the Planck function
(1)where fν is the flux density emitted at the frequency ν, κν is the dust mass absorption coefficient [in the following we will assume κν = κ350(ν/ν350)β], D is the distance and Bν(T) is the Planck function 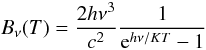 (2)where h is the Planck constant, c the speed of light and T is the dust temperature. We can use Eq. (1) to determine how the 250-to-500 μm flux density ratio varies with temperature:
(2)where h is the Planck constant, c the speed of light and T is the dust temperature. We can use Eq. (1) to determine how the 250-to-500 μm flux density ratio varies with temperature: 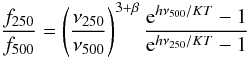 (3)and thus, by combining Eqs. (1) and (3), we can find a functional form that relates, for example, the ratio Mdust/(f350D2) to the 250-to-500 μm ratio. We tested this by varying the dust temperature in the range 5–55 K, assuming a dust mass absorption coefficient of 0.192 at 350 μm (Draine 2003) and β = 2. We choose β = 2 for two reasons. Firstly, a recent analysis of Virgo galaxies (some of which in our sample; Davies et al. 2012) has shown that their dust SEDs are well fitted by a single modified black-body with β = 2. Secondly, this value is very close to the one assumed in the models by Draine & Li (2007), thus simplifying the comparison of our results with more refined dust models (see also Magrini et al. 2011). The result of this test is shown in Fig. 1, where the black line has been obtained by convolving the black-body SED with the SPIRE RSRF for extended sources. Unsurprisingly, the two quantities are strongly correlated and it is easy to fit a polynomial function to the data, suggesting that this method could be easily used to estimate dust masses when SED fitting is not possible.
(3)and thus, by combining Eqs. (1) and (3), we can find a functional form that relates, for example, the ratio Mdust/(f350D2) to the 250-to-500 μm ratio. We tested this by varying the dust temperature in the range 5–55 K, assuming a dust mass absorption coefficient of 0.192 at 350 μm (Draine 2003) and β = 2. We choose β = 2 for two reasons. Firstly, a recent analysis of Virgo galaxies (some of which in our sample; Davies et al. 2012) has shown that their dust SEDs are well fitted by a single modified black-body with β = 2. Secondly, this value is very close to the one assumed in the models by Draine & Li (2007), thus simplifying the comparison of our results with more refined dust models (see also Magrini et al. 2011). The result of this test is shown in Fig. 1, where the black line has been obtained by convolving the black-body SED with the SPIRE RSRF for extended sources. Unsurprisingly, the two quantities are strongly correlated and it is easy to fit a polynomial function to the data, suggesting that this method could be easily used to estimate dust masses when SED fitting is not possible.
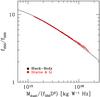 |
Fig. 1 The relation between the ratio Mdust/(F350D2) and the 250 μm-to-500 μm flux density ratio for a modified black-body SED with β = 2 (black, see Table B1) and for the Draine & Li models (red). |
2.2.2. The Draine & Li (2007) model
In order to check the validity of our method, we tested it by using a more detailed description for the dust SED as given by the dust models developed by Draine & Li (2007)5. According to these models the dust mass in a galaxy can be related to the flux density emitted in the far-infrared/submm by the following equation 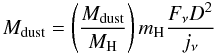 (4)where Mdust/MH is the mass of dust per nucleon (given by the dust model assumed), mH is the mass of the hydrogen nucleon and jν is the dust emissivity per H nucleon. As discussed by Draine & Li (2007), the dust emissivity strongly depends on the properties of the starlight intensities responsible for the dust heating. In particular, they show that the total dust emissivity can be expressed as
(4)where Mdust/MH is the mass of dust per nucleon (given by the dust model assumed), mH is the mass of the hydrogen nucleon and jν is the dust emissivity per H nucleon. As discussed by Draine & Li (2007), the dust emissivity strongly depends on the properties of the starlight intensities responsible for the dust heating. In particular, they show that the total dust emissivity can be expressed as 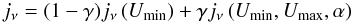 (5)where Umin and Umax are the lowest and highest possible intensities for the interstellar radiation field, (1-γ) is the fraction of dust mass exposed to starlight intensity Umin and α is the index characterizing the distribution of starlight intensities. They find that the SEDs of galaxies in the SINGS sample appear to be satisfactorily reproduced with a fixed α = 2 and Umax = 106, so we use these parameters in the rest of our analysis6. By using the models for a Milky-Way dust (i.e., from MW3.1_00 to MW3.1_60, seven models in total), we computed jν from Eq. (5) by varying γ between 0 and 0.3 (step 0.01) and assuming all the possible values for Umin (from 0.1 to 25, twenty-three in total), see also Muñoz-Mateos et al. (2009), Wiebe et al. (2009), Willmer et al. (2009). Then, we estimated the 250-to-500 μm flux density ratio and, using Eq. (4), the ratio Mdust/(f350D2) assuming Mdust/MH = 0.01 (Draine & Li 2007) and mH = 1.67 × 10-27 kg. The red points in Fig. 1 show the relation between Mdust/(f350D2) and the 250 μm-to-500 μm flux density ratio so obtained. We recover a relation extremely similar to the one found for the modified black-body case (see also Magrini et al. 2011). There is almost no systematic offset (~0.01 dex) between the two methods and the typical scatter between dust mass estimates using the two approaches is ~ 0.02 dex (see also Appendix A). We have also compared the results obtained from this method with the dust masses estimated via SED fitting for those galaxies in the HeViCS footprint for which PACS 100 and 160 μm are available. We find that the two techniques provide consistent results with no systematic effects and a typical scatter of ~ 0.10 dex (see also Appendix A).
(5)where Umin and Umax are the lowest and highest possible intensities for the interstellar radiation field, (1-γ) is the fraction of dust mass exposed to starlight intensity Umin and α is the index characterizing the distribution of starlight intensities. They find that the SEDs of galaxies in the SINGS sample appear to be satisfactorily reproduced with a fixed α = 2 and Umax = 106, so we use these parameters in the rest of our analysis6. By using the models for a Milky-Way dust (i.e., from MW3.1_00 to MW3.1_60, seven models in total), we computed jν from Eq. (5) by varying γ between 0 and 0.3 (step 0.01) and assuming all the possible values for Umin (from 0.1 to 25, twenty-three in total), see also Muñoz-Mateos et al. (2009), Wiebe et al. (2009), Willmer et al. (2009). Then, we estimated the 250-to-500 μm flux density ratio and, using Eq. (4), the ratio Mdust/(f350D2) assuming Mdust/MH = 0.01 (Draine & Li 2007) and mH = 1.67 × 10-27 kg. The red points in Fig. 1 show the relation between Mdust/(f350D2) and the 250 μm-to-500 μm flux density ratio so obtained. We recover a relation extremely similar to the one found for the modified black-body case (see also Magrini et al. 2011). There is almost no systematic offset (~0.01 dex) between the two methods and the typical scatter between dust mass estimates using the two approaches is ~ 0.02 dex (see also Appendix A). We have also compared the results obtained from this method with the dust masses estimated via SED fitting for those galaxies in the HeViCS footprint for which PACS 100 and 160 μm are available. We find that the two techniques provide consistent results with no systematic effects and a typical scatter of ~ 0.10 dex (see also Appendix A).
In summary, we have developed a simple method that allows us to estimate dust masses from just the three SPIRE flux densities. In the rest of the paper we will use the dust masses obtained from the 350 μm flux density and the 250-to-500 μm ratio assuming a modified black-body with β = 2. For the non-detections, upper limits to the dust masses are computed by using the average log (f250/f500) colour observed for the detections (0.75). Given the uncertainty in each flux density measurement, the typical statistical error in the dust mass is ~ 0.2 dex (not including systematics due to assumptions on the dust properties). For the estimate of the dust mass, we also treated as non-detections those objects for which the submm emission is clearly affected by synchrotron emission: i.e., M 84 and M 87 (see also Boselli et al. 2010a; Baes et al. 2010). The exact functional forms used for extended and point sources, as well as the one obtained for different values of β are presented in Appendix B.
2.2.3. The effect of the dust emissivity on the dust mass estimate
We have shown that our empirical method is consistent with a typical SED fitting technique, once the properties of the underlying dust population are fixed. The Draine et al. (2007) model is consistent with β = 2 at these wavelengths, so it is not completely surprising that we obtain similar results when compared with a modified black-body with β = 2. Unfortunately, the absolute value of the dust opacity and its dependence on frequency are still quite uncertain (e.g., Finkbeiner et al. 1999; Dupac et al. 2003; Gordon et al. 2010; Paradis et al. 2010; Planck Collaboration et al. 2011) and it is therefore crucial to investigate how this assumption can affect our analysis. It is easier to address this issue by discussing separately a change in the absolute value of dust opacity and in the β parameter. A variation in the absolute value of κ350 would just shift all our dust estimates up and down without affecting any correlation (and its significance) that we may find. In other words, this will just move systematically the y-axis in all our plots. Much more critical would be a change in the value of β, since this could not only create systematic offsets in the dust mass estimates but also alter the shape of the scaling relations by introducing secondary effects with the quantities we are interested in (e.g., stellar mass, colour and stellar mass surface density), thus undermining the reliability of our analysis. Therefore, in Appendix A, we have investigated how our analysis would be affected by using other values of β: namely, 1, 1.5 and 2.5. We find that, in addition to a systematic shift in the dust mass values (up to ~ 1 dex when moving from β = 2.5 to 1), a change of β would also introduce some artificial trends, in particular with stellar mass and stellar mass surface density. In particular, moving from β = 2.5 to β = 1 dust masses would gradually decrease, but galaxies with higher stellar masses and stellar mass surface densities would be more (~0.2 dex) affected than lower mass systems. Luckily, such differences between high and low stellar mass systems starts to be important only for β < 1.5. For β ≥ 1.5 the scatter in the relations is ≤ 0.1 dex, i.e. comparable to, or lower than, the scatter in our method and, as we will see, significantly lower than the typical dynamical range covered by the scaling relations we investigate here. Moreover, it is important to note that the bluest submm colours in our sample (i.e., f250/f500 > 7.5) cannot be reproduced by a single modified black-body with β = 1 (see also Boselli et al. 2012).
Thus, we can confidently proceed by estimating the dust masses using the technique developed above for a modified black-body with β = 2, and we will discuss throughout the text if and how much different values of β could influence our conclusions. Given all the caveats discussed above, we remind the reader to be cautious of the absolute values of dust masses presented here, and to mainly focus on the trends and differences between the various samples discussed in the rest of the paper.
2.3. Ultraviolet, optical, and HI data
The Herschel/SPIRE data have been combined with multiwavelength observations covering the ultraviolet, optical and Hi regime. A detailed description of these datasets and of the derived quantities is given in Cortese et al. (2011). Briefly, optical broad-band photometry has been obtained from the Sloan Digital Sky Survey DR7 (SDSS-DR7, Abazajian et al. 2009) database. GALaxy Evolution eXplorer (GALEX, Martin et al. 2005) near-ultraviolet (NUV; λ = 2316 Å: Δλ = 1069 Å) images have been mainly obtained as part of two on-going GALEX Guest Investigator programs (GI06-12, P.I. L. Cortese and GI06-01, GALEX Ultraviolet Virgo Cluster Survey, Boselli et al. 2011). Additional frames have been obtained from the GALEX GR6 public release. The SDSS images were registered to the GALEX frames and convolved to the NUV resolution. Isophotal ellipses were then fit to each image, keeping fixed the center, ellipticity and position angle (generally determined in the i-band). The sky background was determined within rectangular regions around the galaxy and subtracted from the images before performing the ellipse fitting. Asymptotic magnitudes have been determined from the growth curves obtained following the technique described by Gil de Paz et al. (2007) and corrected for Galactic extinction assuming a Cardelli et al. (1989) extinction law. An extensive description of GALEX and SDSS measurements as well as all the fluxes will be presented in a future work (Cortese et al., in prep.). Stellar masses M∗ are determined from i-band luminosities Li using the g − i colour-dependent stellar mass-to-light ratio relation from Zibetti et al. (2009), assuming a Chabrier (2003) initial mass function (IMF). We assume a typical uncertainty of 0.15 dex in the stellar mass estimate.
Atomic hydrogen masses have been estimated from Hi 21 cm line emission data (mainly single-dish), available from the literature (e.g., Springob et al. 2005; Giovanelli et al. 2007; Kent et al. 2008; Gavazzi et al. 2003 and the NASA/IPAC Extragalactic Database, NED). As described in Cortese et al. (2011), we estimate the Hi deficiency parameter (DefHI, defined as the difference, in logarithmic units, between the expected Hi mass for an isolated galaxy with the same morphological type and optical diameter of the target and the observed value, following Haynes & Giovanelli 1984) using coefficients that vary with morphological type. These coefficients have been calculated for the following types (see also Table 3 in Boselli & Gavazzi 2009): S0a and earlier (Haynes & Giovanelli 1984), Sa-Sab, Sb, Sbc, Sc (Solanes et al. 1996) and Scd to later types (Boselli & Gavazzi 2009). It is important to remember that, for morphological types earlier than Sa, the estimate of the expected Hi mass is highly uncertain (see also Cortese et al. 2011). In the following, we will consider as “Hi-deficient” galaxies those objects with DefHI ≥ 0.5 (i.e., galaxies with 70% less hydrogen than isolated systems with the same diameter and morphological type).
In order to avoid any possible bias in the comparison among the various scaling relation, in this paper we focus our attention only on those galaxies for which Herschel as well as Hi, NUV and SDSS observations are currently available: 282 galaxies (~87% of the whole HRS, namely 234 late- and 48 early-type galaxies). In Fig. 2, we compare the K-band luminosity distribution of the whole HRS (black) and the one of the sub-sample here investigated (blue). It is clear that our sub-sample provides a fair representation of the HRS and therefore the scaling relations investigated in the rest of the paper should be representative of the local galaxy population as a whole.
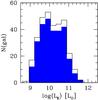 |
Fig. 2 The K-band luminosity distribution for the whole HRS (black) and for the sub-sample analyzed in this paper (blue). |
 |
Fig. 3 The dust-to-stellar mass ratio as function of stellar mass (upper left), NUV − r colour (upper right), concentration index (lower left) and stellar mass surface density (lower right). Circles and triangles show Herschel detections and non-detections, respectively. The typical errors associated with our galaxies are indicated on the bottom-left corner of each panel. |
 |
Fig. 4 The dust-to-stellar mass ratio as function of stellar mass (top row), NUV − r colour (middle row), and stellar mass surface density (bottom row) for HI-normal (first column), HI-deficient (second column) galaxies, systems outside (third column) and inside (fourth column) the Virgo cluster. Circles and black triangles indicate detections and non-detections respectively. The average relations for HI-normal (solid), HI-deficient (long-dashed) galaxies, systems outside (dotted) and inside (short dashed) the Virgo cluster are presented in the fifth column. In the third and fourth column Hi-deficient galaxies outside the Virgo cluster and Hi-normal Virgo galaxies are highlighted in red and blue, respectively. |
3. The dust-to-stellar mass ratio
As a first step in order to quantify how the dust content varies as a function of integrated galaxy properties, we plot in Fig. 3 the dust-to-stellar mass ratio as a function of stellar mass M∗ (upper-left panel), observed NUV − r colour (upper-right), concentration index in r-band [C31(r), defined as the ratio between the radii containing 75% and 25% of the total r-band light7] and stellar mass surface density μ∗ [i.e., 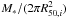 , where R50,i is the radius containing 50% of the total i-band light]. Circles and triangles indicate detections and upper-limits, respectively. The dust-to-stellar mass ratio strongly anti-correlates with M∗, NUV − r (a proxy for SSFR; e.g., Schiminovich et al. 2007) and μ∗, while a very weak non-linear trend is observed with the concentration index. The tightest correlation is with the observed NUV − r colour (Pearson correlation coefficient r = −0.85, dispersion along the y-axis σ = 0.38 dex)8, while the scatter gradually increases for the stellar surface density (r = −0.79, σ = 0.45 dex) and stellar mass (r = −0.68, σ = 0.53 dex). These results are remarkably similar to the scaling relation involving the HI-to-stellar mass ratio (Cortese et al. 2011; Catinella et al. 2010; Fabello et al. 2011), suggesting that the dust and atomic hydrogen content of galaxies might be directly linked.
, where R50,i is the radius containing 50% of the total i-band light]. Circles and triangles indicate detections and upper-limits, respectively. The dust-to-stellar mass ratio strongly anti-correlates with M∗, NUV − r (a proxy for SSFR; e.g., Schiminovich et al. 2007) and μ∗, while a very weak non-linear trend is observed with the concentration index. The tightest correlation is with the observed NUV − r colour (Pearson correlation coefficient r = −0.85, dispersion along the y-axis σ = 0.38 dex)8, while the scatter gradually increases for the stellar surface density (r = −0.79, σ = 0.45 dex) and stellar mass (r = −0.68, σ = 0.53 dex). These results are remarkably similar to the scaling relation involving the HI-to-stellar mass ratio (Cortese et al. 2011; Catinella et al. 2010; Fabello et al. 2011), suggesting that the dust and atomic hydrogen content of galaxies might be directly linked.
As discussed in the previous section, it is important to investigate if and how the assumptions made on the dust properties of our sample can affect the shape and significance of the scaling relations. In Appendix A we show that only for β < 1.5 systematic effects start to be significant (i.e., ~ 0.12 dex). However, when moving from β = 2 to β < 1.5, the decrease in the value of the dust mass would be larger for massive, high stellar mass surface density galaxies, effectively reinforcing the strong correlations between the dust-to-stellar mass ratio and stellar mass, stellar mass surface density and NUV − r colours. Thus we conclude that the main trends shown in Fig. 3 are independent of the assumptions on the dust properties of the HRS.
Recently, Cortese et al. (2011) have shown that the HI scaling relations for the whole HRS are slightly biased towards lower gas content, with respect to the average scaling relation of local galaxies (e.g., Catinella et al. 2010; Fabello et al. 2011). This is because, by construction, nearly half of the galaxies in the HRS belong to the Virgo cluster. In order to test whether this is also the case for the dust scaling relations, and to characterize the relation between dust-to-stellar mass ratio in different environments, we have divided our sample into four different subsets: (a) Hi-normal (i.e., DefHI < 0.5, 158 galaxies) and (b) Hi-deficient (i.e., DefHI ≥ 0.5, 124 galaxies) systems, (c) galaxies outside the Virgo cluster (144 galaxies) and (d) galaxies belonging to one of the Virgo cluster clouds (Virgo A, B, N, E and S as defined by Gavazzi et al. 1999, 138 galaxies). The two pairs (a) − (b) and (c) − (d) are mutually exclusive, while the other combinations are not; thus these are complementary sub-samples. The scaling relations for the four samples are plotted in Fig. 4. In order to properly quantify the difference between different environments, in the right most panel of Fig. 4 and in Table 1 we present the average trends (i.e., ⟨ log (Mdust/M∗) ⟩ ) for each subsample, determined by placing the non-detections to their upper-limit. Although for all four samples the dust-to-stellar mass ratio decreases with stellar mass, colour and stellar mass surface density, galaxies in different environments have different dust contents. In particular, for fixed stellar mass and stellar mass surface density, Virgo and Hi-deficient galaxies have, on average, a lower dust-to-stellar mass ratio than Hi-normal/field galaxies. This difference is particularly strong between Hi-normal and Hi-deficient galaxies (i.e., ~0.5–0.7 dex), while it is less remarkable (i.e., ~0.2–0.4 dex) when galaxies are separated accordingly to the environment they inhabit, suggesting that the atomic hydrogen content is more important than the local environment in regulating the positions of galaxies in the scaling relations.
In order to better quantify the difference between the various subsamples, we estimated the residuals of the Hi-deficient and Virgo galaxies from the mean trends observed for Hi-normal and galaxies outside Virgo, respectively. A simple χ2 test indicates that Hi-deficient and Hi-normal galaxies do not follow the same Mdust/M∗ vs. M∗ and Mdust/M∗ vs. μ∗ relations at >99.99% significance level. Galaxies in and outside Virgo do not follow the same Mdust/M∗ vs. M∗ and Mdust/M∗ vs. μ∗ relations at a ~99.7% and ~98% level, respectively. A similar conclusion is reached if, instead of performing a χ2, we just compare the median residuals of the two populations: while Hi-deficient and Hi-normal galaxies differ by ~7−8σ, galaxies inside and outside the Virgo cluster show just a ~2−3σ difference. The shift towards lower dust content for Hi-deficient/Virgo galaxies is also confirmed by the fact that the vast majority of non-detections are found among gas-poor cluster galaxies. Finally, also the scatter of the Mdust/M∗ vs. M∗ and Mdust/M∗ vs. μ∗ relations varies among the four sub-samples here considered: from ~0.4−0.3 dex to ~0.6−0.5 dex when moving from Hi-normal to Hi-deficient systems and from ~0.57−0.44 dex to ~0.63−0.5 dex when moving from objects outside and inside Virgo, respectively.
Average scaling relations for the four samples discussed in Sect. 3.
It is quite easy to understand why a rough cut in environment is less powerful in isolating dust poor systems than a cut in gas content. On one side, our Virgo sample still includes Hi-normal star-forming galaxies not yet affected by the cluster environment (Boselli & Gavazzi 2006; Cortese & Hughes 2009). On the other side, we find Hi-deficient galaxies also outside Virgo (Cortese et al. 2011). These two factors together reduce the difference between the two samples. This is clearly shown in Fig. 4 where Hi-deficient field galaxies and Hi-normal Virgo galaxies are highlighted. It is also important to remember that, due to the lack of statistics available outside the Virgo cluster (in particular for early-type galaxies), it is impossible to perform a more detailed investigation of environmental effects at the scale of galaxy groups and pairs.
Contrary to the Mdust/M∗ vs. M∗ and Mdust/M∗ vs. μ∗ relations, the relation between Mdust/M∗ vs. NUV − r does not show any clear variation with environment or Hi content. Although gas-poor Virgo systems cover a larger range of colours and are offset towards redder colours than Hi-normal “field” galaxies, all the four sub-samples here considered apparently lie on the same scaling relation at a >85% significance level. This is different from what is observed in the case of the Hi scaling relations (Cortese et al. 2011), where also the HI-fraction vs. NUV − r colour relation showed a variation with the environment. As we will see in the next sections, the independence of the Mdust/M∗ and NUV − r on environment is consistent with a scenario in which dust is removed mainly when the environment is able to strip the ISM directly from the optical disk, thus reducing the star formation and moving a galaxy along the main relation. Being the NUV − r colour a proxy for SSFR, our findings do not only confirm the recent results of da Cunha et al. (2010), who pointed out the existence of a tight relation between star formation and dust mass in nearby galaxies. They also suggest that this relation might be a very useful tool for chemical evolution models, since it is apparently not affected by the environment. It is important to remember that our colours are not corrected for internal dust attenuation and therefore part of the scatter at red colours could easily be due to the fact that we are mixing truly passive objects with highly obscured ones. We plan to investigate in more detail the relation between total SFR and dust mass in a future paper, once accurate dust extinction corrections are developed.
 |
Fig. 5 The Mdust/M∗ as a function of the morphological type. Black filled and red empty circles are HI-normal and HI-deficient galaxies, respectively. Upper limits are indicated by green triangles. The large empty rectangles indicate the average value and its error for HI-normal (black) and HI-deficient (red) galaxies in each morphological type. In case only one galaxy is available in a bin, only a line is shown. |
In summary, once combined our results indicate that, at fixed stellar mass and stellar mass surface density, the dust content of nearby galaxies varies as a function of environment and Hi content, although the effect of the environment on the dust seems to be weaker than in the case of the Hi.
Finally, since galaxy properties are also tightly linked to optical morphology (e.g., Roberts & Haynes 1994), it is interesting to investigate how the Mdust/M∗ ratio varies as a function of morphological type. As shown in Fig. 5, the Mdust/M∗ ratio rapidly decreases when moving from late- to early-type galaxies (see also Skibba et al. 2011). A detailed analysis of the dust properties of early-type galaxies in the HRS is presented by Smith et al. (2012). Not surprisingly, almost all the non-detections are early-type galaxies. Moreover, even at fixed morphological type, we find that Hi-deficient objects have a significantly smaller dust content than Hi-normal systems, reinforcing once more one of the main results emerging from this section: i.e., when the Hi is removed from a galaxy the dust content is affected as well. This is even more evident when the mean Mdust/M∗ ratios per bin of morphological type and their standard deviations (i.e., the large rectangles in Fig. 5) are considered.
 |
Fig. 6 The dust-to-HI mass ratio as a function of stellar mass (right panel), NUV − r colour (central panel) and stellar mass surface density (left panel). Filled and empty circles indicate HI-normal and HI-deficient galaxies, respectively. Arrows show upper limits in either dust or Hi mass. Typical errorbars are shown in the bottom-right corner of each panel. |
4. The dust-to-HI mass ratio
In the previous section we have shown that the Mdust/M ∗ ratio follows scaling relations very similar to the ones observed for the HI-to-stellar mass ratio, suggesting that these two components of the ISM are tightly linked. In this section we investigate the variation of the Mdust/MHI ratio as a function of internal galaxy properties and environment following a similar approach as above. We focus on the separation between Hi-deficient and Hi-normal galaxies, since this turned out to be the ideal one to investigate environmental trends.
In Fig. 6 we show the Mdust/MHI ratio as a function of stellar mass, NUV − r colour and stellar mass surface density. Filled and empty symbols indicate Hi-normal and Hi-deficient galaxies, respectively. Arrows indicate both upper limits in Hi mass or in dust mass. Galaxies not detected at both radio and submm wavelengths are not shown. Contrary to what observed for the Mdust/M∗ ratio, the dust-to-HI ratio varies less than 2 dex. Almost no correlation is found with the stellar mass surface density (r = 0.1) while a weak correlation is found with stellar mass and NUV − r colour (r ~ 0.31 and dispersion along the y-axis ~ 0.37 dex). These relations become even weaker if we focus on Hi-normal galaxies. The Mdust/MHI vs. M∗ relation is still significant (r ~ 0.28), showing that the Mdust/MHI ratio is an increasing function of stellar mass, as expected from the stellar mass vs. gas metallicity relation (e.g., Tremonti et al. 2004). Conversely, the correlation coefficient for the Mdust/M∗ vs. NUV − r relation drops to r ~ 0.07. This is mainly due to the presence of outliers at red colours (NUV − r > 4), some of which are likely red just because they are highly attenuated and not because they are passive. If we limit our analysis to galaxies with NUV − r < 4 the correlation coefficient increases to ~0.4.
One of the most interesting results emerging from Fig. 6 is indeed the different behavior of Hi-deficient and Hi-normal galaxies. The dynamic range covered by the Mdust/MHI ratio almost doubles when Hi-deficient galaxies are included into the picture. At fixed stellar mass, Hi-deficient objects have systematically higher Mdust/MHI ratios than Hi-normal galaxies. A similar offset is observed for the stellar mass surface density, although more pronounced at high μ∗, whereas in the Mdust/MHI vs. NUV − r relation Hi-deficient galaxies appear mainly to extend the relation already seen for Hi-normal galaxies to redder colours, confirming that the gas removal and the reddening of the colours (i.e., quenching of the star formation) are related (Boselli & Gavazzi 2006; Boselli et al. 2008; Cortese & Hughes 2009). This suggests that, when the gas is removed, the fraction of dust stripped from the galaxy is significantly lower than the Hi, thus automatically increasing the Mdust/MHI ratio in these objects. Similar results are obtained if we investigate the variation of the Mdust/MHI ratio as a function of morphological type (see Fig. 7). The Mdust/MHI ratio is almost independent of morphological type, showing (in the case of Hi-normal galaxies) a very small decrease only towards either early-type or irregulars/BCDs, consistent with what previously observed by Draine et al. (2007) for SINGS galaxies. At fixed morphological type, Hi-deficient galaxies have higher Mdust/MHI ratio, confirming that the dust is less affected by the environment than the gas.
In addition to Hi-deficient galaxies showing a higher Mdust/MHI ratio than normal, it is interesting to note the presence of a few outliers having Mdust/MHI significantly lower ( ≲ 10-3) than the average value for Hi-normal systems (~10-2.1), namely: NGC 3657, NGC 4203, NGC 4262, NGC 4636 and UGC 8045. In the case of UGC 8045 and NGC 4636 the low Mdust/MHI could just be due to a problem with the estimate of the Hi mass. UGC 8045 could indeed be confused in Hi (i.e., more than one galaxy included in the Arecibo beam, Kent et al. 2008) and in the case of NGC 4636 values published in the literature vary between ~109 M⊙ (Gavazzi et al. 2003; Knapp et al. 1978) and <8 × 107 M⊙ (Krishna Kumar & Thonnard 1983). Conversely, we can exclude a measurement problem for NGC 3657, NGC 4203 and NGC 4262 and conclude that these systems have significantly higher amounts of atomic hydrogen compared to their dust content. This is confirmed when we look in detail at the properties of these systems. NGC 4203 and NGC 4262 have peculiar Hi morphologies (Krumm et al. 1985; van Driel et al. 1988) and several independent analyses have proposed that these galaxies might have recently accreted cold gas (see Cortese & Hughes 2009 and references therein). Although no Hi interferometric data are available for NGC 3657, the huge ultraviolet extended disk revealed by GALEX images (see Fig. 8) suggests that this galaxy likely contains an extended Hi reservoir. Thus, we speculate that the unusually low Mdust/MHI ratio observed in these systems may be due to the presence of a considerable amount of pristine gas not yet enriched by star formation, either because it has been recently accreted or because it has too low column density to form stars at high rate. Unfortunately, no gas metallicity estimates for the outer parts of these galaxies are available. If confirmed, this result would suggest the use of the Mdust/MHI ratio as an alternative method to identify objects that have recently accreted a significant amount of pristine gas.
 |
Fig. 8 The extended UV disk of NGC 3657. SDSS-optical (left), GALEX-NUV (center) and Herschel/SPIRE 250 μm (right) images are compared on the same spatial scale. |
Finally, there is a caveat to this discussion; as discussed in Appendix A the relation between Mdust/MHI and stellar mass could become gradually weaker for β < 2 (e.g., for β = 1.5 the correlation coefficient of the Mdust/MHI vs. M∗ relation decreases to ~0.27) and it might almost disappear in the extreme case of β ~ 1.
5. Discussion
5.1. The origin of the dust scaling relations
We have shown that the dust-to-stellar mass ratio strongly anti-correlates with stellar mass, stellar mass surface density and colour over the whole dynamic range covered by the HRS, reproducing remarkably well similar scaling relations observed for the Hi-to-stellar mass ratio (Catinella et al. 2010; Cortese et al. 2011). Similarly, the dust-to-stellar mass ratio monotonically decreases when moving from late- to early-type galaxies. Although some of these scaling relations are not new [e.g., da Cunha et al. (2010) has recently shown that the Mdust/M∗ ratio strongly anti-correlates with SSFR], this is the first time that we can accurately quantify them for a volume-limited sample of galaxies spanning all morphologies and for which Hi information is available.
Once the prediction of dust formation and evolution models are taken into account (e.g., Dwek 1998; Edmunds 2001; Calura et al. 2008), it is quite easy to understand where these scaling relations are coming from. As nicely described by da Cunha et al. (2010), the trends shown in Fig. 3 can be seen as the result of the variation of SSFR with stellar mass (e.g., Boselli et al. 2001; Schiminovich et al. 2007). Low mass, late-type systems are characterized by high SSFR and gas fraction. The gas can sustain the star formation activity and, consequently, a large fraction of dust is formed, likely exceeding the amount of dust grains destroyed in the ISM. When we move to higher stellar mass and earlier morphological types, the SSFR and gas fraction start decreasing and, as a result, the amount of dust produced will no longer be able to overcome those destroyed in the meantime. This would naturally explain why the dust-to-stellar mass ratio decreases with stellar mass, SSFR, stellar mass surface density and when moving from irregulars to elliptical galaxies. In other words, what we are looking at is the change of the amount of baryonic mass stored in the ISM as a function of internal galaxy properties, explaining why Hi and dust follow the same scaling relations.
To test this scenario qualitatively, we use the simple analytical approach developed by Edmunds (2001) in the case of a closed-box. We use his Eqs. (5) and (11) to determine how the dust-to-stellar mass ratio evolves as a function of the gas fraction. The model has six free parameters: namely, the efficiency of dust condensation from heavy elements made in stellar winds from massive stars and supernovae (χ1) and from asymptotic giant branch stars (χ2), the effective yield (p), the fraction of mass of the ISM locked into stars (α), the fraction of the ISM where mantles can grow (ϵ) and the fraction of dust destroyed by star formation (δ). Here we assume χ1 = 0.2 (Morgan & Edmunds 2003), χ2 = 0.5 (Zhukovska et al. 2008), p = 0.012 and α = 0.80 (i.e., consistent with a Chabrier 2003 IMF), δ = 0.3 (Edmunds 2001) and ϵ = 0.5. In order to estimate the total amount of gas of our galaxies from the Hi masses, we assume a molecular-to-atomic hydrogen gas ratio of 0.38 (Saintonge et al. 2011) and include the contribution of helium and heavy elements (i.e., a factor 1.36). The overall trend is not significantly affected if we account only for the contribution from atomic gas in the estimate of the gas fraction. We note that the goal of this exercise is just to establish whether the predictions of a simple closed-box model are roughly consistent with the shape of the trends we find. There are many free parameters and assumptions in the modeling, as well as a large uncertainty in the absolute value of our dust masses, thus looking for an exact fit does not seem meaningful at this stage. In addition, this is just a simple close-box model, whereas the evolutionary history of some galaxies in our sample (in particular early-type systems) might have been significantly different. The prediction of this simple model are shown in Fig. 9. As expected, the Mdust/M∗ ratio decreases with the gas fraction confirming that the scaling relations we found are just a consequence of the tight link between dust and the cold gas in the ISM. Interestingly, the five galaxies with unusually low dust-to-Hi ratio, discussed in Sect. 4, are also outliers in Fig. 9. Thus, for these objects, a closed-box approximation is likely inadequate. Our model is also unable to reproduce the very dust-rich systems in our sample. A similar tension between observations and models was recently found by Dunne et al. (2011) studying the properties of galaxies in the H-ATLAS survey. By comparing more detailed models predictions with observations they show how theoretical models are not able to reproduce galaxies with log (Mdust/M∗) > −2.5. The origin of this disagreement is still unclear, but we note that it may partially be solved if β is lower than 2. We plan to investigate further this issue in the future when more accurate dust estimates will become possible.
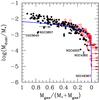 |
Fig. 9 The dust-to-stellar mass ratio as a function of the total gas fractions for HRS galaxies. The solid blue line shows the predictions of a simple closed-box models (Edmunds 2001). See the text for details. The five galaxies with low dust-to-Hi ratio mass discussed in Sect. 4 are highlighted. Symbols are as in Fig. 6. |
 |
Fig. 10 Left: the relation between dust-to-stellar mass and HI deficiency. Right: the relation between dust-to-stellar mass and HI-to-stellar mass ratio. The dotted lines indicate constant HI-to-dust ratios of (from left to right): 30-100-300. The green lines indicate two different models of dust stripping assuming a constant (dashed) or exponential (solid) Hi surface density profile. See text for details. Symbols are as in Fig. 6. |
5.2. Dust stripping
The other important result emerging from our analysis is that at fixed stellar mass, stellar mass surface density and morphology, Hi-deficient/Virgo cluster galaxies have systematically lower Mdust/M∗ and higher Mdust/MHI ratios than Hi-normal/field systems. Once combined, these two independent results provide a consistent picture of the effects of the environment on the dust content of cluster galaxies. On one side, the reduction in the Mdust/M∗ ratio is a clear evidence for dust removal in cluster galaxies. This is reinforced by Fig. 10 (left), where we show that the Mdust/M∗ ratio strongly decreases as a function of Hi deficiency (see also Corbelli et al. 2011). On the other side, the higher Mdust/MHI ratio indicates that the effect of the environment on the dust content is significantly less dramatic compared to the amount of Hi stripped from the disk and dispersed into the intra-cluster medium. As already suggested by Cortese et al. (2010b), this could be easily explained if the dust disk is significantly less extended than the gas disk (Thomas et al. 2004) or, in other words, if the dust-to-gas ratio decreases monotonically with increasing distance from the center of galaxies (Bendo et al. 2010; Muñoz-Mateos et al. 2009; Pohlen et al. 2010; Magrini et al. 2011).
We test this interpretation in the right panel of Fig. 10, where we compare the strong correlation between Mdust/M∗ and MHI/M ∗ found in our data, with the predictions of a very simple toy model. We assume that the stripping of the ISM is outside-in, with the outer parts being affected before the galaxy center, as expected in a ram-pressure stripping scenario (Koopmann et al. 2006; Boselli & Gavazzi 2006; Boselli et al. 2006; Cortese et al. 2011). Once the stripping starts, all the components of the ISM (i.e., both gas and dust) are completely removed from the disk up to the truncation radius. The dust mass surface density profile is exponential while we consider two different surface density distributions for the Hi. In the first one (solid line in Fig. 10), the Hi profile is exponential and the scalelength of the Hi disk is just 1.5 times the one of the dust disk (Thomas et al. 2004). In the second one (dashed line in Fig. 10), the Hi profile is constant (Bigiel et al. 2010) and extends up to 8 times the scalelength of the dust disk. This corresponds to a Hi radius 1.5 times the optical/dust radius assuming that the dust follows the stellar distribution and that the ratio between optical scale-length and optical radius is ~5.3 (Gavazzi et al. 2000). Both models are normalized so that the unperturbed galaxy has the typical log (Mdust/M∗) of Hi-normal galaxies (~−2.46 dex) and Mdust/MHI = 100. We note that these two cases represent two extremes in the difference between the dust and Hi distribution in galaxies. In Fig. 10 (right) we show the evolution of the Mdust/M∗ and MHI/M∗ predicted by the two models for different values of stripping radius. As expected, the range covered by these models reproduces the difference in Mdust/M∗ and MHI/M∗ between Hi-normal and Hi-deficient galaxies. This supports our simple interpretation that the dust is affected by the environment in a less dramatic way than the Hi just because, like the molecular gas, it is more centrally concentrated than the atomic gas component. These results confirm once more dust stripping by environmental effects as an important mechanism for injecting dust grains into the intra-cluster medium, thus contributing to its metal enrichment (Popescu et al. 2000).
The clear evidence of dust stripping emerging from our analysis leaves open the possibility that also the molecular hydrogen component in galaxies could be significantly perturbed in the center of clusters of galaxies. However, this issue is still highly debated (Boselli et al. 2002; Fumagalli et al. 2009) and, as clearly shown by our analysis, only a detailed comparison of molecular hydrogen properties for galaxies in different environment but with the same morphological type and stellar mass, will eventually allow us to quantify if and how molecules are directly removed from the star forming disks of infalling spirals.
6. Summary
In this paper, we have combined Herschel/SPIRE observations with optical, Hi and UV data to investigate the relation between dust content, galaxy properties and environment for the Herschel Reference Survey, a volume- magnitude- limited sample of ~300 galaxies. Our main results are as follows:
-
We find that the dust-to-stellar mass ratio strongly anti-correlateswith stellar mass, stellar mass surface density and NUV − r color across the whole range of parameters covered by our sample. These relations are followed by all galaxies, regardless of environment or gas content, but Virgo/Hi-deficient galaxies show a systematically lower dust-to-stellar mass at fixed stellar mass and morphological type.
-
Significantly weaker correlations are found between the dust-to-Hi mass ratio and internal galaxy properties, with the Mdust/MHI ratio mildly increasing with stellar mass, as expected from the mass-metallicity relation. Gas-poor cluster galaxies have systematically higher dust content per unit of Hi mass than Hi-normal systems.
-
We show that the differences observed between Hi-deficient and Hi-normal galaxies provide strong evidence for dust stripping in cluster galaxies. However, we demonstrate that the fraction of dust removed from the disk is significantly lower than the Hi, and that this is likely just a consequence of the fact that the Hi disk is much more extended than the dust disk or, in other words, that the dust-to-atomic hydrogen ratio quickly declines in the outer regions.
-
Finally, we compare our results with the prediction of simple models of dust formation and evolution showing that the trends here presented are consistent with a simple picture in which the amount of dust in galaxies is regulated by the star formation activity and cold gas content.
Although this work represents just the first step in the understanding of dust properties in galaxies, our investigation highlights the power of the HRS as an ideal local sample for galaxy evolution studies. The natural extension of the present analysis will be the study of the relation between dust properties, molecular hydrogen content and gas metallicity. Only after molecules and heavy elements in the ISM are included into the picture and more accurate dust mass estimates are available, will it be really possible to unveil the role of dust on galaxy evolution not only providing strong constraints for theoretical models but also a reference for high-redshift studies, i.e., the primary goal of a survey such as the HRS.
Online material
Appendix A: Testing the dust mass estimate based on SPIRE flux densities only
In this Appendix we investigate the reliability of the method described in Sect. 2.2 to estimate dust masses. We proceed as follows. We compare our estimates with different methods all based on roughly the same assumptions on the properties of the underlying dust population (i.e., the value of β and its variation with frequency). This is aimed at validating the methodology presented here. Then, we use our method for different values of β to study how the assumption β = 2 made in this paper could affect our results. In both cases we are interested in the average difference and standard deviation between the various methods and in the presence of any possible systematic trend with stellar mass, stellar mass surface density and NUV − r colour.
 |
Fig. A.1 The logarithmic difference between the dust mass estimates presented in this work and those obtained from modified black-body SED fitting of PACS+SPIRE (top row) and SPIRE-only (second row) data, using the SED library of Draine & Li (2007, third row) and using just the 350 μm luminosity without any colour information (bottom row). For each row, the right panel shows the histogram of the difference, its average value and standard deviation of the population. The empty circles in the top two rows indicate points for which the SED fitting routine provided a χ2 > 1. |
The results of the first step are shown in Fig. A.1. In each row we show the difference between the logarithm of the dust mass obtained from two different methods as a function of stellar mass, NUV − r colour and stellar mass surface density. In the right most panel we also present the histogram of the distribution of the difference, its average value and standard deviation.
First of all, we compare our results with the ones obtained by Davies et al. (2012) for the 55 galaxies in common with our work (top row in Fig. A.1). These are obtained using a single modified black-body SED fitting of the five PACS+SPIRE flux densities at 100, 160, 250, 350 and 500 μm and assuming the same dust emissivity as in this paper. In our analysis we only considered the points for which the SED fitting routine gives a χ2 < 1, but in Fig. A.1 we also show as empty circles the galaxies with χ2 > 1. We do not find any systematic difference in the average dust mass estimate and the scatter between the two methods is of the order of ~ 0.1 dex, not significantly larger than the uncertainty of ~0.08 dex in the dust mass estimate from the SED fitting technique (Davies et al. 2012). Small systematic trends in the dust mass estimate are found as a function of stellar mass and stellar mass surface density. However, these are just marginal and within the error assumed throughout the paper.
Secondly, we consider the case of SED fitting of SPIRE-only points, following the same technique described above. Interestingly, we find a perfect agreement between the two methods and we could in theory just use the SED fitting of SPIRE fluxes only. The main reason why we decided not to do so is that the best fitting SED is significantly different from the one obtained by Davies et al. (2012) when combining PACS and SPIRE data since no constraint is provided below 250 μm. Therefore these are likely not a good representation of the far-infrared/submm emission for our galaxies and we preferred not to use them. Moreover, it is sometimes difficult to trust the uncertainty determined from the fitting technique since only based on the three SPIRE data.
Thirdly, we compare the estimate obtained from our method assuming a modified black-body SED and the one obtained from the same method but assuming the Draine & Li (2007) SED (DL07) as described in Sect. 2.2. As shown in the third row of Fig. A.1 we find again a very good agreement between the two methods. This is due to the fact that, in the wavelength range covered by SPIRE, the SED predicted by the Draine & Li (2007) models is very similar to a single temperature modified black-body with β = 2 (see also Magrini et al. 2011).
 |
Fig. A.2 The 250-to-500 μm flux density ratio as a function of stellar mass (left), NUV − r colour (center) and stellar mass surface density (right). |
 |
Fig. A.3 The dust-to-stellar mass ratio as a function of stellar mass (left), NUV − r colour (center) and stellar mass surface density (right), for dust masses estimated from the 350 μm luminosities without taking into account any colour/temperature variation in the sample. Symbols are as in Fig. 3. The orange lines and dashed regions show the average scaling relations and ± 1σ area presented in Fig. 3. |
Finally, we consider the very simple case where only a submm flux density is available and no colour can be used (bottom row in Fig. A.1). In details, we just assumed the same 250-to-500 μm ratio for all our galaxies (i.e., the mean value for the detections in our sample log (f250/f500) = 0.75). This is done to investigate the role played by the colour term in our method and to warn how this very rough technique could affect scaling relations studies, in particular at high-redshift. As expected, this is by far the worse method to estimate dust masses showing a scatter of ~0.2 dex. More importantly, we find systematic trends with stellar mass and stellar mass surface densities showing that, when compared with our method, this technique underestimates dust masses for low-mass galaxies and overestimate those of massive systems. The reason for these systematic trends is due to the fact that the 250-to-500 μm flux density ratio strongly correlates with stellar mass and stellar mass surface density (see Fig. A.2 and Boselli et al. 2012). Thus not accounting for the different colours in our galaxies introduces systematic effects that can be seen in Fig. A.3, where we compare some of the scaling relations discussed in this paper (orange dashed regions) with those obtained using this method. While, as expected, the relation with NUV − r colour is not affected, the trends between dust-to-stellar mass ratio, stellar mass and stellar mass surface density change. We thus suggest caution in using a technique based on only a single luminosity for a detailed quantification of dust properties in galaxies.
In summary, these first tests confirm that our technique does not introduce any significant systematic effect, once the properties of the underlying dust component are fixed.
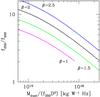 |
Fig. A.4 The relation between the ratio Mdust/(f350D2) and the 250 μm-to-500 μm flux density ratio for a modified black-body SED with β = 2.5 (blue), 2 (black), 1.5 (green) and 1 (magenta). |
The next step is to see what happens if we change the value of β, keeping fixed the value of dust opacity at 350 μm. In the following, we consider modified black-bodies with 1 ≤ β ≤ 2.5 which appear the most favoured range of values according to theoretical models and observations (Finkbeiner et al. 1999; Dupac et al. 2003; Gordon et al. 2010; Paradis et al. 2010; Planck Collaboration et al. 2011). It is important to note that, given the strong degeneracy between β and dust temperature we had to modify the range of dust temperatures investigated in order to recover the range of submm colours observed in the HRS. In detail, while for β = 2 and 2.5 we varied the temperature between 5 and 55 K, for β = 1.5 and 1 we had to vary the temperature between 15 and 230 K. Moreover, the case β = 1 is not able to reproduce the bluest colours observed in our sample (i.e., f250/f500 > 7.5, 37 galaxies in total) suggesting that this case is not a good representation of the dust SED for at least a fraction of our sample (see Fig. A.4). The results of our investigations are summarized in Fig. A.5. As expected, the absolute value of the dust mass varies with β by almost a factor 10. Values of β lower than 2 give dust masses smaller than the one used in this work, and viceversa. However, once this offset is taken into account, the intrinsic scatter in the dust mass estimate stays below ~0.1 dex for 1.5 ≤ β ≤ 2.5 and goes up to just 0.17 dex for β = 1 (for this case only those galaxies with f250/f500 ≤ 7.5 are included), although with a significant tail of outliers. Moreover, very mild systematic trends are observed as a function of stellar mass, colour and stellar mass surface density but these could become important only for β ~ 1. As discussed in the text, this would reinforce the trend observed between the dust-to-stellar mass ratio but weaken the one between dust-to-Hi mass ratio and stellar mass.
 |
Fig. A.5 The logarithmic difference between the dust mass estimates presented in this work and the one obtained assuming a modified black-body with β = 2.5 (top row), 1.5 (middle row) and 1 (bottom row). For each row, the right panel shows the histogram of the difference, its average value and standard deviation of the population. |
In conclusion, we can confidently state that the method presented here to estimate dust masses is a reliable solution when accurate SED fitting is not possible. The typical scatter with respect to our methods is of the order of ~0.2 dex. Although different values of β would imply different values of dust masses, the scaling relations discussed in this paper should remain valid at least for 1.5 ≤ β ≤ 2.5.
Appendix B: Recipes to estimate dust masses with SPIRE data only
In this Appendix we provide the polynomial fit to the relations between the ratio Mdust/(f350D2) in units of kg W-1 Hz and the 250 μm-to-500 μm flux density ratio which we used to estimate dust masses. We provide two different sets of coefficients obtained by convolving modified black-bodies characterized by different values of β (i.e., 1, 1.5, 2 and 2.5) with the SPIRE RSRF for extended and point-like sources (Table B.1). Once the value Mdust/(f350D2) has been computed, the dust mass can be obtained from the following equation 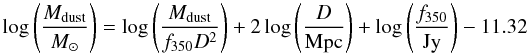 (B.1)
(B.1)
We note that the difference degrees used to fit β ≥ 2 and β < 2 are due to the different range of temperatures adopted for each case. For β < 2 we had to use larger temperature range (15 to 230 K instead of 5 to 55 K) and, as a consequence, an higher order polynomial to fit the relation between the 250 μm-to-500 μm and Mdust/(f350D2) ratios. The fits are optimized for the range of colours covered by our sample, i.e., 3 < f250/f500 < 11.
Relations to determine the Mdust/(f350D2) from the 250 μm-to-500 μm flux density ratio for extended sources and point sources.
With respect to the original selection described in Boselli et al. (2010b), we removed HRS228 because the redshift reported in NED turned out to be incorrect. In addition, after visual inspection and comparison with the literature, we revised the NED-based morphological type classification given in Boselli et al. (2010b) for six galaxies in our sample. In detail, NGC 4179 moved from Sb to S0, NGC 4438 from S0/a to Sb, NGC 4457 from S0/a to Sb, VCC1549 from Sb to dE, NGC 4691 from S0/a to Sa and NGC 5701 from S0/a to Sa (Sandage & Tammann 1981; Binggeli et al. 1985; Gavazzi et al. 2003; Cortese & Hughes 2009).
Acknowledgments
We thank all the people involved in the construction and the launch of Herschel. SPIRE has been developed by a consortium of institutes led by Cardiff University (UK) and including Univ. Lethbridge (Canada); NAOC (China); CEA, LAM (France); IFSI, Univ. Padua (Italy); IAC (Spain); Stockholm Observatory (Sweden); Imperial College London, RAL, UCL-MSSL, UKATC, Univ. Sussex (UK); and Caltech, JPL, NHSC, Univ. Colorado (USA). This development has been supported by national funding agencies: CSA (Canada); NAOC (China); CEA, CNES, CNRS (France); ASI (Italy); MCINN (Spain); SNSB (Sweden); STFC and UKSA (UK); and NASA (USA). HIPE is a joint development (are joint developments) by the Herschel Science Ground Segment Consortium, consisting of ESA, the NASA Herschel Science Center, and the HIFI, PACS and SPIRE consortia. GALEX is a NASA Small Explorer, launched in 2003 April. We gratefully acknowledge NASA’s support for construction, operation and science analysis for the GALEX mission, developed in cooperation with the Centre National d’Etudes Spatiales (CNES) of France and the Korean Ministry of Science and Technology. This publication makes use of data products from Two Micron All Sky Survey, which is a joint project of the University of Massachusetts and the Infrared Processing and Analysis Center/California Institute of Technology, funded by the National Aeronautics and Space Administration and the National Science Foundation. Funding for the SDSS and SDSS-II has been provided by the Alfred P. Sloan Foundation, the Participating Institutions, the National Science Foundation, the US Department of Energy, the National Aeronautics and Space Administration, the Japanese Monbukagakusho, the Max Planck Society, and the Higher Education Funding Council for England. The SDSS Web Site is http://www.sdss.org/. The SDSS is managed by the Astrophysical Research Consortium for the Participating Institutions. The Participating Institutions are the American Museum of Natural History, Astrophysical Institute Potsdam, University of Basel, University of Cambridge, Case Western Reserve University, University of Chicago, Drexel University, Fermilab, the Institute for Advanced Study, the Japan Participation Group, Johns Hopkins University, the Joint Institute for Nuclear Astrophysics, the Kavli Institute for Particle Astrophysics and Cosmology, the Korean Scientist Group, the Chinese Academy of Sciences (LAMOST), Los Alamos National Laboratory, the Max-Planck-Institute for Astronomy (MPIA), the Max-Planck-Institute for Astrophysics (MPA), New Mexico State University, Ohio State University, University of Pittsburgh, University of Portsmouth, Princeton University, the United States Naval Observatory, and the University of Washington. This research has made use of the NASA/IPAC Extragalactic Database (NED) which is operated by the Jet Propulsion Laboratory, California Institute of Technology, under contract with the National Aeronautics and Space Administration; and of the GOLDMine database. The research leading to these results has received funding from the European Community’s Seventh Framework Programme (/FP7/2007-2013/) under grant agreement No 229517. S.B., E.C., L.K.H., S.D.A., L.M. and C.P. acknowledge financial support by ASI through the ASI-INAF grant “HeViCS: the Herschel Virgo Cluster Survey” I/009/10/0. C.V. received support from the ALMA-CONICYT Fund for the Development of Chilean Astronomy (Project 31090013) and from the Center of Excellence in Astrophysics and Associated Technologies (PBF06).
References
- Abazajian, K. N., Adelman-McCarthy, J. K., Agüeros, M. A., et al. 2009, ApJS, 182, 543 [NASA ADS] [CrossRef] [Google Scholar]
- Baes, M., Clemens, M., Xilouris, E. M., et al. 2010, A&A, 518, L53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bell, E. F., McIntosh, D. H., Katz, N., & Weinberg, M. D. 2003, ApJS, 149, 289 [NASA ADS] [CrossRef] [Google Scholar]
- Bendo, G. J., Joseph, R. D., Wells, M., et al. 2002, AJ, 124, 1380 [NASA ADS] [CrossRef] [Google Scholar]
- Bendo, G. J., Wilson, C. D., Warren, B. E., et al. 2010, MNRAS, 402, 1409 [NASA ADS] [CrossRef] [Google Scholar]
- Bianchi, S. 2008, A&A, 490, 461 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bigiel, F., Leroy, A., Walter, F., et al. 2010, AJ, 140, 1194 [NASA ADS] [CrossRef] [Google Scholar]
- Binggeli, B., Sandage, A., & Tammann, G. A. 1985, AJ, 90, 1681 [NASA ADS] [CrossRef] [Google Scholar]
- Boselli, A., & Gavazzi, G. 2006, PASP, 118, 517 [NASA ADS] [CrossRef] [Google Scholar]
- Boselli, A., & Gavazzi, G. 2009, A&A, 508, 201 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boselli, A., Gavazzi, G., Donas, J., & Scodeggio, M. 2001, AJ, 121, 753 [NASA ADS] [CrossRef] [Google Scholar]
- Boselli, A., Lequeux, J., & Gavazzi, G. 2002, A&A, 384, 33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boselli, A., Sauvage, M., Lequeux, J., Donati, A., & Gavazzi, G. 2003, A&A, 406, 867 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boselli, A., Boissier, S., Cortese, L., et al. 2006, ApJ, 651, 811 [NASA ADS] [CrossRef] [Google Scholar]
- Boselli, A., Boissier, S., Cortese, L., & Gavazzi, G. 2008, ApJ, 674, 742 [NASA ADS] [CrossRef] [Google Scholar]
- Boselli, A., Boissier, S., Cortese, L., et al. 2009, ApJ, 706, 1527 [NASA ADS] [CrossRef] [Google Scholar]
- Boselli, A., Ciesla, L., Buat, V., et al. 2010a, A&A, 518, L61 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boselli, A., Eales, S., Cortese, L., et al. 2010b, PASP, 122, 261 [NASA ADS] [CrossRef] [Google Scholar]
- Boselli, A., Boissier, S., Heinis, S., et al. 2011, A&A, 528, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boselli, A., Ciesla, L., Cortese, L., et al. 2012, A&A, in press, DOI: 10.1051/0004-6361/201118602 [Google Scholar]
- Calura, F., Pipino, A., & Matteucci, F. 2008, A&A, 479, 669 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cardelli, J. A., Clayton, G. C., & Mathis, J. S. 1989, ApJ, 345, 245 [NASA ADS] [CrossRef] [Google Scholar]
- Catinella, B., Schiminovich, D., Kauffmann, G., et al. 2010, MNRAS, 403, 683 [NASA ADS] [CrossRef] [Google Scholar]
- Chabrier, G. 2003, PASP, 115, 763 [NASA ADS] [CrossRef] [Google Scholar]
- Clemens, M. S., Jones, A. P., Bressan, A., et al. 2010, A&A, 518, L50 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Compiègne, M., Verstraete, L., Jones, A., et al. 2011, A&A, 525, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Contursi, A., Boselli, A., Gavazzi, G., et al. 2001, A&A, 365, 11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Corbelli, E., Bianchi, S., Cortese, L., et al. 2011, A&A, submitted [Google Scholar]
- Cortese, L., & Hughes, T. M. 2009, MNRAS, 400, 1225 [NASA ADS] [CrossRef] [Google Scholar]
- Cortese, L., Bendo, G. J., Boselli, A., et al. 2010a, A&A, 518, L63 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cortese, L., Davies, J. I., Pohlen, M., et al. 2010b, A&A, 518, L49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cortese, L., Catinella, B., Boissier, S., Boselli, A., & Heinis, S. 2011, MNRAS, 415, 1797 [NASA ADS] [CrossRef] [Google Scholar]
- Cowie, L. L., Songaila, A., Hu, E. M., & Cohen, J. G. 1996, AJ, 112, 839 [Google Scholar]
- da Cunha, E., Charlot, S., & Elbaz, D. 2008, MNRAS, 388, 1595 [NASA ADS] [CrossRef] [Google Scholar]
- da Cunha, E., Eminian, C., Charlot, S., & Blaizot, J. 2010, MNRAS, 403, 1894 [NASA ADS] [CrossRef] [Google Scholar]
- Davies, J. I., Baes, M., Bendo, G. J., et al. 2010, A&A, 518, L48 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Davies, J. I., Bianchi, S., Cortese, L., et al. 2012, MNRAS, 419, 3505 [NASA ADS] [CrossRef] [Google Scholar]
- de Jong, T., Clegg, P. E., Rowan-Robinson, M., et al. 1984, ApJ, 278, L67 [NASA ADS] [CrossRef] [Google Scholar]
- Devereux, N. A., & Hameed, S. 1997, AJ, 113, 599 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T. 2003, ARA&A, 41, 241 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T., & Li, A. 2007, ApJ, 657, 810 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T., Dale, D. A., Bendo, G., et al. 2007, ApJ, 663, 866 [NASA ADS] [CrossRef] [Google Scholar]
- Dunne, L., Eales, S., Edmunds, M., et al. 2000, MNRAS, 315, 115 [NASA ADS] [CrossRef] [Google Scholar]
- Dunne, L., Gomez, H. L., da Cunha, E., et al. 2011, MNRAS, 417, 1510 [NASA ADS] [CrossRef] [Google Scholar]
- Dupac, X., Bernard, J.-P., Boudet, N., et al. 2003, A&A, 404, L11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dwek, E. 1998, ApJ, 501, 643 [NASA ADS] [CrossRef] [Google Scholar]
- Edmunds, M. G. 2001, MNRAS, 328, 223 [NASA ADS] [CrossRef] [Google Scholar]
- Fabello, S., Catinella, B., Giovanelli, R., et al. 2011, MNRAS, 411, 993 [NASA ADS] [CrossRef] [Google Scholar]
- Finkbeiner, D. P., Davis, M., & Schlegel, D. J. 1999, ApJ, 524, 867 [NASA ADS] [CrossRef] [Google Scholar]
- Fumagalli, M., Krumholz, M. R., Prochaska, J. X., Gavazzi, G., & Boselli, A. 2009, ApJ, 697, 1811 [NASA ADS] [CrossRef] [Google Scholar]
- Galametz, M., Madden, S. C., Galliano, F., et al. 2011, A&A, 532, A56 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Galliano, F., Dwek, E., & Chanial, P. 2008, ApJ, 672, 214 [NASA ADS] [CrossRef] [Google Scholar]
- Gavazzi, G., Pierini, D., & Boselli, A. 1996, A&A, 312, 397 [NASA ADS] [Google Scholar]
- Gavazzi, G., Boselli, A., Scodeggio, M., Pierini, D., & Belsole, E. 1999, MNRAS, 304, 595 [NASA ADS] [CrossRef] [Google Scholar]
- Gavazzi, G., Franzetti, P., Scodeggio, M., Boselli, A., & Pierini, D. 2000, A&A, 361, 863 [NASA ADS] [Google Scholar]
- Gavazzi, G., Boselli, A., Donati, A., Franzetti, P., & Scodeggio, M. 2003, A&A, 400, 451 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gil de Paz, A., Boissier, S., Madore, B. F., et al. 2007, ApJS, 173, 185 [NASA ADS] [CrossRef] [Google Scholar]
- Giovanelli, R., Haynes, M. P., Kent, B. R., et al. 2007, AJ, 133, 2569 [Google Scholar]
- Gomez, H. L., Baes, M., Cortese, L., et al. 2010, A&A, 518, L45 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gómez, P. L., Nichol, R. C., Miller, C. J., et al. 2003, ApJ, 584, 210 [NASA ADS] [CrossRef] [Google Scholar]
- Gordon, K. D., Galliano, F., Hony, S., et al. 2010, A&A, 518, L89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Griffin, M. J., Abergel, A., Abreu, A., et al. 2010, A&A, 518, L3 [Google Scholar]
- Haynes, M. P., & Giovanelli, R. 1984, AJ, 89, 758 [NASA ADS] [CrossRef] [Google Scholar]
- Herschel Space Observatory. 2011, SPIRE Observer’s Manual, Version 2.4 (Noordwijk: ESA) [Google Scholar]
- Hildebrand, R. H. 1983, QJRAS, 24, 267 [NASA ADS] [Google Scholar]
- Holland, W. S., Robson, E. I., Gear, W. K., et al. 1999, MNRAS, 303, 659 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Hollenbach, D., & Salpeter, E. E. 1971, ApJ, 163, 155 [NASA ADS] [CrossRef] [Google Scholar]
- Hughes, T. M., & Cortese, L. 2009, MNRAS, 396, L41 [NASA ADS] [CrossRef] [Google Scholar]
- Issa, M. R., MacLaren, I., & Wolfendale, A. W. 1990, A&A, 236, 237 [NASA ADS] [Google Scholar]
- Kent, B. R., Giovanelli, R., Haynes, M. P., et al. 2008, AJ, 136, 713 [Google Scholar]
- Kessler, M. F., Steinz, J. A., Anderegg, M. E., et al. 1996, A&A, 315, L27 [NASA ADS] [Google Scholar]
- Knapp, G. R., Faber, S. M., & Gallagher, J. S. 1978, AJ, 83, 11 [NASA ADS] [CrossRef] [Google Scholar]
- Koopmann, R. A., Haynes, M. P., & Catinella, B. 2006, AJ, 131, 716 [NASA ADS] [CrossRef] [Google Scholar]
- Krishna Kumar, C., & Thonnard, N. 1983, AJ, 88, 260 [NASA ADS] [CrossRef] [Google Scholar]
- Krumm, N., van Driel, W., & van Woerden, H. 1985, A&A, 144, 202 [NASA ADS] [Google Scholar]
- Lewis, I., Balogh, M., De Propris, R., et al. 2002, MNRAS, 334, 673 [NASA ADS] [CrossRef] [Google Scholar]
- Lilly, S. J., Le Fevre, O., Hammer, F., & Crampton, D. 1996, ApJ, 460, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Lisenfeld, U., & Ferrara, A. 1998, ApJ, 496, 145 [NASA ADS] [CrossRef] [Google Scholar]
- Madau, P., Pozzetti, L., & Dickinson, M. 1998, ApJ, 498, 106 [NASA ADS] [CrossRef] [Google Scholar]
- Magrini, L., Bianchi, S., Corbelli, E., et al. 2011, A&A, 535, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Martin, D. C., Fanson, J., Schiminovich, D., et al. 2005, ApJ, 619, L1 [Google Scholar]
- Morgan, H. L., & Edmunds, M. G. 2003, MNRAS, 343, 427 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Muñoz-Mateos, J. C., Gil de Paz, A., Boissier, S., et al. 2009, ApJ, 701, 1965 [NASA ADS] [CrossRef] [Google Scholar]
- Neugebauer, G., Habing, H. J., van Duinen, R., et al. 1984, ApJ, 278, L1 [Google Scholar]
- Paradis, D., Veneziani, M., Noriega-Crespo, A., et al. 2010, A&A, 520, L8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pilbratt, G. L., Riedinger, J. R., Passvogel, T., et al. 2010, A&A, 518, L1 [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration, Ade, P. A. R., Aghanim, N., et al. 2011, A&A, 536, A17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Poglitsch, A., Waelkens, C., Geis, N., et al. 2010, A&A, 518, L2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pohlen, M., Cortese, L., Smith, M. W. L., et al. 2010, A&A, 518, L72 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Popescu, C. C., Tuffs, R. J., Fischera, J., & Völk, H. 2000, A&A, 354, 480 [NASA ADS] [Google Scholar]
- Popescu, C. C., Tuffs, R. J., Völk, H. J., Pierini, D., & Madore, B. F. 2002, ApJ, 567, 221 [NASA ADS] [CrossRef] [Google Scholar]
- Roberts, M. S., & Haynes, M. P. 1994, ARA&A, 32, 115 [NASA ADS] [CrossRef] [Google Scholar]
- Saintonge, A., Kauffmann, G., Kramer, C., et al. 2011, MNRAS, 415, 32 [NASA ADS] [CrossRef] [Google Scholar]
- Sandage, A., & Tammann, G. A. 1981, in Carnegie Inst. of Washington, Publ. 635 [Google Scholar]
- Savage, B. D., & Mathis, J. S. 1979, ARA&A, 17, 73 [NASA ADS] [CrossRef] [Google Scholar]
- Schiminovich, D., Wyder, T. K., Martin, D. C., et al. 2007, ApJS, 173, 315 [NASA ADS] [CrossRef] [Google Scholar]
- Schlegel, D. J., Finkbeiner, D. P., & Davis, M. 1998, ApJ, 500, 525 [NASA ADS] [CrossRef] [Google Scholar]
- Scoville, N., Aussel, H., Brusa, M., et al. 2007, ApJS, 172, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Shetty, R., Kauffmann, J., Schnee, S., & Goodman, A. A. 2009a, ApJ, 696, 676 [NASA ADS] [CrossRef] [Google Scholar]
- Shetty, R., Kauffmann, J., Schnee, S., Goodman, A. A., & Ercolano, B. 2009b, ApJ, 696, 2234 [NASA ADS] [CrossRef] [Google Scholar]
- Skibba, R. A., Engelbracht, C. W., Dale, D., et al. 2011, ApJ, 738, 89 [NASA ADS] [CrossRef] [Google Scholar]
- Skrutskie, M. F., Cutri, R. M., Stiening, R., et al. 2006, AJ, 131, 1163 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, M. W. L., Gomez, H. L., Eales, S. A., et al. 2012, ApJ, 748, 123 [NASA ADS] [CrossRef] [Google Scholar]
- Solanes, J. M., Giovanelli, R., & Haynes, M. P. 1996, ApJ, 461, 609 [NASA ADS] [CrossRef] [Google Scholar]
- Springob, C. M., Haynes, M. P., & Giovanelli, R. 2005, ApJ, 621, 215 [NASA ADS] [CrossRef] [Google Scholar]
- Thomas, H. C., Alexander, P., Clemens, M. S., et al. 2004, MNRAS, 351, 362 [NASA ADS] [CrossRef] [Google Scholar]
- Tremonti, C. A., Heckman, T. M., Kauffmann, G., et al. 2004, ApJ, 613, 898 [NASA ADS] [CrossRef] [Google Scholar]
- Tuffs, R. J., Popescu, C. C., Pierini, D., et al. 2002, ApJS, 139, 37 [NASA ADS] [CrossRef] [Google Scholar]
- van Driel, W., van Woerden, H., Schwarz, U. J., & Gallagher, III, J. S. 1988, A&A, 191, 201 [NASA ADS] [Google Scholar]
- Vlahakis, C., Dunne, L., & Eales, S. 2005, MNRAS, 364, 1253 [NASA ADS] [CrossRef] [Google Scholar]
- Walter, F., Sandstrom, K., Aniano, G., et al. 2011, ApJ, 726, L11 [NASA ADS] [CrossRef] [Google Scholar]
- Werner, M. W., Roellig, T. L., Low, F. J., et al. 2004, ApJS, 154, 1 [Google Scholar]
- Wiebe, D. V., Ade, P. A. R., Bock, J. J., et al. 2009, ApJ, 707, 1809 [NASA ADS] [CrossRef] [Google Scholar]
- Willmer, C. N. A., Rieke, G. H., Le Floc’h, E., et al. 2009, AJ, 138, 146 [NASA ADS] [CrossRef] [Google Scholar]
- Zhukovska, S., Gail, H.-P., & Trieloff, M. 2008, A&A, 479, 453 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zibetti, S., Charlot, S., & Rix, H. 2009, MNRAS, 400, 1181 [NASA ADS] [CrossRef] [Google Scholar]
- Zubko, V., Dwek, E., & Arendt, R. G. 2004, ApJS, 152, 211 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Relations to determine the Mdust/(f350D2) from the 250 μm-to-500 μm flux density ratio for extended sources and point sources.
All Figures
 |
Fig. 1 The relation between the ratio Mdust/(F350D2) and the 250 μm-to-500 μm flux density ratio for a modified black-body SED with β = 2 (black, see Table B1) and for the Draine & Li models (red). |
| In the text | |
 |
Fig. 2 The K-band luminosity distribution for the whole HRS (black) and for the sub-sample analyzed in this paper (blue). |
| In the text | |
 |
Fig. 3 The dust-to-stellar mass ratio as function of stellar mass (upper left), NUV − r colour (upper right), concentration index (lower left) and stellar mass surface density (lower right). Circles and triangles show Herschel detections and non-detections, respectively. The typical errors associated with our galaxies are indicated on the bottom-left corner of each panel. |
| In the text | |
 |
Fig. 4 The dust-to-stellar mass ratio as function of stellar mass (top row), NUV − r colour (middle row), and stellar mass surface density (bottom row) for HI-normal (first column), HI-deficient (second column) galaxies, systems outside (third column) and inside (fourth column) the Virgo cluster. Circles and black triangles indicate detections and non-detections respectively. The average relations for HI-normal (solid), HI-deficient (long-dashed) galaxies, systems outside (dotted) and inside (short dashed) the Virgo cluster are presented in the fifth column. In the third and fourth column Hi-deficient galaxies outside the Virgo cluster and Hi-normal Virgo galaxies are highlighted in red and blue, respectively. |
| In the text | |
 |
Fig. 5 The Mdust/M∗ as a function of the morphological type. Black filled and red empty circles are HI-normal and HI-deficient galaxies, respectively. Upper limits are indicated by green triangles. The large empty rectangles indicate the average value and its error for HI-normal (black) and HI-deficient (red) galaxies in each morphological type. In case only one galaxy is available in a bin, only a line is shown. |
| In the text | |
 |
Fig. 6 The dust-to-HI mass ratio as a function of stellar mass (right panel), NUV − r colour (central panel) and stellar mass surface density (left panel). Filled and empty circles indicate HI-normal and HI-deficient galaxies, respectively. Arrows show upper limits in either dust or Hi mass. Typical errorbars are shown in the bottom-right corner of each panel. |
| In the text | |
 |
Fig. 7 The Mdust/MHI ratios as a function of the morphological type. Symbols are as in Fig. 5. |
| In the text | |
 |
Fig. 8 The extended UV disk of NGC 3657. SDSS-optical (left), GALEX-NUV (center) and Herschel/SPIRE 250 μm (right) images are compared on the same spatial scale. |
| In the text | |
 |
Fig. 9 The dust-to-stellar mass ratio as a function of the total gas fractions for HRS galaxies. The solid blue line shows the predictions of a simple closed-box models (Edmunds 2001). See the text for details. The five galaxies with low dust-to-Hi ratio mass discussed in Sect. 4 are highlighted. Symbols are as in Fig. 6. |
| In the text | |
 |
Fig. 10 Left: the relation between dust-to-stellar mass and HI deficiency. Right: the relation between dust-to-stellar mass and HI-to-stellar mass ratio. The dotted lines indicate constant HI-to-dust ratios of (from left to right): 30-100-300. The green lines indicate two different models of dust stripping assuming a constant (dashed) or exponential (solid) Hi surface density profile. See text for details. Symbols are as in Fig. 6. |
| In the text | |
 |
Fig. A.1 The logarithmic difference between the dust mass estimates presented in this work and those obtained from modified black-body SED fitting of PACS+SPIRE (top row) and SPIRE-only (second row) data, using the SED library of Draine & Li (2007, third row) and using just the 350 μm luminosity without any colour information (bottom row). For each row, the right panel shows the histogram of the difference, its average value and standard deviation of the population. The empty circles in the top two rows indicate points for which the SED fitting routine provided a χ2 > 1. |
| In the text | |
 |
Fig. A.2 The 250-to-500 μm flux density ratio as a function of stellar mass (left), NUV − r colour (center) and stellar mass surface density (right). |
| In the text | |
 |
Fig. A.3 The dust-to-stellar mass ratio as a function of stellar mass (left), NUV − r colour (center) and stellar mass surface density (right), for dust masses estimated from the 350 μm luminosities without taking into account any colour/temperature variation in the sample. Symbols are as in Fig. 3. The orange lines and dashed regions show the average scaling relations and ± 1σ area presented in Fig. 3. |
| In the text | |
 |
Fig. A.4 The relation between the ratio Mdust/(f350D2) and the 250 μm-to-500 μm flux density ratio for a modified black-body SED with β = 2.5 (blue), 2 (black), 1.5 (green) and 1 (magenta). |
| In the text | |
 |
Fig. A.5 The logarithmic difference between the dust mass estimates presented in this work and the one obtained assuming a modified black-body with β = 2.5 (top row), 1.5 (middle row) and 1 (bottom row). For each row, the right panel shows the histogram of the difference, its average value and standard deviation of the population. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


