| Issue |
A&A
Volume 540, April 2012
|
|
|---|---|---|
| Article Number | A52 | |
| Number of page(s) | 17 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201118499 | |
| Published online | 23 March 2012 | |
Online material
Appendix A: Testing the dust mass estimate based on SPIRE flux densities only
In this Appendix we investigate the reliability of the method described in Sect. 2.2 to estimate dust masses. We proceed as follows. We compare our estimates with different methods all based on roughly the same assumptions on the properties of the underlying dust population (i.e., the value of β and its variation with frequency). This is aimed at validating the methodology presented here. Then, we use our method for different values of β to study how the assumption β = 2 made in this paper could affect our results. In both cases we are interested in the average difference and standard deviation between the various methods and in the presence of any possible systematic trend with stellar mass, stellar mass surface density and NUV − r colour.
 |
Fig. A.1
The logarithmic difference between the dust mass estimates presented in this work and those obtained from modified black-body SED fitting of PACS+SPIRE (top row) and SPIRE-only (second row) data, using the SED library of Draine & Li (2007, third row) and using just the 350 μm luminosity without any colour information (bottom row). For each row, the right panel shows the histogram of the difference, its average value and standard deviation of the population. The empty circles in the top two rows indicate points for which the SED fitting routine provided a χ2 > 1. |
| Open with DEXTER | |
The results of the first step are shown in Fig. A.1. In each row we show the difference between the logarithm of the dust mass obtained from two different methods as a function of stellar mass, NUV − r colour and stellar mass surface density. In the right most panel we also present the histogram of the distribution of the difference, its average value and standard deviation.
First of all, we compare our results with the ones obtained by Davies et al. (2012) for the 55 galaxies in common with our work (top row in Fig. A.1). These are obtained using a single modified black-body SED fitting of the five PACS+SPIRE flux densities at 100, 160, 250, 350 and 500 μm and assuming the same dust emissivity as in this paper. In our analysis we only considered the points for which the SED fitting routine gives a χ2 < 1, but in Fig. A.1 we also show as empty circles the galaxies with χ2 > 1. We do not find any systematic difference in the average dust mass estimate and the scatter between the two methods is of the order of ~ 0.1 dex, not significantly larger than the uncertainty of ~0.08 dex in the dust mass estimate from the SED fitting technique (Davies et al. 2012). Small systematic trends in the dust mass estimate are found as a function of stellar mass and stellar mass surface density. However, these are just marginal and within the error assumed throughout the paper.
Secondly, we consider the case of SED fitting of SPIRE-only points, following the same technique described above. Interestingly, we find a perfect agreement between the two methods and we could in theory just use the SED fitting of SPIRE fluxes only. The main reason why we decided not to do so is that the best fitting SED is significantly different from the one obtained by Davies et al. (2012) when combining PACS and SPIRE data since no constraint is provided below 250 μm. Therefore these are likely not a good representation of the far-infrared/submm emission for our galaxies and we preferred not to use them. Moreover, it is sometimes difficult to trust the uncertainty determined from the fitting technique since only based on the three SPIRE data.
Thirdly, we compare the estimate obtained from our method assuming a modified black-body SED and the one obtained from the same method but assuming the Draine & Li (2007) SED (DL07) as described in Sect. 2.2. As shown in the third row of Fig. A.1 we find again a very good agreement between the two methods. This is due to the fact that, in the wavelength range covered by SPIRE, the SED predicted by the Draine & Li (2007) models is very similar to a single temperature modified black-body with β = 2 (see also Magrini et al. 2011).
 |
Fig. A.2
The 250-to-500 μm flux density ratio as a function of stellar mass (left), NUV − r colour (center) and stellar mass surface density (right). |
| Open with DEXTER | |
 |
Fig. A.3
The dust-to-stellar mass ratio as a function of stellar mass (left), NUV − r colour (center) and stellar mass surface density (right), for dust masses estimated from the 350 μm luminosities without taking into account any colour/temperature variation in the sample. Symbols are as in Fig. 3. The orange lines and dashed regions show the average scaling relations and ± 1σ area presented in Fig. 3. |
| Open with DEXTER | |
Finally, we consider the very simple case where only a submm flux density is available and no colour can be used (bottom row in Fig. A.1). In details, we just assumed the same 250-to-500 μm ratio for all our galaxies (i.e., the mean value for the detections in our sample log (f250/f500) = 0.75). This is done to investigate the role played by the colour term in our method and to warn how this very rough technique could affect scaling relations studies, in particular at high-redshift. As expected, this is by far the worse method to estimate dust masses showing a scatter of ~0.2 dex. More importantly, we find systematic trends with stellar mass and stellar mass surface densities showing that, when compared with our method, this technique underestimates dust masses for low-mass galaxies and overestimate those of massive systems. The reason for these systematic trends is due to the fact that the 250-to-500 μm flux density ratio strongly correlates with stellar mass and stellar mass surface density (see Fig. A.2 and Boselli et al. 2012). Thus not accounting for the different colours in our galaxies introduces systematic effects that can be seen in Fig. A.3, where we compare some of the scaling relations discussed in this paper (orange dashed regions) with those obtained using this method. While, as expected, the relation with NUV − r colour is not affected, the trends between dust-to-stellar mass ratio, stellar mass and stellar mass surface density change. We thus suggest caution in using a technique based on only a single luminosity for a detailed quantification of dust properties in galaxies.
In summary, these first tests confirm that our technique does not introduce any significant systematic effect, once the properties of the underlying dust component are fixed.
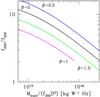 |
Fig. A.4
The relation between the ratio Mdust/(f350D2) and the 250 μm-to-500 μm flux density ratio for a modified black-body SED with β = 2.5 (blue), 2 (black), 1.5 (green) and 1 (magenta). |
| Open with DEXTER | |
The next step is to see what happens if we change the value of β, keeping fixed the value of dust opacity at 350 μm. In the following, we consider modified black-bodies with 1 ≤ β ≤ 2.5 which appear the most favoured range of values according to theoretical models and observations (Finkbeiner et al. 1999; Dupac et al. 2003; Gordon et al. 2010; Paradis et al. 2010; Planck Collaboration et al. 2011). It is important to note that, given the strong degeneracy between β and dust temperature we had to modify the range of dust temperatures investigated in order to recover the range of submm colours observed in the HRS. In detail, while for β = 2 and 2.5 we varied the temperature between 5 and 55 K, for β = 1.5 and 1 we had to vary the temperature between 15 and 230 K. Moreover, the case β = 1 is not able to reproduce the bluest colours observed in our sample (i.e., f250/f500 > 7.5, 37 galaxies in total) suggesting that this case is not a good representation of the dust SED for at least a fraction of our sample (see Fig. A.4). The results of our investigations are summarized in Fig. A.5. As expected, the absolute value of the dust mass varies with β by almost a factor 10. Values of β lower than 2 give dust masses smaller than the one used in this work, and viceversa. However, once this offset is taken into account, the intrinsic scatter in the dust mass estimate stays below ~0.1 dex for 1.5 ≤ β ≤ 2.5 and goes up to just 0.17 dex for β = 1 (for this case only those galaxies with f250/f500 ≤ 7.5 are included), although with a significant tail of outliers. Moreover, very mild systematic trends are observed as a function of stellar mass, colour and stellar mass surface density but these could become important only for β ~ 1. As discussed in the text, this would reinforce the trend observed between the dust-to-stellar mass ratio but weaken the one between dust-to-Hi mass ratio and stellar mass.
 |
Fig. A.5
The logarithmic difference between the dust mass estimates presented in this work and the one obtained assuming a modified black-body with β = 2.5 (top row), 1.5 (middle row) and 1 (bottom row). For each row, the right panel shows the histogram of the difference, its average value and standard deviation of the population. |
| Open with DEXTER | |
In conclusion, we can confidently state that the method presented here to estimate dust masses is a reliable solution when accurate SED fitting is not possible. The typical scatter with respect to our methods is of the order of ~0.2 dex. Although different values of β would imply different values of dust masses, the scaling relations discussed in this paper should remain valid at least for 1.5 ≤ β ≤ 2.5.
Appendix B: Recipes to estimate dust masses with SPIRE data only
In this Appendix we provide the polynomial fit to the relations between the ratio Mdust/(f350D2) in units of kg W-1 Hz and the 250 μm-to-500 μm flux density ratio which we used to estimate dust masses. We provide two different sets of coefficients obtained by convolving modified black-bodies characterized by different values of β (i.e., 1, 1.5, 2 and 2.5) with the SPIRE RSRF for extended and point-like sources (Table B.1). Once the value Mdust/(f350D2) has been computed, the dust mass can be obtained from the following equation 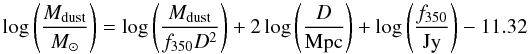 (B.1)
(B.1)
We note that the difference degrees used to fit β ≥ 2 and β < 2 are due to the different range of temperatures adopted for each case. For β < 2 we had to use larger temperature range (15 to 230 K instead of 5 to 55 K) and, as a consequence, an higher order polynomial to fit the relation between the 250 μm-to-500 μm and Mdust/(f350D2) ratios. The fits are optimized for the range of colours covered by our sample, i.e., 3 < f250/f500 < 11.
Relations to determine the Mdust/(f350D2) from the 250 μm-to-500 μm flux density ratio for extended sources and point sources.
© ESO, 2012
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


