| Issue |
A&A
Volume 540, April 2012
|
|
|---|---|---|
| Article Number | A101 | |
| Number of page(s) | 13 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/201118295 | |
| Published online | 04 April 2012 | |
The implications of dust for high-redshift protogalaxies and the formation of binary disks
1 Kapteyn Astronomical Institute, University of Groningen, PO Box 800, 9700 AV Groningen, The Netherlands
e-mail: latife@astro.rug.nl
2 Institut für Astrophysik, Georg-August-Universität, Friedrich-Hund-Platz 1, 37077 Göttingen, Germany
Received: 18 October 2011
Accepted: 21 February 2012
Numerical simulations suggest that the first galaxies are formed in protogalactic halos with virial temperatures ≥104 K. It is likely that such halos are polluted with trace amounts of metals produced by the first generation of stars. The presence of dust can significantly change the chemistry and dynamics of early galaxies. In this article, we aim to assess the role of dust on the thermal and dynamical evolution of the first galaxies in the presence of a background UV flux, and its implications for the observability of Lyman-α emitters and sub-mm sources. We have performed high resolution cosmological simulations using the adaptive mesh refinement code FLASH to accomplish this goal. We have developed a chemical network appropriate for these conditions and coupled it with the FLASH code. The main ingredients of our chemical model include the formation of molecules (both in the gas phase and on dust grains), a multi-level treatment of atomic hydrogen, line trapping of Ly-α photons and, photoionization and photodissociation processes in a UV background. We found that the formation of molecules (H2 and HD) is significantly enhanced in the presence of dust grains as compared to only gas phase reactions by up to two orders of magnitude. The presence of dust may thus establish a molecular ISM in high-redshift galaxies. The presence of a background UV flux strongly influences the formation of molecules by photodissociating them. We explore the evolution after a major merger, leading to the formation of a binary disk. These disks have gas masses of ~107 M⊙ at a redshift of 5.4. Each disk lies in a separate subhalo as a result of the merger event. The disks are supported by turbulent pressure due to the highly supersonic turbulence present in the halo. For values of J21 = 1000 (internal flux), we find that fragmentation may be enhanced due to thermal instabilities in the hot gas. The presence of dust does not significantly reduce the Ly-α emission. The emission of Ly-α is extended and originates from the envelope of the halo due to line trapping effects. We also find that dust masses of a few × 108 M⊙ are required to observe the dust continuum emission from z ~ 5 galaxies with ALMA.
Key words: methods: numerical / dust, extinction / cosmology: theory / galaxies: formation / atomic processes / molecular processes
© ESO, 2012
1. Introduction
The observational frontier of high-redshift galaxies is shifting rapidly (Bouwens et al. 2010; Bunker et al. 2010; Bouwens et al. 2011; Vanzella et al. 2011). High-redshift galaxies have been detected using the spectral imprint of neutral hydrogen. These first galaxies produce copious amounts of Lyman-α radiation and many have now been detected up to z = 7 (Steidel et al. 2000; Matsuda et al. 2004; Saito et al. 2006, 2008; Yang et al. 2009; Ouchi et al. 2009; Lehnert et al. 2010).
From a theoretical point of view, the first galaxies are formed in atomic cooling halos with Tvir ≥ 104 K (Bromm & Yoshida 2011; Johnson 2011). Gas in atomic cooling halos may cool through Ly-α radiation down to 8000 K. Molecular hydrogen is the only efficient coolant in the absence of metals that can cool the gas down to a few 100 K. Trace amounts of H2 can be formed through gas phase reactions (Saslaw & Zipoy 1967; Lepp & Shull 1984; Galli & Palla 1998). HD is another molecule that is a very efficient coolant around 100 K and may cool the gas down close to the cosmic microwave background (CMB) temperature. The presence of deuterium creates a small dipole moment, which allows rotational transitions to take place with an appreciable Einstein A coefficient. Despite the fact that H2 and HD are the efficient coolants, they are very fragile to Lyman-Werner UV radiation (Dijkstra et al. 2008; Latif et al. 2011a; Shang et al. 2010; Wolcott-Green & Haiman 2011).
The first galaxies were preceded by the very first stars, forming in minihalos at redshift ~ 20 (Abel et al. 2002; Bromm & Larson 2004; Yoshida et al. 2008; Clark et al. 2011b,a). These stars emit UV radiation, photoionize gas and photodissociate molecules. Consequently, they influence the subsequent formation of structure in the surrounding intergalactic medium (Johnson et al. 2007; Johnson 2011; Maio et al. 2011). It is likely that atomic cooling halos are polluted by trace amounts of metals through Pop III supernova explosions (Greif et al. 2010). The presence of metals or dust significantly influences the thermal evolution of gas and fragmentation becomes inevitable (Bromm et al. 2001; Schneider et al. 2002, 2003; Bromm & Loeb 2003; Omukai et al. 2005; Santoro & Shull 2006; Smith et al. 2008). Additional metals may originate from the local presence of stellar winds. The impact of dust and metals in the presence of a background UV flux has been studied by Omukai et al. (2008).
The formation of H2 and HD is significantly boosted via grain surface reactions as compared to the gas phase route in the presence of trace amounts of dust (i.e., >10-5 solar) (Cazaux & Spaans 2004, 2009). Dust grains also attenuate UV radiation. The fate of the halo further depends on the content of dust, intensity of the UV radiation field, gas-grain collisional coupling, and the formation of molecules under these conditions (Jappsen et al. 2009a,b; Schneider & Omukai 2010). At high densities, gas-grain collisions have a significant impact on the thermal evolution and the stellar initial mass function (Spaans & Silk 2000; Dopcke et al. 2011). These are therefore the key parameters to study.
Although the number of observed Ly-α emitters has increased manifold during the past years, the inception of Ly-α emitters is not yet fully understood. In our earlier studies (Latif et al. 2011b,a), we focused on metal free halos. However, some observations suggest the presence of dusty Ly-α emitters (Tamura et al. 2009; Ono et al. 2010). The presence of dust has important implications for Ly-α emission. It may absorb Ly-α photons and re-emit them in the continuum at far-infrared frequencies. Neufeld (1991) and Haiman & Spaans (1999) studied the Ly-α radiative transfer in a dusty medium. They found that Ly-α photons face less attenuation than nonresonantly scattered photons if the medium is inhomogeneous.
In this paper, we study the impact of dust on the dynamical evolution of a protogalactic halo, the formation of binary disks, and the implications of dust for the emission of Ly-α photons. We intend to asses how the presence of dust influences the formation of H2 and HD molecules for different strengths of the impinging UV radiation field. To complete this task, we have performed state-of-the-art high resolution cosmological simulations by extending our previous chemical model (Latif et al. 2011a) to include dust physics. The main ingredients of our extended chemical model include the formation of H2 and HD molecules on dust grains, extinction of UV radiation by dust grains and gas-grain collisional coupling. We study the evolution for different dust-to-gas ratios and various strengths of the UV radiation field.
Our paper is organized in the following way. In Sect. 2, we describe the numerical schemes and simulation setup. We briefly summarize our chemical model in Sect. 3. We present the results obtained in Sect. 4. In Sect. 5, we discuss our conclusions.
2. Computational methods
Our numerical simulations have been performed using the extended version of the FLASH code (Dubey et al. 2009). FLASH is an adaptive mesh refinement (AMR), modular, parallel, grid based code. It can run on massively parallel systems and can be used for a wide variety of astrophysical problems. It uses the message passing interface (MPI) to achieve portability and scalability on different systems. It discretizes the computational domain into nested grid cells by making use of the PARAMESH library. It has two exchangeable grids, a uniform grid and an oct-tree based adaptive grid. We exploit the AMR technique to add resolution in the domain of interest. We capitalize the AMR method and add 15 additional levels of refinement. Consequently, we obtain an effective resolution of 5 pc. We resolve the Jeans length by at least 20 cells to make sure that all essential processes are resolved properly (Federrath et al. 2011b). This also ensures the fulfillment of Truelove criterion (Truelove et al. 1997). We use an unsplit hydro solver with a 3rd order piece-wise parabolic (PPM) method for hydrodynamic calculations. A multigrid Poisson solver is employed for self-gravity computations. The particle mesh method is used for the dynamical evolution of a dark matter.
We perform 3-dimensional cosmological simulations and our computational box has a comoving size of 5 Mpc in each dimension. Periodic boundary conditions have been used both for the hydrodynamics and gravity. Our simulations start with cosmological initial conditions and make use of the COSMIC package developed by Bertschinger (1995) to produce Gaussian random field initial conditions. We start our simulations at redshift 90 as computed by the COSMIC code, employing 3.2 × 106 particles for dark matter gravity calculations. The dark matter particles are distributed according to the initial distribution of the baryons (see below). We use constraint realization, available in the grafic code (part of the COSMIC package), to select a massive halo at the center of a box. We start with an effective grid resolution of 5123 in the central 1 Mpc region and set the rest of the box to a resolution of 1283 grid cells. In this way, the resolution in the central Mpc is increased by a factor of 4. Our simulations are based on a ΛCDM cosmology with WMAP 5-years parameters Ωm = 0.2581, H0 = 72 km s-1 Mpc-1, Ωb = 0.0441, assuming a scale invariant power spectrum with σ8 = 0.8. The size of the dark matter halo at z = 5.4 is ~10 kpc and has a mass of ~2 × 1010 M⊙. Simulation results are partly analyzed using YT, i.e., a visualization toolkit for astrophysical data (Turk et al. 2011).
Collisional and radiative rates.
3. Chemical model
The gas in the protogalactic halos is heated up to their virial temperatures where cooling due to Ly-α radiation becomes important. HI can cool the gas down to 8000 K. In the absence of metals, H2 is the only molecule that can cool the gas down to a few × 100 K. Trace amounts of H2 can be formed through the residual fraction of free electrons left over by the recombination epoch. H2 can also be formed in shock heated regions (Tegmark et al. 1997; Anninos et al. 1997). The gas phase formation is dominated by 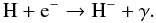 (1)This leads to H2 formation via the reaction
(1)This leads to H2 formation via the reaction 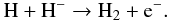 (2)HD is a molecule whose cooling becomes efficient below 200 K. The first excited state of HD can be excited around 150 K. It can cool the gas down to about TCMB = 2.75(1 + z). The main route for HD formation is
(2)HD is a molecule whose cooling becomes efficient below 200 K. The first excited state of HD can be excited around 150 K. It can cool the gas down to about TCMB = 2.75(1 + z). The main route for HD formation is 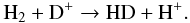 (3)In a previous study (Latif et al. 2011a), we devised a chemical model for a gas of primordial composition, consisting of 36 reactions (23 collisional and 13 radiative). For details, see the Appendix of Latif et al. (2011a). We solve the rate equations of the following 12 species:
(3)In a previous study (Latif et al. 2011a), we devised a chemical model for a gas of primordial composition, consisting of 36 reactions (23 collisional and 13 radiative). For details, see the Appendix of Latif et al. (2011a). We solve the rate equations of the following 12 species: 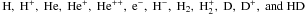 . We include non-equilibrium ionization, photoionization, collisional ionization, radiative recombination and photodissociation of the above mentioned species. We also include a comprehensive model for cooling and heating, i.e., photo-ionization heating, collisional excitation cooling, recombination cooling, collisional ionization cooling, bremsstrahlung cooling and photo-dissociation heating. Our model also comprises cooling due to H2 and HD molecules as well as a multi-level model for atomic hydrogen line cooling (see Appendix: Table 2 of Latif et al. 2011a). We also include the self-shielding of H2 and HD.
. We include non-equilibrium ionization, photoionization, collisional ionization, radiative recombination and photodissociation of the above mentioned species. We also include a comprehensive model for cooling and heating, i.e., photo-ionization heating, collisional excitation cooling, recombination cooling, collisional ionization cooling, bremsstrahlung cooling and photo-dissociation heating. Our model also comprises cooling due to H2 and HD molecules as well as a multi-level model for atomic hydrogen line cooling (see Appendix: Table 2 of Latif et al. 2011a). We also include the self-shielding of H2 and HD.
We have extended our previous chemical model to include dust physics. For the description of the dust abundance, we adopt the dust-to-gas ratio measured in units of the solar value, as suggested by Schneider et al. (2011). Dust models show that supernovae can efficiently produce dust (Todini & Ferrara 2001; Nozawa et al. 2003; Bianchi & Schneider 2007). Indeed, signatures of supernova dust have been observed in the spectra of a high-redshift quasar (Maiolino et al. 2004; Gallerani et al. 2010).
The presence of dust efficiently boosts the formation of H2 and HD molecules (Cazaux & Spaans 2004, 2009) for metallicities as low as Z/Z⊙ = 10-5. In order to include a recipe for the formation of H2 and HD molecules on dust surfaces, we adopted the H2 and HD formation rates on dust grains from Cazaux & Spaans (2009), see Eqs. (12) and (13). The formation efficiency of H2 and HD on dust grain surfaces depends on the gas and dust temperatures as well as on the grain size distribution and composition. We use the grain size distribution of Weingartner & Draine (2001). In this study, we further focus on carbon (PAHs, AC) and silicate dust grains. We have grain sizes of 3.5–300 Å. We assume that dust abundance scales linearly with overall metallicity and that the total dust grain cross section is equal to the the Milky Way for solar metallicity (Cazaux & Spaans 2009). In this way, we take into account the contribution of smaller grain sizes which may further enhance the H2 and HD formation rates due to an increase in surface area. The dust temperature in the presence of a background UV flux is computed as (Hollenbach et al. 1991; Meijerink & Spaans 2005) ![\begin{eqnarray} \rm {\it T}_{d}&=&\{8.9\times10^{-11} \nu_{0}{\it G}_{0}10^{-1.8 {\it A}_{\rm {\nu}}} + {\it T}_{\rm CMB}^{5} +3.4 \times 10^{-2}\\ \nonumber \,\,&&\times \,\,\rm [0.42-log(3.5\times10^{-2}\tau_{100}{\it T}_{0})]\times \tau_{100}{\it T}_{0}^{-0.2} \}^{0.2} \label{dust1} \end{eqnarray}](/articles/aa/full_html/2012/04/aa18295-11/aa18295-11-eq43.png) (4)where ν0 = 2.65 × 1015 s-1, G0 is the far-ultraviolet (FUV) flux in units of the equivalent Habing flux (Habing 1968),
(4)where ν0 = 2.65 × 1015 s-1, G0 is the far-ultraviolet (FUV) flux in units of the equivalent Habing flux (Habing 1968), 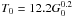 K is the equilibrium dust temperature and
K is the equilibrium dust temperature and 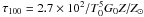 is the optical depth at 100 μm. The dust temperature is computed assuming that each dust grain is illuminated by attenuated FUV flux, CMB radiation, and the infrared radiation field from warm dust emission (Hollenbach et al. 1991). If gas and dust grains have different temperatures, they can exchange heat through collisions. We compute the gas-grain collisional heating and cooling rates as given in the equation below (Meijerink & Spaans 2005)
is the optical depth at 100 μm. The dust temperature is computed assuming that each dust grain is illuminated by attenuated FUV flux, CMB radiation, and the infrared radiation field from warm dust emission (Hollenbach et al. 1991). If gas and dust grains have different temperatures, they can exchange heat through collisions. We compute the gas-grain collisional heating and cooling rates as given in the equation below (Meijerink & Spaans 2005)
 \label{dust33e} \end{eqnarray}](/articles/aa/full_html/2012/04/aa18295-11/aa18295-11-eq49.png) (5)Td and Tk are dust and gas temperatures, respectively, n is the gas number density, and amin is the minimum dust grain size. We set the minimum grain size to 3.5 Å (Meijerink & Spaans 2005). Grain surface reactions are often more effective than their gas-phase counterparts. We have included H2, HD, H, D and He formation on the surfaces of dust grains in our chemical model. The rates for these reactions are taken from Glover & Jappsen (2007) and Cazaux & Spaans (2009), and are listed in Table 1. We have also included the H2 collisional dissociation cooling, photoelectric heating by UV irradiated dust grains, gas-phase H2 formation heating, and heating by H2 formation on dust grains. These are listed in Table 7 of Glover & Jappsen (2007).
(5)Td and Tk are dust and gas temperatures, respectively, n is the gas number density, and amin is the minimum dust grain size. We set the minimum grain size to 3.5 Å (Meijerink & Spaans 2005). Grain surface reactions are often more effective than their gas-phase counterparts. We have included H2, HD, H, D and He formation on the surfaces of dust grains in our chemical model. The rates for these reactions are taken from Glover & Jappsen (2007) and Cazaux & Spaans (2009), and are listed in Table 1. We have also included the H2 collisional dissociation cooling, photoelectric heating by UV irradiated dust grains, gas-phase H2 formation heating, and heating by H2 formation on dust grains. These are listed in Table 7 of Glover & Jappsen (2007).
During the epoch of reionization, a background UV flux is produced by stellar populations. The background UV flux can photoheat and photoionize the gas, and can photodissociate molecules. We have modeled the background UV flux in the following way (Omukai et al. 2008) ![\begin{equation} \rm {\it J}_{\nu}^{ex} = {\it J}_{21}10^{-21}[{\it B}_{\nu}({\it T}_{*})/{\it B}_{\nu H}] {\it f}(\nu)~ erg~cm^{-2}\,sr^{-1}\,s^{-1}\,Hz^{-1}, \label{jrad} \end{equation}](/articles/aa/full_html/2012/04/aa18295-11/aa18295-11-eq54.png) (6)where J21 is the background UV radiation field intensity below the Lyman limit and T∗ is the color temperature of a star. We assume a black body radiation spectrum with T∗ = 104 K. f(ν) is one for non-ionizing radiation and is equal to fesc for ionizing radiation. BνH is the black body spectrum at the Lyman limit (J21 = 10-21 erg/cm2/s/Hz/sr). Bν is the stellar radiation spectrum (i.e., black body spectrum) as given by
(6)where J21 is the background UV radiation field intensity below the Lyman limit and T∗ is the color temperature of a star. We assume a black body radiation spectrum with T∗ = 104 K. f(ν) is one for non-ionizing radiation and is equal to fesc for ionizing radiation. BνH is the black body spectrum at the Lyman limit (J21 = 10-21 erg/cm2/s/Hz/sr). Bν is the stellar radiation spectrum (i.e., black body spectrum) as given by 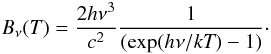 (7)Here h is Planck’s constant, ν is the frequency of radiation, c is the speed of light, k is Boltzmann’s constant and T is the radiation temperature. JIH = J21 × fesc is the ionizing flux, where fesc is again the escape fraction of ionizing radiation. These ionizing photons are attenuated while propagating through intergalactic medium. We have taken this effect into account in an approximate manner by computing the optical depth for each frequency bin in the following manner
(7)Here h is Planck’s constant, ν is the frequency of radiation, c is the speed of light, k is Boltzmann’s constant and T is the radiation temperature. JIH = J21 × fesc is the ionizing flux, where fesc is again the escape fraction of ionizing radiation. These ionizing photons are attenuated while propagating through intergalactic medium. We have taken this effect into account in an approximate manner by computing the optical depth for each frequency bin in the following manner 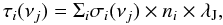 (8)where i stands for the specie and j denotes the frequency bin, σi is the photoionization cross section of the specie, n is the gas number density and λJ is the local Jeans length. The radiation flux also becomes attenuated by dust grains. These grains both absorb and scatter the radiation. The dust opacity strongly depends on the frequency of the UV flux. We use a fit to the extinction curve by Roberge et al. (1991) to compute the dust opacity as given by
(8)where i stands for the specie and j denotes the frequency bin, σi is the photoionization cross section of the specie, n is the gas number density and λJ is the local Jeans length. The radiation flux also becomes attenuated by dust grains. These grains both absorb and scatter the radiation. The dust opacity strongly depends on the frequency of the UV flux. We use a fit to the extinction curve by Roberge et al. (1991) to compute the dust opacity as given by 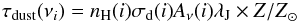 (9)here nH is the number density of hydrogen, σd is the effective dust cross section, and Aν is the dust extinction coefficient. Total attenuation of the radiation field is given by
(9)here nH is the number density of hydrogen, σd is the effective dust cross section, and Aν is the dust extinction coefficient. Total attenuation of the radiation field is given by 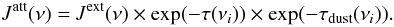 (10)The stellar sources formed inside the halos will produce a local UV flux. We have also modeled this flux and studied its influence on the collapse and chemistry of the gas physics. As these sources are formed in the high density regions, we enhance the background UV flux by factors of 100 and 1000 above densities of 1 cm-3.
(10)The stellar sources formed inside the halos will produce a local UV flux. We have also modeled this flux and studied its influence on the collapse and chemistry of the gas physics. As these sources are formed in the high density regions, we enhance the background UV flux by factors of 100 and 1000 above densities of 1 cm-3.
 |
Fig. 1 Time sequence of density snapshots at different redshifts. Redshift and distance scales are mentioned in each panel, and shown for model A. The values of density shown in the colorbar are in comoving units [g/cm3]. The merging of clumps is shown inside the black circle. |
 |
Fig. 2 Average density radial profiles for different strengths of the background UV field and dust-to-gas ratios at z = 5.4. The values of the background UV flux and metallicities are shown inside each figure. The right hand side panel is for an internal UV radiation flux (model E, F, G, H) in addition to a background UV flux of J21 = 1. The value of the escape fraction for ionizing radiation is 10% for both panels. |
 |
Fig. 3 Average radial profiles for different background UV fields and dust-to-gas ratios at z = 5.4. The upper left panel of this figure shows the temperature radial profile of the halo. The HII abundance radial profile for the halo is depicted in the upper right panel. H2 abundance is shown in the lower left panel. The lower right panel shows the HD radial profile of the halo. The escape fraction of ionizing radiation is 10% for all the panels shown in the figure. |
 |
Fig. 4 Density weighted projection of gas density for different background UV fields and dust-to-gas ratios at redshift 5.4. The top left panel shows the density for model A. The density structure for model B is shown in the upper right panel. The bottom left panel shows the density structure for model C while the bottom right panel shows the density structure for model D. The escape fraction of ionizing radiation is 10% for all the panels. The values of density shown in the colorbar are in comoving units [g/cm3]. |
4. Results
4.1. Global dynamics
We have performed a grid of simulations for different strengths of external and internal UV fluxes as well as for two different dust-to-gas ratios as shown in Table 2. We start our simulations at redshift 90 with cosmological initial conditions. Density perturbations decouple from the Hubble flow and begin to collapse through gravitational instability at redshift 20. The gas falls into the dark matter potentials and gets shock heated. The virialization processes partly transform the gravitational binding energy into kinetic energy of the gas and dark matter. Part of the gravitational potential energy goes into thermal energy of the gas and is radiated away. We also see the merging of smaller clumps into bigger ones. The occurrence of a major merger is shown in Fig. 1. This process of merging helps in the transfer of angular momentum, which is necessary for the gas to settle in the gravitational potential (Mayer et al. 2010). We switch on the radiative backgrounds at z = 8, where we expect reionization to be already in its final phase. The temperature of the gas is increased above 104 K due to photoheating, depending on the strength of the radiation field. At these temperatures, the recombination cooling kicks in and the gas begins to recombine. The gas in the filaments is relatively denser, becomes self-shielded and falls into the center of the galaxy through cold streams (Haiman et al. 2000; Dijkstra & Loeb 2009). These cold streams have typical temperatures of 104 K and number densities on the order of 0.01−1 cm-3. The average density radial profiles for different strengths of the background UV fields are shown in Fig. 2. The variations in the density radial profiles are due to the substructure in the halo and vary with the strength of the radiation field and dust-to-gas ratio. Before discussing the disk morphologies and dynamics in more detail, we will explore the impact of dust and radiation backgrounds in Sect. 4.2.
4.2. Chemical and thermal evolution
The average temperature radial profiles for two different dust-to-gas ratios and various strengths of a background UV radiation field are shown in the upper left panel of Fig. 3. It can be seen that gas is photoheated by a UV radiation flux in the envelope of a halo and consequently its temperature is raised to above 104 K. It can also be seen that the maximum temperature is 105 K for ionizing flux (J21 × fesc) of 1 in units of J21. The cooling due to helium lines becomes important at ≥5 × 104 K and thus keeps the gas temperature at 105 K. Recombination cooling becomes effective above 10-24 g/cm3 and cools the gas down to 104 K. It is found that for model A, gas cools efficiently due to the enhanced fraction of H2 and HD molecules in the presence of dust grains. The H2 and HD cooling begins to become effective around 10-22 g/cm3, where gas is cooled down to ~150 K. For model B, the temperature in the center of the halo is increased to approximately 250 K. Similarly, for models C and D (i.e., J21 = 10) the temperature is higher in the center of a halo due to the photodissociation of H2 and HD molecules.
The temperature evolution is significantly different for higher and lower dust-to-gas ratios. The ionization degree of the gas is shown in the top right panel of Fig. 3. The ionization fraction of HII is higher in the surroundings of the halo, depending on the intensity of ionizing radiation, and goes down toward the center of the halo. The overall degree of ionization is higher for a stronger radiation field and lower for a weaker radiation field. At radii <1019.7 cm, the ionization fraction decreases sharply as gas becomes neutral and is efficiently shielded from the ionizing radiation flux. The results are in agreement with our previous study (Latif et al. 2011a).
The bottom left panel of Fig. 3 depicts the H2 radial profiles. It is found that the molecular hydrogen abundance is very low in the envelope of the halo as gas is highly ionized. There is a sharp rise in H2 abundance at radii between 1021.5 cm and 1022 cm. This is due to the substructure in the halo where gas self-shields against the background UV radiation field and molecular hydrogen survives. The H2 abundance sharply increases toward the center of the halo as its photodissociation becomes ineffective due to further self-shielding. For a weaker radiation field and higher dust-to-gas ratio (i.e., model A), the H2 fraction is higher compared to the stronger radiation field and lower dust-to-gas ratio cases. The H2 abundance is significantly boosted in the core of the halo due to the formation of H2 molecules on dust grains at high gas densities. This increase in H2 abundance in the presence of dust grains is consistent with earlier studies of Cazaux & Spaans (2009, 2004). Similar behavior is found for HD molecules, as shown in the bottom right panel of Fig. 3. The HD abundance is lower for a stronger UV background flux and higher for a weaker flux. A maximum HD abundance of 10-4.5 is found for model A. The HD abundance remains lower than the critical value (i.e., 10-6) for J21 ≥ 0.1 in agreement with previous studies (Wolcott-Green & Haiman 2011; Latif et al. 2011a).
4.3. Disk formation and morphology
Estimates of dust continuum emission for different UV radiation fields.
The properties of simulations for different strengths of background UV flux and dust-to-gas ratios at redshift 5.4 are illustrated in Fig. 4. It is found that binary disks are formed for model A, as shown in the top left panel of Fig. 4, in different subhalos. We note that the upper disk is formed first and the second disk appears a few megayears after the formation of first. Each disk has spiral arms and gas masses of 4 × 107 M⊙ and 2 × 107 M⊙, respectively, and sizes of ~1 kpc. We see indications for the formation of an additional disk during later stages of the evolution. For the same radiation field, but with lower dust-to-gas ratio (i.e., model B), the halo fragments again and forms binary disks. The morphology of the halo is shown in the top right panel of Fig. 4 and is very different from the previous case. The temperature of the halo is higher due to the lower dust-to-gas ratio. The gas masses of the lower and upper disks are 2.3 × 107 M⊙ and 1.4 × 107 M⊙, respectively. We found that the lower disk is formed first (opposite to the previous case) and the second disk is formed after 6 megayears. The bottom left panel of Fig. 4 shows the structure of a halo for model C. It can be seen that again binary disks are formed. The formation process is different, the top disk is formed first while the second disk is formed through the merging of smaller clumps. Moreover, the formation of the bottom disk is delayed compared to the lower radiation background UV field case and is formed 19 megayears after the formation of the first disk. The overall collapse of the halo is also delayed due to the stronger radiation field. The gas masses of the lower and upper disks are 2.0 × 107 M⊙ and 3 × 107 M⊙, respectively. The bottom right panel of Fig. 4 shows the state of the halo for model D. Similar to the other cases, two disks are formed. The upper disk is formed first and the second disk is formed after 20 megayears. This delay is due to the enhanced strength of the radiation field and lower dust-to-gas ratio. Gas masses of the lower and upper disks are 2.2 × 107 M⊙, 1.7 × 107 M⊙, respectively. The binary disk formation in our simulations is due to the presence of subhalos after a major merger. Employing different initial conditions may result in single or multiple disks.
4.4. Disk dynamics and stability
We have computed the circular velocity (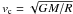 , M is the disk mass) and rotational velocity (vrot = L/R, where L is the specific angular momentum of the disk) for each disk. The ratio of rotational to circular velocity for disk 1 (the massive disk in each case) is shown in the top left panel of Fig. 5, while for disk 2 (the less massive one in each case) is shown in the top right panel of Fig. 5. The rotational velocity remains lower than the circular velocity which means that the collapse is never halted by rotational support. In the very central region, there is a central massive clump with no spiral arm structure, and with very little rotational support. This is because the turbulent velocities are much larger than the rotational velocity, leading to a spherical rather than a disk-type structure. At larger scales >1019.6 cm, the rotational velocity is increased and we see a disk with spiral arms. We found that both disks are co-rotating, independent of metallicity. The sign change in the rotational velocity is a result of the two spiral arms, as the arms between the disks then move in opposite directions. We found that disk 2 in each case has higher rotational support than disk 1. We also computed the turbulent energy for the system and compared it with the thermal energy. The ratio of turbulent to thermal energy is plotted for both disks in the middle panel of Fig. 5. It is found that turbulence is highly supersonic and turbulent pressure is more important than the thermal pressure. This is due to the high virial temperature, which is reflected in the kinetic energy of the gas. Our results are similar to Aykutalp & Spaans (2011). To investigate the stability of each disk, we computed the Toomre instability parameter Q, given by
, M is the disk mass) and rotational velocity (vrot = L/R, where L is the specific angular momentum of the disk) for each disk. The ratio of rotational to circular velocity for disk 1 (the massive disk in each case) is shown in the top left panel of Fig. 5, while for disk 2 (the less massive one in each case) is shown in the top right panel of Fig. 5. The rotational velocity remains lower than the circular velocity which means that the collapse is never halted by rotational support. In the very central region, there is a central massive clump with no spiral arm structure, and with very little rotational support. This is because the turbulent velocities are much larger than the rotational velocity, leading to a spherical rather than a disk-type structure. At larger scales >1019.6 cm, the rotational velocity is increased and we see a disk with spiral arms. We found that both disks are co-rotating, independent of metallicity. The sign change in the rotational velocity is a result of the two spiral arms, as the arms between the disks then move in opposite directions. We found that disk 2 in each case has higher rotational support than disk 1. We also computed the turbulent energy for the system and compared it with the thermal energy. The ratio of turbulent to thermal energy is plotted for both disks in the middle panel of Fig. 5. It is found that turbulence is highly supersonic and turbulent pressure is more important than the thermal pressure. This is due to the high virial temperature, which is reflected in the kinetic energy of the gas. Our results are similar to Aykutalp & Spaans (2011). To investigate the stability of each disk, we computed the Toomre instability parameter Q, given by 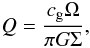 (11)where Ω is the Keplerian orbital frequency, Σg is the surface density of the disk,
(11)where Ω is the Keplerian orbital frequency, Σg is the surface density of the disk, 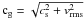 , cs is the isothermal sound speed and vrms is the root mean square velocity
, cs is the isothermal sound speed and vrms is the root mean square velocity 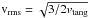 and G is the gravitational constant. The bottom left panel of Fig. 5 shows the spatial evolution of the Q parameter for disk 1. It is found that only for R < 1019.6 cm the value of Q is larger than one and the disk is stable. The sharp increase toward the center of the disks is due to the increase in epicyclic frequency. The Toomre instability parameter Q for disk 2 is shown in the bottom right panel of Fig. 5. The value of the Toomre parameter is not well defined on large scales (i.e., > 1020 cm), as there is no well defined disk and the overall spatial evolution of mass is much larger than the Jeans mass. We also computed the specific angular momentum spatial evolution. We found that angular momentum increases with radius according to expectation. We have a specific angular momentum on the order of 1031 cm2/s and our results are again in agreement with Aykutalp & Spaans (2011). Our stability analysis shows that disks are stable and are supported by turbulent pressure. In spite of the global stability, the high turbulent Mach numbers considered will locally produce strong overdensities in shocks, and may lead to a star formation mode regulated by turbulence (Mac Low & Klessen 2004; Krumholz & Tan 2007; Braun & Schmidt 2012). The final fate of the disks depends on the ambient conditions. They may merge with each other and lead to the formation of a protogalaxy. They may form stars if they become Toomre unstable.
and G is the gravitational constant. The bottom left panel of Fig. 5 shows the spatial evolution of the Q parameter for disk 1. It is found that only for R < 1019.6 cm the value of Q is larger than one and the disk is stable. The sharp increase toward the center of the disks is due to the increase in epicyclic frequency. The Toomre instability parameter Q for disk 2 is shown in the bottom right panel of Fig. 5. The value of the Toomre parameter is not well defined on large scales (i.e., > 1020 cm), as there is no well defined disk and the overall spatial evolution of mass is much larger than the Jeans mass. We also computed the specific angular momentum spatial evolution. We found that angular momentum increases with radius according to expectation. We have a specific angular momentum on the order of 1031 cm2/s and our results are again in agreement with Aykutalp & Spaans (2011). Our stability analysis shows that disks are stable and are supported by turbulent pressure. In spite of the global stability, the high turbulent Mach numbers considered will locally produce strong overdensities in shocks, and may lead to a star formation mode regulated by turbulence (Mac Low & Klessen 2004; Krumholz & Tan 2007; Braun & Schmidt 2012). The final fate of the disks depends on the ambient conditions. They may merge with each other and lead to the formation of a protogalaxy. They may form stars if they become Toomre unstable.
4.5. The implications of internal radiation fields
 |
Fig. 5 Average radial profiles of disks for different background UV fields and dust-to-gas ratios at z = 5.4. The left panels of this figure show radial profiles for disk 1 and the right panels show the radial profiles for disk 2. The top two panels show the ratio of rotational to orbital velocity for the disks. The middle panels show the ratio of turbulent to thermal energy for each disk. The Toomre parameter Q for each disk is depicted in the bottom panel. The escape fraction of ionizing radiation is 10% for all panels. |
 |
Fig. 6 Average radial profiles for different internal UV field strengths and dust-to-gas ratios at z = 5.4. The upper left panel of this figure shows the temperature radial profile of the halo. The HII abundance radial profile for the halo is depicted in the upper right panel. The lower left panel shows the H2 abundance. The HD radial profile of the halo is depicted in the lower right panel. The escape fraction of ionizing radiation is 10%. |
 |
Fig. 7 Density weighted projections of gas density for various internal UV field strengths and dust-to-gas ratios at redshift 5.4. The top left panel show the density for model E. The density structure for model F is depicted in the upper right panel. The left panel shows the density structure for model G. The state of a halo for model H is shown in the right panel. The escape fraction of ionizing radiation is 10% for all panels. The values of density shown in the colorbar are in comoving units [g/cm3]. |
 |
Fig. 8 Density weighted projections of temperature for different internal UV field strengths and dust-to-gas ratios at redshift 5.4. The left panel shows the temperature for model G. The temperature for model H is depicted in the right panel. The panels show temperatures corresponding to the density panels of Fig. 7. This shows that thermal instability leads to the formation of gas clumps at these temperatures. The values of temperature are shown in the colorbar. |
 |
Fig. 9 Average radial profiles of the disks for different strengths of internal UV fields and dust-to-gas ratios at z = 5.4. The left panel of this figure shows radial profiles for disk 1 and right panels shows the radial profiles for disk 2. The top two panels show the ratio of rotational to orbital velocity for the disks. The Toomre parameter Q for each disk is depicted in the bottom panels. The value of an escape fraction for ionizing radiation is 10% for both panels. |
We also performed simulations with a given strength (i.e., J21 = 1) of the background UV radiation field, but for an enhanced internal radiation flux of 100 and 1000 times the background at densities >1 cm-3 due to the formation of stellar sources inside the halo. Figure 6 shows the radial profiles for temperature, ionization degree of the gas, abundances of H2 and HD molecules. It is found that the temperature of the gas is relatively higher as compared to the cases with no internal radiation sources. The degree of ionization is also enhanced. The gas still cools and recombines inside the HII regions, which is why the degree of ionization declines toward the center of a halo. The H2 and HD abundances are shown in the bottom panel of Fig. 6. It is found that due to the enhanced strength of the internal UV flux, photodissociation of molecules becomes effective and H2 and HD are almost two orders of magnitude lower than in the no internal radiation case. The state of the simulations for internal radiation sources at redshift 5.4 is shown in Fig. 7. It is found that the collapse of a halo is delayed for these cases. We find that for model E, gas is still able to cool down to a few hundred Kelvin, while for the lower dust-to-gas ratio case (i.e., model F) the temperature increases up to 1000 K. A binary system is again formed irrespective of the dust-to-gas ratio. The gas masses of disk 1 and 2 are 1.9 × 107 M⊙ and 1.7 × 107 M⊙ for Z/Z⊙ = 10-2, and 1.6 × 107 M⊙ and 8 × 106 M⊙ for Z/Z⊙ = 10-4. Despite the higher temperatures in the core of a halo due to photodissociation of molecules, surprisingly, fragmentation is enhanced for J21 = 1000 irrespective of the dust-to-gas ratio. This is due to cooling instabilities because the temperature lies in the unstable regime of 2000 to 5000 K. The formation and dissociation of H2 is very sensitive to the above-mentioned temperature range. As the temperature increases above 3700 K, the H2 survival time sharply decreases and the cooling time scale increases. On the other hand, if the temperature is slightly decreased, this leads to longer H2 survival times (see Fig. 4 of Oh & Haiman 2002). This process initiates thermal instabilities. The gas masses of the fragments are on the order of a few 106 M⊙. Figure 8 shows the temperature corresponding to the density projections in Fig. 7 (i.e., models G and H). It can be seen that in the high density regions fine-grained thermal substructure occurs, which indicates small pockets of gas that quickly cool down to low temperatures. This supports our hypothesis of thermal instabilities leading to the local cooling and collapse of gas.
We also computed the ratio of rotational to circular velocity of the disks for internal radiation field cases (i.e., models E, F, G and H). These are shown in the top panels of Fig. 9. The ratio remains less than unity as in previous cases. We find that for a lower dust-to-gas ratio, the disks are now counter-rotating while they are co-rotating for higher dust-to-gas ratio case. Dynamical evolution is faster in high dust-to-gas ratio environments (Aykutalp & Spaans 2011). Therefore, the lower-mass disk falls behind in its evolution compared to the higher-mass one for lower dust-to-gas ratio. Subsequently, the lower-mass disk is forced to accrete gas from the trailing spiral arm of the higher-mass disk and counter-rotation ensues. We also computed the turbulent and thermal energy of the system and found that turbulence is again highly supersonic and the disks are supported by turbulent pressure. The Toomre stability parameter Q is larger than unity in the central region (i.e., <1019.6 cm), where we see a well-defined disk. The disk is therefore expected to be stable, similar to previous cases, as shown in the bottom panels of Fig. 9.
4.6. Lyman-α emission from high-redshift protogalaxies
We estimate the Ly-α flux emanating from the galaxy forming halo. Our results for the Ly-α emission in the presence of dust are shown in Fig. 10. We found that above columns of 1022 cm2 and optical depths of τ ≥ 107 trapping of Ly-α photons becomes effective, consistent with previous studies (Spaans & Silk 2006; Latif et al. 2011a,b,c). That is why Ly-α emission sharply declines toward the center of the halo. It can be seen that the Ly-α flux emerges from the envelope of the halo. The value of the flux depends upon the strength of the external UV radiation field and the dust-to-gas ratio. The local variations in the flux are due to the clumpiness of the medium. We assume a constant dust-to-gas ratio, leading to a highly inhomogeneous, clumpy interstellar medium as a result of the high Mach numbers in our simulation (see models of Neufeld 1991; Haiman & Spaans 1999; Shimizu et al. 2011). As dust sits in the center of the dense clumps, Ly-α photons scatter off these clumps and are able to escape the halo due to large scattering cross sections. This depends on the clump covering factor, i.e., average number of gas clouds along the line of sight. We compute the column density distribution and use it to determine the clump covering factor. We use the model of Haiman & Spaans (1999) to compute the HI Ly-α escape fraction. Our findings are in agreement with Neufeld (1991); Haiman & Spaans (1999); Shimizu et al. (2011).
The presence of a background UV flux excites the emission of Ly-α photons and enhances its luminosity. Moreover, flux predominantly arises from collisional excitation of atomic hydrogen and the contribution from recombination line emission is a few orders of magnitude lower. For further details on the origin and source of Ly-α emission see our previous studies (Latif et al. 2011b,a). Our results also agree with previous studies that emission of Ly-α is extended and emerges from the warm gas in the surroundings of the galaxy (Dijkstra et al. 2006a,b; Dijkstra & Loeb 2009; Faucher-Giguère et al. 2010; Latif et al. 2011a). We found that a flux on the order of 10-14−10-12 erg/cm2/s emanates from the the protogalactic halo at redshift 5.4. The redshifted wavelength of Ly-α photons at redshift 5.4 is 0.78 micron. This should be detectable with present-day telescopes like Subaru1 and VLT2. Further details on the issue of line trapping of Ly-α photons and the role of background UV flux in the emission of Ly-α photons are given by Schleicher et al. (2010b) and Latif et al. (2011a). Ly-α emission, apart from dust content, also depends on the velocity structure of a halo. The variation in Doppler velocity shift does not strongly influence the escape fraction of Ly-α photons (Haiman & Spaans 1999). We also checked the consistency of intrinsic Ly-α luminosity with the adopted internal UV flux. We computed flux from intrinsic Ly-α luminosity by normalizing it with Ly-α line width and found it consistent with the adopted UV flux. In the presence of dust, the contribution of the internal stellar feedback, on top of the background UV field, can vary strongly. For Z/Z⊙ = 10-4, UV continuum optical depths range from 10-6 to almost unity, and are a factor 100 times larger for Z/Z⊙ = 10-2. In our simulations, column densities range from 1018 to 1024 cm-2, a similarly wide range as found by Wada et al. (2009). For the dust-free case, we expect internal stellar feedback to be quite effective, and to partly photo-dissociate H2. However, in the presence of a strong background UV field, the role of the intrinsic luminosity again diminishes.
4.7. Dust emission from high-redshift protogalaxies
We further compute the dust temperatures for different UV background fluxes and dust-to-gas ratios for the cases listed in Table 2. We found that for lower background UV fluxes (i.e., J21 = 1), the dust temperature remains close to the TCMB while for higher fluxes (i.e., J21 = 100) it is well above TCMB. We have a maximum dust temperature of 34 K for the model H in our case. Our results are in agreement with observed dust temperatures of high-redshift quasars (Omont et al. 2001; Yang et al. 2012). We found that for the given dust-to-gas ratios and the halo masses considered here (dust masses, 106 M⊙ for Z/Z⊙ = 10-2 and 104 M⊙ for Z/Z⊙ = 10-4), the dust continuum emission is far below the detection limits of the Atacama Large Millimeter Array (ALMA)3 at z = 5.4. However, ALMA will be able to explore the dust content in larger systems or in the presence of higher dust-to-gas ratios. Our calculations show that a 3 sigma detection is possible with ALMA band 9 in five hours of integration if dust masses (for calculation see equation 1 of Omont et al. 2001) of 6.75 × 108 M⊙, 3.27 × 108 M⊙, and 1.54 × 108 M⊙ are present (assuming dust temperatures of 20 K, 30 K, and 50 K, respectively). One requires roughly solar metallicity for a ~1010 M⊙ protogalactic halo to be detectable at z > 5.
 |
Fig. 10 Ly-α emission for different magnitudes of the background UV field and dust-to-gas ratios. The right hand side panel shows the flux for different background UV radiation fields. The left panel shows the Ly-α flux for an internal UV radiation field in addition to a background UV flux J21 = 1. The value of the escape fraction for ionizing radiation is 10% for both panels. |
5. Discussion and conclusions
In all, we have performed 9 cosmological simulations to study the dynamics of disk formation in protogalactic halos under the influence of different UV radiation field strengths and dust-to-gas ratios. We used the AMR code FLASH to carry out this task and coupled it with a chemical network. Our chemical model includes photoionization, collisional excitation, collisional ionization, radiative recombination, photodissociation processes and the formation of molecules on dust grains as well as a multi-level treatment of the hydrogen atom. We found that gas in the atomic cooling halo is photoionized by a background UV flux and that photoheating raises the gas temperature to above 104 K. At densities ≥ 10-24 g/cm-3, gas cools, recombines and falls into the center of a halo through cold streams of gas. The later thermal evolution of a halo depends on the strength of a background UV flux and the dust-to-gas ratio. The formation of H2 and HD molecules is significantly enhanced (by two orders of magnitude) in the presence of dust grains as compared to gas phase reactions. We found that the formation of molecules is more effective for higher dust-to gas ratio (i.e., Z/Z⊙ = 10-2) as compared to lower dust-to-gas ratio (i.e., Z/Z⊙ = 10-4). The minimum temperature in the core of a halo is ~ 200 K for model A. This value is higher (800 K) for lower dust-to-gas ratio and stronger UV radiation flux. We conclude that the thermal evolution of a protogalactic halo is strongly influenced by the presence of dust and a UV radiation field.
Our results show that binary disks are formed in the protogalactic halo at redshift 5.4 irrespective of the background UV radiation field strength and dust-to-gas ratio in our simulations. However, the morphology and the formation time of disks does strongly depend on the dust-to-gas ratio and strength of a background UV flux. We found that disks are stable as the value of Toomre instability parameter Q is greater than one at radii < 1019.5 cm. We also found that the turbulence in the halo is highly supersonic due to the higher virial temperature of the halo. Moreover, disks are more supported by turbulent pressure than thermal pressure. It may happen that disks merge with one another at lower redshifts. There is also a possibility that more than 2 disks are formed in some cases, which will lead to the formation of a multiple disk system. We could not follow the evolution of a halo to a lower redshift than 5.4 as this becomes a computationally too expensive task. Nevertheless, we have explored an important phase of disk formation, which may be observed with future planned surveys.
We also performed a set of simulations with different Gaussian random field initial conditions to determine whether the origin of binary disk formation comes from cosmological initial conditions. We found that a single disk is formed in the center of a halo instead of binary disks for a different random seed. We thus think that the origin of binary disk formation is associated with the underlying dynamics of the dark matter in the halo. In an upcoming paper, we will address the issue of how often these binary disks form in atomic cooling halos.
We performed additional simulations for the cases where the background UV flux is enhanced by factors of 100 and 1000 due to the formation of radiation sources like stars inside the halo. It was found that the collapse of a halo is delayed in HII regions formed by the internal radiation sources and the photodissociation of molecules (H2 and HD) is strongly enhanced in this case. We found that despite the higher temperatures in the halo for an internal radiation flux of J21 = 100, in addition to a background UV flux of J21 = 1, again binary disks are formed for both Z/Z⊙ = 10-2 and Z/Z⊙ = 10-4. For a higher strength of the internal radiation flux, J21 = 1000, the temperature of the halo in the center is increased to a few thousand Kelvin. We found that for this case cooling instabilities lead to the formation of multiple clumps for both dust-to-gas ratios, Z/Z⊙ = 10-2 and Z/Z⊙ = 10-4 at redshift 5.4. Due to significant local overdensities in the high-Mach turbulence, we expect a star formation mode that is regulated by the turbulent density PDF (Mac Low & Klessen 2004; Krumholz & Tan 2007; Braun & Schmidt 2012). The further fate of these clumps depends on how they transfer angular momentum. They may merge with each other and form a disk if they lose angular momentum. It may also happen that they keep cooling, and collapsing, and fragment further.
We estimated the Ly-α emission from protogalactic halos for different strengths of UV radiation fields and dust-to-gas ratios. We found that even in the presence of dust, for Z/Z⊙ = 10-2 and Z/Z⊙ = 10-4, Ly-α photons scatter off dusty gas clouds and an inhomogeneous dust distribution leads to the efficient escape of Ly-α photons. Our results are in agreement with the models of Haiman & Spaans (1999). It was found that a flux of the order of 10-14 − 10-12 erg/cm2/s emerges from the envelope of the halo due to effective line trapping of Ly-α photons in the center of a halo, consistent with previous studies (Spaans & Silk 2006; Schleicher et al. 2010b; Latif et al. 2011a,b). Such a flux should be observable with present-day telescopes like Subaru and the VLT. Our results provide a conservative lower limit to the Ly-α flux as we have computed the flux for minimum velocity gradient along the line of sight. Radiative transfer of Ly-α photons strongly depends on the amount of structure in the halo as well as on velocity gradients. Therefore, cosmological simulations coupled with Ly-α radiative transfer should be performed in the future to obtain more robust results.
Finally, we computed the dust emission from the protogalactic halo in our simulations. We found that due to the low dust masses such systems cannot be observed with ALMA at z = 5.4. Only galaxies with higher metal content and high dust temperatures can be probed. However, we also found that dust masses of few × 108 M⊙ yield ~0.1 mJy of flux and thus a 3-sigma detection in 5 h. Given that our protogalactic halos are likely to build up a solar content of metals within 1–2 Gyr, they should be detectable for z ≤ 5.
The formation of disks may also have significant implications for magnetic fields in the first galaxies. In the absence of rotation, the small-scale dynamo is expected to produce tangled magnetic fields, close to equipartition with turbulent energy (Arshakian et al. 2009; Schleicher et al. 2010a). This process was shown to be efficient for a large range of turbulence models and Mach numbers (Federrath et al. 2011a; Schober et al. 2012). The presence of rotating disks, on the other hand, gives rise to large-scale dynamo effects amplifying the mean magnetic field (Brandenburg & Subramanian 2005). The presence of magnetic fields in high-redshift galaxies will be probed in the future with the SKA4.
Acknowledgments
The FLASH code was in part developed by the DOE-supported Alliance Center for Astrophysical Thermonuclear Flashes (ACS) at the University of Chicago. We thank Stephanie Cazaux, Seyit Hocuk, and Gustavo Dopcke for valuable discussions on the topic. D.R.G.S. acknowledges funding from the DFG priority program 1573 (project number SCHL 1964/1-1) and the SFB 963 (project A12). D.R.G.S. also thanks the German Science Foundation for funding via the SPP 1573 (project number SCHL 1964/1-1) and the SFB 963/1 Astrophysical Flow Instabilities and Turbulence. We also thank the anonymous referee for a careful reading of the manuscript and useful feedbacak. Our simulations were carried out on the Gemini machines at the Kapteyn Astronomical Institute, University of Groningen.
References
- Abel, T., Bryan, G. L., & Norman, M. L. 2002, Science, 295, 93 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Anninos, P., Zhang, Y., Abel, T., & Norman, M. L. 1997, New A, 2, 209 [Google Scholar]
- Arshakian, T. G., Beck, R., Krause, M., & Sokoloff, D. 2009, A&A, 494, 21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Aykutalp, A., & Spaans, M. 2011, ApJ, 737, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Bertschinger, E. 1995, unpublished [arXiv:9506070] [Google Scholar]
- Bianchi, S., & Schneider, R. 2007, MNRAS, 378, 973 [NASA ADS] [CrossRef] [Google Scholar]
- Bouwens, R. J., Illingworth, G. D., Oesch, P. A., et al. 2010, ApJ, 709, L133 [NASA ADS] [CrossRef] [Google Scholar]
- Bouwens, R. J., Illingworth, G. D., Labbe, I., et al. 2011, Nature, 469, 504 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Brandenburg, A., & Subramanian, K. 2005, Phys. Rep., 417, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Braun, H., & Schmidt, W. 2012, MNRAS, in press [arXiv:1104.5582] [Google Scholar]
- Bromm, V., & Larson, R. B. 2004, ARA&A, 42, 79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bromm, V., & Loeb, A. 2003, Nature, 425, 812 [NASA ADS] [CrossRef] [EDP Sciences] [PubMed] [Google Scholar]
- Bromm, V., & Yoshida, N. 2011, ARA&A, 49, 373 [NASA ADS] [CrossRef] [Google Scholar]
- Bromm, V., Ferrara, A., Coppi, P. S., & Larson, R. B. 2001, MNRAS, 328, 969 [NASA ADS] [CrossRef] [Google Scholar]
- Bunker, A. J., Wilkins, S., Ellis, R. S., et al. 2010, MNRAS, 409, 855 [NASA ADS] [CrossRef] [Google Scholar]
- Cazaux, S., & Spaans, M. 2004, ApJ, 611, 40 [NASA ADS] [CrossRef] [Google Scholar]
- Cazaux, S., & Spaans, M. 2009, A&A, 496, 365 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Clark, P. C., Glover, S. C. O., Klessen, R. S., & Bromm, V. 2011a, ApJ, 727, 110 [NASA ADS] [CrossRef] [Google Scholar]
- Clark, P. C., Glover, S. C. O., Smith, R. J., et al. 2011b, Science, 331, 1040 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Dijkstra, M., & Loeb, A. 2009, MNRAS, 400, 1109 [NASA ADS] [CrossRef] [Google Scholar]
- Dijkstra, M., Haiman, Z., & Spaans, M. 2006a, ApJ, 649, 14 [NASA ADS] [CrossRef] [Google Scholar]
- Dijkstra, M., Haiman, Z., & Spaans, M. 2006b, ApJ, 649, 37 [NASA ADS] [CrossRef] [Google Scholar]
- Dijkstra, M., Haiman, Z., Mesinger, A., & Wyithe, J. S. B. 2008, MNRAS, 391, 1961 [NASA ADS] [CrossRef] [Google Scholar]
- Dopcke, G., Glover, S. C. O., Clark, P. C., & Klessen, R. S. 2011, ApJ, 729, L3 [NASA ADS] [CrossRef] [Google Scholar]
- Dubey, A., Antypas, K., Ganapathy, M. K., et al. 2009, Parallel Computing, 35, 512 [CrossRef] [Google Scholar]
- Faucher-Giguère, C., Kereš, D., Dijkstra, M., Hernquist, L., & Zaldarriaga, M. 2010, ApJ, 725, 633 [NASA ADS] [CrossRef] [Google Scholar]
- Federrath, C., Chabrier, G., Schober, J., et al. 2011a, Phys. Rev. Lett., 107, 114504 [NASA ADS] [CrossRef] [Google Scholar]
- Federrath, C., Sur, S., Schleicher, D. R. G., Banerjee, R., & Klessen, R. S. 2011b, ApJ, 731, 62 [NASA ADS] [CrossRef] [Google Scholar]
- Gallerani, S., Maiolino, R., Juarez, Y., et al. 2010, A&A, 523, A85 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Galli, D., & Palla, F. 1998, A&A, 335, 403 [NASA ADS] [Google Scholar]
- Glover, S. C. O., & Jappsen, A. 2007, ApJ, 666, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Greif, T. H., Glover, S. C. O., Bromm, V., & Klessen, R. S. 2010, ApJ, 716, 510 [NASA ADS] [CrossRef] [Google Scholar]
- Habing, H. J. 1968, Bull. Astron. Inst. Netherlands, 19, 421 [Google Scholar]
- Haiman, Z., & Spaans, M. 1999, ApJ, 518, 138 [NASA ADS] [CrossRef] [Google Scholar]
- Haiman, Z., Spaans, M., & Quataert, E. 2000, ApJ, 537, L5 [NASA ADS] [CrossRef] [Google Scholar]
- Hollenbach, D. J., Takahashi, T., & Tielens, A. G. G. M. 1991, ApJ, 377, 192 [NASA ADS] [CrossRef] [Google Scholar]
- Jappsen, A.-K., Klessen, R. S., Glover, S. C. O., & Mac Low, M.-M. 2009a, ApJ, 696, 1065 [NASA ADS] [CrossRef] [Google Scholar]
- Jappsen, A.-K., Mac Low, M.-M., Glover, S. C. O., Klessen, R. S., & Kitsionas, S. 2009b, ApJ, 694, 1161 [NASA ADS] [CrossRef] [Google Scholar]
- Johnson, J. L. 2011 [arXiv:1105.5701] [Google Scholar]
- Johnson, J. L., Greif, T. H., & Bromm, V. 2007, ApJ, 665, 85 [NASA ADS] [CrossRef] [Google Scholar]
- Krumholz, M. R., & Tan, J. C. 2007, ApJ, 654, 304 [NASA ADS] [CrossRef] [Google Scholar]
- Latif, M. A., Schleicher, D. R. G., Spaans, M., & Zaroubi, S. 2011a, A&A, 532, A66 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Latif, M. A., Schleicher, D. R. G., Spaans, M., & Zaroubi, S. 2011b, MNRAS, 413, L33 [NASA ADS] [CrossRef] [Google Scholar]
- Latif, M. A., Zaroubi, S., & Spaans, M. 2011c, MNRAS, 411, 1659 [NASA ADS] [CrossRef] [Google Scholar]
- Lehnert, M. D., Nesvadba, N. P. H., Cuby, J., et al. 2010, Nature, 467, 940 [NASA ADS] [CrossRef] [Google Scholar]
- Lepp, S., & Shull, J. M. 1984, ApJ, 280, 465 [NASA ADS] [CrossRef] [Google Scholar]
- Mac Low, M.-M., & Klessen, R. S. 2004, Rev. Mod. Phys., 76, 125 [NASA ADS] [CrossRef] [Google Scholar]
- Maio, U., Khochfar, S., Johnson, J. L., & Ciardi, B. 2011, MNRAS, 414, 1145 [NASA ADS] [CrossRef] [Google Scholar]
- Maiolino, R., Schneider, R., Oliva, E., et al. 2004, Nature, 431, 533 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Matsuda, Y., Yamada, T., Hayashino, T., et al. 2004, AJ, 128, 569 [NASA ADS] [CrossRef] [Google Scholar]
- Mayer, L., Kazantzidis, S., Escala, A., & Callegari, S. 2010, Nature, 466, 1082 [NASA ADS] [CrossRef] [Google Scholar]
- Meijerink, R., & Spaans, M. 2005, A&A, 436, 397 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Neufeld, D. A. 1991, ApJ, 370, L85 [NASA ADS] [CrossRef] [Google Scholar]
- Nozawa, T., Kozasa, T., Umeda, H., Maeda, K., & Nomoto, K. 2003, ApJ, 598, 785 [NASA ADS] [CrossRef] [Google Scholar]
- Oh, S. P., & Haiman, Z. 2002, ApJ, 569, 558 [NASA ADS] [CrossRef] [Google Scholar]
- Omont, A., Cox, P., Bertoldi, F., et al. 2001, A&A, 374, 371 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Omukai, K., Tsuribe, T., Schneider, R., & Ferrara, A. 2005, ApJ, 626, 627 [NASA ADS] [CrossRef] [Google Scholar]
- Omukai, K., Schneider, R., & Haiman, Z. 2008, ApJ, 686, 801 [NASA ADS] [CrossRef] [Google Scholar]
- Ono, Y., Ouchi, M., Shimasaku, K., et al. 2010, MNRAS, 402, 1580 [NASA ADS] [CrossRef] [Google Scholar]
- Ouchi, M., Ono, Y., Egami, E., et al. 2009, ApJ, 696, 1164 [NASA ADS] [CrossRef] [Google Scholar]
- Roberge, W. G., Jones, D., Lepp, S., & Dalgarno, A. 1991, ApJS, 77, 287 [NASA ADS] [CrossRef] [Google Scholar]
- Saito, T., Shimasaku, K., Okamura, S., et al. 2006, ApJ, 648, 54 [NASA ADS] [CrossRef] [Google Scholar]
- Saito, T., Shimasaku, K., Okamura, S., et al. 2008, ApJ, 675, 1076 [NASA ADS] [CrossRef] [Google Scholar]
- Santoro, F., & Shull, J. M. 2006, ApJ, 643, 26 [NASA ADS] [CrossRef] [Google Scholar]
- Saslaw, W. C., & Zipoy, D. 1967, Nature, 216, 976 [NASA ADS] [CrossRef] [Google Scholar]
- Schneider, R., & Omukai, K. 2010, MNRAS, 402, 429 [NASA ADS] [CrossRef] [Google Scholar]
- Schneider, R., Ferrara, A., Natarajan, P., & Omukai, K. 2002, ApJ, 571, 30 [NASA ADS] [CrossRef] [Google Scholar]
- Schneider, R., Ferrara, A., Salvaterra, R., Omukai, K., & Bromm, V. 2003, Nature, 422, 869 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Schleicher, D. R. G., Banerjee, R., Sur, S., et al. 2010a, A&A, 522, A115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schleicher, D. R. G., Spaans, M., & Glover, S. C. O. 2010b, ApJ, 712, L69 [NASA ADS] [CrossRef] [Google Scholar]
- Schneider, R., Omukai, K., Bianchi, S., & Valiante, R. 2011, MNRAS, 1743 [Google Scholar]
- Schober, J., Schleicher, D., Federrath, C., Klessen, R., & Banerjee, R. 2012, Phys. Rev. E, 85, 026303 [NASA ADS] [CrossRef] [Google Scholar]
- Shang, C., Bryan, G. L., & Haiman, Z. 2010, MNRAS, 402, 1249 [NASA ADS] [CrossRef] [Google Scholar]
- Shimizu, I., Yoshida, N., & Okamoto, T. 2011, MNRAS, 418, 2273 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, B., Sigurdsson, S., & Abel, T. 2008, MNRAS, 385, 1443 [NASA ADS] [CrossRef] [Google Scholar]
- Spaans, M., & Silk, J. 2000, ApJ, 538, 115 [NASA ADS] [CrossRef] [Google Scholar]
- Spaans, M., & Silk, J. 2006, ApJ, 652, 902 [NASA ADS] [CrossRef] [Google Scholar]
- Steidel, C. C., Adelberger, K. L., Shapley, A. E., et al. 2000, ApJ, 532, 170 [Google Scholar]
- Tamura, Y., Kohno, K., Nakanishi, K., et al. 2009, Nature, 459, 61 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Tegmark, M., Silk, J., Rees, M. J., et al. 1997, ApJ, 474, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Todini, P., & Ferrara, A. 2001, MNRAS, 325, 726 [NASA ADS] [CrossRef] [Google Scholar]
- Truelove, J. K., Klein, R. I., McKee, C. F., et al. 1997, ApJ, 489, L179 [NASA ADS] [CrossRef] [Google Scholar]
- Turk, M. J., Smith, B. D., Oishi, J. S., et al. 2011, ApJS, 192, 9 [NASA ADS] [CrossRef] [Google Scholar]
- Vanzella, E., Pentericci, L., Fontana, A., et al. 2011, ApJ, 730, L35 [NASA ADS] [CrossRef] [Google Scholar]
- Wada, K., Papadopoulos, P. P., & Spaans, M. 2009, ApJ, 702, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Weingartner, J. C., & Draine, B. T. 2001, ApJ, 548, 296 [NASA ADS] [CrossRef] [Google Scholar]
- Wolcott-Green, J., & Haiman, Z. 2011, MNRAS, 412, 2603 [NASA ADS] [CrossRef] [Google Scholar]
- Yang, Y., Zabludoff, A., Tremonti, C., Eisenstein, D., & Davé, R. 2009, ApJ, 693, 1579 [NASA ADS] [CrossRef] [Google Scholar]
- Yang, Y., Decarli, R., Dannerbauer, H., et al. 2012, ApJ, 744, 178 [NASA ADS] [CrossRef] [Google Scholar]
- Yoshida, N., Omukai, K., & Hernquist, L. 2008, Science, 321, 669 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Time sequence of density snapshots at different redshifts. Redshift and distance scales are mentioned in each panel, and shown for model A. The values of density shown in the colorbar are in comoving units [g/cm3]. The merging of clumps is shown inside the black circle. |
| In the text | |
 |
Fig. 2 Average density radial profiles for different strengths of the background UV field and dust-to-gas ratios at z = 5.4. The values of the background UV flux and metallicities are shown inside each figure. The right hand side panel is for an internal UV radiation flux (model E, F, G, H) in addition to a background UV flux of J21 = 1. The value of the escape fraction for ionizing radiation is 10% for both panels. |
| In the text | |
 |
Fig. 3 Average radial profiles for different background UV fields and dust-to-gas ratios at z = 5.4. The upper left panel of this figure shows the temperature radial profile of the halo. The HII abundance radial profile for the halo is depicted in the upper right panel. H2 abundance is shown in the lower left panel. The lower right panel shows the HD radial profile of the halo. The escape fraction of ionizing radiation is 10% for all the panels shown in the figure. |
| In the text | |
 |
Fig. 4 Density weighted projection of gas density for different background UV fields and dust-to-gas ratios at redshift 5.4. The top left panel shows the density for model A. The density structure for model B is shown in the upper right panel. The bottom left panel shows the density structure for model C while the bottom right panel shows the density structure for model D. The escape fraction of ionizing radiation is 10% for all the panels. The values of density shown in the colorbar are in comoving units [g/cm3]. |
| In the text | |
 |
Fig. 5 Average radial profiles of disks for different background UV fields and dust-to-gas ratios at z = 5.4. The left panels of this figure show radial profiles for disk 1 and the right panels show the radial profiles for disk 2. The top two panels show the ratio of rotational to orbital velocity for the disks. The middle panels show the ratio of turbulent to thermal energy for each disk. The Toomre parameter Q for each disk is depicted in the bottom panel. The escape fraction of ionizing radiation is 10% for all panels. |
| In the text | |
 |
Fig. 6 Average radial profiles for different internal UV field strengths and dust-to-gas ratios at z = 5.4. The upper left panel of this figure shows the temperature radial profile of the halo. The HII abundance radial profile for the halo is depicted in the upper right panel. The lower left panel shows the H2 abundance. The HD radial profile of the halo is depicted in the lower right panel. The escape fraction of ionizing radiation is 10%. |
| In the text | |
 |
Fig. 7 Density weighted projections of gas density for various internal UV field strengths and dust-to-gas ratios at redshift 5.4. The top left panel show the density for model E. The density structure for model F is depicted in the upper right panel. The left panel shows the density structure for model G. The state of a halo for model H is shown in the right panel. The escape fraction of ionizing radiation is 10% for all panels. The values of density shown in the colorbar are in comoving units [g/cm3]. |
| In the text | |
 |
Fig. 8 Density weighted projections of temperature for different internal UV field strengths and dust-to-gas ratios at redshift 5.4. The left panel shows the temperature for model G. The temperature for model H is depicted in the right panel. The panels show temperatures corresponding to the density panels of Fig. 7. This shows that thermal instability leads to the formation of gas clumps at these temperatures. The values of temperature are shown in the colorbar. |
| In the text | |
 |
Fig. 9 Average radial profiles of the disks for different strengths of internal UV fields and dust-to-gas ratios at z = 5.4. The left panel of this figure shows radial profiles for disk 1 and right panels shows the radial profiles for disk 2. The top two panels show the ratio of rotational to orbital velocity for the disks. The Toomre parameter Q for each disk is depicted in the bottom panels. The value of an escape fraction for ionizing radiation is 10% for both panels. |
| In the text | |
 |
Fig. 10 Ly-α emission for different magnitudes of the background UV field and dust-to-gas ratios. The right hand side panel shows the flux for different background UV radiation fields. The left panel shows the Ly-α flux for an internal UV radiation field in addition to a background UV flux J21 = 1. The value of the escape fraction for ionizing radiation is 10% for both panels. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


