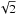| Issue |
A&A
Volume 540, April 2012
|
|
|---|---|---|
| Article Number | A38 | |
| Number of page(s) | 15 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/201116622 | |
| Published online | 22 March 2012 | |
The intracluster magnetic field power spectrum in A2199
1 Dipartimento di Fisica, Università degli studi di Cagliari, Cittadella Universitaria, 09042 Monserrato (CA), Italy
e-mail: vvacca@oa-cagliari.inaf.it
2 INAF – Osservatorio Astronomico di Cagliari, Poggio dei Pini, Strada 54, 09012 Capoterra (CA), Italy
3 INAF – Istituto di Radioastronomia, via Gobetti 101, 40129 Bologna, Italy
4 Dipartimento di Astronomia, Univ. Bologna, via Ranzani 1, 40127 Bologna, Italy
5 National Radio Astronomy Observatory, Socorro, NM 87801, USA
6 Department of Physics and Astronomy, University of New Mexico, Albuquerque NM, 87131, USA
Received: 1 February 2011
Accepted: 2 December 2011
Aims. We investigate the magnetic field power spectrum in the cool core galaxy cluster A2199 by analyzing the polarized emission of the central radio source 3C 338.
Methods. The polarized radiation from the radio emitting plasma is modified by the Faraday rotation as it passes through the magneto-ionic intracluster medium. We use Very Large Array observations between 1665 and 8415 MHz to produce detailed Faraday rotation measure and fractional polarization images of the radio galaxy. We simulate Gaussian random three-dimensional magnetic field models with different power-law power spectra and we assume that the field strength decreases radially with the thermal gas density as neη. By comparing the synthetic and the observed images with a Bayesian approach, we constrain the strength and structure of the magnetic field associated with the intracluster medium.
Results. We find that the Faraday rotation toward 3C 338 in A2199 is consistent with a magnetic field power law power spectrum characterized by an index n = (2.8 ± 1.3) between a maximum and a minimum scale of fluctuation of Λmax = (35 ± 28) kpc and Λmin = (0.7 ± 0.1) kpc, respectively. By including in the modeling X-ray cavities coincident with the radio galaxy lobes, we find a magnetic field strength of ⟨B0⟩ = (11.7 ± 9.0) μG at the cluster center. Further out, the field decreases with the radius following the gas density to the power of η = (0.9 ± 0.5).
Key words: galaxies: clusters: general / galaxies: clusters: individual: Abell 2199 / magnetic fields / polarization / large-scale structure of Universe
© ESO, 2012
1. Introduction
In the past decade, significant progress has been made in characterizing the properties of the intracluster magnetic field. Most of what we know about intracluster magnetic field strength and structure is derived from the study of diffuse synchrotron emission (radio halos, mini-halos, and relics) and Faraday rotation measures of polarized radio galaxies located inside or behind galaxy clusters (e.g., Carilli & Taylor 2002; Govoni & Feretti 2004; Ferrari et al. 2008, and references therein).
The study of the Faraday rotation of cluster radio galaxies provides a detailed view of the intracluster magnetic field on scales ≲ 100 kpc. Linearly polarized radiation propagating through a magnetized plasma experiences a rotation of the plane of polarization that is proportional to the thermal gas density and the magnetic field strength along the line-of-sight (e.g., Burn 1966; Taylor et al. 1999). Indeed, it is possible to obtain important information about the intracluster magnetic fields by combining polarization images of radio sources located inside or behind galaxy clusters with X-ray observations of the thermal gas.
The rotation measure (RM) distributions seen over extended radio sources are generally patchy, indicating that the intracluster magnetic fields are not regularly ordered, but instead have turbulent structures on linear scales as small as a few kpc or less, both in merging and in relaxed clusters. Actually, magnetic field fluctuations seem to cover a wide range of spatial scales. In a few galaxy clusters containing radio sources with very detailed rotation measure images, the magnetic field power spectrum has been estimated (Enßlin & Vogt 2003; Vogt & Enßlin 2003, 2005; Murgia et al. 2004; Govoni et al. 2006; Guidetti et al. 2008, 2010; Laing et al. 2008; Bonafede et al. 2010; Kuchar & Enßlin 2011). The rotation measure studies generally show central magnetic field strengths of a few μG in merging galaxy clusters. Higher values of about 10–40 μG are typical of relaxed cooling core clusters (e.g. Dreher et al. 1987; Allen et al. 2001; Taylor et al. 2002), where the observed extreme RM magnitudes appear to be roughly proportional to the cooling flow rate (Taylor et al. 2002). In this paper, we investigate the magnetic field power spectrum in the nearby galaxy cluster A2199 by analyzing multifrequency polarization observations of the central radio source 3C 338 taken with the Very Large Array (VLA).
Details of the VLA observations of 3C 338.
Chandra observations by Johnstone et al. (2002) revealed X-ray cavities in the cluster center associated with the radio lobes. The temperature of the intracluster medium decreases from 4.2 keV to 1.6 keV over radii from 100 kpc to 5 kpc, implying a drop in the radiative cooling time from 7 Gyr to 0.1 Gyr. These features seem to be consistent with a cooling flow, even if the action of radiative cooling should cool the central ICM to kT < 1 keV. Therefore, as in many other cool core clusters, in A2199, it has been proposed that some heating mechanism (e.g., Tucker & Rosner 1983; Gaetz 1989; David et al. 2000) prevents the ICM from cooling down to temperatures below 1 keV. Kawano et al. (2003) suggest that previous AGN activity could be responsible for such heating in A2199.
The radio source 3C 338 (otherwise known as B2 1626+39) is associated with the multiple nuclei cD galaxy NGC 6166, the brightest galaxy at the center of the cluster (Burns et al. 1983; Fanti et al. 1986), and it is classified as a restarting Fanaroff-Riley type I radio galaxy (see Murgia et al. 2011, and references therein). On parsec scales, 3C 338 was the first established example of a symmetric, two-sided source in a radio galaxy (Feretti et al. 1993), consisting of a compact core and two symmetric relativistic jets (Giovannini et al. 2001). On kiloparsec scales, Burns et al. (1983) and Giovannini et al. (1998) showed that the radio structure consists of an active region, which includes the core and two symmetric jets terminating in two faint hot spots and two steep-spectrum radio lobes. The radio lobes are clearly associated with cavities in the central X-ray emission, as shown by Johnstone et al. (2002) and Gentile et al. (2007). Burns et al. (1983) pointed out a displacement between the large-scale structure with respect to the restarted symmetric jets, which could indicate a possible motion of the central AGN inside the galaxy, but we speculate that the displacement could also be due to an interaction between the old radio lobes with bulk motions in the surrounding medium caused by the sloshing of the cluster core (Markevitch & Vikhlinin 2007).
A2199 is an interesting target for Faraday rotation studies because the presence of X-ray cavities associated with the radio galaxy lobes indicates that the rotation of the polarization plane is likely to occur entirely in the intracluster medium, since comparatively little thermal gas should be present inside the radio-emitting plasma. A previous rotation measure study has been done by Ge & Owen (1994) based on 5000 MHz VLA data. These authors show that 3C 338 radio emission suffers a significant depolarization and is characterized by high RM values. By combining the information from this rotation measure image with deprojected ROSAT data, and assuming a very simple magnetic field model, Eilek & Owen (2002) infer an averaged magnetic field value along the line of sight of 15 μG.
In this paper we try to improve upon the previous estimate by analyzing additional data and by performing a numerical modeling of the intracluster magnetic field fluctuations. We use VLA observations between 1665 and 8415 MHz to produce detailed Faraday rotation measure and fractional polarization images of the radio galaxy. Following Murgia et al. (2004), we simulate Gaussian random three-dimensional magnetic field models with different power-law power spectra, and we compare the synthetic and the observed images in order to constrain the strength and structure of the magnetic field associated with the intracluster medium.
In Sect. 2 we present the radio observations and the data reduction. In Sect. 3 we describe the polarization properties of 3C 338. In Sect. 4 we present the Faraday rotation modeling. In Sects. 5 and 6 we describe the results of the two-dimensional and three-dimensional simulations. Finally, in Sect. 7 we summarize our conclusions. Throughout this paper we adopt a ΛCDM cosmology with H0 = 71 km s-1 Mpc-1, Ωm = 0.27, and ΩΛ = 0.73. At the distance of 3C 338 (z = 0.0311, Smith et al. 1997), 1′′ corresponds to 0.61 kpc.
Relevant parameters of the total intensity and polarization images between 1665 and 8415 MHz.
2. Radio observations and data reduction
We present polarimetric archival observations of 3C 338 at 1665, 4585, 4685, 4885, 4985, and 8415 MHz performed at the VLA in the A, B, and C configurations between 1987 December and 2000 February. All observations were made with a bandwidth of 50 MHz. The pointing center is identified by the coordinates RA(J2000) = 16h28m38s, and Dec(J2000) = +39d33m04s, and the details are provided in Table 1.
All data were reduced using the NRAO’s Astronomical Image Processing System (AIPS) package. The radio source 3C 286 was used both as primary flux density calibrator and as reference for the absolute polarization angles. Phase calibration was derived from nearby sources, periodically observed over a wide range in parallactic angle to separate the source polarization properties from the antenna polarizations. We proceeded with the standard calibration procedures, imaging and self-calibration. Once all the data were calibrated for each configuration and frequency, all visibilities corresponding to the same frequency were combined using the task DBCON in order to improve (u,v) coverage and sensitivity. The combined data were then self-calibrated to produce the final images. The images of total intensity I and Stokes parameters Q and U were restored with a circular beam of 2.5″. The noise levels of I, U, and Q are summarized in Table 2. Polarized intensity (corrected for the positive bias), 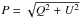 , polarization angle, Ψ = 0.5tan-1(U/Q), and fractional polarization FPOL = P/I images were produced for each frequency.
, polarization angle, Ψ = 0.5tan-1(U/Q), and fractional polarization FPOL = P/I images were produced for each frequency.
The total intensity contours of the radio galaxy 3C 338 overlaid on the DSS2 red plate1 are showed in Fig. 1. The 8415 MHz radio galaxy emission peaks at RA(J2000) = 16h28m38s and Dec(J2000) = +39d33m04s. It is also the same location of the X-ray peak to within the image resolution. Therefore we chose this reference location for our analysis.
3. Polarization analysis
In Fig. 2 we present the total intensity radio contours and polarization vectors at 1665, 4585, and 8415 MHz at a resolution of 2.5″ × 2.5″. The length of the vectors is proportional to the fractional polarization, while their orientation is the same as the projected E-field. The fractional polarization and the polarization angle were obtained by considering only those pixels where the fractional polarization is above 3σFPOL at the corresponding frequency. The total intensity emission of the source extends out to about 1′ from the cluster center. The total flux density of the radio source and all the relevant parameters of the I, Q, and U images are reported in Table 2.
 |
Fig. 1 Total intensity radio contours of 3C 338 at 8415 MHz with an FWHM of 2.5″ × 2.5″. The first contour level is drawn at 0.06 mJy/beam and the rest are spaced by a factor |
 |
Fig. 2 Total intensity contours and polarization vectors at 1665 (top), 4585 (middle), and 8415 MHz (bottom). The angular resolution is 2.5″ × 2.5″. Contour levels start at 3σI, and increase by factors of two. The lines give the orientation of the electric vector position angle (E-field) and are proportional in length to the fractional polarization (1″ ~ 5%). |
3.1. Rotation measure
The presence of a magnetic field in an ionized plasma creates a difference in the phase velocities for left versus right circularly polarized radiation. As a consequence, the polarized emission from a radio source propagating through the plasma experiences a phase shift between the two components. This corresponds to a rotation in the polarization angle. For a completely foreground screen (Burn 1966), which we expect here, the rotation is 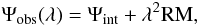 (1)where Ψobs(λ) is the observed position angle at wavelength λ, Ψint the intrinsic polarization angle of the polarized emission, and RM the rotation measure. Under this assumption, by observing radio galaxies at different wavelengths, the rotation measure can be derived from a linear fit of the polarization position angle Ψobs(λ) versus λ2. By considering an electron density ne (cm-3), a magnetic field B (μG), and a path length l (kpc), the Faraday RM is
(1)where Ψobs(λ) is the observed position angle at wavelength λ, Ψint the intrinsic polarization angle of the polarized emission, and RM the rotation measure. Under this assumption, by observing radio galaxies at different wavelengths, the rotation measure can be derived from a linear fit of the polarization position angle Ψobs(λ) versus λ2. By considering an electron density ne (cm-3), a magnetic field B (μG), and a path length l (kpc), the Faraday RM is ![\begin{equation} \mathrm{RM}=812\int _{\rm 0}^{\rm l}n_{\rm e[{\rm cm}^{\rm -3}]}\vec{B}_{\rm [\mu G]}\cdot{\rm d} \vec{l}_{\rm [kpc]}~~~\mathrm{rad}~\mathrm{m}^{\rm -2}. \label{eq2} \end{equation}](/articles/aa/full_html/2012/04/aa16622-11/aa16622-11-eq52.png) (2)We produced the Faraday RM image by running the FARADAY code (Murgia et al. 2004). The software requires as input Q and U images for each frequency and outputs the RM, the intrinsic polarization angle Ψint, their errors images, and χ2 maps. The RM image is created pixel by pixel by fitting the observed polarization angle Ψobs versus the squared wavelength λ2 for all the frequencies. To reduce the problems associated with nπ ambiguities, the fitting algorithm can perform a sequence of improvement iterations. In the first iteration, only a subset of high signal-to-noise pixels is considered. In the successive iterations, lower signal-to-noise pixels are gradually included and the information from the previous iteration is used to assist the fit of the λ2 law.
(2)We produced the Faraday RM image by running the FARADAY code (Murgia et al. 2004). The software requires as input Q and U images for each frequency and outputs the RM, the intrinsic polarization angle Ψint, their errors images, and χ2 maps. The RM image is created pixel by pixel by fitting the observed polarization angle Ψobs versus the squared wavelength λ2 for all the frequencies. To reduce the problems associated with nπ ambiguities, the fitting algorithm can perform a sequence of improvement iterations. In the first iteration, only a subset of high signal-to-noise pixels is considered. In the successive iterations, lower signal-to-noise pixels are gradually included and the information from the previous iteration is used to assist the fit of the λ2 law.
We considered only those regions of the radio source where the total intensity emission at 8415 MHz is above 5σI. Only pixels with an uncertainty in polarization angle below 10° at each wavelength were considered. The RM fit is generated if this condition is satisfied for at least five frequency maps. Almost half of the total number of the pixels in the RM image are based on a five-frequency fit. The remainder are based on a six-frequency fit.
Statistics of the rotation measure distribution.
The final rotation measure image of 3C 338 is shown in Fig. 3 (top left panel) with total intensity contours at 8415 MHz overlaid. The image has a resolution of 2.5″, which corresponds to 1.5 kpc at the distance of 3C 338. The RM has a patchy structure with values ranging from − 1300 to 900 rad/m2. As shown by the histogram in Fig. 3 (top right panel), the RM distribution is characterized by a mean value of ⟨RM⟩= −54 rad/m2 and a standard deviation σRM = 460 rad/m2. The RM fit is characterized by a mean error Errfit = 18 rad/m2. In Table 3 we report the statistics of the RM distribution of the entire source and, separately, of the east and west lobes. The mean and dispersion of the RM are quite different, but the “total power” 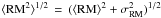 is very similar. Therefore, we cannot constrain the inclination to the line of sight of the source, and in the following analysis we assume that 3C 338 is on the plane of the sky. Examples of the observed position angle Ψobs as a function of λ2 for four high signal-to-noise pixels are shown in the bottom panels of Fig. 3. The observed fits are linear, as expected in the case of a foreground Faraday screen.
is very similar. Therefore, we cannot constrain the inclination to the line of sight of the source, and in the following analysis we assume that 3C 338 is on the plane of the sky. Examples of the observed position angle Ψobs as a function of λ2 for four high signal-to-noise pixels are shown in the bottom panels of Fig. 3. The observed fits are linear, as expected in the case of a foreground Faraday screen.
We have estimated the contribution of our own Galaxy to the Faraday rotation in the direction of 3C 338. In galactic coordinates, the radio source is located at l = 62.9° and b = 43.7°. We computed the average of the RM values reported in Taylor et al. (2009) for a region of about 3° around this direction and from this estimated a Galactic contribution of ~ 13 rad/m2. Since the Galactic foreground is small compared to the RM intrinsic to 3C 338, it has a negligible impact on the RM.
3.2. Depolarization
In Table 4 we report the average fractional polarization levels of 3C 338 obtained by considering the same pixels as we used to calculate the RM image. The radio source is less polarized at longer wavelengths. This behavior can be interpreted in terms of variation in the RM on smaller scales than the beam of the radio images.
Fractional polarization between 1665 and 8415 MHz.
These unresolved RM structures in the foreground screen cause a depolarization of the signal which, to first order, can be approximated by 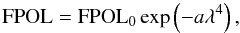 (3)where a is a value related to the RM gradient within the observing beam and FPOL0 is the intrinsic fractional polarization (Burn 1966; see also Laing et al. 2008, for a more recent derivation). We fitted the Burn law only between 4585 and 8415 MHz (6 and 3.6 cm) observations, since the formula is not applicable in the long-wavelength regime (20 cm/1665 MHz) (see Tribble 1991 and Sect. 5). We find a = (66 ± 6) × 103 rad2/m4.
(3)where a is a value related to the RM gradient within the observing beam and FPOL0 is the intrinsic fractional polarization (Burn 1966; see also Laing et al. 2008, for a more recent derivation). We fitted the Burn law only between 4585 and 8415 MHz (6 and 3.6 cm) observations, since the formula is not applicable in the long-wavelength regime (20 cm/1665 MHz) (see Tribble 1991 and Sect. 5). We find a = (66 ± 6) × 103 rad2/m4.
 |
Fig. 3 Top left: total intensity radio contours of 3C 338 at 8415 MHz overlaid on the RM image. The angular resolution is 2.5″ × 2.5″. Contour levels are drawn at: 0.06, 0.12, 0.24, and 0.96 mJy/beam. Top right: the histogram of the RM values. Bottom: sample plots of the observed position angle versus the squared wavelength at different source locations. The inset is a zoom of the observed polarization angle corresponding to frequencies between 4585 and 8415 MHz. |
4. Faraday rotation modeling
Our aim is to constrain the intracluster magnetic field strength and structure in A2199 by using the information from the radio galaxy RM and polarization images presented in the previous section. Our modeling is based on the assumption that the Faraday rotation is occurring entirely in the intracluster medium. In particular, we suppose that there is no internal Faraday rotation inside the radio lobes, as suggested by the X-ray cavities detected by Johnstone et al. (2002) and by the observed linearity of the polarization angle Ψobs versus λ2 (see Fig. 3). Moreover, we suppose that any possible local RM enhancement occurring at the interface between the radio lobes and the surrounding medium is negligible compared to the total RM across the cluster (but see Rudnick & Blundell 2003, for a contrary viewpoint).
As shown in Eq. (2), the rotation measure is the integral along the line-of-sight of the intracluster magnetic field and the thermal gas density. To derive useful information about the intracluster magnetic field we first need a model for the spatial distribution of the thermal electron density.
 |
Fig. 4 Left panel: adaptively smoothed Chandra X-ray image (Obs. ID 497) in the 0.2–10 keV band of the galaxy cluster A2199 with the VLA contour levels at 8415 MHz overlaid. Pronounced X-ray cavities can be identified in correspondence of the radio galaxy lobes. Top right panel: deprojected thermal gas density profile (Johnstone et al. 2002). Bottom right panel: pixel distribution of the rotation measure image as a function of the distance from the cluster center. |
4.1. Thermal gas modeling
The distribution of the thermal electrons was modeled using the Chandra X-ray observation of A2199 by Johnstone et al. (2002). In the left panel of Fig. 4 we show a superposition of the VLA 8415 MHz contour levels on the Chandra X-ray image in the 0.2–10 keV band of the central region of A2199. In the top righthand panel of Fig. 4 we show the deprojected thermal gas density ne(r) profile derived by Johnstone et al. (2002). In the bottom righthand panel we show the rotation measure pixel distribution as a function of the distance from the cluster center. The RM pixels are sampled at distances from the cluster core in the range 3 to 30 kpc, with a higher concentration between 10 and 20 kpc.
We initially fit the deprojected thermal gas density profile with a single β-model 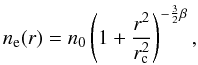 (4)where r is the distance from the cluster X-ray centroid, n0 the central electron density, and rc the cluster core radius (Cavaliere & Fusco-Femiano 1976). But this thermal gas model does not allow a good description of the central jump owing to the high central density, typical of cooling core galaxy clusters. Therefore, we tried to improve the fit by considering a double β-model,
(4)where r is the distance from the cluster X-ray centroid, n0 the central electron density, and rc the cluster core radius (Cavaliere & Fusco-Femiano 1976). But this thermal gas model does not allow a good description of the central jump owing to the high central density, typical of cooling core galaxy clusters. Therefore, we tried to improve the fit by considering a double β-model, 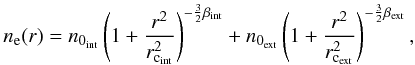 (5)where n0int and n0ext are the internal and external central electron densities, while rcint and rcext are the internal and external cluster core radii, respectively. We do not discuss the physical validity of this model here. Our purpose is to empirically obtain an analytic profile that provides a reasonable continuous description of the deprojected gas density observed by Johnstone et al. (2002). This analytic profile can be conveniently extrapolated to both the cluster center and to large radii so that the integral in Eq. (2) can be performed.
(5)where n0int and n0ext are the internal and external central electron densities, while rcint and rcext are the internal and external cluster core radii, respectively. We do not discuss the physical validity of this model here. Our purpose is to empirically obtain an analytic profile that provides a reasonable continuous description of the deprojected gas density observed by Johnstone et al. (2002). This analytic profile can be conveniently extrapolated to both the cluster center and to large radii so that the integral in Eq. (2) can be performed.
The double β-model best-fit parameters are reported in Table 5, while the best-fit profile is shown as a continuous line in the righthand panel of Fig. 4. In the same plot we also show, as a dotted line, the external part of the model that has been constrained by a fit of the data points with r > 18 kpc. The total central density we find is n0 = n0int + n0ext = 0.101 cm-3.
Double β-model parameters.
4.2. Magnetic field modeling
The patchy structure characterizing the RM image in Fig. 3 can be interpreted as a signature of the turbulent intracluster magnetic field. In particular, the dispersion of the RM values can be related to the strength and structure of the magnetic field. If the magneto-ionic medium is approximated by uniform cells of size Λc with random orientation in space, the Faraday rotation from a physical depth L ≫ Λc is expected to be a Gaussian with zero mean and dispersion given by 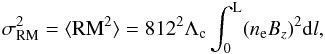 (6)where Bz is the magnetic field component along the line-of-sight (e.g., Felten 1996).
(6)where Bz is the magnetic field component along the line-of-sight (e.g., Felten 1996).
Magnetic field model parameters.
More generally, the magnetic field auto-correlation function CBz(r) and the rotation measure auto-correlation function CRM are related by the Abel transform (Enßlin & Vogt 2003), 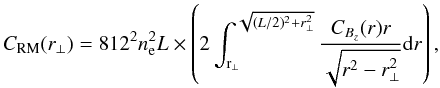 (7)where, for simplicity, the thermal gas density ne is considered constant here.
(7)where, for simplicity, the thermal gas density ne is considered constant here.
If the characteristic fluctuation scale of the magnetic field is much smaller than the physical depth of the Faraday screen (such that ⟨B⟩= 0 and ⟨RM⟩= 0), in the limit r⊥ → 0, we obtain 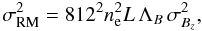 (8)where
(8)where 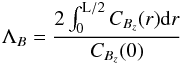 (9)defines the magnetic field auto-correlation length, which should be the appropriate scale to use for Λc in Eq. (6).
(9)defines the magnetic field auto-correlation length, which should be the appropriate scale to use for Λc in Eq. (6).
For an isotropic divergence-free random field, it can be shown that ΛB is related to the magnetic field power spectrum, |Bk|2, by 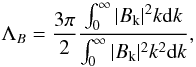 (10)where k = 2π/Λ is the wave number (Enßlin & Vogt 2003).
(10)where k = 2π/Λ is the wave number (Enßlin & Vogt 2003).
This is a particularly important result, since it implies that we must know the power spectrum of the magnetic field fluctuations to determine the strength of the field from the RM image. We also note that the RM power spectrum is proportional to the magnetic field power spectrum, 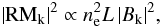 (11)but the RM auto-correlation length,
(11)but the RM auto-correlation length, 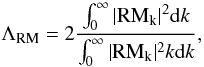 (12)is not the same as ΛB.
(12)is not the same as ΛB.
To limit the number of free parameters, in this work we choose to model a power-law power spectrum2 with index n of the form 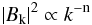 (13)in the wave number range from kmin to kmax and 0 outside. Moreover, we suppose that the power-spectrum normalization varies with the distance from the cluster center such that the average magnetic field strength scales as a function of the thermal gas density according to
(13)in the wave number range from kmin to kmax and 0 outside. Moreover, we suppose that the power-spectrum normalization varies with the distance from the cluster center such that the average magnetic field strength scales as a function of the thermal gas density according to ![\begin{equation} \langle B(r)\rangle=\langle B_{\rm 0}\rangle\left[\frac{n_{\rm e}(r)}{n_{\rm 0}}\right]^{\rm \eta}, \label{eq4} \end{equation}](/articles/aa/full_html/2012/04/aa16622-11/aa16622-11-eq132.png) (14)where ⟨B0 ⟩ is the average magnetic field strength at the center of the cluster, and ne(r) is the thermal electron gas density. We have to note that the tapering of the magnetic field power spectrum due to the thermal gas density may not preserve exactly the magnetic-field power-spectrum power-law shape at the edges (see Fig. 10).
(14)where ⟨B0 ⟩ is the average magnetic field strength at the center of the cluster, and ne(r) is the thermal electron gas density. We have to note that the tapering of the magnetic field power spectrum due to the thermal gas density may not preserve exactly the magnetic-field power-spectrum power-law shape at the edges (see Fig. 10).
Overall, our magnetic field model depends on the five parameters listed in Table 6: the strength at the cluster center ⟨B0 ⟩ , the radial slope η, the power spectrum index n, and finally the minimum and maximum scales of fluctuation, Λmin = 2π/kmax and Λmax = 2π/kmin, respectively.
4.3. Bayesian inference
To constrain the magnetic field strength and structure, we proceeded in two steps. First, we performed a two-dimensional analysis of the RM fluctuations and of the source depolarization to constrain the slope n and the range of scales of the power spectrum. Second, we performed three-dimensional numerical simulations to constrain the strength of the field and its scaling with the gas density. In both cases, we made use of the FARADAY code to produce synthetic polarization images of 3C 338 and to compare them to the observed ones. We compared model and data using the Bayesian inference, whose use was first introduced in the RM analysis by Enßlin & Vogt (2003). Because of the random nature of the intracluster magnetic field, the RM image we observe is just one possible realization of the data. Different realizations of magnetic field characterized by the same power spectrum will generate different RM images. Thus, rather than try to determine the particular set of power spectrum parameters that best reproduces the given realization of the data, it is perhaps more meaningful to search for that distribution of model parameters that maximizes the probability of the model given the data. The Bayesian inference offers a natural theoretical framework for this approach.
The Bayesian rule relates our prior information on the distribution P(θ) of model parameters θ to their posterior probability distribution P(θ | D) after the data D have been acquired 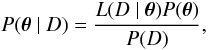 (15)where L(D | θ) is the likelihood function, while P(D) is called the evidence. The evidence acts as a normalizing constant and represents the integral of the likelihood function weighted by the prior over all the parameters space
(15)where L(D | θ) is the likelihood function, while P(D) is called the evidence. The evidence acts as a normalizing constant and represents the integral of the likelihood function weighted by the prior over all the parameters space 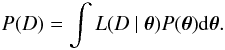 (16)The most probable configuration for the model parameters is obtained by maximizing the joint posterior given by the product of the likelihood function with the prior probability. We used a Markov Chain Monte Carlo (MCMC) method to extract samples from the posterior probability distribution. In particular, we implemented the Metropolis-Hastings algorithm, which is capable of generating a sample of the posterior distribution without the need to calculate the evidence explicitly, which is often extremely difficult to compute since it would require exploring the entire prior space. The MCMC is started from a random initial value θ0 and the algorithm is run for many iterations by selecting new states according to a transitional kernel, Q(θ,θ′), between the actual, θ, and the proposed position, θ′. The proposed position is accepted with probability
(16)The most probable configuration for the model parameters is obtained by maximizing the joint posterior given by the product of the likelihood function with the prior probability. We used a Markov Chain Monte Carlo (MCMC) method to extract samples from the posterior probability distribution. In particular, we implemented the Metropolis-Hastings algorithm, which is capable of generating a sample of the posterior distribution without the need to calculate the evidence explicitly, which is often extremely difficult to compute since it would require exploring the entire prior space. The MCMC is started from a random initial value θ0 and the algorithm is run for many iterations by selecting new states according to a transitional kernel, Q(θ,θ′), between the actual, θ, and the proposed position, θ′. The proposed position is accepted with probability ![\begin{equation} h=\min \left[1, \frac{L(D~\vert~\vec\theta^{\rm \prime}) P(\vec\theta^{\rm \prime}) Q(\vec\theta^{\rm \prime},\vec\theta) } { L(D~\vert~\vec\theta) P(\vec\theta) Q(\vec\theta,\vec\theta^{\rm \prime}) } \right]\cdot \end{equation}](/articles/aa/full_html/2012/04/aa16622-11/aa16622-11-eq144.png) (17)We chose for Q a multivariate Gaussian kernel. The MCMC starts with a number of “burn-in” steps during which, according to common practice, the standard deviation of the transitional kernel is adjusted so that the average acceptance rate stays in the range 25–50%. After the burn-in period, the random walk forgets its initial state and the chain reaches an equilibrium distribution. The burning steps are discarded, and the remaining set of accepted values of θ is a representative sample of the posterior distribution that can be used to compute the final statistics on the model parameters.
(17)We chose for Q a multivariate Gaussian kernel. The MCMC starts with a number of “burn-in” steps during which, according to common practice, the standard deviation of the transitional kernel is adjusted so that the average acceptance rate stays in the range 25–50%. After the burn-in period, the random walk forgets its initial state and the chain reaches an equilibrium distribution. The burning steps are discarded, and the remaining set of accepted values of θ is a representative sample of the posterior distribution that can be used to compute the final statistics on the model parameters.
5. 2D analysis
We performed a preliminary two-dimensional analysis of the RM fluctuations and of the source depolarization to constrain the slope n and the range of scales of the power spectrum. The two-dimensional analysis relies on the proportionality between the magnetic field and the rotation measure power spectra. On the basis of this proportionality, the index n of the two-dimensional rotation measure power spectrum is the same as the three-dimensional magnetic field power spectrum: 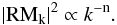 (18)At this stage, we are only interested in the shape of the power spectrum and not in the exact value of the normalization. Indeed, as a first approximation, we do not consider the effect of the spatially variable gas density; i.e., we suppose that the depth of the Faraday screen is on average the same over all of the source. We simulated synthetic images with a given power spectrum in a two-dimensional grid. The simulations start in the Fourier space, where the amplitudes of the RM components are selected according to Eq. (18), while the phases are completely random. The RM image in the real space is obtained by a fast Fourier transform (FFT).
(18)At this stage, we are only interested in the shape of the power spectrum and not in the exact value of the normalization. Indeed, as a first approximation, we do not consider the effect of the spatially variable gas density; i.e., we suppose that the depth of the Faraday screen is on average the same over all of the source. We simulated synthetic images with a given power spectrum in a two-dimensional grid. The simulations start in the Fourier space, where the amplitudes of the RM components are selected according to Eq. (18), while the phases are completely random. The RM image in the real space is obtained by a fast Fourier transform (FFT).
 |
Fig. 5 Top left panel: Bayesian analysis of the RM structure function. The dots represent the data (error bars are comparable to the size of the symbols). The shaded area represents the population of synthetic RM structure functions from the posterior distribution. The dashed line corresponds to the most probable value for the model parameters (see text). Top right, bottom left, and bottom right panel: one-dimensional (histograms) and two-dimensional (colors and contours) marginalization of the posterior for the model parameters. The contours are traced at 0.9, 0.75, and 0.5 of the peak value. |
 |
Fig. 6 Top left panel: Bayesian analysis of the source depolarization. The dots represent the data. The shaded area represents the population of synthetic polarization from the posterior distribution. The dashed line corresponds to the most probable value for the model parameters (see text). Top right, bottom left, and bottom right panel: one-dimensional (histograms) and two-dimensional (colors and contours) marginalization of the posterior for the model parameters. The contours are traced at 0.9, 0.75, and 0.5 of the peak value. |
As a compromise between computational speed and spatial dynamical range, we adopted a computational grid of 2048 × 2048 pixels with a pixel size of 0.05 kpc. This grid allowed us to explore RM fluctuations on scales as small as Λmin ≃ 0.1 kpc, i.e. one order of magnitude smaller than the beam of the observations (FWHM ≃ 1.5 kpc). Simultaneously, we were able to investigate fluctuations as large as Λmax ≃ 100 kpc, i.e., comparable to the linear size of 3C 338. We determined the distribution of the best-fit parameters using the Bayesian approach outlined in Sect. 4.3. In particular, we characterize the RM image by its structure function ![\begin{equation} S_{\rm RM}(r_{\rm \perp})=\left\langle \left[{\rm RM}(x,y)-{\rm RM}(x+\Delta x, y+\Delta y)\right] ^{\rm 2}\right\rangle_{(x,y)}, \end{equation}](/articles/aa/full_html/2012/04/aa16622-11/aa16622-11-eq149.png) (19)which is obtained by averaging the difference in RM values corresponding to pixels located at the scale distance
(19)which is obtained by averaging the difference in RM values corresponding to pixels located at the scale distance 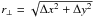 , and is related to the RM auto-correlation function
, and is related to the RM auto-correlation function 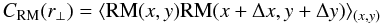 (20)by the simple relation
(20)by the simple relation 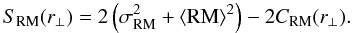 (21)The observed structure function is shown in the top lefthand panel of Fig. 5, the formal error bars are comparable to the size of the dots. For an isotropic field, the RM auto-correlation function and power spectrum are related by the Hankel transform
(21)The observed structure function is shown in the top lefthand panel of Fig. 5, the formal error bars are comparable to the size of the dots. For an isotropic field, the RM auto-correlation function and power spectrum are related by the Hankel transform 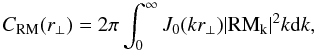 (22)where
(22)where 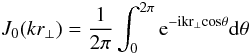 (23)is the zero-order Bessel function. For the power-law power spectrum in Eq. (18), we can identify three regimes in the RM structure function. In the asymptotic small-separation regime, r⊥ ≪ 2π/kmax, the structure function increases as
(23)is the zero-order Bessel function. For the power-law power spectrum in Eq. (18), we can identify three regimes in the RM structure function. In the asymptotic small-separation regime, r⊥ ≪ 2π/kmax, the structure function increases as 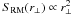 . In the intermediate regime, where 2π/kmax ≪ r⊥ ≪ 2π/kmin,
. In the intermediate regime, where 2π/kmax ≪ r⊥ ≪ 2π/kmin, 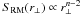 . Finally for r⊥ ≫ 2π/kmin, the structure function saturates to the constant value of
. Finally for r⊥ ≫ 2π/kmin, the structure function saturates to the constant value of 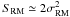 . However, it can be hard to discern these three regimes directly from the observed structure function because of the coarse resolution of the radio images and the undersampling of the large separations because of the finite size of the RM image. Indeed, we need to resort to numerical simulations in order to account for the effects of these window functions. The synthetic images are thus gridded to the same geometry as the data and are convolved to the same angular resolution. Moreover, we masked the synthetic images using the observations to reproduce the window function imposed by the shape of 3C 338, and we added Gaussian noise with an rms value of Errfit, in order to mimic the noise of the observed RM image.
. However, it can be hard to discern these three regimes directly from the observed structure function because of the coarse resolution of the radio images and the undersampling of the large separations because of the finite size of the RM image. Indeed, we need to resort to numerical simulations in order to account for the effects of these window functions. The synthetic images are thus gridded to the same geometry as the data and are convolved to the same angular resolution. Moreover, we masked the synthetic images using the observations to reproduce the window function imposed by the shape of 3C 338, and we added Gaussian noise with an rms value of Errfit, in order to mimic the noise of the observed RM image.
 |
Fig. 7 Examples of observed (left) fractional polarizations images at 8415, 4585, 1665 MHz compared with synthetic realizations (right) corresponding to the best fit parameters from the depolarization analysis. |
 |
Fig. 8 Top panel: X-ray cavity model. The darker region indicates the location where the thermal gas has been subtracted from the double β-model. Bottom panel: horizontal slice passing through the X-ray cavities at the cluster center. Continuous line represents the observations from the Chandra image, dashed line simulations with cavities, dotted line simulations without cavities. |
 |
Fig. 9 Bayesian 3-dimensional analysis of the RM structure function for the model with Λmax = 35 kpc. Top panel: the dots represent the data (error bars are comparable to the size of the symbols). The shaded area represents the population of synthetic RM structure functions from the posterior distribution. The dashed line corresponds to the most probable value for the model parameters (see text). Bottom panel: one-dimensional (histograms) and two-dimensional (colors and contours) marginalizations of the posterior for the model parameters. The contours are traced at 0.9, 0.75, and 0.5 of the peak value. |
We then applied the Bayesian method described in Sect. 4.3 by choosing uniform priors for the four power spectrum parameters: the normalization norm, the slope n, the minimum, and the maximum wave number kmin and kmax. The statistics of the simulated RM fluctuations are Gaussian, so their structure function at a given separation has a log-normal distribution. At each step of the MCMC, we performed 30 realizations of the same power spectrum with different random seeds and evaluated the average and the dispersion of the logarithm of the model structure function. We averaged the offsets and the dispersions at all the individual separations. From these values we computed the likelihood of the observed structure function.
In Fig. 5 we show the results of the Bayesian analysis of the rotation measure structure function. The output from the MCMC is a 4-dimensional hypercube containing a sample of the posterior distribution of the power spectrum parameters. The top-right, bottom-left, and bottom righthand panels show the two-dimensional marginalization of this hypercube as color images. In addition, one-dimensional marginalizations are shown as histograms along each axis of these images. The two-dimensional marginalizations represent the projected density of samples in the MCMC, which is proportional to the posterior probability of that particular couple of model parameters. The maximum scale of the fluctuation, the normalization, and the slope of the power spectrum appear to be characterized by a peak that corresponds to the maximum posterior probability for that configuration of parameters, while for the minimum scale of fluctuation we only have an upper limit.
To provide a visual comparison between model and data, in the top lefthand panel of Fig. 5 we show the observed structure function along with the population of synthetic structure functions contained in the posterior sample and the structure function for which posterior is maximum (best fit). The brighter pixels in the shaded image occur where many different synthetic structure functions overlap each other. The probability of the model given the data is higher in the brighter regions and is lower in the darker regions. The shaded region is relatively narrow for small separations but widens significantly for r⊥ > 10 kpc, indicating that our sensitivity to the large-scale separations is lower. Overall, the data stay close to the high-probability region, indicating that the model is doing a good job reproducing the observed RM structure. However, for r⊥ > 20 kpc the observed structure function decreases while the model stays relatively constant. The turnover of the observed structure function is very likely due to the lower gas density at large distances from the cluster center, which results in a systematic decrease in the power spectrum normalization, hence of the Faraday rotation on large scales. This effect is not included in the current modeling, but it will be investigated with the aid of three-dimensional simulations in Sect. 6.
The power spectrum used to model the RM image should also be consistent with the observed depolarization of the radio source at increasing wavelengths (see Sect. 3.2). The depolarization is caused by RM variations on smaller scales than the beam that results in an incoherent sum of the radio signal. Indeed, modeling of the polarization amplitude can be used to place more stringent constraints on the minimum scale of fluctuation of the magnetic field and on the slope of the power spectrum. Using the same simulation set-up presented above, we reproduced the expected polarized signal from 3C 338 as a function of the wavelength. We first constructed an image of the source polarization at λ = 0, which is characterized by an intrinsic degree of polarization FPOL0. We then simulated different RM images at full resolution and used them to rotate the intrinsic polarization vectors according to Eq. (1). These full-resolution images are finally convolved at the same resolution as the observations, resulting in beam depolarization of the signal at longer wavelengths.
We used the Bayesian inference and a Gaussian likelihood to estimate the distribution of the power spectrum parameters, which maximizes the probability that the observed depolarization is a realization of the model. In Fig. 6 the posterior from the depolarization analysis is shown for the five free parameters: the intrinsic degree of polarization FPOL0, the normalization norm, the slope n, the minimum, and the maximum scale of fluctuation Λmin, and Λmax of the magnetic field power spectrum. In the top right and bottom panels the two-dimensional (colors and contours) and one-dimensional (histograms) marginalization of the posterior are shown for three different combinations of the model parameters. All the model parameters appear to be well constrained, and their values are consistent with the structure function analysis. In the top lefthand panel, the observed fractional polarization as a function of the fourth power of the wavelength is shown, together with the sample of realizations from the posterior and the best fit. In Fig. 7 the observed fractional polarization images are compared with synthetic realizations corresponding to the best fit parameters. The synthetic fractional polarization trend at higher frequencies (4585 to 8415 MHz) is consistent with a Burn law, FPOL = FPOL0exp( − aλ4), with asynth = (61 ± 3) × 103 rad2/m4, in very good agreement with the observed value aobs = (66 ± 6) × 103 rad2/m4. However, it is clear from the top lefthand panel of Fig. 6 that our simulations are also able to explain the observed polarization levels reasonably well at low frequencies (1400 MHz) where the Burn law breaks down.
Overall, the combined two-dimensional analysis, RM image, and depolarization allowed us to obtain a first insight into the shape of the magnetic field power spectrum. We constrained the power spectrum index to n = (2.8 ± 1.3), and the minimum and maximum scales in the range from Λmin = (0.7 ± 0.1) kpc to Λmax = (35 ± 28) kpc, where the given errors represent the dispersion of the one-dimensional marginalizations. In the next step we fix these values and constrain the strength of the magnetic field and its scaling with the gas density with the aid of three-dimensional simulations.
6. 3D simulations
We can construct a three-dimensional model of the intracluster magnetic field by following the numerical approach described in Murgia et al. (2004). The simulations begin in Fourier space by extracting the amplitude of the magnetic field potential vector, 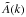 , from a Rayleigh distribution whose standard deviation varies with the wave number according to |Ak|2 ∝ k − n − 2. The phase of the potential vector fluctuations is taken to be completely random. The magnetic field is formed in Fourier space via the cross product
, from a Rayleigh distribution whose standard deviation varies with the wave number according to |Ak|2 ∝ k − n − 2. The phase of the potential vector fluctuations is taken to be completely random. The magnetic field is formed in Fourier space via the cross product 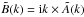 . This ensures that the magnetic field is effectively divergence free. We then perform a three-dimensional FFT inversion to produce the magnetic field in the real space domain. The field is then Gaussian and isotropic, in the sense that there is no privileged direction in space for the magnetic field fluctuations. The power-spectrum normalization is set such that the average magnetic field strength scales as a function of the thermal gas density according to Eq. (14). The gas density profile is described by the double-beta model in Eq. (5). Actually, we know that the gas density distribution in A2199 deviates from spherical symmetry because of the X-ray cavities corresponding to the radio lobes of 3C 338. Hence, we include the X-ray cavities in the three-dimensional simulations by removing from the gas density modeling all the magneto-ionic material inside two ellipsoidal regions centered on the radio lobes, as shown in the top panel of Fig. 8. In the bottom panel we trace the profile of the X-ray brightness along an horizontal slice passing through the radio lobes for the double beta-model with and without cavities. The model with cavities provides a better description of the observed X-ray brightness along the slice.
. This ensures that the magnetic field is effectively divergence free. We then perform a three-dimensional FFT inversion to produce the magnetic field in the real space domain. The field is then Gaussian and isotropic, in the sense that there is no privileged direction in space for the magnetic field fluctuations. The power-spectrum normalization is set such that the average magnetic field strength scales as a function of the thermal gas density according to Eq. (14). The gas density profile is described by the double-beta model in Eq. (5). Actually, we know that the gas density distribution in A2199 deviates from spherical symmetry because of the X-ray cavities corresponding to the radio lobes of 3C 338. Hence, we include the X-ray cavities in the three-dimensional simulations by removing from the gas density modeling all the magneto-ionic material inside two ellipsoidal regions centered on the radio lobes, as shown in the top panel of Fig. 8. In the bottom panel we trace the profile of the X-ray brightness along an horizontal slice passing through the radio lobes for the double beta-model with and without cavities. The model with cavities provides a better description of the observed X-ray brightness along the slice.
We simulated the random magnetic field by using a cubical grid of 10243 pixels with a cell size of 0.16 kpc/pixel. The synthetic RM images were obtained by integrating numerically the gas density and the magnetic field product along the line-of-sight accordingly to Eq. (2). In a similar way to the two-dimensional simulations, the synthetic RM images were gridded, convolved, blanked, and noised as the observed RM image before the comparison with the data. We used the Bayesian approach to find the posterior distribution for ⟨B0 ⟩ and η, which maximizes the probability that the observed structure function is a realization of the model. The slope n and the scales kmin and kmax were kept fixed at the values found with the two-dimensional analysis.
 |
Fig. 10 The magnetic field power spectra (left panel) and radial profiles (right panel) for the models corresponding to the three values of Λmax = 10, 35, and 164 kpc are shown as dotted, continuous, and dashed lines, respectively. The model with Λmax = 35 kpc provides the best description of the observed RM structure function, see text. |
 |
Fig. 11 Qualitative comparison between the observed rotation measure image (left) and a synthetic 3-dimensional realization (right). |
We started with uniform priors for ⟨B0 ⟩ and η and we evaluated the likelihood of the structure function by mean of 30 different configurations for the magnetic field phases at each step of the MCMC. The result of the Bayesian analysis is shown in Fig. 9. In the bottom panel we present the two-dimensional (colors and contours) and one-dimensional marginalizations of the posterior. The two parameters appear well constrained. We found a magnetic field with a central strength ⟨B0 ⟩ = (11.7 ± 9.0) μG, and a radial slope η = (0.9 ± 0.5). In the top panel we show the observed structure function along with the synthetic structure functions from the posterior and the best fit. The three-dimensional modeling represents a significant improvement over the two-dimensional analysis. In fact, we are now able to describe the overall shape of the observed structure function with good accuracy, including the turnover at large separations that is most likely due to the decrease in the Faraday rotation with radius. In the three-dimensional simulations we kept the maximum scale of the magnetic field fluctuation fixed to Λmax = 35 kpc, which is the value found from the two-dimensional analysis in Sect. 5. The consequences of a different choice of this parameter are discussed in further detail in the Appendix where we also tested the cases Λmax = 10 and 164 kpc. The value Λmax = 35 kpc still provides the best description of the observed RM structure function. In Fig. 10 we plot the magnetic field power spectra and radial profiles corresponding to the maximum posterior for the three values of Λmax.
We performed the same Bayesian analysis also not taking the X-ray cavities into account (not shown). We found very similar results to those including the cavities and we conclude that the presence of these voids in the gas density distribution has a second-order impact on the Faraday rotation measures we are analyzing. This could be because the most of the lines of sight sampled from our observed RM image do not intercept the regions of the cluster affected by the cavities.
Finally, in Fig. 11 we present a qualitative comparison between the observed and a synthetic RM images taken from the simulations with cavities. Although very simple, the power-spectrum model adopted here provides a reasonable description of the patchy RM structure seen in the data.
It is interesting to compare our result with the independent estimate based on the theoretical work by Kunz et al. (2011). By assuming that turbulent dissipation balances radiative cooling at all radii inside the cluster core, Kunz et al. (2011) find in the bremsstrahlung regime (that is T ≳ 1 keV) 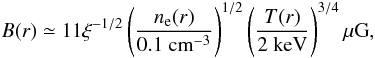 (24)where T is the temperature, while on average ξ2 is expected to range between 0.25 and 1 in a turbulent plasma. By considering a central density n0 ≃ 0.1 cm-3 and a central temperature T ≃ 2 keV, according Johnstone et al. (2002), they found B0 ≃ 11ξ − 1/2 μG, very close to our estimate based on the Faraday rotation.
(24)where T is the temperature, while on average ξ2 is expected to range between 0.25 and 1 in a turbulent plasma. By considering a central density n0 ≃ 0.1 cm-3 and a central temperature T ≃ 2 keV, according Johnstone et al. (2002), they found B0 ≃ 11ξ − 1/2 μG, very close to our estimate based on the Faraday rotation.
7. Conclusions
We investigated the magnetic field power spectrum in the cool core galaxy cluster A2199 by analyzing the polarized emission of the central radio source 3C 338. We used archival VLA observations between 1665 and 8415 MHz to produce detailed Faraday rotation measure and fractional polarization images of the radio galaxy. We observed a significant depolarization of the radio emission of the radio galaxy and high RM values. This agrees with the analysis performed by Ge & Owen (1994) at 5000 MHz, although our result takes the additional information at 1665 and 8415 MHz into account.
We simulated Gaussian random three-dimensional magnetic field models with different power-law power spectra, and we assumed that the field strength decreases radially as a power of the thermal gas density as neη. By comparing the synthetic and the observed images with a Bayesian approach, we constrained the strength and structure of the magnetic field associated with the intracluster medium. We found that the Faraday rotation toward 3C 338 in A2199 is consistent with a magnetic field power-law power spectrum characterized by an index n = (2.8 ± 1.3) between a maximum and a minimum scale of fluctuation of Λmax = (35 ± 28) kpc and Λmin = (0.7 ± 0.1) kpc, respectively. The corresponding magnetic field auto-correlation length is ΛB = 5.2 kpc. In addition, by including in the modeling the presence of X-ray cavities in coincidence with the radio galaxy lobes, we found a magnetic field strength of ⟨B0 ⟩ = (11.7 ± 9.0) μG at the cluster center. Farther out, the field decreases with radius following the gas density to the power of η = (0.9 ± 0.5). To a comparison with other values reported in the literature, the radially averaged magnetic field strength calculated over the central 1 Mpc3 is ~0.19 μG. The additional data and the numerical modeling of the intracluster magnetic field fluctuations allowed us to improve upon the previous estimate of 15 μG (Eilek & Owen 2002), with more stringent constraints not only on the magnetic field strength but also on its structure.
From the literature the central magnetic field strength found in merger galaxy clusters is a few μG (e.g., 2.5 μG in A2255 by Govoni et al. 2006 and 4.7 μG in Coma by Bonafede et al. 2010). In cooling-core galaxy clusters the magnetic field central strength is still uncertain. Typically it is a few tens μG (as in Hydra A, where values between 19 and 80 μG have been indicated, e.g. Laing et al. 2008; Kuchar & Ensslin 2011), even if lower values have also been found, as in the galaxy cluster A2634 (3 μG, Vogt & Ensslin 2003). In A2199 we found a magnetic field strength of about 10 μG that seems to confirm values of the magnetic field central strength in cooling-core galaxy clusters that are higher than in merging clusters.
Acknowledgments
We thank the anonymous referee for the useful comments fundamental for improving this work. We are grateful to A. Bonafede for useful discussions. This work made use of results produced by the Cybersar Project managed by the Consorzio COSMOLAB, a project cofunded by the Italian Ministry of University and Research (MIUR) within the Programma Operativo Nazionale 2000–2006 “Ricerca Scientifica, Sviluppo Tecnologico, Alta Formazione” per le Regioni Italiane dell’ Obiettivo 1 (Campania, Calabria, Puglia, Basilicata, Sicilia, Sardegna) – Asse II, Misura II.2 “Società dell′Informazione”, Azione a “Sistemi di calcolo e simulazione ad alte prestazioni”. More information is available at http://www.cybersar.it. This research was partially supported by PRIN-INAF2009. The National Radio Astronomy Observatory (NRAO) is a facility of the National Science Foundation, operated under cooperative agreement by Associated Universities, Inc. We are grateful to Antonella Fara for the assistance with the Cybersar-OAC computer cluster.
References
- Allen, S. W., Taylor, G. B., Nulsen, P. E. J., et al. 2001, MNRAS, 324, 842 [NASA ADS] [CrossRef] [Google Scholar]
- Bonafede, A., Feretti, L., Murgia, M., et al. 2010, A&A, 513, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Burn, B. J. 1966, MNRAS, 133, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Burns, J. O., Schwendeman, E., & White, R. A. 1983, ApJ, 271, 575 [NASA ADS] [CrossRef] [Google Scholar]
- Carilli, C. L., & Taylor, G. B. 2002, ARA&A, 40, 319 [NASA ADS] [CrossRef] [Google Scholar]
- Cavaliere, A., & Fusco-Femiano, R. 1976, A&A, 49, 137 [NASA ADS] [Google Scholar]
- David, L. P., Nulsen, P. E. J., McNamara, B. R., Forman, W., & Robertson, B. 2000, BAAS, 32, 1208 [NASA ADS] [Google Scholar]
- Dreher, J. W., Carilli, C. L., & Perley, R. A. 1987, ApJ, 316, 611 [NASA ADS] [CrossRef] [Google Scholar]
- Eilek, J. A., & Owen, F. N. 2002, ApJ, 567, 202 [NASA ADS] [CrossRef] [Google Scholar]
- Enßlin, T. A., & Vogt, C. 2003, A&A, 401, 835 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fanti, C., Fanti, R., de Ruiter, H. R., & Parma, P. 1986, A&AS, 65, 145 [NASA ADS] [Google Scholar]
- Felten, J. E. 1996, Clusters, Lensing, and the Future of the Universe, 88, 271 [Google Scholar]
- Feretti, L., Comoretto, G., Giovannini, G., Venturi, T., & Wehrle, A. E. 1993, ApJ, 408, 446 [NASA ADS] [CrossRef] [Google Scholar]
- Ferrari, C., Govoni, F., Schindler, S., Bykov, A. M., & Rephaeli, Y. 2008, Space Sci. Rev., 134, 93 [NASA ADS] [CrossRef] [Google Scholar]
- Gaetz, T. J. 1989, ApJ, 345, 666 [NASA ADS] [CrossRef] [Google Scholar]
- Ge, J., & Owen, F. N. 1994, AJ, 108, 1523 [NASA ADS] [CrossRef] [Google Scholar]
- Gentile, G., Rodríguez, C., Taylor, G. B., et al. 2007, ApJ, 659, 225 [NASA ADS] [CrossRef] [Google Scholar]
- Giovannini, G., Cotton, W. D., Feretti, L., Lara, L., & Venturi, T. 1998, ApJ, 493, 632 [NASA ADS] [CrossRef] [Google Scholar]
- Giovannini, G., Cotton, W. D., Feretti, L., Lara, L., & Venturi, T. 2001, ApJ, 552, 508 [NASA ADS] [CrossRef] [Google Scholar]
- Govoni, F., & Feretti, L. 2004, Int. J. Mod. Phys. D, 13, 1549 [NASA ADS] [CrossRef] [Google Scholar]
- Govoni, F., Murgia, M., Feretti, L., et al. 2006, A&A, 460, 425 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Guidetti, D., Murgia, M., Govoni, F., et al. 2008, A&A, 483, 699 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Guidetti, D., Laing, R. A., Murgia, M., et al. 2010, A&A, 514, A50 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Johnstone, R. M., Allen, S. W., Fabian, A. C., & Sanders, J. S. 2002, MNRAS, 336, 299 [NASA ADS] [CrossRef] [Google Scholar]
- Kawano, N., Ohto, A., & Fukazawa, Y. 2003, PASJ, 55, 585 [NASA ADS] [Google Scholar]
- Kuchar, P., & Enßlin, T. A. 2011, A&A, 529, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kunz, M. W., Schekochihin, A. A., Cowley, S. C., Binney, J. J., & Sanders, J. S. 2011, MNRAS, 410, 2446 [NASA ADS] [CrossRef] [Google Scholar]
- Laing, R. A., Bridle, A. H., Parma, P., & Murgia, M. 2008, MNRAS, 391, 521 [NASA ADS] [CrossRef] [Google Scholar]
- Markevitch, M., & Vikhlinin, A. 2007, Phys. Rep., 443, 1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Murgia, M., Govoni, F., Feretti, L., et al. 2004, A&A, 424, 429 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Murgia, M., Parma, P., Mack, K.-H., et al. 2011, A&A, 526, A148 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rudnick, L., & Blundell, K. M. 2003, ApJ, 588, 143 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, R. J., Lucey, J. R., Steel, J., & Hudson, M. J. 1997, MNRAS, 291, 461 [NASA ADS] [Google Scholar]
- Taylor, G. B., Allen, S. W., & Fabian, A. C. 1999, Diffuse Thermal and Relativistic Plasma in Galaxy Clusters, 77 [Google Scholar]
- Taylor, G. B., Fabian, A. C., & Allen, S. W. 2002, MNRAS, 334, 769 [NASA ADS] [CrossRef] [Google Scholar]
- Taylor, A. R., Stil, J. M., & Sunstrum, C. 2009, ApJ, 702, 1230 [NASA ADS] [CrossRef] [Google Scholar]
- Tribble, P. C. 1991, MNRAS, 250, 726 [NASA ADS] [CrossRef] [Google Scholar]
- Tucker, W. H., & Rosner, R. 1983, ApJ, 267, 547 [NASA ADS] [CrossRef] [Google Scholar]
- Vogt, C., & Enßlin, T. A. 2003, A&A, 412, 373 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vogt, C., & Enßlin, T. A. 2005, A&A, 434, 67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Appendix A: Maximum scale of fluctuation
In this appendix we briefly discuss the determination of the outer scale of the magnetic field fluctuations. On the basis of the two-dimensional and three-dimensional simulations, we find that a maximum fluctuation scale of Λmax = 35 kpc provides a very good description of the observed structure function.
The observed rotation measure structure function is affected by a turnover in the large-separation regime (r⊥ ≫ 2π/kmin). The drop comes from a lowering of the gas density at large distances from the cluster center, resulting in a systematic decrease of the power of the Faraday rotation on large scales. This effect cannot be modeled by the two-dimensional simulations (see top-left panel of Fig. 5), while it is reproduced perfectly by the three-dimensional simulations (see top panel of Fig. 9). However, since we know that the tapering imposed by the gas density distribution on the RM structure function at large separations may limit the possibility to determine the maximum fluctuation scale of the magnetic field, we may ask which is our actual sensitivity on Λmax.
An accurate analysis would require considering Λmax as a free model parameter in the three-dimensional simulations as well, but the computational burden would be heavy. Indeed, we decided to explore only two more different values of Λmax, namely, a value of Λmax = 10 kpc, which is lower than the best-fit value, and a value of Λmax = 164 kpc, which is the maximum allowed by our computational grid of 10243 pixels.
 |
Fig. A.1 Bayesian 3-dimensional analysis of the RM structure function for the model with cavities for Λmax = 10 kpc (left) and Λmax = 164 kpc (right). Top panels: the dots represent the data (error bars are comparable to the size of the symbols). The shaded area represents the population of synthetic RM structure functions from the posterior distribution. The dashed line corresponds to the most probable value for the model parameters (see text). Bottom panels: one-dimensional (histograms) and two-dimensional (colors and contours) marginalizations of the posterior for the model parameters. The contours are traced at 0.9, 0.75, and 0.5 of the peak value. |
We performed the Bayesian analysis of the RM structure function with the same magnetic-field configuration as is described in Sect. 5, except for the maximum scale of fluctuations. The results are presented in Fig. A.1 for Λmax = 10 kpc and Λmax = 164 kpc (left and right panels, respectively). In the bottom panels of Fig. A.1 we present the two-dimensional (colors and contours) and one-dimensional (histograms) marginalizations of the posterior. The magnetic field central strength and radial decrease are constrained to
-
⟨B0⟩ = (33.1 ± 9.7) μG, and η = (1.7 ± 0.4) for Λmax = 10 kpc;
-
⟨B0⟩ = (16.4 ± 8.9) μG, and η = (1.2 ± 0.5) for Λmax = 164 kpc.
In the top panels we show the observed structure function (dots) along with the synthetic structure functions from the posterior. The blue line is the best fit. We note that Λmax = 10 kpc does not give a good description of the data because there is not enough power on large scales.
On the other hand, a maximum scale of fluctuation of Λmax = 164 kpc provides a better description of the observed structure function, even if it predicts slightly too much power for separations larger than r⊥ > 20 kpc. In this regime, the magnetic field model with Λmax = 35 kpc is still better.
Indeed, we may conclude that Λmax should be surely larger than 10 kpc. Although the drop in the gas density limits our sensitivity, we may infer that Λmax should be around 35 kpc, possibly lower than 164 kpc.
All Tables
Relevant parameters of the total intensity and polarization images between 1665 and 8415 MHz.
All Figures
 |
Fig. 1 Total intensity radio contours of 3C 338 at 8415 MHz with an FWHM of 2.5″ × 2.5″. The first contour level is drawn at 0.06 mJy/beam and the rest are spaced by a factor |
| In the text | |
 |
Fig. 2 Total intensity contours and polarization vectors at 1665 (top), 4585 (middle), and 8415 MHz (bottom). The angular resolution is 2.5″ × 2.5″. Contour levels start at 3σI, and increase by factors of two. The lines give the orientation of the electric vector position angle (E-field) and are proportional in length to the fractional polarization (1″ ~ 5%). |
| In the text | |
 |
Fig. 3 Top left: total intensity radio contours of 3C 338 at 8415 MHz overlaid on the RM image. The angular resolution is 2.5″ × 2.5″. Contour levels are drawn at: 0.06, 0.12, 0.24, and 0.96 mJy/beam. Top right: the histogram of the RM values. Bottom: sample plots of the observed position angle versus the squared wavelength at different source locations. The inset is a zoom of the observed polarization angle corresponding to frequencies between 4585 and 8415 MHz. |
| In the text | |
 |
Fig. 4 Left panel: adaptively smoothed Chandra X-ray image (Obs. ID 497) in the 0.2–10 keV band of the galaxy cluster A2199 with the VLA contour levels at 8415 MHz overlaid. Pronounced X-ray cavities can be identified in correspondence of the radio galaxy lobes. Top right panel: deprojected thermal gas density profile (Johnstone et al. 2002). Bottom right panel: pixel distribution of the rotation measure image as a function of the distance from the cluster center. |
| In the text | |
 |
Fig. 5 Top left panel: Bayesian analysis of the RM structure function. The dots represent the data (error bars are comparable to the size of the symbols). The shaded area represents the population of synthetic RM structure functions from the posterior distribution. The dashed line corresponds to the most probable value for the model parameters (see text). Top right, bottom left, and bottom right panel: one-dimensional (histograms) and two-dimensional (colors and contours) marginalization of the posterior for the model parameters. The contours are traced at 0.9, 0.75, and 0.5 of the peak value. |
| In the text | |
 |
Fig. 6 Top left panel: Bayesian analysis of the source depolarization. The dots represent the data. The shaded area represents the population of synthetic polarization from the posterior distribution. The dashed line corresponds to the most probable value for the model parameters (see text). Top right, bottom left, and bottom right panel: one-dimensional (histograms) and two-dimensional (colors and contours) marginalization of the posterior for the model parameters. The contours are traced at 0.9, 0.75, and 0.5 of the peak value. |
| In the text | |
 |
Fig. 7 Examples of observed (left) fractional polarizations images at 8415, 4585, 1665 MHz compared with synthetic realizations (right) corresponding to the best fit parameters from the depolarization analysis. |
| In the text | |
 |
Fig. 8 Top panel: X-ray cavity model. The darker region indicates the location where the thermal gas has been subtracted from the double β-model. Bottom panel: horizontal slice passing through the X-ray cavities at the cluster center. Continuous line represents the observations from the Chandra image, dashed line simulations with cavities, dotted line simulations without cavities. |
| In the text | |
 |
Fig. 9 Bayesian 3-dimensional analysis of the RM structure function for the model with Λmax = 35 kpc. Top panel: the dots represent the data (error bars are comparable to the size of the symbols). The shaded area represents the population of synthetic RM structure functions from the posterior distribution. The dashed line corresponds to the most probable value for the model parameters (see text). Bottom panel: one-dimensional (histograms) and two-dimensional (colors and contours) marginalizations of the posterior for the model parameters. The contours are traced at 0.9, 0.75, and 0.5 of the peak value. |
| In the text | |
 |
Fig. 10 The magnetic field power spectra (left panel) and radial profiles (right panel) for the models corresponding to the three values of Λmax = 10, 35, and 164 kpc are shown as dotted, continuous, and dashed lines, respectively. The model with Λmax = 35 kpc provides the best description of the observed RM structure function, see text. |
| In the text | |
 |
Fig. 11 Qualitative comparison between the observed rotation measure image (left) and a synthetic 3-dimensional realization (right). |
| In the text | |
 |
Fig. A.1 Bayesian 3-dimensional analysis of the RM structure function for the model with cavities for Λmax = 10 kpc (left) and Λmax = 164 kpc (right). Top panels: the dots represent the data (error bars are comparable to the size of the symbols). The shaded area represents the population of synthetic RM structure functions from the posterior distribution. The dashed line corresponds to the most probable value for the model parameters (see text). Bottom panels: one-dimensional (histograms) and two-dimensional (colors and contours) marginalizations of the posterior for the model parameters. The contours are traced at 0.9, 0.75, and 0.5 of the peak value. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.