| Issue |
A&A
Volume 539, March 2012
|
|
|---|---|---|
| Article Number | A87 | |
| Number of page(s) | 9 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201118371 | |
| Published online | 27 February 2012 | |
The instability strip of ZZ Ceti white dwarfs
I. Introduction of time-dependent convection
1 Institut d’Astrophysique et de Géophysique, Université de Liège, 17 allée du 6 Août, 4000 Liège, Belgium
e-mail: valerie.vangrootel@ulg.ac.be
2 Chargé de recherches, Fonds de la Recherche Scientifique, FNRS, 5 rue d’Egmont, 1000 Bruxelles, Belgium
3 Département de Physique, Université de Montréal, CP 6128, Succursale Centre-Ville, Montréal, QC H3C 3J7, Canada
4 Centro de Astrofisica da Universidade do Porto, Rua das Estrelas, 4150-762 Porto, Portugal
5 Agence Spatiale Canadienne, 6767 route de l’Aéroport, Longueuil, QC J3Y 8Y9, Canada
Received: 1 November 2011
Accepted: 6 January 2012
Aims. The determination of the location of the theoretical ZZ Ceti instability strip in the log g − Teff diagram has remained a challenge over the years due to the lack of a suitable treatment for convection in these stars. For the first time, a full nonadiabatic approach including time-dependent convection is applied to ZZ Ceti pulsators, and we provide the appropriate details related to the inner workings of the driving mechanism.
Methods. We used the nonadiabatic pulsation code MAD with a representative evolutionary sequence of a 0.6 M⊙ DA white dwarf. This sequence is made of state-of-the-art models that include a detailed modeling of the feedback of convection on the atmospheric structure. The assumed convective efficiency in these models is the so-called ML2/α = 1.0 version. We also carried out, for comparison purposes, nonadiabatic computations within the frozen convection approximation, as well as calculations based on models with standard grey atmospheres.
Results. We find that pulsational driving in ZZ Ceti stars is concentrated at the base of the superficial H convection zone, but at depths, near the blue edge of the instability strip, somewhat larger than those obtained with the frozen convection approach. Despite the fact that this approach is formally invalid in such stars, particularly near the blue edge of the instability strip, the predicted boundaries are not dramatically different in both cases. The revised blue edge for a 0.6 M⊙ model is found to be around Teff = 11 970 K, some 240 K hotter than the value predicted within the frozen convection approximation, in rather good agreement with the empirical value. On the other hand, our predicted red edge temperature for the same stellar mass is only about 5600 K (80 K hotter than with the frozen convection approach), much lower than the observed value.
Conclusions. We correctly understand the development of pulsational instabilities of a white dwarf as it cools at the blue edge of the ZZ Ceti instability strip. Our current implementation of time-dependent convection however still lacks important ingredients to fully account for the observed red edge of the strip. We will explore a number of possibilities in the future papers of this series.
Key words: stars: oscillations / white dwarfs
© ESO, 2012
1. Introduction
The ZZ Ceti stars constitute the coolest pulsating white dwarfs in the Hertzsprung-Russell diagram. These H-atmosphere (DA) white dwarfs are in a phase of their cooling sequence where hydrogen in the outer envelope, essentially pure due to the gravitational settling of other elements, recombines around Teff ~ 12 000 K. This leads to a huge increase of the envelope opacity which, in turn, strangles the flow of radiation, and finally causes pulsational instabilities as g-modes oscillations (see, e.g., Winget et al. 1982; Winget 1982).
On the observational front, mapping the ZZ Ceti instability strip to precisely determine the empirical boundaries has been a long-term objective carried out by the Montréal group, in particular (see, e.g., Gianninas et al. 2007, and references therein). These efforts, started with the important contribution of Bergeron et al. (1995), and continued over the years (the most recent developments have been presented by Gianninas et al. 2010; Tremblay et al. 2011, on the spectroscopic front), have led to a solid confirmation of the initial suggestion made by Fontaine et al. (1982) that the ZZ Ceti strip must be pure. That is, all DA white dwarfs are to become ZZ Ceti pulsators as they cool across the strip. Figure 1, based on the data presented in the review of Fontaine & Brassard (2008), gives an enlightening overview of the empirical ZZ Ceti instability strip. Note that there is a log g − Teff correlation for the boundaries in the sense that the edge occurs at lower effective temperatures for lower surface gravity stars. Furthermore, the slope is more pronounced at the red edge than at the blue edge.
 |
Fig. 1 Empirical instability domain in the log g − Teff diagram for the ZZ Ceti white dwarfs. The positions of pulsating stars are indicated by the filled circles, while those of the nonvariable stars are given by the open circles. The error cross in the lower left part gives the typical uncertainties on the atmospheric parameters. The dotted curves illustrate evolutionary tracks for DA white dwarfs of different masses, from 0.4 M⊙ above to 1.1 M⊙ below in steps of 0.1 M⊙. The dashed lines illustrate the empirical boundaries of the strip. |
The earliest theoretical investigations of the boundaries of the instability strip for ZZ Ceti stars were made, for lack of a better approach, within the frozen convection (FC) approximation (see, e.g., Dolez & Vauclair 1981; Dziembowski & Koester 1981; Winget et al. 1982; Winget 1982; Starrfield et al. 1982). It was in the meantime realized (see, e.g., Brickhill 1983, and references therein) that, at least at the blue edge, the turnover timescale in the convection zone of a ZZ Ceti star is, in fact, much smaller than the pulsation periods of interest. This justified the opposite assumption, in which the convective flux reacts instantaneously to pulsations. Such an instantaneous convection response was numerically implemented by Brassard & Fontaine (1997, 1999) in a complete nonadiabatic pulsation code in a white dwarf context. They were able to determine a realistic theoretical blue edge, but they did not find any credible red edge localization. This concurs with the independent results of Wu & Goldreich (1999), who also found the theoretical red edge to be rather elusive. No further developments were made since then, and the red edge problem remains very much a challenge. We still have no consistent global picture of the interaction between convection and pulsations in white dwarfs, and, therefore, a consistent description of the driving of instabilities in the ZZ Ceti stars does not exist. A more complete story of the past developments on the excitation physics front in pulsating white dwarfs can be found in Fontaine & Brassard (2008), in their Sect. 5, in particular.
The problem of interactions between convection and pulsations has been studied by many authors, following different approaches (Unno 1967; Gough 1977). Following the original ideas put forward by Unno (1967), a time-dependent convection (TDC) treatment in the framework of the mixing-length theory (MLT) has been developed by Gabriel et al. (1974) and Gabriel (1996). This theory is presented in a unified form, along with the latest improvements about the energy closure equation, in Grigahcène et al. (2005). The nonradial nonadiabatic code MAD (Dupret 2002) is, to our knowledge, the only one to have implemented such a TDC theory. We propose, in this series of papers, to apply the MAD code to ZZ Ceti white dwarf models, with the aim to progress on the theoretical determination of the instability boundaries. Similar efforts have recently been carried out on variable He-atmospheres (DB) white dwarfs, with some promising results (Dupret et al. 2008; Quirion et al. 2008). For the ZZ Ceti stars, this is the first time here that a time-dependent convection treatment is applied in a full consistent way. Sections 2 and 3 of this paper present the ZZ Ceti evolutionary models and the TDC theory, respectively. Section 4 gives the results obtained for 0.6 M⊙ DA models, including a discussion of the eigenfunctions obtained with the TDC treatment compared to the FC approximation. Section 5 presents conclusions and prospects for future work.
2. ZZ Ceti models
2.1. Properties of evolutionary models
We used in this study evolutionary models computed with the white dwarf stellar code presented in Fontaine et al. (2001). They are made of a pure C core surrounded by a pure He mantle containing a mass fraction log q = log (1 − M(r)/M∗) = −2.0, itself surrounded by a pure H envelope with a fractional mass loq q = −4.5. These particular choices of model parameters do not affect in any significant way the nonadiabatic physics associated with the driving mechanism. Indeed, Fontaine et al. (1994) showed that the theoretical blue edge temperature of the ZZ Ceti instability strip is insensitive to the H envelope mass fraction for log q ≥ − 12. Our evolutionary tracks were computed for nine stellar masses from 0.4 to 1.2 M⊙ in steps of 0.1 M⊙ covering a very wide range of effective temperature, from above 60 000 K down to about 1000 K, more than enough to cover the empirical ZZ Ceti instability strip. In addition, we considered three different flavors of the MLT, as well as two distinct treatments of the atmospheric layers in presence of convection. In the present paper, we focus primarily on the introduction of TDC in a ZZ Ceti context, and use only two of these sequences at this time, however. These sequences of models are similar in that they are both characterized by a total mass of 0.6 M⊙, and a choice of the ML2/α = 1.0 version of the MLT. The ML2/α = 1.0 flavor is defined by α = l/HP = 1.0, and the following numerical constants related to the geometry of the convective elements: a = 1, b = 2 and c = 16 (Bohm & Cassinelli 1971). The two sequences differ in that one incorporates the feedback effect of the convection zone on the atmospheric layers (see below), while the other does not.
Figure 2 shows the profile of the convection zone (small filled circles) and contours of the Rosseland opacity log κ (small dots, with some indicated values) as functions of the fractional mass depth log q for our 0.6 M⊙ evolutionary sequence between Teff = 17 000 K and 1000 K. On this scale, the center of the star is at log q = 0; only the outermost layers are depicted here. A very large opacity bump develops as the effective temperature decreases, and is due to ionization/recombination of neutral hydrogen HI. As a consequence, a large superficial convection zone develops, as clearly illustrated in the figure. It has to be mentioned that the top of the convection zone always resides in the photospheric layers1, while the base initially sinks deeper into the star as it cools. The convection zone extends from about log q ~ −6 up to log q ~ −14.5 near the photosphere at Teff = 5000 K. At this effective temperature, the base of the convection zone reaches for the first time the upper boundary of the degenerate core (where very efficient conductive transport prevails), thus coupling the surface with the core. This “convective coupling” increases considerably the rate of energy transfer from the core across the outer opaque envelope beyond what is possible through radiative transfer alone, and constitutes a significant event in the evolution of cool white dwarfs (Fontaine et al. 2001).
 |
Fig. 2 Structure of the envelope of our representative evolving 0.6 M⊙ DA white dwarf. The ordinate gives the fractional mass depth in logarithmic units. The small dots define “isocontours” of opacity, and some are labelled by their value of log κ. The small filled circles indicate the boundaries of the superficial convection zone. The vertical dashed lines indicate the blue and red edges obtained with our TDC treatment with ML2/α = 1.0. |
In the range of effective temperature of interest for ZZ Ceti stars, most of the energy is transported by convection in the outer layers. This is illustrated in Fig. 3 on the left, where the fraction of the convective flux Fc to the total flux F is indicated. For its part, the right panel of Fig. 3 shows contours of log τc, the convective turnover timescale (in seconds). The contours are separated by 0.5 dex, also with some indicated values. The typical pulsation periods in ZZ Ceti white dwarfs are in the range 100−1500 s (i.e., in logarithmic units, 2.00 − 3.18; Fontaine & Brassard 2008). For the hot models above Teff ~ 10 000 K, the lifetimes of convective elements are much smaller than the pulsation periods, so convection adapts quasi-instantaneously to the pulsations, as is well known. This state of affair is not true anymore for the cooler models: the lifetimes become of the same order as the pulsation periods, especially at the base of the convection zone. In that case, neither the approximations of instantaneous response or frozen convection are valid anymore, and a full TDC treatment like ours is formally required.
 |
Fig. 3 Left panel: similar to Fig. 2, but the small dots define here isocontours of the ratio of the convective to total flux, with values Fc/F = 0.99, 0.95, 0.9, 0.8, 0.7, 0.6, 0.5, 0.4, 0.3, 0.2, 0.1, and 0.01. Right panel: similar, but for the convective turnover timescale log τc expressed in seconds. |
Figure 4 shows the details of the driving/damping region for a typical unstable g-mode (l = 1, k = 7, period of 447.8 s) culled from a representative ZZ Ceti star model (0.6 M⊙, Teff = 11 500 K). The running work integral W (blue curve, left ordinate axis) is arbitrarily normalized. A negative slope of W at a given depth means that the mode is locally damped, while, conversely, a positive slope implies that the mode is locally driven. The mode illustrated here has a final positive value of its work integral at the surface, and is therefore globally excited and potentially observable. Conversely, a negative value of the work integral at the surface would imply that the mode is globally damped and should not be seen. One can notice that, unlike the traditional κ-mechanism, maximum driving does not occur at the depth where the opacity reaches its maximum value, but somewhat below. Also, the driving region is concentrated at the base of the convection zone: the pulsation driving in ZZ Ceti stars is thus intimately associated with the physical conditions near the base of the superficial convection zone.
2.2. Detailed atmospheric structures
The precise location of the convection zone, and especially of its base where the driving region is concentrated, is of prime importance for the accurate determination of the development of pulsational instabilities in the ZZ Ceti white dwarfs. A proper treatment of the feedback effect of the convection zone on the atmospheric structure – usually neglected in stellar evolution codes – must then be considered. We followed in this the prescription of Brassard & Fontaine (1997), and incorporated it into our stellar evolution code. Briefly, at large optical depths, the radiative gradient is given with good accuracy by the diffusion approximation: 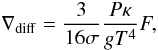 (1)where the symbols have their standard meaning. For optically thin regions, the usual approximation in stellar evolution codes is to use a grey atmosphere, and the temperature gradient is then given by
(1)where the symbols have their standard meaning. For optically thin regions, the usual approximation in stellar evolution codes is to use a grey atmosphere, and the temperature gradient is then given by ![\begin{equation} \label{eq2} \nabla_{\rm grey} = \frac{3}{16\sigma} \frac{P \kappa}{g T^4} F [1+H'(\tau)] \end{equation}](/articles/aa/full_html/2012/03/aa18371-11/aa18371-11-eq33.png) (2)where H(τ) is the Hopf function, as appropriate for a purely radiative grey atmosphere. By analogy with these expressions, we define a realistic temperature gradient which is particularly of interest in the presence of convection,
(2)where H(τ) is the Hopf function, as appropriate for a purely radiative grey atmosphere. By analogy with these expressions, we define a realistic temperature gradient which is particularly of interest in the presence of convection, 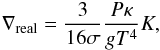 (3)where K = K(P,T,τ) is a function extracted from detailed atmospheric computations, such that the atmospheres computed in our evolutionary models have the same temperature stratifications as those of complete (non-grey) model atmospheres. In this way, a feedback of the convection on the global structure of the atmosphere is allowed to occur, which is not taken into account with a standard grey atmosphere.
(3)where K = K(P,T,τ) is a function extracted from detailed atmospheric computations, such that the atmospheres computed in our evolutionary models have the same temperature stratifications as those of complete (non-grey) model atmospheres. In this way, a feedback of the convection on the global structure of the atmosphere is allowed to occur, which is not taken into account with a standard grey atmosphere.
Figure 5 shows the profiles of the convection zone, respectively for evolutionary models with standard grey atmospheres (blue dots) and for similar evolutionary models but obtained from the solution of the transfer Eq. (3) (red dots). At a given effective temperature, both the top and the base of the convection zone are moved upward in the star in the case of a detailed atmosphere including feedback. The consequence is to “cool down” the blue edge somewhat when these more realistic atmospheres are incorporated in the evolutionary models. These detailed model atmospheres are an optional choice for the surface boundary conditions in our evolutionary models, and this is the choice we picked in this paper. Otherwise, the other option is the use of the standard grey atmospheres.
 |
Fig. 4 Details of the driving/damping region for a typical unstable g-mode in a representative model of a ZZ Ceti star. The boundaries of the superficial convection zone are indicated by the two vertical dashed black lines. The vertical dashed red lines are, respectively, the position of the photosphere (Rosseland optical depth of 2/3) on the right, and of the base of the atmosphere (Rosseland optical depth of 100) on the left. The green curve (right ordinate axis) illustrates the profile of the Rosseland opacity, while the blue curve (left ordinate axis) shows the running (from left to right) work integral for the excited mode. |
 |
Fig. 5 Comparison of the profiles of the superficial HI convection zone from two 0.6 M⊙ evolutionary sequences having the same parameters, except for the way the atmospheric layers are handled. The blue dots depict the expected zone for models using standard grey atmosphere structures, while the red dots correspond to the models with the inclusion of convective feedback on the atmospheric structure. |
3. Time-dependent convection theory
We briefly recall the basic features of the time-dependent convection treatment originally developed by Gabriel et al. (1974; see also Gabriel 1996), and described in detail in Grigahcène et al. (2005). The TDC treatment is built within the framework of the mixing-length theory, and the stability of the solution is studied by a linear perturbative method. The treatment of convection is local, for consistency with the white dwarf models. While a non-local treatment of convection is implemented in the MAD pulsation code, it remains so far to be built in the white dwarf evolutionary sequence. Such a global convection treatment is beyond the scope of this paper. Let us mention that attempts of a non-local treatment of convection, with hydrodynamically simulated convective surface layers supplemented with standard interior models, could not reproduce theoretically the observed location of the blue edge of ZZ Ceti stars (Gautschy et al. 1996).
The variables are splitted in two parts, describing respectively the average model and the convection: 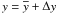 (y is any scalar variable) and v = u + V (where v is the velocity vector).
(y is any scalar variable) and v = u + V (where v is the velocity vector). 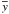 and u are the average values, while Δy and V describe the convection. The substraction of the mean equations of mass, momentum and energy conservations from the corresponding non-averaged ones gives the equations for convection. They are then simplified in such a way that their stationary solutions lead to the classical mixing-length theory in its “ML2 version” of Bohm & Cassinelli (1971) adopted in our white dwarf models. This procedure ensures the compatibility between the theories used to compute the white dwarf models and to evaluate their pulsational stability.
and u are the average values, while Δy and V describe the convection. The substraction of the mean equations of mass, momentum and energy conservations from the corresponding non-averaged ones gives the equations for convection. They are then simplified in such a way that their stationary solutions lead to the classical mixing-length theory in its “ML2 version” of Bohm & Cassinelli (1971) adopted in our white dwarf models. This procedure ensures the compatibility between the theories used to compute the white dwarf models and to evaluate their pulsational stability.
The perturbations of the mean equations of mass, momentum and energy conservations give the linear pulsation equations, where new terms appear such as the perturbation of the convective flux and the Reynolds stress tensor. Of these terms, only the perturbation of the convective flux vector is taken into account in this paper and is given by: 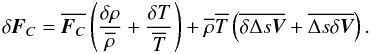 (4)The unknown correlation terms (δΔsV) and (ΔsδV) in Eq. (4) can be obtained by perturbing the equations for convection solutions (assuming constant coefficients) of the form δ(ΔX) = δ(ΔX)keik·reiσt. These solutions are then integrated over all values of kθ and kΦ such as k
(4)The unknown correlation terms (δΔsV) and (ΔsδV) in Eq. (4) can be obtained by perturbing the equations for convection solutions (assuming constant coefficients) of the form δ(ΔX) = δ(ΔX)keik·reiσt. These solutions are then integrated over all values of kθ and kΦ such as k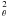 + k
+ k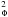 = Ak
= Ak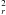 (A is a constant, = 1/2 for isotropic turbulence) and assuming that every direction of the horizontal component of k has the same probability. The horizontal averages are computed. The perturbed convective flux takes finally the following form:
(A is a constant, = 1/2 for isotropic turbulence) and assuming that every direction of the horizontal component of k has the same probability. The horizontal averages are computed. The perturbed convective flux takes finally the following form: 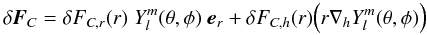 (5)with a natural separation of the problem in spherical harmonics. δFC,r(r) and δFC,h(r) are related to the perturbed mean quantities by first order differential equations. Explicit forms are given by Eqs. (18) and (20) in Grigahcène et al. (2005). In this procedure, the timescales of pulsation and convection (coming respectively from the perturbation of the left side of the motion equation and right side of the energy equation for convection) are both taken into account, and our treatment therefore does not assume instantaneous adaptation of convection or frozen convection.
(5)with a natural separation of the problem in spherical harmonics. δFC,r(r) and δFC,h(r) are related to the perturbed mean quantities by first order differential equations. Explicit forms are given by Eqs. (18) and (20) in Grigahcène et al. (2005). In this procedure, the timescales of pulsation and convection (coming respectively from the perturbation of the left side of the motion equation and right side of the energy equation for convection) are both taken into account, and our treatment therefore does not assume instantaneous adaptation of convection or frozen convection.
The frozen convection approach in what follows consists in neglecting the Lagragian variations of the convective luminosity, i.e. δ(r2FC,r) = 0 and δFC,h = 0 (see Grigahcène et al. 2007).
The main source of uncertainty in any MLT treatment of convection-pulsation interaction comes from the adopted expression for the perturbation of the mixing length l = αHp (Hp is the pressure scale height). In this paper, we chose, as discussed in Grigahcène et al. (2005): 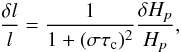 (6)from which we retrieve the two limits cases δl/l → δHp/Hp when στc ≪ 1 (instantaneous adaptation of convection) and δl/l → 0 when στc ≫ 1 (frozen convection).
(6)from which we retrieve the two limits cases δl/l → δHp/Hp when στc ≪ 1 (instantaneous adaptation of convection) and δl/l → 0 when στc ≫ 1 (frozen convection).
 |
Fig. 6 Work integral for the l = 1 g4 mode of a 0.6 M⊙ ZZ Ceti model with our TDC treatment. Top and middle panel: at Teff = 5600 K, with β = (0,0) and β = (1, −1) respectively. Bottom panel: at Teff = 8850 K, also with β = (0,0) (dashed curve) and β = (1, −1) (solid curve). |
A well known problem of this treatment is the occurrence of spatial oscillations of the thermal eigenfunctions with a wavelength much shorter than the mixing-length, which are not physical (see Fig. 6). These oscillations occur in the part of the convective envelope where στc ≫ 1 and most of the energy is transported by convection. Grigahcène et al. (2005) proposed an improvement of the TDC treatment able to solve this problem in a local way. A new free parameter β of the order of unity was introduced in the perturbation of the closure term of the energy equation, such as 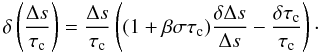 (7)With this free parameter, phase lags between the oscillations and the way the turbulence cascade adapts to them are allowed to occur, while they have been neglected in the original MLT approach.
(7)With this free parameter, phase lags between the oscillations and the way the turbulence cascade adapts to them are allowed to occur, while they have been neglected in the original MLT approach.
For ZZ Ceti white dwarfs, the oscillations of eigenfunctions slowly appear for the low effective temperatures of the cooling sequence, below ~ 7000 K. Figure 6 shows the running work integral W for the l = 1 g4 mode (i.e., the k = 4 g-mode) at Teff = 5600 K, with β = (0,0) (top panel) and β = (1, − 1) (middle panel). The introduction of β importantly reduces the oscillations of the work integral, and trials/errors showed that a real part close to unity and a negative imaginary part also close to unity is the best compromise. It is also important to mention that when the short-wavelength oscillations are not present, the results obtained with a zero or with a non-zero value of β are very close (bottom panel of Fig. 6, for the same oscillation mode of a 0.6 M⊙ model at Teff = 8850 K).
 |
Fig. 7 Periods (in seconds) of the excited l = 1 g-modes as functions of the effective temperature along the 0.6 M⊙ evolutionary sequence computed with the detailed atmosphere modeling. The size of a dot is a measure of the excitation of that particular mode. Top panel: FC. Middle panel: TDC with β = (0,0). Bottom panel: TDC with β = (1, −1). |
4. Results
4.1. The instability strips
We applied the MAD code with the TDC treatment (in the ML2/α = 1.0 version) to our two representative 0.6 M⊙ evolutionary sequences, from an initial effective temperature of 35 000 K to a final value of 2000 K. For comparison purposes, we also carried out nonadiabatic computations within the frozen convection approximation. Table 1 summarizes the results for the values of the effective temperature at the boundaries of the instability strip, while Fig. 7 illustrates how the spectrum of excited l = 1 modes behaves across the strip.
Theoretical boundaries of the ZZ Ceti instability strip.
The comparison between the middle and bottom panel (TDC treatment with β = (0,0) and β = (1, − 1), respectively) of Fig. 7 shows that the introduction of the parameter β in the TDC treatment is necessary to obtain a well-defined location for the red edge. Without it, the pulsations appear to be excited somewhat “randomly” for Teff ~ 6000 K and below, in relation with the increasing presence of short-wavelength oscillations in the eigenfunctions of the modes at these effective temperatures (see Fig. 6). Table 1 indicates that, with the detailed atmosphere modeling, the locations of both edges are shifted towards lower effective temperatures. As shown in Fig. 5, the convection zone is moved higher in the star in the case where convective feedback is taken into account. This is equivalent to “repel” the blue edge, defined by a precise depth of the base of the convection zone, to a lower effective temperature model. The shift is about 230 K for the blue edge and 370 K for the red one in TDC. This is a small, but significant effect when comes the time to compare with the location of the empirical ZZ Ceti instability strip (Fig. 1).
The most striking feature that comes out of Table 1 and Fig. 7, however, is the fact that the predicted boundaries of the ZZ Ceti instability strip are not largely different in TDC compared to FC. The predicted effective temperatures at both boundaries are systematically larger in TDC than in FC, by about 240 K at the blue edge2, and by about 80 K only at the red edge for our 0.6 M⊙ models computed with detailed atmospheres. That these differences are relatively small is both a blessing and a curse in the sense that the predictions of past investigations based on the FC approximation are somehow “comforted” by our results, even though the physical conditions under which FC is justified are clearly not met in ZZ Ceti stars. And indeed, only at effective temperatures much lower than those defining the empirical red edge does the convective turnover timescale become comparable to, and eventually larger than, the pulsation periods of interest. Near the blue edge, FC is certainly not justified on a formal basis, since the conditions are rather those found at the other extreme of the spectrum of possibilities, i.e., they are compatible with instantaneous adaptative convection. Yet, the predicted blue edge temperatures reported in Table 1 are not dramatically different from each other, i.e., in TDC or FC. We note that similar results have been obtained by Dupret et al. (2008) and Quirion et al. (2008) for pulsating DB (V777 Her) white dwarfs. At the very least, such results indicate that the precise way the convective flux is modulated in a ZZ Ceti (or V777 Her) model does not have a dramatic impact on the predicted locations of instability regions.
We further note that the theoretical blue edge obtained with our computations for the 0.6 M⊙ ZZ Ceti sequence models is globally coherent with the empirical blue edge, observed around Teff ~ 12 000 K (Fig. 1). We will investigate in detail the dependence of the blue edge on the mass (surface gravity) of the models, as well as its dependence on the assumed convective efficiency used in the equilibrium structures in Paper II of this series. As for the red edge, our current implementation of TDC is unable to account for its empirical location. Our predicted red edge temperature is, as in the case of FC, much too low to be compatible with the empirical value of Teff ~ 11 000 K (Fig. 1) for 0.6 M⊙ stars. Clearly, our current approach is still missing an important piece of physics. Possible upgrades include the time variations of the turbulent pressure, of non diagonal components of the Reynolds stress tensor, and of the dissipation rate of turbulent kinetic energy into heat. It also might be related to the non-local nature of convection. We will consider such possible improvements in Paper III of this series. For the time being, we next turn to a discussion of the details of driving/damping in our models of ZZ Ceti stars, emphasizing, in particular, the differences between TDC and FC.
 |
Fig. 8 Work integrals (solid curve: TDC treatment, dashed curve: FC approximation) for three 0.6 M⊙ models along the evolutionary sequence, from Teff = 11 750 K to Teff = 8000 K. The limits of the convection zone are indicated in each panel by the vertical dashed lines. |
 |
Fig. 9 Entropy variation ℜ(δs) (solid curve: TDC treatment, dashed curve: FC approximation) for three 0.6 M⊙ models along the evolutionary sequence. The limits of the convection zone are indicated in each panel by the vertical dashed lines. The insert figure is a zoom of the base of the convection zone. |
 |
Fig. 10 Total luminosity variation δL/L (solid curve: TDC treatment, dashed curve: FC approximation), with contributions of radiation (dotted curve) and convection (dot-dashed curve), along the evolutionary sequence. The limits of the convection zone are indicated in each panel by the vertical dashed lines. |
4.2. Eigenfunctions
Figures 8–10 present the eigenfunctions (work integral W, real part of entropy variation ℜ(δs) and total luminosity variation δL/L, with contributions of radiation and convection) along the evolutionary sequence. Three panels are shown in each figure: near the computed blue edge at Teff = 11 750 K, at Teff = 10 650 K where the number of excited modes reaches a maximum, and towards the red edge at Teff = 8000 K. The mode considered in these figures is characterized by l = 1, g4. Its period ranges from 311.9 s at Teff = 11 750 K to 369.1 s at Teff = 8000 K. The results are shown both with the FC approximation and with the TDC treatment, with β = (1, −1). We considered here the case of a detailed atmosphere modeling, including the convective feedback.
The work integrals in Fig. 8 are normalized, in such a way that the surface value gives the growth rate of the mode multiplied by the dynamical time. The main driving of the mode always occurs near the base of the convection zone, and the mode considered here is always globally excited. Significant differences between the FC and TDC results are observed near the blue edge, with a driving in the TDC case slightly below the base of the convection zone. The mode is therefore globally more excited in the TDC case. The generalization of this situation leads to a blue edge at slightly higher effective temperatures with the TDC treatment, as observed in Fig. 7. The differences in the work integrals are less pronounced as we progress along the evolutionary sequence towards lower effective temperatures.
Figure 9 shows the real part of the entropy variation ℜ(δs) along the cooling sequence. Near the blue edge, the convective turnover timescale is much smaller than the pulsations periods, so the convection adapts quasi-instantaneously to the oscillations. Such a situation is allowed to occur in TDC models, and is the opposite of frozen convection. Convection is very efficient in the deep regions, and a small entropy gradient is able to transport energy. The TDC treatment does not allow significant entropy gradient to occur and a plateau of δs is predicted contrary to the FC approximation. We can show that the relative perturbation of the convective flux (Eq. (18) of Grigahcène et al. 2005) is, in the case of an instantaneous adaptation of convection to pulsations (στc ≪ 1 and A, B, C and D coefficients of Eq. (18) of Grigahcène et al. 2005, tending to unity), directly related to the relative perturbation of the entropy gradient (only the dominant term is given here): 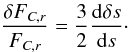 (8)On the contrary in FC models, the entropy gradient is allowed to have unrealistic high values in the upper part of the convection zone, without any control of it by the energy equation throughout the convective flux variations. This is what we observe in the top panel of Fig. 9. The plateau in TDC models leads to a gain of heat ρTδs near the base of the convection zone much larger in this case than within the FC approximation. This large energy input is transformed in mechanical work driving the oscillations more efficiently in TDC models than in FC models. As δT and therefore δs must be continuous, it does not drop directly to zero below the convection zone, which explains why the driving begins slightly below the convection zone boundary in the TDC blue edge model. This differs from the FC models, in which the driving only results from convective blocking in the bottom part of the convection zone. The upper part of the convection zone has practically no influence on the driving, as the density ρ and temperature T rapidly decrease towards the surface of the star.
(8)On the contrary in FC models, the entropy gradient is allowed to have unrealistic high values in the upper part of the convection zone, without any control of it by the energy equation throughout the convective flux variations. This is what we observe in the top panel of Fig. 9. The plateau in TDC models leads to a gain of heat ρTδs near the base of the convection zone much larger in this case than within the FC approximation. This large energy input is transformed in mechanical work driving the oscillations more efficiently in TDC models than in FC models. As δT and therefore δs must be continuous, it does not drop directly to zero below the convection zone, which explains why the driving begins slightly below the convection zone boundary in the TDC blue edge model. This differs from the FC models, in which the driving only results from convective blocking in the bottom part of the convection zone. The upper part of the convection zone has practically no influence on the driving, as the density ρ and temperature T rapidly decrease towards the surface of the star.
At Teff = 10 650 K (middle panels of Figs. 8–10), the convective turnover timescales is again smaller than the oscillations periods, especially at the base of the convection zone. The plateau of δs in TDC models is still observed near the base of the convection zone at these effective temperatures, albeit at a much lower level than the blue edge plateau (see the inserts in Fig. 9). Since the base of the convection zone is now located deeper in the star, at higher densities and temperatures, a very small entropy gradient is able to transport energy. The physical behavior in FC models is again basically different, with a huge entropy variation in the upper part of the convection zone. However, the energy input ρTδs near the base of the convection zone able to drive the oscillations is the same order in the TDC and FC models. This explains the little differences in the work integrals of TDC and FC models in the middle panel of Fig. 8, despite the fact that the physics of the driving is intrinsically different and the frozen convection approximation is again not justified at Teff = 10 650 K.
As long as we progress along the cooling sequence, the convective turnover timescale becomes of the order of the oscillation periods. The plateau of δs disappears. Again there are little differences in the energy input of TDC and FC models at the base of the convection zone where the pulsational driving is located, and the work integrals look alike (bottom panel of Fig. 8).
The evolution of the entropy variation in the convection zone along the cooling sequence is closely related to the evolution of the luminosity variations δL/L presented in Fig. 10, through the energy equation 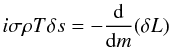 (9)valid for regions without nuclear reactions as is the case here for the convection zone, and neglecting the divergence of the horizontal flux. At the high effective temperatures of the instability strip, a plateau of δs is observed at the base of the convection zone in TDC models (Fig. 9). This constant δs leads to huge variations of the radiative luminosity δLr/L (dotted curves in Fig. 10) near the base of the convection zone, but they are counterbalanced thanks to the high convection efficiency by a huge δLc/L (dot-dashed curves in Fig. 10). The total luminosity variations (solid curves in Fig. 10) hence keep reasonable values. This figure clearly shows the basic discrepancy of the frozen convection approximation, where the convective luminosity variations δLc are supposed to be negligible compared to the radiative luminosity variations δLr.
(9)valid for regions without nuclear reactions as is the case here for the convection zone, and neglecting the divergence of the horizontal flux. At the high effective temperatures of the instability strip, a plateau of δs is observed at the base of the convection zone in TDC models (Fig. 9). This constant δs leads to huge variations of the radiative luminosity δLr/L (dotted curves in Fig. 10) near the base of the convection zone, but they are counterbalanced thanks to the high convection efficiency by a huge δLc/L (dot-dashed curves in Fig. 10). The total luminosity variations (solid curves in Fig. 10) hence keep reasonable values. This figure clearly shows the basic discrepancy of the frozen convection approximation, where the convective luminosity variations δLc are supposed to be negligible compared to the radiative luminosity variations δLr.
As long as the effective temperature decreases along the evolutionary sequence, the entropy variations δs become smaller at the base of the convection zone (Fig. 9), located deeper in the star, at higher densities and temperatures. Oscillations are thus quasiadiabatic in this region. Not only δL but also δLr are continuous at the convective zone boundary, and therefore δLc ~ 0. This implies that |δLc| ≪ |δLr|, which corresponds to the frozen convection approximation. Eigenfunctions act “like” in the FC limit, despite the fact that the convective turnover timescales is still smaller or of the order of the oscillation periods (and not higher than them) at these effective temperatures.
5. Conclusion and prospects
We applied, for the first time, a full time-dependent convection treatment to study the development of pulsational instabilities in ZZ Ceti white dwarfs. We also carried out, for comparison purposes, similar calculations within the frozen convection approximation. Although it has been realized long ago that the latter approach is not generally justified in the convection zone of a ZZ Ceti star, it has still been used many times because a better recipe has been lacking. In this paper, we considered two representative 0.6 M⊙ evolutionary sequences for DA white dwarfs, differing only in their respective treatment of the feedback effect of convection on the atmospheric structure.
The theoretical blue edge temperature obtained in our computations incorporating TDC and convective feedback is quite consistent with the value found at the empirical blue edge, i.e., Teff ~ 12 000 K for 0.6 M⊙ stars. This theoretical value is slightly (240 K), but significantly larger than the blue edge temperature found in the same equilibrium models, but analyzed with the FC approach. Despite the fact that the physical details of the driving mechanism found in both cases are quite different (as observed in our analysis of the behaviors of the eigenfunctions), and despite the fact that the FC approximation is not justified, especially near the blue edge of the instability strip, the predicted blue edge temperature in the FC framework as well as the development of the pulsational instabilities across the strip (as can be seen by comparing the upper with the lower panel in Fig. 7) are not dramatically different from the results derived with TDC. This is puzzling, but Brassard & Fontaine (1997, 1999) already have found a similar result with their instantaneous convection approach to the study of the blue edge of the ZZ Ceti instability strip, and Dupret et al. (2008) and Quirion et al. (2008) also found a comparable behavior in their study of the pulsational instabilities found in models of pulsating DB white dwarfs. It thus would seem that the exact way the convective flux is modulated in pulsating white dwarfs does not have a spectacular effect on the predicted range of excited periods. What matters, for the driving, is mainly the size of the convection zone. This situation is similar to the one encountered in γ Doradus stars (see, e.g., Dupret et al. 2005).
The TDC results presented in this paper, based on a full nonadiabatic approach incorporating convective perturbations, are certainly the best physical description put forward so far of how pulsational instabilities develop at the blue edge of the ZZ Ceti instability strip. The fact that we have been able to reproduce quite well the value of the effective temperature at the blue edge of the empirical strip for stars with 0.6 M⊙ is encouraging and is motivating us to map in more detail the theoretical blue edge. Hence, in Paper II of this series, we will examine the dependence of the blue edge temperature on the mass (surface gravity) of the models, as well as its dependence on various flavors of the MLT theory.
Our results for the red edge are, in contrast to the blue edge, still not satisfactory. Despite the introduction of the TDC treatment giving a well-defined red edge, its location remains far too cold compared to the empirical value. This strongly implies that one or several key ingredients are still missing here. In Paper III, we will explore several possibilities, such as the introduction of other MLT versions for convection, non-local treatment of convection, and the introduction of turbulent pressure and other parameters in (hopefully) improved implementations of our TDC approach. We are aware also that the red edge may arise from nonlinear effects. In that case, we will need more complex theoretical developments. Our long-term goal, if it can be met, is to provide a complete physical understanding of pulsational instabilities as they develop and subside in a DA white cooling across the ZZ Ceti instability strip.
We note that the temperature difference at the blue edge that we find here is entirely compatible with the instantaneous convection adaptation results of Brassard & Fontaine (1997, 1999) at that edge.
Acknowledgments
This work was supported in part by the Natural Sciences and Engineering Research Council of Canada. G.F. also acknowledges the contribution of the Canada Research Chair Program.
References
- Bergeron, P., Wesemael, F., Lamontagne, R., et al. 1995, ApJ, 449, 258 [NASA ADS] [CrossRef] [Google Scholar]
- Bohm, K. H., & Cassinelli, J. 1971, A&A, 12, 21 [NASA ADS] [Google Scholar]
- Brassard, P., & Fontaine, G. 1997, in White dwarfs, ed. J. Isern, M. Hernanz, & E. Garcia-Berro (Dordrecht: Kluwer Academic Publishers), Astrophys. Space Sci. Lib., 214, 451 [Google Scholar]
- Brassard, P., & Fontaine, G. 1999, in Stellar Structure: Theory and Test of Connective Energy Transport, ed. A. Gimenez, E. F. Guinan, & B. Montesinos (San Francisco: ASP), ASP Conf. Ser., 173, 329 [Google Scholar]
- Brickhill, A. J. 1983, MNRAS, 204, 537 [NASA ADS] [Google Scholar]
- Dolez, N., & Vauclair, G. 1981, A&A, 102, 375 [NASA ADS] [Google Scholar]
- Dupret, M.-A. 2002, Bulletin de la Société Royale des Sciences de Liège, 71, 249 [Google Scholar]
- Dupret, M.-A., Grigahcène, A., Garrido, R., et al. 2005, MNRAS, 360, 1143 [Google Scholar]
- Dupret, M.-A., Quirion, P.-O., Fontaine, G., Brassard, P., & Grigahcène, A. 2008, J. Phys. Conf. Ser., 118, 012051 [NASA ADS] [CrossRef] [Google Scholar]
- Dziembowski, W., & Koester, D. 1981, A&A, 97, 16 [NASA ADS] [Google Scholar]
- Fontaine, G., & Brassard, P. 2008, PASP, 120, 1043 [NASA ADS] [CrossRef] [Google Scholar]
- Fontaine, G., Lacombe, P., McGraw, J. T., Dearborn, D. S. P., & Gustafson, J. 1982, ApJ, 258, 651 [Google Scholar]
- Fontaine, G., Brassard, P., Wesemael, F., & Tassoul, M. 1994, ApJ, 428, L61 [NASA ADS] [CrossRef] [Google Scholar]
- Fontaine, G., Brassard, P., & Bergeron, P. 2001, PASP, 113, 409 [NASA ADS] [CrossRef] [Google Scholar]
- Gabriel, M. 1996, BASI, 24, 233 [Google Scholar]
- Gabriel, M., Scuflaire, R., Noels, A., & Boury, A. 1974, Bulletin de l’Académie Royale de Belgique, 60, 866 [Google Scholar]
- Gautschy, A., Ludwig, H.-G., & Freytag, B. 1996, A&A, 311, 493 [NASA ADS] [Google Scholar]
- Gianninas, A., Bergeron, P., & Fontaine, G. 2007, in 15th European Workshop on White Dwarfs, ed. R. Napiwotzki, & M. R. Burleigh (San Francisco: ASP), ASP Conf. Ser., 372, 577 [Google Scholar]
- Gianninas, A., Bergeron, P., Dupuis, J., & Ruiz, M. T. 2010, ApJ, 720, 581 [NASA ADS] [CrossRef] [Google Scholar]
- Gough, D. O. 1977, ApJ, 214, 196 [NASA ADS] [CrossRef] [Google Scholar]
- Grigahcène, A., Dupret, M.-A., Gabriel, M., Garrido, R., & Scuflaire, R. 2005, A&A, 434, 1055 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Grigahcène, A., Dupret, M.-A., & Garrido, R. 2007, in EAS Publ. Ser. 26, ed. C. W. Straka, Y. Lebreton, & M. J. P. F. G. Monteiro, 137 [Google Scholar]
- Quirion, P.-O., Dupret, M.-A., Fontaine, G., Brassard, P., & Grigahcène, A. 2008, in Hydrogen-Deficient Stars, ed. A. Werner, & T. Rauch (San Francisco: ASP), ASP Conf. Ser., 391, 183 [Google Scholar]
- Starrfield, S., Cox, A. N., Hodson, S., & Pesnell, W. D. 1982, in Pulsations in Classical and Cataclysmic Variable Stars, ed. J. P. Cox, & C. J. Hansen (Boulder: University of Colorado and National Bureau of Standards), 78 [Google Scholar]
- Tremblay, P.-E., Bergeron, P., & Gianninas, A. 2011, ApJ, 730, 128 [NASA ADS] [CrossRef] [Google Scholar]
- Unno, W. 1967, PASJ, 19, 140 [NASA ADS] [Google Scholar]
- Winget, D. E. 1982, Ph.D. Thesis, The University of Rochester [Google Scholar]
- Winget, D. E., van Horn, H. M., Tassoul, M., et al. 1982, ApJ, 252, L65 [NASA ADS] [CrossRef] [Google Scholar]
- Wu, Y., & Goldreich, P. 1999, ApJ, 519, 783 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Empirical instability domain in the log g − Teff diagram for the ZZ Ceti white dwarfs. The positions of pulsating stars are indicated by the filled circles, while those of the nonvariable stars are given by the open circles. The error cross in the lower left part gives the typical uncertainties on the atmospheric parameters. The dotted curves illustrate evolutionary tracks for DA white dwarfs of different masses, from 0.4 M⊙ above to 1.1 M⊙ below in steps of 0.1 M⊙. The dashed lines illustrate the empirical boundaries of the strip. |
| In the text | |
 |
Fig. 2 Structure of the envelope of our representative evolving 0.6 M⊙ DA white dwarf. The ordinate gives the fractional mass depth in logarithmic units. The small dots define “isocontours” of opacity, and some are labelled by their value of log κ. The small filled circles indicate the boundaries of the superficial convection zone. The vertical dashed lines indicate the blue and red edges obtained with our TDC treatment with ML2/α = 1.0. |
| In the text | |
 |
Fig. 3 Left panel: similar to Fig. 2, but the small dots define here isocontours of the ratio of the convective to total flux, with values Fc/F = 0.99, 0.95, 0.9, 0.8, 0.7, 0.6, 0.5, 0.4, 0.3, 0.2, 0.1, and 0.01. Right panel: similar, but for the convective turnover timescale log τc expressed in seconds. |
| In the text | |
 |
Fig. 4 Details of the driving/damping region for a typical unstable g-mode in a representative model of a ZZ Ceti star. The boundaries of the superficial convection zone are indicated by the two vertical dashed black lines. The vertical dashed red lines are, respectively, the position of the photosphere (Rosseland optical depth of 2/3) on the right, and of the base of the atmosphere (Rosseland optical depth of 100) on the left. The green curve (right ordinate axis) illustrates the profile of the Rosseland opacity, while the blue curve (left ordinate axis) shows the running (from left to right) work integral for the excited mode. |
| In the text | |
 |
Fig. 5 Comparison of the profiles of the superficial HI convection zone from two 0.6 M⊙ evolutionary sequences having the same parameters, except for the way the atmospheric layers are handled. The blue dots depict the expected zone for models using standard grey atmosphere structures, while the red dots correspond to the models with the inclusion of convective feedback on the atmospheric structure. |
| In the text | |
 |
Fig. 6 Work integral for the l = 1 g4 mode of a 0.6 M⊙ ZZ Ceti model with our TDC treatment. Top and middle panel: at Teff = 5600 K, with β = (0,0) and β = (1, −1) respectively. Bottom panel: at Teff = 8850 K, also with β = (0,0) (dashed curve) and β = (1, −1) (solid curve). |
| In the text | |
 |
Fig. 7 Periods (in seconds) of the excited l = 1 g-modes as functions of the effective temperature along the 0.6 M⊙ evolutionary sequence computed with the detailed atmosphere modeling. The size of a dot is a measure of the excitation of that particular mode. Top panel: FC. Middle panel: TDC with β = (0,0). Bottom panel: TDC with β = (1, −1). |
| In the text | |
 |
Fig. 8 Work integrals (solid curve: TDC treatment, dashed curve: FC approximation) for three 0.6 M⊙ models along the evolutionary sequence, from Teff = 11 750 K to Teff = 8000 K. The limits of the convection zone are indicated in each panel by the vertical dashed lines. |
| In the text | |
 |
Fig. 9 Entropy variation ℜ(δs) (solid curve: TDC treatment, dashed curve: FC approximation) for three 0.6 M⊙ models along the evolutionary sequence. The limits of the convection zone are indicated in each panel by the vertical dashed lines. The insert figure is a zoom of the base of the convection zone. |
| In the text | |
 |
Fig. 10 Total luminosity variation δL/L (solid curve: TDC treatment, dashed curve: FC approximation), with contributions of radiation (dotted curve) and convection (dot-dashed curve), along the evolutionary sequence. The limits of the convection zone are indicated in each panel by the vertical dashed lines. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


