| Issue |
A&A
Volume 539, March 2012
|
|
|---|---|---|
| Article Number | A120 | |
| Number of page(s) | 14 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/201118000 | |
| Published online | 05 March 2012 | |
Modelling self-similar appearance of galaxy clusters in X-rays
1 Max-Planck-Institut für extraterrestrische Physik, 85748 Garching, Germany
e-mail: hxb@mpe.mpg.de
2 Max-Planck-Institut für Astrophysik, 85748 Garching, Germany
3 Universitätssternwarte München, Scheinerstr. 1, 81679 München, Germany
Received: 1 September 2011
Accepted: 28 November 2011
Context. The largest uncertainty for cosmological studies using clusters of galaxies is introduced by our limited knowledge of the statistics of galaxy cluster structure and the related scaling relations between observables and cluster mass. A large effort has therefore been made to compile global galaxy cluster properties, in particular those obtained through X-ray observations, and to study their scaling relations. However, the scaling schemes used in the literature differ.
Aims. The present paper aims to clarify this situation by providing a thorough review of the scaling laws within the standard model of large-scale structure growth and to discuss various steps in practical approximations.
Methods. We derived the scaling laws for X-ray observables and cluster mass within the pure gravitational structure growth scenario. Using N-body simulations we tested the recent formation approximation used in earlier analytic approaches. It involves a redshift-dependent overdensity parameter. We find this approximation less precise than using a fiducial radius based on a fixed overdensity with respect to critical density.
Results. Inspired by the comparison of the predicted scaling relations with observations, we propose a first-order modification of the scaling scheme to include the observed effects of hydrodynamics in structure formation. This modification involves a cluster-mass dependent gas-mass fraction. We also discuss the observational results of the reshift evolution of the most important scaling relations and find that a redshift dependence of the gas mass to total mass relation also has to be invoked within our modification scheme.
Conclusions. We find that the current observational data are, within their uncertainties, consistent with the proposed modified scaling laws.
Key words: galaxies: clusters: general / galaxies: clusters: intracluster medium / cosmology: observations / X-rays: galaxies: clusters
© ESO, 2012
1. Introduction
Galaxy clusters form from overdense regions in the large-scale matter distribution, which have small amplitudes at early epochs and only have collapsed to objects very recently. In the standard cosmological model the large-scale matter distribution is described by a random Gaussian field characterized by a power spectrum with a smoothly changing power law index over relevant length scales. This implies that the structure evolution will feature a high degree of self-similarity in scale and time (e.g. Peebles 1980). Consequently, galaxy clusters, which form an integral part of this large-scale structure, also show an imprint of this general self-similarity. This connection between the framework of the evolution of the gravitating matter on large scales and galaxy cluster formation and their observed structure was realized in early studies, e.g. by Gunn & Gott (1972), Fillmore & Goldreich (1984), Bertschinger (1985), Hoffman & Shaham (1985) and in simulations, e.g. Frenk et al. (1985), Zureck et al. (1988), Efstathiou et al. (1988), West et al. (1987). It resulted in a comprehensive description of the structure of dark matter halos, of which galaxy clusters are the most massive representatives, in a series of papers by Navarro et al. (1995, 1996, 1997) and in the follow-up literature. In this picture of purely dark matter structure growth, dark matter halos form a nearly self-similar, two-parameter family, with the two parameters being mass and a concentration or time-of-formation parameter. This structural model of clusters describes an average behavior of the cluster population, where the different statistical realizations of mass distributions in the protoclusters produce a significant scatter in the observed structural parameters around this mean. Deviations from the equilibrium state after merger events further contribute to this scatter.
The addition of baryons to this model leads to a modification of this picture, which for clusters can be seen as a perturbation of the dark matter structure evolution. In this sense galaxy clusters mark a very interesting transition region where a first-order description involving only the large-scale structure’s gravitational physics provides a very effective guideline and the more complicated hydrodynamics, including radiative cooling, feedback from star formation, and AGN activity, constitutes a perturbative refinement. On smaller scales, for galaxies the gaseous astrophysics dominants for the appearance of the visible objects, and the observed evolution of the large-scale structure on galaxy scales becomes very nonlinear. It is therefore on galaxy cluster scales that we can still apply analytical descriptions very successfully as a useful guideline for the understanding of structure evolution. This paper builds on this property of galaxy clusters.
X-ray observations currently provide the most detailed account of galaxy cluster structure and are consequently used extensively to test the predictions of the large-scale structure growth models. However, they do not directly provide a picture of the dark matter halo distribution, but the distribution of the hot intracluster medium (ICM) that fills the entire cluster volume and radiates in X-rays. Therefore the X-ray appearance of clusters includes aspects of the hydrodynamics of how the gas reacts to the dark matter density distribution and how the ICM evolves in its thermodynamic properties (e.g. Voit 2005). One can use it as a tracer of the dark matter distribution, for example through the assumption that it is located in the dark matter potentials in hydrostatic equilibrium. We can thus expect that the X-ray appearance of galaxy clusters features some hydrodynamic modification compared to the more readily described dark matter distribution.
Because the galaxy cluster formation is so tightly connected to the large-scale structure evolution and because there is a well described self-similar structure statistics in the purely gravitational cluster formation model (Navarro et al. 1997), we can expect that there are simple, analytically derivable scaling relations for the global X-ray observables as a function of cluster mass. These relation have been studied already early by, e.g., Kaiser (1986) and Evrard & Henry (1991), and this theoretical work has been supported by simulations (e.g. Bryan & Norman 1998; Borgani 2004; Kravtsov et al. 2006; Evrard et al. 2008; Stanek et al. 2010; Short et al. 2010; Borgani & Kravtsov 2010).
After the detailed observational studies of cluster structure in X-rays by means of the advanced X-ray observatories Chandra and XMM-Newton, large sets of observational data on cluster structure and scaling relations have become available now, and the detailed testing of the theoretical predictions for the scaling laws is in full swing (e.g. Markevitch et al. 1998; Arnaud & Evrard 1999; Mohr & Evrard 1997; Finoguenov et al. 2001; Ikebe et al. 2002; Reiprich & Böhringer 2002; Ponman et al. 2003; Ettori et al. 2004; Vikhlinin et al. 2005; Pointecouteau et al. 2005; Arnaud et al. 2005; Pratt et al. 2006; Kotov & Vikhlinin 2006; Zhang et al. 2006; Maughan et al. 2006; Maughan 2007; Arnaud et al. 2007; Pratt et al. 2009; Mantz et al. 2010; Arnaud et al. 2010; Sun et al. 2011; Reichert et al. 2011). An investigation of the relevant literature shows, however, that a number different methods are used for scaling the data at different redshifts. The aim of this paper is therefore to critically review these methods and to determine the best approach based on comparison with simulations and observations.
In the above-mentioned literature, mostly analytical formulations of the scaling relations have been used, based on general considerations of structure formation. To provide the basis for higher precision in analysing the evolution of the cluster structure, the simplifications made in the analytical models should be replaced by tests and calibrations with N-body simulations. This situation can be compared to the theoretical prediction of the dark matter halo (galaxy cluster) mass function, where the analytical model by Press & Schechter (1974) has paved the way for the general formulation of the solution for the mass function, but the actual formulae now applied are the result of careful calibration with N-body simulations (e.g. Jenkins et al. 2001; Evrard et al. 2002; Warren et al. 2006; Tinker et al. 2008). Here we adopt a similar approach. We first present the theoretical framework for describing the evolution of the scaling relations in the classical form, based on the assumption of the recent formation approximation, and compare it to an alternative scheme used in the literature. We then resort to the results of N-body simulations to test the predictions of the analytical approaches and discuss which of the presently used methods in the literature is best.
In the second part of the paper we compare the theoretical scaling relations to observations, inspect the deviations in the observed scaling relations from the predictions based on dark matter structure evolution (often called “gravitational scaling relations”), and discuss these deviations in the context of the influence of hydrodynamical processes. We then explore a simple empirical modification scheme of the scaling relation using a mass-dependent depletion factor for the ICM gas to account for the hydrodynamical scaling effects and compare this new set of scaling relations to observations. In a last step we consider how this modification depends on redshift to be consistent with the observational data.
The paper is structured as follows. In Sect. 2 we derive the “gravitational scaling relations” based on dark matter structure evolution with the assumption that the baryonic matter follows the dark matter. In Sect. 3 we investigate the dependence of these scaling relations on the redshift-dependent overdensity parameter in a ΛCDM cosmology and test this model against the method using a fixed overdensity parameter in Sect. 4 using numerical simulations. In Sect. 5 we discuss the redshift dependence of the overdensity parameter, which defines the proper fiducial radius of the clusters, in the context of numerical studies of the redshift dependence of the concentration parameter of galaxy clusters. Section 6 then starts the second part of the paper where we discuss the modification of the scaling relations to include hydrodynamical effects. After comparing the description of the evolution of the scaling relations in terms of the parameters E(z) and (1 + z) in Sect. 7 and a brief comparison with some recent simulations in Sect. 8, we provide a comprehensive comparison of scaling relation results in the literature with the model predictions in Sect. 9. Finally Sect. 10 contains a discussion and conclusions.
2. Analytic gravitational self-similar model
In describing the self-similar structure of galaxy clusters in the purely gravitational picture, we will first consider the cluster formation by collapse in an Einstein-deSitter model (EdS), which is a universe with critical density and zero cosmological parameter. When we describe the self-similar evolution for other cosmologies in the second step, this model is used as the reference model. For illustration, as sketched in Fig. 1, we use a “top-hat overdensity” for the initial conditions characterized by a homogeneous overdensity within a sphere. Under realistic conditions, protoclusters will have a wide range of morphologies, but we can reasonably assume that the morphology distribution with respect to the top-hat model is similar for different masses or formation times. The statistical realizations are strictly self-similar only as far as the power spectrum of the density fluctuations, P(k), is described by a power law.
 |
Fig. 1 Schematic illustration of how the galaxy cluster structure scaling depends on the formation epoch of the cluster and on the critical density of the universe in an Einstein-de Sitter (densities are blue) and in a concordance cosmological model (green). The left panel provides a sketch of cluster collapse for a cluster with a formation redshift of z = 0, and the right panel shows a cluster forming at z = 0.5. For further explanations see the text. |
The theoretical background to the proper scaling has been worked out some time ago, with a seminal paper provided for example by Kitayama & Suto (1996). The aspects of this model, which are crucial for our discussion, are illustrated in Fig. 1, and will first be interpreted in the framework of an EdS cosmological model. The lefthand side of Fig. 1 shows a cluster that virializes at redshift zero, where the point of virialization is in general defined by the time when an ideal homogeneous sphere would have collapsed to a point. A good time of reference in the collapse process is the epoch when the overdensity stops expanding and turns around to collapse, which happens for this cluster at z = 0.78, when the mean matter density inside the protocluster is about 6.5 times the background density. This is true for all clusters with different mass that virialize at z = 0. All these clusters finish their formation at the same time – twice the turnaround time – and, in the same way, from the spherical overdensity with same amplitude to a self-similar structure with the same density shape and amplitude but just with different radial scaling. Therefore, for clusters formed at the same epoch we can defined a fiducial outer radius by a mean cluster density threshold in units of the mean or critical density of the EdS universe.
Inspecting now the evolution of a cluster that forms at higher redshift, like the cluster sketched on the righthand side of Fig. 1, we find a similar picture. The protocluster has a higher mean density when it forms compared to younger clusters, but the ratio of mean protocluster density to the background density at turnaround is the same factor of ~6.5. From the turnaround epoch, cluster collapse will be self-similar to the formation at earlier (later) epochs, just scaled to higher (lower) density. Also the background density of the universe will evolve self-similarly during cluster collapse, since in the EdS universe we have ρm = ρcrit ∝ t-2. Therefore, if we define a fiducial outer radius by the radius at which the mean density of the cluster has the same overdensity ratio, Δ, to the mean density of the universe, we can compare self-similar radii for clusters at different epochs and different sizes. For the EdS, a popular choice for the fiducial radius, rΔ is, for example the virial radius (with Δ ~ 18π2 ~ 180; e.g. Peebles 1980).
A self-similar fiducial radius of the clusters is thus defined by 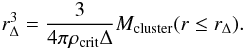 (1)The picture becomes more complicated when we change to a low-density universe (possibly also including a Λ term). For the overdense regions developing into clusters there is no change. According to the Birkhoff theorem, where a local region of the universe evolves like a universe with these local density and expansion parameters irrespective of the embedding cosmology, the cluster evolution is not concerned with the background universe1. Therefore we can keep the knowledge we have gained in the EdS reference frame, and just have to introduce another conversion that links the critical density of a general model universe with the density of a coevolving EdS universe. To make this more transparent, we illustrate this point for the case of the concordance cosmological model (CCM, with Ωm = 0.3 and ΩΛ = 0.7) which seems to provide a close approximation to the structure of the real Universe (e.g. Spergel et al. 2007; Komatsu et al. 2011).
(1)The picture becomes more complicated when we change to a low-density universe (possibly also including a Λ term). For the overdense regions developing into clusters there is no change. According to the Birkhoff theorem, where a local region of the universe evolves like a universe with these local density and expansion parameters irrespective of the embedding cosmology, the cluster evolution is not concerned with the background universe1. Therefore we can keep the knowledge we have gained in the EdS reference frame, and just have to introduce another conversion that links the critical density of a general model universe with the density of a coevolving EdS universe. To make this more transparent, we illustrate this point for the case of the concordance cosmological model (CCM, with Ωm = 0.3 and ΩΛ = 0.7) which seems to provide a close approximation to the structure of the real Universe (e.g. Spergel et al. 2007; Komatsu et al. 2011).
 |
Fig. 2 Evolution with lookback time of the mean density, ρm and critical density ρcrit in the concordance cosmological model in comparison with the matter density of a coevolving Einstein-de Sitter reference model, ρ0. The curves are from top to bottom: ρcrit, ρ0, and ρm. The two models are compared at the same times after the starting point of the coevolving calculations at 13 Gyr. |
This is again illustrated in Fig. 1 where a lookback time of 13 Gyr (corresponding to a redshift of z = 10 in the CCM) was used as a good approximation to set an EdS and CCM model to the same density initial conditions and look at their coevolution in time, which is shown in Fig. 2. For a given time, the redshifts of the two models will differ. We see that approaching present time the CCM model has a lower density than the EdS model, but a higher critical density, which is due to the accelerating expansion. Defining the ratios of the critical densities in Fig. 2 as η(time) = η(zCCM) = ρcrit(CCM)/ρm(EdS), where zCCM is the redshift in the CCM (with an index that we will drop in the following), we can adapt the overdensity parameter to the new situation by defining 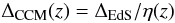 (2)and
(2)and 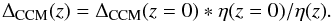 (3)Thus, as illustrated in Fig. 1, a ΔEdS = 200 in EdS for example corresponds to a ΔCCM ~ 101 for z = 0 in the CCM model since η(z = 0) ~ 2. It corresponds to Δ ~ 138 at z = 0.5 in the CCM model, however, since with increasing redshift the difference between the two models shrinks. In the following we drop the index of Δ and use it only for the CCM. This formalism has been worked out in detail for the general case by Kitayama & Suto (1996) and Eke et al. (1998), and useful approximate formulae for Δ(z) for a range of cosmological models including nonflat universes can be found e.g. in Pierpaoli et al. (2001).
(3)Thus, as illustrated in Fig. 1, a ΔEdS = 200 in EdS for example corresponds to a ΔCCM ~ 101 for z = 0 in the CCM model since η(z = 0) ~ 2. It corresponds to Δ ~ 138 at z = 0.5 in the CCM model, however, since with increasing redshift the difference between the two models shrinks. In the following we drop the index of Δ and use it only for the CCM. This formalism has been worked out in detail for the general case by Kitayama & Suto (1996) and Eke et al. (1998), and useful approximate formulae for Δ(z) for a range of cosmological models including nonflat universes can be found e.g. in Pierpaoli et al. (2001).
Gravitational scaling relations.
For the dependence of the fiducial radius on mass we have a simple geometrical scaling, while for the scaling with time we have a proportionality of the mean density of the cluster to the critical density of the universe, ρ0, taken either at the time of turnaround or at collapse (for the EdS model). The mean density as a function of redshift is: 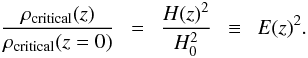 (4)The evolution of the radius at fixed overdensity (e.g. Δ = 200) is thus given by
(4)The evolution of the radius at fixed overdensity (e.g. Δ = 200) is thus given by 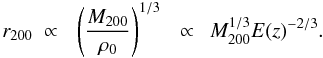 (5)As mentioned above, the radius at fixed overdensity describes a self-similar region in clusters at different epochs only in the EdS scenario. Thus if we stay true to the described modeling, and if we want to compare like with like, we have to use the radii, rΔ(z) for any comparison. Thus Eq. (5) becomes
(5)As mentioned above, the radius at fixed overdensity describes a self-similar region in clusters at different epochs only in the EdS scenario. Thus if we stay true to the described modeling, and if we want to compare like with like, we have to use the radii, rΔ(z) for any comparison. Thus Eq. (5) becomes 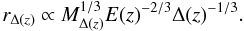 (6)We ought to note here that in this approach it has been assumed that the clusters we observe have just collapsed. This is only true in a very broad sense, since clusters are always accreting material, and we always see them in a stage where they have just completed some late accretion. This scenario is termed “recent formation approximation” in the literature. A more critical inspection of cluster formation, e.g., in N-body simulations shows, however, that the cluster structure depends in more detail on the whole recent accretion history. We should therefore be especially concerned about this approximation within the frame of the presently preferred ΛCDM cosmology. While in an Einstein-de Sitter cosmological model, structure growth continues into the future, it starts to cease in a universe with a low matter density as soon as the matter density drops below the critical density value. Thus clusters have accreted matter more slowly in the recent past than at higher redshift and will practically stop growing in the distant future (e.g. Busha et al. 2007). Thus even though we recognize the beauty and logic of the above approach, we have to critically test what deviations are introduced by these approximations by finally comparing to N-body simulations.
(6)We ought to note here that in this approach it has been assumed that the clusters we observe have just collapsed. This is only true in a very broad sense, since clusters are always accreting material, and we always see them in a stage where they have just completed some late accretion. This scenario is termed “recent formation approximation” in the literature. A more critical inspection of cluster formation, e.g., in N-body simulations shows, however, that the cluster structure depends in more detail on the whole recent accretion history. We should therefore be especially concerned about this approximation within the frame of the presently preferred ΛCDM cosmology. While in an Einstein-de Sitter cosmological model, structure growth continues into the future, it starts to cease in a universe with a low matter density as soon as the matter density drops below the critical density value. Thus clusters have accreted matter more slowly in the recent past than at higher redshift and will practically stop growing in the distant future (e.g. Busha et al. 2007). Thus even though we recognize the beauty and logic of the above approach, we have to critically test what deviations are introduced by these approximations by finally comparing to N-body simulations.
After the radius – mass relation given in Eq. (4), the next basic equation is the one linking the X-ray gas temperature with the cluster mass. The heat of the ICM comes from the conversion of potential energy during the formation of the cluster. We therefore expect the temperature to be proportional to the depth of the gravitational potential. so we find 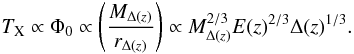 (7)In a similar way, other essential scaling relations for important X-ray properties can be constructed (see also Kaiser 1986). In Table 1 we list a set of scaling relations involving the cluster mass or the temperature as scaling parameter (the latter being a prime observable parameter) for X-ray determined properties as X-ray luminosity, LX2, gas mass, Mgas, ICM entropy, K, density, ρ, YX-parameter, with YX = Mgas × TX, and pressure, P. We have termed these relations “gravitational”, since they only include the physics of structure evolution of the dark matter, which only interacts gravitationally. The baryonic matter is assumed here to follow the dark matter and hydrodynamical effects have been neglected. Consequently we will term the relations taking these effects into account as “hydrodynamical relations”, which describe the observations better (e.g. Voit 2005).
(7)In a similar way, other essential scaling relations for important X-ray properties can be constructed (see also Kaiser 1986). In Table 1 we list a set of scaling relations involving the cluster mass or the temperature as scaling parameter (the latter being a prime observable parameter) for X-ray determined properties as X-ray luminosity, LX2, gas mass, Mgas, ICM entropy, K, density, ρ, YX-parameter, with YX = Mgas × TX, and pressure, P. We have termed these relations “gravitational”, since they only include the physics of structure evolution of the dark matter, which only interacts gravitationally. The baryonic matter is assumed here to follow the dark matter and hydrodynamical effects have been neglected. Consequently we will term the relations taking these effects into account as “hydrodynamical relations”, which describe the observations better (e.g. Voit 2005).
In these relations the redshift scaling factor E(z)2 × Δ(z) always appears in the same combination but with different powers, and thus one can introduce the abbreviation, F(z) ≡ E(z) × Δ(z)1/2. Note that all the integral observables or parameters appearing in Table 1, such as LX, Mtot, Mgas, and YX, have to be integrated out to RΔ(z) if a comparison between clusters at different redshifts are made. Thus, M in the table should actually be written as MΔ(z), but we have chosen the simplified version of the formulae in the table for easier reading.
3. Dependence on the overdensity parameter
The appearance of the parameter Δ(z) in the above equations is a nuisance, in particular as it can only be calculated by numerical integration or from approximate formulae given in the literature, e.g. Pierpaoli et al. (2001). Thus some effort has been made to check with simulations if this parameter is really necessary and if the scaling relations can simply be derived from simulations without a redshift dependent overdensity parameter. The work by Evrard et al. (2002) and (2008) has been, for example, performed in this spirit.
On the other hand, we have seen in the previous chapter that this parameter has nothing to do with cluster formation. It comes solely from the break in the self-similar evolution in the background cosmology in going from an EdS to a CCM scenario. Therefore, the overdensity parameter should not be easily abandoned without further checking.
In the following we investigate wether the unwanted parameter can be eliminated if we make assumptions about the structural parameters of the clusters. One of the most fundamental relations is the one between temperature and mass. Making the very simple assumption that the mass profile is given by an isothermal sphere, where M(r) ∝ r, we find with some arithmetics involving Eq. (1) that MΔ ∝ Δ − 1/2.
Equation (7) can be rewritten as 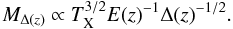 (8)With the above suggested mass dependence on Δ(z) we find that
(8)With the above suggested mass dependence on Δ(z) we find that 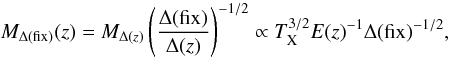 (9)where Δ(fix) is the fixed value for the Δ parameter independent of redshift. We note that, for the isothermal sphere mass profile, the redshift dependent overdensity parameter is eliminated from the equation of the mass-temperature relation.
(9)where Δ(fix) is the fixed value for the Δ parameter independent of redshift. We note that, for the isothermal sphere mass profile, the redshift dependent overdensity parameter is eliminated from the equation of the mass-temperature relation.
In the more general case of M(r) ∝ rγ, we find 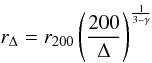 (10)and
(10)and 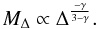 (11)The most widely used model for cluster mass profiles established by simulations and best confirmed by observations is the NFW model (Navarro et al. 1995, 1997)3. In Fig. 3 we show the logarithmic slope of this mass profile as a function of radius and the logarithmic slope for the function M(Δ(z)) for a typical value of c = 5. For the range of interest for overdensities of 100 to 2500 the slope parameter for the latter function is in the range 0.3 to 0.6, not far from the case of the isothermal model, and therefore we can expect an approximate elimination of the Δ(z) parameter. Most of the observational results have been obtained for radii corresponding to overdensities of 500 for the CCM model which corresponds roughly to an overdensity of 1000 for EdS at redshift zero and a lower value for higher redshifts. The isothermal sphere approximation best applies in the interval 500 to 1000 where the slope parameter for the M(Δ(z)) function is in the range 0.4 to 0.5. The maximum deviation introduced in the comparison between z = 0 and z = 1 clusters at these overdensities is on the order of 4%, so much smaller than the uncertainties in all observed relations and also smaller than the errors in relations derived from simulations. Thus, for the current precision of the results, we can easily neglect the Δ(z) dependence in the mass-temperature relation. This will, however, not be true for any relation such as those listed in Table 1. In this table we apply the conversion to Δ(fix) formulation in an analogous way to the mass profile above, with results shown in Col. 5. For parameters such as luminosity, entropy, and pressure, the Δ dependence does not cancel for the case of the recent formation approximation.
(11)The most widely used model for cluster mass profiles established by simulations and best confirmed by observations is the NFW model (Navarro et al. 1995, 1997)3. In Fig. 3 we show the logarithmic slope of this mass profile as a function of radius and the logarithmic slope for the function M(Δ(z)) for a typical value of c = 5. For the range of interest for overdensities of 100 to 2500 the slope parameter for the latter function is in the range 0.3 to 0.6, not far from the case of the isothermal model, and therefore we can expect an approximate elimination of the Δ(z) parameter. Most of the observational results have been obtained for radii corresponding to overdensities of 500 for the CCM model which corresponds roughly to an overdensity of 1000 for EdS at redshift zero and a lower value for higher redshifts. The isothermal sphere approximation best applies in the interval 500 to 1000 where the slope parameter for the M(Δ(z)) function is in the range 0.4 to 0.5. The maximum deviation introduced in the comparison between z = 0 and z = 1 clusters at these overdensities is on the order of 4%, so much smaller than the uncertainties in all observed relations and also smaller than the errors in relations derived from simulations. Thus, for the current precision of the results, we can easily neglect the Δ(z) dependence in the mass-temperature relation. This will, however, not be true for any relation such as those listed in Table 1. In this table we apply the conversion to Δ(fix) formulation in an analogous way to the mass profile above, with results shown in Col. 5. For parameters such as luminosity, entropy, and pressure, the Δ dependence does not cancel for the case of the recent formation approximation.
The X-ray determined temperature and the velocity dispersion of the galaxies in optical observations have generally been used as two of the most reliable proxies for the estimate of cluster masses4 (e.g. Arnaud & Evrard 1999; Carlberg et al. 1996; Biviano et al. 2006). Therefore it is interesting that it is exactly for this relation that the Δ(z) dependence can be neglected. Indeed in the observational work by Kotov & Vikhlinin (2006), for example, the evolution of the mass-temperature relation is explained without the need of Δ(z), and likewise simulations by Evrard et al. (2008) show a perfect relation for the one-dimensional dark matter velocity dispersion and cluster mass of the form 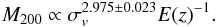 (12)From these two examples, we cannot conclude, however, that Δ(z) is an unnecessary parameter in general. This is illustrated through the scaling of density and radius with redshift. According to the relations given in Table 1 and from the illustration in Fig. 1, the density scales as ρ(z) ∝ E(z)2Δ(z). To see how this works we need a reference density within the density profile of the cluster. In a cored density profile, we can use the central density, ρ0. For the NFW density profile, described by
(12)From these two examples, we cannot conclude, however, that Δ(z) is an unnecessary parameter in general. This is illustrated through the scaling of density and radius with redshift. According to the relations given in Table 1 and from the illustration in Fig. 1, the density scales as ρ(z) ∝ E(z)2Δ(z). To see how this works we need a reference density within the density profile of the cluster. In a cored density profile, we can use the central density, ρ0. For the NFW density profile, described by 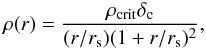 (13)where ρcrit is a reference density that is obviously proportional to Δ(z), we can, for example, use ρs = ρ(r = rs) as reference density for comparison. This density is characterized by the break in the slope in the density profile. If we compare this density point in different clusters, it should have the same overdensity in the EdS cosmology, and in the CCM it should scale according to the above relation. The radius of this point should then scale as given by Eq. (6) and expressed as a function of temperature as
(13)where ρcrit is a reference density that is obviously proportional to Δ(z), we can, for example, use ρs = ρ(r = rs) as reference density for comparison. This density is characterized by the break in the slope in the density profile. If we compare this density point in different clusters, it should have the same overdensity in the EdS cosmology, and in the CCM it should scale according to the above relation. The radius of this point should then scale as given by Eq. (6) and expressed as a function of temperature as 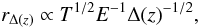 (14)in which the Δ(z) dependence can be eliminated according to the relations used in Eq. (9) to yield
(14)in which the Δ(z) dependence can be eliminated according to the relations used in Eq. (9) to yield 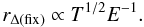 (15)This then implies that in comparing density profiles, we do not observe any dependence on the Δ(z) parameter in the radial scaling around r500 to r1000, but we should observe the influence of this parameter on the amplitude scaling of the density profiles at smaller radii according to Table 1
(15)This then implies that in comparing density profiles, we do not observe any dependence on the Δ(z) parameter in the radial scaling around r500 to r1000, but we should observe the influence of this parameter on the amplitude scaling of the density profiles at smaller radii according to Table 1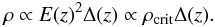 (16)From z = 0 to z = 0.5 (z = 1), the parameter Δ(z) changes by a factor of 1.36 (1.55). We test this relation in the next section.
(16)From z = 0 to z = 0.5 (z = 1), the parameter Δ(z) changes by a factor of 1.36 (1.55). We test this relation in the next section.
 |
Fig. 3 Upper panel: logarithmic slope of the NFW mass profile as a function of scaled radius. Lower panel: logarithmic slope of the NFW mass profile a function of the mean density of the cluster over the critical density. |
For any observable, ObsΔ, the influence of the Δ(z) parameter can be investigated in the following way (using a logarithmic Taylor expansion): 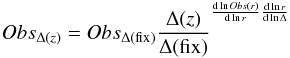 (17)where the last factor in the exponent is again approximately − 0.5. For example, for the total bolometric luminosity inside rΔ, we find for a β-model surface brightness profile with β ~ 2/3 a behavior of Lbol(r) ∝ r0.5 and consequently
(17)where the last factor in the exponent is again approximately − 0.5. For example, for the total bolometric luminosity inside rΔ, we find for a β-model surface brightness profile with β ~ 2/3 a behavior of Lbol(r) ∝ r0.5 and consequently 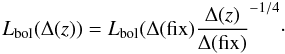 (18)For a profile that is steeper than the β-model, the exponent is even smaller and the Δ(z) dependence is even less important.
(18)For a profile that is steeper than the β-model, the exponent is even smaller and the Δ(z) dependence is even less important.
For the radial profile of entropy and pressure, which depend on the temperature profile, we used the observational results that entropy is approximately proportional to radius (e.g. Pratt 2010), which implies TX(r) ∝ r − 1/3 and the scaling for pressure listed in Table 1. For YX, which is defined as gas mass times global temperature and which is an integral quantitiy, we take the global temperature to be independent of radius, which then implies that YX has the same radial dependence as gas mass and total mass.
It is thus clear that in the frame of high-precision cosmology, we cannot just drop the variable overdensity scenario, as long as the recent formation approximation provides a precise picture. Therefore, in the next step, we critically test this approximation.
4. Testing the density scaling with redshift by N-body simulations
With the discovery that, in the temperature – mass or velocity dispersion – mass relation, the overdensity parameter can be neglected (Evrard et al. 2008), we observe a change in the literature in the use of scaling relations. In the recent literature a scaling with fixed overdensity and no overdensity evolution is preferred. Therefore in this chapter we test which of these relations is described better by simulations. We are still concerned with the pure gravitational case and therefore apply our test to the dark matter distribution. Thus the most fundamental test we can perform here is to study wether the dark matter density distribution scales as Eqs. (15) and (16), which we term the variable overdensity scaling model, or just proportional to E(z)2, to which we refer as fixed overdensity scaling model.
 |
Fig. 4 Upper panel: testing the redshift evolution of the self-similar scaling of the dark matter density distribution with the variable overdensity scaling model. The density profiles are given for redshifts of z = 0 (heavy line) and z = 0.2521, 0.5073, 0.7695, 1.0013. Dashed lines show the unscaled and solid lines the scaled profiles. Lower panel: redshift evolution of the self-similar scaling of the dark matter density distribution with the fixed overdensity scaling model. This model clearly is better than the model shown above. We also show, displaced by a factor of 0.1, the density profiles after applying the full scaling corrections described in Sect. 5. Apart from some numerical fluctuations we observe a perfect fit of the scaling corrections. |
For the test we used the simulations by Dolag et al. (2004) which are based on resimulations of clusters taken from a large cosmological simulation described in Yoshida et al. (2001) and Jekins et al. (2001). The cosmological simulation was performed with 5123 particles in a 479 h-1 kpc side length box and cosmological parameters of h = 0.7, Ωm,0 = 0.3, and ΩΛ = 0.7 and a power spectrum normalization of σ8 = 0.9. These resimulations have a mass resolution in the range 2 × 109 to 6 × 109 h-1 M⊙ and a gravitational softening parameter of 5 h-1 kpc. The simulation data set used here is for dark matter particles only to sample the purely gravitational evolution of the clusters.
In Fig. 4 we show the test of the two scaling models. In the upper panel, which shows the variable overdensity model, we note that the unscaled density increases with increasing redshift, as expected, but when this increase is corrected by dividing by the factor ρ × Δ(z), we observe an overcorrection of the profiles in the center, where we can most sensitively test the density scaling. Based on all the reasoning given above, we have to conclude that the central density of the clusters does not decrease as much with descreasing redshift as expected from the recent formation approximation. More explicitly, if mass accretion slowly ceases at low redshifts, the clusters keep a more compact shape than expected in the simplified model. In other words, clusters observed at high redshift are relatively younger and more recently formed than clusters observed at low redshift. The recent formation approximation is therefore not a good approximation in a ΛCDM model.
The lower panel of Fig. 4 shows the scaling behavior of the fixed overdensity model. It features much better because the correction made for the density increase with redshift is smaller, so the overcorrection is less. We think that there is no other fundamental reason for the better match of this model than just fortuitous smaller overcorrection. At larger radii, r > 0.15 × r500, the profiles rescaled with the variable overdensity model fit very well and actually slightly better than in the fixed overdensity case.
5. Overdensity scaling based on the evolution of the concentration parameter
Since the fixed overdensity scaling model also does not perfectly describe the evolution of the dark matter density distribution, we now seek a more perfect description for the gravitational scaling relations and take a closer look at the predictions from N-body simulations. Since a lot of effort was put into an evolutionary description of the universal dark matter halo mass profiles, the answer to our problem should be sought in this approach.
In the literature the change in the shape of the dark matter halo profiles with redshift is described in the framework of the NFW model (see. Eq. (13)) by means of the concentration parameter, which depends on the halo mass and the redshift of formation. The concentration is defined as 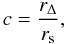 (19)where rΔ is the fiducial cluster radius, which can be taken as rΔ(z), r200, or rm200, with r200 being the radius for a mean overdensity of 200 above critical density and rm200 refers to mean background density (see e.g. Duffy et al. 2008). The redshift evolution of this parameter has been studied by Navarro et al. (1997), Bullock et al. (2001), Eke et al. (2001), Dolag et al. (2004), Duffy et al. (2008), and Gao et al. (2008). We use here the results of Dolag et al. (2004), which come from the same simulations as used for our testing. The result they find is approximated well by
(19)where rΔ is the fiducial cluster radius, which can be taken as rΔ(z), r200, or rm200, with r200 being the radius for a mean overdensity of 200 above critical density and rm200 refers to mean background density (see e.g. Duffy et al. 2008). The redshift evolution of this parameter has been studied by Navarro et al. (1997), Bullock et al. (2001), Eke et al. (2001), Dolag et al. (2004), Duffy et al. (2008), and Gao et al. (2008). We use here the results of Dolag et al. (2004), which come from the same simulations as used for our testing. The result they find is approximated well by 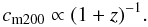 (20)The same result is derived by Duffy et al. (2008, Table 1). Gao et al. (2008) do not give the redshift evolution explicitly, but get similar results with slightly flatter evolution. The earlier work finds qualitatively similar results with small discrepancies as discussed in Dolag et al. (2004). For high-precision cosmology, the current exercise should be based on simulations with higher statistics to be obtained in the future. But the methodical approach will still be the same as outlined here.
(20)The same result is derived by Duffy et al. (2008, Table 1). Gao et al. (2008) do not give the redshift evolution explicitly, but get similar results with slightly flatter evolution. The earlier work finds qualitatively similar results with small discrepancies as discussed in Dolag et al. (2004). For high-precision cosmology, the current exercise should be based on simulations with higher statistics to be obtained in the future. But the methodical approach will still be the same as outlined here.
We use the findings of Dolag et al. for the concentration parameter to impose a second-order correction on the above relations. We apply the corrections to the relations with fixed overdensity, since they have a simpler form and they are closer to the simulation results. Thus we have to transform the behavior of cm200 to fixed overdensity scaling with respect to critical density, 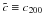 ,
, 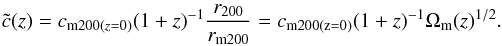 (21)In addition we have to correct the radius scaling by the additional factor. As clusters get less compact with increasing redshift, their radii will be larger than expected and have to be scaled it down accordingly by
(21)In addition we have to correct the radius scaling by the additional factor. As clusters get less compact with increasing redshift, their radii will be larger than expected and have to be scaled it down accordingly by 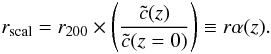 (22)To observe mass conservation, the change in radial scaling has to be compensated for by a corresponding scaling of the density normalization. For the NFW profile the density normalization depends on the concentration parameter through the proportionality
(22)To observe mass conservation, the change in radial scaling has to be compensated for by a corresponding scaling of the density normalization. For the NFW profile the density normalization depends on the concentration parameter through the proportionality ![\begin{equation} \rho_{c\star} \propto {c^3 \over \left[{\rm ln} (1+c) - c/(1+c)\right]}\cdot \end{equation}](/articles/aa/full_html/2012/03/aa18000-11/aa18000-11-eq168.png) (23)The amplitude of the density profile will be less than expected with increasing redshift, as clusters get less compact, and we have to scale the density up accordingly by
(23)The amplitude of the density profile will be less than expected with increasing redshift, as clusters get less compact, and we have to scale the density up accordingly by 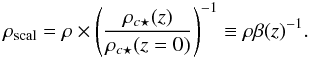 (24)The correction terms α(z) and β(z) in Eqs. (22) and (24) are shown in Fig. 5 (together with the correction terms that apply for the recent formation approximation approach). The magnitude of the correction is 35% for α and 17% for β at z = 1. The values are derived for the reference cosmology model and a mass-independent concentration parameter c(z = 0) = 5. When these corrections are applied to the density profiles from different epochs, a perfect scaling within a few percent numerical uncertainty is obtained, as shown in the lowel panel of Fig. 4.
(24)The correction terms α(z) and β(z) in Eqs. (22) and (24) are shown in Fig. 5 (together with the correction terms that apply for the recent formation approximation approach). The magnitude of the correction is 35% for α and 17% for β at z = 1. The values are derived for the reference cosmology model and a mass-independent concentration parameter c(z = 0) = 5. When these corrections are applied to the density profiles from different epochs, a perfect scaling within a few percent numerical uncertainty is obtained, as shown in the lowel panel of Fig. 4.
 |
Fig. 5 Correction factors α(z) and β(z) as a function of redshift for the fixed overdensity model (thick lines) and recent formation approximation (rfa) model (thin lines and parameters labeled with index rfa). |
The correction has a significant effect on the central density, while the effect is minor at larger radii (r ≥ 0.2r500) as can be seen implicitly from the lower panel of Fig. 4, because the corrections α(z) and β(z) in Eqs. (22) and (24) have a compensating effect. In general the compensating effect for the radial profile of an observable can be evaluated (analogous to Eq. (9)): 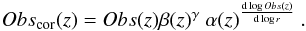 (25)We expect this correction to be small (a few percent). Thus we do not elaborate on this further here, because it will be more useful once we have a better description of the change of the dark matter halo profiles from simulations with better statistics.
(25)We expect this correction to be small (a few percent). Thus we do not elaborate on this further here, because it will be more useful once we have a better description of the change of the dark matter halo profiles from simulations with better statistics.
6. Modifications due to hydrodynamics
While the first part of this paper is concerned with the more theoretical aspect, of which model provides the best approach to describe the scaling relations in the purely gravitational picture of cosmic structure growth, the second part now explores how the actually observed X-ray scaling relations of galaxy clusters can be described within a scenario, including hydrodynamical effects in an empirical way. Only the most basic relations like those of ICM temperature or galaxy velocity dispersion with mass are approximately consistent with the pure gravitational scaling relation model given in Table 1. Most other relations involving ICM properties show deviations. The most famous of these deviations is the Lbol − Tx relation that shows an exponent in many observational studies closer to 2.9 than to the expected value of 2 (e.g. Edge & Stewart 1991; Ebeling et al. 1996; Markevitch 1998; Arnaud & Evrard 1999; Ikebe et al. 2001; Pratt et al. 2009). A clue to an explanation from the observational side comes from the fact that the X-ray surface brightness, the line-of-sight-integrated emission measure profile, and the density profile (all very closely related) can all be brought to match surprisingly close at radii r ≥ 0.15r500 with an appropriate amplitude scaling (Arnaud et al. 2002; Croston et al. 2008). At smaller radii, ICM cooling and central AGN feedback are known to modify the density profiles (e.g. Fabian 1994; Voit 2005). The fact that the shape of the ICM density profile matches so well, while the scaling of the normalization is different from the scaling in Table 1 implies that the ICM gas mass fraction is not constant as a function of cluster mass. An early discussion of the change in the gas mass fraction with cluster mass can be found in David et al. (1990).
Specifically, Arnaud et al. (2002) find a line-of-sight emission measure scaling of the form 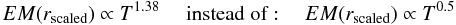 (26)where the second relation stands for the purely gravitational scaling. Since the integrated emission measure is proportional to the squared density and the line-of-sight integration path ( ∝ rΔ ∝ T0.5), the amplitude scaling of the ICM density is given by ∝ T0.44. Croston et al. (2008) find for the matching of the deprojected density profiles, a best fitting scaling of
(26)where the second relation stands for the purely gravitational scaling. Since the integrated emission measure is proportional to the squared density and the line-of-sight integration path ( ∝ rΔ ∝ T0.5), the amplitude scaling of the ICM density is given by ∝ T0.44. Croston et al. (2008) find for the matching of the deprojected density profiles, a best fitting scaling of 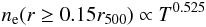 (27)for the clusters of the REXCESS sample that span a temperature range of 2 to 10 keV. Pratt et al. (2009) directly present the gas mass fractions of the REXCESS clusters at r500 and adding the results of Vikhlinin et al. (2006), Arnaud et al. (2007) and Sun et al. (2009); they find a best-fitting description of
(27)for the clusters of the REXCESS sample that span a temperature range of 2 to 10 keV. Pratt et al. (2009) directly present the gas mass fractions of the REXCESS clusters at r500 and adding the results of Vikhlinin et al. (2006), Arnaud et al. (2007) and Sun et al. (2009); they find a best-fitting description of 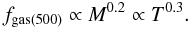 (28)The variation in the temperature exponent seen in these results is partly an effect of sample variance, but is also caused by the ratio of the gas mass fraction and entropy of clusters of different mass being a function of radius (see e.g. Nagai et al. 2007; Pratt et al. 2010).
(28)The variation in the temperature exponent seen in these results is partly an effect of sample variance, but is also caused by the ratio of the gas mass fraction and entropy of clusters of different mass being a function of radius (see e.g. Nagai et al. 2007; Pratt et al. 2010).
Neglecting this radial dependence as a higher order effect, we explore further the consequences of the mass dependent gas mass fraction on the scaling relations by adopting a mean value of 0.45 for the temperature exponent of the gas fraction relation. Thus we find a variation of fgas with cluster mass of the form: 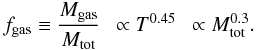 (29)The decreasing gas mass fraction with decreasing system mass is explained within the structure formation scenario by an increasing specific energy introduced into the ICM by star formation and AGN feedback (e.g. Voit 2005). In more theoretical approaches, the reasoning for the modification of structure is derived from entropy arguments (e.g. Ponman et al. 1999; Bryan & Voit 2000; Voit 2005; Ostriker et al. 2005). For the present derivation given here we prefer the more direct observational approach based on the gas mass fraction.
(29)The decreasing gas mass fraction with decreasing system mass is explained within the structure formation scenario by an increasing specific energy introduced into the ICM by star formation and AGN feedback (e.g. Voit 2005). In more theoretical approaches, the reasoning for the modification of structure is derived from entropy arguments (e.g. Ponman et al. 1999; Bryan & Voit 2000; Voit 2005; Ostriker et al. 2005). For the present derivation given here we prefer the more direct observational approach based on the gas mass fraction.
With this observationally implied modification to the scaling relations, including the fgas variation with cluster mass, we can obtain a new set of scaling relations that are approximately consistent with the observations. These relations are given in Table 2 (where Col. 2 gives the redshift evolution assuming that the fgas − TX relation does not evolve with redshift).
Hydrodynamic scaling relations.
By compiling all the major scaling relation data from the literature and adding new data for high-redshift clusters from the XDCP project (Böhringer et al. 2005; Fassbender 2008) and from other newly detected distant clusters in Reichert et al. (2011), we found the first significant constraints on the reshift evolution of some major ICM scaling relations. For the mass – temperature relation a result of 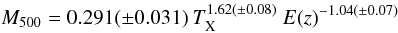 (30)is found with mass given in units of 1014 M⊙ and TX in units of keV. The relation shows a redshift evolution that is close to the one expected in the gravitational scenario (expectation E(z)-1). For the relation of bolometric luminosity and temperature (involving two independent observational parameters) they find
(30)is found with mass given in units of 1014 M⊙ and TX in units of keV. The relation shows a redshift evolution that is close to the one expected in the gravitational scenario (expectation E(z)-1). For the relation of bolometric luminosity and temperature (involving two independent observational parameters) they find 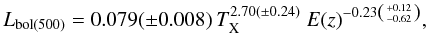 (31)and a mass luminosity relation of
(31)and a mass luminosity relation of 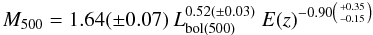 (32)where Lbol is given in units of 1044 erg s-1. The last relation can in principle also be derived from the first two, and these results are consistent with each other within the error limits.
(32)where Lbol is given in units of 1044 erg s-1. The last relation can in principle also be derived from the first two, and these results are consistent with each other within the error limits.
Therefore, we focus on the implications of the luminosity – temperature relation. To satisfy the redshift evolution of this relation by means of a redshift-dependent gas mass fraction, we have to imply a relation of the form: 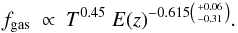 (33)This relation can now be folded into the relations of other properties according to their dependence on fgas as listed in Table 2, to find their “empirically” predicted redshift dependence which is listed in Col. 4 of the table.
(33)This relation can now be folded into the relations of other properties according to their dependence on fgas as listed in Table 2, to find their “empirically” predicted redshift dependence which is listed in Col. 4 of the table.
7. Expressions as powers of (1 + z)
In past studies, trends in cluster evolution and the evolution of scaling relations has most often been modeled with a redshift dependence of powers 1 + z in the absence of any better knowledge. For comparison with these results we studied how well the parameter E(z) can be expressed by powers of 1 + z. For the redshift range from zero to a given upper limit, we have determined which power of 1 + z provides the best approximation with the smallest maximum deviation from the function. Table 3 provides the results for upper redshift limits of z = 0.5, 0.7, 1.0, and 1.5. These approximations and the functions are shown in Fig. 6. The figure immediately reveals that the approximations are not very good, but for limited redshift ranges (as are typical of the present surveys) the deviations are still much smaller than any typical observational uncertainties, and these simplified relations may therefore still be helpful at the present stage.
Thus for the relation of bolometric luminosity and temperature (in the fixed overdensity approximation) we find, for example, 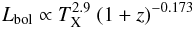 (34)for the best fit in the redshift range z = 0−1.
(34)for the best fit in the redshift range z = 0−1.
8. Comparison to some recent simulations
In the Millenium gas simulations (Springel et al. 2005; Hartly et al. 2008), the scaling relations were studied by Stanek et al. (2010). For the zero redshift simulations, they find slopes of the scaling relations with masses of 0.559(±0.002) and 0.576(±0.002) for the mean temperature and spectroscopic-like temperature compared to an expectation value of 2/3. For Lbol and Yx they get 1.825(±0.003) and 1.868(±0.006) compared to 2.018 and 1.9667, respectively, as given in Table 2. The results are in fair agreement with the major difference that the TX – mass relation is less steep in the simulations, which is then also reflected in a slightly shallower slope of all other relations.
For the evolution of the parameters they find that fICM, Lbol, and YX evolve with E(z) with exponents of −0.44, 1.39, and 0.352 compared to −0.315, 1.39, and 0.33. Except for Lbol there is again a fair agreement with a slightly larger negative evolution of the gas mass fraction in the simulations than is implied by the results by Reichert et al. (2011).
Using the same basic simulations, Short et al. (2010) investigated the dependence of the scaling relations on the feedback physics used in the simulations. As already discussed in detail in Reichert et al. (2011), there is fair agreement of the observations with the preheating models which involve an early input of energy and elevation of entropy of the ICM. In contrast, late feedback models with most of the energy input at redshifts below 1 are clearly inconsistent with the data.
Approximations of E(z) in powers of (1 + z).
9. Comparison to observations
In this section we compare the model predictions to recent observations. We use a representative set of more recently published results and do not aim for a complete coverage of the literature. In particular, the earlier results either suffer from low quality statistics or they rely on lower quality observational data. Many more results for scaling relations and their evolution with redshift are expected to appear in the near future with a more comprehensive exploitation of the XMM-Newton and Chandra archives and the completion of several large-survey projects, which will be used for a more critical test and refinement of the model.
One of the caveats to keep in mind when interpreting the following results is that some of the cluster surveys in the literature are affected by selection-bias effects. These effects arise, e.g., from the use of flux-limited surveys, which tend to sample primarily the most luminous clusters in any distribution. We discussed and modeled this effect for these types of data sets in the paper by Reichert et al. (2011). A number of the data sets come from the analysis of galaxy clusters in the data archives; also these clusters are usually studied as a result of discovery in flux-limited surveys. Only in a few cases, such as Ikebe et al. (2001) as an earlier paper and Vikhlinin et al. (2009), have efforts been made to correct for the biasing effects. In most cases, the bias effects on the slope of the relation, which is what concerns us most here, are weaker than the statistical uncertainties, and so we do not consider the selection bias effects in the following discussion5.
9.1. Mass–temperature relation
 |
Fig. 6 Evolution parameter, E(z)2, as a function of redshift. The dashed lines show the power law functions of (1 + z) with exponents of 1.26, 1.36, 1.5, 1.68 corresponding to the best approximations given in Table 3. |
Observationally determined slopes of the M − T relation.
Observationally determined slopes of the L − T relation.
We begin with the comparison for the mass temperature relation. Table 4 provides a large, representative, but not complete list of the literature results. The results by Reichert et al. (2011) are based on a compilation of data from 14 data sets taken from the literature and supplemented by recent published results on individual distant galaxy clusters. It therefore gives a summary or average of the largest and most recent observational data samples. Most of the values for the correlation slope range from 1.5 to 1.7 for an expected value of 1.5. The observed relation is thus slightly steeper, but it is closer to the expectation for samples without low-mass (low-temperature) systems. For samples with a lower temperature limit above 3 keV the slopes are shallower and closer to the self-similar scaling.
9.2. X-ray luminosity–temperature relation
The luminosity–temperature relation is the relation with the two observables derived almost independently. The luminosity is obtained from imaging data with tiny corrections from spectral data, while the temperatures are derived from the interpretation of X-ray spectra. In Table 5 we summarize the observational results for the luminosity–temperature relation for both luminosities derived for certain energy bands and bolometric luminosities, Lbol.
The band-limited luminosity scaling relations have observed slopes in the range 2–2.5 with an expected value of about 2.4, while most of the Lbol–T relation slopes show observed values of 2.6 − 3.7 with an expected value of about 2.9. The results are thus in good agreement with the predictions of the modified scaling relations within the observational uncertainties.
9.3. Luminosity – mass relation
The X-ray luminosity – mass relation is one of the most important relations for cosmological modeling of X-ray cluster surveys. Published results are listed in Table 6. Again we find good agreement for the observed slopes of 1.4–1.7 (for Lband) and 1.6–2 (for Lbol) with the predictions for the slopes of 1.6 and 1.93, respectively.
Observationally determined slopes of the L − M relation.
9.4. Entropy – temperature relation
Table 7 lists the results for the entropy temperature relation from the observational analysis of Pratt et al. (2010). We note that the slope of the relation depends on the scaled radius at which the measurement is taken. In contrast to the observational parameters above, which are integrated values like luminosity, this is the local entropy value at a given radius. The change in slope comes from the fact that the gas density reduction in low-mass systems is not completely self-similar with radius, somewhat contrary to what is suggested, e.g., by the very tight scaling of the density profiles in Fig. 2 of Croston et al. (2008).
The gravitational scaling model would predict the relation K ∝ T, while our modified scaling relation predicts K ∝ T0.7. The latter prediction is approximately met at intermediate radii. For larger radii, the results seem to approach the gravitational scaling relations.
Observationally determined slopes of the Entropy – T and entropy – mass relation.
9.5. Gas mass – temperature relation
Some results for the gas mass – temperature relation are listed in Table 8. The observed range of values for the slope of 1.88–2.22 corresponds well to the predicted value of 1.95.
Observationally determined slopes of the Mgas − T relation.
9.6. Other relations
Observational results for some other interesting relations are presented in Table 9. The YX parameter is a quantity motivated by cluster observations in the Sunyaev-Zeldovich effect (SZE). Since the SZE signal is proportional to the intracluster plasma temperature and the total number of electrons, the YX-parameter is defined as YX = T × Mgas. This parameter has been promoted as a very good mass proxy for galaxy clusters (Motl et al. 2005; Kravtsov et al. 2006).
Values for the slope of the Lbol − YX relation of 0.65–1.1 and for the Lband − YX relation of 0.8–1.14 agree well with the predictions (combining the LX − T and YX − T relations) of values of 0.98 and 0.81, respectively. The M500 − YX relation with slope values of 0.57–0.62 is also not far off the precdited value of 0.51.
Finally the Mtot − Mgas relation with a predicted slope of 0.76 is shallower than the listed result of 0.9 by Zhang et al. (2008) and also somewhat shallower than the slope inferred from Fig. 9 in Vikhlinin et al. (2009) which roughly corresponds to a slope of 0.83 in the mass range 1014 to 1015 M⊙. But our prediction is supported very well by (and partly comes from) the results of Pratt et al. (2009), which are based on a large and representative sample of galaxy clusters with high-quality XMM-Newton data.
Observationally determined slopes for various relations.
9.7. Evolution with redshift
Vikhlinin et al. (2009) quote a result for the evolution of the LX2 − M relation of 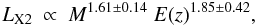 (35)which has to be compared to Eq. (32) based on the result of Reichert et al. (2011). Inverting relation (32) and converting from Lbol to LX2 we find LX2 ∝ LbolT-0.5 ∝ T-0.5M1.92E(z)1.73. Substituting Eq. (7) without the Δ-factor we get
(35)which has to be compared to Eq. (32) based on the result of Reichert et al. (2011). Inverting relation (32) and converting from Lbol to LX2 we find LX2 ∝ LbolT-0.5 ∝ T-0.5M1.92E(z)1.73. Substituting Eq. (7) without the Δ-factor we get 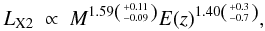 (36)showing agreement between the two results within the uncertainties.
(36)showing agreement between the two results within the uncertainties.
More effort has been put into studing the evolution of the luminosity – temperature relation. Here we find a different picture, such that most previous works find a positive evolution. In the earlier literature, the evolution has most often been parameterized in the form 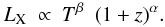 (37)Taking this functional form and the correspondence of E(z) ~ (1 + z)0.75 from Table 3 for the redshift range z = 0 − 1 we find a proportionality of the evolution of the LX − T relation of ∝
(37)Taking this functional form and the correspondence of E(z) ~ (1 + z)0.75 from Table 3 for the redshift range z = 0 − 1 we find a proportionality of the evolution of the LX − T relation of ∝ 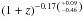 for the results of Reichert et al. (2011). Earlier works find α = 1.5 ± 0.3 in Vikhlinin et al. (2002) and Lumb et al. (2004), and α = 1.8 ± 0.3 in Kotov & Vikhlinin (2005). Maughan et al. (2006) find a value of α = 1.3 ± 0.2 when they combine their WARPS cluster sample with that of Vikhlinin et al. (2002) and a value of α = 0.8 ± 0.4 for the WARPS sample alone. Ettori et al. (2004) find the least positive evolution with values for the exponent of (1 + z) in the range 0.04 to 0.98 when using Markevitch (1998) and Arnaud & Evrard (1999) as local reference, but partly negative values in the range –0.48 to +0.54 when combining their results with those of Novicki et al. (2002). Common to all these studies is their use of the data of Markevitch (1998) and Arnaud & Evrard (1999) for the local (z ~ 0) reference. The normalization of the LX − T relation in the last two works is lower by a factor of very roughly 1.5 than that of Pratt et al. (2009), which has been used in Reichert et al. as the most important local reference. Therefore, the most obvious reason for these earlier works finding a positive evolution in contrast to the slightly negative evolution found by Reichert et al. (2011) is the different local reference in addition to the small sample sizes and selection bias effects.
for the results of Reichert et al. (2011). Earlier works find α = 1.5 ± 0.3 in Vikhlinin et al. (2002) and Lumb et al. (2004), and α = 1.8 ± 0.3 in Kotov & Vikhlinin (2005). Maughan et al. (2006) find a value of α = 1.3 ± 0.2 when they combine their WARPS cluster sample with that of Vikhlinin et al. (2002) and a value of α = 0.8 ± 0.4 for the WARPS sample alone. Ettori et al. (2004) find the least positive evolution with values for the exponent of (1 + z) in the range 0.04 to 0.98 when using Markevitch (1998) and Arnaud & Evrard (1999) as local reference, but partly negative values in the range –0.48 to +0.54 when combining their results with those of Novicki et al. (2002). Common to all these studies is their use of the data of Markevitch (1998) and Arnaud & Evrard (1999) for the local (z ~ 0) reference. The normalization of the LX − T relation in the last two works is lower by a factor of very roughly 1.5 than that of Pratt et al. (2009), which has been used in Reichert et al. as the most important local reference. Therefore, the most obvious reason for these earlier works finding a positive evolution in contrast to the slightly negative evolution found by Reichert et al. (2011) is the different local reference in addition to the small sample sizes and selection bias effects.
Pacaud et al. (2007) also quote an LX − T evolution best fit by α = 1.5 ± 0.4, but the fit is poor and the data are different from this approximation at z ≥ 0.7 as can be seen in their Fig. 4. In a recent paper Maughan et al. (2012) also find a positive evolution with substantial deviations from the overall trend at intermediate redshifts. Unlike these other results, O’Hara et al. (2007) find a negative evolution with a value of α = −0.25 ± 0.56.
In summary, it is clear that the sparsity and inhomogeneity of the data used in the past to study the redshift evolution of the scaling relations lead to inconclusive results and we are just beginning to see some trends now. The uncertainties of the parameterized evolution of the relations are still very large, and in the case of the LX − T relation, for example, the results are still consistent with no evolution in the LX − T relation.
10. Discussion and conclusion
By studying the evolution of the dark matter mass density profiles of simulated galaxy clusters in detail, we have shown that the older model of self-similar scaling relations based on the recent formation approximation, which uses a scenario where the fiducial overdensity radius, rΔ(z), is taken to be redshift-dependent, is not accurate. A scaling with a fixed overdensity provides a better and currently sufficiently precise description of self-similar evolution. For a precise analysis of future cosmological surveys of the galaxy cluster population, we should improve this description even further. We envision to do this with larger N-body/hydrodynamical simulations, which are performed at present and therefore give no detailed recipes for the scaling corrections in this paper. The corrections as shown in Fig. 5 depend on the cosmological model used, and therefore these corrections will have to be worked separately for each model case explored.
Studying the different types of scaling relations involving parameters derived from X-rays, we can distinguish two types of scaling behavior: the mass - temperature relation mostly depends on the scaling of the dark matter potentials and is therefore very close to the gravitational scaling prediction. Most other relations involving gas density or gas mass are affected by the inconstancy of the gas mass to total mass ratio. With the introduction of modified scaling relations to take this hydrodynamical effects into account, we can describe the currently available data sets within the given uncertainties.
Looking at the evolution of the scaling relations with redshift, we find an analogous situation: the M − T relation corresponds to the prediction of the gravitational self-similar scenario within the current uncertainties. All other relations involving parameters that depend on the gas density show deviations, which implies that the gas mass fraction is not constant for any given cluster mass with redshift. This is just the consequence of the following effects. At higher redshifts, clusters of given mass are more compact, and the ICM has to be squeezed into a deeper and narrower potential. Since in preheating models, which seem to explain the data best, the gas starts out with an elevated entropy before cluster formation is complete, the gas is less tightly squeezed into the earlier, narrower potentials than into the later wider potentials.
Our modified scaling relation model does not describe all observational effects. As shown in Pratt et al. (2010), the entropy scaling depends on the radius at which the entropy is measured. These results imply that the ICM depletion is greater in the center of groups and clusters than in the outer parts. More data are required that extend out to large cluster radii (to r500 and beyond) to substantiate this result.
The redshift evolution of the L − T scaling relation, which is predicted to be ∝ E(z) in the simple self-similar scenario, is now found in recent studies to be much less positive or even negative (e.g. O’Hara et al. 2007; Reichert et al. 2011). This has the important consequence that one will find fewer high-redshift galaxy clusters in future X-ray and SZE surveys than predicted based on the simple scaling models (Reichert et al. 2011). More important, a precise measurement of this evolution effect is crucial for using the future X-ray survey data on galaxy clusters for the test of cosmological models.
As shown by the comparison of the evolution of the scaling relations compiled by Reichert et al. (2011) and the simulations by Short et al. (2010), studying the evolution of the scaling relations also provides important insight into the astrophysics of the ICM. Currently the observational data strongly favor a model with early preheating of the ICM.
In the coming years both the observational data as well as the simulation results will experience further strong improvements. Therefore we see the importance of this paper more in elucidating how the scaling relations should be analyzed and applied, rather than already providing the best parameterization of the results.
For the scaling of the X-ray luminosity in a specific band, LX, we assume that the energy band is chosen such that the X-ray emissivity is independent of the ICM temperature at temperatures above 2 keV. This is, for example, almost fulfilled for the 0.5 to 2 keV energy band used in most imaging analysis of galaxy clusters, where the change in emissivity in the temperature range from 2 to 10 keV is less than 6% for given emission measure.
In the recent literature, notably in Kravtsov et al. (2006), the parameter, YX, is often promoted as the best mass proxy.
Acknowledgments
The paper is based on observations obtained with XMM-Newton, an ESA science mission with instruments and contributions directly funded by ESA Member States and the USA (NASA). The XMM-Newton project is supported by the Bundesministerium für Bildung und Forschung, Deutsches Zentrum für Luft und Raumfahrt (BMBF/DLR), the Max-Planck Society, and the Haidenhain-Stiftung. H.B. acknowledges support from the DfG Transregio Program TR33 and the Munich Excellence Cluster “Structure and Evolution of the Universe”. K.D. acknowledges support by the DfG Priority Programme 1177 and additional support by the DfG Cluster of Excellence “Structure and Evolution of the Universe”. We thank the anonymous referee for helpful comments and Andrey Kravtsov for discussions.
References
- Allen, S. W., & Fabian, A. C. 1998, MNRAS, 297, L57 [NASA ADS] [CrossRef] [Google Scholar]
- Arnaud, M., & Evrard, A. E. 1999, MNRAS. 305, 631 [Google Scholar]
- Arnaud, M., Aghanim, N., & Neumann, D. M. 2002, A&A, 389, 1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Arnaud, M., Pointecouteau, E., & Pratt, G. W. 2005, A&A, 441, 893 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Arnaud, M., Pointecouteau, E., & Pratt, G. W. 2007, A&A, 474, L40 [Google Scholar]
- Arnaud, M., Pratt, G. W., Piffaretti, R., et al. 2010, A&A, 517, A92 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bertschinger, E. 1985, ApJS, 58, 39 [NASA ADS] [CrossRef] [Google Scholar]
- Biviano, A., Murante, G., Borgani, S., et al., A&A, 456, 23 [Google Scholar]
- Böhringer, H., Mullis, C., Rosati, P., et al. 2005, The Messenger, 120, 33 [NASA ADS] [Google Scholar]
- Borgani, S., & Kravtsov, A. 2009 [arXiv:0906.4370] [Google Scholar]
- Borgani, S., Murante, G., & Springel, V. 2004, MNRAS, 348, 1078 [NASA ADS] [CrossRef] [Google Scholar]
- Branchesi, M., Gioia, I. M., Fanti, C., & Fanti, R. 2007, A&A, 472, 739 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bryan, G. L., & Norman, M. L. 1998, ApJ, 495, 80 [NASA ADS] [CrossRef] [Google Scholar]
- Bryan, G. L., & Voit, G. M. 2001, ApJ, 556, 590 [NASA ADS] [CrossRef] [Google Scholar]
- Bullock, J. S., Kolatt, T. S., Sigad, Y., et al. 2001, MNRAS, 321, 559 [Google Scholar]
- Carlberg, R. G., Yee, H. K. C., Ellingson, E., et al. 1996, ApJ, 462, 32 [Google Scholar]
- Croston, J. H., Pratt, G. W., Böhringer, H., et al. 2008, A&A, 487, 431 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- David, L. P., Arnaud, K. A., Forman, W., & Jones, C. 1990, ApJ, 356, 32 [NASA ADS] [CrossRef] [Google Scholar]
- Dolag, K., Bartelmann, M., Perrotta, F., et al. 2004, A&A, 416, 853 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Duffy, A. R., Schaye, J., Kay, S. T., & Dalla Vecchia, C. 2008, MNRAS, 390, 64 [Google Scholar]
- Ebeling, H., Voges, W., Böhringer, H., et al. 1996, MNRAS, 281, 799 [NASA ADS] [CrossRef] [Google Scholar]
- Edge, A. C., & Stewart, G. C. 1991, MNRAS, 252, 414 [NASA ADS] [CrossRef] [Google Scholar]
- Eke, V. R., Cole, S., Frenk, C. S., & Henry, J. P. 1998, MNRAS, 298, 1145 [NASA ADS] [CrossRef] [Google Scholar]
- Ettori, S., Tozzi, P., Borgani, S., & Rosati, P. 2004, A&A, 417, 13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Evrard, A. E., & Henry, J. P. 1991, ApJ, 383, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Evrard, A. E., MacFarland, T. J., Couchman, H. M. P., et al. 2002, ApJ, 573, 7 [NASA ADS] [CrossRef] [Google Scholar]
- Evrard, A. E., Bialek, J., Busha, M., et al. 2008, ApJ, 672, 122 [NASA ADS] [CrossRef] [Google Scholar]
- Fabian, A. C., Crawford, C. S., Edge, A. C., & Mushotzky, R. F. 1994, MNRAS, 267, 779 [NASA ADS] [CrossRef] [Google Scholar]
- Fassbender, R. 2008, Ph.D. Thesis Ludwig-Maximilians-Universitaet Muenchen [arXiv:0806.0861] [Google Scholar]
- Fillmore, J. A., & Goldreich, P. 1984, ApJ, 281, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Finoguenov, A., Reiprich, T. H., & Böhringer, H. 2001, A&A, 368, 749 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gao, L., Navarro, J. F., Cole, S., et al. 2008, MNRAS, 387, 536 [NASA ADS] [CrossRef] [Google Scholar]
- Gunn, J., & Gott, J. R. 1972, ApJ, 176, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Hartley, W. G., Gazzola, L., Pearce, F. R., Kay, S. T., & Thomas, P. A. 2008, MNRAS, 386 2015 [Google Scholar]
- Hicks, A. K., Ellingson, E., Bautz, M., et al., ApJ, 680, 1022 [Google Scholar]
- Hoffman, Y., & Shaham, J. 1985, ApJ, 297, 16 [NASA ADS] [CrossRef] [Google Scholar]
- Ikebe, Y., Reiprich, T. H., Böhringer, H., Tanaka, Y., & Kitayama, T. 2002, A&A, 383, 773 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jenkins, A., Frenk, C. S., & White, S. D. M. 2001, MNRAS, 321, 372 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Kaiser, N. 1986, MNRAS, 222, 323 [NASA ADS] [CrossRef] [Google Scholar]
- Kitayama, T., & Suto, Y. 1996, ApJ, 469, 480 [CrossRef] [Google Scholar]
- Komatsu, E., Smith, K. M., Dunkley, J., et al. 2011, ApJS, 192, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Kotov, O., & Vikhlinin, A. 2005, ApJ, 633, 781 [NASA ADS] [CrossRef] [Google Scholar]
- Kotov, O., & Vikhlinin, A. 2006, ApJ, 641, 752 [NASA ADS] [CrossRef] [Google Scholar]
- Kravtsov, A. V., Vikhlinin, A., & Nagai, D. 2006, ApJ, 650, 128 [NASA ADS] [CrossRef] [Google Scholar]
- Lacey, C., & Cole, S. 1993, MNRAS, 262, 627 [NASA ADS] [CrossRef] [Google Scholar]
- Lumb, D. H., Bartlett, J. G., Romer, A. K., et al. 2004, A&A, 420, 853 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mantz, A., Allen, S. W., Ebeling, H., et al. 2010, MNRAS, 406, 1773 [NASA ADS] [Google Scholar]
- Markevitch, M. 1998, ApJ, 504, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Maughan, B. J. 2007, ApJ, 668, 772 [NASA ADS] [CrossRef] [Google Scholar]
- Maughan, B. J., Jones, L. R., Ebeling, H., & Scharf, C. 2006, MNRAS, 365, 509 [NASA ADS] [CrossRef] [Google Scholar]
- Maughan, B. J., Giles, P. A., Randall, S. W., et al. 2012, MNRAS, in press [arXiv:1108.1200] [Google Scholar]
- Mohr, J. J., & Evrard, A. E. 1997, ApJ, 491, 38 [NASA ADS] [CrossRef] [Google Scholar]
- Motl, P. M., Hallman, E. J., Burns, J. O., & Norman, M. L. 2005, ApJ, 623, L63 [NASA ADS] [CrossRef] [Google Scholar]
- Navarro, J. F., Frenk, C. S., & White, S. D. M. 1995, MNRAS, 275, 720 [NASA ADS] [CrossRef] [Google Scholar]
- Navarro, J. F., Frenk, C. S., & White, S. D. M. 1996, ApJ, 462, 563 [NASA ADS] [CrossRef] [Google Scholar]
- Navarro, J. F., Frenk, C. S., & White, S. D. M. 1997, ApJ, 490, 493 [NASA ADS] [CrossRef] [Google Scholar]
- Navarro, J. F., Hayashi, E., Power, C., et al. 2004, MNRAS, 349, 1039 [NASA ADS] [CrossRef] [Google Scholar]
- Novicki, M. C., Sornig, M., & Henry, J. P. 2002, AJ, 124, 2413 [NASA ADS] [CrossRef] [Google Scholar]
- O’Hara, T. B., Mohr, J. J., & Sanderson, A. J. R. 2007, ApJ, unpublished [arXiv:0710.5782] [Google Scholar]
- Ostriker, J. P., Bode, P., & Babul, A. 2005, ApJ, 634, 964 [NASA ADS] [CrossRef] [Google Scholar]
- Peebles, P. E. J. 1980 The Large Scale Structure of the Universe, Princeton Series in Physics, Princeton [Google Scholar]
- Pierpaoli, E., Scott, D., & White, M. 2001, MNRAS, 325, 77 [NASA ADS] [CrossRef] [Google Scholar]
- Pointecouteau, E., Arnaud, M., & Pratt, G. W. 2005, A&A, 435, 1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ponman, T. J., Cannon, D. B., & Navarro, J. F. 1999, Nature, 397, 135 [NASA ADS] [CrossRef] [Google Scholar]
- Ponman, T. J., Sanderson, A. J. R., & Finoguenov, A. 2003, MNRAS, 343, 331 [NASA ADS] [CrossRef] [Google Scholar]
- Pratt, G. W., Arnaud, M., & Pointecouteau, E. 2006, A&A, 446, 429 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pratt, G. W., Croston, J. H., Arnaud, M., & Böhringer, H. 2009, A&A, 498, 361 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pratt, G. W., Arnaud, M., Piffaretti, R., et al. 2010, A&A, 511, A85 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Press, W. H., & Schechter, P. 1974, ApJ, 187, 425 [NASA ADS] [CrossRef] [Google Scholar]
- Reichert, A., Böhringer, H., Fassbender, R., & Mühlegger, M. 2011, A&A, 535, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Reiprich, T. H., & Böhringer, H. 2002, ApJ, 567, 716 [NASA ADS] [CrossRef] [Google Scholar]
- Short, C. J., Thomas, P. A., Young, O. E., et al. 2010, MNRAS, 408, 2213 [NASA ADS] [CrossRef] [Google Scholar]
- Spergel, D. N., Bean, R., Doré, O., et al. 2007, ApJS, 170, 377 [NASA ADS] [CrossRef] [Google Scholar]
- Springel, V. 2005, MNRAS, 364, 1105 [NASA ADS] [CrossRef] [Google Scholar]
- Stanek, R., Rasia, E., Evrard, A. E., et al. 2010, ApJ, 715, 1508 [NASA ADS] [CrossRef] [Google Scholar]
- Sun, M., Voit, G. M., Donahue, M., et al. 2009, ApJ, 693, 1142 [NASA ADS] [CrossRef] [Google Scholar]
- Sun, M., Sehgal, N., Voit, G. M., et al. 2011, ApJ, 727, L49 [NASA ADS] [CrossRef] [Google Scholar]
- Tinker, J., Kravtsov, A. V., Klypin, A., et al. 2008, ApJ, 688, 709 [NASA ADS] [CrossRef] [Google Scholar]
- Vikhlinin, A., Van Speybroeck, L., Markevitch, M., Forman, W., & Grego, L. 2002, ApJ, 578, L107 [NASA ADS] [CrossRef] [Google Scholar]
- Vikhlinin, A., Markevitch, M., & Murray, S. S. 2005, ApJ, 628, 655 [NASA ADS] [CrossRef] [Google Scholar]
- Vikhlinin, A., Kravtsov, A., Forman, W., et al. 2006, ApJ, 640, 691 [NASA ADS] [CrossRef] [Google Scholar]
- Vikhlinin, A., Burenin, R. A., Ebeling, H., et al. 2009, ApJ, 692, 1033 [NASA ADS] [CrossRef] [Google Scholar]
- Voit, M. 2005, Rev. Mod. Phys., 77, 207 [NASA ADS] [CrossRef] [Google Scholar]
- Warren, M. S., Abazajian, K., Holz, D. E., & Teodoro, L. 2006, ApJ, 646, 881 [NASA ADS] [CrossRef] [Google Scholar]
- West, M. J., Dekel, A., & Oemler, A. Jr. 1987, ApJ, 316, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Yoshida, N., Colberg, J., White, S. D. M., et al. 2001, MNRAS, 325, 803 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, Y.-Y., Böhringer, H., Finoguenov, A., et al. 2006, A&A, 456, 55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zhang, Y. Y., Finoguenov, A., Böhringer, H., et al. 2008, A&A, 482, 451 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
Observationally determined slopes of the Entropy – T and entropy – mass relation.
All Figures
 |
Fig. 1 Schematic illustration of how the galaxy cluster structure scaling depends on the formation epoch of the cluster and on the critical density of the universe in an Einstein-de Sitter (densities are blue) and in a concordance cosmological model (green). The left panel provides a sketch of cluster collapse for a cluster with a formation redshift of z = 0, and the right panel shows a cluster forming at z = 0.5. For further explanations see the text. |
| In the text | |
 |
Fig. 2 Evolution with lookback time of the mean density, ρm and critical density ρcrit in the concordance cosmological model in comparison with the matter density of a coevolving Einstein-de Sitter reference model, ρ0. The curves are from top to bottom: ρcrit, ρ0, and ρm. The two models are compared at the same times after the starting point of the coevolving calculations at 13 Gyr. |
| In the text | |
 |
Fig. 3 Upper panel: logarithmic slope of the NFW mass profile as a function of scaled radius. Lower panel: logarithmic slope of the NFW mass profile a function of the mean density of the cluster over the critical density. |
| In the text | |
 |
Fig. 4 Upper panel: testing the redshift evolution of the self-similar scaling of the dark matter density distribution with the variable overdensity scaling model. The density profiles are given for redshifts of z = 0 (heavy line) and z = 0.2521, 0.5073, 0.7695, 1.0013. Dashed lines show the unscaled and solid lines the scaled profiles. Lower panel: redshift evolution of the self-similar scaling of the dark matter density distribution with the fixed overdensity scaling model. This model clearly is better than the model shown above. We also show, displaced by a factor of 0.1, the density profiles after applying the full scaling corrections described in Sect. 5. Apart from some numerical fluctuations we observe a perfect fit of the scaling corrections. |
| In the text | |
 |
Fig. 5 Correction factors α(z) and β(z) as a function of redshift for the fixed overdensity model (thick lines) and recent formation approximation (rfa) model (thin lines and parameters labeled with index rfa). |
| In the text | |
 |
Fig. 6 Evolution parameter, E(z)2, as a function of redshift. The dashed lines show the power law functions of (1 + z) with exponents of 1.26, 1.36, 1.5, 1.68 corresponding to the best approximations given in Table 3. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


