EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 538 (February 2012) A&A, 538 (2012) A134 Full HTML
Free Access
Issue
A&A
Volume 538, February 2012
Article Number A134
Number of page(s) 5
Section Astrophysical processes
DOI https://doi.org/10.1051/0004-6361/201117754
Published online 14 February 2012

© ESO, 2012

1. Introduction

Gamma-ray busts (GRBs) are one of the most powerful and energetic explosive events in the Universe. The observations of GRBs up to redshifts higher than eight (Salvaterra et al. 2009; Cucchiara et al. 2011) cause GRBs to be among the farthest known astrophysical sources. Taking their considerable event rate into consideration, GRBs may be good candidates that can be used to probe our Universe. Several interesting correlations have been suggested for GRBs (Amati et al. 2002; Norris et al. 2000; Ghirlanda et al. 2004a; Liang & Zhang 2005; Dainotti et al. 2010; Qi & Lu 2010). Based on them, the cosmology parameters have been tentatively constrained (e.g., Fenimore & Ramirez-Ruiz 2000; Schaefer 2003, 2007; Dai et al. 2004; Ghirlanda et al. 2004b, 2006; Amati et al. 2008; Wang & Dai 2006; Dainotti et al. 2008; Wang et al. 2009, 2011).

To derive a meritorious constraint on the cosmology parameters, the most important thing is to find a credible standard candle relation for GRBs. Currently, no such a relation can be established when all GRBs are involved (Butler et al. 2009; Yu et al. 2009). The reason may be that different GRBs should be produced via various mechanisms. Interestingly, for a subsample of long GRBs with known redshifts and with a plateau phase in the afterglow, an anticorrelation has been reported to exist between the end time of the plateau phase (Ta, measured in the GRB rest frame) and the corresponding X-ray luminosity (LX) at that moment (Dainotti et al. 2010, hereafter D2010). In this paper, we denote the Dainotti et al. two-parameter correlation as the L-T correlation. The intrinsic scatter of this correlation is still too large to be directly applied as a redshift estimator (Dainotti et al. 2011). Additionally, normal long-duration GRBs and the intermediate duration GRBs do not obey the same correlation equation (D2010), and the intermediate class seems to be more scattered in the plot.

In this study, we have tried to add a third parameter, i.e. the isotropic γ-ray energy release (Eγ,iso), into the correlation. We find that the new three-parameter correlation (designated as the L-T-E correlation) is much tighter than the previous L-T correlation. It is also obeyed by both the long GRBs and the intermediate-calss GRBs. The L-T-E correlation may hopefully give a better measure for our Universe. In Sect. 2, we describe our GRB sample and the method of data analysis. Our results are presented in Sect. 3. Section 4 contains our discussion and conclusions.

2. Sample and data analysis

According to Swift observations, many GRBs show a plateau phase in the early afterglow, prior to the normal power-law decay phase (Zhang et al. 2006; Nousek et al. 2006). In this study, we mainly concentrate on the GRBs with such a characteristics. All our GRBs are taken from the Dainotti et al. sample (D2010). In D2010’s data table, a total of 77 GRBs are initially included, with known redshift and with a plateau phase in the afterglow light curve. After removing the intermediate-class GRBs and some GRBs with relatively large errors, they finally limited their major statics to only 62 long GRBs. Here, we have reselected the events by taking the following three criteria into account in our studies: (1) the plateau should be obvious (GRBs 050318, 050603, 060124, 060418, 061007, 070518, and 071031 are removed by us, since their phateau phase is not clear enough.); (2) the data in the plateau phase should be rich enough to show the profile of the plateau and the end time of the plateau as well (GRBs 050820A, 060512, 060904, and 060124 are removed by us due to this constraint.); and (3) there should be no flares during the plateau phase, since flares may affect the shape of the plateau light curve and lead to errors in the quantities that we are interested in (GRBs 050904, 050908, 060223A, and 060526 are removed by us according to this condition.). As a result, our “golden sample” consisted of 55 events in total, i.e., 47 long GRBs and eight intermediate-class GRBs. (Intermediate-class GRB are characterized by a short initial burst followed by an extended low intensity emission phase; Norris et al. 2006). The redshifts of our sample range from 0.08 to 8.26.

For the end times of the plateau phase (Ta, in the GRB rest frame) and the X-ray afterglow luminosities at that moment (LX ≡ LX(Ta)), we use the values of D2010. In D2010, Ta is derived through a phenomenological fitting model (Willingale et al. 2007), and LX is derived from the equation, 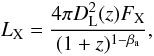(1)where z is the redshift, DL(z) the luminosity distance, FX the observed flux by Swift − XRT at the end time of the plateau phase, and βa the spectral index of the X-ray afterglow (Evans et al. 2009).

The isotropic γ-ray energy release in the prompt emission phase is 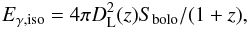(2)where Sbolo is the bolometric fluence, which can be taken from Wang et al. (2011). In this, Sbolo is calculated from the observed energy spectrum Φ(E) as (Schaefer 2007): 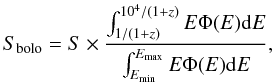(3)where S is the observed fluence in units of erg   cm-2 for each GRB, and (Emin,   Emax) are the detector thresholds. The energy spectrum Φ(E) is assumed to be the Band function (Band et al. 1993), 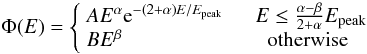(4)where Epeak is the peak energy of the spectrum, and α, β are the power-law indices for photon energies below or above the break energy, respectively. Finally, the complete data set of all our 55 GRBs are shown in Table 1, where the error bars are in the 1σ range.

We investigate whether an intrinsic correlation exists between the three parameters of LX,   Ta, and Eγ,iso as 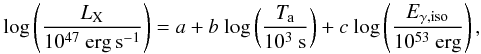(5)where a,   b, and c are constants to be determined from the fit to the observational data. In this equation, a is the constant of the intercept, while b and c are actually the power-law indices of time and energy when we approximate LX as power-law functions of Ta and Eγ,iso. Due to the complexity of GRB sampling, an intrinsic scattering parameter, σint, is introduced in our analysis, as is usually done by other researchers (Reichart 2001; Guidorzi et al. 2006; Amati et al. 2008). This extra variable that follows a normal distribution of 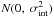is engaged to represent all the contribution to LX from other unknown hidden variables.

To derive the best fit to the observational data with the above three-parameter correlation, we use the method presented in D′Agostini (2005). Here, to simplify, we first define 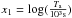, , 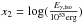and . The joint likelihood function for the coefficients of a,   b,   c, and σint is (D’Agostini 2005) (6)where i is the corresponding serial number of GRBs in our sample.

To get the best-fit coefficients, the so-called Markov-chain Monte Carlo techniques are used in our calculations. For each Markov chain, we generate 106 samples according to the likelihood function. Then we derive the the coefficients of a,   b,   c, and σint according to the statistical results of the samples.

Our likelihood function can also be conveniently applied to the two-parameter L-T correlation case studied by D2010, by simply taking c = 0. We have checked our method by comparing our result for the L-T correlation with that of D2010. The results are generally consistent, which proves the reliability of our codes.

3. Results

In our study, we assume a flat ΛCDM cosmology with H = 69.7   km   s-1   Mpc-1 and ΩM = 0.291 (the same values as D2010). By using the method described in Sect. 2, we find that the best-fit correlation between LX, Ta and Eγ,iso is (7)Figure 1 shows the above correlation. It is clearly shown that this three-parameter correlation is tight for all the 55 GRBs.

thumbnail Fig. 1

The best-fit correlation between LX, Ta, and Eγ,iso for our “golden sample”. Y-axis is the X-ray luminosity at the end time of the plateau phase, i.e. LX, in units of 1047 erg/s. The X-axis is a combined quantity of Ta (in units of 103 s) and Eγ,iso (in units of 1053 erg), i.e. 1.17 − 0.87log Ta + 0.88log Eγ,iso. The filled points correspond to the observed data of 47 long GRBs and the hollow square points correspond to the eight intermediate-class GRBs. The solid line is plotted from Eq. (7), which is the best fit of the 55 observational data points.

Comparing Eqs. (5) and (7), we find that the best values for the constants of a, b, and c in Eq. (5) are a = 1.17, b =  −0.87, and c = 0.88, respectively. Figure 1 also clearly shows that there is still obvious scatter in the L-T-E correlation. To give a quantitative description of the scatter, we need to derive the 1σ errors of these constants.

The probability distributions of these constants, as well as the intrinsic scattering parameter (σint), are displayed in Fig. 2. From this figure, we find that the probability distributions of these coefficients can be well fitted by Gauss functions, so we can easily get the 1σ error bars for these parameters. Actually, the best values and the 1σ errors for the coefficients are a = 1.17 ± 0.09, b =  −0.87 ± 0.09, c = 0.88 ± 0.08, and σint = 0.43 ± 0.05, respectively.

thumbnail Fig. 2

The probability distributions of the constants of a (upper left panel), b (upper right panel), c (lower left panel) in Eq. (5), and the probability distribution of the intrinsic scattering parameter σint (lower right panel). According to these panels, the best values and the 1σ errors for the coefficients are a = 1.17 ± 0.09, b =  −0.87 ± 0.09, c = 0.88 ± 0.08, σint = 0.43 ± 0.05, respectively.

We have also explored the three-parameter correlation for all the 77 GRB events listed in D2010, using the same analytical method as for our “golden sample” of 55 GRBs. The best-fit result is shown in Fig. 3. The best parameter values and the 1σ errors for the coefficients are a = 0.81 ± 0.07, b =  −0.91 ± 0.09, c = 0.59 ± 0.05, and σint = 1.15 ± 0.12. Comparing with the result of the “golden sample”, although there is still an obvious correlation among LX, Ta, and Eγ,iso for all the 77 GRBs, the intrinsic scatter of the L-T-E correlation is much larger now. However, it is very important to note that we exclude the 22 samples because they most likely do not physically belong to the same group as the “golden sample” (for example, many of them do not have an obvious plateau phase), as judged from the three criteria in Sect. 2.

thumbnail Fig. 3

The best-fit correlation between LX, Ta and Eγ,iso for all the 77 GRBs of D2010. The units of all physical quantity are the same as Fig. 2. The X-axis is a combined quantity of 0.81−0.91log Ta + 0.59log Eγ,iso. The filled points correspond to the observed data of 55 “golden” GRBs with error bars. The hollow diamonds correspond to 7 GRBs with too large error bars to be plotted in the figure, and the hollow circles correspond to other 15 discarded events. The solid line is the best fit for all the 77 data points.

To directly compare with the L-T correlation suggested by D2010, we also fit the two-parameter correlation for our sample. The best-fit equation is (8)This equation is consistent with the L-T correlation derived in D2010. Comparing Eq. (8) with Eq. (7), and from Fig. 2, we find that the error bars of the constants in Eq. (8) (i.e. the L-T correlation) are generally significantly larger than those of Eq. (7) (i.e. the L-T-E correlation). Also, in the two-parameter fitting of Eq. (8), the intrinsic scatter is 0.85 ± 0.10, which is also markedly larger than in the three-parameter correlation case (0.43 ± 0.05). From the comparison, we see that the L-T-E correlation is really significantly tighter than the L-T correlation.

For our GRB sample, we also find that the correlation coefficient of our L-T-E statistics is r = 0.92, and the chance probability is P = 1.05 × 10-20. In contrast, the correlation coefficient of the L-T statistics of the same sample is r =  −0.73 and the corresponding chance probability P = 5.55 × 10-8. This also shows that the L-T-E correlation is much tighter than the L-T correlation.

Table 1

55 GRBs of our sample.

4. Discussion and conclusions

In this paper, a new three-parameter correlation is found for the GRBs with an obvious plateau phase in the afterglow. This L-T-E correlation is tighter than the L-T correlation reported in D2010. It has been shown that the intrinsic scattering of our L-T-E correlation is significantly smaller than that of the L-T correlation, and the correlation coefficient is correspondingly larger. However, we note that the intrinsic scatter of the L-T-E correlation is still larger than that of some correlations derived from prompt GRB emission (Guidorzi et al. 2006; Amati et al. 2008). In the future, more samples and more delicate selections might help to improve the result.

The plateau phase (or the shallow decay segment) is an interesting characteristic of many GRB afterglows (Zhang et al. 2006; Nousek et al. 2006). This phenomenon can be explained as continuous energy injection from the central engine after the prompt burst (Rees & Mészáros 1998; Dai & Lu 1998; Zhang & Mészáros 2001; Dai 2004; Kobayashi & Zhang 2007; Yu & Dai 2007; Xu et al. 2009; Yu et al. 2010; Dall′Osso et al. 2011) or by the two-component models (Corsi & Mészáros 2009), or by structured jets (Eichler & Granot 2006; Granot et al. 2006; Panaitescu 2007; Yamazaki 2009; Xu & Huang 2010), or even as due to dust scattering (Shao & Dai 2007; Shao et al. 2008). According to our L-T-E correlation (Eq. (7)), the X-ray luminosity at the end time of the plateau can be expressed as a function of the end time and the isotropic γ-ray energy release as (9)We believe that this relation can give useful constraints on the underlying physics.

For the energy injection model, a natural mechanism is the dipole radiation from the spinning down of a magnetar at the center of the fireball. Note that the injected energy may not be Poynting flux, but can be electron-positron pairs (Dai 2004). These pairs interact with the fireball material, leading to the formation of a relativistic wind bubble. When the energy injection dominates the dynamical evolution of the external shock, the afterglow intensity should naturally be proportional to the energy injection power, so LX is actually a measure of the energy injection rate. According to Eq. (9), LX is roughly inversely proportional to the timescale of the energy injection, Ta. It hints that the energy reservoir should be roughly a constant. This is consistent with the energy injection model, which usually assumes that the central engine is a rapidly rotating millisecond magnetar. In different GRBs, the surface magnetic field intensities of the central magnetars may be quite different, leading to various energy injection luminosities and energy injection timescales. But the total energy available for energy injection is relatively constant (about rotational energy of the magnetar). It is mainly constrained by the limiting angular velocity of the magnetar, which again is determined by the equation of state of neutron stars. Additionally, according to Dai (2004), to produce an obvious plateau in the afterglow lightcurve, the total injected energy must be comparable to the original fireball energy (which may be comparable to Eγ,iso). This requirement is again roughly consistent with the item of 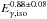in Eq. (9). Based on the above analyses, we argued that the L-T-E correlation strongly supports the energy injection model of magnetars. It also indicates that the newly born millisecond magnetars associated with GRBs provide a good standard candle in our Universe. Thus the L-T-E correlation may potentially be used to test the cosmological models.

Our sample contains 47 long GRBs and eight intermediate-class GRBs. From Fig. 1, we see that both of these two classes are consistent with the same L-T-E correlation. Howerer, they do behave very differently in frame work of the two-parameter L-T correlation. This is another important advantage of our three-parameter correlation. It indicates that magnetars may also form in intermediate-class GRBs, and their limiting spinning is simply similar to those magnetars born in long GRBs. A natural problem will be raised as to whether short GRBs with plateau phase in the afterglow also obey the same correlation. Unfortunately, the number of short GRBs meeting the requirement is currently too small.

It is worth noting that many interesting physical principles could be involved in newly born magnetars (Dall′Osso et al. 2009), which include the emission of gravitational waves, the cooling process, the evolution of the magnetic axis, etc. Some of the physics may affect the the energy injection process of the newly born magnetar delicately. We believe that further studies of the new three-parameter correlation may give useful constraints on the physics of newly born magnetars.

Acknowledgments

We thank the anonymous referee for many useful suggestions and comments. We also would like to thank Z. G. Dai, S. Qi, and F. Y. Wang

for helpful discussion. This work was supported by the National Natural Science Foundation of China (Grant No. 11033002) and the National Basic Research Program of China (973 Program, Grant No. 2009CB824800).

References

  1. Amati, L., Frontera, F., Tavani, M., et al. 2002, ApJ, 390, 81 [Google Scholar]
  2. Amati, L., Guidorzi, C., Frontera, F., et al. 2008, MNRAS, 391, 577 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
  3. Band, D., Matteson, J., Ford, L., et al. 1993, ApJ, 413, 281 [NASA ADS] [CrossRef] [Google Scholar]
  4. Butler, N. R., Kocevski, D., & Bloom, J. S. 2009, ApJ, 694, 76 [NASA ADS] [CrossRef] [Google Scholar]
  5. Corsi, A., & Mészáros, P. 2009, ApJ, 702, 1171 [NASA ADS] [CrossRef] [Google Scholar]
  6. Cucchiara, A., Levan, A. J., Fox, D. B., et al. 2011, ApJ, 736, 7 [NASA ADS] [CrossRef] [Google Scholar]
  7. D′Agostini, G. 2005 [arXiv:astroph/0511182] [Google Scholar]
  8. Dai, Z. G. 2004, ApJ, 606, 1000 [NASA ADS] [CrossRef] [Google Scholar]
  9. Dai, Z. G., & Lu, T. 1998, A&A, 333, L87 [NASA ADS] [Google Scholar]
  10. Dai, Z. G., Liang, E. W., & Xu, D. 2004, ApJ, 612, L101 [NASA ADS] [CrossRef] [Google Scholar]
  11. Dainotti, M. G., Cardone, V. F., & Capozziello, S. 2008, MNRAS, 391, L79 [NASA ADS] [CrossRef] [Google Scholar]
  12. Dainotti, M. G., Willingale, R., Capozziello, S., Fabrizio Cardone, V., & Ostrowski, M. 2010, ApJ, 722, L215 [NASA ADS] [CrossRef] [Google Scholar]
  13. Dainotti, M. G., Cardone, V. F., Capozziello, S., Ostrowski, M., & Willingale, R. 2011, ApJ, 730, 135 [NASA ADS] [CrossRef] [Google Scholar]
  14. Dall′Osso, S., Shore, S. N., & Stella, L. 2009, MNRAS, 398, 1869 [NASA ADS] [CrossRef] [Google Scholar]
  15. Dall′Osso, S., Stratta, G., Guetta, D., et al. 2011, A&A, 526, A121 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  16. Eichler, D., & Granot, J. 2006, ApJ, 641, L5 [NASA ADS] [CrossRef] [Google Scholar]
  17. Evans, P., Beardmore, A. P., Page, K. L., et al. 2009, MNRAS, 397, 1177 [NASA ADS] [CrossRef] [Google Scholar]
  18. Fenimore, E. E., & Ramirez-Ruiz, E. 2000 [arXiv:astro-ph/0004176] [Google Scholar]
  19. Ghirlanda, G., Ghisellini, G., & Lazzati, D. 2004a, ApJ, 616, 331 [NASA ADS] [CrossRef] [Google Scholar]
  20. Ghirlanda, G., Ghisellini, G., Lazzati, D., & Firmani, C. 2004b, ApJ, 613, L13 [NASA ADS] [CrossRef] [Google Scholar]
  21. Ghirlanda, G., Ghisellini, G., & Firmani, C. 2006, New J. Phys., 8, 123 [NASA ADS] [CrossRef] [Google Scholar]
  22. Granot, J., Königl, A., & Piran, T. 2006, MNRAS, 370, 1946 [NASA ADS] [CrossRef] [Google Scholar]
  23. Guidorzi, C., Frontera, F., Montanari, E., et al. 2006, MNRAS, 371, 843 [Google Scholar]
  24. Kobayashi, S., & Zhang, B. 2007, ApJ, 655, 973 [NASA ADS] [CrossRef] [Google Scholar]
  25. Liang, E. W., & Zhang, B. 2005, ApJ, 633, 611 [NASA ADS] [CrossRef] [Google Scholar]
  26. Norris, J. P., & Bonnell, J. T. 2006, A&A, 643, 266 [Google Scholar]
  27. Norris, J. P., Marani, G. F., & Bonnell, J. T. 2000, ApJ, 534, 248 [NASA ADS] [CrossRef] [Google Scholar]
  28. Nousek, J. A., Kouveliotou, C., Grupe, D., et al. 2006, ApJ, 642, 389 [NASA ADS] [CrossRef] [Google Scholar]
  29. Panaitescu, A. 2007, MNRAS, 379, 331 [NASA ADS] [CrossRef] [Google Scholar]
  30. Qi, S., & Lu, T. 2010, ApJ, 717, 1274 [NASA ADS] [CrossRef] [Google Scholar]
  31. Rees, M. J., & Mészáros, P. 1998, ApJ, 496, L1 [NASA ADS] [CrossRef] [Google Scholar]
  32. Reichart, D. E. 2001, ApJ, 553, 235 [NASA ADS] [CrossRef] [Google Scholar]
  33. Salvaterra, R., Della Valle, M., Campana, S., et al. 2009, Nature, 461, 1258 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  34. Schaefer, B. E. 2003, ApJ, 583, L67 [NASA ADS] [CrossRef] [Google Scholar]
  35. Schaefer, B. E. 2007, ApJ, 660, 16 [NASA ADS] [CrossRef] [Google Scholar]
  36. Shao, L., & Dai, Z. G. 2007, ApJ, 660, 1319 [NASA ADS] [CrossRef] [Google Scholar]
  37. Shao, L., Dai, Z. G., & Mirabal, N. 2008, ApJ, 675, 507 [NASA ADS] [CrossRef] [Google Scholar]
  38. Wang, F. Y., & Dai, Z. G. 2006, MNRAS, 368, 371 [NASA ADS] [CrossRef] [Google Scholar]
  39. Wang, F. Y., Dai, Z. G., & Qi, S. 2009, A&A, 507, 53 [Google Scholar]
  40. Wang, F. Y., Qi, S., & Dai, Z. G. 2011, MNRAS, 415, 3423 [NASA ADS] [CrossRef] [Google Scholar]
  41. Willingale, R. W., O′Brien, P. T., Osborne, J. P., et al. 2007, ApJ, 662, 1093 [NASA ADS] [CrossRef] [Google Scholar]
  42. Xu, M., & Huang, Y. F. 2010, A&A, 523, 5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  43. Xu, M., Huang, Y. F., & Lu, T. 2009, RAA, 9, 1317 [Google Scholar]
  44. Yamazaki, R. 2009, ApJ, 690, L118 [NASA ADS] [CrossRef] [Google Scholar]
  45. Yu, Y. W., & Dai, Z. G. 2007, A&A, 470, 119 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  46. Yu, B., Qi, S., & Lu, T. 2009, ApJ, 705, 15 [NASA ADS] [CrossRef] [Google Scholar]
  47. Yu, Y. W., Cheng, K. S., & Cao, X. F. 2010, ApJ, 715, 477 [NASA ADS] [CrossRef] [Google Scholar]
  48. Zhang, B., & Mészáros, P. 2001, ApJ, 552, L35 [NASA ADS] [CrossRef] [Google Scholar]
  49. Zhang, B., Fan, Y. Z., Dyks, J., et al. 2006, ApJ, 642, 354 [NASA ADS] [CrossRef] [Google Scholar]

All Tables

Table 1

55 GRBs of our sample.

In the text

All Figures

thumbnail Fig. 1

The best-fit correlation between LX, Ta, and Eγ,iso for our “golden sample”. Y-axis is the X-ray luminosity at the end time of the plateau phase, i.e. LX, in units of 1047 erg/s. The X-axis is a combined quantity of Ta (in units of 103 s) and Eγ,iso (in units of 1053 erg), i.e. 1.17 − 0.87log Ta + 0.88log Eγ,iso. The filled points correspond to the observed data of 47 long GRBs and the hollow square points correspond to the eight intermediate-class GRBs. The solid line is plotted from Eq. (7), which is the best fit of the 55 observational data points.
In the text
thumbnail Fig. 2

The probability distributions of the constants of a (upper left panel), b (upper right panel), c (lower left panel) in Eq. (5), and the probability distribution of the intrinsic scattering parameter σint (lower right panel). According to these panels, the best values and the 1σ errors for the coefficients are a = 1.17 ± 0.09, b =  −0.87 ± 0.09, c = 0.88 ± 0.08, σint = 0.43 ± 0.05, respectively.
In the text
thumbnail Fig. 3

The best-fit correlation between LX, Ta and Eγ,iso for all the 77 GRBs of D2010. The units of all physical quantity are the same as Fig. 2. The X-axis is a combined quantity of 0.81−0.91log Ta + 0.59log Eγ,iso. The filled points correspond to the observed data of 55 “golden” GRBs with error bars. The hollow diamonds correspond to 7 GRBs with too large error bars to be plotted in the figure, and the hollow circles correspond to other 15 discarded events. The solid line is the best fit for all the 77 data points.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.