EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 538 (February 2012) A&A, 538 (2012) A136 Full HTML
Free Access
Issue
A&A
Volume 538, February 2012
Article Number A136
Number of page(s) 10
Section Stellar structure and evolution
DOI https://doi.org/10.1051/0004-6361/201117452
Published online 14 February 2012

© ESO, 2012

1. Introduction

SiO maser emission associated with asymptotic giant branch (AGB) stars occurs at the inner region of circumstellar envelopes (CSEs). Maser emission has been detected in several vibrationally-excited rotational transitions of the SiO molecule (e.g. Humphreys et al. 1997; Pardo et al. 1998; Soria-Ruiz et al. 2007). A series of very long baseline array (VLBA), high-resolution observations of the SiO masers around Mira variables have shown that the maser emission is confined to a region, sometimes ring-shaped, between the stellar photosphere and the dust formation zone (e.g. Cotton et al. 2008, 2006; Diamond et al. 1994). On scales probed by very long baseline interferometry (VLBI), the masers are confined to localized spots with lifetimes of a few months. The resolution of the VLBI observations of SiO masers is a small fraction of the ring. The above points imply that SiO masers can be used as powerful probes of the processes that drive the mass loss and dynamics in the inner region of the CSEs.

SiO masers can also be important for understanding the evolutionary path from the spherically symmetric AGB stars to aspherical planetary nebulae (PNe). Magnetic fields very likely play an important role in shaping the CSEs of evolved stars (e.g. Garcia-Segura 1997). Polarization observations of circumstellar masers enable us to determine the magnetic field strength and morphology at different distances from the central stars. Observations indicate that SiO masers are significantly linearly polarized, with polarization vectors mainly tangential to the maser ring. For example, multi-epoch polarization VLBA observations of the Mira star TX Cam have revealed the linear polarization morphology tangential to the projected shell of SiO maser emission (e.g. Kemball et al. 2009). However, Cotton et al. (2008) observed five Mira variables with the VLBA at 43 GHz, but not all sources showed a tangential linear polarization morphology. It therefore remains unclear whether the tangential linear polarization morphology is a generic property of the SiO maser region of evolved stars. The circular polarization of the masers is in the range 3% to 5% (e.g. Barvainis et al. 1987; Kemball et al. 2009). Polarimetric observations of a sample of evolved stars indicate an average magnetic field of several Gauss (Herpin et al. 2006; Kemball & Diamond 1997). The SiO maser magnetic fields are consistent with those measured using H2O and OH masers farther out in the envelope, assuming a dipole (B ∝ r-3) or solar-type (B ∝ r-2) magnetic field (Vlemmings et al. 2005).

VLBI studies of SiO masers have so far focused on Mira variables and a handful of post-AGB objects and water fountain sources (e.g. Cotton et al. 2008; Desmurs et al. 2007; Imai et al. 2005), and as far as we can tell, no high-resolution VLBI observation has been performed to image SiO masers in OH/IR stars. These objects have larger CSEs and much longer periods up to 2000 days than do Mira variables (Herman & Habing 1985b). They are strong 1612 MHz OH maser emitters (Baud et al. 1979). The stars are surrounded by thick dust shells, which makes them optically obscured. The SiO maser pump mechanism in OH/IR stars may be different from the one operating in Mira variables (Doel et al. 1995). Owing to the higher mass loss of these objects, the CSE is denser at least an order of magnitude more than those of Mira variables.

Here, we report the SiO maser polarimetric observations of the OH/IR star OH44.8-2.3 with the VLBA. The observations enable us to obtain the spatial distribution of the SiO maser features in OH/IR stars for the first time. Additionally, our experiment probes the magnetic field strength and morphology in the SiO maser region of OH/IR stars and compares them with those of Mira variables. We also reduced the 1612 MHz OH maser observations of this star from the VLA archive to determine whether any large scale asymmetry exists in the OH maser shell of this star.

OH 44.8-2.3 is identified as a moderate OH/IR star with a warm and thin CSE and a period of 534 days (Groenewegen 1994). The mass loss of this star is estimated to be  ~4.6    ×    10-6   M⊙/yr (de Beck et al. 2010). The OH masers of this source show a double-peak profile at −88.9 and −53.8 km s-1 with a peak flux density of 14.4 Jy for the red-shifted part of the spectrum (Engels & Jiménez-Esteban 2007). A distance of 1.13  ±  0.34 kpc was measured for this star using the phase-lag method based on the characteristic 1612 MHz double-peak profile of the OH masers of this source (Van Langevelde et al. 1990). The H2O masers of this star were detected by Engels et al. (1986) at  ~5 Jy. However, further single-dish monitoring of this source did not result in any detection (Shintani et al. 2008; Kim et al. 2010). The v = 1, J = 1 → 0 SiO masers of this star were observed by Nyman et al. (1998) with a flux density of 17.6 Jy. Kim et al. (2010) observed the v = 1, 2 , J = 1 → 0 emission from this star with an integrated flux density of  ~25 Jy and  ~28 Jy, respectively.

The outline of the paper is as follows. The observations are described in Sect. 2. Before giving the results in Sect. 4, we introduce the necessary background on maser polarization in Sect. 3. We discuss the interpretation of the results in Sect. 5. This is followed by the conclusion in Sect. 6.

2. Observations

We observed the v = 1, J = 1 → 0 SiO maser emission toward OH 44.8-2.3 on 6 July 2010 using the NRAO1 Very Long Baseline Array (VLBA) operating in the 43 GHz band. Auxiliary Extended Very Large Array (EVLA) interferometer observations were also performed on 2 and 11 July 2010 to allow for the absolute calibration of the electric vector polarization angle (EVPA). Furthermore, we retrieved the 1612 MHz OH maser very large array (VLA) observations of OH 44.8-2.3 from the NRAO archive. The VLBA, EVLA, and VLA observations are discussed below.

thumbnail Fig. 1

Linearly polarized map of the polarization calibrator J2253+16 obtained with the EVLA (left panel) and the VLBA (right panel). The vectors are rotated by 15° in the VLBA image.

2.1. VLBA observations and reduction

The data were recorded in dual circular polarization spectral line mode, which generates all four polarization combinations in the correlator. The DiFX correlator was used with a bandwidth of 4 MHz and 1024 spectral channels, which results in 0.03 km s-1 spectral resolution. The observations were performed in one spectral window centered at a fixed frequency corresponding to the v = 1, J = 1 → 0 SiO maser transition at a rest frequency of 43.12208 GHz and a stellar velocity of −72 km s-1 with respect to the local standard of rest (LSR), determined from OH maser observations. The total observing time was 6 h, balanced between the target source, OH 44.8-2.3, and the continuum calibrators, J2253+1608, J1751+0939, and J1800+3848. We achieved a spatial resolution of 0.5  ×  0.2 mas.

We used the Astronomical Image Processing Software Package (AIPS) to perform the rest of the calibration, editing, and imaging of the data. The first calibration steps were performed on the data set with modest spectral resolution (128 channels). The solutions were then applied to the high spectral resolution data set (1024 channels). Parallactic angle corrections were performed on all calibrators. The North Liberty (NL) and Saint Croix (SC) antennas had to be flagged, owing to the bad weather conditions at the time of the observations.

Since the SiO molecule is nonparamagnetic, the fractional circular polarization is low (mc ~ 1−3%). To preserve the low stokes V signature, we performed amplitude calibration of OH 44.8-2.3 using the AIPS task “ACFIT”. In this method, each circular polarization autocorrelation spectrum was calibrated independently using the method described by Reid et al. (1980). A template auto-correlation spectrum was selected for  ~20 min interval from the Los Alamos antenna at a time range with sufficiently high elevation. The template spectrum was fit to all other total power spectra from all antennas, and the relative gains of the antennas as a function of time were determined. We used the system temperature measurements provided with the data to perform the amplitude calibration for the calibrators.

The complex band pass solutions were obtained using J2253+1608 on each data set separately. Fringe fitting for the residual relay and rate for the parallel hand data was done using the continuum calibrators J2253+1608 and J1751+0939. The fringe rate solutions for OH 44.8-2.3 were determined on the strongest feature. The delay offset between the right and left circular polarizations at the reference antenna was determined for J2253+1608 on the Los Alamos – Fort Davis baseline. The solutions were transferred to all other baselines and sources. The polarization leakage terms were determined using J2253+1608. After the solutions were applied to both data sets image cubes could be created with 50 μarcsec pixel spacing. The rms noise in the modest spectral resolution and the high spectral resolution individual channel images correspond to 8 mJy and 26 mJy, respectively.

thumbnail Fig. 2

The 1612 MHz OH maser map of OH 44.8-2.3 obtained with the VLA. The top-left and bottom-right panels show the blue- and red-shifted peaks. The red-shifted peak exhibits the highest flux density of 8.1 Jy. The contour levels are at 1.62, 3.24, 4.86, 6.48 and 8.1 Jy. The top-right and bottom-left panels exhibit emission summed over several channels close to the stellar velocity. The contour levels are at 0.005, 0.011, 0.016, 0.022, and 0.027 Jy. The star symbol indicates the position of the peak in the red-shifted emission which probably indicates the position of the central star.

2.2. EVLA observations and reductions

The absolute phase difference between the right and left circular polarizations at the reference antenna is not known, which implies that the absolute EVPA of linearly polarized emission cannot be measured accurately in our VLBA observations. Therefore, auxiliary EVLA observations were performed to measure the absolute polarization angle of the polarization calibrators with respect to a primary polarization calibrator with known polarization angle.

The continuum sources J2253+1608 and J1751+0939 were observed as transfer calibrators on 2 and 11 July 2010, respectively. The observations were performed in continuum mode and full polarization, using two 128 MHz spectral windows. The data reduction was performed for each spectral window separately. We achieved a beam size of 2.6  ×  1.7 arcsec during the observations.

We reduced the data according to the standard EVLA data calibration and imaging recipe in the appendix of the AIPS Cook Book. Since the delays are not set accurately in EVLA observations, we solved for the phase slope using the AIPS task FRING. A  ~1 min solution interval was chosen for J2253+1608 and J1751+0939 to solve for the phase slope as a function of frequency. The bandpass solutions were determined using J2253+1608 and J1751+0939. The flux density of the primary flux calibrators 3C 286 and 3C 48 was determined using the model provided within the AIPS software. The AIPS task “CALIB” was used to perform phase calibration for 3C 286 and 3C 48 using a model of the sources. Subsequently, the phase solution was determined for the secondary calibrators J2253+1608 and J1751+0939. The amplitude of the secondary calibrators was adjusted with respect to the flux density of the primary flux calibrator. We used 3C 286 and 3C 48 for polarization calibration. The delay difference between the right and left circular polarizations were determined using the AIPS task “RLDLY”. The feed parameters for each polarization were determined both in continuum and spectral mode since the EVLA feeds show significant variations in frequency. Images were produced in each spectral window in Stokes Q, U, I by adopting a pixel spacing of 0.2 arcsec. The rms noise for J2253+16 was  ~8 mJy and for J1751+9839 was  ~1 mJy.

The absolute EVPA of J2251608 and J1751+0939 were measured with respect to 3C 48 and 3C 286, respectively. The final absolute EVPA was calculated as the mean of the EVPA in each spectral window. This corresponds to the measured EVPA of 62° for J2253+1608 and −44° for J1751+0939. Figure 1 shows the EVPA of the linearly polarized emission for J2253+1608 for both EVLA and VLBA observations. The EVPA in the VLBA image is rotated by 15°, which corresponds to the difference in the EVPA between the EVLA and VLBA images. We note that the linearly polarized emission of the other polarization calibrator, J1751+0939 shows two polarized components separated by  ~90° in the VLBA image. Therefore we were not able to use this source as a robust EVPA calibrator.

2.3. VLA observations of the 1612 MHz OH masers of OH 44.8-2.3

We found the previous observations of the 1612 MHz OH masers of OH 44.8-2.3 observed on 25 September 1983 using the Very Large Array (VLA) from the NRAO archive. The observations were performed under the project name “AH127” in the A configuration with the largest spacing of 36.5 km, which gives a resolution of 1′′. The band width of 1.5 MHz was used for the observations, which gives a velocity resolution of 1.4 km s-1 at 1612 MHz, and 3C 286 was observed as a flux density calibrator with 1741-038 as the secondary phase calibrator. The data reduction was performed following the recipe provided in the AIPS cookbook.

Figure 2 displays the OH maser map of OH 44.8-2.3. The emission covers a velocity range of −87 to −56 km s-1. The figure shows the blue- and red-shifted peaks, as well as emission summed over several channels close to the stellar velocity.

3. SiO maser polarization theory

The SiO maser emission at 43.12208 GHz involves the rotational transition J = 1 → 0 in the excited vibrational state v = 1. Since the SiO molecule is nonparamagnetic, its response to the magnetic field is weak. This implies that the Zeeman splitting is smaller than the line width.

3.1. Linear polarization

SiO masers present high fractional linear polarization (e.g. Kemball & Diamond 1997). It was shown that anisotropic background radiation from the central star generates anisotropic pumping, potentially producing a high degree of linear polarization in the SiO emission region (e.g. Watson 2002). In the case where the SiO masers are radiatively pumped, the magnetic substates may be anisotropically populated, which can generate high linear polarization fraction for saturated masers (Western & Watson 1983). However, the results from Nedoluha & Watson (1990) show that the polarization vectors still trace the direction of the magnetic field despite the possibility that the linear polarization develops generally from anisotropic pumping.

thumbnail Fig. 3

The total intensity spectrum of OH 44.8-2.3 for the v = 1, J = 1 → 0 SiO maser emission obtained with the VLBA.

thumbnail Fig. 4

The VLBA map of v = 1, J = 1 → 0 SiO maser emission towards the OH/IR star OH 44.8-2.3. The features are color-coded according to the flux density (Jy/beam) integrated over all velocity channels.

3.2. Potential non-Zeeman effects for circular polarization

The non-Zeeman mechanism prohibits one from interpreting circular polarization as a measure of the magnetic field strength. This stems from the competition between the stimulated emission rate (R), the Zeeman coefficient rate (gΩ), and the radiative decay rate (Γ). The circular polarization can be created by the change in the axis of symmetry for the molecular quantum states when the condition gΩ ≃ R > Γ is satisfied (Nedoluha & Watson 1994). For some distance along the maser path gΩ ≥ R is satisfied and the magnetic field is the quantization axis. As the radiation propagates farther into the maser path and the rate of stimulated emission rises, the inequality R ≥ gΩ is satisfied and the molecule interacts more strongly with the radiation. This implies that the axis of the symmetry of the molecule changes from parallel to the magnetic field to parallel to the direction of propagation. The resulting circular polarization would have the antisymmetric profile which resembles the one produced by the ordinary Zeeman effect. The intensity-dependent circular polarization can be higher than that created by the Zeeman effect by a factor as large as 1000. This scenario is an inherent part of the radiative transfer process and does not require anisotropic pumping or high fractional linear polarization.

Wiebe & Watson (1998) introduce yet another non-Zeeman effect in which the propagation of a strong linear polarization can create circular polarization if the condition gΩ ≫ R > Γ is satisfied. The circular polarization can be generated if the magnetic field orientation changes along the direction of maser propagation. The circular polarization produced from this scenario is on average 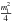 ~, where ml indicates the linear polarization fraction. For a typical linear polarization fraction around 30%, the circular polarization results from that formula above corresponds to  ~2–3%, which agrees with the observed circular polarization (e.g. Barvainis et al. 1987); however, in individual maser features the circular polarization fraction can go up to  ~20%. This mechanism would then generate circular polarization with only 10–20 mG fields. Moreover, if there is no velocity gradient along the maser path, the circular polarization profile would have the shape of the S-curve. However, the intrinsic profiles can be distorted as a result of saturation, as can with velocity and magnetic gradients along the amplification path. A correlation between the linear and circular polarization fraction is expected for the individual features.

4. Results

4.1. Total intensity

Figure 3 shows the total intensity spectrum of the SiO maser emission towards OH 44.8-2.3. The emission covers a velocity range of  ~7 km s-1. The SiO emission actually implies a stellar velocity 3–4 km s-1 offset from the stellar velocity of −72 km s-1 based on OH maser observations of this star. Figure 4 displays the SiO maser emission map of OH 44.8-2.3 summed over all velocity channels covering emission. The maser features form a partial ring of 4.75 mas corresponding to 5.4 AU, assuming a distance of 1.13 kpc (Van Langevelde et al. 1990). The masers appear to be absent from the north-east and south-west part of the ring. The ring pattern observed in the SiO maser region of this star implies that the masers are tangentially amplified. This is typically interpreted to indicate that large velocity gradients exist in the SiO maser region, which prohibits radial amplification. The peak flux density for the maser features are displayed in Table 1. Feature 1 exhibits the largest flux density of 2.8 Jy.

Table 1

Results of the magnetic field determination of the SiO maser features of OH 44.8-2.3 obtained from the VLBA observations.

4.2. Linear polarization

The polarization morphology is shown in Fig. 5. In this plot, the polarized emission is plotted as vectors with a length proportional to the polarization intensity. The position angle of the vectors corresponds to the EVPA of the emission. All Stokes parameters are summed over frequency before making this plot. The maps of Stokes I, Q, and U are available via CDS. The background contours represent the total intensity image. The fractional linear polarization for the individual maser features is shown in Table 1. The average linear polarization fraction for the SiO maser features of this star is  ~30%. In particular it reaches 100% for feature 8. This most likely implies that the (radiative or collisional) pumping of SiO masers is not isotropic.

thumbnail Fig. 5

Contour plot of the Stokes I image at levels [1, 2, 5, 10, 20, 40, 80, 100]% of the peak. Vectors are overlaid proportional to the linearly polarized intensity (on a scale 1 mas = 1.25 Jy beam-1) and drawn at a position angle of the EVPA. All Stokes parameters (I,   Q,   U) are summed over velocity.

thumbnail Fig. 6

Total power (I) and circular polarization (V) spectra of the brightest SiO maser feature of OH 44.8-2.3. The dashed line is the fit to the observed V-spectrum. The V spectrum is shown after removing the scaled down replica of Stokes I.

4.3. Circular polarization

The instrumental gain differences between the RCP and LCP spectra can cause a residual, scaled-down version of the Stokes I spectrum to appear in the circular polarization profile. The Zeeman splitting for the Stokes V spectra for the SiO maser features of OH 44.8-2.3 can be determined by measuring the residual curve having the shape of the derivative of the total intensity spectrum in the least square sense (Troland & Heiles 1982): 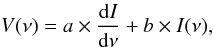(1)where a is the measure of the circular polarization due to the Zeeman splitting, and b denotes the instrumental differential amplitude. This method assumes that intrinsically equal flux is present in the RCP and LCP spectra, which implies that the circular polarization spectra have the antisymmetric S-curve pattern. However, theoretical models of circular polarization produce asymmetric profiles, depending on the velocity gradient along the amplification path (Wiebe & Watson 1998). We find a tentative detection of the circular polarization for the brightest maser feature in Fig. 4 (feature 1 from Table 1). Figure 6 displays the circular polarization, together with the total intensity spectra for this feature. The figure also shows the fit to the circular polarization profile after removing the scaled-down replica of Stokes I. The circular polarization fraction is measured as 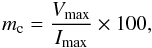(2)where Vmax corresponds to the maximum of the fit to the observed Stokes V spectrum (Eq. (1): 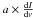). For the modest spectral resolution data (128 channels), we measured circular polarization of mc ~ 0.7    ±    0.2%. However, owing to the increased noise in individual channels in the high spectral resolution data, we cannot confirm the detection. The magnetic field derived from circular polarization corresponds to the following equation (Kemball & Diamond 1997; derived from Elitzur 1996): 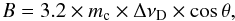(3)where mc, ΔνD, and θ indicate the fractional circular polarization, the maser line width, and the angle between the magnetic field and line of sight, respectively. The full width half maximum line with for the Stokes I spectrum of feature 1 corresponds to  ~0.8 km s-1. Using the preceding relation, a magnetic field of 1.8  ±  0.5 G is derived for feature 1.

4.3.1. Cross-correlation method and magnetic field strength

Alternatively, we use the cross-correlation method introduced by Modjaz et al. (2005) to measure the magnetic field due to the Zeeman splitting. In this method the right circular polarization (RCP) and the left circular polarization (LCP) spectra are cross-correlated to determine the velocity splitting. The magnetic field is determined by applying the Zeeman splitting coefficient for SiO masers. This method can even work for complex spectra, assuming that the velocity shift is the same over the spectrum, which means the magnetic field strength and direction are constant in the maser region. The sensitivity of this method is comparable to the S-curve method, where the stokes V spectrum is used directly for measuring the magnetic field (e.g. Vlemmings et al. 2001; Fiebig & Guesten 1989).

The Zeeman rate for SiO is given by Nedoluha & Watson (1990) as 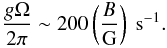(4)This equation implies the Zeeman splitting coefficient for the J = 1 → 0, v = 1 transition of the SiO maser is 8.7  ×  10-3 km s-1 G-1. We present the result of the cross-correlation method in Table 1. We measured a magnetic field of 1.5  ±  0.3 G for feature 1. However, we only place upper limits at the 3σ level for the other features of the SiO emission of this star.

4.4. OH maser observations of OH 44.8-2.3

The VLA results on OH 1612 MHz emission from OH 44.8-2.3 were not presented directly in the scientific literature before, although the original distance determination in Herman et al. (1986) and the one we use from Van Langevelde et al. (1990) depend directly on it. We have access to the results of the original analysis in which a shell radius of 1.302′′ ± 0.023′′ was obtained (van Langevelde, priv. comm.). The new processing we performed gave consistent images with these previous results, but we note that the OH at intermediate velocities is quite elongated (Fig. 2). The inferred size of the region is of course much larger than the SiO, spanning  ~1471 AU compared to 5.4 AU. One should note that, with the typical outflow velocities of  ~16 km s-1 and 5 km s-1 for OH and SiO masers, the dynamical timescales are also very different:  ~440 years for the OH and  ~5 years for the SiO.

5. Discussion

5.1. Linear polarization

To the compare the two conflicting polarization theories (a magnetic versus anisotropic pumping origin of the linear polarization implying a Zeeman or non-Zeeman origin of the circular polarization), we need to determine in which theoretical regime the masers were observed. This includes determining of the stimulated emission rate (R), the Zeeman rate (gΩ), and the collisional and radiative decay rate Γ. The radiative decay rate for the v = 1, J =    1    →    0 transition of the SiO molecule is estimated as 5 s-1 (Kwan & Scoville 1974; Elitzur 1992). The stimulated emission rate (R) is estimated by (Kemball et al. 2009): 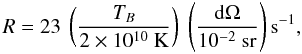(5)where TB is the maser brightness temperature and dΩ is the estimated maser beaming-angle. We obtained an estimate for the brightness temperature for feature 1 (Fig. 4) as 5  ×  1010 K. We adapt an estimated beaming angle of 10-2 sr (Kemball et al. 2009). Replacing these values in Eq. (5) results in R = 57.5 s-1. Substituting the value of  ~1.5 G obtained for feature 1 (Table 1) in Eq. (4), implies gΩ ~ 1900 s-1. Therefore, we are in a regime where gΩ ≫ R > Γ. In this regime the linear polarization vectors appear either parallel or perpendicular to the projected magnetic field, depending on the angle between the magnetic field direction and the line of sight (Goldreich et al. 1973). When taking the EVPA of −50° for feature 8, which has the highest linear polarization fraction, this implies that the magnetic field direction is either parallel (−50°) or perpendicular (40°) to the linear polarization vectors. In either case, the EVPA vectors probably indicate a large-scale magnetic field in the SiO maser region of this star.

The linear polarization morphology of this star is not consistent with the dominant tangential polarization morphologies that were reported for other evolved stars (e.g. TX Cam; Kemball et al. 2009). Based on previous observations of the SiO maser region of TX Cam (Kemball & Diamond 1997; Desmurs et al. 2000), Kemball et al. (2009) conclude that the tangential polarization morphology could be an inter cycle property of the SiO maser emission toward this star. Instead of tangential polarization morphology, the EVPA vectors could indicate a bipolar magnetic field morphology for the SiO maser region of OH 44.8-2.3 (Fig. 5). However, we cannot rule out the other, more complex, morphologies. Polarimetric observations of the OH and H2O masers of this star are required to clarify the magnetic field morphology of this star. A dipole field morphology is reported for the supergiant VX Sgr using the polarimetric observations of high-frequency SiO masers (Vlemmings et al. 2011). This morphology was consistent with the the dipole magnetic field inferred from H2O and OH maser regions at much greater distances from the central star (Szymczak & Cohen 1997; Szymczak et al. 2001; Vlemmings et al. 2005).

5.1.1. The effects of anisotropic pumping

The SiO maser features of this star exhibit high fractional linear polarization up to 100% (Table 1), which very likely indicates that the pumping of the masers is highly anisotropic. Such high linear polarization fractions have been reported previously (Kemball & Diamond 1997; Cotton et al. 2006). The masers occur close to the central star and the infrared radiation incident on the masering region is highly anisotropic. This implies that the magnetic substates are pumped unequally. Additionally, the medium in which they are located most likely has large velocity gradients, which leads to a preferred direction for the propagation of masers (Watson 2002). Western & Watson (1983) show that even for collisionally pumped SiO masers, the magnetic substates are anisotropically pumped and high linear polarization would be expected for saturated and unsaturated masers. In the absence of magnetic fields, collisional pumping causes linear polarization along the radial direction. In contrast, radiative pumping would produce linear polarization vectors tangential to the SiO maser ring. However, our observations show that magnetic fields are present in the SiO maser ring of OH 44.8-2.3, which implies that both magnetic field and anisotropic pumping influence the linear polarization morphology. Therefore, we cannot distinguish between the radiative or collisional pumping from the observations.

5.1.2. Maser saturation

The degree of saturation is the ratio of the rate R for stimulated emission to the loss rate Γ. From the observations we measured the stimulated emission rate for feature 1 as R ~ 57.5 s-1 which implies 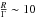. This indicates that the medium is marginally saturated. In contrast, a saturation of 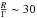is required to achieve a 70% linear polarization fraction in the non-Zeeman scenario (Watson & Wyld 2001). In the standard Zeeman interpretation scenario proposed by Elitzur (1996) the polarization solution does not depend on the saturation level. Nedoluha & Watson (1994) show that the low-level circular polarization observed for SiO masers can come from the saturation of masers.

5.1.3. Jet-like features

Even though the majority of the SiO maser features of OH 44.8-2.3 are coherent and fit the ring model, features 8 and 15 do not conform to the ring pattern. A striking characteristic of feature 8 is the 100% linear polarization fraction. Additionally, the linear polarization vectors of this feature are in the perpendicular direction of the overall linear polarization morphology of this star (Fig. 5). Cotton et al. (2006) report structures aligned with the direction of the photosphere with magnetic field morphology along the features. They refer to them as jet-like features. They explain that these features most likely form from the masering region being dragged along the magnetic field. For the case of OH 44.8-2.3, the 100% linear polarization fraction could imply that this feature is a dynamic part of the envelope. Observations of this feature close in time to study the proper motion is necessary to understand the nature of this feature.

5.2. Circular polarization

We report a tentative detection of  ~0.7% for the circular polarization fraction for feature 1 (Table 1). The measured magnetic field corresponds to 1.5  ±  0.3 G for this feature. We note that the magnetic field measured from the circular polarization fraction (Sect. 4.3: 1.8  ±  0.5 G) and the one measured from the cross-correlation method (Sect. 4.3.1: 1.5  ±  0.3 G) are consistent within errors. Therefore the correspondence of the field measured from the cross-correlation method with the field determination through the circular polarization fraction confirms that the cross-correlation method works properly. The non-Zeeman effect of intensity-dependent circular polarization introduced by Nedoluha & Watson (1994) is ruled out since gΩ ≫ R in our observations. However, since we are in a regime where gΩ ≫ R > Γ, the non-Zeeman effect introduced by Wiebe & Watson (1998) is applicable. For the 7% linear polarization fraction measured for feature 1 (Table 1), the generated circular polarization it causes is 0.12%. This implies that the measured circular polarization for feature 1 is about six times higher than the estimated value from the non-Zeeman effect. Wiebe & Watson (1998) show that if the circular polarization is higher than the average of , the circular polarization stems from other causes, probably the Zeeman effect. Therefore, it is likely that the circular polarization of this star comes from the Zeeman splitting. However, Wiebe & Watson (1998) explain that the average circular polarization in individual features can go up to 20%. Additionally, the determination of Zeeman or non-Zeeman effect from the observed circular polarization profile remains inconclusive, since both models predict the similar antisymmetric S-curve profile.

5.3. CSE morphology and magnetic field

The SiO maser features of OH 44.8-2.3 exhibit two opposite arcs (Fig. 4). Additionally, the OH masers of this star show that the masers have an elongated shell morphology in the direction where there is a gap in the SiO maser emission (Fig. 2). We note that the OH masers occur on much larger scale (~1471 AU) than the SiO masers (5.4 AU) around the star. It is therefore not obvious that both deviations from symmetry are related, but if they are, this indicates that there is a mechanism at work that can support the asymmetry on many scales. Similar gaps or opposite arcs have been seen recently in monitoring observations of the SiO masers of R Cas with the VLBA (Assaf et al. 2011). Of course, with only one epoch of observations we can not determine whether the SiO maser arcs in OH 44.8-2.3 are consistent in time since the region where SiO masers occur is expected to be highly dynamic. Therefore, multi-epoch observations of the SiO masers of this star are essential to probe the motion of the SiO maser features.

As mentioned earlier, the magnetic field morphology for the SiO maser region of this star is either parallel or perpendicular to the linear polarization vectors. Interestingly, the direction of the magnetic field is parallel or perpendicular to the location of the gaps in the SiO maser ring and the OH maser extent. There thus appears to be a generally preferred direction of the outflow imposed by the magnetic field in the CSE of this star. Such asymmetric outflows have already been reported for the CSE of evolved stars. For example, collimated H2O maser jets have been observed in a class of post-AGB objects, the so-called water-fountain sources (Imai et al. 2002; Boboltz & Marvel 2005). Additionally, interferometric observations of the OH maser region of this class of objects have revealed aspherical morphologies with either equatorial or bi-conical distributions (Amiri et al. 2011). High-resolution observations of the SiO masers of the post-AGB object W43A indicates a biconical outflow (Imai et al. 2005). The bipolar jets observed in water-fountain sources are related to the onset of asymmetric PNe (Sahai & Trauger 1998).

The high fractional linear polarization observed for the SiO masers of OH 44.8-2.3, together with the tentative detection of circular polarization, is potentially a strong indication that magnetic fields play a significant role in shaping the circumstellar environment of this star. Significant magnetic fields are observed in different regions of the circumstellar environment of several evolved stars, which indicates the possible role of the magnetic field in shaping the CSEs. Observations of H2O masers reveals significant field strength for Mira variables and supergiants in the range 0.2 G to 4 G (Vlemmings et al. 2002, 2005). In particular, H2O maser polarimetric observations of the water-fountain source W43A shows that the jet is magnetically collimated (Vlemmings et al. 2006). Additionally, polarimetric observations of OH masers reveals large scale magnetic field strength in evolved stars ranging from 0.1 mG to 10 mG (e.g. Etoka & Diamond 2004; Amiri et al. 2010).

However, it should be noted that, by interpreting the morphology of the maser emission in terms of the underlying physical structure, a number of aspects have been ignored. This includes sufficient column density, a velocity coherent path length along the amplification path, and a pumping mechanism. Therefore, it is possible that both SiO and OH molecules exist in spherical shells, but the conditions for the masers mentioned above are not satisfied.

5.4. SiO emission in OH 44.8-2.3

The SiO masers of OH 44.8-2.3 exhibit a ring morphology (Fig. 4). Assuming a distance of 1.13  ±  0.34 kpc, the masers are located at a distance of  ~5.4 AU from the surface of the star. The ring morphology is similar to the ring patterns observed previously for the SiO masers of Mira variables (e.g. Diamond et al. 1994). Moreover, the estimated SiO maser ring radius of OH 44.8-2.3 is similar to those measured for Mira variables (e.g.3-7 AU; Cotton et al. 2008). However, since OH 44.8-2.3 is a high mass loss OH/IR star, the CSE and stellar radius of this star are expected to be larger than Mira variables. The typical stellar radius for OH/IR stars corresponds to  ~2.8 AU (Herman & Habing 1985a). This implies that the SiO masers of OH 44.8-2.3 occur at  ~1.9 stellar radius. This value is similar to the lower end location of SiO masers in Mira variables (2–6 stellar radius; Elitzur 1992). Therefore, even though OH 44.8-2.3 is expected to be larger, the SiO masers occur at the same distance from the stellar photosphere as Mira variables.

The main uncertainty for the discussion above however is the distance to the star. From the 1612 MHz OH maser observations of this source using the phase lag method, a distance of 1.13  ±  0.34 kpc was measured by Van Langevelde et al. (1990). This method assumes spherical symmetry of the OH maser shell. However, the distribution of the OH masers of this star (Fig. 2) does not indicate any spherical expansion of the OH maser shell. Therefore, accurate determination of the distance of this source using the parallax method for the SiO maser features of OH 44.8-2.3 is necessary to understand the size and location of the SiO maser region.

6. Conclusions

Our observations indicate a ring morphology for the SiO maser region of the OH/IR star OH 44.8-2.3. Assuming a distance of 1.13  ±  0.34 kpc (Van Langevelde et al. 1990), the masers are located at  ~5.4 AU from the central star. The ring pattern is similar to what was observed previously for Mira variables.

The linear polarization morphology is consistent with the dipole magnetic field morphology in the SiO maser region of this star. However, we cannot rule out toroidal or solar type field morphologies. Polarimetric observations of the OH and H2O maser regions of the CSE of this star are required to clarify its magnetic field morphology.

We report tentative detection of circular polarization at  ~0.7% for the brightest SiO maser feature in the modest spectral resolution data set. However, the increased noise in high spectral resolution data set means we can not confirm the detection. Further polarimetric VLBI observations of the SiO masers of this star with more integration time are needed to clarify this. We note that, based on polarization studies, we cannot distinguish between the Zeeman and non-Zeeman effects from the observations.

The SiO maser features of OH 44.8-2.3 exhibit two opposite arcs. Furthermore, the 1612 MHz OH masers of this star indicate an elongated shell morphology in the direction where there is a gap in the SiO maser emission. Additionally, the direction of the magnetic field is parallel or perpendicular to the location of the gaps in the SiO maser ring and the OH maser extent. This could be taken as a clue that there is a large-scale magnetic field that imposes a preferred direction on the outflow on scales that span two orders of magnitude. Because of the timescales involved in forming the OH shell, one would then conclude that the magnetic field is important for imposing an asymmetric signature on the neutral outflow in the OH/IR phase. Furthermore, the high fractional linear polarization measured for the SiO masers of this star could indicate the possible role of the magnetic field in shaping the circumstellar environment of this star. However, we cannot differentiate the radiative and collisional pumping for the SiO maser ring of OH 44.8-2.3.

Follow up monitoring of the SiO maser region of OH 44.8-2.3 can give the distance through parallax measurements and this source offers a unique opportunity to check the phase-lag distance previously obtained by Van Langevelde et al. (1990). Additionally, the future observations will enable us to check the evolution of asymmetries in the CSE of this star.

1

The National Radio Astronomy Observatory (NRAO) is a facility of the National Science Foundation operated under cooperative agreement by Associated Universities, Inc.

Acknowledgments

This research program was supported by the ESTRELA fellowship, the EU Framework 6 Marie Curie Early Stage Training program under contract number MEST-CT-2005-19669. W.V. acknowledges support by the Deutsche Forschungsgemeinschaft through the Emmy Noether Research grant VL 61/3-1. We thank Bruce Partridge for giving us access to the EVLA observations of J2253+1608.

References

  1. Amiri, N., Vlemmings, W., & van Langevelde, H. J. 2010, A&A, 509, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  2. Amiri, N., Vlemmings, W., & van Langevelde, H. J. 2011, A&A, 532, A149 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  3. Assaf, K. A., Diamond, P. J., Richards, A. M. S., & Gray, M. D. 2011, MNRAS, 415, 1083 [NASA ADS] [CrossRef] [Google Scholar]
  4. Barvainis, R., McIntosh, G., & Predmore, C. R. 1987, Nature, 329, 613 [NASA ADS] [CrossRef] [Google Scholar]
  5. Baud, B., Habing, H. J., Matthews, H. E., & Winnberg, A. 1979, A&AS, 36, 193 [NASA ADS] [Google Scholar]
  6. Boboltz, D. A., & Marvel, K. B. 2005, ApJ, 627, L45 [NASA ADS] [CrossRef] [Google Scholar]
  7. Cotton, W. D., Vlemmings, W., Mennesson, B., et al. 2006, A&A, 456, 339 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  8. Cotton, W. D., Perrin, G., & Lopez, B. 2008, A&A, 477, 853 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  9. de Beck, E., Decin, L., de Koter, A., et al. 2010, A&A, 523, A18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  10. Desmurs, J. F., Bujarrabal, V., Colomer, F., & Alcolea, J. 2000, A&A, 360, 189 [NASA ADS] [Google Scholar]
  11. Desmurs, J.-F., Alcolea, J., Bujarrabal, V., Sánchez Contreras, C., & Colomer, F. 2007, A&A, 468, 189 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  12. Diamond, P. J., Kemball, A. J., Junor, W., et al. 1994, ApJ, 430, L61 [NASA ADS] [CrossRef] [Google Scholar]
  13. Doel, R. C., Gray, M. D., Humphreys, E. M. L., Braithwaite, M. F., & Field, D. 1995, A&A, 302, 797 [NASA ADS] [Google Scholar]
  14. Elitzur, M. 1992, ARA&A, 30, 75 [NASA ADS] [CrossRef] [Google Scholar]
  15. Elitzur, M. 1996, ApJ, 457, 415 [NASA ADS] [CrossRef] [Google Scholar]
  16. Engels, D., & Jiménez-Esteban, F. 2007, A&A, 475, 941 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  17. Engels, D., Schmid-Burgk, J., & Walmsley, C. M. 1986, A&A, 167, 129 [NASA ADS] [Google Scholar]
  18. Etoka, S., & Diamond, P. 2004, MNRAS, 348, 34 [NASA ADS] [CrossRef] [Google Scholar]
  19. Fiebig, D., & Guesten, R. 1989, A&A, 214, 333 [NASA ADS] [Google Scholar]
  20. Garcia-Segura, G. 1997, ApJ, 489, L189 [NASA ADS] [CrossRef] [Google Scholar]
  21. Goldreich, P., Keeley, D. A., & Kwan, J. Y. 1973, ApJ, 179, 111 [NASA ADS] [CrossRef] [Google Scholar]
  22. Groenewegen, M. A. T. 1994, A&A, 290, 544 [NASA ADS] [Google Scholar]
  23. Herman, J., & Habing, H. J. 1985a, Phys. Rep., 124, 255 [NASA ADS] [CrossRef] [Google Scholar]
  24. Herman, J., & Habing, H. J. 1985b, A&AS, 59, 523 [NASA ADS] [Google Scholar]
  25. Herman, J., Burger, J. H., & Penninx, W. H. 1986, A&A, 167, 247 [NASA ADS] [Google Scholar]
  26. Herpin, F., Baudry, A., Thum, C., Morris, D., & Wiesemeyer, H. 2006, A&A, 450, 667 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  27. Humphreys, E. M. L., Gray, M. D., Yates, J. A., & Field, D. 1997, MNRAS, 287, 663 [NASA ADS] [Google Scholar]
  28. Imai, H., Obara, K., Diamond, P. J., Omodaka, T., & Sasao, T. 2002, Nature, 417, 829 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  29. Imai, H., Nakashima, J., Diamond, P. J., Miyazaki, A., & Deguchi, S. 2005, ApJ, 622, L125 [NASA ADS] [CrossRef] [Google Scholar]
  30. Kemball, A. J., & Diamond, P. J. 1997, ApJ, 481, L111 [NASA ADS] [CrossRef] [Google Scholar]
  31. Kemball, A. J., Diamond, P. J., Gonidakis, I., et al. 2009, ApJ, 698, 1721 [NASA ADS] [CrossRef] [Google Scholar]
  32. Kim, J., Cho, S., Oh, C. S., & Byun, D. 2010, ApJS, 188, 209 [NASA ADS] [CrossRef] [Google Scholar]
  33. Kwan, J., & Scoville, N. 1974, ApJ, 194, L97 [NASA ADS] [CrossRef] [Google Scholar]
  34. Modjaz, M., Moran, J. M., Kondratko, P. T., & Greenhill, L. J. 2005, ApJ, 626, 104 [NASA ADS] [CrossRef] [Google Scholar]
  35. Nedoluha, G. E., & Watson, W. D. 1990, ApJ, 361, L53 [NASA ADS] [CrossRef] [Google Scholar]
  36. Nedoluha, G. E., & Watson, W. D. 1994, ApJ, 423, 394 [NASA ADS] [CrossRef] [Google Scholar]
  37. Nyman, L., Hall, P. J., & Olofsson, H. 1998, A&AS, 127, 185 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  38. Pardo, J. R., Cernicharo, J., Gonzalez-Alfonso, E., & Bujarrabal, V. 1998, A&A, 329, 219 [NASA ADS] [Google Scholar]
  39. Reid, M. J., Haschick, A. D., Burke, B. F., et al. 1980, ApJ, 239, 89 [NASA ADS] [CrossRef] [Google Scholar]
  40. Sahai, R., & Trauger, J. T. 1998, AJ, 116, 1357 [NASA ADS] [CrossRef] [Google Scholar]
  41. Shintani, M., Imai, H., Ando, K., et al. 2008, PASJ, 60, 1077 [NASA ADS] [Google Scholar]
  42. Soria-Ruiz, R., Alcolea, J., Colomer, F., Bujarrabal, V., & Desmurs, J.-F. 2007, A&A, 468, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  43. Szymczak, M., & Cohen, R. J. 1997, MNRAS, 288, 945 [NASA ADS] [Google Scholar]
  44. Szymczak, M., Cohen, R. J., & Richards, A. M. S. 2001, A&A, 371, 1012 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  45. Troland, T. H., & Heiles, C. 1982, ApJ, 252, 179 [NASA ADS] [CrossRef] [Google Scholar]
  46. Van Langevelde, H. J., van der Heiden, R., & van Schooneveld, C. 1990, A&A, 239, 193 [NASA ADS] [Google Scholar]
  47. Vlemmings, W., Diamond, P. J., & van Langevelde, H. J. 2001, A&A, 375, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  48. Vlemmings, W. H. T., Diamond, P. J., & van Langevelde, H. J. 2002, A&A, 394, 589 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  49. Vlemmings, W. H. T., van Langevelde, H. J., & Diamond, P. J. 2005, A&A, 434, 1029 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  50. Vlemmings, W. H. T., Diamond, P. J., & Imai, H. 2006, Nature, 440, 58 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  51. Vlemmings, W. H. T., Humphreys, E. M. L., & Franco-Hernández, R. 2011, ApJ, 728, 149 [NASA ADS] [CrossRef] [Google Scholar]
  52. Watson, W. D. 2002, in Cosmic Masers: From Proto-Stars to Black Holes, ed. V. Migenes, & M. J. Reid, IAU Symp., 206, 464 [Google Scholar]
  53. Watson, W. D., & Wyld, H. W. 2001, ApJ, 558, L55 [NASA ADS] [CrossRef] [Google Scholar]
  54. Western, L. R., & Watson, W. D. 1983, ApJ, 275, 195 [NASA ADS] [CrossRef] [Google Scholar]
  55. Wiebe, D. S., & Watson, W. D. 1998, ApJ, 503, L71 [NASA ADS] [CrossRef] [Google Scholar]

All Tables

Table 1

Results of the magnetic field determination of the SiO maser features of OH 44.8-2.3 obtained from the VLBA observations.

In the text

All Figures

thumbnail Fig. 1

Linearly polarized map of the polarization calibrator J2253+16 obtained with the EVLA (left panel) and the VLBA (right panel). The vectors are rotated by 15° in the VLBA image.
In the text
thumbnail Fig. 2

The 1612 MHz OH maser map of OH 44.8-2.3 obtained with the VLA. The top-left and bottom-right panels show the blue- and red-shifted peaks. The red-shifted peak exhibits the highest flux density of 8.1 Jy. The contour levels are at 1.62, 3.24, 4.86, 6.48 and 8.1 Jy. The top-right and bottom-left panels exhibit emission summed over several channels close to the stellar velocity. The contour levels are at 0.005, 0.011, 0.016, 0.022, and 0.027 Jy. The star symbol indicates the position of the peak in the red-shifted emission which probably indicates the position of the central star.
In the text
thumbnail Fig. 3

The total intensity spectrum of OH 44.8-2.3 for the v = 1, J = 1 → 0 SiO maser emission obtained with the VLBA.
In the text
thumbnail Fig. 4

The VLBA map of v = 1, J = 1 → 0 SiO maser emission towards the OH/IR star OH 44.8-2.3. The features are color-coded according to the flux density (Jy/beam) integrated over all velocity channels.
In the text
thumbnail Fig. 5

Contour plot of the Stokes I image at levels [1, 2, 5, 10, 20, 40, 80, 100]% of the peak. Vectors are overlaid proportional to the linearly polarized intensity (on a scale 1 mas = 1.25 Jy beam-1) and drawn at a position angle of the EVPA. All Stokes parameters (I,   Q,   U) are summed over velocity.
In the text
thumbnail Fig. 6

Total power (I) and circular polarization (V) spectra of the brightest SiO maser feature of OH 44.8-2.3. The dashed line is the fit to the observed V-spectrum. The V spectrum is shown after removing the scaled down replica of Stokes I.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.