| Issue |
A&A
Volume 538, February 2012
|
|
|---|---|---|
| Article Number | A80 | |
| Number of page(s) | 12 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/201117448 | |
| Published online | 08 February 2012 | |
On the origin and composition of Galactic cosmic rays
Institut d’Astrophysique de Paris, UMR7095 CNRS, Univ. P. & M. Curie, 98bis Bd. Arago, 75104 Paris, France
e-mail: prantzos@iap.fr
Received: 9 June 2011
Accepted: 27 December 2011
Context. The composition of Galactic cosmic rays (GCR) presents strong similarities to the standard (cosmic) composition, but also noticeable differences, the most important of which is the high isotopic ratio of 22Ne/20Ne, which is ~5 times higher in GCR than in the Sun. This ratio provides key information on the GCR origin.
Aims. We investigate the idea that GCR are accelerated by the forward shocks of supernova explosions, while they run through the pre-supernova winds of the massive stars and through the interstellar medium.
Methods. We use detailed wind and core yields of rotating and non-rotating models of massive stars with mass loss, as well as simple models for the properties of the forward shock and of the circumstellar medium.
Results. We find that the observed GCR 22Ne/20Ne ratio can be explained if GCR are accelerated only during the early Sedov phase, for shock velocities >1600 km s-1. The acceleration efficiency is found to be of the order of 10-6–10-5, i.e. a few particles out of a million encountered by the shock escape the SN at GCR energies. We also show quantitatively that the widely publicized idea that GCR are accelerated in superbubbles fails to account for the high 22Ne/20Ne ratio in GCR.
Key words: acceleration of particles / shock waves / ISM: supernova remnants / stars: mass-loss
© ESO, 2012
1. Introduction
Supernova (SN) shocks are generally thought to be the main accelerator of the bulk of Galactic cosmic rays (GCR). Indeed, the power of GCR in the Milky Way is estimated to be 1041 erg/s, corresponding to 10–20% of the kinetic power of Galactic supernovae (assuming canonical values of 2 SN per century, each one releasing 1051 erg of kinetic energy).
The site of the acceleration of GCR remains debatable today, despite more than five decades of theoretical and observational studies (e.g. Strong et al. 2007, and references therein). Over the years, it has been suggested that GCR are accelerated in 1) SN remnants (either by the forward or the reverse shock or both), 2) the interstellar medium (ISM), 3) the winds of massive stars, 4) the interiors of superbubbles, excavated by the massive star winds and the subsequent SN explosions of an OB association.
Each one of the proposed sites has its own advantages and shortcomings, regarding the energetics and/or the composition of accelerated matter. For instance, it has been argued that the hot, low-density environment of a superbubble minmizes radiative losses of SN shocks and energy losses of accelerated particles, thus allowing the latter to reach substantial energies, up to the “knee” of the GCR spectrum (e.g. Parizot et al. 2004). On the other hand, reverse SN shocks running into the SN interior carry insufficient energy to explain the bulk GCR energetics (Ramaty et al. 1997). Moreover, they should accelerate 59Ni, a product of explosive nucleosynthesis that is unstable to e−-capture (with a lifetime of 104 yr) and that has not been detected in GCR (Wiedenbeck et al. 1999), while a rapid acceleration would render it practically stable and thus detectable.
It was realized early on that the elemental composition of GCR differs significantly from the one of the ISM. Those differences may provide valuable information on the origin of GCR particles and, perhaps, on the site – and even the mechanism – of acceleration. Volatiles behave differently from refractories: the former display a mass-dependent enrichment with respect to H, which reaches a factor of 10 for the heaviest of them; the latter are all overabundant (w.r.t. H) by a factor of 20, while C and O display intermediate overabundances, by factors of 9 and 5, respectively (e.g. Wiedenbeck 2007, and references therein).
This complex pattern is now thought to result not from ionization effects (as suggested in Cassé & Goret 1978, and further developed by Meyer 1985) but rather from effects related to elemental condensation temperature (Meyer et al. 1997): refractories are locked in dust grains, which are sputtered by repeated SN shocks and the released ions are easily picked-up and accelerated (Ellison et al. 1997). This quite elaborate scheme, which builds on earlier ideas by e.g. Cesarsky & Bibring (1981), accounts quantitatively for most of the observed features of GCR source composition; still, it leaves unanswered the key question about the acceleration site of GCR (and how it affects the composition of accelerated matter).
The most conspicuous feature of GCR source composition is undoubtely the high isotopic 22Ne/20Ne ratio. Its value was measured since the late 1970ies (Garcia-Munoz et al. 1979; Wiedenbeck & Greiner 1981). The most accurate measurement today, obtained from analysis of the CRIS instrument, leads to a best estimate (Binns et al. 2008) of 0.387 ± 0.007 (statistical) ± 0.022 (systematic). This is 5.3 ± 0.3 times the value of the (22Ne/20Ne)⊙ ratio in the solar wind. In contrast to the case of the elemental source GCR abundances, which may be affected by various physico-chemical factors (first ionization potential, condensation temperature, etc.) isotopic ratios can only be affected by nucleosynthetic processes and hence provide crucial information on the origin of cosmic ray particles. It should be noticed that up to now there is no clear evidence for any other GCR isotopic ratio to differ from solar, with the potential exception of 58Fe/56Fe, which is estimated to be 1.687 ± 0.274 times solar (Binns et al. 2008).
Soon after the discovery of the anomalous GCR 22Ne/20Ne ratio, Cassé & Paul (1982) suggested that it could be explained by a mixture of ~2% of material from the wind of a WC star to 98% of material with standard composition. In early He-burning, 14N (produced through the CNO cycle in the previous H-burning phase) is transformed almost totally in 22Ne through 14N(α,γ)18F(β + )18O(α,γ)22Ne. He-burning products (like 12C and 22Ne) are expelled by the stellar winds of massive stars during their WC phase. The observed GCR 22Ne/20Ne ratio is obtained by assuming dilution of WC material with matter of standard composition. Subsequent studies put the aforementionned idea on a quantitative basis, with the use of detailed models of the evolution and nucleosynthesis of massive, mass-losing stars (Maeder 1983; Prantzos 1984; Meyer 1985; Prantzos et al. 1987). In those studies, the acceleration site of GCR was considered as decoupled from the nucleosynthesis site, and unrelated to the fraction of admixtured WC material.
Higdon & Lingenfelter (2003) evaluated quantitatively the 22Ne/20Ne ratio within a superbubble, created by the collective action of stellar winds and SN shockwaves. They adopted stellar wind yields for 20Ne and 22Ne from the models of Schaller et al. (1992) and SN yields from the models of Woosley & Weaver (1995). Higdon & Lingenfelter (2003) found that the 22Ne/20Ne ratio in the superbubble decreases with time (because 22Ne from the winds dominates the evolution of 22Ne/20Ne at early times) and that its time average value is compatible with the GCR source 22Ne/20Ne inferred from observations. In a subsequent paper, Lingenfelter & Higdon (2007) recognised that the Schaller et al. (1992) yields of 22Ne were highly overestimated1 and, consequently, “new detailed calculations of the expected GCR isotopic ratio are called for”, but they did not attempt such a re-evaluation. In the meantime, Binns et al. (2005), using updated wind yields of massive stars with rotation (from the Geneva group, see Sect. 2.2), found good agreement between the observed 22Ne/20Ne ratio and an admixture of ~20% material from WR stars with 80% material of standard composition. According to Binns et al. (2008), since WR stars are evolutionary products of OB stars, such an agreement “suggests that OB associations within superbubbles are the likely source of at least a substantial fraction of GCR”.
Howewer, theoretical studies in the past 10 years are based mostly on the paradigm of GCR being accelerated in SN remnants, not in superbubbles, e.g. Ptuskin & Zirakashivili (2005); Berezhko & Völk (2006); Berezhko et al. (2009); Ptuskin et al. (2010); Caprioli et al. (2010); Schure et al. (2010), Ellison & Bykov (2011) and references therein. The kinetic energy of the bulk motion of the forward shock of the SN explosion is converted into GCR energy through diffusive shock acceleration. The process is highly non-linear and involves the dynamical reaction of both the accelerated particles and of the magnetic field on the system. Those studies usually take into account that the SN explosion often occurs within the cavity excavated in the interstellar medium (ISM) by the wind of the massive star prior to the explosion, e.g. Biermann et al. (2001); however, the structure of the circumstellar environment in that case is quite complex and simplified models are used for its description. Although Caprioli et al. (2011) considered the composition of GCR (H, He, CNO, MgSiAl, Fe) resulting from such an acceleration site, none of those studies considered the 22Ne/20Ne ratio.
In this work we study the 22Ne/20Ne ratio of GCR accelerated by the forward shocks of SN explosions, while they run through the presupernova winds of massive stars and through the interstellar medium. We consider the whole mass spectrum of massive stars (from ~10 to 120 M⊙), including stars with either small or large mass losses prior to their explosions. We consider stellar properties (masses of winds, ejecta, yields etc.) from recent models with mass loss and or without rotation (from Hirschi et al. 2005; and Limongi & Chieffi 2006, respectively), the former having greater 22Ne enhancements in their winds. We adopt a simplified prescription (suggested in Ptuskin & Zirakashvili 2005; and reformulated in Caprioli 2011) to describe the structure of the circumstellar medium at the time of the explosion and we consider that GCR start being accelerated in the Sedov-Taylor (ST) phase of the SN remnant (see e.g. Ptuskin et al. 2010). By requiring the resulting IMF averaged 22Ne/20Ne ratio to equal the observed one RObs = (22Ne/20Ne)GCR/(22Ne/20Ne)⊙ = 5.3 ± 0.3 we are able to constrain the forward shock velocity to values >1600–1900 km s-1 for rotating stars and to >2100–2400 km s-1 for non rotating ones (depending on assumptions on acceleration efficiency), i.e. we find that GCR are accelerated during the early ST phase, lasting for a few 103 yr. Assuming that 10% of the SN kinetic energy is converted to GCR, we find that during the acceleration period a few particles out of a million encountered by the forward shock are accelerated. Finally, we reassess the superbubble paradigm for the origin of GCR, by evaluating consistently the 22Ne/20Ne ratio with the aforementioned stellar yields. We find that it cannot be as high as observed, unless some extremely favorable assumptions are made (only the early period of the superbubble lifetime considered, no gas left over from the formation of the OB association). We conclude that the bulk of GCR cannot originate in superbubbles.
The plan of the paper is as follows. In Sect. 2 we present the general set-up of our model: the adopted stellar models (Sect. 2.2) and their wind yields (Sect. 2.3), the description of the circumstellar environment (Sect. 2.4) and the evolution of the forward shock in the ST phase (Sect. 2.5). In Sect. 3 we present our results for the (time-dependent) composition of the accelerated particles, the limits imposed on the shock velocity by the observed 22Ne/20Ne ratio and the efficiency of the particle acceleration. Finally, in Sect. 4 we explore the 22Ne/20Ne ratio of GCR, assumed to be accelerated inside a superbubble, and we show that it cannot match the oberved one (unless extreme assumptions are made). The results are summarized in Sect. 5.
2. A toy model for the composition of CR accelerated in massive star winds
2.1. The set-up
The method adopted here to calculate the composition of matter accelerated by a single SN explosion is schematically illustrated in Fig. 1. At the end of its life and at the time of its SN explosion, a star of initial mass M∗ is left with a mass MExp, surrounded by a circumstellar shell of mass MWind = M∗ – MExp, which has been lost through stellar wind during its prior hydrostatic evolution After the SN explosion, a mass of ejecta MEj = MExp – MRem (where MRem is the mass of the compact remmant, neutron star or black hole) expands first within the shell of mass MWind and then in the ISM, with the forward shock having initial velocity 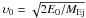 , where E0 is the kinetic energy of the SN explosion.
, where E0 is the kinetic energy of the SN explosion.
 |
Fig. 1 Schematic representation of a supernova exploding in the wind of its parent star. The star of initial mass M∗ explodes with a mass MExp, i.e. it has lost a mass Mwind = M∗ − MExp. The most massive stars become WR stars and their wind expels not only the H-envelope (of mass MEnv, with composition similar to that of the ISM) but also nuclearly processed layers, of mass MProc, i.e. MWind = MEnv + MProc, where MProc = MHeC − MExp and MHeC is the mass of the (H-exhausted) He-core. The star leaves a remnant (neutron star or black hole) of mass MRem; the mass ejected in the SN explosion is MEj = MExp − MRem. Efficient GCR acceleration presumably starts at the beginning of the ST phase, when a mass MS1 ~ MEj is swept up in front of the SN shock wave (which is indicated by arrows). |
For stars ending their lives as WR stars, the wind contains both the original (nuclearly unprocessed) envelope of mass MEnv, and nuclearly processed layers of mass MProc, enriched in products of H-burning, and in some cases of He-burning as well. For those stars, MWind = MProc + MEnv and MProc is calculated as the difference between the mass of the nuclearly processed core MHeC and the mass at the explosion: MProc = MHeC – MExp. For lower mass stars that explode as red supergiants, the wind composition results essentially from the 1st dredge-up, i.e. it is a mixture of H-burning products from the stellar core with the original envelope composition (i.e. mass loss has not uncovered the He-core at the time of the explosion). The limit between the two classes of stars depends on their initial mass, mass-loss rate and rotational velocity and it is rather poorly known at present: in general, in models with no rotation stars with M∗ > 32–35 M⊙ become WR stars (e.g. Heger et al. 2002), while in models with rotation that limit may be as low as 22 M⊙ (Meynet & Maeder 2000).
The first phase of the supernova remnant (“free expansion”) takes place at shock velocity υ ~ const. and ends when a mass MS1 ~ MEj has been swept up in front of the shock wave, at which point the ST phase sets in. Following Ptuskin et al. (2010), we assume that efficient GCR acceleration starts at this time, where the situation is energetically most favourable. In our baseline model we consider constant acceleration efficiency ; time-dependent efficiency of particle acceleration is the subject of current researches (see Ellison & Bykov 2011; Drury 2011, and references therein) and will be briefly discussed in Sect. 3.3.
The ST phase proceeds adiabatically, i.e. at about constant energy and with decreasing velocity, until the temperature of the gas engulfed by the shock front drops to levels allowing a significant fraction (about 50%) of the remaining energy to be radiated away. At that time, an amount of matter MS2 ≫ MEj has been swept up and the shock enters the “snow-plow” phase. At this point – and, perhaps, even earlier, during the ST phase – the forward shock is too weak to accelerate particles to GCR energies any more.
In the aforementioned scenario, GCR are accelerated from a pool of particles with composition characteristic of the mass MWind early on. Depending on the initial stellar mass, this composition may be rich in products of H- (and He-) burning. It is progressively diluted with ambient (first wind – with normal 22Ne – and then interstellar) gas and at the end of the ST phase it closely resembles closely that of the ISM. The GCR source composition observed on Earth should correspond to the average composition between the early ST phase and some later evolutionary stage of the remnant, and should result from the whole mass spectrum of exploding stars, i.e. it should be averaged over a stellar initial mass function (IMF).
2.2. Properties of mass-losing stars
 |
Fig. 2 Input data adopted in this work for solar metallicity massive stars with mass loss. Left: non rotating models from Limongi & Chieffi (2006); right: rotating models from Hirschi, Meynet & Maeder (2005). Top: mass of the (H-exhausted) He core MHeC, of the star at explosion MExp and of the compact remnant MRem as a function of the initial stellar mass M∗. Bottom: derived quantities are the mass of the wind MWind = M∗ − MExp, the mass of the nuclearly processed layer MProc = MHeC − MRem and of the unprocessed (22Ne-normal) envelope MEnv = MWind-MProc and the mass of the SN ejecta MEj = MExp − MRem In all cases, curves are smoothly interpolated between model results. |
We adopt two sets of stellar models in this work. They are calculated for stars of solar metallicity, and in both cases the solar mixture of Anders & Grevesse (1979) is adopted. The corresponding metallicity is Z⊙ = 0.019, substantially higher than more recent values (Lodders 2003; Asplund et al. 2010) and this difference results in particular from the reduction in the past decade of the solar abundances of C, N, O and Ne, which are key elements for the purpose of this work. For obvious consistency reasons, we keep here the Anders & Grevesse (1979) values, when comparing our results for GCR to solar ones.
The first set of stellar models is the one of the Frascati group (Limongi & Chieffi 2006, hereafter LC06). It comprises 15 model stars between 11 and 120 M⊙ with mass loss but no rotation. The model includes all stages of hydrostatic nuclear burning and simulates the final stellar explosion by imparting an initial velocity to a mass coordinate of 1 M⊙ (i.e. well inside the Fe core of the stars); the mass cut (the limit separating the ejecta of mass MEj from the compact remnant of mass MRem) is chosen such that 0.1 M⊙ of 56Ni is ejected by the explosion.
The various masses involved in the “toy model” of Sect. 2.1 and Fig. 1 are provided in Table 2 of LC06 and are displayed in Fig. 2 (top left) of this work, whereas derived quantities are displayed in Fig. 2 (bottom left). It can be seen that stars with M∗ < 20 M⊙ have lost a negligible amount of mass prior to the explosion (MWind < MEj) and the ST phase starts within the ambient ISM. Stars with M∗ > 30 M⊙ have MHeC > MExp, i.e. they explode as WR stars, having expelled nuclearly processed layers in their winds. But only for the most massive stars (M∗ > 60 M⊙) one has MEj < MProc, i.e. in the beginning of the ST phase the shock wave still expands into material with a composition reflecting that of the nuclearly processed core; for lower mass stars (30 < M∗/M⊙ < 60) the ST phase starts when the shock wave encounters material with mixed composition from the core and the envelope, i.e. less enriched in H- and He- burning products. An interesting feature of those models is that the mass of the ejecta MEj ~ 10 M⊙ is similar for all of them, leading to similar properties (duration, swept-up mass) for their corresponding ST phases.
The second set of stellar models is that of the Geneva group, calculated by Hirschi et al. (2005, hereafter HMM05) and includes both mass loss and rotation for stars with mass between 12 and 60 M⊙; it has been complemented with results for stars of 85 and 120 M⊙, kindly provided by Meynet (priv. comm.). The initial rotational velocity is vRot = 300 km s-1 on the ZAMS, corrrsponding to an average velocity of 220 km s-1 on the main sequence, i.e. close to the average observed value. Non-rotating models with the same physical ingredients (for convection, mass loss, etc.) have also been calculated for comparison. The evolution has been calculated to the end of Si-burning but the final SN explosion was not considered. Instead, an empirical prescription was used to evaluate the mass of the compact remnant. The masses of our “toy model”, as given in Table 2 of HMM05, are displayed in Fig. 2. There is an important difference with respect to Table 2 of HMM05: they provide the mass of He-core at the time of the explosion and for the most massive stars this coincides with MExp (i.e. the mass left to the star at explosion is smaller than the maximum extent of the He-core); however, we are interested in the true value of MHeC (since this will determine how much mass of processed material the shock wave will encounter) and that value is obtained through the detailed results of HMM05 (displaying the wind composition as a function of time – or of mass left).
Comparing the results of LC06 and HMM05 one sees that rotation increases the mass loss (MWind larger in HMM05), thus leaving the star with a smaller mass at explosion (MExp smaller in HMM05). Rotation also increases the size of nuclearly processed regions (MHeC larger in HMM05), because matter is rotationally mixed outwards to greater distances than achieved through convection. In turn, this leads to larger amounts of processed material MProc for the HMM05 models.
The aforementioned features of rotating vs non-rotating models, which are explained in detail in e.g. Maeder & Meynet (2000) are crucial for understanding the differences in the corresponding wind yields of the stars.
2.3. The wind composition of massive stars
LC06 provided (private communication) yields yi of all stable nuclear species, from H to Ge, included in their models and ejected through the winds of the stars, up to the moment of the explosion. HMM05 provide (Table 3 in their paper) the net yields yn,i of the winds of their models for stable species from 3He to 23Na, from which the yields can be recovered through 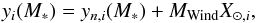 (1)where the adopted solar values X ⊙ ,i are displayed in Table 1 of HMM05.
(1)where the adopted solar values X ⊙ ,i are displayed in Table 1 of HMM05.
The wind yields of a few selected species appear in Fig. 3 for the non-rotating models of LC06 and for both the non-rotating and the rotating models of HMM05. It can be seen that the results for non-rotating models of LC06 and HMM05 generally agree very well for stars up to 40 M⊙. Their results differ only for the 60 M⊙ model (and presumably for higher masses as well) and only for the He-burning products 12C, 16O and 22Ne. Because both HMM05 and LC06 use the same prescriptions for mass loss, the reason for that discrepancy could be the use of a small amount of overshooting in HMM05.
 |
Fig. 3 Total masses of selected isotopes in the winds of the massive stars from the two sets of models adopted in this work. Solid curves are yields from HMM05 (with rotation) and dotted curves from LC06 (no rotation), in both cases interpolated between model results. The points correspond to results of the HMM05 models with no rotation and, in general, agree well with LC06 results except for the 60 M⊙ star. |
Rotation has a twofold effect on stellar yields: it increases the size of the nuclearly processed layers (because it mixes material to greater distances than convection alone) and reduces the escape velocity in the stellar equator, allowing larger amounts of mass to be ejected in the wind. Both effects enhance the wind yields up to a certain mass limit; above it, the wind has removed so much mass that less material is left in the star to be processed in subsequent stages of the evolution, thus reducing the corresponding yields. This is the case, for instance, with the He-burning products 12C and 22Ne, the yields of which decrease above ~60 M⊙ in the rotating HMM05 models (see Fig. 3 and HMM05 for details).
In the following we assume that the wind interaction with the ISM has not substantially changed the wind stratification: the forward shock will first encounter the innermost wind layers, which contain processed material in the most massive stars; later it will encounter the outer wind layers (containing mostly the initial composition), before running into the ISM. Figure 4 displays the mass integrated composition of the wind (for a few key metals), as encountered by the forward shock, moving outwards from MExp, for two rotating model stars of 25 M⊙ and 60 M⊙ (from HMM05). The quantity 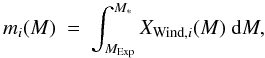 (2)is displayed as a function of mass coordinate M, Xwind,i(M) being the mass fraction of isotope i in the wind of the star of mass M∗. Obviously, one has mi(MExp) = 0. and mi(M∗) = yi(M∗), i.e. at crossing the last (outermost) wind layer, the forward shock has encountered the totality of the yield yi(M∗).
(2)is displayed as a function of mass coordinate M, Xwind,i(M) being the mass fraction of isotope i in the wind of the star of mass M∗. Obviously, one has mi(MExp) = 0. and mi(M∗) = yi(M∗), i.e. at crossing the last (outermost) wind layer, the forward shock has encountered the totality of the yield yi(M∗).
 |
Fig. 4 Composition encountered by the forward shock wave as it moves (from left to right) through the winds of 25 M⊙ (left) and 60 M⊙(right) rotating stars. The shock wave starts at MExp = 10 M⊙and 14.8 M⊙, respectively, and the ST phase sets in when a mass MS1 = MExp has been swept up and has presumably been well mixed. The quantities displayed correspond to the mass integrated composition of the wind, starting at MExp. |
An inspection of Fig. 4 shows that
-
for the 25 M⊙ star (no He-burningproducts encountered by the shock wave), the innermost layerscontain most of the 14N produced by the CNO cycle(its mass increases slowly in the outermost layers), and little of12C and 16O, which are depleted by the CNO cycle(their mass increases rapidly in the outermost layers);20Ne and 22Ne are little affected byH-burning and their integrated wind mass increases in a wayintermediate between 14N and 12C.
-
for the 60 M⊙ star (He-burning, then H-burning products encountered by the shock wave), the quasi-totality of the 12C and 22Ne produced by He-burning are encountered in the inner layers (inside ~ 25 M⊙), while essentially no 14N is left in that region; the majority of 14N is found in the region 25 < M/M⊙ < 50 while substantial 16O is found in the unprocessed envelope (beyond 50 M⊙). Finally, 20Ne is little affected everywhere (almost constant mass fraction) and its integrated mass rises in step with the wind mass of the star.
If detailed information (i.e. wind composition as function of wind mass coordinate) is available, the composition of the material swept-up by the forward shock can be calculated in a consistent way. If only the wind yields yi and the various characteristic masses of Fig. 2 are available, one may adopt the following approximations:
-
(i)
stars that never reach the WR stage (M∗ < 22 M⊙ for rotating models and M∗ < 34 M⊙ for non rotating ones) have their envelopes fully mixed after the 1st dredge-up episode in the red supergiant phase; the wind composition is then simply obtained as
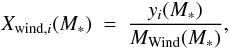 (3)
(3) -
(ii)
stars that do not reach the WR stage first eject their unprocessed envelope of mass MEnv and composition Xenv,i = XISM,i and then the innermost processed layers of mass MProc and composition XPROC,i such that
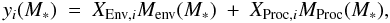 (4)which allows one to derive
XProc,i, i.e. an average abundance
in the processed layers, and obtain thus an average wind composition profile
(4)which allows one to derive
XProc,i, i.e. an average abundance
in the processed layers, and obtain thus an average wind composition profile 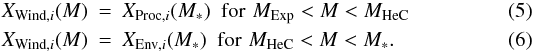
2.4. The circumstellar environment of massive stars
According to the ideas outlined in Sect. 2.1, particle acceleration to GCR energies starts when a mass MS1 ~ MEj has been swept-up by the forward shock. The composition of that material at the very beginning of particle acceleration is that of the material located at mass coordinate A1 = MExp+ MEj and obviously constitutes an extreme for the abundances of the corresponding elements (upper limit for those produced in the stellar interior and lower limit for those destroyed, like H). In the following we shall assume that at the time of the explosion the stellar wind has fully kept the stratification of its various layers, as they were progressively leaving the stellar surface.
The circumstellar region hit by the forward shock has a complex structure that depends on the properties of the exploded star. That structure has been explored in some detail with hydrodynamical models by Garcia-Segura et al. (1996a,b) for non-rotating stars. In the case study of a 35 M⊙ star, they have found that the rapid wind of the O star excavates a large bubble (radius ~36 pc) of low density (10-3 cm-3). Inside it propagates a dense (~1 cm-3), slow wind – released during the red supergiant phase – which occupies the innermost few pc (depending on its assumed velocity, of the order of a few tens of km s-1). The subsequent fast (~103 km s-1) WR wind compresses the RSG wind, and most of the mass of the latter is found within a thin shell.
The aforementioned study illustrates the complexity of the situation, but its results can hardly be generalized to the whole mass range of massive stars (for instance, lower mass stars will not display the fast WR wind). Indeed, its results cannot even be safely used for the 35 M⊙ star, since they depend so critically on the adopted parameters of the model (mass loss rates and wind velocities for the various stages). And they certainly fail to describe the situation for rotating stars, which display slow but intense (and not radially symmetric) mass losses on the main sequence.
In view of these uncertainties, we adopt here a simplified prescription for the structure of the circumstellar bubble, assuming spherical symmetry in all cases. We assume that the winds have excavated a bubble of mean density n0 = 0.1 cm-3 and, consequently, of radius 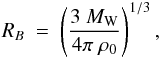 (7)with ρ0 = n0 mp, mp being the proton mass. Inside the bubble, the density profile is ρ(r) ∝ r-2, i.e. it corresponds to a steady stellar wind with mass loss rate
(7)with ρ0 = n0 mp, mp being the proton mass. Inside the bubble, the density profile is ρ(r) ∝ r-2, i.e. it corresponds to a steady stellar wind with mass loss rate 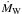 and velocity vW, which is given by
and velocity vW, which is given by 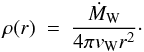 (8)Our choice of ρ0 automatically fixes the ρ(r) profile and corresponds to a combination of
(8)Our choice of ρ0 automatically fixes the ρ(r) profile and corresponds to a combination of 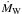 and vW values. Obviously, one has
and vW values. Obviously, one has 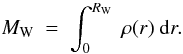 (9)Outside RW we assume an ISM with constant density ρISM = 1 mp cm-3. Our approach is similar to Caprioli (2011), but we do not consider here the more complicate case of a WR wind overtaking a RSG wind.
(9)Outside RW we assume an ISM with constant density ρISM = 1 mp cm-3. Our approach is similar to Caprioli (2011), but we do not consider here the more complicate case of a WR wind overtaking a RSG wind.
2.5. Evolution during the Sedov-Taylor (ST) phase
We follow the propagation of the forward shock first through the wind bubble and then through the ISM with a simple model presented in Ptuskin & Zirakashvili (2005) and, in a more concise form, in Caprioli (2011, his Eqs. (3.4) to (3.9)). We start the calculation from the “free-expansion” (ejecta-dominated) phase, where the swept-up mass is smaller than MEj and which can be described by self-similar analytical solutions. In the subsequent ST phase (swept-up mass < MEj), the model is based on the “thin shell” approximation (e.g. Ostriker & McKee 1988) which assumes that the swept-up mass is concentrated in a thin shell behind the shock. We solve numerically the time-dependent equations for continuity of mass, energy and momentum, to recover shock radius and velocity as a function of time. Unlike Caprioli (2011), we assume full adiabaticity in the ST phase, i.e. we do not take into account the 10–20% energy losses of the shock through CR acceleration, which would reduce the shock velocity ( ∝ 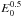 ) by less than 10%. The mass swept-up in the ST phase inside shock radius RS is
) by less than 10%. The mass swept-up in the ST phase inside shock radius RS is 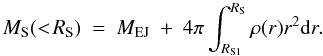 (10)We follow the evolution all the way through the ST phase, which ends when a significant fraction of the energy of the cooling remnant is radiated away (through recombination emission); for a solar mixture this occurs at time
(10)We follow the evolution all the way through the ST phase, which ends when a significant fraction of the energy of the cooling remnant is radiated away (through recombination emission); for a solar mixture this occurs at time 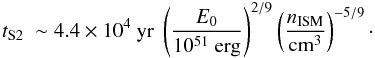 (11)In the framework of this simple model we are able to calculate the composition of the material encountered (and presumably accelerated) by the forward shock as a function of time, or of the swept-up mass: indeed, the integrated mass of each element swept up by the forward shock is given by an equation similar to Eq. (2),
(11)In the framework of this simple model we are able to calculate the composition of the material encountered (and presumably accelerated) by the forward shock as a function of time, or of the swept-up mass: indeed, the integrated mass of each element swept up by the forward shock is given by an equation similar to Eq. (2), 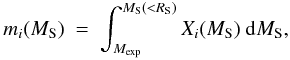 (12)where Xi(MS) = Xwind,i for MS < M∗ (Sect. 2.3) and Xi(M) = XISM,i for MS > M∗, i.e. when the shock propagates into the ISM; the upper limit in the integral is given by Eq. (10).
(12)where Xi(MS) = Xwind,i for MS < M∗ (Sect. 2.3) and Xi(M) = XISM,i for MS > M∗, i.e. when the shock propagates into the ISM; the upper limit in the integral is given by Eq. (10).
Equation (12) allows one to link the stellar model, i.e. the abundance profiles X(M), to the evolution during the ST phase through Eq. (10), and to the properties of the shock wave. Since the mass MS2 swept-up in the end of the ST phase is much larger than the wind mass in all cases (a few 103 M⊙, compared to ~100 M⊙ at most) for the largest part of the ST phase the swept up material has ISM composition. In order to obtain significant deviations from the solar composition, such as the observed 22Ne/20Ne ratio, one should assume that significant acceleration occurs only in the early ST phase, when the forward shock is stronger and its velocity higher.
3. Results
3.1. Composition of matter in the ST phase
 |
Fig. 5 Evolution of the SN remnants of two rotating stars of initial masses 20 M⊙ (dotted) and 60 M⊙ (solid), respectively. Top: velocity of the forward shock and swept-up mass. Middle: shock radius and density profile before shock arrival (see text). Bottom: composition of the matter swept up up to time t by the shock wave, for the 14N/16O and 22Ne/20Ne ratios. In all panels, the thickportions of the curves indicate the period of efficient particle acceleration, i.e. from the beginning of the ST phase and as far as υs > υmin. The value of υmin (=1900 km s-1 for the rotating star models in the figure) is chosen so that the IMF averaged theoretical ratio of 22Ne/20Ne matches the observed one in GCR (see text, Eq. (13) and Fig. 6). |
Figure 5 (top) displays the evolution of the velocity υS and radius RS of the forward shock and of the mass MS(<RS) swept up by it, for a 20 and a 60 M⊙ rotating star, respectively. The density of the unperturbed ISM is taken to be 1 cm-3 in all cases.
The similarity of the curves for υS, RS and MS(<RS) for the 20 and 60 M⊙ stars simply reflects the self-similarity of the ST solution. The small differences in the early ST phase are caused by the difference of the ejected mass MEj in the two stars (6 vs. 10 M⊙, see Fig. 2), since the other parameters (E0 and nISM) are the same.
The bottom panel of Fig. 5 displays the evolution of the 14N/16O and 22Ne/20Ne ratios (i.e. the ratios of the corresponding masses of Eq. (12) for each isotope), expressed in units of the corresponding solar values. In both cases, the forward shock first encounters layers with low 16O and high 14N, resulting in a high 14N/16O ratio (in the 60 M⊙ star, 14N is depleted from He-burning in the innermost layers, resulting in a slightly lower 14N/16O ratio than in the 20 M⊙ case). Subsequently, in the 20 M⊙ star the shock moves rapidly through the small remaining stellar envelope (3.4 M⊙) and starts propagating into the ISM, thus decreasing its mass-integrated 14N/16O ratio rapidly. In the 60 M⊙ star, the shock runs through ~20 M⊙ of processed material, with a high value of 14N/16O, before reaching the ISM; the corresponding 14N/16O ratio decreases more slowly than in the 20 M⊙ case.
The evolution of 22Ne/20Ne is quite different in the two models. In the 20 M⊙ star, no He-burning products are encountered by the shock wave and the 22Ne/20Ne ratio always has its initial (solar) value. A high 22Ne/20Ne ratio is initially encountered in the processed layers of the 60 M⊙ star, which is progressively diluted as the shock moves outwards.
 |
Fig. 6 Abundance ratios of various nuclear species in GCR source normalized to the corresponding solar ones as a function of the initial stellar mass. In all panels, solid curves correspond to models of HMM05 and dotted curves to models of LC06. Upper, thin curves are for GCR accelerated at the beginning of the ST phase and lower, thick curvesfor the time-average at the end of GCR acceleration. An average over a Salpeter IMF (and accounting for the swept-up mass in each case) produces the vertical segments to the right, their top point corresponding to the beginning and the bottom one to the end of the GCR acceleration phase, respectively (also indicated by filled squares). These results are compared to GCR source abundance ratios as derived by ACE data (points at the extreme right with error bars) in Binns et al. (2005). The most significant, unaffected by FIP, volatility etc., is the one of 22Ne/20Ne. The end of the GCR acceleration phase is assumed to correspond to shock velocities υmin such that the time and IMF averaged theoretical ratio (squares) of 22Ne/20Ne matches the observed one (see text). For the set-up adopted here we find υmin = 1900 km s-1 for HMM models and υmin = 2400 km s-1 for LC06 models. |
3.2. Composition of accelerated particles
The composition curves of the bottom panel of Fig. 5 give the time (or mass) integrated composition encountered by the shock wave and, in consequence, the composition of the particles that have been accelerated up to that time. We assume here that particles are accelerated to GCR energies with the same efficiency for shock velocities higher than some critical value υmin, which is the same for all stellar masses. We determine υmin empirically by requiring that, when averaged over a stellar Initial mass function (IMF) Φ(M∗), the ratio 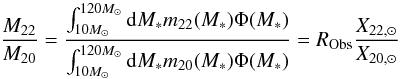 (13)where RObs = 5.3 ± 0.3 is the observationally determined source GCR ratio of 22Ne/20Ne in solar units and m22(M∗) and m20(M∗) are calculated from Eq. (12) for stars of mass M∗ and for swept-up masses MS(υ > υmin).
(13)where RObs = 5.3 ± 0.3 is the observationally determined source GCR ratio of 22Ne/20Ne in solar units and m22(M∗) and m20(M∗) are calculated from Eq. (12) for stars of mass M∗ and for swept-up masses MS(υ > υmin).
We adopt here a Salpeter IMF 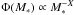 with X = 2.35. The results of the procedure appear in Fig. 6 for a few selected abundance ratios and for the models of both HMM05 (solid curves) and LC06 (dotted curves). In all panels, the upper (thin) curves correspond to the composition accelerated at the beginning of the ST phase (maximal possible deviations from solar composition). Stars with mass < 22 M⊙ (for HMM05) and 32 M⊙ (for LC06) display no He-burning products in their accelerated particles. N is overabundant in lower stellar masses, because of the 1st dredge-up.
with X = 2.35. The results of the procedure appear in Fig. 6 for a few selected abundance ratios and for the models of both HMM05 (solid curves) and LC06 (dotted curves). In all panels, the upper (thin) curves correspond to the composition accelerated at the beginning of the ST phase (maximal possible deviations from solar composition). Stars with mass < 22 M⊙ (for HMM05) and 32 M⊙ (for LC06) display no He-burning products in their accelerated particles. N is overabundant in lower stellar masses, because of the 1st dredge-up.
The lower (thick) curves in all panels of Fig. 6 correspond to a composition accelerated up to the end of the acceleration period which is assumed to occur for a shock velocity υmin. The corresponding IMF-averaged quantities (between 10 and 120 M⊙) are displayed to the right of the curves: their uppermost point corresponds to the beginning of the ST phase and the lower one (also indicated with a filled square) to the end of the acceleration period, i.e. to υmin. The value of υmin is found to be ~1900 km s-1 for the HMM05 models with rotation and ~ 20% higher (2400 km s-1) for the LC06 models without rotation. The reason for that difference is, of course that rotating models have thicker processed layers, requiring more dilution with circumstellar material.
The top and middle panels of Fig. 6 display the corresponding ratios for 12C/16O and 14N/16O, respectively. In both cases, the IMF averaged ratios are higher than the observed ones in GCR (which are, in turn, higher than solar), by factors of 1.5–2. Unlike 22Ne/20Ne, these are ratios of different elements with different atomic properties. The GCR source abundances are known to be affected by atomic effects, e.g. First ionization potential (FIP), or, perhaps more plausibly, volatility and mass/charge ratio (see extensive discussion in Meyer et al. 1997). The analysis of these effects is beyond the scope of this study. We simply notice here that observations indicate that refractory elements are relatively more abundant in GCR sources than volatiles. Meyer et al. (1997) attribute that to the fact that refractories are locked up in grains, which are sputtered by the shock wave and the released ions are easily picked up and accelerated. Because 16O is more refractory than both 14N and 12C, it is expected that its abundance in GCR source will be enhanced by that effect, and the corresponding 12C/16O and 14N/16O ratios in GCR source will be lower than predicted from stellar nucleosynthesis alone. The fact that we obtain higher than observed ratios for 12C/16O and 14N/16O in Fig. 6 is encouraging in that respect, because the aforementioned atomic effects would lower those ratios, hopefully to their observed values2.
3.3. Efficiency of particle acceleration
The material of Sects. 3.1 and 3.2 is summarized in Fig. 7 for the rotating models of HMM05. The forward shock, launched at mass coordinate MExp, sweeps up a mass MS1 ~ MExp and then starts accelerating particles, at mass coordinate A1 = MExp+MS1, up to point A2 (where its velocity becomes υmin). For rotating stars with M < 15 M⊙, A1 lies beyond the stellar surface and only ISM is accelerated. In stars with 15 < M∗/M⊙ < 25, A1 lies beyond the processed/mixed interior MHeC and the forward shock first accelerates envelope and then ISM material. For stars above 35 M⊙, the shock first accelerates processed material (hatched aerea), then the – 22Ne normal – envelope and then ISM. Finally, for stars with M > 70 M⊙, particle acceleration ends when the shock is still within the massive stellar envelope.
 |
Fig. 7 Graphical presentation of the results discussed in Sect. 3.3. Particle acceleration starts at the beginning of the ST phase, located at mass coordinate A1 = MExp+ MEj, i.e. when the forward shock (FS, arrows), launched at MExp, has swept up a mass MS1 = MEj. Acceleration stops at mass coordinate A2, corresponding in the case dicussed here to a shock velocity of 1900 km s-1. The mass sampled by the FS between those two regions is MAcc = A2 − A1. For rotating stars with mass M > 30 M⊙, an increasing part of MAcc includes nuclearly processed material (shaded aerea), while for rotating stars with M < 18 M⊙, MACcc contains only material of ISM (=solar) “composition”. |
The mass of circumstellar material from which particles are accelerated is MACC = A2 − A1 and lies in the range 30–40 M⊙. The mass of particles that have been accelerated is given by 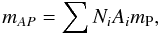 (14)where Ni is the total number of nuclei of species i, Ai the corresponding mass number and mP the proton mass. The number Ni, or rather the product NiAi, can be determined by noticing that the total energy carried by those accelerated particles is a fraction f of the kinetic energy E0 of the supernova
(14)where Ni is the total number of nuclei of species i, Ai the corresponding mass number and mP the proton mass. The number Ni, or rather the product NiAi, can be determined by noticing that the total energy carried by those accelerated particles is a fraction f of the kinetic energy E0 of the supernova 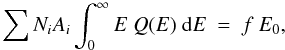 (15)where Q(E) is the spectrum of accelerated particles (Ai appears on the left side of Eq. (15) because energies are expressed in energy units per nucleon). The efficiency f of conversion of E0 to accelerated particles escaping the supernova is estimated to f ~ 0.1, while another 0.1–0.2 goes to the acceleration of particles that are finally trapped in the SN (Ellison & Bykov 2011). The particle spectrum is often described by a power law in momentum
(15)where Q(E) is the spectrum of accelerated particles (Ai appears on the left side of Eq. (15) because energies are expressed in energy units per nucleon). The efficiency f of conversion of E0 to accelerated particles escaping the supernova is estimated to f ~ 0.1, while another 0.1–0.2 goes to the acceleration of particles that are finally trapped in the SN (Ellison & Bykov 2011). The particle spectrum is often described by a power law in momentum 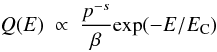 (16)where β = v/c is the velocity expressed as a fraction of the light velocity, p is the particle momentum per nucleon, the factor s is usually 2 < s < 3 (for strong shocks) and EC is a cut-off energy, here taken to be 3 TeV (the results are insensitive to much higher values).
(16)where β = v/c is the velocity expressed as a fraction of the light velocity, p is the particle momentum per nucleon, the factor s is usually 2 < s < 3 (for strong shocks) and EC is a cut-off energy, here taken to be 3 TeV (the results are insensitive to much higher values).
Assuming that the spectrum of accelerated particles escaping the SN is given by Eq. (16), one finds the efficiency with which particles are accelerated from the shocked circumstellar medium, through Eqs. (14) to (16): 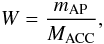 (17)and for rotating stars it is found to be in the range 3–6 × 10-6 i.e. a few particles out of a million encountered ones are accelerated by the forward shock to GCR energies. For non-rotating stars, the energetics is the same, but the swept-up mass is smaller (by a factor of two, on average, to obtain the observed 22Ne/20Ne ratio) and the corresponding efficiency is W ~ 10-5. These estimates constitute only a gross average, since the efficiency of particle acceleration may depend on several factors, not considered here, such as the density of the circumstellar medium or the shock velocity – through a smoothly varying function f(vS) instead of the Heavyside function f(>υmin) = 1 and f(<υmin) = 0 considered here – or the shock radius at the time of acceleration, since particles may subsequently suffer adiabatic cooling before escaping (e.g. Drury 2011; Bykov & Ellison 2011). Notice that some of those effects may have opposite time dependencies. For instance, particles accelerated earlier on (at higher shock velocities and presumably with higher efficiencies) are expected to suffer more from adiabatic cooling (because they are produced at smaller radii). These effects require a much more thorough investigation. As a first step in that direction, we also tested the case where the efficiency of shock acceleration varies with shock velocity as f ∝ υ2 (Drury 2011). In that case, material with high 22Ne/20Ne is efficiently accelerated in the inner layers of the most massive stars. To obtain again the observed GCR source 22Ne/20Ne ratio, one has to dilute the mixture by allowing acceleration for shock velocities lower then the reference values found above: we thus find values of υmin = 1600 km s-1 for the HMM05 yields and 2150 km s-1 for the LC06 yields; the corresponding overall acceleration efficiencies increase then by ~40% from the reference values given above, ranging from 4–7 × 10-6 for HMM05 yields to 1–1.4 × 10-5 for LC06 yields. The reason for obtaining such a small difference (only a few hundreds of km s-1) between the non-realistic reference case and the – perhaps more realistic – case of velocity dependent efficiency, is the adopted unified treatment, which considers acceleration in both low-mass and high-mass supernova: the former accelerate almost pure ISM with low 22Ne/20Ne and the latter almost pure wind material with high 22Ne/20Ne. Allowing for lower values of υmin involves a considerably larger amount of ISM processed by low-mass supernovae, since the lower acceleration efficiency (f ∝ υ2) is more than compensated for by the nISM4πr2dr factor.
(17)and for rotating stars it is found to be in the range 3–6 × 10-6 i.e. a few particles out of a million encountered ones are accelerated by the forward shock to GCR energies. For non-rotating stars, the energetics is the same, but the swept-up mass is smaller (by a factor of two, on average, to obtain the observed 22Ne/20Ne ratio) and the corresponding efficiency is W ~ 10-5. These estimates constitute only a gross average, since the efficiency of particle acceleration may depend on several factors, not considered here, such as the density of the circumstellar medium or the shock velocity – through a smoothly varying function f(vS) instead of the Heavyside function f(>υmin) = 1 and f(<υmin) = 0 considered here – or the shock radius at the time of acceleration, since particles may subsequently suffer adiabatic cooling before escaping (e.g. Drury 2011; Bykov & Ellison 2011). Notice that some of those effects may have opposite time dependencies. For instance, particles accelerated earlier on (at higher shock velocities and presumably with higher efficiencies) are expected to suffer more from adiabatic cooling (because they are produced at smaller radii). These effects require a much more thorough investigation. As a first step in that direction, we also tested the case where the efficiency of shock acceleration varies with shock velocity as f ∝ υ2 (Drury 2011). In that case, material with high 22Ne/20Ne is efficiently accelerated in the inner layers of the most massive stars. To obtain again the observed GCR source 22Ne/20Ne ratio, one has to dilute the mixture by allowing acceleration for shock velocities lower then the reference values found above: we thus find values of υmin = 1600 km s-1 for the HMM05 yields and 2150 km s-1 for the LC06 yields; the corresponding overall acceleration efficiencies increase then by ~40% from the reference values given above, ranging from 4–7 × 10-6 for HMM05 yields to 1–1.4 × 10-5 for LC06 yields. The reason for obtaining such a small difference (only a few hundreds of km s-1) between the non-realistic reference case and the – perhaps more realistic – case of velocity dependent efficiency, is the adopted unified treatment, which considers acceleration in both low-mass and high-mass supernova: the former accelerate almost pure ISM with low 22Ne/20Ne and the latter almost pure wind material with high 22Ne/20Ne. Allowing for lower values of υmin involves a considerably larger amount of ISM processed by low-mass supernovae, since the lower acceleration efficiency (f ∝ υ2) is more than compensated for by the nISM4πr2dr factor.
As approximate as they may be, the results obtained here through the constraint of the observed GCR source 22Ne/20Ne ratio, clearly indicate that acceleration has to occur for shock velocities higher than ~1500 km s-1, and they may help to improve our understanding of particle acceleration in SN remnants.
4. GCR cannot be accelerated (mainly) in superbubbles
The idea that CGR are accelerated mainly in superbubbles has been suggested by Kafatos et al. (1981) and reassessed by Higdon et al. (1998). Massive stars are mainly formed in OB associations and the winds of the most massive of them initiate the formation of superbubbles, while the subsequent SN explosions power the expansion of those superbubbles for a few 107 years. Higdon et al. (1998) argued that the environment of these superbubbles, enriched with the ejecta of stellar winds and core collapse SN explosions, provides a composition that compares favourably to the inferred GCR source composition.
One potential problem with that idea is that 59Ni, a well-known product of SN nucleosynthesis, is absent from GCR arriving on Earth (Wiedenbeck et al. 1999). Since 59Ni is unstable to electron capure, with a lifetime of ~105 y, Higdon et al. (1998) argued that SN explosions occur within the superbubble with a sufficiently low frequency (less than one SN every 3 × 105 y), to allow for the decay of 59Ni between two SN explosions. Prantzos (2005) pointed out that energetic stellar winds can also accelerate particles and they are not intermittent (like SN) but occur continuously in superbubbles; in that case 59Ni is continuously accelerated to GCR energies and, being unable to capture an electron, it becomes effectively stable and it should be detectable in GCR. Binns et al. (2008) counter-argued that the period of energetic WR winds represents a small (albeit not negligible) fraction in the early lifetime of an OB association and therefore only little (and presumably undetectable) amounts of 59Ni would be accelerated, thus saving the “superbubble paradigm”.
In the meantime, Higdon & Lingenfelter (2003) evaluated the isotopic composition of 22Ne/20Ne – the critical abundance anomaly in GCR – expected in a superbubble, based on (a very heterogeneous set of) then available yields of WR stars and SN. They found that the GCR 22Ne/20Ne ratio “can be easily understood as the result of GCR accelerated primarily out of superbubbles with a mean metallicity ZSB = 2.7 ± 0.4 Z⊙” and that this result “provides strong, additional evidence for a superbubble origin of GCR”. In a subsequent paper, Lingenfelter & Higdon (2007) quantitatively explored that senario for other GCR abundances, finding again that results compare favourably to observations.
Despite their apparent sophistication, the aforementioned arguments for a superbubble origin of GCR miss a simple point: massive stars are the principal source of both 20Ne and 22Ne in the Universe. As a result, the 22Ne/20Ne ratio of a generation of massive stars (integrated over an IMF and including WR winds and all kinds of SN ejecta) should be solar3. Because 22Ne is overabundant with respect to 20Ne only in the massive star winds (and not in the SN ejecta or the ISM), a popular exercise in the past 30 years or so consisted in evaluating the mixing ratio of WR ejecta with SN ejecta (or with average ISM), as to obtain the observed 22Ne/20Ne ratio in GCR (see Introduction and references therein).
However, it is expected that a properly weighted mixture of the ejecta of massive stars in a superbubble (i.e. including stellar winds and SN ejecta and folded with a stellar IMF) would produce a solar 22Ne/20Ne ratio. In this section, the same exercise is repeated with the yields of LC06 and HMM05 and by taking into account the corresponding stellar lifetimes. In Fig. 8 we present again the adopted 20Ne and 22Ne yields of LC06 and HMM05 for the stellar winds (solid and dotted curves, i.e. the same as in Fig. 3) and also the total yields (winds plus SN ejecta, points). The latter are from LC06 for stars with mass loss (but no rotation) and from Woosley & Weaver (1995, WW95) for stars without mass loss; they agree well overall, except for 20Ne in stars around 20 M⊙. For the SN ejecta, we consider only stars with M < 40 M⊙, i.e. we assume that more massive stars eject their 20Ne and 22Ne through their winds and then form black holes; in that case we maximize the 22Ne/20Ne ratio expected from massive stars.
 |
Fig. 8 Yields of 20Ne (top) and 22Ne (bottom) as a function of the initial stellar mass. Wind yields are from HMM05 (solid curves) and LC06 (dotted curves), respectively (same as in Fig. 3). Total yields are from LC06 (filled squares) and WW95 (asterisks). |
An inspection of Fig. 8 shows that the total (wind+SN) 22Ne yields of M < 40 M⊙ stars are comparable to the wind 22Ne yields of the most massive (~100 M⊙) stars; however, the corresponding total 20Ne yields of M < 40 M⊙ stars are at least 10 times higher than the wind 20Ne yields of the most massive (~100 M⊙) stars. Thus, while the production of 22Ne receives a sizeable contribution from the most massive stellar winds (at least for the rotating stars), the production of 20Ne is totally dominated by the SN ejecta of M < 40 M⊙ stars. In a coeval stellar population, like the one expected in an OB association or a superbubble, the 22Ne/20Ne ratio will evolve then from higher than solar to ~ solar values, as the M < 40 M⊙ stars eject their core products a few Myr after their more massive counterparts.
 |
Fig. 9 Evolution of composition in a superbubble. Top left: ejection rate of 20Ne (dotted) and 22Ne (solid) in M⊙/Myr per 1 M⊙ of stars formed (assuming a Salpeter IMF between 0.1 and 120 M⊙). Top right: supernova rate per Myr. Middle: total mass of 20Ne (dotted) and 22Ne (solid) accumulated in the superbubble for no initial gas (M0 = 0, left) and for an initial mass of gas equal to 1/5 of the formed stars (M0 = 0.20, right); in the former case 22Ne dominates by mass early on, whereas in the latter the mass of 20Ne dominates from the very beginning. Bottom: corresponding evolution of the O/H (dashed) and of the (22Ne/20Ne)SB ratio (dotted) in the SB gas; the solid curve represents the (22Ne/20Ne)CR ratio of particles accelerated up to that time and has to be compared to the observed GCR source ratio (dotted horizontal line). |
We quantitative illustrate this effect in Fig. 9, where we present the evolution of a stellar population born at time t = 0 with a Salpeter IMF and total mass of 1 M⊙ (results can be directly scaled to masses of OB associations, while abundances and abundance ratios remain the same). The top right panel displays the rate of SN explosions; for a total stellar mass of 104 M⊙, resulting in a ~100 OB stars, there are about 3 SN/Myr, i.e. ~1 SN every 300 000 yr, as evaluated in Higdon et al. (1998) to avoid the problem of 59Ni acceleration. The top left panel displays the ejection rates of 20Ne and 22Ne (in M⊙/Myr per M⊙ of stars formed): 22Ne from stellar winds dominates only for a couple of Myr but ~5 Myr after the stellar formation, 20Ne from M < 40 M⊙ explosions dominates. Notice that, to maximise the 22Ne/20Ne ratio, we adopted only the yields of HMM05 for these calculations (i.e. corresponding to the solid curves in Fig. 8 with wind yields only above M = 40 M⊙).
The instantaneous (22Ne/20Ne)SB ratio in the superbubble at time t is the ratio of the amounts of 20Ne and 22Ne cumulated up to that time, which are provided in the middle panels of Fig. 9. To evaluate those quantities, one needs to make an assumption about the amount of pre-existing gas still left inside the superbubble. In the left middle panel of Fig. 9 it is assumed that no gas is left after star formation: gas is exclusively supplied by the wind and explosive stellar ejecta. In that case, 22Ne dominates early on, but 20Ne takes over after a couple of Myr. In the right middle panel it is assumed that an amount of gas with solar composition and equal to 20% of the mass of formed stars remained in the superbubble; the stellar ejecta are diluted into it and the superbubble composition is now dominated always by 20Ne.
The bottom panels of Fig. 9 display the corresponding (22Ne/20Ne)SB ratios in the superbubble. For zero initial gas (left), the instantaneous (22Ne/20Ne)SB ratio remains high – from 18 to 5 times solar – for a couple of Myr, but soon after stars of M < 40 M⊙ start dying, its value decreases rapidly to solar (as expected from the nucleosynthesis argument presented in the beginning of this section). The (22Ne/20Ne)CR (<t) ratio of particles accelerated to CR energies up to time t is the time integral of the instantaneous (22Ne/20Ne)SB ratio in the superbubble 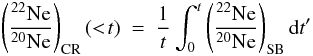 (18)where it is assumed that the efficiency of particle acceleration does not vary with time. (22Ne/20Ne)CR (<t) represents the mean CR composition accelerated by a superbubble which “operates” up to time t.
(18)where it is assumed that the efficiency of particle acceleration does not vary with time. (22Ne/20Ne)CR (<t) represents the mean CR composition accelerated by a superbubble which “operates” up to time t.
In the bottom left panel it is seen that the (22Ne/20Ne)CR (<t) ratio (in solar units) remains above the observed RObs = 5.3 ± 0.3 for about 7 Myr, while it declines steadily after that, tending to an asymptotic value of ~2, considerably smaller than observed. The corresponding metallicity in the superbubble, expressed by the O/H ratio (dashed curve), is quite high – about 10 times solar – since it represents pure core collapse SN ejecta; such high metallicity values have never been reported for any astrophysical environment (except SN remnants).
The bottom right panel of Fig. 9 displays the corresponding quantities in the more realistic case of a superbubble endowed with some gas left over from the star formation. In that case, although metallicity is still high (about 3 times solar after 7 Myr), the 22Ne/20Ne ratios never get above 3 times solar, either in the superbubble or in the accelerated particles; in fact they are close to solar for the largest part of the superbubble lifetime.
The results displayed in Fig. 9 suggest that the observed RObs = 5.3 ± 0.3 ratio in GCR cannot be obtained from material accelerated in a superbubble: even under the most favorable possible conditions, such as those adopted here (yields from rotating massive stars, only wind yields considered above M = 40 M⊙, no gas left over from star formation), the resulting 22Ne/20Ne ratio remains at high values only in the early evolution of the superbubble, during a small fraction of its lifetime. Interestingly, Binns et al. (2008) suggested that no substantial particle acceleration must occur during that early period to avoid the problem of 59Ni acceleration from the WR winds; thus, saving the “superbubble paradigm” for the origin of cosmic rays requires that acceleration occurs only in the late superbubble evolution, when the WR winds have essentially stopped and only SN inject intermittently their kinetic energy in the superbubble. However, we have shown here that during this period, the (22Ne/20Ne)CR ratio is considerably lower than observed. Indeed, under realistic conditions (some initial gas left, explosive yields also above 40 M⊙ considered, at least for some stars), the 22Ne/20Ne ratio in a superbubble would never reach values as high as observed, contrary to claims made in the literature in the past decade. It must be stressed that this conclusion does not depend on detailed adopted yields, but on a simple argument, namely that the IMF averaged 22Ne/20Ne ratio in a superbubble has to be close to solar during the longest period of the superbubble lifetime.
5. Summary
We explore some implications of the idea that cosmic rays are accelerated by the forward shock in supernova remnants during their ST phase. We focus on the chemical composition resulting from such an acceleration and, in particular, on the 22Ne/20Ne ratio, which is the most characteristic feature of the observed GCR source composition and is unaffected by atomic effects. For that purpose, we adopt recent models of the nucleosynthesis and evolution of massive stars with mass loss: those of LC06 with no rotation and those of HMM05 with rotation.
In Sect. 2 we present a detailed summary of the properties of those models and, in particular, of the chemical composition of their winds, insisting that rotating models release more 22Ne in their winds than non-rotating ones. We also present the adopted model for the evolution of a SN remnant within a stellar wind, based on the ideas of Ptuskin & Zirakashvili (2005) and the equations summarized in Caprioli (2011).
In the framework of the simple model adopted here, we follow the time-dependent composition of GCR, accelerated by the forward shock as it runs through either the ISM (for stars with M < 25–35 M⊙, depending on rotation) or through the stellar wind (for more massive stars). Indeed, during the longest part of the ST phase, the shock runs through ISM and encounters a solar composition. In order to reproduce the observed high value of (22Ne/20Ne)CR (RObs = 5.3 ± 0.3 in solar units) after accounting for the stellar IMF, we have then to assume that acceleration is efficient only during a short early period in the ST phase. We chose to use the shock velocity as a criterion for efficient acceleration and, based on the aforementioned GCR composition argument, we find that shock velocities larger than ~1900 km s-1 (for the rotating stellar models) or 2400 km s-1 (for the non-rotating ones) are required. This result is obtained by assuming a step function for the efficiency f of particle acceleration (f = 0 before the ST phase and after υmin, and f = 1 between the two). For the – perhaps more realistic – assumption of a velocity-dependent efficiency f ∝ υ2, we find slightly lower values for υmin (1600 km s-1 for HMM05 yields and 2150 km s-1 for LC06 yields, respectively). In the framework of the adopted models, this corresponds to a circumstellar mass of several tens of M⊙ encountered by the forward shock. Assuming, furthermore, that 10% of the SN kinetic energy is used in acceleration of escaping cosmic rays with standard energy spectra allowed us to evaluate the efficiency of that acceleration: we find that a few particles out of a million encountered by the forward shock are accelerated to CR energies. We also notice that this scheme of GCR acceleration does not suffer from problems related to the absence of unstable 59Ni in observed GCR composition: this heavy nucleus is well inside the SN ejecta and is not reached by the forward shock, which accelerates only wind material and ISM.
The aforementioned scenario assumes that even the most massive stars, up to 120 M⊙, develop strong forward shocks and accelerate the particles of their WR winds. For non-rotating stars, this is probably an extreme assumption, because it has been argued (Heger et al. 2003) that non-rotating massive stars of about solar metallicity collapse into black holes, if their mass is in the 30–60 M⊙ range (see their Fig. 1). Notice that stars in the 60–120 M⊙ range (the most important 22Ne producers) end as black holes in their scheme. However, for slightly higher metallicities – such as those encountered in the inner Galactic disk - these authors find that only neutron stars are formed, because higher stellar mass losses result in a less massive star at explosion. It should be noticed that the details of massive star explosions remain poorly understood at present (see e.g. Hanke et al. 2011) and so is the fate of a massive star above 30 M⊙ (see Fryer et al. 2011, for a recent – but certainly not definitive – assessment). The fate of the rotating mass-losing stars considered here is even less well known.
In view of the aformentioned uncertainties, we feel that the scenario proposed here can be considered as valid at present, although future refinements in our understanding of massive star explosions may change it quantitatively (and even qualitatively, if it turns out that most masive stars above, say, 50 M⊙, end up as black holes).
Finally, we explore the idea that CR are accelerated in superbubbles, in which case their composition results from the ejecta of both stellar winds and SN explosions. We first notice that simple nucleosynthesis arguments suggest that the resulting composition, averaged over the stellar IMF, should be very close to solar. We demonstrate this quantitatively, with a simple model for the evolving composition of a superbubble, enriched first by the (22Ne rich) winds of the most massive stars, then by the (20Ne rich) SN ejecta of less massive stars. We find that, after a few Myr the superbubble (22Ne/20Ne)SB ratio tends to solar, and so does the average (22Ne/20Ne)CR ratio in accelerated particles. We conclude that superbubbles cannot provide the observed high RObs value of GCR sources and, therefore, are not the main site of GCR acceleration. In contrast, SN remnants – including those expanding in the pre-explosion environment of a stellar wind – appear to be suitable sites of GCR acceleration.
One might think that a combined analysis of the 12C/16O and 14N/16O ratios of Fig. 6 could help to constrain the atomic processes shaping the GCR source abundances. However, the abundances of 12C and 16O are affected by the still uncertain value of the 12C(α,γ)16O reaction rate and are unsuitable for such a study.
Acknowledgments
I am grateful to G. Meynet and M. Limongi for providing tables with yields and other properties of their stellar models and to the referee, L. Drury, for constructive remarks.
References
- Anders, E., & Grevesse, N. 1989, GeCoA, 53, 197 [Google Scholar]
- Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Berezhko, E. G., & Völk, H. J. 2006, A&A, 451, 981 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Berezhko, E. G., Pühlhofer, G., & Völk, H. J. 2009, A&A, 505, 641 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bibring, J.-P., & Cesarsky, C. J. 1981, ICRC, 2, 289 [NASA ADS] [Google Scholar]
- Biermann, P. L., Langer, N., Seo, E.-S., & Stanev, T. 2001, A&A, 369, 269 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Binns, W. R., Wiedenbeck, M. E., Arnould, M., et al. 2005, ApJ, 634, 351 [NASA ADS] [CrossRef] [Google Scholar]
- Binns, W. R., Wiedenbeck, M. E., Arnould, M., et al. 2007, SSRv, 130, 439 [Google Scholar]
- Binns, W. R., Wiedenbeck, M. E., Arnould, M., et al. 2008, NewAR, 52, 427 [Google Scholar]
- Caprioli, D. 2011, J. Cosmol. Astropart. Phys., 05, 026 [Google Scholar]
- Caprioli, D., Amato, E., & Blasi, P. 2010, APh, 33, 160 [Google Scholar]
- Caprioli, D., Blasi, P., & Amato, E. 2011, Astropart. Phys., 34, 447 [NASA ADS] [CrossRef] [Google Scholar]
- Casse, M., & Goret, P. 1978, ApJ, 221, 703 [NASA ADS] [CrossRef] [Google Scholar]
- Casse, M., & Paul, J. A. 1982, ApJ, 258, 860 [NASA ADS] [CrossRef] [Google Scholar]
- Drury, L. O’C. 2011, MNRAS, 415, 1807 [NASA ADS] [CrossRef] [Google Scholar]
- Ellison, D. C., Drury, L. O’C., & Meyer, J.-P. 1997, ApJ, 487, 197 [NASA ADS] [CrossRef] [Google Scholar]
- Ellison, D. C., & Bykov, A. M. 2011, ApJ, 731, 87 [NASA ADS] [CrossRef] [Google Scholar]
- Fryer, C., Belczynski, K., Wiktorowicz, G., et al. 2011, ApJ, submitted [arXiv:1110.1726] [Google Scholar]
- Garcia-Munoz, M., Simpson, J. A., & Wefel, J. P. 1979, ApJ, 232, L95 [NASA ADS] [CrossRef] [Google Scholar]
- Garcia-Segura, G., Langer, N., & Mac Low, M.-M. 1996a, A&A, 316, 133 [NASA ADS] [Google Scholar]
- Garcia-Segura, G., Mac Low, M.-M., & Langer, N. 1996b, A&A, 305, 229 [NASA ADS] [Google Scholar]
- Hanke, F., Marek, A., Mueller, B., & Janka, H.-T. 2011, ApJ, submitted [arXiv:1108.4355] [Google Scholar]
- Heger, A., Fryer, C. L., Woosley, S. E., Langer, N., & Hartmann, D. H. 2003, ApJ, 591, 288 [NASA ADS] [CrossRef] [Google Scholar]
- Higdon, J. C., & Lingenfelter, R. E. 2003, ApJ, 590, 822 [NASA ADS] [CrossRef] [Google Scholar]
- Hirschi, R., Meynet, G., & Maeder, A. 2005, A&A, 433, 1013 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kafatos, M., Bruhweiler, F., & Sofia, S. 1981, 17th International Cosmic Ray Conference, 2, 222 [Google Scholar]
- Lingenfelter, R. E., & Higdon, J. C. 2007, ApJ, 660, 330 [NASA ADS] [CrossRef] [Google Scholar]
- Limongi, M., & Chieffi, A. 2006, ApJ, 647, 483 [NASA ADS] [CrossRef] [Google Scholar]
- Limongi, M., & Chieffi, A. 2008, EAS, 32, 233 [Google Scholar]
- Lodders, K. 2003, ApJ, 591, 1220 [NASA ADS] [CrossRef] [Google Scholar]
- Maeder, A. 1983, A&A, 120, 130 [NASA ADS] [Google Scholar]
- Maeder, A., & Meynet, G. 1993, A&A, 278, 406 [NASA ADS] [Google Scholar]
- Maeder, A., & Meynet, G. 2000, ARA&A, 38, 143 [NASA ADS] [CrossRef] [Google Scholar]
- Meyer, J.-P. 1985, ApJS, 57, 173 [NASA ADS] [CrossRef] [Google Scholar]
- Meyer, J.-P., Drury, L. O., & Ellison, D. C. 1997, ApJ, 487, 182 [NASA ADS] [CrossRef] [Google Scholar]
- Ostriker, J. P., & McKee, C. F. 1988, RvMP, 60, 1 [Google Scholar]
- Parizot, E., Marcowith, A., van der Swaluw, E., Bykov, A. M., & Tatischeff, V. 2004, A&A, 424, 747 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Prantzos, N. 1984, AdSpR, 4, 109 [NASA ADS] [Google Scholar]
- Prantzos, N. 2005, in Chemical Abundances and Mixing in Stars in the Milky Way and its Satellites, ESO Astrophysics Symposia (Springer-Verlag), 351 [arXiv:astro-ph/0411569] [Google Scholar]
- Prantzos, N. 2010, IAUS, 268, 473 [Google Scholar]
- Prantzos, N., Arnould, M., & Arcoragi, J.-P. 1987, ApJ, 315, 209 [NASA ADS] [CrossRef] [Google Scholar]
- Schaller, G., Schaerer, D., Meynet, G., & Maeder, A. 1992, A&AS, 96, 269 [Google Scholar]
- Ptuskin, V. S., & Zirakashvili, V. N. 2005, A&A, 429, 755 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [PubMed] [Google Scholar]
- Ptuskin, V., Zirakashvili, V., & Seo, E.-S. 2010, ApJ, 718, 31 [NASA ADS] [CrossRef] [Google Scholar]
- Ramaty, R., Kozlovsky, B., Lingenfelter, R. E., & Reeves, H. 1997, ApJ, 488, 730 [NASA ADS] [CrossRef] [Google Scholar]
- Schure, K. M., Achterberg, A., Keppens, R., & Vink, J. 2010, MNRAS, 406, 2633 [NASA ADS] [CrossRef] [Google Scholar]
- Strong, A. W., Moskalenko, I. V., & Ptuskin, V. S. 2007, ARNPS, 57, 285 [Google Scholar]
- Wiedenbeck, M. E., & Greiner, D. E. 1981, PhRvL, 46, 682 [Google Scholar]
- Wiedenbeck, M. E., Binns, W. R., Christian, E. R., et al. 1999, ApJ, 523, L6 [Google Scholar]
- Wiedenbeck, M. E., Binns, W. R., Cummings, A. C., et al. 2007, SSRv, 130, 415 [Google Scholar]
- Woosley, S. E., & Weaver, T. A. 1995, ApJS, 101, 181 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1 Schematic representation of a supernova exploding in the wind of its parent star. The star of initial mass M∗ explodes with a mass MExp, i.e. it has lost a mass Mwind = M∗ − MExp. The most massive stars become WR stars and their wind expels not only the H-envelope (of mass MEnv, with composition similar to that of the ISM) but also nuclearly processed layers, of mass MProc, i.e. MWind = MEnv + MProc, where MProc = MHeC − MExp and MHeC is the mass of the (H-exhausted) He-core. The star leaves a remnant (neutron star or black hole) of mass MRem; the mass ejected in the SN explosion is MEj = MExp − MRem. Efficient GCR acceleration presumably starts at the beginning of the ST phase, when a mass MS1 ~ MEj is swept up in front of the SN shock wave (which is indicated by arrows). |
| In the text | |
 |
Fig. 2 Input data adopted in this work for solar metallicity massive stars with mass loss. Left: non rotating models from Limongi & Chieffi (2006); right: rotating models from Hirschi, Meynet & Maeder (2005). Top: mass of the (H-exhausted) He core MHeC, of the star at explosion MExp and of the compact remnant MRem as a function of the initial stellar mass M∗. Bottom: derived quantities are the mass of the wind MWind = M∗ − MExp, the mass of the nuclearly processed layer MProc = MHeC − MRem and of the unprocessed (22Ne-normal) envelope MEnv = MWind-MProc and the mass of the SN ejecta MEj = MExp − MRem In all cases, curves are smoothly interpolated between model results. |
| In the text | |
 |
Fig. 3 Total masses of selected isotopes in the winds of the massive stars from the two sets of models adopted in this work. Solid curves are yields from HMM05 (with rotation) and dotted curves from LC06 (no rotation), in both cases interpolated between model results. The points correspond to results of the HMM05 models with no rotation and, in general, agree well with LC06 results except for the 60 M⊙ star. |
| In the text | |
 |
Fig. 4 Composition encountered by the forward shock wave as it moves (from left to right) through the winds of 25 M⊙ (left) and 60 M⊙(right) rotating stars. The shock wave starts at MExp = 10 M⊙and 14.8 M⊙, respectively, and the ST phase sets in when a mass MS1 = MExp has been swept up and has presumably been well mixed. The quantities displayed correspond to the mass integrated composition of the wind, starting at MExp. |
| In the text | |
 |
Fig. 5 Evolution of the SN remnants of two rotating stars of initial masses 20 M⊙ (dotted) and 60 M⊙ (solid), respectively. Top: velocity of the forward shock and swept-up mass. Middle: shock radius and density profile before shock arrival (see text). Bottom: composition of the matter swept up up to time t by the shock wave, for the 14N/16O and 22Ne/20Ne ratios. In all panels, the thickportions of the curves indicate the period of efficient particle acceleration, i.e. from the beginning of the ST phase and as far as υs > υmin. The value of υmin (=1900 km s-1 for the rotating star models in the figure) is chosen so that the IMF averaged theoretical ratio of 22Ne/20Ne matches the observed one in GCR (see text, Eq. (13) and Fig. 6). |
| In the text | |
 |
Fig. 6 Abundance ratios of various nuclear species in GCR source normalized to the corresponding solar ones as a function of the initial stellar mass. In all panels, solid curves correspond to models of HMM05 and dotted curves to models of LC06. Upper, thin curves are for GCR accelerated at the beginning of the ST phase and lower, thick curvesfor the time-average at the end of GCR acceleration. An average over a Salpeter IMF (and accounting for the swept-up mass in each case) produces the vertical segments to the right, their top point corresponding to the beginning and the bottom one to the end of the GCR acceleration phase, respectively (also indicated by filled squares). These results are compared to GCR source abundance ratios as derived by ACE data (points at the extreme right with error bars) in Binns et al. (2005). The most significant, unaffected by FIP, volatility etc., is the one of 22Ne/20Ne. The end of the GCR acceleration phase is assumed to correspond to shock velocities υmin such that the time and IMF averaged theoretical ratio (squares) of 22Ne/20Ne matches the observed one (see text). For the set-up adopted here we find υmin = 1900 km s-1 for HMM models and υmin = 2400 km s-1 for LC06 models. |
| In the text | |
 |
Fig. 7 Graphical presentation of the results discussed in Sect. 3.3. Particle acceleration starts at the beginning of the ST phase, located at mass coordinate A1 = MExp+ MEj, i.e. when the forward shock (FS, arrows), launched at MExp, has swept up a mass MS1 = MEj. Acceleration stops at mass coordinate A2, corresponding in the case dicussed here to a shock velocity of 1900 km s-1. The mass sampled by the FS between those two regions is MAcc = A2 − A1. For rotating stars with mass M > 30 M⊙, an increasing part of MAcc includes nuclearly processed material (shaded aerea), while for rotating stars with M < 18 M⊙, MACcc contains only material of ISM (=solar) “composition”. |
| In the text | |
 |
Fig. 8 Yields of 20Ne (top) and 22Ne (bottom) as a function of the initial stellar mass. Wind yields are from HMM05 (solid curves) and LC06 (dotted curves), respectively (same as in Fig. 3). Total yields are from LC06 (filled squares) and WW95 (asterisks). |
| In the text | |
 |
Fig. 9 Evolution of composition in a superbubble. Top left: ejection rate of 20Ne (dotted) and 22Ne (solid) in M⊙/Myr per 1 M⊙ of stars formed (assuming a Salpeter IMF between 0.1 and 120 M⊙). Top right: supernova rate per Myr. Middle: total mass of 20Ne (dotted) and 22Ne (solid) accumulated in the superbubble for no initial gas (M0 = 0, left) and for an initial mass of gas equal to 1/5 of the formed stars (M0 = 0.20, right); in the former case 22Ne dominates by mass early on, whereas in the latter the mass of 20Ne dominates from the very beginning. Bottom: corresponding evolution of the O/H (dashed) and of the (22Ne/20Ne)SB ratio (dotted) in the SB gas; the solid curve represents the (22Ne/20Ne)CR ratio of particles accelerated up to that time and has to be compared to the observed GCR source ratio (dotted horizontal line). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


