| Issue |
A&A
Volume 538, February 2012
|
|
|---|---|---|
| Article Number | A74 | |
| Number of page(s) | 20 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201015027 | |
| Published online | 06 February 2012 | |
Massive binaries in the Cepheus OB2/3 region⋆
Constraining the formation mechanism of massive stars
Max-Planck-Institut für Astronomie, Königstuhl 17, 69117 Heidelberg, Germany
e-mail: peterd@mpia-hd.mpg.de
Received: 20 May 2010
Accepted: 7 October 2011
Context. Two different formation scenarios for stars of masses larger than 10 M⊙ exist. Although simulations within both scenarios are capable of producing stars up to the highest observed masses, the relevance of the two formation scenarios for massive star-formation is not yet clear.
Aims. We aim to detect companions to massive stars to constrain the binary parameters of the multiple systems. These findings will help to constrain the formation of massive stars.
Methods. We performed z′-band observations of massive and intermediate-mass stars in the Cep OB2/3 associations with the Lucky imaging camera AstraLux on the 2.2 m telescope of the Calar Alto observatory. The analysis aimed at detecting binary systems with separations out to 2'.2 (~1700 AU), the inner limit depending on the contrast. The maximum contrast of 7 mag in z′ (corresponding to a mass contrast of 17:1 versus an O9V primary) requires a minimum separation of 0'.7 (~550 AU).
Results. We found 28 new companions for our sample of 148 intermediate-mass and massive stars in Cep OB2/3. The companion star fraction of the massive stars is 0.7; about 50% of the systems are triples. The mass function of the companions to the massive stars is strongly top-heavy. We found that the sample parameters closely agreed with those found in the Orion Trapezium cluster.
Conclusions. The multiplicity of massive stars seems to be significantly higher than that of intermediate-mass stars, independently of the environment. The comparison of our findings with the theories of massive star-formation favor the formation of massive stars by the fragmentation of proto-stellar cores combined with competitive accretion.
Key words: binaries: close / stars: formation / stars: massive
Appendix A in available in electronic form at http://www.aanda.org
© ESO, 2012
1. Introduction
Understanding the formation of stars is one of the fundamental tasks of astronomy. For low-mass stars there exists a standard model of the formation process (e.g. Shu et al. 1987; Klessen et al. 2004). However, the model of star-formation proposed there cannot be directly applied to massive star-formation (see e.g. Zinnecker & Yorke 2007). The main reason for this is the high photon flux that can prevent further infall and potentially stop the formation at masses of ≈10 M⊙ (e.g. Wolfire & Cassinelli 1987). Historically, the theory of massive star-formation follows two lines.
The first one is a scaled-up version of low-mass star-formation with the following modifications: Firstly, higher accretion rates are presumed, i.e. ≈10-3 M⊙/yr instead of the value of 10-6M⊙/yr as found in low-mass star-forming regions. This value can be reached by taking turbulence and high pressure present in massive star-forming regions into account (McKee & Tan 2002; McKee & Tan 2003). Values of accretion rates even higher than the one stated above have been observed in Orion by Nakano et al. (2000). Secondly, the models include non-spherical accretion, as is indeed common in star-formation. Calculations by Yorke & Bodenheimer (1999), Yorke & Sonnhalter (2002), Krumholz (2006), and Krumholz et al. (2009) for example show that the formation of an accretion disk induces a non-isotropic distribution of the stellar radiative flux. The radiative acceleration is concentrated toward the poles and the radiation pressure on the accretion disc above the equator is reduced. Both effects together can result in a self-shielding of the accretion disk (Jijina & Adams 1996), allowing matter to flow further onto the surface of the star.
The second approach to explain how massive stars form is based on the fact that massive stars usually form within the dense cores of stellar clusters where dynamical interactions play an important role. Massive stars near the center of these star clusters are at the bottom of the gravitational potential well. There they are fed with matter from the entire cluster rather than from their nearest environment only. The term “matter” in this context can also include complete low- or intermediate-mass stars, i.e. this scenario includes the creation of massive stars as the product of collisions between two or more intermediate-mass stars (Bonnell & Bate 2005). A prediction of this hypothesis is that a large part of massive stars harbor close companions (failed mergers), potentially with another wide low-mass star in the system. An important condition for this scenario are minimum stellar densities of ≈ 106 pc-3 as observed in the centers of rich stellar clusters. Note that although both scenarios are capable of producing massive stars, the second scenario works for massive stars only, and the respective validity of each scenario for massive star-formation is not clear.
These two theoretical scenarios differ in their predictions regarding the formation of binary and multiple systems and the eventual distribution of binary parameters (mass ratio, separation, etc.).
In this work, we describe the result of an observing campaign targeting the Cep OB 2/3 associations and aimed at identifying these binary parameters for a sample of massive and intermediate-mass stars. Drawing conclusions from these parameters on the formation mechanism of the companion star(s) allows us to provide constrains on the formation scenario of massive stars.
Note that many groups have undertaken studies of the close environment of massive stars, among them Preibisch et al. (1999), who concluded on a formation mechanism different from low-mass stars owing to an increased average number of companion stars per massive star, Duchêne et al. (2001), who in contrast argue that standard accretion together with cloud fragmentation can explain their results; Turner et al. (2008), who provide count statistics; Mason et al. (2009), who concentrate on comparing the multiplicities of O-stars in associations to runaway and field O-stars; Sana & Evans (2011), who focus on determining the parameter distributions of massive binaries, and Maíz Apellániz (2010), who used the same instrument as we did to derive the multiplicity fraction of 138 massive stars with δ > −25deg.
This paper is organized as follows: the next section will outline the selection process for our target areas and introduce the individual regions. Section 3 describes the observations and the data reduction. Section 4 will define the samples of physical companions. In Sect. 5 we investigate the multiplicity of these samples and present the properties of the companions derived from our observations, and in Sect. 6 the correlations between several binary parameters. The consequences for the formation scenario of high- and intermediate-mass stars will be discussed in Sect. 7. Finally, Sect. 8 will summarize the conclusions.
2. The Cep OB2/3 associations
To detect close companions, we need high linear resolution. This requires high angular resolution images and the proximity of the targets. To provide a statistically significant basis for our sample, the number of massive stars in the target area has to be sufficiently large, i.e., ≫10. A low stellar density at present day and a young age strongly reduce the effect of dynamical interactions on the binary parameters. The Cep OB2/3 associations fulfill all these criteria: they are positioned at a distance of ≈800 pc, and contain a high number of massive (Simonson 1968; Blaauw et al. 1959) and intermediate-mass stars (Sicilia-Aguilar et al. 2005; Contreras et al. 2002). The stellar density of associations is in general not higher than that of the field (Jordi et al. 1996). We measure a maximum projected stellar density of 4.2 pc-2 down to stars of spectral type A for our targets. Assuming the radial extension of the regions to be of the same order of magnitude as the apparent linear size, this translates into a massive-star density of always less than 0.3 pc-3.
Finally the age of the two associations lies between 3 Myr and 10 Myr (Patel et al. 1995; Patel et al. 1998; Sicilia-Aguilar et al. 2004; Blaauw 1964; Blaauw 1991; de Zeeuw & Brand 1985; Jordi et al. 1996).
2.1. The Cepheus OB2/3 association
We now briefly describe the origin of the CepOB2/3 associations and its star formation.
2.1.1. The Cep OB2 association
The Cepheus OB2 association is embedded in the Cepheus bubble, a bubble-like structure of atomic and molecular gas (Simonson & van Someren Greve 1976; Patel et al. 1994; Patel et al. 1998), extending about 120 pc around the center at RA(2000) = 21h24m04s, Dec(2000) = +62°23′18″. Balazs & Kun (1989) and Patel et al. (1995), Patel et al. (1998) derived a model of the bubble and its star-formation. From CO emission data and IRAS point sources, they modeled the bubble as a shell originating from one or more supernova explosions of first-generation stars. Now, the next-generation star-formation triggered by these explosions is taking place on the boundary of the bubble. Already there is a third generation of stars triggered by even more supernova explosions. Based on the expansion of the bubble and an additional instability argument for the rim of the bubble, the age is estimated to be about 7–10 Myr for the center (NGC 7160) and 3 Myr (Tr37) for the rim. Note that kinematic methods usually underestimate the ages of associations (Brown et al. 1997). Additionally, the bubble can also be formed from the strong winds of the massive stars of the first generation (see Gouliermis et al. 2008). However, the age derived for CepOB2 was confirmed by Sicilia-Aguilar et al. (2004). They used stellar spectra in combination with colors, variability, and accretion features of low-mass stars in the association to determine the age.
2.1.2. The Cep OB3 association
The Cep OB3 association is located at a similar distance from the Sun as Cep OB2, i.e., 800 pc (Moreno-Corral et al. 1993). It covers an area on the sky from approximately 22h46m to 23h10m in right ascension and + 61° to + 64° in declination. It can be divided into two subgroups of different ages (10 ± 2 Myr and 7 ± 2 Myr) by isochrone fitting (Blaauw 1964; Blaauw 1991; de Zeeuw & Brand 1985). However, these age determinations based on isochrones are model-dependent and, therefore, have to be taken with caution. Indeed, an age determination from the expansion of the association, which again could be an underestimate, places it at 0.5 Myr (de Vegt 1966; Garmany 1973; Assousa et al. 1977; Sargent 1979; Trullols et al. 1997). The age difference and the spatial separation of the two groups, which are 13 pc apart from each other, is the basis of the hypothesis of sequential star-formation (Elmegreen & Lada 1977; Sargent 1979). In this model, the ionizing radiation from early type stars causes a shock wave to propagate through the cloud. This shock-wave makes the cloud gravitationally unstable, which results in a condensation into new massive stars.
An alternative model by Assousa et al. (1977) places the origin of the star-formation in the younger subgroup in a supernova explosion in the older group. The observational basis of this model was the existence of an Hi expanding shell around Cep OB3 first discovered by Simonson & van Someren Greve (1976) from 21 cm line observations. This shell with a radius of approximately 53 pc and an expansion velocity of 35 km s-1 was identified as (typeII) supernova remnant with an age of 0.43 Myr.
 |
Fig. 1 Targets observed with AstraLux. The different regions are shown by name. The asterisks mark the intermediate-mass stars, the crosses the massive stars. Additionally shown are examples of identified binaries. |
The possible stellar remnant of this supernova is the pulsar PSR 2223+65 with an age of 1.14 Myr. The event is much too recent, however, to have initiated star-formation in the younger subgroup. Another pulsar, PST 2324+60, with an age of 10 Myr also quoted by Assousa et al. (1977) seems to be a much better candidate to have triggered star-formation in the older and the younger subgroups.
3. Observations and data reduction
Observations have been performed at the 2.2 m telescope at the Centro Astronómico Hispano Alemán with the AstraLux lucky imaging camera in Johnson z′-band (Hormuth et al. 2008). This camera uses a 512 × 512 pixel EMCCD as detector, which can be used as a noiseless photon counting device. Therefore, the sensitivity for the detection of companions is limited by the photonic shot noise as produced by the halo of the primary rather than by read out noise effects.
We observed 148 target stars in the Cep OB2/3 region. The lists contains 12 stars of spectral type O, 61 stars of spectral type B down to and including B3, 17 later-type B stars, and 58 A-type stars. The position of the targets on sky is presented in Fig. 1 together with a few examples of identified binaries. The observed targets are summarized in Appendix A, Table A.1.
The field-of-view of the exposures varied between 12″ × 12″ and 24″ × 24″. The typical single frame integration time was 30 ms, the total exposure time per target typically 150 s. The camera gain was varied such that every target star exhibited approximately the same number of counts on the detector, typically 10% to 25% of the full-well capacity after electron multiplication. This makes the observations comparable within the same range of magnitude differences.
Data reduction was made with the standard AstraLux on line pipeline, which largely follows the procedures outlined in Tubbs et al. (2002) and is described in detail in Hormuth et al. (2008). For the detection of companions at the separation of the diffraction limit, we used the 1% selection rate pipeline results. If there were wide (i.e. ≥ 1.0′′ separation) companions, we additionally used the 10% selection rate images, resulting in a lower final Strehl value but higher signal-to-noise ratio for faint sources outside the halo of the bright host star. In these cases, the typically achieved full-width-at-half maximum of the stellar point spread function (PSF) is 110 mas, whereas the theoretical diffraction limit is 87 mas. Note that the broadening is only partly caused by remaining atmospheric contribution, imperfect optics – particularly in the Barlow lens in use, slight undersampling and differential refraction also play a major role here.
For the subarcsecond companions, we used a PSF-fitting algorithm. If possible we used a PSF from the same image, if not we tried several PSFs and used the best fit. Relative photometry and astrometry were performed on the image.
The z′ magnitudes of the target stars were determined by converting literature B,R,I,V brightnesses using the transformation formula given by Smith et al. (2002)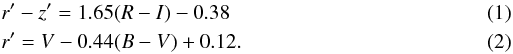 Companion stars are always assumed to be of luminosity class “V”, the z′-magnitudes of of all main-sequence stars were derived in the same way as above using UBVRI colors from (Straižys 1992). Hence, we were able to determine the spectral type of any detected companion by the sole measurement of contrast versus the primary in z′, a method unaffected by distance or variable extinction. The spectral types are then converted to masses consequently mass ratios using the tabulated values again from (Straižys 1992).
Companion stars are always assumed to be of luminosity class “V”, the z′-magnitudes of of all main-sequence stars were derived in the same way as above using UBVRI colors from (Straižys 1992). Hence, we were able to determine the spectral type of any detected companion by the sole measurement of contrast versus the primary in z′, a method unaffected by distance or variable extinction. The spectral types are then converted to masses consequently mass ratios using the tabulated values again from (Straižys 1992).
4. Definition of the samples
4.1. Identification of the physical companions
In the images of the 148 target stars that are members of the Cep OB2/3 association, we detected 182 potential companions.
Background stars were rejected by their spatial position only. To sort them out, we had to use a probability criterion because the observations were performed in one band only. We used the following criterion: from the total number of observations we derived the stellar density ρ for the target area. ρ is the surface density of background stars with a contrast of less than 7 mag versus the primary target in each frame. Since the number of sources per frame is generally low, we used an average value over all frames in our calculations. The cut-off of at 7 mag in contrast versus the primary reflects the variable camera settings that kept the sensitivity of individual frames tied to the primary’s brightness. The cut-off of 7 mag ensures 100% completeness across the whole set of targets, it only decreases at the very inner edge of the field where photon noise from the primary additionally limits detectability.
The probability p of two stars at separation d being a chance projection is then 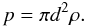 (3)The probability of a single star to be a physical companion is consequently 1 − p. For a sample of N observations the total probability P to observe k chance projections is given by the expression
(3)The probability of a single star to be a physical companion is consequently 1 − p. For a sample of N observations the total probability P to observe k chance projections is given by the expression 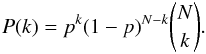 (4)Therefore the most probable number of chance projections for a given maximum separation between the companions can be derived by maximizing P(k). After computing P(k) = 0.95, we excluded the outermost companion from the sample. The result of the procedure is a limiting separation of 2
(4)Therefore the most probable number of chance projections for a given maximum separation between the companions can be derived by maximizing P(k). After computing P(k) = 0.95, we excluded the outermost companion from the sample. The result of the procedure is a limiting separation of 2 2, corresponding to a probability of 95% for a companion of a single observation to be physical – in other words, 1 in 20 stars is wrongly assumed to be physically bound.
2, corresponding to a probability of 95% for a companion of a single observation to be physical – in other words, 1 in 20 stars is wrongly assumed to be physically bound.
4.2. Observational biases
There are two major biases that are potentially introduced by our methods used to constrain the sample of physically bound companions. First, the contrast limit of 7 mag introduces an apparent correlation between primary and secondary mass. It turns out, however, that no stars have been rejected by this criterion that could have been regarded as physical companions. Indeed, most of the contrasts we find are several magnitudes above this limit.
More serious is the decreasing contrast limit caused by the primery’s PSF halo between 0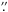 7 and the inner detection limit, 0
7 and the inner detection limit, 0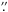 08. Note the bias introduced by this limit shown in Fig. 2: the closer a companion, the brighter, and thus the more massive, it has to be. We will refer to this bias as the “brightness-separation bias”.
08. Note the bias introduced by this limit shown in Fig. 2: the closer a companion, the brighter, and thus the more massive, it has to be. We will refer to this bias as the “brightness-separation bias”.
4.3. The border between intermediate-mass and massive stars
The border between low-mass and massive stars is a matter of definition. In our case, we are trying to find signposts for a change-over in the formation mechanism of stars as, e.g., suggested by Wolfire & Cassinelli (1987). This change might not manifest itself exactly at the conventionally specified border of 8 to 10 M⊙. To define our own sample of massive stars, we first search blindly for a change in the companion star fraction (CSF) as depending on the mass of the primary as a first hint for a different mechanism of formation.
Note that the most massive star in our sample has about 60 M⊙, and about half of the sample are located above the 8 M⊙ limit, most of them between 10 and 15 M⊙.
Of course this approach can be called somewhat phenomenological, but once we detected a significant border between low and high masses, we examined the other parameters mentioned in the previous section and see which formation scenario for the massive stars is supported by the data. The CSF is one of the most straightforward parameters to find an appropriate position for the border to the high-mass regime. On the one hand this parameter is easily calculated for all targets, free of most observational biases and easy to compare across the sample, on the other hand one could naively assume that a change in the dominant mechanism of formation should manifest itself in the number of companions produced.
In Fig. 3 upper panel we show the CSF as a function of the maximum mass of the sample. It starts to rise at a border of ≈ 10 M⊙.
 |
Fig. 2 Brightness vs. separation of the companion stars. The solid curve marks the sample of companions that we assumed to be physical. The left border of the sample is given by the detection limit as a function of brightness. The right border is defined by the change in the behavior of the stellar density with separation (see text). |
To further investigate the significance of this border, the lower panel shows the ratio between the average CSF of stars more massive than a given mass, and the average CSF of stars less massive than that mass, plotted versus the mass where the division is made. The two dashed lines mark the error of the CSF ratio, calculated from the number of incidences via Poissonian statistics. The range displayed lies between spectral type B5 (5 M⊙) and B0 (20 M⊙) (Straižys 1992). There is a clear local maximum around 10 M⊙ which corresponds to a spectral type B2V. We will therefore use this 10 M⊙ border to distinguish between our subsamples. We will refer to the subsample below this border as the “AB” sample, the more massive one will be referred to as the “OB” sample. Interestingly, this limit is consistent with the theoretical mass border around 10 M⊙ between the stars with and without PMS phase.
After the definition of the mass border we can counter-check the spatial separation we set as border between true companions and field stars. It turns out that for the massive sample there are several binaries with brightness contrast of 1.7 mag or less. The spatial border we defined above includes all these massive companions as physical companions. There is no object similarly massive outside this border on any of the images. The bright companions outside the border in Fig. 2 all belong to intermediate-mass stars and have much lower masses. This finding again supports our choice of the spatial border.
 |
Fig. 3 Upper panel: the CSF as function of the maximum primary mass. Lower panel: the ratio of two CSFs. One CSF is calculated for the sample of targets with the value on the x-axis taken as maximum mass, the other one is calculated for the remaining targets. The ratio is calculated as the value of the CSF of the sample of the more massive targets over the value of the CSF of the less massive sample. The dotted lines indicate the error range at the position of the peak and prove that the peak is indeed significant. |
4.4. Individual objects
Before we turn our attention to the general binary parameters, we present a list of objects with interesting properties in Table 1. This compilation includes possible multiple systems from our images as well as findings from the literature. Potential companions farther away than 2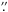 5 are only reported if they can also be found in the literature.
5 are only reported if they can also be found in the literature.
Besides listing the name and spectral type of the target, Cols. 3 and 4 of Table 1 contain information on the separation and position angle of the respective companion. Column 5 contains the number of companions for each target, and in Col. 6 we state whether this companion is newly detected or already known and if so, whether so we can confirm the detection.
List of multiple systems.
5. Investigation of the binary parameters
With the definition of the sample of physical companions in Sect. 4 we are ready to explore the parameters of the binary systems.
5.1. Companion-star fraction and degree of multiplicity
Figure 4 shows the CSF as function of the spectral type of the primary star. The CSF is defined as:
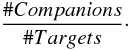 (5)For example a sample of a binary and a single star have a CSF of 0.5 or a sample of one triple and one binary has a CSF of 1.5.
(5)For example a sample of a binary and a single star have a CSF of 0.5 or a sample of one triple and one binary has a CSF of 1.5.
The samples of spectral types are defined as follows: A: all A-stars, AB: all A-stars and B-stars up to the mass border defined above, B: all B-stars, OB: all O-stars and B-stars down to the mass border defined above, and tot: all stars. The CSF rises towards earlier spectral types, yielding values of 0.39 ± 0.08, 0.29 ± 0.08, 0.16 ± 0.06 and 0.16 ± 0.07 for OB-, B-, AB- and A-stars respectively.
 |
Fig. 4 Companion-star fraction as a function of spectral type. |
The values of the OB sample and the AB sample are significantly different, at least on the level of the 1-σ error bars shown. These errors have again been computed using Poissonian statistics on the low number of detected companions. For the degree of multiplicity (DOM) of the two samples we also find significantly different values. The DOM is defined as 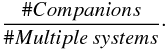 (6)For example a binary has a DOM of 1, a sample of binary and a triple has a DOM of 1.5, and the sample of a binary and a single star has the DOM of 1.
(6)For example a binary has a DOM of 1, a sample of binary and a triple has a DOM of 1.5, and the sample of a binary and a single star has the DOM of 1.
For the OB sample this DOM counts 1.4 ± 0.1. The AB sample consists purely of binaries, i.e. has a DOM of 1.0.
5.2. Mass function of the companion stars
In Sect. 4.1 we used the contrast between primary and companion to define a brightness cutoff for our sample, which translates into a variable mass cutoff depending on primary mass. In the last section, we showed that companions are generally frequent within the OB sample. Knowing that the field stars follow a Salpeter IMF, the question is: does the companion mass function (CMF) of the sample follow the Salpeter IMF? To answer this, we will compare the data to Monte Carlo simulations based on a true Salpeter IMF.
The theoretical sample is constructed as follows: we simulated a theoretical mass function (MF) with a minimum mass of 0.1 M⊙, a maximum mass of 60 M⊙ and a slope of Γ = −1.35. For every target star we applied the following constraints: the maximum detectable mass on the image is given by the mass of the target star itself and the minimum observable mass is given by the detection limit of 7 mag brightness contrast. For every individual image we constructed an observed CMF in this way. All the MFs constructed in this way were then combined into the single CMF that is shown as comparison in Fig. 5. An algorithmic description of this procedure is shown in Alg. 1. In this way, the brightness-separation bias mentioned in Sect. 4.2 is taken into account when constructing the synthetic CMF and we can conclude that any deviation from what we see is really caused by the observed CMF being top-heavy.
 |
Fig. 5 Mass function of companions to stars in the OB sample (dashed) compared to the CMF as it was constructed from individual images under consideration of the brightness-separation bias following the Salpeter law (solid, see text). Overplotted as dotted line is the Salpeter-like mass function but with an exponent Γ of –0.001. |
| Algorithm 1 Construction of the simulated CMF | |
|
|
|
| initialize empty SynthCMF | |
| 2: |
for all Target Stars do initialize empty MF |
| 4: | SIMF = SalpeterIMF(Γ = −1.35, mmin = 0.1 M⊙, mmax = 60 M⊙, Ns = 10 000) for all Stars in SIMF do |
| 6: | if contrast limits render companion star observable AND star is fainter than primary then put star in MF |
| 8: | end if end for |
| 10: | Add CMF to SynthCMF end for |
| 12: | return SynthCMF |
Another argument against the deviation being solely caused by the brightness-separation bias is the following: Fig. 5 clearly shows that the OB star CMF is top-heavy for all samples with minimum separation less than 2′′. Let us assume for a moment that the only reason for the obvious deviation from the Salpeter law is the brightness-separation bias. Then a fit with the Salpeter IMF, reproducing the distribution of companions, will provide us with the companions we miss because of our brightness-separation bias. Such a fit yields more than 300 additional companions outside of our detection limits. As a consequence, every star in the sample would need to have about six unseen companions, a number which we discard as highly unlikely for the moment. A Kolmogorov-Smirnov test in the form described in Stephens (Stephens 1970) yields a probability of basically 0 that the observed mass distribution of companions is compatible with a Salpeter IMF input to Alg. 1. Therefore we conclude that the deviation from the Salpeter distribution is real.
Still, the CMF of the OB star sample can be modeled by a single power law. If we change the exponent of the generation function of SIMF in Alg. 1 to Γ = −0.001, as shown in Fig. 5, we can reproduce the observed mass distribution of the companion stars. A Kolmogorov-Smirnov test computed for compatibility with a modified powerlaw with index Γ = −0.001 yields a probability of 0.9. This probability implies an indication that at least the exponent of the distribution would have to be modified.
Note, however, that we are biased towards bright stars and the modulus of the “true” value of the exponent is probably higher than the one derived here.
5.3. Distribution of parameter ratios
This subsection contains our analyses of the of the binary parameter distributions. The result should be taken with extreme care because the sample size of 19 does not really allow a definite conclusion about whether the quantities in question indeed follow the assumed distributions or not. We derived the distributions of three binary parameters: the magnitude difference (contrast ratio), the mass ratio, and the separation. To derive a functional behaviour, i.e. multiple Gaussian or flat, we performed the following tests: generally, we tried to fit the observed cumulative distribution with a model distribution. As a measure for the goodness of fit we used the Kolmogorov-Smirnov (KS) test. This KS test is preferred over the standard χ2-test because of the low number-statistics we are dealing with – the total number of companions in our sample is 27. For such low numbers the KS test is known to have greater rejection power against false distribution choices than the standard χ2-test (Massey 1951). It is also preferred over the Lilliefors-test, because the underlying distributions cannot generally be assumed to be Gaussian. Again we use the implementation of the KS-test described in Stephens (Stephens 1970), which by the author is described to be a good approximation for sample sizes greater than or equal to eight. Note that the actual fitting procedure does not involve a true maximization of the probability computed by the KS test that the observed parameters have been drawn from the distribution in question, instead the fit was made “by eye” until the test gave a satisfying result. Note also hat the computed KS probabilities show the probability that all observed points of the cumulative distribution are compatible with the corresponding fitted distribution, assuming that the fit model it is indeed the underlying distribution.
Distribution of contrast ratios:
 |
Fig. 6 Histogram of the distribution of magnitude differences between binary components in the OB sample. Overplotted is the best-fit model. The probability is displayed in the bottom of the image. The inset shows the cumulative distribution (steps) on which the fit (curve) was performed. See text for explanations about why a Gaussian fit passes the KS test well while a Bayesian analysis cannot find a significant evidience for either a Gaussian or a Uniform distribution. |
Fig. 6 displays the distribution for OB stars. The fit was performed for a sample with separations larger than 0 4 to reduce the influence of the brightness-separation bias. The goodness of fit is estimated by a Kolmogorov-Smirnov test between the model and the cumulative distributions. The probability that the fit and the data are drawn from the same original distribution is shown in the bottom of the image. The Gaussian models have the following parameters: the center at 1.1 mag and a width of 3.2 mag.
4 to reduce the influence of the brightness-separation bias. The goodness of fit is estimated by a Kolmogorov-Smirnov test between the model and the cumulative distributions. The probability that the fit and the data are drawn from the same original distribution is shown in the bottom of the image. The Gaussian models have the following parameters: the center at 1.1 mag and a width of 3.2 mag.
The alternative model of a flat distribution for the OB star sample has a probability of 0.81.
Distribution of mass ratios:
Fig. 7 shows the distribution of mass ratios for the OB star sample. It is compatible with a Gaussian distribution with a peak at 0.45 and a width of 0.3 and with a flat distribution (not shown here).
 |
Fig. 7 Histogram of the mass ratio distribution for the OB star sample. Overplotted is the Gaussian model derived from the cumulative distribution shown in the inset. See text for an explanation why the KS test is extremly favourable for the Gaussian distribution while a Bayesian analysis actually shows evidence that the distribution is actually uniform. |
This means that the data do not permit conclusion on a distribution of mass ratios.
Distribution of separations:
as first assumption we used a log-normal distribution of the separations as found for low-mass stars by Duquennoy & Mayor (1991). Here, we found that the Kolmogorov-Smirnov test yields only a poor agreement between data and the log-normal distribution. When we combined two different distributions to describe the data, the agreement was much improved. The fit was performed for a sample with a brightness difference lower than 3 mag to reduce the influence of the bias.
Figure 8 shows the histogram of the distribution of separations for OB stars. Overplotted is the best fit to the cumulative distribution (shown in the inset). For the OB stars we used a combination of two Gaussians. One Gaussian is centered at log (r/1″) = 0.2 with a width of 0.7, the other is centered at log (r/1″) = –1.0 with a width of 0.1. Here we have the problem that the distribution peaks towards the inner cut-off and therefore we do not know if the curve has a maximum at this position or towards closer separations. We used the fit whose peak was as far to the right as possible.
 |
Fig. 8 Histogram of the distribution of separations for the OB star sample. Over plotted is the best fit to the cumulative distribution shown in the inset. See text for explanations about why a Gaussian fit passes the KS test well while a Bayesian analysis cannot find a significant evidience for either a Gaussian or a Uniform distribution. |
Again we also tried to fit a flat distribution to the OB star sample. The goodness of fit is 0.71. The steep increase for close separations seriously questions a flat model.
Bayesian evidence for particular models:
given our analyses above, which show satisfactory KS coefficients but can be doubted in terms of significance because of the small sample size, we computed generalized Bayesian evidence ratios between purely random and (double) Gaussian distributions for our data sets. The method closely follows that described in Bailer-Jones (2011). Note that Bayesian evidence ratios do not compare a single best-fit realization of a particular model with a similar one for another model, but take into account the possible variations of parameters and also the amount of available data.
Table 2 shows the distributions and parameter ranges tested according to the method and equations outlined in Bailer-Jones (2011). The outcome of Bayesian evidence ratios is disillusioning: evidence ratios between (double) Gaussian and uniform distributions are 0.6 for the contrast ratios, 5 × 10-8 for the mass ratios, and 0.1 for the log separation. Note that Bayesian evidence ratios are usually considered as inconclusive when they are between 0.1 and 10. This means that although the KS tests favour the Gaussian over the uniform distributions for certain individual best-fit parameter sets, the generalized Bayesian comparison between Gaussian and uniform distributions is always inclined against the Gaussian models and plainly rejects the Gaussian model for the mass ratio distribution.
6. Correlations between binary parameters
While the actual discussion of the correlations between binary parameters and their potential meaning for the discussion about different formation scenarios for massive stars will be outlined in Sect. 7.1, here we concern ourselves with those three correlations that are found useful for distinguishing between scenarios: the correlation between total system mass M and binary separation R, the correlation between mass ratio m and binary separation R, and the correlation between system mass M and mass ratio m. Additionally, we will test the correlation between primary mass M1 and secondary mass M2, because this is predicted to differ depending on the number of stars into which a core fragments (Clarke 2001).
We have seen that for massive stars the number of higher-order systems, especially those including spectroscopic companions, is not negligible. In these systems dynamical interactions will play an important role during their formation. These dynamical interactions potentially reduce the degree of correlation between the binary parameters. Still, we will not exclude the known multiple system from the investigation because we cannot really quantify the effect of these interactions.
6.1. Separation vs. system mass
Figure 9 shows the correlation between separation and system mass. The sample shows an anti-correlation between the two quantities. This relation becomes stronger when we exclude the wide companions and also when we leave out the O stars. Consequently the strongest (anti-)correlation can be found for the B0-B2 stars with separations ≤ 2′′. We have to be careful, however, because the brightness-separation bias works in the direction of the observed correlation. This is especially true for the sample of B0-B2 stars with separations ≤2′′. We conclude that the reality of the anti-correlation we detected is uncertain.
6.2. Mass ratio vs. separation
Distributions and parameter ranges compared in the Bayesian evidence calculation.
 |
Fig. 9 Separation vs. mass correlation for the OB stars. |
 |
Fig. 10 Mass ratio vs. separation correlation for the OB stars. |
In Fig. 10 we show the correlation between mass ratio and separation. Again the removal of the wide companions increases the strength of the anti-correlation and the slope of the relationship. Here the brightness-separation bias also works in the direction of the correlation. Again the spectroscopic binaries will add close pairs with high mass ratios, i.e., support the correlation. Our data alone however cannot clearly support the correlation, as observational biases alone can produce a very similar correlation (cf. Sect. 6.5)
6.3. Mass ratio vs. system mass
 |
Fig. 11 Correlation between mass ratio and system mass for the OB stars. |
From Fig. 11 it is clear that there is a correlation between mass ratio and system mass. This correlation is strongest for the sample of B0-B2 stars. This means it is greatly reduced by the stars of masses greater than 20 M⊙ that are suspected members of multiple systems. Again we have to take care of the influence of the brightness-separation bias: for the sample of B0-B2 stars the correlation is stronger if we do not leave out the wide companions. This indicates that the correlation must be real as the wider companions that increase the degree of correlation are not subject to the brightness-separation bias. Thus the correlation between separation and mass ratio seems to be real.
6.4. Primary mass vs. secondary mass
The correlation between primary and secondary masses is shown in Fig. 12. This correlation has a positive slope, and, according to its correlation coefficient, is the strongest of all. However, the brightness-separation bias is expected to have its strongest effect here, and a Monte Carlo analysis in the next section shows that it might indeed produce the observed correlation alone.
 |
Fig. 12 Correlation between primary and secondary mass for the OB stars. |
6.5. General notes on correlations
Generally, the correlation coefficients derived are low – below the threshold usually taken as reliable indication that a correlation exists. To verify whether the correlations found are indeed real, we performed a Monte-Carlo simulation of samples of massive stars. We generated 100 000 realizations of a 10 000-star sample and subjected them to simulated observations applying the same constraints in z-band contrast and separation as quoted in Sect. 4.1. The mass of the primaries and the secondaries were independently taken from the Salpeter IMF, reversing the ratio where secondaries came out more massive than the primaries. The separations were equally distributed. From every sample the first 19 star systems with detectable companions (according to our criteria defined in Sect. 4.1) were taken, so that we ended up with 100 000 samples of 19 stars to derive the correlation. The results are compared to the actual findings in Table 3.
Table 3 summarizes the observed correlation coefficients r and slopes s and compares them to these randomly generated ones. While the MC simulations deliver error margins for the coefficients and slopes for free from the large number of realizations, the errors on the coefficients of the observed sample were estimated from  where r is the correlation coefficient and N the number of targets Press et al. (1988).
where r is the correlation coefficient and N the number of targets Press et al. (1988).
As can be seen in Table 3, the results are again ambivalent because of the low number of targets. Most of the error ranges – which can be considered 1σ errors – overlap or nearly do so. However, one can safely make the following statements:
-
R vs. M shows a negative correlation that cannot be produced by observational biases (which were of course included in the MC simulations) alone. Still due to the large error bars the correlation is not established;
-
for the pair m vs. R, the result is unclear, the negative correlation appears to be slightly stronger in the observed sample than in the simulated one, but the error bars are too large;
-
m vs. M shows a correlation where the simulations clearly predict none;
-
the last pair, M1 vs. M2, is again unclear.
Because using a Salpeter IMF does not reproduce a top-heavy companion sample as found in Sect. 5.2, we recomputed the MC simulations using the modified power law described in Sect. 5.2 with Γ = −0.001. All the resulting observed correlations do not differ significantly from those where a Salpeter law was used, except for the last one: as could be naively expected, the correlation between M1 and M2 becomes stronger and steeper with a correlation coefficient of 0.57 ± 0.18 and a linear slope of 0.74 ± 0.30.
Correlation coefficients and slopes found on the observed samples, and on the comparison Monte Carlo simulations.
6.6. Summary of the binary parameters
Here, we summarize our results.
From our sample of target stars we constructed the OB sample of massive stars with a lower mass limit of ≈ 10 M⊙, which corresponds to spectral type B2V. For this sample, we derived several multiplicity parameters:
-
1.
The CSF of the OB sample is high(0.39 ± 0.09). This value differs significantly from the CSF of the AB sample (0.17 ± 0.06).
-
2.
The DOM differs significantly between the OB sample (1.4 ± 0.1) and the AB sample (1.0 ± 0.1).
-
3.
There is an anti-correlation between system mass and separation which is, however, not well established.
-
4.
The sample exhibits an anti-correlation between separation and mass ratio, but this is possibly produced by observational biases.
-
5.
There exists a correlation between system mass and mass ratio that is not caused by observational biases.
-
6.
We see a correlation between primary and secondary mass, but this may again caused by to observational biases combined with a modified CMF.
-
7.
The mass function of the companions for the total sample of OB star companions has an exponent Γ of –0.001 instead of –1.35, the value of the Salpeter IMF.
-
8.
Although distributions between mass ratios, brightness differences, and separations can be fitted well by individually chosen Gaussian distributions, a Bayesian analysis shows that one cannot decide between a uniform or a (double) Gaussian distribution in the cases of contrast ratio and separations, while it plainly rejects the Gaussian model for the mass ratio distribution.
7. Discussion
7.1. Companions of massive stars – formation and parameters
We now compare the outcome of our analysis to the predictions that can be derived for binary parameters under the different scenarios for the formation of massive stars.
Both scenarios – scaled-up disk accretion and coalescence or competitive accretion – have in common that the origin of the binaries or multiple systems is either proto-stellar cores gravitationally bound to each other or one proto-stellar core that fragments further. The difference is the evolution of the binary from this starting point. In the case of the scaled-up disk accretion scenario (SADA) each star evolves from its own circum-stellar matter alone, whereas in the case of competitive accretion (CA) all parts of the multiple system have access to additional circum-system matter.
7.2. Binary formation in the case of scaled-up disk accretion
The scaled-up disk accretion (SADA) scenario has three potential channels of binary formation: A pure capture scenario (Moeckel & Bally 2007), formation of the companion by disk fragmentation (Kratter & Matzner 2006; Krumholz 2008), and formation of the companion by fragmentation of the proto-stellar core (Clarke 2001). We will not discuss the first channel, because the pure capture scenario can only explain CSFs up to 0.3 (Moeckel & Bally 2007), and is thus incapable of producing the CSFs found for massive stars. We will also not compare our findings to the second channel in detail, because we are not able to detect the low-mass companions predicted by the disk fragmentation channel.
Regarding SADA, we will therefore solely focus on the channel working via fragmentation of the proto-stellar core (SADA-PSCF).
For the SADA-PSCF scenario we assume that each star is formed from its own fragment and has no access to any circum-binary matter (Krumholz 2006).
The rate of binaries and multiple systems is high in this scenario (see for example Clarke 2001). Additionally, the models predict an increase of the CSF with primary mass. The fact that the two most massive fragments will form the out-coming binary will make the CMF top-heavy. This scenario predicts a correlation between system mass and separation because more massive stars need more matter and consequently a larger volume to form. An anti-correlation would also be possible within SADA-PSCF, but one has to make even more assumptions about a correlation between the density distribution of the core and the core mass. Observational evidence to prove any such assumption is missing. Therefore, we will restrict ourselves to assuming SADA-PSCF is valid only when we find a correlation.
A correlation between system mass and mass ratio is also consistent for SADA-PSCF, when the core fragments into very few parts only. In this case the mass of the companion is predicted to be correlated to the primary mass (Clarke 2001). For a fragmentation of the core in a larger number of fragments one would instead expect an opposite behavior (see Clarke 2001). However, for massive stars the correlation between system mass and mass ratio can be explained also by a different mechanism: if, during fragmentation, the most massive of the fragments starts to heat the core by its accretion luminosity as soon as it becomes a protostar (see Krumholz 2006), it prevents further fragmentation and other fragments must be necessarily more massive because the Jeans mass rises with temperature: The more massive the primary, the earlier and stronger the heating, and thus the more massive and the fewer the companions. The luminosity L of the star depends on the mass M like L ∝ M3.5. Therefore, the companion masses should increase more than linear with system mass.
7.3. Binary formation in the case of competitive accretion and coalescence
In the competitive accretion (CA) scenario the stars compete for the matter of the available reservoir. For global competitive accretion, this reservoir is the entire cluster. In the case of local competitive accretion it is the proto-stellar core, which fragments as for the scaled-up accretion scenario. Note, however, that in contrast to the SADA where every proto-star has only access to circum-stellar matter confined within its fragment, for CA every proto-star additionally has access to matter of the original proto-stellar core outside its fragment. In the extreme case this means every star has access to the entire reservoir of matter contained in the original proto-stellar core.
CA needs stellar densities of ≈ 106 pc-3 to work (Zinnecker & Yorke 2007). As mentioned above, we expect the original global stellar density of the investigated regions to be below 105 pc-3. Locally, however, the threshold could still easily have been exceeded at the time of formation, so CA is still likely to work for our targets.
In both cases (global and local) the binary or multiple systems form as originally wide low-mass systems and undergo evolution during the accretion phase. This evolution strongly affects the binary parameters. The general connection between system mass (M) and separation (R) is given by (see Bonnell & Bate 2005) 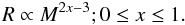 (10)For spherical infall we obtain R ∝ M-3 and for constant angular momentum of the in-falling gas R ∝ M-1 as extreme cases (see Bonnell & Bate 2005). For a turbulent ambient medium that adds mass to the growing stars, Bonnell and coworkers find a relationship of R ∝ M-2.
(10)For spherical infall we obtain R ∝ M-3 and for constant angular momentum of the in-falling gas R ∝ M-1 as extreme cases (see Bonnell & Bate 2005). For a turbulent ambient medium that adds mass to the growing stars, Bonnell and coworkers find a relationship of R ∝ M-2.
This model also predicts a correlation between binary separation and mass ratio as well as between system mass and mass ratio Bate (2000). For more details of this scenario we refer to, e.g., Bate (2000), Bonnell et al. (1998), Bonnell & Bate (2005), and Bonnell (2008). Here we will merely summarize the outcome: within a scenario of accretion onto a wide binary, anti-correlations between separation (R) and system mass (M), and between separation and mass ratio (m) are expected.
We also expect a correlation between system mass and mass ratio as well as between primary mass (M1) and secondary mass (M2). An increase of CSF with primary mass as well as a top-heavy CMF for massive stars is also expected. This top-heavy CMF of the companions is the result of an over-proportionally strong growth of the star with the lower mass in this binary formation scenario.
Table 4 summarizes the parameters we examined and their predicted behavior in the two cases of modified disk and competitive accretion. The parameters that seem to distinguish between the two scenarios are written in boldface.
Examined parameters and their behavior in the cases of modified disk and competitive accretion.
Interestingly, all possibilities to probe the scenarios point towards the CA mechanism, although the parameter x in Eq. (10) comes out as x = 1.22, whereas Bonnell & Bate (2005) give 0 ≤ x ≤ 1.
7.4. Comparison of parameter behavior to observations
Companion star fraction:
the CSF agrees well with both scenarios. A slightly flattened CMF again agrees well with the scenarios.
Companion mass function:
for both evolutionary models we can state that the flatter slope of the CMF compared to the Salpeter mass function is peculiar in the context of stellar evolution from proto-stellar cores to stars: observations of proto-stellar cores Alves et al. (2007), Beuther & Schilke (2004) seem to suggest that already at this evolutionary stage the mass function follows a Salpeter law with a shift in mass (Alves et al. 2007). In other words: if every proto-stellar core only formed one star, the resulting mass function would be the Salpeter IMF. However, these results have to be taken with care because the error bars on the data of Beuther & Schilke (2004) are large and in the case of Alves et al. (2007) it is questionable if the cores will give birth to stars.
If we assume for the moment that their findings are real and further assume that, in the case of fragmentation of the proto-stellar core, the ratio between the fragments’ masses is not related to the system mass then the MF of the cores will be transcribed (with a tendency towards higher secondary masses as argued above) onto the MF of the primaries as well as the secondaries. Our data contradict this scenario.
Further evolution of the binary systems is needed to explain the shape of the mass function. This can be competitive accretion as well as strong dynamical interactions. However, it is not clear if the latter will change the mass function in such a dramatic way.
Correlations:
as stated in Sect. 7.3, most of the correlations fit well to either the fragmentation scenario or the competitive accretion scenario. Exceptions are the relation between separation and system mass, the correlation between mass ratio and separation, and the CMF. Below we will check the consistency of our data with these predicted relations.
The correlation between mass ratio and system mass is well expected for competitive accretion. For a scenario of core fragmentation followed by SADA this correlation is neither given for a N = 2 fragmentation nor for a fragmentation into more parts (see Clarke 2001). The only possible way to still allow for a SADA would be if the total mass in undetected companions is so high that the system mass calculated by us is a strong underestimation. This appears unlikely, however.
For both models, fragmentation and competitive accretion, we can state that the flat slope of the MF of the secondaries in concert with an increase of mass ratio with system mass is consistent with a picture where the primary MF is the Salpeter IMF, whereas the secondaries follow a different MF. As a crude approximation we take the relationship between system mass M and the ratio between primary mass M1 and secondary mass M2 as linear (for large masses this is of course wrong because at some mass the secondary would be more massive than the primary). This roughly complies with the value of the slope for the OB sample. If we then use the formulas 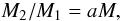 (11)and
(11)and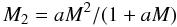 (12)then
(12)then 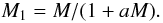 (13)and
(13)and 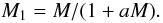 (14)For a low value of aM the secondary mass M2 increases quadratically with system mass and M1 linearly. If the system MF follows the Salpeter IMF then the primary MF does as well. The secondary MF follows the distribution of ≈
(14)For a low value of aM the secondary mass M2 increases quadratically with system mass and M1 linearly. If the system MF follows the Salpeter IMF then the primary MF does as well. The secondary MF follows the distribution of ≈ 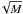 and therefore has an exponent of α = −2.35/2 and consequently for the cumulative distribution of ≈ Γ = −0.2. This value is consistent with our measurement.
and therefore has an exponent of α = −2.35/2 and consequently for the cumulative distribution of ≈ Γ = −0.2. This value is consistent with our measurement.
For the massive stars the anti-correlation between system mass and separation contradicts the SADA scenario, whereas the competitive accretion scenario can easily be applied to the data and is therefore much better suited to explain the formation of the stars. The high multiplicity of the massive targets also fits into this picture. For the case of the CA scenario the fairly qualitative argumentation we used is supported by simulations by Bonnell & Bate (2005).
7.5. Comparison with other star-forming regions
Various studies of the multiplicity of main-sequence and T Tauri stars have been performed in the past. This includes studies on F-type and B-type stars (Abt et al. 1990; Abt & Levy 1976), nearby G-dwarfs (Duquennoy & Mayor 1991), K-dwarfs (Mayor et al. 1992), M-dwarfs (Henry & McCarthy 1990; Tokovinin 1992; Fischer & Marcy 1992), T Tauri stars (Leinert et al. 1993; Brandner & Koehler 1998; Ratzka et al. 2005; Ghez et al. 1997) and OB samples (Duchêne et al. 2001; Preibisch et al. 1998; Nelan et al. 2004; Apai et al. 2007). One can find a decrease in CSF with spectral type from ≥ 100% for OB-type stars to 50%–60% for F- and B-type stars to 45% for K-type stars and 42% for M-type stars. For the T Tauri stars the CSF varies between different star-forming regions. For Taurus itself there is high evidence for a CSF of 100%, whereas in Scorpius and ρ Ophiuchi the CSF seems not to differ significantly from that of main-sequence low-mass stars. Our findings confirm the trend of a decrease in the CSF towards stars of later spectral type.
In Table 5 we compare our CSF with that from the star-forming regions found in the literature in the common regime of spatial separations. The name of the region and the targets under investigation are shown in Cols. 1 and 2. For comparison, we artificially place the region from the literature at the distance of Cep OB2/3 and apply our observational constraints to it. This yields the range of separations presented in Col. 3 of the table. The CSF from the literature shown in Col. 4 is then the CSF derived for this range of separations. As comparison we show the CSF of our OB sample derived for the same range of separations in Col. 5.
CSF for different star-forming regions.
The CSFs found from the literature in most regions are quite similar. The two exceptions are Orion and Taurus. Both have an overly high CSF where Orion has by far the highest one.
CSF:
the CSF of our sample agrees only with regions where the range of separations is relatively small. For samples with a larger regime of separations the CSF we find in Cepheus is usually larger than that found in the literature. The only exception is Orion where the CSF from the literature is comparable to the one we detect.
That the CSF compares well to the regions where the spatial regime is small and not to those with a larger range of separations indicates that the spatial distribution of companions is important for a comparison.
DOM:
the DOM within this regions can be derived from the ratio of single stars (S) to binaries (B), triple systems (T) and quadruple or higher systems (Q). This ratio found in the literature for low-mass and T Tauri stars (Duquennoy & Mayor 1991) is 57:38:4:1 and 60:39:3:2 (Leinert et al. 1993), respectively. If we apply our detection bias to the sample by Preibisch et al. (1999) in Orion we find a distribution for S:B:T:Q of 6:3:3:1.
For the regions mentioned above the DOM is 1.14 ± 0.06 for the G-star sample of Duquennoy and Mayor, 1.16 ± 0.06 for the T Tauri stars and 1.7 ± 0.26 for Orion. The value found in Orion differs significantly from those in the other regions. For our sample of massive stars we find a DOM of 1.4 ± 0.1. Both values are consistent with the values for Orion only.
Preibisch et al. also found a significant difference of the CSF and the DOM for stars earlier and later than a spectral type around B3. In our case we observe something similar with a cut around spectral type B2. The CSF is much higher for the earlier stars and the number of higher-order systems significantly larger.
Parameter distributions:
in Sect. 5.3 we concluded that from our sample we cannot really tell whether distributions of mass ratios, separations and contrasts appear uniform or Gaussian, with the exception of the mass ratio distribution where the Bayesian evidence pointed clearly against the Gaussian. We nevertheless compare these findings to other studies conducted previously to ours.
Distribution of separations:
a pronounced Gaussian distribution of orbital periods was found by Duquennoy & Mayor (1991) for the solar neighborhood. Converting their units to separations, they found a peak at 31 AU and a standard deviation of 0.7 AU. Note that these values are all comprised in our innermost bin, so we cannot verify this distribution here.
Kouwenhoven et al. (2007) and Brandner & Koehler (1998) also found distributions rising towards peaks at their respective inner detection limits, but again owing to the farther distance of the Cep OB regions we cannot compare our distribution with theirs.
Brightness distribution:
our brightness distributions of OB stars is similar to that found by Kouwenhoven et al. (2007). Their distribution, if binned in 0.5 mag bins, is also fairly flat. This finding is confirmed by Ratzka et al. (2005) for ρ Ophiuchi.
CMF:
the CMF derived for the OB sample differs strongly from the Salpeter IMF and has an exponent Γ = −0.001. A similar flattening has been observed in the center of massive young clusters in our galaxy (Figer et al. 1999; Stolte et al. 2002). Values of Γ between –0.65 and –0.8 were measured there.
It is unclear, however, whether Figer et al. (1999) and Stolte et al. (2002) distinguished between primaries and companions. If not, their observed value would then result from a mixture of the two slopes yielding a value intermediate between –0.001 and − 1.35.
Therefore the IMF found in the galactic clusters may be strongly contaminated by binary stars.
Mass ratio distribution:
the behavior of the mass ratios we observed is compatible with values from the literature (i.e. Duquennoy & Mayor 1991), which show a peak around 0.2–0.3 but in general are fairly flat. Distributions from other regions like NGC 6611 (Duchêne et al. 2001) or Scorpius (Kouwenhoven et al. 2007) are also comparable to that of our OB sample. In these regions an overabundance of low mass ratios with respect to high mass ratios were found, as we can also see for the widest companions in our sample.
Correlations between binary parameters:
unfortunately, we cannot compute the correlations between binary parameters for the literature samples. In principle, it would have been possible to compare to the data by Kouwenhoven et al. (2007). But they only have a single target with a mass above 10 M⊙ harboring a companion within our detection limits, so a computation of correlations actually does not make sense. Therefore we conclude:
-
1.
The CSF and the DOM of our OB sample compare well with thefindings in Orion only.
-
2.
The mass limit attached to the change in the CSF and the DOM is in the same range as found in Orion and also agrees with the theoretical border between stars with and without PMS-phase.
-
3.
The exponent of the mass function of the companions for the OB star companions is –0.001 instead of –1.35. This value can explain the flattened IMF found in the centers of massive clusters as a combination of a Salpeter IMF for the primaries and a strongly flattened CMF instead of dynamical mass segregation.
-
4.
The rise towards close separations in the distribution of separations in our OB sample compares well with results found in other star-forming regions.
-
5.
The distribution of brightness differences for the OB star sample compares well to the distributions found in most other star-forming regions.
-
6.
The tendency of wide companions of the OB sample to be less massive compares well with the findings in NGC 6611 and ρ-Oph.
8. Summary and conclusions
We performed a z′-band multiplicity-survey of massive and intermediate-mass stars in the Cep OB2/3 association.
We divided our sample of 126 target members of the association into two subsamples of stars. One subsample, the OB sample, includes all primaries with spectral types earlier than B2, the other – AB sample – those stars with later spectral type. This border fits with the theoretical border between the stars with and without PMS-phase well. This mass border also divides regimes of a different CSF as well as DOM and compares well to the border detected by Preibisch et al. (1999) in Orion.
The CSF of the sample of AB stars was measured to be 17 ± 6%. A completion for missing companions owing to observational biases shows that the CSF of AB-stars is compatible with values ≥ 0.41. This agrees well with measurements on T Tauri stars and G-type stars in other star-forming regions. No multiple systems of higher degree are detected for this sample.The distribution of brightnesses and mass ratios both compare well with the literature. The mass function of the companions is potentially slightly top-heavy but still agrees with the Salpeter IMF.
The (uncorrected) CSF for the OB sample including spectroscopic binaries found in the literature was measured to number 69 ± 9%. A completion for missing companions owing to observational biases shows that the CSF of massive stars is compatible with values ≥1.21. This value compares well with values detected for massive stars in different star-forming regions, especially Orion. The DOM of 1.4 of our OB sample also compares well to the ratios found in Orion and differs significantly from the values found in other star-forming regions.
The mass function of the companion stars fits well with a MF with slope Γ = −0.001. This can explain the findings of a flattened mass function with a slope of Γ = −0.6 to –0.8 in the center of young galactic clusters.
The distribution of separations of the massive sample increases towards our lower detection limit of 0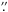 08 and shows a weak maximum at 1
08 and shows a weak maximum at 1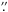 6. This increase towards lower separations compares well to the findings in most other star-forming regions. In Scorpio A Brandner & Koehler (1998) found an additional peak of the distribution as we do for the OB star sample but at the closer separation of 350 AU (0
6. This increase towards lower separations compares well to the findings in most other star-forming regions. In Scorpio A Brandner & Koehler (1998) found an additional peak of the distribution as we do for the OB star sample but at the closer separation of 350 AU (0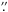 4 at the distance of Cep OB2/3).
4 at the distance of Cep OB2/3).
The distribution of mass ratios is peaked around 0.45 and compares well to other star-forming regions.
More than 60% of the companions of this massive sample have a brightness contrast to the primary of ≤ 1.7 mag. The massive companions apparently have four regions where they reside: spectroscopic, around a separation of 80 AU, 400 AU and 1600 AU. These different regions seem not to result from projection effects. This observation needs to be further confirmed and ifso, will be a challenge to any model of massive star-formation. A possible explanation is that the wide companions reside on highly eccentric orbits. This is additionally hinted at because they are to about 50% members of real or suspected triple systems. It would be interesting to re-observe these targets with larger telescopes and interferometers to possibly detect these close companions. Additionally, an observation with GAIA at least for the companions with intermediate separation (≈0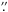 8) could test the hypothesis of eccentricity.
8) could test the hypothesis of eccentricity.
The findings confirm that massive stars tend to form in multiple systems. Dynamical interactions play an important role during the formation.
The correlations between system mass, binary separation mass ratio and primary and secondary mass all agree well with a scenario of the formation of a close binary via competitive accretion onto an originally wide one. A scenario of fragmentation of the proto-stellar core to explain the data needs a fine-tuning of the correlation between core mass and density gradient and is less favorable. A survey of proto-stellar cores with ALMA can test this correlation. All the correlations found agree well with the data found in Scorpius OB2 by Kouwenhoven et al. (2007). This implies that the mechanism of binary formation is universal at least for OB-associations.
A competitive accretion scenario can explain our data of the massive stars best. However, a proper motion study of the region indicates that the stellar density in our region has never been high enough for a competitive accretion scenario to work on a global scale. Thus it seems that the reason for the multiplicity of the stars is intrinsic to their formation and a local effect, i.e., does not depend on the properties of the surrounding cluster or association. Consequently, we favor for the formation of multiple systems in the Cep OB2/3 associations a scenario where the proto-stellar core fragments into a few parts only and the fragments undergo an evolution determined by competitive accretion, giving each component access to the matter reservoir comprising the whole original proto-stellar core. The number of fragments rises with the core mass from two for stars with spectral types later than B2V to three or more for more massive stars.
Online material
Appendix A: Target list
The following Tables A.1 to A.4 contain all targets we observed. The different columns contain the following parameters: Col. 1 the name of the target. Most names are either from the Henry Draper Catalog, the “Bonner Durchmusterung” or from Kun & Pasztor (1990). Column 2 and 3 give the right ascension and declination with equinox 2000. Column 4 shows the spectral type adapted in this work. In Col. 5 we list the separation of the detected companions up to a maximum separation of 3′′. Any companion further out is not shown. The position angle is shown in Col. 6. Column 7 presents the magnitude difference between primary and secondary. The membership of the target to the association is shown in Col. 8. The spectral types found in the literature are then given in Col. 9. The numbers in the table denote the following: 16: Roeser & Bastian (1988), 17: Simonson (1968), 18: Garrison (1970), 19: Contreras et al. (2002), 20: Morgan et al. (1955), 21: Blaauw et al. (1959), 22: Garrison & Kormendy (1976), 23: Walborn (1971), 24: Jaschek et al. (1964), 25: Sicilia-Aguilar et al. (2005), 26: Hiltner & Johnson (1956), 27: Melikian et al. (1988), 28: Skiff (2007), 29: Kharchenko (2001), 30: Garmany & Stencel (1992), 31: Morgan et al. (1953), 32: Mendoza V. (1958).
Target list of AstraLux observations.
Acknowledgments
The authores want to thank the staff of the Calar Alto observatory for their support. The authors also want to express their gratitude to an anonymous referee and language editor who helped to improve the paper.
References
- Abt, H. A., & Levy, S. G. 1976, BAAS, 8, 521 [NASA ADS] [Google Scholar]
- Abt, H. A., Gomez, A. E., & Levy, S. G. 1990, ApJS, 74, 551 [NASA ADS] [CrossRef] [Google Scholar]
- Alves, J., Lombardi, M., & Lada, C. J. 2007, A&A, 462, L17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Apai, D., Bik, A., Kaper, L., Henning, T., & Zinnecker, H. 2007, ApJ, 655, 484 [NASA ADS] [CrossRef] [Google Scholar]
- Assousa, G. E., Herbst, W., & Turner, K. C. 1977, ApJ, 218, L13 [NASA ADS] [CrossRef] [Google Scholar]
- Balazs, L. G., & Kun, M. 1989, Astron. Nachr., 310, 385 [NASA ADS] [CrossRef] [Google Scholar]
- Bate, M. R. 2000, MNRAS, 314, 33 [NASA ADS] [CrossRef] [Google Scholar]
- Batten, A. H., Fletcher, J. M., & Mann, P. J. 1978, Publications of the Dominion Astrophysical Observatory Victoria, 15, 121 [Google Scholar]
- Beuther, H., & Schilke, P. 2004, Science, 303, 1167 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Blaauw, A. 1964, ARA&A, 2, 213 [NASA ADS] [CrossRef] [Google Scholar]
- Blaauw, A. 1991, in The Physics of Star Formation and Early Stellar Evolution, ed. C. J. Lada, & N. D. Kylafis, NATO ASIC Proc., 342, 125 [Google Scholar]
- Blaauw, A., Hiltner, W. A., & Johnson, H. L. 1959, ApJ, 130, 69 [NASA ADS] [CrossRef] [Google Scholar]
- Bonnell, I. A. 2008, in Pathways Through an Eclectic Universe, ed. J. H. Knapen, T. J. Mahoney, & A. Vazdekis, ASP Conf. Ser., 390, 26 [Google Scholar]
- Bonnell, I. A., & Bate, M. R. 2005, MNRAS, 362, 915 [NASA ADS] [CrossRef] [Google Scholar]
- Bonnell, I. A., Bate, M. R., & Zinnecker, H. 1998, MNRAS, 298, 93 [NASA ADS] [CrossRef] [Google Scholar]
- Brandner, W., & Koehler, R. 1998, ApJ, 499, L79 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, A. G. A., Dekker, G., & de Zeeuw, P. T. 1997, MNRAS, 285, 479 [NASA ADS] [CrossRef] [Google Scholar]
- Clarke, C. J. 2001, in The Formation of Binary Stars, ed. H. Zinnecker, & R. Mathieu, IAU Symp., 200, 346 [Google Scholar]
- Contreras, M. E., Sicilia-Aguilar, A., Muzerolle, J., et al. 2002, AJ, 124, 1585 [NASA ADS] [CrossRef] [Google Scholar]
- de Vegt, C. 1966, ZAp, 64, 268 [NASA ADS] [Google Scholar]
- de Zeeuw, T., & Brand, J. 1985, in Birth and Evolution of Massive Stars and Stellar Groups, ed. W. Boland, & H. van Woerden, Astrophys. Space Sci. Lib., 120, 95 [Google Scholar]
- Dommanget, J., & Nys, O. 2002, VizieR Online Data Catalog, 1274, [Google Scholar]
- Doremus, C. 1970, PASP, 82, 745 [NASA ADS] [CrossRef] [Google Scholar]
- Duchêne, G., Simon, T., Eislöffel, J., & Bouvier, J. 2001, A&A, 379, 147 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Duquennoy, A., & Mayor, M. 1991, A&A, 248, 485 [NASA ADS] [Google Scholar]
- Elmegreen, B. G., & Lada, C. J. 1977, ApJ, 214, 725 [NASA ADS] [CrossRef] [Google Scholar]
- Fabricius, C., Høg, E., Makarov, V. V., et al. 2002, A&A, 384, 180 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Figer, D. F., Morris, M., Kim, S. S., & Serabyn, E. 1999, in The Central Parsecs of the Galaxy, ed. H. Falcke, A. Cotera, W. J. Duschl, F. Melia, & M. J. Rieke, ASP Conf. Ser., 186, 329 [Google Scholar]
- Fischer, D. A., & Marcy, G. W. 1992, ApJ, 396, 178 [NASA ADS] [CrossRef] [Google Scholar]
- Garmany, C. D. 1973, AJ, 78, 185 [NASA ADS] [CrossRef] [Google Scholar]
- Garmany, C. D., & Stencel, R. E. 1992, A&AS, 94, 211 [NASA ADS] [Google Scholar]
- Garrison, R. F. 1970, AJ, 75, 1001 [NASA ADS] [CrossRef] [Google Scholar]
- Garrison, R. F., & Kormendy, J. 1976, PASP, 88, 865 [NASA ADS] [CrossRef] [Google Scholar]
- Ghez, A. M., McCarthy, D. W., Patience, J. L., & Beck, T. L. 1997, ApJ, 481, 378 [NASA ADS] [CrossRef] [Google Scholar]
- Gouliermis, D. A., Chu, Y.-H., Henning, T., et al. 2008, ApJ, 688, 1050 [NASA ADS] [CrossRef] [Google Scholar]
- Henry, T. J., & McCarthy, Jr., D. W. 1990, ApJ, 350, 334 [NASA ADS] [CrossRef] [Google Scholar]
- Hill, G. 1967, ApJS, 14, 301 [NASA ADS] [CrossRef] [Google Scholar]
- Hiltner, W. A., & Johnson, H. L. 1956, ApJ, 124, 367 [NASA ADS] [CrossRef] [Google Scholar]
- Hormuth, F., Hippler, S., Brandner, W., Wagner, K., & Henning, T. 2008, in SPIE Conf. Ser., 7014 [Google Scholar]
- Jaschek, C., Conde, H., & de Sierra, A. C. 1964, Observatory Astronomical La Plata Series Astronomies, 28, 1 [NASA ADS] [Google Scholar]
- Jijina, J., & Adams, F. C. 1996, ApJ, 462, 874 [NASA ADS] [CrossRef] [Google Scholar]
- Jordi, C., Trullols, E., & Galadi-Enriquez, D. 1996, A&A, 312, 499 [NASA ADS] [Google Scholar]
- Kharchenko, N. V. 2001, Kinematika i Fizika Nebesnykh Tel, 17, 409 [NASA ADS] [Google Scholar]
- Klessen, R. S., Ballesteros-Paredes, J., Li, Y., & Mac Low, M.-M. 2004, in The Formation and Evolution of Massive Young Star Clusters, ed. H. J. G. L. M. Lamers, L. J. Smith, & A. Nota, ASP Conf. Ser., 322, 299 [Google Scholar]
- Kouwenhoven, M. B. N., Brown, A. G. A., Portegies Zwart, S. F., & Kaper, L. 2007, A&A, 474, 77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kratter, K. M., & Matzner, C. D. 2006, MNRAS, 373, 1563 [NASA ADS] [CrossRef] [Google Scholar]
- Krumholz, M. R. 2006 [arXiv:0607429] [Google Scholar]
- Krumholz, M. 2008, in Pathways Through an Eclectic Universe, ed. J. H. Knapen, T. J. Mahoney, & A. Vazdekis, ASP Conf. Ser., 390, 16 [Google Scholar]
- Krumholz, M. R., Klein, R. I., McKee, C. F., Offner, S. S. R., & Cunningham, A. J. 2009, Science, 323, 754 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Kun, M., & Pasztor, L. 1990, Ap&SS, 174, 13 [NASA ADS] [CrossRef] [Google Scholar]
- Leinert, C., Zinnecker, H., Weitzel, N., et al. 1993, A&A, 278, 129 [NASA ADS] [Google Scholar]
- Maíz Apellániz, J. 2010, A&A, 518, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mason, B. D., Gies, D. R., Hartkopf, W. I., et al. 1998, AJ, 115, 821 [NASA ADS] [CrossRef] [Google Scholar]
- Mason, B. D., Hartkopf, W. I., Gies, D. R., Henry, T. J., & Helsel, J. W. 2009, AJ, 137, 3358 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Massey, F. J. 1951, J. Am. Statis. Assoc., 46, 68 [CrossRef] [Google Scholar]
- Mayor, M., Duquennoy, A., Halbwachs, J.-L., & Mermilliod, J.-C. 1992, in Complementary Approaches to Double and Multiple Star Research, ed. H. A. McAlister, & W. I. Hartkopf, IAU Colloq., 135, ASP Conf. Ser., 32, 73 [Google Scholar]
- McKee, C. F., & Tan, J. C. 2002, Nature, 416, 59 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- McKee, C. F., & Tan, J. C. 2003, ApJ, 585, 850 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Melikian, N. D., Shevchenko, V. S., Ibragimov, M. A., Jakubov, S. D., & Chernyshev, A. V. 1988, Information Bulletin on Variable Stars, 3187, 1 [NASA ADS] [Google Scholar]
- Mendoza, V. E. E. 1958, ApJ, 128, 207 [NASA ADS] [CrossRef] [Google Scholar]
- Moeckel, N., & Bally, J. 2007, ApJ, 656, 275 [NASA ADS] [CrossRef] [Google Scholar]
- Moreno-Corral, M. A., Chavarria, K. C., de Lara, E., & Wagner, S. 1993, A&A, 273, 619 [NASA ADS] [Google Scholar]
- Morgan, W. W., Whitford, A. E., & Code, A. D. 1953, ApJ, 118, 318 [Google Scholar]
- Morgan, W. W., Code, A. D., & Whitford, A. E. 1955, ApJS, 2, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Nakano, T., Hasegawa, T., Morino, J.-I., & Yamashita, T. 2000, ApJ, 534, 976 [NASA ADS] [CrossRef] [Google Scholar]
- Nelan, E. P., Walborn, N. R., Wallace, D. J., et al. 2004, AJ, 128, 323 [NASA ADS] [CrossRef] [Google Scholar]
- Patel, N. A., Heyer, M. H., Goldsmith, P. F., et al. 1994, in Clouds, Cores, and Low Mass Stars, ed. D. P. Clemens, & R. Barvainis, ASP Conf. Ser., 65, 81 [Google Scholar]
- Patel, N. A., Goldsmith, P. F., Snell, R. L., Hezel, T., & Xie, T. 1995, ApJ, 447, 721 [NASA ADS] [CrossRef] [Google Scholar]
- Patel, N. A., Goldsmith, P. F., Heyer, M. H., Snell, R. L., & Pratap, P. 1998, ApJ, 507, 241 [NASA ADS] [CrossRef] [Google Scholar]
- Pourbaix, D., Tokovinin, A. A., Batten, A. H., et al. 2004, A&A, 424, 727 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Preibisch, T., Zinnecker, H., Guenther, E., et al. 1998, in Cool Stars, Stellar Systems, and the Sun, ed. R. A. Donahue, & J. A. Bookbinder, ASP Conf. Ser., 154, 1780 [Google Scholar]
- Preibisch, T., Balega, Y., Hofmann, K.-H., Weigelt, G., & Zinnecker, H. 1999, New A, 4, 531 [Google Scholar]
- Press, W. H., Teukolsky, S. A., Vetterling, W. T., & Flannery, B. P. 1988, Numerical Recipes in C [Google Scholar]
- Ratzka, T., Köhler, R., & Leinert, C. 2005, A&A, 437, 611 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Roeser, S., & Bastian, U. 1988, A&AS, 74, 449 [NASA ADS] [Google Scholar]
- Samus, N. N., Durlevich, O. V., et al. 2004, VizieR Online Data Catalog, 2250, [Google Scholar]
- Sana, H., & Evans, C. J. 2011, in IAU Symp. 272, ed. C. Neiner, G. Wade, G. Meynet, & G. Peters, 474 [Google Scholar]
- Sargent, A. I. 1979, ApJ, 233, 163 [NASA ADS] [CrossRef] [Google Scholar]
- Shu, F. H., Adams, F. C., & Lizano, S. 1987, ARA&A, 25, 23 [Google Scholar]
- Sicilia-Aguilar, A., Hartmann, L. W., Briceño, C., Muzerolle, J., & Calvet, N. 2004, AJ, 128, 805 [NASA ADS] [CrossRef] [Google Scholar]
- Sicilia-Aguilar, A., Hartmann, L. W., Hernández, J., Briceño, C., & Calvet, N. 2005, AJ, 130, 188 [NASA ADS] [CrossRef] [Google Scholar]
- Simonson, III, S. C. 1968, ApJ, 154, 923 [NASA ADS] [CrossRef] [Google Scholar]
- Simonson, III, S. C., & Van Someren Greve, H. W. 1976, A&A, 49, 343 [NASA ADS] [Google Scholar]
- Skiff, B. A. 2007, VizieR Online Data Catalog, 2277, [Google Scholar]
- Smith, J. A., Tucker, D. L., Kent, S., et al. 2002, AJ, 123, 2121 [Google Scholar]
- Stephens, M. A. 1970, J. Roy. Stat. Soc. Ser. B (Methodological), 32, 115 [Google Scholar]
- Stickland, D. J. 1995, The Observatory, 115, 180 [NASA ADS] [Google Scholar]
- Stolte, A., Grebel, E. K., Brandner, W., & Figer, D. F. 2002, A&A, 394, 459 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Straižys, V. 1992, Multicolor stellar photometry, ed. V. Straižys [Google Scholar]
- Tokovinin, A. A. 1992, A&A, 256, 121 [NASA ADS] [Google Scholar]
- Trullols, E., Jordi, C., & Galadi-Enriquez, D. 1997, in Hipparcos – Venice ’97, ed. R. M. Bonnet, E. Høg, P. L. Bernacca et al., ESA SP, 402, 299 [Google Scholar]
- Tubbs, R. N., Baldwin, J. E., Mackay, C. D., & Cox, G. C. 2002, A&A, 387, L21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Turner, N. H., Ten Brummelaar, T. A., Roberts, L. C., et al. 2008, AJ, 136, 554 [NASA ADS] [CrossRef] [Google Scholar]
- Walborn, N. R. 1971, ApJS, 23, 257 [NASA ADS] [CrossRef] [Google Scholar]
- Wolfire, M. G., & Cassinelli, J. P. 1987, ApJ, 319, 850 [NASA ADS] [CrossRef] [Google Scholar]
- Yorke, H. W., & Bodenheimer, P. 1999, ApJ, 525, 330 [NASA ADS] [CrossRef] [Google Scholar]
- Yorke, H. W., & Sonnhalter, C. 2002, ApJ, 569, 846 [NASA ADS] [CrossRef] [Google Scholar]
- Zinnecker, H., & Yorke, H. W. 2007, ARA&A, 45, 481 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Distributions and parameter ranges compared in the Bayesian evidence calculation.
Correlation coefficients and slopes found on the observed samples, and on the comparison Monte Carlo simulations.
Examined parameters and their behavior in the cases of modified disk and competitive accretion.
All Figures
 |
Fig. 1 Targets observed with AstraLux. The different regions are shown by name. The asterisks mark the intermediate-mass stars, the crosses the massive stars. Additionally shown are examples of identified binaries. |
| In the text | |
 |
Fig. 2 Brightness vs. separation of the companion stars. The solid curve marks the sample of companions that we assumed to be physical. The left border of the sample is given by the detection limit as a function of brightness. The right border is defined by the change in the behavior of the stellar density with separation (see text). |
| In the text | |
 |
Fig. 3 Upper panel: the CSF as function of the maximum primary mass. Lower panel: the ratio of two CSFs. One CSF is calculated for the sample of targets with the value on the x-axis taken as maximum mass, the other one is calculated for the remaining targets. The ratio is calculated as the value of the CSF of the sample of the more massive targets over the value of the CSF of the less massive sample. The dotted lines indicate the error range at the position of the peak and prove that the peak is indeed significant. |
| In the text | |
 |
Fig. 4 Companion-star fraction as a function of spectral type. |
| In the text | |
 |
Fig. 5 Mass function of companions to stars in the OB sample (dashed) compared to the CMF as it was constructed from individual images under consideration of the brightness-separation bias following the Salpeter law (solid, see text). Overplotted as dotted line is the Salpeter-like mass function but with an exponent Γ of –0.001. |
| In the text | |
 |
Fig. 6 Histogram of the distribution of magnitude differences between binary components in the OB sample. Overplotted is the best-fit model. The probability is displayed in the bottom of the image. The inset shows the cumulative distribution (steps) on which the fit (curve) was performed. See text for explanations about why a Gaussian fit passes the KS test well while a Bayesian analysis cannot find a significant evidience for either a Gaussian or a Uniform distribution. |
| In the text | |
 |
Fig. 7 Histogram of the mass ratio distribution for the OB star sample. Overplotted is the Gaussian model derived from the cumulative distribution shown in the inset. See text for an explanation why the KS test is extremly favourable for the Gaussian distribution while a Bayesian analysis actually shows evidence that the distribution is actually uniform. |
| In the text | |
 |
Fig. 8 Histogram of the distribution of separations for the OB star sample. Over plotted is the best fit to the cumulative distribution shown in the inset. See text for explanations about why a Gaussian fit passes the KS test well while a Bayesian analysis cannot find a significant evidience for either a Gaussian or a Uniform distribution. |
| In the text | |
 |
Fig. 9 Separation vs. mass correlation for the OB stars. |
| In the text | |
 |
Fig. 10 Mass ratio vs. separation correlation for the OB stars. |
| In the text | |
 |
Fig. 11 Correlation between mass ratio and system mass for the OB stars. |
| In the text | |
 |
Fig. 12 Correlation between primary and secondary mass for the OB stars. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


