| Issue |
A&A
Volume 537, January 2012
|
|
|---|---|---|
| Article Number | A33 | |
| Number of page(s) | 7 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201117902 | |
| Published online | 23 December 2011 | |
New phase diagrams for dense carbon-oxygen mixtures and white dwarf evolution
1 Facultad de Ciencias Astronómicas y Geofísicas, Universidad Nacional de La Plata, Paseo del Bosque s/n, 1900 La Plata, Argentina
2 Member of CONICET, Argentina
e-mail: althaus@fcaglp.unlp.edu.ar; acorsico@fcaglp.unlp.edu.ar; mmiller@fcaglp.unlp.edu.ar;
3 Departament de Física Aplicada, Universitat Politècnica de Catalunya, c/Esteve Terrades 5, 08860 Castelldefels, Spain
e-mail:garcia@fa.upc.edu
4 Institute for Space Studies of Catalonia, c/Gran Capità 2–4, Edif. Nexus 104, 08034 Barcelona, Spain
5 Institut de Ciències de l’Espai (CSIC), Facultat de Ciències, Campus UAB, Torre C5-parell, 08193 Bellaterra, Spain
e-mail: isern@ieec.cat
Received: 17 August 2011
Accepted: 19 October 2011
Context. Cool white dwarfs are reliable and independent stellar chronometers. The most common white dwarfs have carbon-oxygen dense cores. Consequently, the cooling ages of very cool white dwarfs sensitively depend on the adopted phase diagram of the carbon-oxygen binary mixture.
Aims. A new phase diagram of dense carbon-oxygen mixtures appropriate for white dwarf interiors has been recently obtained using direct molecular dynamics simulations. In this paper, we explore the consequences of this phase diagram in the evolution of cool white dwarfs.
Methods. To do this we employ a detailed stellar evolutionary code and accurate initial white dwarf configurations, derived from the full evolution of progenitor stars. We use two different phase diagrams, that of Horowitz et al. (2010, Phys. Rev. Lett., 104, 231101), which presents an azeotrope, and the phase diagram of Segretain & Chabrier (1993, A&A, 271, L13), which is of the spindle form.
Results. We computed the evolution of 0.593 and 0.878 M⊙ white dwarf models during the crystallization phase, and we found that the energy released by carbon-oxygen phase separation is smaller when the new phase diagram of Horowitz et al. is used. This translates into time delays that are on average a factor ~2 smaller than those obtained when the phase diagram of Segretain & Chabrier is employed.
Conclusions. Our results have important implications for white dwarf cosmochronology, because the cooling ages of very old white dwarfs are different for the two phase diagrams. This may have a noticeable impact on the age determinations of very old globular clusters, for which the white dwarf color-magnitude diagram provides an independent way of estimating their age.
Key words: stars: evolution / white dwarfs / stars: interiors
© ESO, 2012
1. Introduction
White dwarf stars constitute the most common end-point of stellar evolution – see, for instance, Althaus et al. (2010a) for a recent review – and as such are valuable in constraining several properties of a wide variety of stellar populations including globular and open clusters (Von Hippel & Gilmore 2000; Hansen et al. 2007; Winget et al. 2009; García-Berro et al. 2010). Additionally, they can be used to place constraints on exotic elementary particles (Isern et al. 1992; Córsico et al. 2001; Isern et al. 2008) or on alternative theories of gravitation (García-Berro et al. 1995; Benvenuto et al. 2004; García-Berro et al. 2011). This is possible because we have a relatively precise knowledge of the main physical processes responsible for their evolution, although some uncertainties still persist for key aspects of their constitutive physics. One of the processes that is still subject to some uncertainties is crystallization. As early recognized (Van Horn 1968), cool white dwarfs are expected to crystallize as a result of strong Coulomb interactions in their very dense interior. Crystallization results in two additional energy sources that slow down the cooling process. The first source is latent heat, while the second one is the release of gravitational energy resulting from the changes in the carbon-oxygen profile due to the different chemical compositions of the liquid and solid phases (García-Berro et al. 1988a,b). Generally speaking, the solid formed upon cyrstallization is richer in oxygen than the liquid. As the oxygen-rich solid core grows at the center of the white dwarf, the lighter carbon-rich liquid mantle left behind is efficiently redistributed by Rayleigh-Taylor instabilities (Isern et al. 1997). This process releases gravitational energy, and this additional energy source has a substantial impact in the computed cooling times of cool white dwarfs (Segretain et al. 1994; Salaris et al. 1997; Montgomery et al. 1999; Salaris et al. 2000; Isern et al. 2000; Renedo et al. 2010).
Recently, Winget et al. (2009) have used theoretical fits to the observed white dwarf luminosity function of the globular cluster NGC 6397 to provide evidence for the occurrence of crystallization in deep interiors of white dwarfs, and to place constraints on the crystallization temperature of the carbon-oxygen mixture. Thus, it is foreseable that in the near future deep photometry of the cooling sequence of degenerate stars of nearby globular clusters will allow us to check the accuracy of the theoretical cooling sequences, and hence will allow us to study the constitutive physics of matter at the high densities of cool white dwarfs.
Since the pionering works of Stevenson (1980) and Mochkovitch (1983), large theoretical efforts have been paid to study the phase diagram of carbon-oxygen mixtures. In these early efforts the adopted carbon-oxygen phase diagram had a deep eutectic. This resulted in a high enhancement of the oxygen abundance of the solid phase. Consequently, the computed delays in the cooling ages were rather large. The calculations of Stevenson (1980) were subsequently improved by Ichimaru et al. (1988), who obtained a phase diagram of the azeotropic form, and Barrat et al. (1988), who found that the phase diagram was of the spindle form. Later, Ogata et al. (1993) used Monte Carlo simulations and the hypernetted-chain approximation to compute the phase diagram of the carbon-oxygen binary mixture, and obtained a phase diagram of the spindle form. Almost simultaneously, Segretain & Chabrier (1993) used a density-functional approach to obtain the phase diagram for arbitrary binary mixtures as a function of Z1/Z2, being Z1 and Z2 the charge of the two chemical species. In the case of carbon-oxygen mixtures, they obtained a phase diagram of the spindle type. Since in the case of a phase diagram of the spindle form the solid phase is less oxygen-enriched, the time delays computed using this type of phase diagrams turned out to be smaller than those previously computed (Segretain et al. 1994). Since then, the phase diagram of Segretain & Chabrier (1993) has remained a “de facto” standard over the years. However, very recently the phase diagram of dense carbon-oxygen mixtures appropriate for white dwarf star interiors has been re-examined by Horowitz et al. (2010). This work was motivated by the unexpected finding of Winget et al. (2009) that the crystallization temperature of white dwarfs in the globular cluster NGC 6397 was close to that for pure carbon. Horowitz et al. (2010) used an approach completely different of those previously employed. Specifically, they used direct two-phase molecular dynamics simulations for the solid and liquid phases. Their results are in rather good agreement with those of Medin & Cumming (2010), and predict crystallization temperatures considerably lower than those obtained by Segretain & Chabrier (1993). In particular, Horowitz et al. (2010) found the crystallization temperature of carbon-oxygen mixtures with equal mass fractions to be close to that of pure carbon, thus offering a possible explanation for the puzzling result of Winget et al. (2009). Additionally, Horowitz et al. (2010) found that the shape of the carbon-oxygen phase diagram is of the azeotropic form, and not of the spindle type, as previously thought. This may have a large effect on the evolutionary ages of cool white dwarfs.
In this paper we explore the implications for the evolutionary properties of white dwarfs of the new phase diagram of carbon-oxygen mixtures computed by Horowitz et al. (2010). To this end, we employ a detailed stellar evolutionary code and initial accurate white dwarf structures derived from the full evolution of progenitor stars. The paper is organized as follows. In Sect. 2 we briefly describe the phase diagram of Horowitz et al. (2010). We also comment on the main characteristics of our evolutionary code. Particularly we also elaborate on the treatment of the energy sources resulting from crystallization, and the evolutionary sequences used in our study. Section 3 is devoted to explore the consequences of the new phase diagram for the evolutionary times of white dwarfs. Finally, in Sect. 4 we summarize the main results of our calculations and we draw our conclusions.
 |
Fig. 1 Carbon-oxygen phase diagrams used in our evolutionary calculations. The crystallization temperature of the carbon-oxygen binary mixture in terms of the crystallization temperature of pure carbon is shown as a function of the oxygen abundance by mass. Dashed red lines and solid blue lines correspond, respectively, to the phase diagrams of Segretain & Chabrier (1993) and Horowitz et al. (2010). For each diagram, the upper curve gives the crystallization temperature for a given oxygen abundance of the liquid, while the lower curve provides the equilibrium oxygen abundance of the solid at this temperature. The dotted line corresponds to the case in which no phase separation occurs, and the mixture is treated as the average of the chemical species. Finally, the circles denote the crystallization temperature of the carbon-oxygen mixture for the case of an oxygen mass abundance of 0.7, a typical value found in the evolutionary calculations of white dwarf progenitors. |
2. Numerical tools
2.1. Carbon-oxygen phase diagrams
Horowitz et al. (2010) have recently determined the phase diagram of dense carbon-oxygen mixtures appropriate for white dwarf star interiors. They argue that their results, based on direct two-phase molecular dynamics simulations, are less affected by small errors in the free energy difference between the liquid and solid phases than previous studies. Moreover, they predict that the crystallization temperature of the carbon-oxygen binary mixture is considerably lower than that resulting from the phase diagram of Segretain & Chabrier (1993). This can be seen Fig. 1, in which several phase diagrams for the carbon-oxygen mixture are displayed. In particular, in this figure we show both the crystallization temperature (upper curves) as a function of the oxygen abundance by mass of the liquid phase and the equilibrium abundances in the solid phase (lower curves) at this temperature. The crystallization temperature T of the carbon-oxygen mixture is expressed in terms of the crystallization temperature of pure carbon (TC). Crystallization for pure carbon occurs when the Coulomb coupling parameter (Γ) reaches the value Γcrys = 178.4 (Horowitz et al. 2010), where the Coulomb coupling parameter is defined as: 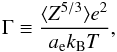 (1)being ae the interelectronic distance, ⟨ Z5/3 ⟩ an average (by number) over the ion charges, and kB Boltzmann’s constant. The rest of the symbols have their usual meaning. In particular, the crystallization temperature for pure carbon composition results
(1)being ae the interelectronic distance, ⟨ Z5/3 ⟩ an average (by number) over the ion charges, and kB Boltzmann’s constant. The rest of the symbols have their usual meaning. In particular, the crystallization temperature for pure carbon composition results 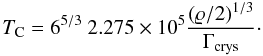 (2)The shape of the phase diagram for a carbon-oxygen mixture as calculated by Horowitz et al. (2010) is displayed in Fig. 1 using solid blue lines. In addition, we also show (dashed red lines) the carbon-oxygen phase diagram of Segretain & Chabrier (1993). Finally, the crystallization temperature when phase separation is not taken into account, and the mixture is treated as the average of the chemical species, is represented as well (black dotted line). It is worth highlighting some important features of the phase diagrams illustrated in Fig. 1. To begin with, we note that the phase diagram of Horowitz et al. (2010) predicts a crystallization temperature of the carbon-oxygen mixture substantially lower than that predicted by the phase diagram of Segretain & Chabrier (1993), which in turn is also much lower than that obtained in the case in which phase separation is disregarded. This implies that for a white dwarf of a given mass and core composition, crystallization will set in at smaller stellar luminosities when the phase diagram of Horowitz et al. (2010) is adopted. The second relevant point is that the width of the phase diagram of Segretain & Chabrier (1993) is considerably larger than that of Horowitz et al. (2010). Hence, the oxygen enhancement in the solid phase (with respect to the composition of the fluid phase from which it formed) will be substantially smaller when the phase diagram of Horowitz et al. (2010) is adopted. These two differences have opposite effects. On the one hand, the gravitational energy released by carbon-oxygen phase separation will be smaller in the case in which the phase diagram of Horowitz et al. (2010) is adopted. On the other, this energy is released at smaller luminosities. The impact of these two effects on the delays introduced by phase separation upon crystallization can only be reliably assessed using a full evolutionary code. Finally, there is as well another effect which is also worth noting. The phase diagram of Horowitz et al. (2010) presents an azeotrope at XO ~ 0.3, while that of Segretain & Chabrier (1993) is approximately of the spindle form. This means that when the fluid phase reaches the azeotropic composition, the solid phase has the same composition of the liquid. Consequently, phase separation no longer occurs, and the subsequent evolution during the crystallization phase is only driven by the release of latent heat. Nevertheless, if the abundance of oxygen in the outer layers is smaller than the azeotropic one, the solid that forms is oxygen poor as compared with the liquid and raises until it melts, leaving behind a liquid that gradually aproaches to the azeotropic composition. When this happens a solid with the azeotropic composition forms. Therefore, in this case, the process of separation continues until the entire white dwarf core has frozen.
(2)The shape of the phase diagram for a carbon-oxygen mixture as calculated by Horowitz et al. (2010) is displayed in Fig. 1 using solid blue lines. In addition, we also show (dashed red lines) the carbon-oxygen phase diagram of Segretain & Chabrier (1993). Finally, the crystallization temperature when phase separation is not taken into account, and the mixture is treated as the average of the chemical species, is represented as well (black dotted line). It is worth highlighting some important features of the phase diagrams illustrated in Fig. 1. To begin with, we note that the phase diagram of Horowitz et al. (2010) predicts a crystallization temperature of the carbon-oxygen mixture substantially lower than that predicted by the phase diagram of Segretain & Chabrier (1993), which in turn is also much lower than that obtained in the case in which phase separation is disregarded. This implies that for a white dwarf of a given mass and core composition, crystallization will set in at smaller stellar luminosities when the phase diagram of Horowitz et al. (2010) is adopted. The second relevant point is that the width of the phase diagram of Segretain & Chabrier (1993) is considerably larger than that of Horowitz et al. (2010). Hence, the oxygen enhancement in the solid phase (with respect to the composition of the fluid phase from which it formed) will be substantially smaller when the phase diagram of Horowitz et al. (2010) is adopted. These two differences have opposite effects. On the one hand, the gravitational energy released by carbon-oxygen phase separation will be smaller in the case in which the phase diagram of Horowitz et al. (2010) is adopted. On the other, this energy is released at smaller luminosities. The impact of these two effects on the delays introduced by phase separation upon crystallization can only be reliably assessed using a full evolutionary code. Finally, there is as well another effect which is also worth noting. The phase diagram of Horowitz et al. (2010) presents an azeotrope at XO ~ 0.3, while that of Segretain & Chabrier (1993) is approximately of the spindle form. This means that when the fluid phase reaches the azeotropic composition, the solid phase has the same composition of the liquid. Consequently, phase separation no longer occurs, and the subsequent evolution during the crystallization phase is only driven by the release of latent heat. Nevertheless, if the abundance of oxygen in the outer layers is smaller than the azeotropic one, the solid that forms is oxygen poor as compared with the liquid and raises until it melts, leaving behind a liquid that gradually aproaches to the azeotropic composition. When this happens a solid with the azeotropic composition forms. Therefore, in this case, the process of separation continues until the entire white dwarf core has frozen.
2.2. Evolutionary code
All the calculations reported here have been done using the LPCODE stellar evolutionary code. This code has been used to study different problems related to the formation and evolution of white dwarfs – see Althaus et al. (2010b), Renedo et al. (2010), and references therein for details. The only difference with respect to previous evolutionary calculations of cooling white dwarfs is the treatment of crystallization. For the results presented here, crystallization sets in according to the phase diagram considered. That is, when no phase separation is assumed the crystallization temperature of the carbon-oxygen core is obtained from Eq. (1), and imposing Γ = 180, while in all other cases this temperature is obtained from the corresponding phase diagram.
The energy sources associated to the crystallization of the white dwarf core comprise the release of latent heat and gravitational energy associated with changes in the carbon-oxygen profile induced by crystallization. In LPCODE, the inclusion of these two energy sources is done self-consistently and locally coupled to the full set of equations of stellar evolution. That is, the structure and evolution of white dwarfs is computed with the changing composition profile and with the luminosity equation appropriately modified to account for both the local contribution of energy released from the core chemical redistribution and latent heat. At each evolutionary timestep, the crystallization temperature and the change of the chemical profile resulting from phase separation are computed using the appropriate phase diagram. In particular, the carbon-enhanced convectively-unstable liquid layers overlying the crystallizing core are assumed to be instantaneously mixed, a reasonable assumption considering the long evolutionary timescales of white dwarfs (Isern et al. 1997). After computing the chemical compositions of both the solid and liquid phases the net energy released in the process is assessed as in Isern et al. (1997, 2000). The latent heat contribution is taken to be 0.77kBT per ion (Salaris et al. 2000). Both energy contributions are distributed over a small mass range around the crystallization front. We mention that the magnitude of both energy sources are calculated at each iteration during the convergence of the model – see Althaus et al. (2010c) for the numerical details.
The input physics of the code include the equation of state of Segretain et al. (1994) for the high-density regime – which accounts for all the important contributions for both the liquid and solid phases (Althaus et al. 2007) – complemented with an updated version of the equation of state of Magni & Mazzitelli (1979) for the low-density regime. Radiative opacities are those of OPAL (Iglesias & Rogers 1996), including carbon- and oxygen-rich compositions, complemented with the low-temperature opacities of Alexander & Ferguson (1994), whilst conductive opacities are taken from Cassisi et al. (2007). During the white dwarf regime, the metal mass fraction Z in the envelope is not assumed to be fixed. Instead, it is specified consistently according to the prediction of element diffusion. To account for this, we considered radiative opacities tables from OPAL for arbitrary metallicities. For effective temperatures less than 10 000 K, outer boundary conditions for the evolving models are given by detailed non-gray model atmospheres that incorporate non-ideal effects in the gas equation of state and chemical equilibrium (based on the occupation probability formalism), radiative and convective transport (mixing length theory) of energy, collision-induced absorption from molecules, and the Lyα quasi-molecular opacity (Rohrmann et al. 2011). This provides detailed and accurate outer boundary conditions which are required for a proper treatment of the evolutionary behavior of cool white dwarfs.
2.3. Evolutionary sequences
Instead of exploring the evolution of white dwarfs with different arbitrary chemical profiles for the core, we focus on evolutionary sequences that are provided by detailed calculations of the evolutionary history of progenitor stars. Our aim is to explore the impact of the new phase diagram of Horowitz et al. (2010) on existing grids of white dwarf evolutionary sequences that incorporate a realistic chemical profile in the stellar interior. Specifically, the white dwarf initial configurations considered in this investigation are those obtained from the full evolution of progenitor stars we computed in previous studies (Renedo et al. 2010). In those studies progenitor stars were evolved from the zero age main sequence, through the thermally-pulsing and mass-loss phases on the asymptotic giant branch (AGB), to the white dwarf cooling phase. Extra-mixing episodes beyond each formal convective boundary were taken into account, particularly during the core helium burning stage, but not during the evolutionary stages corresponding to the thermally-pulsing AGB phase. Moreover, the outer chemical profiles of our white dwarf sequences are the result of element diffusion processes that lead to the formation of pure hydrogen envelopes – see Althaus et al. (2010b) for details.
 |
Fig. 2 Inner oxygen distribution (abundance by mass) for the 0.593 M⊙ white dwarf model at different evolutionary stages. The (red) dot-dashed line corresponds to the oxygen distribution before the occurrence of crystallization. The final oxygen profile when most of the white dwarf has crystallized is also shown for the phase diagram of Horowitz et al. (2010) – (blue) dashed line – and for the phase diagram of Segretain & Chabier (1993) – (black) solid line. |
For the sake of conciseness, we concentrate on two white dwarf sequences, with masses 0.593 and 0.878 M⊙, which are the result of the evolution of 1.75 and 5.0 M⊙ progenitors with metallicity Z = 0.01. The total mass of hydrogen in their envelopes is 1.1 × 10-4 and 1.17 × 10-5 M⊙, respectively. For each stellar mass, we have computed the white dwarf cooling phase down to very low luminosities, when most of the white dwarf has already crystallized. Each sequence has been computed considering the phase diagrams of Segretain & Chabrier (1993) and Horowitz et al. (2010). In the interests of comparison, we have computed additional evolutionary sequences considering the chemical profiles obtained using these two phase diagrams but adopting a crystallization temperature resulting from imposing Γ = 180. In this way the effects of chemical differentiation upon crystallization can be disentangled from those resulting from a smaller crystallization temperature.
3. Evolutionary results
We start by examining the impact of the shape of the phase diagram on the oxygen abundance distribution expected in the interior of a crystallized white dwarf. This is illustrated in Figs. 2 and 3, which display the inner oxygen abundance profile at different evolutionary stages for the 0.593 and 0.878 M⊙ white dwarf models, respectively. In each figure, the dot-dashed line shows the oxygen distribution before the onset of crystallization, and the dashed and solid lines show, respectively, the oxygen distribution after crystallization is almost complete, when the phase diagrams of Horowitz et al. (2010) and Segretain & Chabrier (2003) are employed. As anticipated in Sect. 2, because of the very different shapes of both phase diagrams, we expect a distinct oxygen distribution in the white dwarf interior by the end of the crystallization process. This is apparent from Figs. 2 and 3, where it can be seen that the final oxygen distributions predicted by the two phase diagrams are clearly different. Note that, for both masses, the phase diagram of Horowitz et al. (2010) yields smaller oxygen abundances in the central regions, compared with those obtained using the phase diagram of Segretain & Chabrier (1993). In particular, for the 0.593 M⊙ model, the crystallization process increases the oxygen abundance at the center by ~10% when the phase diagram of Horowitz et al. (2010) is used, and by ~19% when the phase diagram of Segretain & Chabrier (1993) is adopted. These figures turn out to be ~11% and ~27%, respectively, for the 0.878 M⊙ model white dwarf.
 |
Fig. 4 Surface luminosity versus age for the 0.593 M⊙ white dwarf sequences undergoing carbon-oxygen phase separation. Solid and dashed curves correpond to the predictions of the phase diagrams of Segretain & Chabrier (1993) and Horowitz et al. (2010), respectively. The cooling curve in the case that carbon-oxygen phase separation is not considered is also shown as a dotted line. |
Clearly, the amount of matter redistributed by phase separation during crystallization for a given stellar mass is markedly smaller when the phase diagram of Horowitz et al. (2010) is considered. This results in a smaller energy release from carbon-oxygen differentiation. Since for the 0.59 M⊙ model the initial oxygen abundance is XO ~ 0.7 when crystallization sets in (see Fig. 2), the crystallization temperature is not too different for both phase diagrams (see Fig. 1). Specifically, for the phase diagram of Horowitz et al. (2010) the crystallization temperature is ~1.19TC, whereas for that of Segretain et al. (1993) is ~1.35TC. Consequently, this energy is released at similar luminosities – log (L/L⊙) ≃ −3.84 for the phase diagram of Horowitz et al. (2010) and log (L/L⊙) ≃ −3.70 for that of Segretain & Chabrier (1993) – and the impact on the white dwarf cooling times is smaller in the case in which the phase diagram of Horowitz et al. (2010) is adopted. The same occurs for the more massive white dwarf (see Fig. 3). All this becomes clear by examining Figs. 4 and 5 which depict, respectively, the relationship between the surface luminosity and age for the 0.593 and 0.878 M⊙ white dwarf sequences that undergo carbon-oxygen phase separation. In each figure, solid and dashed curves correpond to the predictions of the phase diagrams of Segretain & Chabrier (1993) and Horowitz et al. (2010), respectively. In addition, the cooling curve obtained when the carbon-oxygen phase separation upon crystallization is neglected is shown with a dotted line – for this sequence, crystallization and the release of latent heat are assumed to occur at Γ = 180. Note that for both stellar masses, the phase diagram of Horowitz et al. (2010) results in white dwarf cooling times that are smaller than those predicted by the phase diagram of Segretain & Chabrier (1993). This is, as mentioned, a consequence of the smaller composition changes predicted by the Horowitz et al. (2010) phase diagram.
 |
Fig. 6 Age delays, in percentage with respect to the case in which phase separation is not considered, due to carbon-oxygen phase separation according to the phase diagram of Horowitz et al. (2010) and Segretain & Chabrier (1993), dashed and solid lines, respectively. Upper and bottom panel correspond to the 0.593 and 0.878 M⊙ white dwarf sequences, respectively. |
The dependence of the age delays induced by chemical differentiation on stellar mass for both phase diagrams is more difficult to assess, since they depend not only on gravity but also on the temperature at which crystallization occurs. Since gravity is larger for the more massive white dwarf, the energy released by chemical redistribution is larger as well. However, for the more massive white dwarf crystallization takes place at higher stellar luminosities, and the delay in the cooling times introduced by chemical differentiation is smaller in this case – see, for instance, Salaris et al. (1997). In addition, the magnitude of the age delays are influenced by the initial chemical profile of the white dwarf, which is different for each stellar mass. This is more important in the case of the phase diagram of Segretain & Chabrier (1993), for which the age delays strongly depend on the initial composition (Salaris et al. 2000), but less relevant in the case of the phase diagram of Horowitz et al. (2010), for which the predicted composition changes are smaller, see Fig. 1.
 |
Fig. 7 Same as Fig. 4 but including the cooling curves (thin lines) that result from imposing that crystallization occurs at Γ = 180. |
The situation can be clarified with the help of Fig. 6, which illustrates the age delays resulting from carbon-oxygen phase separation (in percentage with respect to the case in which phase separation is disregarded) for the 0.593 and 0.878 M⊙ white dwarf cooling sequences (top and bottom panel, respectively), for both the phase diagram of Horowitz et al. (2010) – dashed lines – and that of Segretain & Chabrier (1993) – solid lines. Note that when the phase diagram of Horowitz et al. (2010) is employed, the age delays are negative at moderately high luminosities, between − 3.8 ≳ log (L/L⊙) ≳ −4.1 for the 0.593 M⊙ model. This is simply because the phase diagram of Horowitz et al. (2010) predicts a lower crystallization temperature than that obtained using Eq. (1) with Γ = 180. Hence, crystallization occurs at lower stellar luminosities when the phase diagram of Horowitz et al. (2010) is employed, with the consequence that the corresponding cooling sequence has initially shorter cooling ages. It is also worth emphasizing that when the phase diagram of Horowitz et al. (2010) is adopted, the bulk of the delay in the cooling ages of an otherwise typical white dwarf of 0.593 M⊙ occurs at luminosities ranging from log (L/L⊙) ~ −4.2 to log (L/L⊙) ~ −4.5, whereas for the phase diagram of Segretain & Chabrier (1993) this occurs at luminosities between log (L/L⊙) ~ −4.0 and − 4.4, when a sizable part of the core is already crystallized. But the most relevant aspect that Fig. 6 puts forward is that when the phase diagram of Horowitz et al. (2010) is adopted, carbon-oxygen phase separation is less relevant for the evolution of white dwarfs. In particular, for the 0.593 M⊙ at log (L/L⊙) ≃ −4.5, the age delay is only ~0.5 Gyr when the phase diagram of Horowitz et al. (2010) is adopted, whilst in the case in which that of Segretain & Chabrier (1993) is used the delay amounts to ~1.3 Gyr.
We also note that for the 0.593 M⊙ white dwarf cooling sequence, the phase diagram of Horowitz et al. (2010) predicts ages that are up to ≈ 8% shorter at log (L/L⊙) = −4.0 when compared with the ages derived using the phase diagram of Segretain & Chabrier (1993). The differences are larger for the 0.878 M⊙ white dwarf sequence, reaching up to ≈ 17% also at log (L/L⊙) = −4.0. In this case the differences are larger because the smaller initial oxygen abundance translates into a larger relative enrichment of the solid phase when the phase diagram of Segretain & Chabrier (1993) is used – but not in the Horowitz et al. (2010) phase diagram. This, in turn, results in a larger energy release, and consequently in larger delays. This merely reflects the fact that age delays resulting from carbon-oxygen separation are less sensitive to the initial chemical profile when using the Horowitz et al. (2010) phase diagram.
To isolate the effect on the cooling ages of the shape of the phase diagram from the different crystallization temperature of both phase diagrams, in Fig. 7 we compare the cooling curves for several 0.593 M⊙ white dwarf sequences. In addition to the cooling curves considered in Fig. 4, we also plot the cooling curves computed for both phase diagrams when the crystallization temperature is given by the relation Γ = 180, rather than being obtained using the upper curve of the phase diagram. These cooling curves are shown using thin lines. The results deserve some comments. As already noted, the phase diagram of Horowitz et al. (2010) predicts lower crystallization temperatures (and luminosities) than that of Segretain & Chabrier (1993), and even lower than the crystallization temperature when no phase separation is considered. Specifically, for the 0.593 M⊙ sequence, crystallization starts at log (L/L⊙) = −3.70 when the phase diagram of Segretain & Chabrier (1993) is used, and at log (L/L⊙) = −3.84 when that of Horowitz et al. (2010) is adopted, while when no phase separation is considered, crystallization occurs at log (L/L⊙) = −3.68. This explains the initially larger cooling ages in the latter sequence. But at smaller luminosities, the trend is reversed. We thus conclude that it is the shape of the phase diagram that is the most relevant factor influencing the delays in the ages of cool white dwarfs, and not the specific value of the crystallization temperature. Finally, it is worth mentioning as well that the value of Γ at the onset of crystallization is 186 and 210 for the phase diagrams of Segretain & Chabrier (1993) and Horowitz et al. (2010). These values turn out to be somewhat higher, 190 and 218, respectively, for the 0.878 M⊙ sequence, because of the initially lower oxygen abundance of this sequence.
4. Conclusions
Winget et al. (2009) suggested that the crystallization temperature of carbon-oxygen white dwarf cores in the globular cluster NGC 6397 is close to that of pure carbon. This unexpected result prompted Horowitz et al. (2010) to determine a new phase diagram for carbon-oxygen mixtures using direct molecular dynamics simulations for the solid and liquid phases. They found crystallization temperatures considerably lower than those given by the most usually adopted prescription, which is obtained imposing Γ = 180, and neglecting carbon-oxygen phase separation. In particular, Horowitz et al. (2010) found that the crystallization temperature for carbon-oxygen mixtures with equal mass fractions of carbon and oxygen to be close to that of pure carbon, thus offering an explanation for the puzzling result of Winget et al. (2009). They also found that the shape of the phase diagram of binary carbon-oxygen mixtures is of the azeotropic form, instead of the spindle phase diagram (Segretain & Chabrier 1993) previously employed in the most accurate calculations of cooling white dwarfs (Renedo et al. 2010) available so far. The core feature of this paper has been precisely to explore the consequences for white dwarf evolution of this new phase diagram. To this end, we used the LPCODE stellar evolutionary code, and we computed several cooling sequences for white dwarfs of masses 0.593 and 0.878 M⊙. The initial white dwarf configurations were extracted from the full and detailed evolution of progenitor stars we computed in previous studies, which also provided realistic initial chemical profiles.
The lower crystallization temperature predicted by the Horowitz et al. (2010) phase diagram means that the onset of crystallization in white dwarfs occurs at stellar luminosities smaller than those predicted by the phase diagram of Segretain & Chabrier (1993). For a typical white dwarf of mass ~0.6 M⊙, we find that the phase diagram of Horowitz et al. (2010) predicts crystallization to occur at log (L/L⊙) = −3.84, while the luminosity at which crystallization sets in when the phase diagram of Segretain & Chabrier (1993) is used is log (L/L⊙) = −3.70, and when no phase separation is considered the white dwarf core crystallizes at log (L/L⊙) = −3.68. Additionally, for this new phase diagram the value of Coulomb coupling parameter at the onset of crystallization for a 0.6 M⊙ white dwarf is Γ ≃ 210.
The amount of matter that is redistributed by phase separation during crystallization is notably smaller in the new phase diagram than in previous calculations of this kind. Hence, we find that carbon-oxygen phase separation becomes less relevant for white dwarf evolution when this phase diagram is adopted. At the luminosities for which a large fraction of the white dwarf mass has crystallized, we find age delays due to carbon-oxygen phase separation that are on average a factor ~2.5 smaller than the delays obtained using the phase diagram of Segretain & Chabrier (1993). Another interesting feature of the new phase diagram of Horowitz et al. (2010) is that composition changes are less sensitive to the initial chemical profile of the white dwarf. This is a relevant point, since it means that the magnitude of the age delays induced by carbon-oxygen phase separation will be less affected by current uncertainties in the initial carbon-oxygen composition of white dwarfs.
Our results have implications for the age determinations of stellar populations using the white dwarf cooling sequence, which should be investigated in subsequent works. This is particularly relevant for the well-studied, old, metal-poor globular cluster NGC 6397, which has been imaged down to very faint luminosities and for which a reliable color-magnitude diagram and a white dwarf luminosity function have been derived. As mentioned, this cluster has been recently used to constrain the properties of crystallization in the deep interior of cool white dwarfs (Winget et al. 2009). In particular, Winget et al. (2010) have shown that the observed white dwarf luminosity function in NGC 6397 seems to be consistent with pure carbon core white dwarfs crystallizing at Γ ≈ 178, or, alternatively, carbon-oxygen core white dwarfs crystallizing at Γ values larger than 178, the theoretical value for a one component plasma. This finding is in line with the predicions of molecular dynamics simulations of Horowitz et al. (2010). These results together with the ones reported in this paper call for the need of studying the cooling sequence of crystallizing white dwarfs in other old stellar clusters on the basis of Horowitz et al. (2010) phase diagram. Work in this direction is in progress.
Acknowledgments
This research was supported by AGAUR, by MCINN grants AYA2008-04211-C02-01 and AYA08-1839/ESP, by the ESF EUROCORES Program EuroGENESIS (MICINN grant EUI2009-04170), by the European Union FEDER funds, by AGENCIA: Programa de Modernización Tecnológica BID 1728/OC-AR, and by PIP 2008-00940 from CONICET.
References
- Alexander, D. R., & Ferguson, J. W. 1994, ApJ, 437, 879 [NASA ADS] [CrossRef] [Google Scholar]
- Althaus, L. G., García-Berro, E., Isern, J., Córsico, A. H., & Rohrmann, R. D. 2007, A&A, 465, 249 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Althaus, L. G., Córsico, A. H., Isern, J., & García-Berro, E. 2010a, A&AR, 18, 471 [CrossRef] [Google Scholar]
- Althaus, L. G., Córsico, A. H., Bischoff-Kim, A., et al. 2010b, ApJ, 717, 897 [NASA ADS] [CrossRef] [Google Scholar]
- Althaus, L. G., García-Berro, E., Renedo, I., et al. 2010c, ApJ, 719, 612 [NASA ADS] [CrossRef] [Google Scholar]
- Barrat, J. L., Hansen, J. P., & Mochkovitch, R. 1988, A&A, 199, L15 [NASA ADS] [Google Scholar]
- Benvenuto, O. G., García-Berro, E., & Isern, J. 2004, Phys. Rev. D, 69, 082002 [NASA ADS] [CrossRef] [Google Scholar]
- Cassisi, S., Potekhin, A. Y., Pietrinferni, A., Catelan, M., & Salaris, M. 2007, ApJ, 661, 1094 [NASA ADS] [CrossRef] [Google Scholar]
- Córsico, A. H., Benvenuto, O. G., Althaus, L. G., Isern, J., & García-Berro, E. 2001, New A, 6, 197 [Google Scholar]
- García-Berro, E., Hernanz, M., Mochkovitch, R., & Isern, J. 1988a, A&A, 193, 141 [NASA ADS] [Google Scholar]
- García-Berro, E., Hernanz, M., Isern, J., & Mochkovitch, R. 1988b, Nature, 333, 642 [NASA ADS] [CrossRef] [Google Scholar]
- García-Berro, E., Hernanz, M., Isern, J., & Mochkovitch, R. 1995, MNRAS, 277, 801 [NASA ADS] [CrossRef] [Google Scholar]
- García-Berro, E., Torres, S., Althaus, L. G., et al. 2010, Nature, 465, 194 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- García-Berro, E., Lorén-Aguilar, P., Torres, S., Althaus, L. G., & Isern, J. 2011, J. Cosmology Astropart. Phys., 5, 21 [Google Scholar]
- Hansen, B. M. S., Anderson, J., Brewer, J., et al. 2007, ApJ, 671, 380 [NASA ADS] [CrossRef] [Google Scholar]
- Horowitz, C. J., Schneider, A. S., & Berry, D. K. 2010, Phys. Rev. Lett., 104, 231101 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Ichimaru, S., Iyetomi, H., & Ogata, S. 1988, ApJ, 334, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Iglesias, C. A., & Rogers, F. J. 1996, ApJ, 464, 943 [NASA ADS] [CrossRef] [Google Scholar]
- Isern, J., Hernanz, M., & García-Berro, E. 1992, ApJ, 392, L23 [NASA ADS] [CrossRef] [Google Scholar]
- Isern, J., Mochkovitch, R., Garcia-Berro, E., & Hernanz, M. 1997, ApJ, 485, 308 [NASA ADS] [CrossRef] [Google Scholar]
- Isern, J., García-Berro, E., Hernanz, M., & Chabrier, G. 2000, ApJ, 528, 397 [NASA ADS] [CrossRef] [Google Scholar]
- Isern, J., García-Berro, E., Torres, S., & Catalán, S. 2008, ApJ, 682, L109 [NASA ADS] [CrossRef] [Google Scholar]
- Magni, G., & Mazzitelli, I. 1979, A&A, 72, 134 [NASA ADS] [Google Scholar]
- Medin, Z., & Cumming, A. 2010, Phys. Rev. E, 81, 036107 [NASA ADS] [CrossRef] [Google Scholar]
- Mochkovitch, R. 1983, A&A, 122, 212 [NASA ADS] [Google Scholar]
- Montgomery, M. H., Klumpe, E. W., Winget, D. E., & Wood, M. A. 1999, ApJ, 525, 482 [NASA ADS] [CrossRef] [Google Scholar]
- Ogata, S., Iyetomi, H., Ichimaru, S., & Van Horn, H. M. 1993, Phys. Rev. E, 48, 1344 [NASA ADS] [CrossRef] [Google Scholar]
- Renedo, I., Althaus, L. G., Miller Bertolami, M. M., et al. 2010, ApJ, 717, 183 [NASA ADS] [CrossRef] [Google Scholar]
- Rohrmann, R. D., Althaus, L. G., & Kepler, S. O. 2011, MNRAS, 411, 781 [NASA ADS] [CrossRef] [Google Scholar]
- Salaris, M., Domínguez, I., García-Berro, E., et al. 1997, ApJ, 486, 413 [NASA ADS] [CrossRef] [Google Scholar]
- Salaris, M., García-Berro, E., Hernanz, M., Isern, J., & Saumon, D. 2000, ApJ, 544, 1036 [NASA ADS] [CrossRef] [Google Scholar]
- Segretain, L., & Chabrier, G. 1993, A&A, 271, L13 [NASA ADS] [Google Scholar]
- Segretain, L., Chabrier, G., Hernanz, M., et al. 1994, ApJ, 434, 641 [NASA ADS] [CrossRef] [Google Scholar]
- Stevenson, D. J. 1980, J. Phys., 41, 2 [Google Scholar]
- Van Horn, H. M. 1968, ApJ, 151, 227 [NASA ADS] [CrossRef] [Google Scholar]
- von Hippel, T., & Gilmore, G. 2000, AJ, 120, 1384 [NASA ADS] [CrossRef] [Google Scholar]
- Winget, D. E., Kepler, S. O., Campos, F., et al. 2009, ApJ, 693, L6 [NASA ADS] [CrossRef] [Google Scholar]
- Winget, D. E., Montgomery, M. H., Kepler, S. O., Campos, F., & Bergeron, P. 2010, AIP Conf. Ser., 1273, 146 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1 Carbon-oxygen phase diagrams used in our evolutionary calculations. The crystallization temperature of the carbon-oxygen binary mixture in terms of the crystallization temperature of pure carbon is shown as a function of the oxygen abundance by mass. Dashed red lines and solid blue lines correspond, respectively, to the phase diagrams of Segretain & Chabrier (1993) and Horowitz et al. (2010). For each diagram, the upper curve gives the crystallization temperature for a given oxygen abundance of the liquid, while the lower curve provides the equilibrium oxygen abundance of the solid at this temperature. The dotted line corresponds to the case in which no phase separation occurs, and the mixture is treated as the average of the chemical species. Finally, the circles denote the crystallization temperature of the carbon-oxygen mixture for the case of an oxygen mass abundance of 0.7, a typical value found in the evolutionary calculations of white dwarf progenitors. |
| In the text | |
 |
Fig. 2 Inner oxygen distribution (abundance by mass) for the 0.593 M⊙ white dwarf model at different evolutionary stages. The (red) dot-dashed line corresponds to the oxygen distribution before the occurrence of crystallization. The final oxygen profile when most of the white dwarf has crystallized is also shown for the phase diagram of Horowitz et al. (2010) – (blue) dashed line – and for the phase diagram of Segretain & Chabier (1993) – (black) solid line. |
| In the text | |
 |
Fig. 3 Same as Fig. 2 but for 0.878 M⊙ white dwarf model sequence. |
| In the text | |
 |
Fig. 4 Surface luminosity versus age for the 0.593 M⊙ white dwarf sequences undergoing carbon-oxygen phase separation. Solid and dashed curves correpond to the predictions of the phase diagrams of Segretain & Chabrier (1993) and Horowitz et al. (2010), respectively. The cooling curve in the case that carbon-oxygen phase separation is not considered is also shown as a dotted line. |
| In the text | |
 |
Fig. 5 Same as Fig. 4 but for the 0.878 M⊙ white dwarf sequences. |
| In the text | |
 |
Fig. 6 Age delays, in percentage with respect to the case in which phase separation is not considered, due to carbon-oxygen phase separation according to the phase diagram of Horowitz et al. (2010) and Segretain & Chabrier (1993), dashed and solid lines, respectively. Upper and bottom panel correspond to the 0.593 and 0.878 M⊙ white dwarf sequences, respectively. |
| In the text | |
 |
Fig. 7 Same as Fig. 4 but including the cooling curves (thin lines) that result from imposing that crystallization occurs at Γ = 180. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


