| Issue |
A&A
Volume 537, January 2012
|
|
|---|---|---|
| Article Number | A100 | |
| Number of page(s) | 7 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201117801 | |
| Published online | 16 January 2012 | |
Plasma diagnostic in eruptive prominences from SDO/AIA observations at 304 Å
SUPA, School of Physics and Astronomy, University of Glasgow, Glasgow, G12 8QQ, Scotland, UK
e-mail: Nicolas.Labrosse@glasgow.ac.uk
Received: 1 August 2011
Accepted: 16 November 2011
Context. Theoretical calculations have shown that when solar prominences move away from the surface of the Sun, their radiative output is affected via the Doppler dimming or brightening effects.
Aims. In this paper we ask whether observational signatures of the changes in the radiative output of eruptive prominences can be found in EUV (extreme ultraviolet) observations of the first resonance line of ionised helium at 304 Å. We also investigate whether these observations can be used to perform a diagnostic of the plasma of the eruptive prominence.
Methods. We first look for suitable events in the SDO/AIA database. The variation of intensity of arbitrarily selected features in the 304 channel is studied as a function of velocity in the plane of the sky. These results are then compared with new non-LTE radiative transfer calculations of the intensity of the He ii 304 resonance line.
Results. We find that observations of intensities in various parts of the four eruptive prominences studied here are sometimes consistent with the Doppler dimming effect on the He ii 304 Å line. However, in some cases, one observes an increase in intensity in the 304 channel with velocity, in contradiction to what is expected from the Doppler dimming effect alone. The use of the non-LTE models allows us to explain the different behaviour of the intensity by changes in the plasma parameters inside the prominence, in particular the column mass of the plasma and its temperature.
Conclusions. The non-LTE models used here are more realistic than what was used in previous calculations. They are able to reproduce qualitatively the range of observations from SDO/AIA analysed in this study. With the help of non-LTE modelling, we can infer the plasma parameters in eruptive prominences from SDO/AIA observations at 304 Å.
Key words: radiative transfer / Sun: filaments, prominences / Sun: corona / line: formation
© ESO, 2012
1. Introduction
Solar prominences are strongly sensitive to the radiation coming from the solar disc, which creates conditions far from local thermodynamic equilibrium (LTE – see Hirayama 1963). They are also optically thick in several spectral lines. To model the emitted radiation it is necessary to use non-LTE radiative transfer codes.
Non-LTE radiative transfer calculations have shown that when the prominences move away from the surface of the Sun, for instance when they become active or eruptive, their radiative output is affected (see review by Labrosse et al. 2010, and references therein). If this can be observed then this opens a new door to diagnose the prominence plasma in the eruption phase. This predicted change in the radiation output is due to the so-called Doppler dimming/brightening effect (Hyder & Lites 1970), and is widely used to diagnose the solar wind speed from the observation of resonance lines (see e.g., Kohl & Withbroe 1982).
In this study we investigate whether observational signatures of the changes in the radiative output from eruptive prominences can be found in EUV observations, in particular in the 304 Å line emitted by ionised helium. This line has been shown to be very sensitive to the radial motion of the prominence, because it is mostly formed by scattering of the incident radiation coming from the Sun (Labrosse et al. 2007, 2008). The present work is therefore an attempt to develop an observational answer to the questions raised by the aforementioned theoretical studies. To do this, we look for suitable events in the SDO/AIA database, and measure the intensities emitted by these prominences. Atmospheric imaging assembly (AIA, Lemen et al. 2011) is a multi-band imager including the He ii 304 Å channel and is one of three instruments embarked on the Solar Dynamics Observatory (SDO). These observations are then compared with a new grid of 1D non-LTE models. The main objective of this research is to characterise the variation in the radiation of active and eruptive prominences as they move away from the solar surface and therefore receive a variable incident radiation. The small sample of well-observed prominence eruptions selected for this study allows us to answer the questions posed by the theoretical studies, namely 1) can we observe the predicted intensity variations; and 2) if yes can we use this effect to diagnose the prominence plasma? These objectives are primarily related to a number of open issues in solar prominence physics (Labrosse et al. 2010).
The paper is organised as follows: observations are described in Sect. 2. The non-LTE models are described in Sect. 3. In Sect. 4 we discuss our results before the conclusions in Sect. 5.
2. Observations
Launched in February 2010 by NASA, AIA onboard SDO is the most advanced solar imager to date. It consists of 4 dual-channel telescopes with filters centered at 94 Å, 131 Å, 171 Å, 193 Å, 211 Å, 304 Å, 335 Å and 1600 Å. Here we use observations at 304 Å, corresponding primarily to He ii emission coming from the chromosphere and the transition region at a temperature of about log T = 4.7. In that passband, however, lies another line at 303.3 Å emitted by Si xi (see Sect. 4.1). The main advantage of AIA over previous solar imagers is both its high spatial and temporal resolutions. The apparatus uses a 4096 × 4096 CCD chip with a pixel size of 0.6′′ (level 1.5 data), allowing it to probe into the fine structures of the Sun. AIA takes an image approximately every 12 seconds at each wavelength, allowing it to closely track even the most rapidly evolving features – which is useful for our investigation.
We select four events in the SDO/AIA database. The main selection criteria are that the eruptions must be well developed and last long enough to facilitate manual feature tracking. We choose four events exhibiting different morphologies. In each case, we produce a movie (available on request) from the level 1.5 data and follow individual features. Intensities are averaged over nine pixels to produce the intensity plots shown below (Figs. 2–5). All intensities are normalised by the exposure time (2.9 s). In order to make the comparison with the theoretical intensities presented in Sect. 3, the observed intensities are normalised by the intensity corresponding to the lowest velocity. Hence all intensity values greater than 1 indicate a brightening of the prominence with velocity, while intensity values lower than 1 indicate a dimming of the prominence with velocity. The variation of the relative intensity as a function of velocity shown in the bottom panels of Figs. 2–5 has been plotted with the same axis scales in intensity and velocity for the four events in order to ease the comparison between each of them. In Fig. 2 an inset has been added to show this intensity variation on a more appropriate scale for this specific event.
Figure 1 shows the evolution of the velocity of selected features in four distinct eruptive prominences as a function of time elapsed since the beginning of tracking.
 |
Fig. 1 Temporal variation of the velocity of the selected features for the four prominence eruptions studied. The inset shows this velocity variation in more details for fast-evolving events. |
This gives an overview of the dynamics of the selected events. While most of them evolve quite rapidly (reaching velocities larger than 100 km s-1 within a few minutes), the prominence eruption observed on 13 June 2010 is much less dynamic, with velocities of a few tens km s-1 after 1–2 h.
The following subsections present the details of individual events used in this work, and the intensity variations as a function of velocity for the selected features.
 |
Fig. 2 Top: evolution of the 2010-06-13 prominence eruption. The circle marks the part of the prominence which was tracked and used to calculate the intensities. The field of view in the images is 300′′ × 300′′. Bottom: variation of relative intensity as a function of velocity in the plane of the sky. Intensities are normalised by the intensity corresponding to the lowest velocity. The inset shows the relative intensity variation with axis scales specific to this event. The time evolution is coded in color (with the time-scale indicated on the right of the plot) in the online version of the figure. |
2.1. Prominence eruption on 2010-06-13 at 00:00
This moderate-sized prominence eruption takes place on the 13th June 2010 at 00:00 on the North-West limb. For the first few hours of the event there is a slow rise phase. From around 03:00 onwards however the top part of the prominence begins to detach itself from the base as the motion becomes more prominent. At around 05:00 there is a clear detachment of the structure and this then moves outward. This rise continues for several hours until it suddenly stretches before fading away. The base of the prominence rises by a small amount during this time, and then blows away and disappears from view. This eruption has been recently studied by Régnier et al. (2011) who investigated the thermal and magnetic structure of the coronal cavity located above the prominence.
We start our feature tracking at 04:15 UT in the middle part of the prominence body, but close to the edge to the coronal cavity. Differing from other events studied in this paper by being a substantially longer lasting, slower event, images were taken at 15 min intervals. The tracking was taken over 11 images, ending at 06:45, just before the detached plasma is stretched. Figure 2 shows six images of the evolution of the eruptive prominence and the feature which was tracked, and the variation of relative intensity (normalised to the intensity at the lowest velocity over the tracking period) as a function of velocity. The circles on the images highlight the pixels used in calculating the intensities. The velocities are much lower in this event than in the others studied in this paper.
This event shows a decrease of the observed intensity of the He ii 304 channel with an increasing velocity. The trend of an intensity decrease with increasing velocity is reminiscent of the Doppler dimming effect as illustrated by the theoretical calculations of Labrosse et al. (2007, 2008). However, these theoretical calculations were done by varying only the radial velocity of the moving prominence, and keeping all the plasma parameters constant throughout the activation/eruption. In fact, we do not exclude that the physical parameters of the prominence plasma may vary during the eruption.
2.2. Prominence eruption on 2010-09-08 at 22:30
This prominence eruption took place on September 8th, 2010. The eruption began at approximately 22:30 UT at the north-west limb. It was associated with a GOES Class B3.4 flare near AR 11105. Any appreciable outward motion of the plasma did not occur until approximately 23:08. The tracking starts at 23:11 over 14 frames until 23:24 at a one minute cadence. Figure 3 shows the same information as Fig. 2 only for the 2010-09-08 event.
 |
Fig. 3 Same as Fig. 2 for the 2010-09-08 prominence eruption. The field of view in the images (top panel) is 450′′ × 450′′. |
Here again, the main feature of the relative intensity vs. velocity graph is the decrease in intensity with increasing velocity.
2.3. Prominence eruption on 2011-03-19 at 11:30
This other prominence eruption took place on the 19th March 2011. Beginning at 11:10 UT, AIA observed a large kinking loop eruption from AR 11171. Located in the south west quadrant of the Sun, this eruption exhibits a strong sweeping motion as it moves further south. Helical motions are visible in the prominence legs during the eruption. We start the manual tracking at 11:49 of a bright patch of plasma on the ridge of the prominence over 11 images ending at 11:59. Figure 4 shows the same information as Fig. 2 only for the 2011-03-19 event.
 |
Fig. 4 Same as Fig. 2 for the 2011-03-19 prominence eruption. The field of view in the images (top panel) is 390′′ × 390′′. |
It highlights what was already visible in Figs. 2 and 3, namely that a decrease of intensity with velocity is observed during the eruption.
2.4. Prominence eruption on 2011-06-10 at 17:43
This prominence eruption took place on the 10th June 2011 and was associated to a C2.9 flare in AR 11227. First appearing as a compact flaring region on the south west limb, the prominence soon developed into a very tight looped structure at around 17:49, very different to the other cases explored here. This is a good example of a so-called failed eruption, with most of the plasma falling back towards the surface of the Sun.
For this particular prominence, two parts were tracked. The first feature-tracking started at 17:48 on the part of the loop which evolves into the jet of plasma. The feature was tracked over 10 images, ending at 17:57. The second blob of plasma is chosen in a different part of the prominence. Tracking started at 17:52 for 10 images, ending at 18:01. Figure 5 shows the same information as Fig. 2 only for the 2011-06-10 event. In this case however the first tracked feature is indicated in the first three images in the sequence, while the last three images show the second feature.
 |
Fig. 5 Same as Fig. 2 for the 2011-06-10 prominence eruption. The first tracked feature is indicated on the first three images in the sequence, while the last three images show the second tracked feature. The field of view in the images is 276′′ × 276′′. For the intensity-velocity graph the cross symbols correspond to the event beginning at 17:48 and the diamond symbols correspond to the 17:52 event. |
This case is interesting, since instead of having a decrease of intensity with velocity as was expected from the simple theoretical models of Labrosse et al. (2007, 2008), and supported by the observations shown in previous sections, one now observes an increase in intensity with velocity. The two independent parts of plasma tracked show a differing intensity profile from each other. In Sect. 3 we discuss in more details what are the possible causes for this increasing intensity with velocity, but it is likely that this is an effect of a variation of the physical conditions of the prominence plasma during the eruption, which was not taken into account in the isothermal models of Labrosse et al. (2007) or in the prominence models including a transition region (Labrosse et al. 2008).
3. Modelling
The motivation to construct new non-LTE models to study the Doppler dimming effect on the He ii 304 Å resonance line is two-fold. First, we want to test if these models are able to reproduce the observations presented in Sect. 2, at least on a qualitative basis. Second, the calculations presented in Labrosse et al. (2007, 2008) were carried out for simplified models which allowed these authors to understand the basic Doppler dimming mechanisms and their effects on the spectral lines produced by neutral and ionised helium. These calculations showed that the resonance lines of neutral, and to a greater extent, ionised helium, are sensitive to the Doppler dimming effect. This is because resonance scattering plays such an important role in the formation of these lines. However, the physical conditions inside their eruptive prominence models were not very realistic, since all the plasma parameters were kept constant during the eruption as the structure was moving upwards. In reality, the physical conditions within the eruptive structures may vary, depending mainly on the driving mechanisms of the eruption.
In the following we describe our new prominence models where we relax all the model input parameters, allowing them to vary in order to study how the emergent intensities are modified when both the velocity and the other plasma parameters change during the eruption.
3.1. Description of the models
The details of the computations are the same as in Labrosse et al. (2007, 2008). Our eruptive prominence is represented by a 1D plane-parallel slab standing vertically above the solar surface (see Fig. 6).
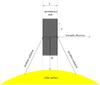 |
Fig. 6 Schematic representation of the 1D plane-parallel prominence slab of geometrical width L, altitude H above the solar surface, moving radially at a velocity V. |
The model input parameters are the radial velocity (V) at which the prominence slab is moving, the temperatures and pressures at the centre of the slab and at the boundary with the corona, the steepness γ of the temperature gradient in the prominence-to-corona transition region (PCTR), the total column mass (or equivalently the slab width L), the microturbulent velocity, and the altitude of the slab H (viz., the height of the line-of-sight above the limb where it intersects the plane of the sky). The temperature and pressure profiles are taken from Anzer & Heinzel (1999).
 |
Fig. 7 Histogram densities of the prominence model parameters varying as indicated in Table 1. a) Central temperature (103 K); b) Surface pressure (dyn cm-2); c) Central pressure (dyn cm-2); d) Slab thickness (103 km); e) Column mass (10-4 g cm-2); f) γ; g) Microturbulent velocity (km s-1); h) Altitude (103 km); i) Radial velocity (km s-1). |
Input parameters for non-LTE models.
For this study we compute a new grid of models from randomly chosen input parameters within realistic ranges of values. These are indicated in Table 1. We calculated 100 models with these input parameters. The realistic range of values taken by our input parameters allows us to investigate the effect of the variation of the plasma parameters on the evolution of the emergent intensity of the He ii 304 line in different types of eruptive prominence models. The histogram densities for all input parameters are shown in Fig. 7. There is a reasonable number of models covering all possible values of the plasma parameters. In this study, the slab width is determined from the solution of the hydrostatic equilibrium, with the column mass, the temperature and the pressure as input. For each model, we solve the radiative transfer and statistical equilibrium equations for Hydrogen and Helium to obtain the emergent intensities in the He ii 304 Å line. For more details on theoretical investigations of the Doppler dimming and brightening effects on active and eruptive prominences, see the review by Labrosse et al. (2010).
3.2. Results
Within our randomly generated grid of models, we look for the model that has the lowest possible velocity. This model has the following characteristics: Tcen ≈ 8800 K, pressures of 0.7 and 0.086 dyn cm-2 at the centre of the slab and at the coronal boundary respectively, and a column mass of 4.8 × 10-5 g cm-2 (slab thickness of 2500 km). The mean temperature of the model across the slab is 11 300 K. Its radial velocity is null. With these parameters, we can consider that this model is representative of a random quiescent prominence, and we therefore call it our reference model. Starting from this reference model, we compute ten additional models where all the plasma parameters are kept constant and identical to the parameters of the reference model described above, with the radial velocity being the only variable changing. Hence we are able to clearly identify how the Doppler dimming effect alone affects the emergent intensity of the He ii 304 line for our reference model.
Our results (shown in Fig. 8) indicate that when all the plasma parameters are allowed to vary, models with a non-zero velocity yield in equal proportions computed intensities in the He ii line either greater or lower than the intensity of the reference (static) model.As our aim here is to compare our theoretical results with the observations presented in the previous section, and also to identify under what conditions an erupting prominence might become dimmer or brighter as its radial velocity increases, we look at relative intensities in the 304 line, i.e. intensities normalised to the intensity of our reference model (which has a null radial velocity).
As was already pointed out by Labrosse et al. (2008) in cases where a PCTR is included in the modelling, the Doppler dimming effect will be stronger for models with a low column mass. This is explained by the fact that, as the column mass increases, the amount of material at high temperatures becomes more important. The sensitivity of this high temperature plasma to Doppler dimming is less strong due to the enhanced role of thermal processes in the formation of the line. We find that among the dimmer models, 67% have a lower column mass than the reference model (Fig. 8).
 |
Fig. 8 Effect of the column mass of the model on the relative intensities of the He ii 304 Å line (normalised to the intensity of the reference model where the prominence is at rest) as a function of the radial velocity of the prominence. The solid line shows the variation of intensity with radial velocity when all the model parameters are kept constant. |
On the other hand, among the brighter models, 79% have a larger column mass than the reference model. Hence, with these PCTR models, our results indicate that the main physical parameter giving a hint of whether the intensity at 304 Å will decrease or increase with radial velocity is the column mass. If the column mass increases during the eruption process, for instance as a result of mass loading or rearrangement of the prominence plasma along the line of sight (due, e.g., to the rotation of the filament structure – see Kurokawa et al. 1987; Bemporad et al. 2011), there is a high probability that the intensity will increase despite an increase of the radial velocity.
Another factor that will determine the relative importance of scattering of the incident radiation versus collisional processes in the formation of the He ii 304 Å line is the temperature of the plasma. The majority (62%) of models with a larger column mass than our reference model will have a lower emergent intensity at 304 Å in a moving prominence if the central temperature of the slab is lower than that of the reference model. Similarly, the majority of these higher column mass models are brighter at a non-zero velocity if their central temperature is larger.
These results indicate that the behaviour of the He ii 304 line intensity with velocity changes according to the plasma parameters inside the prominence, in particular the column mass of the plasma and its temperature.
4. Discussion
4.1. Contributing ions in the 304 Å channel
One difficult aspect of interpreting observations in the 304 channel is that the He ii line at 303.8 Å is not the only contributor. The Si xi line at 303.3 Å (formed at ~1.2 MK) also contributes in the filter spectral band.
In the context of AIA data, it is believed that the Si xi line can contribute to up to 20% of the observed intensity in an active region on the disk (Lemen et al. 2011). Based on results obtained by the SOHO/CDS spectrometer, Thompson & Brekke (2000) also point out that the relative contribution of Si xi 303.3 Å can be larger than 90% above the limb in a typical region of the quiet corona. However, typical prominence conditions are much more akin to on-disk quiet-sun conditions, for which the contribution of the Si xi line is reduced to around 4% (Thompson & Brekke 2000). This aspect has also been recently discussed by Bemporad (2011) in the context of STEREO/EUVI observations. There will also be a contribution from Si xi from the corona in front of the prominence. However, it can be neglected since the observed prominences exhibit a rather sharp edge (i.e., the corona surrounding the prominence is much dimmer).
While the relative contributions of these two lines will vary according to the conditions inside the plasma, and in the absence of detailed line profiles, we can safely assume based on the above discussion that in prominences, the main contributor in the 304 channel is the He ii line.
4.2. Projection effects
Another observational limitation is the lack of three-dimensional information on the eruptive structure. We are led to make the assumption that all motions take place in the plane of the sky, and that motions take place along the radial direction. A possible approach to overcome this limitation is to use spectroscopic data to measure Doppler shifts along high-cadence imaging to measure transverse motions.
Bemporad (2011) mentions some of the most successful attempts at characterising the 3D motion of eruptive prominences. As found by, e.g., Zapiór & Rudawy (2010), the trajectories of eruptive prominences are generally not purely in the radial direction. However, we do not have enough information with the available data set used in this paper to refine our radial velocity estimates. What really matters in determining the Doppler dimming/brightening effect is the radial velocity of the plasma, and we will assume that the velocities measured from the observed motions in the plane of the sky are reasonable estimates of the radial velocity of the erupting structure. Our derived values are in agreement with values given, e.g., by Régnier et al. (2011) and Krall & Sterling (2007).
In a future study, we plan to make a quantitative analysis of one particular event, studying its evolution and determining the velocity of the plasma in 3D using additional data from the STEREO spacecrafts (Thompson 2009; Joshi & Srivastava 2011; Bemporad et al. 2011), and comparing calibrated intensities with our radiative transfer calculations.
4.3. Local prominence plasma conditions
The fact that our computations can explain an increase in intensity with increasing radial velocity does not contradict the fact that the He ii 304 Å line is strongly sensitive to the Doppler dimming effect. The effect of Doppler dimming alone (i.e., the variation of intensity with velocity as all plasma parameters are kept constant) is shown by the solid curve in Fig. 8. The sensitivity of the emergent intensity to Doppler dimming is explained by the predominance of resonant scattering of incoming photons from the Sun in the formation of the He ii 304 Å line. This Doppler dimming effect (diminution of emergent intensity) is due to the fact that the incident radiation becomes out of resonance with the absorption profile of the 304 Å transition as the velocity increases. However, it is possible that changes in the physical conditions of the prominence plasma will more than compensate the Doppler dimming effect, implying that a higher emergent intensity will be observed.
We looked at the AIA data for these four events at other wavelengths to seek signs of temperature variations of the prominence region which was tracked. In particular, all four eruptive prominences investigated here show up in some degree in the 171 Å channel (which has quite a broad temperature response), especially for the 2011-06-10 event in which the structure is very well preserved (see Sect. 2.4). For three of these events, as time elapses it is only the prominence edges that remain apparent in the 171 Å waveband. Only the 2011-06-10 eruptive prominence remains fairly well seen for most of the event at this wavelength. This could be interpreted as evidence for localised heating of the plasma during the eruption.
5. Conclusions
The first detailed computations of the helium spectrum in a quiescent prominence were obtained by Labrosse & Gouttebroze (2001, 2004). They showed that the ionised helium resonance lines were mostly formed by scattering of the incident radiation under typical quiescent prominence conditions. This was confirmed in a recent observational study by Labrosse et al. (2011). As a consequence it is natural to expect that active and eruptive prominences with pronounced radial outflows are very sensitive to the Doppler dimming effect in these lines, as demonstrated by Labrosse et al. (2007, 2008).
This paper investigates the intensity variations as a function of velocity in eruptive prominences observed with the SDO/AIA imager in the 304 channel. We study four well-observed eruptive prominences and find three cases where the intensities of small features inside the eruptive structures decrease with increasing velocity, while in the fourth case, the intensities of the small features increase with velocity. We then compare our observations with a grid of randomly generated non-LTE models allowing us to study the effects of the plasma parameters and of the radial
velocity of the prominence plasma on the emergent intensity of the He ii 304 Å line. Our theoretical results confirm that the intensity of the He ii line can increase as well as decrease when the velocity of the prominence plasma increases and the model plasma parameters are allowed to vary.
The answer to the question of whether the emergent intensity in the He ii 304 line decreases or increases with increasing radial velocity of the eruptive prominence depends on the variations of the local plasma conditions as well as on the velocity of the prominence. Even if previous theoretical studies showed that this line is strongly sensitive to the Doppler dimming effect, variations in the plasma parameters also play an important role in determining the behaviour of the emergent intensity. Specifically, the column mass and the temperature of the plasma are found to be the two most important parameters in determining the evolution of the intensity of the 304 Å line with velocity of the prominence plasma.
This non-LTE modelling of eruptive prominences opens the door for improved diagnostics, allowing us to shed light on the variations of the plasma parameters of eruptive prominences from SDO/AIA observations at 304 Å. This diagnostic technique, applied in the present study to SDO/AIA observations, can be applied to any other past (EIT on SOHO, Delaboudinière et al. 1995), current (EUVI, part of SECCHI on STEREO, Howard et al. 2008), or future EUV observations of prominence eruptions observed at a sufficiently high cadence in the He ii 304 Å channel.
In a future study we plan to make a more detailed diagnostic of the eruptive prominence plasma by comparing absolute intensities in the 304 Å line with a suitable grid of non-LTE models.
Acknowledgments
We thank the referee for helpful suggestions to improve the clarity of the paper. Part of this work was supported by a Nuffield Foundation Undergraduate Research Bursary to KM (URB/39921). Financial support by the International Space Science Institute (ISSI) is gratefully acknowledged, and NL thanks colleagues from the ISSI International Team 174 on “Solar Prominence Formation and Equilibrium: New Data, New Models” for stimulating discussions. The data used are provided courtesy of NASA/SDO and the AIA science team. We thank Greg Slater for his help with the processing of the Level 1 AIA data. This research has made use of NASA’s Astrophysics Data System.
References
- Anzer, U., & Heinzel, P. 1999, A&A, 349, 974 [NASA ADS] [Google Scholar]
- Bemporad, A. 2011, J. Atmosph. Sol.-Terrestr. Phys., 73, 1117 [NASA ADS] [CrossRef] [Google Scholar]
- Bemporad, A., Mierla, M., & Tripathi, D. 2011, A&A, 531, A147 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Delaboudinière, J.-P., Artzner, G. E., Brunaud, J., et al. 1995, Sol. Phys., 162, 291 [NASA ADS] [CrossRef] [Google Scholar]
- Hirayama, T. 1963, PASJ, 15, 122 [NASA ADS] [Google Scholar]
- Howard, R. A., Moses, J. D., Vourlidas, A., et al. 2008, Space Sci. Rev., 136, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Hyder, C. L., & Lites, B. W. 1970, Sol. Phys., 14, 147 [NASA ADS] [Google Scholar]
- Joshi, A. D., & Srivastava, N. 2011, ApJ, 730, 104 [Google Scholar]
- Kohl, J. L., & Withbroe, G. L. 1982, ApJ, 256, 263 [NASA ADS] [CrossRef] [Google Scholar]
- Krall, J., & Sterling, A. C. 2007, ApJ, 663, 1354 [NASA ADS] [CrossRef] [Google Scholar]
- Kurokawa, H., Hanaoka, Y., Shibata, K., & Uchida, Y. 1987, Sol. Phys., 108, 251 [Google Scholar]
- Labrosse, N., & Gouttebroze, P. 2001, A&A, 380, 323 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Labrosse, N., & Gouttebroze, P. 2004, ApJ, 617, 614 [NASA ADS] [CrossRef] [Google Scholar]
- Labrosse, N., Gouttebroze, P., & Vial, J.-C. 2007, A&A, 463, 1171 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Labrosse, N., Vial, J.-C., & Gouttebroze, P. 2008, Ann. Geophys., 26, 2961 [NASA ADS] [CrossRef] [Google Scholar]
- Labrosse, N., Heinzel, P., Vial, J., et al. 2010, Space Sci. Rev., 151, 243 [Google Scholar]
- Labrosse, N., Schmieder, B., Heinzel, P., & Watanabe, T. 2011, A&A, 531, A69 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lemen, J. R., Title, A. M., Akin, D. J., et al. 2011, Sol. Phys., 115 [Google Scholar]
- Régnier, S., Walsh, R. W., & Alexander, C. E. 2011, A&A, 533, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Thompson, W. T. 2009, Icarus, 200, 351 [NASA ADS] [CrossRef] [Google Scholar]
- Thompson, W. T., & Brekke, P. 2000, Sol. Phys., 195, 45 [Google Scholar]
- Zapiór, M., & Rudawy, P. 2010, Sol. Phys., 267, 95 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Temporal variation of the velocity of the selected features for the four prominence eruptions studied. The inset shows this velocity variation in more details for fast-evolving events. |
| In the text | |
 |
Fig. 2 Top: evolution of the 2010-06-13 prominence eruption. The circle marks the part of the prominence which was tracked and used to calculate the intensities. The field of view in the images is 300′′ × 300′′. Bottom: variation of relative intensity as a function of velocity in the plane of the sky. Intensities are normalised by the intensity corresponding to the lowest velocity. The inset shows the relative intensity variation with axis scales specific to this event. The time evolution is coded in color (with the time-scale indicated on the right of the plot) in the online version of the figure. |
| In the text | |
 |
Fig. 3 Same as Fig. 2 for the 2010-09-08 prominence eruption. The field of view in the images (top panel) is 450′′ × 450′′. |
| In the text | |
 |
Fig. 4 Same as Fig. 2 for the 2011-03-19 prominence eruption. The field of view in the images (top panel) is 390′′ × 390′′. |
| In the text | |
 |
Fig. 5 Same as Fig. 2 for the 2011-06-10 prominence eruption. The first tracked feature is indicated on the first three images in the sequence, while the last three images show the second tracked feature. The field of view in the images is 276′′ × 276′′. For the intensity-velocity graph the cross symbols correspond to the event beginning at 17:48 and the diamond symbols correspond to the 17:52 event. |
| In the text | |
 |
Fig. 6 Schematic representation of the 1D plane-parallel prominence slab of geometrical width L, altitude H above the solar surface, moving radially at a velocity V. |
| In the text | |
 |
Fig. 7 Histogram densities of the prominence model parameters varying as indicated in Table 1. a) Central temperature (103 K); b) Surface pressure (dyn cm-2); c) Central pressure (dyn cm-2); d) Slab thickness (103 km); e) Column mass (10-4 g cm-2); f) γ; g) Microturbulent velocity (km s-1); h) Altitude (103 km); i) Radial velocity (km s-1). |
| In the text | |
 |
Fig. 8 Effect of the column mass of the model on the relative intensities of the He ii 304 Å line (normalised to the intensity of the reference model where the prominence is at rest) as a function of the radial velocity of the prominence. The solid line shows the variation of intensity with radial velocity when all the model parameters are kept constant. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


