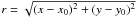| Issue |
A&A
Volume 537, January 2012
|
|
|---|---|---|
| Article Number | A25 | |
| Number of page(s) | 16 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/201117755 | |
| Published online | 22 December 2011 | |
Fossil group origins
II. Unveiling the formation of the brightest group galaxies through their scaling relations
1 Instituto Astrofísico de Canarias, C/ Vía Láctea s/n, 38200 La Laguna, Spain
2 Departamento de Astrofísica, Universidad de La Laguna, C/ Astrofísico Francisco Sánchez, 38205 La Laguna, Spain
e-mail: jairo@iac.es
3 European Southern Observatory, Alonso de Córdova 3107, Vitacura, Santiago, Chile
4 Fundación Galileo Galilei-INAF, Rambla José Ana Fernández Pérez 7, 38712 Breña Baja, Spain
5 Dipartimento di Astronomia, Università di Padova, vicolo dell’Osservatorio 3, 35122 Padova, Italy
6 UNINOVA/CA3, Campus da FCT/UNL, Quinta da Torre, 2825-149 Caparica, Portugal
7 Harvard-Smithsonian Center for Astrophysics, 60 Garden Street, Cambridge, MA 02138, USA
8 Dipartimento di Fisica-Sezione Astronomia, Università degli Studi di Trieste, via Tiepolo 11, 34143 Trieste, Italy
9 INAF-Osservatorio Astronomico di Trieste, via Tiepolo 11, 34143 Trieste, Italy
10 Instituto de Astrofísica de Andalucia-CSIC, 18008 Granada, Spain
11 Centro Astronómico Hispano Alemán, C/ Jesús Durbán Remón 2-2, 04004 Almería, Spain
12 INAF-Osservatorio Astronomico di Capodimonte, Salita Moiariello 16, 80131 Napoli, Italy
Received: 22 July 2011
Accepted: 30 September 2011
Context. Fossil systems are galaxy associations dominated by a relatively isolated, bright elliptical galaxy, surrounded by a group of smaller galaxies lacking L∗ objects. Because of this extreme environment, fossil groups (FGs) are ideal laboratories for studying the mass assembly of brightest group galaxies (BGGs).
Aims. We analyzed the near-infrared photometric and structural properties of a sample of 20 BGGs present in FGs to better understand their formation mechanisms. They represent the largest sample studied to date.
Methods.Ks-band deep images were used to study the structural properties of our sample galaxies. Their surface-brightness distribution was fitted to a Sérsic profile using the GASP2D algorithm. Then, the standard scaling relations were derived for the first time for these galaxies and compared with those of normal ellipticals and brightest cluster galaxies in non-fossil systems.
Results. The BGGs presented in this study represent a subset of the most massive galaxies in the Universe. We find that their ellipticity profiles are continuously increasing with the galactocentric radius. Our fossil BCGs follow closely the fundamental plane described by normal ellipticals. However, they depart from both the log σ0 vs. log LKs and log re vs. log LKs relations described by intermediate-mass ellipticals. This occurs in the sense that our BGGs have larger effective radii and smaller velocity dispersions than those predicted by these relations. We also find that more elliptical galaxies systematically deviate from the previous relations, while rounder objects do not. No similar correlation was found with the Sérsic index.
Conclusions. The derived scaling relations can be interpreted in terms of the formation scenario of the BGGs. Because our BGGs follow the fundamental plane tilt but have larger effective radii than expected for intermediate-mass ellipticals, we suggest that they only went through dissipational mergers in an early stage of their evolution and then assembled the bulk of their mass through subsequent dry mergers, contrary to previous claims that BGGs in FGs were mainly formed by the merging of gas-rich galaxies.
Key words: galaxies: photometry / galaxies: structure / galaxies: evolution / galaxies: formation / galaxies: elliptical and lenticular; cD / galaxies: fundamental parameters
© ESO, 2012
1. Introduction
Fossil groups (FGs) are observationally defined as X-ray bright systems (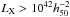 erg s-1), dominated in the optical by a giant elliptical galaxy at the center and with an R-band difference in the absolute magnitude of ΔM12 > 2 (Jones et al. 2003) between the two brightest galaxies located within half the virial radius of the system. These relatively rare systems were first identified by Ponman et al. (1994) and were the target of several studies in the past few years (Vikhlinin et al. 1999; Jones et al. 2003; Mendes de Oliveira et al. 2006; Cypriano et al. 2006; Khosroshahi et al. 2006; Mendes de Oliveira et al. 2009; Zibetti et al. 2009; Démoclès et al. 2010; Aguerri et al. 2011).
erg s-1), dominated in the optical by a giant elliptical galaxy at the center and with an R-band difference in the absolute magnitude of ΔM12 > 2 (Jones et al. 2003) between the two brightest galaxies located within half the virial radius of the system. These relatively rare systems were first identified by Ponman et al. (1994) and were the target of several studies in the past few years (Vikhlinin et al. 1999; Jones et al. 2003; Mendes de Oliveira et al. 2006; Cypriano et al. 2006; Khosroshahi et al. 2006; Mendes de Oliveira et al. 2009; Zibetti et al. 2009; Démoclès et al. 2010; Aguerri et al. 2011).
Observationally, these systems are massive galaxy associations with typical masses of rich groups or poor clusters. They follow also the scaling relations of groups or clusters such as X-ray luminosity (LX) vs. gas temperature (TX), total mass (M) vs. TX, gas entropy vs. TX , LX vs. cluster velocity dispersion (σcl), optical luminosity (Lopt) vs. σcl, σcl vs. TX , gas fraction (fgas) vs. TX (Khosroshahi et al. 2007; Sun et al. 2009). Some differences have been found in the optical vs. X-ray luminosity (Lopt-LX) relation (Khosroshahi et al. 2007) even if this is still controversial (Voevodkin et al. 2010). Detailed X-ray observations of some FGs also indicate that these systems were assembled at early epochs in high centrally concentrated dark matter (DM) halos with high mass-to-light ratios (M/L) (Démoclès et al. 2010). Nevertheless, they do not show cooling cores such as those detected in galaxy clusters, which points toward the presence of other heating mechanisms, like active galactic nuclei (AGN) feedback (Sun et al. 2004; Khosroshahi et al. 2004, 2006; Mendes de Oliveira et al. 2009).
From numerical simulations, and due to the interesting nature of these systems, their formation scenarios have been matter of debate in recent years (D’Onghia et al. 2005; Sommer-Larsen 2006; von Benda-Beckmann et al. 2008; Romeo et al. 2008; Díaz-Giménez et al. 2011; Cui et al. 2011). One scenario attributes their properties to their dynamical history, implying that fossil systems are formed if a group/cluster remains undisturbed for a long period of time. Therefore, if fossil systems were assembled in an early epoch of the Universe throughout a fast and efficient process of merging, they should have had time enough for their L∗ galaxies to merge, thus producing the observed lack of intermediate-luminosity galaxies and the large magnitude gap between the brightest and the second brightest galaxy of the group (D’Onghia et al. 2005; von Benda-Beckmann et al. 2008). An alternative explanation for FG formation is that such systems are “failed” groups that suffer from a lack of L∗ galaxies as an accident of birth (Mulchaey & Zabludoff 1999). On the other hand, some authors suggest that FGs might represent a transitory phase in the cluster life, with an absence of significant mergers for a long time, enough for cluster relaxation (von Benda-Beckmann et al. 2008; Cui et al. 2011).
The merger history underlying the origin of the central galaxies in FGs continue to be discussed in the literature. Their brightest group galaxies (BGGs) are among the most massive galaxies known in the Universe. Originally, they were thought to be possible results of group evolution as driven by dynamical friction (Ponman et al. 1994; Jones et al. 2003). Recent N-body simulations and semi-analytic calculations have suggested that BGGs formed on a short time-scale as consequence of mergers with low angular momentum (Sommer-Larsen 2006), pushing dynamical friction to a less likely scenario for the evolution of BGGs.
Observations show that BGGs also have different observational properties than other bright elliptical galaxies. In particular, they present disky isophotes in the center and their luminosities correlate with the velocity dispersions of the groups. These different properties suggest a different formation scenario for bright ellipticals in fossil and non-fossil systems (Khosroshahi et al. 2006). Whereas bright ellipticals in FGs would grow out of gas-rich mergers, giant ellipticals in non-fossil systems would suffer more dry mergers. However, neither recent samples of BGGs (La Barbera et al. 2009) nor numerical simulations (Díaz-Giménez et al. 2008) show these differences (La Barbera et al. 2009). All previous results on fossil systems have the drawback of being obtained using small samples of FGs. This could be the reason for the contradictory findings found by different studies. The lack of a large and homogeneous statistical study of this kind of system makes the previous results inconclusive.
In the framework of the fossil groups origins (FOGO) project (Aguerri et al. 2011), which aims to carry out a systematic, multiwavelength study of a sample of 34 FGs selected from the Sloan Digital Sky Survey (SDSS; Santos et al. 2007), near-infrared images in the Ks-band were taken for the central regions of 17 groups using the long-slit intermediate resolution infrared spectrograph (LIRIS) at the 4.2-m William Herschel Telescope (WHT). This represents the largest sample of BGGs studied to date at these wavelengths. Near-infrared observations have the advantage of mapping the distribution of the mass-carrying evolved stars and diminishing the influence of dust. In this work, we analyze in detail the photometric properties of the BGGs present on these FGs to perform a systematic study of their structural properties and shed light on their formation/evolution scenarios.
The remainder of this paper is as follows: the data sample, observations, and data reduction are summarized in Sect. 2. In Sect. 3 we describe the surface photometry and photometric decomposition. The scaling relations are presented in Sect. 4. The discussion of the results and conclusions are presented in Sects. 5 and 6, respectively.
Throughout this paper we assume a flat cosmology with ΩM = 0.3, ΩΛ = 0.7, and a Hubble parameter H0 = 70 km s-1 Mpc-1.
2. Data sample, observations, and data reduction
2.1. LIRIS data
Near-infrared imaging of a sample of 17 FG systems belonging to the FOGO project was carried out at the WHT in January 2010. We observed in the Ks-band using the LIRIS imaging mode. LIRIS is a near-infrared (0.9–2.4 μm) instrument with an optical system based on a classical camera design (Manchado et al. 2004). The detector is a Hawaii 1024 × 1024 HgCdTe array operating at 70 K with a pixel scale of 0 25 pixel-1.
25 pixel-1.
We exposed a total of 3000 s per field, developing several cycles of a five points dithering for each target. The exposure time of individual frames was 10–12 s. The dithering cycling procedure allowed us to estimate and then correct the background contributions of the sky and its significant oscillations. In addition, the dithering and flat frames helped us to clean the cosmetic effects of the CCDs. After these corrections, we obtained maximum variations of about 0.4% in the background across the full image.
Data reduction was carried out in the IRAF1 environment and with LIRIS specific packages. To maintain the quality of the point spread function (PSF) across the whole field of view after stacking individual frames, the geometry effect of the distorted field was corrected. In the combined images, the PSF is consistent with that of the single ones. This is true even close to the edges of the field.
Our observations were carried out under photometric conditions and within a seeing range of 0 6–1
6–1 1 (FWHM) as measured by fitting a Moffat PSF to field stars in our images. The photometric calibration was performed by observing United Kingdom Infra-Red Telescope (UKIRT) faint near-infrared standards (Casali & Hawarden 1992). We checked our photometric calibration taking the Two Micron All Sky Survey (2MASS) photometry as reference. Our zero-point estimations agree with those of 2MASS within ± 0.02 mag.
1 (FWHM) as measured by fitting a Moffat PSF to field stars in our images. The photometric calibration was performed by observing United Kingdom Infra-Red Telescope (UKIRT) faint near-infrared standards (Casali & Hawarden 1992). We checked our photometric calibration taking the Two Micron All Sky Survey (2MASS) photometry as reference. Our zero-point estimations agree with those of 2MASS within ± 0.02 mag.
Finally we identified galaxies in our Ks-band images and measured their magnitudes with the SExtractor package (Bertin & Arnouts 1996). Objects were identified by requiring that they cover a certain minimum area and have a number counts above a limiting threshold with the local sky background as a reference. The limiting size and flux were nine pixels and 1.5 standard deviation of the sky counts, respectively. The selected limiting size corresponds to an apparent size of 0 75, which is about the typical seeing FWHM obtained from our combined images. We performed careful visual inspections of the frames in order to deal with the best combination of the above parameters that removes spurious objects from the catalogs.
75, which is about the typical seeing FWHM obtained from our combined images. We performed careful visual inspections of the frames in order to deal with the best combination of the above parameters that removes spurious objects from the catalogs.
 |
Fig. 1 Ks-band counts per square degree per 0.5 mag bin for the fields observed with LIRIS. The continuous curve and vertical dotted lines represent the logarithmic function fit to the histogram, completeness, and limit magnitudes, respectively. |
Figure 1 shows the Ks-band counts for the fields observed with LIRIS. The counts follow the count-magnitude relation expected for a homogeneous galaxy distribution in a universe with Euclidean geometry. The completeness was computed as the magnitude where the measured counts are less than 10% with respect to the fit, whereas the limit magnitude was assumed to be that of the faintest detected objects. For our sample, the completeness and limit magnitudes correspond to targets with signal-to-noise ratio S/N = 5 and 3, and are Ks = 18.7 and 20.3, respectively. The characteristics of the observed sample are listed in Table 1.
2.2. Additional data
2.2.1. UKIDSS data
Since we were not able to observe the whole sample of 34 FGs of the FOGO sample, we carried out a search in the UKIRT Infrared Deep Sky Survey (UKIDSS) eigth data release database to complete our sample. We found seven galaxies out of the 17 already observed with LIRIS. In addition, five new groups not previously observed with LIRIS were found.
 |
Fig. 2 Distribution of redshift (left panel), X-ray luminosity (middle panel), and r-band absolute magnitude (right panel) for the FOGO FGs (solid black line) and of FGs studied in this work (red dotted line). |
Since the quality and depth of the UKIDSS data is clearly poorer than those of images obtained using LIRIS, we analyzed the images of the seven common BGGs (see Table 1) to understand whether the UKIDSS data could be useful to our scientific purpose. We performed a photometric decomposition of the surface-brightness distribution of the BGGs measured on the UKIDSS images as we did for the LIRIS data (see Sect. 3.1 for details). By comparing the total magnitudes obtained from both fits, we found that only for four BGGs (see Table 1) the results are comparable within 0.2 mag. After analyzing the results of the fits we concluded that to obtain a reliable fit we need a suitable combination of surface-brightness dynamical range and Sérsic index; i.e., we found that galaxies with Sérsic index n > 3 need at least a range of 6 mag arcsec-2 to be well fitted within the observational errors. Instead, for n ≤ 3 we need only a range of 4 mag arcsec-2, applying these criteria to the five images of the BGGs without counterpart in LIRIS we found that three groups (SDSSJ154855.85+085044.3, SDSSJ161431.10+264350.3, SDSSJ225630.04-003210.8) satisfy the conditions and so only these were included in the analysis.
It is worth noticing that we do not cover the complete sample of 34 FGs comprised by the FOGO project. This subsample of 20 groups is missing mainly the fainter end of the FOGO sample in both optical magnitude of the BGG and X-ray luminosity of the groups. However, this bias does not affect the results obtained in this article. In Fig. 2 we show the distribution of the complete FOGO sample and the studied in this paper as function of the redshift, X-ray luminosity, and r-band absolute magnitude.
2.2.2. SDSS data
Since all our BGGs were observed spectroscopically by the Sloan Digital Sky Survey (SDSS), we searched for the presence of velocity dispersion measurements in the SDSS database. We found the stellar velocity dispersions for the whole sample using the SDSS-III eighth data release (Aihara et al. 2011). However, since the SDSS spectroscopy was performed using fibers with 3′′ of diameter, the measurement of the velocity dispersion could be contaminated by the presence of another object inside this radius. For this reason, we visually checked the galaxies in order this effect into account, for this effect and we did not use the velocity dispersions of the BGGs in the SDSSJ084257.55+362159.2 and SDSSJ133559.98-033129.1 groups. Therefore, our final sample of velocity dispersion includes 18 galaxies. The velocity dispersions were corrected for the aperture size effect following the prescription by Jørgensen et al. (1995) and adopting a fixed physical aperture of re/8. The measurements after aperture corrections are given in Table 1.
Characteristics of our sample of FGs and BGGs.
3. Surface photometry
3.1. Photometric decomposition
The two-dimensional photometric decomposition of the sample galaxies was performed using the GASP2D algorithm described in Méndez-Abreu et al. (2008). This algorithm has been successfully applied to several galaxy samples (Morelli et al. 2008; Pizzella et al. 2008; Beifiori et al. 2011). In particular, it has been applied to a large sample of brightest cluster galaxies (BCGs) in non-fossil systems (Ascaso et al. 2011).
 |
Fig. 3 Observed (black points) and model (green solid line) surface-brightness radial profiles of the sample galaxies. The observed radial profiles were obtained by fitting ellipses to the isophotes of the Ks-band images. The model profiles follow a Sérsic law. These profiles were not corrected for cosmological dimming, K- or evolutionary corrections. The short vertical lines mark the effective radius. Semi-major axes of fitted ellipses are given in arcsec (bottom) and kpc (top). The inset in the upper panels shows the surface brightness in logarithmic scale to enhance the quality of the fit in the inner regions. The residuals of the fit are represented by a gray region in the lower panels. |
 |
Fig. 3 continued. |
 |
Fig. 3 continued. |
 |
Fig. 3 continued. |
The GASP2D algorithm is based on a χ2 minimization. Therefore, the choice of the initial trials for free parameters is crucial to obtain a good fit. To this aim, the ellipse-averaged radial profiles of surface brightness, ellipticity, and position angle were analyzed by following the prescriptions by Méndez-Abreu et al. (2008). Starting from these initial trial parameters the different photometric models of the surface brightness were fitted iteratively by GASP2D to the pixels of the galaxy image to derive its photometric structural parameters. Each image pixel was weighted according to the variance of its total observed photon counts due to the contribution of both galaxy and sky, and determined by assuming photon noise limitation and taking the detector read-out noise into account. Seeing effects were also taken into account by convolving the model image with a circular Moffat PSF with a FWHM matching the observed one (see Table 1). The convolution was performed as a product in the Fourier domain before the least-squares minimization.
We tested three different parametric models to fit the galaxy surface-brightness distribution. The de Vaucouleurs profile (de Vaucouleurs 1948) was extensively used to describe the light distribution of elliptical galaxies and to look for central dominant galaxies (cDs) in clusters by searching light excess over the model de Vaucouleurs profile in the outer parts of the profile (Matthews et al. 1964; Schombert 1987). The Sérsic profile (Sérsic 1968) is nowadays believed to be the most suitable model for describing the surface-brightness distribution of elliptical galaxies in a wide range of luminosities and masses (e.g., Caon et al. 1993; Graham & Guzmán 2003; Aguerri et al. 2004; Kormendy et al. 2009). It is parametrized by re, Ie, and n, which are the effective radius, surface brightness at re and a shape parameter describing the curvature of the radial profile, respectively. When n = 4 we recover the de Vaucouleurs profile, and for n = 1 we obtain the exponential one. Figure 3 shows the best fit of the observed surface-brightness radial profile to a Sérsic model obtained for our sample galaxies. In addition to the previous models, we also fitted a two-component (Sérsic+exponential) model to the data. This allowed us to fit the low surface-brightness and extended component that BCGs could present (Nelson et al. 2002; Gonzalez et al. 2003, 2005; Seigar et al. 2007; Liu et al. 2008; Ascaso et al. 2011). We found that 7 galaxies are described by this two-component model, however, since all galaxies can be successfully modelled by a Sérsic profile and in order to work with a self-comparable set of structural parameters, we decided to only use the Sérsic structural parameters in this paper. In addition, we found that a high fraction (14 out of 20) of our sample galaxies are compatible within the errors bars with following a de Vaucouleurs profile. Following the criteria given by Schombert (1987) to identify cDs based on looking for an upward break in the surface-brightness profile with respect to the typical de Vaucouleurs profile, we identified SDSSJ124742.07+413137.6 as the only candidate to be a cD galaxy. However, this classification should be interpreted as tentative, since the surface-brightness limits reached in our photometry are not directly comparable to those of Schombert (1987).
The parameters derived for the structural components of the sample galaxies using a Sérsic fit are collected in Table 2. The values of this table were corrected for galaxy inclination, cosmological dimming, K-correction, and evolutionary effects. The K-correction and evolutionary effect were taken into account using the recipes by Poggianti (1997). All the quantities plotted in the figures of this paper show these corrected values, unless otherwise stated.
Structural parameters in the Ks-band derived by fitting a Sérsic model to our sample of BGGs.
3.2. Internal errors in the structural parameters
The errors given in Table 2 for each structural parameter were obtained through a series of Monte Carlo simulations. Because the formal errors obtained from the χ2 minimization method are usually not representative of the real errors (Méndez-Abreu et al. 2008), we carried out extensive simulations on artificial galaxies to reliably estimate these errors. Monte Carlo simulations also have the advantage of getting rid of systematic biases in our measurements, such as those introduced by the effects of seeing in our images (see Trujillo et al. 2001).
A set of 2000 images of galaxies modeled with a Sérsic profile was generated. The structural parameters of the artificial galaxies were randomly chosen among the following ranges: 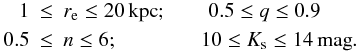 (1)To mimic the same instrumental setup, we added a background level and photon noise to these artificial images similar to the observed images. They were also convolved by simulating the seeing that we have in our observations. Finally, these simulated galaxies were fitted with the same conditions as the real ones. Then, simulated galaxies were used to determine the errors of the fitted structural parameters. To assign the corresponding error to every single galaxy for every structural parameter, we divided our catalog of artificial galaxies in bins of 0.5 mag and assumed that the errors were normally distributed, with mean and standard deviations corresponding to the systematic and typical errors, respectively. Then, we placed our observed galaxy in its magnitude bin and assigned the corresponding error to each parameter.
(1)To mimic the same instrumental setup, we added a background level and photon noise to these artificial images similar to the observed images. They were also convolved by simulating the seeing that we have in our observations. Finally, these simulated galaxies were fitted with the same conditions as the real ones. Then, simulated galaxies were used to determine the errors of the fitted structural parameters. To assign the corresponding error to every single galaxy for every structural parameter, we divided our catalog of artificial galaxies in bins of 0.5 mag and assumed that the errors were normally distributed, with mean and standard deviations corresponding to the systematic and typical errors, respectively. Then, we placed our observed galaxy in its magnitude bin and assigned the corresponding error to each parameter.
3.3. Radial profiles
The surface photometry was measured by fitting ellipses to the isophotes of the galaxies using the IRAF task ELLIPSE. This routine fits a large number of free parameters to every isophote using the iterative method described by Jedrzejewski (1987). Bad pixels, foreground stars, and other spurious sources were masked before performing the fit. Figure 4 shows the ellipticity (ϵ), centroid position (x0,y0), fourth-order cosine Fourier moment (a4), and position angle (PA) radial profiles of the isophotes. It is worth noticing that the surface-brightness profiles of 16 galaxies extend at least to 2re at a level of μKS ≈ 21 mag arcsec-2 corresponding to 1σ of the sky counts, and nine reach at least 3re, denoting thus the depth of our images.
 |
Fig. 4 A) Ellipticity, B) centroid ( |
No galaxies with ellipticities greater than 0.7 were found, which agrees with typical ellipticals (Fig. 4A). We found that in almost all cases the ellipticity profile increases with radius up to large distances. We checked that this effect was caused neither by a bad sky subtraction nor by light contamination from a close object. This behavior cannot be explained by assuming that these galaxies are oblate (or prolate) spheroids, therefore suggesting the presence of another component or a structural distortion in the outer parts (Porter et al. 1991; Méndez-Abreu et al. 2010). There is no correlation with the Sérsic shape parameter, whereas we found a weak dependence of the ellipticity on the galaxy magnitude. Less luminous galaxies are rounder.
The variations in the galaxy centroid do not show any correlation with the magnitude (Fig. 4B). Nevertheless, these variations seem to be larger for radii greater than re, at least for some galaxies, possibly indicating the presence of distortions in the outer parts of these galaxies.
The fourth-order cosine Fourier coefficient is related to the isophotes shape. Negative values indicate boxy isophotes. In contrast, positive values are related to disky isophotes. These profiles are too noisy for our sample galaxies, and this prevented us assigning a single value or even defining a trend (Fig. 4C). Therefore, no obvious correlation was found between this coefficient and either the Sérsic shape parameter or galaxy magnitude.
The position angle profiles are shown in Fig. 4D. We did not find any correlation between these profiles and other galaxy parameters. In addition, the profiles are very flat with variations |PA − PA(re)| < 10°.
4. Scaling relations
We studied the structural scaling relations for our sample of BGGs in FGs by analyzing the results from the photometric decomposition presented in Sect. 3.1. We also considered the sample of early-type galaxies by Pahre et al. (1998, hereafter P98), described in detail in Pahre (1999), as a control sample. This represents a statistically significant sample of galaxies in clusters and groups observed homogeneously in the Ks band. We selected the P98 BCGs to compare the same type of object. The P98 BCGs showed in the figures are the following: NGC 4874 and NGC 4889 (Coma), NGC 545 and NGC 547 (Abell 194), NGC 6166 (Abell 2199), NGC 7720 (Abell 2634), NGC 4696 (Centaurus), NGC 1316 (Fornax), NGC 3309 and NGC 3311 (Hydra), NGC 1272 and NGC 1275 (Perseus), NGC 4486 (Virgo), and NGC 1407 (Eridanus).
 |
Fig. 5 A) luminosity, B) effective radius, C) mean effective surface-brightness, and D) velocity dispersion differences between the aperture photometry and photometric decomposition measurements. Abscissa axes represent a number assigned to each galaxy. Blue solid lines represent the mean difference taking all points into account. Error bars represent the errors listed in Tables 1 and 2. |
4.1. Consistency with P98 data
The P98 data represent a large sample of early-type galaxies observed in the near infrared with a photometric depth similar to that of our images. Therefore, it is ideal to compare them with our sample of BGGs in fossil systems. However, their structural parameters (LKs, re, and ⟨ μe ⟩ ) were derived from circular aperture photometry, which differs from our approach of performing two-dimensional photometric decompositions.
To check for possible biases between the two datasets that could contaminate our results, we calculated the structural parameters for our sample data also using circular aperture photometry onto our images. The actual computation was done with the IRAF package ELLIPSE, as done by P98. Figure 5 shows the results from this comparison. A clear bias appears in all the photometric parameters under study. The luminosity (Lks), effective radius (re), and mean effective surface-brightness ( ⟨ μe ⟩ ) derived by the photometric decomposition are 0.11 dex, 0.13 dex, and 0.44 mag arcsec-2, which are greater than those derived by aperture photometry. These differences are expected and are pointed out in other studies. For instance, Aguerri et al. (2005) and Trujillo & Aguerri (2004) find that the differences in magnitudes between the two methods is never more that 0.5 mag, in agreement with our result. The main reason for these differences is that models used in the photometric decomposition approach are extrapolated to the infinite, therefore given larger magnitudes, effective radius, and effective surface-brightness.
Figure 5 also shows the comparison between the central velocity dispersion of the galaxies using P98 and this work. As explained in Sect. 2.2.2, we corrected our velocity dispersions using a physical aperture of re/8, whereas P98 use a physical scale of 1.53 kpc. These different aperture corrections do not introduce a bias between the two samples, and it only could increase the scatter in the relations.
These biases must be kept in mind in the following, but they are not enough to change the results presented in this work. In fact, most of the differences are within the error bars of the measurements. To avoid confusion, we have corrected for these biases in all the figures where we compare our measurements with P98 data.
4.2. Structural parameters vs. luminosity
Figure 6 shows the relation between the absolute rest-frame magnitude in Ks-band (or equivalently also the Ks-band luminosity in solar units) obtained from the Sérsic fit to the surface-brightness distribution of the sample galaxies and the mean effective surface brightness, or Sérsic shape parameter.
Some of our sample galaxies are among the brightest galaxies located in cluster/group environments in the Universe. They are brighter than the BCGs present in nearby clusters such as Virgo or Coma. However, they are not the most concentrated, nor do they possess the highest central surface brightness. In fact, the mean effective surface brightness correlates well with the galaxy magnitude and follows the same trend as normal ellipticals and BCGs.
The P98 sample does not provide any information about the shape of the surface-brightness profile, which in our case is represented by the Sérsic index, so we cannot make a direct comparison. However, it is worth noticing the wide range of Sérsic index values obtained for our BGGs, ranging from 1.7 to 5.3 with a mean value of 3.0. This indicates that the shape of the surface-brightness profile can be very different from a typical de Vaucouleurs profile.
4.3. Fundamental plane
It is well known that the structural parameters of classical bulges and elliptical galaxies follow a tight relation called the fundamental plane (FP; Djorgovski & Davis 1987; Dressler et al. 1987) among the effective radius (log re), mean effective surface brightness (⟨μe⟩), and central stellar velocity dispersion (log σ0). The small intrinsic dispersion of the FP relation is a consequence of the virial theorem and demonstrate that these systems are in dynamical equilibrium. Possible deviations from the FP are related to a variation in the mass-luminosity ratio with the luminosity and/or a nonhomology in the structure of these galaxies throughout the full range of luminosities (Trujillo et al. 2004). The FP has been widely used as a powerful tool in measuring galactic distances and also in studies of galaxy formation and evolution (Kjaergaard et al. 1993; Jørgensen et al. 1996, 1999; Kelson et al. 1997).
Figure 7 shows the distribution of our sample galaxies in the FP relation defined by the sample of P98. Our BGGs follow an FP that is compatible within the errors with that of normal ellipticals and BCGs, therefore implying that in the innermost regions (r < re) they are relaxed systems similar to normal ellipticals.
4.4. Kormendy relation
 |
Fig. 6 Correlations between ⟨ μe ⟩ (upper panel), n (bottom panel) and the galaxy absolute magnitude in the Ks-band. Large black dots indicate our sample galaxies. Blue dots represent the P98 early-type galaxies. The BCGs in the P98 sample are marked by blue open triangles. |
The effective radius and mean surface brightness of elliptical galaxies are correlated through the so-called Kormendy relation (KR; Kormendy 1977) which represents a projection of the FP. Figure 8 shows the position of our BGGs in the KR with respect to the control sample of P98. The fit to the data points used the FITEXY routine (Press et al. 1992) implemented in IDL2, which estimates the parameters of a straight-line fit and takes data errors into account on both variables. The best-fitted KR to the P98 sample is given by 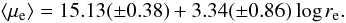 (2)Our galaxies are systematically above the best-fit relation obtained for the P98 sample, even if both relations are similar once the errors are considered. The relation obtained by fitting only our galaxies is
(2)Our galaxies are systematically above the best-fit relation obtained for the P98 sample, even if both relations are similar once the errors are considered. The relation obtained by fitting only our galaxies is 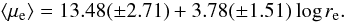 (3)Several works have studied the KR in galaxy clusters, demonstrating that the intrinsic dispersion is approximately 0.4 mag arcsec-2 in ⟨ μe ⟩ (Hoessel et al. 1987; Sandage & Perelmuter 1991; La Barbera et al. 2003). This high intrinsic dispersion can be interpreted in different ways: the KR does not consider the third parameter of FP (i.e., velocity dispersion, Ziegler et al. 1999); because there are both measurement errors and systematic errors due to the photometric calibration and also due to the corrections introduced for different biases (e.g., zero point and color transformation, K-correction, and reddening); or the position of the galaxies in the KR depends on their magnitude (Nigoche-Netro et al. 2008).
(3)Several works have studied the KR in galaxy clusters, demonstrating that the intrinsic dispersion is approximately 0.4 mag arcsec-2 in ⟨ μe ⟩ (Hoessel et al. 1987; Sandage & Perelmuter 1991; La Barbera et al. 2003). This high intrinsic dispersion can be interpreted in different ways: the KR does not consider the third parameter of FP (i.e., velocity dispersion, Ziegler et al. 1999); because there are both measurement errors and systematic errors due to the photometric calibration and also due to the corrections introduced for different biases (e.g., zero point and color transformation, K-correction, and reddening); or the position of the galaxies in the KR depends on their magnitude (Nigoche-Netro et al. 2008).
In the case of our BGGs, we suggest that, since our galaxies represent the brightest galaxies located in cluster/groups, the different position of the BGGs in the KR is produced only by their higher luminosity. In fact, galaxies with increasing magnitudes are placed parallel to the KR but with higher values for the mean surface brightness for a given effective radius, as is the case for our sample galaxies. In addition, the coefficients of our fit are poorly constrained owing to our small number statistics, and both samples are consistent within the errors.
4.5. Faber-Jackson relation
The Faber-Jackson relation (FJ; Faber & Jackson 1976) represents another physically significant projection of the FP. It correlates the galaxy magnitude with the stellar velocity dispersion, and for this reason it is observationally more expensive to obtain than the KR since it requires spectroscopic data. For the sake of clarity, we plot the total luminosity in the Ks-band instead of the magnitude in Fig. 9. The Ks-band luminosities of a given stellar population are less affected by metallicity effects than those in optical passbands. In addition, they are a good proxy of the total stellar mass since the typical M/L ≈ 1 for an old stellar population (e.g., Bruzual & Charlot 2003).
Figure 9 represents the FJ relation for the P98 sample and our sample of BGGs. Recently, Bernardi et al. (2011a,b) have demonstrated that the scaling relations of early-type galaxies present a change in their slope at a characteristic stellar mass (M∗ ~ 2 × 1011 M⊙, see also Tortora et al. 2009). Interestingly, this curvature of the scaling relations is not present when the stellar mass of the galaxies is replaced by the central velocity dispersion. In particular, they find that galaxies with masses higher than 2 × 1011 M⊙ have smaller velocity dispersions and larger effective radii for a given mass than their counterparts in the mass range 3 × 1010 < M∗/M⊙ < 2 × 1011.
Our sample galaxies represent a subset of the most massive galaxies of the Universe. Some of them probably fall in the Bernardi sample (Bernardi et al. 2011a,b) since they have SDSS information. Unfortunately, we cannot compare their work directly since they have optical photometry, whereas we have near-infrared photometry. In Fig. 9 we plot the FJ fit to the range of masses, while Bernardi et al. (2011b) consider that the relation is linear. Most of our BGGs follow the expected curvature in the log σ0 vs. log LKs relation, confirming and extending the results by Bernardi et al. (2011b).
4.6. Effective radius vs. luminosity
Figure 10 shows the relation between the Ks-band luminosity in solar units obtained from the Sérsic fit to the surface brightness and the effective radius of the galaxies.
As in the previous section, we tested the results of Bernardi et al. (2011b) with our sample of massive BGGs. We fitted a straight line on a logarithmic scale to the data in the mass range 3 × 1010 < M∗/M⊙ < 2 × 1011 and extrapolated such a fit to higher masses. From our data, it is clear that most of our BGGs follow the expected curvature in the log re vs. log LKs relation; i.e., galaxies with masses higher than 2 × 1011 M⊙ have larger effective radius for a given mass than do their counterparts in the mass range of 3 × 1010 < M∗/M⊙ < 2 × 1011, in agreement with Bernardi et al. (2011b).
5. Discussion
The BGGs of the fossil systems presented in this study represent a subset of the brightest and most massive galaxies in the Universe. This can be seen by looking at both their Ks-band luminosities and central stellar velocity dispersions. However, they follow the FP scaling relation defined by normal elliptical galaxies and other BCGs closely, suggesting that they are dynamically relaxed systems, at least in their central regions.
FGs are believed to be created fast and in an early epoch of the Universe by the efficient merger of L∗ galaxies inside DM halos (D’Onghia et al. 2005; Díaz-Giménez et al. 2011). In this scenario, the BGGs observed at low redshift had time to reach a virialized status, although some remnant of their merger phase could still be present. The different relaxation time scales between the inner and outer regions imply that the outskirts of galaxies may have fossil information about their past formation. The continuously increasing ellipticity profile observed in almost all galaxies of our sample could be a hint of such a merger history. Porter et al. (1991) reported on this behavior of the ellipticity profiles in a sample of BCGs, and they found that 50% of the BCGs in rich clusters present these characteristics and associated them with the observed absence of rotation in luminous ellipticals (Davies et al. 1983; Carter et al. 1985). This result might be consistent with our findings if the increasing ellipticity profiles are correlated with galaxy luminosity. In addition, Boylan-Kolchin et al. (2006) use numerical simulations to demonstrate that these ellipticity trends can be explained in terms of a high fraction of radial collisions, indicating a preferential direction in the orbits of the mergers.
Assuming that FGs were formed in an early epoch (Dariush et al. 2007; Díaz-Giménez et al. 2011) and then passively evolved for a long time in order to reach a relaxed state, it is customary to consider that dissipational mergers with a high fraction of gas should be predominant in the formation of these systems (Díaz-Giménez et al. 2008). Recent works by Robertson et al. (2006) and Hopkins et al. (2008) demonstrate through simulations and observations, respectively, how the observed tilt of the FP can be explained in terms of the amount of dissipation involved in the formation of elliptical galaxies. They conclude that galaxies formed through dissipationless mergers follow the FP defined by the virial theorem (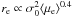 ) perfectly, whereas ellipticals formed through dissipational mergers will present an FP tilt, depending on the fraction of gas involved in the merger. Our galaxies, as normal ellipticals, are described well by a tilted FP, thus indicating that most of them could be the remnants of mergers with a high gas fraction. In addition, numerical simulations show that gas-rich mergers at an early stage of the formation of BGGs are needed to account for the observed properties of elliptical galaxies (Hernquist et al. 1993; Naab & Ostriker 2009).
) perfectly, whereas ellipticals formed through dissipational mergers will present an FP tilt, depending on the fraction of gas involved in the merger. Our galaxies, as normal ellipticals, are described well by a tilted FP, thus indicating that most of them could be the remnants of mergers with a high gas fraction. In addition, numerical simulations show that gas-rich mergers at an early stage of the formation of BGGs are needed to account for the observed properties of elliptical galaxies (Hernquist et al. 1993; Naab & Ostriker 2009).
However, numerical simulations of gas-rich mergers also predict that the remnants will be round and compact galaxies (i.e., with small effective radius) where the stellar velocity dispersions should increase (e.g., Khochfar & Silk 2006; Naab et al. 2007; Hopkins et al. 2008). Recent observational works on early type galaxies by Bernardi et al. (2011a,b) have shown a change in the slope of different scaling relations that involve the stellar mass. This trend is interpreted by the authors in terms of the kind of mergers that have been involved in the formation of these systems. Major dissipationless mergers between galaxies are mechanisms expected to increase the final size of the resulting galaxy but not its central velocity dispersion; however, if minor dry mergers are the predominant mechanism, they are expected to change both the size and velocity dispersion (Bernardi et al. 2011a). Therefore, Bernardi et al. (2011b) claim that the most feasible scenario is that galaxies with M∗ > 2 × 1011 M⊙ are formed mainly by major dissipationless mergers. It is clear that most of our BGGs follow the expected curvature in both the log σ0 vs. log LKs (Fig. 9) and log re vs. log LKs (Fig. 10) relations, confirming the observational trend found by Bernardi et al. (2011b). This interpretation contradicts the previous one and hints at a formation scenario where most of our BGGs formed through major gas-rich merger (Khosroshahi et al. 2006).
 |
Fig. 7 Distribution of our BGGs (large black points) in the edge-on view of the FP defined by the P98 early-type galaxies (small blue points). The BCGs of the P98 sample are marked by blue open triangles. The solid line represents the FP best fit to P98 galaxies. The dotted lines represent the 3σ deviation from the fit. |
 |
Fig. 8 The KR for our BGGs (large black points) and P98 early-type galaxies (small blue points). The BCGs of the P98 sample are marked by blue open triangles. The solid line represents the KR best fit to our sample, and the dotted line represents the best KR fit to P98 sample. |
 |
Fig. 9 Distribution of our BGGs (red stars and large black points) and P98 early-type galaxies (small blue points) in the log σ0 vs. log Lks plane. The BCGs in the P98 sample are marked by blue open triangles. The solid line represents the best fit to the galaxies in the luminosity range 3 × 1010 < LKs/L⊙ < 2 × 1011 as done by Bernardi et al. (2011b). Red stars and large black points represent BGGs with ellipticities ϵ > 0.3 and ϵ ≤ 0.3, respectively. The bottom panel represents the residuals from the best fit. |
 |
Fig. 10 Distribution of our BGGs (red stars and large black points) and P98 early-type galaxies (small blue points) in the log re vs. log LKs plane. The BCGs in the P98 sample are marked by blue open triangles. The solid line represents the best fit to the galaxies in the luminosity range 3 × 1010 < LKs/L⊙ < 2 × 1011 as done by Bernardi et al. (2011b). Red stars and large black points represent BGGs with ellipticities ϵ > 0.3 and ϵ ≤ 0.3, respectively. The bottom panel represents the residuals from the best fit. |
Another commonly used proxy for understanding the formation mechanisms of early-type galaxies is the Sérsic index. Numerical simulations predict Sérsic indexes for the remnants of dry mergers in the range 3 < n < 8 (González-García & Balcells 2005; Naab & Trujillo 2006), whereas they would be in the range 2 < n < 4 in dissipational mergers (Hopkins et al. 2009; Kormendy et al. 2009). We have tentatively divided our sample into galaxies with n ≤ 3 and n > 3 in order to understand whether the shape of the surface-brightness profiles could be used to distinguish the different formation scenarios. We did not find any relation between the departure from the intermediate-mass scaling relations and the Sérsic index. Similarly, several works based on numerical simulations have found that the shape of the isophotes can also be used to trace the merger history of elliptical galaxies (Naab & Burkert 2003; Khochfar & Burkert 2005; Naab et al. 2006). These studies find out that disky isophotes are the result of gas-rich mergers, whereas boxy isophotes are formed primarily in dissipationless collisions. Supported by these results, Khosroshahi et al. (2006) claim that BGGs in fossil systems were formed through dissipational mergers since they show disky isophotes. We measured the isophote shapes by means of the a4 coefficient, however, their noisy profiles (Fig. 4) prevented us from drawing any conclusions about the merger history of our BGGs based on the isophotes shape.
Interestingly, we found that the ellipticity turned out to be a good indicator of the kind of merger involved in the formation of BGGs. Numerical simulations show that the remnants of dissipational mergers are rounder on average than remnants of dissipationless mergers (Cox et al. 2004). In fact, the ellipticity distribution of dissipational merger remnants peaks at about 0.2, which sharps contrasts to the dissipationless remnants whose distribution of ellipticities peaks at about 0.4. We used this information to separate our BGGs into galaxies with ϵ ≤ 0.3 and ϵ > 0.3. We measured the ellipticities at re to mimic simulations. The results are shown in Figs. 9 and 10. It is clear that BGGs with higher ellipticities systematically deviate from the intermediate-mass scaling relation, whereas rounder galaxies are also distributed near this relation. Therefore, we interpret this result as another hint that dissipationless mergers (ϵ > 0.3) are the main processes driven the evolution of BGGs.
We conclude that BGGs in fossil systems suffered major dissipational mergers in an early epoch of their formation, but the bulk of their mass is assembled later in subsequent dissipationless mergers that increased the BGGs size.
6. Conclusions
We analyzed the near-infrared Ks-band photometric properties of a sample of 20 BGGs observed within the framework of the FOGO project (Aguerri et al. 2011). So far, this represent the largest sample of BGGs in fossil systems studied in the near-infrared. Here we summarize our results:
-
The structural parameters of the sample galaxies were derivedusing the GASP2D algorithm (Méndez-Abreuet al. 2008) by fitting a Sérsic modelto their surface-brightness distribution. This model provides agood description for all the galaxies and allows a straightforwardcomparison with the results available in literature.
-
Only one sample BGG is a candidate to be a cD galaxy since it shows an upward break in the surface-brightness profile with respect to a de Vaucouleurs profile.
-
The ellipticity profile of most of our galaxies is an increasing function of the radius. This can be related to the fact that our galaxies represent the very bright end of the luminosity function. The trend in the ellipticity profile cannot be explained in terms of a oblate/prolate spheroid. Together with the variation observed in the galaxy centroid and position angle radial profiles, it might indicate a preferential direction in the orbits of the mergers.
-
We built the Ks-band scaling relations (FP, KR, and FJ) for our sample of BGGs, and we compared them with those of normal elliptical and BCGs. We did not find any significant difference between the FP defined by BGGs and those of ellipticals or BCGs. This suggests that the central regions of BGGs are relaxed with structure similar to those of normal ellipticals. However, we found a change of the slope in the FJ and in the log re vs. log LKs relation for our massive galaxies.
These observational results can be interpreted in terms of the formation scenario of the BGGs. Our BGGs sample follows the FP of ellipticals and therefore are reproduced well by a tilted FP. Therefore, this supports that most of our BGGs probably suffered dissipational mergers during their formation. However, the curvature found in the scaling relation involving the mass of the galaxies can be interpreted as indicating that the stellar mass of these systems grew mainly by dissipationless mergers. Therefore, we suggest that BGGs in fossil system suffered major dissipational mergers in an early epoch of their formation, but the bulk of their mass is assembled later in subsequent dissipationless mergers that increase the BGGs size.
Acknowledgments
We acknowledge the anonymous referee for the positive comments which helped us to improve the paper. J.M.A., J.I.P., and J.V.M. are partially funded by the Spanish MICINN under the Consolider-Ingenio 2010 Program grant CSD2006-00070: First Science with the GTC (http://www.iac.es/consolider-ingenio-gtc). J.M.A. and J.A.L.A. are partially funded by the Spanish MICINN (grants AYA2007-67965-C03-01 and AYA2010-21887-C04-04). J.I.P. and J.V.M. are partially funded by the Spanish MICINN (grants AYA2007-67965-C03-02 and AYA2010-21887-C04-01). C.d.B. is partly funded by the Fundação para a Ciência e a Tecnologia (FCT)-Portugal through the project PEst-OE/EEI/UI0066/2011. E.M.C. is supported by the University of Padua through grants CPDA089220, 60A02-1283/10, and 60A02-5052/11 and by the Italian Space Agency (ASI) through grant ASI-INAF I/009/10/0. This article is based on observations made with the William Herschel Telescope operated on the island of La Palma, in the Spanish Observatorio del Roque de los Muchachos of the Instituto de Astrofísica de Canarias. This work is based in part on data obtained as part of the UKIRT Infrared Deep Sky Survey.
References
- Aguerri, J. A. L., Iglesias-Paramo, J., Vilchez, J. M., & Muñoz-Tuñón, C. 2004, AJ, 127, 1344 [NASA ADS] [CrossRef] [Google Scholar]
- Aguerri, J. A. L., Iglesias-Páramo, J., Vílchez, J. M., Muñoz-Tuñón, C., & Sánchez-Janssen, R. 2005, AJ, 130, 475 [NASA ADS] [CrossRef] [Google Scholar]
- Aguerri, J. A. L., Girardi, M., Boschin, W., et al. 2011, A&A, 527, A143 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Aihara, H., Allen de Prieto, C., An, D., et al. 2011, ApJS, 193, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Ascaso, B., Aguerri, J. A. L., Varela, J., et al. 2011, ApJ, 726, 69 [NASA ADS] [CrossRef] [Google Scholar]
- Beifiori, A., Courteau, S., Corsini, E. M., & Zhu, Y. 2011 [arXiv:1109.6265] [Google Scholar]
- Bernardi, M., Roche, N., Shankar, F., & Sheth, R. K. 2011a, MNRAS, 412, 684 [Google Scholar]
- Bernardi, M., Roche, N., Shankar, F., & Sheth, R. K. 2011b, MNRAS, 412, L6 [NASA ADS] [CrossRef] [Google Scholar]
- Bertin, E., & Arnouts, S. 1996, A&AS, 117, 393 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boylan-Kolchin, M., Ma, C.-P., & Quataert, E. 2006, MNRAS, 369, 1081 [NASA ADS] [CrossRef] [Google Scholar]
- Bruzual, G., & Charlot, S. 2003, MNRAS, 344, 1000 [NASA ADS] [CrossRef] [Google Scholar]
- Caon, N., Capaccioli, M., & D’Onofrio, M. 1993, MNRAS, 265, 1013 [NASA ADS] [CrossRef] [Google Scholar]
- Carter, D., Inglis, I., Ellis, R. S., Efstathiou, G., & Godwin, J. G. 1985, MNRAS, 212, 471 [NASA ADS] [Google Scholar]
- Casali, M. M., & Hawarden, T. G. 1992, in UKIRT Newsletter [Google Scholar]
- Cox, T. J., Primack, J., Jonsson, P., & Somerville, R. S. 2004, ApJ, 607, L87 [NASA ADS] [CrossRef] [Google Scholar]
- Cui, W., Springel, V., Yang, X., De Lucia, G., & Borgani, S. 2011, MNRAS, 416, 2997 [NASA ADS] [CrossRef] [Google Scholar]
- Cypriano, E. S., Mendes de Oliveira, C. L., & Sodré, Jr., L. 2006, AJ, 132, 514 [NASA ADS] [CrossRef] [Google Scholar]
- Dariush, A., Khosroshahi, H. G., Ponman, T. J., et al. 2007, MNRAS, 382, 433 [NASA ADS] [CrossRef] [Google Scholar]
- Davies, R. L., Efstathiou, G., Fall, S. M., Illingworth, G., & Schechter, P. L. 1983, ApJ, 266, 41 [NASA ADS] [CrossRef] [Google Scholar]
- de Vaucouleurs, G. 1948, Annales d’Astrophysique, 11, 247 [NASA ADS] [Google Scholar]
- Démoclès, J., Pratt, G. W., Pierini, D., et al. 2010, A&A, 517, A52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Díaz-Giménez, E., Muriel, H., & Mendes de Oliveira, C. 2008, A&A, 490, 965 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Díaz-Giménez, E., Zandivarez, A., Proctor, R., Mendes de Oliveira, C., & Abramo, L. R. 2011, A&A, 527, A129 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Djorgovski, S., & Davis, M. 1987, ApJ, 313, 59 [NASA ADS] [CrossRef] [Google Scholar]
- D’Onghia, E., Sommer-Larsen, J., Romeo, A. D., et al. 2005, ApJ, 630, L109 [NASA ADS] [CrossRef] [Google Scholar]
- Dressler, A., Lynden-Bell, D., Burstein, D., et al. 1987, ApJ, 313, 42 [NASA ADS] [CrossRef] [Google Scholar]
- Faber, S. M., & Jackson, R. E. 1976, ApJ, 204, 668 [NASA ADS] [CrossRef] [Google Scholar]
- Gonzalez, A. H., Zabludoff, A. I., & Zaritsky, D. 2003, Ap&SS, 285, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Gonzalez, A. H., Zabludoff, A. I., & Zaritsky, D. 2005, ApJ, 618, 195 [Google Scholar]
- González-García, A. C., & Balcells, M. 2005, MNRAS, 357, 753 [NASA ADS] [CrossRef] [Google Scholar]
- Graham, A. W., & Guzmán, R. 2003, AJ, 125, 2936 [NASA ADS] [CrossRef] [Google Scholar]
- Hernquist, L., Spergel, D. N., & Heyl, J. S. 1993, ApJ, 416, 415 [NASA ADS] [CrossRef] [Google Scholar]
- Hoessel, J. G., Oegerle, W. R., & Schneider, D. P. 1987, AJ, 94, 1111 [NASA ADS] [CrossRef] [Google Scholar]
- Hopkins, P. F., Cox, T. J., & Hernquist, L. 2008, ApJ, 689, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Hopkins, P. F., Cox, T. J., Dutta, S. N., et al. 2009, ApJS, 181, 135 [NASA ADS] [CrossRef] [Google Scholar]
- Jedrzejewski, R. I. 1987, MNRAS, 226, 747 [Google Scholar]
- Jones, L. R., Ponman, T. J., Horton, A., et al. 2003, MNRAS, 343, 627 [NASA ADS] [CrossRef] [Google Scholar]
- Jørgensen, I., Franx, M., & Kjaergaard, P. 1995, MNRAS, 276, 1341 [NASA ADS] [Google Scholar]
- Jørgensen, I., Franx, M., & Kjaergaard, P. 1996, MNRAS, 280, 167 [NASA ADS] [CrossRef] [Google Scholar]
- Jørgensen, I., Franx, M., Hjorth, J., & van Dokkum, P. G. 1999, MNRAS, 308, 833 [NASA ADS] [CrossRef] [Google Scholar]
- Kelson, D. D., van Dokkum, P. G., Franx, M., Illingworth, G. D., & Fabricant, D. 1997, ApJ, 478, L13 [NASA ADS] [CrossRef] [Google Scholar]
- Khochfar, S., & Burkert, A. 2005, MNRAS, 359, 1379 [NASA ADS] [CrossRef] [Google Scholar]
- Khochfar, S., & Silk, J. 2006, ApJ, 648, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Khosroshahi, H. G., Raychaudhury, S., Ponman, T. J., Miles, T. A., & Forbes, D. A. 2004, MNRAS, 349, 527 [NASA ADS] [CrossRef] [Google Scholar]
- Khosroshahi, H. G., Maughan, B. J., Ponman, T. J., & Jones, L. R. 2006, MNRAS, 369, 1211 [NASA ADS] [CrossRef] [Google Scholar]
- Khosroshahi, H. G., Ponman, T. J., & Jones, L. R. 2007, MNRAS, 377, 595 [NASA ADS] [CrossRef] [Google Scholar]
- Kjaergaard, P., Jorgensen, I., & Moles, M. 1993, ApJ, 418, 617 [Google Scholar]
- Kormendy, J. 1977, ApJ, 218, 333 [NASA ADS] [CrossRef] [Google Scholar]
- Kormendy, J., Fisher, D. B., Cornell, M. E., & Bender, R. 2009, ApJS, 182, 216 [NASA ADS] [CrossRef] [Google Scholar]
- La Barbera, F., Busarello, G., Merluzzi, P., Massarotti, M., & Capaccioli, M. 2003, ApJ, 595, 127 [NASA ADS] [CrossRef] [Google Scholar]
- La Barbera, F., de Carvalho, R. R., de la Rosa, I. G., et al. 2009, AJ, 137, 3942 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, F. S., Xia, X. Y., Mao, S., Wu, H., & Deng, Z. G. 2008, MNRAS, 385, 23 [NASA ADS] [CrossRef] [Google Scholar]
- Manchado, A., Barreto, M., Acosta-Pulido, J., et al. 2004, in SPIE Conf. Ser. 5492, ed. A. F. M. Moorwood, & M. Iye, 1094 [Google Scholar]
- Matthews, T. A., Morgan, W. W., & Schmidt, M. 1964, ApJ, 140, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Mendes de Oliveira, C. L., Cypriano, E. S., & Sodré, Jr., L. 2006, AJ, 131, 158 [NASA ADS] [CrossRef] [Google Scholar]
- Méndez-Abreu, J., Aguerri, J. A. L., Corsini, E. M., & Simonneau, E. 2008, A&A, 478, 353 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mendes de Oliveira, C. L., Cypriano, E. S., Dupke, R. A., & Sodré, L. 2009, AJ, 138, 502 [NASA ADS] [CrossRef] [Google Scholar]
- Méndez-Abreu, J., Simonneau, E., Aguerri, J. A. L., & Corsini, E. M. 2010, A&A, 521, A71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Morelli, L., Pompei, E., Pizzella, A., et al. 2008, MNRAS, 389, 341 [NASA ADS] [CrossRef] [Google Scholar]
- Mulchaey, J. S., & Zabludoff, A. I. 1999, ApJ, 514, 133 [NASA ADS] [CrossRef] [Google Scholar]
- Naab, T., & Burkert, A. 2003, ApJ, 597, 893 [NASA ADS] [CrossRef] [Google Scholar]
- Naab, T., & Ostriker, J. P. 2009, ApJ, 690, 1452 [NASA ADS] [CrossRef] [Google Scholar]
- Naab, T., & Trujillo, I. 2006, MNRAS, 369, 625 [NASA ADS] [CrossRef] [Google Scholar]
- Naab, T., Jesseit, R., & Burkert, A. 2006, MNRAS, 372, 839 [NASA ADS] [CrossRef] [Google Scholar]
- Naab, T., Johansson, P. H., Ostriker, J. P., & Efstathiou, G. 2007, ApJ, 658, 710 [NASA ADS] [CrossRef] [Google Scholar]
- Nelson, A. E., Simard, L., Zaritsky, D., Dalcanton, J. J., & Gonzalez, A. H. 2002, ApJ, 567, 144 [NASA ADS] [CrossRef] [Google Scholar]
- Nigoche-Netro, A., Ruelas-Mayorga, A., & Franco-Balderas, A. 2008, A&A, 491, 731 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pahre, M. A. 1999, ApJS, 124, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Pahre, M. A., Djorgovski, S. G., & de Carvalho, R. R. 1998, AJ, 116, 1591 [P98] [NASA ADS] [CrossRef] [Google Scholar]
- Pizzella, A., Corsini, E. M., Sarzi, M., et al. 2008, MNRAS, 387, 1099 [NASA ADS] [CrossRef] [Google Scholar]
- Poggianti, B. M. 1997, A&AS, 122, 399 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ponman, T. J., Allan, D. J., Jones, L. R., et al. 1994, Nature, 369, 462 [NASA ADS] [CrossRef] [Google Scholar]
- Porter, A. C., Schneider, D. P., & Hoessel, J. G. 1991, AJ, 101, 1561 [NASA ADS] [CrossRef] [Google Scholar]
- Press, W. H., Teukolsky, S. A., Vetterling, W. T., & Flannery, B. P. 1992, Numerical recipes in FORTRAN. The art of scientific computing [Google Scholar]
- Robertson, B., Cox, T. J., Hernquist, L., et al. 2006, ApJ, 641, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Romeo, A. D., Napolitano, N. R., Covone, G., et al. 2008, MNRAS, 389, 13 [NASA ADS] [CrossRef] [Google Scholar]
- Sandage, A., & Perelmuter, J. 1991, ApJ, 370, 455 [NASA ADS] [CrossRef] [Google Scholar]
- Santos, W. A., Mendes de Oliveira, C., & Sodré, Jr., L. 2007, AJ, 134, 1551 [NASA ADS] [CrossRef] [Google Scholar]
- Schombert, J. M. 1987, ApJS, 64, 643 [NASA ADS] [CrossRef] [Google Scholar]
- Seigar, M. S., Graham, A. W., & Jerjen, H. 2007, MNRAS, 378, 1575 [NASA ADS] [CrossRef] [Google Scholar]
- Sérsic, J. L. 1968, Atlas de galaxias australes, ed.J. L. Sersic [Google Scholar]
- Sommer-Larsen, J. 2006, MNRAS, 369, 958 [NASA ADS] [CrossRef] [Google Scholar]
- Sun, M., Forman, W., Vikhlinin, A., et al. 2004, ApJ, 612, 805 [NASA ADS] [CrossRef] [Google Scholar]
- Sun, M., Voit, G. M., Donahue, M., et al. 2009, ApJ, 693, 1142 [NASA ADS] [CrossRef] [Google Scholar]
- Tortora, C., Napolitano, N. R., Romanowsky, A. J., Capaccioli, M., & Covone, G. 2009, MNRAS, 396, 1132 [NASA ADS] [CrossRef] [Google Scholar]
- Trujillo, I., & Aguerri, J. A. L. 2004, MNRAS, 355, 82 [NASA ADS] [CrossRef] [Google Scholar]
- Trujillo, I., Aguerri, J. A. L., Cepa, J., & Gutiérrez, C. M. 2001, MNRAS, 328, 977 [NASA ADS] [CrossRef] [Google Scholar]
- Trujillo, I., Burkert, A., & Bell, E. F. 2004, ApJ, 600, L39 [NASA ADS] [CrossRef] [Google Scholar]
- Vikhlinin, A., McNamara, B. R., Hornstrup, A., et al. 1999, ApJ, 520, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Voevodkin, A., Borozdin, K., Heitmann, K., et al. 2010, ApJ, 708, 1376 [NASA ADS] [CrossRef] [Google Scholar]
- von Benda-Beckmann, A. M., D’Onghia, E., Gottlöber, S., et al. 2008, MNRAS, 386, 2345 [NASA ADS] [CrossRef] [Google Scholar]
- Zibetti, S., Pierini, D., & Pratt, G. W. 2009, MNRAS, 392, 525 [NASA ADS] [CrossRef] [Google Scholar]
- Ziegler, B. L., Saglia, R. P., Bender, R., et al. 1999, A&A, 346, 13 [NASA ADS] [Google Scholar]
All Tables
Structural parameters in the Ks-band derived by fitting a Sérsic model to our sample of BGGs.
All Figures
 |
Fig. 1 Ks-band counts per square degree per 0.5 mag bin for the fields observed with LIRIS. The continuous curve and vertical dotted lines represent the logarithmic function fit to the histogram, completeness, and limit magnitudes, respectively. |
| In the text | |
 |
Fig. 2 Distribution of redshift (left panel), X-ray luminosity (middle panel), and r-band absolute magnitude (right panel) for the FOGO FGs (solid black line) and of FGs studied in this work (red dotted line). |
| In the text | |
 |
Fig. 3 Observed (black points) and model (green solid line) surface-brightness radial profiles of the sample galaxies. The observed radial profiles were obtained by fitting ellipses to the isophotes of the Ks-band images. The model profiles follow a Sérsic law. These profiles were not corrected for cosmological dimming, K- or evolutionary corrections. The short vertical lines mark the effective radius. Semi-major axes of fitted ellipses are given in arcsec (bottom) and kpc (top). The inset in the upper panels shows the surface brightness in logarithmic scale to enhance the quality of the fit in the inner regions. The residuals of the fit are represented by a gray region in the lower panels. |
| In the text | |
 |
Fig. 3 continued. |
| In the text | |
 |
Fig. 3 continued. |
| In the text | |
 |
Fig. 3 continued. |
| In the text | |
 |
Fig. 4 A) Ellipticity, B) centroid ( |
| In the text | |
 |
Fig. 5 A) luminosity, B) effective radius, C) mean effective surface-brightness, and D) velocity dispersion differences between the aperture photometry and photometric decomposition measurements. Abscissa axes represent a number assigned to each galaxy. Blue solid lines represent the mean difference taking all points into account. Error bars represent the errors listed in Tables 1 and 2. |
| In the text | |
 |
Fig. 6 Correlations between ⟨ μe ⟩ (upper panel), n (bottom panel) and the galaxy absolute magnitude in the Ks-band. Large black dots indicate our sample galaxies. Blue dots represent the P98 early-type galaxies. The BCGs in the P98 sample are marked by blue open triangles. |
| In the text | |
 |
Fig. 7 Distribution of our BGGs (large black points) in the edge-on view of the FP defined by the P98 early-type galaxies (small blue points). The BCGs of the P98 sample are marked by blue open triangles. The solid line represents the FP best fit to P98 galaxies. The dotted lines represent the 3σ deviation from the fit. |
| In the text | |
 |
Fig. 8 The KR for our BGGs (large black points) and P98 early-type galaxies (small blue points). The BCGs of the P98 sample are marked by blue open triangles. The solid line represents the KR best fit to our sample, and the dotted line represents the best KR fit to P98 sample. |
| In the text | |
 |
Fig. 9 Distribution of our BGGs (red stars and large black points) and P98 early-type galaxies (small blue points) in the log σ0 vs. log Lks plane. The BCGs in the P98 sample are marked by blue open triangles. The solid line represents the best fit to the galaxies in the luminosity range 3 × 1010 < LKs/L⊙ < 2 × 1011 as done by Bernardi et al. (2011b). Red stars and large black points represent BGGs with ellipticities ϵ > 0.3 and ϵ ≤ 0.3, respectively. The bottom panel represents the residuals from the best fit. |
| In the text | |
 |
Fig. 10 Distribution of our BGGs (red stars and large black points) and P98 early-type galaxies (small blue points) in the log re vs. log LKs plane. The BCGs in the P98 sample are marked by blue open triangles. The solid line represents the best fit to the galaxies in the luminosity range 3 × 1010 < LKs/L⊙ < 2 × 1011 as done by Bernardi et al. (2011b). Red stars and large black points represent BGGs with ellipticities ϵ > 0.3 and ϵ ≤ 0.3, respectively. The bottom panel represents the residuals from the best fit. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.