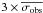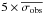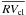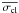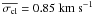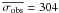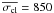| Issue |
A&A
Volume 535, November 2011
|
|
|---|---|---|
| Article Number | A39 | |
| Number of page(s) | 28 | |
| Section | Galactic structure, stellar clusters and populations | |
| DOI | https://doi.org/10.1051/0004-6361/200913582 | |
| Published online | 28 October 2011 | |
VLT multi-epoch radial velocity survey toward NGC 6253⋆,⋆⋆
Analysis of three transiting planetary candidates
1
Centro de Astrofísica da Universidade do Porto, Rua das Estrelas, 4150-762 Porto, Portugal
e-mail: marco.montalto@astro.up.pt
2
Universitaets-Sternwarte der Ludwig-Maximilians-Universitaet, Scheinerstr.1, 81679 Muenchen, Germany
3
Max-Planck-Institute for Extraterrestrial Physics, Giessenbachstr., 85741 Garching b Muenchen, Germany
4 Grupo de Astronomia, Departamento de Fisica, Casilla 160, Universidad de Conception, Chile
5
Universitá di Padova Dipartimento di Astronomia, Vicolo dell’Osservatorio 5, 35122 Padova, Italy
6
INAF – Osservatorio Astronomico di Padova Vicolo dell’Osservatorio 5, 35122 Padova, Italy
7 Dipartimento di Fisica, Universitá di Trento, via Sommarive 14, 38123 Povo (TN), Italy
8 INAF – Osservatorio Astronomico di Brera, via E. Bianchi 46, 23807 Merate (LC), Italy
9
Space Telescope Science Institute, 3800 San Martin Drive, Baltimore, MD 21218, USA
10
ESO Chile, A. de Cordova 3107, Santiago, Chile
Received: 2 November 2009
Accepted: 30 June 2011
Context. One of the most metal-rich open cluster of the Galaxy, NGC 6253 is a target of special interest in the search for extrasolar planets, the study of stellar populations, and the chemical/dynamical evolution of the Galactic disk.
Aims. We present the results of two photometric campaigns and a VLT multi-epoch radial velocity survey toward the open cluster NGC 6253. We complement our analysis with photometric, proper motion, and radial velocity data available from previous studies of this cluster, and analyze three planetary candidates found in the field of NGC 6253.
Methods. We derived homogeneous radial velocity measurements for stars located at the turn-off, sub-giant, red-giant branch, red-clump, and blue straggler regions of the cluster. We also analyzed a comparison sample of surrounding field stars. Spectra were obtained with the UVES and GIRAFFE spectrographs at the VLT during three epochs in August 2008.
Results. The three UVES measurements acquired for our brightest transiting candidate (V = 15.26) are all consistent within their errors (200 m/s), but were acquired at very similar orbital phases. The mean radial velocity of this object is not consistent with the cluster recession velocity, which rules out cluster membership except in the case of a binary system. This star is worth further analysis with high-precision spectroscopy. For our faintest candidate (V = 18.247), we were able to exclude the observed transits being caused by a close-by stellar companion, but more precise measurements will be needed to derive an orbital fit and to study other possible scenarios. For the remaining candidate, no measurements were acquired probably because of bad fiber positioning. The mean radial velocity of the cluster is (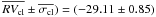 km s-1. Using both radial velocities and proper motions, we identified 35 cluster members. Our results are in good agreement with past radial velocity and photometric measurements. Furthermore, using our photometry, astrometry, and spectroscopy we identified a new eclipsing binary system member of the cluster.
km s-1. Using both radial velocities and proper motions, we identified 35 cluster members. Our results are in good agreement with past radial velocity and photometric measurements. Furthermore, using our photometry, astrometry, and spectroscopy we identified a new eclipsing binary system member of the cluster.
Conclusions. We discussed the possibility of detecting substellar companions (brown dwarfs and planets) with the radial velocity technique (both with UVES/GIRAFFE and HARPS) around turn-off stars of old open cluster. We isolated 5 stars that are optimal targets for searching for planetary mass companions with HARPS. Our optimized strategy minimizes the observing time requested to isolate and followup on the best planetary candidates in cluster with high-precision spectrographs, an important aspect given the faint target stars.
Key words: planetary systems / techniques: radial velocities / open cluster and associations: individual: NGC 6253
Based on observations collected at the European Organization for Astronomical Research in the Southern Hemisphere, Chile, program ID: 381.C-0270(A). Photometric observations relevant for this project were acquired in La Silla, Chile during programs 073.C-0227[A], 083.A-9001[A] and at the Anglo Australian Telescope (AAT) in Siding Spring.
© ESO, 2011
1. Introduction
The advent of multi-object spectrographs feeding large aperture telescopes offers the possibility obtaining simultaneous, repeated, and accurate spectroscopic measurements of a large sample of stars. The application of this technique to the study of open cluster is of particular interest. While open cluster photometric surveys are now routinely performed typically over several consecutive nights, there are relatively few multi-epoch radial velocity surveys that target these objects (Mermilliod et al. 2009; Hole et al. 2009). Besides allowing further culling of cluster members, multiple radial velocity measurements allow a more complete census of binary and multiple systems. Spectroscopic follow-up of eclipsing binary systems that belong to open cluster gives the opportunity to derive accurate stellar masses, thereby constraining models of stellar evolution (e.g. Southworth & Clausen 2006). Moreover, the increasing stability and accuracy of modern spectrographs is leading toward detection of binary systems with low-mass companions (such as brown dwarfs and planets) also in open cluster, where target stars are typically fainter than those observed in common radial velocity planet searches in the solar surroundings.
In this work, we have focused our attention on the old and metal-rich open cluster NGC 6253 (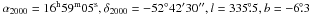 ). This cluster was selected as part of our project aimed at searching for transiting hot-Jupiter planets in metal-rich open cluster (Montalto et al. 2007).
). This cluster was selected as part of our project aimed at searching for transiting hot-Jupiter planets in metal-rich open cluster (Montalto et al. 2007).
In the solar neighborhood, FGK metal-rich dwarf stars have a higher probability hosting Jupiter-like planets (Gonzalez 1998; Santos et al. 2001; Fischer & Valenti 2005). According to the most accredited explanation that the planet-metallicity correlation is of primordial origin, we expect a higher planet discovery rate that targets stars born in metal-rich environments. While at solar metallicity the frequency of planets (with period P < 4 years, and radial velocity semi-amplitude K > 30 m/s) around FGK dwarf stars in the solar neighborhood is about 3%, at the metallicity of NGC 6253, the expected frequency is around 18%, as can be deduced from Fischer & Valenti (2005).
Since the high expected frequency of planets in metal-rich cluster, these objects are top targets for planet searches, and they offer an excellent natural laboratory for testing ideas of planet formation and evolution, while probing at the same time the effects of the environment.
Searches for planets around dwarf stars in cluster have not yet provided even bona-fide planetary candidates. This result may still be due to statistical problems (van Saders & Gaudi 2011), since in particular open cluster are typically loosely populated, and the most widely used technique for detecting planets in such environments is the transit method. However, the increasingly large number of surveys and the lack of detections could start to reveal some fundamental differences between planet formation processes around field and cluster dwarf stars. It is then of primary importance to continue monitoring cluster and establish on a firm observational basis that there is indeed a difference between the planet frequency in these environments and in the field.
In 2004, we monitored the metal-rich open cluster NGC 6253 photometrically for ten consecutive nights, during a multi-site campaign performed simultaneously in La Silla and Siding Spring. In April 2009 we observed the cluster at the 2.2 m La Silla Telescope another 14 nights during Max Planck Institute for Extrterrestrial Physics reserved time.
In August 2008, we followed-up with the VLT three transiting-planet candidates we found in the region of this cluster. We will dedicate a forthcoming contribution to the study of planet frequency in the field and in the cluster. Our observational strategy was also tied to the study of cluster members and surrounding field stars, and here we present the results of the complete multi-epoch radial velocity campaign toward NGC 6253. We used FLAMES in MEDUSA mode, targeting a total of 204 stars in the region of the cluster.
We then explore the possibility of searching for planetary companions around dwarf stars of old open cluster by means of the radial velocity technique. This detection method would greatly increase our chances of detecting planetary mass companions, allowing us to overcome the problem of the small sample of stars available in cluster. However such a technique has been applied systematically only to the Hyades cluster so far (Cochran et al. 2002; Paulson et al. 2002, 2003) given the proximity and consequent brightness of its members. In young cluster, planet detection is significantly hampered and complicated by stellar activity (Paulson et al. 2004a,b). Old open cluster should be better targets, although the faintness of their members seems to significantly limit the application of the radial velocity technique, in general requiring a very large investment of observing time. Here we discuss an optimized observing strategy aimed at isolating only the most promising objects to follow-up with high-precision spectroscopy, involving the use of photometry, astrometry, and multi-object spectroscopy. Besides resulting in a great improvement in the knowledge of cluster properties, this method minimizes the time needed to identify and followup on the best candidates. The application of this technique to the particular case of NGC 6253 is of special interest given the characteristics of this cluster.
NGC 6253 has been studied by several authors in the past, both photometrically (Bragaglia et al. 1997; Piatti et al. 1998; Sagar et al. 2001; Twarog et al. 2003; Anthony-Twarog et al. 2007; Montalto et al. 2009; De Marchi et al. 2010), and spectroscopically (Carretta et al. 2000, 2007; Sestito et al. 2007; Anthony-Twarog et al. 2010). In addition, in Montalto et al. (2009) we calculated proper-motion membership probabilities.
These studies have demonstrated that NGC 6253 is an old (~3.5 Gyr, e.g. Montalto et al. 2009) and metal-rich cluster ([Fe/H] = + 0.39 ± 0.07 Sestito et al. 2007; [Fe/H] = + 0.46 Carretta et al. 2007), since it is in fact one of the most metal-rich open cluster of the Galaxy. It is also one of the few old open cluster located inside the solar ring (Carraro et al. 2005a,b) at a Galactocentric distance of around 6 kpc, where more prohibitive environmental conditions in general prevent cluster survival (Wielen 1971). NGC 6253 is also important in the more general context of stellar population studies, offering homogeneous sample of coeval metal-rich stars against which stellar models at this extreme metallicity can be tested and compared. Its peculiar location in the Galactic disk gives the opportunity of extending toward the inner regions of the Galaxy the baseline for the study of the Galactic disk radial abundance, which is a basic ingredient in Galactic chemical evolution models (Tosi 1996).
This paper is organized as follows. In Sect. 2 we describe the photometric data we have used in this work, which were important to complement the spectroscopic results; in Sect. 3, we describe our radial velocity observations, and in Sect. 4 we give a detailed description of their reduction and calibration. In Sect. 5, we discuss the mean radial velocity of the cluster; in Sect. 6, we analyze our three transiting planetary candidates; in Sect. 7, we present the spectroscopic characterization of additional stars; in Sect. 8, we discuss four detached eclipsing binary systems; in Sect. 9, we present an optimized strategy to search for substellar objects with the radial velocity technique around turn-off stars of old open cluster; in Sect. 10, we discuss a method of constraining the minimum mass and period of cluster close binary systems, detected by RV surveys; and finally in Sect. 11, we summarize and conclude.
2. Photometric data
The photometric data that appear in this work are based on two major photometric campaigns conducted at the 2.2 m La Silla Telescope in 2004 and 2009 respectively. The 2004 photometric campaign was conducted during June 2004 (program ID:073.C-0227[A]). These data have been already presented and discussed in Montalto et al. (2009) and De Marchi et al. (2010) to which the reader is referred for further information.
2.1. The 2009 photometric observations of NGC 6253
In April 2009, we used the 2.2 m Telescope in La Silla for 14 consecutive nights between 1 − 14 April during Max Planck Institute for Extraterrestrial Physics reserved time (program ID:083.A-9001[A]). Only part of the time was allocated to NGC 6253 observations, as it is detailed in the summary presented in Table 1. The observing strategy was the same adopted in 2004, where we saturated turn-off stars and maintain the same pointing across all the nights in order to keep the stars as close as possible on the same pixels to minimize systematic effects arising from residual flat fielding corrections.
2.2. Photometric data reduction
The prereduction of the data used standard reduction software in IRAF. All the images were reduced using image subtraction and the DAOPHOT/ALLSTAR packages as described in Montalto et al. (2007). In particular, the image-subtraction method models the kernel that convolves the PSF of a reference high S/N image to match the PSF of a target image. The convolved reference image is then subtracted from the target image, leaving only variable objects as residuals, with constant objects disappearing. The photometry is then performed for each source of interest on the resulting difference images and compared with the photometry on the reference image.
We used the standard reduction routines in the difference image package ISIS2.2 (Alard & Lupton 1998; Alard 2000). At first, the images were interpolated on the astrometric reference system of the best seeing image. We imposed a second-order degree for the polynomial astrometric transformation between frames. Then we calculated the mean seeing of our images, and ranked them in order of increasing (absolute) seeing difference from the mean value. We then created a reference image considering only the first 50 images in this list. This procedure minimizes the seeing differences between the reference image and the target images. We performed different tests in order to set the best parameters for the subtraction. In the end, we decided to apply a kernel variable at the second order, and a sky background variable at the first order. The reduction was performed simultaneously on the entire image (i.e., we did not apply image splitting). From the reference image, we built up a master list of stars. The photometry and astrometry of the stars was extracted using the ALLSTAR package, using a fitting radius equal to the FWHM of the reference image. The photometry on the subtracted images was instead obtained from aperture photometry. We used the DAOPHOT (Stetson 1987) aperture photometry routine and slightly modified it to accept the subtracted images. The aperture radius was set equal to the FWHM of each image, and the sky background was extracted from a fixed outer annulus around the stars. Then the magnitude of the stars in the subtracted images was obtained by means of the following formula: 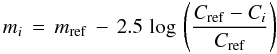 (1)where mi is the magnitude of a generic star in a generic ith subtracted image, mref the magnitude of the correspondent star in the reference image, Cref the counts obtained in the reference image and Ci in the ith subtracted image. We analyzed the lightcurves to search for planetary transit events following the procedure presented in Montalto et al. (2007). A separate paper in preparation accounts for the technical details and for the expected planetary frequency in our field of view. From our analysis three potentially good planetary transit events were identified, which were then analyzed spectroscopically as described in the following.
(1)where mi is the magnitude of a generic star in a generic ith subtracted image, mref the magnitude of the correspondent star in the reference image, Cref the counts obtained in the reference image and Ci in the ith subtracted image. We analyzed the lightcurves to search for planetary transit events following the procedure presented in Montalto et al. (2007). A separate paper in preparation accounts for the technical details and for the expected planetary frequency in our field of view. From our analysis three potentially good planetary transit events were identified, which were then analyzed spectroscopically as described in the following.
3. Spectroscopic observations
The observations were obtained using the FLAMES facility (Pasquini et al. 2002) at the UT2 (Kueyen telescope), in Paranal, Chile. FLAMES is the multi-object, intermediate and high resolution spectrograph of the VLT. It can access targets over a 25 arcmin diameter field of view, and it feeds two different spectrographs: UVES and GIRAFFE. While UVES provides the maximum resolution (R = 47 000), but can access up to eight targets at a time, GIRAFFE has an intermediate resolution (either R ≃ 25 000 or R ≃ 10 000), allowing us to target up to 130 objects at the time or to do integral field spectroscopy.
As reported in the previous section, our main purpose was to followup on three transiting-planet candidates we found in the field of NGC 6253. Then, we used UVES in fiber mode, with the standard setup centered at 580 nm. To maximize the scientific output of our research, we used UVES with GIRAFFE simultaneously and with the high-resolution grating HR9B, covering 21.3 nm centered at 525.8 nm with a resolution R = 25 000.
Given the spatial distribution of the transiting candidates we decided to prepare two different configurations named NGC6253_A and NGC6253_B1. In each configuration the eight fibers of UVES were allocated in the following manner: one fiber was dedicated to the simultaneous calibration, two fibers were allocated to two transiting candidate host stars, four (three in the second configuration) fibers to some known cluster member stars, and one (two in the second configuration) to the sky. Since our faintest candidate planet host star (V = 18.247) was located in between the other two, we were able to observe it in both configurations in order to improve the S/N.
The GIRAFFE fibers were used to target proper motion cluster members (Montalto et al. 2009), photometric variables (De Marchi et al. 2010), and stars previously observed for abundance analysis (Carretta et al. 2007; Sestito et al. 2007), complemented by other stars for comparison purposes. Eleven and twelve fibers were also allocated to the sky in each configuration, and five fibers were dedicated to the simultaneous thorium.
The data were obtained during three nights between August 17, 2008 and August 25, 2008. The exposure time for each configuration was 1875 s (15 min overhead), for a total observing time of ~6 h. The observations were performed in service mode. Table 2 provides a summary of our data.
We targeted a total of 204 stars, 44 of which in both configurations. For a given star, we always used the same fiber (apart from the stars in common to the two configurations) to minimize systematic effects. We measured the radial velocity for a total of 139 stars. We were not able to obtain accurate radial velocities for 65 stars. For 24 objects this was probably due to their faint magnitude, since they had R > 16 while for the remaining 41 stars, either to their intrinsic characteristics (hot temperature, high rotation velocities, etc.) or bad fiber positioning, or blends.
Among the stars analyzed, 106 have three measurements (present only in one configuration), and 33 have six measurements (present in both configurations). We preferred probable cluster members, on the basis of colors, magnitudes, and proper motion membership probabilities (MP). These probabilities were calculated in Montalto et al. (2009), considering likely cluster members those stars located within a rectangle region of dimesion 6.3 × 7.9 arcmin inclusive of the cluster center (see Montalto et al. 2009, for details), with magnitude V < 18, and that have MP > 90% at V = 12.5, down to MP > 50% at V = 18. The selected stars are representative of different stellar evolutionary stages and include a sample of turn-off, subgiant branch, red-giant branch, red-clump, and blue straggler stars. We also considered in our target list 16 stars present in the sample of variable stars compiled by De Marchi et al. (2010). These are (the enumeration of the following objects is the one presented in the catalog of Montalto et al. 2009 or; if not present, the one in De Marchi et al. 2010): the contact binary (EW) 30341; the RS Canum Venaticorum variable (RS CVn) 44079; the detached binary systems (EA) 31195, 24487, 38138, 126376; the rotational variables (RO1, RO2, see De Marchi et al. 2010, for details) 9832, 6430; the long period variables 173273, 153432, 40819, 16649, 50025, 4306; the RR Lyrae (RR) 74452, and the δ Scuti (DSCT) 84206. One of these stars, (RS CVn) 44079, is a likely cluster member. Finally 14 stars in the spectroscopic samples of Carretta et al. (2007), Sestito et al. (2007), and Anthony-Twarog et al. (2010) are included in our list, further improving our chances to detect binarity for these objects. They are stars 45410, 45412, 45413, and 45414 from Carretta et al. (2007), stars 45404, 45421, 45474 from Sestito et al. (2007), and stars 39994, 45404, 45421, 45513, 39810, 45414, 45444, 45410, 16649, 45409, 21555 from Anthony-Twarog et al. (2010). The remaining stars in our list were selected by considering either the need to have a sample of field objects against which comparing the results obtained for cluster stars or technical constraints like that the need to avoid putting the fiber buttons too close to each other.
4. Spectroscopic data reduction and radial velocity measurements
Data were reduced using the UVES and GIRAFFE pipelines (Ballester et al. 2000; Blecha et al. 2000) where raw data were bias-subtracted, flat-field corrected, extracted using the average extraction method, and wavelength-calibrated. GIRAFFE spectra were wavelength-calibrated using both prior and simultaneous calibration-lamp spectra, which assure a final systematic error in radial velocities lower than 100 m/s (Sommariva et al. 2009).
In particular, for each plate the wavelength calibration was first done using the next morning ThAr frame. Then a drift correction measured by the five simultaneous calibration lamps was applied. The drift was of the order of few hundred m/s. Finally, sky subtraction was applied. For what concerns UVES data, echelle orders were flux-calibrated using the master response curve of the instrument. Finally, the orders were merged to obtain a 1D spectrum. Radial velocities were obtained from the IRAF fxcor cross-correlation subroutine. Stellar spectra were cross-correlated with synthetic templates calculated by SPECTRUM2. The selection of a proper template for each star was mandatory because the targets have different spectral types and rotational velocities. For this reason we used three templates: the first calculated for the Sun and valid for stars with effective temperatures in the range Teff = 4000−6500 K; the second calculated for Teff = 3500 K, which includes the strong molecular bands, and is valid for the coolest stars in our sample; the last calculated for Teff = 7000 K, valid for the hottest stars in our sample. In addition, the template for hot stars was divided in seven subtemplates, calculated for rotational velocities equal to 0, 25, 50, 75, 100, 200, and 300 km s-1. For each star we carefully compared the observed spectrum with our templates, and according to the visible spectral lines and to a rough estimation of the rotation, we chose the most appropriate one. Once dealing with double-lined spectroscopic binaries, we in general reported the radial velocity values relative to the star with the strongest peak in the cross-correlation function.
We calculated the mean radial velocity (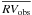 ) and the dispersion (σobs) for each star. To determine the threshold for binary detection, we subdivided the stars into seven magnitude bins 0.5 mag wide between 11 < R < 14.5, plus an additional large magnitude bin between 14 ≥ R < 18 (to account for the fewer stars in this magnitude range). We calculated the mean dispersion in each magnitude bin excluding stars with σobs > 1 km s-1 (σobs > 2 km s-1, in the fainter large bin), applied a σ-clipping algorithm excluding all stars above 3.5 × σ from the mean, and calculated the final value of the mean dispersions. We then performed a linear least square fit of the resulting values separating the brighter bins from the fainter one. Our result for the best-fit mean dispersion of constant stars (
) and the dispersion (σobs) for each star. To determine the threshold for binary detection, we subdivided the stars into seven magnitude bins 0.5 mag wide between 11 < R < 14.5, plus an additional large magnitude bin between 14 ≥ R < 18 (to account for the fewer stars in this magnitude range). We calculated the mean dispersion in each magnitude bin excluding stars with σobs > 1 km s-1 (σobs > 2 km s-1, in the fainter large bin), applied a σ-clipping algorithm excluding all stars above 3.5 × σ from the mean, and calculated the final value of the mean dispersions. We then performed a linear least square fit of the resulting values separating the brighter bins from the fainter one. Our result for the best-fit mean dispersion of constant stars (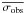 ) is given by the following equations:
) is given by the following equations: 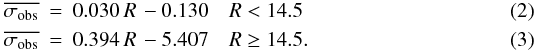 We adopted a conservative threshold for binary detection given that only stars having
We adopted a conservative threshold for binary detection given that only stars having 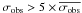 were considered candidate spectroscopic binaries.
were considered candidate spectroscopic binaries.
Throughout this paper we call radial velocity variables simply candidate close binary systems or close binary systems, though it is clear that they could also be multiple systems or that the radial velocity variations may have other physical explanations. In particular, we used the adjective close, because our observations span a period of only eight days, and even when the binarity is inferred by means of a comparison with past results, those observations are separated at most by eight years with respect to our observations3.
In Tables 9 and 10, we present the measured radial velocities for the analyzed objects, distinguishing between stars that are likely to be proper motion cluster members (Table 9) and stars that are not proper motion members, or that have doubtful/absent proper motions (Table 10). The columns in these tables indicate (i) the ID number of the star in the catalog of Montalto et al. (2009), (ii) the IDold number of the star used in the catalog of NGC 6253 variable stars of De Marchi et al. (2010), (iii) the right ascenscion RA(J2000), (iv) the declination Dec(J2000), (v) the mean visual magnitude (V), (vi) the mean R-band magnitude R, (vii) the B − R color, (viii) the mean radial velocity of the star 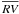 , (ix) the dispersion of the radial velocity measurements (σobs), (x) the ratio of the observed radial velocity dispersion to the dispersion threshold for binary detection
, (ix) the dispersion of the radial velocity measurements (σobs), (x) the ratio of the observed radial velocity dispersion to the dispersion threshold for binary detection 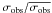 (Eqs. (2) and (3)), (xi) the proper motion membership probability MP (from Montalto et al. 2009), (xii) a classification flag (class) accounting for the position of the star in the color-magnitude diagram and its cluster membership probability, mean radial velocity and/or its classification on the basis of its photometric variability (De Marchi et al. 2010). In particular: MS = main sequence, SGB = sub-giant branch, RGB = red-giant branch, BSS = blue straggler, TRS = transiting planet candidate; LON = long-period variable, RSCVn = RS Canum Venaticorum variable; EW = contact eclipsing binaries; FLD = field star, EA = detached eclipsing binary, RR = RR-Lyrae, DSCT = δ Scuti, RO1 = rotational variable of type one (De Marchi et al. 2010), RO2 = rotational variable of type two (De Marchi et al. 2010); (xiii) binarity (bin) flag where stars considered spectroscopic binaries on the basis of the criterium reported above are flagged with bin = 1, (xiv) the spectrograph (inst) used in this study to observe the star, G = GIRAFFE, U = UVES; (xv) the projected distance D of the star to the center of the cluster, in arcmin, and (xvi) N the number of spectra acquired.
(Eqs. (2) and (3)), (xi) the proper motion membership probability MP (from Montalto et al. 2009), (xii) a classification flag (class) accounting for the position of the star in the color-magnitude diagram and its cluster membership probability, mean radial velocity and/or its classification on the basis of its photometric variability (De Marchi et al. 2010). In particular: MS = main sequence, SGB = sub-giant branch, RGB = red-giant branch, BSS = blue straggler, TRS = transiting planet candidate; LON = long-period variable, RSCVn = RS Canum Venaticorum variable; EW = contact eclipsing binaries; FLD = field star, EA = detached eclipsing binary, RR = RR-Lyrae, DSCT = δ Scuti, RO1 = rotational variable of type one (De Marchi et al. 2010), RO2 = rotational variable of type two (De Marchi et al. 2010); (xiii) binarity (bin) flag where stars considered spectroscopic binaries on the basis of the criterium reported above are flagged with bin = 1, (xiv) the spectrograph (inst) used in this study to observe the star, G = GIRAFFE, U = UVES; (xv) the projected distance D of the star to the center of the cluster, in arcmin, and (xvi) N the number of spectra acquired.
 |
Fig. 2 Observed radial velocity dispersions (σobs) against R-band magnitude. The continuous line indicates our best fit for the typical dispersion ( |
5. Results
5.1. Cluster mean radial velocity
The recession radial velocity of the cluster was calculated by only considering proper motion cluster members. Moreover, we excluded stars that are likely close binaries. Then we calculated the mean radial velocities (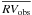 ) for these remaining bona-fide cluster members and used them to derive the cluster mean radial velocity (
) for these remaining bona-fide cluster members and used them to derive the cluster mean radial velocity (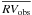 ), after applying an iterative 3-σ clipping algorithm to also exclude long period binaries or residual contaminants. The resulting mean radial velocity of the cluster obtained after this procedure is
), after applying an iterative 3-σ clipping algorithm to also exclude long period binaries or residual contaminants. The resulting mean radial velocity of the cluster obtained after this procedure is 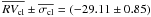 km s-1, where the error is the error of the mean, and the root mean square of the residuals is σcl = 4.26 km s-1, as obtained from a sample of 25 stars.
km s-1, where the error is the error of the mean, and the root mean square of the residuals is σcl = 4.26 km s-1, as obtained from a sample of 25 stars.
The cluster velocity dispersion seems quite high, since typical values for open cluster of similar richness are around 1 − 2 km s-1. This might indicate that there are still long-period binaries inflating the RV distribution. In Fig. 3, we present the radial velocity histogram for the 25 stars used above to calculate the cluster mean radial velocity (upper panel) and for all the remaining objects (bottom panel) in bins of 4 km s-1. Among the stars not considered in our calculation there are other very likely members, which will be discussed in the next section.
Considering only stars with radial velocities within 1-σ from the mean, the result is 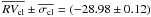 km s-1, and the scatter σcl = 0.4 km s-1, calculated from a sample of ten stars. These estimates are in reasonable agreement with previous literature results. Sestito et al. (2007) obtained a mean radial velocity equal to ( − 29.71 ± 0.79) km s-1 from a sample of four stars. Carretta et al. (2007) obtained ( − 28.26 ± 0.29) km s-1 from a sample of four stars, and more recently Anthony-Twarog et al. (2010) have obtained ( − 29.4 ± 1.3) km s-1 from a sample of 42 probable radial-velocity single members.
km s-1, and the scatter σcl = 0.4 km s-1, calculated from a sample of ten stars. These estimates are in reasonable agreement with previous literature results. Sestito et al. (2007) obtained a mean radial velocity equal to ( − 29.71 ± 0.79) km s-1 from a sample of four stars. Carretta et al. (2007) obtained ( − 28.26 ± 0.29) km s-1 from a sample of four stars, and more recently Anthony-Twarog et al. (2010) have obtained ( − 29.4 ± 1.3) km s-1 from a sample of 42 probable radial-velocity single members.
 |
Fig. 3 Upper panel: radial velocity distribution of stars considered as cluster members on the basis of proper motions and radial velocities. Bottom panel: radial velocity distribution of all the remaining stars in the sample (see text). |
6. Transiting-planet candidates
In this section, we present a preliminary analysis of the three planetary transiting candidates we found in the field of NGC 6253, based on the photometric data described in Sect. 2.2, and on the UVES spectroscopy. In Fig. 4, we present the color-magnitude diagram of proper motion cluster members, together with the colors and magnitudes of the transiting candidates. None of these candidates is located in the region were our proper motions are reliable. Moreover from Fig. 4 it appears that only star 171895 may be compatible with cluster membership, since it is located in the turn-off region. The other objects are likely field stars.
 |
Fig. 4 V, B − V color magnitude diagram of proper motion cluster members of NGC 6253, with highlighted the positions of the three planetary transiting candidates discussed in the text. |
6.1. Star 171895
The magnitude of the target star (2MASS16595146-5253456) is V = 15.260 ± 0.002. From the analysis of the UVES spectra, we obtained the following parameters: Teff = 5720 ± 50 K derived from the excitation equilibrium of the FeI lines, log (g) = 4.50 ± 0.20, [Fe/H] = + 0.36 ± 0.02 (spectral type G2V). Using these parameters and uncertainties, along with and the isochrones with metallicity Z = 0.03 with ages comprised between log (age [Gy] ) = 7.8 and log (age [Gy] ) = 10.25 taken from the Padova database, we constrained the mass, radius, and age of the star, obtaining M = (1.07 ± 0.04) M⊙, R = (1.04 ± 0.07) R⊙, and age < 8 Gyr. We also estimated a projected rotational velocity equal to vsin i ~ 5 km s-1.
In Fig. 5 (upper panels) we present the entire lightcurve of the object obtained using the WFI data. The photometry of the 2009 observing season was more noisy than the photometry of 2004, since we observed in April (at typically higher airmasses than in June 2004), and during a bright time (dark time in 2004). However, we detected three evident transit events (denoted by the roman numerals I, III, and IV in Fig. 5) of around 0.024 mag depth. The first (full) transit was detected in 2004, the other two (a partial transit during the flat bottom region and a full transit) in 2009. The period of the transiting object was deduced using at first the two transits of 2009, which allowed us to guess the closest integer period to the real period (that is, four days), and then folding the lightcurve finding the best solution consistent with all our photometric measurements and able to overlap the two full transits. We assumed a constant period. The result is P = 4.16164 days. Submultiples of this period are then excluded by our photometry. On the basis of this procedure, we also deduced that a few photometric measurements acquired just at the end of the ninth night in 2004 should have been located just at the ingress of the transit (see the epoch denoted by the roman numeral II). In the folded lightcurve presented in Fig. 5 (bottom left panel) we note that the points acquired during that night present a slight photometric offset with respect to the other measurements (~0.002 mag) that the two points just inside the transit present relatively large residuals with respect to the best transit model matching the observations denoted by the red, even accounting for the photometric offset. Whether this indicates that assuming a constant period is not correct, it is not clear from these observations. A few other measurements acquired during epoch IV and with similar phases ~−0.05 days in the same figure, appear to have large residuals as well; however, this is more likely due to the lower photometric quality of the 2009 observing season. Other photometric measurements are cleary needed to clearly understand this system.
The best-fit model was obtained using the Mandel & Agol (2002) algorithm, and a quadratic limb-darkening law, where the limb-darkening coefficients were selected from the table of Claret (2000) according to the spectral type of the host star. The stellar parameters (mass and radius) were also fixed to the mean values we obtained from spectroscopy. The model fully reproduces the shape of the observed transits. The rms of the fit is 0.002 mag, the radius of the transiting object we obtained is Rpl = 1.49 Rjup, and the inclination 87°.
The UVES radial velocity measurements are shown in Fig. 5 (lower right panel), and presented in Table 3. Since we did not know the orbital period at the time of the UVES observations (only one transit was detected in 2004, see above), it was not possible to plan the spectroscopic follow-up of this object accurately. The UVES measurements were unfortunately acquired at very similar orbital phases, as shown in Fig. 5 (lower right panel). As a consequence it is impossible to derive an orbital solution. The measurements are compatible within their errors, which is 200 m/s. Observations at other orbital phases and of higher precision are needed to accurately constrain the mass of the transiting object. The epoch (E) of the eclipses is given by 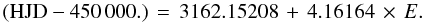 (4)
(4)
6.1.1. Cluster membership of star 171895
As demonstrated above, star 171895 is a very metal-rich star, and it appears located in the cluster turn-off region. However, the mean radial velocity of the system is equal to − 51.81 km s-1, which is not consistent with the recession velocity of the cluster (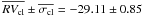 km s-1), and its location in the sky is rather distant from the cluster center (16.2 arcmin). This star has no proper motions in our own catalog, and an attempt to derive proper motions from the UCAC3 catalog has not yielded conclusive results.
km s-1), and its location in the sky is rather distant from the cluster center (16.2 arcmin). This star has no proper motions in our own catalog, and an attempt to derive proper motions from the UCAC3 catalog has not yielded conclusive results.
Given the present observations, the most likely interpretation is that star 171895 is a very metal-rich field star falling by coincidence just at the cluster turn-off. The presence of an additional close stellar companion in the system (e.g. a 0.8 M⊙ star on a ~ 100 day orbit, and presumably a white dwarf, since we did not detect any double peaks in the cross-correlation function) would be required to reconcile the disagreement between the mean radial velocity of this star and the recession velocity of the cluster. Such a scenario appears quite unlikely; otherwise, since additional radial velocity measurements are needed to constrain the mass of the transiting objects, this further hypothesis can be checked automatically. The HARPS instrument will accomplish these tasks perfectly, since we expect a precision of 10 m/s with 1 h of integration time for this star.
 |
Fig. 5 Upper left: lightcurve of star 171895 relative to the 2004 observing season. Red points highlight transit epochs, also indicated by the roman numeration. Upper right: lightcurve of star 171895 relative to the 2009 observing season. Lower left, top panel: folded lightcurve. The continuous line indicates the best-fit model obtained using the Mandel & Agol (2002) algorithm, considering as properties of the host star those derived from the UVES spectroscopy. The roman numeration and the associated symbols are relative to the transit epochs shown in the upper panels. Lower left, bottom panel: observed minus model residuals. Lower right: UVES spectroscopic measurements. |
6.2. Star 56223
The magnitude of the host star is V = 17.789. Its radial distance from the cluster center is 18.5 arcmin. In our photometry we detected eight transit events with a periodicity of 0.8494083 days (Fig. 6, upper panels). No UVES measurements were acquired for this system. This was probably due to a bad positioning of the fiber, also considering the faintness of the object. The transits depth is ~0.008 mag. Assuming that the host is a solar-type star, we obtained the best fit shown in Fig. 6 (bottom panel). The rms of the fit is 0.003 mag, the radius of the transiting object is R = 0.82 Rjup, and the inclination 85°. We observe that the ingress and egress phases do not appear to follow the model closely, although the large scatter does not allow us to draw a definitive conclusion. The epoch (E) of the eclipses is given by 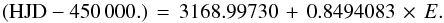 (5)Folding the lightcurve with a period twice as long as the quoted one, we observe the possible presence of an out-of transit flux variation as shown in Fig. 6. This may favor an eclipsing binary (or blend) scenario for this object. Since we are not able to spectroscopically characterize the host star, no additional information on this system is provided here.
(5)Folding the lightcurve with a period twice as long as the quoted one, we observe the possible presence of an out-of transit flux variation as shown in Fig. 6. This may favor an eclipsing binary (or blend) scenario for this object. Since we are not able to spectroscopically characterize the host star, no additional information on this system is provided here.
Journal of UVES radial velocities for star 171895.
 |
Fig. 6 Upper left: lightcurve of star 56223 relative to the 2004 observing season. Upper right: lightcurve of star 56223 relative to the 2009 observing season. Lower left panel, upper figure: folded lightcurve. The continuous line indicates the best-fit model obtained using the Mandel & Algol (2002) algorithm, assuming that the host star is a solar type star. Lower left panel, bottom figure: observed minus model residuals. Lower right panel: lightcurve folded with a period twice the best fitting period, showing the possible presence of out-of-transit variations. |
6.3. Star 23333
The magnitude of the host star is V = 18.247. This object is the closest to the cluster’s center, with a radial distance of 6.4 arcmin. The radial velocity measurements are presented in Table 4. From our photometry we detected four transit events, two full transits in 2004 and two partial transits in 2009 (Fig. 7 upper and lower left panels). The epoch (E) of the eclipses is given by 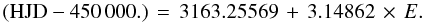 (6)Given the faintness of the object the lightcurve is very noisy. The transits are rather deep, at around 0.03 mag, and the duration is ~1.92 h. The folded radial velocity measurements are shown in the bottom right panel of Fig. 7. In this case radial velocity measurements appear sufficiently well separated. However, the error of each measurement is large (~3.6 km s-1). Even when binning the couple of datapoints we acquired at the same orbital phase, the error is reduced by a
(6)Given the faintness of the object the lightcurve is very noisy. The transits are rather deep, at around 0.03 mag, and the duration is ~1.92 h. The folded radial velocity measurements are shown in the bottom right panel of Fig. 7. In this case radial velocity measurements appear sufficiently well separated. However, the error of each measurement is large (~3.6 km s-1). Even when binning the couple of datapoints we acquired at the same orbital phase, the error is reduced by a 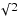 (2.5 km s-1). From the UVES spectroscopy we were able to derive an approximate value of the effective temperature of the host star, which is Teff = (5700 ± 200) K. We were not able to derive the gravity because of the low S/N of the spectra. The best fit obtained with the Mandel & Agol (2002) algorithm, when considering a solar radius host star, would give a radius for the secondary equal to 2.25 Rjup and an inclination of 84°. A 2.25 Rjup stellar companion would have a mass of about 0.2 solar masses using a mass-radius relation (e.g. Pont et al. 2005), yielding an expected RV semiamplitude of ~25 km s-1, which is clearly excluded by the observations. The S/N of the spectra is in this case too low to provide a reasonable estimate of the vsini. Moreover, we did not observe apparent out-of-transit variations in this case. We conclude that this object will require further observations in the future to better clarify its nature.
(2.5 km s-1). From the UVES spectroscopy we were able to derive an approximate value of the effective temperature of the host star, which is Teff = (5700 ± 200) K. We were not able to derive the gravity because of the low S/N of the spectra. The best fit obtained with the Mandel & Agol (2002) algorithm, when considering a solar radius host star, would give a radius for the secondary equal to 2.25 Rjup and an inclination of 84°. A 2.25 Rjup stellar companion would have a mass of about 0.2 solar masses using a mass-radius relation (e.g. Pont et al. 2005), yielding an expected RV semiamplitude of ~25 km s-1, which is clearly excluded by the observations. The S/N of the spectra is in this case too low to provide a reasonable estimate of the vsini. Moreover, we did not observe apparent out-of-transit variations in this case. We conclude that this object will require further observations in the future to better clarify its nature.
Journal of UVES radial velocities for star 23333.
 |
Fig. 7 Upper left: lightcurve of star 23333 relative to the 2004 observing season. Upper right: lightcurve of star 23333 relative to the 2009 observing season. Lower left: folded lightcurve. Lower right: UVES spectroscopic measurements. |
Among the three planetary transiting candidates presented, star 171895 is the most interesting object, both for its brightness and for its characteristics. Follow-up observations of this system (both photometric and spectroscopic in particular with the HARPS instrument) are clearly warranted to accurately determine its properties.
7. Spectroscopic characterization of additional stars
7.1. Proper motion and radial velocity members
Among the sample of proper motion cluster members, stars that have mean radial velocities (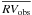 ), satisfying the condition
), satisfying the condition 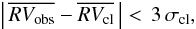 (7)were considered also radial velocity members. In Fig. 8, we present the (R,B − R) color magnitude diagram for proper-motion selected cluster members, highlighting stars also having radial velocity measurements and/or stars likely close binaries (as obtained from our multi-epoch radial velocities). We overplot the best-fit isochrone taken from the Padova database (age = 3.5 Gyr, Z = 0.03), and also the equal mass binary sequence. There are 30 stars in all. As shown in Fig. 8, these stars populate the turn-off, sub-giant, red-giant branch, red-clump and blue straggler regions of the cluster, and are considered secure cluster members. Among them, the following objects are particularly interesting.
(7)were considered also radial velocity members. In Fig. 8, we present the (R,B − R) color magnitude diagram for proper-motion selected cluster members, highlighting stars also having radial velocity measurements and/or stars likely close binaries (as obtained from our multi-epoch radial velocities). We overplot the best-fit isochrone taken from the Padova database (age = 3.5 Gyr, Z = 0.03), and also the equal mass binary sequence. There are 30 stars in all. As shown in Fig. 8, these stars populate the turn-off, sub-giant, red-giant branch, red-clump and blue straggler regions of the cluster, and are considered secure cluster members. Among them, the following objects are particularly interesting.
 |
Fig. 8 R-band magnitude and B − R color for proper motion selected members (small black points). Red squares indicate stars that are also radial velocity members, steel blue squares stars that appear to be radial velocity non members, and black framed squares stars that are likely close binary systems. The continuous line indicates the best-fitting isochrone as discussed in Montalto et al. (2009), and the dashed line the equal mass binary stars sequence. |
 |
Fig. 9 Same as Fig. 8, but for proper motion non-members or for stars whose proper motion membership probabilities are either doubtful or absent, as explained in the legend. |
7.1.1. Star 39810
Star 39810 has a high proper motion membership probability (MP = 95%), its mean radial velocity agrees with the one of the cluster (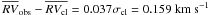 ), and it is located in the turn-off region of the cluster. Since we measured a dispersion σobs = 1.595 km s-1, (
), and it is located in the turn-off region of the cluster. Since we measured a dispersion σobs = 1.595 km s-1, (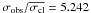 ) from our repeated radial velocities, we conclude that this object is also a candidate cluster close binary system. Anthony-Twarog et al. (2010) measure a mean radial velocity for this object equal to − 29.82 km s-1, which is compatible with our measurement ( − 29.269 km s-1), and also report a dispersion of their three radial velocity measurements equal to 2.28 km s-1.
) from our repeated radial velocities, we conclude that this object is also a candidate cluster close binary system. Anthony-Twarog et al. (2010) measure a mean radial velocity for this object equal to − 29.82 km s-1, which is compatible with our measurement ( − 29.269 km s-1), and also report a dispersion of their three radial velocity measurements equal to 2.28 km s-1.
7.1.2. Star 45387
Star 45387 is a proper motion and radial velocity cluster member (MP = 97%, 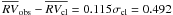 km s-1) located in the blue straggler region, and a likely close binary system (σobs = 1.602 km s-1,
km s-1) located in the blue straggler region, and a likely close binary system (σobs = 1.602 km s-1, 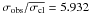 ).
).
7.1.3. Star 45144
Star 45144 is a proper motion and radial velocity cluster member (MP = 97%, 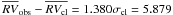 km s-1) in the turn-off region. It is a likely close binary system (σobs = 5.081 km s-1,
km s-1) in the turn-off region. It is a likely close binary system (σobs = 5.081 km s-1, 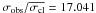 ).
).
7.1.4. Star 45474
Star 45474 is a proper motion and radial velocity cluster member (MP = 97%, 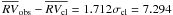 km s-1) in the turn-off region, and a likely close binary system (σobs = 8.090 km s-1,
km s-1) in the turn-off region, and a likely close binary system (σobs = 8.090 km s-1, 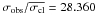 ). This star was also observed by Sestito et al. (2007), who determines a radial velocity equal to (33.49 ± 2.87) km s-1 with a difference of 11.67 km s-1 with respect to our own mean radial velocity, confirming the binarity of the object.
). This star was also observed by Sestito et al. (2007), who determines a radial velocity equal to (33.49 ± 2.87) km s-1 with a difference of 11.67 km s-1 with respect to our own mean radial velocity, confirming the binarity of the object.
7.1.5. Star 45413
Star 45413 at the red-clump, proper-motion, and radial velocity member (MP = 91%, 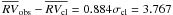 km s-1), does not indicate binarity from our dataset (σobs = 0.467 km s-1,
km s-1), does not indicate binarity from our dataset (σobs = 0.467 km s-1, 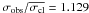 ), though a comparison with the measurement of Carretta et al. (2007) gives a difference of 12.207 km s-1 with respect to our mean radial velocity, suggesting that the star is a binary system likely with a longer period than our time baseline.
), though a comparison with the measurement of Carretta et al. (2007) gives a difference of 12.207 km s-1 with respect to our mean radial velocity, suggesting that the star is a binary system likely with a longer period than our time baseline.
7.1.6. Star 44682
Star 44682 at the turn-off is a double-lined spectroscopic binary, probably with a period much longer than our observing window, since from our radial velocities this star is not variable (MP = 95%; 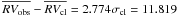 km s-1, σobs = 0.326 km s-1,
km s-1, σobs = 0.326 km s-1, 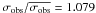 ).
).
7.1.7. Star 45421
Star 45421 on the red-giant branch, has already been classified as a potential binary star by Sestito et al. (2007). Our estimated mean radial velocity differs from their measurement by ~ 2.7 km s-1. Anthony-Twarog et al. (2010) also derives the radial velocity for this object, which differs from our estimate by ~ 6.1 km s-1. It appears then that this star is a likely cluster close binary, though from our measurements it was not classified as a radial velocity variable star (MP = 94%; 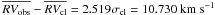 , σobs = 0.339 km s-1,
, σobs = 0.339 km s-1, 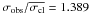 ).
).
7.1.8. Star 39994
Star 39994 at the turn off, is classified as a turn-off cluster star (MP = 92%; 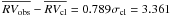 km s-1, σobs = 0.272 km s-1,
km s-1, σobs = 0.272 km s-1, 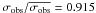 ). We notice that Anthony-Twarog et al. (2010) has obtained four radial velocity measurements for this star with a mean that differs by 1.741 km s-1 from our mean value and a scatter of 4.86 km s-1, which could indicate binarity.
). We notice that Anthony-Twarog et al. (2010) has obtained four radial velocity measurements for this star with a mean that differs by 1.741 km s-1 from our mean value and a scatter of 4.86 km s-1, which could indicate binarity.
7.1.9. Star 45444
The blue straggler star 45444 (MP = 95%; 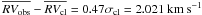 σobs = 0.093 km s-1,
σobs = 0.093 km s-1, 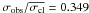 ) is not classified as a binary considering our data. Anthony-Twarog et al. (2010) obtains one radial velocity measurement for this object, which differs by RVMO − RVTW = 6 km s-1 from our mean radial velocity and with an associated uncertainty of 1.79 km s-1. This result suggests that the object is a likely binary system.
) is not classified as a binary considering our data. Anthony-Twarog et al. (2010) obtains one radial velocity measurement for this object, which differs by RVMO − RVTW = 6 km s-1 from our mean radial velocity and with an associated uncertainty of 1.79 km s-1. This result suggests that the object is a likely binary system.
7.1.10. Stars 45404, 45412, 45414, 45410
These stars were also observed by Sestito et al. (2007, star 45404), Carretta et al. (2009, stars 45412, 45414, 454104), and Anthony-Twarog et al. (2010, stars 45404, 45414, 45410). They are not RV variables, and our mean radial velocities agree with the measurements of those authors (within their uncertainties) and with our radial velocity cluster membership criterium.
7.2. Proper motion members with discrepant RV
Stars indicated by steel blue squares (Fig. 8) have mean radial velocities that do not satisfy our cluster membership radial velocity criterium. They are in total six stars. Five of them, are very likely cluster close binaries.
7.2.1. Star 44079
Star 44079, at the cluster turn off, (MP = 90%; 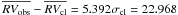 km s-1, σobs = 35.258 km s-1,
km s-1, σobs = 35.258 km s-1, 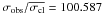 ) is a spectroscopic binary system. De Marchi et al. (2010) report that this star is an RS CVs star with period ~ 2.18 days and that it presents signs of activity and also a shallow eclipse (~0.02 mag). In this case our radial velocities do not appear well phased with the photometric measurements, probably a consequence of activity.
) is a spectroscopic binary system. De Marchi et al. (2010) report that this star is an RS CVs star with period ~ 2.18 days and that it presents signs of activity and also a shallow eclipse (~0.02 mag). In this case our radial velocities do not appear well phased with the photometric measurements, probably a consequence of activity.
7.2.2. Star 45368
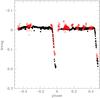 |
Fig. 10 Folded light curve of the eclipsing binary system 45368. Black filled points are relative to the 2004 observing season, and red open circles to the 2009 observing season. |
Star 45368 is a double-lined eclipsing binary system, as we determined by visual inspection of the light curve. The binarity of this object is confirmed by our radial velocity measurements (MP = 95%; 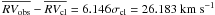 , σobs = 109.131 km s-1,
, σobs = 109.131 km s-1, 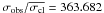 ). Also for this object we derived a rotation velocity of ~30 km s-1, which indicates tidal locking induced by the close-by stellar companion.
). Also for this object we derived a rotation velocity of ~30 km s-1, which indicates tidal locking induced by the close-by stellar companion.
In Fig. 10, we present the photometric observations acquired for this object, distinguishing between 2004 and 2009 observations. We detected four eclipses in all, all of them partial during the ingress of the transits. Moreover, as seen in Fig. 10, the lightcurve is not constant out of the eclipses, since there are some clear light modulations.
The UVES measurements presented in Fig. 11 indicate a very large radial velocity variation (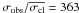 ), which is consistent with the idea of a stellar binary system and a short orbital period. The radial velocities are presented in Table 5. Our result for the epoch (E) of the primary eclipse is
), which is consistent with the idea of a stellar binary system and a short orbital period. The radial velocities are presented in Table 5. Our result for the epoch (E) of the primary eclipse is 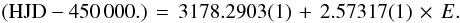 (8)In Fig. 11, we fit the radial velocity measurements with the following models:
(8)In Fig. 11, we fit the radial velocity measurements with the following models: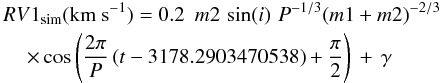 (9)
(9)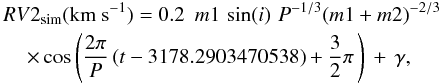 (10)\arraycolsep1.75ptwhere m1 and m2 are the masses of the primary and the secondary stars both in solar masses, P is the period in days, t the epoch of the UVES observations in days, γ the barycentric velocity of the system, i the inclination of the system (assumed equal to 90°), and the result is given in km s-1. We assumed a circular orbit since the short orbital period should imply tidal circularization. The two radial velocity curves represented by Eqs. (6) and (7) are in phase with the observed times of the primary and secondary eclipses respectively. We varied the two masses between 0.6 M⊙ and 10.5 M⊙ in steps of 0.1 M⊙, and γ between ± 4 km s-1 from the recession velocity of the cluster ( − 29.11 km s-1) in steps of 40 m/s. The best solution was found by minimizing the quantity:
(10)\arraycolsep1.75ptwhere m1 and m2 are the masses of the primary and the secondary stars both in solar masses, P is the period in days, t the epoch of the UVES observations in days, γ the barycentric velocity of the system, i the inclination of the system (assumed equal to 90°), and the result is given in km s-1. We assumed a circular orbit since the short orbital period should imply tidal circularization. The two radial velocity curves represented by Eqs. (6) and (7) are in phase with the observed times of the primary and secondary eclipses respectively. We varied the two masses between 0.6 M⊙ and 10.5 M⊙ in steps of 0.1 M⊙, and γ between ± 4 km s-1 from the recession velocity of the cluster ( − 29.11 km s-1) in steps of 40 m/s. The best solution was found by minimizing the quantity: 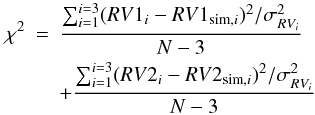 (11)where RV1i and RV2i are the observed radial velocities of the primary and of the secondary, σRVi are the uncertainties of the radial velocity measurements as reported in Table 5 and N − 3 = 3 since we have six independent measurements, and three degrees of freedom (m1, m2, and γ). The result of the fit (Fig. 11) implies m1 = (1.60 ± 0.08) M⊙, m2 = (1.50 ± 0.07) M⊙, γ = −30.2 km s-1, and χ = 1.23, and the errors in the masses have been derived from the rms of all models with χ < 2. The value of the barycentric velocity of the system is then fully consistent with cluster membership.
(11)where RV1i and RV2i are the observed radial velocities of the primary and of the secondary, σRVi are the uncertainties of the radial velocity measurements as reported in Table 5 and N − 3 = 3 since we have six independent measurements, and three degrees of freedom (m1, m2, and γ). The result of the fit (Fig. 11) implies m1 = (1.60 ± 0.08) M⊙, m2 = (1.50 ± 0.07) M⊙, γ = −30.2 km s-1, and χ = 1.23, and the errors in the masses have been derived from the rms of all models with χ < 2. The value of the barycentric velocity of the system is then fully consistent with cluster membership.
 |
Fig. 11 Fill black circles and open circles are UVES radial velocity measurements of the primary and secondary components of the 45368 binary system. The solid curve is the best-fitting model in phase with the primary eclipses. The dotted line is the best-fitting model in phase with the secondary eclipse. The dashed horizontal line indicates the baricentric velocity of the system (γ = −30.19 km s-1). |
Journal of UVES radial velocities for the 45368 eclipsing binary system.
In Table 6, we summarize the results obtained from our analysis. Since the two eclipses are only partial in our photometry, we did not try to fit the lightcurve of this system and constrain the radii of the stars. We note that between the 2004 and 2009 measurements there could be a photometric offset. However, a complete and detailed analysis of this system will be presented once more data is available. The possibility to derive accurate masses and radii for these stars will offer an excellent opportunity to test stellar evolution models predictions at the extreme metallicity of NGC 6253 (Grundahl et al. 2008).
Summary of the parameters derived for the 45368 eclipsing binary system, assuming i = 90° and e = 0.
It is also worth noting that this star showed two eclipses in the 2004 photometry, but we could not determine the period since observations cover them only poorly. For this reason it is not included in the list of variable stars given by De Marchi et al. (2010). When combining 2004 and 2009 photometry, we could derive the period. In turn, we could infer that B-band photometry was acquired during an eclipse (in correspondence of an orbital phase equal to 0.49). This explains why our B − V value (B − V = 1.127, Montalto et al. 2009) is redder than those given by other authors (e.g. Bragaglia et al. 1997, B − V = 0.848), while the V,R, and I photometry as acquired outside the eclipses and are in good agreement with the other authors within the known uncertainties. Therefore, we adopted the B − V value given by Bragaglia et al. (2007) and we could pin the star at the turn-off point. This is a very interesting object, considering that UVES spectroscopy showed that the eclipsing system is also a double-lined spectroscopic binary.
7.2.3. Stars 45528
Star 45528 at the turn off is a double-lined spectroscopic binary system (MP = 97%; 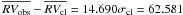 km s-1, σobs = 20.931 km s-1,
km s-1, σobs = 20.931 km s-1, 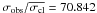 ). Once the radial velocity of both components is considered, the mean radial velocity of the system is equal to − 25.88 km s-1 = 0.758σcl, which allows us to state that the object is a likely radial velocity member binary system.
). Once the radial velocity of both components is considered, the mean radial velocity of the system is equal to − 25.88 km s-1 = 0.758σcl, which allows us to state that the object is a likely radial velocity member binary system.
7.2.4. Stars 45403
Star 45403 at the turn off is a double-lined spectroscopic binary system (MP = 97%; 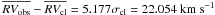 , σobs = 39.078 km s-1,
, σobs = 39.078 km s-1, 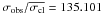 ). The mean radial velocity of the two components is equal to −31.78 km s-1 = 0.627σcl, indicating that this object is a likely radial velocity member binary system.
). The mean radial velocity of the two components is equal to −31.78 km s-1 = 0.627σcl, indicating that this object is a likely radial velocity member binary system.
7.2.5. Star 45300
Star 45300 is located close to the red-giant branch of the cluster. Given its radial velocity, this object could be a candidate cluster close binary, although we have no possibility of checking this hypothesis. From our radial velocities the object is not variable (MP = 94%; 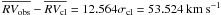 , σobs = 0.256 km s-1,
, σobs = 0.256 km s-1, 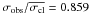 ).
).
7.2.6. Star 30341
Star 30341 is instead almost certainly a field contaminant with similar proper motion of cluster stars, as indicated by its deviant radial velocity (MP = 87%; 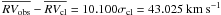 , σobs = 1.277 km s-1,
, σobs = 1.277 km s-1, 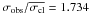 ) and position in the CMD. Its proper motion membership probability is the lowest among the sample of proper motion cluster members listed in Table 3. De Marchi et al. (2010) classify this star as an eclipsing contact binary system (EW) with a 0.27 days period and semi-amplitude ~0.02 mag. From our radial velocities, there is a lack of significant RV variability. Given the small dispersion of the radial velocity measurements and the very small period determined photometrically, we argue that this object may be a rotational variable, rather than a contact binary. As stated in De Marchi et al. (2010), it is very difficult to distinguish between these two classes of variables using only photometric data.
) and position in the CMD. Its proper motion membership probability is the lowest among the sample of proper motion cluster members listed in Table 3. De Marchi et al. (2010) classify this star as an eclipsing contact binary system (EW) with a 0.27 days period and semi-amplitude ~0.02 mag. From our radial velocities, there is a lack of significant RV variability. Given the small dispersion of the radial velocity measurements and the very small period determined photometrically, we argue that this object may be a rotational variable, rather than a contact binary. As stated in De Marchi et al. (2010), it is very difficult to distinguish between these two classes of variables using only photometric data.
In summary, given the high proper motion membership probabilities of these stars and their position in the CMD, it is likely that they are all likely cluster members (with the exception of star 30341). In particular, their deviant radial velocities could be explained by the large dispersions we observed for stars 44079, 45368, 45528, 45403, and by long periods and massive companions for stars 44682, 45421, and 45300.
7.3. Proper motion non-members or stars with doubtful/undefined proper motions
In Fig. 9 and Table 10, we present the results for those stars that are proper motion non-members or that have doubtful/undefined proper motions, as indicated by the different symbols. Different colors separate radial velocity members from non-members. None of the few stars with proper motions met our selection criteria for cluster membership, and most stars have undefined proper motions.
The median radial velocity of this sample of stars is RVfield = −8.98 km s-1 (excluding close binaries) and the root mean square of the residuals is σfield = 48.40 km s-1. By fitting a Gaussian function to this distribution we expect (9 ± 3) stars with radial velocity consistent with cluster membership (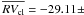 km s-1, 12.78 km s-1 = 3σcl). We count instead 14 potential radial velocity members. Looking at Table 10 and considering the radial distances of these objects from the cluster center, along with their positions in the color magnitude diagram, the most likely cluster members are the detached binary (EA) 31195, located in between the cluster main sequence and the cluster equal mass binary sequence (Fig. 9); the subgiant branch star 254502 and the blue straggler candidates 45392, 45396, 45409, 45427, and 45433. These candidate members must be considered with caution, since their proper motion membership probabilities are not very high ( ≤ 85%).
km s-1, 12.78 km s-1 = 3σcl). We count instead 14 potential radial velocity members. Looking at Table 10 and considering the radial distances of these objects from the cluster center, along with their positions in the color magnitude diagram, the most likely cluster members are the detached binary (EA) 31195, located in between the cluster main sequence and the cluster equal mass binary sequence (Fig. 9); the subgiant branch star 254502 and the blue straggler candidates 45392, 45396, 45409, 45427, and 45433. These candidate members must be considered with caution, since their proper motion membership probabilities are not very high ( ≤ 85%).
7.3.1. Star 16649
Star 16649 (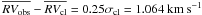 ) has no proper motion measurements. It was classified by De Marchi et al. (2010) as a long period binary, and we classified it also as a candidate radial velocity binary since σobs = 4.725 km s-1,
) has no proper motion measurements. It was classified by De Marchi et al. (2010) as a long period binary, and we classified it also as a candidate radial velocity binary since σobs = 4.725 km s-1, 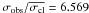 . Anthony-Twarog et al. (2010) obtained three radial velocity measurements for this object, their mean differing only by 0.67 km s-1 from our mean, but presenting a scatter equal to 10.03 km s-1.
. Anthony-Twarog et al. (2010) obtained three radial velocity measurements for this object, their mean differing only by 0.67 km s-1 from our mean, but presenting a scatter equal to 10.03 km s-1.
7.3.2. Star 45409
Star 45409 (MP = 85%; 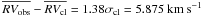 ) is a candidate blue straggler radial velocity binary since σobs = 1.473 km s-1,
) is a candidate blue straggler radial velocity binary since σobs = 1.473 km s-1, 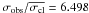 . Anthony-Twarog et al. (2010) obtained one radial velocity measurement for this object, which differs by 1.015 km s-1 from our mean radial velocity and has an associated uncertainty of 5.52 km s-1.
. Anthony-Twarog et al. (2010) obtained one radial velocity measurement for this object, which differs by 1.015 km s-1 from our mean radial velocity and has an associated uncertainty of 5.52 km s-1.
7.4. The frequency of binary systems
The frequency of binaries among cluster and field stars can be investigated thanks to photometric (Montalto et al. 2009; De Marchi et al. 2010) and radial velocity results (Sestito et al. 2007; Carretta et al. 2007, and this work). We consider a star as a likely binary system if either the photometry or the spectroscopy allows us to classify the star as a binary.
Among our sample of 35 likely cluster members, we found that 12 objects are likely cluster binary systems giving a binary frequency of fbin = (34 ± 10)%, where the error accounts for the Poisson statistic5. The frequency remains essentially unaltered, including the sample of seven stars indicated in the previous paragraph as likely members (among which two are variables), fbin = (33 ± 9)%. This result is in good agreement with previous estimates (e.g. Bragaglia et al. 1997; Montalto et al. 2009), though this certainly underestimates the real value, since in general we are not complete for long period binary systems and very low mass companions.
However, a homogeneous comparison with the field’s binary frequency can only be done for binaries detected from our own surveys (both photometric and spectroscopic), since no field objects have been spectroscopically observed by other authors in past years. Just to distinguish the frequency of these binaries from the previous estimate, we use here the term frequency of close binaries (fcb), because both our photometric and spectroscopic surveys covered a few nights of observations.
Then ten out of 35 stars are likely cluster close binary systems of NGC 6253, which gives fcb = (29 ± 9)% (or 29% ± 8% considering the seven stars in the previous paragraph) for the cluster, and equal to fcb,field = (22 ± 5)% (excluding the seven stars of the previous paragraph) for the field. Our estimated cluster binary frequency then appears higher than the field binary frequency, although they are consistent within the uncertainties. We note also that the sample of cluster stars analyzed is still small, and there are some selection effects. As mentioned in the introduction, we have explicitely included some systems whose photometric variability indicate binarity (17 in total). In particular two of them are likely cluster members, the rest are field objects as can be seen in Tables 9 and 10.
Moreover, De Marchi et al. (2010) observed that the class of main-sequence rotational variables is the most numerous, as observed in the surrounding field of NGC 6253. In our sample, there are in fact only two rotational variables. More in general, in this work we have focused on the binarity of turn off and evolved stars, whereas the study of De Marchi et al. (2010) analyzes the variability of fainter objects.
Mermilliod et al. (2009) obtained an overall binary frequency equal to 30% from the analysis of 13 nearby open cluster, considering their 19-year CORAVEL survey, which would be consistent with our estimates.
Mathiew et al. (1990) derived a frequency of binaries with periods less than 1000 days comprised between 9% and 15% among the solar mass M67 members. Latham et al. (2002) obtained a frequency equal to (15.8 ± 1.5)% for the halo population and find no obvious difference with the disk populations. An accurate comparison of our results with previous findings is beyond the scope of this work; moreover, it should be recalled that, for most of our objects, we are only sensitive to short-period variability (a few days) both photometrically and spectroscopically.
We note, however, that our estimated frequency of close binary systems (fcb) appears somehow higher than what derived by these authors in other environments, even if the difference is only significant at ~1.6-σ, considering our errors.
8. Detached eclipsing binary systems
In our target list there are four known detached eclipsing binary systems (see Sect. 1). These objects were selected from the list compiled by De Marchi et al. (2010). As appears evident from their Table A.3, several of these detached systems present very shallow eclipses. In particular, six objects in their list have eclipses with amplitudes ≤ 0.03 mag. We decided to target stars 31195, 126376, 38138 and 24487 with the GIRAFFE spectrograph. They have eclipses of amplitudes 0.02 mag, 0.02 mag, 0.01 mag, and 0.53 mag, and periods equal to 1.8156 days, 1.5896 days, 0.66606 days, and 0.85120 days, respectively. The lightcurves of these objects have already been presented in De Marchi et al. (2010). They tipycally show out-of-eclipse modulations, with the presence of primary and secondary eclipses. The eclipses are also markedly V-shaped. The only exception may be star 38138, where the eclipses are shallow and noisy and not easily distinguished from one another. Assuming that the obseved transits are grazing eclipses caused by very close stellar companions (given the short periods), we should expect to observe large radial velocity variations. For example, a stellar companion just at the limit between the brown dwarf and the stellar regime (M = 0.08 M⊙) in a circular orbit with period equal to P = 1.8156 days would produce a radial velocity semi-amplitude equal to K = 12.5 km s-1 (assuming the primary star is a solar type star). From Table 10 we see instead that only star 24487 has been detected as a binary in our spectroscopic survey. In other words all the three objects presenting shallow eclipses did not appear radial velocity variables.
For star 24487 we verified that our radial velocities are in phase with the transit epoch reported in De Marchi et al. (2010). A preliminary fit to the radial velocities would imply an equal mass system of around 0.6 Msun, though the measurements are quite uncertain with errors typically of 10 − 20 km s-1. We also obtained an estimated rotational velocity vsin i ~ 100 km s-1, which confirms the binary star scenario and tidal locking. However stars 31195 and 126376 have ratational velocities vsin i ~ 0 km s-1, and the S/N was too low for star 38138 to obtain a result.
For star 38138 the observations have been acquired almost at the same phase, that is at phase equal to 0.16, 0.17, 0.19 in chronological order and assuming the time of minimum and the period reported in Table A.3 of De Marchi et al. (2010). For star 127376 the phase is also close to 0 or 0.5 (0.06, 0.58, 0.1). However, it appears that for star 31195 we should have reasonably expected to detect a large radial velocity variation since the observations were acquired at orbital phases equal to 0.11, 0.31, and 0.52. One possible hypothesis is that star 31195 is in fact a blend, where a third unresolved companion determined shallower eclipses and fictitiously small radial velocity variations. Since, as we discussed in Sect. 5 and as also pointed out by De Marchi et al. (2010), this object might be considered a likely cluster member even though its proper motion membership probability is not very high, it would be very important to acquire other observations to better clarify its nature.
9. Radial velocity searches for substellar companions around old open cluster turn-off stars
In this section, we estimated the number of planets we can expect to detect during a radial velocity survey toward NGC 6253, considering different observing strategies. We focused our attention on cluster turn off stars (V = 15), and assumed to use the HARPS spectrograph. At the magnitude of our target stars, considering 1 h of integration time for each star, we expect a radial velocity precision of 10 m/s per measurements (e. g. Bordé et al. 2010). A 3-σ detection threshold implies that only substellar companions that induce radial velocity semi-amplitudes variations K > 30 m/s could be detected. From the Fischer & Valenti (2005) law we expect ~18% FGK dwarf stars having planets that produce radial velocity semi-amplitudes K > 30 m/s, and with orbital periods up to four years, at the metallicity of NGC 6253 ([Fe/H] = + 0.39). We used the following equation to simulate the observations of a planet-host star at some fixed epochs: 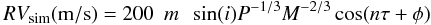 (12)where n is the mean orbital motion ( = 2π/P), and τ corresponds to the 3 epochs of our observations. In the above equation, the period is expressed in days, the mass of the companion (m) in Jupiter masses, the mass of the primary (M) in solar masses, and the resulting radial velocities are in meters per second. Cluster stars with the same magnitude of our targets have masses of ~ 1.3 M⊙ (derived from isochrone fitting), and we adopted this value for the primary’s mass. Random Gaussian scatter was also added to the measurements to account for observational errors. The dispersion was fixed to 10 m/s. The orbital period of the planet was varied between 1 day and 1460 days ( = 4 yr) in steps of 0.5 days, and the mass of the secondary between 0.5 Mjup and 13 Mjup, in steps of 0.1 Mjup. These limits are consistent with the validity domain of the Fischer & Valenti (2005) law. For each couple of period and mass, we performed 1000 simulations randomly varying the orbital phase of the planet, and defined the detection efficiency (eff) as the ratio between the number of simulations for which the standard deviation in the simulated measurements around their mean value exceeded 3 × σ = 30 m/s, with respect to the total number of simulations.
(12)where n is the mean orbital motion ( = 2π/P), and τ corresponds to the 3 epochs of our observations. In the above equation, the period is expressed in days, the mass of the companion (m) in Jupiter masses, the mass of the primary (M) in solar masses, and the resulting radial velocities are in meters per second. Cluster stars with the same magnitude of our targets have masses of ~ 1.3 M⊙ (derived from isochrone fitting), and we adopted this value for the primary’s mass. Random Gaussian scatter was also added to the measurements to account for observational errors. The dispersion was fixed to 10 m/s. The orbital period of the planet was varied between 1 day and 1460 days ( = 4 yr) in steps of 0.5 days, and the mass of the secondary between 0.5 Mjup and 13 Mjup, in steps of 0.1 Mjup. These limits are consistent with the validity domain of the Fischer & Valenti (2005) law. For each couple of period and mass, we performed 1000 simulations randomly varying the orbital phase of the planet, and defined the detection efficiency (eff) as the ratio between the number of simulations for which the standard deviation in the simulated measurements around their mean value exceeded 3 × σ = 30 m/s, with respect to the total number of simulations.
To calculate the expected number of planets, we convolved the detection efficiency with the mass-period functions of extrasolar planets as derived by Jiang et al. (2010). We considered the results obtained by those authors for independent mass functions and, in particular, for the case where all the results from different radial velocity surveys were considered together (the single imaginary survey). Assuming coupled mass-period functions gives similar results, at least for the case of the single imaginary survey, as can be deduced from their Table 5. In such a way the probability (dP) that a single star of metallicity [Fe/H] has a planet with orbital period comprised between P and P + dP, and mass comprised between M and M + dM is given by ![\begin{equation} {\rm d}P=c \left(\frac{M}{M0}\right)^{-\alpha} \left(\frac{P}{P0}\right)^{-\beta} \frac{{\rm d}M}{M} \frac{{\rm d}P}{P} \times 10^{2[{\rm Fe/H}]}\times {\rm eff}(M,P) \end{equation}](/articles/aa/full_html/2011/11/aa13582-09/aa13582-09-eq284.png) (13)where α = −0.143, β = −0.124, c = 0.001316, M0 = 1.5 Mjup, and P0 = 90 days. The efficiency function (eff [M,P] ) depends not only on the mass and period of the orbiting planet, but also on the observing strategy. In the above equation we have assumed that the mass-period functions are independent of both the host-star’s metallicity and the host-star’s mass. Ribas & Miralda-Escudé (2007) find that the host star metallicities decrease with planet mass, however the significance of this result is only marginal considering the present sample of exoplanets. A dependence of planet’s mass and orbital period on the planet’s host mass has also been demonstrated. In particular around M-dwarf stars, hot-Jupiter planets appear relatively rare (e.g. Endl et al. 2006), whereas they seem more frequent around giant stars with respect to dwarf stars, with thier long orbital periods and rather high minimum masses (e.g. Sato et al. 2007). Our considerations are, however, limited to Neptune-Jupiter planets around dwarf stars at the cluster turn off, so are not affected by this problem. Once applied to the period-mass domain of our simulations (see above), assuming solar metallicity and perfect efficiency (eff = 1), Eq. (8) gives a detection probability of 3.1%, in good agreement with the normalization factor of the Fischer & Valenti (2005) law (3%). Once particularized to our case, assuming the metallicity of NGC 6253, the above equation allows calculating the total number of detectable planets and their distribution in period and mass, as reported in Table 7 and shown in Figs. 12 and 13. The main result is that the observing strategy has a strong impact on the expected number of planets. With three epochs equally distributed over 2.66 years, and assuming an initial sample of 26 stars (which means a total of 78 HARPS hours) we can expect to detect 3.23 planets. If taken consecutively, we could expect to detect only 1.42 planets. In general, strategies that involve nonconsecutive observations are the most effective since they allow higher sensitivity to longer period planets.
(13)where α = −0.143, β = −0.124, c = 0.001316, M0 = 1.5 Mjup, and P0 = 90 days. The efficiency function (eff [M,P] ) depends not only on the mass and period of the orbiting planet, but also on the observing strategy. In the above equation we have assumed that the mass-period functions are independent of both the host-star’s metallicity and the host-star’s mass. Ribas & Miralda-Escudé (2007) find that the host star metallicities decrease with planet mass, however the significance of this result is only marginal considering the present sample of exoplanets. A dependence of planet’s mass and orbital period on the planet’s host mass has also been demonstrated. In particular around M-dwarf stars, hot-Jupiter planets appear relatively rare (e.g. Endl et al. 2006), whereas they seem more frequent around giant stars with respect to dwarf stars, with thier long orbital periods and rather high minimum masses (e.g. Sato et al. 2007). Our considerations are, however, limited to Neptune-Jupiter planets around dwarf stars at the cluster turn off, so are not affected by this problem. Once applied to the period-mass domain of our simulations (see above), assuming solar metallicity and perfect efficiency (eff = 1), Eq. (8) gives a detection probability of 3.1%, in good agreement with the normalization factor of the Fischer & Valenti (2005) law (3%). Once particularized to our case, assuming the metallicity of NGC 6253, the above equation allows calculating the total number of detectable planets and their distribution in period and mass, as reported in Table 7 and shown in Figs. 12 and 13. The main result is that the observing strategy has a strong impact on the expected number of planets. With three epochs equally distributed over 2.66 years, and assuming an initial sample of 26 stars (which means a total of 78 HARPS hours) we can expect to detect 3.23 planets. If taken consecutively, we could expect to detect only 1.42 planets. In general, strategies that involve nonconsecutive observations are the most effective since they allow higher sensitivity to longer period planets.
 |
Fig. 12 Probability of detecting a planet around a single turn-off star of NGC 6253, as a function of the planetary orbital period and different simulated HARPS observing strategies. The left panels show the results considering three observing epochs and the right panels considering six observing epochs, as reported by the labels at the top of each group of panels. Each small panel refers to one of the simulations presented in Table 7, as indicated by the inner numbers. |
10. Minimum mass and period of companion objects of cluster members close binary systems
In this section we studied the opposite problem of Sect. 9: assuming we will find a radial velocity variable star during an RV survey and assuming that this variation is determined by the presence of a companion object, which are the most likely minimum mass (m sin [i] ) and period (P) of this object? The effectiveness of an observing strategy should be evaluated not only considering whether it is able to maximize the number of detectable planets, but also considering if it is able to minimize the number of spurious objects that may produce the same signal of the planets.
As an illustration, we considered first the case of the UVES observations and, in particular, of star 39810, which has the smallest dispersion among our sample of cluster candidate close binary systems, as shown in Sect. 5. In Fig. 14, we present a comparison between the radial velocity measurements of stars 39810 and 40519, which is also a turn off cluster member and not a radial velocity variable star. While star 40519 radial velocities are all consistent with the cluster recession velocity, measurements for star 39810 clearly depart from it. We assume in the following that the observed radial velocity variation for star 39810 is determined by the presence of a companion object. On the basis of this hypothesis, we constrain the expected minimum mass and period of this object by means of Monte Carlo simulations. The basic condition that we imposed is that the barycentric radial velocity of the binary system is coincident with the recession velocity of the cluster. This is possible because this star is a very likely cluster member, as demonstrated in Sect. 5. If this object were a common field star, we would nod have had any a priori knowledge of its barycentric radial velocity.
We varied the period P of the orbit between 0.1 to 1000 days (dP = 0.05 days), and the minimum mass of the companion (m sin [i] ) between 0.1 M⊙ to 1000 Mjup (dm sin [i] = 0.05 Mjup). We assumed circular orbits, and we performed 100 simulations for each fixed value of the mass and the period by randomly choosing the orbital phase between 0 < φ < 2π. Then we calculated the observed radial velocity of the primary star (RVsim) by means of Eq. (15), and for each simulation, we calculated the dispersion of the radial velocity measurements σobs,sim, and the mean radial velocity  . We finally imposed the conditions that the simulated dispersions and mean radial velocities matched our observed values:
. We finally imposed the conditions that the simulated dispersions and mean radial velocities matched our observed values: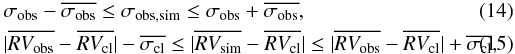 \arraycolsep1.75ptwhere
\arraycolsep1.75ptwhere  is our adopted radial velocity error (
is our adopted radial velocity error (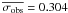 m/s, see Eq. (3)). The likelihood that a given period and minimum companion mass imply orbits for which the simulated mean radial velocities and dispersions are consistent with our observations was calculated by dividing the number of simulations that matched our criteria from the total number of simulations. In the top panel of Fig. 15, we show the likelihood distribution we obtained for star 39810. For periods P < 3 days, the mass is msin(i) ≲ 13 Mjup, then in the range of massive jupiters. We also plot the theoretical curve correspondent to K = 1.4 × σobs, which links the observed scatter to the expected radial velocity amplitude of the companion and the vertical line corresponding to a period equal to ~4 × [t3 − t1] = 36 days, which appears to be the maximum period we should expect for the companion object (coincident with a maximum mass equal to m sin(i) = 40 Mjup), at a confidence level >50%. In the bottom panel of Fig. 15, we show the probability distribution we obtained for the same object, but without the assumption on the barycentric radial velocity of the system (as if the star was a field object). Regions with a probability higher than 50% clearly extend toward longer periods and minimum masses (P > 36 days, m sin(i) > 40 M⊙).
m/s, see Eq. (3)). The likelihood that a given period and minimum companion mass imply orbits for which the simulated mean radial velocities and dispersions are consistent with our observations was calculated by dividing the number of simulations that matched our criteria from the total number of simulations. In the top panel of Fig. 15, we show the likelihood distribution we obtained for star 39810. For periods P < 3 days, the mass is msin(i) ≲ 13 Mjup, then in the range of massive jupiters. We also plot the theoretical curve correspondent to K = 1.4 × σobs, which links the observed scatter to the expected radial velocity amplitude of the companion and the vertical line corresponding to a period equal to ~4 × [t3 − t1] = 36 days, which appears to be the maximum period we should expect for the companion object (coincident with a maximum mass equal to m sin(i) = 40 Mjup), at a confidence level >50%. In the bottom panel of Fig. 15, we show the probability distribution we obtained for the same object, but without the assumption on the barycentric radial velocity of the system (as if the star was a field object). Regions with a probability higher than 50% clearly extend toward longer periods and minimum masses (P > 36 days, m sin(i) > 40 M⊙).
 |
Fig. 14 Radial velocities obtained for stars 39810 and 40519 located in the turn-off region. Dotted lines indicate the stars’ mean radial velocities ( |
To better understand this result, we performed other simulations, assuming different observing epochs. In Fig. 16, we show the results considering three epochs at t1 = 486 days, t2 = 972 days, and t3 = 1458 days (equally distributed over a period of 2.66 years). In both cases (cluster and field star), the overall shape of the probability distribution is the same as in Fig. 15; however, the highest probability regions are clearly more extended toward higher masses and longer periods. The interpretation of Figs. 15 and 16 is that, as long as the period of the companion object is probed by the timescale of the observations (where the timescale can be roughly assumed equal to 4 × [t3 − t1] ), the most likely mass and period of the companion object producing the observed radial velocity scatter are found along the theoretical curve both for the case of the cluster and of the field star (as traced by the highest probability regions). However, a worse result is obtained for the case of the field star in correspondence of resonant periods. Objects with longer periods than the observing timescale may as well produce a scatter compatible with the observations, but their mass should be higher than what is implied by the theoretical curve, since they are forced to produce that scatter during the timescale spanned by the observations. This determines the tail toward high masses and periods visible in Fig. 15. Otherwise, considering the case of the cluster star, this tail is reduced in extension with respect to the case of the field stars, and implies probabilities < 30% thanks to the condition on the barycentric velocity of the system (against < 80% in the case of the field star).
The major conclusion is that if a star belongs to a cluster, and our observations span a period ΔT during which we determine a radial velocity scatter equal to σobs > σcl, and a mean radial velocity consistent with the recession velocity of the cluster, the expected mass and period of the suspected companion object are comprised in the region defined by the conditions K = 1.4 × σobs and P ≲ 4 × Δ T in the mass-period diagram at a confidence level > 50%. This is not true for the field star, where mass and period can be greater than these limits where considering the same confidence level.
10.1. The best observing strategy
 |
Fig. 15 Period-mass probability distribution for the possible companion object of star 39810, obtained from orbital simulations, assuming the real observing epochs and circular obits. In the upper panel we show the results in the hypothesis that the star belongs to the cluster (as demonstrated by proper motions, radial velocities, and position in the CMD), whereas in the bottom panel we show the result if the star is a common field object: σobs = 1595 m/s, |
 |
Fig. 16 Same as Fig. 15, assuming three observing epochs at t1 = 486 days, t2 = 972 days, and t3 = 1458 days and circular orbits, σobs = 1595 m/s, |
 |
Fig. 17 Same as Fig. 15, assuming three observing epochs at t1 = 486 days, t2 = 972 days, and t3 = 1458 days, circular orbits, σobs = 50 m/s, |
In Sect. 9, we found that three observing epochs equally distributed over a period of 2.66 years should provide a good compromise between the number of detectable planets in NGC 6253 and observing time (Table 7). To understand how efficient can be, this observing strategy to isolate potential planetary candidates, we assumed to observe with the HARPS instrument (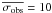 m/s), fixing the observing epochs at t1 = 486, t2 = 972, and t3 = 1458 days. We assume to study a star presenting a radial velocity scatter σobs = 50 m/s. Period and mass of the companion object were varied between 0.05 Mjup and 1000 Mjup, and between 0.05 days and 1000 days respectively (dP = 0.05 days, dm sin(i) = 0.05 Mjup). As shown in Fig. 17, the result for the cluster star resembles the case of the field star more than in previous simulations. The reason is that in this case
m/s), fixing the observing epochs at t1 = 486, t2 = 972, and t3 = 1458 days. We assume to study a star presenting a radial velocity scatter σobs = 50 m/s. Period and mass of the companion object were varied between 0.05 Mjup and 1000 Mjup, and between 0.05 days and 1000 days respectively (dP = 0.05 days, dm sin(i) = 0.05 Mjup). As shown in Fig. 17, the result for the cluster star resembles the case of the field star more than in previous simulations. The reason is that in this case 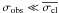 , which reflects the intrinsic dispersion of radial velocities of cluster stars. Then the condition on the mean radial velocity is not as efficient in constraining the period and mass of the orbiting companion as for higher observed σobs values. Still it is clear that a better result can be obtained than in the case of a field object.
, which reflects the intrinsic dispersion of radial velocities of cluster stars. Then the condition on the mean radial velocity is not as efficient in constraining the period and mass of the orbiting companion as for higher observed σobs values. Still it is clear that a better result can be obtained than in the case of a field object.
From our survey we have detected five stars having mean radial velocities consistent with the cluster recession velocity within 0.755 km s-1, as shown in Table 8. Moreover, they are all cluster turn-off stars, very likely cluster members on the basis of our proper motions and radial velocities, and do not present signs of photometric and spectroscopic variability. These objects are 40519, 45512, 44104, 45523, and 45267.
Star 39810, discussed above, may instead be more properly followedup using the same UVES/GIRAFFE spectrographs.
We note that star 45387 also has a small radial velocity dispersion, and it is a radial velocity variable, although this object is located in the blue straggler region, and the assumption on the mass of the primary may not be correct. The other close binary systems in our sample are more likely to host stellar companions.
Searching for substellar objects (brown dwarfs and Jupiter planets) with the radial velocity technique around old open cluster turn-off stars then appears feasible also with present-day instrumentation, but the following are necessary: (i) an efficient preselection of candidate cluster members (by means of colors, magnitudes, and possibly proper motions, and radial velocities); (ii) further identification of massive substellar objects, a task that can be accomplished using multi-object spectrographs like UVES/FLAMES. With just a few hours of observation (6 in our case), it is possible to easily cover most of the turn-off members and identify the best brown dwarf, massive planet candidates, providing at the same time a list of cluster stars that do not appear to be radial velocity variables at the precision of these instruments; (iii) this sample, cleaned of spurious field contaminants and of large mass-ratio binary systems, can be followedup with high-precision spectroscopy, at first using the same technique of UVES/FLAMES, and then covering more intensively only the most promising targets. The previous steps constitute a sort of roadmap towards detection of substellar objects in open cluster. Proceding by steps allows making more efficient use of observational time.
11. Conclusions
We have presented the results of the first multi-epoch radial velocity survey toward the old metal-rich open cluster NGC 6253 with the main goal of followingup on three transiting planetary candidates that we identified in our photometric campaigns. For our brightest planetary candidate (star 171895), we obtained three radial velocity measurements with the UVES spectrograph, which all appeared consistent within their errors (200 m/s), but were acquired at very similar orbital phases. The mean radial velocity of this object is not consistent with the mean radial velocity of cluster members. From the present measurements this system is most likely a field interloper despite its position at the cluster turn off region, unless it is a binary system with a period longer than our observing window. Additional photometric and high-precision spectroscopic measurements are clearly required to clarify the nature of this system. We were not able to derive radial velocities for star 56223 probably because of a bad fiber positioning. We noticed that ingress and egress phases of the transits do not appear to follow planetary models closely, and that there is evidence of out-of-transit variations. For star 23333 we acquired six radial velocity measurements at different orbital phases that allowed us to rule out the possibility that the observed transits are caused by a close-by stellar companion. However, given the faintness of the object, our measurements are not precise enough to derive an orbital fit and to analyze other possible scenarios. We concluded that this object is also worth being further analyzed spectroscopically in the future.
The mean radial velocity of the cluster is 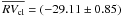 km s-1, where the error is the error of the mean and the rms is 4.26 km s-1, obtained from a sample of 25 cluster members. Using our photometry, proper motions, and radial velocities we identified 35 likely cluster members, populating the turn-off, subgiant, red-giant, red-clump, and blue straggler regions of the cluster. Among this sample, 12 objects are likely close binary systems of the cluster. We isolated five turn-off stars that are optimal targets to search for planetary mass companions with the high precision spectroscopy: stars 40519, 45512, 44104, 45523, 45267. We found a new turn-off eclipsing binary system: star 45368. We compared our results with previous literature radial velocity measurements of a few cluster members, finding in general a good agreement with our study. We showed that searching for substellar objects (brown dwarfs and Jupiter planets) with the radial velocity technique around old open cluster turn off stars also appears feasible with present-day instrumentation, but it is necessary (i) an efficient preselection of candidate cluster members (ii) further identification of likely massive substellar objects by means of multi-object spectroscopy (iii) subsequent follow-up of the best target stars by means of high-precision spectroscopy. We found that three observing epochs uniformly distributed over a period of 2.66 years give a good compromise between expected number of detectable planets and observing time. In Table 12 we report the cross-correlation among the star’s ID introduced in Montalto et al. (2009) and other authors and catalogs.
km s-1, where the error is the error of the mean and the rms is 4.26 km s-1, obtained from a sample of 25 cluster members. Using our photometry, proper motions, and radial velocities we identified 35 likely cluster members, populating the turn-off, subgiant, red-giant, red-clump, and blue straggler regions of the cluster. Among this sample, 12 objects are likely close binary systems of the cluster. We isolated five turn-off stars that are optimal targets to search for planetary mass companions with the high precision spectroscopy: stars 40519, 45512, 44104, 45523, 45267. We found a new turn-off eclipsing binary system: star 45368. We compared our results with previous literature radial velocity measurements of a few cluster members, finding in general a good agreement with our study. We showed that searching for substellar objects (brown dwarfs and Jupiter planets) with the radial velocity technique around old open cluster turn off stars also appears feasible with present-day instrumentation, but it is necessary (i) an efficient preselection of candidate cluster members (ii) further identification of likely massive substellar objects by means of multi-object spectroscopy (iii) subsequent follow-up of the best target stars by means of high-precision spectroscopy. We found that three observing epochs uniformly distributed over a period of 2.66 years give a good compromise between expected number of detectable planets and observing time. In Table 12 we report the cross-correlation among the star’s ID introduced in Montalto et al. (2009) and other authors and catalogs.
Online material
Journal of observations relative to the 2009 photometric campaign.
Journal of observations.
Proper motion cluster member stars.
Proper motion non members or stars with doubtful/undefined proper motions.
ID cross correlation table*.
 |
Fig. 1 The two UVES/MEDUSA configurations reported in the text. Circles denote the positions of the UVES/GIRAFFE targets. The rhombus corresponds to the VLT guide star, and the boxes to the four reference stars used by the Field Acquisition Coherent Bundle (FACB) guide fibers. The crosses represent instead the positions of the fibers allocated to the sky. |
See http://www.phys.appstate.edu/spectrum/spectrum.html for more details.
Acknowledgments
The authors are grateful to the anonynous referee for the numerous useful comments that have allowed a significant improvement in the paper. This work has been supported by grant reference PTDC/CTE-AST/098528/2008, and SFRH/BPD/71230/2010 funded by Fundação para a Ciência e a Tecnologia (FCT), Portugal. M. Montalto is grateful to Dr. Karsten Frank Brogaard of the Aarhus University for the insightful comments regarding the eclipsing binary system 45368. G. Piotto and S. Desidera acknowledge support by INAF through PRIN 2009 “Environmental effects in the formation and evolution of extrasolar planetary systems”.
References
- Alard, C. 2000, A&AS, 144, 363 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Alard, C., & Lupton, R. H. 1998, ApJ, 503, 325 [NASA ADS] [CrossRef] [Google Scholar]
- Anthony-Twarog, B. J., Twarog, B. A., & Mayer, L. 2007, AJ, 133, 1585 [NASA ADS] [CrossRef] [Google Scholar]
- Anthony-Twarog, B. J., Deliyannis, C. P., & Twarog, B. A. 2010, AJ, 139, 2034 [NASA ADS] [CrossRef] [Google Scholar]
- Ballester, G. E., Modigliani, A., Boitquin, O., et al. 2000, Msngr, 101, 31 [Google Scholar]
- Blecha, A., Cayatte, V., North, P., et al. 2000, SPIE, 4008, 467 [Google Scholar]
- Bordé, P., Bouchy, F., Deleuil, M., et al. 2010, A&A, 520, 66 [Google Scholar]
- Bragaglia, A., Tessicini, G., Tosi, M., et al. 1997, MNRAS, 284, 477 [NASA ADS] [CrossRef] [Google Scholar]
- Carraro, G., Mendez, R. A., & Costa, E. 2005a, MNRAS, 356, 647 [NASA ADS] [CrossRef] [Google Scholar]
- Carraro, G., Janes, K. A., & Eastman, J. D. 2005b, MNRAS, 364, 179 [NASA ADS] [CrossRef] [Google Scholar]
- Carretta, E., Bragaglia, A., Tosi, M., et al. 2000, ASPC, 198, 273 [NASA ADS] [Google Scholar]
- Carretta, E., Bragaglia, A., & Gratton, R. G. 2007, A&A, 473, 129 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Claret, A. 2000, A&A, 363, 1081 [NASA ADS] [Google Scholar]
- Cochran, W. D., Hatzes, A. P., & Paulson, D. B. 2002, AJ, 124, 565 [NASA ADS] [CrossRef] [Google Scholar]
- De Marchi, F., Poretti, E., Montalto, M., et al. 2010, A&A, 509, 17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Duquennoy, A., & Mayor, M. 1991, A&A, 248, 485 [NASA ADS] [Google Scholar]
- Endl, M., Cochran, W. D., Küruster, M., et al. 2006, ApJ, 649, 436 [NASA ADS] [CrossRef] [Google Scholar]
- Etzel, P. B. 1981, psbs.conf, 111 [Google Scholar]
- Fischer, D. A., & Valenti, J. 2005, ApJ, 622, 1102 [NASA ADS] [CrossRef] [Google Scholar]
- Gonzalez, G. 1998, A&A, 334, 221 [NASA ADS] [Google Scholar]
- Grundahl, F., Clausen, J. V., Hardis, S., et al. 2008, A&A, 492, 171 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hole, K. T., Geller, A. M., Mathieu, R. D., et al. 2009, AJ, 138, 159 [NASA ADS] [CrossRef] [Google Scholar]
- Jiang, I.-G., Yeh, L.-C., Chang, Y.-C., et al. 2010, ApJS, 186, 48 [NASA ADS] [CrossRef] [Google Scholar]
- Mermilliod, J.-C., Mayor, M., & Udry, S. 2009, A&A, 498, 949 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mandel, K., & Agol, E. 2002, ApJ, 580, 171 [Google Scholar]
- Montalto, M., Piotto, G., Desidera, S., et al. 2007, A&A, 470, 1137 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Montalto, M., Piotto, G., Desidera, S., et al. 2009, A&A, 505, 1129 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pasquini, L., Avila, G., Blecha, A., et al. 2002, Msngr, 110, 1 [Google Scholar]
- Piatti, A. E., Clariá, J. J., Bica, E., et al. 1998, AJ, 116, 801 [NASA ADS] [CrossRef] [Google Scholar]
- Pont, F., Bouchy, F., Melo, C., et al. 2005, A&A, 438, 1123 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Popper, D. M., & Etzel, P. B. 1981, AJ, 86, 102 [NASA ADS] [CrossRef] [Google Scholar]
- Ribas, I., & Miralda-Escudé 2007, A&A, 464, 779 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van Saders, J. L., & Gaudi, B. S. 2011, ApJ, 729, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Sagar, R., Munari, U., & de Boer, K. S. 2001, MNRAS, 327, 23 [NASA ADS] [CrossRef] [Google Scholar]
- Santos, N. C., Israelian, G., & Mayor, M. 2001, A&A, 373, 1019 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sato, B., Izumiura, H., Toyota, E., et al. 2007, ApJ, 661, 527 [NASA ADS] [CrossRef] [Google Scholar]
- Sestito, P., Randich, S., & Bragaglia, A. 2007, A&A, 465, 185 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Southworth, J., & Clausen, J. V. 2006, Ap&SS, 304, 199 [NASA ADS] [CrossRef] [Google Scholar]
- Southworth, J., Maxted, P. F. C., & Smalley, B. 2004a, MNRAS, 351, 1277 [NASA ADS] [CrossRef] [Google Scholar]
- Southworth, J., Maxted, P. F. C., & Smalley, B. 2004b, MNRAS, 355, 986 [NASA ADS] [CrossRef] [Google Scholar]
- Sommariva, V., Piotto, G., Rejkuba, M., et al. 2009, A&A, 493, 947 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stetson, P. B. 1987, PASP, 99, 191 [NASA ADS] [CrossRef] [Google Scholar]
- Tosi, M. 1996, in The Impact of Stellar Physics on Galaxy Evolution, ed. C. Leitherer, U. Fritze-von-Alvensleben, & J. Huchra (San Francisco: ASP), ASP Conf. Ser., 98, 299 [Google Scholar]
- Twarog, B. R., Anthony-Twarog, B. J., & De Lee, N. 2003, AJ, 125, 1383 [NASA ADS] [CrossRef] [Google Scholar]
- Wielen, R. 1971, A&A, 13, 309 [NASA ADS] [Google Scholar]
All Tables
Summary of the parameters derived for the 45368 eclipsing binary system, assuming i = 90° and e = 0.
All Figures
 |
Fig. 2 Observed radial velocity dispersions (σobs) against R-band magnitude. The continuous line indicates our best fit for the typical dispersion ( |
| In the text | |
 |
Fig. 3 Upper panel: radial velocity distribution of stars considered as cluster members on the basis of proper motions and radial velocities. Bottom panel: radial velocity distribution of all the remaining stars in the sample (see text). |
| In the text | |
 |
Fig. 4 V, B − V color magnitude diagram of proper motion cluster members of NGC 6253, with highlighted the positions of the three planetary transiting candidates discussed in the text. |
| In the text | |
 |
Fig. 5 Upper left: lightcurve of star 171895 relative to the 2004 observing season. Red points highlight transit epochs, also indicated by the roman numeration. Upper right: lightcurve of star 171895 relative to the 2009 observing season. Lower left, top panel: folded lightcurve. The continuous line indicates the best-fit model obtained using the Mandel & Agol (2002) algorithm, considering as properties of the host star those derived from the UVES spectroscopy. The roman numeration and the associated symbols are relative to the transit epochs shown in the upper panels. Lower left, bottom panel: observed minus model residuals. Lower right: UVES spectroscopic measurements. |
| In the text | |
 |
Fig. 6 Upper left: lightcurve of star 56223 relative to the 2004 observing season. Upper right: lightcurve of star 56223 relative to the 2009 observing season. Lower left panel, upper figure: folded lightcurve. The continuous line indicates the best-fit model obtained using the Mandel & Algol (2002) algorithm, assuming that the host star is a solar type star. Lower left panel, bottom figure: observed minus model residuals. Lower right panel: lightcurve folded with a period twice the best fitting period, showing the possible presence of out-of-transit variations. |
| In the text | |
 |
Fig. 7 Upper left: lightcurve of star 23333 relative to the 2004 observing season. Upper right: lightcurve of star 23333 relative to the 2009 observing season. Lower left: folded lightcurve. Lower right: UVES spectroscopic measurements. |
| In the text | |
 |
Fig. 8 R-band magnitude and B − R color for proper motion selected members (small black points). Red squares indicate stars that are also radial velocity members, steel blue squares stars that appear to be radial velocity non members, and black framed squares stars that are likely close binary systems. The continuous line indicates the best-fitting isochrone as discussed in Montalto et al. (2009), and the dashed line the equal mass binary stars sequence. |
| In the text | |
 |
Fig. 9 Same as Fig. 8, but for proper motion non-members or for stars whose proper motion membership probabilities are either doubtful or absent, as explained in the legend. |
| In the text | |
 |
Fig. 10 Folded light curve of the eclipsing binary system 45368. Black filled points are relative to the 2004 observing season, and red open circles to the 2009 observing season. |
| In the text | |
 |
Fig. 11 Fill black circles and open circles are UVES radial velocity measurements of the primary and secondary components of the 45368 binary system. The solid curve is the best-fitting model in phase with the primary eclipses. The dotted line is the best-fitting model in phase with the secondary eclipse. The dashed horizontal line indicates the baricentric velocity of the system (γ = −30.19 km s-1). |
| In the text | |
 |
Fig. 12 Probability of detecting a planet around a single turn-off star of NGC 6253, as a function of the planetary orbital period and different simulated HARPS observing strategies. The left panels show the results considering three observing epochs and the right panels considering six observing epochs, as reported by the labels at the top of each group of panels. Each small panel refers to one of the simulations presented in Table 7, as indicated by the inner numbers. |
| In the text | |
 |
Fig. 13 Same as Fig. 12, but in function of the planetary mass. |
| In the text | |
 |
Fig. 14 Radial velocities obtained for stars 39810 and 40519 located in the turn-off region. Dotted lines indicate the stars’ mean radial velocities ( |
| In the text | |
 |
Fig. 15 Period-mass probability distribution for the possible companion object of star 39810, obtained from orbital simulations, assuming the real observing epochs and circular obits. In the upper panel we show the results in the hypothesis that the star belongs to the cluster (as demonstrated by proper motions, radial velocities, and position in the CMD), whereas in the bottom panel we show the result if the star is a common field object: σobs = 1595 m/s, |
| In the text | |
 |
Fig. 16 Same as Fig. 15, assuming three observing epochs at t1 = 486 days, t2 = 972 days, and t3 = 1458 days and circular orbits, σobs = 1595 m/s, |
| In the text | |
 |
Fig. 17 Same as Fig. 15, assuming three observing epochs at t1 = 486 days, t2 = 972 days, and t3 = 1458 days, circular orbits, σobs = 50 m/s, |
| In the text | |
 |
Fig. 1 The two UVES/MEDUSA configurations reported in the text. Circles denote the positions of the UVES/GIRAFFE targets. The rhombus corresponds to the VLT guide star, and the boxes to the four reference stars used by the Field Acquisition Coherent Bundle (FACB) guide fibers. The crosses represent instead the positions of the fibers allocated to the sky. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.