| Issue |
A&A
Volume 534, October 2011
|
|
|---|---|---|
| Article Number | A16 | |
| Number of page(s) | 8 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201117597 | |
| Published online | 22 September 2011 | |
Spin-orbit measurements and refined parameters for the exoplanet systems WASP-22 and WASP-26⋆,⋆⋆
1
Astrophysics Group, Keele University, Staffordshire ST5 5BG, UK
e-mail: dra@astro.keele.ac.uk
2
SUPA, School of Physics and Astronomy, University of St. Andrews, North Haugh, Fife KY16 9SS, UK
3 Institut d’Astrophysique et de Géophysique, Université de Liège, 17 Allée du 6 Août, Bât. B5C, Liège 1, Belgium
4
Observatoire de Genève, Université de Genève, 51 Chemin des Maillettes, 1290 Sauverny, Switzerland
5
Oversky, 47 Allée des Palanques, 33127 Saint Jean d’Illac, France
Received: 30 June 2011
Accepted: 1 September 2011
We report on spectroscopic and photometric observations through transits of the exoplanets WASP-22b and WASP-26b, intended to determine the systems’ spin-orbit angles. We combine these data with existing data to refine the system parameters. We measure a sky-projected spin-orbit angle of 22 ± 16° for WASP-22b, showing the planet’s orbit to be prograde and, perhaps, slightly misaligned. We do not detect the Rossiter-McLaughlin effect of WASP-26b due to its low amplitude and observation noise. We place 3-σ upper limits on orbital eccentricity of 0.063 for WASP-22b and 0.050 for WASP-26b. After refining the drift in the systemic velocity of WASP-22 found by Maxted et al. (2010, AJ, 140, 2007), we find the third body in the system to have a minimum-mass of 5.3 ± 0.3 MJup (a3 / 5 AU)2, where a3 is the orbital distance of the third body.
Key words: binaries: eclipsing / planetary systems / stars: individual: WASP-22 / stars: individual: WASP-26
Based on observations made with the HARPS spectrograph on the 3.6-m ESO telescope (proposal 085.C-0393), the 0.6-m Belgian TRAPPIST telescope, and the CORALIE spectrograph and the Euler camera on the 1.2-m Euler Swiss telescope, all at the ESO La Silla Observatory, Chile.
The photometric time-series and radial velocity data used in this work are available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/534/A16
© ESO, 2011
1. Introduction
By taking spectra of a star whilst an exoplanet transits across it we can measure the sky-projected obliquity λ, where obliquity is the angle between the stellar rotation axis and the planetary orbital axis. As the planet obscures a portion of the rotating star it causes a distortion of the observed stellar line profile, which manifests as an anomalous radial-velocity (RV) signature known as the Rossiter-McLaughlin (RM) effect (Holt 1893; Rossiter 1924; McLaughlin 1924). The shape of the RM effect is sensitive to the path a planet takes across the disc of a star relative to the stellar spin axis, thus by observing it we can determine λ. If we can determine the stellar inclination with respect to the sky plane I then we can determine the system’s true obliquity Ψ. For example, the light curve of a photospherically active star may exhibit rotational modulation, from which the true stellar rotation velocity can be determined. This can be compared with the spectroscopically-determined, sky-projected rotation velocity to get the stellar inclination (e.g., Winn et al. 2007; Hellier et al. 2011).
It is thought that the obliquity of a short-period, giant planet is indicative of the manner by which it arrived in its current orbit from farther out, where it presumably formed. As the angular momenta of a star and its planet-forming disc both derive from that of their parent molecular cloud, stellar spin and planetary orbital axes are expected to at least initially be aligned. Migration via tidal interaction with the gas disc is expected to preserve this initial spin-orbit alignment (Lin et al. 1996; Marzari & Nelson 2009), but a significant fraction of the few dozen systems so far measured1 are misaligned and some are even retrograde (e.g., see Hébrard et al. 2011, and the references therein). Triaud et al. (2010) interpreted this as indicating that some or all close-in planets arrive in their orbits by a mixture of: planet-planet scattering and the Kozai mechanism, which can drive planets into eccentric, misaligned orbits; and tidal friction, which circularises and shortens orbits (e.g., Fabrycky & Tremaine 2007; Nagasawa et al. 2008; Matsumura et al. 2010; Naoz et al. 2011). Morton & Johnson (2011) found the current spin-orbit distribution to be well described by migration via a combination of such alignment-preserving and misaligning mechanisms.
Winn et al. (2010a) and Schlaufman (2010) showed that the stars in misaligned systems tend to be hot (Teff > 6250 K). Winn et al. (2010a) suggested that this indicates either that planetary formation and migration mechanisms depend on stellar mass, or that cooler stars, with their larger convective zones, are able to more effectively realign orbits via tidal dissipation. The number of possible exceptions to this trend is increasing, such as HAT-P-9 with Teff = 6350 K and λ = −16 ± 8°, though rather than having been realigned, such systems may simply have never been very misaligned (Moutou et al. 2011).
In addition to the scattering route, it has been suggested that misaligned systems can arise when stars are misaligned with their discs (Lai et al. 2011) or when discs are misaligned with their stars (Bate et al. 2010).
In this paper we present observations of spectroscopic and photometric transits of WASP-22b (Maxted et al. 2010, hereafter M10) and WASP-26b (Smalley et al. 2010, hereafter S10), from which we attempt to determine the obliquities and refine the parameters of the systems.
WASP-22b is a 0.59-MJup planet that transits its solar metallicity ([Fe/H] = 0.05 ± 0.08) G0V, V = 12.0 host star every 3.53 days. M10 found a linear trend in the RV measurements of WASP-22 suggestive of either a second planet, a low-mass M-dwarf or a white dwarf companion.
WASP-26b is a 1.03-MJup planet that transits its solar metallicity ([Fe/H] = − 0.02 ± 0.09) G0V, V = 11.3 host star every 2.76 days. S10 found WASP-26 to be a visual double with a K-type star, separated in the sky-plane by 3800 AU, and used it to infer a common age of 6 ± 2 Gyr.
2. Observations
2.1. Spectroscopic transits and orbits
A spectroscopic transit comprises a large number of RVs taken in quick succession, during which the target star may have a specific activity level that could bias the measured systemic velocity and hence the determination of λ. Typically, the stellar rotation period is much longer than the orbital period. So, to first order, stellar activity would manifest as a slow variation in the apparent RV of the system’s centre of mass, which is negligibly small on the time-scale of a transit. To mitigate against the potential effects of activity, we obtained spectra of the two host stars outside of transit on the nights of the measured RM effects, and to refine the planets’ masses and orbital eccentricities we obtained spectra across the full orbits.
We obtained spectra of WASP-22 and WASP-26 using the HARPS spectrograph on the ESO 3.6-m telescope at La Silla. Calibration spectra of the thorium-argon lamp were taken at the start of each night, thus avoiding contamination of the stellar spectra by the lamp. This is made possible by the stability of HARPS, which is at the 1 m s-1 night-1 level.
On 2009 Nov. 19, we obtained 20 spectra of WASP-22 through a transit with HARPS. The exposures were 15–20 min and the signal-to-noise ratio (SNR) per pixel at 550 nm was in the range 16–34, with 20 being typical. During the sequence, the airmass of the target decreased from 1.11 to 1.01 and then increased to 1.70. We sampled the full 3.53-day orbit of WASP-22b by obtaining a pair of spectra per night, well-spaced in time, on the night of the transit and on each of the preceeding three nights. With exposures of 30 min for these eight spectra, the SNR was 24–48.
On 2010 Sep. 12, we obtained 24 spectra of WASP-26 through a transit with HARPS. The exposures were 10–15 min and the SNR per pixel at 550 nm was in the range 10–32, with 22 being typical. During the sequence, the airmass of the target decreased from 1.62 to 1.03 and then increased to 1.08. As the focus was improved at BJD (UTC) = 2 455 451.641 the SNR and measurement precision improved, despite a decrease in the exposure time from 15 to 10 min. We sampled the full 2.76-day orbit of WASP-26b by obtaining six spectra over a period of five days around the transit. With exposures of 15–20 min, the SNR of these spectra was 26–40.
Stellar parameters.
 |
Fig. 1 a) The CORALIE (blue circles) and HARPS (green diamonds) RVs of WASP-22 from M10, and the HARPS RVs from this paper (brown diamonds). b) An expansion of the region around the spectroscopic transit, as measured by HARPS on 2009 Nov. 19. c) The transit light curves, from top to bottom, obtained by TRAPPIST on 2010 Nov. 18 and 2010 Dec. 2 through an I+z filter and by EulerCam on 2010 Dec. 2 through a Gunn r filter. The data obtained by TRAPPIST on 2010 Dec. 2 prior to the meridian flip are denoted by green triangles and blue dots denote the data obtained post-flip. In each panel, the data are phase-folded on the ephemeris given in Table 3 and the best-fitting models of Sect. 3 are superimposed. |
 |
Fig. 2 a) The CORALIE (blue circles) and HARPS (brown diamonds) RVs of WASP-26. b)–d) Expansions of the region around the spectroscopic transit, as measured by HARPS on 2010 Sep. 12, in which the RM effect is not modelled b), the RM effect is modelled and a prior is imposed on vsinIc), the RM effect is modelled without a prior on vsinId). e): The Sloan r′-band transit light curve obtained at Oversky on 2010 Oct. 28/29. |
After removing the instrumental blaze function (Triaud et al. 2010), RV measurements were computed for each star by weighted cross-correlation with a numerical G2-spectral template (Baranne et al. 1996; Pepe et al. 2005). These are available at the CDS. We ascribe the fact that the first five RVs in the transit sequence of WASP-26 are lower precision than the rest to higher airmass and poorer focus.
We also incorporated in our analysis the 37 CORALIE RVs and 6 HARPS spectra of WASP-22 reported in M10 and the 16 CORALIE RVs of WASP-26 reported in S10. For consistency with the new measurements, we recalculated RVs from the existing HARPS spectra of WASP-22 after removal of the instrumental blaze function, which had not been done previously. We present these recomputed RVs along with the new RVs in the online tables (at the CDS). The new and old RVs are plotted in Fig. 1a for WASP-22 and in Fig. 2a for WASP-26, folded on the ephemerides of Table 3.
We estimated the sky-projected stellar rotation velocity2vsinI from the HARPS spectra by fitting the profiles of several unblended Fe i lines. For this we determined an instrumental broadening of 0.060 ± 0.005 Å from telluric lines around 6300 Å and used the Bruntt et al. (2010) calibration to assume values for macroturbulence: vmac = 3.2 ± 0.3 km s-1 for WASP-22 and vmac = 3.0 ± 0.3 km s-1 for WASP-26. We obtained vsinI values of 4.5 ± 0.4 km s-1 for WASP-22 and 3.9 ± 0.4 km s-1 for WASP-26.
We determined the typical activity indices (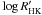 and SMW) of each star by measuring the weak emission in the cores of the Ca ii H+K lines in the HARPS spectra with the highest SNR per pixel at 550 nm: 13 spectra with SNR > 32 for WASP-22 and 11 spectra with SNR > 27 for WASP-26 (Noyes et al. 1984; Santos et al. 2000; Boisse et al. 2009). The values given in Table 1 are the averages and standard deviations of the values from individual spectra, determined using B − V values of 0.57 for WASP-22 and 0.59 for WASP-26. For each star, we estimated the true stellar-rotation period, Prot, using the activity-rotation calibration of Mamajek & Hillenbrand (2008), and combined this with the stellar radius derived in Sect. 3 to estimate the true stellar-rotation velocity, v (Table 1). For each star, the similarity of the values of v and vsinI suggests the stellar spin axis is not significantly inclined relative to the sky plane.
and SMW) of each star by measuring the weak emission in the cores of the Ca ii H+K lines in the HARPS spectra with the highest SNR per pixel at 550 nm: 13 spectra with SNR > 32 for WASP-22 and 11 spectra with SNR > 27 for WASP-26 (Noyes et al. 1984; Santos et al. 2000; Boisse et al. 2009). The values given in Table 1 are the averages and standard deviations of the values from individual spectra, determined using B − V values of 0.57 for WASP-22 and 0.59 for WASP-26. For each star, we estimated the true stellar-rotation period, Prot, using the activity-rotation calibration of Mamajek & Hillenbrand (2008), and combined this with the stellar radius derived in Sect. 3 to estimate the true stellar-rotation velocity, v (Table 1). For each star, the similarity of the values of v and vsinI suggests the stellar spin axis is not significantly inclined relative to the sky plane.
2.2. Photometric transits
The cadence of spectroscopic transit observations tends to be much lower than that of photometric observations and, at least for HARPS measurements of WASP systems, the spectroscopic exposure time tends to be similar to the durations of transit ingress and egress. As such, the accurate measurement of λ requires the times of the four transit contact points during the spectroscopic transit to be accurately determined. This is best achieved using high-quality photometric transit observations. As M10 presented only a partial transit of WASP-22b and as the two transits of WASP-26b presented by S10 were obtained nine months prior to the RM measurement, we obtained additional transit photometry of the two systems.
2.2.1. WASP-22b
We used TRAPPIST3, a 60-cm robotic telescope located at ESO La Silla (Gillon et al. 2011) to observe two transits of WASP-22b. Both transits were observed through a special I+z filter, in the 2 MHz read-out mode, and with 1 × 1 binning, resulting in a typical combined readout and overhead time of 8 s and a readout noise of 13.5 e−. With a pixel size of 15 × 15 μm, the pixel scale is 0.65″ pixel-1 and the field of view is 22 × 22′. The guiding system of TRAPPIST, based on absolute astrometry performed on each image, kept the stars at the same positions on the chip to within 3″ (5 pixels) over the course of the observations (Jehin et al. 2011).
The data from both transits were processed in the same way. After a standard pre-reduction (bias, dark and flat-field correction), the stellar fluxes were extracted from the images using the IRAF/DAOPHOT4 aperture photometry software (Stetson 1987). We tested several sets of reduction parameters and chose the set that gave the most precise photometry for the stars of similar brightness to WASP-22. We carefully selected a set of reference stars and then performed differential photometry.
The first transit of WASP-22b that we observed occurred on 2010 Nov. 18. We obtained little pre-transit data as the transit started soon after dusk. We also obtained little post-transit data as WASP-22 passed through the meridian soon after the transit ended, at which time a meridian flip would have been necessary as TRAPPIST uses a German equatorial mount. The post-flip light curve would thus have been of little value as, due to potential systematics, it would have needed to be detrended separately to the post-flip light curve. The second WASP-22b transit we observed occurred on 2010 Dec. 2. We needed to perform a meridian flip shortly after beginning observations and shortly before the transit began, so we divided the data into pre-flip and post-flip light curves.
We also observed the 2010 Dec. 2 transit of WASP-22b with EulerCam on the 1.2-m Swiss telescope at ESO La Silla. Installed at the Swiss telescope in September 2010, EulerCam uses a 4k × 4k, back-illuminated, deep-depletion e2V silicon chip. Read-out of the entire chip takes ~6 s in four-port mode and ~25 s in one-port mode. In both modes the readout noise is 5 electrons. The field of view of EulerCam is 15.6 × 15.6′, though the corners are shadowed by the filter wheel. With a pixel size of 15 × 15 μm the pixel scale is 0.23″ pixel-1. EulerCam employs a very similar guiding system to that of TRAPPIST. Details of EulerCam will be provided in Lendl et al. (in prep.).
We observed WASP-22 for 4.8 h through a Gunn r filter with slight defocus and using one-port readout (as there were issues with four-port readout at the time). Conditions were good, with a seeing of 0.5–1.0″. The target remained below airmass 1.8 as we observed from 35 min prior to the start of transit until 45 min after the transit ended. We bias-subtracted and flat-fielded the images before performing differential aperture photometry using a reference source created by co-adding the two most favourable reference stars.
The two transit light curves of WASP-22b from TRAPPIST and the one from Euler are shown in Fig. 1c. We also incorporated in our analysis of WASP-22 the photometry of M10: two seasons of WASP photometry covering the full orbit and a partial transit measured by Faulkes Telescope South through a Pan-STARRS z filter.
2.2.2. WASP-26b
We observed a full transit of WASP-26b on 2010 Oct 28/29 through a Sloan r′ filter using the SBIG STL-1001E CCD camera installed at the prime focus of the 0.35-m Celestron C14 Schmidt-Cassegrain telescope at the robotic Oversky Observatory, La Palma. The field of view is 19.9 × 19.9′ and the exposure time was 15 s, with only a small degree of defocus employed so as to avoid blending with a star located 15″ from the target. The data were processed using MUNIPACK5 and the transit light curve is shown in Fig. 2e.
We also incorporated in our analysis of WASP-26 the photometry of S10: two seasons of WASP photometry covering the full orbit and two full transits measured through a Pan-STARRS z filter, one by Faulkes Telescope North (FTN) and the other by Faulkes Telescope South (FTS). In-transit noise in the FTN light curve of S10 (see their Fig. 4) appears to have affected its normalisation. Thus, the transit depth and, in turn, the stellar and plantetary radii may have been biased. As such we chose to detrend that light curve using only the post-transit data. S10 noted that WASP-26 is blended in the WASP data with the common-proper-motion star located 15″ away that is ~2.5 mag fainter. We made an approximate correction to the WASP photometry for this contamination so as to prevent dilution of the transit.
3. Combined model and analysis
For each system, we determined the system parameters from a simultaneous fit to the data described in the previous section. The fit was performed using the current version of the Markov-chain Monte Carlo (MCMC) code described by Collier Cameron et al. (2007) and Pollacco et al. (2008).
Limb-darkening coefficients.
The transit light curves were modelled using the formulation of Mandel & Agol (2002) with the assumption that the planet is much smaller than the star. Limb-darkening was accounted for using a four-coefficient, nonlinear limb-darkening model, using coefficients appropriate to the passbands from the tabulations of Claret (2000, 2004). The coefficients were interpolated once using the values of log g∗ and [Fe/H] from M10 and S10 (Table 1), but were interpolated at each MCMC step using that step’s value of Teff. The coefficient values corresponding to the best-fitting value of Teff are given in Table 2. The transit light curve is parameterised by the epoch of mid-transit T0, the orbital period P, the planet-to-star area ratio (Rpl/R∗)2, the duration of the transit from initial to final contact T14, and the impact parameter b = acosi/R∗ (the distance, in fractional stellar radii, of the transit chord from the star’s centre in the case of a circular orbit), where a is the semimajor axis and i is the inclination of the orbital plane with respect to the sky plane. At each MCMC step, each light curve was decorrelated with a linear function of phase using singular value deconvolution. As noted in Sect. 2.2, we detrended the FTN transit of WASP-26b from S10 using only the post-transit data, specifically those measurements with an orbital phase greater than 1.018. From a fit to all data, this gives a slightly smaller (Rpl/R∗)2 of 0.01022 ± 0.00034 as compared to the 0.01075 ± 0.00033 obtained when detrending using the entire light curve. This results in slightly smaller derived stellar and planetary radii (1.303 ± 0.059 R⊙ cf. 1.334 ± 0.051 R⊙ and 1.281 ± 0.075 RJup cf. 1.346 ± 0.067 RJup).
The eccentric Keplerian RV orbit is parameterised by the stellar reflex velocity semi-amplitude K1, the systemic velocity γ, an instrumental offset between the HARPS and CORALIE spectrographs ΔγHARPS, a linear drift in the systemic velocity 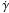 , and
, and 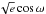 and
and 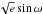 (Collier Cameron, in prep.), where e is orbital eccentricity and ω is the argument of periastron. The RM effect was modelled using the formulation of Giménez (2006) and is parameterised by
(Collier Cameron, in prep.), where e is orbital eccentricity and ω is the argument of periastron. The RM effect was modelled using the formulation of Giménez (2006) and is parameterised by 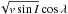 and
and 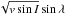 .
.
The linear scale of the system depends on the orbital separation a which, through Kepler’s third law, depends on the stellar mass M∗. At each step in the Markov chain, the latest values of ρ∗, Teff and [Fe/H] are input in to the empirical mass calibration of Enoch et al. (2010) to obtain M∗. The shapes of the transit light curves and the RV curve constrain ρ∗ (Seager & Mallén-Ornelas 2003), which combines with M∗ to give R∗. Teff and [Fe/H] are proposal parameters constrained by Gaussian priors, by means of Bayesian penalties on χ2, with mean values and variances derived directly from the stellar spectra (Table 1).
As the planet-star area ratio is determined from the measured transit depth, Rpl follows from R∗. The planet mass Mpl is calculated from the values of K1 and M∗, and planetary density ρpl and surface gravity log gpl then follow. We also calculate the ingress and egress durations, T12 and T34, and the planetary equilibrium temperature Teql, assuming zero albedo and efficient redistribution of heat from the planet’s presumed permanent day side to its night side.
At each step in the MCMC procedure, model transit light curves and RV curves are computed from the proposal parameter values, which are perturbed from the previous values by a small, random amount. The χ2 statistic is used to judge the goodness of fit of these models to the data and a step is accepted if χ2 is lower than for the previous step. A step with higher χ2 is accepted with a probability proportional to exp( − Δχ2/2), which gives the procedure some robustness against local minima and leads to the thorough exploration of the parameter space around the best-fitting solution. To give proper weighting to each photometry dataset, the uncertainties were scaled at the start of the MCMC so as to obtain a photometric reduced-χ2 of unity. With a similar purpose, a jitter term of 4 m s-1 was added in quadrature to the formal errors of the HARPS RVs of WASP-22, as may be due to stellar activity (though there is no evidence of this here), correlated noise or the finite number of data-points. This was determined from an initial MCMC from which the in-transit RVs were excluded. With spectroscopic reduced-χ2 values of less than unity, it was not necessary to add any jitter to the RVs of WASP-26.
To prevent a specific stellar activity level during a spectroscopic transit observation from biasing the fitting of the RM effect, RVs through a transit have previously been grouped separately to RVs spread over a long baseline (Triaud et al. 2010). WASP-22 and WASP-26 both appear to be chromospherically inactive though (M10; S10), so we grouped RVs only by spectrograph so as to be able to determine the rate of drift in the systemic velocity whilst allowing for an instrumental offset. We did check that this choice did not affect the spin-orbit determination. The systemic velocity at the time of the spectroscopic transit is set by the RVs taken around that time, thus assisting in the accurate measurement of the projected spin-orbit angle. In the case of WASP-22, combining these HARPS RVs with those measured a year prior results in an improved determination of the linear drift in the systemic velocity noted in M10 and in tighter constraints on orbital eccentricity.
For each system, the improvement in the fit to the RV data resulting from the use of an eccentric orbit model is small and is consistent with the underlying orbit being circular. We thus impose circular orbits, as is prudent to do for such short-period, Jupiter-mass planets in the absence of evidence to the contrary (e.g., Anderson et al. 2011). This did not result in significant differences in the best-fitting values of the system parameters or their associated uncertainties. The 3-σ upper limits on e are 0.063 for WASP-22b and 0.050 for WASP-26b.
We imposed a Gaussian prior on vsinI, by means of a Bayesian penalty on χ2, with mean and variance as determined from the HARPS spectra (see Sect. 2.1). For WASP-22, this prior prevents vsinI from wandering to unrealistically large values of up to 168 km s-1. This occurs due to a degeneracy between vsinI and λ when b is low: an RM effect with a similar amplitude and shape can result both when a planet transits near-parallel to the equator of a slowly rotating star and when a planet in a near-polar orbit transits a rapidly rotating star. The MCMC posterior distribution of vsinI and λ shown in Fig. 3a results when a prior is imposed, and the distribution shown in Fig. 3b results when no prior is imposed.
 |
Fig. 3 The MCMC posterior distributions of λ and vsinI for WASP-22 when a) a Gaussian prior of 4.5 ± 0.4 km s-1 is imposed on vsinI and b) no prior is imposed on vsinI. Note that, though the abscissa ranges of each graph are equal, the ordinate ranges are not. The white, blue and black contours are, respectively, the 1-, 2- and 3-σ confidence limits. The shading of each bin is proportional to the logarithm of the number of MCMC steps within. Aligned spin-orbit axes would have λ = 0°, which is marked by the dotted, brown line. |
We checked if the fitting of the RM effect, which involves the inclusion of the two parameters vsinI and λ, results in a significant improvement to the fit to the data for each system. For this we performed an F-test of the null hypothesis that we did not detect the RM effect, using a probability of P(F) = 0.05 as our significance threshold.
For WASP-22, we find a highly significant improvement to the fit when modelling the RM effect with a prior on vsinI: P(F) ~ 0. So, we have made a significant detection of the RM effect of the WASP-22 system, with λ = 22 ± 16°, which is clearly visible in the star’s RVs (Fig. 1b). Without the quadrature addition of the 4 m s-1 jitter term to the HARPS RVs, a value of λ = 25 ± 13° is obtained.
For WASP-26, we are unable to reject the null hypothesis as the data are fit equally well by both a model with no RM effect and by a model with the RM effect and a prior on vsinI, for which λ = 6 ± 6° (P(F) ~ 1; see Figs. 1b and c). When modelling the RM effect with no prior on vsinI, for which λ = 7 ± 50°, we find the improvement in the fit is too slight to reject the null hypothesis (P(F) = 0.50; Fig. 1d). Also, the resulting best-fitting projected stellar rotation speed (vsinI = 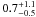 km s-1) is discrepant with the spectral determination (vsinI = 3.9 ± 0.4 km s-1). It can be seen in Fig. 2c that two in-transit RVs lie above the model. The seeing was poorer when those two measurements were obtained (1.1″) than during the rest of the RM sequence (0.5–0.8″). We explored excluding the four RVs (the two in-transit and two others outside of transit) with seeing greater than 1″, but found that a model with the RM effect and a prior on vsinI, for which λ = 13 ± 6°, was still not strongly favoured over a model with no RM effect: P(F) = 0.09. On the night of the RM measurement, three RVs were obtained prior to the re-focussing of the instrument. These data-points lie below the best-fitting model (Fig. 2). Having omitted these three RVs, a similar (slightly worse) fit to the RVs data resulted when fitting the RM effect with the prior on vsinI as compared to when not fitting the RM effect. As such, we did not make a significant detection of the RM effect for WASP-26 and we adopt a Keplerian orbit with no RM effect as our model for that system. We note, though, that in Fig. 2b there appears to be some structure in the in-transit RVs.
km s-1) is discrepant with the spectral determination (vsinI = 3.9 ± 0.4 km s-1). It can be seen in Fig. 2c that two in-transit RVs lie above the model. The seeing was poorer when those two measurements were obtained (1.1″) than during the rest of the RM sequence (0.5–0.8″). We explored excluding the four RVs (the two in-transit and two others outside of transit) with seeing greater than 1″, but found that a model with the RM effect and a prior on vsinI, for which λ = 13 ± 6°, was still not strongly favoured over a model with no RM effect: P(F) = 0.09. On the night of the RM measurement, three RVs were obtained prior to the re-focussing of the instrument. These data-points lie below the best-fitting model (Fig. 2). Having omitted these three RVs, a similar (slightly worse) fit to the RVs data resulted when fitting the RM effect with the prior on vsinI as compared to when not fitting the RM effect. As such, we did not make a significant detection of the RM effect for WASP-26 and we adopt a Keplerian orbit with no RM effect as our model for that system. We note, though, that in Fig. 2b there appears to be some structure in the in-transit RVs.
System parameters from RV and transit data from our adopted, circular solutions.
We explored the degree to which the new transit photometry was assisting in the fitting of the RM effect by excluding it from MCMCs for the two systems. For WASP-22b, the uncertainty in the transit mid-point at the epoch of the RM measurement was reduced from 3 to 1 min, and the uncertainty in the durations of the transit, ingress and egress fell from 6.5 to 1.4 min. For comparison, the ingress and egress durations are 20 min. Also reduced were the uncertainties in b (from 0.16 to 0.12) and Rpl/R∗ (from 0.024 to 0.013). These parameters, relevant to the fitting of the RM effect, and others were previously less certain due to the lack of available high-quality transit photometry. This led to the imposition of a main-sequence prior on the host star in M10, which was not imposed here in the MCMC omitting the new photometry. Without the new photometry 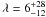 ° is obtained. For WASP-26b, the uncertainty in the transit mid-point at the epoch of the RM measurement was reduced from 2 to 1 min, and the uncertainty in the durations of the transit, ingress and egress fell from 7.7 to 1.4 min. The ingress and egress durations are 34 min.
° is obtained. For WASP-26b, the uncertainty in the transit mid-point at the epoch of the RM measurement was reduced from 2 to 1 min, and the uncertainty in the durations of the transit, ingress and egress fell from 7.7 to 1.4 min. The ingress and egress durations are 34 min.
By measuring the inclination of the stellar spin axis with respect to the sky plane I, we could determine the true, rather than the sky-projected, obliquity. A measurement of the stellar rotation period Prot, in combination with R∗, would give the stellar rotation velocity v. By comparing this to the sky-projected rotation velocity vsinI, determined from the spectra, we could obtain I. Prot can be measured if a star has an active photosphere that induces rotational modulation in its light curve (e.g., Hellier et al. 2011). However, M10 found no evidence for modulation in the WASP-22 light curves, and S10 found none in the WASP-26 light curves.
3.1. Results and discussion
The results of the MCMC model fits are presented in Table 3. The corresponding transit and orbit models are superimposed on the new transit light curves and on all RVs, respectively, in Fig. 1 for WASP-22 and in Fig. 2 for WASP-26.
With λ = 22 ± 16°, WASP-22b is in a prograde orbit around its host star. The best-fitting model suggests that the planetary orbital axis is slightly misaligned with the stellar spin axis, but the current uncertainty allows for quite a range in λ (Fig. 3a). The similarity of our estimates of vsinI and v (Table 1), which agrees with the prediction of Schlaufman (2010) that v = 3.2 ± 1.0 km s-1, suggests that the spin axis of WASP-22 is not significantly inclined relative to the sky plane (i.e., Ψ ~ λ). With Teff = 6000 ± 100 K, WASP-22 is consistent with the observation of Winn et al. (2010a) that the orbits of planets around stars cooler than ~6250 K tend to be aligned. Conversely, the orbits of planets around hotter stars tend to be misaligned, as noted by both Winn et al. (2010a) and Schlaufman (2010). A few possible expections to this trend are now known, including HAT-P-9 with Teff = 6350 K and λ = −16 ± 8° (Moutou et al. 2011). Though it may be that such systems were never very misaligned. Winn et al. (2010a) suggested the observed trend either indicates that planetary formation and migration mechanisms depend on stellar mass, or that the larger convective envelopes of cooler stars are able to more effectively realign with orbits via tidal dissipation, though this does depend on speculative, long-lived core-envelope decoupling.
M10 detected a linear trend of 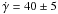 m s-1 in the RVs of WASP-22, which span a duration of 16 months. The new HARPS RVs presented herein make possible a more precise determination of the trend of
m s-1 in the RVs of WASP-22, which span a duration of 16 months. The new HARPS RVs presented herein make possible a more precise determination of the trend of 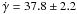 m s-1 (Fig. 4). We can obtain an order of magnitude estimate of the minimum mass of the third body, M3sini3, scaled by its orbital distance, a3, from the primary. Following Winn et al. (2010b), by assuming the third body to be in a near-circular orbit and to have a mass much smaller than that of the primary, we may set
m s-1 (Fig. 4). We can obtain an order of magnitude estimate of the minimum mass of the third body, M3sini3, scaled by its orbital distance, a3, from the primary. Following Winn et al. (2010b), by assuming the third body to be in a near-circular orbit and to have a mass much smaller than that of the primary, we may set 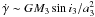 to obtain:
to obtain: 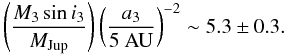 (1)The RM effect of WASP-26b, predicted to have a semi-amplitude of ~15 m s-1, was not detected with significance in our data, for which the median in-transit uncertainty was 7 m s-1. This was due to observation noise and the small amplitude of the signal. For comparison, we measured the semi-amplitude of the RM effect of WASP-22b to be ~30 m s-1, which agrees well with our prediction of 27 m s-1. The median in-transit RV uncertainty was 8 m s-1. The predicted amplitude of the RM effect of WASP-26b is smaller than that of WASP-22b due to the higher impact parameter and, to a lesser extent, the slower stellar rotation velocity. The similarity of our estimates of vsinI and v (Table 1), which agrees with the prediction of Schlaufman (2010) that v = 3.1 ± 0.3 km s-1, suggests that the spin axis of WASP-26 is not significantly inclined relative to the sky plane. Thus it is unlikely that the non-detection of the RM effect is due to the orientation of WASP-26 being close to pole-on. Though it is possible that the planet is in a polar orbit, it can not be transiting over the stellar spin axis as the impact parameter is non-zero. Hence, there will be an observable RM signal and thus further measurements are warranted.
(1)The RM effect of WASP-26b, predicted to have a semi-amplitude of ~15 m s-1, was not detected with significance in our data, for which the median in-transit uncertainty was 7 m s-1. This was due to observation noise and the small amplitude of the signal. For comparison, we measured the semi-amplitude of the RM effect of WASP-22b to be ~30 m s-1, which agrees well with our prediction of 27 m s-1. The median in-transit RV uncertainty was 8 m s-1. The predicted amplitude of the RM effect of WASP-26b is smaller than that of WASP-22b due to the higher impact parameter and, to a lesser extent, the slower stellar rotation velocity. The similarity of our estimates of vsinI and v (Table 1), which agrees with the prediction of Schlaufman (2010) that v = 3.1 ± 0.3 km s-1, suggests that the spin axis of WASP-26 is not significantly inclined relative to the sky plane. Thus it is unlikely that the non-detection of the RM effect is due to the orientation of WASP-26 being close to pole-on. Though it is possible that the planet is in a polar orbit, it can not be transiting over the stellar spin axis as the impact parameter is non-zero. Hence, there will be an observable RM signal and thus further measurements are warranted.
The available RVs of WASP-26 are not a very sensitive probe of a long-term drift as the CORALIE RVs span only 95 days and the HARPS RVs span only 5 days, with a gap of 1 year between the two datasets. Any drift could therefore have been taken up within the fitted instrumental offset between the two spectrographs. However, the similarity in the offsets for the two systems (Table 3) suggests that any drift in the systemic velocity of WASP-26 is likely to be smaller than that of WASP-22.
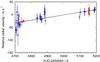 |
Fig. 4 Radial velocities of WASP-22 showing a linear drift in the systemic velocity of |
René Heller maintains a list of measurements and references at http://www.aip.de/People/rheller/content/main_spinorbit.html
TRAnsiting Planets and PlanetesImals Small Telescope; http://arachnos.astro.ulg.ac.be/Sci/Trappist
Acknowledgments
TRAPPIST is a project funded by the Belgian Fund for Scientific Research (Fond National de la Recherche Scientifique, FNRS) under the grant FRFC 2.5.594.09.F, with the participation of the Swiss National Science Fundation (SNF). M. Gillon and E. Jehin are FNRS Research Associates.
References
- Anderson, D. R., Collier Cameron, A., Gillon, M., et al. 2011 [arXiv:1105.3179] [Google Scholar]
- Baranne, A., Queloz, D., Mayor, M., et al. 1996, A&AS, 119, 373 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bate, M. R., Lodato, G., & Pringle, J. E. 2010, MNRAS, 401, 1505 [NASA ADS] [CrossRef] [Google Scholar]
- Boisse, I., Moutou, C., Vidal-Madjar, A., et al. 2009, A&A, 495, 959 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bruntt, H., Bedding, T. R., Quirion, P., et al. 2010, MNRAS, 405, 1907 [NASA ADS] [Google Scholar]
- Claret, A. 2000, A&A, 363, 1081 [NASA ADS] [Google Scholar]
- Claret, A. 2004, A&A, 428, 1001 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Collier Cameron, A., Wilson, D. M., West, R. G., et al. 2007, MNRAS, 380, 1230 [NASA ADS] [CrossRef] [Google Scholar]
- Enoch, B., Collier Cameron, A., Parley, N. R., & Hebb, L. 2010, A&A, 516, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fabrycky, D., & Tremaine, S. 2007, ApJ, 669, 1298 [NASA ADS] [CrossRef] [Google Scholar]
- Gillon, M., Jehin, E., Magain, P., et al. 2011, Detection and Dynamics of Transiting Exoplanets, St. Michel l’Observatoire, France, ed. F. Bouchy, R. Díaz, & C. Moutou, EPJ Web of Conferences, 11, 6002 [Google Scholar]
- Giménez, A. 2006, ApJ, 650, 408 [NASA ADS] [CrossRef] [Google Scholar]
- Hébrard, G., Ehrenreich, D., Bouchy, F., et al. 2011, A&A, 527, L11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hellier, C., Anderson, D. R., Collier-Cameron, A., et al. 2011, ApJ, 730, L31 [NASA ADS] [CrossRef] [Google Scholar]
- Holt, J. R. 1893, A&A, 12, 646 [Google Scholar]
- Jehin, E., Gillon, M., Queloz, D., et al. 2011, The Messenger, 145, 2 [NASA ADS] [Google Scholar]
- Lai, D., Foucart, F., & Lin, D. N. C. 2011, MNRAS, 412, 2790 [NASA ADS] [CrossRef] [Google Scholar]
- Lin, D. N. C., Bodenheimer, P., & Richardson, D. C. 1996, Nature, 380, 606 [NASA ADS] [CrossRef] [Google Scholar]
- Mamajek, E. E., & Hillenbrand, L. A. 2008, ApJ, 687, 1264 [NASA ADS] [CrossRef] [Google Scholar]
- Mandel, K., & Agol, E. 2002, ApJ, 580, L171 [NASA ADS] [CrossRef] [Google Scholar]
- Marzari, F., & Nelson, A. F. 2009, ApJ, 705, 1575 [NASA ADS] [CrossRef] [Google Scholar]
- Matsumura, S., Peale, S. J., & Rasio, F. A. 2010, ApJ, 725, 1995 [NASA ADS] [CrossRef] [Google Scholar]
- Maxted, P. F. L., Anderson, D. R., Gillon, M., et al. 2010, AJ, 140, 2007 [NASA ADS] [CrossRef] [Google Scholar]
- McLaughlin, D. B. 1924, ApJ, 60, 22 [NASA ADS] [CrossRef] [Google Scholar]
- Morton, T. D., & Johnson, J. A. 2011, ApJ, 729, 138 [NASA ADS] [CrossRef] [Google Scholar]
- Moutou, C., Diaz, R. F., Udry, S., et al. 2011, A&A, 533, A113 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nagasawa, M., Ida, S., & Bessho, T. 2008, ApJ, 678, 498 [NASA ADS] [CrossRef] [Google Scholar]
- Naoz, S., Farr, W. M., Lithwick, Y., Rasio, F. A., & Teyssandier, J. 2011, Nature, 473, 187 [NASA ADS] [CrossRef] [Google Scholar]
- Noyes, R. W., Weiss, N. O., & Vaughan, A. H. 1984, ApJ, 287, 769 [NASA ADS] [CrossRef] [Google Scholar]
- Pepe, F., Mayor, M., Queloz, D., et al. 2005, The Messenger, 120, 22 [NASA ADS] [Google Scholar]
- Pollacco, D., Skillen, I., Collier Cameron, A., et al. 2008, MNRAS, 385, 1576 [NASA ADS] [CrossRef] [Google Scholar]
- Rossiter, R. A. 1924, ApJ, 60, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Santos, N. C., Mayor, M., Naef, D., et al. 2000, A&A, 361, 265 [NASA ADS] [Google Scholar]
- Schlaufman, K. C. 2010, ApJ, 719, 602 [NASA ADS] [CrossRef] [Google Scholar]
- Seager, S., & Mallén-Ornelas, G. 2003, ApJ, 585, 1038 [NASA ADS] [CrossRef] [Google Scholar]
- Smalley, B., Anderson, D. R., Collier Cameron, A., et al. 2010, A&A, 520, A56 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stetson, P. B. 1987, PASP, 99, 191 [NASA ADS] [CrossRef] [Google Scholar]
- Triaud, A. H. M. J., Collier Cameron, A., Queloz, D., et al. 2010, A&A, 524, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Winn, J. N., Holman, M. J., Henry, G. W., et al. 2007, AJ, 133, 1828 [NASA ADS] [CrossRef] [Google Scholar]
- Winn, J. N., Fabrycky, D., Albrecht, S., & Johnson, J. A. 2010a, ApJ, 718, L145 [NASA ADS] [CrossRef] [Google Scholar]
- Winn, J. N., Johnson, J. A., Howard, A. W., et al. 2010b, ApJ, 718, 575 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 a) The CORALIE (blue circles) and HARPS (green diamonds) RVs of WASP-22 from M10, and the HARPS RVs from this paper (brown diamonds). b) An expansion of the region around the spectroscopic transit, as measured by HARPS on 2009 Nov. 19. c) The transit light curves, from top to bottom, obtained by TRAPPIST on 2010 Nov. 18 and 2010 Dec. 2 through an I+z filter and by EulerCam on 2010 Dec. 2 through a Gunn r filter. The data obtained by TRAPPIST on 2010 Dec. 2 prior to the meridian flip are denoted by green triangles and blue dots denote the data obtained post-flip. In each panel, the data are phase-folded on the ephemeris given in Table 3 and the best-fitting models of Sect. 3 are superimposed. |
| In the text | |
 |
Fig. 2 a) The CORALIE (blue circles) and HARPS (brown diamonds) RVs of WASP-26. b)–d) Expansions of the region around the spectroscopic transit, as measured by HARPS on 2010 Sep. 12, in which the RM effect is not modelled b), the RM effect is modelled and a prior is imposed on vsinIc), the RM effect is modelled without a prior on vsinId). e): The Sloan r′-band transit light curve obtained at Oversky on 2010 Oct. 28/29. |
| In the text | |
 |
Fig. 3 The MCMC posterior distributions of λ and vsinI for WASP-22 when a) a Gaussian prior of 4.5 ± 0.4 km s-1 is imposed on vsinI and b) no prior is imposed on vsinI. Note that, though the abscissa ranges of each graph are equal, the ordinate ranges are not. The white, blue and black contours are, respectively, the 1-, 2- and 3-σ confidence limits. The shading of each bin is proportional to the logarithm of the number of MCMC steps within. Aligned spin-orbit axes would have λ = 0°, which is marked by the dotted, brown line. |
| In the text | |
 |
Fig. 4 Radial velocities of WASP-22 showing a linear drift in the systemic velocity of |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


