| Issue |
A&A
Volume 534, October 2011
|
|
|---|---|---|
| Article Number | A17 | |
| Number of page(s) | 6 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201014357 | |
| Published online | 22 September 2011 | |
A relationship between the solar rotation and activity in the period 1998–2006 analysed by tracing small bright coronal structures in SOHO-EIT images
1
Physics Department, University of Rijeka Omladinska 14, 51000 Rijeka, Croatia
e-mail: jurdana@phy.uniri.hr; ipoljancic@phy.uniri.hr
2
Hvar Observatory, Faculty of Geodesy, University of Zagreb, Kačićeva 26, 10000 Zagreb, Croatia
e-mail: romanb@geof.hr
3
Kiepenheuer-Institut für Sonnenphysik, Schöneckstr. 6, 79104 Freiburg, Germany
e-mail: hw@kis.uni-freiburg.de
4
Institut für Physik, IGAM, Universität Graz, Universitätsplatz 5, 8010 Graz, Austria
e-mail: arnold.hanslmeier@uni-graz.at
5
Stanford University, HEPL, Stanford, CA 94305-4085, USA
e-mail: leif@leif.org
6
SIDC, Royal Observatory of Belgium, Ave. Circulaire 3, 1180 Brussels, Belgium
e-mail: sgissot@oma.be
Received: 5 March 2010
Accepted: 4 August 2011
Aims. The study aims to find a relationship between the rotation of the small bright coronal structures (SBCS) described by the solar rotation parameters and indices of solar activity on monthly and yearly temporal scales.
Methods. We analyse precise measurements of the solar differential rotation determined by tracing SBCS in SOHO-EIT images and compare the derived solar rotation parameters with the status of solar activity in the period 1998 − 2006. Full-disc solar images obtained with the Extreme ultraviolet Imaging Telescope (EIT) on board the Solar and Heliospheric Observatory (SOHO) were used to analyse solar differential rotation determined by tracing SBCS. An automatic method to identify and track the SBCS in EIT full-disc images with a six hour cadence is applied. We performed a statistical analysis of the monthly and yearly values of solar sidereal rotation velocity parameters A and B (corresponding to the equatorial rotation velocity and the gradient of the solar differential rotation, respectively) as a function of various solar activity indices.
Results. The dependence of the solar rotation on the phase of the solar cycle was found. It is clearly visible for the solar rotation parameter A, whilst the results are not conclusive for parameter B. The relationship between the solar rotation and activity, expressed by the monthly relative sunspot number, the smoothed monthly relative sunspot number, the yearly relative sunspot number, and the interdiurnal variability (IDV) index was investigated. The statistically significant correlation was found for the solar rotation parameter A, whilst a very low and insignificant correlation was obtained for the rotation parameter B.
Conclusions. During the maximum of the solar cycle 23 and just after it, the equatorial solar rotation velocity was lower than in other phases of the cycle, when there was less activity. This is consistent with other observational findings, obtained by different tracers and methods.
Key words: Sun: rotation / Sun: corona / Sun: activity
© ESO, 2011
1. Introduction
Measurements of the solar differential rotation provide precisely determined observational constraint on theoretical models of the solar convection zone and the solar MHD dynamo. The conservation of angular momentum, its transport to maintain the differential rotation profile, and an interplay with magnetic field are very important for understanding physical properties of the Sun and solar-type stars. Many indications of cycle-related variations in the solar rotation have been reported using different tracers and methods (e.g., Howard 1984; Schröter 1985; Snodgrass 1992; Stix 2002). Most often, sunspots and sunspot groups were used as tracers mainly because of the long term data sets available from various observatories. For the investigation of possible variations in the solar rotation, the Greenwich data set was used by Balthasar & Wöhl (1980), Arévalo et al. (1982), and Balthasar et al. (1986); the Kanzelhöhe data set by Lustig (1983); the Mt. Wilson data set by Gilman & Howard (1984) and by Hathaway & Wilson (1990); the Mitaka data set by Kambry & Nishikawa (1990); the Suzuka data set by Suzuki (1998); the extended Greenwich data set by Pulkkinen & Tuominen (1998), Javaraiah (2003), Zuccarello & Zappalá (2003), Javaraiah et al. (2005), Javaraiah & Ulrich (2006), and Brajša et al. (2006, 2007); the Kodaikanal data set by Gupta et al. (1999); and the Abastumani data set by Khutsishvili et al. (2002). Also, temporal variations in the solar rotation were studied using other features, e.g., magnetic fields (Sheeley et al. 1987; Brajša et al. 1992; Sheeley et al. 1992), coronal holes (Nash et al. 1988), observations of the corona in the green line (Rybák 1994; Altrock 2003), Hα filaments (Japaridze & Gigolashvili 1992; Brajša et al. 1997; Gigolashvili et al. 2003), microwave low-brightness-temperature regions (Brajša et al. 1997, 1999, 2000), and faculae (Meunier et al. 1997). Changes in the solar rotation were also investigated by the helioseismological method using the GONG and SOHO-MDI data at the base of the convective zone (Howe et al. 2000a,b, 2001) and at high latitudes (Antia & Basu 2001). Recently, the time-series analysis was applied to investigate temporal changes of the solar rotation, especially using the radio data (Heristchi & Mouradian 2009; Chandra et al. 2009). Various frequencies correspond to various altitudes in the solar corona and different methods have been used (e.g., the Sun analysed as a star with no latitudinal dependence, autocorrelation analysis with a time lag, etc.). However, it seems that up to now either a very weak or no correlation between the coronal rotational period and the sunspot activity can be verified (Vats et al. 2010; Chandra & Vats 2011). This result refers to the height of about 60 000 km and the observing frequency of 2.8 GHz.
If we adopt the working hypothesis of the corrrelation between the solar rotation and activity, then the strongest effect should have been observed during the Maunder minimum (1645 − 1715). In spite of many investigations (e.g., Eddy et al. 1976; Abarbanell & Wöhl 1981; Ribes & Nesme-Ribes 1993; Mendoza 1999; Vaquero et al. 2002; Casas et al. 2006), the results are still not conclusive, owing the general uncertainty of measurements in those times and the different time subintervals when particular observations were performed (just before or at the very beginning of the Maunder minimum, during the Maunder minimum, during the deep Maunder minimum, and just after the regular cycles started again). In addition, new discoveries and reductions of the observations from that time have often been reported. However, there is a strong evidence that sunspots rotated faster at low latitudes with a more pronounced differential profile during the Maunder minimum (Eddy et al. 1976).
In the present paper small bright coronal structures (SBCS) are used as tracers for the solar rotation determination and for a comparison of the deduced solar rotation parameters with indices of solar activity on monthly and yearly temporal scales. The main physical characteristics of SBCS were summarised by Brajša et al. (2004, 2008, and references therein), whilst their good latitudinal coverage on the Sun was described by, e.g. Brajša et al. (2005, and references therein). Solar rotation determined tracing SBCS and its comparison with the sidereal angular rotation velocity of subphotospheric layers were recently analysed by Zaatri et al. (2009) and by Wöhl et al. (2010, hereafter denoted as Paper I). In this work we use the same data set and the same automatic method of data reduction for the determination of the monthly and yearly solar rotation parameters, as in Paper I. Besides the automatic method of data reduction applied in the present work, in Paper I also the interactive method was used, the results of the two methods were compared, the north-south asymmetry of the solar rotation and the rigid rotational component at high solar latitudes were investigated. Also, a detailed comparison of the measured solar rotation of SBCS with the results of other tracers and methods was presented in Paper I. In the present paper we extend that analysis by studying the temporal evolution of the solar rotation determined tracing SBCS and a relationship between the solar rotation and activity during most of the 23rd solar cycle (1998 − 2006). As proxies for the solar activity we use the relative sunspot number (monthly, monthly smoothed and yearly values) and the strength of the interplanetary magnetic field represented by the interdiurnal variability (IDV) index (Svalgaard & Cliver 2005).
2. The SOHO-EIT data set and the automatic method of data reduction
Several thousand full-disc full resolution solar filtergrams recorded in the Fe XV line at the wavelength of 28.4 nm taken with the Extreme Ultraviolet Imaging Telescope (EIT) in the years 1998 − 2006 were analysed. In these images SBCS were identified and used as tracers for the solar rotation determination. The detailed description of the data set and the automatic method of data reduction are presented in Paper I (and references therein). The total amount of reduced data exceeds 50 000 triplets of SBCS (Paper I), which is of the same order of magnitude as the number of pairs of daily position measurements of sunspot groups analysed in the Greenwich Photoheliographic Results by Balthasar et al. (1986). In the present work we use the monthly and yearly parameters of the solar differential rotation published in Paper I and compare them with various solar activity proxies.
3. Results
3.1. Temporal evolution
As usually, the solar differential rotation is represented by 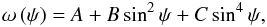 (1)where ω represents the angular rotation velocity expressed in deg/day, ψ the heliographic latitude, and A − C the solar rotation parameters. In the present work we put C = 0 to compare it with the indices of solar activity easier and to use the monthly and yearly differential rotation parameters from the Paper I.
(1)where ω represents the angular rotation velocity expressed in deg/day, ψ the heliographic latitude, and A − C the solar rotation parameters. In the present work we put C = 0 to compare it with the indices of solar activity easier and to use the monthly and yearly differential rotation parameters from the Paper I.
The time dependence of the solar sidereal differential rotation velocity parameters A and B for the time interval 1998 − 2006 was analysed and represented graphically. Monthly and annual dependences of the solar rotation parameters A and B are displayed in Figs. 1 and 2, respectively. Errors for the data concerning monthly values are given in Paper I.
On the time scale of months, the parameter A shows a slight increase after the activity maximum, and the parameter B shows no evidence of a statistically significant time dependence (Figs. 1 and 2). On the annual time scale, the variation in parameter A represented in Fig. 1 is more pronounced than those of the parameter B given in Fig. 2. Solar sidereal equatorial rotation velocity, represented by the parameter A, decreases up to the year 2003 and then the A values increases (Fig. 1).
3.2. A relationship between the solar rotation and activity
To examine correlation between the solar rotation and activity, we performed a statistical analysis of the monthly and yearly values of solar sidereal rotation velocity parameters A and B as a function of different solar activity indices. Solar activity was represented by the monthly relative sunspot number (SN), also called the Wolf number and monthly smoothed relative sunspot number (SSN). This data series is provided by the solar influences data analysis center (SIDC) of the Royal Observatory of Belgium (SIDC-team 1998 − 2006). The solar cycle dependence of solar sidereal rotation parameters Ast and Bst, obtained from selected stable structures, was also examined. The stable structures were identified by searching for pairs of triplets with a difference in latitude of less than 0.5 deg and continuing values in longitude, i.e., in the central meridian distance (CMD). In general, less than half of the structures were found to be stable (Paper I).
 |
Fig. 1 Solar sidereal rotation parameter A as function of time; monthly (black dots) and yearly values (open circles) with corresponding error bars for yearly values and typical mean value uncertainties given in the right corner of the figure. |
 |
Fig. 2 Solar sidereal rotation parameter B as function of time; monthly (black dots) and yearly values (open circles) with corresponding error bars for yearly values and typical uncertainties given in the right corner of the figure. |
Statistical results for monthly and yearly solar sidereal rotation velocity parameters A and B as functions of solar activity.
 |
Fig. 3 Solar sidereal rotation parameter A as function of the relative sunspot number (SN); monthly (black dots, full line) and yearly values (open circles, dotted line). Typical uncertainties are given in the right corner of the figure. |
 |
Fig. 4 Solar sidereal rotation parameter B as function of the relative sunspot number (SN); monthly (black dots, full line) and yearly values (open circles, dotted line). Typical uncertainties are given in the right corner of the figure. |
 |
Fig. 5 Monthly values of the solar sidereal rotation parameter A as a function of the monthly smoothed relative sunspot number (SSN). Typical uncertainty is given in the right corner of the figure. |
 |
Fig. 6 Monthly values of the solar sidereal rotation parameter B as a function of the monthly smoothed relative sunspot number (SSN). Typical uncertainty is given in the right corner of the figure. |
The statistical analysis for the annual values of the solar sidereal rotation parameters A and B have been determined as a function of the solar activity (represented with SN and SSN) and also as a function of the interplanetary magnetic field strength, derived from the IDV index (Svalgaard & Cliver 2005). The following values were calculated in the statistical analysis: the correlation coefficient ρ, the slope of the straight lines fitted through the statistical set of data points b, and the corresponding standard error Mb. The values are given in Table 1 and represented in Figs. 3 − 8. Typical uncertainties are also given in these figures. In Figs. 7, 8 the error bars are not repeated, since they are the same as in previous cases for the yearly values.
According to results given in Table 1 and displayed in Figs. 3 − 8 we obtained the highest correlation between the solar sidereal rotation parameter A and the yearly activity proxies. Generally, solar sidereal rotation parameters obtained from selected stable structures Ast and Bst have lower correlations with solar activity than the parameters A and B. However, the parameter Bst shows slightly higher correlation with solar activity in comparison with the parameter B. Concerning yearly data, the correlation of the parameter A with the relative sunspot number (SN), and the interplanetary magnetic field strength derived from the IDV index is very high, and in all cases correlation coefficient ρ exceeds 0.80.
 |
Fig. 7 Yearly values of the solar sidereal rotation parameter A as a function of the interplanetary magnetic field strength derived from the interdiurnal variability (IDV) index. |
 |
Fig. 8 Yearly values of the solar sidereal rotation parameter B as a function of interplanetary magnetic field strength derived from the interdiurnal variability (IDV) index. |
4. Discussion, interpretation, and conclusion
In this paper we have found a dependence of the solar rotation on the phase of the solar cycle (Figs. 1, 2). This is clearly visible for the solar rotation parameter A, corresponding to the equatorial rotation velocity (Fig. 1), whilst the results are not conclusive for the gradient of the solar differential rotation, expressed by parameter B (Fig. 2). As expected, these results are visible more clearly when the yearly values (Figs. 1, 2) are considered instead of the monthly values (Figs. 1, 2), where the noise is much greater.
We note that Gissot (2009) developed an automatic procedure for identifying and tracking structures in sequences of full-disc solar images. This procedure is based on a tracking algorithm of solar features derived from wavelet transformation of the images. Among various subtopics, that procedure was applied to determining the solar rotation using the archive of EIT He II 30.4 nm images that now covers more than the 23rd solar cycle. As in the present paper, stronger noise was found in the temporal evolution of the rotation parameter B than of the rotation parameter A. In spite of some similarities, the dependence of the solar rotation parameter A on the time is not the same for the two investigations (present work and Gissot 2009).
Furthermore, a relationship between the solar rotation and activity, expressed by different proxies (the monthly relative sunspot number, the smoothed monthly relative sunspot number, the yearly relative sunspot number, and the IDV index) was also investigated. These results are presented in Table 1 and in Figs. 3 − 8. Again, the statistically significant correlation was found for the solar rotation parameter A, whilst a very low and insignificant correlation was obtained for rotation parameter B. As can be seen in Table 1, the slope of the linear least-square fitting is statistically significant on the 3σ level for all cases where the parameter A is considered. For them, the correlation coefficient is in the range from 0.34 to 0.57 for the monthly values and in the range from 0.83 to 0.85 for the yearly values (Table 1), clearly indicating a higher correlation when the yearly values are considered. Statistical significance of correlations was determined testing the null hypothesis (ρ = 0, “no correlation exists”) at the level of 0.05. For monthly values the degree of freedom is 91. As seen from Table 1 calculated test parameter t is for all “A-correlations” greater than Student’s distribution value of t at a chosen level of significance of say t(0.05,91) = 1.64; therefore, the null hypothesis is rejected. On the other hand, all calculated values of t for “B-correlations” except for the Bst = f(SN) dependence given in Table 1 are lower than the value t(0.05,91) = 1.64. Therefore for B values the null hypothesis is accepted in all cases except for Bst = f(SN). For yearly values, where the degree of freedom is 7 and t(0.05,7) = 1.89 the null hypothesis is rejected for both A correlations and accepted for both B correlations (Press et al. 1989).
Our most important result is that during the maximum of the solar cycle 23 and just after it, the equatorial solar rotation velocity, expressed by the rotation parameter A, was lower than in other phases of the cycle, when there was less activity. This agrees with the high correlation between the rotation parameter A and various indices of solar activity. This result is consistent with many other observational findings, obtained by different tracers and methods, so a higher average rotation velocity in activity minima was found by many authors who analysed the solar rotation using various sunspot data series by different methods (Lustig 1983; Gilman & Howard 1984; Balthasar et al. 1986; Hathaway & Wilson 1990; Gupta et al. 1999; Khutsishvili et al. 2002; Zuccarello & Zappalá 2003; Brajša et al. 2006). Moreover, Chandra et al. (2010) measured the differential rotation of the soft X-ray solar corona and investigated its variation with the solar activity. They find that the equatorial rotation velocity correlates well with the corresponding solar cycle phase, whilst parameters B and C do not show any systematic variations. Our results obtained in the present paper agree with the results of Chandra et al. (2010).
Another implication of the correlation between the solar rotation and activity is a higher solar rotation that should have been observed during the Maunder minimum. Some modern analyses of the data from the period of Maunder minimum suggest exactly this type of behaviour, although there is no general agreement on this topic, as we have seen in Sect. 1. Since the floor of the interplanetary magnetic field is about 4 nT, this is an expected value for the Maunder minimum (Svalgaard & Cliver 2007, 2010), and we can find a corresponding value for the solar rotation parameter A, describing the equatorial rotation velocity, from Fig. 7. It is about 0.2 deg/day higher than average value for sunspots in usual solar activity conditions and in good agreement with the value reported by Eddy et al. (1976) for the Maunder minimum.
We note that the equatorial rotation velocity of SBCS, averaged over the whole observing period 1998 − 2006, is very similar to the equatorial rotation velocity of sunspots and sunspot groups (solar rotation parameter A, Table 16 in Paper I), so the solar rotation parameter A determined tracing SBCS is a very good proxy for the solar equatorial rotation determined by sunspots and sunspot groups.
The most probable theoretical interpretation of the observed phenomena is based on the interaction between the solar differential rotation and magnetic field, as discussed in detail in the papers by Brajša et al. (2006, 2007, and references therein). A higher rotation velocity at low latitudes is consistent with a lower magnetic activity on the Sun. This is the result of the numerical simulations performed by Brun (2004), and by Brun et al. (2004), in agreement with an analytical approach to solve the angular momentum equation (Lanza 2006, 2007).
Finally, we can raise the question why in our analysis no significant dependence of the differential rotation parameter B on time and/or on the activity level was found. During the periods of high magnetic activity on the Sun, a more rigid (i.e., a less differential) rotational component should be observed, yielding a lower absolute B value (Brun 2004; Lanza 2007). The most probable explanation for our lack of finding this is that to determine the solar rotation parameters we used data from all latitudes, even in polar regions, i.e., above 80 deg of latitude (Paper I). At those high latitudes the noise and various sources of systematic errors are much larger than at the low latitudes, so these effects smear the variations of the parameter B, whilst having barely any influence on the parameter A. Also, the effect of the height of the tracers on the measured rotation velocity increases with the latitude and has the strongest influence in polar regions (e.g., Roša et al. 1998). Moreover, the north-south rotational asymmetry in our data set is much greater at medium and high latitudes than at the lower ones (Paper I). As a suggestion for a future work, we will repeat the analysis by imposing different cut-offs in the latitude (especially excluding the polar regions) and performing the data reduction separately for the two solar hemispheres.
Acknowledgments
This project was started with the support of the Alexander von Humboldt Foundation and is related to the SOHO-EIT Proposal Brajsa_206: “an analysis of the solar rotation velocity by tracing coronal features” (http://umbra.nascom.nasa.gov/eit/proposals/) submitted in March 1999 by R. Brajša, B. Vršnak, V. Ruždjak, D. Roša, H. Wöhl, & F. Clette. SOHO is a project of international cooperation between ESA and NASA. We would like to thank the EIT team for developing and operating the instrument, and F. Clette, J.-F. Hochedez, and J. de Patoul for providing the EIT images and helpful discussions. The authors would also like to thank E. W. Cliver and J. Rybák for useful comments and suggestions. This work is sponsored by the Air Force Office of Scientific Research, Air Force Material Command, USAF, under grant number FA8655-07-1-3093. Further, the research leading to the results presented in this paper has partly received funding from European Community’s Seventh Framework Programme (FP7/2007 − 2013) under grant agreement No. 218816, and R.B. and A.H. acknowledge also the support from the Austrian-Croatian Bilateral Scientific Project, whilst S.F.G. acknowledges the support from the Belgian government through ESA-PRODEX.
References
- Abarbanell, C., & Wöhl, H. 1981, Sol. Phys., 70, 197 [NASA ADS] [CrossRef] [Google Scholar]
- Altrock, R. C. 2003, Sol. Phys., 213, 23 [NASA ADS] [CrossRef] [Google Scholar]
- Antia, H. M., & Basu, S. 2001, ApJ, 559, L67 [NASA ADS] [CrossRef] [Google Scholar]
- Arévalo, M. J., Gomez, R., Vázquez, M., Balthasar, H., & Wöhl, H. 1982, A&A, 111, 266 [NASA ADS] [Google Scholar]
- Balthasar, H., & Wöhl, H. 1980, A&A, 92, 111 [NASA ADS] [Google Scholar]
- Balthasar, H., Vázquez, M., & Wöhl, H. 1986, A&A, 155, 87 [NASA ADS] [Google Scholar]
- Brajša, R., Vršnak, B., Ruždjak, V., et al. 1992, Hvar Obs. Bull., 16, 13 [NASA ADS] [Google Scholar]
- Brajša, R., Ruždjak, V., Vršnak, B., et al. 1997, Sol. Phys., 171, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Brajša, R., Ruždjak, V., Vršnak, B., et al. 1999, Sol. Phys., 184, 281 [NASA ADS] [CrossRef] [Google Scholar]
- Brajša, R., Ruždjak, V., Vršnak, B., et al. 2000, Sol. Phys., 196, 279 [NASA ADS] [CrossRef] [Google Scholar]
- Brajša, R., Wöhl, H., Vršnak, B., et al. 2004, A&A, 414, 707 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brajša, R., Wöhl, H., Vršnak, B., et al. 2005, Sol. Phys., 231, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Brajša, R., Ruždjak, D., & Wöhl, H. 2006, Sol. Phys., 237, 365 [NASA ADS] [CrossRef] [Google Scholar]
- Brajša, R., Wöhl, H., Ruždjak, D., et al. 2007, Astron. Nachr., 328, 1013 [NASA ADS] [CrossRef] [Google Scholar]
- Brajša, R., Wöhl, H., Vršnak, B., et al. 2008, CEAB, 32, 165 [Google Scholar]
- Brun, A. S. 2004, Sol. Phys., 220, 333 [NASA ADS] [CrossRef] [Google Scholar]
- Brun, A. S., Miesch, M. S., & Toomre, J. 2004, ApJ, 614, 1073 [NASA ADS] [CrossRef] [Google Scholar]
- Casas, R., Vaquero, J. M., & Vázquez, M. 2006, Sol. Phys., 234, 379 [Google Scholar]
- Chandra, S., & Vats, H. O. 2011, MNRAS, 414, 3158 [NASA ADS] [CrossRef] [Google Scholar]
- Chandra, S., Vats, H. O., & Iyer, K. N. 2009, MNRAS, 400, L34 [NASA ADS] [Google Scholar]
- Chandra, S., Vats, H. O., & Iyer, K. N. 2010, MNRAS, 407, 1108 [NASA ADS] [CrossRef] [Google Scholar]
- Eddy, J. A., Gilman, P. A., & Trotter, D. E. 1976, Sol. Phys., 46, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Gigolashvili, M. S., Mdzinarishvili, T. G., Japaridze, D. R., & Chargeishvili, B. B. 2003, New Astron., 8, 529 [NASA ADS] [CrossRef] [Google Scholar]
- Gilman, P., & Howard, R. 1984, ApJ, 283, 385 [NASA ADS] [CrossRef] [Google Scholar]
- Gissot, S. 2009, in Ph.D. Thesis, Université Catholique de Louvain, Ch. 5, 79 [Google Scholar]
- Gupta, S. S., Sivaraman, K. R., & Howard, R. F. 1999, Sol. Phys., 188, 225 [NASA ADS] [CrossRef] [Google Scholar]
- Hathaway, D. H., & Wilson, R. M. 1990, ApJ, 357, 271 [NASA ADS] [CrossRef] [Google Scholar]
- Heristchi, D., & Mouradian, Z. 2009, A&A, 497, 835 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Howard, R. 1984, ARA&A, 22, 131 [NASA ADS] [CrossRef] [Google Scholar]
- Howe, R., Christensen-Dalsgaard, J., Hill, F., et al. 2000a, Science, 287, 2456 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Howe, R., Christensen-Dalsgaard, J., Hill, F., et al. 2000b, ApJ, 533, L163 [NASA ADS] [CrossRef] [Google Scholar]
- Howe, R., Hill, F., Komm, R. W., et al. 2001, in Recent insights into the physics of the Sun and heliosphere: Highlights from SOHO and other space missions, ed. P. Brekke, B. Fleck, & J. Gurman (San Francisco: ASP), 40 [Google Scholar]
- Japaridze, D. R., & Gigolashvili, M. S. 1992, Sol. Phys., 141, 267 [NASA ADS] [CrossRef] [Google Scholar]
- Javaraiah, J. 2003, Sol. Phys., 212, 23 [NASA ADS] [CrossRef] [Google Scholar]
- Javaraiah, J., & Ulrich, R. K. 2006, Sol. Phys., 237, 245 [NASA ADS] [CrossRef] [Google Scholar]
- Javaraiah, J., Bertello, L., & Ulrich, R. K. 2005, Sol. Phys., 232, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Kambry, M. A., & Nishikawa, J. 1990, Sol. Phys., 126, 89 [NASA ADS] [CrossRef] [Google Scholar]
- Khutsishvili, E. V., Gigolashvili, M. S., & Kvernadze, T. M. 2002, Sol. Phys., 206, 219 [NASA ADS] [CrossRef] [Google Scholar]
- Lanza, A. F. 2006, MNRAS, 373, 819 [NASA ADS] [CrossRef] [Google Scholar]
- Lanza, A. F. 2007, A&A, 471, 1011 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lustig, G. 1983, A&A, 125, 355 [NASA ADS] [Google Scholar]
- Mendoza, B. 1999, Sol. Phys., 188, 237 [NASA ADS] [CrossRef] [Google Scholar]
- Meunier, N., Nesme-Ribes, E., & Grosso, N. 1997, A&A, 319, 673 [NASA ADS] [Google Scholar]
- Nash, A. G., Sheeley, N. R. J., & Wang, Y.-M. 1988, Sol. Phys., 117, 359 [NASA ADS] [CrossRef] [Google Scholar]
- Press, W. H., Flannery, B. P., Teukolsky, S. A., & Vetterling, W. T. 1989, Numerical Recipes in Pascal (Cambridge University Press), 498 [Google Scholar]
- Pulkkinen, P., & Tuominen, I. 1998, A&A, 332, 755 [NASA ADS] [Google Scholar]
- Ribes, J. C., & Nesme-Ribes, E. 1993, A&A, 276, 549 [NASA ADS] [Google Scholar]
- Roša, D., Vršnak, B., Božić, H., et al. 1998, Sol. Phys., 179, 237 [NASA ADS] [CrossRef] [Google Scholar]
- Rybák, J. 1994, Sol. Phys., 152, 161 [NASA ADS] [CrossRef] [Google Scholar]
- Schröter, E.-H. 1985, Sol. Phys., 100, 141 [NASA ADS] [CrossRef] [Google Scholar]
- Sheeley, N. R. J., Nash, A. G., & Wang, Y.-M. 1987, ApJ, 319, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Sheeley, N. R. J., Wang, Y.-M., & Nash, A. G. 1992, ApJ, 401, 378 [NASA ADS] [CrossRef] [Google Scholar]
- SIDC-team 1998 − 2006, World Data Center for the Sunspot Index, Monthly Report on the International Sunspot Number, Online catalogue of the sunspot index, Royal Observatory of Belgium, http://www.sidc.be/sunspot-data [Google Scholar]
- Snodgrass, H. 1992, in The Solar Cycle, ed. K. Harvey (San Francisco: ASP), ASP Conf. Ser., 27, 205 [Google Scholar]
- Stix, M. 2002, in The Sun (Berlin: Springer-Verlag), 2nd edn., 277 [Google Scholar]
- Suzuki, M. 1998, Sol. Phys., 178, 259 [NASA ADS] [CrossRef] [Google Scholar]
- Svalgaard, L., & Cliver, E. 2005, J. Geophys. Res., 110, A12103 [NASA ADS] [CrossRef] [Google Scholar]
- Svalgaard, L., & Cliver, E. 2007, ApJ, 661, L203 [Google Scholar]
- Svalgaard, L., & Cliver, E. 2010, J. Geophys. Res., 115, A09111 [Google Scholar]
- Vaquero, J. M., Sánchez-Bajo, F., & Gallego, M. C. 2002, Sol. Phys., 207, 219 [NASA ADS] [CrossRef] [Google Scholar]
- Vats, H. O., Chandra, S., & Iyer, K. N. 2010, in Magnetic Coupling between the Interior and Atmosphere of the Sun, ed. S. S. Hasan, & R. J. Rutten (Berlin Heidelberg: Springer), 526 [Google Scholar]
- Wöhl, H., Brajša, R., Hanslmeier, A., & Gissot, S. 2010, A&A, 520, A29 (Paper I) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zaatri, A., Wöhl, H., Roth, M., Corbard, T., & Brajša, R. 2009, A&A, 504, 589 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zuccarello, F., & Zappalá, R. 2003, Astron. Nachr., 324, 464 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Statistical results for monthly and yearly solar sidereal rotation velocity parameters A and B as functions of solar activity.
All Figures
 |
Fig. 1 Solar sidereal rotation parameter A as function of time; monthly (black dots) and yearly values (open circles) with corresponding error bars for yearly values and typical mean value uncertainties given in the right corner of the figure. |
| In the text | |
 |
Fig. 2 Solar sidereal rotation parameter B as function of time; monthly (black dots) and yearly values (open circles) with corresponding error bars for yearly values and typical uncertainties given in the right corner of the figure. |
| In the text | |
 |
Fig. 3 Solar sidereal rotation parameter A as function of the relative sunspot number (SN); monthly (black dots, full line) and yearly values (open circles, dotted line). Typical uncertainties are given in the right corner of the figure. |
| In the text | |
 |
Fig. 4 Solar sidereal rotation parameter B as function of the relative sunspot number (SN); monthly (black dots, full line) and yearly values (open circles, dotted line). Typical uncertainties are given in the right corner of the figure. |
| In the text | |
 |
Fig. 5 Monthly values of the solar sidereal rotation parameter A as a function of the monthly smoothed relative sunspot number (SSN). Typical uncertainty is given in the right corner of the figure. |
| In the text | |
 |
Fig. 6 Monthly values of the solar sidereal rotation parameter B as a function of the monthly smoothed relative sunspot number (SSN). Typical uncertainty is given in the right corner of the figure. |
| In the text | |
 |
Fig. 7 Yearly values of the solar sidereal rotation parameter A as a function of the interplanetary magnetic field strength derived from the interdiurnal variability (IDV) index. |
| In the text | |
 |
Fig. 8 Yearly values of the solar sidereal rotation parameter B as a function of interplanetary magnetic field strength derived from the interdiurnal variability (IDV) index. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


