| Issue |
A&A
Volume 533, September 2011
|
|
|---|---|---|
| Article Number | A102 | |
| Number of page(s) | 6 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/201117413 | |
| Published online | 07 September 2011 | |
Discovery of gamma- and X-ray pulsations from the young and energetic PSR J1357−6429 with Fermi and XMM-Newton
1
Université Bordeaux 1, CNRS/IN2P3, Centre d’Études Nucléaires de Bordeaux
Gradignan,
33175
Gradignan,
France
e-mail: lemoine@cenbg.in2p3.fr; smith@cenbg.in2p3.fr
2
Space Science laboratory, Universities Space Research
Association, NASA MSFC
VP62, Huntsville,
AL
35805,
USA
e-mail: vyacheslav.zavlin-1@nasa.gov
3
Institut für Astronomie und Astrophysik, Universität
Tübingen, 72076
Tübingen,
Germany
e-mail: grondin@astro.uni-tuebingen.de
4
CSIRO Astronomy and Space Science, Australia Telescope National
Facility, Epping
NSW
1710,
Australia
e-mail: Ryan.Shannon@csiro.au
5 INAF – Cagliari Astronomical Observatory, 09012 Capoterra
( CA), Italy
6
Columbia Astrophysics Laboratory, Columbia
University, New York,
NY
10027,
USA
7
Laboratoire Univers et Particules de Montpellier, Université
Montpellier 2, CNRS/IN2P3, Montpellier, France
8
Max-Planck-Institut für Radioastronomie,
Auf dem Hügel 69, 53121
Bonn,
Germany
9
High Energy Space Environment Branch, Naval Research
Laboratory, Washington, DC
20375,
USA
10 Jodrell Bank Centre for Astrophysics, School of Physics and
Astronomy, The University of Manchester, M13 9PL, UK
11
W. W. Hansen Experimental Physics Laboratory, Kavli Institute for
Particle Astrophysics and Cosmology, Department of Physics and SLAC National
Accelerator Laboratory, Stanford University, Stanford, CA
94305,
USA
12
Center for Earth Observing and Space Research, College of Science,
George Mason University, Fairfax, VA 22030, resident at Naval Research
Laboratory, Washington, DC
20375,
USA
13
Santa Cruz Institute for Particle Physics, Department of Physics
and Department of Astronomy and Astrophysics, University of California at Santa
Cruz, Santa Cruz,
CA
95064,
USA
Received: 6 June 2011
Accepted: 20 July 2011
Context. Since the launch of the Fermi satellite, the number of known gamma-ray pulsars has increased tenfold. Most gamma-ray detected pulsars are young and energetic, and many are associated with TeV sources. PSR J1357−6429 is a high spin-down power pulsar (Ė = 3.1 × 1036 erg s-1), discovered during the Parkes multibeam survey of the Galactic plane, with significant timing noise typical of very young pulsars. In the very-high-energy domain (E > 100 GeV), H.E.S.S. has reported the detection of the extended source HESS J1356−645 (intrinsic Gaussian width of 12′) whose centroid lies 7′ from PSR J1357−6429.
Aims. We search for gamma- and X-ray pulsations from this pulsar, characterize the neutron star emission and explore the environment of PSR J1357−6429.
Methods. Using a rotational ephemeris obtained with 74 observations made with the Parkes telescope at 1.4 GHz, we phase-fold more than two years of gamma-ray data acquired by the Large Area Telescope on-board Fermi as well as those collected with XMM-Newton, and perform gamma-ray spectral modeling.
Results. Significant gamma- and X-ray pulsations are detected from PSR J1357−6429. The light curve in both bands shows one broad peak. Gamma-ray spectral analysis of the pulsed emission suggests that it is well described by a simple power-law of index 1.5 ± 0.3stat ± 0.3syst with an exponential cut-off at 0.8 ± 0.3stat ± 0.3syst GeV and an integral photon flux above 100 MeV of (6.5 ± 1.6stat ± 2.3syst) × 10-8 cm-2 s-1. The X-ray spectra obtained from the new data provide results consistent with previous work. Upper limits on the gamma-ray emission from its potential pulsar wind nebula (PWN) are also reported.
Conclusions. Assuming a distance of 2.4 kpc, the Fermi LAT energy flux yields a gamma-ray luminosity for PSR J1357−6429 of Lγ = (2.13 ± 0.25stat ± 0.83syst) × 1034 erg s-1, consistent with an 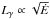 relationship. The Fermi non-detection of the pulsar wind nebula associated with HESS J1356−645 provides new constraints on the electron population responsible for the extended TeV emission.
relationship. The Fermi non-detection of the pulsar wind nebula associated with HESS J1356−645 provides new constraints on the electron population responsible for the extended TeV emission.
Key words: pulsars: individual: PSR J1357 / 6429 / gamma rays: general / pulsars: general
© ESO, 2011
1. Introduction
Since the launch of the Fermi Gamma-ray Space Telescope, the number of known gamma-ray pulsars has increased dramatically. The first Fermi Large Area Telescope (LAT) catalog of pulsars (Abdo et al. 2010a) also marks the birth of new classes of gamma-ray pulsars, such as millisecond (Abdo et al. 2009a) and radio-faint gamma-ray pulsars (Abdo et al. 2009b). The rest are young pulsars, discovered via an efficient collaboration among gamma-ray, radio and X-ray astronomers. Interestingly, many of the detected pulsars are found to be powering pulsar wind nebulae (PWN), and some are associated with TeV sources.
PSR J1357−6429 is a very young, energetic pulsar discovered during the Parkes multibeam survey of the Galactic plane, as reported in Camilo et al. (2004). From its dispersion measure of (127.2 ± 0.5) cm-3 pc, the NE2001 model of the Galactic electron distribution (Cordes & Lazio 2002) assigns PSR J1357−6429 a distance of d = 2.4 ± 0.6 kpc. With a spin period of 166 ms and a period derivative of 3.6 × 10-13 s s-1, the characteristic age is τ = 7300 yr.
No EGRET source is coincident with PSR J1357−6429. Recently, Very Large Telescope data were used to search for optical emission from PSR J1357−6429 (Mignani et al. 2011). No counterpart was found, and an upper limit of V ≃ 27 was determined. Using X-ray Chandra data collected in 2005, Zavlin (2007) reported a hint of pulsed emission using an accurate, contemporaneous radio rotation ephemeris. While of low significance (2–3σ), it is nevertheless more compelling than the non-detection of pulsations reported by Esposito et al. (2007), who folded the same data with an older ephemeris as a starting point to scan for a rotation period for which X-ray pulsations might appear. This pulsar’s timing noise imposes a high number of period trials, which in turn diminishes the significance of what was, at best, a weak signal. In this article, we confirm the detection using new XMM-Newton data from 2009.
PSR J1357−6429 was highlighted by Abdo et al. (2010a) because of the absence of gamma-ray pulsations, and might have become a candidate “gamma-faint” pulsar (Romani et al. 2011). Nearby, with a high spin-down power Ė = 3.1 × 1036 erg s-1, it has 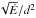 that is 1% of Vela’s, a threshold above which the LAT detects most pulsars. Here we show that the previous non-detection was not the fault of beaming or emission physics, but happened because the timing noise typical of very young pulsars made it difficult to construct an accurate rotation ephemeris after a large glitch early in the Fermi epoch. Once enough post-glitch radio observations had been obtained to build a phase-connected timing model, the gamma-ray pulsations became immediately apparent. We note that Pellizzoni et al. (2009) reported a weak detection with AGILE.
that is 1% of Vela’s, a threshold above which the LAT detects most pulsars. Here we show that the previous non-detection was not the fault of beaming or emission physics, but happened because the timing noise typical of very young pulsars made it difficult to construct an accurate rotation ephemeris after a large glitch early in the Fermi epoch. Once enough post-glitch radio observations had been obtained to build a phase-connected timing model, the gamma-ray pulsations became immediately apparent. We note that Pellizzoni et al. (2009) reported a weak detection with AGILE.
Very often, young and energetic pulsars are embedded in compact nebulae powered by relativistic pulsar winds. Short X-ray observations were performed in 2005 with XMM-Newton and Chandra to search for X-ray emission from a PWN (Esposito et al. 2007; Zavlin 2007). Using the XMM-Newton data, Esposito et al. (2007) found marginal evidence of diffuse emission in the 2−4 keV energy band consisting of a faint elongated structure starting from PSR J1357−6429. These authors also set a 3σ upper limit on the luminosity of ~3 × 1031 erg s-1 in the 2−10 keV range on putative diffuse emission using the Chandra data. On the other hand, Zavlin (2007) reported the detection of tail-like emission associated with the pulsar with a 0.5–10 keV luminosity of ~2.5 × 1031 erg s-1. In the very high energy domain (E > 100 GeV) the H.E.S.S. data show significantly extended emission (intrinsic Gaussian width of 0.20° ± 0.02°) lying close to PSR J1357−6429 (Abramowski et al. 2011). In this article, a GeV upper limit is derived on the emission from the possible PWN observed in the TeV band, providing new constraints on the leptonic population responsible for the very high energy emission.
2. LAT description and observations
The LAT is a gamma-ray telescope that detects photons by conversion into electron-positron pairs in the energy range between 20 MeV to more than 300 GeV, as described by Atwood et al. (2009). It is made of a high-resolution converter/tracker (for direction measurement of the incident gamma rays), a CsI(Tl) crystal calorimeter (for energy measurement) and an anti-coincidence detector to identify the background of charged particles. Compared to EGRET, the LAT has a larger effective area (~8000 cm2 on-axis above 1 GeV), a broader field of view (~2.4 sr) and superior angular resolution (~0.6° 68% containment at 1 GeV for events converting in the front section of the tracker). The on-orbit calibration is described in Abdo et al. (2009c).
The analysis used 29 months of data collected starting August 4, 2008, and extending until January 15, 2011. We selected events with energies greater than 0.1 GeV but excluded those with zenith angles larger than 100° to minimize contamination from secondary gamma-rays from the Earth’s atmosphere (Abdo et al. 2009d). We selected events in the Source class, as described in Atwood et al. (2009). Source events optimize the trade-off between gamma-ray detection efficiency and residual charged-particle contamination in a manner well-suited to localized, persistent sources, as distinct from the Transient or Diffuse classes. We used the most recent analysis version, called “Pass 7”, documented at the Fermi Science Support Center1.
3. Radio timing observations
As part of the space- and ground-based pulsar timing campaign supporting Fermi (Smith et al. 2008), the pulsar PSR J1357−6429 is being observed at the 64-m Parkes radio telescope (Weltevrede et al. 2010b). A total of 74 observations spanning MJDs 54 220 to 55 575 were made in a band centered at 1369 MHz. In this band, the pulsar has a flux density of 440 μJy (Camilo et al. 2004). Observations were made using the central beam of the 20 cm Multibeam Receiver (Staveley-Smith et al. 1996) and recorded using one of the digital filterbanks (DFBs) built by the Australia Telescope National Facility. The DFBs employed real time pulse phase folding to average data into 30 s sub-integrations using 256 MHz of total bandwidth. After calibration, pulse profiles for ~5 min observations were cross-correlated with a template to obtain times-of-arrival. The TEMPO2 timing package (Hobbs et al. 2006) was then used to build the timing solution, taking into account a significant glitch at MJD 54 786 and strong timing noise prevalent in young pulsars. The glitch was modeled by including jumps in spin phase, spin frequency, and spin frequency derivative at the glitch epoch. Higher-order spin frequency derivatives and harmonically related sinusoids (Hobbs et al. 2004) were used to model the timing noise. The post-fit rms is 1.4 ms, or 0.8% of a pulsar rotation. This timing solution will be made available through the FSSC1.
4. X-ray observations and data reduction
XMM-Newton observed PSR J1357−6429 on October 14−15, 2009, with the EPIC-pn instrument operated in Small Window mode and two EPIC-MOS detectors in Full Window mode (for 55.5 and 78.1 ks effective exposures, respectively). The data were reprocessed and reduced with the XMM-Newton Science Analysis Software (SAS v. 11.0).
The pulsar was also observed on October 8−9, 2009, with the Chandra ACIS-I instrument operated in Timed Exposure (Very Faint) mode for a 59.2 ks effective exposure. The Chandra Interactive Analysis of Observations software (CIAO v. 4.3; the calibration database CALDB v. 4.4.3) was used to generate the “level 2” event file for this observation.
5. Analysis and results
5.1. Gamma- and X-ray light curves
PSR J1357−6429 is located 2.5° below the Galactic plane where the diffuse gamma radiation is still intense. For the timing analysis, we took photons within a radius of 0.8° with respect to the radio pulsar position (l = 309.922705°, b = −2.514079°) using an energy-dependent cone of radius 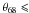
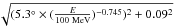 . This choice takes into account the instrument performance and maximizes the signal-to-noise ratio over a broad energy range (Atwood et al. 2009). The arrival times of events were corrected to the solar system barycenter using the JPL DE405 solar system ephemeris (Standish 1998), and the events were folded using the radio ephemeris from Parkes, using the TEMPO2 fermi plugin.
. This choice takes into account the instrument performance and maximizes the signal-to-noise ratio over a broad energy range (Atwood et al. 2009). The arrival times of events were corrected to the solar system barycenter using the JPL DE405 solar system ephemeris (Standish 1998), and the events were folded using the radio ephemeris from Parkes, using the TEMPO2 fermi plugin.
A total of 8707 gamma rays remain above 100 MeV in our energy-dependent circular region, and among them 915 ± 161 pulsed photons after background subtraction. We estimated the background level represented by the dashed horizontal line in Fig. 1 (top panel) using two circular regions 1.5° from PSR J1357−6429 and at the same Galactic latitude. Nearby sources were avoided, and we normalized to the solid angle of the source region. An H-test value of 89.6 is obtained above 100 MeV, corresponding to a pulsed detection significance of ~8σ (de Jager & Büsching 2010). Figure 1 shows the 25 bin gamma-ray light curve (top panel) as well as the 1.4 GHz radio profile (bottom panel) derived from observations with the Parkes radio telescope (Weltevrede et al. 2010b). The gamma-ray peak is offset from the radio pulse by 0.37 ± 0.03 ± 0.01 according to a Lorentzian fit with a full width at half maximum (FWHM) of ~0.25. The first phase uncertainty arises from the gamma-ray fit. The uncertainty in DM of 0.5 pc cm-3 causes an uncertainty in the extrapolation of the radio pulse time-of-arrival to infinite frequency of 0.01 in phase. There is no significant evolution of the gamma-ray peak with energy as can be seen from Fig. 1 (middle panels). We defined the “off-pulse interval” as the pulse minimum between 0.8 and 1.1 in phase.
Figure 1 also shows the pulse profile obtained from the XMM-Newton EPIC-pn data with 6 ms time resolution. For the timing analysis, 1543 events were extracted (with 270 background counts) from a 15′′-radius circle centered at the pulsar position in the 0.5−2 keV range to maximize the signal-to-noise ratio. The photons plugin2 TEMPO2 package was used to assign a phase to each selected photon. This allowed us to use the full complexity of the ephemeris parameters including those for the glitch mentioned in Sect. 3 in the timing model. Performing an unbinned maximum-likelihood fit of the phases to a constant plus single Gaussian, we obtained an intrinsic pulsed fraction of 0.56 ± 0.13 (accounting for the contribution of the diffuse emission surrounding the pulsar; see Sect. 5.2), with a Gaussian of width 0.48 ± 0.18 centered at phase 0.83 ± 0.03. The H-test yields a value of H = 52.42 corresponding to the probability of a chance occurrence in a single trial p = 1.6 × 10-11, or a 6.7σ detection significance. The main contribution to the H value comes from the fundamental and first harmonics, in accordance with the shape of the X-ray light curve with a single broad pulse. This pulse profile can be produced by a thermal radiation emitted from the neutron star surface (see Sect. 5.2). This result unambiguously confirms the previous evidence of pulsations found by Zavlin (2007) in the Chandra data taken in 2005.
 |
Fig. 1 Top panel: phase-aligned histogram of PSR J1357−6429 above 0.1 GeV and within an energy-dependent circular region as defined in Sect. 5.1. Two rotations are plotted with 25 bins per period. The dashed line shows the background level estimated using two nearby circular regions as described in Sect. 5.1. Three following panels: phase histograms for PSR J1357−6429 in the three indicated energy ranges, each with 25 bins per pulse period. Second panel from bottom: X-ray pulse profile extracted from the XMM-Newton data of 2009 in the 0.5–2 keV energy band. Two rotations are plotted with 15 bins per period. Bottom panel: radio pulse profile based on Parkes observations at a center frequency of 1.4 GHz with 256 phase bins (Weltevrede et al. 2010b). |
5.2. Spatial and spectral analysis of the X-ray data
We used the XMM-Newton data from 2009 to derive the spectrum of PSR J1357−6429. Photons were extracted from a 20′′-radius circle centered at the pulsar position in the EPIC-pn and MOS data. Background was evaluted from similar regions in the vicinity of the pulsar. The estimated numbers of source counts are 2266 ± 72, 1000 ± 40 and 996 ± 39 for the EPIC-pn, MOS1 and MOS2 data sets (respectively). The instrumental responses were generated with the SAS rmfgen and arfgen tools. The purely non-thermal interpretation of the pulsar’s X-ray emission can be most likely ruled out because the single power-law (PL) fit to the obtained spectra results in a best estimate of the hydrogen column density, nH < 2 × 1019 cm-2, significantly lower than the value suggested by the pulsar dispersion measure, nH ≃ 4 × 1021 cm-2 (see Zavlin 2007 for details). Adding a thermal component, blackbody (BB) or neutron star magnetized atmosphere model (NSA; see Zavlin 2009 for a review) yields reasonable values of nH and provides good fit quality (with 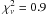 –1; see Fig. 2). Generally, the results derived with the two-component model fits to the new data are consistent with those reported in Zavlin (2007). For example, the NSA-plus-PL fit gives the estimate on the neutron star effective temperature Teff = (0.95 ± 0.05) × 106 K (assuming the standard star mass M = 1.4 M⊙ and radius R = 10 km, and the distance d = 2.4 kpc). The non-thermal component is well described by the PL model with a photon index Γ = 1.43 ± 0.14 and (unabsorbed) flux FX ≃ 2.0 × 10-13 erg cm-2 s-1 in 0.5−10 keV (this range is used for the estimates on all non-thermal fluxes below), whereas the hydrogen column density is nH = (3.9 ± 0.4) × 1021 cm-2.
–1; see Fig. 2). Generally, the results derived with the two-component model fits to the new data are consistent with those reported in Zavlin (2007). For example, the NSA-plus-PL fit gives the estimate on the neutron star effective temperature Teff = (0.95 ± 0.05) × 106 K (assuming the standard star mass M = 1.4 M⊙ and radius R = 10 km, and the distance d = 2.4 kpc). The non-thermal component is well described by the PL model with a photon index Γ = 1.43 ± 0.14 and (unabsorbed) flux FX ≃ 2.0 × 10-13 erg cm-2 s-1 in 0.5−10 keV (this range is used for the estimates on all non-thermal fluxes below), whereas the hydrogen column density is nH = (3.9 ± 0.4) × 1021 cm-2.
 |
Fig. 2 Spectra of PSR J1357−6429 detected with the XMM-Newton EPIC instruments (upper panel) fitted with a two-component, NSA-plus-PL, model (lower panel). The middle panel shows residuals in the spectral fit. |
In addition to the results yielded by the new XMM-Newton observation, the Chandra ACIS-I data of 2009 reveal diffuse emission both surrounding PSR J1357−6429 and extending 15′′–20′′ from the pulsar in the northeast direction (see Fig. 3). Despite the low number of counts (55 ± 9) estimated in the elongated and bent feature (outlined with the dashed contour in Fig. 3), its detection is significant at a 6.1σ level. The spectrum of this feature, extracted with the CIAO tool specextract, which yields both the spectra and instrumental responses, is fitted with a PL model of Γ = 1.51 ± 0.28 and unabsorbed flux FX ≃ 0.2 × 10-13 erg cm-2 s-1. This confirms the earlier detection of a potential PWN reported by Zavlin (2007). The diffuse emission surrounding the pulsar (denoted with the elliptical contour in Fig. 3, with the estimated number of 224 ± 15 source counts), is characterized by a PL spectrum of Γ = 1.48 ± 0.18 and FX ≃ 0.7 × 10-13 erg cm-2 s-1. A detailed analysis of the detected nebula is outside the scope of this paper, but see Chang et al. (2011) for more results on the X-ray PWN.
But it should be noted that the diffuse emission is included in the extraction region used to derive the X-ray spectra from the XMM-Newton EPIC instruments. Therefore, a fraction of the non-thermal flux measured from the EPIC data is contributed by the PWN. This is clearly visible in Fig. 4, which shows the pulsar’s spectrum extracted from the 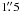 -radius circle centered at its radio position in the Chandra ACIS-I data (456 ± 21 source counts; see Fig. 3). While the thermal component (and the hydrogen column density) is described well by the NSA model yielded by the XMM-Newton data, the non-thermal component is fitted with a PL model of photon index Γ = 1.45 ± 0.16 and unabsorbed X-ray flux FX ≃ 0.9 × 10-13 erg cm-2 s-1 (with
-radius circle centered at its radio position in the Chandra ACIS-I data (456 ± 21 source counts; see Fig. 3). While the thermal component (and the hydrogen column density) is described well by the NSA model yielded by the XMM-Newton data, the non-thermal component is fitted with a PL model of photon index Γ = 1.45 ± 0.16 and unabsorbed X-ray flux FX ≃ 0.9 × 10-13 erg cm-2 s-1 (with 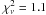 ; Fig. 4). We note that the sum of the non-thermal fluxes estimated in the Chandra data for the pulsar, the surrounding emission and the elongated tail match that derived from the XMM-Newton spectra well.
; Fig. 4). We note that the sum of the non-thermal fluxes estimated in the Chandra data for the pulsar, the surrounding emission and the elongated tail match that derived from the XMM-Newton spectra well.
Another interesting point to mention is that the elongation of the detected X-ray PWN, about 60° to northeast, may indicate the direction of the pulsar’s proper motion (see also Mignani et al. 2011).
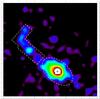 |
Fig. 3 Chandra ACIS-I image of PSR J1357−6429 (in 0.5−10 keV) surrounded by an extended structure. The dashed contour indicates the jet-like feature elongated to the northeast direction. The cross and the |
 |
Fig. 4 Spectrum of PSR J1357−6429 detected with the Chandra ACIS-I instrument (crosses in the upper panel) and fitted with a NSA-plus-PL model (solid curves). The thermal (NSA) component, as well as the hydrogen column density, is the same as in Fig. 2. The dashed curve indicates the PL component derived from the EPIC spectra. The lower panel shows residuals in the spectral fit. |
5.3. Fermi LAT spectra and phase-averaged flux
The phase-averaged spectrum of PSR J1357−6429 was obtained using gtlike, a maximum likelihood spectral analysis (Mattox et al. 1996) implemented in the Fermi Science Tools1. This tool fits a source model to the data. The model includes the object under study as well as other gamma-ray sources in a region extending well beyond the LAT’s angular resolution. Sources near PSR J1357−6429 exceeding the background with statistical significance higher than 5σ are extracted from the Fermi LAT 2FGL catalog (Abdo et al., in prep.) Galactic diffuse emission is modeled using the ring-hybrid model ring_2year_P76_v0.fits. The instrumental background and the extragalactic radiation are described by a single isotropic component with the spectral shape in the tabulated model isotrop_2year_P76_source_v0.txt. The likelihood tool gtlike further requires tables of the Instrument Response Functions (IRFs), which are the energy and direction-dependent angular resolution, effective area, and energy resolution. We used the P7_V6 IRFs. These new models and their detailed description will be available through the FSSC.
Assuming a power-law with an exponential cut-off spectral shape, the best-fit result is obtained for a spectral index of 1.5 ± 0.3 ± 0.3 with a cut-off at 0.8 ± 0.3 ± 0.3 GeV and an integral photon flux above 100 MeV of (6.5 ± 1.6 ± 2.3) × 10-8 cm-2 s-1. The integral energy flux is (1.9 ± 0.2 ± 0.8) × 10-5 MeV cm-2 s-1. The first error is statistical, while the second represents our estimate of systematic effects as discussed below. To check the assumption of a cut-off energy in the spectrum, we have also fit the same dataset with a simple power-law. The spectral model using an exponential cut-off is better constrained with a difference between the log likelihoods of ~4 σ, disfavoring the power-law hypothesis. Figure 5 shows the spectral energy distribution of PSR J1357−6429 as seen by Fermi. The Fermi LAT spectral points were obtained by dividing the 100 MeV−100 GeV range into logarithmically-spaced energy bins and performing a maximum-likelihood spectral analysis in each interval, assuming a power-law shape for the source. These points are overlaid with the exponentially cut-off power-law fit over the total energy range.
Two main systematic uncertainties can affect the LAT flux estimation for a point source: uncertainties on the Galactic diffuse background and on the effective area. The dominant uncertainty at low energy comes from the Galactic diffuse emission because PSR J1357−6429 is located only 2.5° from the Galactic plane. By changing the normalization of the Galactic diffuse model artificially by ± 6% as in Abdo et al. (2010c), we estimate the systematic error on the integrated flux of the pulsar to be 50% below 500 MeV, 20% between 500 MeV and 1 GeV, and 7% above 1 GeV. The second systematic is estimated by using modified IRFs whose effective areas bracket those of our nominal IRF. These “biased” IRFs are defined by envelopes above and below the nominal energy dependence of the effective area by linearly connecting differences of (10%, 5%, 20%) at log(E) of (2, 2.75, 4), respectively. We combine the errors in quadrature to obtain our best estimate of the total systematic uncertainty at each energy, and propagate through to the fit model parameters.
As can be seen from Fig. 5, no significant emission is detected above 4.5 GeV at the position of PSR J1357−6429. In very-high-energy gamma rays, the H.E.S.S. experiment has detected significant emission close to the pulsar and significantly extended with an intrinsic Gaussian width of 0.20° ± 0.02°. As a first search for unpulsed emission from the TeV source HESS J1356−645, we fitted a Gaussian of 0.2° to the data in the energy band 4.5−100 GeV where no pulsed emission is detected. No significant signal could be observed and we derived 95% confidence level (CL) upper limits on the flux in the four logarithmically-spaced energy bins between 4.5 and 100 GeV assuming a power-law shape for the source with fixed spectral index of 2. In a second step, we used the off-pulse data selecting photons in the 0.8−1.1 phase interval and fit the same Gaussian of 0.2° to data in the whole energy band 100 MeV−100 GeV. Again, no significant emission could be detected and we derived 95% CL upper limits on the flux in the nine logarithmically-spaced energy bins (assuming the same spectral index). These upper limits are presented in Fig. 5.
 |
Fig. 5 Spectral energy distribution of PSR J1357−6449 in gamma rays. The LAT spectral points (in red dots) are obtained using the maximum-likelihood method gtlike described in Sect. 5.3 in 9 logarithmically-spaced energy bins between 100 MeV and 100 GeV. The statistical errors are shown in red, while the black lines take into account both the statistical and systematic errors as discussed in Sect. 5.3. The magenta solid line presents the result obtained by fitting an exponentially cut-off power law to the data in the 100 MeV−100 GeV energy range using a maximum-likelihood fit. A 95% C.L. upper limit is computed when the statistical significance is lower than 3σ (red dots). Blue filled (open) stars represent the 95% C.L. upper limits derived assuming a Gaussian of 0.2° at the position of HESS J1356-645 in the whole signal (in the off-pulse). |
6. Discussion
Johnston & Weisberg (2006) measured the polarization profiles for 14 young pulsars at Parkes. For PSR J1357−6429 the polarization position angle Ψ increases with a constant slope of 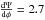 across the radio pulse. In the simplest RVM scenario (rotating vector model, Radhakrishnan & Cooke 1969),
across the radio pulse. In the simplest RVM scenario (rotating vector model, Radhakrishnan & Cooke 1969), 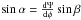 , hence the angle β between the magnetic axis and the line-of-sight is small, β < 22°. The lack of an inflection in Ψ vs. φ and the narrow φ range of the pulse make a full RVM fit unconstraining.
, hence the angle β between the magnetic axis and the line-of-sight is small, β < 22°. The lack of an inflection in Ψ vs. φ and the narrow φ range of the pulse make a full RVM fit unconstraining.
PSR J1357−6429’s gamma-ray profile resembles that of PSR J2229+6114 (Abdo et al. 2009e), PSR J0248+5832 (Theureau et al. 2011), and PSR J1718−3825 (Weltevrede et al. 2010a) in having a single, wide peak offset from the radio pulse by a bit less than a half-rotation. The “Atlas” update by Romani & Watters (2010) provides gamma-ray profiles calculated for different emission models, over a coarse grid of inclination angles α and ζ = α + β, and for four gap widths w approximated by the efficiency, η = Lγ/Ė. We find Lγ = (2.1 ± 0.3 ± 0.8) × 1034fΩ(d/2.4 kpc)2 erg s-1 and η = 0.01fΩ(d/2.4 kpc)2 above 100 MeV, with the beaming correction factor fΩ as defined by Romani & Watters (2010). Two profiles therein resemble the data. They are for w = 0.01, α = 55°, and ζ = 35° and 50° (adjacent plots in the coarse (α,ζ) grid). This is consistent with small β = ζ − α suggested by the RVM. For these geometries, the Atlas predicts fΩ ≃ 1, that is, a small correction to Lγ. This luminosity is within the distance-dominated scatter of the 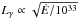 rule shown by Abdo et al. (2010a), with Ė in units of erg s-1.
rule shown by Abdo et al. (2010a), with Ė in units of erg s-1.
The new X-ray data collected from PSR J1357−6429 with XMM-Newton and Chandra in 2009 strongly suggest that the bulk of the pulsar flux at soft X-ray energies (below about 1.5 keV) is of thermal origin, making this pulsar the second youngest neutron star with a detected thermal component known at this time (see Zavlin 2007 for details). Because the X-ray pulsed flux shown in Figs. 1 is extracted in the 0.5−2 keV range, it mostly comes from thermal radiation. This explains the sine-like shape of the light curve with the single broad pulse that is characteristic of the majority of X-ray pulse profiles observed from pulsars with dominating thermal emission. It is also consistent with the phase shift between the pulses in the gamma-ray and X-ray fluxes – the pulses originate at different sites. The thermal component is emitted from the neutron star surface, whereas the high-energy radiation is generated far from the surface (e.g., in the pulsar magnetosphere). Yet the origin of the thermal component remains unclear. It may be emitted from a small hot area (polar caps) of a radius of 1–2 km on the pulsar’s surface, as suggested by the interpretation involving the BB model, or from the entire surface as indicated by the fits with the NSA models. To distinguish between these two interpretations, one should model the pulsed flux, as has been done for X-rays detected from a number of millisecond pulsars (e.g., Zavlin & Pavlov 1998; Bogdanov et al. 2008). This modeling should take into account the effects of the neutron star geometry (orientation of the pulsar spin and magnetic axes with respect to the line of view), surface magnetic and temperature distributions, intrinsic properties (anisotropy) of the thermal emission, and the gravitational bending of photon trajectories near the star surface. If future X-ray observations provide much better photon statistics, this analysis can be supported by phase-resolved spectroscopy and energy-resolved pulse modeling. At present, we can only speculate that the detected thermal flux is intrinsically anisotropic, as predicted by the atmosphere models, otherwise the effect of the gravitational bending would strongly suppress the pulsations.
PSR J1357−6429 also lies within the extended TeV source HESS J1356−645, proposed as its associated PWN (Abramowski et al. 2011). No significant signal is detected using Fermi LAT data above 4.5 GeV, nor in the off-pulse interval below 4.5 GeV. In the context of the leptonic model proposed by Abramowski et al. (2011), our upper limits constrain
the spectrum of the electron population responsible for the extended TeV emission. The best model reproducing both the radio, X-ray and TeV data and the non-detection by Fermi is obtained for a magnetic field of 4 μG (similar to what is seen in other evolved TeV PWNe) and an electron spectrum characterized with a spectral index of 2.4, a minimum energy of 10 GeV, a cut-off energy of 100 TeV and a total energy of 4 × 1047 erg (Abramowski et al. 2011). This energy is only ~10% of the total kinetic energy since the birth of PSR J1357−6429, assuming an initial period of 80 ms.
Acknowledgments
The Fermi LAT Collaboration acknowledges generous ongoing support from a number of agencies and institutes that have supported the development and the operation of the LAT as well as scientific data analysis. These include the National Aeronautics and Space Administration and the Department of Energy in the United States, the Commissariat à l’Énergie Atomique and the Centre National de la Recherche Scientifique/Institut National de Physique Nucléaire et de Physique des Particules in France, the Agenzia Spaziale Italiana, the Istituto Nazionale di Fisica Nucleare, and the Istituto Nazionale di Astrofisica in Italy, the Ministry of Education, Culture, Sports, Science and Technology (MEXT), High Energy Accelerator Research Organization (KEK) and Japan Aerospace Exploration Agency (JAXA) in Japan, and the K. A. Wallenberg Foundation and the Swedish National Space Board in Sweden. Additional support for science analysis during the operations phase from the following agencies is also gratefully acknowledged: the Instituto Nazionale di Astrofisica in Italy and the Centre National d’Études Spatiales in France. The Parkes radio telescope is part of the Australia Telescope, which is funded by the Commonwealth Government for operation as a National Facility managed by CSIRO. We thank our colleagues for their assistance with the radio timing observations. V.E.Z. is grateful to Nataliya Ivanova for discussions and support.
References
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2009a, Science, 325, 848 [NASA ADS] [CrossRef] [Google Scholar]
- Abdo, A. A., Ackermann, M., Atwood, W. B., et al. 2009b, Science, 325, 840 [NASA ADS] [CrossRef] [Google Scholar]
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2009c, ApJ, 696, 1084 [NASA ADS] [CrossRef] [Google Scholar]
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2009d, Phys. Rev. D, 80, 122004 [NASA ADS] [CrossRef] [Google Scholar]
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2009e, ApJ, 706, 1331 [NASA ADS] [CrossRef] [Google Scholar]
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2010a, ApJS, 187, 460 [NASA ADS] [CrossRef] [Google Scholar]
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2010b, ApJS, 188, 405 [NASA ADS] [CrossRef] [Google Scholar]
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2010c, ApJ, 722, 1303 [NASA ADS] [CrossRef] [Google Scholar]
- Abramowski, A., Acero, F., Aharonian, F., et al. (H.E.S.S. collaboration), A&A, in press [Google Scholar]
- Atwood, W. B., Abdo, A. A., Ackermann, M., et al. 2009, ApJ, 697, 1071 [NASA ADS] [CrossRef] [Google Scholar]
- Bogdanov, S., Grindlay, J. E., & Rybicki, G. B. 2008, ApJ, 689, 407 [NASA ADS] [CrossRef] [Google Scholar]
- Camilo, F., Manchester, R. N., Lyne, A. G., et al. 2004, ApJ, 611, L25 [NASA ADS] [CrossRef] [Google Scholar]
- Chang, C., Pavlov, G., & Kargaltsev, O. 2011, ApJ, submitted [arXiv:1107.1819] [Google Scholar]
- Cordes, J. M., & Lazio, T. J. W. 2002 [arXiv:astro-ph/0207156] [Google Scholar]
- de Jager, O. C., & Büsching, I. 2010, A&A, 517, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Esposito, P., Tiengo, A., de Luca, A., & Mattana, F. 2007, A&A, 467, L45 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hobbs, G. B., Edwards, R. T., & Manchester, R. N. 2006, MNRAS, 369, 655 [NASA ADS] [CrossRef] [Google Scholar]
- Johnston, S., & Weisberg, J. M. 2006, MNRAS, 368, 1856 [NASA ADS] [CrossRef] [Google Scholar]
- Mattox, J. R., Bertsch, D. L., Chiang, J., et al. 1996, ApJ, 461, 396 [NASA ADS] [CrossRef] [Google Scholar]
- Mignani, R.P., Shearer, A., De Luca, P., et al. 2011, A&A, 533, A101 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pellizzoni, A., Pilia, M., Possenti, A., et al. 2009, ApJ, 695, L115 [NASA ADS] [CrossRef] [Google Scholar]
- Radhakrishnan, V., & Cooke, D. J. 1969, Astrophys. Lett., 3, 225 [NASA ADS] [Google Scholar]
- Romani, R. W., & Watters, K. P. 2010, ApJ, 714, 810 [NASA ADS] [CrossRef] [Google Scholar]
- Romani, R., Kerr, M., Craig, H. A., et al. 2011, ApJ, 738, 114 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, D. A., Guillemot, L., Camilo, F., et al. 2008, A&A, 492, 923 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Standish, E. M. 1998, JPL Planetary and Lunar Ephemerides, DE405/LE405, Memo IOM 312.F-98-048 [Google Scholar]
- Staveley-Smith, L., Wilson, W. E., Bird, T. S., et al. 1996, PASA, 13, 243 [Google Scholar]
- Theureau, G., Parent, D., Cognard, I., et al. 2011, A&A, 525, A94 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Weltevrede, P., Abdo, A. A., Ackermann, M., et al. 2010a, ApJ, 708, 1426 [NASA ADS] [CrossRef] [Google Scholar]
- Weltevrede, P., Johnston, S., Manchester, R. N., et al. 2010b, PASA, 27, 64 [NASA ADS] [CrossRef] [Google Scholar]
- Zavlin, V. E. 2007, ApJ, 665, L143 [NASA ADS] [CrossRef] [Google Scholar]
- Zavlin, V. E. 2009, in Neutron Stars and Pulsars, Astrophysics and Space Science Library (Springer), 357, 181 [NASA ADS] [CrossRef] [Google Scholar]
- Zavlin, V. E., & Pavlov, G.G. 1998, A&A, 329, 583 [NASA ADS] [Google Scholar]
All Figures
 |
Fig. 1 Top panel: phase-aligned histogram of PSR J1357−6429 above 0.1 GeV and within an energy-dependent circular region as defined in Sect. 5.1. Two rotations are plotted with 25 bins per period. The dashed line shows the background level estimated using two nearby circular regions as described in Sect. 5.1. Three following panels: phase histograms for PSR J1357−6429 in the three indicated energy ranges, each with 25 bins per pulse period. Second panel from bottom: X-ray pulse profile extracted from the XMM-Newton data of 2009 in the 0.5–2 keV energy band. Two rotations are plotted with 15 bins per period. Bottom panel: radio pulse profile based on Parkes observations at a center frequency of 1.4 GHz with 256 phase bins (Weltevrede et al. 2010b). |
| In the text | |
 |
Fig. 2 Spectra of PSR J1357−6429 detected with the XMM-Newton EPIC instruments (upper panel) fitted with a two-component, NSA-plus-PL, model (lower panel). The middle panel shows residuals in the spectral fit. |
| In the text | |
 |
Fig. 3 Chandra ACIS-I image of PSR J1357−6429 (in 0.5−10 keV) surrounded by an extended structure. The dashed contour indicates the jet-like feature elongated to the northeast direction. The cross and the |
| In the text | |
 |
Fig. 4 Spectrum of PSR J1357−6429 detected with the Chandra ACIS-I instrument (crosses in the upper panel) and fitted with a NSA-plus-PL model (solid curves). The thermal (NSA) component, as well as the hydrogen column density, is the same as in Fig. 2. The dashed curve indicates the PL component derived from the EPIC spectra. The lower panel shows residuals in the spectral fit. |
| In the text | |
 |
Fig. 5 Spectral energy distribution of PSR J1357−6449 in gamma rays. The LAT spectral points (in red dots) are obtained using the maximum-likelihood method gtlike described in Sect. 5.3 in 9 logarithmically-spaced energy bins between 100 MeV and 100 GeV. The statistical errors are shown in red, while the black lines take into account both the statistical and systematic errors as discussed in Sect. 5.3. The magenta solid line presents the result obtained by fitting an exponentially cut-off power law to the data in the 100 MeV−100 GeV energy range using a maximum-likelihood fit. A 95% C.L. upper limit is computed when the statistical significance is lower than 3σ (red dots). Blue filled (open) stars represent the 95% C.L. upper limits derived assuming a Gaussian of 0.2° at the position of HESS J1356-645 in the whole signal (in the off-pulse). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


