| Issue |
A&A
Volume 533, September 2011
|
|
|---|---|---|
| Article Number | A71 | |
| Number of page(s) | 5 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/201015808 | |
| Published online | 30 August 2011 | |
No quantum gravity signature from the farthest quasars
1
Dipartimento di Astronomia, Università di Padova, vicolo dell’Osservatorio 3, 35122 Padova, Italy
e-mail: fabrizio.tamburini@unipd.it
2 Dipartimento di Fisica, University of Ferrara, Italy
3
INAF - Osservatorio Astronomico di Capodimonte, salita Moiariello 16, 80131 Napoli, Italy
4
International Center for Relativistic Astrophysics Network, Pescara, Italy
5
European Southern Observatory, Garching bei München, Germany
Received: 22 September 2010
Accepted: 16 July 2011
Context. Strings and other alternative theories describing the quantum properties of space-time suggest that space-time could present a foamy structure and also that, in certain cases, quantum gravity (QG) may manifest at energies much below the Planck scale. One of the observable effects could be the degradation of the diffraction images of distant sources.
Aims. We searched for this degradation effect, caused by QG fluctuations, in the light of the farthest quasars (QSOs) observed by the Hubble Space Telescope with the aim of setting new limits on the fluctuations of the space-time foam and QG models.
Methods. We developed a software that estimates and compares the phase variation in the interference patterns of the high-redshift QSOs, taken from the snapshot survey of HST-SDSS, with those of stars that are expected to not be affected by QG effects. We used a two-parameter function to determine, for each test star and QSO, the maximum of the diffraction pattern and to calculate the Strehl ratio.
Results. Our results go far beyond those already present in the literature. By adopting the most conservative approach where the correction terms, that describe the possibility for space-time fluctuations cumulating across long distances and partially compensate for the effects of the phase variations, are taken into account. We exclude the random walk model and most of the holographic models of the space-time foam. Without considering these correction terms, all the main QG scenarios are excluded. Finally, our results show the absence of any directional dependence of QG effects and the validity of the cosmological principle with an independent method; that is, viewed on a large scale, the properties of the Universe are the same for all observers, including the effects of space-time fluctuations.
Key words: gravitation / quasars: general / methods: data analysis / methods: statistical / cosmology: theory / elementary particles
© ESO, 2011
1. Introduction
Quantum gravity (QG) can be considered the Holy Grail of modern physics. Because of the general Heisenberg’s uncertainty principle, in most of the approaches to the unification of gravitation and quantum physics, the classical geometrical concept of a continuous and smooth space-time support of general relativity is replaced, at very short distances, by a foamy geometric scenario where fluctuations on the order of the Planck length lp ≃ 1.616 × 10-35 m occur at certain characteristic frequencies that are related to the Planck time tp ≃ 5.391 × 10-44 s. For the sake of simplicity, here we will not consider in this discussion more exotic formulations of Heisenberg’s principle, which can be found in the vast literature of quantum gravity.
Without going into too much detail, each model of QG can be naively characterized by its peculiar space-time and energy fluctuation scale, which may occur also at frequencies that are different or even much lower than those expected at Planck scales, 1/tp. The reader can find quite a vast literature describing all the possible scenarios and behavior of gravity on quantum scales, because up to now there has been no theory of QG. This scale is thought to be accompanied by the occurrence of new physical phenomena and macroscopically observable effects, such as the production of mini-black holes at energies much lower than the classical Planck scale, like those expected in the large hadron collider (LHC 2010; Dvali & Sibiryakov 2008; Koch et al. 2005; Hossenfelder 2006, 2002). Other models even describe the possibility of loosing of phase coherence in the light of distant sources, such as the farthest supernovae (SNe) and distant quasars (QSOs). Light, when propagating in the vacuum, will be affected by the fuzzy structure of space-time, with the result of progressively blurring the diffraction images of those sources (Amelino-Camelia 1994; Amelino-Camelia 2000; Ng & van Dam 2000; Ng & van Dam 1994; Ng 2003; Christiansen et al. 2006).
Naively, following the already cited literature, one expects that a photon with energy E = hν is affected by an energy indetermination on the order of δE/E ~ δp/p ~ (E/Ep)α, where α is the characteristic exponent of the power-law distribution of a phenomenological model that describes the energy fluctuations induced in any quanta by QG effects because of the “grainy” structure of space-time. The quantity Ep = h/tP is Planck’s energy. The energy-momentum relationship at the lowest perturbation order is a function of the two parameters a0 and α, ![\begin{equation} p^2 = E^2\left[1\pm a_0\left(E/E_{\rm P}\right)^\alpha\right]. \end{equation}](/articles/aa/full_html/2011/09/aa15808-10/aa15808-10-eq9.png) (1)If this “grainy” structure of space-time emerges on time scales of t∗ ≥ tP, any time interval can be determined with an uncertainty t ≥ t∗ and intrinsic standard deviation derived from the following relationship, σt/t = f(tp/t), where f ≥ 1 for t ≤ tP. When, instead, t ≫ tP, one obtains f = (tp/t)(a0 + a1(tp/t) + a2(tp/t)2 + ...) ≈ a0(tp/t) ≪ 1, where a0 is the lowest order amplitude of the quantum fluctuations in Planck units. This means that this foamy structure of space-time induces a random dispersion of the photon arrival time of a bunch of photons emitted by a source. It is possible to reveal this effect by analyzing the phase coherence of the light of distant sources, as described by Lieu & Hillman (2003) and Ragazzoni et al. (2003). Equivalently, this dispersion is said to generate two differently fluctuating wave velocities that may systematically cumulate during the journey of each photon. The wavelength λ of the traveling photon naturally defines the minimum and characteristic scale length on which physical quantities such as, the phase velocity (vp) and the group velocity (vg), and their respective dispersion relationships can be defined.
(1)If this “grainy” structure of space-time emerges on time scales of t∗ ≥ tP, any time interval can be determined with an uncertainty t ≥ t∗ and intrinsic standard deviation derived from the following relationship, σt/t = f(tp/t), where f ≥ 1 for t ≤ tP. When, instead, t ≫ tP, one obtains f = (tp/t)(a0 + a1(tp/t) + a2(tp/t)2 + ...) ≈ a0(tp/t) ≪ 1, where a0 is the lowest order amplitude of the quantum fluctuations in Planck units. This means that this foamy structure of space-time induces a random dispersion of the photon arrival time of a bunch of photons emitted by a source. It is possible to reveal this effect by analyzing the phase coherence of the light of distant sources, as described by Lieu & Hillman (2003) and Ragazzoni et al. (2003). Equivalently, this dispersion is said to generate two differently fluctuating wave velocities that may systematically cumulate during the journey of each photon. The wavelength λ of the traveling photon naturally defines the minimum and characteristic scale length on which physical quantities such as, the phase velocity (vp) and the group velocity (vg), and their respective dispersion relationships can be defined.
The phase of the electromagnetic wave, associated with the photon propagation, after having crossed the distance λ in the time t = λ/vg, becomes φ = 2πvp/vg. Lieu & Hillman (2003) and Ng et al. (2001) claim that QG fluctuations may induce well-defined phase indeterminations such that an electromagnetic wave, traveling a long distance L, may cumulate a phase variation on the order of ![\begin{eqnarray} \left(\Delta \phi_{\rm QG}\right)_{\min} &\sim& 2 \pi a_0 \frac{l_{\rm p}^\alpha L^{1-\alpha}}{\lambda} \nonumber \\[1.5mm] &\sim& 2 \pi \frac{L}{\lambda} \left[ 1\pm \sqrt{2} \alpha \left(\frac{hc}{\lambda E_{\rm P}} \right)^\alpha \right], \end{eqnarray}](/articles/aa/full_html/2011/09/aa15808-10/aa15808-10-eq23.png) (2)if the emission and detection wavelengths remain equal during the photon propagation. The parameter c is the speed of light and a0 ~ 1 (Ng 2003). If, instead, one also considers the effect of cosmological redshift z, a larger phase dispersion is obtained, as proposed by Steinbring (2007)
(2)if the emission and detection wavelengths remain equal during the photon propagation. The parameter c is the speed of light and a0 ~ 1 (Ng 2003). If, instead, one also considers the effect of cosmological redshift z, a larger phase dispersion is obtained, as proposed by Steinbring (2007) ![\begin{eqnarray} \left(\Delta \phi_{\rm QG}\right)_z &\sim& 2 \pi a_0 \frac{l_{\rm p}^\alpha}{\lambda}\frac{(1-\alpha)c}{H_0q_0} \nonumber \\[1.5mm] &&\times \int_0^z(1+z)L^{-\alpha}\left[1-\frac{1-q_0}{\sqrt{1+2q_0z}}\right]{\rm d}z, \label{eq3} \end{eqnarray}](/articles/aa/full_html/2011/09/aa15808-10/aa15808-10-eq27.png) (3)where H0 is the Hubble constant, q0 the deceleration parameter of the Universe, and the luminosity distance is given by
(3)where H0 is the Hubble constant, q0 the deceleration parameter of the Universe, and the luminosity distance is given by ![\begin{eqnarray} L = \frac{c}{H_0 q_0^2}\left[q_0 z - \left(1 - q_0\right)\left(\sqrt{1+2q_0 z}-1\right)\right]. \end{eqnarray}](/articles/aa/full_html/2011/09/aa15808-10/aa15808-10-eq30.png) (4)This oversimplified phenomenological description of QG models the foamy structure of space-time with only the two parameters a0 and α at the first order in amplitude fluctuations. By varying α, one obtains the three main scenarios of QG. The random walk model has α = 1/2 and random perturbations of space-time add incoherently with a square root dependence in the simplest case, or even following a more general distribution function. Examples are the works by Amelino-Camelia (2000) and Ng & van Dam (1994). The holographic model, which is consistent with Beckenstein-Hawking’s holographic principle and black hole entropy, has α = 2/3 (’t Hooft 2003). The value α = 1 describes the standard model of QG in which the gravitational field fluctuations are close to the Planck time (Smolin 2003; Rovelli 2004).
(4)This oversimplified phenomenological description of QG models the foamy structure of space-time with only the two parameters a0 and α at the first order in amplitude fluctuations. By varying α, one obtains the three main scenarios of QG. The random walk model has α = 1/2 and random perturbations of space-time add incoherently with a square root dependence in the simplest case, or even following a more general distribution function. Examples are the works by Amelino-Camelia (2000) and Ng & van Dam (1994). The holographic model, which is consistent with Beckenstein-Hawking’s holographic principle and black hole entropy, has α = 2/3 (’t Hooft 2003). The value α = 1 describes the standard model of QG in which the gravitational field fluctuations are close to the Planck time (Smolin 2003; Rovelli 2004).
Those effects can in principle be detected by analyzing possible modifications of the interference fringe structures using stellar interferometry. Equivalently, the cumulated phase variation can also be detected by imaging and analyzing, with a diffraction-limited telescope, the ring structure of Airy disks of cosmological point-like sources (Ragazzoni et al. 2003). Airy rings are still observed if the cumulated phase is limited to the value δφ ≤ 2π.
Previous results, based on data from stars and extragalactic sources (Ng & van Dam 1994; Lieu & Hillman 2003), seemed to rule out both the random walk model and the holographic principle and to put severe limits on the standard model. Similarly, the standard model also appeared to be ruled out by data on PKS1413+35 (z = 0.247) and by the detection of the Airy rings from SN 1994D (z = 0.001494) (Ragazzoni et al. 2003). However, in these conclusions the authors did not consider the more recent (Ng 2003) possibility that the space-time fluctuations may cumulate across long distances and partially compensate for the effects of the phase variations. In this case the correction factor is (L/λ) − α and only the random walk model could be excluded with the data available so far. A more sensitive analysis performed by Steinbring (2007), about the Strehl ratios of high-redshift QSOs, pointed out a possible deterioration of the interference structures due to the space time foam.
In this paper we resume the test on QSOs with a new approach to the data analysis and we put new upper limits on the QG fluctuations by analyzing the images of distant QSOs, observed by the Hubble Space Telescope (HST) with a software ad-hoc developed for this purpose.
With our estimates, if we neglect those possible cumulating phase effects, all the models of space-time foam would be immediately ruled out, thereby posing strict limits on the standard model. However, in our paper we use a more conservative approach, in which the space-time fluctuations are expected to compensate for their variations owing to their “averaging” and “smoothing” during the propagation of the light beam, causing the lack of detection of space-time fluctuations.
2. Data analysis
We searched for QG effects on the interference patterns of the high-redshift QSOs taken from the archival HST ACS snapshot survey of Sloan Digital Sky Survey (SDSS) sources (Proposal: 9472, PI: Strauss) and described by Richards et al. (2006). The dataset consists of 157 sources located in the redshift interval 4 < z < 5.4 and acquired with filter F775W (λc = 776.4 nm, bandwidth Δλ = 152.8 nm). Four other sources, located at redshifts 5.7 < z < 6.3, were instead taken with the filter F850LP (λc = 944.5 nm, bandwidth Δλ = 122.9 nm). The detector used in the observations was the High Resolution Camera (HRC), which has a pixel scale of 0.0246 arcsec. We used in our analysis the drizzled (DRZ) images that were corrected for geometric effects. The DRZ files were all reduced by adopting the standard procedure, including the overscan-, bias-, and dark-corrections and the flat-field and the photometrical calibration.
The luminosity distances of the QSOs, L, were calculated by assuming a concordance Universe model described in Krauss (2002): H0 = 72 km s-1 Mpc-1, (ΩM,ΩΛ) = (0.3,0.7), and also by taking the small effects on λ due to the expansion of the Universe into account.
To determine the QG effects through the progressive image degradation of a distant source, we estimated the Strehl ratio S of the source for a given wavelength λ through the empirical phase variation 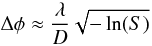 (5)where D = 2.4 m is the telescope diameter. The Strehl ratio S is defined as the ratio between the actual observed peak intensity (Max)source and what is theoretically expected from an unaberrated telescope (Max)th
(5)where D = 2.4 m is the telescope diameter. The Strehl ratio S is defined as the ratio between the actual observed peak intensity (Max)source and what is theoretically expected from an unaberrated telescope (Max)th![\begin{equation} S = \frac{\mathrm{(Max)}_\mathrm{source}}{\mathrm{(Max)}_\mathrm{th}}\sim \exp \left[ -\left(\Delta \phi \frac{D}\lambda \right)^2\right]\cdot \end{equation}](/articles/aa/full_html/2011/09/aa15808-10/aa15808-10-eq53.png) (6)From the Strehl ratio S we obtain the total phase variation Δφ that for QSOs can be written as
(6)From the Strehl ratio S we obtain the total phase variation Δφ that for QSOs can be written as 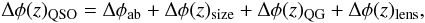 (7)where Δφab is the phase variation due to the aberrations present in the optical path of HST, ΔφQG those due to QG, Δφsize to the resolvability of QSOs and/or their host galaxies, and Δφ(z)lens to the gravitational lensing. The phase variation due to gravitational lensing, averaged in all the exposures of the dataset, is expected to behave as an increase in the blurring already caused by the QG effects, so it cannot, in principle, be easily separated from the latter ones except in special cases. The presence of spikes, caustics, and other typical effects of microlensing were not been observed in our sample. Because of this, the detection of QG effects would be overestimated, because unavoidably entangled with gravitational lensing and optical aberration effects.
(7)where Δφab is the phase variation due to the aberrations present in the optical path of HST, ΔφQG those due to QG, Δφsize to the resolvability of QSOs and/or their host galaxies, and Δφ(z)lens to the gravitational lensing. The phase variation due to gravitational lensing, averaged in all the exposures of the dataset, is expected to behave as an increase in the blurring already caused by the QG effects, so it cannot, in principle, be easily separated from the latter ones except in special cases. The presence of spikes, caustics, and other typical effects of microlensing were not been observed in our sample. Because of this, the detection of QG effects would be overestimated, because unavoidably entangled with gravitational lensing and optical aberration effects.
To reduce the blurring caused by the aberrations of the telescope, we modeled this image degradation effect by analyzing a sample of pictures of stars. The effects of QG are negligible at non cosmological distances and Δφstar ≃ Δφab.
In the case of the QSOs, we now consider the quantity ![\begin{eqnarray} \left(\Delta\phi(z)_{\rm QSO}\right)_\mathrm{Corrected} &=& \Delta \phi(z)_\mathrm{QSO} - \langle\Delta \phi\rangle_\mathrm{star} \nonumber\\[1.5mm] &\simeq& \Delta\phi(z)_\mathrm{size} \!+\! \Delta\phi(z)_\mathrm{QG} \!+\! \Delta\phi(z)_\mathrm{lens} \!\pm\! \delta\phi_{\rm star}. \label{eq6} \end{eqnarray}](/articles/aa/full_html/2011/09/aa15808-10/aa15808-10-eq61.png) (8)To adopt a more conservative approach, we use the averaged value of the phase variation ⟨Δφ⟩ star instead of the dispersion of Δφstar values found in the sample of the stars analyzed by us to calibrate our procedure. The quantity δφstars includes the errors due to the data analysis, the different positions on the detector and the different colors of the stars. The indeterminant δφcolor ≲ 10-8 rad represents the error due to the different colors found between the stars and QSOs. This quantity has been estimated by analyzing the PSFs generated by the Tiny Tim software.
(8)To adopt a more conservative approach, we use the averaged value of the phase variation ⟨Δφ⟩ star instead of the dispersion of Δφstar values found in the sample of the stars analyzed by us to calibrate our procedure. The quantity δφstars includes the errors due to the data analysis, the different positions on the detector and the different colors of the stars. The indeterminant δφcolor ≲ 10-8 rad represents the error due to the different colors found between the stars and QSOs. This quantity has been estimated by analyzing the PSFs generated by the Tiny Tim software.
Our approach is different from the procedure applied by Steinbring (2007), in which the Strehl ratios of QSOs were not corrected but only compared to an appropriate PSF generated for each of the QSOs by the Tiny Tim software. In fact, we did not assume any particular PSF model in our investigation, and we corrected the phase variation of QSOs by using the correction terms derived empirically from galactic stars in Eq. (8).
 |
Fig. 1 Left: HST image of the QSO QSO 0153-0011, IAU name SDSS J015339.60-001104.8 located at z = 4.205. The field of view is 15 × 15 pixels. Center: we show the central region (3 × 3 pixels) reconstructed using the function F (Eq. (10)). We plot the cartesian axes centered on the maximum of the intensity pattern. Here ϵ = 0.23 and α = 0.14 rad. Each pixel of the analyzed area is divided into 15 × 15 sub-pixels. Right: we show the residuals of the central analyzed area (3 × 3 pixels). |
 |
Fig. 2 Top: 1d cut along the x-axis (solid line) and the y-axis (dashed line) of the measured intensity of QSO SDSS J015339.60-001104.8. We analyzed the area within the two dotted lines. Bottom: we show the measured intensity (red line), the interpolated function F (solid blue line), the intensity of the reconstructed image (dashed blu line), and the residuals (dotted blue line) of the 1d cut along the x-axis (left) and the y-axis (right) of the central area (3 × 3 pixels). |
For our analysis we developed a dedicated software to determine the position and the maximum of QSOs and stars. For each source imaged by the ACS camera, we assumed that the central region of the interference structure has an elliptical symmetry. The position and the value of the maximum of the light pattern are determined in a region of 3 × 3 pixels. The light intensity distribution is then interpolated by a 2D function ![\begin{eqnarray} F \left(x,y,\left[mx,cx,cy,\epsilon,\theta, \sigma_1, \sigma_2\right]\right) = \frac{mx}{\sigma_1+\sigma_2} \\[1.5mm] \times \sum^2_{n=1}\sigma_{3-n}\exp\left[-\frac{x_1^2(x,\cdots)-\epsilon x_1^2(x,\cdots) + y_1^2(x,\cdots)}{2\sigma_n^2(1-\epsilon)}\right] \label{methods} \end{eqnarray}](/articles/aa/full_html/2011/09/aa15808-10/aa15808-10-eq74.png) where the pair (cx,cy) identifies the position of the maximum (mx) in the Cartesian coordinate system, the origin of which is placed on the center of the brighter pixel. The quantity ϵ is the eccentricity of the ellipse, and θ is the rotation angle between the axes of the ellipse and the cartesian axes. The parameters σ1 and σ2 modify the shape of the function F, and we write the argument of Eq. (10) as
where the pair (cx,cy) identifies the position of the maximum (mx) in the Cartesian coordinate system, the origin of which is placed on the center of the brighter pixel. The quantity ϵ is the eccentricity of the ellipse, and θ is the rotation angle between the axes of the ellipse and the cartesian axes. The parameters σ1 and σ2 modify the shape of the function F, and we write the argument of Eq. (10) as ![\begin{eqnarray} x_1(x,y,cx,cy,\theta)&=&(x-cx)\,\cos\,\theta-(y-cy)\,\sin\,\theta \nonumber \\[1.5mm] y_1(x,y,cx,cy,\theta)&=&(x-cx)\,\sin\,\theta+(y-cy)\,\cos\,\theta. \end{eqnarray}](/articles/aa/full_html/2011/09/aa15808-10/aa15808-10-eq81.png) (11)With a recursive procedure, we tune the values of the parameters mx, cx, cy, ϵ, θ, σ1, σ2 of the 2D function, F, until minimizing the difference between the measured and the fitted intensity of each pixel, on a 3 × 3 matrix situated around the brightest pixel. In the calculations, each pixel is divided into 15 × 15 subpixels, and for each of these divisions the procedure determines the intensity as a function of the position in the detector. At the end, we obtained both the position of the center and the intensity of the light pattern in the 3 × 3 area with a precision of 15 × 15 division for each pixel (see Figs. 1 and 2). We found deviations between the fitted and measured intensities to be less than 1%. It is important to point out that we considered only the light distribution inside the region delimited by the inner Airy diffraction ring. The values of the maxima of stars and QSOs are normalized with respect to the flux inside an area, centered on the brightest pixel, with a radius of 2 arcsec. An example is reported in Figs. 1 and 2 with the QSO QSO SDSS J015339.60-001104.8 (IAU) (z = 4.205).
(11)With a recursive procedure, we tune the values of the parameters mx, cx, cy, ϵ, θ, σ1, σ2 of the 2D function, F, until minimizing the difference between the measured and the fitted intensity of each pixel, on a 3 × 3 matrix situated around the brightest pixel. In the calculations, each pixel is divided into 15 × 15 subpixels, and for each of these divisions the procedure determines the intensity as a function of the position in the detector. At the end, we obtained both the position of the center and the intensity of the light pattern in the 3 × 3 area with a precision of 15 × 15 division for each pixel (see Figs. 1 and 2). We found deviations between the fitted and measured intensities to be less than 1%. It is important to point out that we considered only the light distribution inside the region delimited by the inner Airy diffraction ring. The values of the maxima of stars and QSOs are normalized with respect to the flux inside an area, centered on the brightest pixel, with a radius of 2 arcsec. An example is reported in Figs. 1 and 2 with the QSO QSO SDSS J015339.60-001104.8 (IAU) (z = 4.205).
 |
Fig. 3 Phase variation of 72 stars imaged with the High Resolution Camera with the filter F775W (upper panel) and 36 stars with the filter F850LP (bottom panel). We plot also the averaged value ⟨ Δφstar ⟩ (solid line) and the error δφstar. The dashed lines show the values ⟨ Δφstar ⟩ ± δφstar. |
 |
Fig. 4 Corrected phase variations of QSOs as a function of the redshift z. No blurring effects due to QG are observed. The linear interpolation of all the data sets show a positive trend, indicating the possible resolvability of the sources – blue solid line (color online). The red (color online) continuous and dashed “z”-shaped lines represent the expected growth of the phase variation, Δφ, as a function of the redshift z. The break of the two curves indicating the limits of QG effects with (red solid line) and without cosmological redshift corrections (red dashed line), are due to the change of filters, F775W and F850LP. |
In Fig. 3 we plot the phase variation of a sample of stars chosen with the values of the maximum of the diffraction pattern in the same range as the QSOs. We indicate with ⟨ Δφstar ⟩ the averaged value of the phase variation of the sample at which we associate the error δφstar defined as the maximum difference between the phase variation values of the stars and ⟨ Δφstar ⟩ .
In Fig. 4 we plot the corrected phase variation of the QSOs, (Δφ(z)QSO)Corrected, at which we associate the error δφstar. We found no blurring effects of QGs. The phase variations observed are much smaller than those expected from the space-time fluctuations described by the holographic principle model having α = 2/3 and a0 = 1. The phase variation (Δφ(z)QSO)Corrected and the redshift z, follow, at the first order, a linear relationship (Δφ(z)QSO)Corrected = az + b, whose coefficients are a = (0.26 ± 0.78) × 10-8 and b = (−0.5 ± 3.5) × 10-8, indicating the possible resolvability of QSOs and/or their host galaxies. We make use of the relations 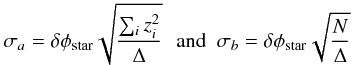 (12)to evaluate the errors on the coefficients a and b, where N is the total number of QSOs and
(12)to evaluate the errors on the coefficients a and b, where N is the total number of QSOs and 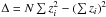 .
.
 |
Fig. 5 Parameter space a0 and α. The red region (colour online) in the left is the portion of the parameter space that is discarded by our observations with the most conservative approach that takes in consideration the cumulating effects of space-time fluctuations (see text). The white region in the middle is the additional portion of the parameter space that would be discarded if no compensation due to the cumulating effect of space-time occurs. The grey region in the right is the portion of the parameter space that cannot be excluded in any case. The data obtained with our analysis from the farthest QSOs exclude the random walk and the holographic models of space-time foam in the range of a0, here reported. These results, indicated by the label QSOs, go far beyond the previous estimates reported in the literature (indicated by z = 5.34 Universe), obtained without considering the cumulating effects of space-time. |
To put our limits to the two parameters of the QG, α and a0, we assume that (Δφ(z)QSO)Corrected ≥ Δφ(z)QG. Our limits are conservative because in the quantity (Δφ(z)QSO)Corrected we cannot disentangle the QG effects from those from the resolvability of the QSOs. In Fig. 5, we compare our results with the upper estimates found in the literature, which refer to the estimates obtained with sources located at distances up to z = 5.34 (Ragazzoni et al. 2003).
As reported in Fig. 6, our results exclude the random walk model and most of the holographic scenario of the space-time foam. For a0 = 1, one obtains (Δφ(z)QSO)Corrected = (0.26 z − 0.5) × 10-8 rad. By using the results previously discussed and the errors on the estimate of the coefficients a and b, one obtains the lower limit αmin = 0.677, with an 83.3% CL lower limit without considering the expansion of the universe, and αz = 0.684 with an 85.5% CL lower limit, if we take the cosmological redshift of the photons emitted by QSOs to the observer’s wavelength into account. Both the results exclude the Holographic scenario, but for low values of the the lowest-order amplitude of the quantum fluctuations, a0 ≲ 5 × 10-2 and a0 ≲ 0.15. The expected value for the amplitude of the quantum fluctuation is a0 ~ 1 (Ng 2003).
 |
Fig. 6 Limitations to the parameters a0 and α from QSOs. The excluded regions are below the dotted-dashed or the solid line depending on whether the photons redshifted to the observer wavelenghts, were taken into account. The holographic model (α = 2/3) of space-time foam is preserved for a0 ≲ 5 10-2 and a0 ≲ 0.15 (upper panel). The random walk model (α = 1/2) is preserved for a0 ≲ 10-13 and a0 ≲ 10-12 (lower panel). |
3. Conclusions
From the analysis of the diffraction images of the most distant QSOs, obtained with HST, we found no blurring effect that could be caused by the interaction of photons with quantum gravity fluctuations. Our results indicate that most of the models of space-time foam consistent with the holographic principle and, consequently, with black hole entropy, can be ruled out for most of the values of the fluctuation amplitude parameter a0.
Surprisingly, we did not find any indirect trace of the magnification of QSO images expected from the geometry of the Universe adopted in our calculations that could generate a possible additional blurring in the diffraction images combined with that expected from QG effects. The linear regression found in our estimates indicates that an eventual combination of QG effects and that possible of QSO magnification does not show any detectable contribution with the dataset available. If a significative trend were found, we should have estimated the QSO luminosities and calculated a QSO luminosity function (Richards et al. 2006) to disentangle this contribution from the one of QG fluctuations. One can suppose that either the Universe is flat in the interval 4 < z < 6 or that QSOs may present some unknown evolutionary effects at large z. Future observations with EELT, when equipped with adaptive optics, of QSOs at higher redshift also imaged with a filter at lower wavelengths should improve our results.
Finally, our results show the absence of any directional dependence on QG effects, since QSOs are located in very different regions of the sky at redshifts between 4 < z < 6.3. This would also limit the effects of intergalactic medium on the light across these cosmological distances in those observation bands. This confirms the cosmological principle on large scales. The isotropy on large scales of the Universe, verified by the distribution of superclusters of galaxies and QSOs on very large scales, is also verified through the independence of the behavior on smaller scales of the quantum fluctuations from any direction in space. Viewed on a large scale, the properties of the Universe and the laws of physics are the same for all observers.
3.1. The effect of QG fluctuations in quantum experiments
We can also infer from our results that quantum states will be preserved for very long distances because they are not affected by the blurring of space-time fluctuations. This is a very important result for quantum information and the foundations of quantum physics: a photon can travel undisturbed for billions of light years within the errors dictated by current HST technology. One can refer to Kok & Yurtsever (2003), Bouwmeester et al. (2000) and Bertlmann et al. (2002) for deeper insight. With our results we can set an upper limit to the phase factor imposed by the foamy structure of space-time to the photons that travel from the farthest QSOs caused by QG fluctuations, which is on the order of δφ ~ 2 × 10-8.
We consider an ideal quantum communication experiment, where Alice on the Earth wants to exchange single quanta of light with Bob located on the most distant QSO observed by HST, with wavelength λ = 1 μm and build a single–photon cryptographic quantum key. The two parties will find that the probability of having one qubit mismatch caused by quantum gravity is almost negligible with respect to the errors usually present in those experiments, affecting at maximum only one qubit over a set of ~5 × 107 qubits used in the building of the key. Earth-Moon and Earth-Mars experiments would cumulate a phase shift Δφ ~ 4.18 × 10-14 and Δφ ~ 2.15 × 10-13, respectively. The value α = 1 suggests a lower limit Δφ ~ 6.15 × 10-17 when noncumulating QG fluctuations occur on the Planck scales. Similar argumentations are valid for entangled photons.
Acknowledgments
The authors would thank B. Bassett, Bo Thidé, M. Stiavelli and the anonymous referee for the useful comments and improvements to the work. One of us, F.T., gratefully acknowledges the support of CARIPARO Foundation within the 2006 Program of Excellence.
References
- Amelino-Camelia, G. 1994, Mod. Phys. Lett. A, 9, 3415 [NASA ADS] [CrossRef] [Google Scholar]
- Amelino-Camelia, G. 2000, Lect. Notes Phys., 541, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Bertlmann, R., & Zeilinger, A. 2002, Quantum [un]speakables: from Bell to quantum information (Berlin, Heidelberg: Springer-Verlag) [Google Scholar]
- Bouwmeester, D., Ekert, A., & Zeilinger, A. 2000, The Physics of Quantum Information (Springer-Verlag) [Google Scholar]
- Christiansen, W. A., Ng, J. Y., & van Dam, H. 2006, Phys. Rev. Lett., 96, 051301 [Google Scholar]
- Dvali, G., & Sibiryakov, S. 2008, JHEP, 03, 007 [NASA ADS] [CrossRef] [Google Scholar]
- Hossenfelder, S. 2006, Nucl. Phys. A, 774, 865 [NASA ADS] [CrossRef] [Google Scholar]
- Hossenfelder, S., Hofmann, S., Bleicher, M., & Stöcker, H. 2002, Phys. Rev. D, 66, 10 [CrossRef] [Google Scholar]
- Hubble Space Telescope Institute – HST STSCI document 1999, http://www.stsci.edu/hst/acs/documents/acs_handout99.pdf [Google Scholar]
- Koch, B., Bleicher, M., & Hossenfelder, S. 2005, J. High Energy Phys., 10, 053 [NASA ADS] [CrossRef] [Google Scholar]
- Kok, P., & Yurtsever, U. 2003, Phys. Rev. D, 68, 085006 [NASA ADS] [CrossRef] [Google Scholar]
- Krauss, L. M. 2002, The State of the Universe: Cosmological Parameters 2002, in Astronomy, Cosmology and Fundamental Physics: Proc. ESO/CERN/ESA Symposium Held at Garching, Germany, 4–7 March, ESO Astrophysics Symposia [arXiv:astro-ph/0301012] [Google Scholar]
- LHC 2010, Official website at CERN, http://lhc.web.cern.ch/lhc/ [Google Scholar]
- Lieu, R., & Hillman, L. W. 2003, ApJ, 585, L77 [NASA ADS] [CrossRef] [Google Scholar]
- Ng, Y. J. 2003, Modern Phys. Lett. A, 18, 16, 1073 [Google Scholar]
- Ng, Y. J., & van Dam, H. 1994, Mod. Phys. Lett. A, 9, 04, 335 [NASA ADS] [CrossRef] [Google Scholar]
- Ng, Y. J., & van Dam, H. 2000, Found. Phys., 30, 795 [CrossRef] [Google Scholar]
- Ng, Y. J., Lee, D. S., Oh, M. C., & van Dam, H. 2001, Phys. Lett. B, 507, 236 [NASA ADS] [CrossRef] [Google Scholar]
- Ragazzoni, R., Turatto, M., & Gaessler, W. 2003, ApJ, 587, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Richards, G. T., Haiman, Z., Pindor, B., et al. 2006, AJ, 131, 49 [NASA ADS] [CrossRef] [Google Scholar]
- Rovelli, C. 2004, QG (Cambridge University Press) [Google Scholar]
- Smolin, L. 2003, unpublished [arXiv:hep-th/0303185] [Google Scholar]
- Steinbring, E. 2007, ApJ, 655, 714 [NASA ADS] [CrossRef] [Google Scholar]
- ’t Hooft, G. 1993, Dimensional Reduction in QG, in Salamfest (Singapore: World Scientific Co.), 284 [Google Scholar]
All Figures
 |
Fig. 1 Left: HST image of the QSO QSO 0153-0011, IAU name SDSS J015339.60-001104.8 located at z = 4.205. The field of view is 15 × 15 pixels. Center: we show the central region (3 × 3 pixels) reconstructed using the function F (Eq. (10)). We plot the cartesian axes centered on the maximum of the intensity pattern. Here ϵ = 0.23 and α = 0.14 rad. Each pixel of the analyzed area is divided into 15 × 15 sub-pixels. Right: we show the residuals of the central analyzed area (3 × 3 pixels). |
| In the text | |
 |
Fig. 2 Top: 1d cut along the x-axis (solid line) and the y-axis (dashed line) of the measured intensity of QSO SDSS J015339.60-001104.8. We analyzed the area within the two dotted lines. Bottom: we show the measured intensity (red line), the interpolated function F (solid blue line), the intensity of the reconstructed image (dashed blu line), and the residuals (dotted blue line) of the 1d cut along the x-axis (left) and the y-axis (right) of the central area (3 × 3 pixels). |
| In the text | |
 |
Fig. 3 Phase variation of 72 stars imaged with the High Resolution Camera with the filter F775W (upper panel) and 36 stars with the filter F850LP (bottom panel). We plot also the averaged value ⟨ Δφstar ⟩ (solid line) and the error δφstar. The dashed lines show the values ⟨ Δφstar ⟩ ± δφstar. |
| In the text | |
 |
Fig. 4 Corrected phase variations of QSOs as a function of the redshift z. No blurring effects due to QG are observed. The linear interpolation of all the data sets show a positive trend, indicating the possible resolvability of the sources – blue solid line (color online). The red (color online) continuous and dashed “z”-shaped lines represent the expected growth of the phase variation, Δφ, as a function of the redshift z. The break of the two curves indicating the limits of QG effects with (red solid line) and without cosmological redshift corrections (red dashed line), are due to the change of filters, F775W and F850LP. |
| In the text | |
 |
Fig. 5 Parameter space a0 and α. The red region (colour online) in the left is the portion of the parameter space that is discarded by our observations with the most conservative approach that takes in consideration the cumulating effects of space-time fluctuations (see text). The white region in the middle is the additional portion of the parameter space that would be discarded if no compensation due to the cumulating effect of space-time occurs. The grey region in the right is the portion of the parameter space that cannot be excluded in any case. The data obtained with our analysis from the farthest QSOs exclude the random walk and the holographic models of space-time foam in the range of a0, here reported. These results, indicated by the label QSOs, go far beyond the previous estimates reported in the literature (indicated by z = 5.34 Universe), obtained without considering the cumulating effects of space-time. |
| In the text | |
 |
Fig. 6 Limitations to the parameters a0 and α from QSOs. The excluded regions are below the dotted-dashed or the solid line depending on whether the photons redshifted to the observer wavelenghts, were taken into account. The holographic model (α = 2/3) of space-time foam is preserved for a0 ≲ 5 10-2 and a0 ≲ 0.15 (upper panel). The random walk model (α = 1/2) is preserved for a0 ≲ 10-13 and a0 ≲ 10-12 (lower panel). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


