| Issue |
A&A
Volume 532, August 2011
|
|
|---|---|---|
| Article Number | A114 | |
| Number of page(s) | 9 | |
| Section | Numerical methods and codes | |
| DOI | https://doi.org/10.1051/0004-6361/201116630 | |
| Published online | 03 August 2011 | |
Modeling supernova remnants: effects of diffusive cosmic-ray acceleration on the evolution and application to observations
1
Astronomical Institute Utrecht, Utrecht University, PO Box 80000, 3508TA Utrecht, The Netherlands
e-mail: D.Kosenko@uu.nl
2
ITEP, Moscow, 117218, Russia
3
SAI, Moscow, 119992, Russia
4
IPMU, Tokyo Universiy, Kashiwa 277-8583, Japan
Received: 2 February 2011
Accepted: 21 May 2011
We present numerical models for supernova remnant evolution, using a new version of the hydrodynamical code SUPREMNA. We added a cosmic-ray diffusion equation to the code scheme, employing a two-fluid approximation. We investigate the dynamics of the simulated supernova remnants with different values of the cosmic-ray acceleration efficiency and the diffusion coefficient. We compare the numerical models with observational data of Tycho’s and SN1006 supernova remnants. We find models that reproduce the observed locations of the blast wave, contact discontinuity, and reverse shock for both remnants, thus allowing us to estimate the contribution of cosmic-ray particles to total pressure and cosmic-ray energy losses in these supernova remnants. We evaluate the energy losses due to cosmic rays escape in Tycho’s supernova remnant to be 10 − 20% of the kinetic energy flux and 20 − 50% in SN1006.
Key words: acceleration of particles / diffusion / hydrodynamics / shock waves / methods: numerical / ISM: supernova remnants
© ESO, 2011
1. Introduction
Clear evidence of the effective acceleration of cosmic-ray (CR) particles in young supernova remnants (SNR) stems from TeV observations of the Galactic sources by H.E.S.S. (Aharonian et al. 2005, 2006), CANGAROO-II (Katagiri et al. 2005), MAGIC (Albert et al. 2007), SHALON (Sinitsyna et al. 2009), and VERITAS (Acciari et al. 2009, 2010). In addition, discoveries of non-thermal X-ray emission from SNRs (see a review by Reynolds 2008) imply that electrons are accelerated to TeV energies in supernova remnants (SNR).
In the past few decades a number of numerical methods to simulate CR acceleration in supernova remnants have been developed. An extensive review of some of these techniques can be found in Malkov & O’C Drury (2001) and Caprioli et al. (2010). Nearby Galactic SNRs provide an excellent opportunity to test these models and to study the efficiency of CR acceleration processes. For example, the proximity of the blast wave (BW) to a contact discontinuity (CD) in Tycho SNR measured by Warren et al. (2005) is inconsistent with adiabatic hydrodynamic models of SNR evolution, and can be explained only if cosmic-ray acceleration of the particles occurs at the forward shock. Similar evidence was presented for SN1006 supernova remnant by Cassam-Chenaï et al. (2008) and Miceli et al. (2009).
Both these objects have been used in testing the numerical and analytical models (e.g. Ellison 2001; Ellison et al. 2007; Völk et al. 2008) of CR acceleration in SNRs. Two-dimensional simulations of Tycho’s SNR evolution and the investigation of Rayleigh-Taylor instability development with the gas adiabatic index values down to γ = 1.1 were performed by Wang (2011). Three-dimentional hydrodynamical modeling of Tycho was conducted by Ferrand et al. (2010).
The effects of the shock modification by cosmic rays in Kepler SNR were studied by Decourchelle et al. (2000), who modeled the X-ray spectra using a non-linear non-equilibrium ionization method. A more detailed study of the acceleration effects on the thermal emission from the shocked supernova ejecta was conducted by Patnaude et al. (2010).
In this study, we present hydrodynamical (HD) simulations of supernova remnant evolution that account for diffusive cosmic-ray acceleration. We introduced a CR diffusion equation into the numerical code supremna, developed by Sorokina et al. (2004); Kosenko (2006). This code calculates the evolution of a supernova remnant assuming spherical symmetry and takes into account time-dependent ionization and thermal conduction. To include the effects of CR acceleration into the scheme, we apply a two-fluid approximation, i.e. we introduce a CR diffusion equation into the system of hydrodynamical equations.
Employing this renewed package, we created sets of hydrodynamical models with different values of CR-related parameters. We compare the results of our simulations with the observations of Tycho’s and SN1006 supernova remnants.
The paper is structured as follows. In Sect. 2, we describe the basic equations we use for the simulations, and in Sect. 3 we show the results of modeling. We compare our models with the observations in Sect. 4. We summarize the results in Sect. 5, discuss them in Sect. 6, and present our conclusions in Sect. 7.
2. Basic equations and method
2.1. Code description
To model the evolution of supernova remnants, we employ the hydrodynamical code supremna, which was originally developed by Sorokina et al. (2004). The method accounts for electron thermal conduction and includes self-consistent calculations of time-dependent ionization processes. The electron and ion temperature equilibration processes are parametrized.
The code uses an implicit Lagranian formulation for a one-dimensional spherical-symmetrical geometry. The hydrodynamical evolution of the remnant is coupled with a system of kinetic equations of ionization balance to calculate self-consistently the non-equillibrium ionization state of the shocked plasma. Ion and electron temperatures are treated separately by taking into account electron thermal conduction (see Appendix A).
To describe the effects of collisionless energy exchange, Sorokina et al. (2004) introduced a parameter qi (0 < qi < 1), which specifies a fraction of artificial viscosity Q. This fraction adds to the pressure of ions in Eqs. (A.3), and (A.5) and plays a role of a source term (the details are presented in Appendix). If only the collisional exchange is taken into account, then qi = (1.0 − me/mp) and the standard system of equations with the heating of only ions at the front is solved.
The artificial viscosity (Richtmyer & Morton 1967) term is defined as follows  (1)with dimensionless parameter Aq = 2 and Δu – velocity difference at neighboring mesh points.
(1)with dimensionless parameter Aq = 2 and Δu – velocity difference at neighboring mesh points.
2.2. Cosmic-ray diffusion equation
To adapt the scheme to simulations of SNRs we need to take into account cosmic-ray (CR) diffusion. We used two-fluid approximation (e.g. Kang & Jones 1990; Ko 1995; Malkov & O’C Drury 2001; Blasi 2002, 2004; Wagner et al. 2006; Zirakashvili & Aharonian 2010) and introduced additional CR diffusion equation into the (A.1) − (A.5) set.
The one-dimensional CR diffusion equation in the Eulerian frame for the plane-parallel case is given by 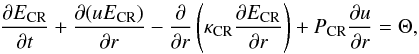 (2)where PCR = (γCR − 1)ECR is CR pressure, ECR – CR energy density, Θ is an external source of CR energy injection, and κCR is the diffusion coefficient. We assume an equation of state for CR matter with the fixed adiabatic exponent of γCR = 4/3,
(2)where PCR = (γCR − 1)ECR is CR pressure, ECR – CR energy density, Θ is an external source of CR energy injection, and κCR is the diffusion coefficient. We assume an equation of state for CR matter with the fixed adiabatic exponent of γCR = 4/3,
We generate a relativistic particle pressure PCR from the artificial viscosity Q term by introducing a parameter qCR that regulates the injection of CR particles. Thus we define the source term as Θ = qCRQ(∂u/∂r) (see Appendix B).
We note that a somewhat similar method was used by Zank et al. (1993), where the introduction of a source term into CR diffusion equation was performed via a “thermal leakage” mechanism. The particle distribution function was divided into two parts: particles with momentum larger than a certain value p0 were treated as CRs that propagate according to the CR diffusion equation. Thermal particles are energized because of the adiabatic compression or anomalous heating within a subshock.
In our study, we are not concerned with the microphysics of the generation and escape of the energetic particles, but more with the hydrodynamical consequences of the acceleration.
After transformation of Eq. (2) to our adopted Lagranian frame, we get 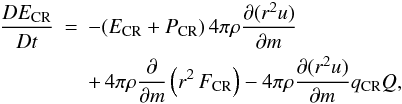 (3)where DECR/Dt = ∂ECR/∂t + 4πr2uρ(∂ECR/∂m).
(3)where DECR/Dt = ∂ECR/∂t + 4πr2uρ(∂ECR/∂m).
We treat cosmic-ray flux FCR in a similar way to the treatment of thermal electron conduction in Sorokina et al. (2004) where 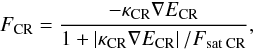 (4)and FsatCR = cPCR/2 (c – speed of light) is the saturated value of the cosmic-ray flux (the Eddington approximation). At this stage, we assume a constant diffusion coefficient κCR, as we do not have any information about the spectrum of cosmic rays.
(4)and FsatCR = cPCR/2 (c – speed of light) is the saturated value of the cosmic-ray flux (the Eddington approximation). At this stage, we assume a constant diffusion coefficient κCR, as we do not have any information about the spectrum of cosmic rays.
In reality, the diffusion will depend on particle energy. In that case, the diffusion coefficient used by us should be regarded as pressure-weighted mean value. Moreover, according to non-linear cosmic-ray acceleration theory, efficient acceleration leads to hard spectra, in which case most of the energy, hence pressure, is contained in the particles with the highest energies. If the maximum energy is around 1015 eV, we expect a typical diffusion coefficient, under the assumption of Bohm-diffusion, of κCR = 1/3rgc = 3 × 1026(B/100 μG)-1(E/1015 eV) cm2 s-1 (rg – gyroradius, B – magnetic field, E – energy of the particle). The most important role of the diffusion coefficient in our calculations is in terms of the CR escape, as it drains energy from the plasma.
And finally, we alter Eq. (A.3) by adding a component of relativistic particle pressure PCR in such a way that 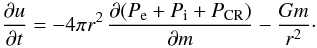 (5)The entire system of Eqs. (A.1), (5), (A.4), (A.5), and (3) describes the method, where electrons, ions, and cosmic-ray components are treated independently. The contributions to the pressure of these three components are governed by two free parameters qi and qCR.
(5)The entire system of Eqs. (A.1), (5), (A.4), (A.5), and (3) describes the method, where electrons, ions, and cosmic-ray components are treated independently. The contributions to the pressure of these three components are governed by two free parameters qi and qCR.
 |
Fig. 1 HD profiles for the SNR models at t = 440 years with ρCSM = 10-24 g cm-3. Top row shows the simulation with qCR = 0.0, middle row – qCR = 0.7, κCR = 1025 cm2 s-1; bottom row – qCR = 0.99, κCR = 1026 cm2 s-1. Left panels: density (black solid line, scale at the left-hand side), ion pressure (blue dash-dotted line, scale at the right-hand side), and CR pressure (blue dashed line, scale at the right-hand side). Right panels: velocity profile (black solid line, scale at the left-hand side), electron temperature profiles (blue dashed line, scale at the right-hand side), and ion temperature profiles (dashed-dotted line, scale at the right-hand side). |
3. Numerical models
We created a library of numerical models with various sets of parameters qCR and κCR. In the simulations, we used a delayed-detonation thermonuclear explosion model with E = 1.4 × 1051 erg (Woosley et al. 2007), where the CR pressure is initially 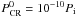 , and the temperature of the homogeneous ambient medium is T0 = 104 K. Using the artificial viscosity source term, we begin CR generation only at the forward shock.
, and the temperature of the homogeneous ambient medium is T0 = 104 K. Using the artificial viscosity source term, we begin CR generation only at the forward shock.
We considered two sets of models of supernova remnants. Parameters for one set (Tycho’s case) were assumed to be similar to those of Tycho’s SNR: the remnant is surrounded by homogeneous circumstellar matter of density ρ0 = 10-24 g cm-3 and the age of the system is 440 years. There are indications that the real ambient density in Tycho vicinity is lower. For example, Katsuda et al. (2010) from proper motion measurements found that n0 ≲ 0.2 cm-3, thus ρ0 ≲ 0.4 × 10-24 g cm-3. Nevertheless, taking into account that we consider an over-energetic initial explosion and that the radius of the remnant R ∝ (E/ρ0)1/5 is a weak function of ambient density, we assume that our input parameters match those of Tycho’s SNR.
 |
Fig. 2 HD profiles for the SNR models at t = 1000 years with ρCSM = 4 × 10-26 g cm-3. Top row shows the simulation with qCR = 0.0, middle row – qCR = 0.7, κCR = 1025 cm2 s-1; bottom row – qCR = 0.99, κCR = 1026 cm2 s-1. Left panels: density (black solid line, scale at the left-hand side), ion pressure (blue dash-dotted line, scale at the right-hand side), and CR pressure (blue dashed line, scale at the right-hand side). Right panels: velocity profile (black solid line, scale at the left-hand side), electron temperature profiles (blue dashed line, scale at the right-hand side), and ion temperature profiles (dashed-dotted line, scale at the right-hand side). |
Examples of the hydrodynamical profiles of a few of these models are presented in Fig. 1. The top row presents the simulation with qCR = 0.0, the middle row qCR = 0.7, and κCR = 1025 cm2 s-1; in the bottom row, qCR = 0.99, and κCR = 1026 cm2 s-1. In the left panels, we present the density (black solid, scale at the left-hand side), ion pressure (blue dash-dotted, scale at the right-hand side), CR pressure (blue dashed, scale at the right-hand side), and in the right panels the solid lines show the velocity profiles (scale at the left-hand side), the dashed lines the electron temperature profiles, and the dashed-dotted lines the ion temperature profiles (according to scale at the right-hand side).
Physical parameters of another set of simulations (for SN1006 case) were chosen to match the conditions of the remnant of SN1006, an ambient homogeneous circumstellar matter of density ρ0 = 4 × 10-26 g cm-3 and the age of 1000 years. The hydrodynamical profiles of a few of these models are presented in Fig. 2.
 |
Fig. 3 Top panel: Rankine-Hugoniot relation in Eq. (6) and data points from all the numerical models. The shade of the symbols reflects the efficiency of CR acceleration. Bottom row: left panel shows evolution of compression ration χ, right panel shows evolution of contact discontinuity to blast wave radii ratio, ρ0 = 10-24 g cm-3. Dashed lines show models with qCR = 0.7, solid lines – qCR = 0.9. Different colors indicate different values of the diffusion coefficient (see legend, where κCR values are given in units of cm2 s-1). |
The numerical models were verified to satisfy the Rankine-Hugoniot condition, derived for a system with energy losses (e.g. Malkov & O’C Drury 2001; Bykov et al. 2008; Vink et al. 2010). We checked the relation 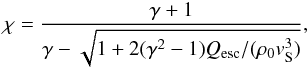 (6)where χ = ρmax/ρ0 is the compression ratio behind the shock, γ is the adiabatic index, Qesc is the energy lost by the system, and vS is the blast wave speed. We rewrite the energy loss term from the energy flux conservation law (e.g. Eq. (12) in Vink et al. 2010) via a dimensionless parameter such as
(6)where χ = ρmax/ρ0 is the compression ratio behind the shock, γ is the adiabatic index, Qesc is the energy lost by the system, and vS is the blast wave speed. We rewrite the energy loss term from the energy flux conservation law (e.g. Eq. (12) in Vink et al. 2010) via a dimensionless parameter such as 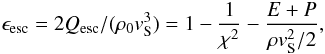 (7)where E,P, and ρ are the total energy density, pressure, and matter density behind the shock.
(7)where E,P, and ρ are the total energy density, pressure, and matter density behind the shock.
 |
Fig. 4 Measured and modeled radii ratios for Tycho’s (left-hand panel) and SN1006 (right-hand panel) SNRs. RCD/RRW (black symbols) and RRS/RRW (grey symbols). Horizontal bars indicate the measurements of Warren et al. (2005) and Miceli et al. (2009). |
The top panel of Fig. 3 shows the relation given in Eq. (6) for γ = 5/3 as a solid line and γ = 4/3 as a dashed line. Data from the numerical models are presented with colored circles. The shade of the symbols indicates the efficiency of the CR acceleration, so that a red point corresponds to the models with qCR = 0.1 and cyan to the models with qCR = 0.99.
The bottom panel of Fig. 3 shows the evolution of the compression ratio and ratio of the contact discontinuity (CD) to blast wave (BW) radii. The profiles are created from the Tycho’s case models with ρ0 = 10-24 g cm-3. The dashed lines show the simulation with qCR = 0.7, and the solid lines qCR = 0.9. Different colors correspond to different values of κCR (see legend). The curves are compared to those from Völk et al. (2008). We see that the χ profiles differ from the curves presented for Tycho’s SNR in Völk et al. (Fig. 1 in 2008). In our approach, the compression ratio is an increasing function of time, whereas in Völk et al. (2008)χ decreases with time. The ratios of the radii in our cases also do not exactly follow the same trend as in Völk et al. (2008).
This divergence in the results can be explained by the magnetic field behind the shock. Völk et al. (2005) show that on average the downstream magnetic field pressure B2/(8π) is proportional to the preshock gas ram pressure 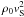 . Both the ram pressure and the magnetic field are diluted as the remnant expands, thus the acceleration then decreases. In our models, the acceleration efficiency depends only on the ram pressure (Eq. (1)) and does not take into account the vanishing magnetic field. Thus with a constant qCR parameter, we somewhat underestimate the efficiency of the CR acceleration at the earlier times of the evolution, and we overestimate it at later times.
. Both the ram pressure and the magnetic field are diluted as the remnant expands, thus the acceleration then decreases. In our models, the acceleration efficiency depends only on the ram pressure (Eq. (1)) and does not take into account the vanishing magnetic field. Thus with a constant qCR parameter, we somewhat underestimate the efficiency of the CR acceleration at the earlier times of the evolution, and we overestimate it at later times.
For the simulation with efficient acceleration qCR = 0.9 and diffusion coefficient κCR = 1027 cm2 s-1 (solid magenta line) at an age of greater than 1000 years, a density spike starts to form. The structure of this spike is illustrated in the bottom rows of Figs. 1 and 2. Similar spikes are also present in the CR dominated shocks in the simulations of Wagner et al. (2009). Nevertheless, this type of structure is produced only for extreme values of the CR parameters and is unlikely to be produced in reality.
The CR precursor can be traced in the hydrodynamical profiles, presented in Figs. 1 and 2, but the precursor region in front of the blast wave is thin (~1017 cm) and cannot be accurately resolved.
4. Comparison with the Galactic SNRs
There is evidence that the shocks of Tycho (e.g. Warren et al. 2005) and SN1006 (Cassam-Chenaï et al. 2008; Orlando et al. 2008; Miceli et al. 2009) are modified by both the acceleration and diffusion of CR particles. Thus, we applied our numerical models to these Galactic supernova remnants. The locations of the blast wave (BW), the contact discontinuity (CD), and the reverse shock (RS) measured by Warren et al. (2005) for Tycho’s SNR, were compared with the corresponding values obtained in our simulations.
The right plot of Fig. 4 shows the measured (horizontal bars) radii ratios and the results of the simulations (asterisks). We accounted for the three-dimentional projection effects and Rayleigh-Taylor (R-T) instabilities1, which can produce fingers of ejecta that protrude out toward the BW (Chevalier et al. 1992; Wang & Chevalier 2001), by adopting a correction factor of 1.07 (Warren et al. 2005; Cassam-Chenaï et al. 2008; Völk et al. 2008, and references therein) to the modeled CD:BW radii ratios. The models that match the observed radii are indicated in boldface.
We also performed simulations with CR acceleration at the reverse shock with the same injection efficiency qCR and diffusion coefficient κCR as at the blast wave. In these models, the layer of the shocked supernova ejecta becomes thinner, and the reverse shock approaches too close to the forward shock compared to the data from Tycho’s SNR. Thus, we did not study these scenarios in details.
From an analysis of the data, presented in Fig. 4, we infer that the most plausible models for Tycho are those with qCR = 0.4 − 0.7, κCR = 1024 − 1025 cm2 s-1. Models with qCR = 0.3, κCR = 1026 cm2 s-1, and qCR = 0.9, κCR = 1024 cm2 s-1 also match the observation. Nevertheless, if we assume that the diffusion coefficient κCR increases with the energy of the CR particles and that the amount of energetic particles increases with the injection efficiency qCR, then we conclude that neither the low efficiency and high diffusion nor the high efficiency and low diffusion scenarios occur in reality.
For Tycho, the simulations yield the compression ratio χ = 4.3−6.8. These results agree with those of Cassam-Chenaï et al. (2007) and Völk et al. (2008).
A similar comparison of the models to SN1006 remnant data (Miceli et al. 2009) is presented in the right plot of Fig. 4. From these models, we obtain the compression ratio behind the blast wave of the remnant χ = 4.7 − 8.3. All the models with qCR = (0.3 − 0.9) match the observational data. The models of SN1006 with a constant adiabatic index γ (Petruk et al. 2011) could not explain the observed small distance between the forward shock and contact discontinuity.
 |
Fig. 5 Left panel: CR pressure versus diffusion coefficient. Right panel: compression ratio χ versus diffusion coefficient κCR for different values of qCR (Tycho’s case). |
5. Results
We have developed a hydro-code to simulate the evolution of a spherically-symmetrical supernova remnants and to account for CR acceleration and time-dependent ionization. We created two sets of hydrodynamical models with different values of parameters for CR acceleration efficiency and CR energy losses. The comparison of these models with the measurement of BW:CD:RS radii of the Galactic SNRs suggests the following.
The simulations with qCR = (0.4−0.7) and κCR = (1024 − 1025) cm2 s-1 match the observed radii ratios of Tycho’s SNR (Fig. 4). This range of values agrees with the estimate of κCR = 2 × 1024 cm2 s-1 found by Wagner et al. (2009) for Tycho and with the findings of Parizot et al. (2006) and Eriksen et al. (2011). We derived the compression ratio of χ = (4.3−6.8), energy losses due to CR diffusion of ϵesc = (0.1−0.2), and distance to Tycho’s SNR of 3.3 kpc2. The distance agrees with the results of Hayato et al. (2010) and Tian & Leahy (2011).
For the SN1006 remnant, we obtained χ = (4.7−8.3) with losses of ϵesc = (0.2−0.5). We inferred the distance to the SN1006 remnant to be 2.0 kpc.
6. Discussion
The observed ratios of the SNR reverse shock, the contact discontinuity, and the forward shock radii may depend on a number of yet unknown factors, such as the structure of the CSM (potential presupernova wind and density enhancement, see discussion in Kosenko et al. 2010; Xu et al. 2011), the CR acceleration, and the diffusion efficiency. Thus the results, presented in this study do not claim to be exhaustive, but rather describe a scenario that is capable of explaining the observations within the cosmic-ray acceleration paradigm.
In the numerical models considered here, we do not turn on the CR acceleration at the reverse shock. The results of the simulations with the same acceleration efficiency (qCR) at the reverse shock do not match the observed RRS/RBW ratio for Tycho’s SNR. Helder & Vink (2008) and Zirakashvili & Aharonian (2010) discovered the possible acceleration of particles by the reverse shock of CasA and SNR RX J1713.7–3946. In addition, numerical simulations of Schure et al. (2010) showed that the reverse shock can re-accelerate particles, provided that the magnetic field is sufficiently strong. However, our models indicate that for Tycho’s SNR the cosmic-ray acceleration at the reverse shock is not as efficient as at the forward shock.
The possible factors that suppress the acceleration at the reverse shock are as follows. The reverse shock velocity in the framework of ejecta is lower in comparison with the blast wave, and acceleration efficiency is probably an increasing function of the shock velocity. Moreover, the initial magnetic field of the progenitor white dwarf is diluted in the remnant by many orders of magnitude. A non-vanishing magnetic field is necessary for the acceleration to take place. In addition, the low efficiency of CR acceleration at the reverse shock was found for Kepler SNR by Decourchelle et al. (2000).
We compared the input and output parameters of the simulation with the Rankine-Hugoniot (RH) relations, which were derived in a two-fluid approach for the steady-state situation and a plane-parallel geometry, presented in Vink et al. (2010). On the one hand, the values of PCR/Ptot measured in the models directly behind the shock cannot be compared to w defined in Vink et al. (2010). The diffusion coefficient κCR implements the CR energy loss, thus the CR pressure PCR is a non-monotonic function of κCR (Fig. 5). The pressure decreases with κCR in the regime of efficient acceleration, where κCR > 3 × 1025 cm2 s-1. This is the opposite of the behavior of w defined by Vink et al. (2010). A possible explanation is that the spherically symmetrical expansion and inward CR diffusion efficiently dilute the pressure, while in the plane-parallel case described by Vink et al. (2010) these effects are absent.
On the other hand, the parameter qCR defines the fraction of the CR pressure taken from the entropy pool created by the shock and in some sense can be attributed to w. Figure 6 shows profiles of the compression ratio ϵesc (left panel) and CR energy losses χ (right panel) as a function of w = PCR/Ptot (Fig. 1 in Vink et al. 2010,for Mach number M0 = 500). In the same panels, we plot ϵesc and χ measured in the models versus the input parameter qCR. The intensity of the data points corresponds to the value of κCR: the lowest value corresponds to the black asterisks, and the models with the highest value of κCR are shaded in light gray.
The right-hand plot of Fig. 6 can be explained with the help of the right-hand plot of Fig. 5, where compression ratios versus diffusion coefficient for different acceleration efficiencies qCR are presented. This plot shows that χ has a maximum at certain κCR. These maximal values of χ for different qCR follow the RH curve, which is plotted with a thick black line in the right plot of Fig. 6. Respectively, the maximum attainable energy losses are skirted by the RH curves presented in the left panel of Fig. 6.
 |
Fig. 6 Left panel: escape CR energy versus w and qCR. Right panel: compression ratio χ versus w and qCR (Tycho’s case). The Rankine-Hugoniot black curve corresponds to Mach number M0 = 500. Intensity of the data point is inversely proportional to the values of diffusion coefficient κCR, i.e. black asterisks correspond to κCR = 1024 cm2 s-1, light grey ones correspond to κCR = 1027 cm2 s-1. |
The parameters qCR and κCR are fixed for each model in our method, while in reality they vary with time and location (e.g. Zirakashvili & Aharonian 2010). The effects of the variability of the diffusion coefficient was also discussed extensively by Lagage & Cesarsky (1983), where they point out that κCR increases away from the shock. Nevertheless, we assume that it is acceptable to use average constant values in this approach.
Even though we used two parameters to describe the CR component in our models, the theory of diffusive CR acceleration assumes that, qCR and κCR are not independent. Hence it will be possible to incorporate a physical relation between those two in the future, reducing the problem to a case with only one free parameter.
Finally, when comparing models with observations, we also considered a case with the lower R-T correction factor of 1.05. In this case, the models that match the observed radii yield a compression ratio for Tycho’s SNR that is systematically higher with χ = 4.6−8.5, but within the uncertainties of our approach and the errors of the radii measurements. Thus our final results are not altered considerably.
7. Conclusion
We have studied hydrodynamical models of supernova remnants evolution that account for diffusive cosmic-ray acceleration. We applied a two-fluid approach to investigate the effects of acceleration efficiency and energy losses on the observable properties on the remnant. We compared the results of our simulations with the measured radii of BW, CD, and RS of Tycho’s and SN1006 SNRs.
We analyzed the numerical models and checked that the Rankine-Hugoniot relation for compression ratio and energy loss is met (Fig. 3). This method has a list of shortcomings but it includes all important relevant physical processes and is easy to use for fast modeling of supernova remnants and comparison with observations.
We found that, to explain the radial properties of Tycho’s SNR, the simulations indicate that the compression ratio behind the blast wave must be in the range (4.3 − 6.8), and that energy loss due to cosmic-ray particle diffusion must be 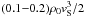 . The distance to the SNR is estimated to be 3.3 kpc. For the case of the SN1006 remnant, we found that χ = (4.7 − 8.3) with losses of
. The distance to the SNR is estimated to be 3.3 kpc. For the case of the SN1006 remnant, we found that χ = (4.7 − 8.3) with losses of 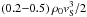 . The distance to the remnant is 2.0 kpc.
. The distance to the remnant is 2.0 kpc.
In the future, we plan to employ the developed package for calculation of detailed thermal X-ray emission from the supernova remnant models modified by the acceleration. The resulting synthetic spectra will allows us to study the effects of different physical conditions of the shock plasma on the X-ray spectra. The analysis will be performed for different explosion models (similar to the method of Badenes et al. 2006, 2008) and later compared with observations of young remnants of type Ia supernova.
Note that the R-T instability is not considerably affected by acceleration at the forward shock (Ferrand et al. 2010; Wang 2011).
Acknowledgments
D.K. is supported by an “open competition” grant and J.V. is supported by a Vidi grant from the Netherlands Organization for Scientific Research (PI J. Vink). The work of S.B. has been supported in part by World Premier International Research Center Initiative, MEXT, Japan, by Agency for Science and Innovations, Russia, contract 02.740.11.0250, and by grants RFBR 10-02-00249-a, Sci. Schools 3458.2010.2, 3899.2010.2, and IZ73Z0-128180/1 of the Swiss National Science Foundation (SCOPES). First of all, we thank the anonymous referee for valuable comments and discussions. The authors are grateful to S. Woosley for providing the models of thermonuclear supernovae. We thank A. Bykov and D. Ellison for useful references and discussion and also F. Bocchino, E.A. Helder, and K. Schure.
References
- Acciari, V. A., Aliu, E., Arlen, T., et al. 2009, ApJ, 698, L133 [NASA ADS] [CrossRef] [Google Scholar]
- Acciari, V. A., Aliu, E., Arlen, T., et al. 2010, ApJ, 714, 163 [Google Scholar]
- Aharonian, F., Akhperjanian, A. G., Bazer-Bachi, A. R., et al. 2005, A&A, 437, L7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Aharonian, F., Akhperjanian, A. G., Bazer-Bachi, A. R., et al. 2006, A&A, 449, 223 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Albert, J., Aliu, E., Anderhub, H., et al. 2007, ApJ, 664, L87 [NASA ADS] [CrossRef] [Google Scholar]
- Badenes, C., Borkowski, K. J., Hughes, J. P., Hwang, U., & Bravo, E. 2006, ApJ, 645, 1373 [NASA ADS] [CrossRef] [Google Scholar]
- Badenes, C., Hughes, J. P., Cassam-Chenaï, G., & Bravo, E. 2008, ApJ, 680, 1149 [NASA ADS] [CrossRef] [Google Scholar]
- Blasi, P. 2002, Astropart. Phys., 16, 429 [Google Scholar]
- Blasi, P. 2004, Astropart. Phys., 21, 45 [Google Scholar]
- Bykov, A. M., Dolag, K., & Durret, F. 2008, Space Sci. Rev., 134, 119 [NASA ADS] [CrossRef] [Google Scholar]
- Caprioli, D., Kang, H., Vladimirov, A. E., & Jones, T. W. 2010, MNRAS, 407, 1773 [NASA ADS] [CrossRef] [Google Scholar]
- Cassam-Chenaï, G., Hughes, J. P., Ballet, J., & Decourchelle, A. 2007, ApJ, 665, 315 [NASA ADS] [CrossRef] [Google Scholar]
- Cassam-Chenaï, G., Hughes, J. P., Reynoso, E. M., Badenes, C., & Moffett, D. 2008, ApJ, 680, 1180 [NASA ADS] [CrossRef] [Google Scholar]
- Chevalier, R. A., Blondin, J. M., & Emmering, R. T. 1992, ApJ, 392, 118 [NASA ADS] [CrossRef] [Google Scholar]
- Decourchelle, A., Ellison, D. C., & Ballet, J. 2000, ApJ, 543, L57 [NASA ADS] [CrossRef] [Google Scholar]
- Ellison, D. C. 2001, Space Sci. Rev., 99, 305 [NASA ADS] [CrossRef] [Google Scholar]
- Ellison, D. C., Patnaude, D. J., Slane, P., Blasi, P., & Gabici, S. 2007, ApJ, 661, 879 [NASA ADS] [CrossRef] [Google Scholar]
- Eriksen, K. A., Hughes, J. P., Badenes, C., et al. 2011, ApJ, 728, L28 [Google Scholar]
- Ferrand, G., Decourchelle, A., Ballet, J., Teyssier, R., & Fraschetti, F. 2010, A&A, 509, L10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hayato, A., Yamaguchi, H., Tamagawa, T., et al. 2010, ApJ, 725, 894 [NASA ADS] [CrossRef] [Google Scholar]
- Helder, E. A., & Vink, J. 2008, ApJ, 686, 1094 [NASA ADS] [CrossRef] [Google Scholar]
- Kang, H., & Jones, T. W. 1990, ApJ, 353, 149 [NASA ADS] [CrossRef] [Google Scholar]
- Katagiri, H., Enomoto, R., Ksenofontov, L. T., et al. 2005, ApJ, 619, L163 [NASA ADS] [CrossRef] [Google Scholar]
- Katsuda, S., Petre, R., Hughes, J. P., et al. 2010, ApJ, 709, 1387 [NASA ADS] [CrossRef] [Google Scholar]
- Ko, C. 1995, Adv. Space Res., 15, 149 [NASA ADS] [CrossRef] [Google Scholar]
- Kosenko, D. I. 2006, MNRAS, 369, 1407 [NASA ADS] [CrossRef] [Google Scholar]
- Kosenko, D., Helder, E. A., & Vink, J. 2010, A&A, 519, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lagage, P. O., & Cesarsky, C. J. 1983, A&A, 118, 223 [NASA ADS] [Google Scholar]
- Malkov, M. A., & O’C Drury, L. 2001, Rep. Prog. Phys., 64, 429 [NASA ADS] [CrossRef] [Google Scholar]
- Miceli, M., Bocchino, F., Iakubovskyi, D., et al. 2009, A&A, 501, 239 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Orlando, S., Bocchino, F., Reale, F., Peres, G., & Pagano, P. 2008, ApJ, 678, 274 [NASA ADS] [CrossRef] [Google Scholar]
- Parizot, E., Marcowith, A., Ballet, J., & Gallant, Y. A. 2006, A&A, 453, 387 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Patnaude, D. J., Slane, P., Raymond, J. C., & Ellison, D. C. 2010, ApJ, 725, 1476 [NASA ADS] [CrossRef] [Google Scholar]
- Petruk, O., Beshley, V., Bocchino, F., Miceli, M., & Orlando, S. 2011, MNRAS, 413, 1643 [NASA ADS] [CrossRef] [Google Scholar]
- Reynolds, S. P. 2008, ARA&A, 46, 89 [Google Scholar]
- Richtmyer, R. D., & Morton, K. W. 1967, Difference methods for initial-value problems (Interscience Publishers) [Google Scholar]
- Schure, K. M., Achterberg, A., Keppens, R., & Vink, J. 2010, MNRAS, 406, 2633 [NASA ADS] [CrossRef] [Google Scholar]
- Sinitsyna, V. G., Musin, F. I., Nikolsky, S. I., & Sinitsyna, V. Y. 2009, J. Phys. Soc. Japan, 78SA, 197 [Google Scholar]
- Sorokina, E. I., Blinnikov, S. I., Kosenko, D. I., & Lundqvist, P. 2004, Astron. Lett., 30, 737 [NASA ADS] [CrossRef] [Google Scholar]
- Tian, W. W., & Leahy, D. A. 2011, ApJ, 729, L15 [NASA ADS] [CrossRef] [Google Scholar]
- Vink, J., Yamazaki, R., Helder, E. A., & Schure, K. M. 2010, ApJ, 722, 1727 [NASA ADS] [CrossRef] [Google Scholar]
- Völk, H. J., Berezhko, E. G., & Ksenofontov, L. T. 2005, A&A, 433, 229 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Völk, H. J., Berezhko, E. G., & Ksenofontov, L. T. 2008, Adv. Space Res., 41, 473 [NASA ADS] [CrossRef] [Google Scholar]
- Wagner, A. Y., Falle, S. A. E. G., Hartquist, T. W., & Pittard, J. M. 2006, A&A, 452, 763 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wagner, A. Y., Lee, J., Raymond, J. C., Hartquist, T. W., & Falle, S. A. E. G. 2009, ApJ, 690, 1412 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, C.-Y. 2011, MNRAS, 415, 83 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, C., & Chevalier, R. A. 2001, ApJ, 549, 1119 [NASA ADS] [CrossRef] [Google Scholar]
- Warren, J. S., Hughes, J. P., Badenes, C., et al. 2005, ApJ, 634, 376 [NASA ADS] [CrossRef] [Google Scholar]
- Woosley, S. E., Kasen, D., Blinnikov, S., & Sorokina, E. 2007, ApJ, 662, 487 [NASA ADS] [CrossRef] [Google Scholar]
- Xu, J.-L., Wang, J.-J., & Miller, M. 2011, Res. Astron. Astrophys., 11, 537 [NASA ADS] [CrossRef] [Google Scholar]
- Zank, G. P., Webb, G. M., & Donohue, D. J. 1993, ApJ, 406, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Zirakashvili, V. N., & Aharonian, F. A. 2010, ApJ, 708, 965 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Basic equations
Originally the method (described by Sorokina et al. 2004) solves the system of hydrodynamical equations 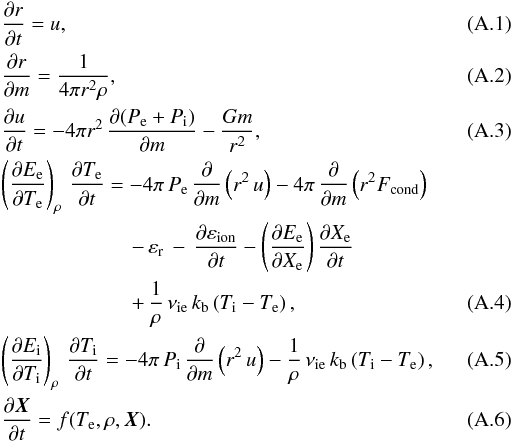 In these equations, the following parameters definitions are assumed: u is the velocity; ρ is the density; Te and Ti are the electron and ion temperatures; Pe and Pi are the respective pressures, taking into account artificial viscosity (see description below); Ee and Ei are the thermal energies per unit mass of the gas element at the Lagrangian coordinate m (corresponding to a mass within a radius r) at the moment of time t; Fcond is the energy flux due to the electron-electron and electron-ion thermal conduction; νie is the electron-ion collision frequency per unit volume; εr is the radiation energy-loss rate per unit mass of the gas element; ∂εion/∂t accounts for the change in specific thermal energy of gas due to the change of ionization state; and X = { XHI,XHII,XHeI,...,XNiXXIX } is the abundance vector of all ions of all included elements relative to the total number of atoms and ions. In addition, Xe = ne/nb for the number of electrons per baryon is introduced. The physical processes described by these equations are discussed in Sorokina et al. (2004).
In these equations, the following parameters definitions are assumed: u is the velocity; ρ is the density; Te and Ti are the electron and ion temperatures; Pe and Pi are the respective pressures, taking into account artificial viscosity (see description below); Ee and Ei are the thermal energies per unit mass of the gas element at the Lagrangian coordinate m (corresponding to a mass within a radius r) at the moment of time t; Fcond is the energy flux due to the electron-electron and electron-ion thermal conduction; νie is the electron-ion collision frequency per unit volume; εr is the radiation energy-loss rate per unit mass of the gas element; ∂εion/∂t accounts for the change in specific thermal energy of gas due to the change of ionization state; and X = { XHI,XHII,XHeI,...,XNiXXIX } is the abundance vector of all ions of all included elements relative to the total number of atoms and ions. In addition, Xe = ne/nb for the number of electrons per baryon is introduced. The physical processes described by these equations are discussed in Sorokina et al. (2004).
Appendix B: On the artificial viscosity
In supremna, the ion pressure was originally defined to be Pi = Pi(phys) + qiQ, thus for the electron pressure we assumed that Pe = Pe(phys) + (1 − qi)Q. The label “(phys)” represents the physical pressure in the system.
The meaning of this pressure can be clarified from the following simple thermodynamical relation. The second law is given by dE + PdV = 0, where E is the internal energy, P the pressure, and dV the volume element. Rewriting the pressure term as P = P(phys) + Q, we get dE + (P(phys) + Q)dV = 0. Thus, the term Q plays a role of a source function in dE + P(phys)dV = −QdV. If there are energy losses ε in the system, then the final relation is given by dE + PdV = −QdV + ε.
After the introduction of the CR component, using the qCR parameter, we define PCR = PCR(phys) + qCRQ (qCR = 0.0 describes a case where the contribution from the cosmic-ray component is zero). Thus, we have the following distribution of the artificial viscosity (Eq. (1)) between ion and electron pressure: Pi = Pi(phys) + (1 − qCR)qiQ and Pe = Pe(phys) + (1 − qCR)(1 − qi)Q. Hence Eq. (2) yields the source term in the form of Θ = qCRQ(∂u/∂r).
All Figures
 |
Fig. 1 HD profiles for the SNR models at t = 440 years with ρCSM = 10-24 g cm-3. Top row shows the simulation with qCR = 0.0, middle row – qCR = 0.7, κCR = 1025 cm2 s-1; bottom row – qCR = 0.99, κCR = 1026 cm2 s-1. Left panels: density (black solid line, scale at the left-hand side), ion pressure (blue dash-dotted line, scale at the right-hand side), and CR pressure (blue dashed line, scale at the right-hand side). Right panels: velocity profile (black solid line, scale at the left-hand side), electron temperature profiles (blue dashed line, scale at the right-hand side), and ion temperature profiles (dashed-dotted line, scale at the right-hand side). |
| In the text | |
 |
Fig. 2 HD profiles for the SNR models at t = 1000 years with ρCSM = 4 × 10-26 g cm-3. Top row shows the simulation with qCR = 0.0, middle row – qCR = 0.7, κCR = 1025 cm2 s-1; bottom row – qCR = 0.99, κCR = 1026 cm2 s-1. Left panels: density (black solid line, scale at the left-hand side), ion pressure (blue dash-dotted line, scale at the right-hand side), and CR pressure (blue dashed line, scale at the right-hand side). Right panels: velocity profile (black solid line, scale at the left-hand side), electron temperature profiles (blue dashed line, scale at the right-hand side), and ion temperature profiles (dashed-dotted line, scale at the right-hand side). |
| In the text | |
 |
Fig. 3 Top panel: Rankine-Hugoniot relation in Eq. (6) and data points from all the numerical models. The shade of the symbols reflects the efficiency of CR acceleration. Bottom row: left panel shows evolution of compression ration χ, right panel shows evolution of contact discontinuity to blast wave radii ratio, ρ0 = 10-24 g cm-3. Dashed lines show models with qCR = 0.7, solid lines – qCR = 0.9. Different colors indicate different values of the diffusion coefficient (see legend, where κCR values are given in units of cm2 s-1). |
| In the text | |
 |
Fig. 4 Measured and modeled radii ratios for Tycho’s (left-hand panel) and SN1006 (right-hand panel) SNRs. RCD/RRW (black symbols) and RRS/RRW (grey symbols). Horizontal bars indicate the measurements of Warren et al. (2005) and Miceli et al. (2009). |
| In the text | |
 |
Fig. 5 Left panel: CR pressure versus diffusion coefficient. Right panel: compression ratio χ versus diffusion coefficient κCR for different values of qCR (Tycho’s case). |
| In the text | |
 |
Fig. 6 Left panel: escape CR energy versus w and qCR. Right panel: compression ratio χ versus w and qCR (Tycho’s case). The Rankine-Hugoniot black curve corresponds to Mach number M0 = 500. Intensity of the data point is inversely proportional to the values of diffusion coefficient κCR, i.e. black asterisks correspond to κCR = 1024 cm2 s-1, light grey ones correspond to κCR = 1027 cm2 s-1. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


