| Issue |
A&A
Volume 532, August 2011
|
|
|---|---|---|
| Article Number | A122 | |
| Number of page(s) | 5 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201014260 | |
| Published online | 04 August 2011 | |
Interstellar H2 toward HD 37903⋆
Institute of Theoretical Physics and Astrophysics, University of Gdańsk, ul. Wita Stwosza 57, 80-952 Gdańsk, Poland
e-mail: pg@iftia9.univ.gda.pl
Received: 15 February 2010
Accepted: 22 April 2011
We present an analysis of interstellar H2 toward HD 37903, which is a hot B 1.5 V star located in the NGC 2023 reflection nebula. Meyer et al. (2001, ApJ, 553, L59) used a rich spectrum of vibrationally excited H2 observed by the HST to calculate a model of the interstellar cloud toward HD 37903. We extend their analysis by including the ν′′ = 0 vibrational level observed by the FUSE satellite.
The temperature calculated from the two lowest rotational levels (J′′ = 0, 1) of the H2 molecule should not be interpreted as a “rotational temperature”, but rather as a temperature of thermal equilibrium between the ortho and para H2. The ortho-to-para H2 ratio is lower for the lowest rotational levels than for the higher levels populated by fluorescence. The PDR model of the cloud located in front of HD 37903 points to a gas kinetic temperature ranging from 110 K on the observer side of the cloud to 377 K on the star side. The hydrogen density changes from nH = 1874 cm-3 on the observer side to 544 cm-3 on the star side. The star-cloud distance in our model is 0.45 pc.
Key words: ISM: molecules / photon-dominated region (PDR) / ISM: general
© ESO, 2011
1. Introduction
A rich spectrum of vibrationally excited H2 in the direction to HD 37903 was first described by Meyer et al. (2001). They observed over 500 interstellar H2 absorption lines from excited vibrational levels ν′′ = 1 − 14 and rotational levels up to J′′ = 13. These lines were detected in a Hubble Space Telescope (HST) spectrum made with the Space Telescope Imaging Spectrograph (STIS). A Far Ultraviolet Spectroscopic Explorer (FUSE) spectrum was made after this publication allowing access to the ν′′ = 0 vibrational level of the ground electronic state. The FUSE spectrum had been used by Rachford et al. (2009) to determine the TOP = 170 K/ln(9N0/N1) = 68 ± 7 K gas “kinetic” temperature and the hydrogen molecular fraction f(H2) = 2N(H2)/(2N(H2) + N(HI)) = 0.53 ± 0.09 in the direction towards HD 37903.
The star HD 37903 was also observed by the Berkeley Extreme and Far–Ultraviolet Spectrometer (BEFS) onboard the Orbiting and Retrievable Far and Extreme Ultraviolet Spectrometer (ORFEUS) telescope. The spectral resolution was R = 3000. Lee et al. (2002) have used this spectra to obtain H2 column densities on ν′′ = 0 and J′′ = 0 − 5 rotational levels. Their column densities agree within an order of magnitude to the column densities derived in this paper from the FUSE spectra. The physical parameters derived by Lee et al. (2002) are TOP = 63 ± 5 K, f(H2) = 0.496 ± 0.017, and the cloud density n = 5600 cm-3.
The H2 molecule exists in two forms: ortho (odd J′′) and para (even J′′) H2. It is caused by the spins of the hydrogen nuclei, which can point “in the same” direction (ortho H2 – triplet state, total nuclei spin I = 1) or in opposite directions (para H2 – singlet state, I = 0). The ratio ortho/para H2 (O/P) is therefore 3:1 at standard temperature and pressure. Conversion between these two spin isomers can take place in gas phase or on the surface of gas grains (Le Bourlot 2000). The ortho-para conversion in the gas phase is caused by the exchange of proton in collisions with H, H+, and H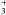 .
.
The fluorescence cascade of H2 that leads to populating the excited ro-vibrational states of H2, as well as to the emission of infrared photons from quadrupole transitions was described by Black & Dalgarno (1976). The first ultraviolet detection of vibrationally excited interstellar H2 was performed by Federman et al. (1995) in the HST spectrum of ζ Ophiuchi.
Section 2 presents the HST and FUSE spectra used in this paper and describes the procedure of calculating the H2 column densities of ro-vibrational energy levels. Section 3 describes the calculation of H2 rotational temperatures, especially the temperatures calculated across the ortho-para divide. Section 4 presents a PDR model of the cloud toward HD 37903.
2. Column densities
We used both HST STIS and FUSE spectra to obtain column densities on H2 ro-vibrational levels. The HST STIS spectrum o59s04010 was averaged because it consists of two subexposures. The HST spectrum is located between 1160 and 1357 Å. We also used the FUSE observation P1160601. We analyzed only spectra from the detectors LiF 1B and LiF 1A. These two spectra have the highest quality. The FUSE spectra coming from the same detector were shifted and coadded using the IRAF tasks poffsets and specalign. A part of the FUSE spectrum is shown in Fig. 1. The whole FUSE spectrum ranges from 987 Å to 1188 Å.
 |
Fig. 1 Fragment of FUSE spectrum with a fit (green line) of H2 absorption lines. The red line represents continuum. |
The Ar I 1048 Å line that lies in the wing of R(0) and R(1) lines was cut out from the spectrum. The wings of H2 lines were calculated up to 60 Å from the line center. The absorption lines in the FUSE spectrum were modeled with the Voigt function, while a Gauss function was used for modeling the H2 lines in the STIS spectrum.
We used a Gaussian point spread function (PSF) with FWHM equal to 15 km s-1 (Jensen et al. 2010) to model the FUSE spectra. The column densities at J′′ = 0, 1 and 2 (ν′′ = 0) were derived from transitions between B and X electronic levels. The vibrational transitions used are (0, 0), (2, 0), (3, 0), and (4, 0), where the first digit is the ν′ on the upper electronic level B and the second digit ν′′ = 0 is the vibrational level of the ground electronic state X. The FUSE spectrum at the (1, 0) vibrational transition was too noisy to perform a good fit. The H2 line positions and oscillator strengths were adopted from Abgrall et al. (1994). The total transition probabilities that include the transitions to continuum (dissociating) states were taken from Abgrall et al. (2000).
The column densities of rotational levels J′′ = 0−9 from the vibrational ν′′ = 0 level, as well as the column density of the ν′′ = 1 J′′ = 0 level, were derived from the FUSE spectrum. Other ro-vibrational levels of the X ground electronic state were derived from the o59s04010 HST STIS spectrum. The continuum level for the FUSE spectrum was placed manually in an iterative process of fitting column densities and changing the continuum level.
The column densities were derived with the profile fitting technique. At each point of the simulated spectrum, the optical depth of many spectral lines was summed. Such a procedure is needed to calculate the profile of blended lines which are ubiquitous in the spectra. The cloud velocity, the doppler broadening parameter and column densities on all observed levels were free parameters, which were fitted to the observed spectra. The cloud velocity and the doppler broadening parameter were common for all H2 absorption lines.
 |
Fig. 2 Fragment of HST STIS spectrum (gray line with dots) fitted with 268 H2 absorption lines (green line). The figure presents only a 5 Å fragment of the spectrum, while the presented fit was done to the whole 200 Å long STIS spectrum (1160–1357 Å) and included 7449 H2 lines. |
 |
Fig. 3 Occupation of H2 X ro-vibrational levels towards HD 37903. Note the different y-axis scale for ν′′ = 0 (left) and for higher ν′′ levels (right). |
Column densities of the H2 ro-vibrational levels towards HD 37903 [cm-2].
The STIS spectrum was fitted with H2 absorption lines from all vibrational ν′′ = 0−14 levels, and rotational levels J′′ = 0−13. H2 lines that were blended with atomic lines were excluded from the fitting procedure. Total 7449 H2 lines were included in the simulated STIS spectrum. The whole STIS spectrum (200 Å long) was fitted at once with all 7449 H2 lines, because of the large number of blended lines. A fragment of the HST STIS spectrum with lines of vibrationally excited molecular hydrogen is presented in Fig. 2. The observed column densities are presented in Table 1 and in Fig. 3. The errors of the column density are about 20% for J′′ = 0 − 7 rotational levels, and up to ~40% for higher rotational levels.
3. Results
The total observed column density of H2 on all vibrational and rotational levels equals N(H2) = (9.6 ± 1.6) × 1020 cm-2. The observed H2 column density is slightly higher than N(H2) = 4 × 1020 cm-2, as estimated by Meyer et al. (2001). The column density of neutral hydrogen is N(HI) = 1.48 × 1021 cm-2 (Diplas & Savage 1994). The hydrogen molecular fraction (assuming 10% error of N(HI)) equals f(H2) = 2N(H2)/(2N(H2) + N(HI)) = 0.56 ± 0.04.
The TOP temperature, calculated from the lowest energy levels of ortho and para H2 (ν′′ = 0), was derived from the equation: 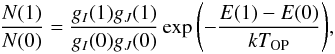 (1)where gI is the spin degeneracy factor gI(I) = 2I + 1. The gI(1) = 3 is the statistical weight for ortho H2, and gI(0) = 1 for the para–H2 spin izomer. The formula gJ(J) = 2J + 1 is the statistical weight for the rotational level J. The TOP is the temperature of thermal equilibrium between the ortho and para spin izomers. The derived TOP = 67 ± 8 K is similar to the temperatures determined by Rachford et al. (2009) (68 K) and by Lee et al. (2002) (63 K). The photon-dominated region (PDR) models of interstellar clouds show that the TOP temperature is correlated to the gas kinetic temperature (Le Petit et al. 2006).
(1)where gI is the spin degeneracy factor gI(I) = 2I + 1. The gI(1) = 3 is the statistical weight for ortho H2, and gI(0) = 1 for the para–H2 spin izomer. The formula gJ(J) = 2J + 1 is the statistical weight for the rotational level J. The TOP is the temperature of thermal equilibrium between the ortho and para spin izomers. The derived TOP = 67 ± 8 K is similar to the temperatures determined by Rachford et al. (2009) (68 K) and by Lee et al. (2002) (63 K). The photon-dominated region (PDR) models of interstellar clouds show that the TOP temperature is correlated to the gas kinetic temperature (Le Petit et al. 2006).
 |
Fig. 4 Theoretical N(J = 1)/N(J = 0) ratio on the ν′′ = 0 vibrational level from Eq. (6) shown as a dark blue dashed line. The light blue dashed lines represent errors introduced by the uncertainty of the Northo/Npara H2 ratio 0.64 ± 0.21. The observed N(1)/N(0) ratio is plotted as a straight black line. The N(1)/N(0) uncertainties are shown as straight gray lines. |
However, if we want to calculate the rotational temperature across the ortho-para divide, we have to take the Northo/Npara H2 ratio into account. The population of the ro-vibrational levels of H2 depends not only on the temperature and radiation field, but also on the total ortho to para ratio. To include the O/P in the Boltzmann equation, we write separate Boltzmann distributions for the ortho and para spin izomers. The Boltzmann distribution for the ortho H2 can be written as 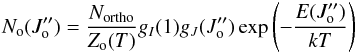 (2)where Northo is the total amount of ortho H2. The partition function Z is
(2)where Northo is the total amount of ortho H2. The partition function Z is 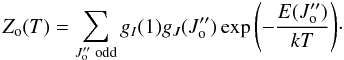 (3)We assume that para H2 has a Boltzmann distribution with the same rotational temperature,
(3)We assume that para H2 has a Boltzmann distribution with the same rotational temperature, 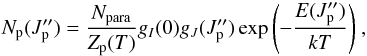 (4)where Npara is the total amount of para H2, and the partition function for para H2
(4)where Npara is the total amount of para H2, and the partition function for para H2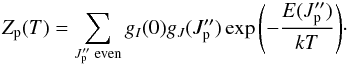 (5)By dividing Eqs. (2) by (4) we obtain
(5)By dividing Eqs. (2) by (4) we obtain 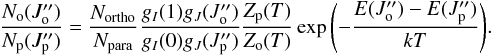 (6)We tried to solve the above equation numerically for the
(6)We tried to solve the above equation numerically for the 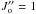 and
and 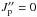 states (ν′′ = 0) to obtain the T01 rotational temperature. The observed Northo/Npara = 0.64 ± 0.21 was calculated from the column densities of ortho and para H2 states on the ν′′ = 0 vibrational level (see Table 1). Figure 4 presents the righthand side of Eq. (6) and the ratio of observed column densities (left side of Eq. (6)), together with maximal errors. As we see in Fig. 4 the rotational temperature T01 can take any value between 0 and 400 K.
states (ν′′ = 0) to obtain the T01 rotational temperature. The observed Northo/Npara = 0.64 ± 0.21 was calculated from the column densities of ortho and para H2 states on the ν′′ = 0 vibrational level (see Table 1). Figure 4 presents the righthand side of Eq. (6) and the ratio of observed column densities (left side of Eq. (6)), together with maximal errors. As we see in Fig. 4 the rotational temperature T01 can take any value between 0 and 400 K.
Equation (6) can be written in another way by making two assumptions that are not valid in the interstellar medium:
-
1.
T > 240 K ⇒ Zp(T)/Zo(T) ≈ 1/3;
-
2.
Northo/Npara = 3 as in standard laboratory conditions.
Under this assumptions, Eq. (6) for rotational temperature reduces to 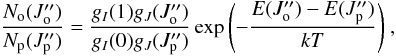 (7)and T01 is the same as the temperature TOP of ortho-para thermal equilibrium.
(7)and T01 is the same as the temperature TOP of ortho-para thermal equilibrium.
The rotational temperatures T02 and T13 involve rotational levels of the same spin isomers of H2, and do not depend on the total Northo/Npara H2 ratio and on the partition function. For the cloud towards HD 37903, the T02 = 132 ± 14 K and T13 = 172 ± 9 K. However, the T12 temperature (which involves both ortho and para spin isomers) calculated from Eq. (6) is 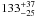 K, while using Eq. (7) gives an incorrect temperature of 263 ± 89 K.
K, while using Eq. (7) gives an incorrect temperature of 263 ± 89 K.
A good illustration that Eq. (6) must be used can be the ν′′ = 1 level. On the ν′′ = 1 level, the temperature T12 = 1223 K (levels ortho and para) is close to the T02 = 921 K and T13 = 1090 K temperatures calculated from the same spin isomers. The temperature calculated with the traditionally used Eq. (7) is negative T = −466 K!
The O/P H2 ratio (O/P)ν′′ = 1 − 14 = 1.35 ± 0.18 was calculated by summing ortho and para H2 on vibrational levels ν′′ = 1 − 14. It is a bit lower than O/P = 1.45 ± 0.08, as given by Meyer et al. (2001). We also used the method proposed by Wilgenbus et al. (2000) to calculate O/P H2 from individual ortho levels, specially 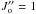 and 3 on ν′′ = 0. For the ν′′ = 0 J′′ = 1 ortho state, the O/P differs significantly from the (O/P)ν′′ = 1 − 14 = 1.35 value and is equal to (O/P)J′′ = 1 = 0.63 ± 0.11. Also for the ν′′ = 0 J′′ = 3 ortho state, the observed O/P is low, only (O/P)J′′ = 3 = 0.70 ± 0.07. For higher rotational and vibrational levels, the Wilgenbus et al. (2000) method gives (O/P)Jo close to 1.3 derived for excited vibrational H2 states.
and 3 on ν′′ = 0. For the ν′′ = 0 J′′ = 1 ortho state, the O/P differs significantly from the (O/P)ν′′ = 1 − 14 = 1.35 value and is equal to (O/P)J′′ = 1 = 0.63 ± 0.11. Also for the ν′′ = 0 J′′ = 3 ortho state, the observed O/P is low, only (O/P)J′′ = 3 = 0.70 ± 0.07. For higher rotational and vibrational levels, the Wilgenbus et al. (2000) method gives (O/P)Jo close to 1.3 derived for excited vibrational H2 states.
 |
Fig. 5 Rotational temperatures for para and ortho H2 toward HD 37903 as a function of the vibrational number ν′′. |
Rotational temperatures for para and ortho H2 as a function of the vibrational level ν′′.
The rotational temperatures for vibrational levels ν′′ = 1 − 14 for para H2 were obtained from the linearized Boltzmann distribution: 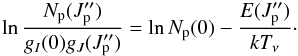 (8)An analogous equation was used for distribution of the ortho H2 states. Figure 3 shows the lefthand side of Eq. (8) versus E/k. Levels fulfilling the Boltzmann distribution should be placed on a straight line on this plot. On the ν′′ = 0 vibrational level, which is partially populated by collisions, the occupation of rotational levels does not follow a straight line, therefore the rotational temperature was not calculated for the ν′′ = 0 vibrational level. For both spin isomers and for vibrational levels ν′′ = 1 − 14 the temperature was calculated using the the linear regression method. The inverse of the line inclination ( − 1/Tν in Eq. (8)) gives us the rotational temperature. The resulting temperatures are presented in Table 2 and in Fig. 5. The rotational temperatures for the ortho isomer are usually higher than for the para H2. However, the ortho H2 rotational temperatures calculated from levels Jo = 1 to penultimate Jo ortho state are in conformity with the para H2 rotational temperatures, so the assumption that the rotational temperatures Tν are the same for ortho and para H2 seems justified. The rotational temperatures fall linearly with the increasing vibrational level.
(8)An analogous equation was used for distribution of the ortho H2 states. Figure 3 shows the lefthand side of Eq. (8) versus E/k. Levels fulfilling the Boltzmann distribution should be placed on a straight line on this plot. On the ν′′ = 0 vibrational level, which is partially populated by collisions, the occupation of rotational levels does not follow a straight line, therefore the rotational temperature was not calculated for the ν′′ = 0 vibrational level. For both spin isomers and for vibrational levels ν′′ = 1 − 14 the temperature was calculated using the the linear regression method. The inverse of the line inclination ( − 1/Tν in Eq. (8)) gives us the rotational temperature. The resulting temperatures are presented in Table 2 and in Fig. 5. The rotational temperatures for the ortho isomer are usually higher than for the para H2. However, the ortho H2 rotational temperatures calculated from levels Jo = 1 to penultimate Jo ortho state are in conformity with the para H2 rotational temperatures, so the assumption that the rotational temperatures Tν are the same for ortho and para H2 seems justified. The rotational temperatures fall linearly with the increasing vibrational level.
4. Model
We used the Meudon PDR code (Le Petit et al. 2006) to calculate a model of the interstellar medium in the direction of HD 37903. The interstellar reddening E(B − V) = 0ṃ35 and RV = 5.5 was chosen to match the values used by Meyer et al. (2001). The radiation source is the HD 37903 star (B 1.5 V spectral type). The model includes 300 H2 ro-vibrational levels and uses exact computation of radiative transfer in H2 spectral lines. The cosmic rays ionization flux was set to 5 × 10-17 s-1. The model is isobaric with thermal balance.
Comparison of cloud models toward HD 37903.
Our models were all two-sided models with an interstellar radiation field on the observer’s side equal to one “Draine” unit. The interstellar radiation field on the star side was varied from 1 to 104 “Draine” units. The best model was chosen among 6917 different models by minimizing the sum 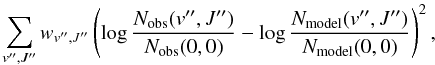 (9)where the weights wv′′,J′′ were chosen such, that the levels populated mainly by collisions J′′ = 0 − 6 (v′′ = 0) have the same influence on the final sum as the rest of the levels (v′′ > 0 and v′′ = 0 J′′ = 7 − 13), which are populated by fluorescence.
(9)where the weights wv′′,J′′ were chosen such, that the levels populated mainly by collisions J′′ = 0 − 6 (v′′ = 0) have the same influence on the final sum as the rest of the levels (v′′ > 0 and v′′ = 0 J′′ = 7 − 13), which are populated by fluorescence.
We varied the star–cloud distance, hydrogen density, and the interstellar radiation field on the star side in order to find a model that matches the observations. Table 3 compares our best model and models presented by Meyer et al. (2001) and Lee et al. (2002). The star-cloud distance of 0.45 pc, which is responsible for filling the fluorescence H2 levels, is similar in our model and in the model presented by Meyer et al. (2001) (d = 0.5 pc). Our cloud kinetic temperature (connected with the collisional-filled levels) equals Tkin = 377 K on the star side of the cloud and Tkin = 110 K on the observer’s side. The hydrogen density obtained in our best model changes from nH = 544 cm-3 on the star side to 1874 cm-3 on the observer’s side. The interstellar radiation field on both sides of our best cloud model is one “Draine” unit. The hydrogen density and gas kinetic temperature in the PDR model of interstellar cloud toward HD 37903 is shown in Fig. 6.
The O/P on excited (ν ≥ 1) vibrational states is equal to 1.57 in our model. The kinetic temperature in our model is higher than the TOP derived from the ν = 0, J = 0 and 1 levels. However, the bulk of molecular hydrogen may be placed in different part of the cloud than H2 in excited states. This behavior is described by Boissé et al. (2005) for the cloud toward HD 34078.
 |
Fig. 6 The hydrogen density (black line) and gas kinetic temperature (dashed red line) in the PDR model of interstellar cloud toward HD 37903. |
5. Conclusions
The molecular cloud toward HD 37903 presents a rare type of spectrum with a large number of absorption lines arising from H2 on vibrationally excited states. We determined the column densities of 191 H2 ro-vibrational energy levels using the HST and FUSE ultraviolet spectra.
Column density of molecular hydrogen toward HD 37903 on all observed H2 levels is N(H2) = 9.6 × 1020 cm-2, the hydrogen molecular fraction equals f(H2) = 0.56 , and the rotational temperatures are T02 = 132 K and T13 = 172 K. Our principal results follow
-
The temperature calculated from the two lowest rotational levels(J′′ = 0, 1) is a temperature of thermal equilibrium between the ortho and para spin isomers and is equal to 67 K.
-
The formula for rotational temperatures calculated across the ortho-para divide (like T12) should include the (O/P)ν H2 ratio.
-
The ortho to para H2 ratio is different on the ground vibrational level and in excited states. The O/P H2 ratio equals 1.35 for the excited levels, but for the J′′ = 1 ortho state (ν′′ = 0) the O/P is only (O/P)J′′ = 1 = 0.63.
-
The best PDR model for the cloud toward HD 37903 gives a gas kinetic temperature Tkin = 110 − 377 K, hydrogen density nH = 544 − 1874 cm-3, and star-cloud distance of 0.45 pc.
Acknowledgments
I would like to thank Herve Abgrall for providing the natural line widths for the H2 lines. The research was supported by University of Gdańsk grant BW/5400-5-0336-0.
References
- Abgrall, H., Roueff, E., Launay, F., & Roncin, J.-Y. 1994, Can. J. Phys., 72, 856 [NASA ADS] [CrossRef] [Google Scholar]
- Abgrall, H., Roueff, E., & Drira, I. 2000, A&AS, 141, 297 [Google Scholar]
- Black, J. H., & Dalgarno, A. 1976, ApJ, 203, 132 [NASA ADS] [CrossRef] [Google Scholar]
- Boissé, P., Le Petit, F., Rollinde, E., et al. 2005, A&A, 429, 509 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Diplas, A., & Savage, B. D. 1994, ApJS, 93, 211 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T., & Bertoldi, F. 1996, ApJ, 468, 269 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Federman, S. R., Cardell, J. A., van Dishoeck, E. F., Lambert, D. L., & Black, J. H. 1995, ApJ, 445, 325 [NASA ADS] [CrossRef] [Google Scholar]
- Jensen, A., Snow, T., Sonneborn, G., & Rachford, B. 2010, ApJ, 711, 1236 [NASA ADS] [CrossRef] [Google Scholar]
- Le Bourlot, J. 2000, A&A, 360, 656 [Google Scholar]
- Le Petit, F., Nehmé, C., Le Bourlot, J., & Roueff, E. 2006, ApJS, 164, 506 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lee, D.-H., Min, K.-W., Federman, S. R., et al. 2002, ApJ, 575, 234 [NASA ADS] [CrossRef] [Google Scholar]
- Meyer, D. M., Lauroesch, J. T., Sofia, U. J., Draine, B. T., & Bertoldi, F. 2001, ApJ, 553, L59 [NASA ADS] [CrossRef] [Google Scholar]
- Rachford, B. L., Snow, T. P., Destree, J. D., et al. 2009, ApJS, 180, 125 [NASA ADS] [CrossRef] [Google Scholar]
- Wilgenbus, D., Cabrit, S., Pineau des Forêts, G., & Flower, D. R. 2000, A&A, 356, 1010 [NASA ADS] [Google Scholar]
All Tables
Rotational temperatures for para and ortho H2 as a function of the vibrational level ν′′.
All Figures
 |
Fig. 1 Fragment of FUSE spectrum with a fit (green line) of H2 absorption lines. The red line represents continuum. |
| In the text | |
 |
Fig. 2 Fragment of HST STIS spectrum (gray line with dots) fitted with 268 H2 absorption lines (green line). The figure presents only a 5 Å fragment of the spectrum, while the presented fit was done to the whole 200 Å long STIS spectrum (1160–1357 Å) and included 7449 H2 lines. |
| In the text | |
 |
Fig. 3 Occupation of H2 X ro-vibrational levels towards HD 37903. Note the different y-axis scale for ν′′ = 0 (left) and for higher ν′′ levels (right). |
| In the text | |
 |
Fig. 4 Theoretical N(J = 1)/N(J = 0) ratio on the ν′′ = 0 vibrational level from Eq. (6) shown as a dark blue dashed line. The light blue dashed lines represent errors introduced by the uncertainty of the Northo/Npara H2 ratio 0.64 ± 0.21. The observed N(1)/N(0) ratio is plotted as a straight black line. The N(1)/N(0) uncertainties are shown as straight gray lines. |
| In the text | |
 |
Fig. 5 Rotational temperatures for para and ortho H2 toward HD 37903 as a function of the vibrational number ν′′. |
| In the text | |
 |
Fig. 6 The hydrogen density (black line) and gas kinetic temperature (dashed red line) in the PDR model of interstellar cloud toward HD 37903. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


