| Issue |
A&A
Volume 685, May 2024
|
|
|---|---|---|
| Article Number | A113 | |
| Number of page(s) | 8 | |
| Section | Atomic, molecular, and nuclear data | |
| DOI | https://doi.org/10.1051/0004-6361/202348645 | |
| Published online | 15 May 2024 | |
Revisiting the rovibrational (de-)excitation of molecular hydrogen by helium★
1
Institute of Physics, Faculty of Physics, Astronomy and Informatics, Nicolaus Copernicus University in Toruń,
Grudzia̧dzka 5,
87-100
Toruń, Poland
e-mail: hubert.jozwiak@doktorant.umk.pl
2
Univ Rennes, CNRS, IPR (Institut de Physique de Rennes) – UMR 6251,
35000
Rennes, France
Received:
17
November
2023
Accepted:
24
February
2024
Context. The collisional (de-)excitation of H2 by He plays an important role in the thermal balance and chemistry of various astro-physical environments, making accurate rate coefficients essential for interpreting observations of the interstellar medium.
Aims. Our goal is to utilize a state-of-the-art potential energy surface (PES) to provide comprehensive state-to-state rate coefficients for He-induced transitions among rovibrational levels of H2.
Methods. We performed quantum scattering calculations for the H2-He system. Thus, we were able to provide state-to-state rate coefficients for 1059 transitions between rovibrational levels of H2, with internal energies up to ≃15 000 cm−1, for temperatures ranging from 20 to 8000 K.
Results. Our results demonstrate a good agreement with previous calculations for pure rotational transitions between low-lying rotational levels. However, we do find significant discrepancies for rovibrational processes involving highly-excited rotational and vibrational states. We attribute these differences to two key factors: (1) the broader range of intramolecular distances covered by ab initio points and (2) the superior accuracy of the PES, resulting from the utilization of the state-of-the-art quantum chemistry methods, compared to previous lower-level calculations.
Conclusions. Radiative transfer calculations performed with the new collisional data indicate that the population of rotational levels in excited vibrational states experiences significant modifications, highlighting the critical need for this updated dataset in models of high-temperature astrophysical environments.
Key words: molecular data / radiative transfer / scattering / ISM: molecules
The ortho- and para-H2 data are available at the CDS via anonymous ftp to cdsarc.cds.unistra.fr (130.79.128.5) or via https://cdsarc.cds.unistra.fr/viz-bin/cat/J/A+A/685/A113
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1 Introduction
As the most abundant molecule in the Universe, H2 plays a crucial role in the chemistry and thermal balance of various astro-physical environments, as a result of collisions. For instance, when a shock wave passes through a molecular gas, heating the medium to temperatures of a few hundred degrees kelvin (or above), inelastic collisions with H2 determine the rate of cooling of the gas at temperatures in the range of 100–1000 K (Aannestad & Field 1973; Shull & Beckwith 1982; Le Bourlot et al. 1999). The collisional excitation of H2 and subsequent infrared emission was also one of the important cooling mechanisms in the post-recombination era, after the first molecules were formed. Despite its low abundance in the early Universe, collisions of H2 and its deuterated isotopologue (HD) dominated the cooling process, leading to the gravitational collapse of inhomogeneities in the primordial gas and to the formation of the first stars (Flower & Pineau des Forêts 2001).
Although it is less abundant than molecular hydrogen, He is one of the most important collisional partners for H2 (along with H, H+, and H2 itself) across a broad variety of astrophysical environments, such as diffuse clouds, dense molecular clouds, protoplanetary disks, and in the early Universe. It is essential to note that typical densities in these environments are not sufficient to achieve local thermodynamic equilibrium (LTE). In such cases, the evolution of molecular populations is determined by two processes: radiative transitions and inelastic collisions. Thus, accurate rate coefficients for collisional processes involving H2 are crucial for a reliable interpretation of observations of the interstellar medium. For instance, rate coefficients for rovibrational excitation and de-excitation of H2 in collisions with He have been used in calculations of the cooling rate of the primordial gas (Flower et al. 2000; Glover & Abel 2008), as well as analyses of populations of H2 in turbulent diffuse interstellar clouds (Cecchi-Pestellini et al. 2005) and the evolution of molecular gas in dark, dense clouds following the passage of C-type shocks (Yuan & Neufeld 2010; Nesterenok 2018), and in studies of protoplanetary disk chemistry (Ruaud 2021).
The astrophysical community typically uses the H2-He rate coefficients calculated by Flower et al. (1998, hereafter, F98), which are available in the BASECOL database (Dubernet et al. 2013). These rate coefficients were obtained from quantum scattering calculations performed on the potential energy surface (PES) reported by Muchnick & Russek (1994). The authors included rovibrational levels up to v = 3, j = 8 in their calculations and provided rate coefficients for temperatures ranging from 100 to 6000 K. Theoretical rate coefficients for vibrational relaxation from rotational levels in the v = 1 manifold are in satisfactory agreement (within a factor of 2) with experimental data of Dove & Teitelbaum (1974) and Audibert et al. (1976). Independent quantum scattering calculations performed on the same PES by Balakrishnan et al. (1999a,b), but using a different approach to performing a rovibrational average of the PES led to a good agreement with the results of Flower et al. (1998) for transitions involving |Δj| = 0,2, and 4. Importantly, the calculations of Balakrishnan et al. (1999b) extended the original dataset of Flower et al. (1998) to v = 4, 5 and 6.
The quality of theoretical rate coefficients is largely determined by the potential energy surface (PES) employed. Since the works of Flower et al. (1998) and Balakrishnan et al. (1999a,b), new PESs have been published that should, in principle, provide a more accurate description of H2-He interaction energies. Lee et al. (2005) conducted a comparative study between the rate coefficients derived from the Muchnick & Russek (1994) (MR) PES and the then most recent PES reported by Boothroyd et al. (2003, BMP). Surprisingly, they discovered that the total quenching rate from the v = 1, j = 0 state calculated with the BMP PES was three orders of magnitude larger than that calculated with the MR PES and the experimental data reported by Audibert et al. (1976). In a joint experimental and theoretical study of low-temperature (between 22 and 180 K), inelastic collisions of H2 and He, Tejeda et al. (2008) found that the rate coefficients for pure rotational de-excitation, kv=0,j=2→v′=0,j′ = 0, obtained from quantum scattering calculations based on the MR PES were in better agreement with the experimental data than those derived from the BMP PES. The two papers confirmed the quality of the MR PES and (indirectly) the rate coefficients calculated by Flower et al. (1998).
However, studies comparing rate coefficients may not be sensitive enough to discern the differences between various PESs. A much more stringent test of the PES can be performed by comparing spectroscopic parameters of molecular lines, such as pressure broadening and shift coefficients (Thibault et al. 2016). Recently, we have shown that the most recent H2-He PES (Thibault et al. 2017, hereafter, BSP3) leads to a subpercent agreement between experimental and theoretical line profiles of molecular hydrogen perturbed in collisions with He (Slowiński et al. 2020). In particular, we have demonstrated that quantum scattering calculations based on the older PESs, such as the improved version from Muchnick & Russek (1994, mMR), fail to reproduce the cavity-enhanced spectra of the 3−0 S(1) and 2−0 Q(1) He-perturbed lines of H2 (Slowiński et al. 2022). The most recent PES has been successfully used in comprehensive calculations of line-shape parameters for He-perturbed H2 (Józwiak et al. 2018) and HD (Thibault et al. 2020; Stankiewicz et al. 2020) lines, which provided a basis for the construction of a new generation of line-shape parameters databases based on ab initio calculations (Wcisło et al. 2021; Stankiewicz et al. 2021). The BSP3 PES has also been used in studies of stereodynamics of cold He-HD (Morita & Balakrishnan 2020a,b) and He-D2 (Jambrina et al. 2022) collisions.
In this paper, we use the most recent PES (Thibault et al. 2017) to perform quantum scattering calculations for the H2-He system and to revise the state-to-state rate coefficients calculated by Flower et al. (1998). The paper is organized as follows. In Sect. 2, we briefly describe the quantum scattering calculations. We present examples of cross-sections and rate coefficients and compare the results with available theoretical and experimental data in Sect. 3. In Sect. 4, we discuss the potential implications of our results on astrophysical models before giving our concluding remarks in Sect. 5. The complete dataset with all state-to-state coefficients will be available online from the BASECOL (Dubernet et al. 2013) website.
2 Methods
We studied the inelastic collisions in the H2-He systems by solving the close-coupling equations in the body-fixed (BF) frame of reference. The theory of non-reactive scattering in systems with arbitrary angular momenta in the BF frame was developed by Launay (1977). It was recently recalled by some of the present authors in the context of scattering calculations for He-perturbed shape of HD rovibrational resonances (Stankiewicz et al. 2020). We chose the BF frame of reference because the coupling matrix exhibits a predominantly block-diagonal structure with blocks interconnected by centrifugal terms (see Fig. 3 in Rabitz 1975), which significantly reduces computational time and memory requirements.
We employed the H2-He potential energy surface reported by Thibault et al. (2017), which extends the PES calculated by Bakr et al. (2013). The PES was computed using the coupled-cluster method with single, double, and perturbative triple excitations [CCSD(T)], supplemented by full configuration interaction corrections. In comparison to the previous version, which covered H–H distances in the range of rHH ∈ [1.1,1.7] a0, this PES encompasses a broader range of intramolecular H–H distances (rHH ∈ [0.65,3.75] a0). This serves as a critical aspect for accurately studying inelastic transitions between excited vibrational states of H2.
The PES is expanded in the Legendre polynomials:
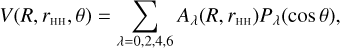 (1)
(1)
where R denotes the distance between He and the center of mass of H2, while θ is the angle between the intra- and intermolecular axis. Since H2 is a homonuclear molecule, λ takes only even values. We use the analytical representation of the expansion terms, Aλ(R, rHH), provided in Eq. (2) of Thibault et al. (2017). The dependence of the expansion coefficients on the stretching coordinate, rHH, is ruled out by averaging the PES over rovibrational wave functions of isolated H2 molecule, χvj(rHH):
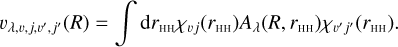 (2)
(2)
We used 703 coupling terms, vλ,v,j,v′,j′ (R), for each λ value. These terms describe couplings between all 37 (see below) rovibrational states included in the calculations. Rovibrational wave functions of H2, χv′j′(rHH), are obtained by solving the Schrödinger equation for nuclear motion of H2 molecule with the potential energy curve of Schwenke (1988), using the discrete variable representation-finite basis representation method.
We recall that the close-coupling equations are diagonal with respect to the total angular momentum (J) and parity (p), namely, they can be solved for each value of J and p separately. Since the PES does not couple states with different nuclear spins (I), we considered the scattering of para-H2 (I = 0, rotational states with even j values) and ortho-H2 (I = 1, rotational states with odd j values) separately. The coupled equations are solved using renormalized Numerov’s algorithm implemented in the in-house scattering code BIGOS (Józwiak 2024)1. The log-derivative matrix is transformed to the space-fixed (SF) frame of reference at a sufficiently large value of R, and the boundary conditions, imposed on the scattering wave functions allow us to obtain the S-matrix elements. The state-to-state cross-sections are calculated from the S-matrix elements as follows
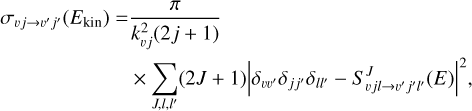 (3)
(3)
where v and j denote pre-collisional vibrational and rotational quantum numbers of H2, l is the angular momentum of the relative motion in the colliding system, E = Ekin + Evj is the total energy (the sum of the relative kinetic energy and the internal energy of H2 in the given rovibrational state), 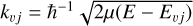 , μ is the reduced mass of the H2-He system, and ℏ is the reduced Planck constant. Primed symbols denote post-collisional values. The sum over J is truncated at a value Jmax large enough to ensure convergence of the elastic and the largest inelastic cross-sections at the level of 10−4 Å2. The range of the sum over l (and l′) is determined by the triangular rule resulting from adding two angular momenta j + l = J (and j′ + l′ = J).
, μ is the reduced mass of the H2-He system, and ℏ is the reduced Planck constant. Primed symbols denote post-collisional values. The sum over J is truncated at a value Jmax large enough to ensure convergence of the elastic and the largest inelastic cross-sections at the level of 10−4 Å2. The range of the sum over l (and l′) is determined by the triangular rule resulting from adding two angular momenta j + l = J (and j′ + l′ = J).
In this study, we are interested in rovibrational transitions between H2 levels with internal energies lower than 15 000 cm−1. There are 26 such levels in ortho-H2, and 27 such levels in para-H2. When all these levels are energetically accessible, there are 676 possible transitions for ortho-H2 and 729 for para-H2. The cross-sections were calculated for total energies ranging between 10−6 and 40 000 cm−1 with various energy steps, in order to accurately describe the channel-opening effects and resonances. We tested the convergence of the cross-sections with respect to the parameters of the propagator and the size of the rovibrational basis. The specific values for these parameters, including the range of propagation (Rmin and Rmax) and the number of steps per half-de Broglie wavelength, are presented in Table 1. The convergence with respect to the size of the rovibrational basis is tested through a series of calculations at the largest collision energy (40 000 cm−1 ). The basis is incrementally expanded by adding rovibrational levels of H2 in order of increasing energy until the state-to-state cross-sections of the 676 (ortho-H2) and 729 (para-H2) transitions differ by less than 1%. This basis (which we refer to as a “fully converged basis”) involves all rovibrational levels of H2 up to υ = 5, j = 6 and υ = 5, j = 7 for para-H2-He and ortho-H2-He collisions, respectively. After establishing a fully-converged basis, we compared the cross-sections derived from smaller basis sets to this benchmark. We set an acceptable level of convergence at 10% when comparing these cross-sections against those obtained from the fully converged basis. Ultimately, the basis set involved 37 rovibrational levels (up to the υ = 2, j = 14 for para-H2 and υ = 5, j = 1 for ortho-H2), which ensured convergence better than 10% with respect to the fully-converged basis for 539 (out of 729) cross-sections in the para-H2 case and 520 (out of 676) cross-sections in the ortho-H2 case related to transitions between levels with internal energies lower than 15 000 cm−1, leading to the total number of 1 059 transitions.
We calculated the thermal rate coefficients by averaging the state-to-state cross-sections over the distribution of relative kinetic energy as follows:
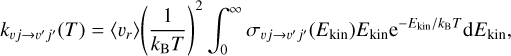 (4)
(4)
where 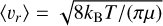 is the mean relative speed of the colliding partners at a given temperature. The range of total energies covered by the scattering calculations (from 10−6 to 40 000 cm−1) allows us to determine thermal rate coefficients ranging from 20 to 8000 K for the 1059 considered transitions.
is the mean relative speed of the colliding partners at a given temperature. The range of total energies covered by the scattering calculations (from 10−6 to 40 000 cm−1) allows us to determine thermal rate coefficients ranging from 20 to 8000 K for the 1059 considered transitions.
Parameters ensuring convergence in scattering calculations.
3 Results
In this section, we discuss the calculated cross-sections and thermal rate coefficients.
3.1 Pure rotational (υ′ = υ) (de-)excitation
We began with the inelastic processes between rotational levels within the ground vibrational state, which are the most populated states in H2 in the 100–1000 K temperature range. Since the PES does not couple ortho- and para-H2, Δ j = ±1 transitions are forbidden. The dominant inelastic processes are the ones that change the rotational quantum number by Δ j = ±2. These are mostly driven by the λ = 2 term in the expansion in Eq. (1), which is the largest anisotropic term in the expansion of the PES. Figure 1 presents the state-to-state cross-sections for pure rotational de-excitation with Δj = −2 of H2 upon collisions with helium up to j = 7. At ultra-low kinetic energies (below 10−3 cm−1, the cross-sections obey the Wigner threshold law (Wigner 1948) for de-excitation cross-section (σ ~ k−1/2). As the kinetic energy increases, more partial waves contribute to the inelastic scattering, the cross-sections pass through a minimum near 20 cm−1 and gradually increase at higher kinetic energies. For the majority of considered kinetic energies, the cross-sections decrease with increasing initial rotational state. This property is translated to thermal rate coefficients (bottom panel in Fig. 1), which also decrease with increasing rotational quantum numbers. This is related to the fact that the rotational spacing between levels increases with j, thus reducing the de-excitation process.
Pure rotational de-excitation (with Δj = −2) within excited vibrational states looks similar to the de-excitation within υ = 0. The only difference is that the cross-sections (and corresponding rate coefficients) increase with the increasing value of υ. Figure 2 presents a comparison between the συ,2→υ,0 (in the top panel) and kυ,2→v,0 (in the bottom panel) for different vibrational quantum numbers. The observed trend is explained by the fact that the energy interval between rotational states decreases with increasing υ, thus enhancing rotational transitions within the same vibrational level. This is in line with an increased contribution from inelastic processes to pressure broadening of rovibrational lines as υ increases (Hartmann et al. 2021), as observed in He-perturbed Q (Thibault et al. 2017), and S and O (Józwiak et al. 2018) lines ofH2.
 |
Fig. 1 State-to-state cross-sections (top panel) and corresponding thermal rate coefficients (bottom panel) for pure rotational de-excitation in υ = 0 with Δj- = −2. |
3.2 Rovibrational (de-)excitation
Figure 3 presents a comparison of the state-to-state cross-sections and corresponding rate coefficients for Δv,Δj = 0 transitions. For reference, we put the elastic scattering cross-section in the ν = 0, j = 0 state (dark blue color), which is at least three orders of magnitude larger than the cross-sections for vibrationally inelastic processes. We recover the expected asymptotic behavior of the elastic cross-section at ultra-low kinetic energies, where it converges to the constant value. The dependence of v-changing cross-sections follows a trend similar to pure rotational de-excitation, with a minimum near 20 cm−1, but the increase in the orders of magnitude of the cross-sections at high (>103 cm−1) is more drastic. For instance, the σ1.0→0,0 cross-section increases by eight orders of magnitude for kinetic energies in the range from 20 to 40 000 cm−1. Overall, the cross-sections and the corresponding thermal rate coefficient decrease rapidly with increasing Δv, owing to the fact that the off-diagonal (in terms of vibrational quantum numbers) radial coupling terms of the potential decrease with Δv. This trend is transferred to thermal rate coefficients. We note that the rate coefficients for vibrational-state-changing collisions are at least three orders of magnitude smaller (at Τ = 8000 Κ) than the rate coefficients for pure rotational de-excitation presented in the top panels of Figs. 1 and 2.
Rate coefficients for simultaneous quenching of both rotational and vibrational excitation are even smaller. Figure 4 presents state-to-state cross-sections and thermal rate coefficients for the v, j = 2 → v′ = 0, j′ = 0 transitions. Contrary to v, j = 0 → v′ = 0, j′ = 0 transitions from Fig. 3, driven only by λ = 0 terms which are off-diagonal in vibrational quantum numbers, transitions in Fig. 4 owe their strength to the anisotropic λ = 2 terms which are off-diagonal in v, v′. Due to the reasons discussed above, the cross-sections and rate coefficients rapidly decrease with increasing Δv.
For the sake of brevity, we do not discuss the analogous (v, j = 1 → v′ = 0, j′ = 1 and v, j = 3 → v′ = 0, j′ = 1) transitions in ortho-H2. The dependence of the cross-sections and rate coefficients on Δv and the overall relation with respect to kinetic energy and temperature remains similar.
 |
Fig. 2 State-to-state cross-sections (top panel) and corresponding thermal rate coefficients (bottom panel) for v, j= 2 → v, j′ = 0 de-excitation with ν = 0,1, 2,3. |
3.3 Comparison with previous results
Here, we compare the new rate coefficients with the available literature data. Due to the large size of the dataset, we begin with a discussion of a few representative rovibrational transitions that highlight the differences and similarities between our results and previous findings.
We begin with the comparison of rate coefficients for pure rotational de-excitation of H2 in the ν = 0 state upon collisions with He. In the top left (k0,2→0,0) and right (k0,3→0,1) panels of Fig. 5 we gathered theoretical rate coefficients calculated in this work, those reported by Flower et al. (1998) and Balakrishnan et al. (1999a), as well as experimental results (Tejeda et al. 2008) determined using Raman spectroscopy in supersonic jets of H2–He mixtures. For theoretical results, we use abbreviations of the names of PESs employed in quantum scattering calculations. We note that both Flower et al. (1998) and Balakrishnan et al. (1999a) performed quantum scattering calculations on the same PES, but used different approach to the rovibrational average in Eq. (2). Flower et al. (1998) approximated the H2 wave functions as harmonic oscillator wave functions (independent of j), while Balakrishnan et al. (1999a,b) obtained χvj(rHH) as expansions in Hermite polynomials using the potential energy curve for H2 taken from Schwenke (1988).
We observe a very good agreement with all previous theoretical calculations, both in the cold (≃10 K) regime, as well as at temperatures of an order of 1000 K. For the ν = 0, j = 2 → v′ = 0, j′ = 0 transitions, our low-temperature results reproduce the experimental datapoints slightly better than other theoretical rate coefficients. We note that Tejeda et al. (2008) also reported results of extensive scattering calculations for the two transitions using the MR PES, its modified (mMR) version (Boothroyd et al. 2003), and the BMP PES. We do not add these results to the top panels in Fig. 5 to maintain the readability of the plot. For the ν = 0, j = 2 → v′ = 0, j′ = 0 de-excitation, using MR and mMR PESs, Tejeda et al. (2008) obtained a perfect agreement with the results of Balakrishnan et al. (1999a), but rate coefficients obtained using the BMP PES deviated significantly from both theoretical and experimental datapoints. A similar agreement between theoretical calculations from the MR and mMR PESs was found for rate coefficients for the ν = 0, j = 3 → v′ = 0, j′ = 1 de-excitations, with results derived from the BMP PES being ≃50% smaller. We also note that rate coefficients for pure rotational de-excitation of H2 by He were studied by Zhou & Chen (2017) who conducted quantum scattering calculations on the BSP PES (Bakr et al. 2013). From Fig. 5 in their paper, we can deduce that rate coefficients for the ν = 0, j = 2 → v′ = 0, j′ = 0 transitions calculated in the range 25 to 150 Κ are slightly lower than the experimental datapoints and are closer to the results of Balakrishnan et al. (1999a).
Now, looking at transitions with ν > 0, we generally obtain a good agreement with the results of Flower et al. (1998) and Balakrishnan et al. (1999a) for transitions with Δv = 0, and Δj = ±2, ±4. As the difference in vibrational and rotational quantum numbers increases, we observe significant differences between our results and previous theoretical calculations. In particular, as shown in the bottom-left (for de-excitation from the ν = 1, j = 0 state) and bottom-right (for a de-excitation from the ν = 2, j = 0 state) of Fig. 5, we observe that rate coefficients for vibrational de-excitation are significantly (by between one and two orders of magnitude) lower than the results of Flower et al. (1998) and Balakrishnan et al. (1999a). We attribute the discrepancies between the results to the quality of the PESs. We recall that the most recent PES was calculated using coupled-cluster method with single, double, and perturbative triple excitations [CCSD(T)], supplemented by full configuration interaction corrections. On the other hand, the MR PES was obtained using much smaller Gaussian basis sets and a lower level of electronic structure theory. Moreover, the BSP3 PES covered a significantly larger range of intramolecular distances (rHH ∈ [0.65, 3.75] a0), which is crucial for the accuracy of quantum scattering calculations involving vibrationally excited H2.
 |
Fig. 3 State-to-state cross-sections (top panel) and corresponding thermal rate coefficients (bottom panel) for v, j = 0 → v′ = 0, j′ = 0 de-excitation with ν = 0, 1, 2, 3. |
 |
Fig. 4 State-to-state cross-sections (top panel) and corresponding thermal rate coefficients (bottom panel) for v, j = 2 → v′ = 0, j′ = 0 de-excitation from the four considered vibrational states. |
 |
Fig. 5 Comparison between the rate coefficients for pure rotational v = 0, j = 2 → v = 0, j = 0 (top left panel), v = 0, j = 3 → v = 0, j = 1 (top-right), and rovibrational v = 1, j = 0 → v′ = 0, j′ = 0 (bottom left panel) and v = 2, j = 0 → v′ = 0, j′ = 0 (bottom-right) de-excitation provided in this work and the available literature data. |
4 Astrophysical applications
As previously mentioned, in the early Universe, as well as in interstellar clouds, the H2 molecules can be excited by collisions with He, H, H2, and H+ which are the dominant heavy projectiles in such media. It is then of interest to compare and discuss the efficiency of all projectiles for (de-)exciting H2 by collisions. Hence, we compare in Fig. 6 the new H2–He collisional data for the rovibrational relaxation of H2(v = 1, j = 0) to H2(v′ = 0, 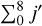 ) to those for H2–H (Lique 2015), H2–H+ (González-Lezana et al. 2021), and H2–p-H2 (Flower & Roueff 1998) as a function of the temperature.
) to those for H2–H (Lique 2015), H2–H+ (González-Lezana et al. 2021), and H2–p-H2 (Flower & Roueff 1998) as a function of the temperature.
As one can see, H+ is by far the most efficient projectile to (de-)excite H2, especially at low temperatures. Such dominance is not surprising and can be explained by the charge of H+ leading to a strong interaction between H2 and H+ and, thus, to an efficient energy transfer during collisions.
For the (de-)excitation induced by neutral projectiles, H is significantly dominating over He and H2 because of its lighter mass and the reactive nature of the system (H2 can be excited by H via inelastic and reactive processes, Lique 2015). Over all the temperature ranges explored in this work, He- and p-H2-rate coefficients exhibit similar magnitude showing that the He:H2 abundance ratio will not be a crucial parameter for determining the excitation conditions of H2 in both the early universe and in interstellar clouds. When modeling of the interstellar spectra, it is customary to use He as a proxy to estimate rate coefficients for the para-H2(j = 0) collider, based on the assumption that their cross sections are equal. Indeed, both He and para-H2(j = 0) possess two electrons and have a spherical shape. One can then use a mass-scaling relation to model para-H2(j = 0) collisional data from He ones:
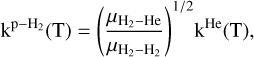 (5)
(5)
where μ is the reduced mass of the collisional system. In the present case, 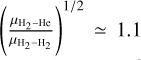 and this approximation seems indeed to aptly justified since He and para-H2(j = 0) collisional data agree well. It should however be mentioned that both sets of collisional data were not performed at the same level of accuracy. It would be desirable, in order to confirm this global agreement, to obtain a new set of para-H2(j = 0) collisional data with a similar level of accuracy to the present He ones.
and this approximation seems indeed to aptly justified since He and para-H2(j = 0) collisional data agree well. It should however be mentioned that both sets of collisional data were not performed at the same level of accuracy. It would be desirable, in order to confirm this global agreement, to obtain a new set of para-H2(j = 0) collisional data with a similar level of accuracy to the present He ones.
Moreover, as a second application and in order to test the impact of the new rate coefficients compared to those of F98 widely used in the astrophysical community, we performed radiative transfer calculations to determine the population of H2 induced by He collisions. Non-local thermodynamic equilibrium (non-LTE) calculations were performed with the RADEX code (van der Tak et al. 2007). Both collisional and radiative processes are taken into account. Only the He projectiles were taken into account. We simulate the excitation conditions of both para- and ortho-H2 induced by He for physical conditions corresponding to the early Universe (Flower et al. 2021) and typical warm molecular clouds where rovibrational lines of H2 are detected (Neufeld & Yuan 2008). Tables 2–3 and 4–5 show a comparison of the H2 fractional population, pv,j, obtained using present and F98 collisional data for a temperature of 5000 K and a He density of 103 cm−3 (typical physical conditions in the early Universe) and for a temperature of 1000 K and a He density of 105 cm−3 (typical physical conditions in warm molecular clouds), respectively. We note that the fractional populations in Tables 2-5 are normalized separately for para-H2 and ortho-H2 species. The relative ortho-to-para ratio is maintained at 3:1, which is consistent with the fact that collisions with He do not induce transitions between para and ortho states.
We can clearly see the population of the different rotational levels in v = 0 vibrational manifold is weakly impacted by the use of the new rate coefficients. A deviation of less than 5% is typically observed for these levels. The effect is the same for both para- and ortho-H2. Such a weak impact can be explained by the good overall agreement between present and F98 pure rotational data. When the vibrational quantum number increases, substantial differences, greater than an order of magnitude, start to appear. These significant deviations reflect the large deviation between present and F98 rovibrational rate coefficients. Globally, the population of rovibrationally excited levels of H2 induced by He collisional is weaker when using present data than when using F98 ones, reflecting new collisional data weaker in magnitude than the former ones.
The magnitude of the line intensities of rovibrational transitions detected by telescopes is directly proportional to the population of the energy levels. The significant deviations seen are likely to modify the observations analysis and the final determination of the abundance of H2 in molecular clouds, even if He is not the dominant collider. The population of υ = 1 energy levels when using the new data are a factor of 3–5 lower than when using the F98 data. We anticipate an increase in the H2 abundance derived from the observations since modeling observational spectra with a weaker population will require to increase in the H2 column density.
Such differences are also likely to modify the cooling function of H2, which is strongly dependent on the H2 populations (Flower et al. 2021). Nevertheless, we note that the largest deviations in the fractional populations are seen for weakly populated levels and we anticipate that the global impact on the cooling function will be moderate.
 |
Fig. 6 Comparison between the rate coefficients for rovibrational v = 1, j = 0 → v′ = 0, |
Comparison between para-H2 fractional population, pv,j, obtained using present and F98 collisional data.
Comparison between ortho-H2 fractional population, pv,j, obtained using present and F98 collisional data.
Comparison between para-H2 pv,j obtained using present and F98 collisional data.
Comparison between ortho-H2 pv,j obtained using present and F98 collisional data.
5 Conclusions
We used the state-of-the-art PES (Thibault et al. 2017) to perform quantum scattering calculations for the H2-He system and to revise the state-to-state rate coefficients calculated by Flower et al. (1998). The revised rates are consistent with the results of previous studies for pure rotational transitions within the ground vibrational state, as reported by Flower et al. (1998) and Balakrishnan et al. (1999a). However, significant discrepancies emerge for rovibrational transitions involving highly-excited rotational and vibrational states. We attribute these discrepancies to the superior accuracy of the PES and the broader range of intramolecular distances in H2 covered by ab initio points, which is crucial for accurate description of inelastic processes involving excited rovibrational states.
The new collisional data have been introduced in a radiative transfer code in order to simulate the excitation conditions of H2 in the early Universe and in warm molecular clouds. We have found that the population of rotational levels in υ = 0 vibrational manifold is weakly impacted by the use of the new collisional data. On the contrary, the population of rotational levels in υ > 0 vibrational manifold is significantly reduced demonstrating the need of using the new set of data in astrophysical models.
Acknowledgements
We acknowledge financial support from the European Research Council (Consolidator Grant COLLEXISM, Grant Agreement No. 811363), and the financial support of the University of Rennes via a grant project dedicated to international collaborations and via the CNRS IRN MCTDH grant. H.J. is supported by the Foundation for Polish Science (FNP) and by the National Science Centre in Poland through Project No. 2019/35/B/ST2/01118. P.W. is supported by the National Science Centre in Poland through Project No. 2022/46/E/ST2/00282. For the purpose of Open Access, the author has applied a CC-BY public copyright license to any Author Accepted Manuscript (AAM) version arising from this submission.
References
- Aannestad, P. A., & Field, G. B. 1973, ApJ, 186, L29 [NASA ADS] [CrossRef] [Google Scholar]
- Audibert, M.-M., Vilaseca, R., Lukasik, J., & Ducuing, J. 1976, Chem. Phys. Lett., 37, 408 [NASA ADS] [CrossRef] [Google Scholar]
- Bakr, B. W., Smith, D. G., & Patkowski, K. 2013, J. Chem. Phys., 139, 144305 [NASA ADS] [CrossRef] [Google Scholar]
- Balakrishnan, N., Forrey, R. C., & Dalgarno, A. 1999a, ApJ, 514, 520 [NASA ADS] [CrossRef] [Google Scholar]
- Balakrishnan, N., Vieira, M., Babb, J. F., et al. 1999b, ApJ, 524, 1122 [NASA ADS] [CrossRef] [Google Scholar]
- Boothroyd, A. I., Martin, P. G., & Peterson, M. R. 2003, J. Chem. Phys., 119, 3187 [NASA ADS] [CrossRef] [Google Scholar]
- Cecchi-Pestellini, C., Casu, S., & Dalgarno, A. 2005, MNRAS, 364, 1309 [NASA ADS] [CrossRef] [Google Scholar]
- Dove, J. E., & Teitelbaum, H. 1974, Chem. Phys., 6, 431 [CrossRef] [Google Scholar]
- Dubernet, M.-L., Alexander, M. H., Ba, Y. A., et al. 2013, A&A, 553, A50 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Flower, D. R., & Pineau des Forêts, G. 2001, MNRAS, 323, 672 [NASA ADS] [CrossRef] [Google Scholar]
- Flower, D. R., & Roueff, E. 1998, J. Phys. B At. Mol. Phys., 31, 2935 [NASA ADS] [CrossRef] [Google Scholar]
- Flower, D. R., Roueff, E., & Zeippen, C. J. 1998, J. Phys. B-At. Mol. Opt., 31, 1105 [NASA ADS] [CrossRef] [Google Scholar]
- Flower, D. R., Le Bourlot, J., Pineau des Forêts, G., & Roueff, E. 2000, MNRAS, 314, 753 [NASA ADS] [CrossRef] [Google Scholar]
- Flower, D. R., Pineau des Forêts, G., Hily-Blant, P., et al. 2021, MNRAS, 507, 3564 [NASA ADS] [CrossRef] [Google Scholar]
- Glover, S. C. O., & Abel, T. 2008, MNRAS, 388, 1627 [NASA ADS] [CrossRef] [Google Scholar]
- González-Lezana, T., Hily-Blant, P., & Faure, A. 2021, J. Chem. Phys., 154, 054310 [CrossRef] [Google Scholar]
- Hartmann, J.-M., Boulet, C., & Robert, D. 2021, Collisional Effects on Molecular Spectra (Elsevier) [Google Scholar]
- Jambrina, P. G., Morita, M., Croft, J. F. E., Aoiz, F. J., & Balakrishnan, N. 2022, J. Phys. Chem., 13, 4064 [Google Scholar]
- Józwiak, H. 2024, The SCATTERING code adjusted for diatom-atom calculations [Google Scholar]
- Józwiak, H., Thibault, F., Stolarczyk, N., & Wcislo, P. 2018, JQSRT, 219, 313 [CrossRef] [Google Scholar]
- Launay, J. M. 1977, J. Phys. B-At. Mol. Opt., 10, 3665 [NASA ADS] [CrossRef] [Google Scholar]
- Le Bourlot, J., Pineau des Forêts, G., & Flower, D. R. 1999, MNRAS, 305, 802 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, T.-G., Rochow, C., Martin, R., et al. 2005, J. Chem. Phys., 122, 024307 [NASA ADS] [CrossRef] [Google Scholar]
- Lique, F. 2015, MNRAS, 453, 810 [NASA ADS] [CrossRef] [Google Scholar]
- Morita, M., & Balakrishnan, N. 2020a, J. Chem. Phys., 153, 091101 [NASA ADS] [CrossRef] [Google Scholar]
- Morita, M., & Balakrishnan, N. 2020b, J. Chem. Phys., 153, 184307 [NASA ADS] [CrossRef] [Google Scholar]
- Muchnick, P., & Russek, A. 1994, J. Chem. Phys., 100, 4336 [NASA ADS] [CrossRef] [Google Scholar]
- Nesterenok, A. V. 2018, Astrophys. Space Sci., 363, 151 [NASA ADS] [CrossRef] [Google Scholar]
- Neufeld, D. A., & Yuan, Y. 2008, ApJ, 678, 974 [NASA ADS] [CrossRef] [Google Scholar]
- Rabitz, H. 1975, J. Chem. Phys., 63, 5208 [NASA ADS] [CrossRef] [Google Scholar]
- Ruaud, M. 2021, ApJ, 916, 103 [CrossRef] [Google Scholar]
- Schwenke, D. W. 1988, J. Chem. Phys., 89, 2076 [Google Scholar]
- Shull, J. M., & Beckwith, S. 1982, ARA&A, 20, 163 [NASA ADS] [CrossRef] [Google Scholar]
- Slowiński, M., Thibault, F., Tan, Y., et al. 2020, Phys. Rev. A, 101, 052705 [CrossRef] [Google Scholar]
- Slowiński, M., Józwiak, H., Gancewski, M., et al. 2022, JQSRT, 277, 107951 [CrossRef] [Google Scholar]
- Stankiewicz, K., Józwiak, H., Gancewski, M., et al. 2020, JQSRT, 254, 107194 [NASA ADS] [CrossRef] [Google Scholar]
- Stankiewicz, K., Stolarczyk, N., Józwiak, H., Thibault, F., & Wcislo, P. 2021, JQSRT, 276, 107911 [NASA ADS] [CrossRef] [Google Scholar]
- Tejeda, G., Thibault, F., Fernández, J. M., & Montero, S. 2008, J. Chem. Phys., 128, 224308 [NASA ADS] [CrossRef] [Google Scholar]
- Thibault, F., Wcisło, P., & Ciurylo, R. 2016, Eur. Phys. J. D, 70, 236 [NASA ADS] [CrossRef] [Google Scholar]
- Thibault, F., Patkowski, K., Żuchowski, P. S., et al. 2017, JQSRT, 202, 308 [NASA ADS] [CrossRef] [Google Scholar]
- Thibault, F., Martínez, R. Z., Bermejo, D., & Wcisło, P. 2020, Mol. Astrophys., 19, 100063 [NASA ADS] [CrossRef] [Google Scholar]
- van der Tak, F. F. S., Black, J. H., Schöier, F. L., Jansen, D. J., & van Dishoeck, E. F. 2007, A&A, 468, 627 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wcisło, P., Thibault, F., Stolarczyk, N., et al. 2021, JQSRT, 260, 107477 [CrossRef] [Google Scholar]
- Wigner, E. P. 1948, Phys. Rev., 73, 1002 [CrossRef] [Google Scholar]
- Yuan, Y., & Neufeld, D. A. 2010, ApJ, 726, 76 [Google Scholar]
- Zhou, B., & Chen, M. 2017, Mol. Phys., 115, 2442 [CrossRef] [Google Scholar]
The scattering code, optimized for H2–He calculations, is publicly available at https://github.com/hjozwiak-umk/bigos_h2he
All Tables
Comparison between para-H2 fractional population, pv,j, obtained using present and F98 collisional data.
Comparison between ortho-H2 fractional population, pv,j, obtained using present and F98 collisional data.
Comparison between ortho-H2 pv,j obtained using present and F98 collisional data.
All Figures
 |
Fig. 1 State-to-state cross-sections (top panel) and corresponding thermal rate coefficients (bottom panel) for pure rotational de-excitation in υ = 0 with Δj- = −2. |
| In the text | |
 |
Fig. 2 State-to-state cross-sections (top panel) and corresponding thermal rate coefficients (bottom panel) for v, j= 2 → v, j′ = 0 de-excitation with ν = 0,1, 2,3. |
| In the text | |
 |
Fig. 3 State-to-state cross-sections (top panel) and corresponding thermal rate coefficients (bottom panel) for v, j = 0 → v′ = 0, j′ = 0 de-excitation with ν = 0, 1, 2, 3. |
| In the text | |
 |
Fig. 4 State-to-state cross-sections (top panel) and corresponding thermal rate coefficients (bottom panel) for v, j = 2 → v′ = 0, j′ = 0 de-excitation from the four considered vibrational states. |
| In the text | |
 |
Fig. 5 Comparison between the rate coefficients for pure rotational v = 0, j = 2 → v = 0, j = 0 (top left panel), v = 0, j = 3 → v = 0, j = 1 (top-right), and rovibrational v = 1, j = 0 → v′ = 0, j′ = 0 (bottom left panel) and v = 2, j = 0 → v′ = 0, j′ = 0 (bottom-right) de-excitation provided in this work and the available literature data. |
| In the text | |
 |
Fig. 6 Comparison between the rate coefficients for rovibrational v = 1, j = 0 → v′ = 0, |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.