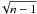| Issue |
A&A
Volume 531, July 2011
|
|
|---|---|---|
| Article Number | A165 | |
| Number of page(s) | 25 | |
| Section | Catalogs and data | |
| DOI | https://doi.org/10.1051/0004-6361/201116769 | |
| Published online | 07 July 2011 | |
The atmospheric parameters and spectral interpolator for the MILES stars⋆
1
Université de Lyon, Université Lyon 1, 69622 Villeurbanne, France ;
CRAL, Observatoire de Lyon, CNRS UMR 5574, 69561 Saint-Genis Laval, France
e-mail: philippe.prugniel@univ-lyon1.fr; isabelle.vauglin@univ-lyon1.fr
2
Instituto de Astrofísica de Canarias, La Laguna, 38200 Tenerife, Spain ;
Departamento de Astrofísica, Universidad de La Laguna, 38205 La Laguna, Tenerife, Spain
e-mail: koleva@iac.es
Received: 22 February 2011
Accepted: 16 April 2011
Context. Empirical libraries of stellar spectra are used to classify stars and synthetize stellar populations. MILES is a medium spectral-resolution library in the optical domain covering a wide range of temperatures, surface gravities and metallicities.
Aims. We redetermine the atmospheric parameters of these stars in order to improve the homogeneity and accuracy. We build an interpolating function that returns a spectrum as a function of the three atmospheric parameters, and finally we characterize the precision of the wavelength calibration and stability of the spectral resolution.
Methods. We used the ULySS program with the ELODIE library as a reference and compared the results with those in the literature.
Results. We obtain precisions of 60 K, 0.13, and 0.05 dex, respectively, for Teff, log g, and [Fe/H] for the FGK stars. For the M stars, the mean errors are 38 K, 0.26, and 0.12 dex and 3.5%, 0.17, and 0.13 dex for the OBA. We construct an interpolator that we test against the MILES stars themselves. We test it also by measuring the atmospheric parameters of the CFLIB stars with MILES as reference and find it to be more reliable than the ELODIE interpolator for the evolved hot stars, like those of the blue horizontal branch in particular.
Key words: stars: fundamental parameters / galaxies: stellar content / stars: abundances
FITS files are only and Table 1 also available in electronic form at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/531/A165
© ESO, 2011
1. Introduction
MILES (Sánchez-Blázquez et al. 2006) is a medium-resolution library of observed stellar spectra in the optical domain. It is comparable to CFLIB (Valdes et al. 2004) and ELODIE (Prugniel & Soubiran 2001), and is of a particular interest for its accurate flux calibration. The three libraries contain normal stars with a wide range of characteristics, from spectral types O to M, all luminosity classes and a wide distribution of metallicities (−2.5 < [Fe/H] < 1) dex.
The empirical libraries have important applications in different fields. They are used as references to classify stars and determine atmospheric parameters (see Wu et al. 2011, and references therein). They are also important ingredients to model stellar populations, which are used to study the history of galaxies (Prugniel et al. 2007a). The most important characteristics of a library are (i) the wavelength range; (ii) the spectral resolution; and (iii) the distribution of the stars in the parameter space whose axes are the effective temperature, Teff, the logarithm of the surface gravity, log g, and the metallicity, [Fe/H]. Other properties, such as the precision and uniformity of the wavelength calibration and spectral resolution or the accuracy of the flux calibration, are also to be considered.
The ELODIE library has been upgraded three times after its publication (Prugniel & Soubiran 2001, 2004; Prugniel et al. 2007b). The last version, ELODIE 3.2 is preliminary described in Wu et al. (2011). It counts 1962 spectra of 1388 stars observed with the eponym echelle spectrograph (Baranne et al. 1996) at the spectral resolution Δλ ≈ 0.13 Å (R = λ/Δλ ≈ 42 000) in the wavelength range 3900 to 6800 Å. CFLIB, also known as the “Indo-US” library, has 1273 stars at a resolution1 Δλ ≈ 1.4 Å ( ) in the range 3460 to 9464 Å. The atmospheric parameters of CFLIB were homogeneously determined by Wu et al. (2011). MILES contains 985 stars at a resolution2 Δλ ≈ 2.56 Å in the range 3536 to 7410 Å. The atmospheric parameters of these stars were compiled from the literature or derived from photometric calibrations by Cenarro et al. (2007). The [Mg/Fe] relative abundances were recently determined by de Castro Milone et al. (2011).
) in the range 3460 to 9464 Å. The atmospheric parameters of CFLIB were homogeneously determined by Wu et al. (2011). MILES contains 985 stars at a resolution2 Δλ ≈ 2.56 Å in the range 3536 to 7410 Å. The atmospheric parameters of these stars were compiled from the literature or derived from photometric calibrations by Cenarro et al. (2007). The [Mg/Fe] relative abundances were recently determined by de Castro Milone et al. (2011).
The goals of this article are to (i) redetermine the atmospheric parameters of the stars of MILES homogeneously using ELODIE as reference; (ii) characterize the resolution and accuracy of the wavelength calibration; and (iii) build an interpolator. The last is a function, based on an interpolation over all the stars of the library, that returns a spectrum for a given set of atmospheric parameters, Teff, log g, and [Fe/H].
In Sect. 2, we describe the steps of the data analysis. In Sect. 3, we present the results and assess their reliability, and Sect. 4 gives the conclusions.
2. Analysis
In this section, we give the details of our analysis. First, we describe the different steps and then present the determination of the atmospheric parameters and line-spread function and the computation of the interpolator in detail.
2.1. Strategy
To determine the atmospheric parameters, we compared the observed MILES spectra with templates built from the ELODIE library. The χ2 minimization, performed with the ULySS program3 (Koleva et al. 2009), was done as described in Wu et al. (2011). The underlying model is ![\begin{equation} {\rm Obs}(\lambda) = P_n(\lambda) \times {\rm G(v_{\rm res},\sigma)}~\otimes {\rm TGM} (T_{\rm eff}, g, {\rm [Fe/H]}, \lambda), \label{eqn:main} \end{equation}](/articles/aa/full_html/2011/07/aa16769-11/aa16769-11-eq13.png) (1)where Obs(λ) is the observed spectrum sampled in log λ, Pn(λ) a series of Legendre polynomials of degree n, and G(vres,σ) a Gaussian broadening function parameterized by the residual velocity vres, and the dispersion σ. The TGM function models a stellar spectrum for given atmospheric parameters. It interpolates the ELODIE 3.2 library described in Sect. 2.2. The program minimizes the squared difference between the observations and the model. The free parameters are the three of TGM, the two of G, and the n coefficients of Pn.
(1)where Obs(λ) is the observed spectrum sampled in log λ, Pn(λ) a series of Legendre polynomials of degree n, and G(vres,σ) a Gaussian broadening function parameterized by the residual velocity vres, and the dispersion σ. The TGM function models a stellar spectrum for given atmospheric parameters. It interpolates the ELODIE 3.2 library described in Sect. 2.2. The program minimizes the squared difference between the observations and the model. The free parameters are the three of TGM, the two of G, and the n coefficients of Pn.
A single minimization provides the atmospheric parameters and the broadening. The advantage of this simultaneity is to reduce the effects of the degeneracy between the broadening and the atmospheric parameters (see Wu et al. 2011).
The function G encompasses the effects of both the finite spectral resolution and the physical broadening of the observation and model. The physical broadening is essentially due to rotation and turbulence. The spectral resolution is represented by the so-called line-spread function (LSF), and in first approximation we can write 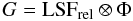 (2)where Φ is the relative physical broadening between the observation and the model (i.e. mismatch of rotation and turbulence) and LSFrel the relative LSF. The absolute LSF of the observed spectrum is LSF = LSFmod ⊗ LSFrel, where LSFmod is the LSF of the model. The approximations are that (i) neither Φ nor LSFrel are strictly Gaussians; and (ii) the LSF generally depends on the wavelength, so we cannot rigorously write convolutions. The Gaussian approximation is certainly acceptable in the present context of moderate spectral resolution because: (i) the physical broadening can often be neglected or can otherwise be assumed Gaussian; and (ii) the MILES spectra were acquired with a relatively narrow slit, thus the top-hat signature of the slit is dominated by the intrinsic broadening due to the disperser.
(2)where Φ is the relative physical broadening between the observation and the model (i.e. mismatch of rotation and turbulence) and LSFrel the relative LSF. The absolute LSF of the observed spectrum is LSF = LSFmod ⊗ LSFrel, where LSFmod is the LSF of the model. The approximations are that (i) neither Φ nor LSFrel are strictly Gaussians; and (ii) the LSF generally depends on the wavelength, so we cannot rigorously write convolutions. The Gaussian approximation is certainly acceptable in the present context of moderate spectral resolution because: (i) the physical broadening can often be neglected or can otherwise be assumed Gaussian; and (ii) the MILES spectra were acquired with a relatively narrow slit, thus the top-hat signature of the slit is dominated by the intrinsic broadening due to the disperser.
The variation in the LSF with the wavelength only has minor consequences on the atmospheric parameters (see Wu et al. 2011), but we explain below how we determine it and inject it in TGM to get the most accurate parameters.
In Eq. (1), the role of the multiplicative polynomial, Pn(λ), is to absorb the mismatch of the shape of the continuum, caused by uncertainties in the flux calibration. It does not bias the measured atmospheric parameters, because it is included in the fitted model rather than determined in a preliminary normalization. In principle, a moderate degree, n ≈ 10, is sufficient, but a higher degree suppresses the “waves” in the residuals and helps the interpretation of the misfits (the residuals are smaller, and it is easier to detect poorly fitted lines). High values of n, up to 100 or more, do not affect the parameters (Wu et al. 2011). The optimal choice of n depends on the resolution, wavelength range, and accuracy of the wavelength calibration. We determined it following the precepts of Koleva et al. (2009). We chose stars of various spectral types and tested different values in order to locate the plateau where the atmospheric parameters are not sensitive to n. We adopted n = 40.
The choice of ELODIE as reference limits the wavelength range where the spectra can be analysed. In particular, the blue end, below the H & K lines, is unfortunately not used. An alternative would have been to use a theoretical library, like the one of Coelho et al. (2005). We tried this solution, but we found that the misfits are significantly larger than with ELODIE (see Sect. 3.1), so we decided to maintain our initial choice.
To handle the wavelength dependence of the LSF, the analysis proceeds in three steps.
-
Determination of the LSF.
We determine thewavelength-dependent LSF of each spectrum of stars in commonbetween the MILES and ELODIE libraries. We use the uly_lsfcommand, as described in Sect. 2.3.
-
Determination of the atmospheric parameters.
We inject the wavelength-dependent relative LSF into the models so that the result has the same resolution characteristics as the observations, and determine the atmospheric parameters calling ulyss.
-
Construction of the spectral interpolator.
Finally, using these atmospheric parameters, we compute an interpolator. For each wavelength element, a polynomial in log Teff, log g, and [Fe/H] is adjusted on all the library stars, to be used as an interpolating function. This process is introduced in Sect. 2.5.
2.2. ELODIE 3.2: library and interpolator
ELODIE 3.2 is based on the same set of stars as ELODIE 3.1 (Prugniel et al. 2007b) and benefited from several improvements concerning various details of the data reduction, in particular a better correction of the diffuse light. We note also that a systematic error of 0.0333 Å (i.e. approximately 2 km s-1) on the wavelengths of the previous version has been corrected (it came from a bug in the computation of the world coordinate system after a rebinning; ELODIE 3.1 was red-shifted).
The ELODIE interpolator approximates each spectral bin with polynomials in Teff, log g, and [Fe/H]. Three different sets of polynomials are defined for the OBA, FGK and M type temperature ranges, and are linearly interpolated in overlapping regions. This interpolator has been noticeably upgraded in the last version, taking the stellar rotation into account and adding some theoretical spectra to extend its range of validity to scarcely populated regions of the parameter space. The ELODIE 3.2 interpolator is publicly available at http://ulyss.univ-lyon1.fr/models.html, and additional details are given in Wu et al. (2011). A similar interpolator is described in Sect. 2.5 for MILES, with the only difference that the rotation terms are omitted.
2.3. Accurate line-spread function
The LSF describes the instrumental broadening, and it may vary with the wavelength. We determined the wavelength-dependent broadening by fitting the spectra of the 303 MILES stars belonging also to ELODIE. (Since ELODIE contains repeated observations of the same stars, this corresponds to 404 comparisons.) These fits were performed with the function uly_lsf in a series of 400 Å intervals separated by 300 Å, hence overlapping by 100 Å on both ends. This procedure gives nine sampling points over the ELODIE range.
The change in broadening with wavelength is a consequence of the characteristics of the disperser and design of the spectrograph, but the shift in these functions with respect to the rest-frame wavelengths should ideally be null. However, the finite precision of the wavelength calibration and uncertain knowledge of the heliocentric velocity of the stars result in residual shifts that may be wavelength dependent. Flexures in the spectrographs or temperature drifts may cause these effects. Their magnitudes are expected to be small fractions of pixels. Sánchez-Blázquez et al. (2006) estimate the precision of their calibration to about 6 km s-1. These residuals are likely to cancel each other out when we average the LSF for all the stars.
We estimated the mean instrumental velocity dispersion and residual shift in each spectral chunk as a clipped average of the individual ones using the IDL procedure biweight_mean that does a bisquare weighting (a median estimation gives identical results).
2.3.1. Absolute LSF
Our analysis provides the relative LSF between MILES and ELODIE. Since the characterization of the LSF has an intrinsic interest, we give the absolute LSF obtained after deconvolving by the LSF of ELODIE.
The FWHM resolution of the ELODIE spectrograph, measured on the thorium lines of calibrating spectra varies from 7.0 km s-1 in the blue to 7.4 in the red (Baranne et al. 1996) or, respectively, 0.09 and 0.17 Å. This corresponds to a mean resolving power of R = 42 000. The low-resolution (i.e. R ≈ 10 000) version of ELODIE 3.2, used in this paper, was produced by convolving the full-resolution spectra with a Gaussian of FWHM = 0.556 Å. Therefore, the final resolution varies from 0.564 to 0.581 Å along the wavelength range, for an average of 0.573 Å.
To check this value, we analysed the LSF of the ELODIE interpolated spectra that have the atmospheric parameters of the MILES stars, using Coelho et al. (2005) as reference. We found a relative broadening of 0.584 ± 0.006 Å, independently of the wavelength. The difference from the value above is definitely compatible with the residual rotational broadening of the interpolated spectra, and we adopted the mean value derived above.
The Gaussian width of the absolute LSF of MILES is therefore the quadratic sum of the width of the LSF relative to ELODIE with the width of the absolute LSF of ELODIE.
2.3.2. Biased LSF
If the effective spectral resolution was the same for all the spectra of MILES, we could simply inject the LSF into the model and adjust only the atmospheric parameters (i.e., omit the convolution in Eq. (1)). However, because of the rotational broadening and dispersion of the instrumental broadening, the effective resolution varies, and we still need to fit the atmospheric parameters and the broadening.
In practice, the model must have a higher spectral resolution than the observation, because it is convolved with G during the analysis (Eq. (1)). If we injected the relative LSF in the model, the result would be broader than the best resolved library spectra. To avoid this difficulty we bias the LSF by subtracting quadratically 40 km s-1 (at any wavelengths) from the width of the mean relative LSF. The resolution of this biased LSF is higher than any spectrum of the library, and it has the correct wavelength dependence.
2.4. Determination of the atmospheric parameters
We fitted the spectra using the ELODIE 3.2 interpolator, injecting the biased LSF previously derived, and assuming a uniform broadening, as described in Eq. (1). In order to avoid trapping in local minimal, we used a grid of initial guesses sampling all the parameter space. The nodes of this grid are
-
Teff ∈ {3500,4000,5600,7000,10 000,18 000,30 000} K;
-
log g ∈ {1.8,3.8} cm s-2;
-
[Fe/H] ∈ {−1.7, −0.3,0.5} .
For the stars belonging to clusters, we adopted and fixed the metallicity to the value given in Cenarro et al. (2007).
The spectra were rebinned into an array of logarithmically spaced wavelengths, each pixel corresponding to 30 km s-1. This choice oversamples the original spectrum by a factor two in the blue and by 20% in the red. We performed the fit in the region 4200–6800 Å, excluding the blue end of the spectra, where the signal-to-noise ratio is lower.
Because the noise estimation in the MILES spectra is not available, we assumed a constant noise, resulting in a uniform weighting of each wavelength bin. We estimated an upper limit to the internal errors on the derived parameters by assuming χ2 = 1.
This first minimization localizes the region of the solution, and we refine our measurements by again running ulyss with the /clean option to identify and discard the spikes in the signal. They result from the imperfect subtraction of sky lines and removal of spikes due to hits of cosmic rays. This process also discards the stellar emission lines. The second set of derived parameters is very close to the first one, because the MILES spectra had already been corrected for most of the observational artifacts.
Finally, the resulting parameters were compared with Cenarro et al. (2007), and the significant outliers were examined by checking the quality of the fit and searching the literature for accurate measurements from high-resolution spectroscopy.
2.5. MILES library interpolator
The goal is to build an interpolator that is similar to the one of the ELODIE library. It may then be used to (i) analyse stellar spectra, for example with ULySS; or (ii) create stellar population models, for example with PEGASE.HR (Le Borgne et al. 2004). The general idea is to approximate each wavelength bin with a polynomial function of Teff, log g and [Fe/H]. This process resembles the fitting functions (Worthey et al. 1994) that are used to predict the equivalent width of some features or spectrophotometric indices, given some atmospheric parameters. It is extended to model each spectral point.
This is a global interpolation, in the sense that each polynomial is valid for a wide range of parameters. An alternative would be to use a local interpolation, like averaging the nearest spectra to a given point in the parameter space. A good example of local interpolation is Vazdekis et al. (2003). Both methods have their own advantages and inconveniences. The global interpolation is less sensitive to the stochasticity of the distribution of the stars, but may not respond accurately in the regions where the spectrum changes rapidly. It is also continuous and derivable everywhere, which are required for using it as a function for a non-linear fit, as in ULySS. In both cases it is possible to control the quality of the interpolation by comparing each star to the interpolated spectrum that matches its parameters.
For the present work, we use the same polynomial developments as for ELODIE 3.2, because this will permit using it directly as a model for a TGM component in ULySS. The first version of this interpolator is described in Prugniel & Soubiran (2001), and we recall below the principles and present the difference introduced in ELODIE 3.2.
2.5.1. Teff regimes
The library contains all types of stars from O to M, and the temperature is the main parameter controlling the shape of the spectra. Modelling all the stars with a single set of polynomials would necessitate including a large number of terms. The result would accordingly be very unstable. It would present oscillations and violently diverge near the edges of the parameter space. For this reason, we defined three temperature ranges, matching the OBA, FGK, and M spectral types, where independent sets of polynomials are adjusted. These three regimes have comfortable overlaps, allowing us to connect them smoothly by a linear interpolation. The limits are
-
OBA regime:
Teff > 7000 K;
-
FGK regime:
4000 < Teff < 9000 K;
-
M regime:
Teff < 4550 K.
The M regime encompasses the cool K-type stars.
2.5.2. Polynomial developments
The developments are the same as for ELODIE.3.2, but truncated to exclude the rotation terms introduced to suppress a bias due to a degeneracy between the stellar rotation and the temperature (see Wu et al. 2011). Because of the lower spectral resolution of MILES, the stellar rotation is mixed with the variation in the resolution from star to star, and the introduction of these terms did not appear relevant.
The terms were chosen iteratively, adding at each step the one leading to the largest reduction of the residuals between the observations and the interpolated spectra. The following developments were used: ![\begin{eqnarray} {\rm TGM}&&(T_{\rm eff}, g, {\rm [Fe/H]}, \lambda) = a_0(\lambda) + a_1(\lambda) \times \log T_{\rm eff} \nonumber\\ &&+a_2(\lambda) \times {\rm [Fe/H]} \nonumber\\ &&+ a_3(\lambda) \times \log g + a_4(\lambda) \times (\log T_{\rm eff})^2 \nonumber\\ &&+ a_5(\lambda) \times (\log T_{\rm eff})^3 + a_6(\lambda) \times (\log T_{\rm eff})^4 \nonumber\\ &&+ a_7(\lambda) \times \log T_{\rm eff} \times {\rm [Fe/H]} + a_8(\lambda) \times \log T_{\rm eff} \times \log g \nonumber\\ &&+ a_9(\lambda) \times (\log T_{\rm eff})^2 \times \log g \nonumber\\ &&+ a_{10}(\lambda) \times (\log T_{\rm eff})^2 \times {\rm [Fe/H]} \nonumber\\ &&+ a_{11}(\lambda) \times (\log g)^2 + a_{12}(\lambda) \times ({\rm [Fe/H]})^2 \nonumber\\ &&+ a_{13}(\lambda) \times (\log T_{\rm eff})^5 + a_{14}(\lambda) \times \log T_{\rm eff} \times (\log g)^2 \nonumber\\ &&+ a_{15}(\lambda) \times (\log g)^3 + a_{16}(\lambda) \times ({\rm [Fe/H]})^2 \nonumber\\ &&+ a_{17}(\lambda) \times \log T_{\rm eff} \times ({\rm [Fe/H]})^2 \nonumber\\ &&+ a_{18}(\lambda) \times \log g \times {\rm [Fe/H]} \nonumber\\ &&+ a_{19}(\lambda) \times (\log g)^2 \times {\rm [Fe/H]} \nonumber\\ &&+ a_{20}(\lambda) \times \log g \times ({\rm [Fe/H]})^2 \nonumber\\ \label{eqn:dev} &&+ a_{21}(\lambda) \times T_{\rm eff} + a_{22}(\lambda) \times (T_{\rm eff})^2, \end{eqnarray}](/articles/aa/full_html/2011/07/aa16769-11/aa16769-11-eq46.png) (3)where TGM is a flux-calibrated interpolated spectrum. Unlike for ELODIE, we did not compute a continuum-normalized interpolator, as it is not needed here. The 23 terms were used for both the FGK and M regimes, but the development was truncated to the first 19 for the OBA one.
(3)where TGM is a flux-calibrated interpolated spectrum. Unlike for ELODIE, we did not compute a continuum-normalized interpolator, as it is not needed here. The 23 terms were used for both the FGK and M regimes, but the development was truncated to the first 19 for the OBA one.
2.5.3. Support for extrapolation
One of the limitations of using empirical libraries is that they do not cover the full range of atmospheric parameters. In particular, to study the stellar populations of galaxies, we would need, for example, young stars of low metallicity, which are obviously missing in a library of Galactic stars. For this reason, it is important that the interpolator preserves its quality at the edges of the parameter space, where only rare stars are present. This is a difficulty for any type of interpolating function.
A solution could have been to supplement the library with theoretical spectra in the margins of the parameter space. However, this would introduce discontinuities because the flux scale of theoretical spectra is not fully consistent with the empirical library. To improve this situation, Prugniel et al. (2007a) introduced a semi-empirical solution where theoretical spectra are used differentially to extend the coverage of the parameter space. This was used to add an [Mg/Fe] dimension to the space, and to model spectra with non-solar abundances, as Galactic globular clusters (Prugniel et al. 2007a; Koleva et al. 2008). The same principle was adopted in ELODIE 3.2 to extend the range of the 3-dimensional parameter space (without the [Mg/Fe] dimension which is not taken into consideration neither in ELODIE 3.2 nor in the present paper).
We computed the differential effect of changing a parameter between a point belonging to the empirical library, and another one located outside of the range of the library. This differential spectrum was built using a theoretical library. Finally, we produced a semi-empirical spectrum, summing the differential one to one generated with the initial version of then interpolator (computed without the semi-empirical extrapolation supports) at the reference location.
We used the Martins et al. (2005) library to add semi-empirical spectra at the following locations: (i) Teff = 40 000 K, log g = 4 and 4.75, and [Fe/H ] = −1, 0 and +0.3 dex, using as reference Teff = 20 000 K, log g = 3.5, [Fe/H ] = 0; (ii) Teff = 55 000 K, log g = 3.5 and 4.75, and [Fe/H ] = −1, and +0.3 dex, using as reference Teff = 30 000 K, log g = 3.5, [Fe/H ] = 0; (iii) Teff = 20 000 K, log g = 3, and 5 and [Fe/H ] = −1, using as reference Teff = 20 000 K, log g = 3.5, [Fe/H ] = 0. We also used the Coelho et al. (2005) library to add some low-metallicity cool dwarfs at the locations Teff = 3500 K, log g = 4.5 and 5.0, [Fe/H ] = −1.5, –2.0 and − 2.5 using as reference Teff = 3500 K, log g = 4.5, [Fe/H ] = −0.5.
 |
Fig. 1 Line-spread function for 10 stars of the MILES library chosen arbitrarily (actually 10 of the first 12), using the interpolated ELODIE spectra for reference. The top panel shows the residual shift of the spectra, illustrating the precision of the wavelength calibration and of the rest-frame reduction. The bottom panel presents the FWHM resolution. The mean formal error on each LSF point is 0.5 km s-1 on the residual shift and 0.025 Å on the FWHM resolution. |
 |
Fig. 2 Histograms of the broadening and residual shift of the line-spread function of the MILES library at 5300 Å. The green histograms are for the 404 direct comparisons with spectra of the ELODIE library. The red ones are the comparisons with the ELODIE interpolator. The top panel is the distribution of the residual shifts, in km s-1, and the bottom ones the distribution of the FWHM Gaussian broadening. |
We affected low weights to these spectra, so they do not affect the region populated with observed stars: each extrapolation-support spectrum has 1/20th of the weight of an observed star. We computed a final version of the interpolator using the semi-empirical spectra. The interpolated spectra in the extrapolated regions are probably not very accurate, but they do not diverge and are sufficient for many applications.
3. Results
In this section, we present the results of the previous procedure. We discuss the determination of the LSF, the measurements of the atmospheric parameters, and finally the computation and validation of the interpolator.
3.1. Line-spread function and wavelength calibration
The broadening was determined individually by comparing MILES and ELODIE spectra for all the stars in common. To increase the statistics, we also did the analysis for all the MILES stars by comparing them with the ELODIE interpolated spectrum corresponding to their atmospheric parameters. This second set of LSFs includes both the instrumental and physical broadening of the individual stars.
Figure 1 presents the individual LSF (using the ELODIE interpolated spectra as reference) for some stars chosen arbitrarily (the firsts of the list). From this small subset alone, it is apparent that the broadening is variable. Some spectra have a lower effective resolution, possibly due to stellar rotation, and some have a higher resolution, maybe because of a better focusing of the spectrograph. It also appears that the rest-frame reduction is not always accurate, with deviation reaching a few 10 km s-1. This may be due to (i) uncertain knowledge of the heliocentric velocities; (ii) imperfect wavelength calibration; or (iii) stellar duplicity. We note also that the residual shift often changes with the wavelength by 10 to 30 km s-1 over the ELODIE range. This results from an uncertainty in the dispersion relation. The effect is slightly stronger than the precision estimated in Sánchez-Blázquez et al. (2006). The values of the broadening and residual shift at 5300 Å are given for each star in Table 1.
The histograms of the broadening and residual shifts are presented in Fig. 2. The Gaussian broadening at 5300 Å spans the range 30 < σins < 92 km s-1, (i.e. 1.3 < FWHM < 3.8 Å), and the histogram is skewed toward the large dispersions. This is likely due to the effect of the rotation. The mean broadening at the same wavelength is 60.5 km s-1, for the direct comparison, with the rms dispersion of 2.4 km s-1 (i.e. respectively 2.52 and 0.10 Å for the FWHM). The mean broadening is similar (60.9 km s-1) and the spread slightly wider (3.6 km s-1), when interpolated spectra are used. The consistency between the two determinations shows that the physical broadening only makes a minor contribution.
As expected, the residual shifts essentially cancel out in the mean LSF. The mean shift is 2 km s-1 (identical for the two analysis), in the sense that MILES is red-shifted. The internal rms spread of these residual shifts is 12 km s-1 or FWHM = 0.50 Å at 5300 Å. If MILES is used to compute population models, this is combined with the instrumental broadening. In other words, the resolution of an interpolated MILES spectrum, or of a population model, will be 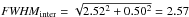 Å (assuming that the effect is uniform over all the parameter space).
Å (assuming that the effect is uniform over all the parameter space).
The mean absolute difference of the residual velocity between the last and first segments of the LSF (i.e. between 6500 and 4100 Å) is 15 km s-1. This reflects the accuracy of the dispersion relation used for the wavelength calibration. As explained in Sánchez-Blázquez et al. (2006), to save observing time, arc spectra were not acquired for each individual spectrum, but only for some spectra representative of each spectral type and luminosity class. It was assumed that the linear dispersion and higher order terms of the dispersion relation were constant, and a global shift was determined by cross-correlating each spectrum to a well-calibrated one. Our present test indicates that the stability of the spectrograph was slightly over-estimated, and the variation in the linear term of the dispersion relation will further degrade the LSF for population models.
 |
Fig. 3 Mean line-spread function of the MILES library, using for reference (i) the interpolated ELODIE spectra (red line and symbols); and (ii) the ELODIE spectra of stars in common (green). The top panel gives the mean residual shift over all the library, and the bottom panel the mean FWHM wavelength resolution. The bars indicate the errors on the mean value (i.e. dispersion/ |
The variation in the LSF with wavelength, as presented in Fig. 3, is consistent for the two sets of templates. The resolution changes from 2.45 Å at 4000 Å to 2.63 Å at 6500 Å, with an average value of 2.56 Å. This is broader than the estimation in Sánchez-Blázquez et al. (2006). In this paper, the authors find FWHM = 2.3 Å by comparison with CFLIB, for which they assumed a resolution of 1 Å. In fact, the resolution of CFLIB is instead ≈ 1.4 Å (Wu et al. 2011; Beifiori et al. 2011), and correcting this error brought the two values to agreement. Beifiori et al. (2011) also measured the resolution of MILES with a similar method and find 2.55 Å, independent of the wavelength. This is consistent with our result.
It is also interesting to characterize the LSF over the whole MILES wavelength range. We therefore repeated the analysis using the Coelho et al. (2005) library. We found consistent results in the ELODIE range, but with a wider spread, certainly due to lower quality fits. The residuals are typically three times larger than those obtained when we compared to ELODIE. A consequence is that the trend of the LSF with the wavelength is smeared out, leaving a uniform FWHM = 2.59 ± 0.08 Å. We similarly analysed the MILES spectra of the five closest analogues of the Sun against the high-resolution spectrum from Kurucz et al. (1984). The results are also consistent with those obtained with ELODIE, but with a large spread resulting from the small statistics. Therefore we cannot constrain the resolution outside of the wavelength range of ELODIE with the same accuracy.
3.2. Atmospheric parameters
We measured the atmospheric parameters for the 985 spectra as indicated in Sect. 2.4. As is known from Wu et al. (2011), the automatic determination is highly reliable for the FGK stars, but lacks faithfulness in some regions of the parameter space. Namely, this concerns the hot evolved stars and the cool stars (Teff < 3600 K). Therefore, for the stars found in these regimes, we searched the literature for recent determinations based on high-resolution spectroscopy. We also examined the very low-metallicity stars, and those for which our derived parameters depart significantly from those listed in Cenarro et al. (2007). Whenever we found values we judged were more credible than ours, we adopted them.
For 77 stars (8% of the library), we adopted parameters compiled and averaged from the literature. For four of them HD 18191, 17491, 54810, and 113285, we adopted either the metallicity or the gravity from the internal inversion of the MILES interpolator (see. Sect. 3.3). For six stars (one A-type star with emission line HD 199478, and five cool stars, Teff < 3000 K, G 156-031 and 171-010, HD 113285, 126327, and 207076), we could not find any reliable source for at least one of the atmospheric parameters.
The most metal-poor star of the library, HD 237846, belongs to a stream discovered by Helmi et al. (1999). We adopted [Fe/H] = −3.15 from recent measurements (Zhang et al. 2009; Ishigaki et al. 2010; Roederer et al. 2010), while Cenarro et al. (2007) catalogued [Fe/H] = −2.59. The inversion with ELODIE returned [Fe/H] = −2.52. The fitted metallicity values for the low metallicity stars ([Fe/H ] < −1.70) were often biased toward higher values by ~0.15 dex. For 13 of these 46 metal-deficient stars, we adopted parameters from the recent literature
The adopted parameters are listed in Table 1, also available in the Vizier database. Figure 4 shows the distribution of the stars in the Teff vs. log g and Teff vs. [Fe/H] diagrams. We compared, in Fig. 5, our parameters to those from Cenarro et al. (2007). We also compared our results with ELODIE 3.2 and CFLIB (Wu et al. 2011) for the stars in common. The corresponding statistics, computed with the IDL command biweight_mean, to discard the outliers, are shown in Table 2. The three lines are for the OBA (Teff > 8000 K), FGK (4000 < Teff ≤ 8000 K), and M (Teff ≤ 4000 K) stars, respectively.
 |
Fig. 4 Distribution in the log (Teff) – log g and log (Teff) – [Fe/H] planes of the adopted atmospheric parameters for the 985 MILES stars. In the top panel, the colour of the symbols distinguishes different metallicity classes. In the bottom panel, it distinguishes different classes of surface gravity. |
 |
Fig. 5 Comparison of the measured atmospheric parameters with the Cenarro et al. (2007) compilation. The abscissae are the parameters measured in the present paper. |
Comparison of the atmospheric parameters with other studies.
The mean deviations with Cenarro et al. are larger than those obtained by Wu et al. (2011) for the CFLIB library, for example, the dispersion is 120 K for the FGK stars, while Wu et al. report dispersions of ~ 70 K when comparing to homogeneous measurements based on high-resolution spectroscopy, and ~ 100 K when comparing to the compilation of Valdes et al. (2004). For the two other parameters, the dispersion is consistent with the comparison between CFLIB and the Valdes et al. (2004) compilation. The comparisons with the ELODIE 3.2 and CFLIB parameters obtained with the same method, are typical of comparisons between accurate spectroscopic measurements.
Comparison between the atmospheric parameters from this papera and Wu et al. (2011)b with those derived using the present MILES interpolator.
There is a statistically significant bias on Teff of the FGK stars (47 K) between our measurements and Cenarro et al. (2007). Although this is within the uncertainties of the present calibrations, such a bias has consequences when the library is used in models of stellar populations. As pointed out on some occasions (Prugniel et al. 2007a; Percival & Salaris 2009), it is sufficient to alter the age derived for old globular clusters by several Gyr.
We compared our measurements with González Hernández & Bonifacio (2009), who used the infrared flux method to measure Teff for FGK stars using 2MASS photometry. After clipping nine outliers out of the 232 stars in common, we found that these values are on average 28 K warmer than ours, with a dispersion of 141 K. Vazdekis et al. (2010) compared the compilation of Cenarro et al. (2007) to González Hernández & Bonifacio (2009) and found a bias of 59 K of the same sign. Our measurements are in better agreement with González Hernández & Bonifacio (2009) than the original MILES compilation, but the different values of the bias are within the accuracy for determing the temperature scale and are only marginally significant.
We used the statistics of the comparison with Cenarro et al. to estimate the external error. We used the ratios of the differences between the two series to the formal errors to rescale the errors, conservatively assuming that the mean precisions of each series are equivalent. This rescaling factor depends on the temperature. It changes from 5 for the G stars to about 20 for both the hottest and the coolest stars. These factors are the same for the three parameters, and the same order of magnitude as those used in Wu et al. (2011). The external errors are significantly larger than the formal error for several reasons, including the internal degeneracies between the atmospheric parameters. They are reported in Table 1.
For the FGK stars, the mean errors are 60 K, 0.13, and 0.05 dex respectively, for Teff, log g, and [Fe/H]. For the M stars, they are 38 K, 0.26, and 0.12 dex, and for the OBA 3.5%, 0.17, and 0.13 dex. The figures are similar to the precision reported by Wu et al. (2011), implying that there is no degradation in the performance of the method because of the lower spectral resolution.
3.3. Interpolator
We adjusted an interpolator to all the stars in MILES, using the atmospheric parameters of Table 1. For the 27 stars presenting a mean residual velocity shift greater than 30 km s-1, we shifted the spectra by an integer number of pixels to reduce the effect. We did not correct all the spectra for the wavelength-dependent shifts derived in Sect. 3.1 to avoid a rebinning by fractions of pixel. We affected a weight to each star depending on its location in the parameter space, in order to compensate for the uneven distribution of the stars. The low-metallicity stars, and the coolest and hottest ones were over-weighted because there are relatively few of them. We did not weight with the signal-to-noise of the spectra because this information is not available.
We checked the residuals between the observed and interpolated spectra to identify and correct outliers. Finally, we assessed the validity of this interpolator performing two tests: (i) we compared the original and interpolated spectra; and (ii) we used the interpolator to measure the atmospheric parameters of MILES and CFLIB with ULySS.
 |
Fig. 6 Fits of MILES spectra with the MILES interpolator for three representative stars. For each star, the top panel represents the flux distribution, normalized to an average of one, and the bottom ones the residuals between the observation and the best-fitted interpolated spectrum (observation − model). The fit was performed with ULySS. The continuous green lines are the ± 1σ errors, assuming a constant error spectrum and χ2 = 1. The clear blue lines are the multiplicative polynomials. |
3.3.1. Detection and treatments of the outliers
We started with all the stars, and we examined the residuals between the observed and interpolated spectra. There are a priori different causes for these residuals: (i) although “normal” stars were targeted, some peculiarities affect some of them (binarity, rotation, chromospheric emission, atypical abundances, etc.); (ii) the atmospheric parameters derived in Sect. 3.2 have uncertainties (or errors); and (iii) the MILES spectra have uncertainties.
The most prominent outliers correspond to spectra whose shape disagree with the interpolator. This is probably not because of errors in the atmospheric parameters, as the spectral features are generally well fitted, but rather because of errors in the flux calibration or in the correction for Galactic extinction. We nevertheless searched the literature for indications of peculiarities that may explain the discrepancies, and whenever we found some plausible reason we excluded the star from the computation of the interpolator. We observe that the spectra with wrong continuum shape are often located at low Galactic latitude or in obscured regions. The most deviant example is HD 18391, a Cepheid variable whose extinction was corrected by assuming E(B − V) = 0.205 mag. Our spectroscopic fit indicates a considerably higher extinction, consistently with Turner et al. (2009) who derived E(B − V) ≈ 1 mag. Another example where the extinction was under-corrected by ~0.7 mag is HD 219978. Although the main outliers correspond to underestimated extinctions, there are cases of over-estimation, like HD 76813.
We suppose that the main source of discrepancy is the correction of the Galactic extinction, but we cannot safely separate this possibility from an error on the flux calibration. Nevertheless, we assumed that for those discrepant cases, the error is due to the extinction correction and we applied an additional correction using a Galactic extinction curve (Schild 1977). Whenever this correction was unsatisfactory (maybe because the source of error is the flux-calibration), we flagged the spectrum reduce its weight or to be excluded. We corrected the extinction for 55 field stars.
All this process was made iteratively, treating the most prominent outliers and recomputing another version of the interpolator. Finally, the mean residuals between the interpolated and observed spectra is 4%, a value comparable to what is obtained for the ELODIE interpolator. A large fraction of these residuals still come from mismatches of the shape of the continuum.
3.3.2. Tests of the interpolator
Wu et al. (2011) have shown that the ELODIE interpolator is not reliable for the hot evolved stars nor for the very cool stars. It is not known if the reason resides in the limited sampling of the parameter space in these regions or from more fundamental characteristics of the interpolator. In order to check this, we used the new interpolator to measure the atmospheric parameters of MILES and CFLIB. The first one is an internal test, where each MILES spectrum is compared to the interpolator based on the whole library. The statistics of the comparisons between these new sets of parameters and the adopted ones are summarized in Table 3. They were computed with the IDL command biweight_mean, to discard the outliers. The different lines are for the OBA (Teff > 8000 K), FGK (4000 < Teff ≤ 8000 K), K5-M (Teff ≤ 4000 K), M (Teff ≤ 3500 K), and BHB (blue horizontal-branch; Teff > 7000 K and [Fe/H] < − 0.7 dex). The M stars for which Wu et al. (2011) give [Fe/H] = −1 were rejected from the statistics on log g and [Fe/H].
For the coolest stars (Teff ≤ 3500 K), the metallicities measured with the ELODIE interpolator were biased toward low values. This effect is absent with the MILES interpolator. For the hot evolved stars (Teff > 7000 K and [Fe/H] < − 0.7 dex), the biases are also considerably reduced compared to those obtained with the ELODIE interpolator.
Figure 6 presents the fits with the MILES interpolator of the MILES spectra of three stars of different spectral types. The residuals are of the order of 1% of the flux, and the multiplicative polynomials are flat and close to unity, reflecting the good quality of the flux calibration of MILES.
These tests show that the MILES interpolator is reliable to measure the atmospheric parameters over their whole range. The lower resolution of MILES does not affect these determinations. The FITS file containing the coefficients of the interpolator is available in Vizier. It can be directly used in ULySS to fit stellar spectra. The interpolated spectra can also be computed online in a Virtual Observatory compliant format (Prugniel et al. 2008).
3.4. Discussion on the flux-calibration
The presumably good flux-calibration of MILES is its most attractive characteristic. It was assessed by comparison with accurate broad-band photometry. To test the photometric precision of the interpolator, we fitted the residuals between the observed and interpolated spectra with a straight line and expressed the result as a B − V colour. For the whole library, we find Δ(B − V) = 0.005 mag and σ(B − V) = 0.039 mag for the bias and dispersion, respectively. This residual colour is small by construction, since the interpolator was built with the observed spectra, but the small dispersion reflects the good spectrophotometric precision. The photometric precision on the individual spectra were determined by Sánchez-Blázquez et al. (2006) to be σ(B − V) = 0.013 ~ 0.025 mag, by comparing synthetic B − V colours with different sets of standards. (The two numbers corresponds to different standards.) Our present values are not as precise, likely because they also include the errors on the Galactic extinction corrections and on the atmospheric parameters, and the cosmic variance introduced by characteristics of individual stars that are not considered in the interpolator.
We can also assess the photometric accuracy of the ELODIE library. This has always been a question, because its flux-calibration results from a complex and indirect process. To test it, we made series of interpolated ELODIE spectra following the main and giant sequences, and we computed the photometric precision as above. We found that the differences between the interpolated ELODIE and MILES spectra are σ(B − V) ≈ 0.02 mag, which is consistent with the estimations made in (Prugniel & Soubiran 2004; Prugniel et al. 2007b).
4. Summary and conclusion
We derived the atmospheric parameters of the stars of the MILES library. We estimated the external precision for the FGK stars to be 60 K, 0.13, and 0.05 dex for Teff, log g, and [Fe/H], respectively. For the M stars, the mean errors are 38 K, 0.26, and 0.12 dex, and for the OBA 3.5%, 0.17, and 0.13 dex. These precisions are comparable to those obtained with the same method for the CFLIB library, whose resolution is significantly higher. This shows that there is no significant degradation due to the resolution.
We characterized the LSF and we found that the residual shift of the rest-frame reduction has a dispersion of 12 km s-1, with an average of 2 km s-1 (MILES is slightly red-shifted). The mean FWHM dispersion of the library is 2.56 Å, changing from 2.45 to 2.63 Å from the blue to the red.
We computed an interpolator for the library. This is a function returning a spectrum for given Teff, log g and [Fe/H]. To check its reliability, we used it to derive the atmospheric parameters of MILES itself and CFLIB. The results are in good agreement with those derived with the ELODIE interpolator in the present paper and in Wu et al. (2011). For some regimes where the ELODIE interpolator has shown deficiencies (hot evolved stars and cool stars), the MILES interpolator gives better performances.
In a companion paper, we will use this interpolator to prepare stellar population models using PEGASE.HR.
Adopted atmospheric parameters for the 985 MILES stars.
Valdes et al. (2004) mention Å, but Beifiori et al. (2011) and Wu et al. (2011) derive 1.4 Å.
The value Å (Sánchez-Blázquez et al. 2006) is underestimated, see Beifiori et al. (2011) and Sect. 3.1.
Acknowledgments
We thank the referee for her/his constructive comments. We acknowledge the support from the French Programme National Cosmologie et Galaxies (PNCG, CNRS). M.K. has been supported by the Programa Nacional de Astronomía y Astrofísica of the Spanish Ministry of Science and Innovation under grant AYA2007-67752-C03-01. She thanks CRAL, Observatoire de Lyon, Université Claude Bernard, Lyon 1, for an Invited Professorship.
References
- Adelman, S. J. 1998, MNRAS, 296, 856 [NASA ADS] [CrossRef] [Google Scholar]
- Adelman, S. J., Pintado, O. I., Nieva, M. F., Rayle, K. E., & Sanders, Jr., S. E. 2002, A&A, 392, 1031 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Aoki, W., Honda, S., Beers, T. C., et al. 2007, ApJ, 660, 747 [NASA ADS] [CrossRef] [Google Scholar]
- Arellano Ferro, A. 2010, Rev. Mex. Astron. Astrofis., 46, 331 [NASA ADS] [Google Scholar]
- Arnone, E., Ryan, S. G., Argast, D., Norris, J. E., & Beers, T. C. 2005, A&A, 430, 507 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Baranne, A., Queloz, D., Mayor, M., et al. 1996, A&AS, 119, 373 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Barbuy, B., Meléndez, J., Spite, M., et al. 2003, ApJ, 588, 1072 [NASA ADS] [CrossRef] [Google Scholar]
- Barzdis, A., Začs, L., & Galazutdinov, G. 2009, Baltic Astron., 18, 65 [NASA ADS] [Google Scholar]
- Beers, T. C., Rossi, S., Norris, J. E., Ryan, S. G., & Shefler, T. 1999, AJ, 117, 981 [NASA ADS] [CrossRef] [Google Scholar]
- Beifiori, A., Maraston, C., Thomas, D., & Johansson, J. 2011, A&A, 531, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bergeat, J., Knapik, A., & Rutily, B. 2001, A&A, 369, 178 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Blanchette, J., Chayer, P., Wesemael, F., et al. 2008, ApJ, 678, 1329 [NASA ADS] [CrossRef] [Google Scholar]
- Bonfils, X., Delfosse, X., Udry, S., et al. 2005, A&A, 442, 635 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Casagrande, L., Flynn, C., & Bessell, M. 2008, MNRAS, 389, 585 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Castelli, F., & Cacciari, C. 2001, A&A, 380, 630 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cenarro, A. J., Peletier, R. F., Sánchez-Blázquez, P., et al. 2007, MNRAS, 374, 664 [NASA ADS] [CrossRef] [Google Scholar]
- Coelho, P., Barbuy, B., Meléndez, J., Schiavon, R. P., & Castilho, B. V. 2005, A&A, 443, 735 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Crowther, P. A., Lennon, D. J., & Walborn, N. R. 2006, A&A, 446, 279 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- de Castro Milone, A., Sansom, A. E., & Sanchez-Blazquez, P. 2011, MNRAS, accepted [Google Scholar]
- For, B., & Sneden, C. 2010, AJ, 140, 1694 [NASA ADS] [CrossRef] [Google Scholar]
- Geier, S., Edelmann, H., Heber, U., & Morales-Rueda, L. 2009, ApJ, 702, 96 [Google Scholar]
- Giridhar, S., Molina, R., Ferro, A. A., & Selvakumar, G. 2010, MNRAS, 406, 290 [NASA ADS] [CrossRef] [Google Scholar]
- González Hernández, J. I., & Bonifacio, P. 2009, A&A, 497, 497 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Helmi, A., White, S. D. M., de Zeeuw, P. T., & Zhao, H. 1999, Nature, 402, 53 [NASA ADS] [CrossRef] [Google Scholar]
- Holmberg, J., Nordström, B., & Andersen, J. 2007, A&A, 475, 519 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
- Honda, S., Aoki, W., Kajino, T., et al. 2004, ApJ, 607, 474 [NASA ADS] [CrossRef] [Google Scholar]
- Houdebine, E. R. 2008, MNRAS, 390, 1081 [NASA ADS] [CrossRef] [Google Scholar]
- Hrivnak, B. J., Van Winckel, H., Reyniers, M., et al. 2008, AJ, 136, 1557 [NASA ADS] [CrossRef] [Google Scholar]
- Ishigaki, M., Chiba, M., & Aoki, W. 2010, PASJ, 62, 143 [NASA ADS] [Google Scholar]
- Kinman, T., Castelli, F., Cacciari, C., et al. 2000, A&A, 364, 102 [NASA ADS] [Google Scholar]
- Kipper, T. 2007, Baltic Astron., 16, 191 [Google Scholar]
- Koleva, M., Gupta, R., Prugniel, P., & Singh, H. 2008, in Pathways Through an Eclectic Universe, ed. J. H. Knapen, T. J. Mahoney, & A. Vazdekis, ASP Conf. Ser., 390, 302 [Google Scholar]
- Koleva, M., Prugniel, P., Bouchard, A., & Wu, Y. 2009, A&A, 501, 1269 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kovtyukh, V. V. 2007, MNRAS, 378, 617 [NASA ADS] [CrossRef] [Google Scholar]
- Kovtyukh, V. V., Soubiran, C., Luck, R. E., et al. 2008, MNRAS, 389, 1336 [NASA ADS] [CrossRef] [Google Scholar]
- Kurucz, R. L., Furenlid, I., Brault, J., & Testerman, L. 1984, Solar flux atlas from 296 to 1300 nm, ed. R. L. Kurucz, I. Furenlid, J. Brault, & L. Testerman [Google Scholar]
- Lai, D. K., Bolte, M., Johnson, J. A., et al. 2008, ApJ, 681, 1524 [NASA ADS] [CrossRef] [Google Scholar]
- LeBorgne, D., Rocca-Volmerange, B., Prugniel, P., et al. 2004, A&A, 425, 881 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lefever, K., Puls, J., Morel, T., et al. 2010, A&A, 515, A74 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Markova, N., & Puls, J. 2008, A&A, 478, 823 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Martins, L. P., González Delgado, R. M., Leitherer, C., Cerviño, M., & Hauschildt, P. 2005, MNRAS, 358, 49 [NASA ADS] [CrossRef] [Google Scholar]
- Meléndez, J., & Barbuy, B. 2009, A&A, 497, 611 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mishenina, T. V., Korotin, S. A., Klochkova, V. G., & Panchuk, V. E. 2000, A&A, 353, 978 [NASA ADS] [Google Scholar]
- Morales, J. C., Ribas, I., & Jordi, C. 2008, A&A, 478, 507 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nordström, B., Mayor, M., Andersen, J., et al. 2004, A&A, 418, 989 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Percival, S. M., & Salaris, M. 2009, ApJ, 703, 1123 [NASA ADS] [CrossRef] [Google Scholar]
- Prugniel, P., & Soubiran, C. 2001, A&A, 369, 1048 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Prugniel, P., & Soubiran, C. 2004 [arXiv:astro-ph/0409214] [Google Scholar]
- Prugniel, P., Koleva, M., Ocvirk, P., Le Borgne, D., & Soubiran, C. 2007a, in IAU Symp., 241, ed. A. Vazdekis, & R. F. Peletier, 68 [Google Scholar]
- Prugniel, P., Soubiran, C., Koleva, M., & Le Borgne, D. 2007b [arXiv:astro-ph/0703658] [Google Scholar]
- Prugniel, P., Koleva, M., Ocvirk, P., Le Borgne, D., & Soubiran, C. 2008, in Astronomical Spectroscopy and Virtual Observatory, ed. M. Guainazzi, & P. Osuna, 219 [Google Scholar]
- Reddy, B. E., & Lambert, D. L. 2008, MNRAS, 391, 95 [Google Scholar]
- Rich, J. A., & Boesgaard, A. M. 2009, ApJ, 701, 1519 [NASA ADS] [CrossRef] [Google Scholar]
- Roederer, I. U., Sneden, C., Thompson, I. B., Preston, G. W., & Shectman, S. A. 2010, ApJ, 711, 573 [NASA ADS] [CrossRef] [Google Scholar]
- Ryde, N., Gustafsson, B., Edvardsson, B., et al. 2010, A&A, 509, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Saffe, C., Gómez, M., Pintado, O., & González, E. 2008, A&A, 490, 297 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sánchez-Blázquez, P., Peletier, R. F., Jiménez-Vicente, J., et al. 2006, MNRAS, 371, 703 [NASA ADS] [CrossRef] [Google Scholar]
- Schild, R. E. 1977, AJ, 82, 337 [NASA ADS] [CrossRef] [Google Scholar]
- Searle, S. C., Prinja, R. K., Massa, D., & Ryans, R. 2008, A&A, 481, 777 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Simmerer, J., Sneden, C., Cowan, J. J., et al. 2004, ApJ, 617, 1091 [NASA ADS] [CrossRef] [Google Scholar]
- Stephens, A., & Boesgaard, A. M. 2002, AJ, 123, 1647 [NASA ADS] [CrossRef] [Google Scholar]
- Takeda, Y., Kang, D., Han, I., Lee, B., & Kim, K. 2009, PASJ, 61, 1165 [NASA ADS] [Google Scholar]
- Takeda, Y., Kambe, E., Sadakane, K., & Masada, S. 2010, PASJ, 62, 1239 [NASA ADS] [CrossRef] [Google Scholar]
- Thompson, H. M. A., Keenan, F. P., Dufton, P. L., et al. 2008, MNRAS, 383, 729 [NASA ADS] [CrossRef] [Google Scholar]
- Trundle, C., Dufton, P. L., Rolleston, W. R. J., et al. 2001, MNRAS, 328, 291 [NASA ADS] [CrossRef] [Google Scholar]
- Turner, D. G., Kovtyukh, V. V., Majaess, D. J., Lane, D. J., & Moncrieff, K. E. 2009, Astron. Nachr., 330, 807 [NASA ADS] [CrossRef] [Google Scholar]
- Valdes, F., Gupta, R., Rose, J. A., Singh, H. P., & Bell, D. J. 2004, ApJS, 152, 251 [NASA ADS] [CrossRef] [Google Scholar]
- Vazdekis, A., Cenarro, A. J., Gorgas, J., Cardiel, N., & Peletier, R. F. 2003, MNRAS, 340, 1317 [NASA ADS] [CrossRef] [Google Scholar]
- Vazdekis, A., Sánchez-Blázquez, P., Falcón-Barroso, J., et al. 2010, MNRAS, 404, 1639 [NASA ADS] [Google Scholar]
- Woolf, V. M., & Wallerstein, G. 2005, MNRAS, 356, 963 [NASA ADS] [CrossRef] [Google Scholar]
- Worthey, G., Faber, S. M., Gonzalez, J. J., & Burstein, D. 1994, ApJS, 94, 687 [NASA ADS] [CrossRef] [Google Scholar]
- Wu, C., Qiu, Y. L., Deng, J. S., Hu, J. Y., & Zhao, Y. H. 2006, A&A, 453, 895 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wu, Y., Singh, H. P., Prugniel, P., Gupta, R., & Koleva, M. 2011, A&A, 525, A71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wylie-de Boer, E. C., & Cottrell, P. L. 2009, ApJ, 692, 522 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, H. W., & Zhao, G. 2005, MNRAS, 364, 712 [NASA ADS] [Google Scholar]
- Zhang, L., Ishigaki, M., Aoki, W., Zhao, G., & Chiba, M. 2009, ApJ, 706, 1095 [NASA ADS] [CrossRef] [Google Scholar]
- Zorec, J., Cidale, L., Arias, M. L., et al. 2009, A&A, 501, 297 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
Comparison between the atmospheric parameters from this papera and Wu et al. (2011)b with those derived using the present MILES interpolator.
All Figures
 |
Fig. 1 Line-spread function for 10 stars of the MILES library chosen arbitrarily (actually 10 of the first 12), using the interpolated ELODIE spectra for reference. The top panel shows the residual shift of the spectra, illustrating the precision of the wavelength calibration and of the rest-frame reduction. The bottom panel presents the FWHM resolution. The mean formal error on each LSF point is 0.5 km s-1 on the residual shift and 0.025 Å on the FWHM resolution. |
| In the text | |
 |
Fig. 2 Histograms of the broadening and residual shift of the line-spread function of the MILES library at 5300 Å. The green histograms are for the 404 direct comparisons with spectra of the ELODIE library. The red ones are the comparisons with the ELODIE interpolator. The top panel is the distribution of the residual shifts, in km s-1, and the bottom ones the distribution of the FWHM Gaussian broadening. |
| In the text | |
 |
Fig. 3 Mean line-spread function of the MILES library, using for reference (i) the interpolated ELODIE spectra (red line and symbols); and (ii) the ELODIE spectra of stars in common (green). The top panel gives the mean residual shift over all the library, and the bottom panel the mean FWHM wavelength resolution. The bars indicate the errors on the mean value (i.e. dispersion/ |
| In the text | |
 |
Fig. 4 Distribution in the log (Teff) – log g and log (Teff) – [Fe/H] planes of the adopted atmospheric parameters for the 985 MILES stars. In the top panel, the colour of the symbols distinguishes different metallicity classes. In the bottom panel, it distinguishes different classes of surface gravity. |
| In the text | |
 |
Fig. 5 Comparison of the measured atmospheric parameters with the Cenarro et al. (2007) compilation. The abscissae are the parameters measured in the present paper. |
| In the text | |
 |
Fig. 6 Fits of MILES spectra with the MILES interpolator for three representative stars. For each star, the top panel represents the flux distribution, normalized to an average of one, and the bottom ones the residuals between the observation and the best-fitted interpolated spectrum (observation − model). The fit was performed with ULySS. The continuous green lines are the ± 1σ errors, assuming a constant error spectrum and χ2 = 1. The clear blue lines are the multiplicative polynomials. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.