| Issue |
A&A
Volume 531, July 2011
|
|
|---|---|---|
| Article Number | A24 | |
| Number of page(s) | 12 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201016367 | |
| Published online | 06 June 2011 | |
WASP-23b: a transiting hot Jupiter around a K dwarf and its Rossiter-McLaughlin effect⋆,⋆⋆,⋆⋆⋆
1
Observatoire Astronomique de l’Université de Genève, Chemin des Maillettes 51, 1290 Sauverny, Switzerland
e-mail: Amaury.Triaud@unige.ch
2
Astrophysics Group, Keele University, Staffordshire, ST55BG, UK
3 Institut d’Astrophysique et de Géophysique, Université de Liège, Allée du 6 Août, 17, Bât. B5C, Liège 1, Belgium
4 Department of Physics and Astronomy, Vanderbilt University, Nashville, TN37235, USA
5
SUPA, School of Physics & Astronomy, University of St Andrews, North Haugh, KY16 9SS, St Andrews, Fife, Scotland, UK
6
Centro de Astrofísica, Universidade do Porto, Rua das Estrelas, 4150-762 Porto, Portugal
7
Institut d’Astrophysique de Paris, CNRS (UMR 7095), Université Pierre & Marie Curie, 98bis bd. Arago, 75014 Paris, France
8
Observatoire de Haute-Provence, CNRS/OAMP, 04870 St Michel l’ Observatoire, France
9
Las Cumbres Observatory, 6740 Cortona Dr. Suite 102, Santa Barbara, CA 93117, USA
10
Astrophysics Research Centre, School of Mathematics & Physics, Queens University, University Road, Belfast, BT71 NN, UK
11
Department of Physics and Astronomy, Universityof Leicester, Leicester, LE17 RH, UK
Received: 20 December 2010
Accepted: 13 March 2011
We report the discovery of a new transiting planet in the southern hemisphere. It was found by the WASP-south transit survey and confirmed photometrically and spectroscopically by the 1.2 m Swiss Euler telescope, LCOGT 2m Faulkes South Telescope, the 60 cm TRAPPIST telescope, and the ESO 3.6 m telescope. The orbital period of the planet is 2.94 days. We find that it is a gas giant with a mass of 0.88 ± 0.10 MJ and an estimated radius of 0.96 ± 0.05 RJ. We obtained spectra during transit with the HARPS spectrograph and detect the Rossiter-McLaughlin effect despite its small amplitude. Because of the low signal-to-noise ratio of the effect and a small impact parameter, we cannot place a strong constraint on the projected spin-orbit angle. We find two conflicting values for the stellar rotation. We find, via spectral line broadening, that v sin I = 2.2 ± 0.3 km s-1, while applying another method, based on the activity level using the index 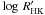 , gives an equatorial rotation velocity of only v = 1.35 ± 0.20 km s-1. Using these as priors in our analysis, the planet might be either misaligned or aligned. This result raises doubts about the use of such priors. There is evidence of neither eccentricity nor any radial velocity drift with time.
, gives an equatorial rotation velocity of only v = 1.35 ± 0.20 km s-1. Using these as priors in our analysis, the planet might be either misaligned or aligned. This result raises doubts about the use of such priors. There is evidence of neither eccentricity nor any radial velocity drift with time.
Key words: binaries: eclipsing / planetary systems / stars: individual: WASP-23 / techniques: spectroscopic / techniques: photometric / stars: rotation
Using WASP-South photometric observations confirmed with LCOGT Faulkes South Telescope, the 60 cm TRAPPIST telescope, the CORALIE spectrograph and the camera from the Swiss 1.2 m Euler Telescope placed at La Silla, Chile, as well as with the HARPS spectrograph, mounted on the ESO 3.6 m, also at La Silla, under proposal 084.C-0185. The data is publicly available at the CDS Strasbourg and on demand to the main author.
RV data is only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/531/A24
Appendix is available in electronic form at http://www.aanda.org
© ESO, 2011
1. Introduction
Finding planets by detecting their transit has proven to be very successful there having been detections past the hundred mark. After the discovery that HD 209458b was transiting (Charbonneau et al. 2000), a plethora of ground-based small aperture wide-angle photometric surveys have been put in place to find similar bodies, such as WASP (Pollacco et al. 2006), the HAT network (Bakos et al. 2004), XO (McCullough et al. 2005), TrES (O’Donovan et al. 2006), or the OGLE search (Udalski et al. 1997; Snellen et al. 2007). WASP is the only survey currently operating in both hemispheres. About 20% of extrasolar planets discovered so far are currently known to transit their host stars, the vast majority of which are the so-called hot Jupiters, planets similar in mass to Jupiter but on orbits with periods <5 days.
Transiting planets provide a treasure trove of observables allowing the study of a special class of planets that is absent from our Solar System. A transiting system, observed with photometry and radial velocities, allows us to measure the planet’s mass ratio with the star, and both the stellar density and ratio of radii. Through observations at the time of occultation, it is possible measure the temperature of the planet. Careful analysis during transit and occultation can provide insight into its atmospherical composition.
Another observable that has been under intense scrutiny recently is the spin-orbit angle. As the planet transits, it covers a part of the approaching or receding hemisphere of the star, therefore red-shifting or blue-shifting the spectrum. This appears as a radial velocity anomaly in the main reflex Doppler motion curve. It is called the Rossiter-McLaughlin effect (Holt 1893; Rossiter 1924; McLaughlin 1924) and was first measured for a planet by Queloz et al. (2000) and modelled by Ohta et al. (2005), Giménez (2006), and Hirano et al. (2010). Recently it was found that hot Jupiters are located on a vast range of orbital planes with respect to the stellar rotation, some even on retrograde orbits (Hébrard et al. 2008; Winn et al. 2009; Narita et al. 2009; Anderson et al. 2010; Queloz et al. 2010). The study of this angle’s distribution is being used to distinguish the processes through which hot Jupiters have arrived at their current orbits (Triaud et al. 2010; Winn et al. 2010a; Morton & Johnson 2011).
All this gathered data helps developments in theoretical physics in regimes beforehand out of reach: intense heat transfer between hot and cold hemispheres (Guillot & Showman 2002) and on supersonic winds (Dobbs-Dixon et al. 2010) to name only two. The few detections of multi-planet systems in which at least one component is transiting can also provide insight into the interior structure (Batygin et al. 2009). Obviously the study of these special exoplanets is also shedding light on how planets form as well as on the evolution of their orbits with time. The hot Jupiters are thought to have experienced a migration to the star after their formation beyond the ice-line, be it through some angular momentum exchange with the primordial protoplanetary disc (Lin et al. 1996), or via dynamical interactions and subsequent tidal friction (Fabrycky & Tremaine 2007; Nagasawa et al. 2008; Malmberg et al. 2011), an explanation now preferred to the previous one. The history of that post formation evolution might hold a key to the understanding of the various processes that planetary systems are likely to experience thus shed light on the events surrounding the origin of our own Solar System.
In this light, we announce the discovery of a new transiting gas giant by the WASP consortium, in close proximity to its host star, which participates in providing a deeper understanding of these objects.
2. Observations
The object, WASP-23, (1SWASP J064430.59-424542.5) is a K1V star with V = 12.68 that was observed during two seasons of the WASP-South survey, located in Sutherland, South Africa, in a single camera field from 2006 October 13 to 2007 March 11 and from 2007 October 11 to 2008 March 11 representing 10 846 photometric measurements. The WASP-South instrument, part of the WASP survey is amply described in Pollacco et al. (2006). The Hunter algorithm (Collier Cameron et al. 2007b) searched the data and found 11 partial transits with a period of 2.94 days and a depth of 1.7% in both seasons (Fig. 1). It was selected for spectroscopic follow-up. No rotational variability could be found in the photometric data, which is indicative of slow rotation and few stellar spots.
 |
Fig. 1 Phased WASP-South photometry, of two seasons, and residuals. R band model superimposed. |
The 1.2 m Euler Swiss telescope, in La Silla, Chile, established the planetary nature of the object by detecting a Doppler variation of semi-amplitude 145 m s-1 with the same period and epoch as the WASP-South photometry. Observations started on 2008 August 31 and were pursued until 2010 April 08 totalling 38 radial velocity measurements (Fig. 2), each a 30 min exposure.
A photometric timeseries was acquired with the camera mounted on the Euler telescope, in the z-band on 2008 December 13. We gathered 254 measurements and confirmed the reality of the photometric signal discovered by WASP-South (Fig. 3). In addition we gathered another 215 measurements in the z band during transit with the Faulkes South Telescope on 2009 September 27. We observed a third transit on 2010 February 7, with Euler, collecting 193 datapoints in the R-band filter (Fig. 3). Two further transits were observed during December 2010 using the newly built 60 cm TRAPPIST robotic telescope (Gillon et al. 2011), also located in La Silla, were finally added to this analysis (Fig. 4).
Under ESO proposal 084.C-0185, we observed with the spectrograph HARPS, mounted on the ESO 3.6 m telescope, at La Silla, Chile, obtaining 35 spectra between 2009 December 18 and 2010 February 9. Twenty-eight spectra at a mean cadence of roughly 600 s were acquired on the first night, 14 of which are positioned as the planet transits (Figs. 2 and 3). The others were observed a few months later because of scheduling contraints and have exposure times of 1200 s.
3. Data analysis
3.1. The Euler z-band transit
The transit was observed in the z-band, on 2008 December 12, from 2h15 to 7h35 UTC using the Euler camera. The z-band filter was used to minimise the impact of stellar limb-darkening on the deduced system parameters. The images were 2 × 2 binned to improve the duty cycle of the observations, resulting in a pixel scale of 0.7 arcsec. We acquired 254 exposures during the run, of exposure times ranging from 45 s to 60 s. Two outliers were removed from our analysis. To keep a good spatial sampling while minimising the impact of interpixel sensitivity inhomogeneities and seeing variations, the telescope was heavily defocused and produced a mean profile width of 4.8 ± 0.2 arcsec. The airmass decreased from 1.43 to 1.03 then increased to 1.09.
After a standard pre-reduction, stellar fluxes were extracted using the IRAF1 version of the DAOPHOT aperture photometry software (Stetson 1987). After a careful selection of reference stars, we subtracted a linear fit from the differential magnitudes as a function of airmass to correct for the different colour dependance of the extinction for the target and comparison stars. The linear fit was calculated from the out-of-transit (OOT) data and applied to all the data. The corresponding fluxes were then normalised using the OOT part of the photometry. Figure 3 shows the resulting timeseries. The OOT rms is 2.2 mmag for a mean time sampling of 75 s. Comparing this OOT rms to the one obtained after binning the data in units of 25 min (a duration comparable to that of ingress/egress) as described by Gillon et al. (2006) indicates that a correlated noise of ~600 ppm is present in the photometry.
 |
Fig. 2 Black triangles: CORALIE data; red discs: HARPS data. Top: radial velocities with model superimposed, and residuals (both in m s-1), as a function of orbital phase. Added are the 1σ error bars. Bottom: phased bisector span and FWHM (both in km s-1). The HARPS data has been translated to have its mean correspond to the CORALIE data. |
 |
Fig. 3 HARPS radial velocity data corrected for the reflex Doppler motion due to the planet and model of the Rossiter-McLaughlin effect with residuals. Below: three photometric transits (instruments are indicated), the best-fit model and residuals. All are presented as a function of the orbital phase. |
3.2. The Euler R-band transit
A similar reduction was performed for the transit of 2010 February 7. After outlier rejection, we were left with 183 images of a mean sampling time of 63 s. In this instance the telescope was not defocused, the mean profile width being 2.3 arcsec. Transparency was good and airmass ranged from 1.03 to 2.22. Five stars were used as reference totalling a comparative flux 4.2 times that of the target. We also observe some correlated noise, of ~600 ppm in the photometry. The photometry is shown in Fig. 3.
3.3. The FTS z-band transit
An additional transit of WASP-23b was obtained with the LCOGT2 2.0 m Faulkes Telescope South (FTS) at Siding Spring Observatory, Australia on the night of 2009 September 27. Observations took place between 15:30 UTC and 19:00 UTC and the airmass decreased throughout the night from 1.9 at the start of the night to 1.1. The em03 Merope camera was used with a 2 × 2 binning mode giving a field of view of 5′ × 5′ and a pixel scale of 0.278 arcsec/pixel. The data were taken through a Pan-STARRS-z filter and the telescope was defocussed to prevent saturation and allow longer 35 s exposure times to be used.
The data were pre-processed in the standard manner to perform the debiassing, dark subtraction, and flatfielding steps. Aperture photometry was performed using DAOPHOT within the IRAF environment using a 10 pixel radius aperture and the differential photometry was performed relative to 14 comparison stars that were within the FTN field of view.
During the course of the FTS observations, we detected a ≳ 0.55 mag deep flat-bottomed partial eclipse on a nearby (~109 arcsec) star (USNO-B1.0 0472-0093932, α = 06h44′37.63′′δ = −42°45′13.5′′) which appears to be an eclipsing binary. A cursory search of the WASP archive indicates that it is has an ephemeris of HJD(Min I) = 2 454 021.573377E + 1.421933 days with an eclipse depth of ~0.75 mag.
 |
Fig. 4 The two I + z band timeseries observed by TRAPPIST, with best-fit model being overplotted. |
3.4. The TRAPPIST I + z band transits
A complete and a partial transit of WASP-23 was also observed with the robotic 60 cm telescope TRAPPIST3) (Gillon et al. 2011). Located at La Silla ESO observatory (Chile), TRAPPIST is equipped with a 2K × 2K Fairchild 3041 CCD camera that has a 22′ × 22′ field of view (pixel scale = 0.64′′/pixel). The transits of WASP-23 were observed on the nights of 2010 December 21 and 30. The sky conditions were clear. We used the 1 × 2 MHz read-out mode with 1 × 1 binning, resulting in a typical read-out + overhead time and read noise of 8.2 s and 13.5 e−, respectively. The integration time was 35 s for both nights. We observed through a special “I + z” filter that has a transmittance of zero below 700 nm, and >90% from 750 nm to beyond 1100 nm. The telescope was defocused to average pixel-to-pixel sensitivity variations and to optimize the duty cycle, resulting in a typical full width at half-maximum of the stellar images of ~5.2 pixels (~3.3′′). The positions of the stars on the chip were maintained to within a few pixels over the course of the two runs, thanks to the “software guiding” system that regularly derives an astrometric solution from the most recently acquired image and sends pointing corrections to the mount if needed. After a standard pre-reduction (bias, dark, flatfield), the stellar fluxes were extracted from the images using the IRAF/DAOPHOT aperture photometry software (Stetson 1987). Several sets of reduction parameters were tested, and we kept the one giving the most precise photometry for the stars of brightness similar to WASP-23. After a careful selection of reference stars, differential photometry was obtained. The data is shows in Fig. 4.
3.5. The spectral analysis
Stellar parameters of WASP-23 from spectroscopic analysis.
A total of 26 individual CORALIE spectra of WASP-23 were coadded to produce a single spectrum with a typical signal-to-noise ratio of around 50:1. The standard pipeline reduction products were used in the analysis.
The analysis was performed using the methods given in Gillon et al. (2009). The Hα line was used to determine the effective temperature (Teff), while the Na i D and Mg i b lines were used as surface gravity (log g) diagnostics. The parameters obtained from the analysis are listed in Table 1. The elemental abundances were determined from equivalent width measurements of several clean and unblended lines. A value for microturbulence (ξt) of 0.8 km s-1 was determined from Fe i using the Magain (1984) method. The quoted error estimates include those given by the uncertainties in Teff, log g and ξt, as well as the scatter due to measurement and atomic data uncertainties.
The projected stellar rotation velocity (vsinI )4 was determined by fitting the profiles of several unblended Fe i lines. Because the value of vsinI was paramount to the model fitting, we used the combined HARPS spectra. A value for macroturbulence (vmac) of 0.8 ± 0.3 km s-1 was assumed, based on work by Bruntt et al. (2010) and an instrumental FWHM of 0.060 Å, determined from the telluric lines around 6300 Å. A best-fitting value of vsinI = 2.2 ± 0.3 km s-1 was obtained. Using a macroturbulence based on the tabulation by Gray (2008) of 1.2 km s-1; we obtain the same result for vsinI showing its robustness.
The HARPS spectra show that there is weak emission in the cores of the calcium H & K lines. Activity levels on the star are estimated by means of the 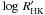 (Noyes et al. 1984; Santos et al. 2000; Boisse et al. 2009) and obtained using a B − V = 0.88 ± 0.05 estimated from the effective temperature. The Mount Wilson index, SMW is also given.
(Noyes et al. 1984; Santos et al. 2000; Boisse et al. 2009) and obtained using a B − V = 0.88 ± 0.05 estimated from the effective temperature. The Mount Wilson index, SMW is also given.
3.6. The RV extraction
The spectroscopic data were reduced using the online Data Reduction Software (DRS) for the HARPS instrument. The radial velocity information was obtained by removing the instrumental blaze function and cross-correlating each spectrum with a K5 mask. This correlation was compared with the Th-Ar spectrum used as a wavelength-calibration reference (see Baranne et al. 1996; Pepe et al. 2002, for details). The DRS was shown to achieve remarkable precision (Mayor et al. 2009) thanks to a revision of the reference lines for thorium and argon by Lovis & Pepe (2007). A similar software package was used the prepare the CORALIE data. A resolving power R = 110 000 for HARPS provided a cross-correlation function (CCF) binned in 0.25 km s-1 increments, while for the CORALIE data, with a lower resolution of 50 000, we used 0.5 km s-1. The CCF window was adapted to be three times the size of the full width at half maximum (FWHM) of the CCF.
1σ error bars on individual data points were estimated from photon noise alone. HARPS is stable in the long term to within 1 m s-1 and CORALIE to better than 5 m s-1. These are smaller than our individual error bars, thus were not taken into account.
The absence of any variation in bisector span correlated with the phase, or any variation in the FWHM, indicate that the photometric and spectroscopic signals are indeed those of a planet. For comparison, we invite the reader to read Santos et al. (2002), studying HD 41004 for which it has been proven that a blend by a star and its brown dwarf companion produced a spectroscopic Doppler shift similar to that of a planet on a foreground object.
4. Modelling the data
The data was fitted using a Markov Chain Monte-Carlo (MCMC) method in a code allowing us to combine both photometry and spectroscopy. It has been used in several occasions (Bouchy et al. 2008; Gillon et al. 2008) and is described at length in Triaud et al. (2009). It is similar to those presented in Collier Cameron et al. (2007a). The code uses a common set of free parameters from which physical parameters can be derived to construct models for the photometric and spectroscopic signals.
4.1. Parameter choice
We used the following free (or jump) parameters: P for the period of the object, T0 the mid-transit time, D the depth of the transit, W its width, b the impact parameter, and K the semi-amplitude of the Doppler reflex motion by the star. To fit the Rossiter-McLaughlin effect, we use 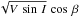 and
and 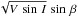 where V sin I is the projected stellar rotation and β the projected spin-orbit angle. To estimate whether the orbit is eccentric, we used
where V sin I is the projected stellar rotation and β the projected spin-orbit angle. To estimate whether the orbit is eccentric, we used 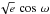 and
and 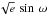 where e is the eccentricity and ω is the argument of the periastron. In addition, we added at times
where e is the eccentricity and ω is the argument of the periastron. In addition, we added at times 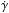 , a radial-velocity drift with time, to assess the presence of an additional body in the system. We also fitted one normalisation factor for each photometric dataset (five in our case) and two γ velocities for the radial velocities, one for each set. We used Gaussian priors to randomly draw each parameter.
, a radial-velocity drift with time, to assess the presence of an additional body in the system. We also fitted one normalisation factor for each photometric dataset (five in our case) and two γ velocities for the radial velocities, one for each set. We used Gaussian priors to randomly draw each parameter.
We decided to use 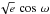 and
and 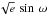 as free parameters instead of the more traditional e cos ω and e sin ω because this would amount to imposing a prior proportional to e2 as noted in Ford (2006). Figure 5 shows the difference between both runs. Considering
as free parameters instead of the more traditional e cos ω and e sin ω because this would amount to imposing a prior proportional to e2 as noted in Ford (2006). Figure 5 shows the difference between both runs. Considering 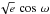 &
& 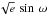 ensures that the eccentricity is less biased towards high values. We therefore made a similar change to another pair of variables, defining
ensures that the eccentricity is less biased towards high values. We therefore made a similar change to another pair of variables, defining 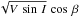 and
and 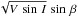 as free parameters rather than using V sin I cos β and V sin I sin β. We conducted checks of these parameters to validate our choice of jump parameters.
as free parameters rather than using V sin I cos β and V sin I sin β. We conducted checks of these parameters to validate our choice of jump parameters.
 |
Fig. 5 In the central box we show the a posteriori probability density function for e and ω, resulting from a chain using |
Limb darkening coefficients used (quadratic law).
4.2. Models and hypotheses
We used the models of Mandel & Agol (2002) to fit the photometric transit and of Giménez (2006) to adjust the Rossiter-McLaughlin effect as well as a classical Keplerian model for the orbital variation in the radial velocities. Limb darkening coefficients for the quadratic law were extracted from Claret (2000, 2004) for the photometry. To fit the Rossiter-McLaughlin effect, we used coefficients specially inferred from HARPS’s spectral response, which were presented in Triaud et al. (2009). Table 2 shows the values we adopted.
These models are compared to the data using a χ2 statistics. A first series of four chains was performed to derive a stellar density estimate. This values were used to determine a stellar mass from the evolutionary models of Girardi et al. (2000) as described in Hebb et al. (2009) using the metallicity and temperature determined in the spectral analysis and the stellar density from fitting the photometric transit. By interpolating between the tracks, we found that 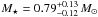 (Fig. 6). This stellar mass was inserted as a prior in a new series of chains. The stellar age could not be constrained but is likely to be old; the star sits above the 10 Gyr isochrone. This first series of chains also allowed the quantification of the correlated noise in the data, which is accounted for in the following chains by increasing the individual error bars. This allows us to place evaluate credible error bars for parameters determined by the photometry.
(Fig. 6). This stellar mass was inserted as a prior in a new series of chains. The stellar age could not be constrained but is likely to be old; the star sits above the 10 Gyr isochrone. This first series of chains also allowed the quantification of the correlated noise in the data, which is accounted for in the following chains by increasing the individual error bars. This allows us to place evaluate credible error bars for parameters determined by the photometry.
Two families of chains, each with 2 000 000 random steps, were run. A family consists of four chains based on different hypotheses:
-
eccentricity and RV drift are allowed to vary freely;
-
no eccentricity but RV drift varie freely;
-
no RV drift but eccentricity varies freely;
-
no eccentricity and no RV drift.
We considered two families, one where the Rossiter-McLaughlin effect is allowed to vary freely and another that neglects this effect, our null hypothesis. Hence from these eight chains we tested for the presence of a linear trend in the radial velocities, for the detection of eccentricity, and for the detection of the Rossiter-McLaughlin effect.
 |
Fig. 6 Modified Hertzprung-Russell diagram comparing the stellar density and temperature of WASP-23 to theoretical stellar evolutionary tracks interpolated for a metallicity of [M/H] = −0.05. The star sits just above the 10 Gyr tracks (dashdotted line). Other tracks are 0.1 Gyr (solid), 1 Gyr (dotted), and 5 Gyr (dashed). Models are those of Girardi et al. (2000). |
 |
Fig. 7 Same legend as in Fig. 5 but here showing V sin I and β, for a circular, non-drifting orbital solution using no prior on V sin I. |
5. Results
We have computed eight different chains, each based on different hypotheses. All chains agree in their results within each others’ error bars in their common parameters, giving strong evidence that they have indeed converged to the solution. Results were extracted from each chain and their comparison with each others led to the final results presented here. This comparison, the most salient points of which are presented in Appendix, made us choose a circular, non-drifting model for the radial velocity. WASP-23b’s parameters were extracted by taking the mode of the marginalised distributions computed by the Markov chains. When two clearly separated mode appeared, each was estimated and its errors bars calculated (see Fig. 8). Error bars are computed by taking the 68.27%, 95.45%, and 99.73% marginalised confidence regions in the a posteriori probability density distribution. Models using eccentricity and a drift as free floating parameters are useful for placing upper constraints on these parameters. Results are presented in Table 3. The final reduced χ2 for the radial velocities, for both CORALIE and HARPS observations, is consistent with one. We therefore saw no need to add any additional terms to our error bars.
Hence, WASP-23b is a 0.88 MJ planet with a 0.96 RJ radius on a 2.94 day orbit, placing it among the normally sized hot Jupiter planets. We can reasonably estimate upper limits to the eccentricity and RV trend at the 99% exclusion level, from the chains that had these as free parameters. Thus, we find that e < 0.062 & 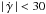 m s-1 yr-1.
m s-1 yr-1.
Using no prior, we detected a radial velocity anomaly compatible with the expected location and shape of the Rossiter-McLaughlin (χ2 changes from 19.6 ± 6.2 to 6.4 ± 3.6 for the 14 data points positioned during transit and one on either side). We detected this effect to a confidence of 3.2 σ from a simple Keplerian model. We see a degeneracy arising between β, V sin I, and b, the impact parameter: V sin I increases to extremely large values (up to 60 km s-1, Fig. 7) by forcing β to a severely misaligned solution and b to becloser to an equatorial transit.
Because of the non-physicality of this result for V sin I we had to resort to using some prior in order to constrain the space within which the MCMC can explore. We do this by imposing a Bayesian penalty on χ2. This additional analysis is presented in the discussion.
Our chains indicate that the effect is mostly symmetrical with respect to the centre of transit (see Fig. 7), and that we can exclude a retrograde orbit.
Fitted and derived parameters for WASP-23 & WASP-23b with their error bars for confidence intervals of 68.27%, 95.45%, and 99.73%. For asterisked parameters, please refer to the text. Underscripted 1 and 2 indicate two distinct solutions for the same parameter.
6. Discussion
 |
Fig. 8 Square boxes present the a posteriori probability density functions for V sin I, β and impact parameter b, from which we extract our results. The white contour marks the 68.27% confidence region. The black dashed contour shows the 95.45%, and the black dotted contour the 99.73% confidence regions. Marginalised distributions are also shown as black histograms in side boxes, normalised to the mode. At the top right, in red, we have the results for a circular, non drifting solution with use of a prior of v = 1.35 ± 0.20 km s-1. On bottom left, in blue, we show a circular, non-drifting solution with the application of a prior of v sin I = 2.2 ± 0.3 km s-1. Grey histograms in V sin I and β show results in the photometry limited runs; for b, we plotted the resulting distribution by fitting the photometry alone without the Rossiter-McLaughlin effect. |
Figure 7 unambiguously shows that we have a strong degeneracy between β and V sin I. This is a well-known problem that was reported in particular in Narita et al. (2010) & Triaud et al. (2010). The spectral line analysis (Sect. 3.5) showed that the projected stellar rotation velocity vsinI = 2.2 ± 0.3 km s-1. From Fig. 7, we observe that a V sin I at such a value would lead to a severely misaligned orbit. This is confirmed when running the MCMC for an additional family of chains using this value of vsinI as a prior on V sin I.
We call this our solution 1: we obtain two modes for β symmetrically opposite each other (see Fig. 8, bottom left corner). We therefore choose to denote this result by its absolute value as | β1 | = 69°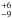
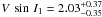 km s-1, and the impact parameter b1 = 0.04 ± 0.05 R ⋆ . This prior choice makes the detection of the Rossiter-McLaughlin effect close to 7.5σ.
km s-1, and the impact parameter b1 = 0.04 ± 0.05 R ⋆ . This prior choice makes the detection of the Rossiter-McLaughlin effect close to 7.5σ.
Before claiming that an additional misaligned planet is present, one around a cool star (thus a strong exception according to Winn et al. 2010a), we searched for another independent estimate of the stellar rotation.
From spectral analysis, we obtained a value quantifying the emission in the calcium II lines expressed in the form of 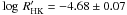 . This value can be used as an indirect measurement of the true stellar rotation period. We used two methods, developed by Noyes et al. (1984), finding
. This value can be used as an indirect measurement of the true stellar rotation period. We used two methods, developed by Noyes et al. (1984), finding 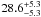 days and a more recent estimate by Mamajek & Hillenbrand (2008) and got the value
days and a more recent estimate by Mamajek & Hillenbrand (2008) and got the value 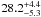 days in very good agreement with the previous value. Using the distribution of R ⋆ computed from our MCMC chains, we transformed these values into the equatorial rotation v obtaining
days in very good agreement with the previous value. Using the distribution of R ⋆ computed from our MCMC chains, we transformed these values into the equatorial rotation v obtaining 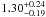 and
and 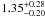 km s-1 respectively. Combining both, we have our new prior that we included as 1.35 ± 0.20 km s-1 into a new series of four chains. The results of these indicate that the planet is most likely on an aligned orbit, but error bars remain large.
km s-1 respectively. Combining both, we have our new prior that we included as 1.35 ± 0.20 km s-1 into a new series of four chains. The results of these indicate that the planet is most likely on an aligned orbit, but error bars remain large.
We refer to these results as our solution 2. We only have one large range of values for the projected spin-orbit angle β2 = −43°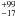 .
. 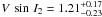 km s-1 and
km s-1 and 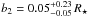 . The detection of the Rossiter-McLaughlin effect is more secure in this case as well, increasing to a value close to 7σ.
. The detection of the Rossiter-McLaughlin effect is more secure in this case as well, increasing to a value close to 7σ.
To test our results, we simulated whether an infinitely precise photometry would help us discriminate between our different solutions for β since the parameter b, for example, is influenced by the adjustment of the Rossiter-McLaughlin model. We therefore removed the Rossiter-McLaughlin effect before running a chain using only photometry to adjust for the transit parameters keeping the non-drifting, non eccentric model. Having photometry as the sole influence on the impact parameter, one finds that 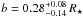 . The value found for b1 and b2 are not at odds with this value. We fixed the parameters controlled by photometry to the most likely values (i.e. b = 0.28) and ran an additional three chains. Those three “photometry limited” chains had the following characteristics:
. The value found for b1 and b2 are not at odds with this value. We fixed the parameters controlled by photometry to the most likely values (i.e. b = 0.28) and ran an additional three chains. Those three “photometry limited” chains had the following characteristics:
-
no imposed prior;
-
a prior of 2.2 ± 0.3 km s-1;
-
a prior of 1.35 ± 0.20 km s-1.
We refer to Fig. 8 for the resulting probability distributions (grey histograms). By fixing all parameters to the values that can be determined by photometry alone and again allowing all remaining parameters to be free, we see some changes in the posterior probability distributions (see grey histograms in Fig. 8). The distribution of V sin I1 is shifted to lower values, while that of β1, although still bimodal, is offset to a far smaller extent. V sin I2 is left almost unchanged, but β2 is more closely confined to zero. This illustrates the effect of our poorly constrained impact parameter on our fit, but this also indicates that, unless a new transit lead us to a higher value of b, even an infinitely precise photometry would not enable us to break entirely the degeneracy between β and V sin I for b < 0.28 R ⋆ .
The measurement of the projected spin-orbit angle β is mostly affected by the small amplitude of the signal and in part by the poorly determined impact parameter, which, floating to small values, creates a degeneracy between small β, small V sin I and high β, high V sin I.
7. Conclusions
After analysing more than four years of photometric and spectroscopic data, we are able to confidently conclude that we have detected a typical hot Jupiter around the K1V star called WASP-23. The analysis was a bit more arduous than anticipated because of a degeneracy that arose when fitting the Rossiter-McLaughlin effect. A total of 19 Markov chains were used to derive our conclusions.
Despite the slow rotation and likely old age of the star, we have managed to detect the Rossiter-McLaughlin effect, which is of similar amplitude to that of WASP-2b (Triaud et al. 2010) and of a similar signal-to-noise as detections such as that on Hat-P-11b (Winn et al. 2010b; Hirano et al. 2011). Imposing priors on V sin I increases our detection level but seriously affects the posterior probability distribution (see Figs. 7 and 8) and thus our results and possible interpretations. This is mostly because of the difference between our two priors, which are 2.7σ away from each other, although our value of v sin I = 2.2 ± 0.3 km s-1 (solution 1) should be seen as a lower value, while v = 1.35 ± 0.20 km s-1 (solution 2) is more of an upper value.
There is strong evidence that for stars colder than 6250 K, planets tend to have a high a priori probability of being aligned with the stellar spin (Winn et al. 2010a). This would then be consistent with our solution 2 , thus imply that the spectral line broadening method is not accurate enough to determine v sin I. This would demonstrate that there is a potential difficulty in estimating v sin I and its use as a prior. However solution 2 is not without its problems either because the determination of the stellar rotation from activity indices could be altered by the presence of a nearby hot Jupiter as well as by long term magnetic cycles.
To resolve WASP-23b’s spin orbit angle, one has several options. One could acquire additional and higher quality photometry. If b were found to be small, then the degeneracy would not be lifted, but the larger its value is found to be, the more likely the system is to be aligned. In addition, further observations of the Rossiter-McLaughlin effect might be needed. There is also a possibility that the current data is enough as one could use the Doppler shadow method pioneered in Collier Cameron et al. (2010) and Miller et al. (2010). This method provides precise determinations of V sin I, β, and b but is most effective best for fast rotators and bright targets.
Either way, the solution to the degeneracy of our results is interesting. If solution 1 (prior on V sin I = 2.2 ± 0.3 km s-1) were confirmed, we would have a misaligned system around a cold star and a need to rectify the determination of stellar rotation based on activity levels. If solution 2 (prior on V sin I = 1.35 ± 0.20 km s-1) were instead the most likely one, then we are observing probably an aligned system and one will need to be careful when using v sin I prior infered by spectral line broadening.
We therefore recommend extreme caution when using priors, as final results can depend entirely on those and a small initial systematic error can lead to dramatic changes in interpretation.
Nota Bene.
We used the UTC time standard and Barycentric Julian Dates in our analysis. Our results are based on the equatorial solar and jovian radii and masses taken from Allen’s Astrophysical Quantities.
Online material
Appendix A: Comparisons between different chains.
In order to lighten the text, here are placed the results of the Markov Chains using various starting hypotheses and from which we estimated upper limits on eccentricity and long term radial velocity trends.
Table A.1 compares the results in χ2 by instrument and during the Rossiter-McLaughlin effect for eights chains. From this we concluded that the eccentric orbit model is compatible with the circular, that a drift that can be fitted is statistically indistinguishable from zero, but that we detect an anomaly in the reflex Doppler motion, corresponding to the location where the Rossiter-McLaughlin effect is expected.
Table A.2 explores the parameters issued from chains where the Rossiter-McLaughlin effect was fitted in order to make sense of the results and see their dependency on initial hypotheses.
Comparison of the results in χ2 by instrument and during the Rossiter-McLaughlin effect 2 different families of chains: having no prior on V sin I, and not fitting the Rossiter-McLaughlin effect.
Results from various Markov chains of the three parameters which control the shape of the Rossiter-McLaughlin effect.
Acknowledgments
The authors would like to acknowledge the use of ADS and of Simbad but mostly the help and the kind attention of the ESO staff at La Silla which with its (now gone and much regretted) completos insured a good and stable supply of energy during the long observing nights. The work is supported by the Swiss Fond National de Recherche Scientifique. TRAPPIST is a project funded by the Belgian Fund for Scientific Research (FNRS) with the participation of the Swiss National Science Fundation (SNF). M. Gillon and E. Jehin are FNRS Research Associates. We also thank R. Heller for providing a copy of Holt’s 1893 paper.
References
- Anderson, D. R., Hellier, C., Gillon, M., et al. 2010, ApJ, 709, 159 [NASA ADS] [CrossRef] [Google Scholar]
- Bakos, G., Noyes, R. W., Kovács, G., et al. 2004, PASP, 116, 266 [NASA ADS] [CrossRef] [Google Scholar]
- Baranne, A., Queloz, D., Mayor, M., et al. 1996, A&A, 119, 373 [Google Scholar]
- Batygin, K., Bodenheimer, P., & Laughlin, G. 2009, ApJ, 704, L49 [NASA ADS] [CrossRef] [Google Scholar]
- Boisse, I., Moutou, C., Vidal-Madjar, A., et al. 2009, A&A, 495, 959 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bouchy, F., Queloz, D., Deleuil, M., et al. 2008, A&A, 482, L25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bruntt, H., Bedding, T. R., Quirion, P.-O., et al. 2010, MNRAS, 405, 1907 [NASA ADS] [Google Scholar]
- Charbonneau, D., Brown, T. M., Latham, D. W., & Mayor, M. 2000, ApJ, 529, L45 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Claret, A. 2000, A&A, 363, 1081 [NASA ADS] [Google Scholar]
- Claret, A. 2004, A&A, 428, 1001 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Collier Cameron, A. C., Bouchy, F., Hébrard, G., et al. 2007a, MNRAS, 375, 951 [NASA ADS] [CrossRef] [Google Scholar]
- Collier Cameron, A. C., Wilson, D. M., West, R. G., et al. 2007b, MNRAS, 380, 1230 [NASA ADS] [CrossRef] [Google Scholar]
- Collier Cameron, A. C., Bruce, V. A., Miller, G. R. M., Triaud, A. H. M. J., & Queloz, D. 2010, MNRAS, 403, 151 [NASA ADS] [CrossRef] [Google Scholar]
- Dobbs-Dixon, I., Cumming, A., & Lin, D. N. C. 2010, ApJ, 710, 1395 [NASA ADS] [CrossRef] [Google Scholar]
- Fabrycky, D., & Tremaine, S. 2007, ApJ, 669, 1298 [NASA ADS] [CrossRef] [Google Scholar]
- Ford, E. B. 2006, ApJ, 642, 505 [NASA ADS] [CrossRef] [Google Scholar]
- Gillon, M., Pont, F., Moutou, C., et al. 2006, A&A, 459, 249 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gillon, M., Triaud, A. H. M. J., Mayor, M., et al. 2008, A&A, 485, 871 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gillon, M., Anderson, D. R., Triaud, A. H. M. J., et al. 2009, A&A, 501, 785 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gillon, M., Jehin, E., Magain, P., et al. 2011, EPJ Web Conf., 11, 06002 [CrossRef] [EDP Sciences] [Google Scholar]
- Giménez, A. 2006, ApJ, 650, 408 [NASA ADS] [CrossRef] [Google Scholar]
- Girardi, L., Bressan, A., Bertelli, G., & Chiosi, C. 2000, A&AS, 141, 371 [Google Scholar]
- Gray, D. F. 2008, The Observation and Analysis of Stellar Photospheres [Google Scholar]
- Guillot, T., & Showman, A. P. 2002, A&A, 385, 156 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hebb, L., Cameron, A. C., Loeillet, B., et al. 2009, ApJ, 693, 1920 [NASA ADS] [CrossRef] [Google Scholar]
- Hébrard, G., Bouchy, F., Pont, F., et al. 2008, A&A, 488, 763 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hirano, T., Suto, Y., Taruya, A., et al. 2010, ApJ, 709, 458 [NASA ADS] [CrossRef] [Google Scholar]
- Hirano, T., Narita, N., Shporer, A., et al. 2011, PASJ, 63, 531 [NASA ADS] [Google Scholar]
- Holt, J. 1893, A&A, XII, 646 [Google Scholar]
- Lin, D. N. C., Bodenheimer, P., & Richardson, D. C. 1996, Nature, 380, 606 [NASA ADS] [CrossRef] [Google Scholar]
- Lovis, C., & Pepe, F. 2007, A&A, 468, 1115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Magain, P. 1984, A&A, 134, 189 [NASA ADS] [Google Scholar]
- Malmberg, D., Davies, M. B., & Heggie, D. C. 2011, MNRAS, 411, 859 [NASA ADS] [CrossRef] [Google Scholar]
- Mamajek, E. E., & Hillenbrand, L. A. 2008, ApJ, 687, 1264 [NASA ADS] [CrossRef] [Google Scholar]
- Mandel, K., & Agol, E. 2002, ApJ, 580, L171 [NASA ADS] [CrossRef] [Google Scholar]
- Mayor, M., Udry, S., Lovis, C., et al. 2009, A&A, 493, 639 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- McCullough, P. R., Stys, J. E., Valenti, J. A., et al. 2005, PASP, 117, 783 [NASA ADS] [CrossRef] [Google Scholar]
- McLaughlin, D. B. 1924, ApJ, 60, 22 [NASA ADS] [CrossRef] [Google Scholar]
- Miller, G. R. M., Collier Cameron, A. C., Simpson, E. K., et al. 2010, A&A, 523, A52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Morton, T. D., & Johnson, J. A. 2011, ApJ, 729, 138 [NASA ADS] [CrossRef] [Google Scholar]
- Nagasawa, M., Ida, S., & Bessho, T. 2008, ApJ, 678, 498 [NASA ADS] [CrossRef] [Google Scholar]
- Narita, N., Sato, B., Hirano, T., & Tamura, M. 2009, PASJ, 61, L35 [NASA ADS] [Google Scholar]
- Narita, N., Hirano, T., Sanchis-Ojeda, R., et al. 2010, PASJ, 62, L61 [NASA ADS] [Google Scholar]
- Noyes, R. W., Weiss, N. O., & Vaughan, A. H. 1984, ApJ, 287, 769 [NASA ADS] [CrossRef] [Google Scholar]
- O’Donovan, F. T., Charbonneau, D., & Hillenbrand, L. 2006, 2007 AAS/AAPT Joint Meeting, 209, 1212 [Google Scholar]
- Ohta, Y., Taruya, A., & Suto, Y. 2005, ApJ, 622, 1118 [NASA ADS] [CrossRef] [Google Scholar]
- Pepe, F., Mayor, M., Galland, F., et al. 2002, A&A, 388, 632 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pollacco, D. L., Skillen, I., Cameron, A. C., et al. 2006, PASP, 118, 1407 [NASA ADS] [CrossRef] [Google Scholar]
- Queloz, D., Eggenberger, A., Mayor, M., et al. 2000, A&A, 359, L13 [NASA ADS] [Google Scholar]
- Queloz, D., Anderson, D., Cameron, A. C., et al. 2010, A&A, 517, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rossiter, R. A. 1924, ApJ, 60, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Santos, N. C., Mayor, M., Naef, D., et al. 2000, A&A, 361, 265 [NASA ADS] [Google Scholar]
- Santos, N. C., Mayor, M., Naef, D., et al. 2002, A&A, 392, 215 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Snellen, I. A. G., van der Burg, R. F. J., de Hoon, M. D. J., & Vuijsje, F. N. 2007, A&A, 476, 1357 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stetson, P. B. 1987, PASP, 99, 191 [NASA ADS] [CrossRef] [Google Scholar]
- Triaud, A. H. M. J., Queloz, D., Bouchy, F., et al. 2009, A&A, 506, 377 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Triaud, A. H. M. J., Cameron, A. C., Queloz, D., et al. 2010, A&A, 524, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Udalski, A., Kubiak, M., & Szymanski, M. 1997, Acta Astron., 47, 319 [NASA ADS] [Google Scholar]
- Winn, J. N., Johnson, J. A., Albrecht, S., et al. 2009, ApJ, 703, L99 [NASA ADS] [CrossRef] [Google Scholar]
- Winn, J. N., Fabrycky, D., Albrecht, S., & Johnson, J. A. 2010a, ApJ, 718, L145 [NASA ADS] [CrossRef] [Google Scholar]
- Winn, J. N., Johnson, J. A., Howard, A. W., et al. 2010b, ApJ, 723, L223 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Fitted and derived parameters for WASP-23 & WASP-23b with their error bars for confidence intervals of 68.27%, 95.45%, and 99.73%. For asterisked parameters, please refer to the text. Underscripted 1 and 2 indicate two distinct solutions for the same parameter.
Comparison of the results in χ2 by instrument and during the Rossiter-McLaughlin effect 2 different families of chains: having no prior on V sin I, and not fitting the Rossiter-McLaughlin effect.
Results from various Markov chains of the three parameters which control the shape of the Rossiter-McLaughlin effect.
All Figures
 |
Fig. 1 Phased WASP-South photometry, of two seasons, and residuals. R band model superimposed. |
| In the text | |
 |
Fig. 2 Black triangles: CORALIE data; red discs: HARPS data. Top: radial velocities with model superimposed, and residuals (both in m s-1), as a function of orbital phase. Added are the 1σ error bars. Bottom: phased bisector span and FWHM (both in km s-1). The HARPS data has been translated to have its mean correspond to the CORALIE data. |
| In the text | |
 |
Fig. 3 HARPS radial velocity data corrected for the reflex Doppler motion due to the planet and model of the Rossiter-McLaughlin effect with residuals. Below: three photometric transits (instruments are indicated), the best-fit model and residuals. All are presented as a function of the orbital phase. |
| In the text | |
 |
Fig. 4 The two I + z band timeseries observed by TRAPPIST, with best-fit model being overplotted. |
| In the text | |
 |
Fig. 5 In the central box we show the a posteriori probability density function for e and ω, resulting from a chain using |
| In the text | |
 |
Fig. 6 Modified Hertzprung-Russell diagram comparing the stellar density and temperature of WASP-23 to theoretical stellar evolutionary tracks interpolated for a metallicity of [M/H] = −0.05. The star sits just above the 10 Gyr tracks (dashdotted line). Other tracks are 0.1 Gyr (solid), 1 Gyr (dotted), and 5 Gyr (dashed). Models are those of Girardi et al. (2000). |
| In the text | |
 |
Fig. 7 Same legend as in Fig. 5 but here showing V sin I and β, for a circular, non-drifting orbital solution using no prior on V sin I. |
| In the text | |
 |
Fig. 8 Square boxes present the a posteriori probability density functions for V sin I, β and impact parameter b, from which we extract our results. The white contour marks the 68.27% confidence region. The black dashed contour shows the 95.45%, and the black dotted contour the 99.73% confidence regions. Marginalised distributions are also shown as black histograms in side boxes, normalised to the mode. At the top right, in red, we have the results for a circular, non drifting solution with use of a prior of v = 1.35 ± 0.20 km s-1. On bottom left, in blue, we show a circular, non-drifting solution with the application of a prior of v sin I = 2.2 ± 0.3 km s-1. Grey histograms in V sin I and β show results in the photometry limited runs; for b, we plotted the resulting distribution by fitting the photometry alone without the Rossiter-McLaughlin effect. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


