| Issue |
A&A
Volume 531, July 2011
|
|
|---|---|---|
| Article Number | A150 | |
| Number of page(s) | 8 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201016115 | |
| Published online | 05 July 2011 | |
Lunar mare single-scattering, porosity, and surface-roughness properties with SMART-1 AMIE
1 Department of Physics, PO Box 64, 00014 University of Helsinki, Finland
e-mail: karri.Muinonen@Helsinki.Fi
2
Finnish Geodetic Institute, PO Box 15, 02431 Masala, Finland
3 Instituto de Astrofísica de Canarias, Calle vía Láctea, 38205 La Laguna (Tenerife), Spain
4
Space Exploration Institute, Case postale 774, 2002 Neuchâtel, Switzerland
5
Micro-cameras & Space Exploration, Puits-Godet 10a, 2000 Neuchâtel, Switzerland
6
IRAP/Observatoire Midi-Pyrénées/CNRS/Université Toulouse III, 14, Avenue Edouard Belin, 31400 Toulouse, France
7
European Space Agency ESA, ESTEC/SRE-S, postbus 299, 2200 AG Noordwijk, The Netherlands
8
European Space Agency ESA, ESAC/SRE-OS, Apdo. de correos 78, 28691 Villanueva de la Cañada, Madrid, Spain
Received: 10 November 2010
Accepted: 19 April 2011
A novel shadowing and coherent-backscattering model is utilized in the analysis of the single-scattering albedos and phase functions, local surface roughness, and regolith porosity of specific lunar mare regions imaged by the AMIE camera (Advanced Moon micro-Imager Experiment) onboard ESA SMART-1 mission. Shadowing due to the regolith particles is accounted via ray-tracing computations for densely-packed particulate media with a fractional-Brownian-motion interface with free space. The shadowing modeling allows us to derive the scattering phase function for a ~100-μm volume element of the lunar mare regolith. The volume-element phase function is explained by coherent-backscattering modeling, where the fundamental single scatterers are the wavelength-scale particle inhomogeneities or the smallest fraction of the particles on the lunar surface. The phase function of the fundamental scatterers is expressed as a sum of two Henyey-Greenstein terms, accounting for increased backward scattering as well as increased forward scattering. Based on the modeling of the AMIE lunar photometry, we conclude that most of the lunar mare opposition effect is caused by coherent backscattering within volume elements comparable in size to typical lunar particles, with only a small contribution from shadowing effects.
Key words: Moon / scattering / techniques: photometric
© ESO, 2011
1. Introduction
The Moon exhibits an opposition effect (Rougier 1933), that is, a nonlinear increase of disk-integrated brightness with decreasing solar phase angle, the angle between the Sun and the observer as seen from the object. Whereas the opposition effect is a ubiquitous phenomenon for atmosphereless solar-system objects at large, the lunar opposition effect is of particular significance as we can witness the brightness of the full Moon with our own bare eyes. In the opposition night, the Moon is roughly twice as bright as in the nights just before and after the opposition.
The lunar opposition effect lacks a widely-accepted physical explanation. It has been traditionally explained by mutual shadowing (Bowell et al. 1989; Hapke & van Horn 1963; Lumme & Bowell 1981; Lumme & Irvine 1982) among regolith particles (sizes in several tens of microns) large compared to the wavelength of incident light (SM; shadowing mechanism): the particles hide their own shadows at exact opposition. More recently, the coherent-backscattering mechanism (CBM) has been introduced as a possible explanation for the opposition effects of selected solar-system objects (e.g., Shkuratov 1988; Muinonen 1990; Hapke 1990; Hapke et al. 1993; Mishchenko & Dlugach 1993). CBM is a multiple-scattering interference mechanism, where electromagnetic waves propagating through the same scatterers in opposite directions interfere constructively in the backward-scattering direction but with varying interference characteristics in other directions.
For accruing knowledge on the properties of fundamental scatterers within the lunar regolith, SM needs to be accurately modeled. SM is affected by surface roughness, that is, the stochastic geometry of the interface between free space and regolith (Parviainen & Muinonen 2009, 2007; Peltoniemi 1993; Lumme et al. 1990). The dependence of SM on the angles of incidence and emergence (as measured from the outward surface normal) as well as the azimuth between the planes of incidence and emergence allows for the estimation of the surface-roughness parameters.
In order to simulate the geometry of the lunar regolith, we make use of a dropping-based algorithm with spherical particles in modeling the bulk particulate medium, as well as fractional-Brownian-motion surfaces (fBm) and Gaussian random surfaces (Gs) in modeling the interface between free space and the particulate medium (Parviainen & Muinonen 2009, 2007; Muinonen et al. 2002, 2001; Peitgen & Saupe 1988). The single spherical particle and its immediate vicinity mimics what we call a volume element of the lunar regolith. The size of the volume element is thus of the order of 100 μm, that is, much larger than the wavelength of incident visible sunlight. We extract the effects of the stochastic geometry from the lunar photometry and, thereby, obtain the volume-element scattering phase function of the lunar regolith locations studied. The volume-element phase function allows us to constrain the physical properties of the typical regolith particles much larger than the wavelength.
We assume, hierarchically, that the volume element consists of a finite random medium of fundamental scatterers and that multiple scattering among these scatterers gives rise to coherent backscattering. In order to compute coherent backscattering by a finite medium large compared to the wavelength, such as the inhomogeneous lunar particles, we rely on the theoretical and computational methods put forward by Muinonen (2004) and Muinonen et al. (2010). To support the validity of the present approach, we refer the reader to the recent comparison to exact electromagnetic methods by Muinonen & Zubko (2010).
Due to the absence of polarimetric observations, we adopt a scalar model for coherent backscattering as summarized in Muinonen et al. (2010). Mishchenko & Dlugach (1992) point out the limited accuracy of the scalar model: the model can result in backscattering enhancement factors overestimated by 20% at maximum. Nevertheless, for the present preliminary and limited analysis, we consider the scalar model to be adequate in the evaluation of the leading scattering effects.
The Clementine space mission has been the first mission to obtain high-resolution photometry over the entire lunar surface. Hillier et al. (1999) have carried out a Clementine-based disk-resolved multispectral photometric study of the Moon. They have analyzed the photometric properties of the lunar surface with the UV/Vis camera in four different photometric channels between 400–1000 nm at a phase-angle range of 0–85° mainly in the nadir-pointing geometry (zero angle of emergence). Hillier et al. have divided the lunar surface into two different types of terrain, mare and highlands, and derived synthesized phase curves for both terrain types over the entire lunar surface for, e.g., photometric corrections in mineralogical studies. According to them, the function fits suggest that the mare regions exhibit broader opposition effects, claimed to be indicative of surfaces more compacted than on the highlands regions. They have also used the Clementine data to study the physical properties of the lunar surface by fitting a photometric model that they have derived from that by Hapke (1984). For the mare regions, they have explained the entire opposition effect by SM with a halfwidth of ~8°.
Shkuratov et al. (1999) have carried out an analysis of the lunar opposition effect analyzing its causes using theoretical, observational, and experimental methods. They have reached the conclusion that the lunar opposition effect is at least partly caused by CBM. Hapke et al. (1993) have measured so-called polarization ratios for a number of lunar samples and suggested diagnostic tools for evaluating the importance of coherent backscattering and shadowing for the lunar opposition effect. Hapke et al. have concluded that SM and CBM contribute to the lunar opposition effect in roughly equal shares.
Kaydash et al. (2009) have analyzed SMART-1 AMIE images of the lunar mare regions and swirls using so-called phase-ratio images and empirical modeling of the photometric dependences in observation and illumination geometries away from opposition. They have indicated regions that show anomalous photometric dependences and have offered interpretations related to the geological evolution of the Moon. Kaydash et al. offer an up-to-date assessment of the various phases of the SMART-1 mission and of the AMIE imaging geometries as well as the status of the image processing.
In what follows, we carry out physical modeling of the shadowing and coherent backscattering phenomena and seek for a plausible interpretation in terms of fundamental physical parameters. In Sect. 2, we describe the SMART-1 AMIE imaging data (Pinet et al. 2005) utilized in our assessment of lunar scattering, porosity, and surface roughness. Section 3 includes the theoretical modeling for the lunar mare scattering law and the inverse methods to derive the model parameters from the imaging data. In Sect. 4, we apply the methods to the chosen set of SMART-1 AMIE data and discuss the results. We close the article with conclusions and future prospects in Sect. 5.
2. Observations
We have used selected data obtained by the AMIE instrument onboard the ESA SMART-1 spacecraft specially operated to provide a wide range of observation geometries (Racca et al. 2002; Foing et al. 2006; Josset et al. 2006). We include four different lunar mare regions in our study (Fig. 1). Mare regions were selected for this study as they offer, in general, a relatively homogeneous surface with little topographic tilts (e.g., crater rims) that could pose difficulties in the determination of the observation geometry. Each of the four regions covers several hundreds of square kilometers of lunar surface. When selecting the regions, we have required that they have been imaged by AMIE across a wide range of phase angles (α), including the opposition geometry. The phase-angle range covered is 0–109°, with incidence and emergence angles as counted from the outward normal vector (ι and ϵ) ranging within 7–87° and 0–53°, respectively. The pixel scale varies from 288 m down to 29 m during the extended mission phase ended by the SMART-1 spacecraft crashing into the lunar surface on September 3, 2006. Note that off-nadir-pointing observations have allowed for the extensive phase-angle coverage. In total, 220 images are used for the present study.
 |
Fig. 1 The lunar regions observed by AMIE onboard ESA SMART-1 (Advanced Moon micro-Imager Experiment) and analyzed in the present study overlaid on the Clementine albedo map: 1) Oceanus Procellarum, around Reiner Gamma; 2) Oceanus Procellarum, between Mons Rümker and the Mairan crater; 3) Mare Imbrium, north of Copernicus crater; and 4) Mare Serenitatis. |
Biases and dark currents were subtracted from the images in the usual way, followed by a flat-field correction. New dark-current reduction procedures have recently been derived from in-flight measurements to replace the ground-calibration images that were rendered practically useless by the large radiation dose that AMIE experienced during the 13-month journey of SMART-1 to the Moon (Grieger 2008). The clear (or panchromatic) filter was chosen for the present study as it provides the largest field of view, consisting of 512 × 512 pixels, and usually also the best signal-to-noise ratio.
Since the surface footprint of a single AMIE image could span several degrees in selenocentric longitude and latitude, the illumination geometry, that is, ι, ϵ, α, and the azimuth angle between the incident and emergent directions φ, was computed separately for each pixel in the images used in the photometric analysis by utilizing the NASA Navigation and Ancillary Information Facility SPICE software toolkit with the latest and corrected SMART-1 AMIE SPICE kernels.
The photometric data points were extracted as follows. First, on average, 50 sample areas of 10 × 10 pixels were chosen by hand from each image, to exclude large craters and albedo anomalies from the analysis. Second, the surface normal, ι, ϵ, φ, and α were computed for each pixel in each sample area. Finally, the illumination angles and the observed intensity were averaged over each sample area. In total, the images used in the study resulted, for the four mare regions, in approximately 12 000 photometric sample points (Fig. 2). We note that the lunar opposition effect in Fig. 2 agrees in steepness over the phase-angle of 0.0–2.5° with the earlier lunar mare analysis using AMIE data by Kaydash et al. (2008).
 |
Fig. 2 The multiangular photometry reduced from the lunar mare regions depicted in Fig. 1 as a function of the phase angle α. The opposition effect shows up as abrupt nonlinear brightening towards opposition. The viewing geometries of the AMIE lunar images are also depicted. Each geometry is fixed by three angles, for example, the angles of incidence and emergence (ι and ϵ) and the azimuth angle φ (that can be replaced by α). |
3. Theoretical and numerical methods
3.1. Scattering model for mare regions
Consider diffuse scattering of light from a semi-infinite particulate regolith with a rough interface towards free space. The reflection coefficient R relates the incident flux density πF0 and the emergent intensity I as 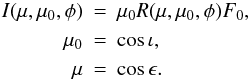 (1)In order to model the scattering from the dark lunar mare regions, we utilize the Lommel-Seeliger reflection coefficient corrected for shadowing as
(1)In order to model the scattering from the dark lunar mare regions, we utilize the Lommel-Seeliger reflection coefficient corrected for shadowing as 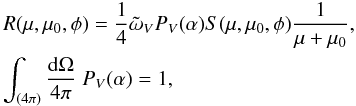 (2)where
(2)where  is the single-scattering albedo of the volume element V, PV is the normalized volume-element scattering phase function, and S accounts for shadowing. For phase angle α = 0°, we have S ≡ 1.
is the single-scattering albedo of the volume element V, PV is the normalized volume-element scattering phase function, and S accounts for shadowing. For phase angle α = 0°, we have S ≡ 1.
Without the shadowing function S, the reflection coefficient in Eq. (2) coincides with the Lommel-Seeliger reflection coefficient, which is the first-order multiple-scattering solution to the radiative transfer equation for a semi-infinite plane-parallel medium of scatterers. The reflection coefficient in Eq. (2) is applicable to dark media such as the lunar mare regolith: the contributions proportional to  , k ≥ 2 are assumed negligible.
, k ≥ 2 are assumed negligible.
Consider next the definition of the volume element. It is well known that the radiative transfer theory succeeds in describing the angular characteristics of regolith reflection coefficients outside the opposition regime. This occurs in spite of the fact that the theory is known to be, strictly, inapplicable to close-packed regoliths of particles. This allows us to assume that the volume element V extends over a typical lunar particle and its immediate vicinity so that the size of the element is of the order of ~100 μm.
The geometric albedo p is the ratio of the disk-integrated brightness of an object and the disk-integrated brightness of a normally illuminated Lambertian disk in the exact backscattering direction α = 0°. Considering a spherical object with surface scattering characteristics described by the reflection coefficient in Eq. (2), we have 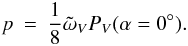 (3)This coincides with the geometric albedo pV of the volume element V: pV = p.
(3)This coincides with the geometric albedo pV of the volume element V: pV = p.
3.2. Coherent-backscattering modeling for p, 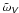 , and PV
, and PV
We model the lunar mare geometric albedo p (Eq. (3)) as well as the volume-element albedo 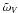 and phase function PV (Eq. (2)) in terms of scalar coherent backscattering by a finite medium of fundamental scatterers (Muinonen et al. 2010). We denote the single-scattering albedo and phase function of the fundamental scatterers by
and phase function PV (Eq. (2)) in terms of scalar coherent backscattering by a finite medium of fundamental scatterers (Muinonen et al. 2010). We denote the single-scattering albedo and phase function of the fundamental scatterers by 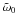 and P0. We further introduce the extinction mean free path ℓ = 1/ke (ke is the extinction coefficient) for the finite medium, which we typically express in a dimensionless form kℓ = 2πℓ/λ, where k and λ are the wave number and wavelength. We assume that the volume element V is spherical and that the radius of the volume element is 60 μm, mimicking a cubic element with an edgelength of 100 μm.
and P0. We further introduce the extinction mean free path ℓ = 1/ke (ke is the extinction coefficient) for the finite medium, which we typically express in a dimensionless form kℓ = 2πℓ/λ, where k and λ are the wave number and wavelength. We assume that the volume element V is spherical and that the radius of the volume element is 60 μm, mimicking a cubic element with an edgelength of 100 μm.
For describing the phase function P0, we utilize double Henyey-Greenstein (H-G) scattering phase functions P2HG: 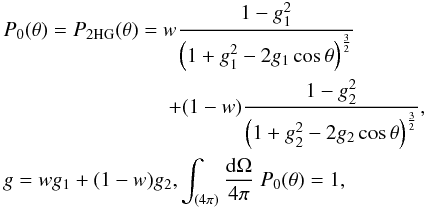 (4)where θ = π − α is the scattering angle, g1 and g2 describe the forward and backward asymmetries, w is the normalized weight of the first H-G term, and g is the asymmetry parameter of the phase function. The first H-G term describes the common increase towards the forward-scattering direction, whereas the second term describes the increase from intermediate scattering angles towards the backward-scattering direction. Note that it remains as an open question what the increase towards the forward-scattering direction means in the case of fundamental scatterers constituting lunar particles much larger than the wavelength.
(4)where θ = π − α is the scattering angle, g1 and g2 describe the forward and backward asymmetries, w is the normalized weight of the first H-G term, and g is the asymmetry parameter of the phase function. The first H-G term describes the common increase towards the forward-scattering direction, whereas the second term describes the increase from intermediate scattering angles towards the backward-scattering direction. Note that it remains as an open question what the increase towards the forward-scattering direction means in the case of fundamental scatterers constituting lunar particles much larger than the wavelength.
In the coherent-backscattering modeling, we require that the resulting lunar mare geometric albedos (Eq. (3)) be p < 0.2 and that the volume-element single-scattering albedos be 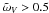 . Such single-scattering albedos are comparable to the corresponding albedos measured in the laboratory for single lunar analog particles large compared to the wavelength (Piironen et al. 1998). The geometric-albedo range for the mare regions has been estimated with the help of the study by Lumme & Irvine (1982).
. Such single-scattering albedos are comparable to the corresponding albedos measured in the laboratory for single lunar analog particles large compared to the wavelength (Piironen et al. 1998). The geometric-albedo range for the mare regions has been estimated with the help of the study by Lumme & Irvine (1982).
3.3. Ray-tracing modeling for R
A numerical geometric-optics ray-tracing code has been developed to derive the volume-element scattering phase function PV and the combined mutual and rough-surface shadowing function S in Eq. (2) for a particulate medium mimicking the lunar regolith (Parviainen & Muinonen 2007, 2009). The code uses Monte-Carlo ray tracing to compute the reflection coefficient R in Eq. (2) for a medium composed of opague spherical particles (Fig. 3).
For deriving PV and S from the lunar photometry, we assume that the particle surfaces, that is, the surfaces of the volume elements, follow the Lommel-Seeliger scattering law (mathematical form equivalent to that in Eq. (2) without the shadowing function; e.g., Bowell et al. 1989). The scattering phase function for the fictituous particle-surface scatterers P∂V is also modeled using a double H-G phase function, P∂V = P2HG. To discriminate between the double H-G parameters of the fundamental scatterers and those of the particle-surface scatterers, we utilize w∂V, g1, ∂V, and g2, ∂V for P∂V. The current shadowing modeling is an advanced version of earlier work in Muinonen et al. (2001) and Stankevich et al. (1999). According to our experience, the present parameterization of the volume element results in excellent fits to lunar mare photometry. We return to the physical interpretation of the modeling below.
Instead of limiting ourselves to the principal plane with varying ι and ϵ and φ = 0° or 180°, we have computed the shadowing function over the entire hemisphere, allowing us to account for azimuthal shadowing effects arising from varying φ. Recent studies (e.g., Shepard & Campbell 1998; Shkuratov et al. 2005; Parviainen & Muinonen 2007; Jehl et al. 2008) have demonstrated that azimuthal shadowing contributes significantly to the photometric response by a planetary regolith surface.
The simulation has consisted of two parts: the generation of the particulate media and the Monte-Carlo ray tracing in the media. First, using a dropping-based random-packing method for five volume densities v = 0.2, 0.3, 0.4, 0.5, and 0.55, we have generated a medium consisting of 106 spherical particles with mean radii of 1/500 of the width of the medium. Second, we have intersected the particulate media by two-dimensional random fields to model the surface roughness with two parameters. We parameterize the fractional-Brownian-motion roughness with the Hurst exponent H and the standard deviation of heights of the whole field σ, while Gaussian roughness is parameterized by the correlation length l and σ. We thus describe the regolith analog media with three parameters v, H or l, and σ. Also, when considering media without external large-scale surface roughness, we remove 20% of the medium in thickness from the surface in order to remove a density gradient arising from the dropping algorithm. For an example fBm surface, see Fig. 3.
 |
Fig. 3 Porous random medium of spherical particles with fractional-Brownian-motion boundary surface: Hurst exponent H = 0.4, standard deviation of heights σ = 0.06, and volume density v = 0.35. |
The Monte-Carlo simulation consists of ray tracing a large number of geometry samples from the medium for each photometric sample point. A single geometry sample consists of information on whether the sample point on the particle surface is illuminated and on the local angles of incidence and emergence as well as the local azimuth angle. Thus, the set of geometry samples represents the distribution of angles visible to the observer (the AMIE camera) for the given observation geometry. Now, the final model reflection coefficient R for a given photometric point can be obtained as a sum of the contributions computed from the illuminated geometry samples. This way of computing the observed angle distribution for a given observation geometry (instead of direct ray tracing for R) allows us to fit arbitrary reflection-coefficient models to the photometric data without a need for computationally expensive additional ray tracing. For each photometric sample point, we have computed 50 geometry samples for 20 rough-surface realizations, yielding 1000 geometry samples in total.
Based on the work by Muinonen et al. (2001) and Stankevich et al. (1999), the shadowing function S can be assumed constant over the surface of an individual spherical particle. This allows us to discriminate between the two parts, PV and S, in the reflection coefficient R derived by least-squares fitting of the ray-tracing model to the lunar photometry. Since the numerical ray-tracing simulations utilize constituent spherical volume elements with Lommel-Seeliger surface scattering laws, the true volume-element scattering phase function PV(θ) is proportional to the product of P∂V(θ) and an additional phase-angle dependent function that results from the integration of the Lommel-Seeliger cosine part over the surface of the spherical volume elements (this integration can be done analytically and independently of S as explained above): ![\begin{eqnarray} &&P_{V}(\theta) = N^{-1} P_{\partial V} (\theta) \left[ 1-\cos\frac{1}{2}\theta\; \cot\frac{1}{2}\theta \; \ln\left(\cot\frac{1}{4}(\pi-\theta)\right) \right], \nonumber\\ &&N = \int_{(4\pi)} \frac{{\rm d}\Omega}{4\pi} \; P_{\partial V} (\theta) \nonumber\\ && \hspace*{8mm} \times\left[ 1-\cos\frac{1}{2}\theta\; \cot\frac{1}{2}\theta \; \ln\left(\cot\frac{1}{4}(\pi-\theta)\right) \right]. \label{eqp11} \end{eqnarray}](/articles/aa/full_html/2011/07/aa16115-10/aa16115-10-eq67.png) (5)The functional form of the shadowing function S now follows from Eq. (2) by dividing the model reflection coefficient by the phase function of Eq. (5) and the Lommel-Seeliger cosine part. Note that the particle-surface scattering phase function P∂V(θ) emerges as an auxiliary computational tool to derive PV(θ) and S.
(5)The functional form of the shadowing function S now follows from Eq. (2) by dividing the model reflection coefficient by the phase function of Eq. (5) and the Lommel-Seeliger cosine part. Note that the particle-surface scattering phase function P∂V(θ) emerges as an auxiliary computational tool to derive PV(θ) and S.
3.4. Inversion
Inversion of the observations for the lunar surface properties consists of two steps. First, the shadowing function S and the volume-element phase function PV (in the relative sense) are derived with the help of the aforedescribed shadowing modeling for particulate media using least-squares analysis of the observations. This step will give us PV as well as the surface roughness parameters H and σ and the regolith porosity v. Second, the resulting PV is explained using scalar coherent-backscattering modeling with realistic assumptions for the geometric albedo of the lunar mare regions or, in other words, 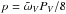 . This step allows us to constrain the single-scattering albedo
. This step allows us to constrain the single-scattering albedo 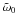 , the single-scattering phase function P0, and the mean free path in the form kℓ for the finite medium of fundamental scatterers mimicking a lunar volume element.
, the single-scattering phase function P0, and the mean free path in the form kℓ for the finite medium of fundamental scatterers mimicking a lunar volume element.
 |
Fig. 4 The multiangular AMIE photometry of the mare regions fitted using the fBm-particulate-medium model with H = 0.80, σ = 0.05, and v = 0.30, and a double Henyey-Greenstein particle-surface phase function with w∂V = 0.001432, g1, ∂V = −0.9228, and g2, ∂V = −0.0546 (uppermost points). Also shown are the residuals shifted downward by 0.2 vertical units for clarity (lowermost points). See Table 1. |
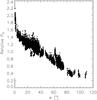 |
Fig. 5 The lunar mare volume-element phase function PV (see Eqs. (2) and (5)). The phase function follows from dividing more than 12 000 SMART-1 AMIE original data points by best-fit model S(μ,μ0,φ)/(μ + μ0) in Eq. (2). |
4. Results and discussion
In order to derive the lunar mare volume-element phase function, a best-fit solution to the photometric observations was searched from the computed fBm scattering models using the differential-evolution global-optimization method (Storn & Price 1997). The effects due to different values of v, H, and σ were small but noticeable (Table 1). After the fit, the first-order approximation for the volume-element phase function was obtained from Eq. (5) based on the fit shown in Fig. 4. The volume-element phase function is depicted in Figs. 5 and 6.
In detail, the best-fit fBm parameters are as follows: v = 0.30, H = 0.80, and σ = 0.05 with the rms value of 2.001 in the units of Fig. 2. For comparison, the best-fit Gaussian model gives v = 0.30, l = 0.50, and σ = 0.03 with the rms value of 2.083, whereas the so-called smooth model gives v = 0.50 with the rms value of 2.151. This offers a preliminary indication that the fBm model is indeed the leading model for the lunar regolith. Table 1 shows how the particle-surface phase function P∂V(θ) and the volume-element phase function PV(θ) (Eq. (5)), as well as the rms values of the least-squares fits vary as a function of the fBm parameters.
Best-fit particle-surface phase functions P∂V(θ) modeled as double Henyey-Greenstein phase functions (H-G) for media with fractional-Brownian-motion surface roughness.
The lunar volume-element phase function exhibits a narrow backscattering intensity surge. The most notable result of the comparison of the photometric observations and numerical SM modeling is that SM does not explain the intensity surge, even for the most porous media considered in the study, v = 0.2. Note that the Lommel-Seeliger scattering law corrected for shadowing in Eq. (2) is largely validated by the fact that, after the division of the observational data with the model data for S(μ,μ0,φ)/(μ + μ0), the remaining variation can be explained, to a precision compatible with the observational errors, by a function that depends on the phase angle α only. This function is then proportional to PV(θ).
The resulting volume-element phase functions differ from those experimentally measured for, e.g., large individual Saharan sand particles (Munoz et al. 2007). This underscores the difference of lunar volume-element scattering characteristics as compared to those of compact, optically rather homogeneous particles with surface roughness.
 |
Fig. 6 The lunar mare volume-element phase function of Fig. 5 averaged using bin size of 0.5°. We show the best-fit volume-element scattering phase function PV (solid line). For the largest phase angles, there is a deviation that is probably due to the incapability of the present model volume-element phase function to fit the observations and to increasing real brightness variegation or correlated observational errors. |
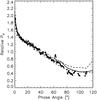 |
Fig. 7 The binned lunar mare volume-element phase function with the corresponding coherent-backscattering modeling including a variation envelope. Double H-G single-scattering phase functions for the fundamental scatterers give rise to coherent-backscattering peaks capable of matching the observations. For the largest phase angles, there is a deviation between the model and the observations potentially due to simplified modeling. |
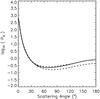 |
Fig. 9 Lunar mare single-scattering phase function P0 of the fundamental scatterers (see Eq. (4)) expressed as a double H-G function with a variation envelope. |
The lunar backscattering intensity surge can be assigned to multiple interactions between the fundamental scatterers within the volume element V. We stress that this multiple scattering is presently included in what we call the lunar volume-element phase function representing a scattering volume large enough to give rise to coherent-backscattering effects.
After carrying out thousands of scalar coherent-backscattering simulations for varying single-scattering albedos and phase functions of the fundamental scatterers, we have converged on computing volume-element scattering characteristics using 31 single-scattering albedos 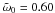 , 0.61, 0.62, ..., 0.90 and 8 extinction mean free paths ℓ with kℓ = 240, 270, 300, ..., 450. We have utilized a total asymmetry parameter of g = 0.60, 0.65, 0.70, 0.75 or 0.8 in the double H-G phase function. In full detail, for the forward and backward-scattering H-G terms, we have assumed g1 = 0.95 and g2 = −0.33, –0.32, –0.31, ..., –0.17, respectively, with the weight factor for the forward-scattering term being determined by the total asymmetry parameter. Thus, we have used altogether 85 different single-scattering phase functions. For the final phase of coherent-backscattering modeling, we have thus computed altogether 21 080 different models for the lunar mare volume element.
, 0.61, 0.62, ..., 0.90 and 8 extinction mean free paths ℓ with kℓ = 240, 270, 300, ..., 450. We have utilized a total asymmetry parameter of g = 0.60, 0.65, 0.70, 0.75 or 0.8 in the double H-G phase function. In full detail, for the forward and backward-scattering H-G terms, we have assumed g1 = 0.95 and g2 = −0.33, –0.32, –0.31, ..., –0.17, respectively, with the weight factor for the forward-scattering term being determined by the total asymmetry parameter. Thus, we have used altogether 85 different single-scattering phase functions. For the final phase of coherent-backscattering modeling, we have thus computed altogether 21 080 different models for the lunar mare volume element.
The single-scattering albedo and total asymmetry parameter of the best-fit solution are 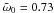 and g = 0.60. In the H-G phase function, we have g1 = 0.95 and g2 = −0.31, giving w = 0.722. The unitless mean free path is kℓ = 450. The resulting geometric albedo for the mare regions is p = 0.176. Figures 7 and 8 show the best-fit coherent-backscattering model with a variation envelope among the sequence of models for spherical media of fundamental scatterers mimicking the volume element in the lunar surface. For 180 data points of the binned volume-element phase function with assumed observational error standard deviation of 0.03 for points with α < 60° and 0.1 for points with α ≥ 60°, the χ2 value of the best fit is 0.928. The variation envelope corresponds to models with χ2-values within a factor of 1.3 from the best-fit value. The threshold χ2-value has been chosen on the basis of the fluctuations of the H-G models to offer a view of how well, overall, the models fit the observations. There are particularly good fits to the observational data all through the parameter phase space of
and g = 0.60. In the H-G phase function, we have g1 = 0.95 and g2 = −0.31, giving w = 0.722. The unitless mean free path is kℓ = 450. The resulting geometric albedo for the mare regions is p = 0.176. Figures 7 and 8 show the best-fit coherent-backscattering model with a variation envelope among the sequence of models for spherical media of fundamental scatterers mimicking the volume element in the lunar surface. For 180 data points of the binned volume-element phase function with assumed observational error standard deviation of 0.03 for points with α < 60° and 0.1 for points with α ≥ 60°, the χ2 value of the best fit is 0.928. The variation envelope corresponds to models with χ2-values within a factor of 1.3 from the best-fit value. The threshold χ2-value has been chosen on the basis of the fluctuations of the H-G models to offer a view of how well, overall, the models fit the observations. There are particularly good fits to the observational data all through the parameter phase space of 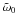 , g, g1, g2, and kℓ and, given the heuristic characteristics of the present modeling, the best-fit solutions have been allowed to occur at the bounds of the parameters g and kℓ. Clearly, acceptable fits could be obtained with less forward scattering double H-G phase functions (i.e., smaller g-values) and longer mean free path lengths. Figure 9 shows the best-fit single-scattering phase function among the models utilized and its variation envelope corresponding to the aforedescribed χ2 analysis.
, g, g1, g2, and kℓ and, given the heuristic characteristics of the present modeling, the best-fit solutions have been allowed to occur at the bounds of the parameters g and kℓ. Clearly, acceptable fits could be obtained with less forward scattering double H-G phase functions (i.e., smaller g-values) and longer mean free path lengths. Figure 9 shows the best-fit single-scattering phase function among the models utilized and its variation envelope corresponding to the aforedescribed χ2 analysis.
There is qualitative agreement between the chosen double H-G function and the numerical light-scattering computations for wavelength-scale Gaussian random particles with the discrete-dipole approximation (Muinonen et al. 2007) as well as agglomerated debris particles (Zubko et al. 2006). In these cases, the phase functions show smooth increase of intensity towards the backward-scattering direction.
Note that the present H-G solution (Fig. 9) resembles the phase function for solar-system particles in Bowell et al. (1989, their Fig. 1). The phase functions from different sources should, however, be compared with caution as their interpretation can significantly differ. We stress that more detailed modeling including polarization is to be carried out in the future using the methods described in Muinonen et al. (2010), Muinonen (2004), and Boehnhardt et al. (2004).
5. Conclusions
Based on the present theoretical modeling of the lunar photometry from SMART-1 AMIE, we conclude that most of the lunar mare opposition effect is caused by coherent backscattering within ~100-μm volume elements comparable to lunar particle sizes, with only a small contribution from shadowing effects. We suggest that the lunar fundamental scatterers exhibit increase in scattered intensity towards the forward direction as well as the backward direction. These characteristics resemble those experimentally measured and theoretically computed for realistic single small particles in free space. Further interpretation for the phase functions of lunar mare volume elements and fundamental scatterers is beyond the scope of the present study.
We find that it is possible to derive information about submicron-to-micron-scale surface properties based on multiangular imaging of the target areas. We put forward a novel method where the stochastic surface geometry is derived from the imaging data, whereafter the reduced data allow the derivation of information on the small-scale physical properties. The present modeling paves the way to quantitative interpretation of the polarization ratios experimentally measured for lunar samples by Hapke et al. (1993). More generally, the modeling can be considered as a beginning of a synoptic approach to explaining all observational and experimental data on scattering by the lunar regolith.
The Moon has been imaged by AMIE onboard SMART-1 with three color filters in addition to the panchromatic channel. A global disk-resolved multi-filter study similar to the one reported in Hillier et al. (1999) for Clementine images is possible and will remain as a topic for future studies. Note that Mare Serenitatis (area 4 in Fig. 1) is one of the Lunar International Calibration Targets (L-ISCT) proposed by Pieters et al. (2008).
Further theoretical and numerical development of the present methods can result in application to other lunar regions observed by various missions. In the recent years, the Moon has been studied by four space missions in addition to SMART-1, namely Kaguya (Selene), Chandrayaan 1, Chang’e 1, and the currently operating Lunar Reconnaissance Orbiter and Chang’e 2. They have extensively mapped the lunar surface with various resolutions in UV/Vis wavelengths. As the calibrated photometric data from these missions is becoming available, applying the present theoretical modelling to the combined data from all possible lunar missions to obtain global disk-resolved analyses of single-scattering phase functions and stochastic surface geometry is emerging as an attractive opportunity.
Acknowledgments
It is a pleasure to thank Kari Lumme, Jukka Piironen, Jani Tyynelä, Tatjana Tchumatchenko, Yurij Shkuratov, Dmitrij Stankevich, Evgenij Zubko, and Olli Wilkman for helping us to interpret the SMART-1 AMIE observations of the Moon. We would like to thank Bruce Hapke for providing critical reviews on the present work. The research has been supported, in part, by the Academy of Finland, and in France by the French Space Agency CNES and PNP (Programme National de Planétologie). Patria Advanced Solutions contributed significantly to the Science Validation of the Flight Model AMIE Camera. The ESA SMART-1 project and operations teams, and the STOC team are also acknowledged.
References
- Boehnhardt, H., Bagnulo, S., Muinonen, K., et al. 2004, A&A, 415, L21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bowell, E. L. G., Hapke, B., Domingue, D., et al. 1989, in Asteroids II, ed. R. P. Binzel, T. Gehrels, & M. Matthews (Tucson: University of Arizona Press), 524 [Google Scholar]
- Foing, B. H., Racca, G. D., & Marini, A., et al. 2006, Adv. Space Res., 1, 6 [NASA ADS] [CrossRef] [Google Scholar]
- Grieger, B. 2008, ESA Technical Note, S1-AMIE-SGS-TN-013 [Google Scholar]
- Hapke, B. 1984, Icarus, 59, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Hapke, B. 1990, Icarus, 88, 407 [NASA ADS] [CrossRef] [Google Scholar]
- Hapke, B., & van Horn, H. 1963, J. Geophys. Res., 68, 4545 [NASA ADS] [CrossRef] [Google Scholar]
- Hapke, B. W., Nelson, R. M., & Smythe, W. D. 1993, Science, 260, 509 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Hillier, J. K., Buratti, B. J., & Hill, K. 1999, Icarus, 141, 205 [NASA ADS] [CrossRef] [Google Scholar]
- Jehl, A., Pinet, P., Baratoux, D., et al. 2008, Icarus, 197, 403 [NASA ADS] [CrossRef] [Google Scholar]
- Josset, J.-L., Beauvivre, S., Cerroni, P., et al. 2006, Adv. Space Res., 1, 14 [NASA ADS] [CrossRef] [Google Scholar]
- Kaydash, V., Kreslavsky, M., Shkuratov, Y. G., et al. 2008, Lunar and Planetary Science XXXIX [Google Scholar]
- Kaydash, V., Kreslavsky, M., Shkuratov, Y., et al. 2009, Icarus, 202, 393 [NASA ADS] [CrossRef] [Google Scholar]
- Lumme, K., & Bowell, E. 1981, AJ, 86, 1694 [NASA ADS] [CrossRef] [Google Scholar]
- Lumme, K., & Irvine, W. M. 1982, AJ, 87, 1076 [NASA ADS] [CrossRef] [Google Scholar]
- Lumme, K., Peltoniemi, J. I., & Irvine, W. M. 1990, Transp. Theory Stat. Phys., 19, 317 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Mishchenko, M. I., & Dlugach, J. M. 1992, Astrophys. Space Sci., 189, 151 [NASA ADS] [CrossRef] [Google Scholar]
- Mishchenko, M. I., & Dlugach, J. M. 1993, Planet. Space Sci., 41, 173 [NASA ADS] [CrossRef] [Google Scholar]
- Muinonen, K. 1990, Ph.D. Thesis, University of Helsinki [Google Scholar]
- Muinonen, K. 2004, Waves in Random Media, 14, 365 [NASA ADS] [CrossRef] [Google Scholar]
- Muinonen, K., & Zubko, E. 2010, in Electromagnetic and Light Scattering XII, ed. K. Muinonen, A. Penttilä, H. Lindqvist, T. Nousiainen, & G. Videen (Helsinki: University of Helsinki), Conf. Proc., 194 [Google Scholar]
- Muinonen, K., Stankevich, D., Shkuratov, Y., Kaasalainen, S., & Piironen, J. 2001, J. Quant. Spec. Radiat. Transf., 70, 787 [NASA ADS] [CrossRef] [Google Scholar]
- Muinonen, K., Shkuratov, Y., Ovcharenko, A., et al. 2002, Planet. Space Sci., 50, 1339 [NASA ADS] [CrossRef] [Google Scholar]
- Muinonen, K., Zubko, E., Tyynelä, J., Shkuratov, Y., & Videen, G. 2007, J. Quant. Spec. Radiat. Transf., 106, 360 [NASA ADS] [CrossRef] [Google Scholar]
- Muinonen, K., Tyynelä, J., Zubko, E., & Videen, G. 2010, Light Scatt. Rev., 5, 477 [CrossRef] [Google Scholar]
- Munoz, O., Volten, H., Hovenier, J., et al. 2007, J. Geophys. Res., 112, [Google Scholar]
- Parviainen, H., & Muinonen, K. 2007, J. Quant. Spec. Radiat. Transf., 106, 398 [NASA ADS] [CrossRef] [Google Scholar]
- Parviainen, H., & Muinonen, K. 2009, J. Quant. Spec. Radiat. Transf., 110, 1418 [NASA ADS] [CrossRef] [Google Scholar]
- Peitgen, H., & Saupe, D. (eds.) 1988, The science of fractal images (New York: Springer-Verlag) [Google Scholar]
- Peltoniemi, J. I. 1993, J. Quant. Spec. Radiat. Transf., 50, 655 [NASA ADS] [CrossRef] [Google Scholar]
- Pieters, C. M., Head, J. W., Isaacson, P., et al. 2008, Adv. Space Res., 2, 248 [NASA ADS] [CrossRef] [Google Scholar]
- Piironen, J., Muinonen, K., Nousiainen, T., et al. 1998, Planet. Space Sci., 46, 937 [NASA ADS] [CrossRef] [Google Scholar]
- Pinet, P., Cerroni, P., Josset, J., et al. 2005, Planet. Space Sci., 53, 1309 [NASA ADS] [CrossRef] [Google Scholar]
- Racca, G. D., Marini, A., & Stagnaro, L., et al. 2002, Planet. Space Sci., 1323 [Google Scholar]
- Rougier, A. 1933, Ann. Obs. Strasbourg, 205 [Google Scholar]
- Shepard, M. K., & Campbell, B. A. 1998, Icarus, 134, 279 [NASA ADS] [CrossRef] [Google Scholar]
- Shkuratov, I. G. 1988, Kinematika i Fizika Nebesnykh Tel, 4, 60 [NASA ADS] [Google Scholar]
- Shkuratov, Y. G., Kreslavsky, M. A., Ovcharenko, A. A., et al. 1999, Icarus, 141, 132 [NASA ADS] [CrossRef] [Google Scholar]
- Shkuratov, Y. G., Stankevich, D. G., Petrov, D. V., et al. 2005, Icarus, 173, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Stankevich, D., Shkuratov, Y. G., & Muinonen, K. 1999, J. Quant. Spec. Radiat. Transf., 63, 445 [Google Scholar]
- Storn, R., & Price, K. 1997, J. Glob. Optim., 11, 341 [Google Scholar]
- Zubko, E., Shkuratov, Y., Muinonen, K., & Videen, G. 2006, J. Quant. Spec. Radiat. Transf., 100, 489 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Best-fit particle-surface phase functions P∂V(θ) modeled as double Henyey-Greenstein phase functions (H-G) for media with fractional-Brownian-motion surface roughness.
All Figures
 |
Fig. 1 The lunar regions observed by AMIE onboard ESA SMART-1 (Advanced Moon micro-Imager Experiment) and analyzed in the present study overlaid on the Clementine albedo map: 1) Oceanus Procellarum, around Reiner Gamma; 2) Oceanus Procellarum, between Mons Rümker and the Mairan crater; 3) Mare Imbrium, north of Copernicus crater; and 4) Mare Serenitatis. |
| In the text | |
 |
Fig. 2 The multiangular photometry reduced from the lunar mare regions depicted in Fig. 1 as a function of the phase angle α. The opposition effect shows up as abrupt nonlinear brightening towards opposition. The viewing geometries of the AMIE lunar images are also depicted. Each geometry is fixed by three angles, for example, the angles of incidence and emergence (ι and ϵ) and the azimuth angle φ (that can be replaced by α). |
| In the text | |
 |
Fig. 3 Porous random medium of spherical particles with fractional-Brownian-motion boundary surface: Hurst exponent H = 0.4, standard deviation of heights σ = 0.06, and volume density v = 0.35. |
| In the text | |
 |
Fig. 4 The multiangular AMIE photometry of the mare regions fitted using the fBm-particulate-medium model with H = 0.80, σ = 0.05, and v = 0.30, and a double Henyey-Greenstein particle-surface phase function with w∂V = 0.001432, g1, ∂V = −0.9228, and g2, ∂V = −0.0546 (uppermost points). Also shown are the residuals shifted downward by 0.2 vertical units for clarity (lowermost points). See Table 1. |
| In the text | |
 |
Fig. 5 The lunar mare volume-element phase function PV (see Eqs. (2) and (5)). The phase function follows from dividing more than 12 000 SMART-1 AMIE original data points by best-fit model S(μ,μ0,φ)/(μ + μ0) in Eq. (2). |
| In the text | |
 |
Fig. 6 The lunar mare volume-element phase function of Fig. 5 averaged using bin size of 0.5°. We show the best-fit volume-element scattering phase function PV (solid line). For the largest phase angles, there is a deviation that is probably due to the incapability of the present model volume-element phase function to fit the observations and to increasing real brightness variegation or correlated observational errors. |
| In the text | |
 |
Fig. 7 The binned lunar mare volume-element phase function with the corresponding coherent-backscattering modeling including a variation envelope. Double H-G single-scattering phase functions for the fundamental scatterers give rise to coherent-backscattering peaks capable of matching the observations. For the largest phase angles, there is a deviation between the model and the observations potentially due to simplified modeling. |
| In the text | |
 |
Fig. 8 As in Fig. 7 for the phase-angle range of 0° ≤ α ≤ 30°. |
| In the text | |
 |
Fig. 9 Lunar mare single-scattering phase function P0 of the fundamental scatterers (see Eq. (4)) expressed as a double H-G function with a variation envelope. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


