| Issue |
A&A
Volume 531, July 2011
|
|
|---|---|---|
| Article Number | A91 | |
| Number of page(s) | 17 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201016006 | |
| Published online | 20 June 2011 | |
Cosmic ray modulation by solar wind disturbances⋆
Hvar Observatory, Faculty of Geodesy,
Kačićeva 26,
10000
Zagreb,
Croatia
e-mail: m.dumbovic@geof.hr
Received: 26 October 2010
Accepted: 30 March 2011
Aims. We perform a systematic statistical study of the relationship between characteristics of solar wind disturbances, caused by interplanetary coronal mass ejections and corotating interaction regions, and properties of Forbush decreases (FDs). Since the mechanism of FDs is still being researched, this analysis should provide a firm empirical basis for physical interpretations of the FD phenomenon.
Methods. The analysis is based on the ground-based neutron monitor data and the solar wind data recorded by the Advanced Composition Explorer, where the disturbances were identified as increases in proton speed, magnetic field, and magnetic field fluctuations. We focus on the relative timing of FDs, as well as on the correlations between various FD and solar wind parameters, paying special attention to the statistical significance of the results.
Results. It was found that the onset, the minimum, and the end of FDs are delayed after the onset, the maximum, and the end of the magnetic field enhancement. The t-test shows that at the 95% significance level the average lags have to be longer than 3, 7, and 26 h, respectively. FD magnitude (| FD|) is correlated with the magnetic field strength (B), magnetic field fluctuations (δB), and speed (v), as well as with combined parameters, BtB, Bv, vtB, and BvtB, where tB is the duration of the magnetic field disturbance. In the |FD|(B) dependence, a “branching” effect was observed, i.e., two different trends exist. The analysis of the FD duration and recovery period reveals a correlation with the duration of the magnetic field enhancement. The strongest correlations are obtained for the dependence on combined solar wind parameters of the product of the FD duration and magnitude, implying that combined parameters are in fact true variables themselves, rather than just a product of variables.
Conclusions. From the time lags we estimate that “the penetration depth” in the disturbance, at which FD onset becomes recognizable, is on the order of 100 Larmor radii and is comparable to a typical shock-sheath dimension. The results for the FD time profile indicate “shadow effect” of the solar wind disturbance before and after it passes the observer. The importance of reduced parallel diffusion during the passage of the disturbance is discussed, along with the influence of terrestrial effects on the observed “branching effect”.
Key words: Sun: coronal mass ejections (CMEs) / solar-terrestrial relations / cosmic rays
Appendices A–C are available in electronic form at http://www.aanda.org
© ESO, 2011
1. Introduction
Sudden short-term decreases in the cosmic ray (CR) count rate, which have typical durations of a few days and a magnitude distinctly larger than the daily CR count rate variations, were reported for the first time by Scott E. Forbush (Forbush 1937) and are nowadays referred to as Forbush decreases (FDs). The term itself is somewhat ambiguous, since there is no consensus for whether the term should be used only for nonrecurrent, short-term decreases, caused by interplanetary coronal mass ejections (ICMEs), or for all short-term decreases, including the recurrent ones, caused by corotating interaction regions (CIRs) (see, e.g., Cane 2000; Belov et al. 2001). In this paper both types are regarded as FDs, regardless of the type of the disturbance causing it (ICME, CIR, or an ICME/CIR combination).
The recurrent FDs, caused by CIRs start gradually and are symmetric in shape (Cane 2000; Belov et al. 2001). The recurrence of these CR depressions is related to the origin of a solar wind disturbance that causes them, since CIR is generated by the interaction of a high-speed solar wind stream, originating in coronal holes, with the slow solar wind. This interaction results in a compressed, heated plasma region with enhanced magnetic field intensity and fluctuations. The boundary region, called stream interface, is characterized by increases in the solar wind speed and proton temperature, along with a decrease in plasma density (see e.g. Burlaga et al. 1984; Richardson et al. 1996; Richardson 2004, and references therein). Typical magnitude of FDs caused by CIRs are 0.5–2% (Čalogović et al. 2009) and have been found to be correlated with both speed (Richardson et al. 1996; Čalogović et al. 2009) and magnetic field strength and solar wind density (Čalogović et al. 2009). The commencement of the CR decrease is associated with the leading edge of the stream, while the minimum is generally found in the vicinity of the maximum in solar wind speed (Richardson et al. 1996).
ICMEs, which are the interplanetary counterparts of coronal mass ejections (CMEs), cause non-recurrent decreases, which have a sudden onset, a short decrease period, and then a much slower recovery. Many are preceded by a precursory increase, but this increase can be (and often is) masked by the increased anisotropies observed near the onset and later in FD (Lockwood 1971; Cane 2000). Since ICMEs are related to CMEs, they are composed of the material coming from the Sun, and they have distinctly different characteristics from the background solar wind (SW), e.g., density, temperature, magnetic field intensity and fluctuations (see Gopalswamy 2006, and references therein). The ICME-related FDs show a variety of shapes and sizes. According to Cane (Cane et al. 1996; Cane 2000), their properties can be related to the characteristics and origin of the associated CMEs on the Sun and could be divided into three types: ejecta with preceding shock, ejecta-only, and shock-only. The so-called classical two-step FD is caused by ICME with preceding shock, with the first decrease occurring in the turbulent shock-sheath region and the second one in the ejecta. Most FDs greater than 4% are of this type (Cane et al. 1996). Shock is generated on its leading edge if ICME is propagating at supersonic speed. If not, only ejection is present and it causes a short-duration one-step decrease (Cane 2000). The ICME source region prescribes the direction of propagation, i.e., determines whether the ICME will reach the observer, pass it by, or hit it with its flank. If it hits with its flank, the observer will only see a shock. Generally, this happens for CMEs originating outside 50° of the Sun’s central meridian (Cane et al. 1996). Only very energetic CMEs can create shocks that are strong enough for the shock-only effect to be seen and are often accompanied by strong solar particle events (solar energetic particle, SEP).
The onset of ICME-caused FD is mostly regarded as simultaneous with the arrival of a shock (e.g. Cane et al. 1996). There are indications, though, that some FD onsets actually occur in the post-shock region (Lockwood et al. 1991) and some even before shock (Cane et al. 1996). The studies of FD recovery characteristics have also shown some conflicting results. It was found by Lockwood et al. (1986) that the characteristic recovery time was independent of rigidity and the magnitude of the decrease. They also found no dependence on the interplaneraty magnetic field (IMF) polarity state. A more recent study of recovery times made by Singh & Badruddin (2006) has shown that the recovery rate does in fact depend on the polarity state of IMF in a way that its faster during the A > 0 epoch than A < 0 epoch. The A > 0 polarity state refers to the state of the field being directed outward in the northern and inward in the southern magnetic hemisphere. As opposed to the previously mentioned findings of Lockwood et al. (1986), Jämsén et al. (2007) examined a larger energy scale of CRs and find characteristic recovery time in some events to be strongly dependent on the median energy of the detector, i.e. rigidity dependent. Studying magnetic clouds Badruddin et al. (1986) found that the duration of the decrease-phase (from FD onset to FD minimum value) does not depend on the duration of the cloud, but their results show a connection between the duration of the cloud and FD recovery time. A study made by Penna & Quillen (2005) shows an anti-correlation between ICME transit time between Sun and Earth and the recovery period, suggesting that slower traveling ICMEs cause longer recovery periods of FDs. These studies therefore indicate the relevance of the ICME size for the duration of the FD recovery phase.
Possible dependence of FD magnitude on some of the ICME parameters has also been studied. Badruddin et al. (1986) reported that a general dependence of FD on IMF and solar wind speed increase can be seen, with indications that an increased degree of turbulence could also be a significant factor. This was later confirmed in a superposed epoch analysis made by Badruddin (1996). Cane (1993) came to a similar conclusion while studying magnetic clouds. No attempts were made, however, to do a statistical analysis to find a correlation between FD magnitude and increase in magnetic field fluctuations. Searches for a positive correlation have mostly focused on magnetic field and speed enhancement. A study by Cane et al. (1996) showed a positive correlation between FD magnitude and ICME shock transit speed, but since for any particular speed there was a broad range of FD magnitudes, shock transit speed was declared to be a poor predictor of FD magnitude. On the other hand, Chilingarian & Bostanjyan (2010) find that FD magnitudes correlate well with speeds and sizes of ICMEs. They also find that correlation between magnetic field enhancement and FD magnitude becomes stronger when events followed by strong geomagnetic storms are excluded.
Although there are a number of papers that cover the relationship between FDs and SW disturbances, the majority of them treat CIRs and ICMEs separately. Since both can be regarded as propagating disturbed conditions in solar wind, we consider that an analysis joining both phenomena could reveal some useful information about the FDs caused by SW disturbances in general. The results would then be applicable to all types of disturbances, in spite of their differences. Such a study was reported by Belov et al. (2001), but they only regarded the FD magnitude; i.e., they did not consider the FD time characteristics. Hereinafter, we present an extensive analysis of FD timing, magnitude, and time profile. We focus on systematically quantifying the relationships between FDs and SW disturbances to provide a complete and firm empirical background for physical interpretations of the FD phenomenon. In a subsequent paper we will analyze separately different types of disturbances, i.e. ICMEs and CIRs, with the distinction between those associated with shock and those not associated with it. In this paper we do that only for the relative timing of FDs.
2. Data and method
The neutron monitor (NM) data was taken from SPIDR website (http://spidr.ngdc.noaa.gov/spidr/). The hourly averaged count rates from 7 NM stations, corrected for atmospheric pressure, were used. The chosen NM stations have similar rigidities, but are located at different longitudes, i.e., have different longitudes of asymptotic arrival directions. The locations and cutoff rigidities for the employed stations are given in Appendix A.
We inspected 20-day intervals around the events from the list of identified CME-ICME pairs prepared by Schwenn et al. (2005) and the SOTERIA-WP4 case-study list (http://soteria-space.eu/doc/reports/SOTERIA_D4_1.pdf). A total of 26 intervals were selected in a period around maximum of 23rd solar cycle, between 1998 and 2005. In that way the possible influence of the solar magnetic field polarity reversal (i.e., the difference in the IMF polarity state between two consecutive solar cycle minima) on the recovery phase of FDs was avoided (Singh & Badruddin 2006). To eliminate daily variations, count rates of three to four stations of different asymptotic-arrival longitudes were averaged. Then, the mean count rate for the first four days of a given 20-day interval was found, to determine count rates relative to this unperturbed mean level. The time intervals were chosen in such a manner that first four days show no recognizable FDs. Similar rigidities were used to avoid the rigidity dependence of FD magnitude (Lockwood 1971) and recovery (Jämsén et al. 2007). The largest difference in cutoff rigidities between two stations used in the same data preparation is 1.6 GV (Irkutsk3 and Magadan; see Appendix A). The power-law rigidity dependence of the FD magnitude (P−γ,0.4 < γ < 1.2; see Cane 2000) can lead to the FD magnitude difference of 0.6 – 0.8%, which is somewhat lower than the daily variations. Since NM stations have different asymptotic arrival directions, and different onset times of FDs are expected (see e.g. Cane 2000; Lockwood 1971). The differences in onset times between the stations for our data sets were found not to exceed 0.2 days, consequently leading to an error of 0.1 day, since an average over the employed stations was used. This has been taken as the accuracy of timing in both cosmic ray (CR) and solar wind (SW) measurements.
The SW and IMF data were taken from the Solar Wind Electron, Proton, and Alpha Monitor (SWEPAM; McComas et al. 1998) and the magnetometer instrument (MAG; Smith et al. 1998) onboard the Advanced Composition Explorer (ACE; Stone et al. 1998). The SWEPAM measures the solar wind plasma electron and ion fluxes as functions of direction and energy, which provides detailed knowledge of the solar wind conditions. For our purpose we used level-2 data (http://www.srl.caltech.edu/ACE/) of 1-h averages of the proton density n [cm3], proton temperature T [K], proton speed (SW bulk speed) v [km s-1], the IMF strength B [nT], and the IMF fluctuations δB [nT]. The last is the RMS variation in the magnetic field vector, 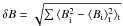 , where 16-s averages are used over the summation interval of one hour. For a typical quiet-condition solar wind (v = 400 km s-1), the interval of 16 s corresponds to the spatial scale of 0.64 × 106 km, which is comparable to the Larmor radius of 0.1 GeV CR.
, where 16-s averages are used over the summation interval of one hour. For a typical quiet-condition solar wind (v = 400 km s-1), the interval of 16 s corresponds to the spatial scale of 0.64 × 106 km, which is comparable to the Larmor radius of 0.1 GeV CR.
In the 26 chosen periods, SW disturbances were identified as increases in SW speed, IMF strength, and the magnetic field fluctuations. The SW density and temperature data were considered, too, mostly to determine the type of the SW disturbance (ICME, CIR, or mixed events; see Burlaga et al. 1984; Richardson et al. 1996; Cane 2000; Richardson 2004). To reduce the role of subjectiveness, the identification of SW disturbances and measurements of their characteristic were performed separately by M.D. and B.V., providing two independent data sets (hereinafter denoted as measurements I and II, respectively). The two samples consist of 56 and 66 events, respectively (see Appendix B), and according to the t-test, the two samples show no statistically significant difference. A more detailed statistical analysis of the two samples is given in Appendix C.
Figure 1 shows the time curves of the CR count and SW parameters for one of the events from the sample. Basic FD parameters that we measure and use are the relative FD magnitude and three specific time points: the onset, the time of minimum count rate, and the end point of FD. The FD magnitude is defined as the amplitude of the CR count depression, |FD|, measured relative to the CR count rate at the FD onset, i.e. the beginning of the decrease in the CR count (Fig. 1). If a pre-increase was present, the magnitude was set relative to the value of CR count before the pre-increase. The end of FD should be, by definition, the time at which the CR count returns to the pre-decreased value, as shown in Fig. 1. However, not all FDs have such a well-defined shape, and in many cases it is difficult, or even impossible, to determine these three specific time points. Especially problematic is the end point, since many FDs do not recover fully at all or show the over-recovery effect. This also affects the estimate of the total duration of FD (Fig. 1) and timing relative to SW disturbance.
Given the intrinsic noise in FD time profiles, a maximal and a minimal value of |FD| were determined, also providing an estimate of the error of measurement (Fig. 2). The same procedure was applied in estimating the relative speed, vrel, the absolute speed, vmax, the magnetic field amplitude, B, and the increase in the magnetic field fluctuations, δB (Fig. 2).
 |
Fig. 1 ICME that occurred 24.09.1998. Predecrese level is marked by a dashed line in the CR count curve, defining the onset and the end point of FD. Along with the minimum of the CR count, these time points are used to obtain the recovery time (trec) and the duration of FD (tFD = tfall + trec), where tfall is the time interval between the onset and the minimum and trec is the time interval between the minimum and the end point. Similarly, dashed lines given as the pre-increase and post-increase levels in magnetic field strength data are used to define the onset (entry into ICME) and the end point (exit from ICME), that give the decay (tdec) and the duration (tB = trise + tdec) of the SW disturbance, trise and tdec representing the time intervals between the onset and the maximum, and the maximum and the end point, respectively. |
 |
Fig. 2 ICME-CIR event that occurred on 12 October 2000. A two-step FD is caused by a shock-related ICME. However, the increased speed after the ICME is due to CIR, which is confirmed by the proton density and temperature data (not shown). Dashed vertical line marks the shock, which is practically simultaneous with the FD onset. The method of estimating the relative maximal and minimal amplitude (MAX and MIN, respectively) and duration (tFD and tB) is sketched for FD and solar wind disturbance. |
3. Results
3.1. Timing
First we analyze the timing of FDs relative to the solar wind disturbances. In particular, we consider the time difference of the FD beginning and the onset of the interplanetary magnetic field (IMF) increase, dTb, the delay of FD minimum after the IMF maximum, dTm, and the delay of the end of the FD recovery after the end of the IMF disturbance, dTe. Furthermore, the data was treated separately for ICMEs, CIRs, and mixed events, and separately for events with a shock and without it.
The mean values of time lags and the corresponding standard deviations are given in Table 1a. The one-sample t-test at a 0.05 significance level was applied to check if the mean value is significantly different from zero (Table 1b). Finally, since we obtained different values for CIR/ICME/mixed events and shock/no-shock events, a two-sample t-test at a 0.05 level was performed for all dataset pairs to check that there is a statistically significant difference between them (Table 1c). The data is listed for measurements I and II separately.
By inspecting Table 1b we see that all listed delays have 95% statistical significance, except dTe for CIRs in measurements II and dTm for mixed events in measurements I. Since in both cases two independent measurements disagree with each other, we find these results inconclusive.
Our results show that generally there is a delay of FD onset after the arrival of the SW disturbance (dTb > 0), in contrast to the result obtained by Cane et al. (1996). The average time delay is 5 and 6 h for measurements I and II, respectively, but there are substantial case-to-case differences, leading to a large standard deviation. The t-test shows that at 95% significance level the mean value of dTb is longer than 3 h for measurements I, and 5 h for measurements II. In both samples five events had a negative dTb delay, out of which only one was common to both measurements (a shock related ICME, which occurred 5 May 1999). The longest negative delay (12 h) was found in measurement II for CIR of 23 January 2001. We note that events with negative delay, i.e., with FDs preceding the disturbance, have already been reported (Cane et al. 1996). The measured FD magnitude and magnetic field enhancement for the events with dTb < 0 are both below average (average FD being 4% and B 15 nT). There were 12 events showing dTb ~ 0, out of which only four were common to both measurements I and II. The longest observed delay in measurements I is 19 h found in two events, one for CIR that occurred on 16 April 2000 and another for the shock-ICME-CIR event that occurred on 6 November 2001. In measurements II the largest delay (34 h) was found for CIR that arrived on 24 November 2001. It should be noted that in both samples, the majority of events had a positive dTb delay (82% in measurements I and 84% in measurements II), clearly showing that in the majority of cases the disturbance onset precedes the onset of FD.
List of delays and their significance.
We also found statistically significant time lags for dTm and dTe, with the average dTm being two times, and dTe four times longer than dTb. The case-to-case differences are also substantial, resulting in a large standard deviation, and 6–7% of the events in the two samples show a negative dTm delay. However, all measured negative dTm delays in both samples are related to positive dTb delays. Some differences in the delay estimates between the two sets of measurements are again present, owing to the noise in time profiles of both CR count and SW characteristics. The longest observed delays dTm are present in the events where ICME was preceded by a shock. These are a 43-h delay for the event that occurred 15 August 1999 (measurements I) and a 60-h delay that occurred 27 November 2000 (measurements II). 89% of events show a positive dTm in the first sample and 86% in the second one. The mean value equals to 11 and 12 h for measurements I and II, respectively, and the t-test shows that at 95% significance level the mean time difference is longer than 7 and 10 h, respectively. Thus, we conclude that the minimum of CR generally lags behind the maximum of IMF increase.
The delays dTe are related to the recovery period of FD. We note that differences in the dTe estimates for the two sets of measurements are larger than in case of dTb and dTm delays. A negative delay was observed in 13% of the events in measurements II and only in one event in measurements I (2%). Thus, in some cases FDs apparently end before, or close to, the end of the SW disturbance. However, it should be noted that many of these events were interrupted by a new FD event, so measured values of some delays might be ambiguous. Nevertheless, looking at the whole sample, information about general characteristics can be obtained. The majority show positive delays, which is 85% for measurements I and 78% for measurements II, with the mean delay of 34 h and 40 h, respectively. The t-test shows that at 95% significance level the mean value of dTe in the two measurements is longer than 26 and 30 h, respectively, so we conclude that at least a one-day delay can be expected in general. The largest observed delays of this type were observed for the same event in both sets of measurements. This was a shock-preceded ICME that occurred on 19 September 2000. The measured dTe for this event was 146 h (measurements I) and 132 h (measurements II).
Inspecting Table 1a, one finds some differences between delays of CIR and ICME events and also between shock and no-shock events. The statistical-significance t-test was applied and the results are shown in Table 1c. The following pairs were tested: shock and no-shock events, CIR and ICME events, ICME and mixed ICME-CIR events, CIR and mixed ICME-CIR events. For all pairs it has been shown that there are no differences in the dTm at 95% significance level, indicating that a similar dTm should be expected for all SW disturbances. This indicates that generally both ICME- and CIR-related FD minima occur after the maximum of the magnetic field maximum.
We also find no difference in the dTb delay between mixed events and ICME events and also mixed events and CIR events. However, tests show that there is a difference in dTb for CIRs and ICMEs, with CIRs having a longer delay. The results for dTb in the case of events with and without shock are inconclusive since measurements I and measurements II disagree. However, we note that results indicate that delays might be somewhat longer for no-shock events, as concluded by Badruddin et al. (1986). There seems to be no difference in dTe delays between shock/no-shock events, CIR/ICME events, and ICME/mixed events, since the outcome is inconclusive, while CIRs seem to have a shorter dTe delays than mixed events.
From the presented analysis it can be concluded that reliable information can only be obtained for the complete sample, but separating the data to various subsamples mostly leads to inconclusive results. This is most likely related to statistically-insufficient number of events in subsamples.
Finally, one might argue that the delays might be because the CR measurements are performed on Earth, while SW observations are made at the ACE satellite, i.e., 1.5 million kilometers closer to the Sun. However, a simple estimate shows that these measurements can be regarded as approximately simultaneous. Even for an SW disturbance speed as low as 400 km s-1, the time difference would be ~1 h, which is smaller than the measurement precision (0.1 days ≈2 h). For the average speed of ~630 km s-1 the time difference is 0.7 h, whereas for the highest measured speed (~1000 km s-1) less than 0.5 h. There are no ACE SW speed data for the most violent events, where even higher values of speed are expected; however, we find for the 2003 October 29 event in Chilingarian & Bostanjyan (2010) a value for speed ~1900 km s-1, giving the time difference between Earth and ACE of 0.2 h. This is one order of magnitude less than the measurement precision of 0.1 days. Thus, when considering average delays presented in Table 1a, this effect can be neglected, since it is already embedded in the standard deviations. However, this is only valid for statistical analysis, whereas in case studies this effect has to be taken into account, especially for slower SW disturbances.
3.2. FD magnitude
 |
Fig. 3 Dependence of |FD| on the solar wind parameters: a) the magnetic field amplitude, b) enhancement of the magnetic field fluctuations, c) the velocity amplitude. Only measurement II data are shown. The least-squares fit is presented by a solid line (r represents the correlation coefficient) and the upper-limit by a dashed line; for δB we also estimated the upper limit in the form of the square-root function (dotted). |
We examined the relationship between FD magnitude, |FD|, and several SW parameters: IMF amplitude (B), IMF fluctuations enhancement (δB), and the solar wind speed (both absolute, vmax, and amplitude, vrel). A linear regression analysis was performed by applying t-tests for the slope and the y-axis intercept. The results are presented in first three rows of Table 2, separately for both sets of measurements. Table 2 reveals a strong correlation for all the listed variables, with very high statistical significance for the slope (very low value of p(a)). Also, it can be deduced from Table 2 that in most cases the y-axis intercept does not differ from zero significantly.
Figure 3 shows dependence of FD magnitude on the magnetic field amplitude, enhancement of IMF fluctuations and relative SW speed. The dependence of |FD| on the magnetic field enhancement B is shown in Fig. 3a. We can see that for higher values of B, the data start to split into two branches almost symmetrically around the regression line. Similar behavior was noticed for ICMEs by Chilingarian & Bostanjyan (2010), whereas data presented by Lockwood et al. (1991) also indicate such a trend. Chilingarian & Bostanjyan (2010) obtained a much better correlation when they excluded FDs accompanied by strong geomagnetic storms, which eliminated one of the two “branches”.
The data points creating the effect of “branching” in Fig. 3a are related to the events that occurred 2003 October 29 and 2005 January 17 (upper-branch data), and 2001 November 06, 2001 November 24, and 2000 July 15 (lower-branch data). All of these are related to the shock-preceded disturbances, four of them being ICMEs and one (06 November 2001) being a mixed ICME-CIR event. This mixed SW disturbance had extremely strong magnetic field enhancement, more than three times more than the observed average. The largest observed FD is, however, not caused by this event, but by the event with largest magnetic field fluctuations (2003 October 29), thus indicating that fluctuations might be the most important factor in the short-term CR modulation. The FD magnitude for this event is approximately 5 times larger than the observed average. The corresponding magnetic field enhancement is over the average, but is almost 2 times less than the largest observed magnetic field enhancement. There were no ACE data for the speed, but we can find the same event in a paper by Chilingarian & Bostanjyan (2010), where they observed a corresponding maximum speed of around 1900 km s-1, thus a very jutted data point. This is probably why they obtained a very strong correlation between FD magnitude and ICME speed (r = 0.87). Our results for |FD|(v) dependence are more in agreement with the results obtained by Cane et al. (1996) for shock related ICMEs. Though a significant positive correlation coefficient is found, there is a span of |FD| values at a given v (Fig. 3c). We emphasize that the highest correlation coefficient was obtained for magnetic field fluctuations δB in measurement I. This agrees with results reported by Badruddin (1996), where fluctuations were found to play a significant role in CR modulation. However, it should be noted that the linear regression in this case is strongly influenced by an outlier, the event that occurred on 29 October 2003. When the analysis is performed without this event, somewhat smaller correlation coefficients are obtained (0.61 and 0.66 in measurements I and II). These values are very similar to those obtained for the magnetic field strength (Table 2). We also found a strong correlation between magnetic field strength and fluctuations for SW disturbances (r = 0.76 and r = 0.83 for measurements I and II, respectively). Thus, we conclude that both B and δB strongly influence |FD|.
Correlation of |FD| and different solar wind parameters.
Error bars shown in Fig. 3 are generally related to the noise in the time curves used to estimate the considered parameters. They are defined as difference between maximum and minimum estimates of the amplitude (see Fig. 2) The majority of |FD| relative errors are less than 25%. However, the largest relative errors for B are due to the presence of shock; i.e., they appear in the events where the shock/sheath region shows a sharp peak of B that is much higher than B in the ICME body itself. For instance, the largest relative error (49%) was measured for the shock-related ICME that occurred on 4 May 1998. The peak of IMF in the shock/sheath region is 2 times higher than the peak within the ejection itself. It is interesting to notice that large relative errors for B do not necessarily correspond to large relative errors for δB.
The data points in Figs. 3 are constrained to a triangular area, so we estimated an upper-limit line on |FD| values. The estimated upper limit can be expressed as |FD| = 0.5 × B, meaning that for, e.g., an increase in IMF of 20 nT, one should expect a maximum FD of ~10%. Similarly, we estimated the boundary line for the SW speed increase, |FD| = 0.035 × v, predicting a maximal depression of ~7% for the speed increase of 200 kms-1. For the magnetic field fluctuations we find |FD| = 6 × δB, but here we also present another option, 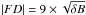 (Fig. 3b). For a fluctuation increase of 1 nT and 4 nT, a square-root curve predicts a maximum depression of 9% and 18%, respectively, while a straight line predicts a maximum depression of 6% and 24%.
(Fig. 3b). For a fluctuation increase of 1 nT and 4 nT, a square-root curve predicts a maximum depression of 9% and 18%, respectively, while a straight line predicts a maximum depression of 6% and 24%.
3.3. FD duration
 |
Fig. 4 Time characteristics of FD vs. solar wind disturbance parameters: a) FD duration vs. disturbance duration, b) FD recovery period vs. disturbance duration, c) FD duration vs. the product BtB, d) FD recovery period vs. the product BtB. The data is taken from the measurement II data set. tFD, tB, and tFD,rec are given in hours (h), BtB is given in nT × h. |
We estimated the duration of FD, tFD, the duration of the magnetic field disturbance, tB, the duration of the FD recovery, trec, and the duration of B decay, tdec (defined in Sect. 2), in order to explore the time profiles of both Forbush decreases and solar wind disturbances and a possible connection between the two. In some studies (e.g. Lockwood et al. 1986; Jämsén et al. 2007), a characteristic time constant for the recovery was employed, since it was found that the recovery phase of FD could be fitted by an exponential curve (see e.g. Lockwood 1971; Cane 2000, and references therein). This method has certain advantages when studying the FD recovery, because of difficulties arising in determining the recovery period, where the recovery is often interrupted by another event or masked by the noise. However, if one wishes to explore and compare time profiles of FDs with morphologically different shapes (and not only the asymmetric ones caused by ICMEs), difficulties arise when an exponential fit is employed.
The duration of the recovery was measured both directly and via exponential fit in measurements I, whereas only direct estimates were employed in measurements II. The exponential fit of the form I = I0e−t/t0 was used (see Lockwood 1971, and references therein), where I0 denotes the amplitude of the decrease, t the relative time expressed in days, and t0 is the characteristic recovery time. In our dataset the exponential fit was found to be inadequate for about 40% of events, mostly due to interrupted recovery (whether by a solar energetic particle event or another decrease), inappropriate shape of FD, or lack of data. In these cases, only the directly measured recovery time was used in the analysis. We note that in measurements II much stronger criteria were imposed in determining tFD and tFD,rec, but the outcome is basically the same (the only difference arises from an outlier present in measurements II as described in Appendix C).
First we examine the correlation of tFD and tFD,rec with the amplitude of B. As can be seen in the first rows of Tables 3a and b, a positive correlation was found, implying that the disturbances with stronger fields cause longer recoveries. Comparing these results with those from Sect. 3.2, where a correlation was found between the magnetic field increase and FD magnitude, one could guess that FD magnitude and recovery time might also be correlated. This is not the case, since no significant correlation between the two has been found, which agrees with the results obtained by Lockwood et al. (1986).
In the next step we studied whether the FD duration and the recovery phase depend on the duration of the SW disturbance, tB. A positive correlation was found in both cases (see Figs. 4a and b, as well as the second rows of Table 3a and b), implying that disturbances that take longer to pass over the Earth cause FDs of longer recoveries, hence longer total duration. The relationship of the recovery time and the SW disturbance duration was also found by Badruddin et al. (1986), but with fewer data and without statistical analysis. The correlation coefficient is somewhat lower in measurements I than in measurements II (see Table 3a), primarily due to an outlier present in measurement II (the event of 8 June 2000). Regardless of the outlier, a significant positive correlation was found between tFD and tB (for details see Appendix C), though the data scatter is substantial, presumably due to the inaccuracy of the duration estimates. This indicates that the FD time profile is influenced by the propagation characteristics and the size of SW disturbances. Since the SW disturbance duration is influenced by a number of factors, e.g., speed, size, and direction of the propagation, it cannot be decided whether the FD recovery is modulated by one of these parameters or by a combination of several effects.
Inspecting the data, we find that the longest FD duration does not necessarily coincide with either the strongest field or with the longest disturbance duration. In measurements I the longest FD duration is observed for the shock-related ICME of average speed and duration that occurred on 17 September 2000. The magnetic field and fluctuations for this event are two times greater than the observed average, as is the corresponding FD magnitude. In measurement II data, the longest FD was caused by a shock-associated ICME on 8 June 2000, which had an average magnetic field enhancement, fluctuations, and speed, while FD was slightly above average.
We also inspected the correlation between the characteristic recovery time t0 obtained by the exponential fit and different SW disturbance (B, tB) and FD (tFD, tFD,rec) parameters. No significant correlation was found. The characteristic recovery time ranges from 0.5 to 8 days, with an average value of ~3.5 days, which is somewhat less than the values obtained by (Lockwood et al. 1986). In our opinion these results reflect that an exponential fit is not really appropriate for our analysis, which includes FDs of various morphological forms and not only simple “text-book” events.
3.4. Combined SW parameters and total CR deficit
 |
Fig. 5 The product of the FD magnitude and duration vs. products of different solar wind parameters. a) magnetic field enhancement and disturbance duration, BtB; b) magnetic field fluctuations and disturbance duration, δBtB; c) magnetic field enhancement, speed and disturbance duration, BvmaxtB; d) magnetic field enhancement and speed, Bvmax. The data is taken from the measurement I data set. |FD|tFD is expressed as % × h, BtB and δBtB are given in nT × h, BvmaxtB in nT × km s-1 × h and Bvmax in nT × km s-1. |
Belov et al. (2001) reveals that the correlation between FD magnitude and the product of the magnetic field enhancement and the SW speed increase is better than correlations for the two SW parameters treated separately. Therefore, we analyzed correlations of FD characteristics and various products of solar wind parameters (BtB, Bv, BvtB, and vtB, where v denotes maximum speed for measurements I and relative speed for measurements II) to find out which of these products is the most relevant one. The product vtB can be regarded as a proxy for the size of the passing disturbance (or to be more specific, the part of it that passes over the Earth). The product BtB can be regarded as a measure of the total “strength” of the disturbance, since it is a proxy for the time integral of the IMF perturbation. The Bv product is actually a proxy for maximum (convective) electric field and can be also regarded as the unit-width magnetic flux that passes over the observer in unit time. The product BvtB is related to the magnetic flux (per unit-width of the disturbance cross-section) associated with the passing perturbation; i.e., it can be considered as the disturbance-related unit-width magnetic flux that has passed over the observer. We also inspected the relationship of the product |FD|tFD with different parameters of SW disturbance, since it is a measure of the total amount of CRs reduced by the passage of the disturbance.
Correlation between different solar wind parameters and a) FD duration, tFD, b) FD recovery, tFD,rec.
Correlation between different combined solar wind parameters and a product of FD magnitude and duration, |FD|tFD.
The results for FD magnitude and combined parameters are given in the last four rows of Table 2. A positive correlation coefficient was found for all the products with a very high statistical significance. Comparison of the results with those obtained by Belov et al. (2001) shows several similarities, particularly in the correlation of |FD| with B, v, and the product Bv. Although we got a somewhat higher correlation coefficient for v than Belov et al. (2001), the Bv product still correlates better than the B and v separately in measurements I.
The relationship of the FD duration, tFD with SW parameter products was also analyzed. Analogously, an analysis was performed for the recovery periods (tFD,rec). The results of the linear regression analysis (the slope and the y-axis intercept) are shown in the last four rows of Table 3a and b. A positive correlation was found in all cases, especially between the recovery time of FD and the BtB product. The dependencies of the FD duration and the recovery period on the product BtB are shown in Figs. 4c and d.
Finally, we analyzed the product of the FD magnitude and the FD duration. The results of the linear regression analysis are shown in Table 4 for different products of solar wind disturbance parameters. Again, t-test for the slope and the y-axis intercept was applied. Inspecting Table 4, one finds that there is a strong correlation for all analyzed products. The regression lines for the data of measurements I are shown in Fig. 5. We can see that the largest total CR deficit, |FD|tFD, which was caused by the shock-related ICME that started on 11 April 2001, corresponds to the highest values of δBtB and BvtB. The values of Bv and BtB for this event are not the highest ones, although they are higher than the average.
Comparing the results displayed in Table 4 with the results presented in Tables 2 and 3, one can see that the product |FD|tFD has a higher correlation coefficient than |FD| and tFD separately. Since correlations between the total CR deficit, |FD|tFD, and various products of the disturbance parameters are generally better than for the parameters taken separately, it can be concluded that the products themselves behave as variables, rather than just being products of independent variables.
4. Discussion
The statistical analysis of the relationship between SW disturbances and FDs revealed that the average lag of the FD onset after the SW disturbance arrival is longer than three hours. Similarly, the average lag of the FD minimum after magnetic field maximum is longer than seven hours. These delays cannot be attributed to the time differences in measurements on the Earth and ACE, or errors of measurements. Thus, our result opposes some previous studies that showed no delay (e.g. Cane et al. 1996).
The length scale L associated with the FD-onset delay can be estimated by multiplying a typical SW disturbance speed, ⟨ vmax ⟩ , and time lag of FDs start after the SW disturbance arrival, ⟨ dtb ⟩ , i.e., L = ⟨ vmax ⟩ ⟨ dtb ⟩ , which gives a value on the order of 1010 m. This is much greater than the Larmor radius for typical conditions (protons with energies E ~ 1 GeV in the magnetic field of ⟨ Bmax ⟩ ~ 20 nT), which can be estimated to E/ce ⟨ Bmax ⟩ ~ 108 m. This implies that the observer has to be well inside the disturbance before starting to experience the CR decrease. In other words, the arrival of the SW disturbance does not immediately initiate the depletion of CRs, as proposed in some studies (e.g., Barnden 1973).
Apparently, there is a critical depth at which the observer starts to experience the CR decrease, which is on the order of 100 Larmor radii. On the other hand, it should be noted that L is comparable to a typical shock-sheath thickness (e.g., Russell & Mulligan 2002). In this respect, we note that no statistically significant correlation was found between L and magnetic field strength or fluctuations. That the FD minimum is delayed after the magnetic field maximum shows that in the majority of events the “shielding” is actually most effective once the peak of magnetic field strength has already passed over the observer.
In some events negative delays were observed; that is, FDs started before the arrival of the disturbance. This can be explained in the same way as Lockwood et al. (1986) explained the recovery phase of FDs. They reasoned that after the disturbance passes, it still “casts a shadow” upon the region of depressed CR area, with the shadow effect weakening as the disturbance “decays”, while propagating away from the observer. This shadow casting could therefore be a relevant factor even before the disturbance reaches the observer, but only in cases when a large portion of the neighboring space (i.e., large solid angle) is covered by the disturbance. Such conditions are met when the disturbance hits the observer by its flank (see Fig. 6-right). The shadow effect is less efficient for disturbances coming frontally (see Fig. 6-left). Furthermore, the occurrence of pre-increase in some FDs, caused by CRs that are reflected towards the observer by the magnetic mirror effect, can mask this effect in the frontal impact.
There are indications that the “shadow effect” might be related to the shape of FD. None of the five events showing negative delays were classical two-step FDs, but rather had a gradual decrease. This might be because the disturbance “casts” even larger “shadows” while approaching the observer. This agrees with observations of symmetric, CIR-like FDs, produced by ICMEs hitting with the flank, where the observer only intercepts shock without ejecta (Cane 2000).
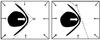 |
Fig. 6 The “shadow effect” of the disturbance before it reaches the observer for the disturbance coming frontally (left) and the disturbance hitting with a flank (right). ICME associated with shock is taken as an example. White arrow marks the direction of propagation, black arrows represent CRs and the observer is marked by × . Dashed lines mark the solid angle covered by the disturbance. |
Regression analysis showed high correlation between the depression amplitude and the increase of the magnetic field and its fluctuations. Therefore, it can be concluded that the timing of FD onset, minimum, and end point is governed by the geometry and propagation characteristics of the disturbance, while depression amplitudes are mainly determined by the increases in the magnetic field strength and turbulence. This is in accordance with the axially symmetric time dependent model proposed by Le Roux & Potgieter (1991) and also the propagating diffusion barrier presented by Wibberenz et al. (1998). These two models point out that the amplitude of the depression is influenced by the local modulation conditions (e.g. undisturbed speed and diffusion coefficient) and characteristics of the disturbance (dimension, amplitude). Furthermore, Le Roux & Potgieter (1991) note that the recovery of FD is not influenced by the local parameters, but by the evolution of the disturbance, as described by the “shadow effect” scenario. Although a correlation with the disturbance speed was found too, the large scatter of the data implies that increased speed is not as important as increases in magnetic field strength and fluctuations. A similar result is obtained by Cane et al. (1996) for ICMEs and by Čalogović et al. (2009) for CIRs, while Richardson et al. (1996) find somewhat different behavior for CIRs. The separate study of the two types of the disturbances will be given in a subsequent paper (in preparation). The results for |FD|(v) presented in Fig. 3c and third row of Table 2 are quantitatively in good agreement with simulations made by Wawrzynczak & Alania (2010), where a similar increase in FD magnitude with SW speed is expected (see Fig. 5 of Wawrzynczak & Alania 2010).
The transport equation of cosmic rays in the heliosphere proposed by Parker (1965) includes contributions from four basic physical effects – diffusion, drifts, convection, and energy change. Our results indicate that the last two effects, related to the SW speed, are not crucial factors for FDs, which does not mean, however, that they do not contribute to a certain degree. The two remaining mechanisms, depletion of CRs due to increased magnetic field, which leads to reduced curvature and gradient drifts, and exclusion due to enhanced fluctuations, which reduces the diffusion mean free path, seem to be more important. We emphasize particularily the results for magnetic field fluctuations, showing the importance of the magnetic field turbulence in short-term CR modulation (e.g. Badruddin 1996) through reduced parallel diffusion coefficient (see e.g. Wibberenz et al. 1998). This agrees with simulations of both short-term and long-term CR modulations depending on the level of magnetic field fluctuations (see e.g. Alania & Wawrzynczak 2008; Alania et al. 2010b,a; Wawrzynczak & Alania 2010).
On the other hand, we note that the influence of the increased magnetic field is not simple. The “branching” present in Fig. 3a might not be related to the mechanisms by which the disturbance reduces the CR flux, but can be a consequence of some other effects, e.g., of terrestrial origin. As mentioned in Sect. 3.2, Chilingarian & Bostanjyan (2010) find a similar data structure for ICMEs and relate it to reduced cutoff rigidity during strong geomagnetic storms, but this was not confirmed by statistical analysis. Whether this branching effect is a consequence of terrestrial effects or some modulation differences in different FDs still needs to be clarified.
The analysis of the FD duration revealed its relation with the duration of the magnetic field disturbance. Furthermore, a large portion of the recovery phase was found to last long after the return of the magnetic field strength to the pre-increase level, indicating that the “shielding” effect is present even after the disturbance has passed the observer, gradually weakening as the disturbance propagates away. This agrees with the “shadow-effect” scenario proposed by Lockwood et al. (1986) and considered within the model of Le Roux & Potgieter (1991). As previously noted, this is related to the geometry of the disturbance. Penna & Quillen (2005) come to a similar conclusion after studying ICME transit times between the Sun and Earth. They also point out that FD recovery time (and therefore FD duration) are not expected to depend on the width of the disturbance or magnetic field amplitude (see Penna & Quillen 2005, and references therein). We however find evidence for the opposite. The duration and recovery period of FDs were found to be correlated with both magnetic field strength and a proxy of the size of the disturbance (vtB), though in a smaller degree than the duration of the disturbance itself. The duration of FDs was found to be longer for the disturbances of larger sizes associated with stronger fields.
Since correlations between SW disturbance parameters and FD magnitudes and also between duration of FDs and SW disturbances were found, it is not surprising that the products of the two were also found to correlate. It is to a certain degree surprising, however, that the correlation of these combined parameters is stronger than for involved parameters separately. This suggests that the products themselves behave as variables, not merely as products of variables, as pointed out in Sect. 3.4. They can be regarded as proxies of time integrals of the physical quantities involved. Therefore, it follows from our statistical analysis that the total CR deficit during the Forbush decrease (| FD|tFD) strongly depends on the “strength” of magnetic field disturbance (BtB). The same conclusions can be drawn for fluctuations (δBtB) and the unit-width magnetic flux (BvtB). The analysis of the “time-integral” of the FD variation indicates that different mechanisms may contribute even to total CR deficit, but their relative contribution to CR depletion might be different in different stages of the passing of the disturbance, as was noted in some studies regarding classical two-step Forbush decreases produced by ICMEs associated with shocks (see Wibberenz et al. 1998).
5. Summary
We summarize the main results of our analysis as follows.
-
In the majority of events the depletion starts when the observer is already engulfed in the disturbance, at a depth that is on the order of 100 Larmor radii and comparable to a typical shock-sheath length. However, depending on the direction of propagation of the disturbance, the observer might experience the “shadow effect” before the arrival of the disturbance.
-
The amplitudes of the CR depression are primarily influenced by the increase in magnetic field strength and fluctuations, which are associated with solar wind disturbances. The latter confirms the hypothesis that relates Forbush decreases with reduced parallel diffusion. The influence of the increased magnetic field was found to be rather complex. There are indications that this might be a consequence of terrestrial effects, but this has yet to be confirmed.
-
The recovery period can be explained by the “shadow effect” of the disturbance: as it propagates away from the observer, its effect on incoming CRs gradually weakens. The recovery phase also depends on the magnetic field strength and size of the disturbance.
-
The best correlations were obtained for combined SW disturbance and FD parameters. Thus, they should be treated as the relevant physical quantities, rather than just a product of physical variables.
Online material
Appendix A: Neutron monitor stations
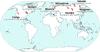 |
Fig. A.1 Stations that provided the neutron monitor data. Cutoff rigidity (Rc), latitude, and longitude are written under the name of the station. |
A grid of ground level cosmic ray detectors, located in a number of stations around the globe, including both high-energy muon detectors and lower energy neutron monitors, cover different geographic latitudes and longitudes. This is important for cosmic ray research owing to the interaction of cosmic rays (i.e. protons, which make up 90% of the incoming cosmic rays) with geomagnetic field. The effects of this interaction is given through vertical geomagnetic cutoff rigidity, i.e. the lowest, latitude-dependent rigidity, associated with a particle penetrating the Earth‘s magnetic field (particles of lower rigidity do not enter the atmosphere). Rigidity (R = pc/|q|,where p and q are particle impulse and charge, and c is speed of light) is dependent on both particle energy and the magnetic field in question, representing the influence of the magnetic field on the trajectory of the particle. Thus, a particle of the energy of 1 GeV will be detected near the pole, where the cutoff rigidity is very low, but not near the equator, where only high-energy particles can penetrate the geomagnetic field deep enough for the secondaries to reach the detector. Consequently, this will influence the CR flux, as detected by the ground-based monitors, since the flux will evidently be larger at higher latitudes (i.e. for smaller cutoff rigidities). Figure A.1 shows the location of neutron monitor stations used in our research, along with the associated cutoff rigidity.
Appendix B: List of events
Notes on Tables B.1 and B.2: The event date was determined by the onset of Forbush decrease. Dashes stand for missing data, whereas question marks are attributed to measurements that are unclear. Events associated with shock are denoted with “Y”, those not associated with shock are denoted N. The phenomenon where CR count in the recovery phase of Forbush decrease reaches higher values than the ones in the pre-decrease phase is referred to as over-recovery. It was determined only in measurements I and categorized as follows:
-
“N” – events that show no over-recovery and are not interrupted by another event;
-
“N*” – events that show no over-recovery, but are interrupted by another event;
-
“Y*” – events that show over-recovery, but start in the recovery phase of another event;
-
“Y” – events that show over-recovery and do not start in the recovery phase of another event.
Measurements I.
Measurements II.
Appendix C: Random sample analysis
In order to also check the reliability of the analysis performed by two independent people, denoted as measurements I and II, random subsamples of events from both measurements were generated. Each subsample consisted of 50 events, where one half was taken randomly from measurement I and another half from measurement II. The correlation coefficient was then calculated for each random subsample, and the procedure was repeated one million times. This provided the distribution of correlation coefficients as shown in Fig. C.1. This also allowed identifying outliers, as they led to a double-peaked distribution, as can be seen in the δB(| FD|) and tFD(tB) data in Figs. C.2 and C.3.
The median values of the distributions of correlation coefficients shown in Fig. C.1 correspond approximately to values obtained by the linear regression analysis of measurements I and II (see Tables 2 and 4 in Sects. 3.2 and 3.4). The situation is somewhat different for the examples in Figs. C.2a and C.3a due to double-peaked distributions. Removal of the outliers (29 october 2003 and 8 June 2000 in Figs. C.2b and C.3b, respectively) results in a quite regular distribution (see Figs. C.2b and C.3b), characterized by somewhat smaller median of correlation coefficients, which match the values obtained by the linear regression analysis of measurements I and II, when the outliers are removed (r = 0.61 for δB(|FD|) in measurements I, r = 0.66 for δB(| FD|) in measurements II and r = 0.54 for tFD(tB) in measurements II). It should be noted that the outlier in tFD(tB) data is only present in measurements II data and is therefore a source of the difference in the correlation coefficients for the two samples (see Table 3).
 |
Fig. C.1 Correlation histogram for a) FD magnitude, |FD|, versus IMF magnitude, B; b) |FD| versus solar wind speed, vrel; c) the product of the FD magnitude and duration, |FD|tFD, versus the product of the magnetic field enhancement and duration, BtB. The y-axis represents the number of correlations in specific correlation coefficient class (x-axis). Each histogram is based on one million calculated correlation coefficients. |
 |
Fig. C.2 Correlation histograms for FD duration, tFD, versus the disturbance duration, tB. a) All events used to generate the samples; b) the event identified as an outlier (29.10.2003.) was removed from the analysis. The y-axis represents the number of correlations in specific correlation coefficient class (x-axis). Each histogram is based on one million calculated correlation coefficients. |
 |
Fig. C.3 Correlation histograms for FD magnitude, |FD|, versus IMF fluctuations enhancement, δB. a) All events used to generate the samples; b) event identified as an outlier (08.06.2000.) was removed from the analysis. The y-axis represents the number of correlations in specific correlation coefficient class (x-axis). Each histogram is based on one million calculated correlation coefficients. |
Acknowledgments
We are grateful to the referee, Dr. Bernd Heber, whose comments and suggestions led to a substantial improvement in the paper. The research leading to these results has received funding from the European Commission’s Seventh Framework Programs (FP7/2007-2013) under the grant agreement No. 218816 (SOTERIA project, www.soteria-space.eu).
References
- Alania, M. V., & Wawrzynczak, A. 2008, Astrophys. Space Sci. Trans., 4, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Alania, M. V., Iskra, K., & Siluszyk, M. 2010a, Adv. Space Res., 45, 1203 [NASA ADS] [CrossRef] [Google Scholar]
- Alania, M. V., Modzelewska, R., & Wawrzynczak, A. 2010b, Adv. Space Res., 45, 421 [NASA ADS] [CrossRef] [Google Scholar]
- Badruddin 1996, Ap&SS, 246, 171 [NASA ADS] [CrossRef] [Google Scholar]
- Badruddin, Yadav, R. S., & Yadav, N. R. 1986, Sol. Phys., 105, 413 [NASA ADS] [CrossRef] [Google Scholar]
- Barnden, L. R. 1973, in International Cosmic Ray Conference, 2, I, 1277 [Google Scholar]
- Belov, A. V., Eroshenko, E. A., Oleneva, V. A., Struminsky, A. B., & Yanke, V. G. 2001, Adv. Space Res., 27, 625 [NASA ADS] [CrossRef] [Google Scholar]
- Burlaga, L. F., McDonald, F. B., Ness, N. F., et al. 1984, J. Geophys. Res., 89, 6579 [NASA ADS] [CrossRef] [Google Scholar]
- Cane, H. V. 1993, J. Geophys. Res., 98, 3509 [NASA ADS] [CrossRef] [Google Scholar]
- Cane, H. V. 2000, Space Sci. Rev., 93, 55 [NASA ADS] [CrossRef] [Google Scholar]
- Cane, H. V., Richardson, I. G., & von Rosenvinge, T. T. 1996, J. Geophys. Res., 101, 21561 [NASA ADS] [CrossRef] [Google Scholar]
- Chilingarian, A., & Bostanjyan, N. 2010, Adv. Space Res., 45, 614 [NASA ADS] [CrossRef] [Google Scholar]
- Čalogović, J., Vršnak, B., Temmer, M., & Veronig, A. M. 2009, in IAU Symp., 257, I, ed. N. Gopalswamy, & D. F. Webb, 425 [Google Scholar]
- Forbush, S. E. 1937, Phys. Rev., 51, 1108 [NASA ADS] [CrossRef] [Google Scholar]
- Gopalswamy, N. 2006, Sun and Geosphere, 1, 020000 [Google Scholar]
- Jämsén, T., Usoskin, I. G., Räihä, T., Sarkamo, J., & Kovaltsov, G. A. 2007, Adv. Space Res., 40, 342 [NASA ADS] [CrossRef] [Google Scholar]
- Le Roux, J. A., & Potgieter, M. S. 1991, A&A, 243, 531 [NASA ADS] [Google Scholar]
- Lockwood, J. A. 1971, Space Sci. Rev., 12, 658 [NASA ADS] [CrossRef] [Google Scholar]
- Lockwood, J. A., Webber, W. R., & Jokipii, J. R. 1986, J. Geophys. Res., 91, 2851 [NASA ADS] [CrossRef] [Google Scholar]
- Lockwood, J. A., Webber, W. R., & Debrunner, H. 1991, J. Geophys. Res., 96, 11587 [NASA ADS] [CrossRef] [Google Scholar]
- McComas, D. J., Bame, S. J., Barker, P., et al. 1998, Space Sci. Rev., 86, 563 [NASA ADS] [CrossRef] [Google Scholar]
- Parker, E. N. 1965, Planet. Space Sci., 13, 9 [Google Scholar]
- Penna, R. F., & Quillen, A. C. 2005, J. Geophys. Res. (Space Phys.), 110, 9 [Google Scholar]
- Richardson, I. G. 2004, Space Sci. Rev., 111, 267 [NASA ADS] [CrossRef] [Google Scholar]
- Richardson, I. G., Wibberenz, G., & Cane, H. V. 1996, J. Geophys. Res., 101, 13483 [Google Scholar]
- Russell, C. T., & Mulligan, T. 2002, Planet. Space Sci., 50, 527 [NASA ADS] [CrossRef] [Google Scholar]
- Schwenn, R., dal Lago, A., Huttunen, E., & Gonzalez, W. D. 2005, ApJ, 23, 1033 [Google Scholar]
- Singh, Y. P., & Badruddin. 2006, Sol. Phys., 234, 339 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, C. W., L’Heureux, J., Ness, N. F., et al. 1998, Space Sci. Rev., 86, 613 [NASA ADS] [CrossRef] [Google Scholar]
- Stone, E. C., Frandsen, A. M., Mewaldt, R. A., et al. 1998, Space Sci. Rev., 86, 1 [Google Scholar]
- Wawrzynczak, A., & Alania, M. V. 2010, Adv. Space Res., 45, 622 [NASA ADS] [CrossRef] [Google Scholar]
- Wibberenz, G., Le Roux, J. A., Potgieter, M. S., & Bieber, J. W. 1998, Space Sci. Rev., 83, 309 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Correlation between different solar wind parameters and a) FD duration, tFD, b) FD recovery, tFD,rec.
Correlation between different combined solar wind parameters and a product of FD magnitude and duration, |FD|tFD.
All Figures
 |
Fig. 1 ICME that occurred 24.09.1998. Predecrese level is marked by a dashed line in the CR count curve, defining the onset and the end point of FD. Along with the minimum of the CR count, these time points are used to obtain the recovery time (trec) and the duration of FD (tFD = tfall + trec), where tfall is the time interval between the onset and the minimum and trec is the time interval between the minimum and the end point. Similarly, dashed lines given as the pre-increase and post-increase levels in magnetic field strength data are used to define the onset (entry into ICME) and the end point (exit from ICME), that give the decay (tdec) and the duration (tB = trise + tdec) of the SW disturbance, trise and tdec representing the time intervals between the onset and the maximum, and the maximum and the end point, respectively. |
| In the text | |
 |
Fig. 2 ICME-CIR event that occurred on 12 October 2000. A two-step FD is caused by a shock-related ICME. However, the increased speed after the ICME is due to CIR, which is confirmed by the proton density and temperature data (not shown). Dashed vertical line marks the shock, which is practically simultaneous with the FD onset. The method of estimating the relative maximal and minimal amplitude (MAX and MIN, respectively) and duration (tFD and tB) is sketched for FD and solar wind disturbance. |
| In the text | |
 |
Fig. 3 Dependence of |FD| on the solar wind parameters: a) the magnetic field amplitude, b) enhancement of the magnetic field fluctuations, c) the velocity amplitude. Only measurement II data are shown. The least-squares fit is presented by a solid line (r represents the correlation coefficient) and the upper-limit by a dashed line; for δB we also estimated the upper limit in the form of the square-root function (dotted). |
| In the text | |
 |
Fig. 4 Time characteristics of FD vs. solar wind disturbance parameters: a) FD duration vs. disturbance duration, b) FD recovery period vs. disturbance duration, c) FD duration vs. the product BtB, d) FD recovery period vs. the product BtB. The data is taken from the measurement II data set. tFD, tB, and tFD,rec are given in hours (h), BtB is given in nT × h. |
| In the text | |
 |
Fig. 5 The product of the FD magnitude and duration vs. products of different solar wind parameters. a) magnetic field enhancement and disturbance duration, BtB; b) magnetic field fluctuations and disturbance duration, δBtB; c) magnetic field enhancement, speed and disturbance duration, BvmaxtB; d) magnetic field enhancement and speed, Bvmax. The data is taken from the measurement I data set. |FD|tFD is expressed as % × h, BtB and δBtB are given in nT × h, BvmaxtB in nT × km s-1 × h and Bvmax in nT × km s-1. |
| In the text | |
 |
Fig. 6 The “shadow effect” of the disturbance before it reaches the observer for the disturbance coming frontally (left) and the disturbance hitting with a flank (right). ICME associated with shock is taken as an example. White arrow marks the direction of propagation, black arrows represent CRs and the observer is marked by × . Dashed lines mark the solid angle covered by the disturbance. |
| In the text | |
 |
Fig. A.1 Stations that provided the neutron monitor data. Cutoff rigidity (Rc), latitude, and longitude are written under the name of the station. |
| In the text | |
 |
Fig. C.1 Correlation histogram for a) FD magnitude, |FD|, versus IMF magnitude, B; b) |FD| versus solar wind speed, vrel; c) the product of the FD magnitude and duration, |FD|tFD, versus the product of the magnetic field enhancement and duration, BtB. The y-axis represents the number of correlations in specific correlation coefficient class (x-axis). Each histogram is based on one million calculated correlation coefficients. |
| In the text | |
 |
Fig. C.2 Correlation histograms for FD duration, tFD, versus the disturbance duration, tB. a) All events used to generate the samples; b) the event identified as an outlier (29.10.2003.) was removed from the analysis. The y-axis represents the number of correlations in specific correlation coefficient class (x-axis). Each histogram is based on one million calculated correlation coefficients. |
| In the text | |
 |
Fig. C.3 Correlation histograms for FD magnitude, |FD|, versus IMF fluctuations enhancement, δB. a) All events used to generate the samples; b) event identified as an outlier (08.06.2000.) was removed from the analysis. The y-axis represents the number of correlations in specific correlation coefficient class (x-axis). Each histogram is based on one million calculated correlation coefficients. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


