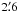| Issue |
A&A
Volume 529, May 2011
|
|
|---|---|---|
| Article Number | A94 | |
| Number of page(s) | 15 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201015393 | |
| Published online | 11 April 2011 | |
Magnetic fields in Local Group dwarf irregulars⋆
1
Obserwatorium Astronomiczne Uniwersytetu Jagiellońskiego, ul. Orla 171, 30-244 Kraków, Poland
e-mail: chris@oa.uj.edu.pl
2
Max-Planck-Institut für Radioastronomie, Auf dem Hügel 69, 53121 Bonn, Germany
3
Ruhr-Universität Bochum, Universitätsstrasse 150, 44780 Bochum, Germany
Received: 14 July 2010
Accepted: 24 January 2011
Aims. We wish to clarify whether strong magnetic fields can be effectively generated in typically low-mass dwarf galaxies and to assess the role of dwarf galaxies in the magnetization of the Universe.
Methods. We performed a search for radio emission and magnetic fields in an unbiased sample of 12 Local Group (LG) irregular and dwarf irregular galaxies with the 100-m Effelsberg telescope at 2.64 GHz. Three galaxies were detected. A higher frequency (4.85 GHz) was used to search for polarized emission in five dwarfs that are the most luminous ones in the infrared domain, of which three were detected.
Results. Magnetic fields in LG dwarfs are weak, with a mean value of the total field strength of <4.2 ± 1.8 μG, three times lower than in the normal spirals. The strongest field among all LG dwarfs of 10 μG (at 2.64 GHz) is observed in the starburst dwarf IC 10. The production of total magnetic fields in dwarf systems appears to be regulated mainly by the star-formation surface density (with the power-law exponent of 0.30 ± 0.04) or by the gas surface density (with the exponent 0.47 ± 0.09). In addition, we find systematically stronger fields in objects of higher global star-formation rate. The dwarf galaxies follow a similar far-infrared relationship (with a slope of 0.91 ± 0.08) to that determined for high surface brightness spiral galaxies. The magnetic field strength in dwarf galaxies does not correlate with their maximum rotational velocity, indicating that a small-scale rather than a large-scale dynamo process is responsible for producting magnetic fields in dwarfs. If magnetization of the Universe by galactic outflows is coeval with its metal enrichment, we show that more massive objects (such as Lyman break galaxies) can efficiently magnetize the intergalactic medium with a magnetic field strength of about 0.8 nG out to a distance of 160–530 kpc at redshifts 5–3, respectively. Magnetic fields that are several times weaker and shorter magnetization distances are expected for primordial dwarf galaxies. We also predict that most star-forming local dwarfs might have magnetized their surroundings up to a field strength about 0.1 μG within about a 5 kpc distance.
Conclusions. Strong magnetic fields (>6 μG) are observed only in dwarfs of extreme characteristics (e.g. NGC 4449, NGC 1569, and the LG dwarf IC 10). They are all starbursts and more evolved objects of statistically much higher metallicity and global star-formation rate than the majority of the LG dwarf population. Typical LG dwarfs are unsuitable objects for the efficient supply of magnetic fields to the intergalactic medium.
Key words: galaxies: evolution / galaxies: magnetic fields / galaxies: dwarf / galaxies: irregular / Local Group / radio continuum: galaxies
© ESO, 2011
1. Introduction
Dwarf galaxies are the most numerous population of galaxies in the Universe (Grebel 2001) and according to the hierarchical clustering scenario, they were the primary building blocks of more massive galaxies in the past. They play a key role in one of the most puzzling problems in the ΛCDM picture of galaxy formation, namely the “missing satellites problem” (e.g. Kravtsov 2010). Much effort has been made to understand the origin of star formation bursts, as well as the formation of filamentary structures in dwarfs (Hunter 2002; Hunter & Gallagher 1990). In contrarast to the massive spiral galaxies, the star formation activity in dwarfs occurs without any strong influence from density waves (Hunter et al. 1998) and usually develops stochastically.
Magnetic fields can bee especially important in these low-mass galaxies because of their lower gravitational potential and the greater ability of their gas to escape via galactic winds. These fields enable magnetic fields to be supplied to the intergalactic medium (IGM) at early cosmological epochs (Kronberg et al. 1999; Bertone et al. 2006). However, the generation of magnetic fields in dwarf galaxies by a classical large-scale dynamo can be inefficient because of the slow or chaotic rotation and hence low differential rotation of these galaxies (Chyży et al. 2003). Star formation activity would produce magnetic fields by generating a small-scale dynamo (Zeldovich et al. 1990), but the magnetic fields and star formation would then be related in a nonlinear way (Chyży 2008). Thus, it is unclear whether strong magnetic fields could be effectively generated in these low-mass galaxies and under stochastically generated star formation the large-scale structures of magnetic fields could be developed.
Surprisingly, very strong magnetic fields were discovered in the optically bright dwarf irregular galaxy NGC 4449, with the total field intensity of about 12 μG and a regular component of up to 8 μG (Chyży et al. 2000). Similar fields were detected in NGC 1569 (Kepley et al. 2010). Weaker total fields, in the range of 5−7 μG, were also observed in some other dwarfs as NGC 6822 (Chyży et al. 2003), IC 10 (Chyży et al. 2003), and the Large Magellanic Cloud (LMC: Gaensler et al. 2005). In the Small Magellanic Cloud (SMC), a weak total field of about 3 μG was found, partly on large-scales (Mao et al. 2008). Since all these galaxies are optically bright and nearby objects, the detection of magnetic fields in them may be influenced by strong selection effects. The question then arises of whether they represent a typical sample of dwarf galaxies and the typical conditions for dynamo processes to occur.
To date, there has been no systematic study of diffuse nonthermal radio emission and polarization in a uniformly selected sample of dwarf galaxies with diverse star formation activities, kinematics, masses, and gas contents. One ideal target for such an investigation is the Local Group (LG), which contains a mixture of small irregular and dwarf galaxies around two giant spirals. Many dwarfs in the Local Group are star-forming objects (Mateo 1998) with a wide range of star-forming activity (Hunter & Elmegreen 2004; Dolphin et al. 2005; Tolstoy et al. 2009). As a complete sample of local galaxies, LG dwarfs can be studied to provide reliable statistical insight into association of magnetic fields with other galactic properties. They also provide a unique opportunity to investigate the relationship between magnetic fields in dwarfs and those in larger stellar systems, giving valuable estimates of the efficiency of galactic dynamo processes working in low-mass objects.
In this paper, we report the results of a systematic attempt to detect diffuse radio emission and magnetic fields in LG irregular and dwarf irregular galaxies. This sensitive study was conducted with the 100-m Effelsberg radio telescope at 4.85 GHz and 2.64 GHz. In the next section, we describe the criteria used to build our sample of dwarf galaxies and in Sect. 3 provide details of the observations and data reduction process. The radio maps, derived radio emission fluxes, and estimates of magnetic field strengths are presented in Sect. 4. In Sect. 5 we investigate how magnetic fields might possibly be influenced by the global and local star formation rate, galactic mass, rotation, metallicity, and star formation history. We also investigate the possibility of the Universe being magnetized by outflows from dwarfs using our current knowledge on the IGM metal enrichment. We then discuss the prevalence of large-scale magnetic fields in dwarfs, and construct a radio-infrared diagram to check whether dwarfs deviate from the general correlation trend followed by optically bright spiral galaxies. We summarize our studies in Sect. 6.
2. The sample
Parameters of the radio observations of all galaxies studied at 2.64 GHz.
The Local Group consists of about 41 members, the most massive and optically bright of which are the three spiral systems the Milky Way, the M 31, and the small M 33. Less significant members include seven galaxies of irregular type (Irr), e.g., LMC, and 31 dwarfs. A subgroup of 14 dwarfs, called dwarf irregulars (dIrr), are low-mass objects (M ≤ 109 M⊙) but like irregulars are gas-rich and display evidence of current or recent star formation (Mateo 1998; Tolstoy et al. 2009). The remaining 31 dwarfs, known as dwarf ellipticals (dE) and dwarf spheroidals (dSph), are prime examples of gas-poor systems dominated by old stellar populations, that show no signs of current star formation. They are low-luminosity (MV ≥ −14 mag), strongly dark-matter dominated systems, with total masses of about 107 M⊙ (Strigari et al. 2008). Although dSphs experienced star formation over extended time intervals in their youth, today all of them but one appear to be completely free of detectable interstellar material (Grebel et al. 2003). A new population of ultrafaint dSphs (UF dSphs) with absolute magnitude MV ≥ −6 were observed by Martin et al. (2008). They are more metal-poor than dSphs, their more luminous counterparts. Ursa Minor and Draco are examples of these systems, whose stellar velocity dispersions are only a few kilometres per second, and whose total masses of less than 106 M⊙ are composed primarily of very old stars.
For our systematic search for radio emission and magnetic fields, only gas-rich systems that display evidence of star formation activity, hence irregular and dwarf irregular galaxies, are suitable. Following Mateo (1998), we do not distinguish between these two types of objects and call them hereafter dwarf irregular galaxies.
There are in total 12 LG dwarf irregular galaxies of declination larger than about −25°, and thus available for radio observations from the site of the 100-m Effelsberg telescope. The details of the sample are presented in Table 1. To detect their radio emission and achieve an adequate balance between resolution and sensitivity we used the 2.64 GHz (11 cm) receiver of the Effelsberg telescope. Using a relatively low frequency, we also minimized the contribution of radio thermal emission. At this frequency, the telescope beam size of 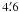 is still sufficient to probe the large-scale radio emission of LG dwarfs, which are often of large angular size (up to 19′; Table 1). Radio interferometers that could provide data of higher resolution are inappropriate for observations of these large and diffuse objects.
is still sufficient to probe the large-scale radio emission of LG dwarfs, which are often of large angular size (up to 19′; Table 1). Radio interferometers that could provide data of higher resolution are inappropriate for observations of these large and diffuse objects.
For a selected subgroup of 5 out of 12 dwarfs with a high star-formation rate (SFR) (see Table 3), we also attempted to investigate in addition radio polarized emission at 4.85 GHz (6.2 cm). We had observed three galaxies, NGC 6822, IC 10 (Chyży et al. 2003), and IC 1613 before with the Effelsberg telescope. For the remaining two galaxies, Sextans A and Sextans B, we carried out separate observations at 4.85 GHz.
3. Observations and data reduction
The Effelsberg observations were made in May 2007 (Table 2). The unbiased sample of 12 LG dwarfs were observed at 2.64 GHz using a single horn receiver. We scanned our objects alternatively along the RA and Dec directions. The subgroup of two galaxies mentioned above were additionally observed at 4.85 GHz using a two-horn (with horn separation of 8′) system in the secondary focus of the radio telescope (see Gioia et al. 1982). The coverages were obtained in this case in the azimuth-elevation frame. At both frequencies, the horns were equipped with two total-power receivers and an IF-polarimeter, resulting in four channels containing the Stokes parameters I (two channels), Q, and U. The telescope pointing was corrected by repeating cross-scans of a bright point source close to the observed galaxy at time intervals of about 1.5 h. The flux density scale was established by mapping the calibration sources 3C 138 and 3C 286. Table 2 presents the details of our observations at 2.64 GHz.
The data reduction was accomplished using the NOD2 data reduction package (Haslam 1974). At 2.64 GHz, the obtained coverages in I, Q, and U channels (from a single horn system) were combined using the spatial-frequency weighting method (Emerson & Gräve 1988), followed by a digital filtering process that removed the spatial frequencies corresponding to noisy structures smaller than the telescope beam.
At 4.85 GHz (dual system used), we combined the data from the two horns, using the “software beam switching” technique (Morsi & Reich 1986), followed by restoration of total intensity channel I (Emerson et al. 1979). We then combined I, Q, and U maps using the same procedure as for 2.64 GHz and obtained the final maps of total power, polarized intensity, polarization degree, and polarization position angles.
4. Results
4.1. Radio detections
Among the 12 observed LG dwarfs, we clearly detected extended radio emission at 2.64 GHz in three cases: IC 10, NGC 6822, and IC 1613. To estimate their radio fluxes reliably or their upper limits in cases of no detection the emission from confusing background sources had to be removed. For identification of background sources, we compared our radio maps with those of the Condon (1987), NVSS1, and FIRST2 surveys. We then applied the “subtraction” method (Chyży et al. 2003) and removed all confusing sources from the maps. For clear detections of dwarfs their total fluxes were obtained by integrating the signal in polygonal areas encompassing all visible radio emission. If there was no detection, we defined the upper limit of flux density as 1.5 times the rms noise level of the map multiplied by the number of beams covering the optical extent of a given galaxy. These estimates are presented in Table. 2. All the detected galaxies are presented below and in Figs. 1–5, which also show background sources. Polarized emission was detected in NGC 6822, IC 10 (Chyży et al. 2003), and IC 1613 (Figs. 4, 5) all at 4.85 GHz. To show the structure of the magnetic field projected on the sky plane, we used the apparent B-vectors defined as E-vectors rotated by 90°. Faraday rotation was expected to be small at 4.85 GHz.
IC 10. – The map of total intensity at 2.64 GHz (Fig. 1) clearly detects, slightly resolved, and elongated radio emission. It appears to be the strongest (250 mJy) source in our sample. The small extension to the west is caused by a weak (9 mJy) background source, also visible in the NVSS map at 1.4 GHz. The emission is fully compatible with the 10.45 GHz map of Chyży et al. (2003). The spectral index between both frequencies is about 0.35 ± 0.05, which is in good agreement with Klein & Gräve (1986). IC 10 is experiencing a massive starburst, apparently triggered by infalling H i gas from the southeast (Grebel 2004). The synchrotron emission detected in this portion of the galaxy indicates gas compression (Chyży et al. 2003). According to several authors (see Grebel 2004 and references therein), the properties of this galaxy suggest that it should be classified as a blue compact dwarf.
 |
Fig. 1 The total power map of IC 10 at 2.64 GHz overlaid onto the DSS blue image. The contours are at 3, 5, 8, 16, 25, 40 × 3.9 mJy/b.a. The map resolution is |
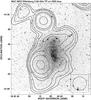 |
Fig. 2 The total power map of NGC 6822 at 2.64 GHz overlaid onto the DSS blue image. The contours are at 3, 5, 8, 15, 20, 40, 80 × 1.2 mJy/b.a. The map resolution is |
NGC 6822. – This galaxy has a three times lower total star formation rate (based on Hα observations) than IC 10 (Woo et al. 2008), but contains several well-defined supernovae remnants and star-forming clumps (Chyży et al. 2003; see also Table 3). Our radio map of the total intensity of NGC 6822 at 2.64 GHz (Fig. 2) shows significant radio emission from this galaxy mainly associated with distinct Hα regions. The emission peaks at the positions RA2000 = 19h45m40s, Dec2000 = −14°34′, RA = 19h45m10s, Dec = −14°37′, and RA = 19h45m15s, Dec = −14°52′ as well as the extension to the south are due to background sources. The overall distribution of radio emission corresponds well with our earlier observations at 4.85 GHz (Chyży et al. 2003).
IC 1613. – This galaxy seems to be a typical LSB Irr evolving slowly in isolation without large bursts of star formation during its entire lifetime (Skillman et al. 2003). The total power map at 2.64 GHz (Fig. 3) reveals radio emission mainly from areas associated with two distinct Hα regions. The emission peaks at RA = 01h04m50s, Dec = 02°04′ and RA = 01h04m25s, Dec = 02°12′ are strong background sources. The higher resolution map at 4.85 GHz (Fig. 4) confirms these findings, while revealing three more background sources (RA = 01h05m15s, Dec = 02°14′ and RA = 01h05m12s, Dec = 02°05′30″ with an extension towards RA = 01h04m55s, Dec = 02°04′ being a weak, though slightly polarized background source). The main radio emission from the galaxy comes from strong H ii regions, whereas the rest of the galaxy remains radio-quiet. The map of polarized intensity of IC 1613 (Fig. 5) shows only two faint patches of emission in the northeastern and southern outskirts of the galaxy. They are however most likely associated with the background sources mentioned above.
To summarize, only 3 out of 12 sources (25%) are detected at radio wavelengths. The failed attempts to detect dwarfs are not due to the lower sensitivity level of their respective radio maps, as illustrated in Fig. 6. They are simply intrinsically weaker than the detected objects. This is not quite an unexpected result as we analyse the volume complete sample of LG dIrrs, unaffected by any selection bias. Although 75% dwarfs from our complete sample are undetected, they still provide important information on the processes of magnetic field generation. By comparing the undetected and detected LG dwarfs and by relating them to other dwarfs observed so far (see Introduction), we can statistically infer which properties of the galaxies influence the radio emission and the generation of magnetic fields in dwarfs (see Sect. 5).
 |
Fig. 3 The total power map of IC 1613 at 2.64 GHz overlaid onto the DSS blue image. The contours are at 3, 5, 8, 20, 40 × 1.1 mJy/b.a. The map resolution is |
 |
Fig. 4 The total power map of IC 1613 at 4.85 GHz with apparent B-vectors of polarized intensity overlaid onto the DSS blue image. The contours are at 3, 5, 8, 12, 16, 25, 40, 100, 200 × 0.3 mJy/b.a., and a vector of 1′ length corresponds to the polarized intensity of 0.3 mJy/b.a. The map resolution is |
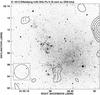 |
Fig. 5 The map of polarized intensity of IC 1613 at 4.85 GHz with apparent B-vectors of polarization degree overlaid onto the DSS blue image. The contours are at 3, 5, 8, 12, 16 × 0.05 mJy/b.a., and a vector of 1′ length corresponds to the polarization degree of 20%. The map resolution is |
 |
Fig. 6 Signal to rms noise level ratio versus the noise level for our maps of LG dwarfs and for maps of the Magellanic Clouds (Haynes et al. 1991) at 2.64 GHz. The undetected objects are marked. |
Magnetic field estimates and physical parameters for our sample of LG dwarfs and comparison dwarfs.
4.2. Magnetic field strengths
After determining the radio emission flux or at least its upper limit for all 12 LG dwarfs, we can calculate either the magnetic field strength or its upper limit, respectively. We derive the thermal contributions to the total radio fluxes mostly from Hα total fluxes. The classical model of H ii regions by Caplan & Deharveng (1986) provides an estimate of the radio thermal emission from Hα fluxes, which we apply to the data at 2.64 GHz. Extinction due to dust is low in these galaxies (Hunter & Elmegreen 2004), therefore Hα clearly traces the bulk of galactic star formation and can be used to estimate the SFRs from simple linear scaling (i.e. Kennicutt 1998). These SFRs taken from the available literature are given in Table 3. For Aquarius and LGS 3, which are undetected in Hα, the SFR and the expected radio thermal emission is derived from the infrared emission (Kennicutt 1998). The thermal radio fluxes are subtracted from the total radio fluxes (or their upper limits) to yield estimates of the synchrotron emission.
To compute the equipartition magnetic field strengths, we employed the formulae given by Beck & Krause (2005) (see Appendix for details). Since the presented calculations include the total magnetic field and its component perpendicular to the line of sight, as well as the pathlength through the medium, it is required to take into account the geometries of the investigated galaxies and the contribution to the total field of both regular and random components. As our aim is to search for the existence of magnetic fields and estimate their upper limits, it is enough to assume ellipsoidal geometries for the studied galaxies, using their minor axes as the synchrotron pathlength. To estimate the uncertainties in the estimated field strengths, we applied a variation in all assumed parameters of 50%. Similar estimates of the magnetic field strengths were obtained at 4.85 GHz for galaxies detected at this frequency. They give values within the uncertainty range of the strengths derived from the 2.64 GHz data.
For comparison, Table 3 also presents data for the LMC and SMC dIrrs, which are also LG members but are situated in the southern sky (thus not included in our unbiased LG sample). We also present data for NGC 1569 and NGC 4449, dIrrs not belonging to the LG but with significant magnetic fields. NGC 1569 is a nearby dwarf galaxy that experienced a very strong starburst more than about 4 million years ago and now displays outflows of hot metal-rich gas (Martin et al. 2002). NGC 4449 is an irregular starburst galaxy, which at optical wavelengths has properties similar to the Lyman-break galaxies (LBG) at high redshift (Annibali et al. 2008).
The mean equipartition magnetic field strengths for our sample of LG dwarfs is <4.2 ± 1.8 μG, including the upper limits of the field strength for the radio-undetected dwarfs at 2.64 GHz (Table 3). The typical magnetic fields in dwarfs are thus significantly weaker than in spiral galaxies, for which the mean field strength is about 10 μG (Beck 2005). In our LG sample, the strongest field is observed in the starburst dwarf IC 10 and its value of 9.7 μG is close to the that of starburst dIrrs (NGC 1569 and NGC 4449) from outside of the LG. Both Magellanic Clouds have magnetic fields close to the estimated mean value for our LG sample.
We also estimated the strength of the ordered magnetic field of the LG dwarfs for which polarized emission was detected at 4.85 GHz (4.5 ± 0.5, 5.1 ± 2.1, and 0.10 ± 0.04 mJy for IC 10, NGC 6822, and IC 1613, respectively). The strengths are in the range of 0.4 − 0.9 μG. The ordered-to-random field ratio of those galaxies is as large as about 0.2, which is similar to the averaged field order in spiral galaxies. For undetected dwarfs, we expect the production of an ordered field to be of the same efficiency or lower.
5. Discussion
As presented in Sect. 4.2, the magnetic fields in LG dwarfs are statistically almost three times weaker than in typical spiral galaxies of various kinds. To estimate the influence of the star formation rate and other galactic properties on the magnetic field production, we compiled various characteristics of our dwarfs available in the literature. Table 3 includes global SFRs, H i masses (MHI), infrared fluxes at 60 μm, and rotational velocities of all dIrrs in our sample. Knowing the global SFR, we calculated the SFR surface density (ΣSFR) using object sizes from Table 1. We obtained the gas surface density Σρ from the disk-averaged H i atomic gas. Since in dwarf galaxies, the molecular gas contributes to the total gaseous mass only up to a few percent for the most massive objects (see e.g. Braine et al. 2001), the atomic component closely represents the total gaseous mass of dwarfs.
Below, we analyse various correlations of magnetic field with other dwarf characteristics. For the sake of comparison we also analyse four other well-known irregular dwarfs: both of the Magellanic Clouds, NGC 1569, and NGC 4449.
 |
Fig. 7 Correlations of the magnetic field strength and SFR with other parameters. LG dwarfs from our sample, LMC, and SMC are marked by circles or in cases when the upper limit of the radio emission was applied – by triangles. Comparison dwarfs are marked by squares. The solid lines present power-law fits. Fits a and c are restricted to radio-detected dwarfs only (circles and squares). |
Correlation coefficients, their significance levels in percentages, and the number of dwarfs included in calculations.
5.1. Main factors regulating magnetic field
We determined mutual correlations between a range of parameters: magnetic field strength B, SFR, ΣSFR, MHI, Σρ, and the dwarf’s unprojected linear size L, taken as the source major axis from Table 1. Where possible, we included in the calculations all 16 dwarfs, including the comparison dwarfs. When searching for correlations with the magnetic field strength, we restricted our calculations to radio-detected dIrrs (seven objects). Owing to small number statistics, we chose to evaluate the Pearson correlation coefficient r and in each case performed a test of its statistical significance. We determined the significance level as the probability of rejecting a hypothesis that r = 0. Results are presented in Table 4. In a similar way, we also performed analogous calculations for the Kendal rank correlation coefficients. This approach led to the same following conclusions.
We found that among the various relations studied the magnetic field strength depends primarily on the density of the star formation rate ΣSFR having the largest correlation coefficient r = 0.94 (significant at the P = 0.2% level). This strong dependence can be intuitively understood because the local SFR determines the population of supernova explosions, which constitute the main source of the turbulent energy, which is in turn vital to the dynamo process (Arshakian et al. 2009, see also Sect. 5.4). This relation shown in Fig. 7a can be quantified by the power-law fit B ∝ ΣSFR0.30 ± 0.04. A similar nonlinear relation between total magnetic field strength and the global SFR has been observed for nearby spiral galaxies (Krause 2009) and fits to the equipartition model for the radio-FIR correlation (Niklas & Beck 1997). A strong influence of the local SFR on the (random) magnetic field has also been observed within the disk of a large spiral galaxy NGC 4254 (Chyży 2008).
The remaining group of radio-undetected dwarfs occupy a common region in the B − ΣSFR plane. If detected, they would possibly move down in this plane as their current positions represent only upper limits to the magnetic field strength. Therefore, the population of undetected dwarfs would likely fulfil the power-law determined for the radio-detected dwarfs alone. We give another argument for this prediction in Sect. 5.5. We also notice a gap in Fig. 7a between dwarfs of weak and strong magnetic fields. This may be evidence of a threshold in either the dynamo action producing magnetic fields, or the SFR above which (ΣSFR ≈ 10-2 M⊙ yr-1 kpc-2) the dynamo activity is enhanced.
The physical processes underlying both the star formation and magnetic fields in our sample of dwarfs are usually modelled by relating the surface density of galactic SFR (ΣSFR) to the gas surface density Σρ (Kennicutt 1998). The empirical fit to a power-law relation ΣSFR ∝ ΣρN with N ≈ 1.4 was found to provide an appropriate parametrization of these processes for different types of galaxies (Schmidt 1959). It follows that the gas density is a major factor influencing the star formation rate. We find that our dwarf galaxies also follow a similar power-law fit (Fig. 7a, Table 4) with a slope of N = 1.83 ± 0.30 and a correlation of r = 0.77 (which is significant at much less than the P = 1% level). The slope is somewhat steeper but agrees within its broad uncertainty limits with the aforementioned Schmidt law. The slightly steeper relation found for dwarfs, which are relatively low-mass objects, is also reasonable, as some star-formation thresholds in low-density (low-mass) galaxies are expected (Kennicutt 1998). It is also likely that the Schmidt law is a strong oversimplification as H i gas is only a weak tracer of star formation, and even CO gas has a too low excitation temperature to serve as a good star formation tracer. Hence, a significant fraction of the gas is unrelated to star formation, explaining the loose correlation shown in Fig. 7b.
The ΣSFR – Σρ relation observed for our dwarfs causes in turn a significant correlation for the gas density and the magnetic field strength (Table 4). Hence, in contrast to the B − ΣSFR relation, we can also describe the magnetic field in dwarfs as being controlled by the local gas density. For the radio-detected dwarfs, we obtained the relationship of B ∝ Σρ0.47 ± 0.09 with a correlation of r = + 0.78 (P = 4%). This relation is very close to that determined for spiral and irregular galaxies by Niklas & Beck (1997), who found an exponent of 0.48 ± 0.05.
It was shown that for a wide range of galaxies the far-infrared luminosity is a linear indicator of the SFR (Kennicutt 1998). Thus, to test this relation for dwarfs we can estimate ΣSFR for all investigated dwarfs independently of the Hα emission using the available infrared 60 μm fluxes (Table 3). After determining the dependence of gas density on star formation (exponent 1.83) and the relation of magnetic field to gas density (exponent 0.47), we can model the relation between magnetic field and the surface-normalized infrared luminosity of  . The observed relation for radio-detected dwarfs gives a power-law fit with the exponent of 0.25 ± 0.04 (correlation r = + 0.90, P = 0.5%), which is in a good agreement with the predicted one. We also found that this relation is compatible with the one determined for the ΣSFR estimated in a similar way from Hα emission (with the slope 0.30 ± 0.04). In summary, we can state that in dwarf galaxies the gas density regulates both the star-formation rate and the magnetic field production in a way similar to the spiral galaxies (Krause 2009) and the late-type galaxies (Chyży et al. 2007) studied so far.
. The observed relation for radio-detected dwarfs gives a power-law fit with the exponent of 0.25 ± 0.04 (correlation r = + 0.90, P = 0.5%), which is in a good agreement with the predicted one. We also found that this relation is compatible with the one determined for the ΣSFR estimated in a similar way from Hα emission (with the slope 0.30 ± 0.04). In summary, we can state that in dwarf galaxies the gas density regulates both the star-formation rate and the magnetic field production in a way similar to the spiral galaxies (Krause 2009) and the late-type galaxies (Chyży et al. 2007) studied so far.
We also found that the magnetic field is stronger in dIrrs of higher global SFR (Fig. 7c). This trend for the seven radio-detected dwarfs can be quantified by the relation B ∝ SFR0.25 ± 0.06 with the correlation coefficient of r = + 0.70 (P = 8%). A similar relation with an exponent of 0.34 ± 0.08 was fitted for the spiral galaxies by Niklas & Beck (1997), while Vallée (2004) obtained an exponent of 0.13 ± 0.04 for a different sample of nearby spirals. In our estimate, the exponent could be just a lower limit, as we took into consideration only the radio-detected (hence possibly relatively brighter) dwarfs (see Fig. 7c). The correlation found between the global SFR and B must involve some additional factors, not accounted for by the local B − ΣSFR dependency discussed above (Fig. 7b).
One possible explanation of the B − SFR relation could be the galactic mass. According to the principal component analysis of various global characteristics of galaxies performed by Disney et al. (2008), the galactic mass is the principal component strongly affecting a wide range of other global galactic properties. Plotted together, the H i mass and SFR of dwarfs are nonlineary related by a power-law slope of 1.45 ± 0.11 (r = + 93, P ≪ 1%, Fig. 7d). However, we do not observe a statistically significant influence of the mass on magnetic field strengths in dwarfs (r = + 0.16, P = 73%). A larger sample of radio-detected dwarfs is certainly needed to confirm this finding at higher statistical confidence.
If star formation in LG dwarfs were also a driver of effective galactic winds (see Sect. 5.3), then one might expect weaker magnetic fields in actively star-forming dwarfs because the fields and CRs could just escape in galactic outflows. To check this idea, we compare the strength of the magnetic field B with the velocity dispersion σv of ISM, which should scale with the star formation activity. In the case of effective winds, larger velocity dispersion should correspond to weaker fields. We present the values of σv estimated from H i observations in Table 3, and the derived B − σv relation in Figure 8. The dIrrs with starbursts (NGC 1569, NGC 4449) have large velocity dispersions (σv > 20 km s-1) but also have strong magnetic fields (B > 10 μG). The larger σv of both these galaxies and the Magellanic Clouds could be caused by galactic winds and/or by specific gas motions due to their tidal interactions. For dIrrs with weak magnetic fields (B < 5 μG), the velocity dispersion is around 10 ± 2 km-1, which is a value typically found in quiescent galaxies. Therefore, to explain the B − σv relation of dIrrs, galactic outflows are not needed, hence we ascribe the presence of weak magnetic fields to low star formation and not to galactic winds.
A possible process that could also influence both the SFR and magnetic fields is the gravitational interaction of galaxies. Young et al. (1996) found that the efficiency of star formation in interacting galaxies is significantly higher than in isolated objects. For the analysed dIrrs, clear signs of gravitational perturbations or gas infall were clearly detected in all most-intensively star-forming objects: NGC 4449, NGC 1569, IC 10, LMC, and SMC (see Table 3). Therefore, in dIrrs gravitational interactions can indeed stimulate massive star formation and promote stronger magnetic fields in a way similar to that observed in the Antennae galaxies (Chyży & Beck 2004). A larger sample of radio detected dIrrs is again necessary to confirm this possibility.
5.2. SFR evolution
 |
Fig. 8 Magnetic field strength versus velocity dispersion for dwarf galaxies. See Fig. 7 for symbol coding. |
The magnetic field in dIrrs, as in normal spiral galaxies, could be related not only to the current state of star-forming activity, as discussed above, but also to their recent star formation history. The production of magnetic fields might then be connected to the galaxy past. The evolution of global star formation can be qualitatively studied in a plane of two dimensionless parameters, p = log (SFR T0/LB) and f = log [MHI/(SFR T0) ] , where LB denotes the total blue luminosity of a galaxy and T0 = 13.7 Gyr the age of the Universe. The former parameter (p) characterizes the past, and the latter (f) the future of the galactic star formation (see Karachentsev & Kaisin 2007 for details). We calculated the values of LB for dwarfs from the absolute B-magnitude given in Mateo (1998) or, if unavailable, from the LEDA database. The other parameters needed are given in Table 3. We found that the investigated LG dIrrs show a similar distribution across the p − f plane (Fig. 9) to the group of dwarf galaxies around the giant spiral M 81 (Fig. 4 in Karachentsev & Kaisin 2007), thus seem to be representative of our nearby region of the Universe.
The majority of all dwarfs with detectable radio emission and magnetic fields are located in the bottom-right quarter of this plane (Fig. 9). Despite being more massive objects, they produce stars so efficiently, that their H i gas would be sufficient for just a short period of time, e.g. for 10% of the Hubble time (f ≈ −1.0) for LMC and IC 10. The most extreme case among all dwarfs is the starburst NGC 1569 with f = −1.5. Its star formation, and accordingly also the production of a magnetic field, should cease soon (the current level of SFR may continue only for the next 400 Myr). Galaxies such as NGC 1569 are presumably at their major star-forming phase (large p value of 1.5), thus might be analogs of starbursting (“young”) objects of the early Universe. This conclusion is supported by an analysis of the star formation history of NGC 1569 derived from a synthetic color-magnitude diagram method incorporating strong episodes of star formation over the past Gyr (Angeretti et al. 2005). Within our unbiased LG sample the only similar dwarf is IC 10 (p ≈ + 0.5) with strong magnetic fields of 9.7 μ G. The LMC is located at a similar location in the p − f diagram. Its star-formation episodes are believed to be triggered by close encounters with the Milky Way over the past 4 Gyr (Bekki & Chiba 2005).
 |
Fig. 9 Dwarf galaxies on the past-future evolution plane: p = log (SFR T0/LB) and f = log [MHI/(SFR T0)] . The comparison galaxies from outside of the Local Group are shown by squares. |
In contrast to the aforementioned bottom-right quarter, the top-left quarter of the p − f plane is occupied by less evolved objects with a relatively weak star-formation activity (negative p) that evolve slowly, despite having enough gas to produce stars. Galaxies such as WLM, Sag DIG, Aquarius, LGS 3, and Leo A (f ≥ 0.5) could even make stars for at least three times the Hubble time with the current SFR. These galaxies are most common among the LG dwarfs and all lack any detectable magnetic field. Thus, the existence of detectable magnetic fields in dwarfs is not coincidental but connected to the whole galaxy evolution.
To check whether the magnetic properties of dwarfs are indeed related to their overall evolution we investigated the relation of magnetic field strength to the mean metallicity (12+O/H) of the dwarfs, which we obtained for all the objects from the compilation of Mateo (1998) and Braine et al. (2001). We found that strong magnetic fields are observed exclusively in the evolved systems of relatively high metallicity. No object of metallicity 12+O/H < 8.1 has a magnetic field stronger than 5 μG, which indicates that the magnetic field production in dwarfs is tightly connected to the galactic gas consumption during their lives. Since the metallicity of dwarfs strongly correlates with their masses (Braine et al. 2001), this can explain the complex and mutual relation of magnetic field strength, global SFR, and mass (Sect. 5.1).
A good example to illustrate these complex issues is the well-studied NGC 4449. It shows a global starburst with a widespread star-formation activity. It forms stars twice as rapidly as the LMC, even though sizes of both galaxies are similar (Table 3). NGC 4449 is also unusual in having neutral hydrogen gas extending to six times its Holmberg radius. The large amount of H i gas places this galaxy closer to the center of the p − f plane than other starburst dwarfs. In the past, the galaxy most likely acquired some gas from an interaction or possibly a merger, as its inner part is counter-rotating with respect to the outer envelope (Hunter et al. 1998). The strong and regular magnetic field of NGC 4449 (almost 10 μG) is therefore likely connected to the star formation history, star-formation triggering mechanisms, the acquired mass, and the entire complicated history of the galaxy. The omission of these processes could have prevented a fully successful numerical MHD modelling of this object (Otmianowska-Mazur et al. 2000). This example also shows that dIrrs do not seem to be simple galaxy systems, nor easier to model than typical spiral galaxies.
5.3. Magnetization of the IGM
The magnetic field strength defines statistical scaling relations with other properties of LG dwarfs, such as ΣSFR, Σρ, and mass (Sect. 5.1). Similar trends can also be observed for local regions within large spiral galaxies (Chyży 2008), indicating in both cases some universal connections between various physical mechanisms. Close links between the global stellar and dynamical properties of dwarfs were also observed by Woo et al. (2008) and modelled for higher-redshift dwarfs by Tassis et al. (2008). We therefore infer that the magnetic properties of LG dwarfs can tell us something about magnetic fields in dwarf galaxies in past cosmological epochs, in particular about the role they might have played in magnetizing the intergalactic medium in the early Universe. Low-mass galaxies with a weak gravitational potential seem to be good candidates to support this process. We perform below a straightforward modelling of whether dwarf galaxies could actually be an efficient supplier of magnetic fields to the IGM. We use the available data concerning the magnetic field characteristics of the low-mass galactic systems that we observed within the Local Group and our current knowledge of protogalaxies and their environments.
According to theoretical considerations, very weak seed magnetic fields of the order of 10-20−10-18 G could have been generated in early cosmological epochs by a number of mechanisms, including phase transitions, the Weibel instability (Medvedev & Loeb 1999), and the Biermann battery (Widrow 2002; Zweibel 2006). Alternatively, seed fields could have been produced by the first stars and amplified by dynamo processes in protogalaxies. The small-scale galactic dynamo could produce strong magnetic fields on timescales of even 107 yr (Brandenburg & Subramanian 2005; Arshakian et al. 2009). Outflows from protogalaxies could then seed the IGM and massive galaxies that assembled at lower redshifts with magnetic fields (Kronberg et al. 2001; Bertone et al. 2006; Donnert et al. 2009; Kronberg et al. 1999; Samui et al. 2009; Dubois & Teyssier 2010). Measurements of integrated Faraday rotation of distant quasars as well as the modelling of the cosmological evolution of the IGM provide hints of a possible significant magnetization of the IGM at z ≈ 4 − 7 (Kronberg 2006).
Modelling of the magnetization of the IGM.
On the other hand, the observations of Ly-α quasar absorption lines indicate that metals are present in the IGM up to z ≈ 5 (Cowie et al. 1995; Songaila & Cowie 1996; Ellison et al. 2000; Bouché at al. 2007). Various estimates suggest that clouds obscuring quasars are located 200–500 kpc from protogalaxies (Meiksin 2009, and references therein). To transport metals into these regions, some mechanisms, such as stellar winds, supernova-driven galactic outflows, or AGN induced outflows, must be at work there. The same galactic outflows that pollute the space with metals could also supply the IGM with magnetic fields produced in protogalaxies.
In our modelling, we study a galactic-wind-blown bubble which energy Eb drives the bubble expansion (Veilleux et al. 2005; Meiksin 2009). Only some net fraction ϵ of the injected energy Ew from supernovae and stellar winds is available for this process (Eb = ϵEw), which can only be roughly estimated to be within 0.01−0.1, as it depends on several unknown factors such as: expansion losses, wind mass loading, radiative cooling, uniformity of the ambient medium, and energy losses intrinsic to the interstellar medium (e.g. Bertone et al. 2006; Cho & Kang 2008; Meiksin 2009). The bubble of radius Rb and thermal pressure  finally reaches an equilibrium with the IGM pressure PIGM ∝ TIGM(1 + z)3 and stops expanding at the stall radius Rs = (Eb/TIGM)1/3(1 + z)-1.
finally reaches an equilibrium with the IGM pressure PIGM ∝ TIGM(1 + z)3 and stops expanding at the stall radius Rs = (Eb/TIGM)1/3(1 + z)-1.
Next, we assume that magnetic fields are also blown out along with the plasma that has escaped from star forming regions and reached the strength Bs at radius Rs. For spherical expansion of the bubble, the strength of the magnetic fields dominated by the random component scales with the bubble’s density as Bb ∝ ρ2/3. Following the results of Sect. 5.1, we relate the initial strength of the magnetic fields B0 within a star forming region of extent R0 to the total galactic mass and the global SFR, using masses and sizes of the protogalaxies estimated from observations (see below) (Table 5).
We calculated the amount of mechanical energy Ew injected by active star-forming regions by modelling an evolutionary stellar population synthesis using the Starburst99 code3 (Leitherer et al. 1999; Vazquez & Leitherer 2005). The main input parameter of this code is the star forming (SF) mass in the case of instantaneous star formation, or the SFR in the case of continuous star formation. For high-z objects, we used the former option to simulate the burst of star formation during the formation process of primordial galaxies, as well as the enhanced Geneva stellar tracks of low metallicity Z = 0.004, appropriate for young galaxies. For the stellar initial mass function, the classical Salpeter law was used in-between 1 and 100 M⊙.
According to the CDM scenario, the first dark matter halos appeared in the Universe at z ≈ 20−8. The observational characteristics of dSphs in the LG (see Sect. 2), which have the common total mass of about 107 M⊙ (Strigari et al. 2008), suggest that they may constitute LG fossils of primordial dSph (Pri dSph) galaxies (Ricotti 2010). Almost all LG dSphs exhibit a prominent stellar population of about 10 Gyr in age, resulting from a SFR of about several hundred M⊙ per Myr (Dolphin et al. 2005) followed by a subsequent decline in SF activity. The lower-mass galaxies, which fossils can now be observed as UF dSphs, were less efficient in forming stars and transformed a smaller fraction of their baryonic mass into stars (Salvadori & Ferrara 2009). In our modelling, we therefore restricted the low-end of the instantaneous SF mass to 2 × 105 M⊙ (Table 5). For a total galactic mass of dSphs of e.g., several 107 M⊙, this corresponds to 14% of the baryonic content, converting 3.5% of the gas into stars in a single outburst. The applied values of SF mass correspond to a mean SFR of 5 × 10-3 M⊙ yr-1 over the time of the starburst ( ≈ 4 × 107 yr), which is close to the SFR estimated by Dolphin et al. (2005) and several orders of magnitude higher than the SFR observed today among LG dSphs. They are also similar to those used in simulations of dwarf galaxy evolution by Ricotti et al. (2008, 2010).
Low-mass systems might have merged in the past to form larger galaxies, as predicted by the model of hierarchical cosmology. The primordial dwarf irregular galaxies (Pri dIrr) probably formed later than Pri dSphs or in more massive halos (Ricotti & Gnedin 2005). In our modelling, we assigned them a SF mass of 107 M⊙ (Table 5). This value corresponds to the case of a strong burst of star formation of about 0.3 M⊙ yr-1 that can be observed currently in the starbursting dwarf NGC 1569 (Table 3). This galaxy was much quieter in the past, including its youth (Angeretti et al. 2005). Most LG dIrrs probably experienced less massive bursts of star formation during their evolution. For example, the SFR mentioned above is two orders of magnitude higher than the current SFR of IC 1613 (Table 3) and about one order of magnitude higher than during the most active stage in the whole evolution of this object (Skillman et al. 2003).
More massive and starbursting galaxies have been detected as Lyman-break galaxies (LBGs) (Verma et al. 2007). These objects are probably progenitors of the present-day early Hubble-type galaxies and bulges of massive galaxies. LBGs evolved with time in mass: those assembled at z ≈ 5 are 10 times less massive and luminous than z ≈ 3 LBGs (Verma et al. 2007). Our modelling includes both types of LBGs (at z = 5 and z = 3) as the high-end mass systems (Table 5). The applied SF masses (4 × 108 and 4 × 108 M⊙) correspond to an equivalent SFR during the starburst of 10 and 100 M⊙ yr-1, respectively. Thus, the second class of LBGs corresponds in terms of their properties to the M 82-like starburst galaxies. In galaxies with masses significantly higher than 109 M⊙, the escape of gas from the galactic disks becomes problematic because of the deep gravitational potential wells (Ferrara & Tolstoy 2000). Therefore, the modelled Rs for LBGs at z = 3 should be regarded as upper limits. We also note that sometimes even relatively massive galaxies with a total mass of up to ≈ 1011 M⊙ are called dwarf galaxies (e.g. Crain et al. 2009) in the sense that they have a sub-galactic mass value compared to the typical galactic systems in the present Universe, such as the Milky Way. However, primordial systems of this mass, as well as LBGs, would not have evolved to become the typical LG dIrrs that we investigate in this paper.
For all kind of objects, we adopt in our modelling TIGM = 104 K (Meiksin 2009) and ϵ = 0.01, for which we get for LBGs at z = 3 the bubble’s stall radius of Rs = 530 kpc (Table 5), in agreement with the modelling of metal enrichment by Madau et al. (2001), Calura & Matteucci (2006), and Samui et al. (2008). Our modelling predicts a small stall radius of 9 kpc for primordial dSphs and 36 kpc for primordial dIrrs (Table 5). Thus, it is quite unlikely that the metal absorption systems seen in the Ly-α forest out to at least 300 kpc from parent objects were produced by low-mass dIrrs.
If these attempts to explain the IGM’s metal enrichment are valid, our modelling indicates that the primordial dIrrs could have magnetized the IGM only locally, out to about a 40 kpc distance, with the strength of magnetic fields of about a few nanogauss (Table 5). Accordingly, the contribution from these galaxies is simply insufficient to have any significant impact on magnetization of the IGM. Our modelling suggests that more massive galaxies, such as LBGs, are more effective in magnetizing the IGM, providing a larger spread (160–530 kpc) and magnetic field strengths of almost one nanogauss. Kinematic signatures of vigorous large-scale winds have been detected among LBGs at z ≈ 3−4 (e.g. Veilleux et al. 2005).
We now examine the effect of varying the model parameters. Raising the energy conversion fraction ϵ from 0.01 (applied in Table 5) to 0.1 doubles the bubble’s stall radius, while decreasing the magnetic field strength by factor of five. Thus, the applied ϵ = 0.01 results in upper limits of Bs presented in Table 5. Extending the lower end of the Salpeter IMF to 0.1 M⊙ or raising its upper level to 120 M⊙ results in an input wind energy that is lower by a factor of 2.5 and in turn, a 35% smaller Rs and 1.8 times stronger magnetic fields. If we decrease R0 by a factor of two, we obtain a four times weaker magnetic field. Altering the other input parameters has a less significant effect; for example, by changing the IMF to the standard Kroupa one decreases the input energy by only 68%. Changing the metallicity from 0.004 to 0.02 gives a wind energy higher by 20%, a stall radius larger by 7%, and a magnetic field strength lower by 15%. A higher star-forming mass or lower IGM temperature by a factor of two yield a stall radius larger by about 25% and a magnetic field strength weaker by about 60%. This analysis demonstrates that the obtained results are most sensitive to the uncertain value of ϵ. However, even assuming that its uncertainty is as large as about one order of magnitude does not affect our conclusion concerning the weak effectiveness of dwarf galaxies in polluting the IGM with metals and magnetic fields.
We also perform similar modelling of spreading the magnetic fields of nearby (z = 0) dwarfs. As LG dIrrs appear to experience continuous star formation with amplitude variations of factors 2 − 3 during their lifetime (e.g. Grebel 2004, 2005), we applied this option to our modelling of stellar population synthesis over a characteristic timescales of 107 yrs, and applied a metallicity of Z = 0.02 (Table 5). Continuous star formation agrees with the detection of significant amounts of gas in these systems (Mateo 1998). We adopted a higher ambient gas temperature (TIGM = 105 K), as the IGM in the LG is not pristine and likely to have a hot component due to galactic feedback, structure formation heating, and the large potential wells of massive spirals (Davé & Oppenheimer 2007; Crain et al. 2009). There are also some predictions that the density of the local IGM is about 10-4 cm-3 (Pildis & McGaugh 1996; Rasmussen et al. 2003; Sembach 2006), which we use to estimate the ambient pressure PIGM.
Our modelling indicates that typical LG dwarfs do not appear capable of providing an efficient supply of magnetic fields to their environments. Typical wind-blown expanding bubbles may reach relatively short distances of about 1 kpc (Table 5). Only around the most starbursting dwarfs (as e.g. IC 10, NGC 1569, NGC 4449) could the IGM be magnetized in this way up to about 0.1 μG and within a distance of about 2–5 kpc.
In the above modelling, the galactic outflows were driven exclusively by thermal pressure. However, the energy of CRs may also play an important role in triggering galactic winds e.g. Breitschwerdt et al. (1991, 1993), Breitschwerdt (2008), Everett et al. (2008, 2010). This source of energy could be highly important in quiescent galaxies, such as our Milky Way (Everett et al. 2010). Nevertheless, we attempt to estimate the possible influence of additional pressure from CRs to blow-out bubbles in our low-mass objects. Treating CRs hydrodynamically and assuming that their pressure could reach approximate equipartition with the thermal pressure Pb, we repeated the modelling of the expansion of the bubble for primordial dSphs and dIrrs. We obtain stall radius of 11 and 45 kpc, respectively. These values are only 26% larger than in the case of purely thermally driven winds. These estimates seems to be upper limits as we do not include any quenching effect of CRs on star formation (Socrates et al. 2008; Samui et al. 2009) and the interaction of CRs with mass-loaded gaseous outflows.
Thus, we conclude that it is highly unlikely that typical dwarf galaxies (e.g. IC 1613) could have had any major role in magnetizing the Universe at any cosmological epoch. Our predictions of the magnetized surroundings of nearby dIrrs should be verified by observations at very long radio wavelengths to possibly reveal an aged population of CR electrons radiating in weak magnetic fields, or by Faraday rotation observations applied to background sources. These possibilities are only now becoming possible with the availability of the LOFAR and SKA pathfinders (Morganti et al. 2010; Beck 2010), as well as the EVLA.
5.4. Production of large-scale fields
We demonstrated that magnetic fields in the LG dIrrs (if detectable) are not more ordered than in typical spiral galaxies (Sect. 4.2) and must be dominated by the random component. This conclusion suggests that LG dwarfs might not fulfil the evolutionary scenario of Arshakian et al. (2009) that local and moderately distant (z ≈ 1) dwarfs can produce highly coherent (unidirectional) fields.
The generation of coherent (regular) fields requires large-scale dynamo process to operate, hence helical turbulence produced by supernovae explosions and Coriolis forces (Widrow 2002). The dynamo efficiency is approximately described by the dynamo number  which depends on the vertical scale height of the galactic disk H, turbulent velocity vt, an angular rotation Ω, and the velocity shear (r∂Ω/∂r). The large-scale α-Ω dynamo works only if D exceeds a critical number of about 9-11, depending on the details of the gas flow pattern. For the LG dwarfs, we estimated the maximum rotational velocities vrot from the galactic rotation curves or velocity dispersions (see Table 3 with notes). As some galaxies show evidence of gravitational interactions, these esimates are only approximate. For example, for strongly interacting NGC 4449 Valdez-Gutiérrez et al. (2002) estimate that the systematic rotation on the receding side of the galaxy is about 40 km s-1 at 2′ radius (from Hα measurements). On the same portion of the galaxy, the H i observations indicate a rotation of about 30 km s-1 (Martin 1998). The typical maximum rotational velocity for dwarfs is about 30 km s-1 at a radius r = 2 kpc. For differential rotation and flat rotation curve, this corresponds to a shear of 15 km s-1 kpc-1. Taking vt = 10 km s-1, H = 0.5 kpc (cf. Elstner et al. 2009), we obtain a dynamo number of D = 5, which is subcritical and hence in agreement with our radio observations. If this rotation were not differential (e.g. more chaotic), then D would be even smaller. This is confirmed by direct simulations of a supernova-driven dynamo by Gressel et al. (2008), who did not find large-scale dynamo action within a galactic disk of corresponding shear 20 km s-1 kpc-1. Recent MHD simulations of a cosmic-ray driven dynamo by Siejkowski et al. (2010) show that the production of regular fields in dwarf galaxies requires mainly fast rotation. The velocity shear is necessary but influences the dynamo efficiency much less.
which depends on the vertical scale height of the galactic disk H, turbulent velocity vt, an angular rotation Ω, and the velocity shear (r∂Ω/∂r). The large-scale α-Ω dynamo works only if D exceeds a critical number of about 9-11, depending on the details of the gas flow pattern. For the LG dwarfs, we estimated the maximum rotational velocities vrot from the galactic rotation curves or velocity dispersions (see Table 3 with notes). As some galaxies show evidence of gravitational interactions, these esimates are only approximate. For example, for strongly interacting NGC 4449 Valdez-Gutiérrez et al. (2002) estimate that the systematic rotation on the receding side of the galaxy is about 40 km s-1 at 2′ radius (from Hα measurements). On the same portion of the galaxy, the H i observations indicate a rotation of about 30 km s-1 (Martin 1998). The typical maximum rotational velocity for dwarfs is about 30 km s-1 at a radius r = 2 kpc. For differential rotation and flat rotation curve, this corresponds to a shear of 15 km s-1 kpc-1. Taking vt = 10 km s-1, H = 0.5 kpc (cf. Elstner et al. 2009), we obtain a dynamo number of D = 5, which is subcritical and hence in agreement with our radio observations. If this rotation were not differential (e.g. more chaotic), then D would be even smaller. This is confirmed by direct simulations of a supernova-driven dynamo by Gressel et al. (2008), who did not find large-scale dynamo action within a galactic disk of corresponding shear 20 km s-1 kpc-1. Recent MHD simulations of a cosmic-ray driven dynamo by Siejkowski et al. (2010) show that the production of regular fields in dwarf galaxies requires mainly fast rotation. The velocity shear is necessary but influences the dynamo efficiency much less.
 |
Fig. 10 Total magnetic field strengths plotted against rotational velocities of dwarfs. |
In typical and even the most starbursting LG dwarf (IC 10), the ordered magnetic fields have indeed been observed so far not to show any large-scale structure that could resemble MHD dynamo fields (Chyży et al. 2003). This confirms the earlier suggestion by Chyży et al. (2003) that small galaxies should mainly produce random magnetic fields maintained by turbulent gas motions. The large irregular dwarf NGC 4449 with its dynamo-like field could be a special case (Sect. 5.2). Rotation in dwarfs is usually not only slower but also more chaotic than in spiral galaxies (e.g. van Eymeren et al. 2009). Larger velocity dispersion and star formation feedback may destroy the regular pattern of magnetic fields and lower the field regularity. No MHD simulations have hitherto addressed these possibilities.
We do not observe a systematic dependence of the maximum rotational velocity on the total magnetic field strength in dwarfs (Fig. 10). For slow rotation (vrot < 40 km s-1), all dwarf galaxies show weak fields (B < 4 μG). Above a velocity of 40 km s-1, dwarfs have either stronger or weaker fields that seems to mainly depend on the actual value of the SFR. Indeed, NGC 6822, LMC, and SMC rotate at least as fast as the starbursting galaxies IC 10, NGC 1569, and NGC 4449, but they have less active and widespread star formation.
According to a study of magnetic fields within the disk of the large spiral galaxy NGC 4254 (Chyży 2008), the random magnetic field scales with the far-infrared based ΣSFR as a powerlaw with an exponent of 0.26 ± 0.01. A similar relation with exponent of 0.25 ± 0.04 has also been found for LG dIrrs (Sect. 5.1). We are currently collecting data on galaxies with properties in-between those of the dwarfs studied in this paper and spiral galaxies to confirm these findings for a larger sample of galaxies.
5.5. Radio-infrared relation
 |
Fig. 11 The radio-infrared correlation diagram for LG dwarfs and comparison dwarfs (plotted with the same symbols as in Fig. 7), and for the sake of reference, the sample of galaxies observed by de Jong (1967) plotted as stars. The surface brightness at 2.64 GHz and at 60 μm is used (in Jy/◻′). The solid line is an orthogonal fit to the reference galaxies. |
We constructed for the first time a radio-infrared correlation diagram for dwarf galaxies (Fig. 11), extending this relation to the lowest limit of galactic mass of about several 107 M⊙, which is 10 times lower than previously studied (Chyży et al. 2007). We used the surface brightness radio emission at 2.64 GHz (or its limits) and the infrared surface brightness emission at 60 μm (Table 3). The relation for detected dwarfs is closely represented by the powerlaw with a slope of 0.91 ± 0.08 and a correlation of r = + 0.91 (P ≪ 1%) determined for a sample of bright galaxies observed by de Jong (1967) with the 100 m NRAO telescope. Hence, typically unevolved, low-mass stellar systems in our local neighbourhood reveal similar physical conditions for star formation, magnetic field, and cosmic-ray generation processes as the massive spirals (e.g. Weżgowiec et al. 2007). A similar relation was extended to young, high-redshift galaxies (Seymour et al. 2008).
However, it cannot be excluded that some radio deficiency might be present in some dwarfs of weak infrared radiation, as only the upper limits of their radio brightness are plotted in Fig. 11. The loss of magnetic fields and CRs by galactic outflows in dwarfs and subsequently their weaker synchrotron emission could be counterbalanced by the lower content of dust as suggested for blue compact dwarfs by Klein at al. (1991). In this case, the radio-infrared relation could be preserved. Because dIrrs at the low-end of the radio flux also have lower metallicity (which scales with the object’s mass) the shortage of dust is indeed likely to occur.
According to the radio-infrared relation, the radio-undetected dwarfs from our LG sample are expected to have a radio brightness at 2.64 GHz of about 1 mJy per 1′ beam or less. This requires a few times higher detecting sensitivity than we have achieved with the Effelsberg telescope. However, these fluxes are below the confusion limit of a single-dish antenna and demand observations of higher resolution. Objects with such weak and extended radio emission are extremely difficult to detect at higher frequencies. Studies at lower frequencies would thus require a high-sensitivity radio interferometer such as LOFAR. If these dwarf galaxies hosted primarily regular magnetic fields of about 1 μG strength (Arshakian et al. 2009), then they could also be detected by the background Faraday rotation method with the upcoming LOFAR or SKA interferometers.
6. Summary and conclusions
We have performed a sensitive search for radio emission in a statistically unbiased sample of the Local Group irregular and dwarf irregular galaxies available at the site of 100-m Effelsberg telescope at 2.64 GHz. We have compared these 12 galaxies to other LG objects, i.e., LMC and SMC, and the starburst dwarfs NGC 4449 and NGC 1569, for which magnetic fields have already been observed. Higher frequency (4.85 GHz) observations were used to search for polarized emission in the five most luminous dwarfs in the infrared domain.
We found the following:
-
The LG dIrrs closely represent the local volume of the Universe and display star-formation characteristics similar to those of other nearby groups of dwarfs (Sect. 5.2). Only 25% of the LG dwarfs (3 out of 12) were detected at 2.64 GHz. We argued that the radio-undetected dwarfs must be intrinsically radio weak.
-
The total magnetic fields in LG dwarfs are very weak: the mean value of the equipartition magnetic field strength of all objects is < 4.2 ± 1.8 μG, taking into account the upper limits for radio-undetected dwarfs (9 out of 12). This value is almost three times weaker than the estimated mean for typical spiral galaxies. The strongest total field of 10 μG is observed in the starburst dwarf IC 10. We found that the magnetic field strength does not correlate with the dwarf rotational velocity.
-
Among the three radio-detected dwarfs, the strength of the ordered field component is in the range 0.4 − 0.9 μG and the ordered-to-random field component ratio is about 0.2. These values are smaller than in typical spiral galaxies indicating that the production of magnetic fields in dwarfs is probably not maintained by the large-scale dynamo process.
-
The production of the total magnetic field in dwarf systems appears to be controlled mainly by the star-formation surface density (B ∝ ΣSFR0.30 ± 0.04), or the gas density (B ∝ Σρ0.47 ± 0.09), as for spiral galaxies (Chyży 2008; Krause 2009). We note a somewhat steeper Schmidt law (a slope N = 1.8) for our LG dwarfs than in typical large-mass disks. Among all the dwarfs, we also found systematically stronger magnetic fields in objects of higher global SFR (B ∝ SFR0.25 ± 0.06).
-
Stronger disk-averaged magnetic fields (>4 μG) were observed in dIrrs of extreme characteristics only (e.g. NGC 4449, NGC 1569, and the LG dwarf IC 10). They are more evolved objects of generally much higher metallicity and global SFR than the majority of LG dwarf population. They also usually show clear signs of current or recent gravitational interactions.
-
We propose that a coeval magnetization of the IGM around primordial galaxies occurs with a metal enrichment caused by galactic outflows maintained by stellar winds and supernovae. However, our modelling of the stellar population synthesis (code Starburst99) and expansion of a blowing bubble indicate that not dIrrs but more massive galaxies of LBG properties can efficiently magnetize the IGM at high (z > 3) redshift. If the current understanding and modelling of metal enrichment is valid, we expect that the most efficient seeding of the IGM is that produced by LBG galaxies with magnetic field strengths of about 0.9 − 0.6 nG at up to distances of 160–530 kpc at redshifts 5–3, respectively. We show that several times weaker fields and shorter distances are expected from primordial dwarf galaxies.
-
The sizes of blowing bubbles around primordial galaxies might be slightly enlarged (by up to 26%) if in addition to the thermal pressure the pressure of CRs is included.
-
We also predict that around local, most star-forming dwarf galaxies, the surrounding IGM is magnetized up to about 0.1 μG to within a distance of about 5 kpc. These predictions should be verified by LOFAR, EVLA, and SKA observations.
-
The dIrrs of different SFR follow the far-infrared relationship determined for high surface brightness spiral galaxies (with a slope 0.91 ± 0.08), showing that similar processes regulate star formation, synchrotron emission, and production of magnetic fields in low-mass dwarfs and large spirals. From the radio-infrared relation, we predict for the radio-undetected dwarfs in our sample a mean total field strength as small as about 1 μG .
NVSS: the NRAO VLA Sky Survey at 1.4 GHz, Condon et al. (1998).
FIRST: Faint Images of the Radio Sky at 20 cm, Becker et al. (1995).
Acknowledgments
We are grateful to Prof. M. Urbanik for permission to present 4.85 GHz data of IC 1613 from our common observation in 2002, and to Dr M. Soida for valuable discussions. K.T. Chyży is grateful to Prof. Claus Leitherer for his help in the compilation and setup of the Starburst99 code. We thank Dr. M. Krause for careful reading of the manuscript and an anonymous referee for helpful comments and suggestions. This work was supported by the Polish Ministry of Science and Higher Education, grant 2693/H03/2006/31, 3033/B/H03/2008/35, and from research funding from the European Community’s sixth Framework Programme under RadioNet R113CT 2003 5058187. We acknowledge the use of the HyperLeda (http://leda.univ-lyon1.fr) and NED (http://nedwww.ipac.caltech.edu) databases.
References
- Annibali, F., Aloisi, A., Mack, J., et al. 2008, AJ, 135, 1900 [NASA ADS] [CrossRef] [Google Scholar]
- Angeretti, L., Tosi, M., Greggio, L., et al. 2005, AJ, 129, 2203 [NASA ADS] [CrossRef] [Google Scholar]
- Arshakian, T. G., Beck, R., Krause, M., & Sokoloff, D. 2009, A&A, 494, 21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Becker, R. H., White, R. L., & Helfand, D. J. 1995, ApJ, 450, 559 [NASA ADS] [CrossRef] [Google Scholar]
- Beck, R. 2005, in Cosmic Magnetic Fields, ed. R. Wielebinski, & R. Beck (Heidelberg: Springer), 41 [Google Scholar]
- Beck, R., 2010, in Wide Field Science and Technology for the Square Kilometre Array, ed. S. A. Torchinsky, et al. (SKADS), 93 [Google Scholar]
- Beck, R., & Krause, M. 2005, Astron. Nachr., 326, 414 [NASA ADS] [CrossRef] [Google Scholar]
- Bekki, K., & Chiba, M. 2005, MNRAS, 356, 680 [NASA ADS] [CrossRef] [Google Scholar]
- Bertone, S., Vogt, C., & Enßlin, T. 2006, MNRAS, 370, 319 [NASA ADS] [Google Scholar]
- Bouché, N., Lehnert, M. D., Aguirre, A., Péroux, C., & Bergeron, J. 2007, MNRAS, 378, 525 [NASA ADS] [CrossRef] [Google Scholar]
- Braine, J., Duc, P.-A., Lisenfeld, U., et al. 2001, A&A, 378, 51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brandenburg, A., & Subramanian, K. 2005, Phys. Rep., 417, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Breitschwerdt, D. 2008, Nature, 452, 826 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Breitschwerdt, D., McKenzie, J. F., & Völk, H. J. 1991, A&A, 245, 79 [NASA ADS] [Google Scholar]
- Breitschwerdt, D., McKenzie, J. F., & Völk, H. J. 1993, A&A, 269, 54 [NASA ADS] [Google Scholar]
- Calura, F., & Matteucci, F. 2006 MNRAS, 369, 465 [NASA ADS] [CrossRef] [Google Scholar]
- Caplan, J., & Deharveng, L. 1986, A&A, 155, 297 [NASA ADS] [Google Scholar]
- Cho, H., & Kang, H. 2008, New A, 13, 163 [Google Scholar]
- Chyży, K. T. 2008, A&A, 482, 755 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chyży, K. T., & Beck, R. 2004, A&A, 417, 541 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chyży, K. T., Beck, R., Kohle, S., Klein, U., & Urbanik, M. 2000, A&A, 355, 128 [NASA ADS] [Google Scholar]
- Chyży, K. T., Knapik, J., Bomans, D. J., et al. 2003, A&A, 405, 513 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chyży, K. T., Bomans, D. J., Krause, M., et al. 2007, A&A, 462, 933 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Condon, J. J. 1987, ApJS, 65, 485 [NASA ADS] [CrossRef] [Google Scholar]
- Condon, J. J., Cotton, W. D., Greisen, E. W., et al. 1998, AJ, 115, 1693 [NASA ADS] [CrossRef] [Google Scholar]
- Cowie, L. L., Songaila, A., Kim, T.-S., & Hu, E. M. 1995, AJ, 109, 1522 [NASA ADS] [CrossRef] [Google Scholar]
- Crain, R. A., Theuns, T., Dal la Vecchia, C., et al. 2009, MNRAS, 399, 1773 [NASA ADS] [CrossRef] [Google Scholar]
- Davé, R., & Oppenheimer, B. D. 2007, MNRAS, 374, 427 [NASA ADS] [CrossRef] [Google Scholar]
- Disney, M. J., Romano, J. D., Garcia-Appadoo, D. A., et al. 2008, Nature, 455, 1082 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Dolphin, A. E., Weisz, D. R., Skillman, E. D., & Holtzman, J. A. 2005 [arXiv:astro-ph/0506430] [Google Scholar]
- Donnert, J., Dolag, K., Lesch, H., & Müller, E. 2009, MNRAS, 392, 1008 [NASA ADS] [CrossRef] [Google Scholar]
- de Jong, M. L. 1967, ApJ, 150, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Dubois, Y., & Teyssier, R. 2010, A&A, 523, A72 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ellison, S. L., Songaila, A., Schaye, J., & Pettini, M. 2000, AJ, 120, 1175 [NASA ADS] [CrossRef] [Google Scholar]
- Elstner, D., Gressel, O., & Rüdiger, G. 2009, in Cosmic Magnetic Fields: From Planets, to Stars and Galaxies, ed. K. G. Strassmeier, et al., IAU Symp. 259, 467 [Google Scholar]
- Emerson, D. T., & Gräve, R. 1988, A&A, 190, 353 [NASA ADS] [Google Scholar]
- Emerson, D. T., Klein, U., & Haslam, C. G. T. 1979, A&A, 76, 92 [NASA ADS] [Google Scholar]
- Everett, J. E., Zweibel, E. G., Benjamin, R. A., et al. 2008, ApJ, 674, 258 [NASA ADS] [CrossRef] [Google Scholar]
- Everett, J. E., Schiller, Q. G., & Zweibel, E. G. 2010, ApJ, 711, 13 [NASA ADS] [CrossRef] [Google Scholar]
- Ferrara, A., & Tolstoy, E. 2000, MNRAS, 313, 291 [NASA ADS] [CrossRef] [Google Scholar]
- Gaensler, B. M., Haverkorn, M., Staveley-Smith, L., et al. 2005, Sci, 307, 1610 [Google Scholar]
- Gressel, O., Elstner, D., Ziegler, U., & Rüdiger, G. 2008, A&A, 486, L35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gioia, I. M., Gregorini, L., & Klein, U. 1982, A&A, 116, 164 [NASA ADS] [Google Scholar]
- Grebel, E. K. 2001, A&SSS, 277, 231 [Google Scholar]
- Grebel, E. K. 2004, Carnegie Observatories Astrophys. Series, 4, 234 [Google Scholar]
- Grebel, E. K. 2005, in Stellar astrophysics with the world’s largest telescopes, AIP Conf. Proc., 752, 161 [Google Scholar]
- Grebel, E. K., Gallagher, J. S. III, & Harbeck, D. 2003, AJ, 125, 1926 [NASA ADS] [CrossRef] [Google Scholar]
- Haslam, C. G. T. 1974, A&AS, 15, 333 [Google Scholar]
- Haynes, R. F., Klein, U., Wayte, S. R., et al. 1991, A&A, 252, 475 [NASA ADS] [Google Scholar]
- Hunter, D. A., 2002, in Modes of Star Formation and the Origin of Field Populations, ed. E. K. Grebel, & W. Brandner, San Francisco, ASP Conf. Proc., 285, 323 [Google Scholar]
- Hunter, D. A., & Gallagher, J. S., 1990, in NASA, Ames Research Center, The Interstellar Medium in External Galaxies, 149 [Google Scholar]
- Hunter, D. A., & Elmegreen, B. G. 2004, AJ, 128, 2170 [NASA ADS] [CrossRef] [Google Scholar]
- Hunter, D. A., Wilcots, E. M., van Woerden, H., Gallagher, J. S., & Kohle, S. 1998, ApJ, 495, L47 [NASA ADS] [CrossRef] [Google Scholar]
- Hunter, D. A., van Woerden, H., & Gallagher, J. S. 1999, AJ, 118, 2184 [NASA ADS] [CrossRef] [Google Scholar]
- Helou, G., & Walker, D. W. 1995, IRAS Small Scale Structure Catalog, Ver 1.00 Vizier Online Data Catalog: VII/73 [Google Scholar]
- Karachentsev, I. D. 2005, AJ, 129, 178 [NASA ADS] [CrossRef] [Google Scholar]
- Karachentsev, I. D., & Kaisin, S. S. 2007, AJ, 133, 1883 [NASA ADS] [CrossRef] [Google Scholar]
- Kennicutt, R. C. 1998, ApJ, 498, 541 [NASA ADS] [CrossRef] [Google Scholar]
- Kepley, A. A., Mühle, S., Everett, J., et al. 2010, ApJ, 712, 536 [NASA ADS] [CrossRef] [Google Scholar]
- Klein, U., & Gräve, R. 1986, A&A, 161, 155 [NASA ADS] [Google Scholar]
- Klein, U., Weiland, H., & Brinks, E. 1991, A&A, 246, 323 [NASA ADS] [Google Scholar]
- Kravtsov, A. 2010, Adv. Astron., 2010, 1 [Google Scholar]
- Krause, M. 2009, Rev. Mex. Astron. Astrofis., 36, 25 [Google Scholar]
- Kronberg, P. P. 2006, AN, 327, 517 [NASA ADS] [Google Scholar]
- Kronberg, P. P., Lesch, H., & Hopp, U. 1999, ApJ, 511, 56 [NASA ADS] [CrossRef] [Google Scholar]
- Kronberg, P. P., Dufton, Q. W., Li, H., & Colgate, S. A. 2001, ApJ, 560, 178 [NASA ADS] [CrossRef] [Google Scholar]
- Leitherer, C., Schaerer, D., Goldader, J. D., et al. 1999, ApJS, 123, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Madau, P., Ferrara, A., & Rees, M. J. 2001, ApJ, 555, 92 [NASA ADS] [CrossRef] [Google Scholar]
- Mao, S. A., Gaensler, B. M., Stanimirović, S., et al. 2008, ApJ, 688, 1029 [NASA ADS] [CrossRef] [Google Scholar]
- Martin, C. L. 1998, ApJ, 506, 222 [NASA ADS] [CrossRef] [Google Scholar]
- Martin, C. L., Kobulnicky, H. A., & Heckman, T. M. 2002, ApJ, 574, 663 [NASA ADS] [CrossRef] [Google Scholar]
- Martin, N. F., de Jong, J. T. A., & Rix, H.-W. 2008, ApJ, 684, 1075 [NASA ADS] [CrossRef] [Google Scholar]
- Mateo, M. 1998, ARA&A, 36, 435 [NASA ADS] [CrossRef] [Google Scholar]
- Medvedev, M. V., & Loeb, A. 1999, ApJ, 526, 697 [NASA ADS] [CrossRef] [Google Scholar]
- Meiksin, A. A. 2009, Rev. Mod. Phys., 81, 1405 [NASA ADS] [CrossRef] [Google Scholar]
- Morganti, R., Rottgering, H., Snellen, I., et al. 2010 [arXiv:1001.2384] [Google Scholar]
- Morsi, H. W., & Reich, W. 1986, A&A, 163, 313 [NASA ADS] [Google Scholar]
- Moshir, M., Copan, G., Conrow, T., et al. 1990, IRAS Faint Source Catalogue, version 2.0, Vizier Online Data Catalog, 2156, [Google Scholar]
- Niklas, S., & Beck, R. 1997, A&A, 320, 54 [NASA ADS] [Google Scholar]
- Otmianowska-Mazur, K., Chyży, K. T., Soida, M., & von Linden, S. 2000, A&A, 359, 29 [NASA ADS] [Google Scholar]
- Pacholczyk, A. G. 1970, Radio Astrophysics: Nonthermal Processes in Galactic and Extragalactic Sources, Series of Books in Astronomy and Astrophysics (San Francisco, CA: Freeman) [Google Scholar]
- Pildis, R. A., & McGaugh, S. S. 1996, ApJ, 470, L77 [NASA ADS] [CrossRef] [Google Scholar]
- Prevot, L., Rousseau, J., & Martin, N. 1989, A&A, 225, 303 [NASA ADS] [Google Scholar]
- Rasmussen, A., Kahn, S. M., & Paerels, F. 2003, in The IGM/Galaxy Connection: The Distribution of Baryons at z = 0, ed. J. L. Rosenberg, & M. E. Putman (Dordrecht: Kluwer Academic Publishers), ASSL Conf. Proc., 281, 109 [Google Scholar]
- Ricotti, M. 2010, Adv. Astron., 2010, 1 [CrossRef] [Google Scholar]
- Ricotti, M., & Gnedin, N. Y. 2005, ApJ, 629, 259 [NASA ADS] [CrossRef] [Google Scholar]
- Ricotti, M., Gnedin, N. Y., & Shull, J. M. 2008, ApJ, 685, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Salvadori, S., & Ferrara, A. 2009, MNRAS, 395, L6 [NASA ADS] [Google Scholar]
- Samui, S., Subramanian, K., & Srianand, R. 2008, MNRAS, 385, 783 [NASA ADS] [CrossRef] [Google Scholar]
- Samui, S., Subramanian, K., & Srianand, R. 2010, MNRAS, 402, 2778 [NASA ADS] [CrossRef] [Google Scholar]
- Schmidt, M. 1959, ApJ, 129, 243 [NASA ADS] [CrossRef] [Google Scholar]
- Segalovitz, A., Shane, W. W., & de Bruyn, A. G. 1976, Nature, 264, 222 [NASA ADS] [CrossRef] [Google Scholar]
- Sembach, K. R. 2006, in The Local Group as an astrophysical laboratory, Proc. of the Space Telescope Science Institute Symposium Series, ed. M. Livio, & T. M. Brown (Cambridge Univ. Press), 17, 86 [Google Scholar]
- Seymour, N., Dwelly, Y., Moss, D., et al. 2008, MNRAS, 386, 1695 [NASA ADS] [CrossRef] [Google Scholar]
- Siejkowski, H., Soida, M., Otmianowska-Mazur, K., Hanasz, M., & Bomans, D. J. 2010, A&A, 510, A97 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Skillman, E. D., Tolstoy, E., Cole, A. A., et al. 2003, ApJ, 596, 253 [NASA ADS] [CrossRef] [Google Scholar]
- Socrates, A., Davis, S. W., & Ramirez-Ruiz, E. 2008, ApJ, 687, 202 [NASA ADS] [CrossRef] [Google Scholar]
- Songaila, A., & Cowie, L. L. 1996, AJ, 112, 335 [NASA ADS] [CrossRef] [Google Scholar]
- Staveley-Smith, L, Sault, R. J., Hatzidimitriou, D., Kesteven, M. J., & McConnell, D. 1997, MNRAS, 289, 225 [NASA ADS] [CrossRef] [Google Scholar]
- Stil, J. M., & Israel, F. P. 2002, A&A, 392, 473 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Strigari, L. E., Bullock, J. S., Kaplinghat, M., et al. 2008, Nature, 454, 1096 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Tabatabaei, F. S., Krause, M., Fletcher, A., & Beck, R. 2008, A&A, 490, 1005 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tassis, K., Kravtsov, A. V., & Gnedin, N. Y. 2008, ApJ, 672, 888 [NASA ADS] [CrossRef] [Google Scholar]
- Tolstoy, E., Hill, V., & Tosi, M. 2009, ARA&A, 47, 371 [NASA ADS] [CrossRef] [Google Scholar]
- Valdez-Gutiérrez, M., Rosado, M., Puerari, I., et al. 2002, ApJ, 124, 3157 [Google Scholar]
- Vallée, J. P. 2004, New Astron. Rev., 48, 763 [NASA ADS] [CrossRef] [Google Scholar]
- van Eymeren, J., Marcelin, M., Koribalski, B., et al. 2009, A&A, 493, 511 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vazquez, G. A., & Leitherer, C. 2005, ApJ, 621, 695 [NASA ADS] [CrossRef] [Google Scholar]
- Veilleux, S., Cecil, G., & Bland-Hawthorn, J. 2005, ARA&A, 43, 769 [Google Scholar]
- Verma, A., Lehnert, M. D., Förster Schreiber, N. M., Bremer, M. N., & Douglas, L. 2007, MNRAS, 377, 1024 [NASA ADS] [CrossRef] [Google Scholar]
- Weżgowiec, M., Urbanik, M., Vollmer, B., et al. 2007, A&A, 471, 93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Widrow, L. M. 2002, Rev. Mod. Phys., 74, 775 [NASA ADS] [CrossRef] [Google Scholar]
- Woo, J., Courteau, S., & Dekel, A. 2008, MNRAS, 390, 1453 [NASA ADS] [Google Scholar]
- Young, J. S., Allen, L., Kenney, J. D. P., Lesser, A., & Rownd, B. 1996, AJ, 112, 1903 [NASA ADS] [CrossRef] [Google Scholar]
- Zeldovich, Y. B., Ruzmaikin, A. A., & Sokoloff, D. D. 1990, The Almighty Chance (Singapore: World Scientific Publication) [Google Scholar]
- Zweibel, E. G. 2006, Astron. Nachr., 327, 505 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Derivation of magnetic field strengths
According to the theory of synchrotron emission (e.g. Pacholczyk 1970), the total synchrotron intensity and the degree of linear polarization obtained from our radio polarimetric observations can be used to calculate the strengths of the total (Btot) and regular (Breg) magnetic field. With the assumption of equipartition between the energy densities of the magnetic field and cosmic rays (εCR = εBtot = Btot/8π), the total magnetic field is (Beck & Krause 2005) ![\appendix \setcounter{section}{1} \begin{equation} B_{\rm tot} = \left[\frac{4\pi(2\alpha_{\rm n}+1)(K_0+1)I_{\rm n}E_{\rm p}^{1-2\alpha_{\rm n}}(\frac{\nu}{2c_1})^{\alpha_{\rm n}}}{(2\alpha_{\rm n}-1)c_2\alpha_{\rm n}Lc_3}\right]^{1 \over{\alpha_{\rm n}+3}}, \end{equation}](/articles/aa/full_html/2011/05/aa15393-10/aa15393-10-eq226.png) (A.1)where K0 is the constant ratio of proton to electron number densities, In is the nonthermal intensity, and αn is the mean synchrotron spectral index, L denotes the pathlength through the synchrotron emitting medium, Ep is the proton rest energy, and c1 is a constant defined as
(A.1)where K0 is the constant ratio of proton to electron number densities, In is the nonthermal intensity, and αn is the mean synchrotron spectral index, L denotes the pathlength through the synchrotron emitting medium, Ep is the proton rest energy, and c1 is a constant defined as 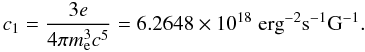 (A.2)The constants c2 and c3 depend on the spectral index and the inclination of the magnetic field, respectively
(A.2)The constants c2 and c3 depend on the spectral index and the inclination of the magnetic field, respectively ![\appendix \setcounter{section}{1} \begin{equation} c_2(\alpha_{\rm n}) = {1\over4}c_3 \frac{(\alpha_{\rm n}+{5\over3})}{(\alpha_{\rm n}+1)} \Gamma\left[{(3\alpha_{\rm n}+1)\over6}\right]\times\Gamma\left[{(3\alpha_{\rm n}+5)\over6}\right], \end{equation}](/articles/aa/full_html/2011/05/aa15393-10/aa15393-10-eq236.png) (A.3)where c3 = (cosi)αn + 1. This is true for a region where the field is totally regular and has a constant inclination i with respect to the sky plane. If the synchrotron intensity is averaged over a large volume (as in estimating the mean field strength), the value of c3 has to be replaced by its average over all occurring values of i. For a totally turbulent field, one needs to use c3 = (2/3)(αn + 1)/2.
(A.3)where c3 = (cosi)αn + 1. This is true for a region where the field is totally regular and has a constant inclination i with respect to the sky plane. If the synchrotron intensity is averaged over a large volume (as in estimating the mean field strength), the value of c3 has to be replaced by its average over all occurring values of i. For a totally turbulent field, one needs to use c3 = (2/3)(αn + 1)/2.
The dependence of the total magnetic field (in μG) of NGC 6822 on the synchrotron pathlength (L) and the proton-to-electron ratio (K0).
To estimate the strength of the regular magnetic field in the sky plane, we can use the observed nonthermal degree of polarization (Segalovitz et al. 1976) ![\appendix \setcounter{section}{1} \begin{equation} P_{\rm nth} = \left(\frac{3\gamma+3}{3\gamma+7}\right)\times \left[1+\frac{(1-q)\pi^{1\over2}\Gamma[(\gamma+5)/4]}{2q\Gamma[(\gamma+7)/4]F(i)}\right]^{-1}, \end{equation}](/articles/aa/full_html/2011/05/aa15393-10/aa15393-10-eq242.png) (A.4)where
(A.4)where 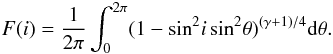 (A.5)In the above formulae, q2/(1 + γ) = Breg/Bturb, γ = 2αn + 1, and θ is the azimuthal angle.
(A.5)In the above formulae, q2/(1 + γ) = Breg/Bturb, γ = 2αn + 1, and θ is the azimuthal angle.
In calculating magnetic field strengths, some uncertainties can be introduced by assuming a proton-to-electron number density ratio, as well as a geometry for the galaxy. We assume ellipsoidal geometries of the studied galaxies, using their minor axes as the synchrotron pathlength. An ellipsoidal approximation of the geometry of a dwarf galaxy was applied by Chyży et al. (2003) to derive the magnetic field strength for NGC 6822 from the 4.85 GHz data. To test the influence of these parameters, we performed calculations of the magnetic field in NGC 6822, varying Ko in the range of 50–150 and L in the range of 1–3 kpc. The results are presented in Table A.1. The largest deviation in our calculations was 32% (see Table A.1), while typically it did not exceed 15%. Therefore, varying these parameters by 50%, as we also did for the nonthermal flux and the degree of polarization, to calculate the global error in the magnetic field strengths (see Sect. 4.2), provides us with errors that thoroughly estimate the possible uncertainties. We also tested whether the magnetic field strength depends on galaxy distance, thus on the location within the Local Group with respect to the Milky Way. For all LG dIrrs, the correlation coefficient r = −0.37 with P = 23%, which means that the distance has no statistically significant influence.
All Tables
Magnetic field estimates and physical parameters for our sample of LG dwarfs and comparison dwarfs.
Correlation coefficients, their significance levels in percentages, and the number of dwarfs included in calculations.
The dependence of the total magnetic field (in μG) of NGC 6822 on the synchrotron pathlength (L) and the proton-to-electron ratio (K0).
All Figures
 |
Fig. 1 The total power map of IC 10 at 2.64 GHz overlaid onto the DSS blue image. The contours are at 3, 5, 8, 16, 25, 40 × 3.9 mJy/b.a. The map resolution is |
| In the text | |
 |
Fig. 2 The total power map of NGC 6822 at 2.64 GHz overlaid onto the DSS blue image. The contours are at 3, 5, 8, 15, 20, 40, 80 × 1.2 mJy/b.a. The map resolution is |
| In the text | |
 |
Fig. 3 The total power map of IC 1613 at 2.64 GHz overlaid onto the DSS blue image. The contours are at 3, 5, 8, 20, 40 × 1.1 mJy/b.a. The map resolution is |
| In the text | |
 |
Fig. 4 The total power map of IC 1613 at 4.85 GHz with apparent B-vectors of polarized intensity overlaid onto the DSS blue image. The contours are at 3, 5, 8, 12, 16, 25, 40, 100, 200 × 0.3 mJy/b.a., and a vector of 1′ length corresponds to the polarized intensity of 0.3 mJy/b.a. The map resolution is |
| In the text | |
 |
Fig. 5 The map of polarized intensity of IC 1613 at 4.85 GHz with apparent B-vectors of polarization degree overlaid onto the DSS blue image. The contours are at 3, 5, 8, 12, 16 × 0.05 mJy/b.a., and a vector of 1′ length corresponds to the polarization degree of 20%. The map resolution is |
| In the text | |
 |
Fig. 6 Signal to rms noise level ratio versus the noise level for our maps of LG dwarfs and for maps of the Magellanic Clouds (Haynes et al. 1991) at 2.64 GHz. The undetected objects are marked. |
| In the text | |
 |
Fig. 7 Correlations of the magnetic field strength and SFR with other parameters. LG dwarfs from our sample, LMC, and SMC are marked by circles or in cases when the upper limit of the radio emission was applied – by triangles. Comparison dwarfs are marked by squares. The solid lines present power-law fits. Fits a and c are restricted to radio-detected dwarfs only (circles and squares). |
| In the text | |
 |
Fig. 8 Magnetic field strength versus velocity dispersion for dwarf galaxies. See Fig. 7 for symbol coding. |
| In the text | |
 |
Fig. 9 Dwarf galaxies on the past-future evolution plane: p = log (SFR T0/LB) and f = log [MHI/(SFR T0)] . The comparison galaxies from outside of the Local Group are shown by squares. |
| In the text | |
 |
Fig. 10 Total magnetic field strengths plotted against rotational velocities of dwarfs. |
| In the text | |
 |
Fig. 11 The radio-infrared correlation diagram for LG dwarfs and comparison dwarfs (plotted with the same symbols as in Fig. 7), and for the sake of reference, the sample of galaxies observed by de Jong (1967) plotted as stars. The surface brightness at 2.64 GHz and at 60 μm is used (in Jy/◻′). The solid line is an orthogonal fit to the reference galaxies. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.