| Issue |
A&A
Volume 529, May 2011
|
|
|---|---|---|
| Article Number | A8 | |
| Number of page(s) | 14 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201014368 | |
| Published online | 21 March 2011 | |
Potential biosignatures in super-Earth atmospheres
I. Spectral appearance of super-Earths around M dwarfs
1
Institut für Planetenforschung, Deutsches Zentrum für Luft- und Raumfahrt, Rutherfordstraße 2, 12489 Berlin, Germany
e-mail: heike.rauer@dlr.de
2
Zentrum für Astronomie und Astrophysik, Technische Universität Berlin, Hardenbergstraße 36, 10623 Berlin, Germany
3
Université de Bordeaux, Observatoire Aquitain des Sciences de l’Univers, 2 rue de l’Observatoire, BP 89, 33271 Floirac Cedex, France
4
CNRS, UMR 5804, Laboratoire d’Astrophysique de Bordeaux, 2 rue de l’Observatoire, BP 89, 33271 Floirac Cedex, France
5
Institut für Methodik der Fernerkundung, Deutsches Zentrum für Luft- und Raumfahrt 82234 Oberpfaffenhofen-Wessling, Germany
Received: 5 March 2010
Accepted: 28 January 2011
Atmospheric temperature and mixing ratio profiles of terrestrial planets vary with the spectral energy flux distribution for different types of M-dwarf stars and the planetary gravity. We investigate the resulting effects on the spectral appearance of molecular absorption bands, which are relevant as indicators for potential planetary habitability during primary and secondary eclipse for transiting terrestrial planets with Earth-like biomass emissions. Atmospheric profiles are computed using a plane-parallel, 1D climate model coupled with a chemistry model. We then calculate simulated spectra using a line-by-line radiative transfer model.
We find that emission spectra during secondary eclipse show increasing absorption of methane, water, and ozone for planets orbiting quiet M0–M3 dwarfs and the active M-type star AD Leo compared with solar-type central stars. However, for planets orbiting very cool and quiet M dwarfs (M4 to M7), increasing temperatures in the mid-atmosphere lead to reduced absorption signals, which impedes the detection of molecules in these scenarios. Transmission spectra during primary eclipse show strong absorption features of CH4, N2O and H2O for planets orbiting quiet M0–M7 stars and AD Leo. The N2O absorption of an Earth-sized planet orbiting a quiet M7 star can even be as strong as the CO2 signal. However, ozone absorption decreases for planets orbiting these cool central stars owing to chemical effects in the atmosphere. To investigate the effect on the spectroscopic detection of absorption bands with potential future satellite missions, we compute signal-to-noise-ratios (SNR) for a James Webb Space Telescope (JWST)-like aperture telescope.
Key words: astrobiology / radiative transfer / planets and satellites: atmospheres
© ESO, 2011
1. Introduction
The majority of the more than 500 extra-solar planets found so far are giant gas planets. However, with improving detection techniques, more and more low-mass planets will be found. At the time of writing this paper, we know of more than 20 planets with (minimum) masses below 10 M⊕. Two systems (around Gliese 581 and HD 40307) host three potential low-mass planets each (Udry et al. 2007; Mayor et al. 2009). The only two low-mass planets where both radius and mass could be measured are CoRoT-7b (Léger et al. 2009; Queloz et al. 2009), a transiting planet of approximately 5 M⊕ and 1.7 R⊕, and GJ 1214b (Charbonneau et al. 2009), with 6.5 M⊕ and 2.7 R⊕. CoRoT-7b, which is likely to be a rocky planet, may therefore be classified as terrestrial (a so called super-Earth).
Whereas atmospheres of close-in gas giant planets around bright stars have been already spectroscopically characterised with the Hubble Space Telescope (HST) and the Spitzer IR-telescope (e.g. Vidal-Madjar et al. 2004; Tinetti et al. 2007; Swain et al. 2008, 2009; Knutson et al. 2008, 2009), terrestrial extra-solar planets seem out of reach with currently available telescopes. However, future satellite missions, such as the JWST (James Webb Space Telescope) or proposed dedicated missions for spectral characterisation, will provide an improved detection range. To which extent their performance will be sufficient to spectroscopically characterise the atmosphere of terrestrial planets in the habitable zone of their central star is the subject of increasing modelling investigations.
Previous major modelling efforts producing synthetic spectra of hypothetical terrestrial extra-solar planets were performed by e.g. Selsis (2000), Selsis et al. (2002), Des Marais et al. (2002), Segura et al. (2003, 2005), Tinetti (2006), Ehrenreich et al. (2006), Kaltenegger et al. (2007), Kaltenegger & Traub (2009) and Kaltenegger & Sasselov (2010). They examined the influence of e.g. stellar type, atmospheric abundances, background atmospheres or atmospheric evolution on the emission and transmission spectra.
This work focuses on emission and transmission spectra of super-Earth planetary atmospheres that orbit in the habitable zone (HZ) around M-dwarf stars because in these cases the highest signal-to-noise-ratios (SNRs) for potentially habitable planets are expected. Spectral resolution and the expected SNRs are studied for a photon-limited telescope with 6.5 m aperture (JWST-sized). Real SNRs will be significantly lower because of instrumental noise and the astronomical background. The values here serve as a “best case” therefore and provide a first estimate on the possible detection performance. A parametric study of expected SNRs for a wide range of star-planet combinations including instrumental noise for the JWST has been performed by Belu et al. (2011). We complement this study by a detailed investigation that includes the effects of atmospheric chemistry on habitable super-Earth planets.
Our approach is similar to that of Selsis (2000), Segura et al. (2003, 2005). We first apply an atmosphere column model to calculate the mean temperature profile and the corresponding chemical profiles assuming an Earth-like planet development and biomass emissions. We chose this approach because the T-p-profiles as well as the atmospheric mixing ratios vary depending on stellar type and planetary parameters. This was first shown for planets orbiting M-dwarf stars by Segura et al. (2005), who demonstrated the effect of the changing atmospheric chemistry on emission flux spectra of these Earth-like extra-solar planets. This early work did not include transit transmission spectra and SNR estimates or a change of planetary gravity though. SNRs were later calculated for a 6.5 m JWST-aperture telescope by Kaltenegger & Traub (2009) in a simplified approach, which kept the planetary atmospheric conditions fixed to those of a modern Earth when changing the central star. Their results showed the difficulty to detect the weak biosignatures in transmission spectra with the JWST, but also discussed how this could be overcome by co-adding several transit measurements. Our main goal is to extend these SNR investigations by including the effect of chemistry to study whether the detection of biosignatures could be favoured by chemical processes, as suggested by Segura et al. (2005). In addition, we also consider transmission and emission spectra.
The paper is organised as follows: Sect. 2 describes the atmospheric and radiative transfer models and the modelled scenarios. In Sect. 3 we show how the SNR calculations are performed. Section 4 compares the resulting emission and transmission spectra with modern Earth spectra, followed by the resolution and SNR calculations. Section 5 summarises the results.
2. Models and simulated scenarios
2.1. Atmospheric and spectral models
We used a 1D radiative-convective photochemical model to calculate the chemistry and climate of planets with an Earth-like atmospheric chemical composition. The model calculates the globally, diurnally-averaged atmospheric temperature, pressure, and composition profiles for cloud-free conditions. The original code has been described in detail by Kasting et al. (1984) and was further developed by Segura et al. (2003), Grenfell et al. (2007a,b). Here, we briefly summarise the model and describe its recent improvements.
The model extends from the ground up to the mid-mesosphere. The climate module grid is divided into 52 layers on a log-pressure grid. Compared with Grenfell et al. (2007a), we improved the calculation of the grid. Depending on how much water is evaporating at the surface, the pressure is re-adjusted in each iteration step. The chemistry module is divided into 64 equidistant layers in altitude. As an upgrade to previous model versions, the top layer is now equal to the top-of-atmosphere (TOA) altitude derived by the climate module. Hence, the model grid consistently takes into account the changing scale height with varying gravity in the climate and chemical modules, allowing the simulation of super-Earth planets with high gravity with consistent resolution.
The radiative transfer for incoming stellar radiation in our climate module covers the wavelength region from 237.6 nm to 4.545 μm with 38 wavelength bands. We used a two-stream radiative transfer method based on Toon et al. (1989). The radiatively active species considered are H2O, CO2, O2, O3, and CH4. Absorption coefficients are calculated by an exponential sum correlated-k method using up to four terms per sum. Rayleigh scattering is included for N2, O2, and CO2.
Stellar parameters used in this study.
For thermal emission we considered the wavelength range from 3.07–1000 μm in 16 bands, using the Rapid Radiative Transfer Model (RRTM, Mlawer et al. 1997). The model includes H2O, CO2, O3, CH4, and N2O as radiative gases in the IR-range. The absorption coefficients were calculated with the 16-term correlated-k method. Because k-coefficients are always calculated for a certain composition, temperature, and pressure range, the model is valid strictly only within 0.01–1050 mbar and for the Earth’s atmospheric temperature profile ± 30 K. For this reason, we limit our coolest input stellar spectra up to M7 dwarf stars for Earth-sized planets, and up to M5-type stars for super-Earth planets. Cooler M dwarfs would result in T-p profiles widely outside the applicable model range. Wet or dry adiabatic H2O lapse rates are used to obtain the temperature profile in the troposphere where applicable. The relative humidity profile is taken from Manabe & Wetherald (1967). We consider a mean solar zenith angle of 60° for the climate model.
The chemistry module includes 55 species with 212 chemical reactions. As in most previous model approaches and for modern Earth simulations, CO2, O2 and N2 are isoprofiles. To calculate the photolysis rates, we took into account a wavelength range from 121.4–855 nm and considered O3, O2, CO2, H2O, SO2, CH4, and H2S as radiative gases. Rayleigh scattering was included for N2, O2, and CO2. The mean solar zenith angle is 45°, following the approach by Segura et al. (2005). In addition to the species considered by Segura et al. (2005), we included H2O and CH4 when calculating the mean molecular weight of air and the concentration of the fill gas nitrogen. We furthermore changed the convergence criterion for the numerical solution from previous model versions to a maximum difference in volume mixing ratio for all species in all model layers of less than 10-4 to ensure convergence for all atmospheric profiles. Moreover, the height of the cold trap is now given by the climate module, and the mixing ratios of all chemical species are adjusted according to how much water is evaporated at the surface.
A main objective of this work is to present simulated spectra for transiting planets, corresponding to our simulated model scenarios. We therefore use the modelled T-p profiles together with the corresponding chemical abundances to calculate spectra for primary and secondary transit geometry. The radiative transfer model SQuIRRL (Schwarzschild Quadrature InfraRed Radiation Line-by-line, Schreier & Schimpf 2001) was used to calculate synthetic spectra in the infrared from 1.8 to 20 μm. SQuIRRL was found to be comparable with other radiative transfer codes (e.g. von Clarmann et al. 2003; Melsheimer et al. 2005). The model takes as input temperature, pressure, and concentration profiles of the following species from the atmospheric model: H2O, CO2, CH4, O3, N2O, CO, SO2, NO2, NO, HCl, HNO3, H2O2, HO2, and CH3Cl. H2O continuum absorption corrections are performed and local thermodynamic equilibrium (LTE) is assumed. Absorption cross sections for all molecules except H2O were computed using the Hitran 2004 line parameter data base (Rothman et al. 2005), for H2O line data from Hitemp 1995 (Rothman et al. 1995) were used. The emission spectra were calculated with a pencil beam looking downwards with a viewing angle of 38° to account for the average illumination. Transmission spectra are calculated for different atmospheric heights (62 layers in total) in limb geometry. The resulting spectra are binned for resolutions (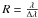 ) of R = 5 − 2000, corresponding to instrumental designs for low- and medium-resolution spectroscopy.
) of R = 5 − 2000, corresponding to instrumental designs for low- and medium-resolution spectroscopy.
2.2. Modelled scenarios
We study planets with Earth-like chemical composition in the habitable zone of M-dwarf stars of types M0–M7. The spectral appearance of the quiet M-dwarfs is approximated as black body emission curves according to effective temperatures and stellar parameters as specified in Kaltenegger & Traub (2009, see Table 1). But these input spectra neglect that many M-dwarf stars show strong activity in the UV range, much more than our Sun, for example. The high UV radiation can have a significant effect on atmospheric chemistry, as discussed in Segura et al. (2005). To illustrate the effect of high stellar UV flux on the expected spectral appearance of transiting planets, we therefore also used a composite spectrum of AD Leo (M4.5V) as central star, as described by Segura et al. (2005). This high-resolution spectrum is based on observations and a stellar model atmosphere. Observations were taken from satellite data (IUE, International Ultraviolet Explorer) and photometry in the visible (Pettersen & Hawley 1989) and near-IR (Leggett et al. 1996). Beyond 2.4 μm, a stellar atmospheric model (NextGen, Hauschildt et al. 1999) was used to calculate a synthetic spectrum. In addition, the Sun was used as a reference case for comparison. The solar spectrum was constructed using measurements provided by Gueymard (2004). The high-resolution spectra were binned appropriately for our broadband climate and chemical code. The stellar parameters are summarised in Table 1 and the input spectra used are shown in Fig. 1. Note the significantly higher UV flux of AD Leo compared with the quiet M4 and M5 dwarfs shortwards of about 310 nm.
 |
Fig. 1 Top: normalised stellar input spectra: Sun (black, solid), AD Leo (dotted), M0 (dashed), M1 (dash-dot), M2 (dash-dot-dot-dot), M3 (long dashes), M4 (red), M5 (green), M6 (blue), and M7 (magenta). Bottom: zoom into the photochemically relevant spectral range. |
We checked for the differences in spectral flux between an approximated Planck function and real spectral data using the Sun and AD Leo as examples. We found that the differences can be up to 20–40% in the visible and near IR and very large in the far UV. Thus, real stellar input spectra should be used whenever possible, especially for detailed chemistry calculations. However, for the parametric study performed here the Planck approximation is acceptable for quiet M-dwarfs.
In our study, planetary gravity was varied from 1g to 3g (9.8 to 29.4 m s-2). Hence, our 1g and 3g cases correspond to 1 and 11.4 Earth masses and 1 and 1.95 Earth radii (Sotin et al. 2007), respectively. The surface pressure was kept fixed at 1 bar. As in previous studies (e.g. Segura et al. 2003, 2005), we set the model parameters surface albedo and fluxes of chemical species in a way that the mean surface temperature of 288 K and observed surface concentrations of the chemical species H2, CO, CH4, N2O and CH3Cl are reproduced for present Earth. For the other model scenarios we kept the surface albedo and fluxes constant and calculated the atmospheric concentrations and surface temperature. However, in contrast to previous studies, we then placed the modelled extra-solar planets at an orbital distance from their central star where their total stellar energy input equals that of 1 solar constant (1366 W/m2). We chose this approach so that habitable surface temperatures were not enforced and allowed the temperature to adjust in a consistent way to the different spectral energy distribution of the M-dwarf stars. Thus, we separated in our investigation the effects of the different spectral energy distributions from variations of the total incoming flux. We will show in Sect. 4 that the resulting surface temperatures are still in the habitable range.
At present, the atmosphere of a terrestrial extrasolar planet has not been detected directly. Assumptions on their composition are therefore more or less arbitrary, and are based on our knowledge of the Solar System. In terms of searching for biomarkers, Earth is the only reference case we know of a planet with a biosphere. In this study, we therefore assume the same initial modern Earth atmospheric composition and biomass emissions for the simulated extra-solar planets. The final atmospheric composition for the star-planet-scenarios studied was then consistently calculated according to the coupled climate-chemistry model. Although the assumption of an Earth-like biosphere for planets orbiting stars that are quite different from our Sun is probably unrealistic, it nevertheless serves as a first step towards understanding the effects of different environmental factors on habitable planets and their atmospheres.
We used specifically the following surface boundary conditions to reproduce mean Earth conditions in our Sun-Earth reference run. Molecular hydrogen was removed at the surface with a constant deposition velocity of 7.7 × 10-4 cms-1. Biomarkers (N2O and CH3Cl) and related compounds (CO and CH4) were emitted with constant upwards fluxes per surface area in a procedure outlined e.g. in Grenfell et al. (2007b). For example a CH4 flux of 531 Tg/year is needed to reproduce modern Earth CH4 surface volume mixing ratios and is kept constant for all other simulated scenarios. This approach is different to the one employed by Segura et al. (2005), who kept the CH4 surface mixing ratio for the quiet M-star runs constant. Furthermore we did not need to change the CO surface boundary condition from a constant flux to a constant deposition velocity as was done in Segura et al. (2005) for their quiet M-star scenarios. As a result, our surface fluxes differ largely from those of Segura et al. (2005) but compare better with the observed values on Earth. Again we chose our approach to vary input parameters step-by-step, not to mix the influence of different effects in our analysis.
To validate our approach, we performed SNR calculations for several modern Earth transmission features, which were also performed by Kaltenegger & Traub (2009, their Table 2, single transit events). When we strictly followed their approach (fixed the atmospheric T-p profiles and composition to modern Earth), we were able to reproduce their values to within 2%. A direct comparison of the model results with observations of the Earth transmission spectra by e.g. Pallé (2010) is unfortunately not possible. The measured spectrum is shortwards of 2.4 μm and thus overlaps only little with our modelling range. Furthermore, because our model is stationary and cloud-free a comparison with real data of a cloudy Earth is difficult and no direct agreement is expected. A comparison with Segura et al. (2005) is discussed in more detail in Sect. 5.
3. SNR calculations
We here consider emission and transmission spectroscopy in the near- to mid-IR wavelength range. We account for photon noise only to give an upper limit on the detection feasibility. Additional noise sources, e.g. instrumental or astrophysical, like zodiacal light, will further decrease the signal-to-noise ratio (SNR) computed here. This section describes the method used to calculate the respective SNR.
3.1. Emission
The planetary emission spectrum, Fp, is obtained by combining fluxes (with equal integration times) observed during (F1) and outside (F2) secondary eclipse 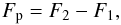 (1)where F1 = Fs and F2 = Fs + Fp, and Fs represents the stellar flux. The SNR for the planetary spectrum is therefore
(1)where F1 = Fs and F2 = Fs + Fp, and Fs represents the stellar flux. The SNR for the planetary spectrum is therefore 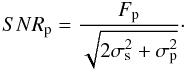 (2)Here, σs and σp denote the stellar and planetary flux standard deviation, respectively. Assuming a photon-limited instrument (hence, only Poisson noise from star and planet) and Fs ≫ Fp, we then reduce (2) to
(2)Here, σs and σp denote the stellar and planetary flux standard deviation, respectively. Assuming a photon-limited instrument (hence, only Poisson noise from star and planet) and Fs ≫ Fp, we then reduce (2) to  (3)with SNRs the stellar SNR and CE the contrast between planetary and stellar signal in the secondary eclipse emission spectrum. The resulting SNR is conservative compared with the continuum flux region.
(3)with SNRs the stellar SNR and CE the contrast between planetary and stellar signal in the secondary eclipse emission spectrum. The resulting SNR is conservative compared with the continuum flux region.
CE is calculated from the integrated fluxes of a hemisphere as
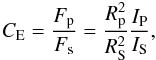 (4)where RP and RS are planetary and stellar radius, respectively, and IP and IS are the spectral energy fluxes (in W m-2 μm-1) from planet and star, respectively. Here, the star is taken as a blackbody with a fixed effective temperature, consistent with previous studies (e.g., Kaltenegger & Traub 2009). The observable stellar signal SS (in J μm-1) is calculated by
(4)where RP and RS are planetary and stellar radius, respectively, and IP and IS are the spectral energy fluxes (in W m-2 μm-1) from planet and star, respectively. Here, the star is taken as a blackbody with a fixed effective temperature, consistent with previous studies (e.g., Kaltenegger & Traub 2009). The observable stellar signal SS (in J μm-1) is calculated by
 (5)where d is the distance to the star, A is the telescope area (assuming a 6.5 m JWST-like aperture in this case) and t the integration time. To convert into the number of photons, we divide SS by
(5)where d is the distance to the star, A is the telescope area (assuming a 6.5 m JWST-like aperture in this case) and t the integration time. To convert into the number of photons, we divide SS by 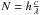 (h Planck constant, c speed of light, λ wavelength). From there, we can calculate the spectrally integrated stellar signal SI (number of photons)
(h Planck constant, c speed of light, λ wavelength). From there, we can calculate the spectrally integrated stellar signal SI (number of photons)
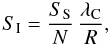 (6)with λC the central wavelength and R the specified spectral resolution.
(6)with λC the central wavelength and R the specified spectral resolution.
Sdet, the signal received from the star by the detector, is calculated as 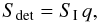 (7)where q is a factor to account for a non-ideal detector and the overall instrument throughput (assumed for JWST: q = 0.15 Kaltenegger & Traub 2009).
(7)where q is a factor to account for a non-ideal detector and the overall instrument throughput (assumed for JWST: q = 0.15 Kaltenegger & Traub 2009).
The signal-to-noise ratio of the star, SNRs, is calculated without taking into account instrumental or read-out noise.
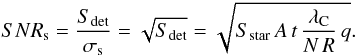 (8)The SNR values are calculated for integration times equal to the transit times of considered scenarios (t = TD). The duration, TD, of a transit is calculated by (assuming that RP ≪ RS, i = 90°)
(8)The SNR values are calculated for integration times equal to the transit times of considered scenarios (t = TD). The duration, TD, of a transit is calculated by (assuming that RP ≪ RS, i = 90°)
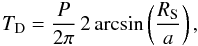 (9)where P is the orbital period and a the planetary orbital distance.
(9)where P is the orbital period and a the planetary orbital distance.
From Eq. (3) we then calculate the planetary SNR (SNRp).
Integration times ti for a certain specified SNRti are obtained from 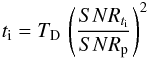 (10)using the
(10)using the  scaling of SNR with integration time.
scaling of SNR with integration time.
Because the SNR scales with  and therefore d-1, the integration times calculated for a specific distance d1 can be easily scaled to any distance d2:
and therefore d-1, the integration times calculated for a specific distance d1 can be easily scaled to any distance d2: 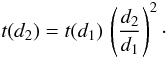 (11)
(11)
3.2. Transmission
The transmission contrast is, to a first order approximation, the photometric transit depth, i.e.
 (12)which is much higher than CE from Eq. (4).
(12)which is much higher than CE from Eq. (4).
In our transmission calculations, we simulated 62 adjacent tangent height rays through the atmosphere, with a diameter corresponding to the altitude layer difference in the chemical module. The central altitudes of the beams correspond to the layer altitudes of our model atmosphere. From there, the effective height h(λ) of the atmosphere is calculated as
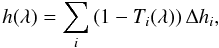 (13)where Ti is the transmission for ray i at wavelength λ and Δhi the altitude difference between consecutive tangent heights. The additional transit depth, fA, provided by the atmosphere is therefore obtained by
(13)where Ti is the transmission for ray i at wavelength λ and Δhi the altitude difference between consecutive tangent heights. The additional transit depth, fA, provided by the atmosphere is therefore obtained by
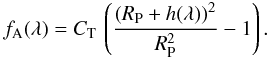 (14)The overall transmission, T, of a beam at a given wavelength λ is calculated by
(14)The overall transmission, T, of a beam at a given wavelength λ is calculated by 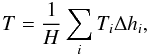 (15)where H is the total height of the considered atmosphere. Because our beams cross the atmosphere in equidistant grid points, T is the simple arithmetic mean of all Ti.
(15)where H is the total height of the considered atmosphere. Because our beams cross the atmosphere in equidistant grid points, T is the simple arithmetic mean of all Ti.
The SNR of a spectral feature in transmission is then calculated by (analogous to Eq. (3))
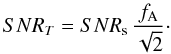 (16)Note the additional factor
(16)Note the additional factor 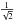 in our SNR compared with Kaltenegger & Traub (2009). The factor results from our approach that considers the planet signal as resulting from the difference of the measured stellar flux in and out of transit.
in our SNR compared with Kaltenegger & Traub (2009). The factor results from our approach that considers the planet signal as resulting from the difference of the measured stellar flux in and out of transit.
Required integration times or integration times vs. distance are then obtained by the same scaling as in Eqs. (10) and (11).
4. Results
4.1. Atmospheric profiles
4.1.1. Temperature profiles
 |
Fig. 2 Influence of gravity: Earth-sized (solid) vs. 3g super-Earth planet (dashed) around the Sun. |
Figure 2 shows the temperature profiles for two different planet gravity values (1g, 3g) with solar radiation in both cases. The temperature profile for the modern Earth control run shows a convective troposphere, and the temperature inversion and stratospheric temperature maximum caused by ozone heating.
The surface temperature decreases for the 3g scenario. This is because we held the surface pressure constant, which consequently lowered the vertical column mass. Less mass means less absorption and therefore less greenhouse effect, hence lower surface temperatures. Furthermore, effective ozone heating occurs at higher pressures, p, and the temperature maximum in the stratosphere accordingly decreases to higher p when increasing gravity. Overall increased stratospheric ozone levels (see Sect. 4.1.2) lead to enhanced heating in these parts of the atmosphere.
 |
Fig. 3 Influence of stellar spectrum: Earth-sized planets around the Sun (black, solid), AD Leo (dotted), M0 (dashed), M1 (dash-dot), M2 (dash-dot-dot-dot), M3 (long dashes), M4 (red), M5 (green), M6 (blue), and M7-type stars (magenta). |
Figure 3 shows the influence of the stellar type on the temperature profile for the Earth control case as well as 1g planets around AD Leo and the M0 to M7 stars from Table 1. Because unlike in previous approaches, we did not fix the surface temperature of our modelled planets by different stellar insolations at TOA, it is interesting to note that although Earth-like planets around M-dwarfs show somewhat increased surface temperatures, they always remain well within the habitable range for a total received energy flux of 1 solar constant. However, surface temperatures for the 1g scenarios are up to 20 K higher than for the Earth-Sun case. For the super-Earth scenarios similar changes occur. Here, surface temperatures are higher for the M-type central stars than for the Sun, and increase from M0 to M4-type stars (not shown). The increase occurs because Rayleigh scattering contributes less to the planetary albedo owing to the λ-4-dependence of the Rayleigh scattering coefficient. In addition, we find enhanced greenhouse warming (see below). Overall, however, the differences in spectral energy distribution alone have only a moderate effect on mean surface temperatures in the context of habitability in general. They may nevertheless significantly alter the planetary environment when studying the detailed atmospheric conditions (for example in a 3D approach that includes dynamical effects such as tidal-locking, see e.g. Joshi et al. 1997).
The main differences between the Sun and the M-star planets are found in the stratosphere, as already noted by Segura et al. (2005). The atmospheres of the modelled M-star planets do not show a stratospheric temperature inversion up to type M5 (M4) for the Earth-sized (super-Earths) planets. This is caused by the different stellar energy flux distribution of M-dwarfs compared with the Sun. The reduced UV flux longwards of about 250 nm results in less heating by ozone and therefore a reduced stratospheric inversion. We confirm this finding by Segura et al. (2005) for the active star AD Leo. In addition, our study also includes model runs for several quiet M-dwarfs with otherwise the same parameters for their orbiting planets. As can be seen in Fig. 3, the planetary stratospheric temperatures increase from hot (M0) to cooler M central stars (M7), even building up a stratospheric inversion again for M6 and M7 stars. This is caused by increasing amounts of methane and water in the mid-atmosphere (see following section) which lead to enhanced absorption and therefore heating of the stratosphere.
As already noted by Segura et al. (2003) and von Paris et al. (2008), the RRTM radiation scheme as applied in the model has been constructed for atmospheres that do not deviate too much from Earth conditions both in terms of temperature structure and composition (Mlawer et al. 1997). When applied to atmospheres that significantly deviate from modern Earth, it is important to check that the atmospheric T-p-profiles do not leave the validity range of RRTM. If this is the case, the resulting effect on the heating and cooling rates must be estimated.
We compared the computed T-p-profiles for the atmosphere considered here to the validity range of RRTM. We found that T-p-profiles for most M-dwarf central stars leave the validity range significantly only in the upper atmosphere. As shown by von Paris et al. (2008), variations in upper stratospheric optical depths have a negligible influence on lower atmospheric temperature profiles. Most of the emission spectra originate in pressures higher than 0.1 bar, except for planets around very cool M dwarfs. For a given chemical composition, the transmission spectra are nearly independent of T-p structure (in contrast to the emission spectra), hence uncertainties in the IR radiative transfer of the climate model are unlikely to significantly influence the transmission spectra. To investigate whether these temperature errors might in turn influence the chemical composition of the atmosphere by means of e.g. temperature-dependent reaction rates, additional tests were performed in which the stratospheric temperatures were arbitrarily changed by ± 10 K. Observed changes in concentrations and column amounts did not exceed 5–20% depending on species, with methane showing the largest effect. However, no difference could be discerned in the spectra. Hence, the influence of errors in stratospheric optical depths on the planetary spectra is likely to be small. A comparison of the thermal fluxes of RRTM with thermal fluxes computed by the line-by-line radiative transfer code SQuIRRL showed an agreement of the total outgoing fluxes within 5.5%.
The surface temperature decreases again for the 1g planet that orbits the M7 star. In view of the above discussion on model validation, we consider the M7 case to be at the limit of the application range. We did not study cooler central stars here, because the results would be out of the application range over most of the atmosphere. For the same reason, we also exclude the M6 and M7 stars from our further analysis of 3g super-Earth scenarios. Nevertheless, the M7 case indicates an interesting trend. Increased absorption of stellar radiation in mid-atmosphere levels owing to massively increased H2O and CH4 concentrations results in less radiation reaching the ground. Whether this trend would continue for planets that orbit even cooler M dwarf stars would need to be further investigated with a model adapted to these conditions.
4.1.2. Chemical profiles
Ozone, nitrous oxide, methyl chloride, methane, and water are the major biomarker molecules and related compounds. In this section we give a broad overview of the concentrations of O3, N2O, CH3Cl, CH4 and H2O. A detailed analysis of the chemical processes for the model runs presented here will be given in a forthcoming publication (Grenfell et al., hereafter Paper II).
 |
Fig. 4 Chemical profiles for an Earth-sized planet (solid) and a 3g super-Earth (dotted) around the Sun. |
Chemical profiles for 1g and 3g scenarios.
Because of the decrease in total column mass for the 3g planetary scenario compared with the 1g case (because of the fixed surface pressure of 1 bar), the decrease in greenhouse effect (GHE) resulted in lower tropospheric temperatures. This in turn led to a small lowering in the tropospheric H2O number densities, as can be seen in the upper left panel of Fig. 4. Although the impact on the number density is small, the impact on the H2O column is large (it is five times lower for the 3g case than for the 1g scenario) owing to the overall decrease in column mass. The decrease in the H2O column led to a lowering in OH to a surface number density of 1.24 × 106 molec. cm-3 compared with 1.31 × 106 molec. cm-3 for the 1g case. Because OH is a major sink for CH4, its number density and column increased. While the surface CH4 number density increased from 3.9 × 1013 molec. cm-3 (1g) to 1.7 × 1014 molec. cm-3 (3g) (see upper right panel in Fig. 4), the column increased by 44% only, again owing to the lower total column mass for the 3g scenario.
The O3 number density increased for the 3g planetary scenario (see lower left panel in Fig. 4) in the lower to mid-atmosphere compared with the 1g case. The overall smaller column amount at 3g led to a small strengthening of the Chapman source at these levels (for more details see Paper II). The main ozone photochemical features typical of the Earth were maintained at 1g and 3g, e.g. in both cases HOx and NOx catalytic cycles were important in the upper and lower atmospheres respectively, whereas the smog cycle was important for ozone production in the troposphere for both 1g and 3g. Compared with changing the stellar type (see below), the effects of increasing gravity are rather small, however. Nevertheless, a more detailed study of the chemical effects in simulated super-Earth planet atmospheres is given in Paper II.
Chemical profiles for different stellar types
The response of biomarkers and important greenhouse gases to different central stars is shown in Fig. 5 for some examples. Increasing the M-dwarf stellar type and consequently decreasing the amount of UV radiation (except for the active star AD Leo) has a significant effect on the photochemical responses in the atmosphere. We briefly discuss the main photochemical responses. For more details we refer to the analysis of the chemical processes made in Paper II.
We first note a strong increase in planetary stratospheric water content when moving from the Sun via M0 stars to our coolest central star, M7. Furthermore, methane significantly increases for cooler central stars. One cause for increased stratospheric water is the increase in tropospheric water abundance owing to higher surface temperatures. Another reason is the reduced UV flux of quiet M dwarfs compared with the Sun, which leads to less photolytic destruction (see Fig. 1). As a result, the abundance of OH is also reduced, which can lead to reduced CH4 destruction. On the other hand, increased methane abundances can lead to faster CH4 oxidation and therefore to increased stratospheric water production, as suggested by Segura et al. (2005). Detailed investigations show that other catalytic cycles also play a role. This analysis is presented in Paper II.
Segura et al. (2005) pointed out that the photolytic destruction of methane in Earth-like, high-oxygen planets is slow, and in combination with drastically reduced sinks by OH this could lead to a “methane runaway”. Possible methane runaway feedbacks are quite well investigated for the Earth’s atmosphere (e.g. Prather 1996). The main feedback is positive, where more methane leads to less OH, therefore slower methane in-situ oxidation, which favours methane even more. There is also an opposing, negative feedback on Earth, e.g. methane warming leads to a damper atmosphere, which favours an increase in OH. There exist potentially complex interactions e.g. with NOx emissions, where increased NOx generally favours fast partitioning of HO2 into OH (via: NO + HO2 → OH + NO2) which in turn affects the CH4 runaway. Lelieveld et al. (2002) provided an overview of these effects. In model simulations as presented here and in Segura et al. (2005), methane runaway can occur as an unphysical scenario for quiet M-dwarfs if the assumed methane fluxes exceed the chemical sinks and loss processes in the model. Our methane fluxes are lower than those of Segura et al. (2005), and this methane runaway does not occur for our scenarios.
 |
Fig. 5 Influence of central star type on chemical atmospheric profiles of an Earth-sized planet: Sun (solid), M0 (long dashed), AD Leo (dotted), M5 (dot-dashed), M7 (triple-dot-dashed). |
 |
Fig. 6 Contrast spectra for an Earth-sized planet (1g) around the Sun (black), AD Leo (red), M0 (green), M5 (blue), and M7 (magenta). |
Figure 5 shows the ozone profiles for the Earth-sized planet scenarios. The ozone profile of the Earth-Sun reference run and the planets that orbit AD Leo are similar, whereas ozone decreases for cooler M-dwarfs and is significantly reduced in the M4 to M7 cases. Ozone abundances are controlled by the balance between photochemical sources via the established Chapman and smog mechanisms and the catalytic O3 sinks, which depend on concentrations of e.g. hydrogen and nitrogen-oxides. A key result of the analysis of chemical processes in Paper II is that ozone production changes from being dominated by the Chapman to the smog mechanism with increasing stellar type, thus with decreasing effective temperature and UV flux. The weaker UV flux from the cooler M dwarfs leads to slower photolysis of the O2 molecule, which is required by the Chapman mechanism. Smog production is still slow in comparison. This explains the decline of ozone for cool, quiet M-dwarf central stars. The simulated planet that orbit the active star AD Leo though shows a pronounced ozone layer similar to the Earth owing to its higher UV flux compared with the quiet M4 and M5 stars. The prominent ozone layer for active M dwarfs was also found by Segura et al. (2005). More details on the changing ozone production mechanisms for cool central stars are explained in Paper II.
The changing stellar flux of M dwarfs with increasing M-star class also leads to a strong increase in N2O densities (Fig. 5). This is again caused by reduced photolysis rates due to the lower UV flux. Again, the effect is smaller for active M-dwarfs like AD Leo, where the photolysis rates are much higher.
We also investigated the abundance of the biomarker molecule CH3Cl (not shown here), because Segura et al. (2005) showed this to potentially cause significant absorption bands for high concentrations and active M-dwarf stars. In contrast to Segura et al. (2005), however, our required surface CH3Cl flux to reproduce mean Earth conditions is a factor of 2 lower, which also better agrees with the observed estimates. We find an increase in CH3Cl abundances for cooler M dwarfs owing to the reduced UV flux, similar to the increase in methane. However, in all cases studied, no significant spectral absorption could be seen in the emission spectra, whereas small absorption at 13.7 μm for the coolest central star (M7) can be found in the transmission spectrum (see Fig. 10). This molecule was therefore not investigated in more detail in this work.
4.2. Emission spectroscopy
4.2.1. Emission spectra
The IR emission spectra of extra-solar planets can be measured for transiting planets by observing the secondary eclipse. The planetary signal is derived from the difference of flux during and out-of-eclipse. Below, we show the expected flux contrast (planet/stellar flux) for computed planetary IR emission spectra.
The modern Earth reference contrast spectrum is shown in Fig. 6 (black line). The spectrum follows a blackbody spectrum with absorption bands of, e.g., water (2.7 μm, the broad 6.3 μm band and the rotation band longwards of 15 μm), methane (at 3.3 and 7.7 μm), ozone (9.6 μm) or carbon dioxide (2.7, 4.3 and 15 μm). The contrast between stellar and planetary flux is very low, reaching 10-6 in the mid-IR. Because of the rapid decrease of the planetary Planck function towards shorter wavelengths, the contrast falls below 10-10 in the near-IR.
 |
Fig. 7 Contrast spectrum of the 9.6 μm ozone band and the 15 μm carbon dioxide band for an Earth-sized planet around the Sun (black), AD Leo (red), M0 (green), M5 (blue), and M7 (magenta). Blue diamonds: binned to R = 20, red: smoothed spectra at the same resolution. |
 |
Fig. 8 Emission spectra: integration time in hours needed for SNR = 3 as a function of stellar distance of the 9.6 μm (dotted) ozone and the 15 μm (solid) carbon dioxide spectral feature at R = 20 for an Earth (black) and a 3g super-Earth (red) around AD Leo (top) and an M5 dwarf central star (bottom). Telescope configuration: JWST. |
Figure 6 also compares the spectra of an Earth-like planet (1g) when changing the central star (Sun, AD Leo, M0, M5, M7). The overall contrast is improved for terrestrial planets around M dwarfs, as expected. Because of the much lower effective temperatures and the smaller radius of M-dwarf stars, the contrast increases by about two orders of magnitude and eventually reaches about 10-4 in the mid-IR, which illustrates the improved potential of detecting planets around M-type dwarf stars.
Concerning molecular absorption bands, noticeable differences to the Earth-Sun system are found in the 2.3, 3.3 and 7.7 μm methane bands and the 3.8 and 4.5 μm band of nitrous oxide. These molecules show higher concentrations in the atmosphere of M dwarf planets compared with Earth (see Fig. 5), therefore we would expect their spectral signatures to be more pronounced. Additionally, the 4.7 μm band of CO becomes more prominent owing to its higher concentrations in the atmosphere (not shown). This can indeed be observed for the planets that orbit the quiet M0–M3 dwarfs stars. However, the absorption bands of N2O, CH4 become weaker for cooler M stars and almost completely disappear for an Earth-sized planet around the M7 star, despite the greatly enhanced abundances. This is caused by the temperature structure of these planets (see Fig. 3). The emission in the CH4 and N2O bands originates in the middle atmosphere because of the large concentrations of these gases, i.e. the atmosphere becomes transparent only at much higher altitudes than for Earth around the Sun. At these altitudes, the temperature is almost as high as the surface temperature, hence the contrast between continuum (transparent atmosphere) and absorption band is reduced. The absorption cannot be discerned from the spectrum any longer. Thus, the atmospheric composition may be difficult to detect via emission spectroscopy in planets orbiting quiet and very cool M dwarfs, despite a more favourable planet/star flux contrast ratio.
Another remarkable difference occurs for the 4.3 and 15 μm fundamental bands of carbon dioxide. The absence of a temperature inversion and the much colder stratosphere for the M0 to M5-type stars (see Fig. 3) have a noticeable effect, as already noted by Segura et al. (2005). The 4.3 μm band absorption is stronger for the M0 and AD Leo cases, and in the 15 μm band the emission peak is absent. However, as already discussed, our model runs for quiet M stars show that for cool stars, e.g. the M7 case, the emission spectrum originates mainly in the upper atmosphere for almost the entire spectrum (not only the CO2 fundamentals), and therefore molecular absorption features are weak.
 |
Fig. 9 Effective tangent heights: Earth and 3g super-Earth (red) around Sun. |
Figure 7 shows the 15 μm carbon dioxide and the 9.6 μm ozone band at high and low wavelength resolutions. The CO2 band is clearly visible already at a resolution of R = 20, although the emission peak close to the line centre is not resolved. This emission peak is an indicator of the atmospheric temperature inversion, hence a potentially important spectral feature. To resolve the emission peak, however, at least R ≈ 200 is necessary. The same conclusion holds for other interesting very narrow features. The ozone absorption at 9.6 μm is still visible at R = 20. For a detection of the molecule, low resolution seems to be sufficient. We also performed simulations for even lower resolution (R = 5). In this extreme, however, ozone is barely visible against the surrounding continuum and becomes difficult to detect.
4.2.2. Signal-to-noise-ratios
We calculated the expected SNR for different planet-star configurations. The chosen telescope aperture is as for JWST with an assumed efficiency of 0.15 (Kaltenegger & Traub 2009). Integration times correspond to a single transit event (i.e., 13 h for super-Earth around Sun and 3 h for super-Earth around AD Leo). For the Sun-Earth case, SNR values (not shown) are always below 0.15. Earth-like planets around M stars also show low SNR values. Table 2 summarises the achievable SNR values for a 3g super-Earth around the Sun, AD Leo, M0, and M5. As can be seen from Table 2, the single transit SNR is below unity for all absorptions, except for low resolution and late M dwarf types.
Table 2 shows that emission spectroscopy of terrestrial planets in the HZ provides very low SNR for a single transit duration exposure for the 3.3 μm methane, the 4.3 μm carbon dioxide, the 6.3 μm water and the 7.7 μm methane band. However, for the 9.6 μm band of ozone and the 15 μm band of carbon dioxide, SNR values are more encouraging at low resolution. Nevertheless, several transits need to be added to reach realistic SNR.
In Fig. 8 we show the integration times needed to obtain a SNR of 3 for R = 20 as a function of stellar distance. The planetary scenarios are the 1g Earth-like and 3g super-Earth planet around AD Leo and an M5 dwarf. As examples, we chose the ozone band and the broad carbon dioxide band at 15 μm. The integration time is indicated in units of transit time on the right y-axis. The figure indicates that for 3g super-Earths a SNR of 3 in the 15 μm CO2 band could be achieved in a single transit for the cool M5 dwarf closer than about 10 pc. Higher resolution is probably required for more detailed characterisation, e.g. for the detection of a temperature inversion.
4.3. Transmission spectroscopy
4.3.1. Transmission spectra
 |
Fig. 10 Comparison of atmospheric transmission of a 1g Earth-like planet around the Sun (black), AD Leo (red), M0 (green), M5 (blue), and M7 (magenta) dwarf stars. |
During primary eclipse the light of the central star passes through the atmosphere of the transiting planet and absorption by atmospheric molecules will change the apparent radius of the planet according to their scale height. Generally, transits are observed in the optical wavelength range because of the higher stellar flux and therefore better SNR. However, M-type stellar radiation is shifted somewhat to IR wavelengths and, furthermore, many interesting biomarker or related molecules show absorption in the IR. Below we therefore investigate the signal for primary transit spectroscopy in the near- to mid-IR range.
The wavelength-dependent effective tangent height of the planetary atmosphere blocks the stellar light, hence increases the apparent radius of the planet. The effective height h (see Eq. (13)) is shown in Fig. 9 for an Earth-sized planet (black line) and a super-Earth (red) around the Sun. h is mainly below 20 km, except for the strong methane 3.3 μm band, the ozone 9.6 μm band and the three 2.7, 4.3 and 15 μm bands of carbon dioxide in the case of the Earth. The super-Earth scenarios, however, may not be best suited for transmission spectroscopy, because the effective tangent height is of the order of the atmospheric scale height, which varies as g-1. From Eq. (14), the planetary signal decreases as g0.4 when using the mass-radius-relationship from Sotin et al. (2007). This effect is illustrated in Fig. 9.
The effect of changing the central star for the 1g scenarios is shown in Fig. 10 for various M-dwarf type central stars. The relative transmission spectrum (from Eq. (13)) of the Earth is shown in black. Absorption from water, ozone, carbon dioxide, and methane are clearly visible. Furthermore, the nitrous oxide 4.5 μm band and 17 μm band as well as a HNO3 band at 11.5 μm can be distinguished. Some interesting differences in the spectra are seen for M dwarfs. The 15 μm band of CO2 changes only by a small amount from the Sun up to the M7 central star. However, the nitrous oxide, methane and water bands continuously increase from earlier (hotter) to later (cooler) M dwarfs. We note that N2O absorption can be as strong as the main CO2 bands for the simulated planet around the M7 star. In this case, the nitrous oxide would be a strong biomarker signal. The HNO3 absorption basically disappears for AD Leo and is weak for the central M0 star case, but strongly increases up to the quiet M7 star.
Ozone is strongest in AD Leo and increases somewhat from M0 to M3 for the quiet central stars. The ozone signal then, however, decreases again for planets around cooler central stars due to the reduced overall O3 column. Thus, although atmospheric absorption signals in transmission may be easier to detect for planets orbiting cooler stars for most species, this may not be the case for ozone.
4.3.2. Signal-to-noise-ratios
Table 3 summarises the achievable SNR for different absorption bands for transmission spectroscopy during a single transit for Earth-sized planets around the Sun and M dwarfs. In contrast to emission spectroscopy, transmission spectroscopy does not probe the temperature structure of an atmosphere, but the chemical composition. Accordingly high resolution is not explicitly necessary. Unfortunately, at mid-IR wavelengths (e.g. 15 μm), the stellar SNR is relatively low, which makes detection harder than at shorter wavelengths (e.g., ozone at 9.6 μm or methane at 3.3 μm). For near-IR absorption bands of CH4 and CO2 a SNR > 1 can be achieved in a single transit, thus providing the possibility to achieve reasonable SNR if several transits can be co-added. Figure 11 illustrates this concept. It shows integration times as a function of required distance to achieve a SNR of 3.
Figure 11 implies that for close stars (closer than 5 pc) a JWST aperture-like telescope would be capable of performing low-resolution transmission spectroscopy for Earth-like planets on all bands for the simulated M5 dwarfs. Earlier types of M dwarfs, however, provide more challenging detection conditions. To cross-check our results and identify the differences of the approach used here, we compared our approach to that used by Kaltenegger & Traub (2009). The difference is that we calculated the atmospheric concentration profiles consistent with different M dwarf spectra, whereas Kaltenegger & Traub (2009) used a fixed modern-Earth reference profile. Both approaches yield quite similar results for the CO2 15 μm band. However, for e.g. the methane and ozone absorption we find significant differences. This shows that a consistent approach is necessary to take into account the effect of stellar spectral energy distribution on atmospheric T-p profiles and biomarker mixing ratios.
5. Summary and conclusions
 |
Fig. 11 Transmission: integration time needed for SNR = 3 as a function of stellar distance of the 3.3 μm methane (dash-dot-dot-dot), 4.3 μm carbon dioxide (dash-dot), 7.7 μm methane (dashed), 9.6 μm (dotted) ozone and the 15 μm (solid) carbon dioxide spectral feature at R = 20 for an Earth (black) and a 3g super-Earth (red) around AD Leo (top) and M5 (bottom). Telescope configuration is JWST. |
We investigated the effect of the stellar energy flux distribution of M-dwarf stars on atmospheric profiles of Earth-like and super-Earth planets. In addition, IR emission and transmission spectra and SNRs were computed to investigate how this affects the spectral appearance and detectability of absorption bands. We studied planets with 1g and 3g (1–2 Earth radii) because this approximately corresponds to the range from Earth to super-Earth planets. The planets were placed at a distance from their host star where the stellar energy input equals the energy of the Earth received by the Sun. To illustrate the detection capabilities for planets with biospheres, we arbitrarily assumed planets with modern Earth atmospheric composition as an initial starting value. However, the actual atmospheric composition was then re-calculated according to the incident stellar spectral flux to obtain a consistent model of the climatic conditions and composition of the atmospheres for these planets.
Our results suggest that the different spectral energy distribution of M dwarfs has a potentially large effect on the atmospheric T-p-profiles and on the chemical profiles of H2O, CH4, O3, N2O, and HNO3. In particular the temperature inversion in the mid-atmosphere disappears for planets around M dwarfs (Fig. 3). This was already found by Segura et al. (2005) for planets around active M-dwarf stars. For quiet stars with low UV flux we find, however, that an inversion can build up again in the planet’s atmosphere owing to enhanced concentrations of water and methane in the mid-atmosphere. In contrast to previous approaches, we did not fix the surface temperature to 288 K through stellar flux adjustments in our simulations. Surface temperatures can be up to 20 K higher for planets around M dwarfs for the same total stellar energy input, but the simulated planets always retain their habitable conditions. The effect on atmospheric structure and composition appears to be weaker when we varied gravity from 1–3g compared with varying the stellar input spectra (Fig. 2).
We found systematic increases in the atmospheric abundances for water, methane, and nitrous oxide owing to the reduced photolysis rates associated with M-dwarf stars compared with the Sun. Abundances generally increase from hot to cool M dwarf stars. For active M dwarfs, like AD Leo, photolysis heating rates are higher, and thus their related chemical processes are stronger than for the quiet M dwarfs of a similar type. Interestingly, planetary ozone abundances decrease for very cool, quiet central stars. This is caused by low photolysis rates which reduce the Chapman ozone production. In Grenfell et al. (Paper II) we present a detailed analysis of the chemical responses of these atmospheres.
The main goal of this work is to present simulated spectra and SNR estimates for the modelled planetary systems. We therefore discussed simulated spectra for secondary and primary transit geometries. During secondary eclipse, the measured emission fluxes depend not only on the composition of the atmosphere, but also on its temperature structure. The influence of the decreasing stellar effective temperature of M0–M7 stars on the planetary atmospheres can be seen in our simulated planet spectra. As already pointed out by Segura et al. (2005), absorption of O3, CH4, and N2O is easier to detect for planets that orbit active M dwarfs. We confirm this result for AD Leo and also for quiet M-dwarf central stars up to about type M3. For cooler central stars, however, the developing temperature inversion in the mid-atmosphere leads to reduced absorption signals, which almost level out for the coolest star considered (M7). Thus, although the abundances for most molecules continuously increase from M0 to M7 central stars, absorption features of atmospheric molecules are very difficult to detect in emission spectroscopy of planets that orbit very cool M dwarfs, which lead to potentially false negative detections of biomarkers in these cases.
Our simulations of transmission spectra during primary eclipses show that the relative transmission in spectral absorption bands of CO2, H2O, CH4 increases from M0 to M7 dwarfs, hence increases towards cooler M central stars. We point out that the increasing relative transmission of the biomarker N2O becomes comparable with the major CO2 band for Earth-sized planets around M7 stars. Because N2O is mainly produced from denitrifying bacteria on Earth, it is considered to be a good biomarker molecule. Unfortunately, for most planet scenarios the N2O absorption bands are far too weak to be detected compared with the dominant atmospheric constituents. This may be different for planets around central stars with very low UV fluxes.
The situation is different for transmission spectra of the biomarker ozone. For active and hot M dwarfs ozone absorption also increases. However, for planets around cool M stars (M4–M7) the ozone absorption is reduced again because of its smaller atmospheric abundances caused by the low UV flux in quiet M dwarf stars.
Our simulations confirm that low spectral resolution (around R = 20) is sufficient to identify most spectral features in the spectrum of a planet with an Earth-like atmosphere for IR emission as well as transmission spectra. A characterisation of an atmospheric temperature structure using IR emission spectra, e.g. by studying the presence of a temperature inversion, would require much higher spectral resolutions (of about >200).
Generally, emission spectra are studied in the IR wavelength range. Our SNR calculations show that the detection of the broad CO2 absorption feature at 15 μm and the ozone band at 9.6 μm could be feasible for planets around very nearby M dwarfs with exposure times of several hours for our modelled planet scenarios.
Transmission spectra obtained during primary eclipse of the planet, on the other hand, favour shorter wavelength ranges owing to the increasing stellar flux and therefore better SNR. In this case, detection of e.g. methane at 3.3 μm may be possible when adding transits for the nearest M dwarfs. Summing many transits with a stable instrument could bring the measurements into a feasible range for future observations.
Of course, the real atmospheric composition and total pressures of super-Earth planets remain unknown until the first spectroscopic detections can be made. Atmospheres even of planets similar to Earth may differ in atmospheric mixing ratios, or show e.g. more extended atmospheres. Clouds will additionally affect the detection of absorption signals (see e.g. Kitzmann et al. 2010). This will result in different SNR from those computed here, where only particular scenarios were studied. Investigations of a wide parameter range would therefore be needed. Looking for yet undetected planets, it is important to be open minded and take into account the unexpected, e.g. when designing instruments. Consistent modelling of climate and chemistry in the atmospheres of extra-solar planets is important, even when possible only in exemplary cases, for understanding effects on T-p-profiles and on the composition and therefore spectral appearance. An example is the effect of the T-p-profiles for emission spectra of cool M dwarf stars, which in the extreme case leads to extremely shallow absorption signals and consequently false negative detections. Another example is the ozone signal in transmission spectra, where the ozone column is significantly reduced for planets around very cool stars owing to chemical effects. For the main CO2 15 μm band, however, the differences are small when only considering detection of the broad absorption band. Nevertheless, if future telescopes will be able to observe terrestrial exoplanets at higher spectral resolution (R > 100), a consistent model approach for CO2 is also mandatory to interpret the temperature inversion peak of this band.
Acknowledgments
This research was partly supported by the Helmholtz Gemeinschaft (HGF) through the HGF research alliance “Planetary Evolution and Life”. We thank the anonymous referee for helpful comments. A. Belu, F. Selsis and P. Hedelt acknowledge support from the European Research Council (Starting Grant 209622: E3ARTHs)
References
- Belu, A. R., Selsis, F., Morales, J., et al. 2011, A&A, 525, A83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Charbonneau, D., Berta, Z. K., Irwin, J., et al. 2009, Nature, 462, 891 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Des Marais, D. J., Harwit, M. O., Jucks, K. W., et al. 2002, Astrobiology, 2, 153 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Ehrenreich, D., Tinetti, G., Lecavelier Des Etangs, A., Vidal-Madjar, A., & Selsis, F. 2006, A&A, 448, 379 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Grenfell, J. L., Grießmeier, J.-M., Patzer, B., et al. 2007a, Astrobiology, 7, 208 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Grenfell, J. L., Stracke, B., von Paris, P., et al. 2007b, Planet Space Sci., 55, 661 [Google Scholar]
- Gueymard, C. A. 2004, Solar Energy, 76, 423 [NASA ADS] [CrossRef] [Google Scholar]
- Hauschildt, P. H., Allard, F., & Baron, E. 1999, ApJ, 512, 377 [NASA ADS] [CrossRef] [Google Scholar]
- Joshi, M. M., Haberle, R. M., & Reynolds, R. T. 1997, Icarus, 129, 450 [NASA ADS] [CrossRef] [Google Scholar]
- Kaltenegger, L., & Traub, W. A. 2009, ApJ, 698, 519 [NASA ADS] [CrossRef] [Google Scholar]
- Kaltenegger, L., & Sasselov, D. 2010, ApJ, 708, 1162 [NASA ADS] [CrossRef] [Google Scholar]
- Kaltenegger, L., Traub, W. A., & Jucks, K. W. 2007, ApJ, 658, 598 [NASA ADS] [CrossRef] [Google Scholar]
- Kasting, J. F., Pollack, J. B., & Crisp, D. 1984, J. Atm. Chem., 403 [Google Scholar]
- Kitzmann, D., Patzer, A. B. C., von Paris, P., Godolt, M., & Rauer, H. 2010, A&A, 511, A66 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Knutson, H. A., Charbonneau, D., Allen, L. E., Burrows, A., & Megeath, S. T. 2008, ApJ, 673, 526 [NASA ADS] [CrossRef] [Google Scholar]
- Knutson, H. A., Charbonneau, D., Burrows, A., O’Donovan, F. T., & Mandushev, G. 2009, ApJ, 691, 866 [NASA ADS] [CrossRef] [Google Scholar]
- Léger, A., Rouan, D., Schneider, J., et al. 2009, A&A, 506, 287 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
- Leggett, S. K., Allard, F., Berriman, G., Dahn, C. C., & Hauschildt, P. H. 1996, ApJS, 104, 117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lelieveld, J., Peters, W., Dentener, F. J., & Krol, M. C. 2002, J. Geophys. Res. (Atmospheres), 107, 4715 [NASA ADS] [CrossRef] [Google Scholar]
- Manabe, S., & Wetherald, R. T. 1967, J. Atm. Sci., 24, 241 [NASA ADS] [CrossRef] [Google Scholar]
- Mayor, M., Udry, S., Lovis, C., et al. 2009, A&A, 493, 639 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Melsheimer, C., Verdes, C., Buehler, S. A., et al. 2005, Radio Sci., 40, 1007 [Google Scholar]
- Mlawer, E. J., Taubman, S. J., Brown, P. D., Iacono, M. J., & Clough, S. A. 1997, J. Geophys. Res., 102, 16663 [NASA ADS] [CrossRef] [Google Scholar]
- Pallé, E. 2010, in EAS Publications Ser., ed. T. Montmerle, D. Ehrenreich, & A.-M. Lagrange, A&A, 41, 505 [Google Scholar]
- Pettersen, B. R., & Hawley, S. L. 1989, A&A, 217, 187 [NASA ADS] [Google Scholar]
- Prather, M. J. 1996, Geophys. Res. Lett., 23, 2597 [NASA ADS] [CrossRef] [Google Scholar]
- Queloz, D., Bouchy, F., Moutou, C., et al. 2009, A&A, 506, 303 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rothman, L., Jacquemart, D., Barbe, A., et al. 2005, J. Quant. Spect. Rad. Trans., 96, 139 [Google Scholar]
- Rothman, L., Wattson, R., Gamache, R., Schroeder, J., & McCann, A. 1995, SPIE, 2471, 105 [Google Scholar]
- Schreier, F., & Schimpf, B. 2001, in IRS 2000: Current Problems in Atmospheric Radiation (A. Deepak) [Google Scholar]
- Segura, A., Krelove, K., Kasting, J. F., et al. 2003, Astrobiology, 3, 689 [Google Scholar]
- Segura, A., Kasting, J. F., Meadows, V., et al. 2005, Astrobiology, 5, 706 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Selsis, F. 2000, in Darwin and Astronomy : the Infrared Space Interferometer, ed. B. Schürmann, ESA Special Publication, 451, 133 [Google Scholar]
- Selsis, F., Despois, D., & Parisot, J. 2002, A&A, 388, 985 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sotin, C., Grasset, O., & Mocquet, A. 2007, Icarus, 191, 337 [NASA ADS] [CrossRef] [Google Scholar]
- Swain, M. R., Vasisht, G., & Tinetti, G. 2008, Nature, 452, 329 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Swain, M. R., Vasisht, G., Tinetti, G., et al. 2009, ApJ, 690, L114 [NASA ADS] [CrossRef] [Google Scholar]
- Tinetti, G. 2006, Origins of Life and Evolution of the Biosphere, 36, 541 [NASA ADS] [Google Scholar]
- Tinetti, G., Vidal-Madjar, A., Liang, M.-C., et al. 2007, Nature, 448, 169 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Toon, O. B., McKay, C. P., Ackerman, T. P., & Santhanam, K. 1989, J. Geophys. Res., 94, 16287 [NASA ADS] [CrossRef] [Google Scholar]
- Udry, S., Bonfils, X., Delfosse, X., et al. 2007, A&A, 469, L43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vidal-Madjar, A., Désert, J.-M., Lecavelier des Etangs, A., et al. 2004, ApJ, 604, L69 [NASA ADS] [CrossRef] [Google Scholar]
- von Clarmann, T., Höpfner, M., Funke, B., et al. 2003, J. Quant. Spect. Rad. Trans., 78, 381 [Google Scholar]
- von Paris, P., Rauer, H., Grenfell, J. L., et al. 2008, Planet Space Sci., 56, 1244 [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Top: normalised stellar input spectra: Sun (black, solid), AD Leo (dotted), M0 (dashed), M1 (dash-dot), M2 (dash-dot-dot-dot), M3 (long dashes), M4 (red), M5 (green), M6 (blue), and M7 (magenta). Bottom: zoom into the photochemically relevant spectral range. |
| In the text | |
 |
Fig. 2 Influence of gravity: Earth-sized (solid) vs. 3g super-Earth planet (dashed) around the Sun. |
| In the text | |
 |
Fig. 3 Influence of stellar spectrum: Earth-sized planets around the Sun (black, solid), AD Leo (dotted), M0 (dashed), M1 (dash-dot), M2 (dash-dot-dot-dot), M3 (long dashes), M4 (red), M5 (green), M6 (blue), and M7-type stars (magenta). |
| In the text | |
 |
Fig. 4 Chemical profiles for an Earth-sized planet (solid) and a 3g super-Earth (dotted) around the Sun. |
| In the text | |
 |
Fig. 5 Influence of central star type on chemical atmospheric profiles of an Earth-sized planet: Sun (solid), M0 (long dashed), AD Leo (dotted), M5 (dot-dashed), M7 (triple-dot-dashed). |
| In the text | |
 |
Fig. 6 Contrast spectra for an Earth-sized planet (1g) around the Sun (black), AD Leo (red), M0 (green), M5 (blue), and M7 (magenta). |
| In the text | |
 |
Fig. 7 Contrast spectrum of the 9.6 μm ozone band and the 15 μm carbon dioxide band for an Earth-sized planet around the Sun (black), AD Leo (red), M0 (green), M5 (blue), and M7 (magenta). Blue diamonds: binned to R = 20, red: smoothed spectra at the same resolution. |
| In the text | |
 |
Fig. 8 Emission spectra: integration time in hours needed for SNR = 3 as a function of stellar distance of the 9.6 μm (dotted) ozone and the 15 μm (solid) carbon dioxide spectral feature at R = 20 for an Earth (black) and a 3g super-Earth (red) around AD Leo (top) and an M5 dwarf central star (bottom). Telescope configuration: JWST. |
| In the text | |
 |
Fig. 9 Effective tangent heights: Earth and 3g super-Earth (red) around Sun. |
| In the text | |
 |
Fig. 10 Comparison of atmospheric transmission of a 1g Earth-like planet around the Sun (black), AD Leo (red), M0 (green), M5 (blue), and M7 (magenta) dwarf stars. |
| In the text | |
 |
Fig. 11 Transmission: integration time needed for SNR = 3 as a function of stellar distance of the 3.3 μm methane (dash-dot-dot-dot), 4.3 μm carbon dioxide (dash-dot), 7.7 μm methane (dashed), 9.6 μm (dotted) ozone and the 15 μm (solid) carbon dioxide spectral feature at R = 20 for an Earth (black) and a 3g super-Earth (red) around AD Leo (top) and M5 (bottom). Telescope configuration is JWST. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


