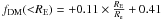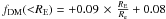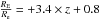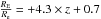| Issue |
A&A
Volume 529, May 2011
|
|
|---|---|---|
| Article Number | A72 | |
| Number of page(s) | 18 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/200913498 | |
| Published online | 05 April 2011 | |
On the evolution of environmental and mass properties of strong lens galaxies in COSMOS⋆
1
Laboratoire d’Astrophysique, École Polytechnique Fédérale de Lausanne (EPFL), Observatoire de Sauverny, 1290 Versoix, Switzerland
2
Centro de Astro-Ingeniería, Departamento de Astronomía y Astrofísica, Pontificia Universidad Católica de Chile, Casilla 306, Santiago, Chile
3
Max Planck Institut für Astronomia, Königstuhl 17, 69117 Heidelberg, Germany
4
Laboratoire AIM, CEA/DSM-CNRS-Universite Paris Diderot, IRFU/SEDI-SAP, Service d’Astrophysique, CEA Saclay, Orme des Merisiers, 91191 Gif-sur-Yvette, France
5
Hubble Fellow, Department of Astronomy, UC Berkeley, 601 Campbell Hall, Berkeley, CA 94720-3411, USA
6
Max-Planck Institut für Extraterrestrische Physik, Giessenbachstrasse, 85748 Garching, Germany
7
Lawrence Berkeley National Laboratory, 1 Cyclotron Road, Berkeley CA 94720, USA
8
Berkeley Center for Cosmological Physics, University of California, Berkeley, CA 94720, USA
9
Institute for Astronomy, ETH Zurich, Wolfgang-Pauli-Strasse 27, 8093 Zurich, Switzerland
10
Laboratoire d’Astrophysique de Marseille, CNRS Université de Provence, 38 rue F. Joliot-Curie, 13388 Marseille Cedex 13, France
11
Jet Propulsion Laboratory, MS 169-327,4800 Oak Grove Drive, Pasadena, CA 91109, USA
12
Space Telescope Science Institute, 3700 San Martin Drive, Baltimore, MD 21218, USA
13
California Institute of Technology, MC 105-24, 1200 East California Boulevard, Pasadena, CA 91125, USA
Received: 19 October 2009
Accepted: 12 February 2011
Context. Nearly 100 new strong-lens candidates have been discovered in the COSMOS field. Among these, 20 lens candidates with 0.34 ≲ zlens ≲ 1.13 feature multiple images of background sources.
Aims. Using the multi-wavelength coverage of the field and its spectroscopic follow-up, we characterize the evolution with redshift of the environment and of the dark-matter (DM) fraction of the lens galaxies.
Methods. We present spectroscopic and new photometric redshifts of the strong-lens candidates. The lens environment is characterized in the following way: we account for the projected 10 closest galaxies around each lens and for galaxies with a projected distance less than 1 Mpc at the lens galaxy redshift. In both cases, we perform similar measurements on a control sample of “twin” non-lens early-type galaxies (ETGs). In addition, we identify group members and field galaxies in the X-ray and optical catalogs of galaxy groups and clusters. From those catalogs, we measure the external shear contribution of the groups/clusters surrounding the lens galaxies. The systems are then modeled using a singular isothermal ellipsoid for the lens galaxies plus the external shear produced by the groups/clusters.
Results. We observe that the average stellar mass of lens galaxies increases with redshift. In addition, we measure that the environment of lens galaxies is compatible with that of the twins over the whole redshift range tested here. During the lens modeling, we notice that when let free, the external shear points in a direction which is the mean direction of the external shear produced by the groups/clusters and of the closest galaxy to the lens. We also notice that the DM fraction of the lens galaxies measured within the Einstein radius significantly decreases as the redshift increases.
Conclusions. Given these observations, we conclude that while the environment of lens galaxies is compatible with that of non-lens ETGS over a wide range of redshifts, their mass properties evolves significantly with redshift: it is still not clear whether this advocates in favor of a stronger lensing bias toward massive objects at high redshift or if it is simply representative of the high proportion of massive and high stellar density galaxies at high redshift.
Key words: gravitational lensing: strong
© ESO, 2011
1. Introduction
In the field of gravitational lensing, studies of strong galaxy-galaxy lenses on statistical grounds have recently become possible. Indeed, within just a few years, searches in the SDSS (SLACS: Bolton et al. 2006, 2008; Allam et al. 2007), in COSMOS (Faure et al. 2008, hereafter Paper I; Jackson 2008), and in the CFHT-LS surveys (SL2S: Cabanac et al. 2007; Limousin et al. 2009b) have delivered more than two hundred new strong galaxy-galaxy lenses, which span a wide range in redshift and image angular separation. The reasons for this interest are manifold. First, strong-lens galaxies provide measurements of the total mass distribution on galaxy scales, which brings additional information about the processes of galaxy formation and evolution (e.g. Ofek et al. 2003; Chae et al. 2006; Koopmans et al. 2006; Tortora et al. 2010). Second, from a statistical point of view, strong lensing occurrences trace the abundance and concentration of matter in the universe, which provides another test for cosmological models (e.g. Keeton 2001; Bartelmann et al. 2003).
Studies of the physical and environmental properties of low-redshift strong-lens galaxies (z ≲ 0.3) have shown that they are bona fide massive early-type galaxies (ETGs; Treu et al. 2006, 2009, T09 hereafter; Gavazzi et al. 2007; Grillo et al. 2009). The strong-lens sample in the COSMOS field (Paper I) spans a higher redshift range (0.33 ≤ z ≤ 1.13) and previous work on this sample have shown that the projected distribution of lens galaxies in COSMOS is comparable to that of ETGs, whether in rich environments such as cosmic filaments, or in the field (Faure et al. 2009, hereafter Paper II). Interestingly, this result means that multiple-mass-sheets do not contribute significantly to make more efficient lenses, contrary to results found in ray tracing through numerical simulations (Wambsganss et al. 2005; Hilbert et al. 2007, 2008). In Paper II we also demonstrate that the presence of large scale structures (LSS) in the lens galaxy environment increases the angular separation of the lensed images of a source, as noticed earlier by Oguri et al. (2005).
In addition, analyses of the mass density profiles of strong-lens galaxies from hydrodynamical N-body simulations (Dobke et al. 2007; Limousin et al. 2009a) and lens samples (Limousin et al. 2007; Auger 2008; Natarajan et al. 2009) show that the mass distribution in galaxies depends on their environment. For example, compared to galaxies centrally placed in their group or cluster, some skewing of the total mass density slope appears in galaxies located at the edges of a group or cluster. This is consistent with tidal stripping of their dark matter halo (T09).
Therefore, it is important to explore the local environment of the COSMOS strong-lenses rather than in LSS as in Paper II. We also aim to learn about the lens galaxy mass properties, in particular to derive information relative to their dark matter (DM) fraction (fDM, defined as fDM = 1 − M ⋆ /(M ⋆ + MDM). This is possible because the COSMOS strong-lenses pertain to one of the best-studied regions of the sky, for which deep multi-wavelength observations have been collected (Koekemoer et al. 2007; Taniguchi et al. 2007; Capak et al. 2007a; Scoville et al. 2007; Lilly et al. 2007; Ilbert et al. 2009). Thus, the properties of the COSMOS galaxy population have been studied extensively (e.g. McCracken et al. 2007; Capak et al. 2007b; Scarlata et al. 2007a,b; Ilbert et al. 2010).
The paper is organized as follows. In Sect. 2 we provide improved redshifts and stellar masses of the COSMOS lens galaxies. In Sect. 3 we examine and discuss the lens environment. In Sect. 4 we present results from our strong-lens mass models for the subsample of triple and quadruple image systems. Discussion and conclusions appear in Sect. 5. Throughout this paper, we assume a WMAP5 ΛCDM cosmology with Ωm = 0.258, ΩΛ = 0.742, H0 = 72 h72 km s-1 Mpc-1.
2. The COSMOS sample of strong-lenses: new redshifts and stellar masses
By visual inspection of stamp images of 10″ × 10″ around ~9500 early photometric type galaxies (with redshifts: 0.2 ≤ z ≤ 1.0, and absolute magnitude: MV < −20) in the COSMOS field, we have discovered 60 strong-lens candidates (Paper I). In addition, in the same study, 7 lens candidates were serendipitously found scattered across the field. Among the whole sample, 19 systems display long curved arcs or multiple images with similar colors (based on SUBARU images, by Taniguchi et al. 2007) around a bright-lens galaxy, and with an image arrangement around the lens galaxy which is consistent with the lensing hypothesis, as probed by lens modeling.
Independently, Jackson (2008) inspected the complete set of galaxies in the COSMOS field, without discrimination. He has discovered two additional convincing strong-lens candidates that produce multiple images:J095930.93+023427.7 and J100140.12+020040.9. The lens galaxies both appear to be ETGs.
Among the 21 multiple-image lenses now available, one system (COSMOS 5921+0638) – which is the only confirmed lensed quasar of the sample – has been studied separately by Anguita et al. (2009, hereafter Paper III). Another system, COSMOS 5737+3424, is a galaxy cluster that is lensing a set of background galaxies. In such a case, the lens covers a different mass scale than in the other 20 systems, and the lens potential is more complex than a single lens galaxy: this target has been dropped from the present analysis.
2.1. Spectroscopic followup
On 2006 March 3 and 2006 April 25 − 26, we have successfully obtained spectra for five of the strong-lenses in the COSMOS field (PI: Faure) using the FORS1 instrument (ESO/VLT) in multi-object spectroscopic mode with 19 slits. For each target, the central slit was located on the lens candidate with an orientation intersecting both the lens galaxy and the brightest lensed image. The other 18 slits in the ~7′ × 7′ field around the lens, were preferentially positioned on galaxies with colors similar to that of the lens galaxy (likely at the same redshift). Leaving aside COSMOS 5921+0638 (discussed in Paper III) and the lens cluster COSMOS 5737+3424, we display the spectra of the other three lens galaxies in Fig. 1. Regarding the source redshifts, from this dataset we could extract only one source redshift, in COSMOS 5921+0638 (Paper III). Positions and redshifts of secondary targets around COSMOS 0012+2015, COSMOS 0013+2249 and COSMOS 0049+5128 are given in Table 2.
 |
Fig. 1 VLT/FORS1 spectra of three strong-lens candidates. The spectral resolution is 5.52 Å per pixel, and has been smoothed by a 3-pixel box to improve the quality of the display. Flux is in arbitrary units. |
 |
Fig. 2 Keck/DEIMOS spectrum of COSMOS 0018+3845. The spectrum is smoothed by 2.3 Å and binned down to 7.5 Å per pixel, taking the wavelength dependent noise into account to improve the apparent signal-to-noise. Flux is in arbitrary units. |
In addition, several COSMOS lens candidates have been observed with the Keck telescopes. Using the Deep Extragalactic Imaging Multi-Object Spectrograph (DEIMOS), a spectrum of COSMOS 0018+3845 has been obtained on 2010 February 11 (Fig. 2). The data were collected in 7 × 1800 s exposures under photometric conditions with 0.5−0.7″ seeing. We used a 1″ slit together with the 830 line/mm grating tilted to 7860 Å and the OG550 blocking filter. The resulting spectral resolution is < 3.3 Å, depending on seeing and object morphology. The objects were dithered along the slit by ± 3″ between exposures to improve background subtraction, as described in Capak et al. (2011). The redshift of the lens was identified using the CaII H & K absorption lines and G-band. The source redshift is estimated based on the Lyman break, which is somewhere in the Subaru IA624-band (λeffective = 6226 Å, FWHM = 299 Å), and yields constraints on the source redshift: 3.9 < zs < 4.1. From there, we find that for zs = 3.96 ± 0.02, SiIV and CII would align with spectral absorption features of the lens. This estimation of the source redshift is used throughout the paper.
Moreover, with the Low Resolution Imaging Spectrometer (LRIS), Lagattuta et al. (2010) measured the redshifts for seven lens galaxies and two sources.
Finally, we retrieved the redshifts of seven strong-lens candidates from our list (based on the G-band and MgI absorption lines) from the z-COSMOS catalog (Lilly et al. 2009). Two of them, re-observed with Keck/LRIS, benefit from a second redshift determination from a higher signal-to-noise spectrum. Both redshifts agree.
A summary of the spectroscopic observations available for this sample is given in Table 1, while the lens redshifts are provided in Table 3.
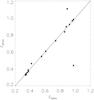 |
Fig. 3 Photometric redshift, zphot, versus spectroscopic redshift, zspec, for 16 of the lens galaxy candidates. The solid line features zphot = zspec. Errors bars on the value of zphot relate to the 68% confidence level. |
Summary of the VLT (FORS1 and VIMOS) and Keck (DEIMOS and LRIS) observations: target name, instrument, and exposure time (in ks).
2.2. Improved photometric redshifts
Recently a new set of photometric redshifts for galaxies in the COSMOS field has been derived by Ilbert et al. (2009), using the code Le Phare (Arnouts & Ilbert1) and the photometric dataset by Capak et al. (2007a, 2011). Compared to the previous set of COSMOS photometric redshifts by Mobasher et al. (2007), which relied on 8 broad bands, the main improvement is the use of 30 bands: the 8 broad bands plus 12 intermediate bands, 2 narrow bands, 7 bands in the near-infrared and 1 band in the ultra-violet. In Fig. 3 we display a comparison between the new photometric redshifts and spectroscopic redshifts for the 17 lens galaxies in our sample for which we have both measurements. For most lens galaxies, the agreement is good within the 68% confidence level error-bars measured for the photometric redshifts. Thus, these new photometric redshifts for the lenses are reliable estimates of their spectroscopic redshifts. Three systems show a strongly deviant photometric redshift (COSMOS 0254+1430: zphot = 0.46 ± 0.01 and zspec = 0.417 ± 0.001; J095930.93+023427.7: 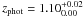 and zspec = 0.892 ± 0.001; COSMOS 0018+3845: zphot = 0.44 ± 0.01 and zspec = 0.9755 ± 0.0003). In those three cases, the photometry of the lens galaxy obtained from ground-based data is contaminated by the close and bright images of the source, and the photometric redshift determination is consequently biased.
and zspec = 0.892 ± 0.001; COSMOS 0018+3845: zphot = 0.44 ± 0.01 and zspec = 0.9755 ± 0.0003). In those three cases, the photometry of the lens galaxy obtained from ground-based data is contaminated by the close and bright images of the source, and the photometric redshift determination is consequently biased.
Position and redshift of galaxies in the FORS1 field around COSMOS 0012+2015, COSMOS 0013+2249, and COSMOS 0049+5128. The error on the redshifts is ± 0.001.
2.3. Stellar masses of the lens galaxies
We derived a first set of stellar masses using the Bayesian code described in Bundy et al. (2006). In brief, a data couple, made of the observed galaxy spectral energy distribution (SED) and its redshift, is referenced to a grid of models that are constructed with the Bruzual & Charlot (2003) synthesis code. The grid includes models that vary in age, star-formation history, dust content and metallicity. At each grid point, the probability that the observed SED fits the model is calculated: the corresponding stellar mass and the stellar mass-to-K-band luminosity ratio are stored. By minimizing over all parameters in the grid, the stellar mass probability distribution is obtained. The median of this distribution is taken as the stellar mass estimate, while the width corresponding to 68% of the probability distribution encodes the error bar that results from degeneracies and uncertainties in the model parameter space. The final error bar on the stellar mass also includes the K-band photometric uncertainty and the expected error on the luminosity distance that results from the uncertainty on the photometric redshift. The stellar masses and uncertainties are provided in Table 3 and plotted in Fig. 4.
 |
Fig. 4 Stellar masses (in M⊙) of the lens galaxies as a function of redshift (spectroscopic when available, photometric otherwise). Black crosses: stellar masses inferred using the method described in Bundy et al. (2006). Grey stars: stellar masses inferred for the IRAC sources in Ilbert et al. (2010). Black and grey lines: the respective least-square fits, with a slope of +0.8 ± 0.3 (black line) and +0.7 ± 0.3 (grey line). |
From the ACS-F814W images (Koekemoer et al. 2007) we infer the contamination from the light of the background-lensed images in the stellar mass measurements. In an aperture of 3″ radius, the lensed images are 3 to 7 mag fainter than their respective lensing galaxy: in all cases this contamination generates an error on the stellar mass ≲ 0.01 dex.
To estimate the reliability of our estimates of the stellar mass (and uncertainties), we retrieved among the 3.6μ IRAC catalog of the Spitzer-COSMOS survey (Sanders et al. 2007) 18 of the 20 strong-lenses; the other two lens galaxies were not detected with Spitzer. For these lenses we compared our estimates of the stellar masses to those inferred by Ilbert et al. (20102): they agree reasonably well (see Fig. 4). The typical difference between the two mass estimators (~0.2 dex) is widely discussed in Ilbert et al. (2010). Both distributions show a tendency of increasing the lens stellar mass with redshift. We will return to this feature in more detail in the discussion (Sect. 5.1).
3. The environment of the lens galaxies
With these more accurate redshift measurements for the lens galaxies and the galaxies in the COSMOS field, we can undertake a study of the local environments of lens galaxies. Indeed, to understand whether high-redshift lensing galaxies (z ≥ 0.3) are representative of the ETG population at their redshift, as the low-redshift lens galaxies are (T09, Auger 2008), we study their environment in comparison to the environment of a population of non-lensing ETGs. Our first analysis of the lens environment with regard to LSS (Paper II) led to the conclusion that lens galaxies are indeed evolving in the same environment as their parent population. Let us now look closer at a more local environment for the lens, using neighbor density measurements as defined and used by T09 for the SLACS sample.
Summary of the properties of the lens galaxy environments (top to bottom: from low to high redshift).
3.1. Projected number of neighbors
3.1.1. The neighbor number densities
In T09, the first estimator is the projected number density of galaxies, Σ10, inside a circle with radius R10, which is equal to the projected distance to the ninth closest neighbor of the lens. The neighbor galaxies are defined in a way that their magnitude is: 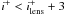 , and the upper or lower bound, z, of their photometric redshift is zlens − δzlens < z < zlens + δzlens, where δzlens is a function of the lens magnitude and redshift, and lies between 0.012 and 0.020 for our sample (see Ilbert et al. 2009). For the two lenses with incorrect photometric redshifts, we used their spectroscopic redshift instead and for the search for neighbors, the δzlens values associated with their spectroscopic redshift in the photometric catalog; this ensures that we are using the same search box for lenses with spectroscopic and photometric redshifts.
, and the upper or lower bound, z, of their photometric redshift is zlens − δzlens < z < zlens + δzlens, where δzlens is a function of the lens magnitude and redshift, and lies between 0.012 and 0.020 for our sample (see Ilbert et al. 2009). For the two lenses with incorrect photometric redshifts, we used their spectroscopic redshift instead and for the search for neighbors, the δzlens values associated with their spectroscopic redshift in the photometric catalog; this ensures that we are using the same search box for lenses with spectroscopic and photometric redshifts.
 |
Fig. 5 Distribution of |
The search for neighbors is performed in the photometric redshift catalog of Ilbert et al. (2009), which contains about one million objects. The limiting magnitude chosen for the neighbors ensures that the scaling in brightness (thus in mass) between a lens galaxy and its neighbors is the same for all lenses, independently of their magnitude. For the faintest lens in our sample, this upper limit corresponds to the completeness limit of the COSMOS photometric catalog (depth: i + ~ 26.2, Capak et al. 2007a). The range chosen for the redshift ensures that, given the error bars on the neighbor photometric redshifts, they are indeed at the same redshift as the lens galaxies (in the 68% confidence limit error bars).
As in T09, we also computed the projected number of galaxies, D1, inside a circle with radius 1 Mpc, at the lens redshift. To select the neighbors, we used the same limiting magnitudes and redshift ranges as for the first estimator.
To achieve comparative measurements for a population of galaxies that are not identified as lenses but have the same morphology (early photometric type), similar brightness and redshift properties, we defined a control sample of “twins” for each lens galaxy. Those twins have the upper or lower bounds, ztwin, of their photometric redshift in a way that zlens − δz < ztwin < zlens + δz with δz = 0.05, and the upper or lower bounds, Itwin, of their magnitude such as: Ilens − δI < Itwin < Ilens − δI, with δI = 0.05 mag. The dispersion authorized around the value of the lens redshift and lens magnitude ensures that the sample of twins is large enough for the results to be statistically reliable (between 22 and 140 twins, see Table 3). In addition, the range in redshift is small enough to avoid possible biases owing to galaxy evolution, and the range in magnitude ensures that the flux difference between a lens and its twins remains lower than 5%. We then measure the average number density of neighbors ⟨ Σ10 ⟩ t and the average projected number of galaxies in a circle with radius 1 Mpc: ⟨ D1 ⟩ t for the control “twin” sample.
For an obvious lack of spectroscopic information, the twins cannot be selected according to their velocity dispersion as it is the case in the analysis by T09. Yet our match in magnitude and redshift mimics up to a certain level of accuracy a match in mass between the lens galaxies and their twins.
3.1.2. Error measurements on the neighbor number densities
In building the photometric catalog of galaxies, masks were necessary to hide bright objects disturbing the galaxy extraction procedure (see Capak et al. 2007a). From these masks we measured at each lens and twin location, the surface that was hidden for the extraction. The hidden surface is typically of a few percents of the total surface used to determine Σ10 or D1. It only gives a positive contribution to the total error budget on the neighbor density estimates: indeed, the surface covered by the circle of radius R10 would be smaller if the ninth closest galaxy were behind the mask, and if one or more galaxies were hidden behind the mask, the number of galaxies in a circle of radius D1 would be larger. Therefore, for a fixed number of galaxies, the surface has to be smaller. In summary, for a lens galaxy the total error bar on the neighbor galaxy density is the quadratic sum of the Poisson error and the error owing to the use of masks on the surface encompassing the neighbors. For its average twin, the error bar is the quadratic sum of the Poisson error, the error owing to the use of masks and the dispersion for the population of twins. The Poisson error largely dominates the error budget for the lens neighbor number densities, while the dispersion largely dominates the error budget for the twins.
3.1.3. Results
The values of Σ10, D1, ⟨ Σ10 ⟩ t and ⟨ D1 ⟩ t depend on the redshift bin and magnitude limit. To circumvent these effects, we only interpret the results in term of ratios: 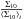 and
and 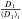 . These ratios quantify the richness of the environment of the lens galaxies in comparison to the environment of their respective twins. They are provided in Table 3. The average distance encompassing the nine closest galaxies to the lens is ⟨ R10 ⟩ = 1.2 Mpc with a 1σ standard deviation of 0.5 Mpc, hence comparable to the radius of 1 Mpc used to calculate D1. In Fig. 5, we display the ratios
. These ratios quantify the richness of the environment of the lens galaxies in comparison to the environment of their respective twins. They are provided in Table 3. The average distance encompassing the nine closest galaxies to the lens is ⟨ R10 ⟩ = 1.2 Mpc with a 1σ standard deviation of 0.5 Mpc, hence comparable to the radius of 1 Mpc used to calculate D1. In Fig. 5, we display the ratios 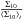 and
and 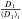 for the COSMOS lenses and for the SLACS lenses (using data from T09), as a function of redshift. A priori, the two distributions cannot be directly compared because they may have different normalization factors (because of their different lens selection function, source redshift distribution and survey sensitivity). Yet, in the redshift range common to the SLACS and COSMOS samples (z ~ [0.33,0.50 ] ), the levels of the distributions for
for the COSMOS lenses and for the SLACS lenses (using data from T09), as a function of redshift. A priori, the two distributions cannot be directly compared because they may have different normalization factors (because of their different lens selection function, source redshift distribution and survey sensitivity). Yet, in the redshift range common to the SLACS and COSMOS samples (z ~ [0.33,0.50 ] ), the levels of the distributions for 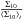 and
and 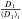 are similar, which suggests that the normalizations are not drastically different. However, to avoid any misinterpretation deriving from intrinsic sample differences, the SLACS sample and the COSMOS sample distributions are separately analyzed.
are similar, which suggests that the normalizations are not drastically different. However, to avoid any misinterpretation deriving from intrinsic sample differences, the SLACS sample and the COSMOS sample distributions are separately analyzed.
The number density ratios displayed in Fig. 5 indicate whether the lens galaxies reside in a typical environment compared to the twin galaxy population. If this were true, the number density ratios should be on the order of 1 at every redshift. This is indeed the case on average for the lenses in the redshift range studied here.
3.2. X-ray and optically detected galaxy groups and clusters
The validity of the estimators used to characterize the environments of lens galaxies in Sect. 3.1 can be checked using the distribution of groups and clusters in the field based on X-ray and spectroscopic data analysis. Indeed, we can access two supplementary pieces of information: (a) the distribution of X-ray emitting gas in the COSMOS field (XMM-Newton survey: Hasinger et al. 2007; and C-COSMOS with Chandra: Elvis et al. 2009), which traces galaxy groups and clusters in the field (Finoguenov et al. 2007, and in prep.), and (b) the identification of optical groups or clusters (Knobel et al. 2009) from the z-COSMOS spectroscopic program (Lilly et al. 2007).
Moreover, because the presence of groups in the direction toward the source generates a different lensing potential compared to that of a single lens galaxy, it is important in preparation of the mass modeling in Sect. 4 to know: 1) if the lens galaxies are group members. If this is indeed the case, the group has to be modeled as an individual potential in the lens modeling; 2) which contribution in terms of shear is produced by the groups and clusters toward and around the lens galaxy. Most of the time this contribution is simply represented by an “external shear” whose parameters are optimized while adjusting the lens model. In this paper, we instead intend to independently measure the external shear using the rich dataset that covers the COSMOS field, in a similar manner than what has been done recently by Wong et al. (2011).
Summary of the contribution of the environment to the lens galaxies.
In the framework of our lensing analysis, each of the group catalogs (X-ray-selected versus spectroscopically selected) has certain advantages and disadvantages. The entire COSMOS region has been mapped through 54 overlapping XMM-Newton pointings while additional Chandra observations have mapped the central region (0.9 square degrees). A composite XMM-Newton and Chandra mosaic has been used to detect and measure the fluxes of groups and clusters to a 4σ detection limit of 1.0 × 10-15 erg cm-2 s-1 over 96% of the ACS field. The general data reduction process can be found in Finoguenov et al. (2007, 2009) and the cluster catalog and weak-lensing analysis are presented in Leauthaud et al. (2010). Therefore, the catalog of X-ray selected groups and clusters is homogeneous and covers the entire COSMOS field. However, it is affected by the sensitivity threshold of the X-ray survey, which is different from the sensitivity cut of the optical dataset. Therefore, groups of modest mass could be missing from the X-ray selected catalog, especially around galaxies at high redshift.
Conversely, the catalog of optically selected groups in COSMOS has the advantage of spanning the same brightness range as the optical imaging dataset from which the strong-lens candidates and the arcs were extracted. Even though the faintest galaxies seen on deep images will remain undetected in the shallower spectroscopic z-COSMOS survey, groups can still be traced and assessed from their central brightest galaxies. Then, the parameters of the galaxy groups can be derived by comparing these detections to a catalog of mock-groups that are subject to the same detection criteria (see Knobel et al. 2009, for an extensive description of the group catalog). The first data release of the z-COSMOS survey (Lilly et al. 2007) covers a fraction of the full COSMOS field, which leaves some of our COSMOS lens candidates outside the coverage of the group catalog.
Let us establish now whether the lens galaxies are group or cluster members (Sect. 3.2.1) and measure the external shear contribution of the groups and clusters at the lens galaxy position (Sect. 3.2.3).
3.2.1. Lens galaxy group members
We cross-correlated the X-ray cluster catalog (Leauthaud et al. 2010) with the sample of strong-lenses. We defined as a group member a lens galaxy located within r200 (radius where the matter density is 200 times the critical density) of the group center, and with a redshift identical to the group redshift (within error bars). We found four matches, and there is a galaxy cluster detected at a lower redshift in direction to J095930.93+023427.7 (see Table 4).
Using the group catalog built from the optical dataset, we did not identify any new groups associated in redshift and space with lens galaxies tin addition to those already identified with the X-ray catalog. In Table 4 we give the probability that galaxies in a 2′ × 2′ field around the lens galaxy are included in the z-COSMOS catalog. This figure roughly establishes the “completeness” of the survey at every lens location and tells us if the z-COSMOS group catalog can be used to characterize the environment of the lens.
3.2.2. Comparison: galaxy group members and projected number density of neighbors
In principle, lens galaxies that are group members are expected to have large neighbor number densities. This should be visible in the ratio measured in Sect. 3.1. This is indeed the case with the first estimator for the lens in COSMOS 0013+2249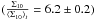 and COSMOS 0216+2955
and COSMOS 0216+2955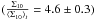 , and it is unclear for COSMOS 0056+1226 and COSMOS 0227+0451 because of the large error bar on the measured density ratios. With the second estimator, the ratio is in average lower than with
, and it is unclear for COSMOS 0056+1226 and COSMOS 0227+0451 because of the large error bar on the measured density ratios. With the second estimator, the ratio is in average lower than with 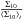 , and it is therefore more difficult to correctly identify an over-dense field. On the contrary, COSMOS 0038+4133 shows a high density ratio
, and it is therefore more difficult to correctly identify an over-dense field. On the contrary, COSMOS 0038+4133 shows a high density ratio 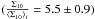 without being associated to any known galaxy group in X-ray or optic.
without being associated to any known galaxy group in X-ray or optic.
3.2.3. The external shear produced by clusters and groups
We estimate the shear and convergence produced by the groups (either X-ray or optical) that is detected around the lens galaxies in order to characterize the contribution of the environment to the total lens potential in future lens models (Sect. 4). To do so we followed the method described in Paper III. In short, we computed the convergence and shear produced by all groups closer in projection than a given radius (5′, as in Paper III), and at any redshift up to that of the source. We assume that the mass profile of every group follows a truncated isothermal sphere (TIS). The choice of this profile is motivated by the fact that the shear and convergence produced by an isothermal sphere are easy to compute (Keeton 2003; Momcheva et al. 2006). Moreover, because we will consider only groups and clusters that do not cross the line-of-sight to the source, estimations of their total masses instead of their mass distributions are sufficient for the accuracy of the result. We selected a truncated profile to avoid to give unrealistically much weight to the most distant groups.
The three-dimensional density distribution of the TIS can be written 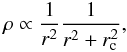 (1)where rc is the truncation radius. The convergence, κ, and shear, γ, produced by this profile are respectively
(1)where rc is the truncation radius. The convergence, κ, and shear, γ, produced by this profile are respectively ![\begin{eqnarray} \kappa &=& \frac{\tilde{b}}{2} \left(\frac{1}{\sqrt{r^2}} - \frac{1}{\sqrt{r_{\rm c}^2+r^2}}\right) \\ \gamma &=& \frac{\tilde{b}}{2} \left[\frac{1}{\sqrt{r^2}} + \frac{1}{\sqrt{r_{\rm c}^2+r^2}} - \frac{2r_{\rm c}}{r^2}\left(\frac{\sqrt{r_{\rm c}^2+r^2}}{r_{\rm c}} - 1\right)\right], \end{eqnarray}](/articles/aa/full_html/2011/05/aa13498-09/aa13498-09-eq255.png) where
where 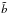 is the impact parameter of the TIS, which relates to the singular isothermal sphere (SIS) impact parameter bSIS as
is the impact parameter of the TIS, which relates to the singular isothermal sphere (SIS) impact parameter bSIS as 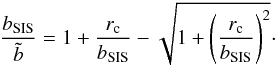 (4)In the limit where rc → ∞ these quantities match those of the SIS.
(4)In the limit where rc → ∞ these quantities match those of the SIS.
To compute the external shear produceded by the groups and clusters we proceed as follows. Whenever P < 0.3 in Table 4 (Col. 2), we only considered the catalog of X-ray-detected groups and clusters. The group’s mass potentials are modeled as TIS using the value M200 and r200 (used as the truncature radius). The error on the X-ray mass comes from the scatter in the relation that is used to derive the mass from the luminosity (Leautaud et al. 2010): it is on the order of ± 20% of M200 (Vikhlinin et al. 2009). Whenever P ≥ 0.3 in Table 4 (Col. 2), we also considered the optical group catalog in addition to the X-ray group catalog. We first correlated the optical and X-ray group catalogs to identify and remove optical groups that might already be accounted for as an X-ray group. Then, we modeled as TIS the remaining optical groups using the “mock” virial mass, Mvir, and the “mock” virial radius, rvir (used as the truncature radius). The upper and lower error on the virial mass are 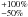 of Mvir (Knobel et al. 2009). These “mock” quantities are the theoretical values associated with the detected groups when subjecting a mock sample of groups to the same selection function and same survey criteria as the observations (see Knobel et al. 2009, for details).
of Mvir (Knobel et al. 2009). These “mock” quantities are the theoretical values associated with the detected groups when subjecting a mock sample of groups to the same selection function and same survey criteria as the observations (see Knobel et al. 2009, for details).
The external shear and associated convergence are calculated individually for each group. They are then re-scaled to the redshift of the lens with the scaling relation given in Momcheva et al. (2006). For a given lens, external shear and convergence are summed following the procedure described in Keeton (2003) and Momcheva et al. (2006). The results are summarized in Table 4. A first set of errors on the shear and on the convergence results from the propagation of the group mass errors.
As mentioned already, in the special case where a galaxy group or cluster has an impact parameter smaller than r200 or rvir (in 5 cases, see Table 4), the shear and convergence calculated under this simple approximation are incorrect (Keeton 2003). Hence, we systematically removed these groups when computing the external shear. Instead, they will have to be accounted for as additional lens potential when we perform the lens modeling.
Regarding the source redshift, it is either known spectroscopically for some lenses (see Table 3), or assumed to be at zs = 2 for lenses with zl < 1, or at zs = 3 for lenses with zl > 1. The convergence and shear contributions depend on the number of groups taken into account, which in turn may depend on the source redshift and on the considered cut-radius. Hence, an error on the source redshift generates an error on the external shear parameter. We estimated this error assuming an uncertainty δz = ± 0.5 on the source redshift when unknown, and using the error on the source redshift in Table 3 when measured (see Table 4). To estimate the error introduced by an arbitrary cut-radius at 5′, we also probed two other radii (7′ and 10′). We found that the incidence of the radius selection on the final lensing contribution is δκ ~ δγ ~ 0.001 and is negligible on the orientation of the shear (δPAγ < 0.5°). Then we calculated the total error on the external shear as the sum in quadrature of the error produced by the group mass uncertainty, the source redshift uncertainty, and the error produced by the choice of aperture.
Lens galaxy luminous profile.
Position of the lensing galaxy (in degree) and relative position (in arc-second) of the images used as constraints for the lens mass model.
We also analyzed the error on the external shear parameters generated when using a single catalog of groups (X-ray) instead of the combination of the two catalogs (X-ray and optical). The comparison is possible for seven systems. While the convergence is different when using a single catalog instead of two, the external shear strength and direction agree within their respective error bars. This means that our calculation realistically associates the largest source of shear with the more massive groups and clusters. It also means that the probable incompleteness of our catalogs in low-mass groups has a minimal impact on the shear measurement: what matters is the completeness of the catalog in large mass groups and clusters. However, the technique is limited for low-redshift sources, because there is no X-ray cluster detected above z = 1.3 in the COSMOS field.
4. The strong-lens modeling
In this section, we focus on the 12 lens galaxies that offer the largest number of observational constraints: the triple and quadruple image systems and the Einstein rings.
4.1. Lens-galaxy light profiles
We re-computed the two-dimensional fit of the galaxy surface brightness distribution of the COSMOS lenses using GIM2D (Simard 1998; Marleau & Simard 1998) to include error bars that were not presented in Paper I. For that purpose, we adopt as in Paper I a Sersic bulge plus an exponential disk parametrization to describe the two-dimensional surface brightness distribution of the lens galaxy light profile. The Sersic profile is parametrized by means of the total flux in the bulge, the Sersic index, n, the bulge ellipticity, ϵ = 1 − b/a, the position angle of the bulge, PA, and the effective radius of the bulge, Re. The exponential profile depends on the photometric disk total flux, the disk scale-length, the disk position angle and the disc inclination. The software gives the best-fitting values for all these parameters. The parameters of the Sersic bulges are summarized in Table 5. The error bars correspond to the 68% confidence level. For most systems, the results are consistent with the surface brightness parameters measured in Paper I. But for others, such as COSMOS 5921+0638, the best-fit parameters differe in Paper I, Paper III, and here. Indeed, the presence of a ring or bright arcs close to the lens galaxy center impide producing a robust fit of the lens-galaxy surface brightness density profile; this is true even when more complex fitting and deconvolution methods are used (see Chantry & Magain 2007).
The relative image positions to the lens galaxies are the main constraints for the lens models. For images that are point like objects, the determination of their positions only depends on the image resolution. This is the case for COSMOS 5921+0638. For this system the error on the relative position is 0.014″ (see Paper III). For the other multiple images systems, we determine the position of the the brightest peak in each image. For theses systems, the error on the relative position of the images is typically 0.05″. For the perfect rings that do not display any peak we place the image arbitrarily around the ring in a symmetric way around the lens center and assume that the error on the relative position of the images is 0.05″. In Table 6 we provide the lens galaxy central coordinates as well as the position of the multiple images relative to the lens galaxy location used in the lens modeling. For J100140.12+020040.9 and J095930.93+023427.7, we retrieved the image position from Jackson 2009.
4.2. The mass models
The purpose of the new lens modeling is first, to measure the total mass of the galaxy within RE: M(<RE) and second, to check if the environment contribution measured in Sect. 3.2.3 is a good estimator of the external shear.
To do so, we used the Lenstool code (Kneib et al. 1993; Jullo et al. 2007) to model the lens-galaxy mass distributions. Lenstool allows a χ2 minimization of parametric mass models either in the source or in the image plane. For higher accuracy, we used the image plane minimization algorithm.
4.2.1. SIE+γ
We performed a set of lens model in which the mass distribution that the lens galaxies follows is that of a singular isothermal ellipsoid (SIE). An SIE is defined by its position, velocity dispersion, orientation, and ellipticity. Assuming that mass follows light, we fix the SIE central position to that of the galaxy light profile (Table 6). We chose its orientation to be that of the Sersic bulge light profile (Table 5) with an additional ± 10° uncertainty to take into account a possible misalignment between the luminous bulge and the DM halo (e.g. Kochaneck 2002). The higher boundary for the SIE ellipticity is set equal to that of the Sersic profile (Table 5); the lowest boundary is set to 0 to take into account a possibly shallower distribution of the DM halo compared to the luminous core observed in ETGs (e.g. Gavazzi et al. 2007).
In addition, we model the contribution of the environment by an “external shear”, which is parametrized by the shear strength and orientation. The group and cluster contributions to the shear at the lens galaxy locations are measured in Sect. 3.2.3. We use the values of γ and PAγ from Table 4, and the corresponding error bars as priors to build the lens models.
Therefore, the total number of free parameters for the models is 5: 3 for the SIE (orientation, ellipticity, velocity dispersion) and 2 for the external shear (strength and direction). The number of observational constraints is 6 for the quads and rings and 4 for the triple image lenses. The χ2 of the best lens models are reported in Table 7 (Col. 3). The best fit models (with χ2 in Col. 3) are displayed in Figs. 7 to 11. Whenever χ2 ≫ 1, we have performed a second lens model, changing the priors on the external shear to the following ones: γ = [0.0,0.9 ] , PAγ = [ − 90°,90° ] , hence letting the external shear parameters free. The χ2 of these second lens models are reported in Table 7 (Col. 4) and referred as χ2′.
Best-fit parameters for the lens models: SIE + shear.
For J095930.93+023427.7, we modeled the group in direction to the lens by a SIS which position is fixed to the position of the group in the X-ray catalog. Hence, the only parameter allowed to vary is the velocity dispersion of the profile. The best-fit model in Table 7 is obtained for a group with velocity dispersion: 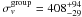 km s-1, if it was at the lens galaxy redshift. From Fig. 11, we see that the fit is not perfect: with additional observational constraints such as the velocity dispersions of individual group members and of the lens galaxy closest neighbor (to the East), one could perform a more detailed model of the lens potential which would most probably improve the fit.
km s-1, if it was at the lens galaxy redshift. From Fig. 11, we see that the fit is not perfect: with additional observational constraints such as the velocity dispersions of individual group members and of the lens galaxy closest neighbor (to the East), one could perform a more detailed model of the lens potential which would most probably improve the fit.
Systems with perfect Einstein rings are mostly satisfactorily modeled by an SIE plus the measured external shear (COSMOS 5947+4752 in Fig. 7, COSMOS 0124+5121 in Fig. 8, COSMOS 5941+3628 in Fig. 9). The reason is that for those lenses, we arbitrarily chose the image positions: they are symmetrically distributed around the lens. In addition, the SIE ellipticity is allowed to be null. Consequently we are artificially correctly fitting the image positions, whatever the external shear values are (as long as the shear strengths are not too large). For those systems, only the Einstein ring and associated mass are reliable measurements in Table 7.
For COSMOS 0049+5128, the fit is poor (χ2 = 35.3). If we let the external shear free, the best-fit shear parameters are different from those measured in Sect. 3.2.3. If we subtract the shear vector given in Table 4 from the best-fit shear vector in Table 7 (Col. 4), we find the direction pointing toward the galaxy closest to the lens (Galaxy 2 in Fig. 7). Galaxy 2 is at a projected distance ~13″ to the lens galaxy. If this were at the lens redshift, it would need to have a velocity dispersion 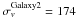 km s-1 to create the shear necessary to obtain χ2′ while fixing the shear parameters to the measured values.
km s-1 to create the shear necessary to obtain χ2′ while fixing the shear parameters to the measured values.
It is the same for the other lenses: if fixed in the lens model, the external shear produced by the groups leads to χ2 ≫ 1. If we set the shear parameters free, the best-fit shear will point in a direction that corresponds to the vectorial summed orientation of the shear produced by the groups and of the shear produced by a secondary (and third in the case of COSMOS 0038+4133) galaxy. In Table 8 we report the projected distance between the lens galaxy and the secondary (third) galaxy as well as the the velocity dispersion of the second (third) galaxy that is needed to obtain χ2′ when fixing the external shear parameters to the one produced by the groups. For COSMOS 0050+4901, the velocity dispersion derived for the main lens and for the secondary galaxy are that of a group rather than that of a galaxy: indeed, when we look at the image of the lens (Fig. 10), we see that the field is crowded with galaxies. However, the neighbor density ratio measured in Sect. 3 does not show any evidence for the presence of a structure at the lens redshift. Therefore, if there is actually a group intervening in this system, it should be at a different redshift than that of the main lens galaxy. For the other systems, the velocity dispersion associated with the secondary lens can be associated with a galaxy mass. For COSMOS 0047+5023, we see in Fig. 9 that the field around the lens is crowded with galaxies: an improved version of the present mass model should take them into account, preferentially using a measurement of their redshift and velocity dispersion.
We conclude that our efforts at measuring the external shear were not in vain because, when using it in the lens model, we clearly identify the missing element: the best fit will point at the closest galaxy to the lens or indicate the realistic presence of a galaxy group in the line-of-sight. We come back to this result in Sect. 5.4.
 |
Fig. 6 Evolution of the dark matter fraction and related parameters for two lens samples: COSMOS (crosses) and JK07 (stars). Top left panels: evolution of the DM fraction in the Einstein radius with the redshift. The least-deviation fits are displayed (solid lines), and follow the relations fDM(<RE) = −0.18 × z + 1.00 for COSMOS and fDM(<RE) = −0.18 × z + 0.38 for JK07. Top right panels: variation of the DM fraction as function of the ratio of the Einstein radius versus effective radius. The least-deviation fits give the following relations: |
The Einstein radius of the lens galaxy and corresponding mass were calculated for the best models and are displayed in Table 7.
Parameters for Galaxy 2.
4.2.2. The proportion of DM in the Einstein radius
We integrated the galaxy light profile density up to the Einstein radius and used the stellar mass of the lens galaxy, identifying the effective radius to the half stellar mass radius, to determine the stellar mass within the Einstein radius, M ⋆ (<RE). Doing so, we can compare it to the total mass within the Einstein radius, M(<RE), which was obtained during the lens modeling. This gives us a measurement of the lens galaxy projected DM fraction within the Einstein radius: 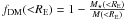 . These values are reported in Table 7. The errors come from the propagation of the uncertainties in M ⋆ , Re, M(<RE) and RE.
. These values are reported in Table 7. The errors come from the propagation of the uncertainties in M ⋆ , Re, M(<RE) and RE.
The negative DM fraction for COSMOS 0038+4133 may indicate that the stellar mass of the lens galaxy is overestimated. This is surprising, because for this system the photometric and spectroscopic redshifts agree, which therefore made us confident that the SED, and consequently the stellar mass, is reliable as well. Another possible explanation is that the light profile fit is not correct and that we measured too large an effective radius. This is indeed a possible explanation, because a bright ring surrounds the lens galaxy and may bias the determination of the light profile. Finally, it is also possible that the source redshift is lower than the one considered here 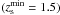 . Indeed, if zs = 0.9, the total mass in the Einstein radius would be M(<RE) = 4.88 × 1011 M⊙, and the corresponding DM fraction fDM(<RE) = 0.6. Because of all these questions, which require further investigation, we did not keep this system for the rest of the analysis.
. Indeed, if zs = 0.9, the total mass in the Einstein radius would be M(<RE) = 4.88 × 1011 M⊙, and the corresponding DM fraction fDM(<RE) = 0.6. Because of all these questions, which require further investigation, we did not keep this system for the rest of the analysis.
For the 11 remaining systems, the fraction of DM varies between 0.58 ± 0.00 (COSMOS 5921+0638) and 0.95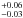 (COSMOS 5947+4752).
(COSMOS 5947+4752).
In Fig. 6 we report the evolution of fDM(<RE) with the redshift. The evolution of fDM(<RE) with redshift is compatible with constant or slight decreasing. The interpretation of this tendency is linked to the evolution of the Einstein radius, RE versus effective radius, Re. Indeed, for a given galaxy if (1) RE ~ Re, the fraction of dark matter in the Einstein radius is expected to be “low” because, in this case, we are probing the region where the galaxy is baryon-dominated: fDM(<RE) is then a lower limit of the total fDM. On the contrary, if (2) RE ≫ Re: we are measuring a fDM(<RE), which is getting close to the total fDM, and therefore it is expected to be larger, on average, than the one determined for (1). This is indeed the case (see Fig. 6, top right panel): fDM(<RE) increases slowly when RE/Re increases. From the same Fig. 6 (bottom left panel) we see that the ratio RE/Re increases quickly with redshift, meaning that as the redshift grows we are measuring fDM(<RE) getting closer to the total fDM of the galaxy. The fact that fDM(<RE) is slightly decreasing or “at best” constant when the redshift grows, suggests that the “total” fraction of dark matter is genuinely lower in the high-redshift lens galaxies than in the low-redshift lens galaxies.
Interestingly, we observe the same tendency if we consider the lens sample from Jiang and Kochanek (2007, JK07 hereafter): they measure the DM fraction (with or without adiabatic compression in their galaxy models and Salpeter initial mass function (IMF)) in the Einstein radius of 22 galaxies spanning a lens redshift zl = [0.0808,1.004 ] . If we look at the 18 galaxies with RE/Re < 10 as in our sample (see Fig. 6), we notice that similarly to our sample that first, fDM(<RE) decreases slightly with redshift with the same slope than for our sample (−0.18), and second, the radius RE/Re increases with redshift while third fDM(<RE) slightly increases when RE/Re increases. The second effect is also observed for eleven ETGs from Strong Lenses in the Legacy Survey (Ruff et al. 2011).
We add that even if the COSMOS sample and the JK07 sample show similar behavior, we chose not to mix them for the display and slope calculations to avoid misinterpretations owing to possible systematics that may affect the measurement of the DM fraction in the two different methods (e.g. different IMFs).
 |
Fig. 7 Mass models overlaid on ACS images for (top to bottom) COSMOS 0049+5128 and COSMOS 5947+4752. The left column displays the best mass model corresponding to the χ2 given in Table 7 (Col. 4 or 3 if no other). The right panel shows a zoom of the central region of the lens models, where the source can be seen. North is to the top and East to the left. Color code: the red circles are the observed images, whose radii correspond to the position uncertainty used in the modeling. In orange are the images produced by the best-lens model (in case of perfect fit, the orange and red crosses are superimposed). The navy blue lines describe the potential. The caustic lines are in yellow, and the critical lines are in cyan. The green ellipses show the position of the source as seen through the best-mass model (one source for each image; when a good fit is reached, the four sources are partially superimposed). We indicate the position of Galaxy 2 (see Sect. 4.2.1 and Table 8). |
 |
Fig. 8 Suite: mass models on top of ACS images for (top to bottom) COSMOS 5921+0638, COSMOS 0038+4133 and COSMOS 0124+5121. The color code for the labels is given in Fig. 7. North is to the top and East to the left. |
 |
Fig. 9 Suite: mass models on top of ACS images for (top to bottom) COSMOS 0047+5023, J100140.12+023427.7 and COSMOS 5941+3628. The color code for the labels is given in Fig. 7. North is to the top and East to the left. |
 |
Fig. 10 Suite: mass models on top of ACS images for (top to bottom) COSMOS 0050+490, COSMOS 0018+3845 and COSMOS 5914+1219. The color code for the labels is given in Fig. 7. North is to the top and East to the left. |
 |
Fig. 11 Suite: mass models for the J095930.93+023427.7. Top left panel: the navy blue circle located north of the image surrounds the group central galaxy. Top right panel: zoom on the lens galaxy and on the images. Bottom panel: zoom on the caustic (yellow curves) and on the favorite source position (green ellipses). The color code for the labels is given in Fig. 7. North is to the top and East to the left. |
5. Discussion and conclusions
From the analysis of the COSMOS strong-lenses in the redshift range 0.34 to 1.13, we obtain three major results: (1) the lens galaxy stellar masses increase with the redshift, (2) the lens galaxy environments are compatible with those of ETGs in this redshift range and (3) the DM fraction of the lens galaxies in the Einstein radius slightly decreases with the redshift when the ratio between the Einstein radius versus the effective radius strongly increases with redshift. Let us discuss each one of these trends.
5.1. Increase of the lens stellar mass with redshift
In Sect. 2.3 we measured that the lens galaxy stellar mass increases with redshift. Is this a result of the selection method used to built the lens sample? At z ~ 0.4, one of our lenses has an effective radius of ~0.3″ and at z ~ 0.9, the smallest lens galaxy effective radius is ~0.2″ (see Table 5). The effective radius is a lower limit for the Einstein radius. These “lower limit Einstein radii” correspond to lower limits in mass within the Einstein radius that are in our case 1010.9 M⊙ at z = 0.4 and 1011.0 M⊙ at z = 0.9, assuming a source at z = 1.5. Hence, for a given source redshift, the minimal lens galaxy mass should increase with the lens redshift to be visually detected; consequently, most probably, the minimal stellar mass might increase as well with redshift. Following this reasoning, we expect the sample average stellar mass to increase with the redshift. While this reasoning is simplistic because the source redshifts are different for every lens, it still partially explains the increasing stellar mass with increasing redshift of the lens galaxies. So far, it is not clear whether this “detection bias” effect is the only reason for the lens galaxy stellar mass increase with redshift. This result should be investigated in dedicated numerical simulations (e.g. van de Ven et al. 2009; Mandelbaum et al. 2009).
5.2. Evolution of the lens galaxy environment
Our study of the environments of COSMOS lens galaxies via the projected galaxy number density in Sect. 3.1 indicates that the environment of lens galaxies is similar to that of ETGs across the whole range of redshifts tested here. This result extends the previous measurements made in the redshift range [0.068; 0.513] with the SLACS sample (T09 and Auger 2008). It is particularly interesting because the COSMOS and SLACS samples have very different selection criteria: therefore, this result is most probably a genuine characteristic of strong-lens galaxies rather than a selection bias.
We also notice that both neighbor density estimators tested here appear to be reliable estimators of the environment of galaxies, because X-ray groups and clusters are actually detected around lenses with high 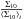 and high
and high 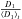 ratios.
ratios.
5.3. The decreasing dark matter fraction with redshift
We measured the lens galaxy DM fraction in the Einstein radius by combining the total mass in the Einstein radius, the light density profile, and the stellar mass in the galaxy. The projected DM fraction decreases with redshift even though the ratio between the Einstein radius and the effective radius increase with the redshift (see Fig. 6). A similar trend is seen in the lens galaxy dataset of JK07, which covers a similar redshift range. Using toy models and a λCDM cosmology and the SLACS lenses, Napolitano et al. (2010) and Tortora et al. (2010) first noticed that for a fixed stellar mass and age, the DM fraction is similar for high- and low- redshift galaxies. They also noticed that the slope of the distribution of fDM versus age is steeper than explained by their model and invoked different scenarios to interpret the discrepancy (including adiabatic compression and different IMF for different galaxy ages). Another possible effect that could be responsible for the DM fraction decrease with redshift is the increasing stellar density of ETGs with redshift as discussed by Bezanson et al. (2009). But to understand if the results are affected by one of these effects, fDM needs to be measured in comparable radius, not different for each galaxy, contrary to the Einstein radius. Results obtained within the effective radius by Ruff et al. (2011) seem to agree with our conclusions. In order to conclude on the favorite ongoing processes on ETGs since z ~ 1 as a function of their age and stellar mass, a joint analysis of the different lens galaxy samples which allow these measurements would certainly be a first step toward a better understanding.
5.4. Some remarks on the lens models
Using lens modeling we measured the Einstein radii and related total masses for the lens galaxies. Doing so, we were able to measure their DM fractions within their Einstein radius. In addition, the lens models were used to test the calculation of the external shear produced by the groups around the lens galaxies. We observed that in every lens model, the difference between the best-fit external shear and the shear produced by the groups points toward the closest galaxy to the lens. We calculate that those secondary galaxies need to have realistic velocity dispersions for the lens models to provide good fits.
Moreover, we have measured that a catalog of high-mass groups and clusters modeled by TIS is giving very similar total shear strengths and orientations than a combination of high-mass and low-mass group catalogs. Therefore we conclude that a measurement of the external shear that affects the lens potential at the lens galaxy location could be made if one could combine a measurement of the redshift and velocity dispersion of the lens galaxy closest neighbor(s) with the locations, masses, and radii of the most massive groups and clusters (such as the one provided by the X-ray observations in the COSMOS field) in a ≳ 5′ radius around the lens galaxy. By fixing the external shear one would break an important source of degeneracy in the lens models.
5.5. Conclusions
On one hand, we have measured that the environment of lens galaxies is similar to that of non-ETGs over a wide redshift range: between 0.068 and 1.13 if we combine the results from the SLACS sample (T09, Auger 2008) and from the COSMOS sample (this paper). On the other hand, we have built up an ensemble of clues suggesting that the mass properties of lens galaxies evolve with redshift.
Indeed, at high redshift, lens galaxies have a large stellar mass and a total dark matter fraction ⟨ fDM ⟩ ~ 0.7 (for z > 0.8). On the contrary, at low redshifts, lens galaxies have lower stellar mass and their DM fraction is ⟨ fDM ⟩ > 0.8.
These results argue in favor of high stellar density of the high-redshift ETGs compared to low-redshift ETGs as suggested by the results of Bezanson et al. (2009). Or it could be that the difference between low- and high- redshift lens galaxy population is a consequence of the stellar population aging and different IMFs at different ages (see Napolitano et al. 2010). It could also be that the effects measured here are related to the lensing efficiency, which in this case would be a complex combination of (1) the lens population number density, (2) the source population distribution in space, redshift, and luminosity, (3) the survey properties (sensitivity, band, size, angular resolution), (4) biases in the lens sample selection.
To distinguish between an evolutionary or a pure lensing origin of the effects discovered in this study, the evolution of lens galaxy properties with redshift needs to be studied in dedicated numerical simulations (e.g. van de Ven et al. 2009; Mandelbaum et al. 2009). Whether the effects are intrinsic to the massive early-type galaxy population or to the lensing efficiency, they must be fully understood if one aims to properly study the galaxy properties gathered from lens galaxy populations.
Available at www.oamp.fr/people/arnouts/LE_PHARE.html
The COSMOS catalogs can be found at http://irsa.ipac.caltech.edu/data/cosmos
Acknowledgments
We acknowledge the anonymous referee for providing a detailed and very useful report. We are gratefully indebted to M. Limousin and R. Gavazzi for enlightening discussions. D.A. thanks CNRS and CEA for support and visits to the Geneva observatory, where this work was finalized. J.P.K. thanks for support from CNRS and SL2S ANR-06-BLAN-0067 and DESIR ANR-07-BLAN-0228. E.J. acknowledges the support of the NPP, administered by Oak Ridge Associated Universities through a contract with NASA.
References
- Allam, S. S., Tucker, D. L., Lin, H., et al. 2007, ApJ, 662, L51 [NASA ADS] [CrossRef] [Google Scholar]
- Anguita, T., Faure, C., Kneib, J.-P., et al. 2009, A&A, 507, 35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Auger, M. W. 2008, MNRAS, 383, L40 [NASA ADS] [Google Scholar]
- Bartelmann, M., Meneghetti, M., Perrotta, F., Baccigalupi, C., & Moscardini, L. 2003, A&A, 409, 449 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bezanson, R., van Dokkum, P. G., Tal, T., et al. 2009, ApJ, 697, 1290 [NASA ADS] [CrossRef] [Google Scholar]
- Bolton, A. S., Burles, S., Koopmans, L. V. E., Treu, T., & Moustakas, L. A. 2006, ApJ, 638, 703 [NASA ADS] [CrossRef] [Google Scholar]
- Bolton, A. S., Burles, S., Koopmans, L. V. E., et al. 2008, ApJ, 682, 964 [NASA ADS] [CrossRef] [Google Scholar]
- Bruzual, G., & Charlot, S. 2003, MNRAS, 344, 1000 [NASA ADS] [CrossRef] [Google Scholar]
- Bundy, K., Ellis, R. S., Conselice, C. J., et al. 2006, ApJ, 651, 120 [NASA ADS] [CrossRef] [Google Scholar]
- Cabanac, R. A., Alard, C., Dantel-Fort, M., et al. 2007, A&A, 461, 813 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Capak, P., Aussel, H., Ajiki, M., et al. 2007a, ApJS, 172, 99 [NASA ADS] [CrossRef] [Google Scholar]
- Capak, P., Abraham, R. G., Ellis, R. S., et al. 2007b, ApJS, 172, 284 [NASA ADS] [CrossRef] [Google Scholar]
- Capak, P., Mobasher, B., Scoville, N. Z., et al. 2011, ApJ, 730, 68 [NASA ADS] [CrossRef] [Google Scholar]
- Chae, K.-H., Mao, S., & Kang, X. 2006, MNRAS, 373, 1369 [NASA ADS] [CrossRef] [Google Scholar]
- Chantry, V., & Magain, P. 2007, A&A, 470, 467 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dobke, B. M., King, L. J., & Fellhauer, M. 2007, MNRAS, 377, 1503 [NASA ADS] [CrossRef] [Google Scholar]
- Elvis, M., Civano, F., Vignali, C., et al. 2009, ApJS, 184, 158 [NASA ADS] [CrossRef] [Google Scholar]
- Faure, C., Kneib, J.-P., Covone, G., et al. 2008, ApJS, 176, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Faure, C., Kneib, J.-P., Hilbert, S., et al. 2009, ApJ, 695, 1233 [NASA ADS] [CrossRef] [Google Scholar]
- Finoguenov, A., Guzzo, L., Hasinger, G., et al. 2007, ApJS, 172, 182 [Google Scholar]
- Finoguenov, A., Connelly, J. L., Parker, L. C., et al. 2009, ApJ, 704, 564 [NASA ADS] [CrossRef] [Google Scholar]
- Gavazzi, R., Treu, T., Rhodes, J. D., et al. 2007, ApJ, 667, 176 [NASA ADS] [CrossRef] [Google Scholar]
- Grillo, C., Gobat, R., Lombardi, M., & Rosati, P. 2009, A&A, 501, 461 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hasinger, G., Cappelluti, N., Brunner, H., et al. 2007, ApJS, 172, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Hilbert, S., White, S. D. M., Hartlap, J., & Schneider, P. 2007, MNRAS, 382, 121 [NASA ADS] [CrossRef] [Google Scholar]
- Hilbert, S., White, S. D. M., Hartlap, J., & Schneider, P. 2008, MNRAS, 386, 1845 [NASA ADS] [CrossRef] [Google Scholar]
- Ilbert, O., Capak, P., Salvato, M., et al. 2009, ApJ, 690, 1236 [NASA ADS] [CrossRef] [Google Scholar]
- Ilbert, O., Salvato, M., Le Floc’h, E., et al. 2010, ApJ, 709, 644 [NASA ADS] [CrossRef] [Google Scholar]
- Jackson, N. 2008, MNRAS, 389, 1311 [NASA ADS] [CrossRef] [Google Scholar]
- Jiang, G., & Kochanek, C. S. 2007, ApJ, 671, 1568 [NASA ADS] [CrossRef] [Google Scholar]
- Jullo, E., Kneib, J.-P., Limousin, M., et al. 2007, New J. Phys., 9, 447 [Google Scholar]
- Keeton, C. R. 2001, ApJ, 561, 46 [NASA ADS] [CrossRef] [Google Scholar]
- Keeton, C. R. 2003, ApJ, 584, 664 [NASA ADS] [CrossRef] [Google Scholar]
- Kneib, J. P., Mellier, Y., Fort, B., & Mathez, G. 1993, A&A, 273, 367 [NASA ADS] [Google Scholar]
- Knobel, C., Lilly, S. J., Iovino, A., et al. 2009, ApJ, 697, 1842 [NASA ADS] [CrossRef] [Google Scholar]
- Kochanek, C. S. 2002, The Shapes of Galaxies and their Dark, 62 [Google Scholar]
- Koekemoer, A. M., Aussel, H., Calzetti, D., et al. 2007, ApJS, 172, 196 [NASA ADS] [CrossRef] [Google Scholar]
- Koopmans, L. V. E., Treu, T., Bolton, A. S., Burles, S., & Moustakas, L. A. 2006, ApJ, 649, 599 [NASA ADS] [CrossRef] [Google Scholar]
- Lagattuta, D. J., Fassnacht, C. D., Auger, M. W., et al. 2010, ApJ, 716, 1579 [NASA ADS] [CrossRef] [Google Scholar]
- Leauthaud, A., Finoguenov, A., Kneib, J.-P., et al. 2010, ApJ, 709, 97 [NASA ADS] [CrossRef] [Google Scholar]
- Lilly, S. J., Le Fèvre, O., Renzini, A., et al. 2007, ApJS, 172, 70 [NASA ADS] [CrossRef] [Google Scholar]
- Lilly, S. J., Le Brun, V., Maier, C., et al. 2009, ApJS, 184, 218 [Google Scholar]
- Limousin, M., Kneib, J. P., Bardeau, S., et al. 2007, A&A, 461, 881 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Limousin, M., Sommer-Larsen, J., Natarajan, P., & Milvang-Jensen, B. 2009a, ApJ, 696, 1771 [NASA ADS] [CrossRef] [Google Scholar]
- Limousin, M., Cabanac, R., Gavazzi, R., et al. 2009b, A&A, 502, 445 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mandelbaum, R., van de Ven, G., & Keeton, C. R. 2009, MNRAS, 1066 [Google Scholar]
- Marleau, F. R., & Simard, L. 1998, ApJ, 507, 585 [NASA ADS] [CrossRef] [Google Scholar]
- McCracken, H. J., Peacock, J. A., Guzzo, L., et al. 2007, ApJS, 172, 314 [NASA ADS] [CrossRef] [Google Scholar]
- Mobasher, B., Capak, P., Scoville, N. Z., et al. 2007, ApJS, 172, 117 [NASA ADS] [CrossRef] [Google Scholar]
- Momcheva, I., Williams, K., Keeton, C., & Zabludoff, A. 2006, ApJ, 641, 169 [NASA ADS] [CrossRef] [Google Scholar]
- Natarajan, P., Kneib, J.-P., Smail, I., et al. 2009, ApJ, 693, 970 [NASA ADS] [CrossRef] [Google Scholar]
- Napolitano, N. R., Romanowsky, A. J., & Tortora, C. 2010, MNRAS, 405, 2351 [NASA ADS] [Google Scholar]
- Ofek, E. O., Rix, H.-W., & Maoz, D. 2003, MNRAS, 343, 639 [NASA ADS] [CrossRef] [Google Scholar]
- Oguri, M., Keeton, C. R., & Dalal, N. 2005, MNRAS, 364, 1451 [NASA ADS] [CrossRef] [Google Scholar]
- Ruff, A. J., Gavazzi, R., Marshall, P. J., et al. 2011, ApJ, 727, 96 [NASA ADS] [CrossRef] [Google Scholar]
- Sanders, D. B., Salvato, M., Aussel, H., et al. 2007, ApJS, 172, 86 [Google Scholar]
- Scoville, N., Aussel, H., Brusa, M., et al. 2007, ApJS, 172, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Scarlata, N., Carollo, C. M., Lilly, S., et al. 2007a, ApJS, 172, 406 [NASA ADS] [CrossRef] [Google Scholar]
- Scarlata, N., Carollo, C. M., Lilly, S. J., et al. 2007b, ApJS, 172, 494 [NASA ADS] [CrossRef] [Google Scholar]
- Simard, L. 1998, Astronomical Data Analysis Software and Systems VII, 145, 108 [NASA ADS] [Google Scholar]
- Taniguchi, Y., Scoville, N., Murayama, T., et al. 2007, ApJS, 172, 9 [NASA ADS] [CrossRef] [Google Scholar]
- Tortora, C., Napolitano, N. R., Romanowsky, A. J., & Jetzer, P. 2010, ApJ, 721, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Treu, T., Koopmans, L. V., Bolton, A. S., Burles, S., & Moustakas, L. A. 2006, ApJ, 640, 662 [NASA ADS] [CrossRef] [Google Scholar]
- Treu, T., Gavazzi, R., Gorecki, A., et al. 2009, ApJ, 690, 670 [NASA ADS] [CrossRef] [Google Scholar]
- Vikhlinin, A., Burenin, R. A., Ebeling, H., et al. 2009, ApJ, 692, 1033 [NASA ADS] [CrossRef] [Google Scholar]
- van de Ven, G., Mandelbaum, R., & Keeton, C. R. 2009, MNRAS, 1067 [Google Scholar]
- Wambsganss, J., Bode, P., & Ostriker, J. P. 2005, ApJ, 635, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Wong, K. C., Keeton, C. R., Williams, K. A., Momcheva, I. G., & Zabludoff, A. I. 2011, ApJ, 726, 84 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Summary of the VLT (FORS1 and VIMOS) and Keck (DEIMOS and LRIS) observations: target name, instrument, and exposure time (in ks).
Position and redshift of galaxies in the FORS1 field around COSMOS 0012+2015, COSMOS 0013+2249, and COSMOS 0049+5128. The error on the redshifts is ± 0.001.
Summary of the properties of the lens galaxy environments (top to bottom: from low to high redshift).
Position of the lensing galaxy (in degree) and relative position (in arc-second) of the images used as constraints for the lens mass model.
All Figures
 |
Fig. 1 VLT/FORS1 spectra of three strong-lens candidates. The spectral resolution is 5.52 Å per pixel, and has been smoothed by a 3-pixel box to improve the quality of the display. Flux is in arbitrary units. |
| In the text | |
 |
Fig. 2 Keck/DEIMOS spectrum of COSMOS 0018+3845. The spectrum is smoothed by 2.3 Å and binned down to 7.5 Å per pixel, taking the wavelength dependent noise into account to improve the apparent signal-to-noise. Flux is in arbitrary units. |
| In the text | |
 |
Fig. 3 Photometric redshift, zphot, versus spectroscopic redshift, zspec, for 16 of the lens galaxy candidates. The solid line features zphot = zspec. Errors bars on the value of zphot relate to the 68% confidence level. |
| In the text | |
 |
Fig. 4 Stellar masses (in M⊙) of the lens galaxies as a function of redshift (spectroscopic when available, photometric otherwise). Black crosses: stellar masses inferred using the method described in Bundy et al. (2006). Grey stars: stellar masses inferred for the IRAC sources in Ilbert et al. (2010). Black and grey lines: the respective least-square fits, with a slope of +0.8 ± 0.3 (black line) and +0.7 ± 0.3 (grey line). |
| In the text | |
 |
Fig. 5 Distribution of |
| In the text | |
 |
Fig. 6 Evolution of the dark matter fraction and related parameters for two lens samples: COSMOS (crosses) and JK07 (stars). Top left panels: evolution of the DM fraction in the Einstein radius with the redshift. The least-deviation fits are displayed (solid lines), and follow the relations fDM(<RE) = −0.18 × z + 1.00 for COSMOS and fDM(<RE) = −0.18 × z + 0.38 for JK07. Top right panels: variation of the DM fraction as function of the ratio of the Einstein radius versus effective radius. The least-deviation fits give the following relations: |
| In the text | |
 |
Fig. 7 Mass models overlaid on ACS images for (top to bottom) COSMOS 0049+5128 and COSMOS 5947+4752. The left column displays the best mass model corresponding to the χ2 given in Table 7 (Col. 4 or 3 if no other). The right panel shows a zoom of the central region of the lens models, where the source can be seen. North is to the top and East to the left. Color code: the red circles are the observed images, whose radii correspond to the position uncertainty used in the modeling. In orange are the images produced by the best-lens model (in case of perfect fit, the orange and red crosses are superimposed). The navy blue lines describe the potential. The caustic lines are in yellow, and the critical lines are in cyan. The green ellipses show the position of the source as seen through the best-mass model (one source for each image; when a good fit is reached, the four sources are partially superimposed). We indicate the position of Galaxy 2 (see Sect. 4.2.1 and Table 8). |
| In the text | |
 |
Fig. 8 Suite: mass models on top of ACS images for (top to bottom) COSMOS 5921+0638, COSMOS 0038+4133 and COSMOS 0124+5121. The color code for the labels is given in Fig. 7. North is to the top and East to the left. |
| In the text | |
 |
Fig. 9 Suite: mass models on top of ACS images for (top to bottom) COSMOS 0047+5023, J100140.12+023427.7 and COSMOS 5941+3628. The color code for the labels is given in Fig. 7. North is to the top and East to the left. |
| In the text | |
 |
Fig. 10 Suite: mass models on top of ACS images for (top to bottom) COSMOS 0050+490, COSMOS 0018+3845 and COSMOS 5914+1219. The color code for the labels is given in Fig. 7. North is to the top and East to the left. |
| In the text | |
 |
Fig. 11 Suite: mass models for the J095930.93+023427.7. Top left panel: the navy blue circle located north of the image surrounds the group central galaxy. Top right panel: zoom on the lens galaxy and on the images. Bottom panel: zoom on the caustic (yellow curves) and on the favorite source position (green ellipses). The color code for the labels is given in Fig. 7. North is to the top and East to the left. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.