| Issue |
A&A
Volume 528, April 2011
|
|
|---|---|---|
| Article Number | A132 | |
| Number of page(s) | 17 | |
| Section | Stellar atmospheres | |
| DOI | https://doi.org/10.1051/0004-6361/201016259 | |
| Published online | 15 March 2011 | |
Abundances of the elements He to Ni in the atmosphere of Sirius A
1 Armagh Observatory, College Hill, Armagh BT61 9DG, Northern
Ireland
e-mail: jls@arm.ac.uk
2 Department of Physics &
Astronomy, University of Western Ontario, London, N6A 3K7
Ontario,
Canada
Received: 3 December 2010
Accepted: 8 February 2011
Context. The abundances of elements in the atmosphere of an individual star provide a very broad range of extremely important information about the formation and evolution history of that star. Specifically, during the main sequence phase, the abundance pattern observed can provide valuable constraints on a range of hydrodynamical processes occurring beneath the visible atmosphere.
Aims. Among middle main sequence (A and B) stars, it is unusual to have abundance determinations for more than about a dozen of the 30 lightest chemical elements, largely because many elements do not have usefully strong spectral lines in the visible wavelength window usually used for abundance analysis. Exceptionally, for the bright, sharp-lined hot Am star Sirius A = HD 48915, high resolution, high signal-to-noise ratio observations of the spectrum are available from 1265 Å to about 1 μm. The aim of this project is to determine generally how useful the UV part of the spectrum is for “generic” abundance determination in A stars, and which abundances of light and iron peak elements can be determined or improved for Sirius A using this nearly unique data set.
Methods. The UV and visible spectrum of Sirius A has been searched for useful spectral lines of all elements up to nickel (2 ≤ Z ≤ 28), as well as the heavy elements Sr, Y, Zr and Ba. Using the spectrum synthesis code ZEEMAN, abundances or upper limits are derived.
Results. Abundances relative to H have been determined for a total of 20 elements, and upper limits are found for 4 others. Useful measurements or limits are possible from these data for all but three of the elements through Ni. In particular, it is found that the light element B is underabundant relative to the Sun by a factor of at least 30.
Conclusions. Recent computations have led to predictions of the abundance pattern of almost all the elements having Z ≤ 28 expected in the atmosphere of Sirius as a result of competition between (1) gravitationally and radiatively driven diffusion and either (2) turbulent mixing or (3) homogeneous mass loss. Comparison of these predictions with observations has been hampered by the limited number of elements for which accurate abundance determinations are available. The work presented here increases the number of elements for which reasonably well-determined abundances are available, and establishes more clearly the uncertainty of the abundance values for most of the elements up to Ni. The new data provide useful tests of the theoretical predictions of the consequences of atomic diffusion in slowly rotating A stars, and in some cases contradict them. These data may also provide some fresh insight into the evolution of the Sirius system. It appears that the new abundance values may be qualitatively consistent with the possibility that significant mass transfer has occurred between the two components of the system during its evolution.
Key words: stars: abundances / stars: chemically peculiar / stars: early-type / stars: evolution / Ultraviolet: stars / stars: individual: HD 48915
Based on observations made with European Southern Observatory telescopes at the La Silla or Paranal Observatories under programme ID 266.D-5655(A) and obtained from the ESO/ST-ECF Science Archive Facility, and on observations made with the NASA/ESA Hubble Space Telescope, obtained from the data archive at the Space Telescope Institute. STScI is operated by the association of Universities for Research in Astronomy, Inc. under the NASA contract NAS 5-26555.
© ESO, 2011
1. Introduction
The Sirius binary system (HD 48915 = HIP 32349), composed of a main sequence A1V star and a hot DA white dwarf, is of great interest as a test case for stellar evolution calculations of various kinds, because so many parameters of both stars can be determined with very high precision.
Sirius is an astrometric visual binary system at a distance of only 2.64 pc. The revised Hipparcos parallax of the system, π = (379.21 ± 1.21) mas (Van Leeuwen 2007) is known to much better than 1% precision, so that the luminosity log (L/L⊙) = 1.405 ± 0.022 is measured with about 5% precision (Kervella et al. 2003).
The two stars orbit one another with a period of 50.09 yr, in an orbit of a = (7.56 ± 0.02) arcsec and e = 0.5923 ± 0.0019. The separation of the two stars varies between 8.1 and 31.7 AU. The astrometric motions of each of the two stars in the system can be measured precisely on the sky, yielding both the mass ratio and the total mass of the system (van den Bos 1960; Gatewood & Gatewood 1978). The masses of Sirius A and B are MA = (2.12 ± 0.06) M⊙ and MB = (1.000 ± 0.016) M⊙.
The diameter of Sirius A has been measured interferometrically (Kervella et al. 2003) as DA = (1.711 ± 0.013) D⊙. The effective temperature Te = (9900 ± 200) K from Strömgren colours (Lemke 1989), in agreement with the value of (9900 ± 130) K derived from the luminosity and radius ( see also Code et al. 1976). The measured mass and radius yield log g = 4.30 ± 0.01.
The initial state of the stars in the Sirius system is that the current Sirius B was once considerably more massive than Sirius A, and thus has had time to evolve to become first a red giant and then a white dwarf while the current Sirius A is still on the main sequence. A possible complication of this evolution is that the two stars may have interacted in an important way during the past, particularly when Sirius B was a red giant or was on the asymptotic giant branch. However, the facts that the mutual orbit is presently quite eccentric, and that the closest approach of the two stars is about 8 AU, have led people to assume that no important interaction occurred.
Making this assumption, one can fit the current position of Sirius A in the HR diagram. It is found (Kervella et al. 2003; Liebert et al. 2005) that this requires that the bulk composition of Sirius A be in the range of Z = 0.014 to 0.016, rather lower than the old value of Z accepted for the Sun, but similar to the value of about 0.134 found by Asplund and collaborators (Asplund et al. 2009). With Z in this range, the elapsed time that Sirius A has spent on the main sequence is found to be in the range of 180 to 250 Myr.
Sirius B is a hot white dwarf, with Te = (25 000 ± 200) K (Liebert et al. 2005). Liebert et al. have argued that the cooling time of a 1.00 M⊙ white dwarf to this effective temperature requires about 125 Myr. Subtracting this cooling time from the main seuqence lifetime deduced for Sirius A, the main sequence lifetime of Sirius B was about 55 to 125 Myr, so this star on the main sequence would have had a mass of about 5–7 M⊙. This value is in agreement with the initial-final mass relationship found for white dwarfs in open clusters (Salaris et al. 2009). Thus the initial state of the Sirius system would have been a binary pair with a star of about 2 M⊙ orbiting a star of about 6 M⊙.
Sirius A is an apparently slow rotator (vesini = 16.5 km s-1; Landstreet 1998), and so the atmospheric abundances are relatively easy to measure. It is found that the star is a hot Am (metallic-line) star, with non-solar abundances of a number of elements (e.g. Sadakane & Ueta 1989). This strongly suggests that the star is an intrinsically slow rotator, and that the small value of vesini is not simply a projection effect. In this case, atomic diffusion (downwards under the influence of gravity, upwards due to radiation pressure from the outward flux of photons acting on specific atoms and ions) is expected to alter the atmospheric abundances from the initial state representative of the stellar bulk chemistry (Richer et al. 2000, Vick et al. 2010).
With so many stellar parameters very precisely determined, including an approximate age, Sirius A should be an excellent test case for computations of the evolution of a suitable stellar model including diffusion. Richer et al. (2000) have computed stellar and atmospheric evolution models for stars like Sirius A assuming turbulent mixing in the stellar envelope, but no mass loss, while Vick et al. (2010) have considered evolution with simple mass loss. Both papers present predictions for the evolution of atmospheric abundance of all the elements with Z ≤ 28 for which sufficient atomic data to predict the evolution of surface chemistry is available, and both make extensive comparison with the observed abundances of elements of Z ≤ 28 in Sirius A, for which abundances of more elements have been measured than for any other A star. It is because of the interest of comparisons with these computations that the abundance analysis here has been largely limited to the elements having Z ≤ 28.
In spite of the relatively large number of elements in Sirius A for which abundances are available, the comparisons with computations are still substantially limited by shortcomings of the observational material. There are two major problem areas. First, the abundances of several light elements with which comparison could be made have not yet been determined. These include Be, B, F, Ne, Cl, Ar, and K. The most recent large study of the abundances of Sirius A, by Qiu et al. (2001) lists abundances for only 17 of the 27 elements from He to Ni. Secondly, several of the elements for which abundances have been determined show substantial differences from one observer to another. Seriously discordant elements include C, Mg, Al, Si, S, Ca, V, Mn, and Ni. Even Fe is somewhat discordant among different studies (± 0.1 dex), in spite of numerous spectral lines and an abundance of relatively well-determined atomic data.
These two limitations of the abundance dataset for even such a well-studied star as Sirius A suggest that a new study would be useful. This is particularly appropriate as a potentially very valuable spectral region, the ultraviolet region between 1250 Å and the Balmer jump at 3646 Å, has hardly been exploited at all in spite of the existence of publicly available spectra covering this entire region. In fact, the use of this region for “generic” abundance analysis of A stars has rarely been explored at all, even though much material is available from Copernicus, IUE, and the HST up to 3200 Å, and from 3000 Å to longer wavelengths from UVES at ESO.
This paper describes an effort to improve our knowledge of the abundances of Sirius A by using publicly available high-signal-to-noise, high resolution spectra covering essentially the full spectral window from 1265 to 10 400 Å. The work has several goals: (1) to determine how generally complete line lists are for spectrum synthesis in the UV, and how accurate the atomic data seem to be; (2) to learn how useful the ultraviolet is (in spite of severe blending) for generic abundance measurements in A stars even of elements that can be studied in the optical, and to explore the factors limiting the precision of UV abundance measurement; (3) to discover whether any of the Z ≤ 28 elements for which the abundance has not been measured for Sirius A in the visible can be studied with the available ultraviolet material; and (4) to find out if the ultraviolet spectra enable us to clarify the abundances of elements with discordant determinations in the optical.
The next section discusses the spectra used in more detail. Section 3 describes the spectrum synthesis method and tools used in the analysis. In Sect. 4, I discuss the abundance analysis, element by element. Section 5 examines the conclusions that can be reached by combining this and complementary abundance studies, considers the implications of the measured abundances for calculations of atmospheric chemical evolution, and re-considers the evolution of the Sirius system in light of recent studies on binary system interactions and of the current abundance information available about Sirius A. The final section summarises the paper.
2. Observational data
The results reported here are based mainly on two sets of spectra of Sirius A, an ultraviolet spectrum from the Hubble Space Telescope, and visible light spectra from the European Southern Observatory.
The ultraviolet spectrum covers the wavelength region between 1265 and 3198 Å. It was obtained with the Goddard High Resolution Spectrograph (GHRS) on the Hubble Space Telescope for GO Proposal 3496 by G. Wahlgren (see Henderson et al. 1999). The spectrum has a resolving power of 25 000, and generally has a continuum signal-to-noise ratio of the order of 100 to 200 throughout. The data were obtained in 1993, when the Sirius AB system was near periastron, with a separation of about 3 arcsec. At this time the HST images still suffered from serious spherical aberration. However, the spectrum was obtained through an aperture of 0.25 arcsec, and the contamination of the spectrum of Sirius A by Sirius B (which has a pure H atmosphere at Te = 25 000 K, so that the fraction of its flux emitted in the UV is much greater than that of Sirius A), which was far out in the distant wings of the point spread function, is negligible. This is confirmed by the fact that even the shortest wavelength spectral regions of Sirius A contain lines that descend to below 1% of the local continuum.
The quality of the GHRS spectrum may be confirmed by comparison with the older ultraviolet scan of this star by the OAO-3 (Copernicus) experiment. This satellite carried out a scan of the ultraviolet spectrum of Sirius between 1649 and 3150 Å with a resolution element of 0.1 Å (the resolving power thus varied between 16 500 at the short wavelength end to 31 500 at the long wavelength end). The Copernicus spectrum of Sirius is presented as an atlas by Rogerson (1987). Although it is difficult to compare the two dataset because of problems of continuum normalisation (see below) and because of an uncertain (but certainly significant) amount of scattered light in the Copernicus spectrum, individual absorption features in the GHRS spectrum are reproduced with excellent fidelity in the slightly different resolution Copernicus spectrum.
The GHRS data were obtained in the form of short segments of spectrum, each of length between 30 and 45 Å. The GHRS reduction pipeline provides an absolute flux calibration for these segments. Comparison of the short overlap regions of a few Å of one segment with the adjacent one shows differences in flux normalisation of typically 5%, rising in some cases (e.g. at 1530 Å) to nearly 20%. This indicates that the accuracy of the flux calibration is not better than about 5–10%, a result which is not surprising, as the spectra were taken at a time when the point-spread function of the telescope placed much of the flux outside the 0.25 arcsec aperture.
The principal difficulty in comparing the GHRS spectrum with the output of a spectrum synthesis programme is in choosing an appropriate normalisation basis for the comparison. Through much of the observed ultraviolet region, the very high density of spectral lines, together with the projected rotation velocity value of about vesini = 16.5 km s-1 (Landstreet 1998), make it unclear on first inspection whether there are any points in the observed spectrum that approach the continuum, which provides the normalisation level conventionally used in abundance analysis. However, the synthetic spectrum suggests that treating continuum normalisation in the conventional manner, by forcing the highest observed data points to 1.0, is actually a reasonable approximation. Therefore the individual GHRS scans were renormalised to this value by the IRAF “continuum” procedure, generally using six segments of cubic splines per scan. In one or two cases, where very broad resonance lines cover a substantial fraction of a scan, a low order polynomial was used instead; the normalisation parameters were adjusted until the overall shape of the spectrum closely resembled a computed spectrum for that wavelength window.
Visible spectra of Sirius A covering almost the entire spectral window between 3050 and 10 400 Å (a gap of 140 Å is present between 8523 and 8663 Å) were obtained from the European Southern Observatory Advanced Data Products archive. These spectra were collected as part of the UVESPOP (UVES Paranal Observatory Project) observation of spectra of a representative sample of stars across the HR diagram (Bagnulo et al. 1993). The spectra were obtained using the UVES spectrograph with a resolving power of 80 000, and have nominal signal-to-noise ratios varying between about 200 for spectral segments shortward of 3800 Å and longward of 8800 Å to several hundred in the intervening segments. However, the standard pipeline reduction of these spectra was not very successful, and the data were not accepted for the UVESPOP final archive. One major problem is that many of the reduced spectra, especially at the UV and IR ends of the spectrum, are found to contain very strong residual signatures of the individual spectral orders observed with this cross-dispersed echelle spectrograph. These data artefacts were successfully removed from the spectrum orders analysed here, by renormalising the individual orders using the IRAF “continuum” procedure. In this part of the spectrum of Sirius, the spectral lines are generally separated by segments of nearly pure continuum, so the renormalisation procedure was usually unambiguous.
A second major problem with the UVES visible-IR data for Sirius A is that the two longest wavelength spectral segments, from 6700 to 8520 Å and from 8670 Å to 1.04 μm, are very badly affected by fringing even after processing with the current UVES pipeline. In these spectra, the SNR deduced from the counts are typically some hundreds, but going from the short to the long wavelength end of each segment, the SNR drops rapidly from values of the order of 100 to about 25. Thus these spectral windows are only useful for quite strong lines. There is also a lot of contamination by atmospheric absorption bands at these long wavelengths.
The UVES spectra as obtained from the ESO Science Archive Facility do have a relative flux calibration, but as these ground-based spectra were obtained through a very narrow slit, this calibration is clearly rather uncertain. I do not know of any accurate spectrophotometric scans of the flux distribution of this star covering the visible and near IR, and without such scans it is not possible to force the relative flux spectra from ESO onto an accurate absolute scale.
The GHRS and UVES spectra overlap in the window 3050–3200 Å. When normalised GHRS and UVES spectra in this interval are overplotted, virtually the only significant differences are attributable to small differences in continuum normalisation. All the features are reproduced with excellent fidelity. In general the differences between the two spectra are at the 1% level, and there does not seem to be any evidence of excess scattered light in either spectrum.
With these two sources of data, a nearly complete high-resolution, high signal-to-noise spectrum of Sirius A is available for the spectral interval 1265 to about 7000 Å, and (with much lower signal-to-noise) out to 10 400 Å, thus covering almost a full decade of the electromagnetic spectrum.
3. Method of abundance determination
Abundances of individual elements were obtained using the FORTRAN spectral synthesis programme ZEEMAN.f (Landstreet 1988, 1989; Wade et al. 2001). This programme computes the emergent spectrum from a stellar atmosphere of specified Te, gravitational acceleration log g, and abundance table. The programme was designed to compute LTE spectral line profiles and polarisation for an atmosphere permeated by a magnetic field (hence the name), but functions quite satisfactorily (and much faster) for a non-magnetic atmosphere.
The programme takes as input a pre-computed stellar atmosphere model (the grid used was computed by Piskunov using a modified version of Kurucz’s ATLAS 9 with solar composition and an experimental set of opacity distribution functions; see Piskunov & Kupka 2001) and a list of spectral lines obtained from the Vienna Atomic Line Database (VALD; Piskunov et al. 1995; Ryabchikova et al. 1997; Kupka et al. 1999, 2000). Line profiles of all listed spectral lines are calculated in a spectral window that is typically 35 to 100 Å in length, and the computed spectrum is adjusted automatically to match the radial velocity and vesini value of an observed spectrum with which comparison is being made. The programme can iteratively adjust the abundance of a single specified chemical element to match the ensemble of sufficiently unblended lines of that element found in an observed spectral window in a least squares sense. For a non-magnetic atmosphere, this adjustment can also include determination of the microturbulence parameter ξ. By adjusting element abundances one after another, convergence on the entire spectrum can be achieved (at least in those happy situations in which the adopted atmospheric and spectral line models are appropriate, the line list is complete and the atomic data are accurate), and an abundance table deduced for all elements for which useful lines are available. For A stars, the abundance determined is of course the abundance relative to the dominant continuous opacity source, which is hydrogen, and so all results are reported in the form of log (nX/nH). The data presented in this paper can be converted to the scale in which log nH ≡ 12 simply by adding 12 to the logarithmic abundances cited.
There are a number of specific aspects of this project that make abundance analysis based on the rocket ultraviolet more difficult than that based on optical spectra of Sirius.
First, the spectrum of Sirius becomes more and more crowded as one moves from the visible towards the Lyman limit. This is mainly because there are many more spectral lines of significant strength per unit wavelength in the ultraviolet than in the visible at the effective temperature of Sirius. This fact, together with the significant line broadening due to the non-zero vesini value, means that below about 2700 Å the lines appear to be almost continuously blended together, rather than mostly isolated as they are in the visible spectrum of Sirius. This in turn means that determining the level of the observational continuum (to which the computed spectrum is conventionally normalised) is difficult and somewhat uncertain.
In light of this problem, it is worth asking whether using continuum-normalised flux for the comparson between model and observation is the most appropriate procedure. In principle, one could consider computing the emergent model stellar flux in physical units, without normalising it to the continuum flux (but rescaling to take account of the accurately known radius and distance of Sirius A), and determine abundances by comparison of this model flux to the calibrated flux produced by the GHRS reduction pipeline. On the face of it, it appears that this might largely eliminate the problem of normalising the observed spectrum. However, it does not appear that this approach would actually improve the precision of the comparison.
On the computational side, the scaling quanitites of radius and distance have some uncertainty (but for Sirius A in particular these only introduce an uncertainty of the order of 2%). More seriously, the theoretical model atmosphere used for Sirius A is only an approximation to the real (chemically peculiar) atmosphere, and especially in the UV below 2000 Å, the emergent flux depends sensitively on having a complete line list and correct atomic data as well as a correct abundance table. It is found (see discussions below) that the computed spectrum in this short wavelength region of the UV is not a very accurate approximation to the observed one, in ways that cannot be attributed simply to poor low-order normalisation of the observed spectrum.
On the observational side, as mentioned above, the absolute flux calibration provided by the GHRS reduction pipeline appears uncertain at about the 10% level, which is roughly the level of renormalisation imposed by the continuum fitting procedure. Thus neither the accuracy of the computed spectra nor that of the observed spectra is good enough to make a comparison of model and observed fluxes advantageous compared to the conventional procedure of comparing continuum normalised spectra.
Because of the continuous blending of lines in the UV, it is necessary to compare the observed spectra with synthetic spectra rather than equivalent width computations. For this it is essential to have a rather complete line list. Fortunately, the line lists available from VALD appear to be reasonably complete for all the stronger lines; perhaps 1% of the strong features in the spectrum have no obvious counterpart in the line list and the computed spectrum, although it is not uncommon for weak features to be unidentified.
Atmospheric abundances of individual elements in Sirius A.
Furthermore, the heavy blending makes severe demands on the accuracy of the oscillator strengths and other atomic parameters of the lines in the list, since a line of interest is almost always blended more or less strongly with other nearby lines. Again, VALD, which summarises many atomic calculations and experiments, has in general achieved an admirable level of overall accuracy longward of 2000 Å, and an adequate level for shorter wavelengths, so that synthetic spectra computed with line lists from that source are similar to the observed spectrum (accurately so for wavelengths longward of 2000 Å; examples will be discussed below). However, one important systematic problem found with the current VALD data is that it contains quite a number of UV lines of Si i (see Moore 1967), for which the available oscillator strengths are clearly far too large. These are lines connecting low lying states with highly excited states near the ionisation potential of Si i, mostly above 63 000 cm-1. Classification of these observed states seems to be rather uncertain, and it is possible that many are incorrectly or inaccurately classified, resulting in incorrect computed gf values. The overly strong lines occur mainly in two clearly delineated spectral regions: 1535–1575 Å, and 1705–1735 Å. In these regions, I have reduced some of the Si i gf values to obtain reasonable agreement between the computed and the observed spectrum.
Another issue is that even with Te ~ 10 000 K, a temperature range at which H bound-free opacity is quite strong, it is essential to include other significant sources of continuous ultraviolet opacity. Since ZEEMAN.f has not previously been used in the region below 3000 Å, several sources important below 2000 Å were not initially included in my continuous opacity subroutine. For this project, I have added approximate expressions for the potentially significant metal continuous opacity derived from the Opacity Project results (Badnell et al. 2005). Since the short wavelength limit of the available spectra is 1265 Å, I have included continuous opacity due to C i, Mg i, and Si i, which have ground state opacity edges at respectively 1445, 1622, and 1521 Å. (He opacity below the Balmer jump was already built into the programme.) None of these turns out to contribute more than a few percent at any important level in the atmosphere of Sirius, and normalised synthetic spectra calculated with solar abundances for the window from 1296 to 1331 Å, with and without the inclusion of continuous opacity from these light elements, differ by at most about 1%. With the abundances found finally for Sirius A, particularly the 1 dex underabundance of C, the spectra with and without light metal continuous opacity are indistinguishable.
A third point that needs to be considered is the value of the microturbulence parameter ξ to use in the ultraviolet. Since this parameter appears to correlate fairly well with the expected amplitude of typical convective velocity (Landstreet 1998), in principle the appropriate values for modelling various regions of the UV spectrum, which are formed at different geometric depths, could be different from the 2.2 km s-1 found for the wavelength window around 4500 Å. This possibility can be explored by exploiting the rather large change in continuous opacity (mainly due to bound-free transitions of neutral H) across the Balmer jump. Through most of the atmosphere of Sirius, the total continuous opacity immediately shortward of this edge is a factor of order ten times larger than it is immediately longward of the edge, and a given continuum optical depth is reached roughly 400 km deeper in the atmosphere on the long wavelength side of the Balmer jump than on the short wavelength side. The values of the total continuous opacity coefficients κc on the two sides of the Balmer jump are the extremes reached for the value of κc throughout the wavelength window considered here.
Thus we can test for a strong variation of the value of the microturbulent parameter ξ with altitude in the atmosphere of Sirius by obtaining values of ξ from abundance analyses using restricted wavelength windows on the two sides of the Balmer jump. The most precise values of ξ may be obtained by finding the value that leads to the most nearly identical values of abundance from weak and strong lines of a single multiplet (or at least of several lines arising from lower atomic terms of similar energy) of a single element. Below the Balmer jump a suitable group of lines with accurate gf values is available in the window 3350–3460 Å with multiplets (3) and (4) of Cr ii. Using Blackwell diagrams as described by Landstreet (1998), the best value of ξ = (2.3 ± 0.4) km s-1. Above the Balmer jump, in a window between 4190 and 4290 Å (to avoid the higher Balmer lines) one may use lines of multiplet (31) of Cr ii, which lead to a value of ξ = (2.2 ± 0.3) km s-1. It appears that there is no major variation in microturbulence parameter over the range of physical depths probed by this experiment, and we adopt a constant microturbulence parameter ξ = 2.2 km s-1 throughout this analysis. This assumption is particularly important in the analysis of spectral lines below about 2500 Å, where the line density is high enough that isolated unsaturated lines are very rare and the microturbulence parameter cannot be determined directly with useful precision.
4. Results for individual elements
 |
Fig. 1 Fits to lines of Be ii (top panel), B ii (2nd panel), C i (1328–30 Å) and ii (1334–37 Å; 3rd panel), and N i (bottom panel). Black curves are observed spectrum of Sirius A. Blue curves show fit with abundances from Table 1, red curves are synthetic spectra with fitted element removed. The vertical axis is intensity normalised to the continuum. The wavelength scale is chosen for each panel so that the length of the boxes are all similar in velocity space, and the width in the figure of unblended single lines is similar regardless of the central wavelength. Exceptionally, in the two upper panels, the syntheses which best fit the observed spectrum do not require any Be or B, and so the red spectra with these elements removed are not shown. Instead the synthesis using the upper limit values to abundance for these elements are shown, and the positions of the relevant lines marked with arrows. |
The abundances found here for individual elements are shown in column 2 of Table 1 and are discussed element by element in the sections below. The next eight columns of this table are comparisons with the literature from the past 30 years; the second last column contains the mean abundance and the standard deviation obtained from a straight average of the individual (logarithmic) data; and the final column gives the abundance relative to H for the elements studied in the Sun (Asplund et al. 2009). The solar abundances are included simply to indicate the level of peculiarity of Sirius A relative to a typical “normal” star. These data will be discussed in Sect. 5. Several representative fits to UV spectral windows are shown in Figs. 1 through 5.
Note that it is not in general the purpose of this project to identify or select the best possible oscillator strengths, but to do the best possible with the generally available data. Only in a few cases have I replaced data from VALD with other data that I prefer. These cases are discussed in the appropriate subsections.
4.1. Helium, Z = 2
With a first ionisation potential of 24.59 eV, He is essentially neutral throughout the atmosphere of Sirius. Because of the large energy gap between the singlet and triplet ground states and the excited levels, the resonance lines lie at shorter wavelengths than the lower wavelength limit of the GHRS spectra. However, several of the strong high-excitation optical lines (e.g. λλ4387, 4471, 5875, 6678) are detectable and not severely blended, with equivalent widths of the order of 10 mÅ. I have used the 4471 and 5875 Å lines to determine the He abundance, which is marginally lower than the He abundance in the Sun.
4.2. Lithium, Z = 3
The strongest visible lines of Li i are the low-excitation lines at 6103 Å and the resonance lines at 6707 Å. The lines at 6103 Å are completely swamped by a line of Fe ii, while the resonance lines at 6707 require an abundance of about − 8.00, about 3 dex above solar, to be visible. As no line is visible at this wavelength, we have an upper limit about 3 dex above the solar Li abundance.
There are no strong Li i lines in the UV.
Li ii is He-like, with an ionisation potential of 75 eV. The lowest excited states are around 50 eV. The resonance lines are far below the Lyman limit, and excited lines require temperatures far higher than that of Sirius A to be seen. The weak upper limit from Li i 6707 is the best constraint available.
4.3. Beryllium, Z = 4
The only lines of Be likely to be strong enough to be detectable are the resonance lines of Be ii at 3130.42 and 3131.06 Å (Fig. 1). This region is available in both the GHRS and UVES spectra. Spectrum synthesis shows that the two lines are blended with lines (of V ii and Ti ii respectively) at slightly different wavelengths. The Be lines are not detected at all, with an upper limit to log (NBe/NH) of − 11.0, about a factor two below the solar abundance.
4.4. Boron, Z = 5
There are only a few lines of B ii that fall within the ultraviolet window (between 1230 and 1624 Å) that might be strong enough to be detected, and none of B i. No useful lines of either ionisation stage are expected in the optical. With the very low solar abundance of this element, only the B ii resonance line at 1362.46 Å (Fig. 1) actually has any realistic chance of being detected in this crowded UV region. Fortuitously, no strong blending lines coincide with this line, and synthesis with solar abundance indicates that the line should be easily detectable. However, it does not seem to be present, and synthesis provides a strong upper limit to the abundance, about a factor of 30 times lower than the solar abundance of this element. The predicted profile of the B ii line for several assumed abundance values is shown in detail in Fig. 2. Note that the log gf value from VALD for the B ii line has been replaced by the value recommended by Morton (2003), which is 0.07 dex larger than the VALD value.
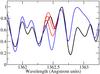 |
Fig. 2 Comparison of computed profiles of the B line at 1362.46 Å (coloured curves) to the observed spectrum (black). Abundances of B assumed in the calculations are log (nB/nH) = −9.3, − 10.3, − 10.8, and − 11.3 (from deepest to shallowest line). The solar abundance of B is − 9.30. |
4.5. Carbon, Z = 6
With a first ionisation potential of 11.26 eV, carbon is predominantly (roughly 90–95%) once ionised throughout most of the Sirius atmosphere, but C i is present in more than trace amounts. Numerous resonance lines and low excitation lines of C i are expected to be useful in the UV. In practice, resonance lines at 1328–29, 1561 and 1656–1659 Å, and low-excitation lines at 1311–16, 1355–1360, 1459–1482 and 1543 Å are sufficiently unblended to provide useful information about C abundance, although these lines are strongly saturated. The best fit abundances to individual lines range from about − 4.5 to − 5.0 with uncertainties of order 0.2 − 0.3 dex, and are globally consistent with an abundance of (− 4.70 ± 0.2) dex. Almost no useful lines of C i in the optical were found, but the line at 5052 Å may be marginally detected, and yields and abundance of − 4.05 ± 0.2. This line is so weak that this measurement should be regarded as an upper limit only.
The best UV lines of C ii are the high-excitation line at 1324, and the resonance lines at 1334–1336 Å (Fig. 1). These lines indicate a log abundance of about (− 4.40 ± 0.2) dex. The only optical lines expected to be detectable are 4267.00/4267.26 Å. These lines are almost undetectable to the eye, but an automated fit gives a best log abundance of about − 4.50 ± 0.2. In any case this line indicates an abundance below − 4.3.
Since the optical spectrum provide at best somewhat conflicting abundances on the basis of lines which are only marginally detectable, while numerous UV lines are clearly detected, frequently not badly blended, and generally well fit with an abundance of about − 4.55 ± 0.2, it is clear that the abundance of C in the atmosphere of Sirius is approximately one dex lower than in the Sun.
4.6. Nitrogen, Z = 7
Nitrogen i has a number of quite strong lines from low-lying levels scattered through the UV spectrum, and many weak high-excitation lines in the optical and near-IR. Because of the high ionisation potentials of N i (14.53 eV) and N ii (29.60 eV), no lines of N ii are expected to be detectable in our spectra, but since the neutral atom is the most common form of N through most of the atmosphere, abundances derived from this ion should be robust. In the UV, all the useful lines are heavily saturated and thus are not well-adapted to precise abundance determination; in addition, almost all of them are at least somewhat blended. I found that the most useful lines are those at 1319.67/.68, 1326.56/.57, 1327.91/.92, 1411.93/.94/.95, 1492.63/.82, 1494.67 (Fig. 1), and 1745.25/.26 Å. These lines are generally consistent with the solar abundance of N with an uncertainty of order 0.2 dex.
In the optical, the N i lines around 4250 Å are too weak to be useful. Some significant IR lines around 8225 Å are in a region where the UVES spectrum is severely degraded by fringing, but several lines between 8680 and 8730 Å are strong enough to model and relatively clean. These lines also yield essentially solar abundance of N, with an uncertainty of about 0.1 dex.
4.7. Oxygen, Z = 8
The very strong lines of O i in the ultraviolet are the allowed resonance lines λλ1302, 1304 and 1306 Å but these lines are very badly blended with similarly strong resonance lines of Si, P and S, and are hardly useful for abundance determination at this temperature. More reliable abundance values may be obtained from the multiplets in the red and infrared optical regions. I have obtained the abundance by fitting (perfectly) the relatively weak group of lines at 6155−6158 Å, which yield an abundance of O of (−3.60 ± 0.1) dex, a factor of two below the solar value.
I also synthesised the very strong O i multiplet (1) lines between 7771 and 7775 Å. From these lines an abundance of −2.75 is deduced, almost one dex larger than from the weaker lines discussed above. This same result was already found by Lambert et al. 1982, whose measured equivalent widths agree with my own to within 2 to 3%. Lambert et al. noted that this problem is caused by strong non-LTE effects in the multiplet (1) lines, as discussed by Baschek et al. 1977. Since my analysis is restricted to LTE, I disregard the result from the multiplet (1) lines.
The lowest even parity levels of O ii are about 15 eV above ground, so the resonance lines are all far below the short wavelength limit of the available spectra, and the longest wavelength low-excitation lines are from about 10 eV above ground. This ion provides no useful information.
4.8. Fluorine, Z = 9
The first ionisation potential of F is at 17.42 eV, so F i is overwhelmingly the dominant ion. The UV resonance lines of F i occur below 1000 Å. The lowest excited state of F i is at 12.6 eV, and so optical lines all arise from levels above 12 eV. As a result, no useful spectral lines of F occur within the available spectra.
4.9. Neon, Z = 10
Neon has a large first ionisation potential of 21.56 eV and a sparse energy level structure throughout most of this range. As a result, the only lines likely to be detectable in Sirius A are in the red, but arise from levels around 18 eV, and are expected to be very weak. The line predicted to be strongest is Ne i 6402.24, which is expected to be at most a few mÅ in equivalent width. This line is not detected in the UVES spectra in spite of a local SNR of more than 300, and an upper limit to the Ne abundance of about a factor of three above solar is established by synthesis.
4.10. Sodium, Z = 11
The only ionisation stage that yields observable lines is Na i. Na ii has an ionisation potential of 47.29 eV, and so all the lines of this state either arise from extremely highly excited levels, or lie far below the Lyman limit. Although the ionisation potential of Na i is only 5.14 eV, the fractional population of this ion rises to about 6 × 10-5 of the total Na in the deep photosphere, and the resonance lines at 5889 and 5895 Å are fairly strong (and contrary to the concern expressed by Qiu et al. 2001, they show no signs, such as sharp components, of interstellar contamination). Fitting these two lines leads to an abundance almost one dex higher than the solar value. These two lines are strongly saturated, so the uncertainty in ξ leads to an uncertainty in abundance of about 0.1 dex. Because the ionisation state used to determine the abundance is not the dominant one, the uncertainty in Te also leads to significant uncertainty. If we assume an uncertainty of 200 K in Te, the inferred abundance of −4.70 is uncertain by about 0.15 dex. Thus the total abundance uncertainty is at least about 0.2 dex, somewhat larger than normal.
The Na i resonance line at 3302.37 Å appears to be weakly detected in a short region that seems free of obvious blends. A fit to this feature yields a logarithmic abundance of −4.75 ± 0.1 dex, consistent with the result from the D lines. I also considered using the lines at λλ8183 and 8194, which Qiu et al. used, but this region is badly distorted by fringing (discussed above) and I do not trust it for weak stellar lines.
The above evidence suggests that the abundance of Na is about 1 dex higher than in the Sun.
4.11. Magnesium, Z = 12
The abundance of Mg may be obtained from the optical region using the strong high-excitation (multiplet (4)) lines of the dominant ionisation stage Mg ii at 4481 Å and the much weaker lines of multiplet (9) nearby, from the UV with the resonance lines of this ion at 2795 and 2802 Å, and from the nearly unblended Mg ii lines at 1737.62 Å that arise from 4.43 eV above ground. All these lines agree reasonably well on an abundance of −4.70 ± 0.1, about a factor of two below the solar value.
The Mg i b triplet of multiplet (2) around 5180 Å is easily detected and modelled. However, like the situation for Na, neutral Mg is very much a minority ion; it never rises to much above 4 10-4 of the total Mg in the atmosphere of Sirius A. Consequently, the discordant abundance of − 4.30 obtained from these lines is not too surprising, and I do not include it in my determination of the abundance of Mg. Note that this discordance suggests that the abundance derived above for Na using the D lines may also be in error by more than the uncertainties estimated from known LTE effects.
 |
Fig. 3 Fits to lines of Al i and ii (top panel), Al ii and iii (2nd panel), Si i and ii (3rd panel), and P i (bottom panel). Black curves are observed spectrum of Sirius A. Blue curves show fit with abundances from Table 1, red curves are synthetic spectra with fitted element removed. In the top two panels, aluminum lines are due to Al ii except as labelled. |
4.12. Aluminum, Z = 13
Aluminum has potentially observable lines of Al i, Al ii and Al iii in the available spectral window, and in fact useful lines of all three ionisation states are found. Resonance lines of Al i at 1766, 1769, 3082, 3092 and 3944 Å are all unblended enough to be useful. Fairly clean lines of Al ii are found in both the ultraviolet (e.g. the strong resonance lines at 1670 Å and a family of low-excitation lines in the region between 1719 and 1767 Å), and in the optical (e.g. at 3900 Å) windows. Two largely unblended lines of Al III are found at 1854 and 1862 Å (Fig. 3). The three ionisation states all lead to a concordant abundance value for Al of − 5.65 ± 0.1, slightly below the solar value of − 5.55.
4.13. Silicon, Z = 14
With a first ionisation potential of 8.15 eV, Si is primarily in the form of Si ii, with a small fraction of Si i and Si iii present. Strong Si i lines occur mainly in the UV, where several series of resonance and low-excitation lines connect the ground and 0.78 eV levels with odd parity levels between 4 and 8 eV. There are two major problems with using these lines to obtain the abundance of Si. First, many of the lines are severely blended. But more seriously, many of the available oscillator strengths, especially for lines for which the upper level is above about 7.9 eV (roughly 63000 cm-1), where the levels themselves are of questionable classification (cf. Moore 1967), are incorrect by one dex or more. Using the log gf values provided by VALD, lines of the Si i series that occur in the spectral windows 1539–1576 Å and 1705–1749 Å are predicted to be far stronger than the observed lines in the spectrum of Sirius A. Because of the problems with Si in VALD, I have replaced (as far as possible) all values from VALD for resonance lines of both Si i and Si ii with those recommended by Morton (2003). In addition I have restricted abundance determinations using Si i to the small number of largely unblended lines with upper levels below 7.9 eV. With these restrictions, the most useful UV lines are found in the window between 1796–1825 Å (Fig. 3). These lines are generally consistent with an abundance of about (−4.45 ± 0.3) dex.
Useful lines of Si ii occur both in the UV and optical regions, and many of the oscillator strength seem to be broadly consistent with one another. The abundance of Si has been obtained using the very strong resonance lines at 1304, 1309, and 1533 Å, and series of weaker but mostly only slightly blended lines in windows at 1475–1486 Å, 1562–1565 Å, and 1807–1818 Å (Fig. 3). The main uncertainty in using the resonance lines is the difficulty of correctly normalising the spectrum through the 8–10 Å-wide windows depressed by the strong line wings, but these wings vary rapidly enough with abundance that they still provide useful constraints. The other UV lines are on the flat part of the curve of growth and thus vary rather slowly with abundance. All of the good UV lines of Si ii in these windows are consistent with an Si abundance of about (−4.6 ± 0.3) dex. On the other hand, groups of lines in windows at 1346–1355 Å and 1403–1418 Å suggest abundances deviating from this value by roughly one dex; the computed lines in the shorter wavelength are too strong, while those in the longer wavelength window are too weak. I have ignored the values from these regions, mainly because they are quite inconsistent with abundance derived from clean lines in the optical spectrum.
Optical lines of Si ii are scattered through the visible window. Relatively unblended lines at 5040 and 5055 Å and at 6347 and 6371 Å were fit. These lines indicate an Si abundance of about (−4.25 ± 0.2) dex. Combining the various results, I adopt (−4.4 ± 0.2) dex, quite close to the solar abundance.
It is clear that the state of UV oscillator strengths for both Si i and Si ii (and probably also classification of high-lying levels of Si i) is rather unsatisfactory, and would greatly benefit from further laboratory work.
 |
Fig. 4 Fits to resonance lines of S i (top panel) and Cl i (2nd panel), and to low-excitation lines of Ca ii (3rd panel) and V ii (bottom panel). Black curves are observed spectrum of Sirius A. Blue curves show fit with abundances from Table 1, red curves are synthetic spectra with fitted element removed. |
4.14. Phosphorus, Z = 15
Because the first even parity level is at about 56 000 cm-1, the longest wavelength resonance lines of P i are expected to be below 1800 Å. With a first ionisation potential of 10.46 eV, a few percent of the total P is neutral in much of the atmosphere, and resonance and low-excitation lines are potentially quite detectable in the UV spectrum. In contrast, the lines of P i in the optical all arise from levels above 6.95 eV, and with generally rather small oscillator strengths are not expected to be detectable.
P ii is the dominant ionisation state. A number of resonance and low-excitation lines are available in the UV, but the optical lines of this ion all arise from levels above 9.4 eV and are undetectably weak in a star as cool as Sirius.
When the first syntheses of various UV regions were done, it was found that the predicted line strengths seemed very inconsistent; at solar abundance some lines were reasonably matched while the computed strengths of others were far too strong. The problems were eventually traced to very old and/or incorrectly transcribed oscillator strengths in the Kurucz on-line database of atomic data (http://www.cfa.harvard.edu/amp/ampdata/kurucz23/sekur.html) and in VALD. The oscillator strengths of the P i resonance line multiplet between 1377 and 1381 Å are about 0.7 dex too small, and were replaced by values from Morton (2003); the values for the multiplet at 1671 to 1679 Å are about 0.8 dex too large and were similarly replaced. For P ii, the isolated line at 1452 Å and the resonance line multiplet between 1532 and 1543 Å have log gf values that are generally 3 dex too large. These oscillator strengths are supposed to come from Hibbert (1988) but there was apparently a transcription error in the Kurucz data that has propagated to VALD. Morton (2003) gives the correct values. In contrast, the oscillator strengths of the P ii multiplet at 1532 to 1544 Å and the isolated line at 1485 Å, also from Hibbert, are given correctly by Kurucz and VALD, so the database errors in this ion are sporadic.
Using corrected oscillator strengths, the computed spectra clearly show that P is present in Sirius at roughly the solar abundance. However, almost all of the reasonably strong lines are badly blended. The most useful lines are P i 1774.94 (almost free of blending) and 1782.82 Å (Fig. 3), and the lines of the P ii multiplet between 1532 and 1544 Å. The P ii lines are all somewhat blended, but are generally consistent with an abundance of about (− 6.55 ± 0.3) dex, while the P i lines, with some scatter, suggest an abundance of about (− 6.8 ± 0.3) dex. The adopted compromise is − 6.7 ± 0.3.
4.15. Sulphur, Z = 16
Neutral S has an ionisation potential of 10.36 eV, so a few percent of S is neutral through much of the atmosphere of Sirius A, although S ii is the dominant ion. The lowest odd parity state of S i has an excitation energy of 6.5 eV, and so neutral sulphur has numerous strong resonance lines below 1900 Å. Many of these are badly blended, but relatively clean lines occur at 1425, 1433, 1436, 1448, 1807, 1820, and 1826 Å (Fig. 4). Synthesis of all these lines suggests an abundance of S of about (− 5.1 ± 0.2) dex, about a factor of two below solar abundance. However, a number of weak high-excitation lines occur in the optical and near-IR region. Most of these are too weak to be detected, or lie in regions in which the available UVES spectra are very noisy, and are not detected, but the group of lines at 6743, 6748, and 6757 Å is clearly present, and these lines are best fit with an abundance of (− 4.58 ± 0.1) dex, slightly above the solar value.
S ii has only a few levels below 12 eV, and transitions among them are mostly parity or spin forbidden. Strong lines are found only below 1260 Å where we have no observations. The optical lines arise from energy levels above about 13 eV, and are too weak to detect.
It is not clear how to resolve the abundance discrepancy between the UV and optical lines of S i. The UV lines are all strongly saturated and mostly slightly blended, and there were significant difficulties to normalise the continuum, so the abundances from this region are certainly less precisely determined than those from the optical. I estimate that the abundance of S is about (− 4.8 ± 0.2) dex, close to the solar value.
4.16. Chlorine, Z = 17
As the ionisation potential of this element is 12.9 eV, a substantial fraction is neutral. The lowest excited level is at 8.88 eV, and optical lines all arise from levels at least this high, and so are quite weak. A group of resonance lines occurs in the UV between 1335 and 1397 Å, most of which are predicted to be quite strong (Fig. 4). Unfortunately, these lines occur in an extremely crowded region filled with other strong lines, many of which are not fully identified. All of the strongest Cl i are heavily blended. Nevertheless several features in this region show some dependence on the abundance of Cl, and all are consistent with an abundance of about − 6.70, not much below the solar value, but the uncertainty is of the order of 0.3 dex.
The lowest level of Cl ii of opposite parity to the ground state is at about 11.5 eV, so the resonance lines and other lines arising from low-lying levels are at shorter wavelength than the available data covers, and the optical lines, all from high-excitation levels, are too weak to detect. No further information is furnished by this ion.
4.17. Argon, Z = 18
Because of its filled 3s and 3p subshells, the lowest excited level of Ar i is 11.5 eV above ground, and all the resonance lines are below 1070 Å, and are outside the spectral region available to me. The strongest observable lines, which arise from levels around 11.5 eV, are in the near infrared, but the abundance of Ar, and the atmospheric temperature of an A star, are not high enough to make these lines detectable in the somewhat noisy IR spectrum. Similarly, the resonance lines of Ar ii are out of reach below 1000 Å, and the potentially useful lines in the optical region arise from levels of such high excitation potentials that they are unobservable in an A star. No useful constraint on this element has been derived.
4.18. Potassium, Z = 19
The low ionisation potential of K i, 4.34 eV, means that almost all of this element is once ionised in the atmosphere of Sirius. Resonance lines of neutral K occur throughout the optical spectrum down to about 3000 Å. However, the pairs of resonance lines of K i at 3446–47, 4044–47, and 7664–98 Å are too weak to be observable. K ii has filled 3s and 3p subshells, so that the first excited level is about 20 eV above ground, the resonance lines are well below the Lyman limit, and the excited lines are too weak to be observed. No useful constraint on this element has been found.
4.19. Calcium, Z = 20
The first ionisation potential of Ca is 6.11 eV, so most of this element is once ionised in the atmosphere of Sirius. However, enough remains neutral that the optical resonance line of Ca i at 4226 Å is easily detected. It is virtually unblended, and modelling leads to an abundance of log nCa/nH = −6.25 ± 0.1.
The strong ultraviolet lines of Ca ii are rather few in number in the accessible available UV region, and almost all the lines I have checked are too badly blended to be useful. Two relatively clean lines are found at 1838.00 (Fig. 4) and 2112.76 Å. Both are strongly saturated and insensitive to small abundance changes, but the abundance deduced from these two lines is about −6.1 ± 0.2. The best available lines for obtaining Ca abundance with the first ion seem to be the three lines of multiplet (4) between 3158 and 3182 Å. These lines are reasonably strong and mostly unblended, and vary rapidly with abundance. From these three lines an abundance of − 5.96 ± 0.1 is obtained; all three lines are nicely consistent with one another, and with the UV lines.
The abundances obtained from the single neutral resonance line and the lines of Ca ii are discordant by 0.3 dex, a factor of two. There is no obvious explanation for this result, unless it is a result of departure of the neutral atom from LTE. However, since several lines of the ion are consistent, I weight these more heavily than the neutral line. In any case, it seems clear that the abundance of Ca in Sirius is a factor of two or so lower than the solar abundance.
4.20. Scandium, Z = 21
Scandium is primarily once ionised in the atmosphere of Sirius. The most useful UV lines appear to be the resonance lines of Sc ii near 2555 Å. Two of these lines, at 2552.35 and 2555.79 Å, are not too badly blended and should be weak enough to vary rather rapidly with abundance. Both these lines are at best marginally detected, and lead to the conclusion that the abundance of Sc is below about − 10.0.
Three lines of Sc ii are weakly detected in the optical UV and visible regions, at 3353.72, 3613.82, and 4246.82 Å. All are (barely) strong enough to model. The three lines agree well on an abundance of − 10.03 ± 0.1, consistent with the upper limit from the UV. The abundance of Sc is more than a factor of 10 smaller than the solar value.
4.21. Titanium, Z = 22
The dominant ion is Ti ii, and a large number of lines are available in the optical. I have synthesized the 3360–3460 Å window containing lines of Ti ii multiplets (1), (53), (54), and (99). This region is very well fit with an abundance of (−6.80 ± 0.1) dex. In the UV, many Ti ii lines occur, but a good fraction are badly blended. A few of the useful lines include one at 1421 Å, several resonance lines between 1890 and 1912 Å, and a very clean low-excitation line at 2154 Å. These windows are best fit with abundances ranging from −6.70 to −7.15, but as the UV lines are all fairly saturated, each fit has an uncertainty of the order of 0.2 dex. I adopt −6.90 ± 0.1 as a reasonable compromise. The abundance of Ti in Sirius A is only a little higher than the solar value.
 |
Fig. 5 Fits to low-excitation lines of Mn ii (top panel), to a mixture of resonance and other lines of Fe ii (2nd panel), to resonance lines of Co ii (3rd panel), and to low-excitation lines of Ni ii (bottom panel). Black curves are observed spectrum of Sirius A. Blue curves show fit with abundances from Table 1, red curves are synthetic spectra with fitted element removed. |
4.22. Vanadium, Z = 23
Vanadium has a relatively small first ionisation potential of 6.74 eV, so most V is once ionised. The NIST database of strong lines (http://www.nist.gov/physlab/data/handbook/) indicates that almost all the strong V ii lines are in the spectral range between 2880 and 3600 Å. I have synthesized several windows in this range, using lines between 2880 and 3160 Å. In all regions the fit is generally quite good, even in the GHRS spectrum from 2868 to 2912 Å (Fig. 4), where the line density is about twice as large as in the region only 200 Å longward. However, the best fits to various lines lead to somewhat discordant abundance values, ranging in log (nV/nH) from about − 7.0 to − 7.5, probably due to inaccuracy of the gf values. I have adopted an intermediate value, with a larger uncertainty than those of the most precisely determined elements. However, it seems clear that V is overabundant in Sirius relative to the solar abundance by a factor of roughly five.
This is an element for which the availability of optical spectral data from below the Balmer jump is extremely valuable. This distinctive feature of UVES spectra has previously found to be a very valuable one in other contexts (e.g. to study Mn and rare earths in the magnetic Ap star HD 66318, as discussed by Bagnulo et al. 2003).
4.23. Chromium, Z = 24
The abundance of Cr is easily determined from optical lines of Cr ii, the dominant ion. It has been shown that the relative gf values within single multiplets of this ion are quite precisely known both from experiment and from computation (Sigut & Landstreet 1990). This situation has already been exploited above to show that the microturbulence parameter of Sirius is very nearly the same above and below the Balmer jump, suggesting that the value determined in the optical spectral region may be used in the UV as well. However, synthesis of various spectral regions lead to small variations in the best-fitting abundances. The window around 3400 Å, in which the lines are dominated by multiplets (3), (4), and (21), gives an abundance of − 5.57 ± 0.15, while the window around 4200 Å, mainly containing lines from multiplet (31), is best fit with an abundance of about − 5.74 ± 0.15.
Several useful lines are found in the ultraviolet spectrum. The region around 2060 Å is relatively uncrowded, and contains both fairly unblended resonance lines (2055.59, 2061.54 Å) and a number of mostly clean low excitation lines. The fit to this region is quite sensitive to abundance, and the best fit from synthesis is (− 5.81 ± 0.1) dex. Another region with a number of rather clean lines of Cr ii is found between 2830 and 2870 Å, which yields an abundance of − 5.90 ± 0.07.
The optical mean of − 5.65 is thus somewhat different from the UV mean of − 5.85. This may be due to systematic differences between the scale of oscillator strengths for optical lines and that for UV lines. I adopt log nCr/nH = −5.75 ± 0.15. Cr is clearly overabundant relative to the abundance in the Sun by about a factor of four.
4.24. Manganese, Z = 25
With a first ionisation potential of 7.43 eV, most Mn in the atmosphere of Sirius is once ionised. In the optical, the strongest lines of Mn ii are multiplets (2) and (3) between 3430 and 3500 Å, and I have used these lines to determine an abundance of −6.00 ± 0.1.
In the UV, some relatively unblended low-excitation lines are found in the region between 1850 and 1950 Å (at 1860, 1861, 1868, 1898, 1908, 1914, 1918, 1919, 1921, 1923, 1925, 1931 and 1935 Å; Fig. 5). Other useful Mn ii lines between 2570 and 2640 Å (including a resonance line at 2576) have also been synthesised. Because these lines are strongly saturated they vary only slowly with abundance, and (with significant line-to-line scatter) are consistent with abundance values ranging from about −5.90 to about −6.50, averaging roughly −6.20 ± 0.2. A final value of −6.05 ± 0.15 seems appropriate, about a factor of three higher than the solar abundance of Mn.
4.25. Iron, Z = 26
Like the other iron peak elements, Fe is mainly once ionised. Because of the higher abundance of this element relative to other iron peak element, there are significant iron lines in almost every part of the UV spectrum, and in many regions in the visible as well. In the optical region, a region with a number of low-excitation Fe ii lines is found near 3180 Å; one with many high-excitation Fe ii lines occurs near 5050 Å, and a large number of Fe i lines are found in the continuous opacity minimum around 4240 Å. All the regions agree on log nFe/nH = −4.10 ± 0.1.
In the UV, it is found that spectral segments below about 1600 Å are quite poorly reproduced by synthesis, but for longer wavelengths the quality of the fit is good. The two shortest wavelength windows computed, around 1310 and 1470 Å, are best fit with Fe abundance of roughly −4.0, while the five longer wavelength UV windows (around 1840, 2330, 2375, 2540, and 2620 Å, mostly dominated by low-excitation lines of Fe ii) are best fit with Fe abundance of −4.35 ± 0.1. The discordance among these regions is disappointing, considering the amount of work that has been put into studying the spectra of iron. I adopt an average value of −4.20 ± 0.15 as a reasonable compromise.
A short window shown in Fig. 5 indicates the extent to which Fe dominates some regions of the spectrum, and demonstrates the quality of the atomic data in this window. Without the Fe lines, the spectral lines in the region around 2380 Å would be as isolated as those in the blue part of the optical spectrum of Sirius A.
4.26. Cobalt, Z = 27
With a first ionisation potential of 7.88 eV, Co is primarily present as Co II, but some Co i is also detected. Five ultraviolet resonance lines of Co ii, at 2011, 2022, 2027, 2049, and 2058 Å are sufficiently unblended to provide useful constraints on the abundance (Fig. 5), and since the line at 2049 is not highly saturated, it varies rapidly enough with abundance to provide a well-determined value. These four lines agree very satisfactorily on log nCo/nH = −6.60 ± 0.1.
In addition, several lines of both Co i and Co ii are detected in the optical window between 3480 and 3570 Å. Most of these lines are near the threshhold for detection, but the Co ii line at 3501.71 Å is unblended and is easily seen and modelled. Both neutral and ionised Co in this region are very well fit with the same abundance as in the UV, with the exception of one line of Co i at 3483.40, for which the value log gf = + 1.00 from VALD is at least one dex too large. (In my synthesis, this is by far the strongest line of Co i in this window, but the laboratory relative intensities in the Revised Multiplet Table of Moore (1967) clearly show that this line is actually one of the weaker lines in the window.)
The abundance of Co is found to be a factor of three larger than the solar abundance, with a precision of about 25%.
4.27. Nickel, Z = 28
Nickel is present in both neutral and once ionised form. Both species have strong spectral lines in the region below the Balmer jump. The abundance was determined from resonance lines of Ni i of multiplets (18), (19), and (20), and from low excitation lines of Ni ii of multiplets (1) and (4). A number of these lines are either unblended or only weakly blended, and judging from the excellent concordance of the line synthesis, the oscillator strengths are very internally consistent. The abundance of this atom is found from these lines to be about log (nNi/nH) = −5.00 ± 0.1.
Numerous lines are also found in the UV spectra. A window at about 2170 Å (Fig. 5) contains a number of reasonably unblended low-excitation lines of Ni ii, and is a region for which the synthetic spectrum with optimised abundances is nearly identical to the observed spectrum. This region yields an abundance of log (nNi/nH) = −5.30 ± 0.1. The two regions are somewhat discrepant, although the internal consistencies of both the UV lines in this window and the optical lines near the Balmer jump are very good.
Ni is overabundant with respect to the solar abundance, by a factor of about four.
4.28. High-Z elements
Although it was generally outside the scope of this project to determine the abundances of elements of Z > 28, in the course of syntheses, abundances were found for the elements Sr, Y, Zr, and Ba, using the lines in the optical region that fell within windows being studied (Sr: 4215 Å; Y: four lines between 3600 and 3635 Å; Zr: resonance lines between 3390 and 3560 Å, especially from multiplet (1); Ba: 4554 and 6141 Å). The resulting abundance values are included in Table 1. Because the lines are on the linear part of the curve of growth, and several are unblended for each of these elements, the uncertainties are quite small. As expected for an Am star, the abundances found for these heavy elements are of the order of three to 30 times higher than in the Sun.
5. Discussion of the abundance analysis
5.1. Comparison with other abundance determinations
It is often useful to compare the results of an abundance analysis with previous work. However, for a survey of abundances of so many elements, it is difficult to draw general conclusions from this exercise.
The most recent large-scale abundance study of Sirius A was carried out by Qiu et al. (2001). For comparison, their results are shown column 3 of Table 1. It will be seen that there are some elements for which agreement is quite satisfactory (the difference is within the uncertainty computed from the individual uncertainties, for example for C, N, Mg, S, Ti, Cr, Fe) and others for which substantially larger differences, up to 1 dex, are found (for example Na, Ca, Co, etc.). A similar mix of agreement and disagreement was found by Qiu et al. in their own comparison of their results with previous work (see their Fig. 9).
The abundances found in a number of earlier studies, going back to the introduction of linear detectors into spectroscopy in the early 1980s, are also listed in Table 1. Some of these studies only concern a few elements, but the studies by Hill & Landstreet (1993) and Sadakane & Ueta (1989) provide numerous results for comparison. Again a mix of good agreement and very poor agreement is found.
Unfortunately there is no single main cause for the differences between the results of different authors, even though the various studies use very similar values of the fundamental parameters of Sirius A. In general, it is found that elements for which a fairly large number of unblended lines, of a variety of strengths, are available for analysis (this is true of Ti, Cr, and Fe, and to a lesser extent of Ni), the abundances derived by different authors are usually in satisfactory agreement. Since the abundances derived for Ti, Cr and Fe all rely on large amounts of excellent atomic data, but still exhibit a dispersion in my study of order 0.10 − 0.15 dex, and the abundances derived in several studies of each of these elements (see Table 1) show a dispersion of order 0.1 dex, it appears reasonable to assume that an uncertainty of order 0.1 dex represents the current limit of accuracy for abundances for favourable A stars, and specifically for Sirius A.
However, as seen in this study, abundance determination for a particular element may rely only on one or a few lines, and these may not cover a wide range of strengths. In these cases, the analysis may not reach a level of accuracy of 0.1 dex because of a large number of reasons. (1) The only available line(s) may be so weak that identification is very uncertain, or there may be unrecognised blends. This probably account for the much larger abundance of Co found by Qiu et al. compared to mine; they use only one very weak line, which appears to be blended with a stronger Ti ii line. A similar problem probably also caused the considerably larger abundance of S found by Hill & Landstreet (1993) compared to that found here. (2) Different analyses use different sets of lines, usually with oscillator strengths from a variety of sources of varied accuracy. Oscillator strengths (especially those of small gf values) are often uncertain by some tenths of a dex, and the errors in these values result directly in errors of abundance. This problem affects most of the elements studied here. (3) Different approximations to the partition functions can also be significant, especially for subordinate ions. (4) Sometimes only lines in the range of strength sensitive to the value of the microturbulence parameter (equivalent widths of order 100 − 200 mÅ) are available. As different authors have adopted values of ξ between about 1.7 and 2.2 km s-1, this sensitivity can, in the worst cases, result in changes of derived abundance by up to 0.2 dex. (5) There seems also to be a category of differences which have no obvious explanation. For example, using the weak Sc ii line at 4246 Å, with the same gf value, Qiu et al. derive an abundance of Sc of − 10.34, while I find − 10.09, almost a factor of two larger. From the Ca i λ4226 line, Qiu et al. find an abundance of − 6.57 while I find − 6.25, even though I agree with their measured equivalent width and gf value. A similar problem occurs with their measurement of the Sr ii λ4215 line. Even worse, using the same lines of Ba ii with the same gf values, Qiu et al. and I derive Ba abundances that differ by a factor of almost 10.
Most commonly, if two abundance determinations of an element for which several lines can be used lead to significantly different abundance values, this is probably best regarded at present as a measure of the real uncertainty of both abundance values. This kind of internal inconsistency between abundances derived from different lines and regions has already led to relatively large estimates of internal uncertainty in this study for the elements C, Si, P, S, Ca, V, Mn, and Ni, most of which also exhibit significant differences in abundance between this study and the others listed in Table 1. To identify the most problematic elements, the second last column of Table 1 contains the mean abundance, a straight average over the logarithmic abundances of all the studies in the table, and the standard deviation of the values about that mean. (In a few cases one strongly deviating value, marked with an asterisk, has been omitted from the mean and standard deviation, usually for a reason mentioned above.) This column provides a summary of the current knowledge of abundances in Sirius, and the standard deviation (whenever it is larger than the uncertainty I find in this study) provides what is probably the most useful measure of the real uncertainty of these abundance values.
According to Table 1, abundances relative to H are now available for 20 of the 27 elements between He and Ni, and useful upper limits have been found for three others. Only Li, F, Ar and K have completely resisted efforts to measure their abundances. Compared to earlier studies, the important additions are good upper limits for Be and B, the first measurements of abundances of P and Cl, and clarification of the low abundance of C. For most of these elements, my uncertainties range from about 0.1 dex for elements with numerous measurable lines to about 0.3 for elements with only a small number of blended lines. This range of uncertainties is confirmed, on the whole, by the standard deviations of abundance determinations for Sirius A from the past 30 years as listed in the second last column of Table 1. Although the standard deviations in this compilation are mostly somewhat larger than my own uncertainties, they are not generally much larger, and fall in approximately the same range of values.
5.2. Diffusion in Sirius A
As discussed in Sect. 1, Sirius A is a slow rotator and hence an Am star. Because of the action of vertical diffusion in the star, the atmospheric abundances are not expected to be representative of the initial (envelope) bulk composition. Instead, as discussed by Richer et al. (2000) and Vick et al. (2010), these surface abundances are expected to evolve with time as a result of gravitational settling, selective radiative levitation, mixing (both convective and turbulent) and mass loss from the atmosphere. The predicted atmospheric abundances are a function of mass, age, and the various processes (some, such as turbulent mixing and mass loss, rather poorly understood) that are assumed to operate. Because Sirius A has so many well-determined parameters (particularly mass and an approximate age), and because abundances of so many elements can be determined for this star, comparisons of the observed abundances of Sirius A with computations are a particularly powerful test of the models.
The observed abundance table of Sirius A has been compared to the computation of evolution assuming gravitational and radiative diffusion, deep turbulent envelope mixing, but no mass loss, by Richer et al. (2000). For most elements a general level of agreement is found. Observed abundances frequently depart from the calculated ones by differences of order 0.3 dex, but this is probably within the real uncertainties of both models and observations. The new measurements do not alter the agreement between predicted and observed abundances for most elements. For the element sulphur, the agreement between the observations and the models is in fact greatly improved by the reduction of the abundance to nearly a solar level, as found by both Qiu et al. and my own measurements. However, the new data reported here reveal a small number of quite significant differences between the computed and observed abundances, assuming that the initial bulk abundances of Sirius A are approximately the same as in the Sun. Boron, which is expected to have between 0 and 0.3 dex lower abundance than the Sun, instead has at least 1.6 dex lower abundance. Carbon, which is predicted to be deficient by 0.2 to 0.6 dex, is observed to be more than 1 dex below solar abundance, and the diffusion models which predict the lowest C also predict considerably lower N than the measured nearly solar abundance. Sodium, expected to be approximately solar in abundance, is observed to be about 1 dex overabundant, but as mentioned above, the abundance value reported here is rather uncertain because of possible non-LTE effects. Finally, phosphorus, expected to be about 0.5 to 0.8 dex overabundant, is found to be slightly underabundant. These differences are sufficiently large to present a significant challenge to the models of Richer et al.
Comparing the observed abundance table with the abundances computed by Vick et al. for a series of models in which the deep turbulent envelope mixing is turned off but fully mixed mass loss is present, we find essentially the same pattern of overall agreement with the computations, but again with the same substantial differences for the elements B, C (together with N), Na, and P. From the observational side, these elements clearly warrant further detailed study to confirm or improve the current abundance values.
A detailed reconsideration of the comparison between these new abundance measurements and the various diffusion models will be presented separately by Michaud, Richer & Vick (in preparation).
5.3. Evolution of the Sirius system
As we have seen in the previous section, the observed abundances of Sirius A now appear to present a significant challenge to models which modify an initial solar abundance table by diffusion with either deep turbulent mixing or a well-mixed stellar wind. However, we should reconsider the assumption of an initially (approximately) solar composition. Recall the description of the Sirius system summarised in Sect. 1: initially, the system was composed of two stars of about 6 M⊙ and 2 M⊙ respectively. We do not know what the orbit was like initially, but the substantial amount of mass lost by Sirius B as an AGB star would suggest that the orbit may have slowly enlarged as the original primary decreased in mass. The high present eccentricity suggests that the initial orbit may also have been quite eccentric, as no catastrophic event such as a supernova explosion was expected in this system which could have abruptly altered the eccentricity. Thus the initial orbit may have carried the present Sirius A from within a few AU of the 6 M⊙ out to some tens of AU at apastron.
Now, as mentioned in Sect. 1, it is usual to consider that the system is (and was always) sufficiently well separated that no “significant” interaction between the two stars occurred, and the evolution of Sirius A from the ZAMS can be realistically computed on the assumption of isolated evolution (e.g. Kervella et al. 2003; Liebert et al. 2005), although Richer et al. 2000 suggested that the surface abundances of CNO in Sirius A might have been altered by accretion of 10-5 M⊙ or more of material from Sirius B. However, the recent calculations of de Val-Borro et al. (2009) call the assumption of essentially isolated evolution into serious question. This group has computed a number of models of wind accretion in symbiotic binaries. Specifically, they consider mass transfer in which the strong wind of a mass-losing AGB star is gravitationally swept up, through an accretion disk, onto the secondary star of the system. Because the wind of the AGB star is slow, if the companion is reasonably massive a large amount of wind gas can be accreted by the secondary star. For systems that are qualitatively similar to the initial Sirius system in mass and separation, they find that of order of 10% of the mass lost from the primary is accreted onto the secondary. Thus the present Sirius A might well have accreted as much as 0.5 M⊙ from its companion.
This material would no longer have had the initial composition of the primary. AGB envelopes and winds contain the products of nuclear fusion in the core as a result of the third dredge-up process which mixes processed material from the core into the convective envelope, and the results of hot bottom burning. As the envelope of the AGB star is carried off by the strong wind, changing conditions at the base of the convection zone lead to changes in the envelope composition as time goes on. Although the evolution during the AGB phase cannot be predicted with certainty, it appears that a star initially as massive as Sirius B is thought to have been (5–6 M⊙) probably undergoes hot bottom burning, and over much of its mass losing phase ejects matter that is somewhat deficient in 12C and perhaps in 16O, and is enhanced in 14N. This material is also probably enhanced in s-process heavy elements (see for example Lattanzio & Wood 2004 or Karakas 2010).
Thus the matter that the present Sirius A accreted, several tens of millions of years into its evolution, could well have increased its mass from ~1.5 M⊙ to the present value of just over 2 M⊙, and furthermore would have given the outer 25% of the mass a chemical composition substantially different from the initial abundance mix. Thus computing the evolution of Sirius A as a single star may well be too simple an approximation. This would of course affect estimations of the bulk composition needed for the model to reproduce the HR Diagram position of the present Sirius A. It would also present different initial conditions for computations of atmospheric abundance evolution due to diffusion.
The abundances found for Sirius A, both by other investigations and in this one, appear to be qualitatively consistent with the possibility that the evolution of Sirius A has been complicated by a major accretion event one-third or half way through its life since the ZAMS, and that the accreted gas did not have the same composition as the initial gas of the two stars. The observed large deficiency of C and smaller deficiency of O, while N seems to be about solar, could in part reflect the composition of the AGB wind, although in the atmosphere this composition would have then been modified by diffusion once the episode of rapid accretion ended. Similarly, some part of the heavy element overabundance, obvious in Table 1, could have come from s-process enrichment of the AGB wind. Thus the possibility of important interaction between the two stars in the Sirius system should probably be considered more seriously than it has been up to now.
6. Discussion and conclusions
This paper has attempted to make some progress towards answering three interesting and significant questions: (1) how well can the ultraviolet spectrum of a reasonably sharp-line A star be reproduced, using conventional spectrum synthesis methods, LTE, reasonable abundances, and standard sources of atomic data, specifically the VALD database, (2) does analysis of the ultraviolet spectrum make it possible to obtain some kinds of information, in particular abundances of interesting elements not detectable in the visible spectral region, and if so, what limits the possible precision of such abundance or other kinds of measurements, and (3) what new information about Sirius A does the UV provide?
It is well known that most of the ultraviolet spectrum of an A or late B star is extremely crowded with lines (see the Figures in this paper). For any star with a non-zero rotational velocity, or any star observed with a resolving power much less than 50 000, this leads to so much overlap of spectral lines that the spectrum can only be studied usefully with spectrum synthesis. Line by line measurements of equivalent width are almost always simply meaningless.
The syntheses carried out for this project have shown consistently that reasonably satisfactory fits to the observed spectrum longward of 1600 or 1800 Å can be obtained using standard procedures developed for the optical region. With continuum normalisation set simply by fitting the highest points in the GHRS spectra with a low-order fitting function, followed by synthesis using normal line lists from VALD, abundances can be adjusted to obtain quite good fits to entire spectral orders of 30 or 40 Å length. Figure 5 shows several examples of typically successful fits.
Fits to windows at shorter wavelengths are still good enough to provide useful and meaningful results, but the quality of fit is definitely worse. The three UV spectra in Fig. 1 all illustrate the difficulties in this shorter wavelength region. Experiments with synthetic spectra computed for no rotation and very high resolving power indicate that, in the spectral region below 1700 Å or so, incompleteness of the line lists seems to be a problem; some significant features do not have corresponding lines in the lists. In addition, the quality of the atomic data (particularly gf values, but possibly also some damping constants of strong lines) seems to be worse in this region.
A further problem is that because not much spectrum synthesis has been done for this region, the available line lists have not been quality-tested in the same way as in the optical. Thus in this study, I found that a number of P ii lines have erroneous or outdated values, and that the current VALD line list contains a large number of Si i lines with high upper levels that clearly have gf values that are much too large.
However, overall, down to at least 1500 Å or so, the VALD line lists are remarkably complete and generally correct. It would simply not be possible to carry out an investigation like the present one without such a resource. Considering the relatively small amount of testing of the UV data, the VALD database is a very robust resource. This robustness, in turn, reflects nearly a century of excellent laboratory and computational atomic spectroscopy.
The number of elements that the UV adds to those that can be studied in the optical is small. In this investigation, the elements Be, P and Cl have been identified in the UV spectral region and approximate abundances or upper limits found. The situation for C, which is barely detected in the optical but has a number of strong lines in the UV, has been clarified. In addition, the little-used optical UV, between 3000 Å and the Balmer Jump at 3646 Å, has been found to be a very useful region. Lines in this region are very valuable for the study of B, Sc, Mn, Co, and Ni, all of which are quite problematic at longer wavelengths in A stars.
A very important limitation of the UV below 3000 Å is that almost all the useful lines are strong and are on the flat portion of the curve of growth. Their profiles are not strongly sensitive to small changes in assumed abundance, but are fairly sensitive to errors in continuum placement, so the abundances derived from these lines are not as well-determined as those from weaker isolated lines in the optical – when such lines are available. Blending is clearly much more of a problem, but is greatly reduced by the excellent quality of the VALD line lists in the longer wavelength part of the GHRS spectra, when used together with the technique of spectrum synthesis.
The result of this study is to show that with nearly one full decade of wavelength available, useful abundance measurements or interesting upper limits for sharp-line A stars can be found for all but five of the 27 elements from He to Ni (the missing five are Li, F, Ne, Ar, and K). This is not yet a list as complete as for the Sun, but it is very encouraging that such a large number of elements is accessible to study in some middle main sequence (and also A supergiant) stars. In particular, the availability of such a wide UV spectrum has has made it possible to increase significantly the number of elements in Sirius A for which abundances are known, and to clarify or improve abundance values for elements previous studied using only spectra longward of the Balmer jump.
The new measurements presented here have identified significant challenges for projects using Sirius as a test case of evolution calculations. The light elements Be, C and N appear to be present in the atmosphere of Sirius A with abundances substantially different from those predicted by evolution calculations based on single star evolution with envelope diffusion plus additional parametrised physics such as deep turbulent envelope mixing or fully mixed mass loss (Richer et al. 2000; Vick et al. 2010).
Even more generally, it appears that these chemical anomalies might point to a failure of the assumption of single star evolution. Sirius A may have undergone substantial accretion 50 or 100 Myr into its evolution, during the AGB phase of the evolution of Sirius B, which could have increased the mass of the original Sirius A by as much as 0.5 M⊙ by the addition of gas from Sirius B that had a somewhat different chemical composition than the original gas cloud (de Val-Borro et al. 2009). The observed abundances of elements with Z ≤ 8 may be symptomatic of such mass transfer. Clearly this possibility might have significantly altered the evolution of Sirius A up to the present time from the predictions of single-star evolution tracks.
It is quite remarkable that such a bright star as Sirius may still have some very interesting lessons to teach about stellar structure and evolution.
Acknowledgments
This work has been supported by the Natural Sciences and Engineering Research Council of Canada. An extended period of residence at the Armagh Observatory has been possible thanks to a Leverhulme Visiting Professorship awarded by the Leverhulme Foundation. A number of very useful suggestions were made by the referee, Dr Elisabetta Caffau. The whole project has been inspired by discussions with Professor Georges Michaud of the Université de Montréal, and has benefitted from his ideas.
References
- Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Badnell, N. R., Bautista, M. A., Butler, K., et al. 2005, MNRAS, 360, 458 [NASA ADS] [CrossRef] [Google Scholar]
- Bagnulo, S., Jehin, E., Ledoux, C., et al. 1993, ESO Messenger, 114, 10 [Google Scholar]
- Bagnulo, S., Landstreet, J. D., Lo Curto, G., Szeifert, T., & Wade, G. A. 2003, A&A, 403, 645 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Baschek, B., Scholz, M., & Sedlmayr, E. 1977, A&A, 55, 375 [NASA ADS] [Google Scholar]
- Code, A. D., Davis, J., Bless, R. C., & Hanbury Brown, R. 1976, ApJ, 203, 417 [NASA ADS] [CrossRef] [Google Scholar]
- de Val-Borro, M., Karovska, M., & Sasselov, D. 2009, ApJ, 700, 1148 [NASA ADS] [CrossRef] [Google Scholar]
- Gatewood, G. D., & Gatewood, C. V. 1978, AJ, 225, 191 [NASA ADS] [CrossRef] [Google Scholar]
- Henderson, M., Irving, R. E., Matulioniene, R., et al. 1999, ApJ, 520, 805 [NASA ADS] [CrossRef] [Google Scholar]
- Hibbert, A. 1988, Phys. Scripta, 38, 37 [Google Scholar]
- Hill, G. M., & Landstreet, J. D. 1993, A&A, 276, 142 [NASA ADS] [Google Scholar]
- Holweger, H., & Stürenburg, S. 1993, in Peculiar Versus Normal Phenomena in A-Type and Related Stars, ed. M. Dworetsky, F. Castelli, & R. Farragiana, ASP Conf. Ser., 44, 356 [Google Scholar]
- Hui-Bon-Hoa, A., Burkhart, C., & Alecian, G. 1997, A&A, 323, 901 [NASA ADS] [Google Scholar]
- Karakas, A. I. 2010, MNRAS, 403, 1413 [NASA ADS] [CrossRef] [Google Scholar]
- Kervella, P., Thévenin, F., Morel, P., Bordé, P., & Di Folco, E. 2003, A&A, 408, 681 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kupka, F., Piskunov, N. E., Ryabchikova, T. A., Stempels, H. C., & Weiss, W. W., 1999, A&AS, 138, 119 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [PubMed] [Google Scholar]
- Kupka, F., Ryabchikova, T. A., Piskunov, N. E., Stempels, H. C., & Weiss, W. W. 2000, Baltic Astronomy, 9, 590 [Google Scholar]
- Lambert, D., Roby, S. W., & Bell, R. A. 1982, ApJ, 254, 663 [NASA ADS] [CrossRef] [Google Scholar]
- Landstreet, J. D. 1988, ApJ, 326, 967 [NASA ADS] [CrossRef] [Google Scholar]
- Landstreet, J. D. 1998, A&A, 338, 1041 [NASA ADS] [Google Scholar]
- Landstreet, J. D., Barker, P. K., Bohlender, D. A., & Jewison, M. S. 1989, ApJ, 344, 876 [NASA ADS] [CrossRef] [Google Scholar]
- Lattanzio, J. C., & Wood, P. R. 2004, in Asymptotic Giant Branch Stars, ed. H. J. Habing, & H. Olofsson (Heidelberg: Springer-Verlag), 23 [Google Scholar]
- Lemke, M. 1989, A&A, 225, 125 [Google Scholar]
- Lemke, M. 1990, A&A, 240, 331 [Google Scholar]
- Liebert, J., Young, P. A., Arnett, D., Holberg, J. B., & Williams, K. A. 2005, ApJ, 630, L69 [NASA ADS] [CrossRef] [Google Scholar]
- Moore, C. E. 1967, Selected Tables of Atomic Spectra, NSRDS-NBS 3, Sect. 2 [Google Scholar]
- Morton, D. C. 2003, ApJS, 149, 205 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Piskunov, N., & Kupka, F. 2001, ApJ, 547, 1040 [NASA ADS] [CrossRef] [Google Scholar]
- Piskunov, N. E., Kupka, F., Ryabchikova, T. A., Weiss, W. W., & Jeffery, C. 1995, A&AS, 112, 525 [Google Scholar]
- Qiu, H. M., Zhao, G., Chen, Y. Q., & Li, Z. W. 2001, ApJ, 548, 953 [NASA ADS] [CrossRef] [Google Scholar]
- Rentzsch-Holm, I. 1997, A&A, 317, 178 [Google Scholar]
- Richer, J., Michaud, G., & Turcotte, S. 2000, ApJ, 529, 338 [NASA ADS] [CrossRef] [Google Scholar]
- Rogerson, J. B. 1987, ApJS, 63, 369 [NASA ADS] [CrossRef] [Google Scholar]
- Ryabchikova, T. A., Piskunov, N. E., Kupka, F., & Weiss, W. W. 1997, Baltic Astron., 6, 244 [Google Scholar]
- Sadakane, K., & Ueta, M. 1989, PASJ, 41, 279 [NASA ADS] [Google Scholar]
- Salaris, M., Serenelli, A., Weiss, A., & Bertolami, M. M. 2009, ApJ, 692, 1013 [NASA ADS] [CrossRef] [Google Scholar]
- Sigut, T. A. A., & Landstreet, J. D. 1990, MNRAS, 247, 611 [NASA ADS] [Google Scholar]
- van den Bos, W. H. 1960, J. D. Obs., 43, 145 [Google Scholar]
- Van Leeuwen, F. 2007, Hipparcos, the New Reduction of the Raw Data (Astrophys. Sp. Sci. Lib.) [Google Scholar]
- Vick, M., Michaud, G., Richer, J., & Richard, O. 2010, A&A, 521, A62 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wade, G. A., Bagnulo, S., Kochukhov, O., et al. 2001, A&A, 374, 265 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Fits to lines of Be ii (top panel), B ii (2nd panel), C i (1328–30 Å) and ii (1334–37 Å; 3rd panel), and N i (bottom panel). Black curves are observed spectrum of Sirius A. Blue curves show fit with abundances from Table 1, red curves are synthetic spectra with fitted element removed. The vertical axis is intensity normalised to the continuum. The wavelength scale is chosen for each panel so that the length of the boxes are all similar in velocity space, and the width in the figure of unblended single lines is similar regardless of the central wavelength. Exceptionally, in the two upper panels, the syntheses which best fit the observed spectrum do not require any Be or B, and so the red spectra with these elements removed are not shown. Instead the synthesis using the upper limit values to abundance for these elements are shown, and the positions of the relevant lines marked with arrows. |
| In the text | |
 |
Fig. 2 Comparison of computed profiles of the B line at 1362.46 Å (coloured curves) to the observed spectrum (black). Abundances of B assumed in the calculations are log (nB/nH) = −9.3, − 10.3, − 10.8, and − 11.3 (from deepest to shallowest line). The solar abundance of B is − 9.30. |
| In the text | |
 |
Fig. 3 Fits to lines of Al i and ii (top panel), Al ii and iii (2nd panel), Si i and ii (3rd panel), and P i (bottom panel). Black curves are observed spectrum of Sirius A. Blue curves show fit with abundances from Table 1, red curves are synthetic spectra with fitted element removed. In the top two panels, aluminum lines are due to Al ii except as labelled. |
| In the text | |
 |
Fig. 4 Fits to resonance lines of S i (top panel) and Cl i (2nd panel), and to low-excitation lines of Ca ii (3rd panel) and V ii (bottom panel). Black curves are observed spectrum of Sirius A. Blue curves show fit with abundances from Table 1, red curves are synthetic spectra with fitted element removed. |
| In the text | |
 |
Fig. 5 Fits to low-excitation lines of Mn ii (top panel), to a mixture of resonance and other lines of Fe ii (2nd panel), to resonance lines of Co ii (3rd panel), and to low-excitation lines of Ni ii (bottom panel). Black curves are observed spectrum of Sirius A. Blue curves show fit with abundances from Table 1, red curves are synthetic spectra with fitted element removed. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


