| Issue |
A&A
Volume 528, April 2011
|
|
|---|---|---|
| Article Number | A127 | |
| Number of page(s) | 14 | |
| Section | Galactic structure, stellar clusters and populations | |
| DOI | https://doi.org/10.1051/0004-6361/201016232 | |
| Published online | 14 March 2011 | |
A lack of close binaries among hot horizontal branch stars in globular clusters⋆
II. NGC 2808
1
Departamento de AstronomíaUniversidad de Concepción,
Casilla 160-C, Concepción,
Chile
e-mail: cmbidin@astro-udec.cl
2
Dipartimento di Astronomia, Università di Padova,
Vicolo dell’Osservatorio 3,
35122
Padova,
Italy
3
European Southern Observatory, Alonso de Cordova 3107, Vitacura, Santiago, Chile
4
INAF- Oss. Astronomico di Padova, Vicolo dell’Osservatorio 5, 35122
Padova,
Italy
Received:
30
November
2010
Accepted:
12
January
2011
Context. The formation mechanism of hot horizontal branch (HB) stars is still one of the most uncertain points of stellar evolution theories. In the past decade, models based on their binary origin have been very successful in reproducing the properties of field subdwarf-B stars, but the observations of their analogues in globular clusters has posed new problems. In addition, the discovery of multiple populations offered an appealing alternative scenario for the formation of these stars.
Aims. We search for binaries of period ℘ ≤ 200 days among a sample of 83 blue horizontal branch stars (Teff = 12 000–22 000 K) in NGC 2808, a cluster known to host three distinct stellar populations and a multimodal horizontal branch. The final sample, after the rejection of stars with incomplete observations or poor quality data, consists of 64 targets.
Methods. The radial velocity of the targets was measured in fourteen epochs, spanning a temporal interval of ~75 days. The significant variations were identified by means of a detailed error analysis and a statistical study.
Results. We detect no RV variable object among stars cooler than the photometric G1 gap at ~17 000 K, while two close (℘ ≤ 10 days) and two intermediate-period (℘ = 10–50 days) systems are found among hotter targets. The close and intermediate-period binary fraction for stars cooler than the gap are fc ≤ 5% and fip ≤ 10%, respectively, with 95% confidence. The most probable values among hotter stars are fc ~ 20% and fip ~ 30%, but the 90%-confidence level intervals are still large (6–42% and 11–72%, respectively).
Conclusions. The G1 gap appears as a discontinuity in the binary faction along the HB, with a higher incidence of binaries among hotter stars, but a constant increase in f with temperature rather than a discontinuity cannot be excluded from our observations. We also find that intermediate-period binaries, never investigated before among cluster HB stars, could play an important role among hotter stars, being more than ~15–20% of the hottest stars of our sample. Our results, compared with previous estimates for other clusters, indicate that fc among hot HB stars is most probably higher for younger clusters, confirming the recently proposed age-fc relation. However, the large observed difference in binary fraction between clusters (e.g. NGC 2808 and NGC 6752) is still not reproduced by binary population synthesis models.
Key words: stars: horizontal-branch / binaries: close / binaries: spectroscopic / globular clusters: individual: NGC 2808
© ESO, 2011
1. Introduction
Horizontal branch (HB) stars in Galactic globular clusters (GCs) are old post-He flash stars of low initial mass (0.7–0.9 M⊙) that, after the exhaustion of hydrogen in the stellar core and their ascension along the red giant branch, eventually ignited helium (Hoyle & Schwarzschild 1955; Faulkner 1966).
GCs display large differences in the HB morphology (see, for example, Piotto et al. 2002). The first parameter responsible for this phenomenon is metallicity, but it alone cannot account for the complex observational picture (the so-called “second parameter problem”, Sandage & Wildey 1967; van den Bergh 1967). While some clusters contain only red HB stars cooler than the RR-Lyrae gap, others host a large population of blue He-burning stars extending even beyond the canonical end of the HB at ~ 35 000 K (e.g. Moehler et al. 2004). Even more puzzling, in the color-magnitude diagram (CMD) of some clusters the HB appears continuous in its whole extension (e.g. NGC 6752, Momany et al. 2002), while in others it is clearly multimodal (e.g. NGC 2808, Sosin et al. 1997). This observational picture still lacks full comprehension, as a consequence of our poor understanding of the formation mechanism of HB stars in GCs. The HB morphology has been linked, among others, to cluster age (Dotter et al. 2010), cluster concentration (Fusi Pecci et al. 1993), stellar rotation (Peterson 1983), cluster mass (Recio-Blanco et al. 2006), helium, and the environment of formation (Fraix-Burnet et al. 2009), but none of the proposed second parameters could satisfactorily reproduce the complex observed behavior (see Catelan 2009, for a review). In particular, the most challenging task is to account for the formation of extreme horizontal branch (EHB) stars at the faint hotter end of HBs (Teff ≥ 20 000 K), observed even in high metallicity clusters (e.g. Rich et al. 1997) and old open clusters (NGC 6791, Buson et al. 2006). Stars hotter than this critical temperature do not have an external envelope massive enough to sustain the shell H-burning, and after the exhaustion of helium in the core they evolve directly to the white dwarf (WD) cooling sequence, without ascending the asymptotic giant branch (AGB manqué stars, Greggio & Renzini 1990). They are extensively observed and studied in the Galactic field, identified as the so-called subdwarf B-type (sdB) stars (Greenstein 1971; Caloi 1972; Heber 1986). However, in GCs they are still poorly studied because of their faintness, and many questions still await an answer (see Catelan 2009; Moni Bidin & Piotto 2010, for recent reviews). Many single-star evolutionary channels have been invoked to explain EHB star formation in GCs, including interactions with a close planet (Soker 1998, see also Silvotti et al. 2007), helium mixing driven by either internal rotation (Sweigart & Mengel 1979; Sweigart 1997) or stellar encounters (Suda et al. 2007), and close encounters with a central intermediate-mass black hole (Miocchi 2007).
The dynamical interactions inside binary systems were proposed early on to be responsible for the heavy mass-loss required to form a EHB star (Mengel et al. 1976; Tutukov & Iungelson 1987). In the past decade, the “binary scenario” has achieved many observational and theoretical successes among field sdB stars, and is now widely accepted as the most satisfactory explanation of their formation. The binary population synthesis model of Han et al. (2002, 2003, 2007) could reproduce their observational properties in great detail, although a small fraction of progenies of single stars is probably required for a perfect match (Lisker et al. 2005). Han’s model considers three main formation channels: the stable Roche Lobe Overflow (RLOF), which produces sdB’s in wide binaries; the common envelope (CE) channel, which forms close systems; and the merging of two WDs, whose progenies are single stars. On the other hand, many surveys have confirmed that a large fraction of field sdB stars reside in binaries (Ferguson et al. 1984; Allard et al. 1994; Ulla & Thejll 1998; Aznar Cuadrado & Jeffery 2001; Maxted et al. 2001; Williams et al. 2001; Reed & Stiening 2004; Napiwotzki et al. 2004), and sdB’s in close systems with periods shorter than ten days are very common (Moran et al. 1999; Saffer et al. 1998; Heber et al. 2002; Morales-Rueda et al. 2003), although the exact close-binary fraction is still uncertain, ranging from 40–45% (Napiwotzki et al. 2004) to 70% (Maxted et al. 2001).
Observations of EHB stars in GCs have so far presented a challenge to the binary scenario, at variance with its well-established successes for field stars. The first surveys surprisingly revealed a lack of EHB close systems in GCs (Moni Bidin et al. 2006, 2009b). Moni Bidin et al. (2008a) fixed at 4% the most probable value of the EHB close-binary fraction (fc) in NGC 6752, proposing that a decrease in fc with the age of the stellar population should be a natural expectation of the binary scenario. The detailed calculations of Han (2008) confirmed that the CE channel becomes very inefficient after the first few Gyrs, and the WD-WD merging should be the predominant mechanism for the formation of EHB stars in old stellar systems. As a consequence, cluster EHBs should be principally single-star products of merging, and close systems should be rare. However, Moni Bidin et al. (2009a) measured a higher fc in M 80 and NGC 5986 (12% and 25%, respectively), and argued that the models proposed by Han (2008) cannot simultaneously account for the low fc measured in NGC 6752 and these much higher values found in clusters only 1–2 Gyr younger. Unfortunately, their results suffered too large uncertainties to be conclusive. In summary, the binary scenario has not been disproved, but its ability to reproduce all the observations in GCs still has to be demonstrated.
An alternative model of EHB star formation has received great attention in recent years: one incorporating the primordial helium enhancement. A super-solar surface helium abundance was recognized early on as a possible cause of the heavy-mass loss underlying the formation of EHB stars, but non-canonical mixing phenomena had to be invoked (von Rudloff et al. 1988; Denissenkov & VandenBerg 2003; Sweigart & Mengel 1979; Sweigart 1997). The discovery of multiple stellar populations in GCs (Bedin et al. 2004; Piotto et al. 2007) opened a new frontier, because the observational results of Piotto et al. (2005) apparently imply that the bluer main-sequence (MS) in ω Cen is most probably populated by He-enriched stars. The currently preferred scenario is that these objects constitute a second stellar generation that formed from material polluted by either intermediate-mass AGB stars (D’Antona et al. 2002; Renzini 2008), or rapidly rotating massive MS stars (Maeder & Meynet 2006; Decressin et al. 2007). The models of multiple populations with different helium abundances successfully reproduce both the MS splitting and the multimodal HB morphology of both ω Cen (Lee et al. 2005) and NGC 2808 (D’Antona et al. 2005). The He-enhancement thus represents a promising model, and alternative to the binary scenario, for the formation of EHB stars in GCs.
In this paper, we present our results of a search for EHB binaries in NGC 2808. Preliminary results, pointing to a close binary fraction higher than in NGC 6752, were presented by Moni Bidin et al. (2008b) and Moni Bidin & Piotto (2010). In this context, this cluster is a key object because it is noticeably younger than NGC 6752 (De Angeli et al. 2005), allowing the study of the fc-age relation foreseen by the binary scenario. Moreover, this cluster represents one of the greatest successes of the He-enhancement scenario, because D’Antona et al. (2005) and D’Orazi et al. (2010) were able to model both its multimodal HB (Bedin et al. 2000) and the multiple MS (Piotto et al. 2007) with three stellar populations of increasing primordial helium abundance.
2. Observations and data reduction
We selected 83 hot HB stars in NGC 2808 from the photometric catalog of Momany et al. (2003), of magnitude between V = 17.4, corresponding approximatively to the Grundahl jump (Grundahl et al. 1999), and the limiting magnitude V = 19.5 imposed by program feasibility. In Table 3, we give the IDs, the coordinates, and the photometric data of the targets from Momany et al. (2003), and their location in the cluster CMDs shown in Fig. 1.
 |
Fig. 1 Position of the targets in the cluster color-magnitude diagrams. Upper panel: V vs. (U − V) diagram, where the arrows indicate the location of the two gaps discussed in the text (G1 and G2), and the magnitude corresponding to T = 20 000 K (the formal definition of the EHB). Lower panel: V vs. (B − V) diagram with superimposed the ZAHB model from Cassisi et al. (1999) used to estimate stellar temperatures. The star #37345 discussed in the text is indicated with an empty triangle. |
Twenty-four single spectra of target stars were collected in fourteen epochs between January 11 and March 24, 2007, with the GIRAFFE spectrograph at the VLT-UT2 telescope, in both visitor and service mode. The instrument setup H7A provided high-resolution (R = 18 000) spectra centered on the Hβ line. The temporal sampling was carefully planned to maximize the detection probability of binaries with any period up to 100 days. Exposures were acquired in pairs to be later summed, except when bad weather conditions forced us to stop observations after the first frame. We thus collected fourteen epochs of data over 2.5 months. The log of the observations is given in Table 1, where each exposure is identified with a unique ID, and the epoch at the middle of the acquisition period is indicated, along with the exposure time and the observing mode (v = visitor, s = service).
Log of the observations.
Data were reduced with the dedicated CPL-based pipeline available at the ESO web site. Because of the extremely low signal collected for the hottest targets, we performed many trial reductions to find the choices and parameter sets that maximized the output quality. The frames were de-biased and flat-fielded with standard procedures based on the frames collected within the standard calibration plan. The dark current was found to be non-negligible only along the top edge of the CCD, not used in our work, and no dark correction was applied to avoid the corresponding decrease in S/N by 10–15%. We gave particular attention to the wavelength calibration (wlc), whose defects can easily affect the radial velocity (RV) measurements. The goodness of the wlc was checked by analyzing the spectra of the lamp fibers acquired simultaneously with target stars. This reduction step was particularly problematic, because we found that running the complete wlc routine resulted in an incorrect solution, with a deviation from the correct one that increased with wavelength and fiber number, up to 10–15 km s-1. We therefore adopted the standard solution for the H7A setup, included in the instrumental package downloadable from the GIRAFFE web site, allowing the pipeline to use the lamp fibers to find rigid shifts and changes in the spectral geometry on the chip. After the final extraction, the lamp fibers showed only small random deviations from laboratory wavelengths (0.3 km s-1 rms). This wlc error is small compared to uncertainties in the RV measurement, and can be safely neglected in the final error budget. Finally, science spectra were extracted using both an optimum algorithm (Horne 1986) and a simple sum. We found that these two methods were in general equivalent and the choice did not alter the results, but in some noisy spectra one or the other returned more precise measurements. This was probably due to small cosmetic defects or noise spikes being treated differently by the two algorithms. We therefore preferred optimum-extracted spectra, but we opted for a simple sum in the few cases in which this clearly returned smaller RV errors. The background flux was estimated by averaging nine fibers allocated to the sky and, after subtracting their mean spectrum from those of the targets, we checked that the weak interstellar emission in the core of the Hβ line had been effectively removed. The spectra were then trimmed to retain only the central region (4780–4930 Å), and we normalized them fitting a linear relation to the continuum on both sides of the Hβ line. We verified that a higher order polynomial was not required in the normalization, as there was no appreciable change in either the fitted function and or the results. As a final step of the reduction, the spectra forming a pair of exposures (see Table 1) were added. Some example spectra are shown in Fig. 2, for two stars at the edge of the temperature range (12 700 and 21 200 K) and one of intermediate temperature, plus the star #37345, discussed later. The presented spectra are the sum of all the spectra collected for each star, after shifting them to laboratory wavelengths.
 |
Fig. 2 Normalized spectra of four target stars, obtained shifting all the collected spectra to laboratory wavelength and summing them. The star ID and temperature is given. The spectra were vertically shifted to avoid overlap. |
The observed HB was fitted with the zero-age HB model (ZAHB) of Cassisi et al. (1999) with metallicity [Fe/H] = − 1.10 (Carretta et al. 2006) to derive a temperature scale along the HB. The procedure was not straightforward using the (U − V) color, and uncertainties remained in the determination of the required distance modulus and reddening. These problems could be due to the use of the U band, because Dalessandro et al. (2011) showed that, at shorter wavelengths, it is impossible to fit the HB of NGC 2808 with one single population of fixed helium content. Therefore, the fit was performed in the V versus (hereafter vs.) (B − V) plane, where the closest match was found by assuming that (m − M)V = 15.7 and E(B − V) = 0.15, in good agreement with Bedin et al. (2000). The fit is shown in the lower panel of Fig. 1. The temperature of each target was then estimated from the point of the model ZAHB closest to the observed position. Varying (m − M)V and E(B − V) between values that still gave a reasonably good fit, we estimated that the uncertainty in the temperature should be on the order of 10%. The temperature derived for each star is given in Table 3.
In the selected sample, there are eight stars hotter than 20 000 K and, following the canonical definition, they can be considered EHB stars. However, in the CMD of NGC 2808 there is no underpopulated region in correspondence to this temperature as in, for example, NGC 6752 and M 80, where the EHB is separated from cooler HB stars. In contrast, Sosin et al. (1997) identified two clear gaps in NGC 2808 at about V = 18.4 (~16 500 K) and V = 20 (~25 000 K), called G1 and G2 respectively, by Bedin et al. (2000). The cluster blue HB is thus divided into three sections, called EBT1 (Teff ≤ 16 500 K), EBT2 (16 000 ≤ Teff ≤ 25 000 K), and EBT3 (Teff ≥ 25 000 K). Following this scheme, the sample contains 62 EBT1 and 21 EBT2 stars, but no star in the faint EBT3 group was observed.
We note that the temperature associated with the gaps was obtained by fitting a canonical model to the observed HB, and the spectroscopic measurements of Moehler et al. (2004) agree with this temperature scale. However, Dalessandro et al. (2011) proposed a new scale, based on a multi-population model of three stellar generations with increasing helium content. In their calculations, the G1 and G2 gaps approximatively coincide with the canonical start (20 000 K) and end (31 000 K) of the EHB, which is thus separated from cooler stars by an underpopulated region even in the CMD of this cluster.
3. RV measurements
The RVs were measured by means of the cross-correlation (CC) technique (Tonry & Davis 1979) implemented in the fxcor IRAF1 task. The CC was restricted to the spectral interval 4840 − 4880 Å, i.e. the Hβ line with its full wings. The template was extracted from the synthetic library of Munari et al. (2005). Experiments with model spectra of different temperature, gravity, and metallicity showed that a change in these parameters does not affect the results, while the errors are very sensitive to this choice, and the templates with a narrower Hβ usually provide smaller errors for all the stars. These conclusions are also supported by the detailed analysis of Morse et al. (1991). Variations in the shape of the template line are indeed not expected to shift the center of the CC function (CCF), but can affect the resulting uncertainties. We also found that the inclusion of weak metallic lines in the synthetic spectra enhanced the errors without adding real information, because they were either absent or not visible in the noisy target spectra. Consequently, the template finally adopted for all the stars was a synthetic profile of the Hβ line, obtained by removing all weaker lines from a synthetic spectrum at 20 000 K, log (g) = 5, and cluster metallicity. It must be noted that the RV measurements are unaffected by any bias or uncertainty in the estimate of the target temperature, because the choice of the template was independent of this temperature and, as discussed, this choice did not alter the results.
The RV was determined by fitting the core of the CCF with a Gaussian profile. While the procedure was straightforward for cool stars, it became problematic for the fainter ones, whose spectra were much noisier down to signal-to-noise ratio (S/N) ≈ 3 in the worst cases. Measuring RVs at such low S/N with only one wide line is a challenging task, and we with experimented different methods to improve the accuracy of the measurements: the application of a narrow Fourier filter (Brault & White 1971) sometimes helped, while the S/N of very noisy spectra was often increased by degrading the resolution by a factor of 2–3 and then rebinning accordingly. Although a lower resolution affects the precision that can be achieved, the noise is by far the dominant source of uncertainty when the stellar flux is very weak. In some cases, we used only one spectrum of a pair, because there was a great difference in the spectral quality of the two, and the addition of the noisier one degraded the resulting measurement. We did not find a unique scheme for returning the optimal results for all the spectra, but we employed in each case the procedures (filtering, rebinning, use of a single spectrum) providing the best results in terms of shape and noise of the CCF, height of its central peak, and goodness of its Gaussian fit. These procedures were designed only to reduce the errors, and the results were stable when experimenting with different combinations of procedures and involved parameters, varying by no more than a few km s-1. When this was not the case, the measurement was judged unreliable and excluded, as when the results were sensitive to changes in either continuum normalization or extraction algorithm.
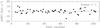 |
Fig. 3 Difference between the RV measured in the first frame (frame 1-1 of Table 1) and the weighted average for each star, plotted as a function of the fiber number. Only the 53 brightest stars, with measurement uncertainty lower than 5 km s-1, are plotted. |
3.1. Systematic errors
 |
Fig. 4 Mean error of each star as a function of effective temperature. |
 |
Fig. 5 Upper panel: histogram of the distribution of the residuals with respect to the weighted average of each star, in unit of the associated error (Eq. (1)). Overplotted to the histogram, a Gaussian with σ = 0.96 and centered in 0.01 is shown. Lower panel: probability plot of the same residuals of the upper panel. The straight line, with intercept 0.01 and slope 0.96, indicates the least squares fit of the data. |
After the correction to heliocentric RVs, we verified that no systematic error was present in the results. First, we checked the zero-point of each frame by averaging the RVs of the 53 brightest stars, excluding measurements with errors larger than 5 km s-1. We thus derived the corrections to reduce each frame to the same zero-point, although they were lower than 1.5 km s-1, i.e. well within the typical error of the 53 stars (3.5–4 km s-1). We then plotted, for each frame, the residual of each star with respect to its weighted-averaged RV as a function of the fiber number, to check for the presence of a systematic effect that varied with position on the CCD, as done by Moni Bidin et al. (2006, Figs. 5 and 7). The plot relative to the first frame is shown in Fig. 3 as an example. The average value of these residuals was always lower than 0.1 km s-1, indicating that any offset between exposures was correctly removed in the previous step. Moreover, the linear and third-order fit never differed from zero by more than 1 km s-1, proving that there is no residual trend in the measured RVs, and the results are free from systematics well beyond the typical random errors of 3–4 km s-1.
3.2. Errors
Any search for binaries by means of multi-epoch RV measurement is based on the comparison between the observed variations and the uncertainties. A precise definition of the errors is therefore of fundamental importance for the correct interpretation of the results.
The uncertainty associated with each measurement was defined as the quadratic sum of the error of the CC technique (as defined by Tonry & Davis 1979), the wlc error defined in Sect. 2, and the uncertainty introduced when correcting the zero-point of each frame (Sect. 3.1). This last quantity was defined as the rms of the corrections applied to each frame, i.e. the scatter in the zero-point of the frames around the mean value. The CC error completely dominates the error budget, being typically 2–3 km s-1 for bright stars and increasing with temperature up to 5–8 km s-1 for the faintest targets. Thus, the quadratic sum of the wlc and zero-point errors (0.3 and 1.1 km s-1, respectively) makes a negligible difference for all but the brightest targets. The mean error for each star is plotted in Fig. 4 as a function of effective temperature. The errors constantly increase with the temperature along the HB, reflecting the decreasing S/N of the collected spectra. The mean value of EBT1 targets (Teff ≤ 17 000 K) ranges from 2.5 to ~4.5 km s-1, with the exception of a couple of deviant stars, with an average value of 3.5 km s-1. Hotter stars show a higher scatter and a steeper gradient, with a mean value of 6.0 km s-1.
To test the reliability of the errors, we analyzed the distribution of the residuals (Δi) of the ith measurement (RVi) with respect to the weighted average (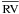 ), in units of the associated error σRV, i
), in units of the associated error σRV, i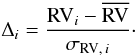 (1)If the observational uncertainties are the only cause of the variations, and the errors σRV, i represent them well, the residuals would follow a normal distribution centered on zero and with unit dispersion. This analysis can easily be spoiled by RV variable stars, which add large values to the wings of the distribution. We therefore excluded all the stars showing one or more residuals Δi ≥ 3.5, as we later demonstrate that no variation above this threshold should be expected from random errors alone (Sect. 4.1). The resulting distribution of Δi is shown in the upper panel of Fig. 5. Both the mean value (0.01) and the standard deviation (0.96) confirm that the errors are indeed well defined, as they account exactly for the random variations. The probability plot (Lutz & Hanson 1992) of these data reveals that they follow a normal distribution, as they are aligned along a straight line of slope 0.96 and intercept 0.01. This would have not happened if, for example, the exclusion of stars with Δi ≥ 3.5 had produced a too narrow cut of the wings of the distribution. In conclusion, the analysis reveals that the errors are reliable, representing well the random uncertainties, and that they can safely be used in a statistical analysis.
(1)If the observational uncertainties are the only cause of the variations, and the errors σRV, i represent them well, the residuals would follow a normal distribution centered on zero and with unit dispersion. This analysis can easily be spoiled by RV variable stars, which add large values to the wings of the distribution. We therefore excluded all the stars showing one or more residuals Δi ≥ 3.5, as we later demonstrate that no variation above this threshold should be expected from random errors alone (Sect. 4.1). The resulting distribution of Δi is shown in the upper panel of Fig. 5. Both the mean value (0.01) and the standard deviation (0.96) confirm that the errors are indeed well defined, as they account exactly for the random variations. The probability plot (Lutz & Hanson 1992) of these data reveals that they follow a normal distribution, as they are aligned along a straight line of slope 0.96 and intercept 0.01. This would have not happened if, for example, the exclusion of stars with Δi ≥ 3.5 had produced a too narrow cut of the wings of the distribution. In conclusion, the analysis reveals that the errors are reliable, representing well the random uncertainties, and that they can safely be used in a statistical analysis.
3.3. Absolute RVs and cluster membership
The absolute RVs were calculated by weight-averaging all the measurements for each star, and the results are given in Col. 7 of Table 3. The histogram of the distribution is shown in Fig. 6. The mean value is 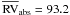 km s-1, in excellent agreement with Harris (1996, February 2003 Web version, 93.6 km s-1, and the observed dispersion is 5.7 km s-1. In Fig. 6, we also overplot a Gaussian curve centered on
km s-1, in excellent agreement with Harris (1996, February 2003 Web version, 93.6 km s-1, and the observed dispersion is 5.7 km s-1. In Fig. 6, we also overplot a Gaussian curve centered on 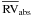 with σ = 5.7 km s-1. The histogram is well described by a normal distribution, with no deviating points, hence all the targets can be considered bona fide cluster members. The only exception is the star #37345, whose spectrum is shown in Fig. 2. This object was immediately recognized as peculiar, because of its very broad Hβ line: rapidly rotating HB stars hotter than ~ 11 500 K have never been found (Recio-Blanco et al. 2002; Behr 2003), while they are very common among hot MS stars. We note that this object is much redder than the other HB stars in terms of U − V color (of Fig. 1), but merges with the HB population in the V − (B − V) diagram (lower panel of the same figure). The RV measurements was highly uncertain because, as a consequence of the line broadening, the fit of the wide peak in the CCF was problematic. When it converged, we derived RV ≈ 150 km s-1, very different from the cluster value. We therefore conclude that the star #37345 is most probably a background field MS B star.
with σ = 5.7 km s-1. The histogram is well described by a normal distribution, with no deviating points, hence all the targets can be considered bona fide cluster members. The only exception is the star #37345, whose spectrum is shown in Fig. 2. This object was immediately recognized as peculiar, because of its very broad Hβ line: rapidly rotating HB stars hotter than ~ 11 500 K have never been found (Recio-Blanco et al. 2002; Behr 2003), while they are very common among hot MS stars. We note that this object is much redder than the other HB stars in terms of U − V color (of Fig. 1), but merges with the HB population in the V − (B − V) diagram (lower panel of the same figure). The RV measurements was highly uncertain because, as a consequence of the line broadening, the fit of the wide peak in the CCF was problematic. When it converged, we derived RV ≈ 150 km s-1, very different from the cluster value. We therefore conclude that the star #37345 is most probably a background field MS B star.
 |
Fig. 6 Distribution of the absolute RVs of the observed stars. The curve shows a Gaussian centered on the mean value (93.2 km s-1) and σ equal to the observed dispersion (5.7 km s-1). The dotted line indicates the cluster RV from Harris (1996). |
4. Analysis
Eleven stars were not considered in our analysis, because their spectra were either too noisy for reliable measurements or strongly contaminated by the emission lines of nearby lamp fibers. All these targets have no data in the last two columns of Table 3. The majority of targets were not allocated the same fiber in both GIRAFFE plates, as these are not equivalent because of broken fibers. As a consequence, the spectra of six stars were free of lamp contamination when observed with one plate, while their spectra collected with the other plate were damaged. Moreover, star #45980 had no fiber allocated in one plate. These seven targets were studied as the others, but were excluded from our statistical analysis because, with only half of the spectra with respect to the other stars, their temporal sampling is very different. Finally, one target was found to be a foreground star (Sect. 3.3). In conclusion, with nineteen stars lost or excluded, the resulting sample comprises 50 EBT1 and 14 EBT2 stars, out of which six EHB targets have Teff ≥ 20 000 K.
The measurements for the four spectra that were not the sum of two exposures, i.e. the frames 3-2, 4-2, 5-1, and 6-3 (Table 1), were in general less reliable, and they were often excluded for faint stars. In the upper panel of Fig. 8, we plot the decrease in the binary detection efficiency, as a function of period, if these four frames are not considered. Their exclusion clearly does not affect the survey much, because the probability of detecting a true binary in general decreases by less than 3%, except for two sensitive periodicities (1 day and ~18 days) where the loss is about 10–15%. Therefore, we finally excluded them from the statistical analysis. The measurements for these lower-quality frames were indeed always more uncertain, and were often excluded anyway, affecting the uniformity of the measurements. We then consider only the remaining ten epochs for each star.
4.1. Detection threshold and detection probability
The identification of binary candidates requires criteria to define when the observed variations can be considered significant. The criteria must satisfy two desiderata: the probability of a false detection (Pfalse) must be negligible, while the probability of detecting a true binary (Pdet) must be as high as possible, within the limitations imposed by the temporal sampling and the observational errors. Usually the first point is satisfied if the statistical expectation is less than one false detection in the whole survey, which in our samples of 64 targets means Pfalse ≤ 0.014. A compromise between these requirements is often needed, because more stringent criteria reducing Pfalse also reduce the efficiency of detecting genuine RV variables.
 |
Fig. 7 Upper panel: probability of a false detection for the “relative” criteria (empty dots and dotted line) and the “absoute” criteria (full dots and line) defined in the text, assuming a 3σ threshold for both. Lower panel: false detection probability for the same criteria, as a function of the threshold, for ten measurements. |
 |
Fig. 8 Upper panel: difference of the binary detection probability, as a function of period, when including or not the four spectra which are not the sum of two exposures (frames 3-2, 4-2, 5-1, and 6-3, see Table 1). For the calculation we assumed an “absolute” criteria with threshold 3.2σ, the same adopted in the present work, and a mean observational error of 3.5 km s-1. Lower panel: detection probability as a function of period, calculated as described in the text. The full and dotted lines indicate the results for the “absolute” criteria with 3.2σ threshold and the “relative” one with 3.8σ criteria, respectively, assuming the typical mean error (3.5 km s-1) of stars cooler than the G1 gap at ~17 000 K. The results for the “absolute” criteria assuming a mean error of 6.0 km s-1, characteristic of hotter stars, are shown with a dashed line. |
The parameter Pdet was estimated as a function of orbital period, generating 2500 synthetic binaries in circular orbits of period ℘, comprising two stars of 0.5 M⊙, uniformly distributed in the sin(i) − θ space, where i is the angle of inclination of the orbital plane and θ is the orbital phase. These systems were then “observed” with the same temporal sampling of our survey, and each star satisfying the criteria under analysis represented a detection. The fraction of detections over the whole sample thus indicated the efficiency of the survey for systems of period ℘. Pfalse was calculated by simulating 100 000 sets of N measurements drawn from a normal distribution centered on zero and of unity dispersion. Each set represented the observations of a star with constant RV, affected by only random errors normalized to unity, and N = 10 for our survey. A false detection was claimed for each set of measurements satisfying the criteria for binary detection, and Pfalse was estimated as the fraction of false detections over the whole sample of 100 000 attempts.
 |
Fig. 9 Maximum residual in units of the error (Eq. (1)) for each star, as a function of temperature. The horizontal line indicates the adopted threshold for binary detection. Empty dots represents stars with only partial temporal coverage, that are excluded from the statistical analysis. The vertical dotted line indicates the approximate position of the G1 gap. |
In previous investigations of HB stars in GCs, the criteria adopted for the detection of a binary candidate was that the measured RV variation was larger than 3σ, where σ was either the error in the spectral shift among two epochs (Moni Bidin et al. 2006, 2009a), or the quadratic sum of the errors in RV measurements (Moni Bidin et al. 2008a). This strategy worked well for surveys based on 4-5 epochs, but is unsuitable for our work: the upper panel of Fig. 7 shows that the probability of a false detection rapidly increases with the number of measurements, and in our 10-epochs survey we should expect 8% of non-binary targets (~6 stars) to violate the threshold due to random errors only. The method could be applied even here, but to reduce the expected false detections to less than one star we should increase the threshold up to 3.8σ, as indicated by the lower panel of Fig. 7, i.e. ~25–30 km s-1 for the hotter stars. In the same figure, we also show Pfalse for an alternative criteria, which we define as “absolute” (while the older one is called “relative”): a star is flagged as binary candidate if one (or more) measurement differs by more than a certain threshold, in units of its associated error, from the weighted average. The plot reveals that the reliability of this criteria is poorly affected by the higher number of measurements, and that in our survey the threshold must be fixed to 3.2σ to have Pfalse ≤ 0.7%, i.e. less than 0.5 false detections expected among our 69 targets. In the present work, we adopt both this criteria and this threshold for the detection of binaries. However, the results are completely equivalent to those for a “relative” criteria with threshold of 3.8σ, because Pfalse is the same, and Pdet is very similar to within a few percent at all periods (see lower panel of Fig. 8).
The efficiency of the survey resulting from the adopted criteria, i.e. the probability of detection as a function of the orbital period, is shown if Fig. 8. We considered two possibilities: a mean error of 3.5 km s-1, typical of the targets brighter than the G1 gap (Teff ≤ 17 000 K), and 6.0 km s-1 for the hotter EBT2 stars. In the first case, the survey can detect binaries with periods up to 400 days and, although the probability of detection drops below 50% for periods longer than 50 days, still more than one-third of the binaries with period 50–200 days can be found with our observations. For hotter stars, the larger errors decrease at all periods the efficiency, which becomes negligible (≤ 20%) for P ≥ 50 days. In any case, the presence of HB binaries with periods longer than 10 days can be tested for the first time in a GC, and these wide systems are poorly studied even among field sdB stars.
4.2. Detected binaries
The results of the search for RV variable stars are summarized in Fig. 9, where for each star we plot the maximum residual Δmax defined in Eq. (1). This value is also given in Col. 8 of Table 3. Five targets show one or more significant deviations from the weighted mean, and they must be considered candidate binaries. The cooler one (star #32670) is one of the seven targets with only partial temporal coverage mentioned at the beginning of this section, and is excluded from the statistical analysis. The other four binary candidates are located in the hotter half of the temperature range, and are all EBT2 stars fainter than the G1 gap. All but one of them (#9715) are hotter than 20 000 K, thus fall within the canonical definition of EHB stars. Their measured RVs are shown in Fig. 10.
 |
Fig. 10 RV measurements of the four binary candidates. The dotted line indicates the weighted mean. |
We note that, although the hotter stars were excluded from the error analysis of Sect. 3.2, the stars with no variation above the threshold show no gradient in Δmax with temperature, indicating that the errors are well-defined across the whole range. Moreover, there is a gap in the distribution of Δmax between these stars and the five binary candidates, which reinforces the idea that they are outliers. This confirms that the adopted threshold is indeed a good separation between statistical random errors and real RV variations.
 |
Fig. 11 Upper panel: detection probability as a function of period, calculated as described in the text, consideting only the first four (full line) or two (dotted line) nights. Lower panel: probability, as a function of period, that an EHB binary would show a significant RV variation only in the fourth night of our observations, as found for the star #7700. |
4.3. Period estimate
Our RV measurements are too few in number, and affected by too large errors, to attempt any estimate of the orbital periods of the binary candidates. However, our survey can detect systems with periods up to 400 days (Sect. 4.1), while previous investigations of GCs and the most extensive surveys among field stars were limited to close binaries with periods shorter than 10 days. This implies that our results are not directly comparable to those works without a minimum classification of the discovered systems. Hereafter, we define close binaries as systems with ℘ ≤ 10 days. They have been the common targets of previous investigations, and should have undergone one or two CE phases. We also define intermediate-period binaries as objects with 10 ≤ ℘ ≤ 400 days. We thus leave the definition of wide binaries to those with periods longer than 400 days, which is the typical product of RLOF (Han et al. 2002), a kind of system undetectable in our survey.
To help classify the binary candidates, we can rely on the adopted temporal sampling: the observations of the first four closely-spaced nights were designed to detect short-period systems, while the later fifth and sixth epochs were planned to help us discover longer periodicities. If our observations had been restricted to the first two nights only, the stars #9715 and #55759 would still have been detected. As can be seen in the upper panel of Fig. 11, systems with periods longer than 5 days would hardly have been found in such a two-night survey, and all binaries with ℘ ≥ 10 days would have passed completely undetected. The period of these two binary stars must therefore be shorter than 10 days, and most probably even shorter than 5 days. These objects can thus safely be classified as close binaries. Figure 11 also reveals that ~80% of the close binaries should have been detected during the first four nights. The remaining 20% mainly consists of nearly face-on systems showing maximum RV variation near or below the detection threshold, as indicated by the inclusion of the other two epochs not noticeably increasing the survey efficiency (compare Figs. 11 and 8). The star #9519 shows variations above the threshold, but not in the first four nights, and therefore can safely be classified as an intermediate-period binary of period longer than 10 days. The classification of the last binary candidate (star #7700) is less straightforward, because it passed undetected during the first three nights but it had a significantly different RV during the fourth one. To clarify its nature, we calculated the probability that a system of a given period behave as observed, i.e. the fraction of the synthetic binaries defined in Sect. 4.1 that would show a significant variation in the fourth epoch only. The results are plotted in the lower panel of Fig. 11. The period is most likely between 5 and 20 days, although shorter values are not impossible, and the most probable period is ~15 days. Taking into account that, as argued by Moni Bidin et al. (2008a), restricting the definition of close binaries to ℘ ≤ 5 days would not make a great difference, we can classify this object as an intermediate-period binary.
Results on the close and intermediate-period binary fraction.
4.4. Binary fraction
The probability of detecting NB binaries in a sample of N stars is given by the expression 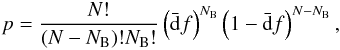 (2)where f is the underlying binary fraction and
(2)where f is the underlying binary fraction and 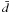 is the average probability of detection weighted by the period distribution. This equation can also be interpreted as the probability that the (unknown) binary fraction is f, when NB systems out of N targets were detected. The calculation requires information about the underlying period distribution, which is unknown. A Gaussian distribution in log (℘) centered on zero has been proposed for close field sdB systems (e.g. Maxted et al. 2001; Napiwotzki et al. 2004), while wider systems are still poorly studied. We assume a flat distribution at all periods, because Moni Bidin et al. (2008a) demonstrated that the results do not change by more than a few percent if other reasonable, but not proven, assumptions are made.
is the average probability of detection weighted by the period distribution. This equation can also be interpreted as the probability that the (unknown) binary fraction is f, when NB systems out of N targets were detected. The calculation requires information about the underlying period distribution, which is unknown. A Gaussian distribution in log (℘) centered on zero has been proposed for close field sdB systems (e.g. Maxted et al. 2001; Napiwotzki et al. 2004), while wider systems are still poorly studied. We assume a flat distribution at all periods, because Moni Bidin et al. (2008a) demonstrated that the results do not change by more than a few percent if other reasonable, but not proven, assumptions are made.
The binary fraction will be estimated separately for the EBT1 and EBT2 sections of the HB, which have different samplings (Fig. 1) and detection probabilities (Fig. 8). These two groups of stars are separated by an underpopulated region in the CMD, and could represent different stellar populations (D’Antona et al. 2005). Stars hotter than 20 000 K will be considered as EHB stars, a sub-group of the EBT2, although this could be only a formal distinction since no known discontinuity separates them from the other EBT2 stars in the CMD. It must also be recalled that this definition strongly depends on the model fixing the temperature scale along the HB, and the multi-population model of Dalessandro et al. (2011) EBT2 and EHB actually coinciding. We also distinguish between the fraction of close and intermediate-period binaries (fc and fip, respectively). The analysis of fip is restricted to ℘ = 10 − 200 days in the EBT1 and to ℘ = 10 − 50 days in the EBT2 and EHB, because the efficiency of the survey rapidly decays for longer periods. In the first case, this choice does not affect the results, because no binary was detected and therefore the solution NB = 0 can be applied to any period interval of interest. In contrast, this restriction could lead to wrong results for the EBT2/EHB because, if one of the two candidate intermediate-period binaries had ℘ ≥ 50 days, fip would be overestimated. However, we have already demonstrated that the star #7700 has ℘ ≤ 30 days (see Fig. 11), and a similar analysis for the star #9519 suggests that the probability that ℘ ≥ 50 days is negligible even for this star.
4.4.1. EBT1
In the EBT1, we have N = 50, and NB = 0 for both close and intermediate-period systems, with 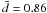 and 0.48, respectively. The resulting probability curves for the two binary fractions are shown in the upper panel of Fig. 12. The curves are narrow-peaked because the efficiency of the survey is high and the sample is sufficiently large, with the curve for fip being wider because of a lower detection probability. As we failed to detect binaries in the EBT1, the most probable value is always zero. The probability of our observations drops below 10% for fc ≥ 5% and fip ≥ 9%, and below 5% for fc ≥ 6% and fip ≥ 11%. These can be adopted as upper limits at the 90% and 95% confidence levels, respectively.
and 0.48, respectively. The resulting probability curves for the two binary fractions are shown in the upper panel of Fig. 12. The curves are narrow-peaked because the efficiency of the survey is high and the sample is sufficiently large, with the curve for fip being wider because of a lower detection probability. As we failed to detect binaries in the EBT1, the most probable value is always zero. The probability of our observations drops below 10% for fc ≥ 5% and fip ≥ 9%, and below 5% for fc ≥ 6% and fip ≥ 11%. These can be adopted as upper limits at the 90% and 95% confidence levels, respectively.
 |
Fig. 12 Curve of probability for the close binary fraction fc (dotted lines), and the intermediate-period binary fraction fip (full lines). Upper panel: EBT1 stars; middle panel: EBT2 stars; Lower panel: EHB stars. |
4.4.2. EBT2
In the EBT2, we have N = 14, and NB = 2 for both close and intermediate-period systems, with 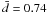 and 0.43, respectively. The curves of probability for the two binary fractions are shown in the middle panel of Fig. 12. The most probable estimate of fc is 19%, and the detection probability is high enough to obtain a relatively narrow curve: the 90% and 95% confidence level intervals are 6–42% and 4–49%, respectively. Stronger constraints could have been obtained only with a larger sample, but this is a typical observational limitation for GCs, because hot, isolated stars outside the inner crowded regions are few in number. The best estimate for fip is 33%, but the large errors affected the efficiency at detecting larger periods, and the probability curve is very wide. The 90% and 95% confidence level intervals are 11–72% and 7–85%, respectively. These results can serve as lower limits, since very low intermediate-period binary fractions can be excluded.
and 0.43, respectively. The curves of probability for the two binary fractions are shown in the middle panel of Fig. 12. The most probable estimate of fc is 19%, and the detection probability is high enough to obtain a relatively narrow curve: the 90% and 95% confidence level intervals are 6–42% and 4–49%, respectively. Stronger constraints could have been obtained only with a larger sample, but this is a typical observational limitation for GCs, because hot, isolated stars outside the inner crowded regions are few in number. The best estimate for fip is 33%, but the large errors affected the efficiency at detecting larger periods, and the probability curve is very wide. The 90% and 95% confidence level intervals are 11–72% and 7–85%, respectively. These results can serve as lower limits, since very low intermediate-period binary fractions can be excluded.
4.4.3. EHB
In the EHB, we have N = 6, NB = 1, and 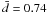 for close binaries, while NB = 2 and
for close binaries, while NB = 2 and 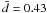 for wider systems. The sample is too small to allow us to place strong constraints on the binary fractions, in particular for fip where the detection probability is low. Therefore, we analyze this sub-group of EBT2 stars only for completeness. The more probable values are fc = 23% and fip = 77%, and the close binary fraction is contained within the interval 3–66% at the 90% confidence level, or 2–78% at the 95% level. Only lower limits can be obtained for fip, because the probability curve does not decrease much after its maximum: at the usual 90% and 95% confidence levels, fip ≥ 24% and 16%, respectively.
for wider systems. The sample is too small to allow us to place strong constraints on the binary fractions, in particular for fip where the detection probability is low. Therefore, we analyze this sub-group of EBT2 stars only for completeness. The more probable values are fc = 23% and fip = 77%, and the close binary fraction is contained within the interval 3–66% at the 90% confidence level, or 2–78% at the 95% level. Only lower limits can be obtained for fip, because the probability curve does not decrease much after its maximum: at the usual 90% and 95% confidence levels, fip ≥ 24% and 16%, respectively.
5. Discussion
The results for the close and intermediate-period binary fraction (fc and fip) obtained in Sects. 4.4.1–4.4.3 are resumed in Table 2, where we present the most probable estimate (fmax), and the 90% and 95% confidence level intervals (P(f) ≥ 10% and P(f) ≥ 5%) separately for the EBT1, EBT2, and EHB stars. Despite our efforts to obtain the most precise measurements, the very low spectral quality of the fainter stars strongly affected our results: the detection efficiency was reduced by the large errors, especially for the longer periods, and one-fourth of the observed EBT2 stars had to be excluded. As a consequence, the binary fractions are not very well determined, as reflected by the large confidence intervals for the EBT2 and EHB groups. However, the statistical analysis still permits us to draw many interesting conclusions.
Data of program stars.
The calculations of Sect. 4.4 are based on the fraction of detected binaries relative to the number of stars observed in each group. Some systematic error in the estimated temperatures could thus alter the results, in particular in the presence of stars evolving off the EHB toward higher luminosities, whose temperature could be underestimated. The temperature and luminosity of the hotter stars are degenerate in the V vs. (B − V) diagram, because the bluer section of the HB is almost vertical. Small luminosity variations or temperature errors should not affect the definition of the EBT1 and EBT2 samples, because it is based on the presence of clear photometric gaps and not on temperature boundaries. Stars ascending the asymptotic giant branch can be identified in the V vs. (U − V) plane, where the temperature-luminosity degeneracy is much less pronounced, and EBT3 stars, evolving directly to the WD cooling sequence, should be at all stages fainter than our magnitude limit. As a consequence, targets assigned to the EBT2 sample should be correctly classified, while two EBT1 targets brighter and/or bluer than the main HB population (see he upper panel of Fig. 1) could be evolved post-HB stars originating from the EBT2 population. One of them was excluded from the statistical analysis for other reasons (Sect. 4), while the other one shows no sign of binarity. Assigning it to the EBT2 group, we would have N = 15 in Sect. 4.4.2, causing a change of about 2% in the values given in Table 2. The results for the EBT1 group are even less sensitive to the change, because of the larger sample. In conclusion, the uncertainties in the definition of the EBT1 and EBT2 samples have a negligible impact on the results. In contrast, even small systematics in the temperature scale can strongly affect the statistical analysis of the EHB group, defined only by a temperature limit, because of the small number of observed targets. For example, when N is varied by ± 1, fc,max and fip,max can vary by ± 5% and ± 15%, respectively. These changes are not large when compared to the uncertainties given in Table 2, and the general conclusions are unaffected, but this result warns us that the results for the EHB group should be regarded as only indicative, as already stated in Sect. 4.4.3.
Binaries with periods longer than 10 days have never been studied in GCs, and have been the target of very few surveys even among field stars (e.g. Morales-Rueda et al. 2006). The most probable estimate of the intermediate-period binary fraction among EHB stars is very high, but is most probably affected by small number statistics as can be deduced from the very wide probability curve in the lower panel of Fig. 12. However, an important result of our investigation is a relatively high (15–20%) lower limit for fip among EHB stars. The estimated close binary fraction in all the clusters studied so far is either comparable to (NGC 2808, NGC 5986, M 80) or much lower than (NGC 6752) this value. The value of fip is most probably higher than fc even in the EBT2, because their probability curves are similar but p(fip) is shifted toward higher values. The most probable values indicate that only one-fifth of the EBT2 stars can reside in close systems, but that even half of them could be binary systems with ℘ ≤ 50 days. Although we cannot provide a more reliable estimate, this result suggests that binaries wider than those investigated so far could play an important role and should deserve more attention, particularly where close systems are lacking.
A second prominent result clearly evident from Table 2 is that the 90% confidence intervals in the EBT1 and EBT2 do not overlap, for both fc and fip. This means that the probability that the binary fraction has the same value in these two sections of the HB is negligible (of the order of 1%): the G1 gap thus appears as a discontinuity in the binary fraction, there being a very small quantity of binaries among the stars cooler than the gap, and about 20–30% for hotter objects. Unfortunately, our data cannot exclude fc and fip monotonically increasing with the temperature rather than showing a real discontinuity at G1. In this regard, we note that there is reasonable agreement between the results in the EBT2 and in its (hotter) sub-group the EHB, in particular for the close binary fraction (compare also the shapes of the dotted curves in the middle and lower panels of Fig. 12). Thus, fc could be quite homogeneous within the EBT2 population, instead of increasing with temperature, but no firm conclusion can be drawn because of the too wide confidence intervals. Future observations should help us to clarify this issue: a sudden increase in the binarity in correspondence with G1 would strongly relate it to the formation of all EBT2 stars, while a fc slowly increasing with temperature may indicate that the progeny of close systems are preferentially hotter.
In the context of the He-enrichment scenario for the formation of hot HB stars in GCs, the difference in binary fraction among EBT1 and EBT2 stars contrasts with the investigation of D’Orazi et al. (2010) in M 4, who found a much lower quantity of binaries among red giants that displayed evidence of chemical enrichment, than among normal ones. They argue that this difference is naturally explained by assuming that the second stellar generation formed in a denser environment, where more frequent dynamical interactions enhanced the disruption rate of binary systems. However, in the multi-population models of NGC 2808, the EBT2 is interpreted as the progeny of the latest and He-richest of the three populations observed in the MS (D’Antona et al. 2005; Dalessandro et al. 2011) and, following D’Orazi et al. (2010), we would expect the EBT2 to be depleted in binaries, at variance with what is observed. If their results were confirmed as a general behavior of the chemically polluted stars in GCs, our results would argue against the link between the EBT2 and the He-enriched stars. However, an alternative interpretation would be that both the He-enrichment and the binary scenarios co-exist in the cluster, as different channels for the formation of blue HB stars. In this case, in the EBT2 both the progeny of He-enriched stars and products of binary interactions would be found. This would cause a higher frequency of EBT2 stars in the HB with respect to the fraction of He-rich MS stars, but binaries in GCs usually represent a minor fraction of the entire population, and this difference could pass unnoticed. No splitting of the red- or sub-giant branch has been detected so far in NGC 2808, but this cluster shows a strong Na-O anticorrelation (Carretta et al. 2006), which has often been interpreted as a consequence of cluster self-pollution. It would therefore be really instructive to repeat the D’Orazi et al.’s investigation among the three different groups of red giants identified by Carretta et al. (2006) on the basis of their Na/O value, for a direct comparison with the values presented in Table 2.
Previous surveys focused mainly on the close binary fraction among EHB stars, defined by the temperature boundary of 20 000 K. This is more than a conventional definition because, as noted in Sect. 1, the post-HB evolution of EHB stars is very distinct from that of cooler stars. However, the formation mechanism does not necessarily differ, and population synthesis models show that sdB stars as cool as 15 000–16 000 K can be formed with the same binary channels used to model the field EHB star population (Han et al. 2003). In addition, massive (0.75 M⊙) EHB stars move to cooler temperatures in the first stages of the post-HB evolution (Han et al. 2002). The previous investigations were not limited to stars hotter than 20 000 K, and the only close system found in M 80, which Moni Bidin et al. (2009a) included in a statistical analysis similar to ours, is actually cooler than this temperature (~18 000 K). For all these reasons, we can safely use our estimate of the close binary fraction in the EBT2 population for comparison with both the results for other clusters, and the expectations of the binary model for sdB star formation. We also recall that the adopted canonical temperature scale might not be appropriate, as the EBT2 and EHB coincide in the model of Dalessandro et al. (2011).
The most reliable estimate of fc is low compared to field values, as observed in all the GCs observed so far. Even the lowest fractions proposed in the literature for the field sdB population are very unlikely (~45%, e.g. Napiwotzki et al. 2004; Morales-Rueda et al. 2006), and the highest ones can safely be excluded (~70%, Maxted et al. 2001). However, even the extremely low fc measured in NGC 6752 (4%, Moni Bidin et al. 2008a) can be excluded with a 95% confidence level. We thus find that NGC 2808 is similar to NGC 5986, where Moni Bidin et al. (2009a) estimated that fc = 25%, although with great uncertainties. The similarity can be drawn even further, because both these clusters are 2–3 Gyr younger than NGC 6752 (De Angeli et al. 2005). While the results of Moni Bidin et al. (2009a) had to be confirmed, the probability that the close binary fraction is equal or very similar in all these three clusters is negligible, and the trend of fc with age depicted in Fig. 1 of Moni Bidin & Piotto (2010) is likely real, following the close binary fraction-age relation proposed by Moni Bidin et al. (2008a) and modeled by Han (2008) in the context of the binary scenario. On the other hand, NGC 2808 also confirms the problems of this scenario pointed out by Moni Bidin et al. (2009a): no model proposed by Han (2008) can predict both the very low fc of NGC 6752 and a steep increase with decreasing age up to fc ≈ 20% for clusters 2–3 Gyr younger. As can be seen from their Fig. 3, the proposed solutions do not have a sufficiently steep gradient, and all the curves with fc(13 Gyr) ≤ 5% are nearly flat for old populations, so that fc ≤ 10% for any cluster older than 8 Gyr. Nevertheless, the simulations of Han (2008) depend strongly on a set of poorly known parameters. In particular, Marsh et al. (1995) deduced a very high CE ejection efficiency (αCE ≈ 1) from their observations of double-degenerate close binaries, but a much lower value (0.2–0.3) was proposed by Zorotovic et al. (2010) as a result of their study of a large sample of post-CE binaries. Han (2008) assumed a αCE = 0.5 − 1.0, but from their Fig. 3 it can be seen that lower values tend to return a steeper slope of the fc-age relation, although still predicting too high values at 13 Gyr. It is therefore possible that, with a different set of parameters, the binary scenario can be reconciled with the observations.
6. Conclusions
We have analyzed the radial velocity variations of a sample of 50 EBT1 stars (Teff = 12 000 − 17 000 K) and 14 EBT2 (Teff = 17 000–22 000 K) stars in the horizontal branch of NGC 2808, which were spectroscopically observed in ten epochs spanning a temporal interval of ~75 days. We detected two close binaries (period ℘ ≤ 10 days), and two wider systems (℘ ≥ 10 days and ℘ = 5 − 20 days, respectively). All these object belong to the EBT2 population, while no binary was detected among the cooler EBT1 stars. We estimated the most probable fraction of close (℘ ≤ 10 days) and intermediate-period (℘ = 10 − 200 days) binaries, fc and fip, plus the ranges corresponding to a 90% and 95% confidence level, respectively, in both the EBT1 and EBT2 groups of stars. Although for hot stars both the sample and the survey efficiency were reduced by the low S/N of the spectra, we were able to draw some important conclusions:
-
We found a relatively high lower limit (15–20%) forfip among EHB stars (Teff ≥ 20 000 K). The intermediate-period binary fraction is most probably higher than fc even for EBT2 stars, where only one-fifth of stars could reside in close systems, but up to half of them could be binaries of period shorter than 50 days. We cannot obtain a better estimate, but this result warns that these so-far unstudied systems could play an important role, in particular in clusters with a strong lack of close EHB binaries (e.g. NGC 6752).
-
The G1 gap separating the EBT1 and the EBT2 in the CMD appears as a discontinuity for both the close and the intermediate-period binary fraction, because the probability that either fc or fip is the same in the two populations is negligible. Nevertheless, a smooth increase in binarity with temperature, rather than a discontinuity, cannot be excluded by our observations. If the observed higher binary frequency among chemically unpolluted RGB stars in M 4 (D’Orazi et al. 2010) should be confirmed as a general behavior of multi-populations in GCs, this could represent a problem for the frequently proposed scenario in which the EBT2 stars are the progeny of the most He-enriched stellar generation observed in the MS.
-
A value of fc as high as that of field stars can be excluded, but close EHB systems are surely much more frequent than in NGC 6752. In contrast, for NGC 2808 we find results very similar to NGC 5986. Both these clusters are 2–3 Gyr younger than NGC 6752, which indicates that an fc-age is present in GCs.
-
The similar fc found in NGC 2808 and NGC 5986 also confirms the problems of reconciling the binary scenario with the observations in GCs, because the predictions proposed so far cannot account for both the extremely low fc of NGC 6752, and the much higher values found in younger clusters. We argue, however, that a change in the model parameters could enable closer agreement to be reached.
Acknowledgments
C.M.B. and S.V. acknowledge the Chilean Centro de Excelencia en Astrofísica y Tecnologías Afines (CATA).
References
- Allard, F., Wesemael, F., Fontaine, G., Bergeron, P., & Lamontagne, R. 1994, AJ, 107, 1565 [NASA ADS] [CrossRef] [Google Scholar]
- Aznar Cuadrado, R., & Jeffery, C. S. 2001, A&A, 368, 994 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bedin, L. R., Piotto, G., Zoccali, M., et al. 2000, A&A, 363, 159 [NASA ADS] [Google Scholar]
- Bedin, L. R., Piotto, G., Anderson, J., et al. 2004, ApJ, 605, L125 [NASA ADS] [CrossRef] [Google Scholar]
- Behr, B. B. 2003, ApJS, 149, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Brault, J. W., & White, O. R. 1971, A&A, 13, 169 [NASA ADS] [Google Scholar]
- Buson, L. M., Bertone, E., Buzzoni, A., & Carraro, G. 2006, Baltic Astronomy, 15, 49 [Google Scholar]
- Caloi, V. 1972, A&A, 20, 357 [NASA ADS] [Google Scholar]
- Carretta, E., Bragaglia, A., Gratton, R. G., et al. 2006, A&A, 450, 523 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cassisi, S., Castellani, V., degl’Innocenti, S., Salaris, M., & Weiss, A. 1999, A&AS, 134, 103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Catelan, M. 2009, Ap&SS, 320, 261 [NASA ADS] [CrossRef] [Google Scholar]
- Dalessandro, E., Salaris, M., Ferraro, F. R., et al. 2011, MNRAS, 410, 694 [NASA ADS] [CrossRef] [Google Scholar]
- D’Antona, F., Caloi, V., Montalbán, J., Ventura, P., & Gratton, R. 2002, A&A, 395, 69 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- D’Antona, F., Bellazzini, M., Caloi, V., et al. 2005, ApJ, 631, 868 [NASA ADS] [CrossRef] [Google Scholar]
- De Angeli, F., Piotto, G., Cassisi, S., et al. 2005, AJ, 130, 116 [NASA ADS] [CrossRef] [Google Scholar]
- Decressin, T., Meynet, G., Charbonnel, C., Prantzos, N., & Ekström, S. 2007, A&A, 464, 1029 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Denissenkov, P. A., & VandenBerg, D. A. 2003, ApJ, 598, 1246 [NASA ADS] [CrossRef] [Google Scholar]
- D’Orazi, V., Gratton, R., Lucatello, S., et al. 2010, ApJ, 719, L213 [NASA ADS] [CrossRef] [Google Scholar]
- Dotter, A., Sarajedini, A., Anderson, J., et al. 2010, ApJ, 708, 698 [NASA ADS] [CrossRef] [Google Scholar]
- Faulkner, J. 1966, ApJ, 144, 978 [NASA ADS] [CrossRef] [Google Scholar]
- Ferguson, D. H., Green, R. F., & Liebert, J. 1984, ApJ, 287, 320 [NASA ADS] [CrossRef] [Google Scholar]
- Fraix-Burnet, D., Davoust, E., & Charbonnel, C. 2009, MNRAS, 398, 1706 [NASA ADS] [CrossRef] [Google Scholar]
- Fusi Pecci, F., Ferraro, F. R., Bellazzini, M., et al. 1993, AJ, 105, 1145 [NASA ADS] [CrossRef] [Google Scholar]
- Greenstein, J. L. 1971, in White Dwarfs, ed. W. J. Luyten (Dordrecht: Reidel), IAU Symp., 42, 46 [NASA ADS] [Google Scholar]
- Greggio, L., & Renzini, A. 1990, ApJ, 364, 35 [Google Scholar]
- Grundahl, F., Catelan, M., Landsman, W. B., Stetson, P. B., & Andersen, M. I. 1999, ApJ, 524, 242 [NASA ADS] [CrossRef] [Google Scholar]
- Han, Z. 2008, A&A, 484, L31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Han, Z., Podsiadlowski, P., Maxted, P. F. L., Marsh, T. R., & Ivanova, N. 2002, MNRAS, 336, 449 [NASA ADS] [CrossRef] [Google Scholar]
- Han, Z., Podsiadlowski, P., Maxted, P. F. L., & Marsh, T. R. 2003, MNRAS, 341, 669 [NASA ADS] [CrossRef] [Google Scholar]
- Han, Z., Podsiadlowski, P., & Lynas-Gray, A. E. 2007, MNRAS, 380, 1098 [NASA ADS] [CrossRef] [Google Scholar]
- Harris, W. E. 1996, AJ, 112, 1487 [NASA ADS] [CrossRef] [Google Scholar]
- Heber, U. 1986, A&A, 155, 33 [NASA ADS] [Google Scholar]
- Heber, U., Moehler, S., Napiwotzki, R., Thejll, P., & Green, E. M. 2002, A&A, 383, 938 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Horne, K. 1986, PASP, 98, 609 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hoyle, F., & Schwarzschild, M. 1955, ApJS, 2, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, Y., Joo, S., Han, S., et al. 2005, ApJ, 621, L57 [NASA ADS] [CrossRef] [Google Scholar]
- Lisker, T., Heber, U., Napiwotzki, R., et al. 2005, A&A, 430, 223 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lutz, T. E., & Hanson, R. B. 1992, in Astronomical Data Analysis Software and Systems I, ed. D. M. Worrall, C. Biemesderfer, & J. Barnes, ASP Conf. Ser., 25, 257 [Google Scholar]
- Maeder, A., & Meynet, G. 2006, A&A, 448, L37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marsh, T. R., Dhillon, V. S., & Duck, S. R. 1995, MNRAS, 275, 828 [NASA ADS] [CrossRef] [Google Scholar]
- Maxted, P. F. L., Heber, U., Marsh, T. R., & North, R. C. 2001, MNRAS, 326, 1391 [NASA ADS] [CrossRef] [Google Scholar]
- Mengel, J. G., Norris, J., & Gross, P. G. 1976, ApJ, 204, 488 [NASA ADS] [CrossRef] [Google Scholar]
- Miocchi, P. 2007, MNRAS, 381, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Moehler, S., Sweigart, A. V., Landsman, W. B., Hammer, N. J., & Dreizler, S. 2004, A&A, 415, 313 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Momany, Y., Piotto, G., Recio-Blanco, A., et al. 2002, ApJ, 576, L65 [NASA ADS] [CrossRef] [Google Scholar]
- Momany, Y., Cassisi, S., Piotto, G., et al. 2003, A&A, 407, 303 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Moni Bidin, C., & Piotto, G. 2010, Ap&SS, 156 [Google Scholar]
- Moni Bidin, C., Moehler, S., Piotto, G., et al. 2006, A&A, 451, 499 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Moni Bidin, C., Catelan, M., & Altmann, M. 2008a, A&A, 480, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Moni Bidin, C., Catelan, M., Villanova, S., et al. 2008b, in Hot Subdwarf Stars and Related Objects, ed. U. Heber, C. S. Jeffery, & R. Napiwotzki, ASP Conf. Ser., 392, 27 [Google Scholar]
- Moni Bidin, C., Moehler, S., Piotto, G., Momany, Y., & Recio-Blanco, A. 2009a, A&A, 498, 737 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Moni Bidin, C., Moehler, S., Piotto, G., et al. 2009b, Globular Clusters – Guides to Galaxies, ed. T. Richtler, & S. Larsen, 37 [Google Scholar]
- Morales-Rueda, L., Maxted, P. F. L., Marsh, T. R., Kilkenny, D., & O’Donoghue, D. 2006, Baltic Astron, 15, 187 [Google Scholar]
- Morales-Rueda, L., Maxted, P. F. L., Marsh, T. R., North, R. C., & Heber, U. 2003, MNRAS, 338, 752 [Google Scholar]
- Moran, C., Maxted, P., Marsh, T. R., Saffer, R. A., & Livio, M. 1999, MNRAS, 304, 535 [NASA ADS] [CrossRef] [Google Scholar]
- Morse, J. A., Mathieu, R. D., & Levine, S. E. 1991, AJ, 101, 1495 [NASA ADS] [CrossRef] [Google Scholar]
- Munari, U., Sordo, R., Castelli, F., & Zwitter, T. 2005, A&A, 442, 1127 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Napiwotzki, R., Karl, C. A., Lisker, T., et al. 2004, Ap&SS, 291, 321 [NASA ADS] [CrossRef] [Google Scholar]
- Peterson, R. C. 1983, ApJ, 275, 737 [NASA ADS] [CrossRef] [Google Scholar]
- Piotto, G., King, I. R., Djorgovski, S. G., et al. 2002, A&A, 391, 945 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Piotto, G., Villanova, S., Bedin, L. R., et al. 2005, ApJ, 621, 777 [NASA ADS] [CrossRef] [Google Scholar]
- Piotto, G., Bedin, L. R., Anderson, J., et al. 2007, ApJ, 661, L53 [NASA ADS] [CrossRef] [Google Scholar]
- Recio-Blanco, A., Piotto, G., Aparicio, A., & Renzini, A. 2002, ApJ, 572, L71 [NASA ADS] [CrossRef] [Google Scholar]
- Recio-Blanco, A., Aparicio, A., Piotto, G., de Angeli, F., & Djorgovski, S. G. 2006, A&A, 452, 875 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Reed, M. D., & Stiening, R. 2004, PASP, 116, 506 [NASA ADS] [CrossRef] [Google Scholar]
- Renzini, A. 2008, MNRAS, 391, 354 [NASA ADS] [CrossRef] [Google Scholar]
- Rich, R. M., Sosin, C., Djorgovski, S. G., et al. 1997, ApJ, 484, L25 [Google Scholar]
- Saffer, R. A., Livio, M., & Yungelson, L. R. 1998, ApJ, 502, 394 [NASA ADS] [CrossRef] [Google Scholar]
- Sandage, A., & Wildey, R. 1967, ApJ, 150, 469 [NASA ADS] [CrossRef] [Google Scholar]
- Silvotti, R., Schuh, S., Janulis, R., et al. 2007, Nature, 449, 189 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Soker, N. 1998, AJ, 116, 1308 [NASA ADS] [CrossRef] [Google Scholar]
- Sosin, C., Dorman, B., Djorgovski, S. G., et al. 1997, ApJ, 480, L35 [NASA ADS] [CrossRef] [Google Scholar]
- Suda, T., Tsujimoto, T., Shigeyama, T., & Fujimoto, M. Y. 2007, ApJ, 671, L129 [NASA ADS] [CrossRef] [Google Scholar]
- Sweigart, A. V. 1997, ApJ, 474, L23 [NASA ADS] [CrossRef] [Google Scholar]
- Sweigart, A. V., & Mengel, J. G. 1979, ApJ, 229, 624 [NASA ADS] [CrossRef] [Google Scholar]
- Tonry, J., & Davis, M. 1979, AJ, 84, 1511 [NASA ADS] [CrossRef] [Google Scholar]
- Tutukov, A., & Iungelson, L. 1987, in Second Conference on Faint Blue Stars, ed. A. G. D. Philip, D. S. Hayes, & J. W. Liebert, IAU Colloq., 95, 435 [Google Scholar]
- Ulla, A., & Thejll, P. 1998, A&AS, 132, 1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van den Bergh, S. 1967, AJ, 72, 70 [NASA ADS] [CrossRef] [Google Scholar]
- von Rudloff, I. R., Vandenberg, D. A., & Hartwick, F. D. A. 1988, ApJ, 324, 840 [NASA ADS] [CrossRef] [Google Scholar]
- Williams, T., McGraw, J. T., Mason, P. A., & Grashuis, R. 2001, PASP, 113, 944 [NASA ADS] [CrossRef] [Google Scholar]
- Zorotovic, M., Schreiber, M. R., Gänsicke, B. T., & Nebot Gómez-Morán, A. 2010, A&A, 520, A86 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Position of the targets in the cluster color-magnitude diagrams. Upper panel: V vs. (U − V) diagram, where the arrows indicate the location of the two gaps discussed in the text (G1 and G2), and the magnitude corresponding to T = 20 000 K (the formal definition of the EHB). Lower panel: V vs. (B − V) diagram with superimposed the ZAHB model from Cassisi et al. (1999) used to estimate stellar temperatures. The star #37345 discussed in the text is indicated with an empty triangle. |
| In the text | |
 |
Fig. 2 Normalized spectra of four target stars, obtained shifting all the collected spectra to laboratory wavelength and summing them. The star ID and temperature is given. The spectra were vertically shifted to avoid overlap. |
| In the text | |
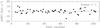 |
Fig. 3 Difference between the RV measured in the first frame (frame 1-1 of Table 1) and the weighted average for each star, plotted as a function of the fiber number. Only the 53 brightest stars, with measurement uncertainty lower than 5 km s-1, are plotted. |
| In the text | |
 |
Fig. 4 Mean error of each star as a function of effective temperature. |
| In the text | |
 |
Fig. 5 Upper panel: histogram of the distribution of the residuals with respect to the weighted average of each star, in unit of the associated error (Eq. (1)). Overplotted to the histogram, a Gaussian with σ = 0.96 and centered in 0.01 is shown. Lower panel: probability plot of the same residuals of the upper panel. The straight line, with intercept 0.01 and slope 0.96, indicates the least squares fit of the data. |
| In the text | |
 |
Fig. 6 Distribution of the absolute RVs of the observed stars. The curve shows a Gaussian centered on the mean value (93.2 km s-1) and σ equal to the observed dispersion (5.7 km s-1). The dotted line indicates the cluster RV from Harris (1996). |
| In the text | |
 |
Fig. 7 Upper panel: probability of a false detection for the “relative” criteria (empty dots and dotted line) and the “absoute” criteria (full dots and line) defined in the text, assuming a 3σ threshold for both. Lower panel: false detection probability for the same criteria, as a function of the threshold, for ten measurements. |
| In the text | |
 |
Fig. 8 Upper panel: difference of the binary detection probability, as a function of period, when including or not the four spectra which are not the sum of two exposures (frames 3-2, 4-2, 5-1, and 6-3, see Table 1). For the calculation we assumed an “absolute” criteria with threshold 3.2σ, the same adopted in the present work, and a mean observational error of 3.5 km s-1. Lower panel: detection probability as a function of period, calculated as described in the text. The full and dotted lines indicate the results for the “absolute” criteria with 3.2σ threshold and the “relative” one with 3.8σ criteria, respectively, assuming the typical mean error (3.5 km s-1) of stars cooler than the G1 gap at ~17 000 K. The results for the “absolute” criteria assuming a mean error of 6.0 km s-1, characteristic of hotter stars, are shown with a dashed line. |
| In the text | |
 |
Fig. 9 Maximum residual in units of the error (Eq. (1)) for each star, as a function of temperature. The horizontal line indicates the adopted threshold for binary detection. Empty dots represents stars with only partial temporal coverage, that are excluded from the statistical analysis. The vertical dotted line indicates the approximate position of the G1 gap. |
| In the text | |
 |
Fig. 10 RV measurements of the four binary candidates. The dotted line indicates the weighted mean. |
| In the text | |
 |
Fig. 11 Upper panel: detection probability as a function of period, calculated as described in the text, consideting only the first four (full line) or two (dotted line) nights. Lower panel: probability, as a function of period, that an EHB binary would show a significant RV variation only in the fourth night of our observations, as found for the star #7700. |
| In the text | |
 |
Fig. 12 Curve of probability for the close binary fraction fc (dotted lines), and the intermediate-period binary fraction fip (full lines). Upper panel: EBT1 stars; middle panel: EBT2 stars; Lower panel: EHB stars. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


