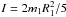Eccentric binaries

E. Moreno; G. Koenigsberger; D. M. Harrington

doi:10.1051/0004-6361/201015874

Home

All issues

Volume 528 (April 2011)

A&A, 528 (2011) A48

Full HTML

Free Access

Issue		A&A Volume 528, April 2011


Article Number		A48
Number of page(s)		15
Section		Stellar structure and evolution
DOI		https://doi.org/10.1051/0004-6361/201015874
Published online		28 February 2011

A&A 528, A48 (2011)

Tidal flows and periastron events

E. Moreno¹, G. Koenigsberger² and D. M. Harrington³

¹ Instituto de Astronomía, Universidad Nacional Autónoma de México, México D. F. 04510, Mexico
e-mail: edmundo@astroscu.unam.mx
² Instituto de Ciencias Físicas, Universidad Nacional Autónoma de México, Cuernavaca, Morelos 62210, Mexico
e-mail: gloria@astro.unam.mx
³ Institute for Astronomy, University of Hawaii, 2680 Woodlawn Drive, Honolulu, HI, 96822, USA
e-mail: dmh@ifa.hawaii.edu

Received: 5 October 2010
Accepted: 12 January 2011

Abstract

Context. A number of binary systems present evidence of enhanced activity around periastron passage, suggesting a connection between tidal interactions and these periastron effects.

Aims. The aim of this investigation is to study the time-dependent response of a star’s surface as it is perturbed by a binary companion. Here we focus on the tidal shear energy dissipation.

Methods. We derive a mathematical expression for computing the rate of dissipation, Ė, of the kinetic energy by the viscous flows that are driven by tidal interactions on the surface layer of a binary star. The method is tested by comparing the results from a grid of model calculations with the analytical predictions of Hut (1981, A&A, 99, 126) and the synchronization timescales of Zahn (1977, A&A, 57, 383; 2008, EAS Pub. Ser., 29, 67).

Results. Our results for the dependence of the average (over orbital cycle) energy dissipation, Ė_ave, on orbital separation are consistent with those of Hut (1981) for model binaries with an orbital separation at periastron r_per/R₁ ≳ 8, where R₁ is the stellar radius. The model also reproduces the predicted pseudo-synchronization angular velocity for moderate eccentricities (e ≤ 0.3). In addition, for circular orbits our approach yields the same scaling of synchronization timescales with orbital separation as given by Zahn (1977, 2008) for convective envelopes. The computations give the distribution of Ė over the stellar surface, and show that it is generally concentrated at the equatorial latitude, with maxima generally located around four clearly defined longitudes, corresponding to the fastest azimuthal velocity perturbations. Maximum amplitudes occur around periastron passage or slightly thereafter for supersynchronously rotating stars. In very eccentric binaries, the distribution of Ė over the surface changes significantly as a function of orbital phase, with small spatial structures appearing after periastron. An exploratory calculation for a highly eccentric binary system with parameters similar to those of δ Sco (e = 0.94, P = 3944.7 d) indicates that Ė_ave changes by ~ 5 orders of magnitude over the 82 days before periastron, suggesting that the sudden and large amplitude variations in surface properties around periastron may, indeed, contribute toward the activity observed around this orbital phase.

Key words: binaries: general / stars: oscillations / stars: rotation

© ESO, 2011

1. Introduction

A number of binary systems present evidence of enhanced activity around periastron passage. Among these, η Car and the Wolf-Rayet systems WR 140 and WR 125 are the most extreme and best documented examples of periodic brightening at X-ray, visual and IR wavebands associated with periastron passages. Recently, van Genderen & Sterken (2007) suggested that these periastron events may have the same physical cause as the milder “periastron effects” exhibited by many renowned eccentric binaries in which small enhancement (Δm_v ~ 0.01–0.03^mag) in the visual brightness of the system around periastron passage are observed. They suggest that the fundamental cause of the effects may reside in the enhanced tidal force that is present during periastron passage. In addition to brightness enhancements, binary interactions are frequently invoked to explain certain mass-ejection phenomena. For example, Koenigsberger et al. (2002) raised the question of whether tidal forces play a role in changing the wind structure in the massive Small Magellanic Cloud binary system HD 5980, and suggested a possible link between tidal forces and the instability producing the 1994 eruptive event. Bonacić Marinović et al. (2008) proposed a tidally-enhanced model of mass-loss from AGBs. Observational data supporting the idea of mass-loss events associated with periastron passage exist for the highly eccentric (e ~ 0.94) binary δ Sco (Bedding 1993; Miroshnichenko et al. 2001; Tango et al. 2009). And Millour et al. (2009) suggested that the dusty circumbinary environment in HD 87643 might be associated with repeated close encounters in the long period and possible highly eccentric binary. In this paper we explore a mechanism that has the potential of providing a theoretical framework for analyzing these phenomena.

Tidal interactions are ubiquitous in binary systems of all types. They lead to the deformation of the stellar surface. When the system is in equilibrium¹, the deformation remains constant. However, if the stellar rotation is not synchronized with the orbital motion, the shape of the star is time-dependent. In eccentric binaries, the orbital separation changes as the stars move from periastron to apastron, thus leading to a time-dependent gravitational force. In addition, because the orbital angular velocity, Ω, is a function of the orbital separation, the departure from synchronicity between the stellar rotation angular velocity, ω, and Ω is orbital-phase dependent. Hence, eccentric binaries are never in synchronous rotation. The asynchronicity leads to the appearance of potentially large horizontal motions on the stellar surface, which are referred to as tidal flows.

The energy that is dissipated because of shearing motions is ultimately converted into heat that is deposited in the stellar layers. Whether this process leads to detectable observational effects is one of the questions that has driven our investigation of the detailed tidal interaction effects. In the first paper of this series, a very simple model was presented for computing the stellar surface motions in a component of a binary system (Moreno & Koenigsberger 1999, hereafter Paper I). In that model we computed only the motion of surface elements on the equatorial plane of a star. We followed a Lagrangian approach in a quasi-hydrodynamic scheme, solving the equations of motion of small surface elements, as they respond to gravitational, gas pressure, viscous, centrifugal, and Coriolis forces. The model was applied to the ι Ori binary system (Paper I), the ϵ Per system (Moreno et al. 2005, hereafter Paper II), and the optical counterpart of the X-ray binary 2S0114+650 (Koenigsberger et al. 2006). In Paper II we computed the absorption line profiles obtained with the model, taking an ad-hoc extension to stellar polar angles of the motion computed on the stellar equator. This extension was also used in the analysis of energy dissipation rates and synchronization time scales in binary systems with circular orbits (Toledano et al. 2007). Here we improve the model by computing explicitly the motion of elements along different parallels that cover the stellar surface. This new scheme in the computation of energy dissipation was applied in the LBV/WR system HD 5980 (Koenigsberger & Moreno 2008), and in the study of tidal flows in α Virginis (Harrington et al. 2009).

This paper is organized as follows: in Sect. 2 we generalize the mathematical expression for the calculation of shear energy dissipation rates, Ė, that was presented in Toledano et al. (2007); in Sects. 3 and 4 we compare the predictions of our model for Ė with the analytical results of Hut (1981) and the synchronization timescales with the analytical expression of Zahn (1977, 2008), respectively; in Sect. 5 we explore the orbital-phase dependent effects and their possible relation to the observational periastron effects; in Sect. 6 we present a discussion, and Sect. 7 lists the conclusions.

2. The extended model

As in the first version of the model, we assume that the main stellar body, below the thin surface layer, behaves as a rigid body. In the quasi-hydrodynamic method used in Paper I, for every surface element a detailed analysis of the positions of neighboring elements is needed to assign a local dimension. If an initial well ordered arrangement of the elements begins to mix freely in the azimuthal and polar directions, the assignment of a physical dimension to an element and its corresponding interactions with neighboring elements is not treatable in our current scheme. Thus, we make the simplifying assumption that the surface elements move only in the radial and azimuthal directions; that is, an element always stays in its initial parallel, and there is no meridional motion². The energy dissipation computation performed in Sect. 2.3 requires the motions of the surface elements. In this section we give the procedure to compute this motion in either of the two stars in the binary system, say star 1, with mass m₁ and initial radius R₁. Star 2 has a mass m₂ and instantaneous position r₂₁ with respect to the center of m₁, and an orbital angular velocity Ω. The motions of the surface elements in m₁ are computed in a primed non-inertial reference frame with its origin at the center of m₁, and Cartesian axes rotating with the orbital angular velocity Ω; the x′ axis always points to m₂.

In Paper II the total acceleration a′ of a surface element, measured in the non-inertial frame, is shown to be $\begin{matrix} a^{'} & = & a_{⋆} - \frac{G m_{1} r^{'}}{| r^{'} |^{3}} - G m_{2} [\frac{r^{'} - r_{21}}{| r^{'} - r_{21} |^{3}} + \frac{r_{21}}{| r_{21} |^{3}}] \\ - Ω \times (Ω \times r^{'}) - 2 Ω \times v' - \frac{d Ω}{d t} \times r^{'}, \end{matrix}$ $\begin{eqnarray} {\bf a}'& =& {\bf a}_{\star}- \frac{Gm_1 {\bf r}'}{|{\bf r}'|^3}-Gm_2 \left [ \frac{{\bf r}'- {\bf r}_{21}} {|{\bf r}'- {\bf r}_{21}|^3}+ \frac{{\bf r}_{21}} {|{\bf r}_{21}|^3} \right ] \nonumber \\ \label{ecmov} && - {\bf {\Omega}} \times \left ( {\bf \Omega} \times {\bf r}' \right ) -2 {\bf {\Omega}} \times \vec{v}'- \frac{{\rm d} {\bf {\Omega}}}{{\rm d}t} \times {\bf r}', \end{eqnarray}$ (1)with a_⋆ the acceleration of a surface element produced by gas pressure and viscous forces exerted by the stellar material surrounding the element, and r′, v′ the position and velocity of the element in the non-inertial frame. A nearly spherical shape is assumed for m₁ throughout its motion.

The computation starts at time t = 0 with no relative motion between the surface elements, so that at this initial time the acceleration a_⋆, with value a_⋆0, has only the contribution of gas pressure. To compute this acceleration we consider a second, double-primed, non-inertial reference frame, whose origin is also at the center of m₁, and has axes rotating with the assumed constant angular velocity ω_⋆ of the inner rigid region of star 1. This angular velocity is written as ω_⋆ = β₀Ω₀, that is, equal to a certain fraction β₀ of the initial orbital angular velocity³. The condition for initial equilibrium 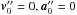$v \begin{matrix} ′′ \\ 0 \end{matrix} = 0, a \begin{matrix} ′′ \\ 0 \end{matrix} = 0$ $\hbox{$\vec{v}''_0 = 0, \vec{a}''_0 = 0$}$ on the surface of m₁ is (with r′′ = r′) $\begin{matrix} a_{⋆ o} & = & {\frac{G m_{1} r^{'}}{| r^{'} |^{3}} + G m_{2} [\frac{r^{'} - r_{21}}{| r^{'} - r_{21} |^{3}} + \frac{r_{21}}{| r_{21} |^{3}}]}_{t = 0} \\ + β_{0}^{2} Ω_{0} \times (Ω_{0} \times {r_{0}^{'}}^{)} . \end{matrix}$ $\begin{eqnarray} {\bf a}_{{\star}o}& =& \left \{ \frac{Gm_1 {\bf r}'}{|{\bf r}'|^3}+Gm_2 \left [ \frac{{\bf r}'- {\bf r}_{21}}{|{\bf r}'- {\bf r}_{21}|^3}+ \frac{{\bf r}_{21}}{|{\bf r}_{21}|^3} \right ] \right \}_{t=0} \nonumber\\ \label{aeso} && +\,\beta^2_0 {\bf {\Omega}}_0 \times \left ( {\bf {\Omega}}_0 \times {\bf r}'_0 \right ). 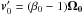\end{eqnarray}$ (2)The initial position r $\begin{matrix} ' \\ 0 \end{matrix}$ $\hbox{$_0'$}$ of a surface element is obtained with an initial spherical shape of star 1, and its initial velocity is, $v \begin{matrix} ' \\ 0 \end{matrix} = (β_{0} - 1) Ω_{0}$ $\hbox{$\vec{v}_0' = ({\beta}_0 - 1) \bf {\Omega}_0$}$ × r $\begin{matrix} ' \\ 0 \end{matrix}$ $\hbox{$_0'$}$ .

The contribution of the m₂- term in Eq. (2) makes a_⋆0 in a given parallel have a non-constant azimuthal component. Thus the assumed initial spherical shape would not be the proper shape consistent with this azimuthal behavior. In our computations, at t = 0 we impose only the radial equilibrium resulting from Eq. (2), and allow unbalanced forces in the azimuthal direction. We found that with appropriate parameters (e.g. viscosity) this non-equilibrium initial condition will be followed by a transient phase and a steady state (dependent on the orbital phase) at later times.

At t > 0 the acceleration produced by gas pressure is conveniently written in terms of the radial component of a_⋆0. Thus the radial component in Eq. (2), which is used in the following section, is $\begin{matrix} a ⋆ 0 r' & = & \frac{G m_{1}}{{r_{0}^{'}}^{2}} + G m_{2} [\frac{r_{0}^{'} - {r_{21}}_{0} \sin θ^{'} \cos ϕ_{0}^{'}}{{({r_{0}^{'}}^{2} + {r_{21}^{2}}_{0} - 2 r_{0}^{'} {r_{21}}_{0} \sin θ^{'} \cos {ϕ_{0}^{'}}^{)}}^{3 / 2}}] \\ + G m_{2} [\frac{\sin θ^{'} \cos ϕ_{0}^{'}}{{r_{21}^{2}}_{0}}] - β_{0}^{2} Ω_{0}^{2} r_{0}^{'} \sin^{2} θ^{'}, \end{matrix}$ $\begin{eqnarray} a_{{\star}0r'} &= &\frac{Gm_1}{{r'_0}^2}+ Gm_2 \left [ \frac{r'_0-{r_{21}}_0\sin{\theta}'\cos{\varphi}'_0} {\left ({r'_0}^2+{r^2_{21}}_0-2r'_0{r_{21}}_0\sin{\theta}' \cos{\varphi}'_0 \right )^{3/2}}\right] \nonumber\\ \label{aesor} &&+ \,Gm_2 \left [\frac{\sin{\theta}'\cos{\varphi}'_0}{{r^2_{21}}_0}\right ]- {\beta}_0^2{\Omega}_0^2r'_0\sin^2{\theta}', \end{eqnarray}$ (3)with θ′ the polar angle of the given parallel and $ϕ_{0}^{'}$ $\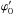hbox{${\varphi}'_0$}$ the initial azimuthal angle of the element.

2.1. The acceleration a_⋆

An element on the stellar surface of m₁ has lateral surfaces facing in the three directions of spherical coordinates, r′, ϕ′, θ′ in the primed non-inertial frame. The x′-axis points to m₂ and ϕ′ = 0 on the positive side of this axis; the polar axis is z′, which is also the stellar rotation axis. We will denote with i the parallel’s number and with j the number of the element. 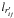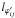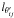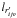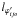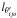The lengths of an element in the three directions are $l_{r_{ij}^{'}}$ $\hbox{$l_{r'_{ij}}$}$ , $l_{ϕ_{ij}^{'}}$ $\hbox{$l_{{\varphi}'_{ij}}$}$ , and $l_{θ_{ij}^{'}}$ $\hbox{$l_{{\theta}'_{ij}}$}$ , with initial values $l_{r_{ijo}^{'}}$ $\hbox{$l_{r'_{ijo}}$}$ , $l_{ϕ_{ijo}^{'}}$ $\hbox{$l_{{\varphi}'_{ijo}}$}$ , $l_{θ_{ijo}^{'}}$ $\hbox{$l_{{\theta}'_{ijo}}$}$ . 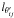The length $l_{θ_{ij}^{'}}$ $\hbox{$l_{{\theta}'_{ij}}$}$ is assumed constant in time for all elements in a given parallel. 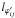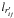In our scheme, for a given element at any time $l_{ϕ_{ij}^{'}}$ $\hbox{$l_{{\varphi}'_{ij}}$}$ is the mean of its azimuthal distances to the centers of mass of the two adjacent elements in this azimuthal direction, and $l_{r_{ij}^{'}}$ $\hbox{$l_{r'_{ij}}$}$ is twice the distance between the center of mass of the element and the boundary of the inner stellar region. At t = 0 all the elements in a given parallel have the same lengths.

The acceleration a_⋆ has contributions from gas pressure and viscous shear. Below we describe the components of these contributions in spherical coordinates.

2.1.1. Gas pressure

The gas pressure inside a surface element is p_ij, and we assume a polytropic state equation p_ij = p_ij0(ρ_ij/ρ_ij0)^γ′, with γ′ = 1 + 1/n; n is the polytropic index and ρ the mass density. The pressure on the element exerted by the neighboring stellar inner region is taken as p_int = p_ij/q, 0 < q < 1. We consider in particular the half value q = 0.5. 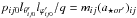Thus the initial radial equilibrium is $p_{ij 0} l_{θ_{ij 0}^{'}} l_{ϕ_{ij 0}^{'}} / q = m_{ij} (a ⋆ or')_{ij}$ $\hbox{$p_{ij0}l_{{\theta}'_{ij0}}l_{{\varphi}'_{ij0}}/q = m_{ij}(a_{{\star}or'})_{ij}$}$ , with m_ij the constant mass of the element. 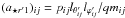At t > 0 the radial pressure acceleration is $(a_{⋆ r^{'} 1})_{ij} = p_{ij} l_{θ_{ij}^{'}} l_{ϕ_{ij}^{'}} / q m_{ij}$ $\hbox{$(a_{{\star}r'1})_{ij} = p_{ij}l_{{\theta}'_{ij}}l_{{\varphi}'_{ij}}/ qm_{ij}$}$ . 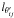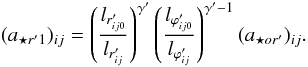This relation combined with the polytropic equation, the initial radial equilibrium, and with the constant value of $l_{θ_{ij}^{'}}$ $\hbox{$l_{{\theta}'_{ij}}$}$ , gives $(a_{⋆ r^{'} 1})_{ij} = {(\frac{l_{r_{ij 0}^{'}}}{l_{r_{ij}^{'}}})}^{γ^{'}} {(\frac{l_{ϕ_{ij 0}^{'}}}{l_{ϕ_{ij}^{'}}})}^{γ^{'} - 1} (a ⋆ or')_{ij} .$ $\begin{equation} (a_{{\star}r'1})_{ij} = \left ( \frac{l_{r'_{ij0}}} {l_{r'_{ij}}} \right )^{{\gamma}'} \left ( \frac{l_{{\varphi}'_{ij0}}} {l_{{\varphi}'_{ij}}} \right )^{{\gamma}'-1}(a_{{\star}or'})_{ij}. \label{aesr1} \end{equation}$ (4)The azimuthal gas pressure acceleration on a given element, (a_⋆ ϕ′1)_ij, is computed with the difference of the gas pressure forces exerted by the two adjacent elements in this azimuthal direction. Then 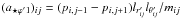$(a_{⋆ ϕ^{'} 1})_{ij} = (p_{i,j - 1} - p_{i,j + 1}) l_{r_{ij}^{'}} l_{θ_{ij}^{'}} / m_{ij}$ $\hbox{$(a_{{\star}{\varphi}'1})_{ij} = (p_{i,j-1}-p_{i,j+1})l_{r'_{ij}}l_{{\theta}'_{ij}}/m_{ij}$}$ . With the polytropic form for each pressure, the corresponding initial radial equilibrium conditions on the adjacent elements, and the same initial mass density for each surface element (thus the same mass of elements in the given parallel, because their initial lenghts are the same), this expression is $\begin{matrix} (a_{⋆ ϕ^{'} 1})_{ij} & = & q \frac{l_{r_{ij}^{'}}}{l_{ϕ_{ij 0}^{'}}} {[l_{r_{ij 0}^{'}} l_{ϕ_{ij 0}^{'}}]}^{γ^{'}} \\ \times {(a ⋆ 0 r')_{i,j - 1} {[l_{r_{i,j - 1}^{'}} l_{ϕ_{i,j - 1}^{'}}]}^{- γ^{'}} - (a ⋆ 0 r')_{i,j + 1} {[l_{r_{i,j + 1}^{'}} l_{ϕ_{i,j + 1}^{'}}]}^{- γ^{'}}} . \end{matrix}$ $\begin{eqnarray} (a_{{\star}{\varphi}'1})_{ij}& =& q \frac{l_{r'_{ij}}}{l_{{\varphi}'_{ij0}}} \left [ l_{r'_{ij0}}l_{{\varphi}'_{ij0}} \right ]^{{\gamma}'} \nonumber \\ \label{aesfi1} &&\hspace{-11mm}\times \,\left \{(a_{{\star}0r'})_{i,j-1}\left [ l_{r'_{i,j-1}}l_{{\varphi}'_{i,j-1}} \right ]^{-{\gamma}'} \!\! -\! (a_{{\star}0r'})_{i,j+1}\left [ l_{r'_{i,j+1}}l_{{\varphi}'_{i,j+1}} \right ]^{-{\gamma}'} \right \}. \end{eqnarray}$ (5)

2.1.2. Viscous force

The shear part of the kinematic stress tensor is given by (e.g., Symon 1971) $P η = - η [\nabla^{'} v' + {(\nabla^{'} v')}^{trp} - \frac{2}{3} 1 (\nabla^{'} \cdot v')],$ $\begin{equation} \vec{P}_{\eta} = -{\eta} \left [ {\nabla}' \vec{v}' + \left ( {\nabla}' \vec{v}' \right )^{\rm trp} - \frac{2}{3} {\bf 1} \left ({\nabla}' \cdot \vec{v}' \right ) \right ], \label{tensor} \end{equation}$ (6)where 1 is the unit matrix, trp indicates the transposed, and η is the coefficient of dynamic viscosity, related with the coefficient of kinematic viscosity, ν, by η = νρ, with ρ the mass density. 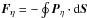The total force on a given surface element from shear stresses is $\hbox{$\vec{F}_{\eta} = - \oint \vec{P}_{\eta} \cdot {\rm d}\vec{S}$}$ , with the integration over its surface. We picture each element with lateral faces in the three directions of spherical coordinates, and corresponding lateral areas A_r′, A_ϕ′, A_θ′. 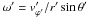Because we do not compute the motion in the polar direction, with $ω^{'} = v_{ϕ^{'}}^{'} / r^{'} \sin θ^{'}$ $\hbox{${\omega}' = v'_{{\varphi}'}/r'\sin{\theta}'$}$ , the relevant radial and azimuthal components of the viscous force are $\begin{matrix} (F_{η})_{r^{'}} & = & A_{r^{'}} Δ [η (\frac{4}{3} r^{'} \frac{\partial}{\partial r^{'}} (\frac{v_{r^{'}}^{'}}{r^{'}}) - \frac{2}{3} \frac{\partial ω^{'}}{\partial ϕ^{'}})] \\ + A_{ϕ^{'}} Δ [η (r^{'} \frac{\partial ω^{'}}{\partial r^{'}} \sin θ^{'} + \frac{1}{r^{'} \sin θ^{'}} \frac{\partial v_{r^{'}}^{'}}{\partial ϕ^{'}})] \\ + A_{θ^{'}} Δ [\frac{η}{r^{'}} \frac{\partial v_{r^{'}}^{'}}{\partial θ^{'}}], \\ (F_{η})_{ϕ^{'}} & = & A_{r^{'}} Δ [η (r^{'} \frac{\partial ω^{'}}{\partial r^{'}} \sin θ^{'} + \frac{1}{r^{'} \sin θ^{'}} \frac{\partial v_{r^{'}}^{'}}{\partial ϕ^{'}})] \\ + A_{ϕ^{'}} Δ [η (- \frac{2}{3} r^{'} \frac{\partial}{\partial r^{'}} (\frac{v_{r^{'}}^{'}}{r^{'}}) + \frac{4}{3} \frac{\partial ω^{'}}{\partial ϕ^{'}})] \\ + A_{θ^{'}} Δ [η \frac{\partial ω^{'}}{\partial θ^{'}} \sin θ^{'}], \end{matrix}$ $\begin{eqnarray} (F_{\eta})_{r'} &=& A_{r'}{\Delta}\left [\eta \left ( \frac{4}{3}r'\frac{\partial}{\partial r'}\left ( \frac{v'_{r'}}{r'} \right )-\frac{2}{3}\frac{\partial {\omega}'}{\partial {\varphi}'} \right ) \right ]\nonumber \\ &&+ A_{{\varphi}'}{\Delta} \left [\eta \left ( r' \frac{\partial {\omega}'}{\partial r'}\sin{\theta}'+ \frac{1}{r'\sin{\theta}'}\frac {\partial v'_{r'}}{\partial {\varphi}'} \right ) \right ] \nonumber\\ \label{frvis} && + A_{{\theta}'}{\Delta} \left [ \frac{\eta}{r'} \frac{\partial v'_{r'}}{\partial {\theta}'} \right ], \\ (F_{\eta})_{{\varphi}'} &=& A_{r'}{\Delta}\left [\eta \left ( r'\frac{\partial {\omega}'}{\partial r'}\sin{\theta}'+ \frac{1}{r'\sin{\theta}'}\frac {\partial v'_{r'}}{\partial {\varphi}'} \right ) \right ]\nonumber \\ &&+ A_{{\varphi}'}{\Delta} \left [\eta \left ( -\frac{2}{3}r' \frac {\partial}{\partial r'}\left ( \frac{v'_{r'}} {r'} \right ) + \frac{4}{3}\frac{\partial {\omega}'}{\partial {\varphi}'} \right ) \right ]\nonumber \\ \label{ffivis} && + A_{{\theta}'}{\Delta} \left [\eta \frac{\partial {\omega}'}{\partial {\theta}'}\sin{\theta}' \right ], \end{eqnarray}$ with Δ meaning the difference of values of the function inside a square parenthesis computed at the corresponding lateral faces in the direction given by the lateral area factor.

In our macroscopic element description, for the evaluation of the several terms in this surface integration we consider as important the gradients across the lateral faces of an element and ignore local gradients along these faces. Thus, given that the density drops to zero at the outer face and the radial velocity is also zero at the inner rigid region, we approximate the radial and azimuthal components of the viscous force as $\begin{matrix} (F_{η})_{r^{'}} & ≃ & A_{ϕ^{'}} Δ [\frac{η}{r^{'} \sin θ^{'}} \frac{\partial v_{r^{'}}^{'}}{\partial ϕ^{'}}] + A_{θ^{'}} Δ [\frac{η}{r^{'}} \frac{\partial v_{r^{'}}^{'}}{\partial θ^{'}}], \\ (F_{η})_{ϕ^{'}} & ≃ & - A_{r^{'}} [η r^{'} \frac{\partial ω^{'}}{\partial r^{'}} \sin θ^{'}] + \frac{4}{3} A_{ϕ^{'}} Δ [η \frac{\partial ω^{'}}{\partial ϕ^{'}}] \\ + A_{θ^{'}} Δ [η \frac{\partial ω^{'}}{\partial θ^{'}} \sin θ^{'}], \end{matrix}$ $\begin{eqnarray} \label{apfrvis} (F_{\eta})_{r'} &\simeq & A_{{\varphi}'}{\Delta} \left [ \frac{\eta}{r'\sin{\theta}'}\frac {\partial v'_{r'}}{\partial {\varphi}'} \right ] + A_{{\theta}'}{\Delta} \left [\frac{\eta}{r'} \frac{\partial v'_{r'}}{\partial {\theta}'} \right ], \\ (F_{\eta})_{{\varphi}'} &\simeq & -A_{r'}\left [\eta r'\frac{\partial {\omega}'}{\partial r'}\sin{\theta}' \right ] + \frac{4}{3}A_{{\varphi}'}{\Delta} \left [\eta \frac{\partial {\omega}'}{\partial {\varphi}'} \right ] \nonumber\\ \label{apffivis} && +A_{{\theta}'}{\Delta} \left [\eta \frac{\partial {\omega}'}{\partial {\theta}'}\sin{\theta}' \right ], \end{eqnarray}$ with the first term in Eq. (10) computed at the boundary with the inner rigid region.

The terms in Eq. (9) give second and third contributions to the radial acceleration, besides that in Eq. (4). Taking the coefficient of kinematic viscosity, ν, to be the same in all the elements, the acceleration corresponding to the first term is approximated as in Eq. (11) of Paper II $(a_{⋆ r^{'} 2})_{ij} ≃ \frac{ν}{l_{ϕ_{ij}^{'}}^{2}} [v_{{r^{'}}_{i,j + 1}}^{'} + v_{{r^{'}}_{i,j - 1}}^{'} - 2 {v_{{r^{'}}_{ij}}^{'}}^{]},$ $\begin{equation} (a_{{\star}r'2})_{ij} \simeq \frac{\nu} {l^2_{{\varphi}'_{ij}}} \left [ v'_{{r'}_{i,j+1}} + v'_{{r'}_{i,j-1}} -2 v'_{{r'}_{ij}} \right ], \label{aesr2} \end{equation}$ (11)likewise, the second term in Eq. (9) gives the acceleration $(a_{⋆ r^{'} 3})_{ij} ≃ \frac{ν}{l_{θ_{ij}^{'}}^{2}} [v_{{r^{'}}_{i + 1,j}}^{' *} + v_{{r^{'}}_{i - 1,j}}^{' *} - 2 {v_{{r^{'}}_{ij}}^{'}}^{]},$ $\begin{equation} (a_{{\star}r'3})_{ij} \simeq \frac{\nu} {l^2_{{\theta}'_{ij}}} \left [ v'^{\ast}_{{r'}_{i+1,j}} + v'^{\ast}_{{r'}_{i-1,j}} -2 v'_{{r'}_{ij}} \right ], \label{aesr3} \end{equation}$ (12)with $v_{{r^{'}}_{i - 1,j}}^{' *}$ $\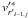hbox{$v'^{\ast}_{{r'}_{i-1,j}}$}$ , $v_{{r^{'}}_{i + 1,j}}^{' *}$ $\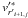hbox{$v'^{\ast}_{{r'}_{i+1,j}}$}$ the mean radial velocities of the elements in the polar direction adjacent to the element ij.

In the first term of Eq. (10) we approximate 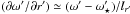$(\partial ω^{'} / \partial r^{'}) ≃ (ω^{'} - ω_{⋆}^{'}) / l_{r^{'}}$ $\hbox{$(\partial {\omega}'/\partial r') \simeq ({\omega}'-{\omega}'_{\star}) /l_{r'}$}$ , with 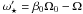$ω_{⋆}^{'} = β_{0} Ω_{0} - Ω$ $\hbox{${\omega}'_{\star} = {\beta}_0{\Omega}_0-\Omega$}$ the angular velocity of the inner stellar region as measured in the primed non-inertial frame. In the second term we make a similar approximation as that used to obtain Eq. (11) and ignore the factor 4/3. Thus, the corresponding accelerations are $\begin{matrix} (a_{⋆ ϕ^{'} 2})_{ij} & ≃ & - \frac{ν}{l_{r_{ij}^{'}}^{2}} (r_{ij}^{'} - \frac{1}{2} l_{r_{ij}^{'}}) [\frac{v_{ϕ_{ij}^{'}}^{'}}{r_{ij}^{'}} - (β_{0} Ω_{0} - Ω) \sin θ_{i}^{'}], \\ (a_{⋆ ϕ^{'} 3})_{ij} & ≃ & \frac{ν}{l_{ϕ_{ij}^{'}}^{2}} [v_{ϕ_{i,j + 1}^{'}}^{'} + v_{ϕ_{i,j - 1}^{'}}^{'} - 2 v_{ϕ_{ij}^{'}}^{'}], \end{matrix}$ $\begin{eqnarray} \label{aesfi2} (a_{{\star}{\varphi}'2})_{ij} &\simeq& - \frac{\nu} {l^2_{r'_{ij}}} \left( r'_{ij}- \frac{1}{2}l_{r'_{ij}}\right) \left [ \frac {v'_{{\varphi}'_{ij}}}{r'_{ij}} - \left ( {\beta}_0{\Omega}_0 - \Omega \right )\sin{\theta}'_i \right ], \\ \label{aesfi3} (a_{{\star}{\varphi}'3})_{ij} &\simeq& \frac{\nu} {l^2_{{\varphi}'_{ij}}} \left [ v'_{{\varphi}'_{i,j+1}} + v'_{{\varphi}'_{i,j-1}} - 2 v'_{{\varphi}'_{ij}} \right ], \end{eqnarray}$ and finally, the last term in Eq. (10) gives the azimuthal acceleration $(a_{⋆ ϕ^{'} 4})_{ij} ≃ \frac{ν r_{ij}^{'}}{l_{θ_{ij}^{'}}^{2}} [(ω_{i + 1,j}^{' *} - ω_{ij}^{'}) \sin θ_{i,i + 1}^{'} - (ω_{ij}^{'} - ω_{i - 1,j}^{' *}) \sin {θ_{i - 1,i}^{'}}^{]},$ $\begin{equation} (a_{{\star}{\varphi}'4})_{ij}\! \simeq\! \frac {{\nu}r'_{ij}}{l^2_{{\theta}'_{ij}}}\! \left [ ({\omega}'^{\ast}_{i+1,j}\!-\!{\omega}'_{ij})\sin{\theta}'_{i,i+1}\!-\! 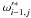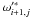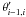({\omega}'_{ij}\!-\!{\omega}'^{\ast}_{i-1,j})\sin{\theta}'_{i-1,i} \right ], \label{aesfi4} \end{equation}$ (15)with $ω_{i - 1,j}^{' *}$ $\hbox{${\omega}'^{\ast}_{i-1,j}$}$ , $ω_{i + 1,j}^{' *}$ $\hbox{${\omega}'^{\ast}_{i+1,j}$}$ the mean angular velocities of the elements in the polar direction adjacent to the element ij, and $θ_{i - 1,i}^{'}$ $\hbox{${\theta}'_{i-1,i}$}$ , $θ_{i,i + 1}^{'}$ $\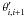hbox{${\theta}'_{i,i+1}$}$ the polar angles of the boundaries of the adjacent parallels.

2.2. Equations of motion

The acceleration a_⋆ of a surface element produced by gas pressure and viscous forces has a radial component a⋆r′ given by the sum of Eqs. (4), (11), and (12), and the corresponding azimuthal component a⋆ϕ′ is the sum of Eqs. (5), (13), (14), and (15). In the primed non-inertial reference frame, the pair of radial and azimuthal equations of motion of a surface element are $\begin{matrix} {r^{'}}_{¨} & = & - \frac{G m_{1}}{{r^{'}}^{2}} - G m_{2} [\frac{r^{'} - r_{21} \sin θ^{'} \cos ϕ^{'}}{{({r^{'}}^{2} + r_{21}^{2} - 2 r^{'} r_{21} \sin θ^{'} \cos ϕ^{'})}^{3 / 2}} \\ {ϕ^{'}}_{¨} & = & \frac{1}{r^{'} \sin θ^{'}} {a ⋆ ϕ' - G m_{2} [\frac{r_{21}}{{({r^{'}}^{2} + r_{21}^{2} - 2 r^{'} r_{21} \sin θ^{'} \cos ϕ^{'})}^{3 / 2}} \end{matrix}$ $\begin{eqnarray} \ddot{r}' & = & -\, \frac{Gm_1}{{r'}^2}- Gm_2 \Bigg [ \frac{r'-r_{21}\sin{\theta}'\cos{\varphi}'} {\left ({r'}^2+r^2_{21}-2r'r_{21}\sin{\theta}'\cos{\varphi}' \right )^{3/2}} \nonumber \\ &&+\,\frac{\sin{\theta}'\cos{\varphi}'}{r^2_{21}} \Bigg ] + a_{{\star}r'}+(\Omega + \dot{\varphi}')^2r'\sin^2{\theta}', \label{emr} \\ \ddot{\varphi}' & = & \frac{1}{r'\sin{\theta}'} \left \{ a_{{\star}{\varphi}'}- Gm_2 \left [ \frac{r_{21}} {\left ({r'}^2+r^2_{21}-2r'r_{21}\sin{\theta}'\cos{\varphi}' \right )^{3/2}}\right.\right. \nonumber \\&&\left.\left.\phantom{\frac{r_{21}} {\left ({r'}^2+r^2_{21}-2r'r_{21}\sin{\theta}'\cos{\varphi}' \right )^{3/2}}}\hspace{-4.9cm}-\, \frac{1}{r^2_{21}} \right ]\sin{\varphi}' \right \} -\dot{\Omega} - \frac{2}{r'}(\Omega + \dot{\varphi}')\dot{r}'. \label{emfi} \end{eqnarray}$ All pairs of equations in all surface elements are solved simultaneously, along with the orbital motion of m₂ around m₁. The values of r₂₁, Ω, $\hbox{$\dot{\Omega}$}$ are obtained from this orbital motion. We used a seventh-order Runge-Kutta algorithm (Fehlberg 1968) to solve the equations. With some forty parallels covering the stellar surface, more than 10⁴ elements are employed.

2.3. Method for Ė calculation

The rate of energy dissipation per unit volume can be expressed in terms of the tensor in Eq. (6), and is given by the matrix product (e.g., McQuarrie 1976) 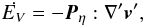$\dot{E_{V}} = - P η : \nabla^{'} v',$ $\begin{equation} \dot{E_V} = - \vec{P}_{\eta}:{\nabla}' \vec{v}', \label{dis1} \end{equation}$ (18)which can be written as $\dot{E_{V}} = - 2 η [\frac{1}{3} {(\nabla^{'} \cdot v')}^{2} - {(\nabla^{'} v')}_{s} : {(\nabla^{'} v')}_{s}],$ $\begin{equation} \dot{E_V} = -2\eta \left [\frac{1}{3} \left ({\nabla}' \cdot \vec{v}' \right )^2 - \left ( {\nabla}' \vec{v}' \right )_s : \left ( {\nabla}' \vec{v}' \right )_s \right ], \label{dis2} \end{equation}$ (19)where $(\nabla^{'} v {}^{'})_{s}$ $\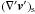hbox{$(\nabla'\vec{v}')_{\rm s}$}$ is the symmetric tensor $(\nabla^{'} v {}^{'})_{s} = \frac{1}{2} [\nabla^{'} v^{'} + (\nabla^{'} v {}^{'})^{trp}]$ $\hbox{$({\nabla}'\vec{v}')_{\rm s} = \frac{1}{2} [{\nabla}'\vec{v}'+ ({\nabla}'\vec{v}')^{\rm trp}]$}$ .

The computations in our model show that the gradient in azimuthal velocity dominates that in radial velocity. Thus, Eq. (19) can be approximated as 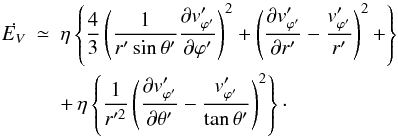$\begin{matrix} \dot{E_{V}} & ≃ & η \begin{matrix} ⎧ \\ ⎪ \\ ⎪ \\ ⎨ \\ ⎪ \\ ⎪ \\ ⎩ \end{matrix} \frac{4}{3} {(\frac{1}{r^{'} \sin θ^{'}} \frac{\partial v_{ϕ^{'}}^{'}}{\partial ϕ^{'}})}^{2} + {(\frac{\partial v_{ϕ^{'}}^{'}}{\partial r^{'}} - \frac{v_{ϕ^{'}}^{'}}{r^{'}})}^{2} + \begin{matrix} ⎫ \\ ⎪ \\ ⎪ \\ ⎬ \\ ⎪ \\ ⎪ \\ ⎭ \end{matrix} \end{matrix}$ $\begin{eqnarray} \dot{E_V}&\simeq&{\eta} \left \{ \frac{4}{3} \left ( \frac{1}{r'\sin{\theta}'} \frac{\partial v'_{{\varphi}'}}{\partial {\varphi}'} \right )^2 + \left (\frac{\partial v'_{{\varphi}'}}{\partial r'} - \frac{v'_{{\varphi}'}}{r'}\right )^2 +\right\} \nonumber\\ &&+\, {\eta}\left \{\frac{1}{r'^2} \left (\frac{\partial v'_{{\varphi}'}}{\partial{\theta}'} - \frac {v'_{{\varphi}'}}{\tan{\theta}'} \right )^2 \right \}\cdot \label{dis3} \end{eqnarray}$ (20)Now with $ω^{'} = v_{ϕ^{'}}^{'} / r^{'} \sin θ^{'}$ $\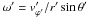hbox{${\omega}' = v'_{{\varphi}'}/r'\sin{\theta}'$}$ , it follows that $\frac{\partial v_{ϕ^{'}}^{'}}{\partial r^{'}} - \frac{v_{ϕ^{'}}^{'}}{r^{'}} = r^{'} \frac{\partial ω^{'}}{\partial r^{'}} \sin θ^{'},$ $\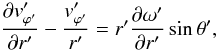begin{equation} \frac{\partial v'_{{\varphi}'}}{\partial r'} - \frac{v'_{{\varphi}'}}{r'} = r' \frac{\partial {\omega}'}{\partial r'}\sin{\theta}', \label{trans1} \end{equation}$ (21) $\frac{\partial v_{ϕ^{'}}^{'}}{\partial ϕ^{'}} = r^{'} \frac{\partial ω^{'}}{\partial ϕ^{'}} \sin θ^{'},$ $\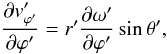begin{equation} \frac{\partial v'_{{\varphi}'}}{\partial {\varphi}'} = r' \frac{\partial {\omega}'}{\partial {\varphi}'}\sin{\theta}', \label{trans2} \end{equation}$ (22) $\frac{\partial v_{ϕ^{'}}^{'}}{\partial θ^{'}} - \frac{v_{ϕ^{'}}^{'}}{\tan θ^{'}} = r^{'} \frac{\partial ω^{'}}{\partial θ^{'}} \sin θ^{'},$ $\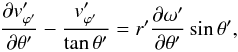begin{equation} \frac{\partial v'_{{\varphi}'}}{\partial {\theta}'} - \frac{v'_{{\varphi}'}}{\tan{\theta}'} = r' \frac{\partial {\omega}'}{\partial {\theta}'}\sin{\theta}', \label{trans3} \end{equation}$ (23)and Eq. (20) reduces to $\dot{E_{V}} ≃ η \begin{matrix} ⎧ \\ ⎪ \\ ⎪ \\ ⎨ \\ ⎪ \\ ⎪ \\ ⎩ \end{matrix} \frac{4}{3} {(\frac{\partial ω^{'}}{\partial ϕ^{'}})}^{2} + [r^{' 2} {(\frac{\partial ω^{'}}{\partial r^{'}})}^{2} + {(\frac{\partial ω^{'}}{\partial θ^{'}})}^{2}] \sin^{2} θ^{'} \begin{matrix} ⎫ \\ ⎪ \\ ⎪ \\ ⎬ \\ ⎪ \\ ⎪ \\ ⎭ \end{matrix} .$ $\begin{equation} \dot{E_V} \simeq {\eta} \left \{ \frac{4}{3} \left ( \frac{\partial {\omega}'}{\partial {\varphi}'} \right )^2 + \left [ r'^2 \left ( \frac{\partial {\omega}'}{\partial r'} \right )^2 + \left ( \frac{\partial {\omega}'}{\partial {\theta}'} \right )^2 \right ]{\sin}^2{\theta}' \right \}. 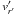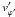\label{dis4} \end{equation}$ (24)For an accretion disk (θ′ = π/2, and the primed reference frame is taken as inertial in this case) with ω′ a function only of the radial distance r′, and $v_{r^{'}}^{'}$ $\hbox{$v'_{r'}$}$ small compared with $v_{ϕ^{'}}^{'}$ $\hbox{$v'_{{\varphi}'}$}$ , Eq. (24) gives 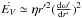$\dot{E_{V}} ≃ η r^{' 2} (\frac{d ω^{'}}{d r^{'}})^{2}$ $\hbox{$\dot{E_V} \simeq {\eta}r'^2(\frac{{\rm d}{\omega}'}{{\rm d}r'})^2$}$ (Lynden-Bell & Pringle 1974); this result was used in Eq. (14) of Toledano et al. (2007), multiplied by the volume of an element.

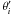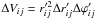
The j-surface element on the parallel with polar angle $θ_{i}^{'}$ $\hbox{${\theta}'_i$}$ has a volume 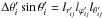$Δ V_{ij} = r_{ij}^{' 2} Δ r_{ij}^{'} Δ ϕ_{ij}^{'}$ $\hbox{${\Delta}V_{ij} = r'^2_{ij}{\Delta}r'_{ij}{\Delta}{\varphi}'_{ij}$}$ $Δ θ_{i}^{'} \sin θ_{i}^{'} = l_{r_{ij}^{'}} l_{ϕ_{ij}^{'}} l_{θ_{ij}^{'}}$ $\hbox{${\Delta}{\theta}'_i\sin{\theta}'_i = l_{r'_{ij}}l_{{\varphi}'_{ij}} l_{{\theta}'_{ij}}$}$ , with 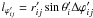$l_{ϕ_{ij}^{'}} = r_{ij}^{'} \sin θ_{i}^{'} Δ ϕ_{ij}^{'}$ $\hbox{$l_{{\varphi}'_{ij}} = r'_{ij}\sin{\theta}'_i{\Delta}{\varphi}'_{ij}$}$ and $l_{θ_{ij}^{'}} = r_{ij}^{'} Δ θ_{i}^{'}$ $\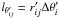hbox{$l_{{\theta}'_{ij}} = r'_{ij}{\Delta}{\theta}'_i$}$ . The rate of energy dissipation in the element is Ė_ij = Ė_VijΔV_ij, with Ė_Vij the evaluation of Eq. (24) at the position of the element.

As already done to approximate Eq. (10), we take $\begin{matrix} {(\frac{\partial ω^{'}}{\partial r^{'}})}_{ij} & = & \frac{ω_{ij}^{'} - ω_{⋆}^{'}}{l_{r_{ij}^{'}}}, \\ {(\frac{\partial ω^{'}}{\partial ϕ^{'}})}_{ij} & = \\ {(\frac{\partial ω^{'}}{\partial θ^{'}})}_{ij} & = & \frac{\frac{1}{2} (ω_{i + 1,j}^{' *} - ω_{i - 1,j}^{' *})}{l_{θ_{ij}^{'}} / r_{ij}^{'}}, \end{matrix}$ $\begin{eqnarray} \label{par1} \left (\frac{\partial {\omega}'}{\partial r'} \right )_{ij} &=& \frac{{\omega}'_{ij}-{\omega}'_{\star}}{l_{r'_{ij}}}, \\ \left (\frac{\partial {\omega}'}{\partial {\varphi}'} \right )_{ij} &=& \frac{\frac{1}{2} \left ({\omega}'_{i,j+1}-{\omega}'_{i,j-1} \right )}{l_{{\varphi}'_{ij}}/r'_{ij}\sin{\theta}'_i}, \label{par2} \\ \label{par3} \left (\frac{\partial {\omega}'}{\partial {\theta}'} \right )_{ij} &=& \frac{\frac{1}{2} \left ({\omega}'^{\ast}_{i+1,j}- {\omega}'^{\ast}_{i-1,j} \right )}{l_{{\theta}'_{ij}}/r'_{ij}}, \end{eqnarray}$ Eqs. (25)–(27) are inserted in Eq. (24), giving Ė_Vij which has three contributions (Ė_Vij)_r′, (Ė_Vij)_ϕ′, and (Ė_Vij)_θ′, corresponding to the three gradients of angular velocity in spherical coordinates. The total rate of energy dissipation in the surface layer is $Ė = \sum i,j [{({Ė}_{Vij})}_{r^{'}} + {({Ė}_{Vij})}_{ϕ^{'}} + {({Ė}_{Vij})}_{θ^{'}}] Δ V_{ij} .$ $\begin{equation} {\dot{E}} = \sum_{i,j}^{} \left [\left ({\dot{E}}_{Vij} \right )_{r'} + \left ({\dot{E}}_{Vij} \right )_{{\varphi}'} + \left ({\dot{E}}_{Vij} \right )_{{\theta}'} \right ]{\Delta}V_{ij}. \label{etot} \end{equation}$ (28)In our computations the major contribution to Ė comes from (Ė_Vij)_r′.

3. Energy dissipation rates

3.1. Sample Ė(ϕ′,θ′) calculation

We can compute Ė_ij, the rate of energy dissipation in the element j in a given parallel i, as a function of the azimuthal angle ϕ′ of the element. Also, it is of interest to compute Ė_i, the total rate of energy dissipation in the parallel i, as a function of the corresponding polar angle θ′. As an example, in this section we show results from our model in the particular polytropic case with n = 1.5 and using a surface layer depth ΔR₁/R₁ = 0.03, with corresponding average mass density ρ = 8.66 × 10^-7 gr cm^-3. The other input parameters are M₁ = 5 M_⊙, M₂ = 4 M_⊙, R₁ = 3.2 R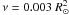_⊙, $ν = 0.003 R_{⊙}^{2}$ $\hbox{$\nu = 0.003 ~R^2_{\odot}$}$ day^-1, an orbital period P = 10 days (a = 40.62 R_⊙), and with two different values β₀ = 1.2 and 2.

Fig. 1

Rate of energy dissipation Ė_ij as a function of ϕ′ in a few selected parallels, for the n = 1.5 polytropic case ΔR₁/R₁ = 0.03, ν = 0.003 $R_{⊙}^{2}$ $\hbox{$R^2_{\odot}$}$ day^-1, ρ = 8.66 × 10^-7 g cm^-3, orbital period P = 10 days (a = 40.62 R_⊙), and β₀ = 1.2. The top curve shows results for the stellar equator, and following curves from top to bottom correspond to parallels with θ′ ≈ 81°, 73°, 64°, 55°, 46°, 38°, 29°, and 20°. Calculations with β₀ = 2.0 yield identical curves, but the Ė_ij values are higher for by ~ 1.5 mag.

Figure 1 shows the run of Ė_ij as a function of ϕ′ in some selected parallels for β₀ = 1.2. The upper curve corresponds to the stellar equator, θ′ = 90°, and following curves from top to bottom give results for the parallels with θ′ ≈ 81°, 73°, 64°, 55°, 46°, 38°, 29° and 20°. A very similar results is obtained for the β₀ = 2 calculation, although the energy dissipation rates are significantly larger.

Fig. 2

Rate of energy dissipation in the parallel i as a function of its polar angle, corresponding to the computations in Fig. 1. Results with β₀ = 1.2 and 2 are shown with empty and filled squares, respectively. The continuous lines show functions with a sin⁷θ′ dependence.

Figure 2 shows the total rate of energy dissipation in the parallel i, Ė_i, as a function of its polar angle. Both cases β₀ = 1.2 and 2 are shown in this figure, with empty and filled squares, respectively. The continuous lines show functions with a sin⁷θ′ dependence. Thus, our computations give the approximate dependence 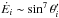$Ė_{i} ~ \sin^{7} θ_{i}^{'}$ $\hbox{$\dot{E}_i \sim \sin^7{\theta}'_i$}$ , excluding polar angles in a region of approximately 10° around the poles. 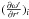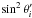This implies that in our model $(\frac{\partial ω^{'}}{\partial r^{'}})_{i}$ $\hbox{$(\frac{\partial {\omega}'}{\partial r'})_i$}$ has a $\sin^{2} θ_{i}^{'}$ $\hbox{$\sin^2{\theta}'_i$}$ dependence, thus the dominant radial gradient in Eq. 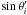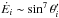(24) integrated in the volume of the parallel, which has a $\sin θ_{i}^{'}$ $\hbox{$\sin{\theta}'_i$}$ dependence, gives $Ė_{i} ~ \sin^{7} θ_{i}^{'}$ $\hbox{$\dot{E}_i \sim \sin^7{\theta}'_i$}$ . Concerning this result, there is a theoretical study by Scharlemann (1981), which gives the tidal velocity field in a differentially rotating convective envelope of a component in a binary system in circular relative orbit, in the limit β₀ → 1. For the case in which the star rotates uniformly, Eq. (40c) of Scharlemann (1981) gives the azimuthal component of the tidal velocity field. 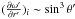This equation implies, in our notation, $(\frac{\partial ω^{'}}{\partial r^{'}})_{i} ~ \sin^{3} θ^{'}$ $\hbox{$(\frac{\partial {\omega}'}{\partial r'})_i \sim \sin^3{\theta}'$}$ , which differs from our result. Yet we find in our computations with β₀ = 1.2, 2.0 that the surface layer does not rotate uniformly, contrary to the assumption in Scharlemann’s equation. Thus, the difference between the two results most likely stems from Scharlemann’s assumption of uniform rotation over the stellar surface which, for β ≠ 1, is incorrect.

3.2. Dependence of Ė on orbital separation

In this section, we analyze the behavior of the total rate of energy dissipation, Ė for binary system models with different orbital separations and a variety of orbital eccentricities.

3.2.1. Circular orbits

As in Toledano et al. (2007), we adopt as the test binary system one with masses m₁ = 5 M_⊙ and m₂ = 4 M_⊙; m₁ with a radius R₁ = 3.2 R_⊙. The analysis was made for circular relative orbits with several different values of orbital separation a. The energy dissipation rate given by Eq. (28) was computed in m₁; we used 20 parallels distributed between the equator and polar angle 85°, with more than 10⁴ surface elements, and a polytropic index n = 1.5. In the coefficient of dynamic viscosity η = νρ the same approach as that of Toledano et al. (2007) was adopted. That is, the average mass density for the surface layer, ΔR₁/R₁, is taken from a BEC stellar structure model computation⁴. For this paper we used a model⁵ kindly provided by Brott (2010, priv. comm.). The value of the kinematic viscosity ν was taken as the lowest value allowed by the code (see discussion in Harrington et al. 2009, regarding this parameter). For the shortest period binary models with circular orbits, this value is ν = 0.003 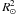$R_{⊙}^{2}$ $\hbox{$R^2_{\odot}$}$ day^-1, which we adopted for the whole set of circular orbit models discussed in this section. Three different values of the thickness of the surface layer in m₁ were considered, ΔR₁/R₁ = 0.01, 0.03, 0.06⁶. The corresponding average mass densities are, 1.19 × 10^-8, 1.68 × 10^-7 and 8.66 × 10^-7 g cm^-3, respectively. The computations were made for two values β₀ = 1.2, 2.0 of the synchronicity parameter.

Fig. 3

Energy dissipation in m₁ as a function of the separation a of the circular orbit. A polytropic index n = 1.5 is used. Empty symbols correspond to β₀ = 1.2 and filled symbols to β₀ = 2.0. The correspondence with the layer thickness ΔR₁/R₁ is, in triangles: ΔR₁/R₁ = 0.01, in squares: ΔR₁/R₁ = 0.03, in pentagons: ΔR₁/R₁ = 0.06. The continuous line is a function with an a^-9 dependence on a.

Figure 3 shows the energy dissipation Ė in m₁ as a function of the radius of the circular orbit. Empty symbols correspond to β₀ = 1.2 and filled symbols to β₀ = 2.0. Triangles, squares, and pentagons show results for ΔR₁/R₁ = 0.01, 0.03, and 0.06, respectively. A clear linear behavior is obtained on this log-log plot. For comparison, the continuous line in this figure shows a function with an a^-9 dependence on the orbital radius a. The data in the three cases ΔR₁/R₁ would shift vertically for different values of the mass density and viscosity, but the functional dependence on orbital separation remains the same.

3.2.2. Elliptic orbits

Elliptical orbit binary systems differ from those in circular orbits in that the synchronicity parameter, β, does not remain constant over the orbital cycle. This is because of the variation of the orbital angular velocity, Ω. The computation takes into account the changing value of β, but we characterize each model by its synchronicity parameter at periastron, β₀.

The energy dissipation rates for a grid of elliptical orbit binary systems were computed following a similar procedure as in Sect. 3.2.1 for the m₁ + m₂ = 5 + 4 M_⊙ binary system, but in this case eccentricities e = 0.1, 0.3, 0.5 0.7 and 0.8 were assigned, and 20 latitude grid points were used in each hemisphere of m₁. The remaining parameters were held constant: R₁ = 3.2, β₀ = 1.2, ΔR₁/R₁ = 0.06, n = 1.5, 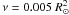$ν = 0.005 R_{⊙}^{2}$ $\hbox{$\nu=0.005~R^2_\odot$}$ day^-1. The changing separation of the two stars over the orbital cycle leads to a strong dependence of the energy dissipation rate on the orbital phase. Thus, in order to assign a value of Ė to each model calculation, an average value of the energy dissipation rate over orbital cycle, Ė_ave, was computed by numerically integrating Ė obtained at many phases distributed over the orbital cycle, and then dividing by the corresponding orbital period. The values of Ė_ave are plotted in Fig. 4 as a function of the major semi-axis of the orbit.

Fig. 4

Energy dissipation rates (in erg s^-1) from our model calculations for β₀ = 1.2 and different eccentricities as indicated. The dashed lines show the absolute value of Ė_orb given by Eq. (A31) of Hut (1981), as written in our Eq. (30). The dotted lines connect the points corresponding to each eccentricity. The short dot-dashed lines show the values of Ė_Hut for e = 0.8 and lag angles α = 10° and 50°.

Two aspects of this figure stand out: 1) there is a “family” of curves, one for each value of the eccentricity; 2) in each case, the scaling of Ė_ave with a does not follow a unique linear (in the log-log plane) plot, as in the circular orbit case. Instead, for very short orbital periods, the slope is steeper and for very long periods, the slope is flatter than the Ė_ave ~ a^-9 relation for circular orbits. It is also interesting to note that the departure from this relation grows with increasing orbital eccentricity.

3.3. Comparison with the “weak friction” model

Hut (1981) provided a derivation of the differential equations for the tidal evolution under the “weak friction, equilibrium tide” model representation for the tidal interaction (Darwin 1880; Alexander 1973). The fundamental assumption of this model is that the tidal bulges that are raised by the external perturbing potential are only slightly misaligned with respect to the axis that connects the two stars. The system is then driven toward an equilibrium configuration through the action of the torques acting on the “retarded body”. The misalignment of the bulges is caused by dissipation (i.e., friction) in the perturbed star. Hut’s formalism includes high order terms in the orbital eccentricity, as required to properly assess the energy dissipation rates in very eccentric systems⁷. In this section we test our model by computing the energy dissipation rates for a 5 + 4 M_⊙ polytropic (n = 1.5) binary system with a primary star’s radius R₁ = 3.2 R_⊙ for a range in orbital separations and eccentricities. Each binary system of the grid is characterized by the energy dissipation rates averaged over the orbital cycle, Ė_ave. We show that for a variety of orbital eccentricities, the behavior of Ė_ave is consistent with the predicted energy dissipation rates in the “weak friction” approximation given by Hut (1981) within the domain of applicability of this approximation. Our model also adequately predicts the pseudo-synchronization angular velocity obtained by Hut (1981) for moderate eccentricities (e ≤ 0.3).

3.3.1. Energy dissipation rates

The rate of energy dissipation within the primary star associated with the decrease in the orbital and rotation energy in the system is given by Hut (1981) in his Eq. (A31) $\begin{matrix} Ė Hut = - 3 \frac{k}{T} G (m_{1} + m_{2}) (\frac{m_{2}^{2}}{m_{1}}) (\frac{R_{1}^{8}}{a^{9}}) (1 - e^{2})^{- 15 / 2} [A - 2 Bx + C x^{2}] \end{matrix}$ $\begin{eqnarray} \dot{E}_{\rm Hut} = -3 \frac{k}{T} G(m_1\!+\!m_2)\left ( \frac{m_2^2}{m_1} \right ) \left(\frac{R_1^8}{a^9}\right ) (1\!-\!e^2 )^{-15/2} \left [A\!-\!2Bx\!+\!Cx^2 \right ] \nonumber \end{eqnarray}$ (28)where k is a constant that depends on the stellar structure, and x = ω/n, with ω the angular rotation velocity of m₁ and n = n_p(1 − e²)^3/2/(1 + e)² the mean orbital angular velocity, with n_p the orbital angular velocity at periastron. 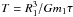$T = R_{1}^{3} / G m_{1} τ$ $\hbox{$T=R_1^3/Gm_1\tau$}$ , where τ is the lag time, and $\begin{matrix} A & = & 1 + \frac{31}{2} e^{2} + \frac{255}{8} e^{4} + \frac{185}{16} e^{6} + \frac{25}{64} e^{8}, \\ B & = & 1 + \frac{15}{2} e^{2} + \frac{45}{8} e^{4} + \frac{5}{16} e^{6}, \\ C & = & 1 + 3 e^{2} + \frac{3}{8} e^{4} . 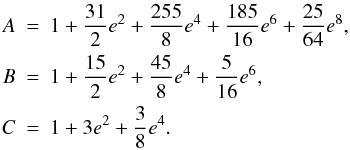\end{matrix}$ $\begin{eqnarray} A&=&1+\frac{31}{2}e^2+\frac{255}{8}e^4+\frac{185}{16}e^6+\frac{25}{64}e^8, \nonumber \\ B&=&1+\frac{15}{2}e^2+ \frac{45}{8}e^4+ \frac{5}{16}e^6, \nonumber \\ C&=&1 +3 e^2+\frac{3}{8}e^4. \end{eqnarray}$ (29)After converting masses and distances to solar units, and writing ω/n in terms of n_p, and recalling that ω/n_p = β₀, the above equation can be rewritten as $\begin{matrix} Ė Hut & = & - 4.4 \times 10^{42} kτ (\frac{m_{1} + m_{2}}{M_{⊙}}) {(\frac{m_{2}}{M_{⊙}})}^{2} {(\frac{R_{1}}{R_{⊙}})}^{5} {(\frac{a}{R_{⊙}})}^{-9} \\ \times (1 - e^{2})^{- 15 / 2} [A - 2 Bx + C x^{2}], \end{matrix}$ $\begin{eqnarray} \dot{E}_{\rm Hut}& =& -4.4\times10^{42} k \tau \left ( \frac{m_1+m_2}{M_\odot} \right ) \left (\frac{m_2}{M_\odot} \right)^2 \left (\frac{R_1}{R_\odot} \right )^5 \left(\frac{a}{R_\odot} \right)^{-9} \nonumber \\ \label{eqhut2} &&\times (1-e^2)^{-15/2} \left [A - 2 Bx+Cx^2 \right ], \end{eqnarray}$ (30)with Ė_Hut given in erg s^-1 and x = β₀(1 + e)².

For the lag time, Hut (1981, Eq. (4)) gives τ = α/(ω − Ω), where ω and Ω are the rotational and instantaneous orbital angular velocity, respectively. α is the lag angle, and is measured from the line that joins the centers of m₁ and m₂. This expression may be re-written in terms of the instantaneous synchronicity parameter, β, as τ = α/Ω(β − 1).

In eccentric binary systems, α is generally very small around periastron, but it can be quite large at other orbital phases⁸. At the same time, the amplitude of the tidal bulges is largest around periastron and, given that this is when m₁ and m₂ have their closest approach, the tidal interaction effects are strongest. Hence, for the purpose of these exploratory calculations, we now make the following approximation: To compute the energy dissipation rates using Eq. (30), we adopt τ ~ α_per/Ω₀(β₀ − 1), where α_per is the lag angle at periastron which we assume is relatively small, and here tentatively adopt α = 1°. We thus also use β = β₀. Using Kepler’s relation Ω₀ = G^1/2(m₁ + m₂)^1/2a^− 3/2(1 + e)²(1 − e²)^− 3/2 and converting to solar units, 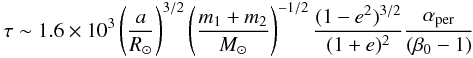$\begin{matrix} τ ~ 1.6 \times 10^{3} {(\frac{a}{R_{⊙}})}^{3 / 2} {(\frac{m_{1} + m_{2}}{M_{⊙}})}^{- 1 / 2} \frac{(1 - e^{2})^{3 / 2}}{(1 + e)^{2}} \frac{α_{per}}{(β_{0} - 1)} \end{matrix}$ $\begin{eqnarray} \tau \sim 1.6\times10^3 \left(\frac{a}{R_\odot}\right)^{3/2} \left (\frac{m_1+m_2}{M_\odot}\right )^{-1/2} \frac{(1-e^2)^{3/2}}{(1+e)^2} \frac{\alpha_{\rm per}}{(\beta_0-1)} \label{eqT} \end{eqnarray}$ (31)with α_per given in radians and τ is in seconds. Note that when Eq. (31) is introduced into Eq. (30), the dependence of Ė_Hut on orbital separation ~ a^− 15/2, thus flattening the slope from the a^-9 relation that holds for a circular orbit.

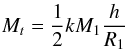For the value of k, we use the expression given in Lecar et al. (1976, their Eq. (2)) for the mass in the tidal bulge, M_t: $\begin{matrix} M_{t} = \frac{1}{2} k M_{1} \frac{h}{R_{1}} \end{matrix}$ $\begin{eqnarray} M_t=\frac{1}{2} k M_1 \frac{h}{R_1} \label{k_lecar} \end{eqnarray}$ (32)where h is the height of the tide. Consider, for example, the model binary system with e = 0.8, P = 15 d, from the grid of models discussed in the previous section. The height of the tide at periastron is ~ 0.03 R_⊙ (see below). The mass in the bulge is M_t = f_tM_layer, where f_t is the fraction of the mass in the outer layer, M_layer, that goes into to the bulge. 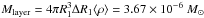For the particular case in question, $M_{layer} = 4 π R_{1}^{3} Δ R_{1} ⟨ ρ ⟩ = 3.67 \times 10^{-6} M_{⊙}$ $\hbox{$M_{\rm layer}=4\pi R_1^3 \Delta R_1 \langle \rho\rangle=3.67\times10^{-6}~M_\odot$}$ , where ΔR₁ = 0.06 R_⊙ is the layer thickness and ⟨ ρ ⟩ = 8.66 × 10^-7 g cm^-3, is the average density of the layer. The maximum in the primary bulge approximately extends over 20° in azimuth, so f_t ~ 10^-4. Hence, this estimate yields k ~ 10^-8.

With these considerations, we use Eq. (30) to estimate the energy dissipation rates in the “weak friction” approximation, Ė_Hut, for the binary model parameters m₁ = 5 M_⊙, m₂ = 4 M_⊙, R₁ = 3.2 R_⊙, β₀ = 1.2, and k = 5 × 10^-8. The dashed lines in Fig. 4 correspond to the absolute values of Ė_Hut given by Eq. (30). The coincidence between the general behavior of these lines and that of the numerical computations is encouraging. Note that no relative shift or scaling is introduced, and yet the relative separation between the curves corresponding to the different eccentricities is reproduced by our models. In addition, our model reproduces the general trend in the slope of the Ė_ave vs. a relation, particularly for large orbital separations. Thus, we find that our numerical calculation captures to a large extent the general scaling in the energy dissipation rates predicted analytically within the “weak friction” tidal model.

However, although the scaling with e predicted by Eq. (30) is adequately captured by our model, the dependence on a^− n, with n = const. is not satisfied. Specifically, there is a marked excess in Ė_ave for smaller orbital separations, with respect to Ė_Hut. Several factors may be responsible for this difference. First, the assumption of a constant lag angle, α, is quite inadequate. For example, assuming that for the e = 0.8 calculation α = 10° and 50°, instead of the 1° used to draw the dash lines, significantly higher Ė_Hut values are obtained⁹. This is illustrated by the short dashed lines in Fig. 4. Second, the applicability of the standard “equilibrium tide” model for high eccentricities is questionable (Efroimsky & Williams 2009). Finally, we note that our model assumes a spherical rigidly-rotating interior region, and that this approximation is less applicable for small orbital separations, where the deformation of the star is greater.

Fig. 5

Energy dissipation rates of the previous figure but here plotted as a function of the periastron distance, r_per. In this representation, the different curves for each eccentricity “collapse” onto a common region. The dashed lines show the absolute value of Ė_orb given by Eq. (A31) of Hut (1981) for e = 0.1 and 0.8, also plotted as a function of r_per. Symbols correspond to the different eccentricities: e = 0.00 (open triangles), 0.01 (filled triangles), 0.10 (small pentagons), 0.30 (large pentagons), 0.50 (crosses), 0.70 (stars) and 0.8 (filled pentagons).

It is interesting to note that if Ė is plotted as a function of r_per, the orbital separation at periastron, instead of the semi-major axis, the curves corresponding to the different eccentricities “collapse” toward a single curve. This is illustrated in Fig. 5. Thus, the periastron distance is a more convenient parameter for the purpose of analyzing the average energy dissipation rates than the semi-major axis.

3.3.2. Pseudo-synchronization angular velocity

Pseudo-synchronization in an eccentric binary is a term used to describe the state that is closest to an equilibrium configuration. Hut (1981) demonstrated that the rotational angular velocity for pseudo-synchronization, ω_ps < Ω₀, where Ω₀ is the orbital angular velocity at periastron. Specifically, 0.8 < ω_ps/Ω₀ < 1¹⁰.

We computed sets of models with e = 0.1, 0.3, 0.5 (P = 6 d) and 0.8 (P = 20 d) holding all other parameters fixed except for β₀, which was varied from ~ 0.4 to the highest value admitted by the calculation.¹¹ Figure 6 illustrates the dependence of Ė_ave on β₀. In all cases, there is a minimum in Ė_ave at a particular value (or range of values) of β₀. For e = 0.1 and 0.3, the minimum occurs around β₀ ~ 0.8–0.9, consistent with the “weak friction” approximation. For e = 0.5 and 0.8, however, the minimum occurs for 1.0 < β₀ < 1.4, a result that is likely related to the caveats already mentioned at the end of the previous section.

Fig. 6

Energy dissipation rates Ė_ave/10³⁵ ⟨ ρ ⟩ as a function of β₀ = ω/Ω₀ for four different eccentricities, e = 0.1 (top left), 0.3 (top right), 0.5 (bottom left) and 0.8 (bottom right). The first three cases are for an orbital period P = 6 d and the last is for 20 d. The ordinate is in units of 10³⁵ ⟨ ρ ⟩ erg s^-1, where ⟨ ρ ⟩ is the average density. The dotted line indicates the level of minimum Ė_ave which, for e = 0.1 and 0.3 coincides with the analytical results of Hut (1981).

4. Synchronization timescales

In this section we analyze the synchronization time scales, which will be defined below, using the model presented in Sect. 2, the procedure to compute the energy dissipation in Sect. 2.3, and the Ė_ave values described in the previous section. The results will be compared with the earlier results of Toledano et al. (2007) and with a theoretical result given by Zahn (1977, 2008).

4.1. Circular orbits

As in Toledano et al. (2007), we now procede to estimate the synchronization time scale between the stellar rotation period and the orbital period. The synchronization time scale is the time needed by the system to arrive at a state in which both periods are equal, and this state is here assumed to be attained as a consequence of the energy dissipation in the surface layer. In our computations, at time t = 0 the whole star, including the surface layer, is rotating with an angular velocity ω_⋆ = β₀Ω₀, with Ω₀ the reference orbital angular velocity. For circular orbits, Ω₀ is directly the angular velocity in the circular orbit while for e > 0 it is the angular velocity at periastron. We adopt here as the condition for synchronicity¹²β₀ = 1. Thus, with β₀ > 1 there is an initial excess of rotational kinetic energy over that in the synchronized state. As a first approximation, ignoring the orbital change suffered by the binary system to reach the β₀ = 1 state, the excess of rotational kinetic energy is proportional to 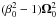$(β_{0}^{2} - 1) Ω_{0}^{2}$ $\hbox{$({\beta}^2_0 -1){\bf {\Omega}}^2_0$}$ , with the proportionality constant being I/2, with I the moment of inertia. 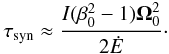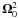Thus for star m₁ the synchronization time is on the order of $τ_{syn} \approx \frac{I (β_{0}^{2} - 1) Ω_{0}^{2}}{2 Ė} \cdot$ $\begin{equation} {\tau}_{\rm syn} \approx \frac{I({\beta}^2_0 -1){\bf {\Omega}}^2_0}{2{\dot{E}}}\cdot \label{tsin} \end{equation}$ (33)From Kepler’s law, $Ω_{0}^{2}$ $\hbox{${\bf {\Omega}}^2_0$}$ has an a^-3 dependence on the major semi-axis a. Thus, for a fixed value of β₀ and with the approximate a^-9 dependence of Ė from Fig. 3, τ_syn will have an a⁶ dependence on a for circular orbits.

On the other hand, Zahn (1977) has analyzed theoretically the tidal friction in close binary stars, also arriving at an a⁶ dependence for stars in which a turbulent viscosity may be the main mechanism that produces the tidal friction. In a recent review of the topic (Zahn 2008), this expression for circular orbits is given as 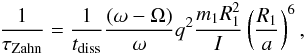$\frac{1}{τ_{Zahn}} = \frac{1}{t_{diss}} \frac{(ω - Ω)}{ω} q^{2} \frac{m_{1} R_{1}^{2}}{I} {(\frac{R_{1}}{a})}^{6},$ $\begin{equation} \frac{1}{{\tau}_{\rm Zahn}} = \frac{1}{t_{\rm diss}} \frac{(\omega-\Omega)}{\omega} q^2 \frac{m_1R_1^2}{I}\left (\frac{R_1}{a}\right )^6, \label{tZsin} \end{equation}$ (34)with q = m₂/m₁, I the moment of inertia of m₁, Ω is the orbital angular velocity which for circular orbits is constant. 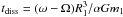$t_{diss} = (ω - Ω) R_{1}^{3} / αG m_{1}$ $\hbox{$t_{\rm diss}=(\omega-\Omega)R_1^3/\alpha G m_1$}$ is the dissipation time, with α the lag angle and G the universal constant of gravitation. 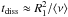Zahn (2008) suggests an approximation $t_{diss} \approx R_{1}^{2} / ⟨ ν ⟩$ $\hbox{$t_{\rm diss} \approx R_1^2/\langle \nu\rangle$}$ , where ⟨ ν ⟩ is an average kinematical viscosity, and we rewrite Eq. 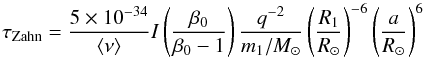(34) as: $τ_{Zahn} = \frac{5 \times 10^{-34}}{⟨ ν ⟩} I (\frac{β_{0}}{β_{0} - 1}) \frac{q^{-2}}{m_{1} / M_{⊙}} {(\frac{R_{1}}{R_{⊙}})}^{-6} {(\frac{a}{R_{⊙}})}^{6}$ $\begin{equation} \tau_{\rm Zahn} = \frac{5\times 10^{-34}}{\langle \nu\rangle} I \left ( \frac{\beta_0}{\beta_0-1}\right ) \frac{q^{-2}}{m_1/M_\odot} \left (\frac{R_1}{R_\odot} \right)^{-6} \left (\frac{a}{R_\odot} \right)^{6} \label{tZsin2} \end{equation}$ (35)where τ_Zahn is in seconds.

In order to compare our synchronization times obtained from Eq. (33) with those predicted in Eq. (35), we now make the simplifying assumption of uniform density, from which 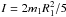$I = 2 m_{1} R_{1}^{2} / 5$ $\hbox{$I = 2m_1 R_1^2/5$}$ .

Fig. 7

Synchronization time computed with Eq. (33) using the results given in Fig. 3. The meaning of symbols stays the same as in Fig. 3. The continuous lines are the theoretical result obtained by using Eq. (2.5) from Zahn (2008), under the assumption of a uniform density structure ( $I = 2 m_{1} R_{1}^{2} / 5$ $\hbox{$I=2m_1R_1^2/5$}$ ), and with ⟨ ν ⟩ = 3.4 × 10¹² cm² s^-1. The top line is for β₀ = 1.2 and the bottom one for β = 2.0.

In Fig. 7 we show the values of τ_syn obtained from our Ė values and Eq. (33). These results have approximately the predicted a⁶ dependence, as obtained in Toledano et al. (2007) with our earlier model. We also see that the derived synchronization times depend on stellar rotation, with the faster rotating stars (β₀ = 2) attaining synchronization significantly faster than slower rotators (β = 1.2).

The two continuous lines are Zahn’s theoretical result given by Eq. (35) for the two values of β₀, using m₁ = 5 M_⊙, m₂ = 4 M_⊙, R₁ = 3.2 R_⊙, and ⟨ ν ⟩ = 3.4 × 10¹² cm² s^-1. Our results are consistent with this theoretical result, except that the value we used for the kinematical viscosity in the calculations is significantly higher, 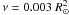$ν = 0.003 R_{⊙}^{2}$ $\hbox{$\nu =0.003 ~R^2_\odot$}$ d^-1 = 1.7 × 10¹⁴ cm² s^-1. It is important to note that in our calculation the tidal friction comes from the shear at the interface of each surface element with its neighbors and with the inner (rigidly rotating) boundary. This means that the action of the kinematical viscosity is limited to these shearing surfaces. In addition, because ours is a single-layer approximation, there is no buoyancy, and therefore our viscosity values are not associated with convection, as are those of Zahn (1977, 2008). Hence, at this stage, we are only able to draw an equivalence between the viscosity parameter used in our model and that used in Zahn’s formalism through the comparison of the synchronization timescales, as shown in Fig. 7. That ⟨ ν ⟩ ~ 10^-2ν is likely because in our calculations the whole energy dissipation is forced to occur in the surface layer, whereas in Zahn’s formalism deeper layers are also involved in these processes.

4.2. Eccentric orbits

Equation (33) can be conveniently written¹³ for an eccentric orbit in terms of the synchronicity parameter at periastron, β₀ and the orbital eccentricity e, as 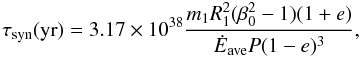$τ_{syn} (yr) = 3.17 \times 10^{38} \frac{m_{1} R_{1}^{2} (β_{0}^{2} - 1) (1 + e)}{Ė ave P (1 - e)^{3}},$ $\begin{equation} \tau_{\rm syn} ({\rm yr})=3.17\times 10^{38} \frac{m_1R_1^2(\beta_0^2-1)(1+e)}{\dot{E}_{\rm ave} P(1-e)^3}, \label{tsinecc} \end{equation}$ (36)where m₁ and R₁ are the primary star’s mass and radius, respectively, in solar units, and P is the orbital period in days. The synchronization times obtained with the above equation, using the Ė_ave values that are plotted in Fig. 4 are shown in Fig. 8. Several features of this plot are notable: 1) there is a clear difference between moderately eccentric (e ≲ 0.3) and the very eccentric systems; 2) at large orbital separations (a ≥ 100 R_⊙), the slope significanlty flattens from the τ_syn ~ (a/R_⊙)⁶ that applies for circular orbits¹⁴; and 3) for a fixed value of a, the timescale for synchronization of the eccentric binaries is shorter than the corresponding circular orbit binary, with differences as large as five orders of magnitude visible in Fig. 8.

Fig. 8

Synchronization from the energy dissipation rates computed with our model using a kinematical viscosity $ν = 0.005 R_{⊙}^{2}$ $\hbox{$\nu=0.005~R^2_\odot$}$ d^-1 and Eq. (36). The different “families” are labeled by their corresponding eccentricity. The solid line is the synchronization timescale from Zahn’s (2008) relation, assuming a constant density structure and ⟨ ν ⟩ = 1.4 × 10¹² cm² s^-1. This relation is valid only for e ~ 0.0. The dotted lines illustrate the trends for higher eccentricities from our computed models. Note that τ_syn ~ a^4.125 for high value of e and a. τ_syn is in units of years.

Fig. 9

Same synchronization times in the previous figure, but here plotted as a function of periastron distance, r_per. The dotted lines connect the points corresponding to each of the eccentricities. τ_syn is in units of years.

The separation into these different “families” is eliminated in part by using the periastron distance, r_per, instead of the semi-major axis of the orbit. Figure 9 illustrates the same values of Ė shown in Fig. 8, but in this case τ_syn is plotted as a function of r_per. The different curves “collapse” onto a common region in the log (τ_syn) vs. log (r_per) plane, with significant differences occuring only for very large orbital separations. This is consistent with the fact that, although the mean distance between the two stars increases with e, the distance at periastron strongly decreases, and as emphasized by Leconte et al. (2010), most of the work caused by tidal forces occurs at this point of the orbit.

The actual values of τ_syn depend on the values of ν and k. But the scaling of τ_syn with separation at periastron is as plotted in Fig. 8, unless ν and k depend on orbital separation¹⁵.

5. Orbital phase-dependence and periastron events

Consider the binary system with e = 0.8 and P = 15 d from the grid of models described in the previous sections. With β₀ = 1.2, the primary star, m₁, is rotating at 193 km s^-1. The maps in the top panels of Fig. 10 are a color-coded Mollweide projection of the stellar surface, with white corresponding to the maximum elevation from the unperturbed stellar surface and black to the largest depression below the unperturbed stellar surface. Azimuth angle ϕ = 0°, corresponding to the location of m₂, is on the left edge of the map, ϕ = 360° on the right edge, and ϕ = 180° is at the center. At periastron (Fig. 10, left), the surface acquires a shape that is typical of that assumed in the “equilibrium tide” approximation. That is, a tidal bulge is raised on both hemispheres with the larger bulge pointing in the general direction of the companion, m₂, but “lagging" slightly behind. The maximum height of the primary bulge at the equator (Fig. 10, bottom left) is ~ 0.03 R_⊙¹⁶.

Fig. 10

Top: maps of radius residuals (r(ϕ′) − R₁) for e = 0.8, P = 15 d, β₀ = 1.2 at periastron (left) and 0.833 days after (right). The sub-binary longitude (ϕ′ = 0) is at the far left on each map and ϕ′ = 180° is at the center. The sense of the stellar rotation is from left-to-right. White/black represents maximum/minimum residuals. Bottom: corresponding plots of the radius residuals along the equator.

Fig. 11

Top: maps of tangential velocity residuals for e = 0.8, P = 15 d, β₀ = 1.2 at periastron (left) and 0.833 days after (right). The sub-binary longitude (ϕ′ = 0) is at the far left on each map and ϕ′ = 180° is at the center. The sense of the stellar rotation is from left-to-right. White/black represents positive/negative residuals; i.e., particles moving faster/slower than the unperturbed stellar rotation velocity. Bottom: corresponding plots along the equator.

The “equilibrium tide” configuration does not subsist very long, however. The right-hand panel of Fig. 10 illustrates the deformations just 0.833 day after periastron, and clearly the “equilibrium tide” approximation no longer represents the stellar surface shape. Now it is best described in terms of a large number of smaller-scale spatial structures. These would fall into the “dynamical tide” representation, if they were associated with the normal modes of oscillation of the stellar interior¹⁷. The amplitude of these structures declines with orbital phase as apastron is approached. A more in-depth analysis of the smaller spatial structures and their dependence on the model input parameters goes beyond the scope of the current paper, but the important point to note is that the “equilibrium tide” approximation is valid only around periastron passage for this particular highly eccentric model binary case. We find that for systems in our computed grid with low eccentricities and/or large orbital periods, the approximation remains valid over the orbital cycle, but not in the more extreme cases. However, even there, the tidal bulges raised by the secondary cannot be assumed to be steady over the orbital cycle, neither in amplitude nor in location.

We illustrate the azimuthal velocity field, v_ϕ′, in Fig. 11. The explanation given by Tassoul (1987) in the context of circular orbits is most appropriate to describe the phenomenon displayed at periastron (left): “Assume that at some initial instant the primary is rotating rigidly with a constant supersynchronous angular velocity. If there were no companion, the system would remain forever axisymmetric. Because of the presence of the secondary, however, a fluid particle moving on the free surface of the primary will experience small accelerations and decelerations in the azimuthal direction. 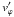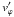Hence, in the sectors 0° < ϕ′ < π/2 and π < ϕ′ < 3π/2, the azimuthal component $v_{ϕ}^{'}$ $\hbox{$v_\varphi'$}$ , of this fluid particle will be smaller than the typical value by a small amount. On the contrary, in the other sectors, $v_{ϕ}^{'}$ $\hbox{$v_\varphi'$}$ will be larger”. Note that in the case shown in Fig. 11 the pattern of positive and negative residuals is slightly rotated with respect to Tassoul’s description because this is not a circular-orbit case, and also because of the “lag” of the primary tidal bulge. This quadrupolar pattern rapidly breaks down into smaller scale structures after periastron, corresponding to the smaller spatial structures of Fig. 10 (right).

Fig. 12

Top: maps of energy dissipation rate for e = 0.8, P = 15 d, β₀ = 1.2 at periastron (left) and 0.833 days after (right). The sub-binary longitude (ϕ′ = 0) is at the far left on each map and ϕ′ = 180° is at the center. The sense of the stellar rotation is from left-to-right. White/black represents maximum/minimum residuals. Bottom: corresponding plots along the equator.

Highest energy dissipation rates are associated with the regions having large perturbations in the azimuthal motion, both positive and negative. At periastron (Fig. 12, left), the highest Ė values occur close to the sub-binary longitude. But by 0.833 day later (Fig. 12, right), the large regions where most of the Ė was generated have broken down into small spatial scale structures. It is noteworthy, however, that some of these smaller structures are associated with significantly high values of Ė. Also noteworthy is that nearly the entire Ė occurs at ± 45° from the equatorial latitude.

The main conclusions we draw from this example are that 1) periastron passage causes a sudden and brief change in the surface perturbations, leading to significant dynamical effects; 2) the tidal shear energy dissipation rates are concentrated (in this example) around the equatorial latitude. Hence, the question arises as to whether these phenomena may provide a natural explanation for the periastron events described in the introduction, as well as the creation of a disk from the ejected material. The topic of how the material may be ejected goes beyond the scope of this paper¹⁸, but a plausible scenario is that additional energy is fed into sub-photospheric layers by the tidal shear, combined with the possible additional turbulence caused by the rapidly-changing motions on the stellar surface. We suggest that one of the crucial ingredients is the extremely rapid and strong forcing to which the stellar surface is subjected during periastron passage in very eccentric systems. Figure 13 shows a plot of Ė as a function of orbital phase for the e = 0.8, P = 15 d binary model discussed above and two other cases for comparison.¹⁹ The rapid rise in the Ė value at periastron is evident.

Fig. 13

Tidal shear energy dissipation rate for very eccentric binary systems as a function of orbital phase measured from periastron passage. Ė is in erg s^-1 and ρ in g cm^-3. Shown in this figure are two cases with e = 0.8 (P = 15 and 350 days) and a case for δ Sco. Note that peristron passage is always associated with a very large time variation of Ė.

The second case depicted in Fig. 13 corresponds to a e = 0.8, P = 350 d model from our grid, and the unperturbed equatorial rotation velocity of m₁ is ~8 km s^-1. The Ė values undergo a ~6 order-of-magnitude variation between apastron and periastron, most of which occurs within ± 70 days of periastron passage. Finally, the third case illustrated in Fig. 13 is an exploratory model calculation for the extremely eccentric (e = 0.94) Be-type binary system δ Sco²⁰. The primary star in this system has an estimated equatorial rotation velocity of ~200 km s^-1, which means that it is rotating extremely fast, compared to the orbital angular velocity of m₂. The star undergoes an increase in Ė by ~9 orders of magnitude between apastron and periastron, with a very steep rise to maximum just 15 days before periastron.

6. Discussion

A large body of research, starting with Darwin (1880), exists on the effects produced by tidal interactions on the long-term evolution of binary systems. The primary concern of these investigations is generally the timescales for circularization of the orbit and synchronization of the rotational and orbital angular velocities. The three general approaches that have been developed for analyzing the effect of tidal dissipation in these investigations are 1) the “equilibrium tide” model; 2) the “dynamical tide” model; and 3) the hydrodynamical model of Tassoul (1987).

In the “equilibrium tide” model (Darwin 1880; Alexander 1973; Hut 1980, 1981; and see Eggleton et al. 1998, and references therein)²¹ the shape of the stellar surface is approximated to that which it would adopt in equilibrium under the effect of the gravitational-centrifugal potential of the system. The viscous nature of the stellar material leads to a misalignment (refereed to as “lag”) between the axis that connects the two tidal bulges and the line that connects the centers of the two stars. The action of the external gravitational field on this misaligned body leads to a torque which, in turn, leads to an interchange of energy and angular momentum between stellar rotation and orbital motion. Dissipation by viscosity results in the decrease in the eccentricity of the orbit and the synchronization of the rotational and orbital motions. It is important to note that the “equilibrium tide” approach implicitly assumes that the star goes through a succession of rigidly rotating states, until the equilibrium configuration is reached.

The “dynamical tide” approach is based on the assumption that the star may be viewed as an oscillator whose normal modes may be excited by the variation in the gravitational potential. Among the first mathematical formulations available in the published literature are those of Fabian et al. (1975), Zahn (1975), and Press & Teukolsky (1977). In more recent years, a large amount of effort has been invested in further developing these concepts, as reviewed by Savonije (2008) (see, also McMillan et al. 1987; Goldreich & Nicholson 1989; Dolginov & Smel’Chakova 1992; Lai 1996; Mardling 1995; Kumar & Goodman 1996; Kumar & Quataert 1997). Three types of modes are believed to be excited a) the internal gravity modes, where the restoring force is the bouyancy force in stably stratified regions (Zahn 1975, 1977; Goldreich & Nicholson 1989; Rocca 1989); b) the acoustic modes, where the restoring force is the compressibility of the gas; and c) the inertial modes where the restoring force is the Coriolis force (Witte & Savonije 1999a,b). These modes are the mechanism by which energy from the orbital motion is absorbed by the star. The system is driven toward the equilibrium state by the damping of these modes. Hence, it is necessary to make an assumption concerning the damping mechanism. In stars with an outer convective layer, it is generally assumed that turbulent viscosity is the dominant mechanism. In stars with outer radiative layers, radiation damping is assumed to be the dissipative mechanism. It is interesting that in an eccentric system, the gravitational forcing goes through a large range of frequencies as the orbit progresses from apastron to periastron. Hence, there is a good chance that one of these frequencies will resonate with the star’s normal modes, thus exciting the particular oscillation mode in the star. At the same time, as periastron is approached, however, the star becomes more deformed, thus potentially modifying its normal modes. The above methods rely on a mathematical formulation of the star’s response to the perturbing potential of its companion, and are usually treated in the linear regime. Thus, they are generally limited to slow rotational velocities and/or low orbital eccentricites.

The third approach, introduced by Tassoul (1987) for early-type binaries, involves large-scale hydrodynamical motions within the tidally distorted star. It is based on the assumed presence of large-scale meriodional circulation, superposed on the mean azimuthal motion of stellar rotation. This circulation is believed to arise because a fluid particle moving on the free surface of the primary will experience small accelerations and decelerations in the azimuthal direction, depending on its location with regard to the sub-binary longitude²². These meridional circulation currents transport angular momentum very efficiently, which leads to very rapid synchronization timescales; i.e., the spin-down time primarily depends on (a/R)^4.125. This mechanism is thus a more long-range mechanism compared with the other two. The method recognizes that near the surface, the Coriolis force and the viscous force must play a donominant role in the mechanical balance. Hence, this approach significantly differs from the other two in that it captures the hydrodynamic processes near the stellar surface.

Contrary to the three methods described above, where the primary concern is the long-term ( ≥ 10⁶ yr) evolution of the orbital and stellar rotation parameters, our method was developed to analyze the tidal effects on orbital timescales (~days). However, we are able to compare the results of our model with results from the other models through the energy dissipation rates which, in turn, allow an estimate to be made of the synchronization timescales. We find that the results of our model for circular orbits are fully consistent with the results of Zahn (1977, 2008) for stars with convective envelopes. We also find that for eccentric orbits, our results for the scaling of the energy dissipation rates with orbital eccentricity and separation are consistent with the predictions of Hut (1981).

Zahn’s synchronization timescale for convective envelopes is based on the “dynamical tide” formalism, while Hut’s method is based on the “equilibrium tide” approximation. Our method does not rely on any a priori assumption regarding the mathematical formulation of the tidal flow structure. Instead, we solve the equations of motion of a thin, deformable surface layer that is allowed to respond to the gravitational field of m₁ and m₂, the Coriolis force, the centrifugal force, the gas pressure and the viscous forces from the shearing flows. The numerical solution of this system of equations yields the velocity field on the stellar surface, from which the energy dissipation rates may be computed. Thus, ours is a computation from first principles, the only simplifying assumptions being those which are inherent to the one-layer approximation. In particular, our method neglects the deformations produced by the tidal effects on the layers below the surface layer. However, because the tidal forces decline as 1/r³, the tidal effects are weaker in deeper layers of the star than on the surface (see, for example, Dolginov & Smelch’akova 1992). On the other hand, we are fully aware that the detailed behavior of underlying layers will be coupled to that of the surface layer. Thus, at this stage our results are merely indicative of the detailed behavior of the surface layer as a function of the orbital phase.

Among the advantages of our method is that it allows a qualitative assessment of the response of the stellar surface under arbitrary conditions and it captures the essence of the three general approaches described above. That is, the solution of the equations of motion yields a first-order deformation attributable to the equilibrium tide and a lag angle; a second order deformation attributable to dynamical effects²³; and because of the inclusion of gas pressure, it captures some of the hydrodynamical effects. Interestingly, our results for the synchronization timescales in eccentric orbits are consistent with the equilibrium tide approach at intermediate orbital separations, but suggest much faster synchronization timescales for larger orbital separations, consistent with Tassoul’s hydrodynamic model²⁴. From the observational standpoint, Abt & Boonyarak (2004) found that B and A stars in binaries with periods as long as 500 days have rotational periods significantly shorter than the corresponding single stars. They therefore concluded that the synchronization process can have an inpact on the stellar rotation even for relatively wide binaries with periods as long as 500 days, thus supporting the presence of a longer-range mechanism. Claret et al. (1995) and Claret & Cunha (1997) also have noted that the Zahn models and the Tassoul models each can explain the observational data only in part.

The major limitation of a one-layer model lies in neglecting the oscillatory nature of the stellar interior. In particular, the interaction of the normal modes of oscillation of the star with the external forcing frequency provides a means by which orbital energy might be captured by the star and deposited as thermal energy. Hence, we cannot at this time probe interesting situations associated with resonances. On the other hand, in long-period, very eccentric binary systems the peristron passage involves very large temporal gradients in the surface properties of the star. The tidal shear energy dissipation rates, in particular, change dramatically over a very small portion of the orbital cycle. Our exploratory calculation for the δ Sco binary system (orbital period P = 3944.7 days) indicates that Ė changes by five orders of magnitude over the 82 days before periastron, two of these occurring over the 15 days before peristron. The combination of added energy, extended radius, and high surface flow velocities may be envisaged to produce a destabilizing effect that leads to a mass-ejection event. Interestingly, we expect that the ejecta should form a disk-like structure, because the strongest tidal effects occur in the equatorial plane. Observational evidence for such a disk-forming event actually exists for the previous orbital cycle (Miroshnichenko et al. 2003). Confirming this behavior in the upcoming periastron passage of 2011 would strengthen the hypothesis.

Finally, we note that it may be productive to use the periastron distance, r_per, instead of the semi-major axis, a, when comparing statistical studies of observational properties with theoretical models of tidal evolution. We show that by using r_per, the synchronization timescales for binaries with different orbital eccentricities “collapse” into a small region in the τ_syn vs. r_per diagram, whereas on the τ_syn vs. a diagram, there is a different “family” of curves corresponding to each eccentricity. This means that for a fixed value of a, the synchronization timescale derived from eccentric binary systems is significantly shorter (by orders of magnitude) than a corresponding e = 0 system. However, if r_per is used instead, the spread between systems with different eccentricites is smaller.

We emphasize moreover that there is a significant dependence of τ_syn on the stellar rotational velocity. However, it must be kept in mind that the important parameter is not only the equatorial rotational velocity, but also the synchronicity parameter, β₀. Hence, slowly rotating stars may undergo strong tidal interaction effects if, for example, β₀ ≪ 1. Whether strong tidal effects can contribute to alter chemical abundances is a question that merits examination, because this could potentially be an explanation for some of the discrepancies recently found between stellar structure evolutionary models and observations (Hunter et al. 2008; Brott et al. 2011).

Clearly, many of the outstanding questions associated with tidal interactions require a more complete treatment than that of any of the currently developed models. In particular, the departures from spherical symmetry imply that a one-dimensional treatment of the radiative transfer processes is inadequate. Furthermore, the energy that is dissipated due to tidal interactions, regardless of the mechanism invoked, is an added source of energy that is deposited in sub-photospheric layers of the star and needs to be considered when analyzing energy transport processes and determining the structure of the outer stellar layers.

7. Conclusions

We derived a mathematical expression for computing the rate of dissipation, Ė, of kinetic energy by the viscous flows that are driven by tidal interactions and used it to explore the effects caused by periastron passage in eccentric binary systems. Our method does not rely on any a priori assumptions regarding the mathematical formulation for the perturbations in the star caused by its companion. We show that our results for the scaling of Ė with orbital separation for circular orbits are the same as those derived analytically by Hut (1981), and that our results yield the same scaling of synchronization timescales with orbital separation as found by Zahn (1977, 2008) for convective envelopes. For elliptical orbits, our results reproduce the dependence of Ė on the eccentricity and the general trend with orbital separation as predicted by Hut (1981). In addition, the model also adequately predicts the pseudo-synchronization angular velocity for moderate eccentricities (e ≤ 0.3), as obtained by Hut (1981).

We explored the distribution of Ė over the stellar surface, and found that its configuration in small eccentricity binaries is consistent with the quadrupolar morphology of the “equilibrium tide”. That is, maximum Ė values tend to be located at four longitude regions where the fastest azimuthal motions are present. In very eccentric systems, however, the morphology significantly changes as a function of orbital phase. Although generally quadrupolar-like at periastron, shortly after this time Ė is distributed into smaller spatial structures, which suggests an analogy with the “dynamical tide” models. In addition, the perturbations are in general strongest around the equatorial latitude²⁵.

We speculate that the very large and sudden increase in Ė that occurs around periastron, combined with the rapid growth rate of the velocity perturbations is a promising mechanism for explaining the increased stellar activity and mass-ejection events often observed around this orbital phase. Two factors may be involved in causing the periastron events. First, Ė is an additional source of energy that is deposited in sub-photospheric layers and represents a time-dependent perturbation to the temperature and differential velocity structure of these layers.

Second, in very eccentric binaries, the growth rate of the surface perturbations increases very abruptly at periastron. For example, in the very eccentric binary system δ Sco (e = 0.94, P = 3944.7 d), our exploratory calculation indicates that Ė changes by five orders of magnitude over the 82 days before periastron, with a two-orders of magnitude increase over the 15 days before peristron. The qualitative phenomenon is one in which portions of the stellar surface are forced to suddenly rotate faster or slower than their neighboring inner layers, thus leading to a variable differentially-rotating structure which significantly differs from its unperturbed structure. Furthermore, most of the activity occurs around the equatorial latitude. The consequence for the stability of the outer layers under these conditions is a problem that merits further attention.

¹

A binary star is defined to be in equilibrium (Hut 1980) when it is in a circular orbit (e = 0), its rate of equatorial rotation equals the rate of orbital motion (ω_rot = Ω) and the axes of stellar and orbital angular velocity are both perpendicular to the orbital plane.

²

Equations (40b) and (40c) given in Scharlemann (1981) indicate that for a colatitude angle θ > 70°, the maximum perturbation in the azimuthal direction is more than 15 times greater than the maximum perturbation in the polar direction.

³

The expression β_per = ω₀/Ω_per = 0.02 P $\frac{v_{rot} (1 - e)^{3 / 2}}{R_{1} (1 + e)^{1 / 2}}$ $\hbox{$\frac{v_{\rm rot}(1-e)^{3/2}}{R_1(1+e)^{1/2}}$}$ is a convenient form to compute the synchronicity parameter at periastron. P is in days, v_rot in km s^-1, and R₁ in R_⊙.

⁴

The Binary Evolutionary Code, Langer (1991).

⁵

m₁ = 5 M_⊙, with an age of 4.29125 × 10⁷ yrs, at which time its radius is 3.156 R_⊙.

⁶

Appendix A shows the manner in which the Ė results depend on the chosen depth of the surface layer.

⁷

The model has recently been revisited by Leconte et al. (2010) in the context of tidal heating in exoplanets. These authors extended Hut’s equations to the case in which the orbital plane and the rotational equatorial plane of the objects do not coincide. A similar extension was also given in Eggleton et al. (1998).

⁸

An example of the orbital-phase dependence of α computed with our model may be found in Koenigsberger et al. (2003).

⁹

We note that at periastron, α is indeed very small (see, for example, Fig. 10), but grows after periastron passage.

¹⁰

Recall that in circular orbits, equilibrium configuration is at β₀ = ω/Ω₀ = 1, where Ė = 0.

¹¹

For the fixed value of ν chosen for these calculations, very high stellar rotation rates cause neighboring surface elements to overlap, a condition which halts the computation.

¹²

Note, however, as shown by Hut (1981), the lowest energy state for the eccentric system corresponds to the pseudosynchronization period which, for moderate eccentricities, is β ~ 0.8–0.9.

¹³

Using Ω₀ = 1.428 × 10^-4v_rot/R₁β₀, and v_rot = β₀R₁(1 + e)^1/2/ [0.02P(1 − e)^3/2], where v_rot is in km s^-1, P is in days, and R₁ in R_⊙.

¹⁴

Note that for a ≥ 100 R_⊙, τ_syn ~ (a/R_⊙)^4.125, similar to the synchronization timescale predicted by Tassoul (1987).

¹⁵

Because ν is generally associated with turbulence, and because the perturbations of the surface velocity field in short-period binaries is very strong, the turbulent component in these systems may be much stronger than in wider binary systems. Thus, the use of a constant viscosity for all orbital separations may not be the most appropriate.

¹⁶

A rough estimate (cf., Zahn 2008) of the tidal bulge elevation for a non-rotating star with similar characteristics, δR/R₁ ~ (m₁/m₂)(R₁/r_per)⁴ ~ 0.02, thus predicting δR = 0.07 R_⊙, a factor 2.5 larger than predicted by our model.

¹⁷

Recall that the stellar interior here is a rotating, rigid body.

¹⁸

See, for example, Lee (1993).

¹⁹

Note that actual binary systems with this eccentricity and orbital period are extremely rare or non-existent, as can be seen in Fig. 1 of Mazeh (2008), which is probably because of the very large Ė, which should rapidly tend to circularize the orbit.

²⁰

The parameters used for this calculation are m₁ = 15 M_⊙, m₂ = 2 M_⊙, P = 3944.7 d, R₁ = 7 R_⊙, β₀ = 28.5, ΔR₁/R₁ = 0.06, β₀ = 28.5, ν = 0.08 R²_⊙ d^-1.

²¹

An illustrative description and discussion of the limitations of this model may be found in Ferraz-Mello et al. (2008).

²²

Indeed, our simulations show that these azimuthal motions are the dominant cause of photospheric line-profile variability on orbital timescales (Harrington et al. 2009).

²³

Clearly, the dynamical effects predicted by the model refer to the surface layer only.

²⁴

Note, however, that our model does not currently include meridional motions. The connection with the Tassoul model resides in the concept of the azimuthal flow velocities. These have significantly faster speeds than those of meridional flows and act on very short timescales.

²⁵

The equator coincides with the orbital plane in our models.

Acknowledgments

We express our gratitude to Frederic Masset for a critical reading of this paper and very helpful suggestions, and to the referee, Peter Eggleton, for important comments. We also thank J. Kuhn, P. Garaud, and A. Maeder for motivating and helpful discussions; I. Brott for the 5 M_⊙ stellar model; and Alfredo Díaz and Ulises Amaya for computing assistance. This research was funded under grants DGAPA/PAPIIT/UNAM 106708; CONACYT 48929; travel support to GK and DMH from the CONACYT-NSF collaborative program is acknowledged.

References

Abt, H. A., & Boonyarak, C. 2004, ApJ, 616, 562 [Google Scholar]
Alexander, M. E. 1973, A&ASS, 23, 459 [Google Scholar]
Bedding, T. R. 1993, AJ, 106, 768 [Google Scholar]
Bonacić Marinović, A. A., Glebbeek, E., & Pols, O. R. 2008, A&A, 480, 797 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Brott, I., Langer, N., de Koter, A., et al. 2011, A&A, in press [Google Scholar]
Claret, A., & Cunha, N. C. S. 1997, A&A, 318, 187 [NASA ADS] [Google Scholar]
Claret, A., Giménez, A., & Cunha, N. C. S. 1995, A&A, 299, 724 [NASA ADS] [Google Scholar]
Darwin, G. H. 1880, Philos. Trans. R. Soc. London, 171, 713 [NASA ADS] [CrossRef] [Google Scholar]
Dolginov, A. Z., & Smelch’akova, E. V. 1992, A&A, 257, 783 [NASA ADS] [Google Scholar]
Efroimsky, M., & Williams, J. G. 2009, Celestial Mechanics and Dynamical Astronomy, 104, 257 [Google Scholar]
Eggleton, P. P., Kiseleva, L. G., & Hut, P. 1998, ApJ, 499, 853 [NASA ADS] [CrossRef] [Google Scholar]
Fabian, A. C., Pringle, J. E., & Reese, M. J. 1975, MNRAS, 172, 15 [NASA ADS] [CrossRef] [Google Scholar]
Fehlberg, E. 1968, NASA TR R-287 [Google Scholar]
Ferraz-Mello, S., Rodtríguez, A., & Hussmann, H. 2008, Celestial Mechanics and Dynamical Astronomy, 101, 171 [NASA ADS] [CrossRef] [Google Scholar]
Goldreich, P., & Nicholson, P. D. 1989, ApJ, 342, 1079 [NASA ADS] [CrossRef] [Google Scholar]
Harrington, D., Koenigsberger, G., Moreno, E., & Kuhn, J. 2009, ApJ, 704, 813 [NASA ADS] [CrossRef] [Google Scholar]
Hunter, I., Brott, I., Lennon, D. J., et al. 2008, ApJ, 676, L29 [NASA ADS] [CrossRef] [Google Scholar]
Hut, P. 1980, A&A, 97, 167 [NASA ADS] [Google Scholar]
Hut, P. 1981, A&A, 99, 126 [NASA ADS] [Google Scholar]
Koenigsberger, G., & Moreno, E. 1997, in Luminous Blue Variables: Massive Stars in Transition, ed. A. Nota, & H. Lamers, ASP Conf. Ser., 120, 233 [Google Scholar]
Koenigsberger, G., & Moreno, E. 2008, Rev. Mex. Astron. Astrofis. (SC), 33, 108 [Google Scholar]
Koenigsberger, G., Moreno, E., & Cervantes, F. 2002, Interacting winds from Massive Stars, ed. A. F. J. Moffat, & N. St-Louis, ASPCS, 260, 507 [Google Scholar]
Koenigsberger, G., Moreno, E., & Cervantes, F. 2003, A massive star Odyssey, from Main Sequence to Supernova, ed. K. A. van der Hucht, A. Herrero, & C. Esteban, Proc. IAU Symp., 212, 101 [Google Scholar]
Koenigsberger, G., Georgiev, L., Moreno, E., et al. 2006, A&A, 458, 513 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Kumar, P., & Quataert E. J. 1997, ApJ, 479, L51 [NASA ADS] [CrossRef] [Google Scholar]
Kumar, P., & Goodman, J. 1996, ApJ, 466, 946 [NASA ADS] [CrossRef] [Google Scholar]
Lai, D. 1996, ApJ, 466, L35 [NASA ADS] [CrossRef] [Google Scholar]
Langer, N. 1991, A&A, 252, 669 [NASA ADS] [Google Scholar]
Leconte, J., Chabrier, G., Baraffe, I., & Levrard, B. 2010, A&A, 516, A64 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Lee, U. 1993, ApJ, 417, 697 [NASA ADS] [CrossRef] [Google Scholar]
Lynden-Bell, D., & Pringle, J. E. 1974, MNRAS, 168, 603 [NASA ADS] [CrossRef] [Google Scholar]
Mardling, R. A. 1995, ApJ, 450, 732 [NASA ADS] [CrossRef] [Google Scholar]
Mazeh, T. 2008, in Tidal Effects in Stars, Planets and Disks, ed. M.-J. Goupil, & J.-P. Zahn, EAS Pub. Ser., 29, 1 [Google Scholar]
McMillan, S. L. W., McDermott, P. N., & Taam, R. E. 1987, ApJ, 318, 261 [NASA ADS] [CrossRef] [Google Scholar]
McQuarrie, D. A. 1976, Statistical Mechanics (New York: Harper & Row) [Google Scholar]
Millour, F., Chesneau, O., Borges Fernandes, M., et al. 2009, A&A, 507, 317 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Miroshnichenko, A. S., Fabregat, J., Bjorkman, D. S., et al. 2001, A&A, 377, 485 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Miroshnichenko, A. S., Bjorkman, K. S., Morrison, N. D., et al. 2003, A&A, 408, 305 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Moreno, E., & Koenigsberger, G. 1999, Rev. Mex. Astron. Astrofis., 35, 157 [NASA ADS] [Google Scholar]
Moreno, E., Koenigsberger, G., & Toledano, O. 2005, A&A, 437, 641 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Press, W. H., & Teukolsky, S. A. 1977, ApJ, 213, 183 [NASA ADS] [CrossRef] [Google Scholar]
Rocca, A. 1989, A&A, 213, 114 [NASA ADS] [Google Scholar]
Savonije, G. 2008, in Tidal Effects in Stars, Planets and Disks, ed. M.-J. Goupil, & J.-P. Zahn, EAS Pub. Ser., 29, 91 [Google Scholar]
Scharlemann, E. T. 1981, ApJ, 246, 292 [NASA ADS] [CrossRef] [Google Scholar]
Symon, K. R. 1971, Mechanics (Addison-Wesley) [Google Scholar]
Tango, W. J., Davis, J., Jacob, A. P., et al. 2009, MNRAS, 396, 842 [NASA ADS] [CrossRef] [Google Scholar]
Tassoul, J. L. 1987, ApJ, 322, 856 [NASA ADS] [CrossRef] [Google Scholar]
Toledano, O., Moreno, E., Koenigsberger, G., Detmers, R., & Langer, N. 2007, A&A, 461, 1057 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
van Genderen, & Sterken 2007, IBVS, 5782 [Google Scholar]
Zahn, J. P. 1975, A&A, 41, 329 [NASA ADS] [Google Scholar]
Zahn, J. P. 1977, A&A, 57, 383 [NASA ADS] [Google Scholar]
Zahn, J. P. 2008, in Tidal Effects in Stars, Planets and Disks, ed. M.-J. Goupil, & J.-P. Zahn, EAS Pub. Ser., 29, 67 [Google Scholar]

Appendix A: Grid of model calculations

Table A.1

Summary of the 5 + 4 M_⊙ model binary system models for ΔR₁/R₁ = 0.06 and 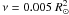$ν = 0.005 R_{⊙}^{2}$ $\hbox{$\nu=0.005~R_\odot^2$}$ day^-1 (unless noted otherwise).

Table A.1 lists the input parameters of the grid of model calculations used in this paper. The first column identifies the set number; the second column lists the eccentricity; the third column lists the range in orbital periods included in the given set; the fourth column lists the value of β₀ used in the calculation, or the range in β₀ values; and the last column contains comments. Unless otherwise noted, all calculations were performed with a kinematical viscosity parameter, 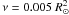$ν = 0.005 R_{⊙}^{2}$ $\appendix \setcounter{section}{1} \hbox{$\nu=0.005~R^2_\odot$}$ day^-1 = 2.8 × 10¹⁴ cm²/s.

Appendix B: Dependence of Ė_ave on layer depth

We examined the manner in which the energy dissipation rates depend on the choice of the depth (ΔR₁/R₁) of the surface layer that is modeled. This was done holding all parameters fixed, except for the values of dR₁/R₁, which were varied from 0.02 to 0.10. The results for e = 0.1, 0.3 and 0.8 are illustrated in Fig. B.1, which show that for the models we have run for this paper, the calculations using different layer depths yield values of Ė_ave that differ by no more than a factor of two.

Fig. B.1

Dependence of Ė_ave on the choice of layer depth for models computed with e = 0.1, 0.3 and e = 0.8, and corresponding orbital periods as listed in the label. The average density for each layer depth used for the Ė_ave calculation were obtained from the stellar structure model of a 5 Mo, 3.15 Ro star (Brott 2010, private communication). This shows that for a fixed set of binary parameters, the energy dissipation rates depend on the choice of layer depth only within a factor of ~2.

All Tables

Table A.1

Summary of the 5 + 4 M_⊙ model binary system models for ΔR₁/R₁ = 0.06 and 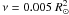$ν = 0.005 R_{⊙}^{2}$ $\hbox{$\nu=0.005~R_\odot^2$}$ day^-1 (unless noted otherwise).

In the text

All Figures

Fig. 1

Rate of energy dissipation Ė_ij as a function of ϕ′ in a few selected parallels, for the n = 1.5 polytropic case ΔR₁/R₁ = 0.03, ν = 0.003 $R_{⊙}^{2}$ $\hbox{$R^2_{\odot}$}$ day^-1, ρ = 8.66 × 10^-7 g cm^-3, orbital period P = 10 days (a = 40.62 R_⊙), and β₀ = 1.2. The top curve shows results for the stellar equator, and following curves from top to bottom correspond to parallels with θ′ ≈ 81°, 73°, 64°, 55°, 46°, 38°, 29°, and 20°. Calculations with β₀ = 2.0 yield identical curves, but the Ė_ij values are higher for by ~ 1.5 mag.

In the text

	Fig. 2 Rate of energy dissipation in the parallel i as a function of its polar angle, corresponding to the computations in Fig. 1. Results with β₀ = 1.2 and 2 are shown with empty and filled squares, respectively. The continuous lines show functions with a sin⁷θ′ dependence.
In the text

Fig. 3

Energy dissipation in m₁ as a function of the separation a of the circular orbit. A polytropic index n = 1.5 is used. Empty symbols correspond to β₀ = 1.2 and filled symbols to β₀ = 2.0. The correspondence with the layer thickness ΔR₁/R₁ is, in triangles: ΔR₁/R₁ = 0.01, in squares: ΔR₁/R₁ = 0.03, in pentagons: ΔR₁/R₁ = 0.06. The continuous line is a function with an a^-9 dependence on a.

In the text

Fig. 4

Energy dissipation rates (in erg s^-1) from our model calculations for β₀ = 1.2 and different eccentricities as indicated. The dashed lines show the absolute value of Ė_orb given by Eq. (A31) of Hut (1981), as written in our Eq. (30). The dotted lines connect the points corresponding to each eccentricity. The short dot-dashed lines show the values of Ė_Hut for e = 0.8 and lag angles α = 10° and 50°.

In the text

Fig. 5

Energy dissipation rates of the previous figure but here plotted as a function of the periastron distance, r_per. In this representation, the different curves for each eccentricity “collapse” onto a common region. The dashed lines show the absolute value of Ė_orb given by Eq. (A31) of Hut (1981) for e = 0.1 and 0.8, also plotted as a function of r_per. Symbols correspond to the different eccentricities: e = 0.00 (open triangles), 0.01 (filled triangles), 0.10 (small pentagons), 0.30 (large pentagons), 0.50 (crosses), 0.70 (stars) and 0.8 (filled pentagons).

In the text

Fig. 6

Energy dissipation rates Ė_ave/10³⁵ ⟨ ρ ⟩ as a function of β₀ = ω/Ω₀ for four different eccentricities, e = 0.1 (top left), 0.3 (top right), 0.5 (bottom left) and 0.8 (bottom right). The first three cases are for an orbital period P = 6 d and the last is for 20 d. The ordinate is in units of 10³⁵ ⟨ ρ ⟩ erg s^-1, where ⟨ ρ ⟩ is the average density. The dotted line indicates the level of minimum Ė_ave which, for e = 0.1 and 0.3 coincides with the analytical results of Hut (1981).

In the text

Fig. 7

Synchronization time computed with Eq. (33) using the results given in Fig. 3. The meaning of symbols stays the same as in Fig. 3. The continuous lines are the theoretical result obtained by using Eq. (2.5) from Zahn (2008), under the assumption of a uniform density structure ( $I = 2 m_{1} R_{1}^{2} / 5$ $\hbox{$I=2m_1R_1^2/5$}$ ), and with ⟨ ν ⟩ = 3.4 × 10¹² cm² s^-1. The top line is for β₀ = 1.2 and the bottom one for β = 2.0.

In the text

Fig. 8

Synchronization from the energy dissipation rates computed with our model using a kinematical viscosity $ν = 0.005 R_{⊙}^{2}$ $\hbox{$\nu=0.005~R^2_\odot$}$ d^-1 and Eq. (36). The different “families” are labeled by their corresponding eccentricity. The solid line is the synchronization timescale from Zahn’s (2008) relation, assuming a constant density structure and ⟨ ν ⟩ = 1.4 × 10¹² cm² s^-1. This relation is valid only for e ~ 0.0. The dotted lines illustrate the trends for higher eccentricities from our computed models. Note that τ_syn ~ a^4.125 for high value of e and a. τ_syn is in units of years.

In the text

	Fig. 9 Same synchronization times in the previous figure, but here plotted as a function of periastron distance, r_per. The dotted lines connect the points corresponding to each of the eccentricities. τ_syn is in units of years.
In the text

Fig. 10

Top: maps of radius residuals (r(ϕ′) − R₁) for e = 0.8, P = 15 d, β₀ = 1.2 at periastron (left) and 0.833 days after (right). The sub-binary longitude (ϕ′ = 0) is at the far left on each map and ϕ′ = 180° is at the center. The sense of the stellar rotation is from left-to-right. White/black represents maximum/minimum residuals. Bottom: corresponding plots of the radius residuals along the equator.

In the text

Fig. 11

Top: maps of tangential velocity residuals for e = 0.8, P = 15 d, β₀ = 1.2 at periastron (left) and 0.833 days after (right). The sub-binary longitude (ϕ′ = 0) is at the far left on each map and ϕ′ = 180° is at the center. The sense of the stellar rotation is from left-to-right. White/black represents positive/negative residuals; i.e., particles moving faster/slower than the unperturbed stellar rotation velocity. Bottom: corresponding plots along the equator.

In the text

	Fig. 12 Top: maps of energy dissipation rate for e = 0.8, P = 15 d, β₀ = 1.2 at periastron (left) and 0.833 days after (right). The sub-binary longitude (ϕ′ = 0) is at the far left on each map and ϕ′ = 180° is at the center. The sense of the stellar rotation is from left-to-right. White/black represents maximum/minimum residuals. Bottom: corresponding plots along the equator.
In the text

	Fig. 13 Tidal shear energy dissipation rate for very eccentric binary systems as a function of orbital phase measured from periastron passage. Ė is in erg s^-1 and ρ in g cm^-3. Shown in this figure are two cases with e = 0.8 (P = 15 and 350 days) and a case for δ Sco. Note that peristron passage is always associated with a very large time variation of Ė.
In the text

Fig. B.1

Dependence of Ė_ave on the choice of layer depth for models computed with e = 0.1, 0.3 and e = 0.8, and corresponding orbital periods as listed in the label. The average density for each layer depth used for the Ė_ave calculation were obtained from the stellar structure model of a 5 Mo, 3.15 Ro star (Brott 2010, private communication). This shows that for a fixed set of binary parameters, the energy dissipation rates depend on the choice of layer depth only within a factor of ~2.

In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.

[1] Abt, H. A., & Boonyarak, C. 2004, ApJ, 616, 562 [Google Scholar]

[2] Alexander, M. E. 1973, A&ASS, 23, 459 [Google Scholar]

[3] Bedding, T. R. 1993, AJ, 106, 768 [Google Scholar]

[4] Bonacić Marinović, A. A., Glebbeek, E., & Pols, O. R. 2008, A&A, 480, 797 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[5] Brott, I., Langer, N., de Koter, A., et al. 2011, A&A, in press [Google Scholar]

[6] Claret, A., & Cunha, N. C. S. 1997, A&A, 318, 187 [NASA ADS] [Google Scholar]

[7] Claret, A., Giménez, A., & Cunha, N. C. S. 1995, A&A, 299, 724 [NASA ADS] [Google Scholar]

[8] Darwin, G. H. 1880, Philos. Trans. R. Soc. London, 171, 713 [NASA ADS] [CrossRef] [Google Scholar]

[9] Dolginov, A. Z., & Smelch’akova, E. V. 1992, A&A, 257, 783 [NASA ADS] [Google Scholar]

[10] Efroimsky, M., & Williams, J. G. 2009, Celestial Mechanics and Dynamical Astronomy, 104, 257 [Google Scholar]

[11] Eggleton, P. P., Kiseleva, L. G., & Hut, P. 1998, ApJ, 499, 853 [NASA ADS] [CrossRef] [Google Scholar]

[12] Fabian, A. C., Pringle, J. E., & Reese, M. J. 1975, MNRAS, 172, 15 [NASA ADS] [CrossRef] [Google Scholar]

[13] Fehlberg, E. 1968, NASA TR R-287 [Google Scholar]

[14] Ferraz-Mello, S., Rodtríguez, A., & Hussmann, H. 2008, Celestial Mechanics and Dynamical Astronomy, 101, 171 [NASA ADS] [CrossRef] [Google Scholar]

[15] Goldreich, P., & Nicholson, P. D. 1989, ApJ, 342, 1079 [NASA ADS] [CrossRef] [Google Scholar]

[16] Harrington, D., Koenigsberger, G., Moreno, E., & Kuhn, J. 2009, ApJ, 704, 813 [NASA ADS] [CrossRef] [Google Scholar]

[17] Hunter, I., Brott, I., Lennon, D. J., et al. 2008, ApJ, 676, L29 [NASA ADS] [CrossRef] [Google Scholar]

[18] Hut, P. 1980, A&A, 97, 167 [NASA ADS] [Google Scholar]

[19] Hut, P. 1981, A&A, 99, 126 [NASA ADS] [Google Scholar]

[20] Koenigsberger, G., & Moreno, E. 1997, in Luminous Blue Variables: Massive Stars in Transition, ed. A. Nota, & H. Lamers, ASP Conf. Ser., 120, 233 [Google Scholar]

[21] Koenigsberger, G., & Moreno, E. 2008, Rev. Mex. Astron. Astrofis. (SC), 33, 108 [Google Scholar]

[22] Koenigsberger, G., Moreno, E., & Cervantes, F. 2002, Interacting winds from Massive Stars, ed. A. F. J. Moffat, & N. St-Louis, ASPCS, 260, 507 [Google Scholar]

[23] Koenigsberger, G., Moreno, E., & Cervantes, F. 2003, A massive star Odyssey, from Main Sequence to Supernova, ed. K. A. van der Hucht, A. Herrero, & C. Esteban, Proc. IAU Symp., 212, 101 [Google Scholar]

[24] Koenigsberger, G., Georgiev, L., Moreno, E., et al. 2006, A&A, 458, 513 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[25] Kumar, P., & Quataert E. J. 1997, ApJ, 479, L51 [NASA ADS] [CrossRef] [Google Scholar]

[26] Kumar, P., & Goodman, J. 1996, ApJ, 466, 946 [NASA ADS] [CrossRef] [Google Scholar]

[27] Lai, D. 1996, ApJ, 466, L35 [NASA ADS] [CrossRef] [Google Scholar]

[28] Langer, N. 1991, A&A, 252, 669 [NASA ADS] [Google Scholar]

[29] Leconte, J., Chabrier, G., Baraffe, I., & Levrard, B. 2010, A&A, 516, A64 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[30] Lee, U. 1993, ApJ, 417, 697 [NASA ADS] [CrossRef] [Google Scholar]

[31] Lynden-Bell, D., & Pringle, J. E. 1974, MNRAS, 168, 603 [NASA ADS] [CrossRef] [Google Scholar]

[32] Mardling, R. A. 1995, ApJ, 450, 732 [NASA ADS] [CrossRef] [Google Scholar]

[33] Mazeh, T. 2008, in Tidal Effects in Stars, Planets and Disks, ed. M.-J. Goupil, & J.-P. Zahn, EAS Pub. Ser., 29, 1 [Google Scholar]

[34] McMillan, S. L. W., McDermott, P. N., & Taam, R. E. 1987, ApJ, 318, 261 [NASA ADS] [CrossRef] [Google Scholar]

[35] McQuarrie, D. A. 1976, Statistical Mechanics (New York: Harper & Row) [Google Scholar]

[36] Millour, F., Chesneau, O., Borges Fernandes, M., et al. 2009, A&A, 507, 317 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[37] Miroshnichenko, A. S., Fabregat, J., Bjorkman, D. S., et al. 2001, A&A, 377, 485 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[38] Miroshnichenko, A. S., Bjorkman, K. S., Morrison, N. D., et al. 2003, A&A, 408, 305 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[39] Moreno, E., & Koenigsberger, G. 1999, Rev. Mex. Astron. Astrofis., 35, 157 [NASA ADS] [Google Scholar]

[40] Moreno, E., Koenigsberger, G., & Toledano, O. 2005, A&A, 437, 641 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[41] Press, W. H., & Teukolsky, S. A. 1977, ApJ, 213, 183 [NASA ADS] [CrossRef] [Google Scholar]

[42] Rocca, A. 1989, A&A, 213, 114 [NASA ADS] [Google Scholar]

[43] Savonije, G. 2008, in Tidal Effects in Stars, Planets and Disks, ed. M.-J. Goupil, & J.-P. Zahn, EAS Pub. Ser., 29, 91 [Google Scholar]

[44] Scharlemann, E. T. 1981, ApJ, 246, 292 [NASA ADS] [CrossRef] [Google Scholar]

[45] Symon, K. R. 1971, Mechanics (Addison-Wesley) [Google Scholar]

[46] Tango, W. J., Davis, J., Jacob, A. P., et al. 2009, MNRAS, 396, 842 [NASA ADS] [CrossRef] [Google Scholar]

[47] Tassoul, J. L. 1987, ApJ, 322, 856 [NASA ADS] [CrossRef] [Google Scholar]

[48] Toledano, O., Moreno, E., Koenigsberger, G., Detmers, R., & Langer, N. 2007, A&A, 461, 1057 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]