| Issue |
A&A
Volume 528, April 2011
|
|
|---|---|---|
| Article Number | A53 | |
| Number of page(s) | 25 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201015867 | |
| Published online | 01 March 2011 | |
Transit timing variations in eccentric hierarchical triple exoplanetary systems
I. Perturbations on the time scale of the orbital period of the perturber
1
Baja Astronomical Observatory of Bács-Kiskun County,
6500 Baja, Szegedi út,
Kt.
766,
Hungary
e-mail: borko@electra.bajaobs.hu; hege@electra.bajaobs.hu
2
Deutsches Zentrum für Luft- und Raumfahrt (DLR), Institut für
Planetenforschung, Rutherfordstr.
2, 12489
Berlin,
Germany
e-mail: szilard.csizmadia@dlr.de
3 Eötvös University, Department of Astronomy, 1518 Budapest,
Pf. 32, Hungary
e-mail: E.Forgacs-Dajka@astro.elte.hu
Received:
5
October
2010
Accepted:
16
December
2010
Aims. We study the long-term time scale (i.e. period comparable to the orbital period of the outer perturber object) transit timing variations (TTVs) in transiting exoplanetary systems that contain another more distant (a2 ≫ a1) planetary or stellar companion.
Methods. We give an analytical form of the O−C diagram (which describes such TTVs) in a trigonometric series, which is valid for arbitrary mutual inclinations, up to the sixth order in the inner eccentricity.
Results. We show that the dependence of the O−C on the orbital and physical parameters can be separated into three parts. Two of these are independent of the real physical parameters (i.e. masses, separations, periods) of a concrete system and only depend on dimensionless orbital elements, so can be analysed in general. We find that, for a specific transiting system, where eccentricity (e1) and the observable argument of periastron (ω1) are known, say, from spectroscopy, the main characteristics of that TTV, which is caused by a possible third-body can be mapped simply. Moreover, as the physical attributes of a given system only occur as scaling parameters, the real amplitude of the O−C can also be estimated for a given system, simply as a function of the m3/P2 ratio. We analyse the above-mentioned dimensionless amplitudes for different arbitrary initial parameters, as well as for two particular systems, CoRoT-9b and HD 80606b. We find in general that, while the shape of the O−C strongly varies with the angular orbital elements, the net amplitude (departing from some specific configurations) depends only weakly on these elements, but strongly on the eccentricities. As an application, we illustrate how the formulae work for the weakly eccentric CoRoT-9b and the highly eccentric HD 80606b. We also consider the question of detection, as well as the correct identification of such perturbations. Finally, we illustrate the operation and effectiveness of Kozai cycles with tidal friction (KCTF) in the case of HD 80606b.
Key words: methods: analytical / planets and satellites: individual: CoRoT-9b / planets and satellites: individual: HD 80606b / methods: numerical / planetary systems / binaries: close
© ESO, 2011
1. Introduction
The rapidly increasing number of exoplanetary systems, as well as the lengthening time interval of the observations naturally leads to the search for perturbations in the motion of the known planets, and this can provide the possibility of detecting additional planetary (or stellar) components in a given system, can produce further information about the oblateness of the host star (or the planet), or might even refer to evolutionary effects.
The detection and the interpretation of such perturbations in the orbital revolution of the exoplanets usually depends on such methods and theoretical formulae, which are well known and have been applied for a long time in the field of the close eclipsing and spectroscopic binaries. We mainly refer to the methods developed in connection with the observed period variations in eclipsing binaries. These period variations manifest themselves in non-linear variations of the difference between the observed and the predicted time of mid-eclipses (either transits or occultations). In the nomenclature of exoplanet studies, this phenomenon is called transit timing variation (TTV). Plotting the observed minus the calculated mid-transit times with respect to the cycle numbers, we get the O−C diagram, which has been the main tool for period studies by observers of variable stars (not only for eclipsing binaries) for more than a century. Consequently, the effect of the various types of period variations (both real and apparent) for the O−C diagram have already been widely studied in the past one hundred years. Some of these are less relevant in the case of transiting exoplanets, but others are important. For example, the two classical cases are the simple geometrical light-time effect (LITE) (of another, more distant companion), and the apsidal motion effect (AME) (of both the stellar oblateness in eccentric binaries and the relativistic effect). LITE has been widely used for identifying other stellar companions of many variable stars (not only eclipsing binaries) from the pioneering papers of Chandler (1892), Hertzsprung (1922), Woltjer (1922), and Irwin (1952) to a copious number of recent applications. Owing to its small amplitude, however, it is less significant in the case of a planetary-mass wide component. Nevertheless in recent years, there have been some efforts to discover exoplanets in this manner (see e.g. Silvotti et al. 2007, V391 Pegasi; Deeg et al. 2008, CM Draconis; Qian et al. 2009, QS Virginis; Lee et al. 2009, HW Virginis). The importance of AME in close exoplanet systems has been investigated in several papers; see e.g. Miralda-Escudé (2002), Heyl & Gladman (2007), and Jordán & Bakos (2008, and further references thereins). This effect has been studied since the pioneering works of Cowling (1938), and Sterne (1939), and besides its evident importance in the checking of the general relativity theory, it plays also an important role in studies of the inner mass distributions of stars (via their quadrupol moment); i.e. it provides observational verification of stellar models.
Besides their similarities, there are also several differences between the period variations of close binary and multiple stars, and of planetary systems. For example, most of the known stellar multiple systems form hierarchic subsystems (see e.g. Tokovinin 1997). This is mainly the consequence of the dynamical stability of these configurations, or put another way, the dynamical instability of the non-hierarchical stellar multiple systems. In contrast, a multiple planetary system may form a stable (or at least long-time quasi-stable) non-hierarchical configuration, as we can see in our solar system, and furthermore, the same result has been shown by numeric integrations for several known exoplanet systems (see e.g. Sándor et al. 2007). This means we can expect several different configurations, the examination of which has, until now, not been considered in the field of the period variations of multiple stellar systems. Examples of these phenomena are the perturbations of both an inner planet and a companion on a resonant orbit (Agol et al. 2005) or, as a special case of the latter, the possibility of Trojan exoplanets (Schwarz et al. 2009). Recently, the detectability of exomoons has also been studied (Simon et al. 2007; Kipping 2009a,b).
Furthermore, thanks to the enhanced activities related to extrasolar planetary searches, which led to missions like CoRoT and Kepler that produce long-term, extraordinarily accurate data, we can expect in the near future other such observations to make it possible to detect and study more phenomena never observed earlier. For example, it is well known that neither the close binary stars nor the hot-Jupiter-type exoplanets could have been formed in their present positions. Different orbital shrinking mechanisms are described in the literature. Instead of listing them, we refer to the short summaries by Tokovinin et al. (2006), Tokovinin (2008), and Fabrycky & Tremaine (2007). Here we note only that one of the most preferred theories for the formation of close binary stars, which also might have produced at least a portion of hot Jupiters, as well, is the combination of the Kozai cycles with tidal friction (KCTF). The Kozai resonance (recently and frequently referred to as Kozai cycle[s]) was first described by Kozai (1962) when investigating secular perturbations of asteroids. The first (theoretical) investigation of this phenomenon with respect to multiple stellar systems can be found in the studies by Harrington (1968, 1969), Mazeh & Saham (1979), and Söderhjelm (1982). A higher, third-order theory of Kozai cycles was given by Ford et al. (2000), while the first application of KCTF to explain the present configuration of a close, hierarchical triple system (the emblematic Algol, itself) was presented by Kiseleva et al. (1998). According to this theory, the close binaries (as well as hot-Jupiter systems) should have originally formed as significantly wider primordial binaries having a distant, inclined third companion. Due to the third object’s induced Kozai oscillation, the inner eccentricity becomes cyclically so large, that around the periastron passages, the two stars (or the host star and its planet) approach each other so closely that tidal friction may be effective, which shrinks the orbit remarkably, during one or more Kozai cycles. Owing to the smaller separation, the tidal forces remain effective on a larger and larger portion of the whole revolution, and finally, they will switch off the Kozai cycles, producing a highly eccentric, moderately inclined, small-separation intermediate orbit. After the last Kozai cycle, some additional, tidally forced circularization may then form close systems in their recent configurations.
Nevertheless, independently of the question, as to which mechanism(s) is (are) the really effective ones, up to now we have not been able to study these mechanisms in operation, so only the end-results have been observed. This is mainly the consequence of selection effects. In order to study these phenomena when they are effective, one should observe the variation in the orbital elements of such extrasolar planets, as well as binary systems that are in the period range of months to years. The easisest way to carry out such observations is to monitor the TTVs of these systems. However, there are only a few known transiting extrasolar planets in this period regime. Furthermore, although binary stars are also known with such separations, they are not appropriate subjects for this investigation because of their non-eclipsing nature.
The continuous long-term monitoring of several hundred stars with the CoRoT and Kepler satellites, as well as the long-term systematic terrestrial surveys, provide an excellent opportunity to discover transiting exoplanets (or as by-products: eclipsing binaries) with the period of months. Then continuous, long-term transit monitoring of these systems (combining the data with spectroscopy) may allow dynamical evolutionary effects (i.e. orbital shrinking) to already be traced within a few decades. Furthermore, the larger the characteristic size of a multiple planetary, stellar (or mixed) system the greater the amplitude of even the shorter period perturbations in the TTVs, as shown in detail in the discussion of Borkovits et al. (2003).
In the past few years, several papers have been published on TTVs, both from theoretical aspects (e.g. Agol et al. 2005; Holman & Murray 2005; Nesvorný & Beaugé 2010; Holman 2010; Cabrera 2010; Fabrycky 2010, see further references therein) and from large numbers of papers on observational aspects for individual transiting exoplanetary systems. Nevertheless, most (but not all) of the theoretical papers above mainly concentrate on the detectibility of additional companions (especially super-Earths) from the TTVs.
In this paper we consider this question in greater detail. We calculate the analytical form of the long-period1 (i.e. with a period close to the orbital period of the ternary component P2), time-scale perturbations of the O−C diagram for hierarchical (i.e. P2 ≫ P1) triple systems. (As we mainly concentrated on transiting systems with a period of weeks to months, we omitted the possible tidal forces. However, our formulae can be practically applied even for the closest exoplanetary systems, because the tidal perturbations usually become effective on a notably longer time scale.) This work is a continuation and extension of the previous paper of Borkovits et al. (2003). In that paper we formulated the long-period perturbations of an (arbitrarily eccentric and inclined) distant companion to the O−C diagram for a circular inner orbit. (Our formula is more general than that of Agol et al. 2005. For the coplanar case the two results become identical.) Now we extend the results to the case of an eccentric inner binary (formed either a host star with its planet or two stars). As shown, our formulae have a satisfactory accuracy even for high eccentricity, such as e1 = 0.9. In the period regime of a few months, the tidal forces are ineffective, so we expect eccentric orbits. This is especially valid in the case of the predecessor systems of hot Jupiters, in which case the formation theory mentioned above predicts very high eccentricities.
In the next section we give a very brief summary of our calculations. (A somewhat detailed description can be found in Borkovits et al. 2003, 2007; nevertheless for self-consistency of the present paper we provide a brief overview.) In Sect. 3 we discuss our results, while in Sect. 4 we illustrate the results with both analytical and numerical calculations on two individual systems, CoRoT-9b and HD 80606b. Finally in Sect. 5 we draw conclusions from our results, and, furthermore, we compare our method and results with those of Nesvorný & Morbidelli (2008), and Nesvorný (2009).
2. Analytical investigations
2.1. General considerations and equations of the problem
As is well known, at the moment of the mid-transit (which for an eccentric orbit usually
does not coincide with half the whole transit event) 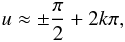 (1)where
u is the true longitude measured from the intersection of the orbital
plane and the plane of sky, and k is an integer. (Since, traditionally
the positive z-axis is directed away from the observer, the primary
transit occurs at u = −π/2.) An exact equality is
valid only if the binary has a circular orbit, or if the orbit is seen edge-on exactly.
The correct inclination dependence of the occurrence of the mid-eclipses can be found in
Gimènez & Garcia-Pelayo (1983).
Nevertheless, the observable inclination of a potentially month-long period transiting
extrasolar planet should be close to i = 90°, if the latter condition is
to be satisfied. Due to its key role in the transits we use u as our
independent time-like variable, instead of the usual variables. It is known from the
textbooks of celestial mechanics that
(1)where
u is the true longitude measured from the intersection of the orbital
plane and the plane of sky, and k is an integer. (Since, traditionally
the positive z-axis is directed away from the observer, the primary
transit occurs at u = −π/2.) An exact equality is
valid only if the binary has a circular orbit, or if the orbit is seen edge-on exactly.
The correct inclination dependence of the occurrence of the mid-eclipses can be found in
Gimènez & Garcia-Pelayo (1983).
Nevertheless, the observable inclination of a potentially month-long period transiting
extrasolar planet should be close to i = 90°, if the latter condition is
to be satisfied. Due to its key role in the transits we use u as our
independent time-like variable, instead of the usual variables. It is known from the
textbooks of celestial mechanics that 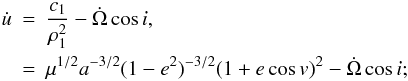 (2)consequently,
the moment of the Nth primary minimum (transit) after an epoch
t0 can be calculated as
(2)consequently,
the moment of the Nth primary minimum (transit) after an epoch
t0 can be calculated as ![\begin{eqnarray} \int^{t_N}_{t_0}\mathrm{d}t&=&\int_{-\pi/2}^{2N\pi-\pi/2}\frac{a^{3/2}}{\mu^{1/2}}\frac{(1-e^2)^{3/2}}{[1+e\cos(u-\omega)]^2}\frac{\mathrm{d}u}{1-\frac{\rho_1^2}{c_1}\dot\Omega\cos{i}}, \nonumber\\ \label{eq:TN} &\approx&\int\frac{a^{3/2}}{\mu^{1/2}}\frac{(1-e^2)^{3/2}}{[1+e\cos(u-\omega)]^2}\left(1+\frac{\rho_1^2}{c_1}\dot\Omega\cos{i}\right)\mathrm{d}u. \end{eqnarray}](/articles/aa/full_html/2011/04/aa15867-10/aa15867-10-eq18.png) (3)In
the equations above, c1 denotes the specific angular momentum
of the inner binary, ρ1 is the radius vector of the planet
with respect to its host star, and the orbital elements have their usual meanings.
Furthermore, in Eq. (3) we write the true
anomaly as v = u − ω. To evaluate
Eq. (3) we first have to express the
perturbations in the orbital elements with respect to u. Assuming that
the orbital elements (except of u) are constant, the first term of the
right-hand side (r.h.s.) yields the following closed solution
(3)In
the equations above, c1 denotes the specific angular momentum
of the inner binary, ρ1 is the radius vector of the planet
with respect to its host star, and the orbital elements have their usual meanings.
Furthermore, in Eq. (3) we write the true
anomaly as v = u − ω. To evaluate
Eq. (3) we first have to express the
perturbations in the orbital elements with respect to u. Assuming that
the orbital elements (except of u) are constant, the first term of the
right-hand side (r.h.s.) yields the following closed solution ![\begin{eqnarray} \overline{P}_{\rm I,II}= \!\frac{P}{2\pi}\!\left[2\!\arctan\!\left(\!\sqrt{\frac{1-e}{1+e}}\frac{\mp\cos\omega}{1\mp\sin\omega}\right)\!\pm(1-e^2)^{1/2}\!\frac{e\cos\omega}{1\mp e\sin\omega}\right], \label{eq:apsisclosed} \end{eqnarray}](/articles/aa/full_html/2011/04/aa15867-10/aa15867-10-eq22.png) (4)for
the two types of minima, respectively. (Here P denotes the anomalistic or
Keplerian period which is considered to be constant.) Instead of the exact forms above,
widely used is the expansion (as in this paper), which, up to the fifth order in
e, is
(4)for
the two types of minima, respectively. (Here P denotes the anomalistic or
Keplerian period which is considered to be constant.) Instead of the exact forms above,
widely used is the expansion (as in this paper), which, up to the fifth order in
e, is ![\begin{eqnarray} \overline{P}_{\rm I,II}&=& P_\mathrm{s}E+\frac{P}{2\pi}\left[\mp\frac{1}{2}\pi\pm2e\cos\omega+\left(\frac{3}{4}e^2+\frac{1}{8}e^4\right)\sin2\omega\right. \nonumber \\ \label{eq:apsisexp} &&\quad \left.\mp\left(\frac{1}{3}e^3+\frac{1}{8}e^5\right)\cos3\omega-\frac{5}{32}e^4\sin4\omega\pm\frac{3}{40}e^5\cos5\omega\right], \end{eqnarray}](/articles/aa/full_html/2011/04/aa15867-10/aa15867-10-eq25.png) (5)where
Ps is the sidereal (or eclipsing) period of, for example,
the first cycle, and E the cycle-number. In the present case the orbital
elements cease to remain constant. Nevertheless, as can be seen from Eqs. (8)–(14), their variation on the P2 time scale is related
to P1/P2 ≪ 1, which allows
linearization of the problem; i.e., in such a case, Eq. (5) is formally valid in the same form, but e,
ω, and Ps are no longer constant. Then a
further integration of Eq. (5) with respect
to v2 gives the analytical form of the perturbed O−C on the
P2 time scale. To this, as a next step, we have to calculate
the long-period and apse-node perturbations in u. Some of these arise
simply from the similar perturbations of the orbital elements (or directly of the
ecosω, esinω
functions), while others (we refer to them as direct perturbations in u)
come from the variations in the mean motion (for more details see Borkovits et al. 2007)2. (In other
words this means that in such a case P will no longer be constant.)
(5)where
Ps is the sidereal (or eclipsing) period of, for example,
the first cycle, and E the cycle-number. In the present case the orbital
elements cease to remain constant. Nevertheless, as can be seen from Eqs. (8)–(14), their variation on the P2 time scale is related
to P1/P2 ≪ 1, which allows
linearization of the problem; i.e., in such a case, Eq. (5) is formally valid in the same form, but e,
ω, and Ps are no longer constant. Then a
further integration of Eq. (5) with respect
to v2 gives the analytical form of the perturbed O−C on the
P2 time scale. To this, as a next step, we have to calculate
the long-period and apse-node perturbations in u. Some of these arise
simply from the similar perturbations of the orbital elements (or directly of the
ecosω, esinω
functions), while others (we refer to them as direct perturbations in u)
come from the variations in the mean motion (for more details see Borkovits et al. 2007)2. (In other
words this means that in such a case P will no longer be constant.)
At this point, to avoid any confusion, we emphasize that during our calculations we use different sets of the angular orbital elements. As we are interested in a phenomenon that primarily depends on the relative positions of the orbiting celestial bodies with respect to the observer, the angular elements (i.e. u, ω, i, Ω) should be expressed in the “observational” frame of reference with the plane of the sky as the fundamental plane, and u, as well as ω, is measured from the intersection of the binary’s orbital plane with that plane, while Ω is measured along the plane of the sky from an arbitrary origin. On the other hand, the physical variations in the motion of the bodies depend on their positions relative to each other, and it is consequently more beneficial (and convenient) to express the equations of perturbations of the orbital elements in a different frame of reference (we refer to it as the dynamical frame), determined only by the relative positions of the bodies. The fundamental plane of this frame of reference is the invariable plane of the triple system, i.e. the plane perpendicular to the net angular momentum vector of the complete triple system. In this frame of reference, the longitude of the ascending node (h) gives the arc between the sky and the corresponding intersection of the two orbital planes measured along the invariable plane, while the true longitude (w) and the argument of periastron (g) are measured from that ascending node, along the respected orbital plane. To avoid a further confusion, the relative inclination of the orbits to the invariable plane is denoted by j. The meaning and the relation between the different elements can be seen in Fig. 1, and are also listed in Appendix A.
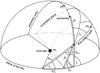 |
Fig. 1 The spatial configuration of the system. |
2.2. Long-period perturbations
From now on we refer to the orbital elements of the inner binary (i.e. the pair formed by
either a host star and the inner planet, or two stellar mass objects) by subscript
1, while those of the wider binary (i.e. the orbit of the third component
around the centre of mass of the inner system) by subscript 2. The differential
perturbation equations of the orbital elements are listed in Borkovits et al. (2007)3. In order
to get the long-period terms of the perturbation equations, the usual method involves
averaging the equations for the short-period (≈P1)
variables, which is usually the mean anomaly (l1) or the true
anomaly (v1) of the inner binary, but in our special case it
is the true longitude u1. This means that we get the variation
in the orbital elements averaged over an eclipsing period. Furthermore, in the case of the
averaged equations we change the independent variable from u1
to (the averaged) v2, by the use of
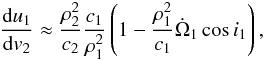 (6)from which, after
averaging, we get
(6)from which, after
averaging, we get ![\begin{eqnarray} \frac{\mathrm{d}\overline{u_1}}{\mathrm{d}\overline{v_2}}&\approx& \frac{\mu_1^{1/2}}{a_1^{3/2}}\frac{\rho_2^2}{\sqrt{\mu_2a_2(1-e_2^2)}}-\frac{\mathrm{d}\overline{\Omega_1}}{\mathrm{d}\overline{v_2}}\cos i_1 \nonumber \\[-1mm] \label{Eq:dudvaverage} &\approx& \frac{P_2}{P_1}\frac{(1-e_2^2)^{3/2}}{(1+e_2\cos v_2)^2}-\frac{\mathrm{d}\Omega_1}{\mathrm{d}v_2}\cos i_1. \end{eqnarray}](/articles/aa/full_html/2011/04/aa15867-10/aa15867-10-eq47.png) (7)In
the following we omit the overlining. Furthermore, as one can see from Eq. (13) below, the second term on the r.h.s.
of (7) is of the order
P1/P2, so can be neglected.
For the long-period perturbations of the orbital elements of the close orbit we get
(7)In
the following we omit the overlining. Furthermore, as one can see from Eq. (13) below, the second term on the r.h.s.
of (7) is of the order
P1/P2, so can be neglected.
For the long-period perturbations of the orbital elements of the close orbit we get
![\begin{eqnarray} \frac{\mathrm{d}a_1}{\mathrm{d}v_2}&=&0, \label{Eq:da1dv2}\\[-1mm] \frac{\mathrm{d}e_1}{\mathrm{d}v_2}&=&A_\mathrm{L}(1-e_1^2)^{1/2}e_1(1+e_2\cos v_2)\nonumber \\[-1mm] &&\times\left[\left(1-I^2\right)\sin2g_1\right. \nonumber \\ &&-\frac{1}{2}(1+I)^2\sin(2v_2+2g_2-2g_1) \nonumber \\ &&\left.+\frac{1}{2}(1-I)^2\sin(2v_2+2g_2+2g_1)\right], \label{Eq:de1dv2}\\ \frac{\mathrm{d}g_1}{\mathrm{d}v_2}&=&A_\mathrm{L}(1-e_1^2)^{1/2}(1+e_2\cos v_2)\nonumber \\ &&\times\left\{\frac{3}{5}\left(I^2-\frac{1}{3}\right)\right. \nonumber \\ &&+\left(1-I^2\right)\left[\cos2g_1+\frac{3}{5}\cos(2v_2+2g_2)\right] \nonumber \\ &&+\frac{1}{2}(1+I)^2\cos(2v_2+2g_2-2g_1)\nonumber \\ &&\left.+\frac{1}{2}(1-I)^2\cos(2v_2+2g_2+2g_1)\right\} \nonumber \\ &&-\frac{\mathrm{d}h_1}{\mathrm{d}v_2}\cos{j_1}, \label{Eq:dg1dv2}\\ \frac{\mathrm{d}h_1}{\mathrm{d}v_2}&=&-A_\mathrm{L}(1-e_1^2)^{-1/2}\frac{\sin i_\mathrm{m}}{\sin{j_1}}(1+e_2\cos v_2)\nonumber \\ &&\times\left[\frac{2}{5}\left(1+\frac{3}{2}e_1^2\right)I\right. \nonumber \\ &&-e_1^2I\cos2g_1 \nonumber \\ &&-\frac{2}{5}\left(1+\frac{3}{2}e_1^2\right)I\cos(2v_2+2g_2) \nonumber \\ &&+\frac{1}{2}e_1^2(1+I)\cos(2v_2+2g_2-2g_1) \nonumber \\ &&\left.-\frac{1}{2}e_1^2(1-I)\cos(2v_2+2g_2+2g_1)\right], \label{Eq:dh1dv2} \nonumber \\ \frac{\mathrm{d}j_1}{\mathrm{d}v_2}&=&A_\mathrm{L}(1-e_1^2)^{-1/2}\sin i_\mathrm{m}(1+e_2\cos v_2) \nonumber \\ &&\times\left[\frac{2}{5}\left(1+\frac{3}{2}e_1^2\right)\sin(2v_2+2g_2)\right. \nonumber \\ &&+e_1^2I\sin2g_1 \nonumber \\ &&-\frac{1}{2}e_1^2(1+I)\sin(2v_2+2g_2-2g_1) \nonumber \\ &&\left.+\frac{1}{2}e_1^2(1-I)\sin(2v_2+2g_2+2g_1)\right], \label{Eq:dj1dv2} \\ \frac{\mathrm{d}\omega_1}{\mathrm{d}v_2}&=&A_\mathrm{L}(1-e_1^2)^{1/2}(1+e_2\cos v_2)\nonumber \\ &&\times\left\{\frac{3}{5}\left(I^2-\frac{1}{3}\right)\right. \nonumber \\ &&+\left(1-I^2\right)\left[\cos2g_1+\frac{3}{5}\cos(2v_2+2g_2)\right] \nonumber \\ &&+\frac{1}{2}(1+I)^2\cos(2v_2+2g_2-2g_1)\nonumber \\ &&\left.+\frac{1}{2}(1-I)^2\cos(2v_2+2g_2+2g_1)\right\} -\frac{\mathrm{d}\Omega_1}{\mathrm{d}v_2}\cos{i_1}, \label{Eq:domega1dv2} \end{eqnarray}](/articles/aa/full_html/2011/04/aa15867-10/aa15867-10-eq49.png)
![\begin{eqnarray} \frac{\mathrm{d}\Omega_1}{\mathrm{d}v_2}&=&A_\mathrm{L}(1-e_1^2)^{-1/2}\frac{\sin i_\mathrm{m}}{\sin{i_1}}(1+e_2\cos v_2)\nonumber \\ &&\times\left[\frac{2}{5}\left(1+\frac{3}{2}e_1^2\right)I\cos(\omega_1-g_1)\right. \nonumber \\ &&+\frac{1}{5}\left(1+\frac{3}{2}e_1^2\right)(1-I)\cos\left(2v_2 +2g_2-\omega_1+g_1\right) \nonumber \\ &&-\frac{1}{5}\left(1+\frac{3}{2}e_1^2\right)(1+I)\cos\left(2v_2 +2g_2+\omega_1-g_1\right) \nonumber \\ &&-e_1^2I\cos(\omega_1+g_1) \nonumber \\ &&+\frac{1}{2}e_1^2(1+I)\cos(2v_2+2g_2-\omega_1-g_1) \nonumber \\ &&\left.-\frac{1}{2}e_1^2(1-I)\cos(2v_2+2g_2+\omega_1+g_1)\right], \label{Eq:dOm1dv2}\\ \frac{\mathrm{d}i_1}{\mathrm{d}v_2}&=&A_\mathrm{L}(1-e_1^2)^{-1/2}\sin i_\mathrm{m}(1+e_2\cos v_2)\nonumber \\ &&\times\left[-\frac{2}{5}\left(1+\frac{3}{2}e_1^2\right)I\sin(\omega_1-g_1)\right. \nonumber \\ &&+\frac{1}{5}\left(1+\frac{3}{2}e_1^2\right)(1-I)\sin\left(2v_2+2g_2-\omega_1+g_1\right) \nonumber \\ &&+\frac{1}{5}\left(1+\frac{3}{2}e_1^2\right)(1+I)\sin\left(2v_2+2g_2+\omega_1-g_1\right) \nonumber \\ &&+e^2I\sin(\omega_1+g_1) \nonumber \\ &&-\frac{1}{2}e_1^2(1+I)\sin(2v_2+2g_2-\omega_1-g_1) \nonumber \\ &&\left.+\frac{1}{2}e_1^2(1-I)\sin(2v_2+2g_2+\omega_1+g_1)\right]. \label{Eq:di1dv2} \end{eqnarray}](/articles/aa/full_html/2011/04/aa15867-10/aa15867-10-eq50.png) Finally,
the direct term is
Finally,
the direct term is 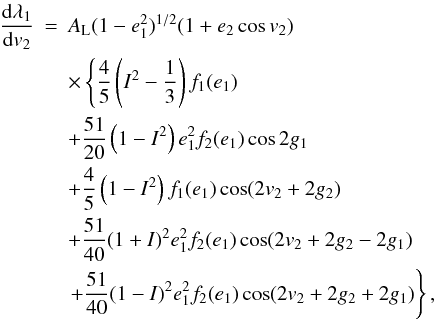 (15)where
(15)where
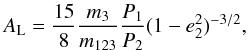 (16)and
(16)and
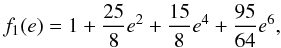 (17)\pagebreak
(17)\pagebreak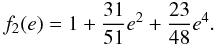 (18)Furthermore,
im denotes the mutual inclination of the two orbital planes,
while
(18)Furthermore,
im denotes the mutual inclination of the two orbital planes,
while 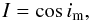 (19)and
m123 stands for the total mass of the system. Formal
integration of the first five of the equations above (i.e. those that refer to the orbital
elements in the dynamical system, Eqs. (8) − (11)) reproduce the results
of Söderhjelm (1982).
(19)and
m123 stands for the total mass of the system. Formal
integration of the first five of the equations above (i.e. those that refer to the orbital
elements in the dynamical system, Eqs. (8) − (11)) reproduce the results
of Söderhjelm (1982).
Strictly speaking, some of the equations above are only valid when both orbits are non-circular, and the orbital planes are inclined to each other and/or to the plane of the sky. For example, if the outer orbit is circular, neither v2 nor g2 has any meaning. Nevertheless, their sum i.e. v2 + g2 is meaningful, as before. Similarly, although the derivative of g1 has no meaning in the case of a circular inner orbit, the derivatives of e1cosg1, e1sing1 (or e1cosω1, e1sinω1), i.e. the so-called Lagrangian elements can be calculated correctly. (Instead of the “pure” derivatives of e1 and g1 (or ω1) these occur directly in the O−C.) Similar redefenitions can be done in the case of coplanarity. For practical reasons and for the sake of clarity, we therefore retain the original formulations, even in such cases, when it is formally not valid.
As one can see, there are some terms on the r.h.s. of these equations that do not depend
on v2. Primarily, these terms give the so-called apse-node
time-scale contribution to the variation in the orbital elements and the TTVs.
Nevertheless, to get a correct result for the long-term behaviour of the orbital elements,
these terms must nevertheless be retained in our long-term formulae. These terms were
calculated for tidally distorted triplets in Borkovits et al. (2007). Such formulae (after omitting the tidal terms) are also
valid for the present case in the low mutual inclination (i.e. approx.
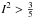 )
domain. (Formulae valid for arbitrary mutual inclinations will be presented in a
subsequent paper.)
)
domain. (Formulae valid for arbitrary mutual inclinations will be presented in a
subsequent paper.)
Carrying out the integrations, all the orbital elements on the r.h.s. of these equations
with the exception of v2 are considered as constants. This can
be justified for two reasons. First, as one can see, the amplitudes of the long-period
perturbative terms (AL) remain small for
P2 ≫ P1 (which is especially
valid for the case where the host star is orbited by two planets, when
m3 ≪ m123)4, and second, although the amplitude of the apse-node perturbative
terms can reach unity, the period is usually so long
(~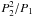 , see e.g. Brown 1936) that its contribution can be safely ignored
during one revolution of the outer object5. The
, see e.g. Brown 1936) that its contribution can be safely ignored
during one revolution of the outer object5. The
final result of such an analysis is an analytical form of the TTVs, i.e. the long-period
O−C diagram: ![\begin{eqnarray} {\rm O}{-}{\rm C}_{P_2}&=& \frac{P_1}{2\pi}A_\mathrm{L}(1-e_1^2)^{1/2}\left\{\left(\frac{4}{5}+\frac{5}{2}e_1^2\mp\frac{6}{5}e_1\sin\omega_1\right)\right. \nonumber \\ &&\quad\times\left[\left(I^2-\frac{1}{3}\right){\cal{M}}+\frac{1}{2}\left(1-I^2\right){\cal{S}}(2v_2+2g_2)\right]\nonumber \\ &&\quad+\left[\frac{51}{20}e_1^2\cos2g_1\mp2e_1\sin(\omega_1-2g_1)\right]\nonumber \\ &&\quad\times\left[\left(1-I^2\right){\cal{M}}+\frac{1}{2}\left(1+I^2\right){\cal{S}}(2v_2+2g_2)\right]\nonumber \\ &&\quad-\left[\frac{51}{20}e_1^2\sin2g_1\mp2e_1\cos(\omega_1-2g_1)\right]I{\cal{C}}(2v_2+2g_2)\nonumber \\ &&\quad+\cot i_1\sin i_\mathrm{m}\left\{-\frac{2}{5}\left(1\mp2e_1\sin\omega_1\right)\cos u_\mathrm{m1}I\right. \nonumber \\[-1mm] &&\quad\times\left[{\cal{M}}-\frac{1}{2}{\cal{S}}(2v_2+2g_2)\right] \nonumber \\[-1mm] &&\quad\left.\left.+\frac{1}{5}(1\mp2e_1\sin\omega_1)\sin u_\mathrm{m1}{\cal{C}}(2v_2+2g_2)\right\}\right\} \nonumber \\[-1mm] &&\quad-\frac{m_3}{m_{123}}\frac{a_2\sin i_2}{c}\frac{\left(1-e_2^2\right)\sin(v_2+\omega_2)}{1+e_2\cos v_2} \nonumber \\[-1mm] &&\quad +{\cal{O}}(e_1^2), \label{Eq:O-Clonge1} \end{eqnarray}](/articles/aa/full_html/2011/04/aa15867-10/aa15867-10-eq71.png) (20)where
(20)where
![\begin{eqnarray} {\cal{M}}&=& \int 1+e_2\cos v_2\mathrm{d}v_2 \nonumber \\[-1mm] &=& v_2-l_2+e_2\sin v_2 \label{Eq:kozeppontiegyenlites} \\[-1mm] &=& 3e_2\sin v_2-\frac{3}{4}e_2^2\sin2v_2+\frac{1}{3}e_2^3\sin3v_2+{\cal{O}}(e_2^4) \nonumber \\[-1mm] &=& 3e_2\left(1-\frac{3}{8}e_2^2\right)\sin l_2+\frac{9}{4}e_2^2\sin2l_2+\frac{53}{24}e_2^3\sin3l_2+{\cal{O}}(e_2^4), ~~~~~~~~~ \label{Eq:M-tag} \end{eqnarray}](/articles/aa/full_html/2011/04/aa15867-10/aa15867-10-eq72.png) and
and
![\begin{eqnarray} {\cal{S}}(2v_2+x) &=& \sin(2v_2+x)+e_2\sin(v_2+x)+\frac{1}{3}e_2\sin(3v_2+x) \nonumber \\ & = & \left(1-4e_2^2\right)\sin(2l_2+x) +e_2\left[-\left(1-\frac{13}{8}e_2^2\right)\sin(l_2+x)\right. \nonumber \\ &&\quad \left.+\frac{7}{3}\left(1\!-\!\frac{207}{56}e_2^2\right)\sin(3l_2\!+\!x)\right] \! +\!e_2^2\left[-\frac{1}{4}\sin{x}\!+\!\frac{17}{4}\sin(4l_2\!+\!x)\right] \nonumber \\ && \quad+e_2^3\left[\frac{1}{24}\sin(l_2-x)+\frac{169}{24}\sin(5l_2+x)\right]+{\cal{O}}(e_2^4), \label{Eq:S(2v+x)} \\ &&{\cal{C}}(2v_2+x) = \cos(2v_2+x)+e_2\cos(v_2+x)+\frac{1}{3}e_2\cos(3v_2+x) \nonumber \\ & = & \left(1-4e_2^2\right)\cos(2l_2+x)\nonumber \\ &&\quad +e_2\left[-\left(1-\frac{13}{8}e_2^2\right)\cos(l_2+x)\right.\nonumber \\ && \quad\left.+\frac{7}{3}\left(1-\frac{207}{56}e_2^2\right)\cos(3l_2+x)\right] \nonumber \\ && \quad+e_2^2\left[-\frac{1}{4}\cos{x}+\frac{17}{4}\cos(4l_2+x)\right] \nonumber \\ &&\quad +e_2^3\left[-\frac{1}{24}\cos(l_2-x)+\frac{169}{24}\cos(5l_2+x)\right]+{\cal{O}}(e_2^4), \label{Eq:C(2v+x)} \end{eqnarray}](/articles/aa/full_html/2011/04/aa15867-10/aa15867-10-eq73.png) and
and
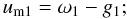 (25)i.e.,
um1 is the angular distance of the intersection of the two
orbits from the plane of the sky, or, in other words, the longitude of the (dynamical)
ascending node of the inner orbit along the orbital plane, measured from the sky. Here we
give the result up to the first order in the inner eccentricity, while a more extended
result up to the sixth order in the inner eccentricity can be found in Appendix B, where we give also the perturbation equations
directly for the
(25)i.e.,
um1 is the angular distance of the intersection of the two
orbits from the plane of the sky, or, in other words, the longitude of the (dynamical)
ascending node of the inner orbit along the orbital plane, measured from the sky. Here we
give the result up to the first order in the inner eccentricity, while a more extended
result up to the sixth order in the inner eccentricity can be found in Appendix B, where we give also the perturbation equations
directly for the 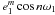 ,
,
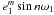 expressions. The upper signs refer to the exoplanetary transits (primary minima), and the
lower signs to the secondary occultations (secondary minima). Furthermore, we assumed the
formally second-order
expressions. The upper signs refer to the exoplanetary transits (primary minima), and the
lower signs to the secondary occultations (secondary minima). Furthermore, we assumed the
formally second-order 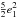 , and
, and
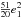 terms to be first
order, as their values exceed e1 for medium eccentricities. We
also included the pure geometrical light-time contribution, shown in the last row. Here
c denotes the speed of light. The minus sign arises because this term
reflects the motion of the inner pair around the common centre of mass, whose true
longitude differs by π from the one of the third component. In Eq. (21) the mean anomaly of the outer body
(l2) appears because of (the constant part of) the
difference between the anomalistic P and sideral (eclipsing, or
transiting) Ps period included into the first term on the
r.h.s. of Eq. (5).
terms to be first
order, as their values exceed e1 for medium eccentricities. We
also included the pure geometrical light-time contribution, shown in the last row. Here
c denotes the speed of light. The minus sign arises because this term
reflects the motion of the inner pair around the common centre of mass, whose true
longitude differs by π from the one of the third component. In Eq. (21) the mean anomaly of the outer body
(l2) appears because of (the constant part of) the
difference between the anomalistic P and sideral (eclipsing, or
transiting) Ps period included into the first term on the
r.h.s. of Eq. (5).
3. Discussion of the results
As one can easily see, the result for a circular inner orbit (i.e. e1 = 0) is identical with the formula (46) of Borkovits et al. (2003). Consequently, the discussion in Sect. 4 of that paper is also valid. Nevertheless, as one can also see in Figs. 2, 3, a significant inner eccentricity produces notably higher amplitudes and is consequently easier to detect. Furthermore, some other attributes of the TTVs also change drastically. For example, in contrast to the previously studied coplanar (I = ± 1), circular inner orbit (e1 = 0) case (Borkovits et al. 2003; Agol et al. 2005), the dynamical term does not disappear even if the outer orbit is circular (e2 = 0), as long as the inner orbit is eccentric. Another important feature for an eccentric inner orbit is that the amplitude, the phase, and the shape of the O−C variations cease to depend simply on the physical (i.e. relative) positions of the celestial bodies, but also on the orientation of the orbit with respect to the observer. These last elements (i.e. e1sinω1, e1cosω1, and their combinations) can also be determined from (a) radial velocity measurements, (b) the shape of the transit light curves, and (c) the time delay between the two different eclipsing events. (Naturally, the last one requires the detection of the secondary occultations or minima.) While the relative, i.e., physical angular parameters (i.e. periastron distances from the intersection of the two orbits, g1, g2, and mutual inclination im) cannot be aquired from other, generally used methods (e.g. light-curve, or simple radial velocity curve analysis), these observational geometrical parameters could be determined from other sources of information, and then can be simply built into such a fitting algorithm, which was described in Borkovits et al. (2003), or could be included in procedures like those presented by Pál (2010).
 |
Fig. 2 Left panels: the dependence on the inner eccentricity
(e1) of the amplitudes Aℳ,
|
 |
Fig. 3 Transit timing variatons caused by a hypothetical P2 = 10 000 day-period m3 = 1 M⊙ mass, moderately eccentric e2 = 0.3 third companion for CoRoT-9b, at different initial orbital elements for four different initial inner eccentricities (e1 = 0, 0.11, 0.5, 0.9). The various initial elements of each panel are as follows. Panel a): g1 = 7°, g2 = 90°, im = 0°; b): the same, but for im = 90°; c): g1 = 7°, g2 = 45°, im = 30°; d): g1 = 337°, g2 = 45°, im = 60°; e): g1 = 307°, g2 = 45°, im = 30°; f): same as previous, but for im = 90°; g): g1 = 277°, g2 = 45°, im = 0°; h): same as previous, but for im = 90°. (For better comparison the curves are corrected for the different average transit periods, and zero point shifts.) |
In the following we omit terms multiplied by coti1, because for
the considered relatively longer period transiting systems
i1 ≈ 90° holds. In Borkovits et al. (2003) we only considered triple stellar systems, where the three
masses were usually nearly equal, and the inner period was a few days. In such cases, the
light-time term dominates. The amplitude of the light-time effect is simply 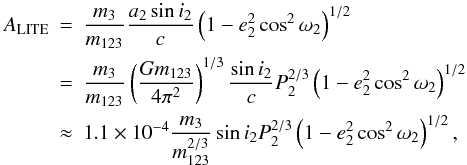 (26)where
masses should be expressed in solar units, and P2 in days.
(26)where
masses should be expressed in solar units, and P2 in days.
The amplitude of the dynamically forced O−C and, consequently, the detectability limit of
such perturbations depends on almost all the dynamical, as well as geometrical, variables.
We can therefore give only some limits on the detectability limit. Nevertheless, for an
easier, and somewhat general study, we separate the physical and geometrical variables from
each other and, furthermore, also separate the elements of the inner orbit from those of the
outer perturber (with the exception of the mutual inclination). To do this, we introduce the
following quantities, all of which depend on eccentricity (e1),
the two types of periastron arguments (g1,
ω1), and mutual inclination (im),
via its cosine: ![\begin{eqnarray} \alpha&=&\left\{\frac{2}{5}+\frac{5}{4}e_1^2\left(1+\cos2g_1\right)\mp e_1\left[\frac{3}{5}\sin\omega_1+\sin(\omega_1-2g_1)\right]\right. \nonumber \\ &&-I^2\left\{\frac{2}{5}+\frac{5}{4}e_1^2\left(1-\cos2g_1\right)\right. \nonumber \\ &&\left.\left.\mp e_1\left[\frac{3}{5}\sin\omega_1-\sin(\omega_1-2g_1)\right]\right\}\right\}\left(1-e_1^2\right)^{1/2}, \\ \beta&=&-\left(1-e_1^2\right)^{1/2}2I\left[\frac{5}{4}e_1^2\sin2g_1\mp e_1\cos(\omega_1-2g_1)\right], \\ \gamma&=&\left\{\!-\frac{4}{15}\!+\!\frac{5}{2}e_1^2\left(\cos2g_1-\frac{1}{3}\right)\mp2e_1\left[\sin(\omega_1-2g_1)-\!\frac{1}{5}\sin\omega_1\!\right]\right.\nonumber \\ &&+I^2\left\{\frac{4}{5}+\frac{5}{2}e_1^2\left(1-\cos2g_1\right)\right. \nonumber \\ &&\left.\left.\mp2e_1\left[\frac{3}{5}\sin\omega_1-\sin(\omega_1-2g_1)\right]\right\}\right\}\left(1-e_1^2\right)^{1/2}. \end{eqnarray}](/articles/aa/full_html/2011/04/aa15867-10/aa15867-10-eq112.png) Then
Then
![\begin{equation} {\rm O}{-}{\rm C}_\mathrm{dyn}\approx\frac{P_1}{2\pi}A_\mathrm{L}\left[\gamma{\cal{M}}+\!\!\sqrt{\alpha^2+\beta^2}{\cal{S}}(2v_2+\phi)\right], \label{eq:OminCdyntomor} \end{equation}](/articles/aa/full_html/2011/04/aa15867-10/aa15867-10-eq113.png) (30)where
(30)where
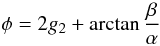 (31)or,
in trigonometric form,
(31)or,
in trigonometric form, 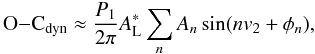 (32)where (up to third order
in e2)
(32)where (up to third order
in e2) 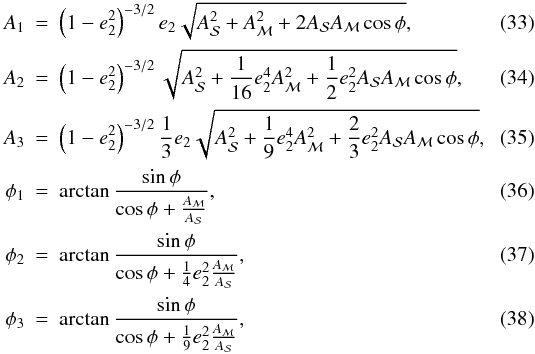 and
and
 and,
furthermore,
and,
furthermore, 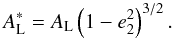 (41)For a circular outer
orbit (e2 = 0)
(41)For a circular outer
orbit (e2 = 0)  As
one can see, both sets of amplitudes, i.e.
As
one can see, both sets of amplitudes, i.e. 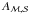 and A1,2,3 are independent of the real physical parameters of
the current exoplanetary system. Furthermore, the dependence on the elements of the outer
orbit (i.e. e2, g2) appears only in
the A1,2,3 Fourier amplitudes. The masses (or more accurately
mass ratios) and the periods and period ratios (and indirectly the physical size of the
system) only occur as a scaling parameter. In this way, the following general statements are
valid for all hierarchical triple systems (as long as the initial model assumptions are
valid). To get the real, i.e. physical values for the O−C amplitudes in a given system,
one must multiply the general system-independent, dimensionless amplitudes by the system
specific number
and A1,2,3 are independent of the real physical parameters of
the current exoplanetary system. Furthermore, the dependence on the elements of the outer
orbit (i.e. e2, g2) appears only in
the A1,2,3 Fourier amplitudes. The masses (or more accurately
mass ratios) and the periods and period ratios (and indirectly the physical size of the
system) only occur as a scaling parameter. In this way, the following general statements are
valid for all hierarchical triple systems (as long as the initial model assumptions are
valid). To get the real, i.e. physical values for the O−C amplitudes in a given system,
one must multiply the general system-independent, dimensionless amplitudes by the system
specific number 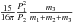 .
.
Considering first the (nearly) coplanar case, i.e. when I ≈ ± 1, then the
(half-)amplitude of the two sinusoidals becomes 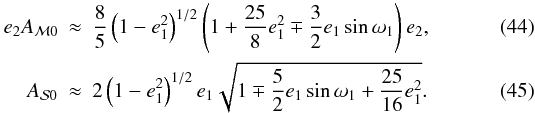 This
illustrates the above-mentioned fundamental differences to the previously-studied coplanar,
e1 = 0 case (Borkovits et al.
2003; Agol et al. 2005), as according to our
new result for eccentric inner orbits, the dynamical term does not disappear even if the
outer orbit is circular (e2 = 0). Furthermore, the amplitudes
strongly depend on the orientation of the orbital axis with respect to the observer. When
the apsidal line coincides (more or less) with the line of sight (i.e.
ω1 = ± 90°), there can be very significant differences both
in the shape and amplitude of the primary (transit) and secondary (occultation)
O−C curves. However, when the apsidal line lies nearly in the sky, then these differences
disappear. Another interesting feature of the ω1 = ± 90°
configuration is that for eclipse events that occur around apastron, there is a full square
under the square-root sign in the
This
illustrates the above-mentioned fundamental differences to the previously-studied coplanar,
e1 = 0 case (Borkovits et al.
2003; Agol et al. 2005), as according to our
new result for eccentric inner orbits, the dynamical term does not disappear even if the
outer orbit is circular (e2 = 0). Furthermore, the amplitudes
strongly depend on the orientation of the orbital axis with respect to the observer. When
the apsidal line coincides (more or less) with the line of sight (i.e.
ω1 = ± 90°), there can be very significant differences both
in the shape and amplitude of the primary (transit) and secondary (occultation)
O−C curves. However, when the apsidal line lies nearly in the sky, then these differences
disappear. Another interesting feature of the ω1 = ± 90°
configuration is that for eclipse events that occur around apastron, there is a full square
under the square-root sign in the 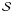 -term,
with the root of e1 = 0.8, which means that this term would
disappear in this situation. Nevertheless, for such high eccentricity, the first order
approximation is far from being valid, as is illustrated in Fig. 2.
-term,
with the root of e1 = 0.8, which means that this term would
disappear in this situation. Nevertheless, for such high eccentricity, the first order
approximation is far from being valid, as is illustrated in Fig. 2.
For highly inclined (I ≈ 0) orbits the (half-)amplitudes are as follows:
![\begin{eqnarray} e_2A_{{\cal{M}}90}&\approx&\frac{4}{5}\left(1-e_1^2\right)^{1/2}\left\{-1-\frac{25}{8}e_1^2\left(1-3\cos2g_1\right)\right. \nonumber \\ &&\left.\pm\frac{3}{2}e_1\left[\sin\omega_1-5\sin(\omega_1-2g_1)\right]\right\}e_2, \\ A_{{\cal{S}}90}&\approx&\frac{2}{5}\left(1-e_1^2\right)^{1/2}\left\{1+\frac{25}{8}e_1^2\left(1+\cos2g_1\right)\right. \nonumber \\ &&\left.\mp\frac{3}{2}e_1\left[\sin\omega_1+\frac{5}{3}\sin(\omega_1-2g_1)\right]\right\}, \label{Eq:AmpliP2dynperpendic} \end{eqnarray}](/articles/aa/full_html/2011/04/aa15867-10/aa15867-10-eq127.png) and
the phase of the
and
the phase of the 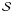 -term
is simply
-term
is simply 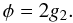 (48)In this case
another parameter, namely, the periastron distance of the inner planet from the intersection
of the two orbital planes (g1) also plays an important role.
(48)In this case
another parameter, namely, the periastron distance of the inner planet from the intersection
of the two orbital planes (g1) also plays an important role.
Finally we also mention a very specific case, the maximum eccentricity phase of the Kozai
mechanism driven e-cycles. During this phase,
cos2g1 takes one definite value, namely
cos2g1 = −1. Furthermore, the mutual inclination of the two
orbits here reaches its minimum. The actual value depends on both the maximum mutual
inclination im or, more strictly, on
j1 and the minimal inner eccentricity
e1. Nevertheless, in the case of an initially almost circular
inner orbit, the minimum mutual inclination is almost independent of its maximum value and
takes j1( ≈ 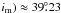 (or its retrograde counterpart,
j1( ≈
(or its retrograde counterpart,
j1( ≈ 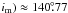 ),
i.e. I2 = 3/5. For this scenario
),
i.e. I2 = 3/5. For this scenario 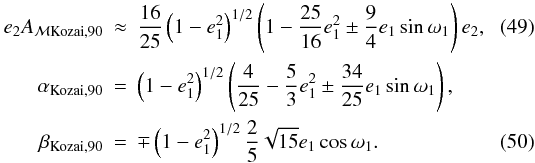 In
order to get a better overview of the parameter dependence of the formulae above, we
investigate the
In
order to get a better overview of the parameter dependence of the formulae above, we
investigate the 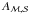 ,
as well as the A1,2,3, amplitudes graphically. Due to the
complex dependence of these amplitudes on many parameters, it is difficult to give general
statements. Therefore we investigate only the dependence of the amplitudes on the inner
eccentricity, while the effects of other parameters are considered in Sect. 4 for specific systems, where some of the parameters can be
fixed.
,
as well as the A1,2,3, amplitudes graphically. Due to the
complex dependence of these amplitudes on many parameters, it is difficult to give general
statements. Therefore we investigate only the dependence of the amplitudes on the inner
eccentricity, while the effects of other parameters are considered in Sect. 4 for specific systems, where some of the parameters can be
fixed.
Figure 2 shows the inner eccentricity
(e1) dependence of the amplitudes for some specific values of
the other parameters. In general, one sees that the e1 increase
with amplitude, but this growth usually remains within one order of magnitude. Although the
shapes of the individual O−C curves may differ significantly, the net amplitudes vary over
a narrow range. The graphs also suggest another, perhaps suprising, fact that the amplitude
of O−CP2dyn only weakly depends on the mutual inclination
(im). This is especially valid for medium inner
eccentricities, since in this case all  amplitudes have similar values, at least for the cases shown in Fig. 2. Moreover, the numerically generated sample O−C curves of Fig. 3 also suggest this conclusion. Nevertheless, there are
several exceptions. There are particular configurations where one of the two amplitudes, or
even both of them (and consequently, the corresponding terms), vanish. Such a situation is
discussed in Sect. 4.1. We return to this question in
detail in all of Sect. 4, where the dependence of the
amplitudes on other parameters will also be studied for the systems of CoRoT-9b and HD
80606b.
amplitudes have similar values, at least for the cases shown in Fig. 2. Moreover, the numerically generated sample O−C curves of Fig. 3 also suggest this conclusion. Nevertheless, there are
several exceptions. There are particular configurations where one of the two amplitudes, or
even both of them (and consequently, the corresponding terms), vanish. Such a situation is
discussed in Sect. 4.1. We return to this question in
detail in all of Sect. 4, where the dependence of the
amplitudes on other parameters will also be studied for the systems of CoRoT-9b and HD
80606b.
Returning now to the LITE amplitude and comparing it with the dynamical case, we see that
an increment of P2 (keeping P1
constant) results in an increment of
ALITE/AP2 − dyn by
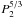 .
Consequently, for more distant systems, the pure geometrical effect tends to exceed the
dynamical one, as is the case in all but one (λ Tau, see e.g. Söderhjelm
1975) of the known hierarchical eclipsing triple stellar systems. Nevertheless, as
we illustrate in this paper (see Fig. 5), we have a
good chance of finding the opposite situation in some of the recently discovered transiting
exoplanetary systems. We can make the following crude estimation. Consider a system with a
solar-like host star, and two approximately Jupiter-mass companions)
(m123 ≈ m1 = 1 M⊙,
m2 = m3 = 10-3 M⊙),
choosing A = 10-3 day for the case of a certain detection, then
the LITE term for the most ideal case gives
P2 ≥ 106 d ≈ 2700 y. Alternatively, after setting
m3 = 10-2 M⊙ and
allowing A = 10-4 for detection limit, the result is
P2 ≥ 103 d ≈ 2.7 y. Similarly, for two
Jupiter-mass planet, in the coplanar case, for small e1, the
A = 10-3 day limit gives the
.
Consequently, for more distant systems, the pure geometrical effect tends to exceed the
dynamical one, as is the case in all but one (λ Tau, see e.g. Söderhjelm
1975) of the known hierarchical eclipsing triple stellar systems. Nevertheless, as
we illustrate in this paper (see Fig. 5), we have a
good chance of finding the opposite situation in some of the recently discovered transiting
exoplanetary systems. We can make the following crude estimation. Consider a system with a
solar-like host star, and two approximately Jupiter-mass companions)
(m123 ≈ m1 = 1 M⊙,
m2 = m3 = 10-3 M⊙),
choosing A = 10-3 day for the case of a certain detection, then
the LITE term for the most ideal case gives
P2 ≥ 106 d ≈ 2700 y. Alternatively, after setting
m3 = 10-2 M⊙ and
allowing A = 10-4 for detection limit, the result is
P2 ≥ 103 d ≈ 2.7 y. Similarly, for two
Jupiter-mass planet, in the coplanar case, for small e1, the
A = 10-3 day limit gives the 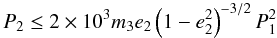 (51)condition
for the detectability of a third companion by its long-term dynamical perturbations. For the
perpendicular case the same limit is
(51)condition
for the detectability of a third companion by its long-term dynamical perturbations. For the
perpendicular case the same limit is 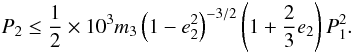 (52)We note that for
m3 ≪ m1 the above equations are
linear for m3, so it is very easy to give the limiting period
P2 in the function of m3.
Nevertheless, we emphasize again that there are so many terms with different periodicities
and phases that these equations give only a very crude first estimation. For
P1 = 1, 10, 100 days, (at zero outer eccentricity) gives
P2 ≤ 0.5, 50, 5000 days, respectively,
(52)We note that for
m3 ≪ m1 the above equations are
linear for m3, so it is very easy to give the limiting period
P2 in the function of m3.
Nevertheless, we emphasize again that there are so many terms with different periodicities
and phases that these equations give only a very crude first estimation. For
P1 = 1, 10, 100 days, (at zero outer eccentricity) gives
P2 ≤ 0.5, 50, 5000 days, respectively,
These results refer to the total amplitude of the O−C curve, i.e. the variation in the
transit times during a complete revolution of the distant companion, which can take as long
as several years or decades. Naturally, the perturbations in the transit times could be
observed within a much shorter period, from the variation in the interval between
consecutive minima. This estimation can be calculated, e.g., from Eq. (30) or even directly from Eq. (15). According to the meaning of the O−C
curve, the transiting or eclipsing period (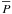 ) between two
consecutive (let us assume the nth and (n + 1)th) minima
is
) between two
consecutive (let us assume the nth and (n + 1)th) minima
is ![\begin{eqnarray} \overline{P}_n&=&t_{n+1}-t_{n} = \left({\rm O}{-}{\rm C}\right)(t_{n+1})-\left({\rm O}{-}{\rm C}\right)(t_n) \nonumber \\ &\approx&P_\mathrm{s}+\frac{P_1}{2\pi}A_\mathrm{L}\left(1-e_1^2\right)^{1/2}\Delta v_{2n}\left(1+e_2\cos v_{2n}\right) \nonumber \\ &&\times\left[\gamma+2\sqrt{\alpha^2+\beta^2}\cos(2v_{2n}+\phi)\right], \label{Eq:onetransit} \end{eqnarray}](/articles/aa/full_html/2011/04/aa15867-10/aa15867-10-eq158.png) (53)where
up to third order in
e2
(53)where
up to third order in
e2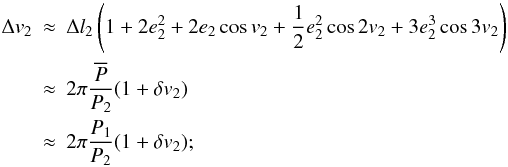 (54)i.e.,
we approximated the variation of the mean anomaly of the outer companion
(l2) by the constant value of
(54)i.e.,
we approximated the variation of the mean anomaly of the outer companion
(l2) by the constant value of
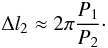 (55)(Here, and in the
following text we neglect the pure geometrical LITE contribution.) Then the variation in the
length of the consecutive transiting periods becomes
(55)(Here, and in the
following text we neglect the pure geometrical LITE contribution.) Then the variation in the
length of the consecutive transiting periods becomes ![\begin{eqnarray} \Delta\overline{P}&\approx&-\frac{15}{4}\pi\frac{m_3}{m_{123}}\frac{P_1^4}{P_2^3}\frac{\left(1-e_1^2\right)^{1/2}}{\left(1-e_2^2\right)^{3/2}}\nonumber \\ &&\times\left\{\gamma\left[3e_2\left(1+\frac{9}{2}e_2^2\right)\sin v_2-6e_2^2\sin2v_2-\frac{9}{2}e_2^3\sin3v_2\right]\right. \nonumber \\ &&+2\sqrt{\alpha^2+\beta^2}\left[2\left(1+8e_2^2\right)\sin(2v_2+\phi)\right. \nonumber \\ &&+\frac{7}{2}e_2\left(1+\frac{9}{2}e_2^2\right)\sin(v_2+\phi)\nonumber \\ &&+\frac{13}{2}e_2\left(1+\frac{9}{2}e_2^2\right)\sin(3v_2+\phi)\nonumber \\ &&\left.\left.+\frac{1}{4}e_2^3\sin(-v+\phi)+\frac{19}{4}e_2^3\sin(5v_2+\phi)\right]\right\}. \label{Eq:deltaPv2} \end{eqnarray}](/articles/aa/full_html/2011/04/aa15867-10/aa15867-10-eq161.png) (56)Comparing
(the amplitude of) this result with Eqs. (1, 2) of Holman
& Murray (2005), one can see that the power of the period ratio differs.
(Furthermore, in the original paper π stands at the same place, i.e. in the
numerator as above but later, in Holman 2010, this
was declared as an error, and it was put into the denominator.) There is a principal
difference in the background. Holman & Murray
(2005) state that they “estimate the variation in transit intervals between
successive transits”, but what they really calculate is the departure of a transiting period
(i.e. the interval between two successive transits) from a constant mean value. This
quantity was estimated in our Eq. (53). In
other words, the Lagrangian perturbation equations gives the instantaneous period of the
perturbed system, so its integration gives the time left between two consecutive minima. The
first derivative of the perturbation equation gives the instantaneous period variation, and
so the variation in the length of two consecutive transiting period can be deduced by
integrating the latter. As a consequence, the best possibility for detecting the TTV, hence
for the presence of some perturber, occurs when the absolute value of the second derivative
of the O−C diagram, or practically Eq. (56) (the period variation during a revolution) is maximum. We illustrate this
statement in the next section for specific systems.
(56)Comparing
(the amplitude of) this result with Eqs. (1, 2) of Holman
& Murray (2005), one can see that the power of the period ratio differs.
(Furthermore, in the original paper π stands at the same place, i.e. in the
numerator as above but later, in Holman 2010, this
was declared as an error, and it was put into the denominator.) There is a principal
difference in the background. Holman & Murray
(2005) state that they “estimate the variation in transit intervals between
successive transits”, but what they really calculate is the departure of a transiting period
(i.e. the interval between two successive transits) from a constant mean value. This
quantity was estimated in our Eq. (53). In
other words, the Lagrangian perturbation equations gives the instantaneous period of the
perturbed system, so its integration gives the time left between two consecutive minima. The
first derivative of the perturbation equation gives the instantaneous period variation, and
so the variation in the length of two consecutive transiting period can be deduced by
integrating the latter. As a consequence, the best possibility for detecting the TTV, hence
for the presence of some perturber, occurs when the absolute value of the second derivative
of the O−C diagram, or practically Eq. (56) (the period variation during a revolution) is maximum. We illustrate this
statement in the next section for specific systems.
4. Case studies
4.1. CoRoT-9b
 |
Fig. 4 Left panels: the dependence on the mutual inclination
(im) of the amplitudes Aℳ,
|
CoRoT-9b is a transiting giant planet that revolves around its host star approximately at the distance of Mercury (Deeg et al. 2010). Consequently, tidal forces (including the possible rotational oblateness) can safely be neglected in this system. Furthermore, thanks to the relatively large absolute separation of the planet from its star, we can expect a large amplitude signal from the perturbations of a hypothetical, distant (but not too distant) additional companion. To illustrate this possibility, and, furthermore, to check our formulae, we both calculated and plotted the amplitudes with the measured parameters of this specific system, and carried out short-term numeric integrations for comparison. The physical parameters and some of the orbital elements of CoRoT-9b were taken from Deeg et al. (2010). These data are listed in Table 1. (We added 180° to the ω1 published in that paper, as the spectroscopic ω1 refers to the orbit of the host star around the common centre of mass of the star-planet double system, so it differs by 180° from the observational argument of periastron of the relative orbit of the transiting planet around its host star.) In the case of the numerical integrations, the inner planets were started from periastron and the outer one from its apastron.
The initial parameters of the transiting planetary subsytems.
Fixing the observationally aquired data, 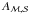 only depend on two parameters, namely g1 and
im. In the left panels of Fig. 4, we plotted the im versus
only depend on two parameters, namely g1 and
im. In the left panels of Fig. 4, we plotted the im versus
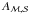 graphs for g1 = 69° and g1 = 158°.
We find that the amplitudes reach their extrema around these periastron arguments; i.e.
for other g1 values, results occur within the areas limited by
these lines6. In the middle and right panels, the
effect of the two other free parameters, i.e. outer eccentricity
(e2), and dynamical (relative) argument of periastron
(g2) were also considered. The middle panels show
A1,2 for e2 = 0.3, the right
panels for e2 = 0.7, for both
g2 = 0° (upper panels), and
g2 = 90° (bottom panels).
(
graphs for g1 = 69° and g1 = 158°.
We find that the amplitudes reach their extrema around these periastron arguments; i.e.
for other g1 values, results occur within the areas limited by
these lines6. In the middle and right panels, the
effect of the two other free parameters, i.e. outer eccentricity
(e2), and dynamical (relative) argument of periastron
(g2) were also considered. The middle panels show
A1,2 for e2 = 0.3, the right
panels for e2 = 0.7, for both
g2 = 0° (upper panels), and
g2 = 90° (bottom panels).
(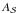 ,
plotted in the left panel is identical to A2 for
e2 = 0, in which case A1,3 = 0.)
,
plotted in the left panel is identical to A2 for
e2 = 0, in which case A1,3 = 0.)
These figures clearly show again that the amplitudes, and consequently, the actual full
amplitude of the dynamical O−C curve remains within one order of magnitude over a wide
range of orbital parameters. This once more verifies the very crude estimations given by
Eqs. (51), (52). As a consequence, for a given system we
can very easily estimate the expected amplitude of the O−C variations induced by an
additional companion. For a planet-mass third body, the
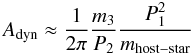 (57)gives
a likely estimation at least in magnitude. For example, for CoRoT-9b,
(57)gives
a likely estimation at least in magnitude. For example, for CoRoT-9b,  (58)i.e.,
a Jupiter-mass additional planet could produce 0ḍ001 half-amplitude already from the
distance of the Mars. (Of course, if e1 and
ω1 are known, a more precise estimation can be provided
easily using the formulae of the present paper.)
(58)i.e.,
a Jupiter-mass additional planet could produce 0ḍ001 half-amplitude already from the
distance of the Mars. (Of course, if e1 and
ω1 are known, a more precise estimation can be provided
easily using the formulae of the present paper.)
Nevertheless, while the net amplitudes usually vary in a narrow range, the dominances of
the two main terms (with period P2 and
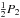 ) can alternate
and, although it is not shown, their relative phase can also vary, so the shape of the
actual curves may show great diversity, as is illustrated in Figs. 3, 5. Furthermore, for specific
values of the parameters, one or other of the amplitudes might disappear. At CoRoT-9b particularly interesting is the
g1 = 69°im ~ 45°configuration
since in this case both Aℳ and
) can alternate
and, although it is not shown, their relative phase can also vary, so the shape of the
actual curves may show great diversity, as is illustrated in Figs. 3, 5. Furthermore, for specific
values of the parameters, one or other of the amplitudes might disappear. At CoRoT-9b particularly interesting is the
g1 = 69°im ~ 45°configuration
since in this case both Aℳ and
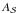 disappear very close to each other. This means that the dynamical O−C almost disappears
for specific e2, g2 values. This
possibility warns us that from the absence of TTV in a given system one cannot
automatically exclude the presence of an additional planet (which should be observed
according to its parameters).
disappear very close to each other. This means that the dynamical O−C almost disappears
for specific e2, g2 values. This
possibility warns us that from the absence of TTV in a given system one cannot
automatically exclude the presence of an additional planet (which should be observed
according to its parameters).
 |
Fig. 5 Sample of transit timing variations caused by a hypothetical P2 = 10 000 day-period m3 = 0.005 M⊙ (≈5 MJ) mass third companion for CoRoT-9b at four different initial mutual inclinations (im = 0°, 40°, 46°, 90°, from up to down), and three different initial outer eccentricities (e2 = 0, 0.3, 0.7, from left to right). The dynamical (relative) arguments of periastrons are set to g1 = 69°, g2 = 90°. The curves show the sum of the geometrical LITE, and the dynamical terms obtained both from numeric integrations, and analytic calculations up to sixth order in e1. The pure LITE contributions are also plotted separately. Note that the vertical scale of the individual columns (i.e. different e2-s) are different. |
This can be seen clearly in Fig. 5, where we plotted the corresponding O−C curves for coplanar, perpendicular, and the above-mentioned interesting im = 40° and 46° configurations. In this figure we plotted O−C curves obtained from both numerical integrations of the three-body motions and analytical calculations with our sixth-order formula. (According to Fig. 2, for the small inner eccentricity of CoRoT-9b, e1 = 0.11, the first-order approximation would have given practically the same results.) Comparing the analytical and the numerical curves, the best similarity can be seen in the perpendicular case (last row). In the coplanar case some minor discrepancies can be observed both in the shape and amplitude, while the discrepancies are expressed more in the particular im = 46° case, where for high outer eccentricity (right panel in the third row) our solution fails. (Nevertheless, the total amplitude of the analytical curve is similar to the numerical one in this case, too.) Although a thorough analysis of the sources of the discrepancies is beyond the scope of this paper, we suppose that in these situations the discrepancies come from the higher order perturbative terms. As was shown by Söderhjelm (1982) and Ford et al. (2000, among others), the higher order contributions are the most significant for e1 ~ 0, im = (0,1) × 180°. Although these authors only considered the secular, or apse-node term perturbations, the same might be the case for the long-period ones. This might explain the better correspondence in the perpendicular configuration than in the coplanar one. We suppose there is some similar reason in the im = 46° case. As in this situation the first order contributions almost disappear, whereas the small higher order terms can also be more significant. Furthermore, numeric integrations in this case show a disappearence of the identity between the g1, g1 + 180° initial conditions, which also suggests a significance of the higher order terms, because in these terms we can expect the appearance of trigonometric functions with g1 and 3g1 in their arguments.
 |
Fig. 6 The first and the second 8 years of O−C-s plotted in the first and the last rows of Fig. 5. The periods of the individual curves were set equal to the respective initial transiting periods. |
As expected, the highly eccentric-distant-companion scenario produces the largest amplitude TTV, at least when a complete revolution is considered. Nevertheless, on a shorter time scale, the length of the observing window necessary for the detection depends highly on the phase of the curve. To illustrate this, in Fig. 6 we plotted the first, and second 8 years of the three primary transit O−C curves for both the coplanar, and the perpendicular cases, shown in the first and last rows of Fig. 5. The transiting periods for each curve were calculated in the usual observational manner; i.e., the time interval between the first (some) transits were used. In the e2 = 0.7 cases, according to Fig. 6, it would be unlikely to detect the perturbations within the first eight years, despite that they show the largest (total) amplitude. The same conclusion can be drawn for the coplanar e2 = 0.3 case. The most certain detection would be possible in the two smallest amplitude, circular e2 = 0 configurations. Nevertheless, if the observations start at those phases plotted in the right panels (8−16 years), the pictures completely differ. In this latter interval, the circular cases produce the smallest curvature O−C-s, and the discrepancy from the linear trend reaches 0ḍ001 days (which can be considered as a limit for certain detection) occurring towards the end of the interval. On the other hand, in the case of the highly eccentric configurations, the “moment of truth” comes after some years. Nevertheless, we have to stress that, although we plotted the O−C curves with continuous lines, in reality they would contain only 3 − 4 points during the phase of the seemingly abrupt jump, which is a further complicating factor with regards to “certain” detection.
 |
Fig. 7 Checking the validity of hierarchical approximation for closer systems. In the first two rows the initial conditions were set to be the same as at the uppermost middle panel of Fig. 5, with the exception of P2 = 1000 (first row) and 2000 days (second row), i.e. a2/a1 ≈ 4.8 and ≈ 7.6, respectively, while the third and last rows have initial conditions similar to the bottom middle panel of Fig. 5, with the exception of P2 = 1000 (third row) and 952.7 days (last row). This latter illustrates the case of a 1:10 mean-motion resonance. The left panels represent a 20-year-long time scale, while the right ones show the TTV behaviour during a century. In the left panel of the last row the blue (quadratic) curve shows the O−C curve calculated by including a quadratic term. See text for details. |
In the sample runs above, a moderately hierarchic scenario
a2 ≈ 22a1 was studied. To get
some picture about the lower limit of the validity of our low-order, hierarchical
approximation, we carried out other integrations for less hierarchic configurations. In
Fig. 7 we show the results of some of these runs,
which were carried out with the same initial conditions as used in the middle panel of the
first and last rows (coplanar and perpendicular cases, respectively) of Fig. 5, but for P2 = 1000 days
(i.e. a2 ≈ 4.8a1),
P2 = 2000 days
(a2 ≈ 7.6a1), and
P2 ≈ 952.7 days
(a2 ≈ 4.6a1), in which last case
the two planets orbit in 1:10 mean motion resonance. In the left panels of Fig. 7 we plot 20-year-long intervals, while in right ones
show century-long time scales. As one can see, on this time scale, apse-node effects
already reach or exceed the magnitude of the long period ones. This naturally arises from
the fact that the typical time scales of these high-amplitude perturbations are
proportional to 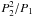 ; i.e., in the
present cases these are ~ 100 × faster than in the previously investigated
case. For the sake of a better comparison, the analytical curves in the right panels were
calculated by including these apse-node terms, although these terms will only be presented
in a forthcoming paper. Turning back to the 20-year-long integrations, one can see that
the limit of the validity of the present approximation indeed strongly depends on the
mutual inclination. While for the im = 90° configurations the
long period analytical results are in remarkably good agreement with the numerical curves
even for a2 < 5a1 (left
panels of third and forth rows), for the coplanar (im = 0°)
case our approximation is clearly insufficient for such low
a2/a1 ratios, and even for the
doubled outer period case (i.e.
a2 ≈ 8a1) the amplitude of the
analytical curve is highly underestimated.
; i.e., in the
present cases these are ~ 100 × faster than in the previously investigated
case. For the sake of a better comparison, the analytical curves in the right panels were
calculated by including these apse-node terms, although these terms will only be presented
in a forthcoming paper. Turning back to the 20-year-long integrations, one can see that
the limit of the validity of the present approximation indeed strongly depends on the
mutual inclination. While for the im = 90° configurations the
long period analytical results are in remarkably good agreement with the numerical curves
even for a2 < 5a1 (left
panels of third and forth rows), for the coplanar (im = 0°)
case our approximation is clearly insufficient for such low
a2/a1 ratios, and even for the
doubled outer period case (i.e.
a2 ≈ 8a1) the amplitude of the
analytical curve is highly underestimated.
We also investigated the case of the 1:10 mean-motion resonance. Our results for the
perpendicular case are plotted in the last row. In this case the numerical integration
shows very high amplitude apse-node scale variations that do not occur in the analytical
curve. To better compare the analytical and numerical long-term variations in this case,
we removed the apse-node effect from the numerical curve by using a quadratic term; i.e.,
the (blue) O−C curve was calculated in the form of
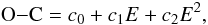 (59)where
E is the cycle number. As one can see, this quadratic (blue) curve
shows similar agreement with the analytical curve, which was found in the similar
a2/a1 ratio non-resonant case.
Consequently, we can state that our long term formulae are capable of producing the same
accuracy even around mean-motion resonances.
(59)where
E is the cycle number. As one can see, this quadratic (blue) curve
shows similar agreement with the analytical curve, which was found in the similar
a2/a1 ratio non-resonant case.
Consequently, we can state that our long term formulae are capable of producing the same
accuracy even around mean-motion resonances.
Nevertheless, from these few arbitrary trial runs we cannot make general statements about the limits of our approximations. A detailed discussion of this point is postponed to a forthcoming paper, where we will include the apse-node time scale terms.
While CoRoT-9b served as an illustration for the TTVs in the low inner eccentricity case, our next sample exoplanet HD 80606b represents the extremely eccentric case.
4.2. HD 80606b
The high-mass gas giant exoplanet HD 80606b features an almost 4-month long period and an extremely eccentric orbit around its solar-type host star. It was discovered spectroscopically by Naef et al. (2001). Recently both secondary occultation (with the Spitzer space telescope, Laughlin et al. 2009), and primary transit (Moutou et al. 2009; Fossey et al. 2009) have been detected. A thorough analysis of the collected data around the February 2009 primary transit led to the conclusion that there is a significant spin-orbit misalignment in the system, i.e. the orbital plane of HD 80606b fails to coincide with the equatorial plane of its host star (Pont et al. 2009). These facts suggest that this planet might be seen at an instant close to the maximum eccentricity phase of a Kozai cycle induced by a distant, inclined third companion (cf. Wu & Murray 2003; Fabrycky & Tremaine 2007). Although HD 80606 itself forms a binary with HD 80607, due to the large separation, one may expect an additional, not so distant companion for an effective Kozai mechanism. The very distant companion HD 80607 may nevertheless play an indirect role in the initial triggering of the Kozai mechanism, by the effect described in Takeda et al. (2009). The most important parameters of the system are summarized in Table 1.
Due to its very high eccentricity, the periastron distance of this planet is q1 = a1(1 − e1) ≈ 0.03 AU, at which distance the tidal forces and especially tidal dissipation should be effective. (As a comparison we note that this separation corresponds to the semi-major axis of an approx. 2 day period orbit.) Furthermore, we can also expect a significant relativistic contribution to the apsidal motion. Although such circumstances do not invalidate the following conclusions (as the time scales of these effects are significantly longer than the ones investigated), we nevertheless provide a quantitive estimation of their effects. Furthermore, the effect of dissipation will also be considered numerically at the end of this section.
The apsidal advance speed, averaged for one orbital revolution, can be written in the
following form: 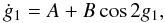 (60)where the non-zero
contributions of the third-body, tidal, and relativistic terms are as follows:
(60)where the non-zero
contributions of the third-body, tidal, and relativistic terms are as follows:
![\begin{eqnarray} A_{3^\mathrm{rd}}&=&A_\mathrm{L}\frac{P_1}{P_2}\left(1-e_1^2\right)^{-1/2}\left[I^2-\frac{1}{5}\left(1-e_1^2\right)+\frac{2}{5}\left(1+\frac{3}{2}e_1^2\right)\frac{C_1}{C_2}I\right], \nonumber \\ \\ B_{3^\mathrm{rd}}&=&A_\mathrm{L}\frac{P_1}{P_2}\left(1-e_1^2\right)^{-1/2}\left[\left(1-e_1^2\right)-I^2-e_1^2\frac{C_1}{C_2}I\right], \\ A_\mathrm{tidal}&=&\frac{5{\cal{T}}}{2a_1^5}\frac{1+\frac{3}{2}e_1^2+\frac{1}{8}e_1^4}{\left(1-e_1^2\right)^5}+\frac{\cal{R}}{a_1^2\left(1-e_1^2\right)^2}, \\ A_\mathrm{rel}&=&6\pi\frac{Gm_1}{c^2a_1(1-e_1^2)}, \end{eqnarray}](/articles/aa/full_html/2011/04/aa15867-10/aa15867-10-eq224.png) where
where
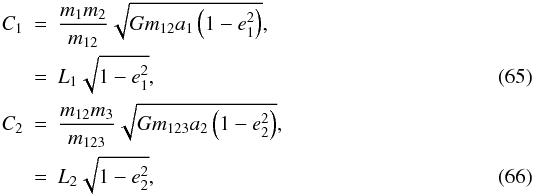 moreover,
moreover,
![\begin{eqnarray} {\cal{T}}&=&6\left(\frac{m_2}{m_1}k_2^{(1)}R_1^5+\frac{m_1}{m_2}k_2^{(2)}R_2^5\right), \nonumber\\ &=&6\frac{m_2}{m_1}R_1^5\left[k_2^{(1)}+k_2^{(2)}\left(\frac{\overline{\rho}_1}{\overline{\rho}_2}\right)^2\frac{R_1}{R_2}\right], \\ {\cal{R}}&=&\frac{k_2^{(1)}R_1^5\omega^2_{z'_1}}{Gm_1}+\frac{k_2^{(2)}R_2^5\omega^2_{z'_2}}{Gm_2} \nonumber \\ &=&\frac{3k_2^{(1)}}{4\pi G\overline{\rho}_1}v^2_{\mathrm{e}_1}+\frac{3k_2^{(2)}}{4\pi G\overline{\rho}_2}v^2_{\mathrm{e}_2}. \end{eqnarray}](/articles/aa/full_html/2011/04/aa15867-10/aa15867-10-eq226.png) In
these equations m1, R1,
In
these equations m1, R1,
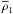 ,
,
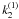 ,
,
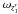 , and
ve1 refer to the mass, radius, average density,
first apsidal motion constant, uni-axial rotational angular velocity, and equatorial
rotational velocity of the host star, respectively, while subscript 2 denotes
the same quantities for the inner planet. Also, the rotational term is only valid for
non-aligned rotation, and consequently only provides a crude estimation for HD 80606b. Nevertheless, for the present purpose it seems
satisfactory. First consider the third-body term. Substituting
cos2g = −1, I2 = 3/5,
, and
ve1 refer to the mass, radius, average density,
first apsidal motion constant, uni-axial rotational angular velocity, and equatorial
rotational velocity of the host star, respectively, while subscript 2 denotes
the same quantities for the inner planet. Also, the rotational term is only valid for
non-aligned rotation, and consequently only provides a crude estimation for HD 80606b. Nevertheless, for the present purpose it seems
satisfactory. First consider the third-body term. Substituting
cos2g = −1, I2 = 3/5, ![\begin{eqnarray} \dot g_{3^\mathrm{rd}}&=&\frac{3\pi}{2}\frac{m_3}{m_{123}}\left(\frac{P_1}{P_2}\right)^2\left(1-e_2^2\right)^{-3/2}\left(1-e_1^2\right)^{-1/2} \nonumber \\ &&\times\left[3e_1^2\pm\sqrt{\frac{3}{5}}\left(1+4e_1^2\right)\frac{L_1}{L_2}\sqrt{\frac{1-e_1^2}{1-e_2^2}}\right], \label{eq:g1p_3rd} \end{eqnarray}](/articles/aa/full_html/2011/04/aa15867-10/aa15867-10-eq233.png) (69)from
which the last term is usually omittable in hierarchical systems, since
C1 ≪ C2, which is more
expressively true for high e1. For example, in the present
situation
(69)from
which the last term is usually omittable in hierarchical systems, since
C1 ≪ C2, which is more
expressively true for high e1. For example, in the present
situation 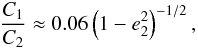 (70)so for HD 80606b we find that
(70)so for HD 80606b we find that
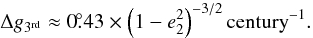 (71)(This result is in
excellent correspondence with Fig. 11.)
(71)(This result is in
excellent correspondence with Fig. 11.)
There are several uncertainties in the calculation of the tidal contribution. While the
k2 constant is relatively well-known for ordinary stars, it
is very ambigous for exoplanets. Furthermore, we know nothing about the rotational
velocity of HD 80606b. For the numeric
integrations, according to the tables of Claret &
Gimènez (1992) we thus set 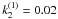 for the host star, and assume
for the host star, and assume
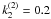 for its planet, which is the
same order of magnitude as for Jupiter and for
WASP-12b (Campo et al. 2011). The stellar rotation is set to
Vrot = 1.8 km s-1 (i.e.
Prot = 27ḍ5;
for its planet, which is the
same order of magnitude as for Jupiter and for
WASP-12b (Campo et al. 2011). The stellar rotation is set to
Vrot = 1.8 km s-1 (i.e.
Prot = 27ḍ5; 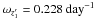 )
(Fischer & Valenti 2005), while for the
planet we take (arbitrarily) a one-day rotation period, i.e.
)
(Fischer & Valenti 2005), while for the
planet we take (arbitrarily) a one-day rotation period, i.e.
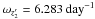 .
With these values, the classical tidal contribution to the apsidal motion becomes
.
With these values, the classical tidal contribution to the apsidal motion becomes
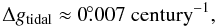 (72)which can be neglected.
(72)which can be neglected.
Finally, the relativistic contribution is estimated to be
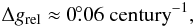 (73)i.e. it is smaller by one
magnitude than the third-body term, so does also not play any important role.
(73)i.e. it is smaller by one
magnitude than the third-body term, so does also not play any important role.
Returning to the P2 time scale variations of the TTVs, we
carried out our calculations and integration runs with the supposition that a second,
similar mass giant planet is the source of this comet-like orbit, which is seen at the
instant of the maximum eccentricity phase of the Kozai-cycle. Consequently, we set
g1 = 90°, and 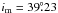 .
With these values from the sixth-order formula, we get
Aℳ = −0.38,
.
With these values from the sixth-order formula, we get
Aℳ = −0.38, 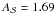 for primary transits, and Aℳ = −1.06,
for primary transits, and Aℳ = −1.06,
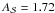 for secondary occultations. Consequently, for primary transits, the O−C is evidently
dominated by the
for secondary occultations. Consequently, for primary transits, the O−C is evidently
dominated by the  -term.
(The negative Aℳ indicates a simple 180° phase shift.) In
Fig. 8 the A1,2,3
amplitudes are plotted as a function of the outer eccentricity
(e2). Due to the more than four and a half-times larger
primary transit
-term.
(The negative Aℳ indicates a simple 180° phase shift.) In
Fig. 8 the A1,2,3
amplitudes are plotted as a function of the outer eccentricity
(e2). Due to the more than four and a half-times larger
primary transit  amplitude, the g2 dependence of the amplitudes here are weak,
and therefore we show only A1,2,3-s for
g2 = 0°.
amplitude, the g2 dependence of the amplitudes here are weak,
and therefore we show only A1,2,3-s for
g2 = 0°.
 |
Fig. 8 The A1,2,3 amplitudes for HD 80606b for primary transits (left), and secondary occultations (right), supposing that the planet is seen at the instant of the maximum phase of a Kozai-cycle. |
In Fig. 9 we present both the numerically generated short-term O−C curves and the analytically calculated cases up to the sixth order in eccentricity (see Appendix B) for three different eccentricities (e2 = 0, 0.3, 0.7) of the outer perturber’s orbit. We plotted the O−C-s for both primary transits and secondary occultations. Also shown are the corresponding primary minus secondary curves.
As one can see, the sixth-order formulae gave satisfactory results even for such high
eccentricities, although the analytical amplitudes are somewhat overestimated.
Nevertheless, a more detailed analysis shows that the accuracy of our formulae for such
high inner eccentricities strongly depends on the other orbital parameters. This is
illustrated even in the present situation, where, for the secondary-occultation curves,
(which correspond to ω1 = 301°), the discrepancies are clearly
larger. From this point of view, the e2 = 0 case (first row)
is even more interesting, because in this situation, where the only one non-vanishing
amplitude is 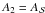 ,
the similar AS values would lead to almost identical O−C
curves (compare the corresponding dashed analytical curves). However, according to the
numerical results (see the solid curves), this, in fact, is not the case.
,
the similar AS values would lead to almost identical O−C
curves (compare the corresponding dashed analytical curves). However, according to the
numerical results (see the solid curves), this, in fact, is not the case.
 |
Fig. 9 Transit timing variatons caused by a hypothetical P2 = 10 000 day-period m3 = 0.005 M⊙( ≈ 5 MJ) mass third companion for HD 80606b at the maximum eccentricity phase of the induced Kozai-cycles. Top: e2 = 0; middle: e2 = 0.3; bottom: e2 = 0.7 (g2 = 0° in all cases); left panels: primary transits; middle panels: secondary occultations; right panels: primary minus secondary difference. See text for further details. (For better comparison the curves are corrected for the different average transit periods, and zero point shifts.) |
Considering the case of fastest possible detection of the amplitudes, in Fig. 10 we also plotted the first and second 8 years of the three primary transit O−C curves shown in Fig. 9. The transiting periods for each curves were calculated in the usual observational manner, i.e. with the time interval between the first (some) transits. According to Fig. 10, in the first eight years, i.e. after the apastron of the outer body, the fastest detection would be possible in the smallest (total) amplitude circular third body case, while the curvature of the highly eccentric curve is so small that it needs almost seven years to exceed the 0ḍ001 difference, which could promise certain detection. (Of course, this is a non-realistic ideal case, where all the transits are measured without any observational error.) Around periastron (right panel), the situation is completely different, similar to the case of CoRoT-9b.
 |
Fig. 10 The first and second 8 years of the left panels of Fig. 9. The periods of the individual curves was set equal to the each initial transiting periods. |
 |
Fig. 11 Dynamical evolution of the orbital elements of HD 80606b in the presence of a hypothetical P2 = 10 000 day-period m3 = 0.005 M⊙(≈5 MJ) mass third companion. The initial orbital elements correspond to the last row of Fig. 9. Red curves: tidal effects and dissipation are considered; blue curves: three point-mass model. (Relativistic contributions are omitted.) Note, the semi-major axis (a1) is given in R⊙. |
We also carried out numerical integrations to investigate the possible orbital evolution of HD 80606b in the presence of such a perturber. We have shown that both relativistic and tidal effects can be omitted in the present configuration of the system. However, this assumption is only correct in those cases where tidally forced dissipation is not considered. Consequently, we have integrated the dynamical evolution of the system both with tidal effects (both dissipative and conservative tidal terms) and without them (i.e. in the frame of pure three, point-mass gravitational interactions). The equations of the motion (including tidal and dissipative terms and stellar rotation) are given in Borkovits et al. (2004), where the description of our integrator can also be found. In the dissipative case, our dissipation constant was selected in such a way that it produced Δt1 ≈ 2ḍ16 × 10-7 tidal lag-time for the host-star, and Δt1 ≈ 5ḍ21 × 10-4 for the planet, which are equivalent to Q1 ≈ 4.1 × 107, Q2 ≈ 1.7 × 104 dissipation parameters, respectively. Figure 11 shows the variation in most of the orbital elements (both dynamical and observational) for 100 and 1 million years in the dynamically most-excited e2 = 0.7 case. Thin lines represent the dissipative case, while thick curves show the point-mass result. The century-long left panel demonstrates that, apart from the shrinking semi-major axis, there is no detectable variation in the orbital elements during such a short time interval. And, of course, if this is true for the extremum of the Kozai cycle, it is more expressly valid for other situations, as this phase produces the fastest orbital element variations. Furthermore, on such a short time scale, the orbital variations in a point-mass or non-Keplerian, tidal framework are indistinguishable. (Again, we do not take the semi-major axis into account.) This provides further verification of the effects discussed previously, namely that we have neglected the tidal and relativistic effects completely and considered all the orbital elements as constant.
Now, we consider orbital shrinking due to dissipation. As one can see, in the present situation the decrease in a1 during the first 100 years is Δa1 ≈ 6 × 10-4 R⊙. Converting this into a period variation suggests ΔP1 ≈ 10-3 d. This gives a Ṗ1 ≈ 3 × 10-6 day cycle-1 rate for one transiting period. From the point of view of an eclipsing binary observer, this is an incredibly high value. For comparison, a typical, secular period variation rate measured for many of the eclipsing binaries is about a 10-9 − 10-11 day cycle-1. Such a high rate would produce 0ḍ001 departure in transit time during ~26 cycles, i.e. during approximately eight years. This period variation ratio is close to the ratio produced by typical long-term perturbations within a few years. This illustrates that, if the data-length is significantly shorter than the period of the long-term periodic perturbations, then the effect has arisen from such perturbations, and other effects of i.e. orbital shrinking can overlap each other and can as a result, be misinterpreted easily. (The question of such kinds of misinterpretations or false identifications were considered in general in Sect. 2 of Borkovits et al. 2005.)
Finally, we consider the right panel of Fig. 11, which illustrates the frequently mentioned Kozai-mechanism (with and without tidal friction) in operation. In the present situation, because of the high outer eccentricity and along with the relatively weak hierarchicity of the system (i.e. a1/a2 ≈ 0.05), the higher order terms of the perturbation function are also significant, which results in very different consecutive cycles even in the point-mass case. This manifests itself not only as different periods and maximum eccentricities, but also in how the argument of (dynamical) periastron (g1) shows both circulation and libration, alternately (cf. Ford et al. 2000). Nevertheless, the detailed investigation of the apse-node time scale behaviour of the TTV, as well as other orbital elements and observables, will be the subject of a subsequent paper.
5. Conclusions
We have studied the long-term P2 time scale TTVs in transiting exoplanetary systems, which feature an additional, more distant (a2 ≫ a1) planetary, or else stellar, companion. We gave the analytical form of the O−C diagram, which describes such TTVs. Our result is an extension of our previous work Borkovits et al. (2003) for arbitrary orbital elements of both the inner transiting planet and the outer companion. We showed that the dependence of the O−C on the orbital and physical parameters can be separated into three parts. Two of these are independent of the real physical parameters (i.e. masses, separations, periods) of a concrete system and only depend on dimensionless orbital elements, and so can be analysed in general. For the two other kinds of parameters, which are amplitudes and phases of trigonometric functions, we separated the orbital elements of the inner from the outer planet. The practical importance of such a separation is that in the case of any actual transiting exoplanets, if eccentricity (e1) and the observable argument of periastron (ω1) are known, e.g., from spectroscopy, then the main characteristics of any, caused by a possible third body, TTVs can be mapped simply by the variation in two free parameters (dynamical, relative argument of periastron, g1, and mutual inclination, im), which then can be refined by the use of the other derived parameters, including two additional parameters for the possible third body (eccentricity, e2, and dynamical, relative argument of periastron, g2). Moreover, as the physical attributes of a given system only occur as scaling parameters, the real amplitude of the O−C can also be estimated for a given system, simply as a function of the m3/P2 ratio.
At this point it would be beneficial to compare our results with the conclusions of Nesvorný & Morbidelli (2008) and Nesvorný (2009). These authors have investigated the same problem, i.e. the fast detection of outer perturbing planets and the determination of their orbital and physical parameters from their perturbations on the transit timing of the inner planet, by the help of the analytical description of the perturbed transiting O−C curve. For the mathematical description, they use the explicit perturbation theory of Hori (1966) and Deprit (1969), based on canonical transformations and on the use of Lie-series. This theory does not require the hierarchical assumption; i.e., the α = a1/a2 parameter, although less than unity, is not required to be small. This suggests a somewhat greater generality of the results, so it is applicable systems similar to our solar system. Nevertheless, perhaps a small disadvantage to this method over the hierarchical approximation is that, for large mutual inclinations, the number of terms in the perturbation function needed for a given accuracy grows very fast, while our formulae have the same accuracy even for the highest mutual inclinations. There is also a similar discomfort in the case of high eccentricities, in which case the general formulae of Nesvorný (2009) are more sensitive to these parameters than in the hierarchical case. For example, we could reproduce satisfactory accuracy even for e1 = 0.9, in which case the classical formulae are divergent. (Although we concentrate only on the long-period perturbations, the same is valid for the apse-node time scale variations, as will be illustrated in the next paper.) As a conclusion, the method used by Nesvorný & Morbidelli (2008) and Nesvorný (2009) beyond the evident non-hierarchical configurations is similarly (or even better) applicable in the nearly coplanar case, too, especially when the inner orbit is nearly circular (a special case where the first-order hierarchical approximation becomes insufficient, see e.g. Ford et al. 2000), but in other cases, our approach could give a faster and simpler method, as long as the hierarchical assumption is satisfied. Furthermore, since in the hierarchical approximation, the principal small parameter in the perturbation equations is the ratio of the separations instead of the mass ratio, these formulae are valid for stellar mass objects as well, and can also be applied to planets orbiting an S-type orbit in binary stars, or even for hierarchical triple stellar systems.
We analysed the above-mentioned dimensionless amplitudes for different arbitrary initial parameters, as well as for two concrete systems CoRoT-9b and HD 80606b. We found in general that, while the shape of the O−C strongly varies with the angular orbital elements, the net amplitude (departing from some specific configurations) depends only weakly on these elements, but strongly on the eccentricities. Nevertheless, we found some situations around im = 45° for the specific case of CoRoT-9b, where the O−C almost disappeared.
We used CoRoT-9b and HD 80606b for case studies. Both giant planets revolve on several monthly
orbits. The former has an almost circular orbit, while the latter has a comet-like,
extremely eccentric orbit. These large-period systems are ideal for searching for other
perturbing components, since the amplitude of the O−C is multiplied by
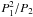 and consequently, as
the magnitude of the perturbations determined by
P1/P2, the same amplitude
perturbations cause a more detectable effect, if the characteristic size of the system (i.e.
P1) is larger.
and consequently, as
the magnitude of the perturbations determined by
P1/P2, the same amplitude
perturbations cause a more detectable effect, if the characteristic size of the system (i.e.
P1) is larger.
We also considered the questions of both detection and the correct identification of such perturbations. We emphasize again that the O−C curve is a very effective tool for detecting any period variations, thanks to its cumulative nature. Nevertheless, some care is necessary. First, it has to be kept in mind that the detectability of a period variation depends on the curvature of the O−C curve. (If the plotted O−C is simply a straight line, with any given slope, it means that the period is constant, which is known with an error equal to that slope.) This implies that the interval needed to detect the period variation coming from a periodic phenomenon depends more strongly on which phase is observed than on the amplitude of the total variation. (We illustrated this possibility for both systems sampled.) We also illustrated that, in the case of a very eccentric third companion, the fastest rate period variation lasts a very short interval, which consists of only a few transit events. This emphasizes the importance of observing all possible transit (and, of course ,occultation) events, with great accuracy. Another question is the possible misinterpretation of the O−C diagram. For example, as was shown, in the HD 80606b system we can expect a secular period change due to tidal dissipation. On a short time scale of decades it may happen that this change is of the same order as the one expected from periodic perturbations of a third companion. These two types of perturbations could be separated in two different ways. One way is simply a question of time. In the case of an enough long observing window, a periodic pertubation would separate from a secular one, which would in turn produce a parabola-like O−C continuously. But, there is also a faster possibility. In the case that not only primary transits, but also secondary occultations, are observed with similar frequency and accuracy, then, on subtracting the two (primary and secondary) O−C curves from each other, the secular change – i.e., the effect of dissipation – would disappear, since it is similar for primary transits and secondary occultations. This also makes it desirable to collect as many occultation observations as possible too.
In this paper we follow the original classification of Brown (1936), which divided the periodic perturbations occurring in hierarchical systems into the following three groups:
-
short-period perturbations. The typical period is equal to the orbital period of the close pair, while the amplitude has the order ;
-
long-period perturbations. This group has a typical period of , and magnitude of the order ;
-
apse-node terms. In this group the typical period is about , and the order of the amplitude reaches unity.
The minus signs on the r.h.s. of Eqs. (10) and (11) of Borkovits et al. (2007) should be replaced by plus.
In that paper, from practical considerations, we did not restrict ourselves to the most usual representation of the perturbation equations, i.e. the Lagrange equations with the perturbing function; rather, we used the somewhat more general form that expresses the perturbations with the three orthogonal components of the perturbing force. Nevertheless, as long as only conservative, three-body terms are considered, the two representations are perfectly equivalent. (In the denominator of Eqs. (14) and (15) for and , a closing bracket is evidently missing, and furthermore, the equation for should be divided by for the correct result.)
This assumption is analogous to that of the classical low-order perturbation theory where the squares of the orbital element changes are neglected, as they should be proportional to (mperturber/mstar)2, but with the difference that here the small parameter is the ratio of the semi-major axes a1/a2 instead of the mass ratio. Consequently, this assumption remains valid even if the perturber is a sufficiently distant stellar-mass object.
This is not necessarily true in the presence of other perturbative effects. Nevertheless, in such cases one can assume that if there is a physical effect producing apse-node time scale perturbations having a period comparable to the period of the long-period perturbations arising from some other sources, then the amplitudes of these long-period perturbations are usually so small with respect to the amplitudes of the apse-node perturbations that their effect can be neglected.
Acknowledgments
This research made use of NASA’s Astrophysics Data System Bibliographic Services. We thank Drs. John Lee Greenfell and Imre Barna Bíró for the linguistic corrections. We thank for the referee and the language editor for their valuable suggestions and comments.
References
- Agol, E., Steffen, J., Sari, R., & Clarkson, W. 2005, MNRAS, 359, 567 [NASA ADS] [CrossRef] [Google Scholar]
- Borkovits, T., Érdi, B., Forgács-Dajka, E., & Kovács, T. 2003, A&A, 398, 1091 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Borkovits, T., Forgács-Dajka, E., & Regály, Zs. 2004, A&A, 426, 951 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Borkovits, T., Elkhateeb, M. M., Csizmadia, Sz., et al. 2005, A&A, 441, 1087 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Borkovits, T., Forgács-Dajka, E., & Regály, Zs. 2007, A&A, 473, 191 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brown, E. W. 1936, MNRAS, 97, 62 [NASA ADS] [Google Scholar]
- Campo, C. J., Harrington, J., Hardy, R. A., et al. 2011, ApJ, 727, 125 [NASA ADS] [CrossRef] [Google Scholar]
- Claret, A., & Gimènez, A. 1991, A&AS, 96, 255 [Google Scholar]
- Cabrera, J. 2010, EAS Publ. Ser., 42, 109 [CrossRef] [EDP Sciences] [Google Scholar]
- Chandler, S. C. 1892, AJ, 11, 113 [NASA ADS] [CrossRef] [Google Scholar]
- Cowling, T. G. 1938, MNRAS, 98, 734 [NASA ADS] [Google Scholar]
- Deeg, H. J., Ocana, B., Kozhevnikov, V. P., et al. 2008, A&A, 480, 563 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Deeg, H. J., Moutou, C., Erikson, A., et al. 2010, Nature, 464, 384 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Deprit, A. 1969, Cel. Mech., 1, 12 [Google Scholar]
- Fabrycky, D. 2010, [arXiv:1006.3834] [Google Scholar]
- Fabrycky, D., & Tremaine, S. 2007, ApJ, 669, 1298 [NASA ADS] [CrossRef] [Google Scholar]
- Fischer, D. A., & Valenti, J. 2005, ApJ, 622, 1102 [NASA ADS] [CrossRef] [Google Scholar]
- Ford, E. B., Kozinsky, B., & Rasio, F. A. 2000, ApJ, 535, 385 [NASA ADS] [CrossRef] [Google Scholar]
- Fossey, S. J., Waldman, I. P., & Kipping, D. M. 2009, MNRAS, 396, L16 [NASA ADS] [CrossRef] [Google Scholar]
- Gimènez, A., & Garcia-Pelayo, J. M. 1983, Ap&SS, 92, 203 [NASA ADS] [CrossRef] [Google Scholar]
- Harrington, R. S. 1968, AJ, 73, 190 [NASA ADS] [CrossRef] [Google Scholar]
- Harrington, R. S. 1969, Cel. Mech., 1, 200 [NASA ADS] [CrossRef] [Google Scholar]
- Hertzsprung, E. 1922, B.A.N., 1, 87 [NASA ADS] [Google Scholar]
- Heyl, J. S., & Gladman, B. J. 2007, MNRAS, 377, 1511 [NASA ADS] [CrossRef] [Google Scholar]
- Holman, M. J. 2010, EAS Pub. Ser., 42, 39 [CrossRef] [EDP Sciences] [Google Scholar]
- Holman, M. J., & Murray, N. W. 2005, Science, 307, 1288 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Hori, G. 1966, PASJ, 18, 287 [NASA ADS] [Google Scholar]
- Irwin, J. B. 1952, ApJ, 116, 211 [NASA ADS] [CrossRef] [Google Scholar]
- Jordán, A., & Bakos, G. Á. 2008 ApJ, 685, 543 [Google Scholar]
- Kiseleva, L. G., Eggleton, P. P., & Mikkola, S. 1998, MNRAS, 300, 292 [NASA ADS] [CrossRef] [Google Scholar]
- Kipping, D. M. 2009a, MNRAS, 392, 181 [NASA ADS] [CrossRef] [Google Scholar]
- Kipping, D. M. 2009b, MNRAS, 396, 1797 [NASA ADS] [CrossRef] [Google Scholar]
- Kozai, Y. 1962, AJ, 67, 591 [Google Scholar]
- Laughlin, G., Deming, D., Langton, J., et al. 2009, Nature, 457, 562 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Lee, J. W., Kim, S.-L., Kim, C.-H., et al. 2009, AJ, 137, 3181 [NASA ADS] [CrossRef] [Google Scholar]
- Mazeh, T., & Saham, J. 1979, A&A, 77, 145 [Google Scholar]
- Miralda-Escudé, J. 2002, ApJ, 564, 1019 [NASA ADS] [CrossRef] [Google Scholar]
- Moutou, C., Hebrard, G., Bouchy, F., et al. 2009, A&A, 498, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Naef, D., Latham, D. W., Mayor, M., et al. 2001, A&A, 375, L27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nesvorný, D., 2009, ApJ, 701, 1116 [NASA ADS] [CrossRef] [Google Scholar]
- Nesvorný, D., & Beaugé, A. 2010, ApJ, 709, L44 [NASA ADS] [CrossRef] [Google Scholar]
- Nesvorný, D., & Morbidelli, A. 2008, ApJ, 688, 636 [NASA ADS] [CrossRef] [Google Scholar]
- Pál, A. 2010, MNRAS, 409, 975 [NASA ADS] [CrossRef] [Google Scholar]
- Pont, F., Hébrard, G., Irwin, J. M., et al. 2009, A&A, 502, 695 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Qian, S.-B., Liao, W.-P., Zhu, L.-Y., et al. 2009, MNRAS, 401, L34 [Google Scholar]
- Sándor, Zs., Süli, Á., Érdi, B., Pilat-Lohinger, E., & Dvorak, R. 2007, MNRAS, 375, 1495 [NASA ADS] [CrossRef] [Google Scholar]
- Schwarz, R., Süli, Á., Dvorak, R., & Pilat-Lohinger, E. 2009, CeMDA, 104, 69 [NASA ADS] [CrossRef] [Google Scholar]
- Simon, A., Szatmáry, K., & Szabó, Gy. M. 2007, A&A, 470, 727 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Silvotti, R., Schuh, S., Janulis, R., et al. 2007, Nature, 449, 189 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Söderhjelm, S. 1975, A&A, 42, 229 [NASA ADS] [Google Scholar]
- Söderhjelm, S. 1982, A&A, 107, 54 [NASA ADS] [Google Scholar]
- Söderhjelm, S. 1984, A&A, 141, 232 [NASA ADS] [Google Scholar]
- Sterne, T. E. 1939, MNRAS, 99, 451 [NASA ADS] [Google Scholar]
- Takeda, G., Kita, R., & Rasio, F. A. 2009, IAU Symp., 253, 181 [NASA ADS] [Google Scholar]
- Tokovinin, A. A. 1997, A&AS, 124, 75 http://www.ctio.noao.edu/atokovinin/stars/index.php (continuously refreshed) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tokovinin, A. A. 2008, MNRAS, 389, 925 [NASA ADS] [CrossRef] [Google Scholar]
- Tokovinin, A. A., Thomas, S., Sterzik, M., & Udry, S. 2006, A&A, 450, 681 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Woltjer, J., Jr. 1922, B.A.N., 1, 93 [Google Scholar]
- Wu, Y., & Murray, N. 2003, ApJ, 589, 605 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Appendix A: Relation between the observable, and the dynamical orbital elements.
First we emphasize that some of the relations between the elements, given in this section, are strictly valid only for the case shown in Fig. 1. According to the actual orientations of the orbital planes, the spherical triangle (with sides um1, um2, Ω1 − Ω2) could be oriented in different ways, and so some precise discussion is necessary, which is omitted in the present appendix.
The relation between the pericentrum arguments is  Consequently,
the true longitudes measured from the sky (u) and from the intersection
of the two orbital planes (w) are
Consequently,
the true longitudes measured from the sky (u) and from the intersection
of the two orbital planes (w) are 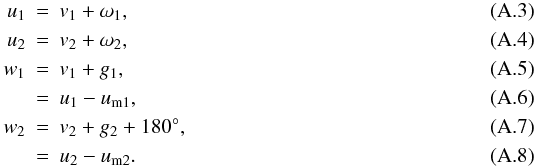 There
are two relations between the mutual inclination (im) and the
two dynamical inclinations (j1,2). One of these is trivial,
while the second comes from the relation of the inclinations to the orbital angular
momenta. The trivial case is
There
are two relations between the mutual inclination (im) and the
two dynamical inclinations (j1,2). One of these is trivial,
while the second comes from the relation of the inclinations to the orbital angular
momenta. The trivial case is 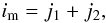 (A.9)while the
non-trivial case comes from the fact that
(A.9)while the
non-trivial case comes from the fact that  i.e.
i.e.
 where
C1,2 represents the orbital angular momentum
vector of the two orbits, C the net orbital angular momentum
vector, and
where
C1,2 represents the orbital angular momentum
vector of the two orbits, C the net orbital angular momentum
vector, and 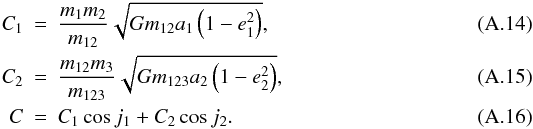 (The
rotational angular momenta were neglected.) At this point we notice that for hierarchical
systems it is a very reasonable to assume
(The
rotational angular momenta were neglected.) At this point we notice that for hierarchical
systems it is a very reasonable to assume
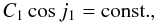 (A.17)
(since the
first-order, doubly averaged Hamiltonian of such systems does not contain its conjugated
variable, h1), which property, together with the constancy of
the semi-major axis, connects the eccentricity (e1) with the
dynamical inclination (j1).
(A.17)
(since the
first-order, doubly averaged Hamiltonian of such systems does not contain its conjugated
variable, h1), which property, together with the constancy of
the semi-major axis, connects the eccentricity (e1) with the
dynamical inclination (j1).
Further relations can be written by the use of the several identities of spherical
triangles, for example 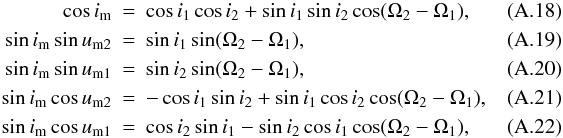 and
similar ones can be written for the two smaller spherical triangles. Finally, in
hierarchical systems, usually
C2 ≫ C1, so we can take the
following as a first approximation:
and
similar ones can be written for the two smaller spherical triangles. Finally, in
hierarchical systems, usually
C2 ≫ C1, so we can take the
following as a first approximation:  In
Fig. 1, for practical reasons, we chose the
intersection of the invariable plane and the sky for the arbitrary starting point of the
observable nodes (Ω1, Ω2). Traditionally, in astrometry, these
quantities are measured from north to east on the sky; nevertheless, such a practical
choice is valid since the Ω-s only appear in the equations in the form of their
differences, and derivatives. (Nodes cannot be determined from photometry and
spectroscopy, as both the light curves and the radial velocity curves are invariant for
any orientation of the orbital planes projected onto the sky.)
In
Fig. 1, for practical reasons, we chose the
intersection of the invariable plane and the sky for the arbitrary starting point of the
observable nodes (Ω1, Ω2). Traditionally, in astrometry, these
quantities are measured from north to east on the sky; nevertheless, such a practical
choice is valid since the Ω-s only appear in the equations in the form of their
differences, and derivatives. (Nodes cannot be determined from photometry and
spectroscopy, as both the light curves and the radial velocity curves are invariant for
any orientation of the orbital planes projected onto the sky.)
Appendix B: The derivatives used for calculating the long-period dynamical O–C up to sixth order in e1
The derivatives of the indirect terms are as follows:
![\appendix \setcounter{section}{2} \begin{eqnarray} \frac{\mathrm{d}{e_1\cos\omega_1}}{\mathrm{d}{v_2}}&=&A_\mathrm{L}\left(1+e_2\cos v_2\right)\left\{(1-e_1^2)^{1/2}\left\{-\frac{3}{5}e_1\sin\omega_1\left[\left(I^2-\frac{1}{3}\right)+\left(1-I^2\right)\cos(2v_2+2g_2)\right]\right.\right. \nonumber \\ &&-e_1\sin(\omega_1-2g_1)\left[\left(1-I^2\right)+\left(1+I^2\right)\cos(2v_2+2g_2)\right] \nonumber \\ &&\left.-e_1\cos(\omega_1-2g_1)2I\sin(2v_2+2g_2)\right\}\nonumber \\ &&+\frac{\sin i_\mathrm{m}\cot i_1}{\left(1-e_1^2\right)^{1/2}}\left\{\left[\frac{2}{5}\left(1+\frac{3}{2}e_1^2\right)\cos u_\mathrm{m1}-e_1^2\cos(2g_1+u_\mathrm{m1})\right]e_1\sin\omega_1I\left[1-\cos(2v_2+2g_2)\right]\right. \nonumber \\ &&\left.\left.+\left[\frac{2}{5}\left(1+\frac{3}{2}e_1^2\right)\sin u_\mathrm{m1}+e_1^2\sin(2g_1+u_\mathrm{m1})\right]e_1\sin\omega_1\sin(2v_2+2g_2)\right\}\right\}, \end{eqnarray}](/articles/aa/full_html/2011/04/aa15867-10/aa15867-10-eq299.png) (B.1)
(B.1)![\appendix \setcounter{section}{2} \begin{eqnarray} \frac{\mathrm{d}{e_1^2f_3(e_1)\sin2\omega_1}}{\mathrm{d}{v_2}}&=&A_\mathrm{L}\left(1+e_2\cos v_2\right)\left\{(1-e_1^2)^{1/2}\left\{\frac{6}{5}e_1^2f_3\cos2\omega_1\left[\left(I^2-\frac{1}{3}\right)+\left(1-I^2\right)\cos(2v_2+2g_2)\right]\right.\right. \nonumber \\ &&+\left[2e_1^2f_4\cos(2\omega_1-2g_1)-\frac{1}{6}e_1^4f_5\cos(2\omega_1+2g_1)\right]\left[\left(1-I^2\right)+\left(1+I^2\right)\cos(2v_2+2g_2)\right] \nonumber \\ &&\left.-\left[2e_1^2f_4\sin(2\omega_1-2g_1)+\frac{1}{6}e_1^4f_5\sin(2\omega_1+2g_1)\right]2I\sin(2v_2+2g_2)\right\}\nonumber \\ &&+\frac{\sin i_\mathrm{m}\cot i_1}{\left(1-e_1^2\right)^{1/2}}f_3\left\{\left[-\frac{4}{5}\left(1+\frac{3}{2}e_1^2\right)\cos u_\mathrm{m1}+2e_1^2\cos(2g_1+u_\mathrm{m1})\right]e_1^2\cos2\omega_1I\left[1-\cos(2v_2+2g_2)\right]\right. \nonumber \\ &&\left.\left.-\left[\frac{4}{5}\left(1+\frac{3}{2}e_1^2\right)\sin u_\mathrm{m1}+2e_1^2\sin(2g_1+u_\mathrm{m1})\right]e_1^2\cos2\omega_1\sin(2v_2+2g_2)\right\}\right\}, \end{eqnarray}](/articles/aa/full_html/2011/04/aa15867-10/aa15867-10-eq300.png) (B.2)
(B.2)![\appendix \setcounter{section}{2} \begin{eqnarray} \frac{\mathrm{d}{e_1^3f_6(e_1)\cos3\omega_1}}{\mathrm{d}{v_2}}&=&A_\mathrm{L}\left(1+e_2\cos v_2\right)\left\{(1-e_1^2)^{1/2}\left\{-\frac{9}{5}e_1^3f_6\sin3\omega_1\left[\left(I^2-\frac{1}{3}\right)+\left(1-I^2\right)\cos(2v_2+2g_2)\right]\right.\right. \nonumber \\ &&-\left[3e_1^3f_7\sin(3\omega_1-2g_1)-\frac{3}{8}e_1^5\sin(3\omega_1+2g_1)\right]\left[\left(1-I^2\right)+\left(1+I^2\right)\cos(2v_2+2g_2)\right] \nonumber \\ &&-\left.\left[3e_1^3f_7\cos(3\omega_1-2g_1)+\frac{3}{8}e_1^5\cos(3\omega_1+2g_1)\right]2I\sin(2v_2+2g_2)\right\}\nonumber \\ &&+\frac{\sin i_\mathrm{m}\cot i_1}{\left(1-e_1^2\right)^{1/2}}f_6\left\{\left[\frac{6}{5}\left(1+\frac{3}{2}e_1^2\right)\cos u_\mathrm{m1}-3e_1^2\cos(2g_1+u_\mathrm{m1})\right]e_1^3\sin3\omega_1I\left[1-\cos(2v_2+2g_2)\right]\right. \nonumber \\ &&\left.\left.+\left[\frac{6}{5}\left(1+\frac{3}{2}e_1^2\right)\sin u_\mathrm{m1}+3e_1^2\sin(2g_1+u_\mathrm{m1})\right]e_1^3\sin3\omega_1\sin(2v_2+2g_2)\right\}\right\}, \end{eqnarray}](/articles/aa/full_html/2011/04/aa15867-10/aa15867-10-eq301.png) (B.3)
(B.3)![\appendix \setcounter{section}{2} \begin{eqnarray} \frac{\mathrm{d}{e_1^4f_8(e_1)\sin4\omega_1}}{\mathrm{d}{v_2}}&=&A_\mathrm{L}\left(1+e_2\cos v_2\right)\left\{(1-e_1^2)^{1/2}\left\{\frac{12}{5}e_1^4f_8\cos4\omega_1\left[\left(I^2-\frac{1}{3}\right)+\left(1-I^2\right)\cos(2v_2+2g_2)\right]\right.\right. \nonumber \\ &&+\left[4e_1^4f_5\cos(4\omega_1-2g_1)-\frac{3}{5}e_1^6\cos(4\omega_1+2g_1)\right]\left[\left(1-I^2\right)+\left(1+I^2\right)\cos(2v_2+2g_2)\right] \nonumber \\ &&\left.-\left[4e_1^4f_5\sin(4\omega_1-2g_1)+\frac{3}{5}e_1^6\sin(4\omega_1+2g_1)\right]2I\sin(2v_2+2g_2)\right\}\nonumber \\ &&+\frac{\sin i_\mathrm{m}\cot i_1}{\left(1-e_1^2\right)^{1/2}}f_8\left\{\left[-\frac{8}{5}\left(1+\frac{3}{2}e_1^2\right)\cos u_\mathrm{m1}+4e_1^2\cos(2g_1+u_\mathrm{m1})\right]e_1^4\cos4\omega_1I\left[1-\cos(2v_2+2g_2)\right]\right. \nonumber \\ &&\left.\left.-\left[\frac{8}{5}\left(1+\frac{3}{2}e_1^2\right)\sin u_\mathrm{m1}+4e_1^2\sin(2g_1+u_\mathrm{m1})\right]e_1^4\cos4\omega_1\sin(2v_2+2g_2)\right\}\right\}, \end{eqnarray}](/articles/aa/full_html/2011/04/aa15867-10/aa15867-10-eq302.png) (B.4)
(B.4)![\appendix \setcounter{section}{2} \begin{eqnarray} \frac{\mathrm{d}{e_1^5\cos5\omega_1}}{\mathrm{d}{v_2}}&=&A_\mathrm{L}\left(1+e_2\cos v_2\right)\left\{(1-e_1^2)^{1/2}\left\{-3e_1^5\sin5\omega_1\left[\left(I^2-\frac{1}{3}\right)+\left(1-I^2\right)\cos(2v_2+2g_2)\right]\right.\right. \nonumber \\ &&-5e_1^5\sin(5\omega_1-2g_1)\left[\left(1-I^2\right)+\left(1+I^2\right)\cos(2v_2+2g_2)\right] \nonumber \\ &&\left.-5e_1^5\cos(5\omega_1-2g_1)2I\sin(2v_2+2g_2)\right\}\nonumber \\ &&+\frac{\sin i_\mathrm{m}\cot i_1}{\left(1-e_1^2\right)^{1/2}}\left\{\left[2\left(1+\frac{3}{2}e_1^2\right)\cos u_\mathrm{m1}-5e_1^2\cos(2g_1+u_\mathrm{m1})\right]e_1^5\sin5\omega_1I\left[1-\cos(2v_2+2g_2)\right]\right. \nonumber \\ &&\left.\left.+\left[2\left(1+\frac{3}{2}e_1^2\right)\sin u_\mathrm{m1}+5e_1^2\sin(2g_1+u_\mathrm{m1})\right]e_1^5\sin5\omega_1\sin(2v_2+2g_2)\right\}\right\}, \end{eqnarray}](/articles/aa/full_html/2011/04/aa15867-10/aa15867-10-eq303.png) (B.5)
(B.5)![\appendix \setcounter{section}{2} \begin{eqnarray} \frac{\mathrm{d}{e_1^6\sin6\omega_1}}{\mathrm{d}{v_2}}&=&A_\mathrm{L}\left(1+e_2\cos v_2\right)\left\{(1-e_1^2)^{1/2}\left\{\frac{18}{5}e_1^6\cos6\omega_1\left[\left(I^2-\frac{1}{3}\right)+\left(1-I^2\right)\cos(2v_2+2g_2)\right]\right.\right. \nonumber \\ &&+6e_1^6\cos(6\omega_1-2g_1)\left[\left(1-I^2\right)+\left(1+I^2\right)\cos(2v_2+2g_2)\right] \nonumber \\ &&\left.-6e_1^6\sin(6\omega_1-2g_1)2I\sin(2v_2+2g_2)\right\}\nonumber \\ &&+\frac{\sin i_\mathrm{m}\cot i_1}{\left(1-e_1^2\right)^{1/2}}f_8\left\{\left[-\frac{12}{5}\left(1+\frac{3}{2}e_1^2\right)\cos u_\mathrm{m1}+6e_1^2\cos(2g_1+u_\mathrm{m1})\right]e_1^4\cos6\omega_1I\left[1-\cos(2v_2+2g_2)\right]\right. \nonumber \\ &&\left.\left.-\left[\frac{12}{5}\left(1+\frac{3}{2}e_1^2\right)\sin u_\mathrm{m1}+6e_1^2\sin(2g_1+u_\mathrm{m1})\right]e_1^6\cos6\omega_1\sin(2v_2+2g_2)\right\}\right\}. \end{eqnarray}](/articles/aa/full_html/2011/04/aa15867-10/aa15867-10-eq304.png) (B.6)The
direct terms are coming from
(a3/2emcos(nv)
and
(B.6)The
direct terms are coming from
(a3/2emcos(nv)
and  )
are as follows:
)
are as follows: ![\appendix \setcounter{section}{2} \begin{eqnarray} \left(\frac{\mathrm{d}e_1\cos v}{\mathrm{d}v_2}\right)_\mathrm{dir}&=&A_\mathrm{L}\left(1+e_2\cos v_2\right)(1-e_1^2)^{1/2}\left\{-\frac{2}{5}\left(1+\frac{1}{2}e_1^2\right)\left[\left(I^2-\frac{1}{3}\right)+\left(1-I^2\right)\cos(2v_2+2g_2)\right]\right. \nonumber \\ &&-e_1^2\cos2g_1\left[\left(1-I^2\right)+\left(1+I^2\right)\cos(2v_2+2g_2)\right] \nonumber \\ &&\left.-e_1^2\sin2g_12I\sin(2v_2+2g_2)\right\}+..., \end{eqnarray}](/articles/aa/full_html/2011/04/aa15867-10/aa15867-10-eq307.png) (B.7)
(B.7)![\appendix \setcounter{section}{2} \begin{eqnarray} \left(\frac{\mathrm{d}e_1^2f_3(e_1)\cos2v}{\mathrm{d}v_2}\right)_\mathrm{dir}&=&A_\mathrm{L}\left(1+e_2\cos v_2\right)(1-e_1^2)^{1/2}\left\{\frac{3}{5}e_1^2\left(1+\frac{1}{4}e_1^2+\frac{1}{18}e_1^4\right)\left[\left(I^2-\frac{1}{3}\right)+\left(1-I^2\right)\cos(2v_2+2g_2)\right]\right. \nonumber \\ &&-\frac{1}{5}e_1^2\left(1-\frac{53}{12}e_1^2-\frac{3}{2}e_1^4\right)\cos2g_1\left[\left(1-I^2\right)+\left(1+I^2\right)\cos(2v_2+2g_2)\right] \nonumber \\ &&\left.-\frac{1}{5}e_1^2\left(1-\frac{53}{12}e_1^2-\frac{3}{2}e_1^4\right)\sin2g_12I\sin(2v_2+2g_2)\right\}+..., \end{eqnarray}](/articles/aa/full_html/2011/04/aa15867-10/aa15867-10-eq308.png) (B.8)
(B.8)![\appendix \setcounter{section}{2} \begin{eqnarray} \left(\frac{\mathrm{d}e_1^3f_6(e_1)\cos3v}{\mathrm{d}v_2}\right)_\mathrm{dir}&=&A_\mathrm{L}\left(1+e_2\cos v_2\right)(1-e_1^2)^{1/2}\left\{-\frac{3}{5}e_1^4\left(1+\frac{1}{2}e_1^2\right)\left[\left(I^2-\frac{1}{3}\right)+\left(1-I^2\right)\cos(2v_2+2g_2)\right]\right. \nonumber \\ &&+\frac{1}{5}e_1^2\left(1+e_1^2-\frac{49}{16}e_1^4\right)\cos2g_1\left[\left(1-I^2\right)+\left(1+I^2\right)\cos(2v_2+2g_2)\right] \nonumber \\ &&\left.+\frac{1}{5}e_1^2\left(1+e_1^2-\frac{49}{16}e_1^4\right)\sin2g_12I\sin(2v_2+2g_2)\right\}+..., \end{eqnarray}](/articles/aa/full_html/2011/04/aa15867-10/aa15867-10-eq309.png) (B.9)
(B.9)![\appendix \setcounter{section}{2} \begin{eqnarray} \left(\frac{\mathrm{d}e_1^4f_8(e_1)\cos4v}{\mathrm{d}v_2}\right)_\mathrm{dir}&=&A_\mathrm{L}\left(1+e_2\cos v_2\right)(1-e_1^2)^{1/2}\left\{\frac{1}{2}e_1^6\left[\left(I^2-\frac{1}{3}\right)+\left(1-I^2\right)\cos(2v_2+2g_2)\right]\right. \nonumber \\ &&-\frac{2}{5}e_1^4\left(1+\frac{3}{4}e_1^2\right)\cos2g_1\left[\left(1-I^2\right)+\left(1+I^2\right)\cos(2v_2+2g_2)\right] \nonumber \\ &&\left.-\frac{2}{5}e_1^4\left(1+\frac{3}{4}e_1^2\right)\sin2g_12I\sin(2v_2+2g_2)\right\}+..., \end{eqnarray}](/articles/aa/full_html/2011/04/aa15867-10/aa15867-10-eq310.png) (B.10)
(B.10)![\appendix \setcounter{section}{2} \begin{eqnarray} \left(\frac{\mathrm{d}e_1^5\cos5v}{\mathrm{d}v_2}\right)_\mathrm{dir}&=&A_\mathrm{L}\left(1+e_2\cos v_2\right)(1-e_1^2)^{1/2}\left\{\frac{1}{2}e_1^6\cos2g_1\left[\left(1-I^2\right)+\left(1+I^2\right)\cos(2v_2+2g_2)\right]\right. \nonumber \\ &&\left.+\frac{1}{2}e_1^6\sin2g_12I\sin(2v_2+2g_2)\right\}+..., \end{eqnarray}](/articles/aa/full_html/2011/04/aa15867-10/aa15867-10-eq311.png) (B.11)
(B.11)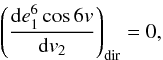 (B.12)where
+ ... refer to those terms which come from the normal force component,
and will be cancelled by equal but opposite in sign direct
(B.12)where
+ ... refer to those terms which come from the normal force component,
and will be cancelled by equal but opposite in sign direct
 -terms.
Furthermore, from
-terms.
Furthermore, from ![\appendix \setcounter{section}{2} \begin{eqnarray} \left(\mu^{-1/2}\frac{\mathrm{d}a^{3/2}}{\mathrm{d}v_2}\frac{\left(1-e_1^2\right)^{3/2}}{(1+e_1\cos v)^2}\right)_\mathrm{dir}&=&\frac{P_1}{2\pi}A_\mathrm{L}\left(1+e_2\cos v_2\right)(1-e_1^2)^{1/2}\left\{\frac{6}{5}e_1^2\left(1+\frac{9}{16}e_1^2+\frac{7}{16}e_1^4\right)\left[\left(I^2-\frac{1}{3}\right)+\left(1-I^2\right)\cos(2v_2+2g_2)\right]\right. \nonumber \\ &&+\frac{21}{20}e_1^2\left(1+\frac{9}{14}e_1^2+\frac{57}{112}e_1^4\right)\cos2g_1\left[\left(1-I^2\right)+\left(1+I^2\right)\cos(2v_2+2g_2)\right] \nonumber \\ &&\left.+\frac{21}{20}e_1^2\left(1+\frac{9}{14}e_1^2+\frac{57}{112}e_1^4\right)\sin2g_12I\sin(2v_2+2g_2)\right\}, \end{eqnarray}](/articles/aa/full_html/2011/04/aa15867-10/aa15867-10-eq315.png) (B.13)and
from
(B.13)and
from  -term:
-term:
![\appendix \setcounter{section}{2} \begin{eqnarray} \left(\frac{\mathrm{d}\Omega}{\mathrm{d}v_2}\cos{i_1}\frac{\left(1-e_1^2\right)^{3/2}}{(1+e_1\cos v)^2}\right)_\mathrm{dir}&=&A_\mathrm{L}\left(1+e_2\cos v_2\right)\frac{\sin i_\mathrm{m}\cot i_1}{(1-e_1^2)^{1/2}}\left\{\left[-\frac{2}{5}\left(1+\frac{3}{2}e_1^2\right)\cos u_\mathrm{m_1}+e_1^2\cos(u_\mathrm{m1}+2g_1)\right]I\left[1-\cos(2v_2+2g_2)\right]\right. \nonumber \\ &&\left.\left[-\frac{2}{5}\left(1+\frac{3}{2}e_1^2\right)\sin u_\mathrm{m_1}+e_1^2\sin(u_\mathrm{m1}+2g_1)\right]\sin(2v_2+2g_2)\right\}-... \end{eqnarray}](/articles/aa/full_html/2011/04/aa15867-10/aa15867-10-eq316.png) (B.14)By
the use of equations above, and integrating for v2, finally we
get:
(B.14)By
the use of equations above, and integrating for v2, finally we
get: ![\appendix \setcounter{section}{2} \begin{eqnarray} (O-C)_{v_2}&=&\frac{P_1}{2\pi}A_\mathrm{L}\left\{\left(1-e_1^2\right)^{1/2}\left\{\left[\frac{4}{5}f_1(e_1)+\frac{6}{5}K_1(e_1,\omega_1)\right]\left[\left(I^2-\frac{1}{3}\right){\cal{M}}+\frac{1}{2}\left(1-I^2\right){\cal{S}}(2v_2+2g_2)\right]\right.\right. \nonumber \\ &&+\left[\frac{51}{20}e_1^2f_2(e_1)\cos2g_1+2K_2(e_1,\omega_1,g_1)+\frac{1}{8}e_1^2K_4(e_1,\omega_1,g_1)\right]\left[\left(1-I^2\right){\cal{M}}+\frac{1}{2}\left(1+I^2\right){\cal{S}}(2v_2+2g_2)\right] \nonumber \\ &&\left.-\frac{1}{2}\left[\frac{51}{20}e_1^2f_2(e_1)\sin2g_1+2K_3(e_1,\omega_1,g_1)+\frac{1}{8}e_1^2K_5(e_1,\omega_1,g_1)\right]2I{\cal{C}}(2v_2+2g_2)\right\} \nonumber \\ \nonumber \\ &&+\frac{\sin i_\mathrm{m}\cot i_1}{\left(1-e_1^2\right)^{1/2}}\left\{\left[-\frac{2}{5}\left(1+\frac{3}{2}e_1^2\right)\cos u_\mathrm{m1}+e_1^2\cos(2g_1+u_\mathrm{m1})\right]\left[1+2K_1(e_1,\omega_1)\right]I\left[{\cal{M}}-\frac{1}{2}{\cal{S}}(2v_2+2g_2)\right]\right. \nonumber \\ &&\left.\left.+\frac{1}{2}\left[\frac{2}{5}\left(1+\frac{3}{2}e_1^2\right)\sin u_\mathrm{m1}+e_1^2\sin(2g_1+u_\mathrm{m1})\right]\left[1+2K_1(e_1,\omega_1)\right]{\cal{C}}(2v_2+2g_2)\right\}\right\}, \end{eqnarray}](/articles/aa/full_html/2011/04/aa15867-10/aa15867-10-eq318.png) (B.15)where
(B.15)where
 and
and
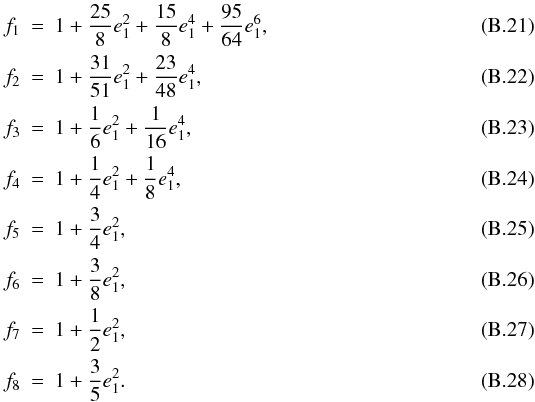
All Tables
All Figures
 |
Fig. 1 The spatial configuration of the system. |
| In the text | |
 |
Fig. 2 Left panels: the dependence on the inner eccentricity
(e1) of the amplitudes Aℳ,
|
| In the text | |
 |
Fig. 3 Transit timing variatons caused by a hypothetical P2 = 10 000 day-period m3 = 1 M⊙ mass, moderately eccentric e2 = 0.3 third companion for CoRoT-9b, at different initial orbital elements for four different initial inner eccentricities (e1 = 0, 0.11, 0.5, 0.9). The various initial elements of each panel are as follows. Panel a): g1 = 7°, g2 = 90°, im = 0°; b): the same, but for im = 90°; c): g1 = 7°, g2 = 45°, im = 30°; d): g1 = 337°, g2 = 45°, im = 60°; e): g1 = 307°, g2 = 45°, im = 30°; f): same as previous, but for im = 90°; g): g1 = 277°, g2 = 45°, im = 0°; h): same as previous, but for im = 90°. (For better comparison the curves are corrected for the different average transit periods, and zero point shifts.) |
| In the text | |
 |
Fig. 4 Left panels: the dependence on the mutual inclination
(im) of the amplitudes Aℳ,
|
| In the text | |
 |
Fig. 5 Sample of transit timing variations caused by a hypothetical P2 = 10 000 day-period m3 = 0.005 M⊙ (≈5 MJ) mass third companion for CoRoT-9b at four different initial mutual inclinations (im = 0°, 40°, 46°, 90°, from up to down), and three different initial outer eccentricities (e2 = 0, 0.3, 0.7, from left to right). The dynamical (relative) arguments of periastrons are set to g1 = 69°, g2 = 90°. The curves show the sum of the geometrical LITE, and the dynamical terms obtained both from numeric integrations, and analytic calculations up to sixth order in e1. The pure LITE contributions are also plotted separately. Note that the vertical scale of the individual columns (i.e. different e2-s) are different. |
| In the text | |
 |
Fig. 6 The first and the second 8 years of O−C-s plotted in the first and the last rows of Fig. 5. The periods of the individual curves were set equal to the respective initial transiting periods. |
| In the text | |
 |
Fig. 7 Checking the validity of hierarchical approximation for closer systems. In the first two rows the initial conditions were set to be the same as at the uppermost middle panel of Fig. 5, with the exception of P2 = 1000 (first row) and 2000 days (second row), i.e. a2/a1 ≈ 4.8 and ≈ 7.6, respectively, while the third and last rows have initial conditions similar to the bottom middle panel of Fig. 5, with the exception of P2 = 1000 (third row) and 952.7 days (last row). This latter illustrates the case of a 1:10 mean-motion resonance. The left panels represent a 20-year-long time scale, while the right ones show the TTV behaviour during a century. In the left panel of the last row the blue (quadratic) curve shows the O−C curve calculated by including a quadratic term. See text for details. |
| In the text | |
 |
Fig. 8 The A1,2,3 amplitudes for HD 80606b for primary transits (left), and secondary occultations (right), supposing that the planet is seen at the instant of the maximum phase of a Kozai-cycle. |
| In the text | |
 |
Fig. 9 Transit timing variatons caused by a hypothetical P2 = 10 000 day-period m3 = 0.005 M⊙( ≈ 5 MJ) mass third companion for HD 80606b at the maximum eccentricity phase of the induced Kozai-cycles. Top: e2 = 0; middle: e2 = 0.3; bottom: e2 = 0.7 (g2 = 0° in all cases); left panels: primary transits; middle panels: secondary occultations; right panels: primary minus secondary difference. See text for further details. (For better comparison the curves are corrected for the different average transit periods, and zero point shifts.) |
| In the text | |
 |
Fig. 10 The first and second 8 years of the left panels of Fig. 9. The periods of the individual curves was set equal to the each initial transiting periods. |
| In the text | |
 |
Fig. 11 Dynamical evolution of the orbital elements of HD 80606b in the presence of a hypothetical P2 = 10 000 day-period m3 = 0.005 M⊙(≈5 MJ) mass third companion. The initial orbital elements correspond to the last row of Fig. 9. Red curves: tidal effects and dissipation are considered; blue curves: three point-mass model. (Relativistic contributions are omitted.) Note, the semi-major axis (a1) is given in R⊙. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


