| Issue |
A&A
Volume 528, April 2011
|
|
|---|---|---|
| Article Number | A66 | |
| Number of page(s) | 8 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201015603 | |
| Published online | 03 March 2011 | |
Long-period thermal oscillations in superfluid millisecond pulsars
Departamento de Astronomía y AstrofísicaPontificia Universidad Católica de Chile, Casilla 306 Santiago 22, Chile
e-mail: cpetrovi@astro.princeton.edu
Received: 18 August 2010
Accepted: 29 January 2011
Context. In previous papers, we have shown that, as the rotation of a neutron star slows down, it will be internally heated as a consequence of the progressively changing mix of particles (rotochemical heating). In previously studied cases (non-superfluid neutron stars or superfluid stars with only modified Urca reactions), this leads to a quasi-steady state in which the star radiates thermal photons for a long time, possibly accounting for the ultraviolet radiation observed from the millisecond pulsar J0437-4715.
Aims. For the first time, we explore the phenomenology of rotochemical heating with direct Urca reactions and uniform and isotropic superfluid energy gaps of different sizes.
Methods. We first do exploratory work by integrating the thermal and chemical evolution equations numerically for different energy gaps, which uncovers a rich phenomenology of stable and unstable solutions. To understand these, we perform a stability analysis around the quasi-steady state, identifying the characteristic times of growing, decaying, and oscillating solutions.
Results. For small gaps, the phenomenology is similar to the previously studied cases, in the sense that the solutions quickly converge to a quasi-steady state. For large gaps ( ≳ 0.05 MeV), these solutions become unstable, leading to a limit-cycle behavior of periodicity ~106−7 yr, in which the star is hot (Ts ≳ 105 K) for a small fraction of the cycle (~5–20%), and cold for a longer time.
Key words: stars: neutron / dense matter / stars: rotation / pulsars: general / pulsars: individual: PSR J0437-4715
© ESO, 2011
1. Introduction
The observation of thermal emission from the surface of a neutron star (NS) has the potential to provide constraints on its inner structure. In the existing literature, several detailed cooling calculations have been compared to the few estimates available for the surface temperatures of neutron stars (see Yakovlev & Pethick 2004, for a review and references). These calculations are based on passive cooling, at first neutrino-dominated, and later driven by photon emission at ages ≳ 105 yr.
Several proposed mechanisms could keep NSs hot beyond the standard cooling timescale ~107 yr (see, e.g., Schaab et al. 1999, but note that this paper gives an incorrect parameterization of rotochemical heating, as explained in Gonzalez & Reisenegger 2010). Gonzalez & Reisenegger (2010) compared the abilities of these mechanisms to reheat NSs, concluding that two of them might be important in old NSs, namely, reheating by frictional motion of superfluid neutron vortices (Alpar et al. 1984; Shibazaki & Lamb 1989) and rotochemical heating. The latter was first proposed by Reisenegger (1995) and then improved by Fernández & Reisenegger (2005), and considered the internal structure of non-superfluid NSs with realistic equations of state (EOSs) in the framework of general relativity. It works as follows. As the NS’s rotation rate decreases, the reduction in the centrifugal force makes it contract. This perturbs each fluid element, raising the local pressure and causing deviations from beta equilibrium. Eventually, the system reaches a quasi-steady configuration, where the rate at which spin-down modifies the equilibrium concentrations is the same as that at which neutrino reactions restore the equilibrium. These reactions heat the stellar interior, making the star emit thermal radiation. The potential presence of superfluid nucleons in the NS’s interior has been widely considered to model their thermal evolution (see, e.g. Yakovlev & Pethick 2004, for cooling models) since it considerably reduces the neutrino reactions and the specific heat involving superfluid species (Yakovlev et al. 2001), and opens new neutrino emission processes, namely pair breaking and formation reactions (Flowers et al. 1976).
In a previous paper (Petrovich & Reisenegger 2010), we modeled rotochemical heating of millisecond pulsars with only modified Urca reactions in the presence of uniform and isotropic Cooper pairing gaps of neutrons Δn and protons Δp. We verified the order-of-magnitude predictions of Reisenegger (1997), finding that the chemical imbalances in the star grow up to the threshold value Δthr = min(Δn + 3Δp,3Δn + Δp), which is higher than in the quasi-steady state achieved in the absence of superfluidity. Therefore, the old superfluid NSs will take longer to reach the quasi-steady state than their nonsuperfluid counterparts, and they have a higher a luminosity in this state, given by 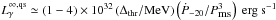 , where Ṗ-20 is the period derivative in units of 10-20 and Pms is the period in milliseconds. With the previous relation, we found that energy gaps in the range 0.05 [MeV] ≲ Δthr ≲ 0.45 [MeV] are consistent with the ultraviolet emission of PSR J0437-4715 (Kargaltsev et al. 2004).
, where Ṗ-20 is the period derivative in units of 10-20 and Pms is the period in milliseconds. With the previous relation, we found that energy gaps in the range 0.05 [MeV] ≲ Δthr ≲ 0.45 [MeV] are consistent with the ultraviolet emission of PSR J0437-4715 (Kargaltsev et al. 2004).
We extend our previous analysis to the case where the much faster direct Urca reactions are allowed. We find a qualitatively new behavior of rotochemical heating, where the temperature and chemical imbalances oscillate around the quasi-steady state.
The structure of this paper is the following. In Sect. 2, we present the basic equations of rotochemical heating and the phase-space integrals for direct Urca reactions with Cooper pairing gaps and chemical imbalances. In Sect. 3, we describe our results for the thermal evolution and the linear stability analysis of old NSs. We summarize our main conclusions in Sect. 4.
2. Theoretical framework
2.1. Rotochemical heating: basic equations
The basic framework for rotochemical heating is explained in detail in Fernández & Reisenegger (2005), and the modifications made to consider the Cooper pairing effects are described in Petrovich & Reisenegger (2010). The latter is the framework we use throughout this paper. Therefore, we just point out the fundamental equations for completeness and to clarify the notation of the present paper.
We consider the simplest model of a neutron star core, composed of neutrons, protons, electrons, and muons (npeμ matter), ignoring the potential presence of exotic particles.
The internal temperature, redshifted to a distant observer, T∞, is taken to be uniform inside the star because we are modeling the thermal evolution over timescales much longer than the diffusion time (Reisenegger 1995). Thus, the evolution of the internal temperature for an isothermal interior is given by the thermal balance equation (Thorne 1977) 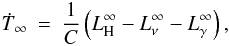 (1)where C is the total heat capacity of the star,
(1)where C is the total heat capacity of the star, 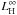 is the total power released by the heating mechanism,
is the total power released by the heating mechanism,  the total power emitted as neutrinos due to Urca reactions, and
the total power emitted as neutrinos due to Urca reactions, and 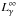 the power released as thermal photons.
the power released as thermal photons.
The amount of energy released by each Urca-type reaction is ηnpl = μn − μp − μl (l = e,μ), where μi is the chemical potential of the particle species i. Thus, we write the total energy dissipation rate as 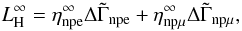 (2)where
(2)where 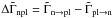 is the net reaction rate of the Urca reaction integrated over the core involving the lepton l.
is the net reaction rate of the Urca reaction integrated over the core involving the lepton l.
The photon luminosity is calculated by assuming black-body radiation 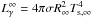 , where R∞ and Ts,∞ are the radius and the surface temperature of the star measured by an observer at infinity, respectively. To relate the internal and the surface temperatures, the fully accreted envelope model of Potekhin et al. (1997) is used.
, where R∞ and Ts,∞ are the radius and the surface temperature of the star measured by an observer at infinity, respectively. To relate the internal and the surface temperatures, the fully accreted envelope model of Potekhin et al. (1997) is used.
The evolution of the redshifted chemical imbalances, also uniform throughout the core, is given by 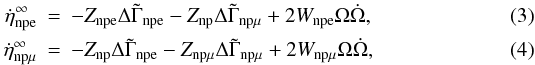 where the terms Znp, Znpe, Znpμ, Wnpe, and Wnpμ are constants that depend on the stellar structure and are kept unchanged with respect to their latest definition in Reisenegger et al. (2006), and
where the terms Znp, Znpe, Znpμ, Wnpe, and Wnpμ are constants that depend on the stellar structure and are kept unchanged with respect to their latest definition in Reisenegger et al. (2006), and 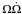 is the product of the angular velocity and its time derivative (proportional to the spin-down power).
is the product of the angular velocity and its time derivative (proportional to the spin-down power).
As Petrovich & Reisenegger (2010) showed, the results of the evolution with rotochemical heating when computing 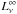 and
and 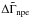 in the presence of superfluid nucleons are substantially different from their superfluid counterparts calculated by Fernández & Reisenegger (2005), since superfluidity strongly inhibits these reactions. Thus, the chemical imbalances become larger during the quasi-steady state, lengthening the timescale to arrive at this state compared with the non-superfluid case, and predicting higher temperatures in old NSs. In this paper, we include the powerful direct Urca reactions to our previous study.
in the presence of superfluid nucleons are substantially different from their superfluid counterparts calculated by Fernández & Reisenegger (2005), since superfluidity strongly inhibits these reactions. Thus, the chemical imbalances become larger during the quasi-steady state, lengthening the timescale to arrive at this state compared with the non-superfluid case, and predicting higher temperatures in old NSs. In this paper, we include the powerful direct Urca reactions to our previous study.
2.2. Cooper pairing
In the core, neutrons are believed to form Cooper pairs because of their interaction in the triplet 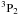 states via the anisotropic channels |mJ| = 0 (type B) or |mJ| = 2 (type C), while protons form isotropic, singlet
states via the anisotropic channels |mJ| = 0 (type B) or |mJ| = 2 (type C), while protons form isotropic, singlet 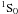 pairs (type A) (Yakovlev et al. 2001). Additionally, in the outermost core and inner crust, neutrons are believed to form singlet-state
pairs (type A) (Yakovlev et al. 2001). Additionally, in the outermost core and inner crust, neutrons are believed to form singlet-state 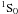 pairs. The
pairs. The 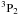 (types B and C) state description is rather uncertain in the sense that the energetically most probable state of nn-pairs (|mJ| = 0,1,2) is not known, being extremely sensitive to the still unknown nn-interaction (see, e.g. Amundsen & Østgaard 1985). Taking this classification into account, Villain & Haensel (2005) solve numerically the suppression due to each type of superfluidity of the net reaction rate for direct Urca and modified Urca reactions out of beta equilibrium, finding that the suppression due to type A superfluidity is of strength between the suppression due to anisotropic channels type B and type C superfluidity, respectively. For simplicity, we consider the energy gaps for the neutrons Δn and the protons Δp at zero temperature, redshifted to a distant observer, as parameters that are isotropic (
(types B and C) state description is rather uncertain in the sense that the energetically most probable state of nn-pairs (|mJ| = 0,1,2) is not known, being extremely sensitive to the still unknown nn-interaction (see, e.g. Amundsen & Østgaard 1985). Taking this classification into account, Villain & Haensel (2005) solve numerically the suppression due to each type of superfluidity of the net reaction rate for direct Urca and modified Urca reactions out of beta equilibrium, finding that the suppression due to type A superfluidity is of strength between the suppression due to anisotropic channels type B and type C superfluidity, respectively. For simplicity, we consider the energy gaps for the neutrons Δn and the protons Δp at zero temperature, redshifted to a distant observer, as parameters that are isotropic (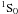 pairs) and uniform throughout the core of the NS.
pairs) and uniform throughout the core of the NS.
The phase transition for a nucleon species into a superfluid state takes place when its temperature falls below a critical value Tc. This temperature is related to the energy gap at zero temperature Δ(T = 0); for the isotropic pairing channel 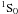 , Δ(T = 0) = 1.764kTc. Additionally, when the transition occurs, the amplitude of the energy gap depends on the temperature by means of the BCS equation (Yakovlev et al. 2001), which can be fitted by the practical formula of Levenfish & Yakovlev (1994) for the isotropic gap
, Δ(T = 0) = 1.764kTc. Additionally, when the transition occurs, the amplitude of the energy gap depends on the temperature by means of the BCS equation (Yakovlev et al. 2001), which can be fitted by the practical formula of Levenfish & Yakovlev (1994) for the isotropic gap 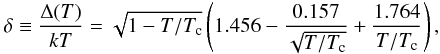 (5)where δ is the variable used in the phase-space integrals in Sect. 2.3. It is straightforward to check that the limiting cases are reproduced by Eq. (5), i.e. δ = 0 when T = Tc and δ = Δ(T = 0)/kT when T ≪ Tc. Levenfish & Yakovlev (1994) claim that intermediate values of T/Tc are also reproduced by this formula with a maximum error less than 5%, which is accurate enough for the purposes of this work.
(5)where δ is the variable used in the phase-space integrals in Sect. 2.3. It is straightforward to check that the limiting cases are reproduced by Eq. (5), i.e. δ = 0 when T = Tc and δ = Δ(T = 0)/kT when T ≪ Tc. Levenfish & Yakovlev (1994) claim that intermediate values of T/Tc are also reproduced by this formula with a maximum error less than 5%, which is accurate enough for the purposes of this work.
Having defined the energy gap of the nucleon Δi with i = n, p, it is possible to express the momentum dependence of the nucleon energy ϵi(pi) near the Fermi level, i.e. |pi − pFi| ≪ pFi, as follows (Yakovlev et al. 2001) 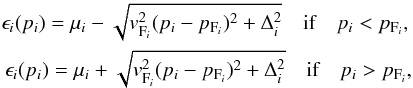 (6)where pi, pFi, vFi, and μi are the momentum, the Fermi momentum, the Fermi velocity, and the chemical potential of species i = n, p, respectively.
(6)where pi, pFi, vFi, and μi are the momentum, the Fermi momentum, the Fermi velocity, and the chemical potential of species i = n, p, respectively.
2.3. Neutrino emissivity
The fastest reactions in NS cores are the direct Urca processes  where l = e, μ. If these reactions are kinematically allowed, their emissivity is much greater than those produced by the modified Urca reactions (Yakovlev et al. 2001).
where l = e, μ. If these reactions are kinematically allowed, their emissivity is much greater than those produced by the modified Urca reactions (Yakovlev et al. 2001).
We write the neutrino emissivity and the net reaction rate of direct Urca reactions involving the lepton l and integrated over the core, respectively, as  where constants
where constants 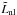 and
and 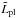 are defined in terms of the neutrino luminosities for a nonsuperfluid NS in beta equilibrium, as
are defined in terms of the neutrino luminosities for a nonsuperfluid NS in beta equilibrium, as 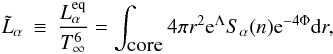 (11)where the term Sl is a slowly varying function of the baryon number density n (e.g., Yakovlev et al. 2001), and Λ and Φ are the usual Schwarzschild metric terms. The quantities ID,ϵ and ID,Γ
(11)where the term Sl is a slowly varying function of the baryon number density n (e.g., Yakovlev et al. 2001), and Λ and Φ are the usual Schwarzschild metric terms. The quantities ID,ϵ and ID,Γ
are dimensionless phase-space integrals that contain the dependence of the emissivity and the net reaction rate, respectively, on the chemical imbalances 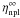 and the energy gaps Δn and Δp.
and the energy gaps Δn and Δp.
To introduce these integrals, it is useful to define the usual dimensionless variables normalized by the thermal energy kT, as follows 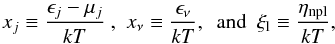 (12)which represent the energy of the non-superfluid degenerate particle j, the neutrino, and the chemical imbalance involving the lepton l, respectively, while for the superfluid nucleon i we write
(12)which represent the energy of the non-superfluid degenerate particle j, the neutrino, and the chemical imbalance involving the lepton l, respectively, while for the superfluid nucleon i we write 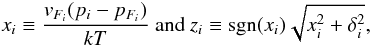 (13)where δi is defined in Eq. (5) in terms of Δi. Thus, in terms of these variables,
(13)where δi is defined in Eq. (5) in terms of Δi. Thus, in terms of these variables, ![\begin{eqnarray} \label{eq:integral_durca_emis} I_{\rm D,\epsilon}&=&\frac{914}{5040\pi^6}\int_0^{\infty}{\rm d}x_{\nu} x_{\nu}^3 \int_{-\infty}^{\infty} \int_{-\infty}^{\infty}\int_{-\infty}^{\infty} {\rm d}x_{\rm n}{\rm d}x_{\rm p}{\rm d}x_{\rm e}\nonumber \\[2mm] &&\times\, f(z_{\rm n}) f(z_{\rm p}) f(x_{\rm e}) \left[\delta(x_{\nu}+\xi_{\rm l}-z_{\rm n}-z_{\rm p}-x_{\rm e}) \right. \nonumber \\[2mm] &&\,+\left. \delta(x_{\nu}-\xi_{\rm l}-z_{\rm n}-z_{\rm p}-x_{\rm e}) \right] \end{eqnarray}](/articles/aa/full_html/2011/04/aa15603-10/aa15603-10-eq82.png) (14)and
(14)and ![\begin{eqnarray} \label{eq:integral_durca_gamma} I_{\rm D,\Gamma}&=&\frac{914}{5040\pi^6}\int_0^{\infty}{\rm d}x_{\nu} x_{\nu}^2 \int_{-\infty}^{\infty} \int_{-\infty}^{\infty}\int_{-\infty}^{\infty} {\rm d}x_{\rm n}{\rm d}x_{\rm p}{\rm d}x_{\rm e}\nonumber \\[2mm] &&\times\, f(z_{\rm n}) f(z_{\rm p}) f(x_{\rm e}) \left[\delta(x_{\nu}+\xi_{\rm l}-z_{\rm n}-z_{\rm p}-x_{\rm e}) \right. \nonumber \\[2mm] &&-\,\left. \delta(x_{\nu}-\xi_{\rm l}-z_{\rm n}-z_{\rm p}-x_{\rm e}) \right], \end{eqnarray}](/articles/aa/full_html/2011/04/aa15603-10/aa15603-10-eq83.png) (15)where f(·) is the Fermi function f(x) = 1/(1 + ex), and the numerical factor in front of the integral is normalizes ID,ϵ to 1 when the energy gaps and the chemical imbalances are zero.
(15)where f(·) is the Fermi function f(x) = 1/(1 + ex), and the numerical factor in front of the integral is normalizes ID,ϵ to 1 when the energy gaps and the chemical imbalances are zero.
In the nonsuperfluid case (i.e. δn = δp = 0), these integrals reduce to the polynomials calculated by Reisenegger (1995)![\begin{eqnarray} \label{eq:F_D_def} I_{\rm D,\epsilon} (\delta_{\rm n}=\delta_{\rm p}=0)&=&F_{\rm D}(\xi_{\rm l}) \nonumber \\[2mm] &=& 1 + \frac{1071\xi_{\rm l}^2}{457\pi^2} + \frac{315\xi_{\rm l}^4}{457\pi^4} + \frac{21\xi_{\rm l}^6}{457\pi^6},\\[2mm] \label{eq:H_D_def} I_{\rm D,\Gamma} (\delta_{\rm n}=\delta_{\rm p}=0)&=&H_{\rm D}(\xi_{\rm l})= \frac{714\xi_{\rm l}}{457\pi^2}+\frac{420\xi_{\rm l}^3}{457\pi^4}+\frac{42\xi_{\rm l}^5}{457\pi^6} \cdot \end{eqnarray}](/articles/aa/full_html/2011/04/aa15603-10/aa15603-10-eq87.png) The phase-space integrals ID,ϵ and ID,Γ cannot be solved analytically when one or two nucleon species are superfluid. Thus, Villain & Haensel (2005) and Petrovich & Reisenegger (2010) computed these integrals numerically and described the suppression produced by the Cooper pairs by means of the so-called reductions factors. The latter are defined as the ratio of the phase-space integrals with superfluid particle species to the non-superfluid integrals, i.e. RD,ϵ = ID,ϵ/FD(ξl) and RD,Γ = ID,Γ/HD(ξl). Hereafter, we calculate these integrals numerically by using the numerical method explained in Petrovich & Reisenegger (2010), which is based on the Gauss-Laguerre quadrature, taking advantage of the exponentially decaying behavior of the Fermi functions appearing in the integrand.
The phase-space integrals ID,ϵ and ID,Γ cannot be solved analytically when one or two nucleon species are superfluid. Thus, Villain & Haensel (2005) and Petrovich & Reisenegger (2010) computed these integrals numerically and described the suppression produced by the Cooper pairs by means of the so-called reductions factors. The latter are defined as the ratio of the phase-space integrals with superfluid particle species to the non-superfluid integrals, i.e. RD,ϵ = ID,ϵ/FD(ξl) and RD,Γ = ID,Γ/HD(ξl). Hereafter, we calculate these integrals numerically by using the numerical method explained in Petrovich & Reisenegger (2010), which is based on the Gauss-Laguerre quadrature, taking advantage of the exponentially decaying behavior of the Fermi functions appearing in the integrand.
3. Results and discussion
3.1. Evolution
In this section, we show the peculiar behavior of rotochemical heating in MSPs with superfluid nucleons and direct Urca reactions. To do so, we numerically compute the evolution of Eqs. (1), (3), and (4). Hereafter, we omit the ∞ subscript in the temperature and the ∞ superscript in the chemical imbalances to simplify the notation.
The NS interior structure is modeled by the BPAL21 EOS of Prakash et al. (1988) for the core, supplemented with those of Pethick et al. (1995) and Haensel & Pichon (1994) for the inner and outer crust, respectively. This model opens electron direct Urca reactions in the core when the NS mass is greater than 1.67 M⊙ and muon direct Urca reactions when its mass is greater than 1.69 M⊙, and reaches a maximum mass value of 1.71 M⊙. Thus, the direct Urca reactions are allowed within the mass range 1.76 ± 0.2 M⊙ of the MSP J0437-4715 (Verbiest et al. 2008), the only MSP whose thermal radiation has been measured so far and, therefore, there is an estimate of its surface temperature (Kargaltsev et al. 2004).
For numerical calculations, the evolution of 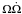 is computed by assuming magnetic dipole braking with no field decay, and relating the magnetic field on the magnetic equator, rotation period, and period derivative by the conventional formula B = 3.2 × 1019(PṖ)1/2 G, where P is measured in seconds. The magnetic field is chosen to be B = 2.8 × 108 G, so as to match the currently measured values of P and Ṗ of PSR J0437-4715.
is computed by assuming magnetic dipole braking with no field decay, and relating the magnetic field on the magnetic equator, rotation period, and period derivative by the conventional formula B = 3.2 × 1019(PṖ)1/2 G, where P is measured in seconds. The magnetic field is chosen to be B = 2.8 × 108 G, so as to match the currently measured values of P and Ṗ of PSR J0437-4715.
In Fig. 1, we show the evolution for three different values of the neutron energy gap, with non-superfluid protons and no muons, illustrating the appearance of strong thermal oscillations at larger gaps. The left top panel, where Δn = 0.01 MeV, shows that rotochemical heating converges rapidly to a stable solution given by the quasi-steady solution calculated from 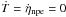 , as it happens when no superfluid nucleon species are considered (Fernández & Reisenegger 2005) or when superfluid nucleons are present, but only modified Urca reactions are allowed (Petrovich & Reisenegger 2010). A hint of an oscillation is seen before the solution converges.
, as it happens when no superfluid nucleon species are considered (Fernández & Reisenegger 2005) or when superfluid nucleons are present, but only modified Urca reactions are allowed (Petrovich & Reisenegger 2010). A hint of an oscillation is seen before the solution converges.
In the left bottom panel of Fig. 1, we increase the value of the energy gap to Δn = 0.03 MeV. In this case, there is a clearly visible damped oscillation before the variables settle to their quasi-state values.
 |
Fig. 1 Evolution of the internal temperature T and the chemical imbalance ηnpe for a 1.68 M⊙ star without muons built with the BPAL21 EOS (Prakash et al. 1988), with the initial conditions T = 108 K and ηnpe = 0. The spin-down is assumed to be caused by magnetic dipole radiation, with dipolar field strength B = 2.8 × 108 G and initial period P0 = 1 ms. The dashed lines are the quasi-steady state solution calculated from |
In the upper right panel of Fig. 1, we use Δn = 0.05 MeV to show strong oscillations without a clear damping effect. This behavior can be understood as follows. Once the chemical imbalance increases to a critical value ~Δn, the reaction rates increase dramatically, suddenly increasing the temperature and thus decreasing the imbalance. At this point, the imbalance is substantially below the energy gap and the direct Urca reactions are strongly inhibited (see Petrovich & Reisenegger 2010, for more details on the reduction factors). Thus, the star begins to cool almost exclusively by photon emission, and the spin-down compression forces the chemical imbalance to grow almost unimpeded by the neutrino reactions until it reaches its critical value again. This process is repeated cyclically in a timescale given, essentially, by the time taken by the chemical imbalance to come back to its critical value ~Δn, where it erases any record of the previous cycles.
The lower right panel of Fig. 1, shows a close-up of one of the peaks depicting the evolution with Δn = 0.05 MeV in order to resolve and illustrate the rather sharp peaks. We also illustrate in this figure that the timescale involved in the rapid increase in temperature is on the order of ~105 yr, while the decrease happens on a timescale of ~106 yr.
This unexpected behavior will be the focus of our analysis.
3.2. Stability analysis
In this section, we analyze the local stability of the temperature and chemical imbalance by perturbing the evolution Eqs. (1) and (3) around the quasi-steady state 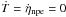 and computing the growth rates of these small displacements. For simplicity, we ignore the presence of muons in our analysis.
and computing the growth rates of these small displacements. For simplicity, we ignore the presence of muons in our analysis.
We can safely neglect the modified Urca reactions of the electrons because the direct Urca reactions are much more efficient and the superfluid suppression is similar in both cases. Thus, the evolution equations (with ηnpe in units of temperature) can be written as ![\begin{eqnarray} \label{eq:evol_1} \dot{T} & =&\frac{1}{C}\left\{\tilde{L}_{\rm D}\left[ \xi_{\rm e} I_\Gamma -I_\epsilon \right]T^6 - \tilde{L}_\gamma T^\alpha \right\} \equiv \mathcal{F}(T,\eta_{\rm npe}),\\ \label{eq:evol_2} \dot{\eta}_{\rm npe} & = & -\frac{Z_{\rm npe}}{k^2}\left(\tilde{L}_{\rm D} I_\Gamma T^5\right) + \frac{2W_{\rm npe}}{k} \Omega \dot{\Omega} \equiv \mathcal{G}(T,\eta_{\rm npe}). \end{eqnarray}](/articles/aa/full_html/2011/04/aa15603-10/aa15603-10-eq110.png) We considered the fully accreted envelope model of Potekhin et al. (1997) to express the photon luminosity in terms of the internal temperature as
We considered the fully accreted envelope model of Potekhin et al. (1997) to express the photon luminosity in terms of the internal temperature as 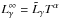 , where
, where 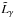 is a numerical factor that depends on the stellar structure, and α = 2.42. Additionally, we defined the functions ℱ and
is a numerical factor that depends on the stellar structure, and α = 2.42. Additionally, we defined the functions ℱ and 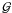 to save notation in the subsequent analysis.
to save notation in the subsequent analysis.
We write the perturbed solutions to these equations as 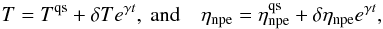 (20)where Tqs and
(20)where Tqs and 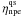 are the solutions of
are the solutions of 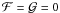 , which are unique for each combination of input parameters, i.e. energy gaps, spin-down power, and structure constants. We define γ as the growth rate of the perturbations δT and δηnpe. Replacing these perturbed solutions in the differential equations leads to the usual eigenvalue problem for the growth rates of these perturbations
, which are unique for each combination of input parameters, i.e. energy gaps, spin-down power, and structure constants. We define γ as the growth rate of the perturbations δT and δηnpe. Replacing these perturbed solutions in the differential equations leads to the usual eigenvalue problem for the growth rates of these perturbations 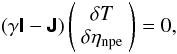 (21)where I is the 2 × 2 identity matrix and J is the Jacobian matrix resulting from the linearization of Eqs. (18) and (19) and evaluated at Tqs and
(21)where I is the 2 × 2 identity matrix and J is the Jacobian matrix resulting from the linearization of Eqs. (18) and (19) and evaluated at Tqs and 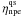 . Thus, we write the Jacobian matrix elements, replacing the quasi-steady state and taking logarithmic derivatives, as
. Thus, we write the Jacobian matrix elements, replacing the quasi-steady state and taking logarithmic derivatives, as ![\begin{eqnarray} \label{eq:J_{11}} \tens{J_{11}}&=&\frac{\partial\mathcal{F} } {\partial T} = \frac{\tilde{L}_\gamma}{\tilde{C}} T^{\alpha-1} \left(\frac{\partial \ln (\xi_{\rm e}I_\Gamma-I_\epsilon)}{\partial \ln T} +(6-\alpha) \right),\\[2mm] \label{eq:J_{12}} \tens{J_{12}}&=& \frac{\partial\mathcal{F} } {\partial \eta_{\rm npe}}= \frac{\tilde{L}_\gamma}{\tilde{C}} T^{\alpha-1} \left(\frac{\partial \ln (\xi_{\rm e}I_\Gamma-I_\epsilon)}{\partial \ln \eta_{\rm npe}} \right), \\[2mm] \label{eq:J_{21}} \tens{J_{21}} &=&\frac{\partial\mathcal{G} } {\partial T}= \frac{2W_{\rm npe}\Omega\dot{\Omega}}{ kT} \left(\frac{\partial \ln (\xi_{\rm e}I_\Gamma)}{\partial \ln T} +6 \right),\\[2mm] \label{eq:J_{22}} \tens{J_{22}}&=&\frac{\partial\mathcal{G} } {\partial \eta_{\rm npe}} =\frac{2W_{\rm npe}\Omega\dot{\Omega}}{ k\eta_{\rm npe}} \left(\frac{\partial \ln (\xi_{\rm e}I_\Gamma)}{\partial \ln \eta_{\rm npe}} -1\right). \end{eqnarray}](/articles/aa/full_html/2011/04/aa15603-10/aa15603-10-eq127.png) We solve for the two growth rates γ + and γ − by simply calculating
We solve for the two growth rates γ + and γ − by simply calculating 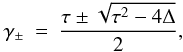 (26)where τ and Δ are the trace and the determinant of J, respectively. The stability of this system of differential equations, at least when the linear approximations is valid, i.e. close to quasi-steady solutions, depends on these growth rates. Thus, if Re(γ ± ) < 0, the fixed point solutions will be stable, as happens when we have only modified Urca reactions or no superfluid nucleons are considered. Otherwise, if Re(γ ± ) > 0 the solutions will diverge. Moreover, the solution will oscillate if Im(γ ± ) ≠ 0, and the oscillations become important during the evolution if |Im(γ ± )| are comparable to or greater than |Re(γ ± )|.
(26)where τ and Δ are the trace and the determinant of J, respectively. The stability of this system of differential equations, at least when the linear approximations is valid, i.e. close to quasi-steady solutions, depends on these growth rates. Thus, if Re(γ ± ) < 0, the fixed point solutions will be stable, as happens when we have only modified Urca reactions or no superfluid nucleons are considered. Otherwise, if Re(γ ± ) > 0 the solutions will diverge. Moreover, the solution will oscillate if Im(γ ± ) ≠ 0, and the oscillations become important during the evolution if |Im(γ ± )| are comparable to or greater than |Re(γ ± )|.
 |
Fig. 2 Real and imaginary parts of the growth rates γ + and γ − (upper panel) calculated from Eq. (26) and components of the Jacobian matrix (lower panel) in Eqs. (22)–(25), for different values of Δn. In both panels, the stellar parameters are the same as in Fig. 1 and we assume that |
In the upper panel of Fig. 2, we show the real and imaginary parts of the two growth rates for different values of Δn. We fix the value of the spin-down parameters to ![\hbox{$\Omega\dot{\Omega}=-3\times 10^{-9}~[\mbox{rad}^2/\mbox{s}^3]$}](/articles/aa/full_html/2011/04/aa15603-10/aa15603-10-eq138.png) in order to compare our results to those of Fig. 1, where
in order to compare our results to those of Fig. 1, where 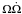 reaches this value at the age of 5 × 106 yr and slowly changes until ~ 108 yr. When the energy gap is Δn = 0.01 MeV (top panel of Fig. 1), the system is locally stable because Re(γ ± ) < 0, and the oscillation is highly damped because | Re(γ ± ) | ≫ | Im(γ ± ) | . Then, if we take Δn = 0.03 MeV (middle panel of Fig. 1), we can see that the system is still locally stable, but Re(γ + ) and Re(γ−) increase in such a way that | Re(γ ± ) | < | Im(γ ± ) | /(2π), and therefore the oscillations are less damped than those with lower energy gaps. Up to here, the linearized system predicts that the fixed point Tqs and
reaches this value at the age of 5 × 106 yr and slowly changes until ~ 108 yr. When the energy gap is Δn = 0.01 MeV (top panel of Fig. 1), the system is locally stable because Re(γ ± ) < 0, and the oscillation is highly damped because | Re(γ ± ) | ≫ | Im(γ ± ) | . Then, if we take Δn = 0.03 MeV (middle panel of Fig. 1), we can see that the system is still locally stable, but Re(γ + ) and Re(γ−) increase in such a way that | Re(γ ± ) | < | Im(γ ± ) | /(2π), and therefore the oscillations are less damped than those with lower energy gaps. Up to here, the linearized system predicts that the fixed point Tqs and 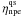 behaves as a stable spiral(also known as an attractor or a sink) in the T − ηnpe space, hence the linear analysis ensures that it is also correct for the non-linear system close to this fixed point (Strogatz 1994).
behaves as a stable spiral(also known as an attractor or a sink) in the T − ηnpe space, hence the linear analysis ensures that it is also correct for the non-linear system close to this fixed point (Strogatz 1994).
Increasing the energy gap to a value higher than Δn = 0.03 MeV, the linearized system becomes unstable because Re(γ ± ) changes from being negative to positive. Beyond this point, the non-linear system acts as an unstable spiral (also known as a repeller or source) in the T − ηnpe space. If the initial condition of the system of Eqs. (18) and (19) is close to the fixed point, it will diverge from it. Afterwards, the amplitude of the perturbations becomes large enough to make the non-linear terms significant, and the linear analysis is no longer valid. We show in section Sect. 3.4 that, for high energy gaps, the highly non-linear system converges to a stable limit cycle.
3.3. Superfluidity driving the oscillations
The oscillations are exclusively caused by the appearance of the superfluid energy gaps at the Fermi level of the nucleons. This drastically changes the dependence of the neutrino emissivity and the net reaction rate on the internal temperature and chemical imbalance, which causes the oscillations, as we show in this section.
In the lower panel of Fig. 2, we show the previous effect by means of the components of the Jacobian matrix in Eqs. (22)–(25), evaluated at the quasi-steady state. From here, we can observe that close to the quasi-steady state, the evolution represented by Eqs. (18) and (19) becomes unstable, essentially, because the component J11 = ∂ℱ/∂T changes from being negative to positive as we increase Δn, changing the sign of the trace of the Jacobian τ.
To understand why this happens, we analyze the dimensionless net heating function ξeIΓ − Iϵ that appears in Eq. (18). For the non-superfluid case, one finds from the polynomials given in Eqs. (16) and (17) that, in the quasi-steady state, where T ≪ η, ξeIΓ − Iϵ ~ 21/(457π6)(η/T)6, which gives ∂ln(ξeIΓ − Iϵ)/∂lnT ~ − 6 , i.e. from Eq. (22) J remains negative. In contrast, for the superfluid case, we find that this function can increase with temperature for values of the energy gaps sufficiently greater than the temperature. We know that both of the functions IΓ and Iϵ increase with temperature since this increases the phase-space available to the particles. However, as Petrovich & Reisenegger (2010) showed by means of the reduction factors, superfluidity blocks the phase-space of the integrals Iϵ and IΓ quite differently, and for the quasi-steady state we find that Rϵ ≪ RΓ (see Fig. 2 of Petrovich & Reisenegger 2010), which forces ξeIΓ − Iϵ to be an increasing function of the temperature. Finally, this happens until the temperature is high enough to make the reduction factors comparable and the function decreases with temperature in a similar way to its non-superfluid counterpart.
3.4. Limit cycle in ηnpe – T: existence and Δ-dependence
In the upper panel of Fig. 3, we show the evolution of rotochemical heating in the ηnpe − T space for different initial conditions that converge to the same the limit cycle. Moreover, we know that the trajectories inside the limit cycle are repelled by the fixed point of ℱ and 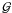 , which in this case is an unstable spiral, as discussed in Sect. 3.2. Thus, we could construct a trapping region, excluding the fixed point, such as the vector that field points inward at the boundary of this region and, therefore, argue by means of the Poincaré-Bendixson theorem that there is a closed orbit, i.e. a stable limit cycle (see, e.g. Strogatz 1994, for details on limit cycles).
, which in this case is an unstable spiral, as discussed in Sect. 3.2. Thus, we could construct a trapping region, excluding the fixed point, such as the vector that field points inward at the boundary of this region and, therefore, argue by means of the Poincaré-Bendixson theorem that there is a closed orbit, i.e. a stable limit cycle (see, e.g. Strogatz 1994, for details on limit cycles).
 |
Fig. 3 Evolution of rotochemical heating in the ηnpe − T space for a superfluid star with the same parameters of Fig. 1. Upper panel: evolution with Δn = 0.05 MeV for different initial conditions (dotted-dashed lines) that converge to the same limit cycle (solid line). The quasi-steady state is indicated (star). Lower panel: evolution of the limit cycle for Δn = 0.04, 0.05, 0.06 MeV. The arrows indicate the path of the cycles A-B, B-C, and C-A for the star with Δn = 0.05 MeV. |
In the lower panel of Fig. 3, we show different limit cycles by changing the energy gap and label three sections of the evolution curve with Δn = 0.05 MeV, namely A-B, B-C, and C-A. Along the path A-B, the chemical imbalance is ~Δn and some reactions are opened, increasing the temperature until it reaches node B, without changing the chemical imbalance. Along the path B-C, the temperature is high enough to open abruptly many reactions that tend to restore the beta equilibrium, and ηnpe drops rapidly. Finally, along the path C-A, the chemical imbalance is sufficiently below the energy gap to strongly inhibit the neutrino reactions. Thus, no heating mechanism is present and the star cools by photon emission. Moreover, no restoring mechanism for the beta equilibrium is present and the chemical imbalance grows by the spin-down compression.
We observe from this figure that the amplitude of the limit cycles increases with the gap Δn, which we can easily understand from the previous analysis. For the path A-B, the chemical imbalance must be larger for larger Δn to open reactions. Then, from B to C, we note from the linear analysis in Sect. 3.2 that for larger gaps the system becomes more unstable or, more precisely, the heating function ξeIΓ − Iϵ becomes more sensitive to small perturbations in temperature reaching higher temperatures, forcing the chemical imbalances to reach lower values in node C. Finally, from C to A, all the curves are parallel since the photon emission and spin-down compression do not depend on Δn.
3.5. Limit cycle timescales and the MSP J0437
We can observe from the bottom panel of Fig. 1 that there are two very different scales governing the limit cycles. The first and shorter one involves the rapid increase in temperature and ends with a rapid decrease in the chemical imbalance, i.e. it goes from A to C in the lower part of Fig. 3. The second scale goes from C to A and is substantially dominant in the rotochemical heating evolution.
The first is quite stable and on the order of the timescales shown in Fig. 2 for the growth rates γ, i.e. a timescale of ~105 yr. However, the second scale depends strongly on the energy gap, because the latter sets the amplitude of the drop in ηnpe. It also depends on 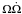 , since it accounts for the rate at which the chemical imbalance grows. For the examples displayed in Figs. 1 and 3, the longer timescale is ~106−107 yr.
, since it accounts for the rate at which the chemical imbalance grows. For the examples displayed in Figs. 1 and 3, the longer timescale is ~106−107 yr.
Considering the large difference between both timescales, we check that the fraction of the time in which the thermal emission would be detectable, i.e. the surface temperature Ts ≳ 105 K, is in the range ~5–25%, mainly depending on the energy gaps and spin-down parameters. Moreover, it is also unlikely to find it close to its quasi-steady state and therefore are unable to draw further conclusions about the pairing gaps needed to explain observations as in Petrovich & Reisenegger (2010).
However, we can account for the maximum energy gap combination Δthr = Δn + Δp at which rotochemical heating evolves to a stable solution, i.e. its quasi-steady state, and predict a surface temperature. Thus, for the spin-down parameters of MSP J0437 and the set of EOSs from Prakash et al. (1988) that allow direct Urca reactions of electrons and muons for its mass range 1.76 ± 0.2 M⊙ (Deller et al. 2008), namely BPAL21, BPAL31, BPAL 32, and BPAL33, the maximum gap combination that predict a quasi-steady state is in the range of Δthr ~ 0.01−0.1 MeV. Thus, the temperatures predicted when including superfluidity are a few times higher than those predicted by the non-superfluid case (Fernández & Reisenegger 2005). They are quite close to 105 K and for some cases can explain the likely thermal emission of the MSP J0437 (Kargaltsev et al. 2004).
Finally, given the rapid increase in temperature, we could ask whether the finite thermal diffusion timescales are relevant to our study or make any difference to the validity of our assumption of an isothermal NS interior. We claim that this assumption is fairly safe, since the increase in temperature takes ~105 yr, while the thermal diffusion time is just a few decades for these low temperatures.
 |
Fig. 4 Evolution of the internal temperature T and the chemical imbalances ηnpe and ηnpμ with the initial condition T = 108 K and null chemical imbalances. The spin-down is assumed to be caused by the magnetic dipole radiation, with dipolar field strength B = 2.8 × 108 G and initial period of P0 = 1 ms. The dashed lines indicate the energy gap Δn = 0.05 MeV. Upper panel: evolution of a 1.69 M⊙ star built with the BPAL21 EOS (Prakash et al. 1988), which allows muon direct Urca reactions, and we add the vortex creep reheating term of Eq. (27) with an excess of angular momentum J = 1043 erg s. Lower panel: evolution of a 1.68 M⊙ star built with the BPAL21 EOS (Prakash et al. 1988), which forbids direct Urca reactions with muons. |
3.6. Effect of muons and other reheating mechanisms.
The presence of muons does not introduce changes to the previous analysis, as long as direct Urca reactions with muons are allowed. On the other hand, if they react only by means of the modified Urca channels, the oscillations are damped and finally vanish.
In the upper panel of Fig. 4, we observe that the only effect to be considered is that the oscillations would be driven by the reactions involving muons, instead of those with electrons. This happens because the departure from beta equilibrium with muons, i.e. ηnpμ, is more strongly affected by the spin-down compression, and the direct Urca reactions with muons will lead the oscillations since they reach the critical value ~Δn first.
Moreover, including another reheating mechanism does not alter the existence of the oscillations as long as the temperature increase produced by this mechanism is not so high as to overcome the quasi-steady value of the temperature. As Gonzalez & Reisenegger (2010) argued, the two most relevant mechanisms to reheat an old neutron star are rotochemical heating and vortex creep (Alpar et al. 1984; Shibazaki & Lamb 1989). Therefore we include the latter in the upper panel of Fig. 4 to show that the oscillations persist even when another reheating mechanism is included. The energy dissipation rate that must be included as a heating term in Eq. (1) is given by (Alpar et al. 1984) 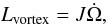 (27)where J is the excess of angular momentum. By choosing an intermediate value of J = 1043 erg s for the models in Shibazaki & Lamb (1989), we observe that the only effect of the extra heating term is to provide a higher floor to the internal temperature. This results in a straightforward way from the analysis in Sect. 3.2, since the Jacobian element in Eq. (22) is unaltered by the new term in Eq. (27). However, if this mechanism keeps the NS at substantially higher temperatures, it could displace the quasi-steady state and change the behavior of the oscillations.
(27)where J is the excess of angular momentum. By choosing an intermediate value of J = 1043 erg s for the models in Shibazaki & Lamb (1989), we observe that the only effect of the extra heating term is to provide a higher floor to the internal temperature. This results in a straightforward way from the analysis in Sect. 3.2, since the Jacobian element in Eq. (22) is unaltered by the new term in Eq. (27). However, if this mechanism keeps the NS at substantially higher temperatures, it could displace the quasi-steady state and change the behavior of the oscillations.
In the lower panel of Fig. 4, we show the evolution when direct Urca reactions with muons are forbidden, but modified Urca reactions involving muons are present. At first, the chemical imbalance of the muons reaches a value close to the energy gaps and reheats the star by means of modified Urca reactions. The chemical imbalance of the electrons then reaches this threshold value and the oscillations start to work normally until the chemical imbalance of the muons reaches its quasi-steady state, which predicts higher temperatures than those without muons (see the bottom panel of Fig. 1). Hence, the oscillations vanish and the quasi-steady state is mostly governed by the chemical imbalance of the muons.
 |
Fig. 5 Evolution of the internal temperature T and the chemical imbalance ηnpe for a 1.68 M⊙ star built with the EOS BPAL21 and no muons, with the initial condition T = 109 K and null chemical imbalance. The spin-down is assumed to be caused by the magnetic dipole radiation, with dipolar field strengths B = 1011 G (dashed line) and B = 1012 G (solid line) initial period of P0 = 5 ms. The dotted-dashed line indicates the energy gap Δn = 0.05 MeV. |
3.7. Effect on classical pulsars
In this section, we show the effects of these oscillations on classical pulsars. In Fig. 5, we illustrate their unstable behavior by showing the evolution of rotochemical heating for a NS with an energy gap Δn = 0.05 MeV, electron direct Urca reactions, no muons, and two magnetic fields of B = 1011 G and B = 1012 G.
From this figure, we observe that the temperature and the chemical imbalance can oscillate only during half of the period for B = 1011 G or a full period for B = 1012 G since the rotation rate is insufficient for the imbalance to recover from its drop and, therefore, produce any other oscillation. Thus, after the sudden increase in temperature at ~105 yr, the star cools almost exclusively by means of photon emission, while the chemical imbalance grows slowly, never reaching the threshold of the energy gap again.
If we changed the initial period to lower values (e.g. P0 = 1 ms), we could observe from the case with B = 1011 G one full oscillation period and another half, similar to the lower panel of Fig. 4. Similarly, lower values of the energy gap could produce more oscillations. In contrast, if we increase the initial period, the rotation energy to increase the chemical imbalance may not be enough to reach the energy gap threshold, and oscillation may not occur at all.
In conclusion, the oscillating behavior generally does not persist in classical pulsars, and the standard cooling governs their thermal evolution.
4. Conclusions
We have studied a new kind of oscillations of the temperature and chemical imbalances, produced during the evolution of rotochemical heating when the direct Urca reactions are allowed in superfluid MSPs with relatively high uniform and isotropic Cooper pairing gaps.
The oscillations work as follows. The direct Urca reactions are strongly blocked until the chemical imbalances grow up to a threshold value Δthr = Δn + Δp. Soon after this happens, strong reactions are suddenly turned on, increasing the temperature and decreasing the chemical imbalances. As this happens, the reactions are again strongly blocked and the star cools down by photon emission, while the chemical imbalances again increase until they reach the threshold value required to repeat the cycle after 106 − 7 yr. The temperature stays high for only a
small fraction of the cycle, making it difficult to detect this effect and predict a NS temperatures at a given time. For gaps below ~ 0.05 MeV or with muons reacting only by modified Urca processes, the oscillations vanish and the system reaches a quasi-steady state, as previously found in the non-superfluid or modified Urca cases.
Acknowledgments
We thank Denis González and Nicolás González for discussions and comments that benefited the present paper, and Rodrigo Fernández for letting us use his rotochemical heating code. This work was supported by Proyecto Regular FONDECYT 1060644, the FONDAP Center of Astrophysics (15010003), Proyecto Basal PFB-06/2007, and Proyecto Límite VRAID No 15/2010.
References
- Alpar, M. A., Anderson, P. W., Pines, D., & Shaham, J. 1984, A&A, 276, 325 [Google Scholar]
- Amundsen, L., & Østgaard, E. 1985, Nucl. Phys. A, 442, 163 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Akmal, A., Pandharipande, V. R., & Ravenhall, D. G. 1998, Phys. Rev. C, 58, 1804 [NASA ADS] [CrossRef] [Google Scholar]
- Deller, A., Verbiest, J., Tingay, S., & Bailes, M., 2008, ApJ, 685, L67 [NASA ADS] [CrossRef] [Google Scholar]
- Fernández, R., & Reisenegger, A. 2005, ApJ, 625, 291 [NASA ADS] [CrossRef] [Google Scholar]
- Flowers, E., Ruderman, M., & Sutherland, P. 1976, A&A, 205, 541 [Google Scholar]
- Gonzalez, D., & Reisenegger, A., 2010, A&A, 522, A16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Haensel, P., & Pichon, B. 1994, A&A, 283, 313 [NASA ADS] [Google Scholar]
- Hansen, B. M. S., & Phinney, E. S. 1998, MNRAS, 294, 569 [NASA ADS] [CrossRef] [Google Scholar]
- Kargaltsev, O., Pavlov, G. G., & Romani, R. 2004, ApJ, 602, 327 [NASA ADS] [CrossRef] [Google Scholar]
- Levenfish, K. P., & Yakovlev, D. G. 1994, Astron. Rep., 38, 247 [NASA ADS] [Google Scholar]
- Lombardo, U., & Schulze, H., 2001, Lect. Notes Phys., 578, 30 [NASA ADS] [CrossRef] [Google Scholar]
- Maxwell, O.V., 1979, A&A, 231, 201 [Google Scholar]
- Pethick, C. J., Ravenhall, D. G., & Lorentz, C. P. 1995, Nucl. Phys. A, 584, 675 [NASA ADS] [CrossRef] [Google Scholar]
- Petrovich, C., & Reisenegger, A., 2010, A&A, 521, A77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Potekhin, A. Y., Chabrier, G., & Yakovlev, D. G. 1997, A&A, 323, 415 [NASA ADS] [Google Scholar]
- Prakash, M., Ainsworth, T. L., & Lattimer, J. M. 1988, Phys. Rev. Lett., 61, 2518 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Reisenegger, A. 1995, ApJ, 442, 749 [NASA ADS] [CrossRef] [Google Scholar]
- Reisenegger, A. 1997, ApJ, 485, 313 [NASA ADS] [CrossRef] [Google Scholar]
- Reisenegger, A., Jofré, P., Fernández, R., & Kantor, E. 2006, ApJ, 653, 568 [Google Scholar]
- Schaab, Ch., Sedrakian, A., Weber, F., & Weigel, M. K. 1999, A&A, 346, 465 [NASA ADS] [Google Scholar]
- Shibazaki, N., & Lamb, F. K. 1989, ApJ, 346, 808 [NASA ADS] [CrossRef] [Google Scholar]
- Strogatz, S. H. 1994, Nonlinear dynamics and chaos (Addison-Wesley) [Google Scholar]
- Thorne, K. S. 1977, ApJ, 212, 825 [NASA ADS] [CrossRef] [Google Scholar]
- Villain, L., & Haensel, P. 2005, A&A, 444, 539 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Verbiest, J. P. W., Bailes, M., van Straten, W., et al. 2008, ApJ, 679, 675 [NASA ADS] [CrossRef] [Google Scholar]
- Yakovlev, D. G. 2001, Phys. Rep., 354, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Yakovlev, D. G., & Pethick, C. J. 2004, ARA&A, 42, 169 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
All Figures
 |
Fig. 1 Evolution of the internal temperature T and the chemical imbalance ηnpe for a 1.68 M⊙ star without muons built with the BPAL21 EOS (Prakash et al. 1988), with the initial conditions T = 108 K and ηnpe = 0. The spin-down is assumed to be caused by magnetic dipole radiation, with dipolar field strength B = 2.8 × 108 G and initial period P0 = 1 ms. The dashed lines are the quasi-steady state solution calculated from |
| In the text | |
 |
Fig. 2 Real and imaginary parts of the growth rates γ + and γ − (upper panel) calculated from Eq. (26) and components of the Jacobian matrix (lower panel) in Eqs. (22)–(25), for different values of Δn. In both panels, the stellar parameters are the same as in Fig. 1 and we assume that |
| In the text | |
 |
Fig. 3 Evolution of rotochemical heating in the ηnpe − T space for a superfluid star with the same parameters of Fig. 1. Upper panel: evolution with Δn = 0.05 MeV for different initial conditions (dotted-dashed lines) that converge to the same limit cycle (solid line). The quasi-steady state is indicated (star). Lower panel: evolution of the limit cycle for Δn = 0.04, 0.05, 0.06 MeV. The arrows indicate the path of the cycles A-B, B-C, and C-A for the star with Δn = 0.05 MeV. |
| In the text | |
 |
Fig. 4 Evolution of the internal temperature T and the chemical imbalances ηnpe and ηnpμ with the initial condition T = 108 K and null chemical imbalances. The spin-down is assumed to be caused by the magnetic dipole radiation, with dipolar field strength B = 2.8 × 108 G and initial period of P0 = 1 ms. The dashed lines indicate the energy gap Δn = 0.05 MeV. Upper panel: evolution of a 1.69 M⊙ star built with the BPAL21 EOS (Prakash et al. 1988), which allows muon direct Urca reactions, and we add the vortex creep reheating term of Eq. (27) with an excess of angular momentum J = 1043 erg s. Lower panel: evolution of a 1.68 M⊙ star built with the BPAL21 EOS (Prakash et al. 1988), which forbids direct Urca reactions with muons. |
| In the text | |
 |
Fig. 5 Evolution of the internal temperature T and the chemical imbalance ηnpe for a 1.68 M⊙ star built with the EOS BPAL21 and no muons, with the initial condition T = 109 K and null chemical imbalance. The spin-down is assumed to be caused by the magnetic dipole radiation, with dipolar field strengths B = 1011 G (dashed line) and B = 1012 G (solid line) initial period of P0 = 5 ms. The dotted-dashed line indicates the energy gap Δn = 0.05 MeV. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


