| Issue |
A&A
Volume 528, April 2011
|
|
|---|---|---|
| Article Number | A36 | |
| Number of page(s) | 10 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/201015413 | |
| Published online | 23 February 2011 | |
A search for faint low surface brightness galaxies in the relaxed cluster Abell 496⋆
1
LAM, Pôle de l’Étoile Site de Château-Gombert, 38 rue Frédéric
Joliot-Curie,
13388
Marseille Cedex 13,
France
2
Department of Physics and Astronomy, Northwestern
University, 2131 Sheridan
Road, Evanston
IL
60208-2900,
USA
3
UPMC Université Paris 06, UMR 7095, Institut d’Astrophysique de
Paris, 75014
Paris,
France
e-mail: durret@iap.fr
4
CNRS, UMR 7095, Institut d’Astrophysique de Paris,
75014
Paris,
France
Received: 16 July 2010
Accepted: 15 January 2011
Context. Cluster faint low surface brightness galaxies (fLSBs) are difficult to observe. Consequently, their origin, physical properties and number density are not well known. After a first search for fLSBs in the highly substructured Coma cluster, we present here a search for fLSBs in the nearly relaxed Abell 496 cluster.
Aims. Abell 496 appears to be a much more relaxed cluster than Coma, but still embedded in a large scale filament of galaxies. Our aim is to compare the properties of fLSBs in these two very different clusters, to search for environmental effects.
Methods. Based on deep CFHT/Megacam images in the u∗, g′, r′ and i′ bands, we selected galaxies with r′ > 21 and μr′ > 24 mag arcsec-2. We estimated photometric redshifts for all these galaxies and kept the 142 fLSBs with photo-z < 0.2.
Results. In a g′ − i′ versus i′ color–magnitude diagram, we find that a large part of these fLSBs follow the red sequence (RS) of brighter galaxies. The fLSBs within ± 1σ of the RS show a homogeneous spatial distribution, while those above the RS appear to be concentrated along the large scale filament of galaxies.
Conclusions. These properties are interpreted as agreeing with the idea that RS fLSBs are formed in groups prior to cluster assembly. The formation of red fLSBs could be related to infalling galaxies.
Key words: galaxies: clusters: individual: Abell 496 / galaxies: luminosity function: mass function
Based on observations obtained with MegaPrime/MegaCam, a joint project of CFHT and CEA/DAPNIA, at the Canada-France-Hawaii Telescope (CFHT) which is operated by the National Research Council (NRC) of Canada, the Institut National des Sciences de l’Univers of the Centre National de la Recherche Scientifique (CNRS) of France, and the University of Hawaii. The data processing were performed by the TERAPIX Data Centre.
© ESO, 2011
1. Introduction
Faint low surface brightness galaxies (fLSBs hereafter) remain a poorly known class of galaxies, though they are interesting objects for several reasons, as already discussed in detail by Adami et al. (2009a). We define fLSBs as galaxies with a central surface brightness fainter than μr′ = 24 mag arcsec-2 and a total magnitude r′ > 21, to be consistent with Adami et al. (2006, hereafter ASU06). Briefly: fLSBs could account for part of the missing low luminosity structures predicted by CDM models of hierarchical structure formation (White & Rees 1978), in particular since they appear dominated by dark matter (e.g. McGaugh et al. 2001; de Blok et al. 2001). CDM models predict the existence of low luminosity galaxies in all environments, but fLSBs seem to be present in higher numbers in clusters than in the field (see e.g. Sabatini et al. 2005; ASU06, and references therein).
Many fLSBs are fainter than the night sky and clearly extend toward fainter brightnesses than predicted by the Freeman law (1970), as shown for example by Bothun et al. (1997). Due to their extreme faintness both in terms of surface brightness and of total magnitude, fLSBs are therefore very difficult to detect, hence their origin, physical properties and number density are not well known in a statistical way over a large number of clusters, despite numerous studies (e.g. Binggeli et al. 1985; Schombert et al. 1992; Bothun et al. 1993; Bernstein et al. 1995; Impey et al. 1996; Sprayberry et al. 1996; Ulmer et al. 1996; Impey & Bothun 1997; O’Neil et al. 1997; Kuzio de Naray et al. 2004).
In order to increase the number of fLSBs detected in clusters, our team has searched for Coma cluster fLSBs in the total magnitude versus central surface brightness space (ASU06; Adami et al. 2009a) and found for example that these objects tended to be more concentrated in several areas (not always central). Furthermore, based on their position in the (B − R) versus R plane, we found that we could identify three distinct types of fLSBs. Those that fall on the color magnitude relation extrapolated from the bright normal galaxy population we called sequence fLSBs. We interpreted sequence fLSBs as galaxies that formed in small groups prior to the cluster assembly. Then we interpreted the reddest fLSBs as faint stripped ellipticals and the blue fLSBs as galaxies made of material stripped from spiral infalling galaxies. However, the Coma cluster is highly substructured (e.g. Adami et al. 2005) and we do not know how substructure could affect the spatial distribution of the fLSB population. We therefore decided to analyze in the same way the distribution and properties of fLSBs in a more relaxed cluster where substructures will not complicate the picture.
Abell 496 is one of the rare nearby nearly relaxed clusters (see e.g. Durret et al. 2000). Boué et al. (2008) reported the detailed analysis of the galaxy luminosity functions of Abell 496, based on deep CFHT Megacam images in four bands which are ideal to search for fLSBs. They confirmed that this cluster appears very relaxed, with no particular structure at the cluster scale, though at larger scale an extended filament of galaxies with redshifts close to that of Abell 496 was found to spread from the north-west to the south-east of the cluster (see Fig. 10 in Boué et al. 2008).
The mean heliocentric velocity of Abell 496 is cz = 9885 km s-1, corresponding to a redshift z = 0.0329, its distance modulus is 35.69, and the scale is 0.666 kpc arcsec-1, assuming H0 = 72 km s-1 Mpc-1, ΩM = 0.3 and ΩΛ = 0.7. It has an angular virial radius of 0.77° (1.85 Mpc), obtained by extrapolating the radius of overdensity 500 (Markevitch et al. 1999), measured relative to the critical density of the Universe to the radius of overdensity 100. We will give magnitudes in the AB system.
The paper is organized as follows. The data and method to search for fLSBs are described in Sect. 2. Results concerning the color–magnitude relation, spatial distribution and luminosity function of fLSBs are presented in Sect. 3 and discussed in Sect. 4. We give in the Appendix the list of the 142 fLSBs with photo-z < 0.2 as well as the images in the four bands and the surface brightness profile for one of them.
2. The data and method
2.1. The optical data
This work is based on deep images obtained at the CFHT with the Megaprime/Megacam camera (program 03BF12, P.I. V. Cayatte) in the four bands u∗, g′, r′, i′ already described in detail by Boué et al. (2008). The images are centered on the cluster centre as defined by NED: J2000.0 equatorial coordinates 04h33mn37.1s, − 13°14′46′′. They were reduced by the TERAPIX pipeline. Since simple detection with SExtractor (Bertin & Arnouts 1996) is not always sufficient to measure fLSB magnitudes unambiguously, we applied the same elaborate technique as in ASU06, which is briefly described below.
2.2. The method to search for fLSBs
In order to make the comparison with the fLSBs in Coma straightforward, we detected fLSBs with the same method as described in ASU06. In brief, we started with a catalog produced by SExtractor from the Abell 496 CFHT Megacam images. Then, since our fLSB dedicated software could not be applied to such large images, we divided each image (and the corresponding catalogue) in 25 subimages, each 0.2 × 0.2 deg2.
The first cut was to eliminate bright objects (total magnitudes r′ < 21) from our analysis in order to be consistent with the ASU06 selection process. This selection criterion is based on the fact that part of the cluster fLSBs could be tidal dwarf galaxies (see ASU06). Tidal dwarf galaxies have masses as low as 107 or 108 M⊙ (Bournaud et al. 2003), and as shown in ASU06 this translates to magnitudes fainter than r′ ~ 21. Each of the 25 subimages was then examined visually, in order to note areas around diffraction spikes and between CCDs, and all SExtractor objects in these areas were removed from further analysis.
As we had images in four bands and our software was designed to process only two bands at once, we first considered the r′ and u∗ bands, in order to encompass the 4000 Å break at the redshift of Abell 496 (z = 0.0329). We then ran a three-step iterative selection process on each of the 25 subimages and for the r′ and u∗ bands to generate a primary data set.
First, we fit a Gaussian form plus a constant background to the linear-scale surface brightness profiles on the images, as in ASU06. Although fLSBs have exponential surface brightness profiles, Ulmer et al. (1996) found that fLSB selection based on exponential profiles generates a large number of false candidates in rich environments, due to the proximity of neighboring objects. Instead of using exponential profiles, ASU06 therefore selected fLSBs by χ2-fitting of Gaussian curves to the radial surface brightness profiles of fLSBs. This does not mean that an exponential is not the proper form of fLSB profile. Rather, the Gaussian profile is the result of the intrinsic (exponential) shape convolved with instrumental effects (the PSF, due to seeing, had typical values between 0.4 and 0.6 arcsec). Initially, we let the radial profiles extend to a maximum radius θmax = 2.5 arcsec from the center of each object, which, as determined by visual inspection, encompasses the entire range of fLSB sizes.
Second, we selected initial fLSB candidates with radius greater than 0.6 arcsec. The radius is defined here as the σ and not as the FWHM of the profile (FWHM = 2.35σ). The size threshold was chosen above the seeing radius in order to limit contamination by globular clusters which at the distance of Abell 496, appear as point sources. The r′ central surface brightness was chosen fainter than μr′ = 24 mag arcsec-2 to be consistent with ASU06.
Third, we optimized the final value of θmax for all the selected candidates to ensure that none of their surface brightness profiles were contaminated by surrounding objects. This process is explained in more detail in ASU06. The optimized θmax for each candidate was determined by visual inspection. We then repeated the two previous steps. After inspecting all candidates visually we selected as final fLSBs the candidates that yielded an acceptable Gaussian fit to a distance of θmax (see also ASU06 for more details). By “acceptable” we mean that the probability of finding a better fit (by changing the parameters) is smaller than 10%. An example is shown in Fig. A.2.
The convergence/non-convergence was done as follows: if the chi-squared changed by less than 0.1% within 20 iterations, this was called convergence. If the chi-squared failed to decrease by less than 0.1% in 20 iterations or if the chi-squared actually grew without bound, then this was called non-convergence.
The final data set was defined requiring a good (i.e. converging) fit for both the r′ and u∗ bands simultaneously. We then computed magnitudes for this sample in the g′ and i′ images. The automated analysis produced valid Gaussian fits most of the time. For objects with a non converging process (for example only 3 cases for the g′ band), we calculated the missing i′ and g′ band magnitudes by comparing the SExtractor magnitudes with the results from our dedicated code for the fLSBs with a converging process. Then we applied the relation deduced in this way to the fLSBs with a non converging process.
2.3. Cluster membership of the fLSBs
Independently, we calculated the photometric redshifts (hereafter photo-zs) for all the galaxies detected in the images, based on the SExtractor magnitudes in the four bands by applying the LePhare software (Ilbert et al. 2006). The zero point of each band was adjusted using a spectroscopic catalog of 596 galaxies brighter than i′ ~ 19.5. Figure 1 clearly shows that we can efficiently discriminate between z ≥ 0.2 and z < 0.2, as most objects with photo-zs < 0.2 also have spectroscopic redshifts < 0.2. This redshift value of 0.2 was also found to be optimal by Adami et al. (2008) with similar data.
 |
Fig. 1 Upper figure: i′ band magnitude histogram of our spectroscopic sample. Lower figure: photometric versus spectroscopic redshifts. |
We thus produced the two following fLSB samples: (a) fLSBs with a photo-z below 0.2 (142 galaxies); (b) fLSBs with a photo-z above 0.2 (783 galaxies).
The goal being to study cluster galaxies, we must estimate the contamination of the sample of 142 fLSBs by non cluster galaxies. From Fig. 1, the expected contamination of the z < 0.2 redshift interval by z ≥ 0.2 fLSBs is of the order of 5% (7 galaxies among the 142).
We must also estimate how many fLSBs at z < 0.2 are not part of Abell 496. Since Abell 496 is at z ~ 0.033, there is a non-negligible cosmological volume behind the cluster, as the photometric redshift technique is not accurate enough to distinguish between a cluster member and a z < 0.2 non-cluster galaxy.
One method to estimate the number of z < 0.2 non cluster member fLSBs is to estimate the volume density of field fLSBs. This is not a trivial task as our selection function is quite specific and is not reproduced by most literature studies. However we can take advantage of the deep spectroscopic follow up of the Coma cluster of Adami et al. (2009b), where a spectroscopic redshift was successfully measured for eleven fLSBs along the line of sight to Coma, selected exactly in the same way as in the present paper. These fLSBs all had a photometric redshift (computed in the same way as here) lower than 0.2 and were brighter than I = 22.7. Four of these eleven galaxies proved not to be part of the Coma cluster, though they were at redshifts lower than 0.2. This gives 21 galaxies per deg2 at photo-z < 0.2 and I ≤ 22.7 which are not cluster members. Along the line of sight to Abell 496, we detected 122 fLSBs brighter than i′ = 23.2 (equivalent to I = 22.7, see Fukugita et al. 1995) in a 1 deg2 field, so 21 of these should therefore not be part of the cluster. Extrapolating this number to the complete magnitude range, 24 of the 142 detected fLSBs at photo-z < 0.2 are expected not to be members of Abell 496.
Another method to estimate how many fLSBs at z < 0.2 are not part of Abell 496 is based on the assumption that cluster fLSBs follow a King number density distribution. This method results in ~ 24 ± 22 fLSBs at z ≤ 0.2 being non cluster members (also see Sect. 3.2), in agreement with the previous estimate, though with a large error.
We therefore conclude that among our 142 photo-z < 0.2 fLSBs, about 30 galaxies (24 effectively located at z < 0.2 but not in the cluster, plus 7 at z > 0.2 but classified as being at z < 0.2), or 21%, may not be part of Abell 496.
3. Results
The list of our 142 z < 0.2 candidate fLSBs is given in Tables A.1–A.3 with their positions, four band magnitudes as measured by the present process, and photometric redshifts.
3.1. Color–magnitude relation
 |
Fig. 2 Color–magnitude relation for all the fLSBs in the direction of Abell 496 (in black), and for the 142 galaxies for which the photo-z is less than 0.2 (in blue). The red line corresponds to the red sequence for bright galaxies (see text). |
 |
Fig. 3 Zoom on the color–magnitude relation for the fLSBs in the direction of Abell 496 with photo-z < 0.2 (142 objects). The red line corresponds to the red sequence for bright galaxies (see text). The green lines delineate the region above and below the red sequence, that we will respectively call red and blue fLSBs. The separation between these two lines corresponds to the approximate 1σ loci, ± 0.29 mag on either side of the red sequence. |
The g′ − i′ versus i′ color–magnitude relation obtained for our fLSBs is plotted in Fig. 2, together with the color–magnitude relation found by Boué et al. (2008) for the “normal” galaxies of Abell 496. The red sequence defined for the galaxies belonging to Abell 496 was computed by Boué et al. (2008) for galaxies brighter than i′ ~ 21 to be: g′ − i′ = −0.05i′ + 1.75. We can see in Fig. 3 that most of the fLSBs with photo-z < 0.2 fall close to the color–magnitude relation defined by brighter normal galaxies from Boué et al. (2008), though there is a non-negligible scatter.
In contrast, the fLSBs with photo-z > 0.2 are mostly located above the color–magnitude relation, suggesting that they are mostly redder and therefore background objects. This is not surprising, as the photometric redshift selection is primarily based on colors and therefore defines relatively blue colors at low redshift and relatively red colors for higher redshift.
We show in Fig. 3 a zoom of the color–magnitude relation for the 142 fLSBs with photo-z < 0.2. We can define three subsamples: the sequence fLSBs (within ± 1σ, or ± 0.29 mag from the red sequence), the blue fLSBs (more than 1σ below the red sequence), and the red fLSBs (more than 1σ above the red sequence). This classification is similar to that already proposed for fLSBs in Coma (ASU06), suggesting that a large fraction (here about 2/3) of fLSBs follows an evolutionary path comparable to that of normal ellipticals in clusters. We will discuss this result in more detail in Sect. 4.
3.2. Spatial distribution of the fLSBs and cluster substructure
A bi-dimensional Kolmogorov Smirnov (KS hereafter) test shows that the α, δ spatial distribution of fLSBs at z < 0.2 is different at the 92% level from a uniform distribution; the same KS test shows that the spatial distributions of the z < 0.2 and z ≥ 0.2 fLSBs are different at the 99.9% level. The fLSBs with a high probability of belonging to Abell 496 are therefore not as uniformly distributed throughout the cluster as the galaxies likely to be non-cluster members.
The α, δ spatial distributions of the photo-z < 0.2 sequence, red, and blue fLSBs shown in Fig. 4 are also different. The distribution of blue fLSBs is different from a uniform spatial distribution only with a probability of less than 1% from a KS test, so we can say that blue fLSBs are relatively uniformly distributed. On the other hand, sequence and red fLSBs are different from a uniform spatial distribution with respective probabilities of 90 and 99%, based on a KS test. In Fig. 4, the red fLSBs generally tend to be found preferentially along the large scale filament of galaxies found by Boué et al. (2008). This suggests that red fLSBs could be linked with this filament made up of groups infalling toward the Abell 496 center.
 |
Fig. 4 Positions of the fLSBs with photo-z < 0.2. Black, cyan and red points correspond to fLSBs within ± 1σ of the red sequence, below, and above this interval respectively. The black line indicates the direction of the very large scale filament of galaxies found by Boué et al. (2008) – see their Fig. 10. The contours correspond to the X-ray emission from the XMM-Newton EPIC MOS1 image (Laganá et al. 2008). |
 |
Fig. 5 Spatial distribution of galaxies of various types with the following symbols: red hexagones for ellipticals, purple squares for early-type spirals, green triangles for intermediate spirals, and blue diamonds for late-type spirals. The spectral types of these galaxies were determined in the photo-z computation process fixing the redshifts to their spectroscopic values. The black open symbols (squares, triangles and circles) show the three main dynamically distinct groups. Contours correspond to the XMM-Newton X-ray emission. The black line indicates the direction of the very large scale filament of galaxies found by Boué et al. (2008). |
Since the cluster Abell 496 is believed to be nearly relaxed (Durret et al. 2000), it is important to determine if it is still experiencing an infalling activity. We searched for substructures in Abell 496 by applying the Serna & Gerbal (1996) method to our large spectroscopic redshift sample of 596 galaxies (Durret et al. 1999). We show in Fig. 5 the spatial distribution of galaxies belonging to various independent dynamical structures inside the Abell 496 cluster.
We only detected three such structures and they are all low mass structures of a few 1012 M⊙. These masses are very small compared to the overall cluster mass of the order of 3.5 × 1014 M⊙ (e.g. Laganá et al. 2010) and do not prevent us from classifying the cluster from being relatively well relaxed. The description of the Serna & Gerbal method and the full analysis of the results thus obtained can be found in Appendix B.
We also see from Fig. 5 that the two main substructures are located towards the northwest and southeast of the cluster, that is roughly along the direction of the large scale filament feeding the cluster. A third less massive structure is located towards the west. Cold dark matter hierarchical structure formation models (e.g. Colberg et al. 1999) predict that clusters of galaxies grow via group accretion. In this context, the cluster substructures detected along the path of the large scale filament are probably recent infallen groups.
 |
Fig. 6 Upper figure: number of galaxies per square arcmin versus distance to the cluster center, considering the 142 fLSBs with photo-z < 0.2. The vertical dashed line shows the cluster central galaxy radius. Lower figure: number of galaxies per square arcmin versus distance to the cluster center, considering the 5766 galaxies with photo-z < 0.2 (fLSBs and normal galaxies). The red lines show the best King model fits in both cases. The green horizontal lines show the respective background contributions. |
We also quantified the spatial distribution of galaxies with photo-z < 0.2 as a function of radius both for the fLSBs and for the entire sample of galaxies in our images (including non-fLSB galaxies). For this, we counted the numbers of galaxies in concentric annuli with radii varying between 5 and 30 arcmin in steps of 5 arcmin. The density distributions (number of galaxies per arcmin2) thus obtained are drawn in Fig. 6.
These distributions were fit by a King model and we added a constant background to take into account non-cluster photo-z < 0.2 galaxies:
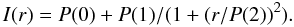 For the 142 fLSBs with photo-z < 0.2, the best fit was obtained for the following parameters: P(0) = (6.8 ± 6.3) × 10-3 arcmin-2, P(1) = 0.12 ± 0.03 arcmin-2, P(2) = 11.19 ± 0.03 arcmin.
For the 142 fLSBs with photo-z < 0.2, the best fit was obtained for the following parameters: P(0) = (6.8 ± 6.3) × 10-3 arcmin-2, P(1) = 0.12 ± 0.03 arcmin-2, P(2) = 11.19 ± 0.03 arcmin.
For all the galaxies, the corresponding numbers are: P(0) = 1.87 ± 0.09 arcmin-2, P(1) = 2.45 ± 0.54 arcmin-2, P(2) = 5.29 ± 0.51 arcmin.
As can be seen in Fig. 6, fLSBs in Abell 496 are not uniformly distributed, but are preferentially found toward the cluster center, except for a decrease of the number of fLSBs per arcmin2 in the cluster innermost point. This data point is most likely low because it is located inside the central galaxy radius, thus fLSBs in this region would have been missed by our analysis. Note that although the fLSBS are concentrated toward the cluster center they are less concentrated than the whole galaxy population, as discussed in Sect. 4.
 |
Fig. 7 Upper figure: r′-band magnitude histogram of the 783 fLSBs with available photo-zs. Lower figure: luminosity function for the 142 fLSBs with photo-z < 0.2 as a function of absolute r′-band magnitude (assuming these objects are cluster members). The vertical line shows the approximate completeness level of the fLSB sample derived from our simulations. The oblique line shows the mean slope of the luminosity function for absolute r′-band magnitude brighter than − 12.9 (see text). |
 |
Fig. 8 Dispersion σ (in arcsec) of the photo-z < 0.2 fLSBs. The vertical dashed line represents the size of our simulated fLSBs. |
3.3. Luminosity function of the fLSBs
Before computing a luminosity function for fLSBs, it is important to investigate the completeness level of our sample. We show in Fig. 7 the magnitude histogram of the 783 fLSBs with available photo-zs and the luminosity function of the 142 fLSBs with photo-z < 0.2. The peak of the magnitude histogram for the 783 fLSBs is located close to r′ = 22.7. This gives a first estimate of the completeness limit of the sample. We also performed simulations in order to have an independent estimate of the completeness in the r′ images.
The simulation adds artificial objects of different shapes and magnitudes to the CCD images and then attempts to recover them by running SExtractor again with the same parameters used for primary object detection (see Adami et al. 2006, for more details). In this way, the completeness is measured on the original CCD frames. We estimated the completeness of our catalog for fLSBs using simulated point-like objects with a Gaussian profile of FWHM 3.3 arcsec (σ = 1.4 arcsec). This is the typical maximal size of a fLSB in our catalog (see Fig. 8). We also divided the full field of view in 100 different sub-regions to have the completeness at different locations in the cluster. The percentage of recovered fLSBs as a function of the r′ magnitude is shown in Fig. 9, where error bars show the variation among these 100 regions. We can see that we reach a 50% completeness at r′ ~ 22.8. This estimate is similar to the value of the peak of the fLSB magnitude histogram. It also represents an underestimate of the true fLSB completeness level, as most fLSBs are more compact than a 3.3 arcsec FWHM Gaussian profile, and therefore easier to detect.
We can see in Fig. 7 that the luminosity function decreases for magnitudes fainter than the completeness limit, as expected. A power-law fit of the bright part of the luminosity function gives a mean slope of − 1.2 ± 0.1. This is significantly shallower than the global luminosity function of Boué et al. (2008), who found a slope of − 1.55 ± 0.05. This means that the fLSBs cannot be responsible for all the increase of the global galaxy luminosity function of the cluster at faint magnitudes. We probably start missing fLSBs for r′ magnitudes fainter than ~ 22.8. At the cluster redshift, this translates to Mr′ ~ −12.9.
 |
Fig. 9 Percentage of recovered fLSBs in our simulations as a function of the r′ magnitude. The dotted lines show the 50% completeness level. |
4. Discussion
As described above, we have found 142 fLSBs in the direction of Abell 496 with photo-z < 0.2, out of which about 80% are probably cluster members. Their angular density profile is well fit by a King model with a core radius about twice as large as for normal galaxies. The King distribution of fLSBs in Abell 496 is very different from what was observed in Coma by ASU06, where fLSBs do not follow any King-like distribution. This difference is consistent with the idea that Abell 496 is relaxed while Coma is not. Furthermore, the wider radial distribution of the fLSBs versus normal galaxies in Abell 496 is consistent with the idea that mass segregation has occurred in Abell 496.
The detected fLSBs fall reasonably well on the extension of the bright end of the color–magnitude relation established by Boué et al. (2008). The fact that we have found (see Sect. 3.1) the ± 1σ interval for the fLSBs around the red sequence similar in Abell 496 and Coma, one a relaxed cluster, the other not, fits with the idea that the relaxation state of the cluster does not influence the position of the fLSBs on the red-sequence. The similar red-sequence width in both clusters could be attributed to sequence fLSBs having evolved in similar groups that fell into the clusters later, as suggested by ASU06.
On scales of ≥ 1 Mpc, we note that there is a filament in the normal galaxy population with redshifts < 0.2 found by Boué et al. (2008). The filament extends along a north-west to south-east line. In Fig. 4 we can see that red fLSBs (with redshifts < 0.2) seem to have an anisotropic distribution similar to the filament found by Boué et al. However, blue fLSBs show no obvious anisotropic distribution, suggesting they had a different evolutionary history. Blue fLSBs are perhaps the remnants of tidally disrupted late-type galaxies as hypothesized by ASU06 for Coma.
In terms of tidal disruption, we note that the spatial distribution of fLSBs seems to show no holes in the cluster center, which is not the case for Coma (ASU06). For Coma the fLSBs could have been destroyed by tidal disruption due to the massive D galaxies in the Coma core. In contrast, there is only one central galaxy in the center of Abell 496, which could produce much less tidal disruption. It is beyond the scope of this work, though, to carry out numerical simulations to verify or falsify the idea that fLSBs are tidally destroyed in the core of Coma and not in Abell 496.
Acknowledgments
We thank the referee for useful comments. We acknowledge our collaboration with G. Boué and V. Cayatte during the first stages of this project and are grateful to T. Laganá for giving us her XMM-Newton images. M. Ulmer thanks UPMC, IAP, Aix-Marseille I University, and LAM for their hospitality during the different stages of this project, and Bryant Smith and Nicholas Logenbaugh for software support.
References
- Adami, C., Biviano, A., & Mazure, A. 1998, A&A, 331, 439 [NASA ADS] [Google Scholar]
- Adami, C., Biviano, A., Durret, F., & Mazure, A. 2005, A&A, 443, 17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Adami, C., Scheidegger, R., Ulmer, M., et al. 2006, A&A, 459, 679 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Adami, C., Ilbert, O., Pelló, R., et al. 2008, A&A, 491, 681 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Adami, C., Pelló, R., Ulmer, M. P., et al. 2009a, A&A, 495, 407 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Adami, C., Le Brun, V., Biviano, A., et al. 2009b, A&A, 507, 1225 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bernstein, G. M., Nichol, R. C., Tyson, J. A., Ulmer, M. P., & Wittman, D. 1995, AJ, 110, 1507 [NASA ADS] [CrossRef] [Google Scholar]
- Bertin, E., & Arnouts, S. 1996, A&AS, 117, 393 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Binggeli, B., Sandage, A., & Tammann, G. A. 1985, AJ, 90, 1681 [NASA ADS] [CrossRef] [Google Scholar]
- Biviano, A., & Katgert, P. 2004, A&A, 424, 779 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bothun, G. D., Schombert, J. M., Impey, C. D., Sprayberry, D., & McGaugh, S. S. 1993, AJ, 106, 530 [NASA ADS] [CrossRef] [Google Scholar]
- Bothun, G. D., Impey, C. D., & McGaugh, S. 1997, PASP, 109, 745 [NASA ADS] [CrossRef] [Google Scholar]
- Bournaud, F., Duc, P. A., & Masset, F. 2003, A&A, 411, L469 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boué, G., Adami, C., Durret, F., Mamon, G., & Cayatte, V. 2008, A&A, 479, 335 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Colberg, J. M., White, S. D. M, Jenkins, A, & Pearce, F. R. 1999, MNRAS, 308, 593 [NASA ADS] [CrossRef] [Google Scholar]
- de Blok, W. J. G., McGaugh, S. S., & Rubin, V. C. 2001, AJ, 122, 2396 [NASA ADS] [CrossRef] [Google Scholar]
- Durret, F., Felenbok, P., Lobo, C., Slezak, E. 1999, A&AS, 139, 525 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Durret, F., Adami, C., Gerbal, D., & Pislar, V. 2000, A&A, 356, 815 [NASA ADS] [Google Scholar]
- Freeman, K. C. 1970, ApJ, 160, 811 [NASA ADS] [CrossRef] [Google Scholar]
- Fukugita, M., Shimasaku, K., & Ichikawa, T. 1995, PASP, 107, 945 [NASA ADS] [CrossRef] [Google Scholar]
- Impey, C. D., & Bothun, G. D. 1997, ARA&A, 35, 267 [NASA ADS] [CrossRef] [Google Scholar]
- Impey, C. D., Sprayberry, D., Irwin, M. J., & Bothun, G. D. 1996, ApJS, 105, 209 [NASA ADS] [CrossRef] [Google Scholar]
- Ilbert, O., Arnouts, S., McCracken, H. J., et al. 2006, A&A, 457, 841 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kuzio de Naray, R., McGaugh, S. S., & de Blok, W. J. G. 2004, MNRAS, 355, 887 [NASA ADS] [CrossRef] [Google Scholar]
- Laganá, T. F., Lima Neto, G. B., Andrade-Santos, F., & Cypriano, E. S. 2008, A&A, 485, 633 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Laganá, T. F., de Souza, R. S., & Keller, G. R. 2010, A&A, 510, 76 [Google Scholar]
- Łokas, E. L., & Mamon, G. A. 2003, MNRAS, 343, 401 [NASA ADS] [CrossRef] [Google Scholar]
- Markevitch, M., Vikhlinin, A., Forman, W. R., & Sarazin, C. L. 1999, ApJ, 527, 545 [NASA ADS] [CrossRef] [Google Scholar]
- McGaugh, S. S., Rubin, V. C., & de Blok, W. J. G. 2001, AJ, 122, 2381 [NASA ADS] [CrossRef] [Google Scholar]
- O’Neil, K., Bothun, G. D., & Cornell, M. E. 1997, AJ, 113, 1212 [NASA ADS] [CrossRef] [Google Scholar]
- Sabatini, S., Davies, J., van Driel, W., et al. 2005, MNRAS, 357, 819 [NASA ADS] [CrossRef] [Google Scholar]
- Schombert, J. M., Bothun, G. D., Schneider, S. E., & McGaugh, S. S. 1992, AJ, 103, 1107 [NASA ADS] [CrossRef] [Google Scholar]
- Serna, A., & Gerbal, D. 1996, A&A, 309, 65 [NASA ADS] [Google Scholar]
- Sprayberry, D., Impey, C. D., & Irwin, M. J. 1996, ApJ, 463, 535 [NASA ADS] [CrossRef] [Google Scholar]
- Ulmer, M. P., Bernstein, G. M., Martin, D. R., et al. 1996, AJ, 112, 2517 [NASA ADS] [CrossRef] [Google Scholar]
- White, S. D. M., & Rees, M. J. 1978, MNRAS, 183, 341 [NASA ADS] [CrossRef] [Google Scholar]
- Wojtak, R., & Łokas, E. L. 2010, MNRAS, 408, 2442 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Example of postage stamp images
Postage stamps images in the four bands are shown for one of the 142 fLSB candidates with photo-z < 0.2 in Fig. A.1 (galaxy #128 in Table A.3). The corresponding surface brightness profile is given in Fig. A.2.
Properties of the fLSBs with photo-z < 0.2 (objects #1 to #55).
 |
Fig. A.2 r′ band surface brightness profile (in mag arcsec-2 as a function of radius in arcsec for the galaxy of Fig. A.1). The dot-dashed and dotted lines show the Gaussian and exponential fits respectively. |
Appendix B: Search for substructures in Abell 496
Based on the large spectroscopic and photometric catalogues acquired for Abell 496 (Boué et al. 2008), we have estimated the spectral type of each galaxy with the Le Phare photometric redshift software. Galaxies are then assigned a spectral type: type 1 for ellipticals, type 2 for early type spirals, type 3 for intermediate type spirals and type 4 for late type spirals.
In order to search for substructures, we applied the Serna & Gerbal (1996) software to galaxies with measured spectroscopic redshifts and magnitudes. This hierarchical method allows to extract galaxy substructures or groups from a catalogue containing positions, magnitudes and redshifts, based on the calculation of their relative (negative) binding energies. The method gives as output a list of galaxies belonging to each group, as well as the information on the binding energy of the group itself, and on the mass of each substructure, assuming a mass to luminosity ratio (M/L). We used here a M/L ratio in the r′ band of 200, as previously assumed for the Coma cluster by Adami et al. (2005), based on the Coma cluster M/L ratio given by Łokas & Mamon (2003).
The Serna & Gerbal analysis shows the existence of three substructures (also see Sect. 4). These all have low masses (smaller than a few 1012 M⊙) and therefore their existence does not contradict the overall relaxed structure of the cluster.
If we analyze the morphological type distribution of the galaxies belonging to these three substructures (also see Fig. 5), we find that only one galaxy is of type 4 (late type spiral), corresponding to ~ 1% of all the galaxies in substructures. If we estimate the percentage of type 4 galaxies in the cluster (i.e. in the [0.0229, 0.0429] redshift range) that are not included in substructures, we find a value of 23%. The difference between these two values could be interpreted as indicating that late type spirals tend to avoid substructures and fall individually into the cluster, while earlier type galaxies fall into the cluster inside groups.
All Tables
All Figures
 |
Fig. 1 Upper figure: i′ band magnitude histogram of our spectroscopic sample. Lower figure: photometric versus spectroscopic redshifts. |
| In the text | |
 |
Fig. 2 Color–magnitude relation for all the fLSBs in the direction of Abell 496 (in black), and for the 142 galaxies for which the photo-z is less than 0.2 (in blue). The red line corresponds to the red sequence for bright galaxies (see text). |
| In the text | |
 |
Fig. 3 Zoom on the color–magnitude relation for the fLSBs in the direction of Abell 496 with photo-z < 0.2 (142 objects). The red line corresponds to the red sequence for bright galaxies (see text). The green lines delineate the region above and below the red sequence, that we will respectively call red and blue fLSBs. The separation between these two lines corresponds to the approximate 1σ loci, ± 0.29 mag on either side of the red sequence. |
| In the text | |
 |
Fig. 4 Positions of the fLSBs with photo-z < 0.2. Black, cyan and red points correspond to fLSBs within ± 1σ of the red sequence, below, and above this interval respectively. The black line indicates the direction of the very large scale filament of galaxies found by Boué et al. (2008) – see their Fig. 10. The contours correspond to the X-ray emission from the XMM-Newton EPIC MOS1 image (Laganá et al. 2008). |
| In the text | |
 |
Fig. 5 Spatial distribution of galaxies of various types with the following symbols: red hexagones for ellipticals, purple squares for early-type spirals, green triangles for intermediate spirals, and blue diamonds for late-type spirals. The spectral types of these galaxies were determined in the photo-z computation process fixing the redshifts to their spectroscopic values. The black open symbols (squares, triangles and circles) show the three main dynamically distinct groups. Contours correspond to the XMM-Newton X-ray emission. The black line indicates the direction of the very large scale filament of galaxies found by Boué et al. (2008). |
| In the text | |
 |
Fig. 6 Upper figure: number of galaxies per square arcmin versus distance to the cluster center, considering the 142 fLSBs with photo-z < 0.2. The vertical dashed line shows the cluster central galaxy radius. Lower figure: number of galaxies per square arcmin versus distance to the cluster center, considering the 5766 galaxies with photo-z < 0.2 (fLSBs and normal galaxies). The red lines show the best King model fits in both cases. The green horizontal lines show the respective background contributions. |
| In the text | |
 |
Fig. 7 Upper figure: r′-band magnitude histogram of the 783 fLSBs with available photo-zs. Lower figure: luminosity function for the 142 fLSBs with photo-z < 0.2 as a function of absolute r′-band magnitude (assuming these objects are cluster members). The vertical line shows the approximate completeness level of the fLSB sample derived from our simulations. The oblique line shows the mean slope of the luminosity function for absolute r′-band magnitude brighter than − 12.9 (see text). |
| In the text | |
 |
Fig. 8 Dispersion σ (in arcsec) of the photo-z < 0.2 fLSBs. The vertical dashed line represents the size of our simulated fLSBs. |
| In the text | |
 |
Fig. 9 Percentage of recovered fLSBs in our simulations as a function of the r′ magnitude. The dotted lines show the 50% completeness level. |
| In the text | |
 |
Fig. A.1 Postage stamp images of one fLSB in the four photometric bands (galaxy #128 in Table A.3). |
| In the text | |
 |
Fig. A.2 r′ band surface brightness profile (in mag arcsec-2 as a function of radius in arcsec for the galaxy of Fig. A.1). The dot-dashed and dotted lines show the Gaussian and exponential fits respectively. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


