| Issue |
A&A
Volume 528, April 2011
|
|
|---|---|---|
| Article Number | A60 | |
| Number of page(s) | 11 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/201015400 | |
| Published online | 01 March 2011 | |
Inhomogeneous metal distribution in the intracluster medium
Institut für Astro- und Teilchenphysik, Universität Innsbruck,
Technikerstr. 25,
6020
Innsbruck,
Austria
e-mail: Lorenzo.Lovisari@uibk.ac.at
Received: 15 July 2010
Accepted: 14 January 2011
Context. The hot gas that fills the space between galaxies in clusters is rich in metals. In their large potential wells, galaxy clusters accumulate metals over the whole cluster history and hence retain important information on cluster formation and evolution.
Aims. We use a sample of five cool core clusters to study the distribution of metals in the ICM. We investigate whether the X-ray observations yield good estimates for the metal mass and whether the heavy elements abundances are consistent with a certain relative fraction of SN Ia to SNCC.
Methods. We derived detailed metallicity maps of the clusters from XMM - Newton observations and used them as a measure for the metal mass in the ICM. We determined radial profiles for several elements, and using population synthesis and chemical enrichment models, we studied the agreement between the measured abundances and the theoretical yields.
Results. We show that the distribution of metals show a lot of inhomogeneities even in relaxed clusters. Using metal maps usually gives a metal mass 10–30% higher than the metal mass computed using a single extraction region, so it is expected that most previous metal mass determination have underestimated metal mass. The abundance ratio of α-elements to Fe, even in the central parts of clusters, are consistent with an enrichment thanks to the combination of SN Ia and SNCC.
Key words: X-rays: galaxies: clusters / galaxies: clusters: general / supernovae: general / galaxies: abundances
© ESO, 2011
1. Introduction
Since the first X-ray observations of the 7 keV iron line feature in the 1970’s by Mitchell et al. (1976) we know that the intracluster medium (ICM) contains not only primordial elements but also heavy elements. As heavy elements are only produced in stars that reside mainly in galaxies, the enriched material must have been ejected into the ICM by the member galaxies. Thanks to the large potential wells of galaxy clusters, they retain all the enriched material, so it makes them excellent laboratories for studying nucleosynthesis and the chemical enrichment history of the universe. Because the gas transfer affects the galaxy and galaxy cluster evolution, it is important to know when and how the enrichment takes place.
The components in a galaxy cluster interact with each other in many different ways, so that studying the distribution of the ejected metals can give us important information on the mechanisms that transports the enriched gas into the ICM. Several processes have been proposed to explain the observed enrichment in the ICM: ram-pressure stripping (Gunn & Gott 1972), galactic winds (De Young 1978), galaxy-galaxy interactions (Gnedin 1998), AGN outflows (De Young 1986; Hasinger et al. 2002), intracluster supernovae (Gerhard et al. 2002), and others. Simulations show an inhomogeneous distribution of the metals independent of the enrichment processes (Kapferer et al. 2006; Schindler & Diaferio 2008). Although both AGN outflows and galaxy-galaxy interactions can add metals to the ICM (Kapferer et al. 2005; Heath et al. 2007), simulations suggest that the metal enrichment of the ICM is caused primarily by galactic winds and ram-pressure stripping. A detailed comparison between the enrichment due to galactic winds and ram-pressure stripping has revealed that these two processes yield different metal distributions and a different time dependence of the enrichment (Kapferer et al. 2007b). In massive clusters, ram-pressure stripping provides a much more centrally concentrated distribution than galactic winds, because galactic winds can be suppressed in the cluster center, while ram-pressure stripping is most efficient there because the ICM density and the galaxies velocities are higher in the cluster center (Kapferer et al. 2006).
X-ray spectra are the only measure for the metallicity of the ICM. The metallicity is derived mainly by measuring the equivalent width of the iron line once the continuum (almost entirely given by thermal bremsstrahlung) is known. With the first generation of satellites it was just possible to determine the radial metallicity profiles (e.g. Mushotzky & Loewenstein 1997; De Grandi et al. 2004). With deep observations of bright clusters of galaxies by Chandra and XMM-Newton satellites it is now possible to extract metallicities in certain regions of a galaxy cluster and construct X-ray weighted metallicity maps (Schmidt et al. 2002; Sanders et al. 2004; Durret et al. 2005; O’Sullivan et al. 2005; Sauvageot et al. 2005; Werner et al. 2006; Sanders & Fabian 2006; Hayakawa et al. 2006; Simionescu et al. 2009; Lovisari et al. 2009).
In this paper we present the results of analysis of a sample of five cool core clusters (Centaurus, Hydra A, Sérsic 159-03, A496 and A2029) observed with XMM-Newton. Our first goal is to show that, even in relaxed clusters, the distribution of metals shows a lot of inhomogeneities that cause an underestimation of the metal mass.
The paper is structured as follows: Sect. 2 the data sets and data reduction techniques, in Sect. 3 spatially resolved measurements of metals abundances, in Sect. 4 the metallicity and temperature maps, in Sect. 5 the total gas and metal mass of the clusters. A summary of our conclusion is given in Sect. 6. Throughout the paper we assume H0 = 70 km s-1 Mpc-1, ΩΛ = 0.73 and ΩM = 0.27. The elemental abundances presented in this paper are given relative to the solar abundances from Anders & Grevesse (1989). We plot and tabulate values with the error quoted at the 90% level of confidence.
2. X-ray observations and analysis
2.1. Sample selection
Our first aim is to derive the metallicity maps of the cluster. Because a lot of photons are required to determine metallicities in many different regions of a cluster, we selected clusters observed with long enough exposure from the XMM-Newton archive. We found five clusters suitable for our study: Centaurus, A496, Sérsic 159-03, Hydra A and A2029. We did not take the Perseus Cluster into account, because there is already a detailed metallicity map that uses Chandra data (Sanders et al. 2005). We decided to include Centaurus, because Sanders & Fabian (2006) derived abundance maps for several elements but only for the inner part of the cluster (~80 kpc).
2.2. Data reduction
Observation data files (ODFs) were retrieved from the XMM archive and reprocessed with the XMM-Newton Science Analysis System (SAS) v7.1.0. We used tasks emchain and epchain to generate calibrated event files from raw data. Throughout this analysis single pixel events for the pn data (PATTERN 0) were selected, while the PATTERNs 0–12 were used for the MOS data sets. In addition, events next to CCD edges and next to bad pixels were excluded for all cameras (FLAG==0).
The data were cleaned for periods of high background due to the soft proton solar flares using a two-stage filtering process. In 100 s bins we first accumulated the light curve in the [10–12] keV band for MOS and [12–14] keV for pn, where the emission is dominated by the particle-induced background, and exclude all the intervals of exposure time having a count rate that deviated by more than 3σ from the mean (see Pratt & Arnaud 2002, for details). After filtering using the good time intervals from this screening, the event lists was then re-filtered in a second pass as a safety check for possible flares with soft spectra (Nevalainen et al. 2005; Pradas & Kerp 2005). In this case light curves were made with 10 s bins in the full [0.3–10] keV band. The resulting exposure times after cleaning are listed in Table 1.
Following the method presented by Simionescu et al. (2009), we used a combination of blank-sky maps and closed-filter observations for the background subtraction. From deep sky observations collected with XMM, we selected the data with the most similar background for each cluster. Both the blank-sky and the closed filter events were selected by applying the same PATTERN selection, vignetting correction, flare rejection criteria, and point source removal as used for the observation events. In addition we transformed the coordinates of the background files such that they were the same as for the associated cluster data set. We calculated the count rates in the hard energy band (10–12 keV for MOS and 12–14 keV for pn) outside of field of view (OOFOV) for each observation, blank sky maps and closed filter observations. For each detector we added a fraction of the closed filter observation to the corresponding blank sky background set to compensate for the difference between the OOFOV hard-band count rate in the observation and in the blank-sky data.
To correct for the vignetting effect, we used the photon-weighting method (Arnaud et al. 2001). The weight coefficients were computing by applying the SAS task evigweight to each event file. Point sources were detected using the task ewavelet in the energy band [0.3–10] keV and checked by eye on images generated for each detector. We produced a list of selected point sources from all available detectors, and the events in the corresponding regions were removed from both the blank field and the observation data set.
 |
Fig. 1 Radial profiles of the a) iron, b) oxygen, c) silicon, d) sulfur, and e) argon in solar units, derived from the EPIC spectra. |
2.3. Spectral analysis
All the spectral fits were performed with the XSPEC package (version 12.5.0, Arnaud 1996). To model the emission from a single (or multi) temperature plasma we fit the spectra with an APEC (+APEC) model (Smith et al. 2001) multiplied by the Galactic hydrogen column density, NH, fixed at the Galactic values (Dickey & Lockman 1990) through the wabs absorption model (Morrison & McCammon 1983). To determine the abundance profiles a VAPEC (+VAPEC) is used. We fit jointly MOS1, MOS2, and pn spectra, enforcing the same normalization value for MOS spectra and allowing the pn spectrum to have a separate normalization. In the spectral fitting we used the 0.3–10 keV energy range. Because of the low number of counts and the high background at large radii, the spectra are fitted in the 0.3–9 keV band and 0.5–7.5 keV energy range for MOS and pn, respectively. For the pn data we excluded the energy above 7.5 keV in order to discard strong instrumental lines around 8 keV. The redistribution and ancillary files (RMF and ARF) were created with the SAS tasks rmfgen and arfgen for each camera and each region that we analyzed.
Cluster sample, sorted in order of increasing redshift.
3. Abundances profiles
To know how the ICM has been enriched, we need to measure the amount and distribution of metals in the ICM. Since Ar and Fe are synthetized mainly in SNe Ia, O in core-collapse supernovae (SNCC), S, and Si in both SN Ia and SNCC, the measure of these elements can give hints to the past enrichment process in the ICM by supernovae.
For each cluster we extracted the spectra from several annular regions. Metal abundance profiles are determined for O, Si, S, Ar, and Fe. We fitted the data with the procedure presented in Lovisari et al. (2009) to avoid the degeneracy of the parameters: (1) we fitted the data with an absorbed APEC model in the 0.4–7 keV band to obtain the temperature (metallicity and normalization are considered free parameters); (2) we fixed the temperature and use a VAPEC model in the same energy band to determine the iron abundance (O, Mg, Si, S, Ar, Ni were left free. The other elements were fixed to the solar value); (3) we kept temperature and iron fixed to measure the oxygen abundance in the 0.4–1.5 keV band; (4) we fix the values of temperature, iron, and oxygen to estimate the silicon, sulfur, and argon abundances in the 1.5–5 keV band. Fixing to the solar value the abundances of elements, which cannot be significantly detected, may introduce a bias in the abundance measurements of other elements if the average cluster abundance is not solar. Thus, as a safety check we fitted the spectra with C, N, and Ne fixed at 0.3. Apart from Centaurus, the resulting abundance of the interested elements (O, Si, S, Fe) do not change significantly. Furthermore, we note that, in general, when we examined all abundances to be free in the fits, the resulting parameters did not change within the statistical errors.
Since there are still cross-calibration issues at energies below ~ 2 keV we fit the MOS and pn spectra separately to investigate how robust the derived values are. In general the values appear to be consistent within the errors in the two instruments, although the abundances of several elements are clearly not for some annuli. In particular O shows a strong discrepancy for Centaurus, A2029, and Hydra A up to 0.5 arcmin, while Si is not consistent for Sersic and Hydra A for the annulus between 0.5 and 1 arcmin. The systematic difference between MOS and pn is 3% for Fe, 17% for O, and 11% for Si.
In general the single temperature model (1T) provided a good fit to the spectra. However, in the inner region of all the clusters, a 2T model significantly improved the fit over a single temperature model as already found by Sanders & Fabian (2006) and Matsushita et al. (2007a) for Centaurus, by Simionescu et al. (2009) for Hydra A and by de Plaa et al. (2006) for Sérsic 159-03. The Fe abundances changed significantly as compared to the single temperature fit (the so-called Fe-bias, see for example Buote 2000; and Molendi & Gastaldello 2001). For these regions we use the abundances derived from this 2T model for the discussion below.
The abundance value for Si, S, Ar, and Fe and their radial variation look quite similar to each other. They commonly decline to about 1/4 of the central value in the outermost annulus (see Fig. 1). The error on the Si, S, and Ar abundance determination is larger than on iron. Nevertheless, their profiles indicate a central increase similar to the iron distribution.
Fit results for spatially resolved EPIC spectra.
The O profile looks more complex compared with the other elements. It shows several discontinuities, probably due to the fact that O is strongly related to episodes of star formation, in fact the O abundance seems to increase in the outer rings, where we expect higher star formation. On the other hand, while in the central regions the flux is high enough to get an accurate measurement, at large radii, the oxygen abundance could be overestimated because the oxygen in the galactic foreground emission starts to play an important role. This effect is most apparent if the background is high with respect to the source emission. Apart from Centaurus, in the outermost bin of each cluster we found approximately an S/N of 4, thus the O abundance should be used with caution there.
We computed abundance ratio of O, Si, S, and Ar over Fe as a function of the projected radius (see Table 2). The ratios Si/Fe and S/Fe are consistent with constant values around 1–2 and 0.7–1.5 respectively, while the O/Fe ratio for the innermost region is lower around 0.5–1 (see Fig. 2). In addition, the O/Fe ratio suggests some increase with radius with the exception of Hydra A for which both O/Fe and Si/Fe ratio seems to be constant. If we do not consider the outermost bin the O/Fe show a slight increase with radius, in agreement with the results obtained by Simionescu et al. (2009).
Using Suzaku observations, Sato et al. (2007, 2008, 2009a,b), Tokoi et al. (2008), and Matsushita et al. (2007b) have presented abundances of groups and clusters of galaxies. All systems show very similar values for the Si/Fe ratio, 1–1.5, in good agreement with our results. Tamura et al. (2004) reported abundance ratios for 19 clusters (among them A496, Hydra A, Sérsic, but with shorter exposure time) studied with XMM-Newton , and the mean Si/Fe was ~1.4. Their O/Fe, ~0.6, is a bit lower than our results. A ratio of 1–2 for the Si/Fe ratio was also found by De Grandi & Molendi (2009) when analyzing 26 clusters. Sanders & Fabian (2006) show the abundances ratios for the Centaurus cluster with Chandra and XMM-Newton, and the radial abundance ratios of O/Fe and Si/Fe to be 0.5–1 and 1–1.5 respectively, were consistent with our results.
Number ratio of SNCC to SN Ia (NII/NIa) and integrated number of SNCC computed using the abundance of O for each considered region.
Therefore, in general our results agree with previous studies, suggesting that cluster and groups have passed the same metal-enrichment process in the ICM.
 |
Fig. 2 Radial profiles of the a) O/Fe, b) Si/Fe and c) S/Fe ratio in solar units. |
 |
Fig. 3 Radial profiles of the relative fraction of SNCC using the O/Fe (red) and Si/Fe (black) ratio. |
3.1. Number ratio of SNCC to SN Ia
We investigated the SNe Ia and SNCC (including type Ib and Ic) contribution to the ICM metals following the method presented in Lovisari et al. (2009). Using the SNe Ia of the WDD2 model (the currently favored SN Ia explosion scenario) adapted from Iwamoto et al. (1999) and SNCC yields by Tsujimoto et al. (1995) we computed which SNCC/Ia ratio reproduces the observed abundances better. Although the models adopted here (SNe yields, Salpeter IMF, spherical symmetry in the ICM, etc.) are probably too simplified, and we should take other effects into account (i.e metals locked in stars), we want to show if there is agreement between the measured abundances and the theoretical yields for different elements. Table 3 and Fig. 3 summarize the results. We found good agreement in the O, Si, and Fe abundances for A496, Sérsic, and Centaurus for which the relative fraction of SNCC seems to increase toward the outskirts, and for Hydra A for which the relative fraction of SNCC seems to be constant. Due to the large error bars in the SN determination of A2029, it is difficult to say whether there is any agreement between the same elements. The flatness profile of the relative fraction of SNCC in Hydra A up to 370 kpc could be a consequence of the mixing due to the central AGN. Simionescu et al. (2009) show that the O/Fe in the cooler gas extending in arm-like structures caused by the central AGN is consistent with the average O/Fe ratio in the inner 3′. Concerning A2029, we found agreement between the O, Si, and Fe only in a few regions probably because the spectral lines are weaker at a high temperature so determining the elements becomes difficult. When the S/Fe ratio increases, the SNCC fraction computed using Si/Fe ratio does not agree with what is obtained using O/Fe ratio. Furthermore, even for most of the considered regions in the other clusters, the S/Fe ratio suggests a very low contribution to the enrichment due to SNCC that contradicts the idea of an early enrichment due to massive stars. In other words, either the yields of sulfur from theoretical works are underestimated or determining sulfur becomes very difficult when the abundances of Si is high. We note that (Baumgartner et al. 2005) found that clusters with a temperature between 6 and 8 keV (as for A2029) show a general increase in sulfur corresponding to a decrease in silicon.
 |
Fig. 4 Left: metallicity maps based on spectra from all three EPIC camera. Right: temperature maps, obtained fitting the spectra with a single temperature model, with the same resolution of the metal maps. The scale for the metallicity and temperature is in solar units and keV, respectively. |
Apart from A2029, the abundances of the other four clusters are consistent with an SNCC to SN Ia ratio of around 1.5–3. This ratio means that almost 75–85% of Fe, 15–25% of Si, and <20% of S were synthetized by SN Ia. Using deep observations of 2A 0335+096 and Sérsic 159-03 Werner et al. (2006) and de Plaa et al. (2006) find a ratio of 2–2.5, in agreement with our result. Based on XMM-Newton observations of 22 clusters de Plaa et al. (2007) found a ratio in the range 1.7–3.5 depending on the supernovae models (using a WDD2 model, as in this work, they obtained 1.7 in good agrement with our result).
The efficiency of the metal enrichment may depend on parameters as age, star-formation efficiency, and contribution from cD galaxies. However, the relative contribution of SNe Ia and SNCC and the processes of metal mixing in the ICM seem to be quite similar among different clusters as claimed also by Sato et al. (2009a). Our results are therefore consistent with an enrichment due to the combination of SN Ia and SNCC. This conclusion contrasts with the general views that the central iron excess in cool core clusters is from Type Ia supernovae alone (Matsushita et al. 2003).
4. 2D Distribution of metals
To study the distribution of metals, we prepared adaptively binned abundance maps of the clusters. Appropriately cleaned data sets for all the three cameras, with point sources removed were used to create the source spectra. To obtain a metallicity measurement with a good accuracy requires a high statistic. Thus, to ensure an acceptable error also in the outskirts of the clusters we set a minimum count number (~5000 source counts per region) necessary for proceeding with the spectral fit. The spectral regions for the map were selected following the method presented in Lovisari et al. (2009) that we can summarize in this way: a square region centered on the X-ray peak was defined to include the area with high surface brightness. The region size of the pixels was optimized to be as small as possible by splitting it into horizontal or vertical segments through its center, while including at least 5000 source counts. For all the selected regions, spectra were extracted for source and background in all three cameras.
The obtained metallicity maps are shown in Figs. 4 and 5. The metallicity distribution appears very inhomogeneous for all the clusters. For Centaurus and Sérsic 159-03, there is a peak in the center and then it decrease in the outskirts while A496, A2029, and Hydra A show high metallicity clumps both in the center and in the outskirts. Since Centaurus is at very low redshift, in these observations we are looking in the very central part of the cluster (r < 200 kpc) compared with the others four clusters, and it could explain its different shape. On the other hand, Sérsic, for which we map the metal distribution for more than 350 kpc, we observe the same shape of Centaurus. Since it is difficult to distinguish real metallicity clumps from statistical noise we quantified the inhomogeneities through the significance maps. First, we smoothed the metallicity profiles applying a Savitzky-Golay filter, and we subtracted it from the metallicity maps. Finally we divided each bin of the resultant maps by the uncertainty in the pixel metallicity. The results are shown in Fig. 6. The blue and red spots represent regions that deviate significatively (99% c.l.) from the average profile.
 |
Fig. 6 Significance maps of all the clusters. |
 |
Fig. 7 Plot of abundance against temperature for each bin. |
There are several maxima visible in the metal distribution, which are not associated with the cluster center. From simulations (Kapferer et al. 2008, 2009), we know that the maxima are typically at places where galaxies just have lost a lot of gas due to the ram-pressure. Since the gas lost by galaxies is obviously not mixed immediately with the ICM at the place where we observe a metal blob, we should observe also a low temperature because the gas in galaxies is cooler than the ICM. Thus, we produced the temperature maps (fitting the spectra with a single temperature model) of the clusters with the same spatial resolution obtained for the metal maps, and then we plotted the abundance of bins against their temperature, which are shown in Fig. 7. Since we are searching for cool high-metallicity clumps due to the ejection of gas from galaxies and not the cool high-metallicity bins found in the cool cores, we did not plot the inner bins (where we used a two temperature model to fit the spectra).
Best-fit results of the spectral and spatial analysis of the sample of galaxy clusters at an overdensity corresponding to 4500.
Apart from Centaurus, we see a deviation from the expected temperature-metallicity relation. The deviation could be due to the combination of the iron bias and inverse iron bias effects. The iron bias effects cause an underestimation of the metallicity when we pretend to fit with a single temperature model a plasma that is, instead characterized by a combination of different temperatures (Buote 2000; Rasia et al. 2008). On the contrary the inverse iron bias effect causes an overestimation of the metal abundance (Gastaldello et al. 2010). The combination of these two effects could explain the spread in the distribution of Fig. 7. On the other hand, these effects seems to be more important in the range of temperature between 2 and 4 keV, while our clusters also show regions with temperatures higher than 4 keV. One possible explanation could be that the ejected gas, with T < 1 keV and metallicity in the range 0.5–1.5 (Matsushita et al. 2000; Athey & Bregman 2009), will be heated up to the temperature of the surrounding gas (ICM) on the shorter time scale than that of metal mixing. In this case, after a while we should observe a region of high metallicity (not yet dispersed) and high temperature (heated up at the ICM temperature). Another possible explanation could be related to the number of intracluster supernovae. In fact, during ram-pressure stripping events a lot of stars are forming in the tail of stripped gas. The stars are evolving and exploding as SNe directly in the ICM, and they can enrich the ICM very efficiently. In this case we should see a clumps of high metallicity (due to SNe explosions) and high temperature. Obviously, more complex heating and cooling processes are at work, thus the simple picture of stripped gas does not hold.
5. Mass determination
Using simulated galaxy clusters, Kapferer et al. (2007a) show that the more inhomogeneous the metals are distributed within the cluster, the more underestimated is metal mass. They show that the true metal mass in the inner parts (r < 500 kpc) of galaxy cluster can be up to three times higher than the metal mass obtained by X-ray observations. They suggest that the discrepancies occur because the metallicity is not constant throughout the extraction area, thus the integration of thermal bremsstrahlung and of line emission can lead to underestimated metal masses.
We used the metallicity maps to estimate the metal mass in the center parts of the clusters and compare the results with the estimations obtained from a single extraction area of the cluster.
First, we computed a background-subtracted, vignetting-corrected, radial surface brightness profile in the 0.3–10 keV energy band for each cluster. All of the X-ray point sources were excluded from the data. The annuli were chosen such that all the widths are larger than the FWHM of the point-spread function (PSF) at that radius. With this choice, all the bins contain at least 2000 counts after background subtraction. With these very good statistics, the error bars of the surface brightness are very small. The profiles were fitted using a β-model (Cavaliere & Fusco-Femiano 1976): 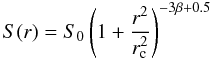 (1)where rc is the core radius. The advantage of using a β-model to parametrize surface brightness is that assuming hydrostatic equilibrium and spherical symmetry the gas density and total mass profile can be recovered analytically and expressed by the simple formula:
(1)where rc is the core radius. The advantage of using a β-model to parametrize surface brightness is that assuming hydrostatic equilibrium and spherical symmetry the gas density and total mass profile can be recovered analytically and expressed by the simple formula: 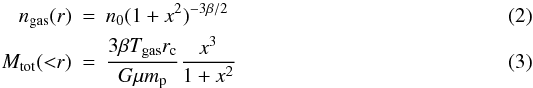 where x = r/rc, n0 is the central electron density, μ the mean molecular weight in atomic mass (=0.6), G the gravitational constant, and mp the proton mass. The best-fit parameters obtained from the spectral and spatial analysis are shown in Table 4. We then evaluate RΔ as the radius encompassing a fixed density contrast with respect to the critical density ρc. This is necessary to compare different clusters. Since Centaurus, is at very low redshift with the analyzed XMM-Newton observation we are looking at an overdensity of 4500. Thus we used such overdensity to estimate the mass of the clusters. For the other four clusters we estimated also the parameter at an overdensity of 2500 and at an overdensity corresponding to the area covered by the metal maps. We compute than the metal mass as
where x = r/rc, n0 is the central electron density, μ the mean molecular weight in atomic mass (=0.6), G the gravitational constant, and mp the proton mass. The best-fit parameters obtained from the spectral and spatial analysis are shown in Table 4. We then evaluate RΔ as the radius encompassing a fixed density contrast with respect to the critical density ρc. This is necessary to compare different clusters. Since Centaurus, is at very low redshift with the analyzed XMM-Newton observation we are looking at an overdensity of 4500. Thus we used such overdensity to estimate the mass of the clusters. For the other four clusters we estimated also the parameter at an overdensity of 2500 and at an overdensity corresponding to the area covered by the metal maps. We compute than the metal mass as 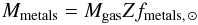 (4)where Z is the metallicity of the gas and fmetals, ⊙ is the metal mass fraction of the Sun. The results are shown in Table 4.
(4)where Z is the metallicity of the gas and fmetals, ⊙ is the metal mass fraction of the Sun. The results are shown in Table 4.
5.1. Metal mass estimation using metallicity maps
In the ionized intracluster plasma the ratio between the proton density np and the electron density ne is approximately 0.82. Thus, the emission integral (EI) could be written as 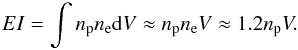 (5)For each spectrum the emission integral (EI) can be derived easily using the normalization K of the thermal spectrum measured within XSPEC:
(5)For each spectrum the emission integral (EI) can be derived easily using the normalization K of the thermal spectrum measured within XSPEC: ![\begin{equation} EI=K\times10^{14}[4\pi d^{2}_{\rm ang}(1+z)^2]. \end{equation}](/articles/aa/full_html/2011/04/aa15400-10/aa15400-10-eq162.png) (6)For each pixel the gas mass along the line of sight is determined using
(6)For each pixel the gas mass along the line of sight is determined using 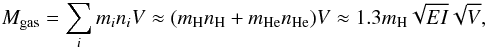 (7)where nH and nHe are the proton and helium number density, respectively, mH is the proton mass, mHe = 4mp, and V the volume of the emitting region. This was determined (assuming that the properties of the material in each region are constant and that there is no material projected onto them) as
(7)where nH and nHe are the proton and helium number density, respectively, mH is the proton mass, mHe = 4mp, and V the volume of the emitting region. This was determined (assuming that the properties of the material in each region are constant and that there is no material projected onto them) as 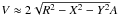 , where A is the area of the region, R the radius emcompassing the fixed density contrast, and X and Y are the projected distances in the east-west and north-south directions, respectively. We assumed the solar He/H fraction, nHe/nH ≈ 0.095 and did not consider the mass contribution of ions heavier than He, which are negligible compared to H and He. Then using Eq. (4) we determined the metal mass along the line of sight for each pixel and summed them up for all the pixels.
, where A is the area of the region, R the radius emcompassing the fixed density contrast, and X and Y are the projected distances in the east-west and north-south directions, respectively. We assumed the solar He/H fraction, nHe/nH ≈ 0.095 and did not consider the mass contribution of ions heavier than He, which are negligible compared to H and He. Then using Eq. (4) we determined the metal mass along the line of sight for each pixel and summed them up for all the pixels.
We found that the metal mass is higher than the metal mass obtained by assuming the metallicity mean of the investigated area (see Table 4). The explanation is that, when we determine the metal mass using the mean metallicity, we do not properly take into account that there are a lot of metals at positions of low density. Since the metallicity is not constant throughout the galaxy cluster, as shown with the metallicity maps, using the maps we are estimating the metal mass along the line of sight more precisely. The discrepancy changes from cluster to cluster, and we consider different radii. In the very inner part at an overdensity of 4500, the metal mass can be underestimated up to 30%. At larger radii the discrepancies can reachs more than two times.
From simulations we know that ram-pressure is more important than galactic winds in the center. The interstellar material in a galaxy feels the rampressure of the intracluster medium as it flows past. This ram-pressure is 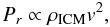 (8)where ρICM is the ICM density and v the relative velocity between the galaxy and the ICM.
(8)where ρICM is the ICM density and v the relative velocity between the galaxy and the ICM.
From the virial theorem we know that the velocity of the galaxies is related to the total mass of the cluster. A higher mass of cluster will translate into a higher velocity of galaxy and thanks to Eq. (8), to a higher metal mass as a consequence of ram-pressure stripping. De Grandi et al. (2004) find that the iron mass associated with the abundance excess does not favor a scenario where the iron mass is accreted from the cooling flow, and the excess can be entirely produced by the brightest cluster galaxy (BCG) at the center of cool core clusters. On the other hand, in our sample of five clusters we found that in the very central part at an overdensity of 4500, the metal mass seems to be correlated with the total mass. The clusters with higher mass are able to strip more gas from the galaxies and to explain at least part of the central mass.
6. Conclusions
Using XMM-Newton observations, we studied the spatial distribution of metal abundances in a sample of five relaxed clusters. Below we summarize the main results.
-
Even for relaxed clusters, the distribution of metals is clearly nonspherical. It looks very inhomogeneous with several maxima separated by low-metallicity regions.
-
The deviation from the expected temperature-metallicity relation suggests that several processes are at work in galaxy clusters and that the simple picture of stripped gas does not hold.
-
The radial profiles are consistent with the current idea that the relative contribution of SN Ia to SNCC increases towards the cluster center, and the O/Fe is more sensitive to this ratio than Si/Fe.
-
Varying from cluster to cluster, the relative number of core-collapse supernovae needed to reproduce the observed abundances ranges between 65–80%.
-
Using a single extraction region to determine the metallicity gives a systematic underestimation of the metal mass: the metal masses are typically understimated by 10–30%.
Acknowledgments
The authors are grateful to R. Paladino and C. Ferrari for useful comments and discussions, and to the anonymous referee for his/her constructive suggestions. We thank M. Murgia for the use of the SYNAGE++ program. This work was supported by the Austrian Science Foundation (FWF) through grants P18523-N16 and P19300-N16.
References
- Anders, E., & Grevesse, N. 1989, Geochim. Cosmochim. Acta, 53, 197 [Google Scholar]
- Arnaud, K. A. 1996, in Astronomical Data Analysis Software and Systems V, ed. G. H. Jacoby, & J. Barnes, ASP Conf. Ser., 101 [Google Scholar]
- Arnaud, M., Neumann, D. M., Aghanim, N., et al. 2001, A&A, 365, L80 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Athey, A. E., & Bregman, J. N. 2009, ApJ, 696, 681 [NASA ADS] [CrossRef] [Google Scholar]
- Baumgartner, W. H., Loewenstein, M., Horner, D. J., & Mushotzky, R. F. 2005, ApJ, 620, 680 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Buote, D. A. 2000, MNRAS, 311, 176 [NASA ADS] [CrossRef] [Google Scholar]
- Cavaliere, A., & Fusco-Femiano, R. 1976, A&A, 49, 137 [NASA ADS] [Google Scholar]
- De Grandi, S., & Molendi, S. 2009, A&A, 508, 565 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- De Grandi, S., Ettori, S., Longhetti, M., & Molendi, S. 2004, A&A, 419, 7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- de Plaa, J., Werner, N., Bykov, A. M., et al. 2006, A&A, 452, 397 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- de Plaa, J., Werner, N., Bleeker, J. A. M., et al. 2007, A&A, 465, 345 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- De Young, D. S. 1978, ApJ, 223, 47 [NASA ADS] [CrossRef] [Google Scholar]
- De Young, D. S. 1986, ApJ, 307, 62 [NASA ADS] [CrossRef] [Google Scholar]
- Dickey, J. M., & Lockman, F. J. 1990, ARA&A, 28, 215 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Durret, F., Lima Neto, G. B., & Forman, W. 2005, A&A, 432, 809 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gastaldello, F., Ettori, S., Balestra, I., et al. 2010, A&A, 522, A34 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gerhard, O., Arnaboldi, M., Freeman, K. C., & Okamura, S. 2002, ApJ, 580, L121 [NASA ADS] [CrossRef] [Google Scholar]
- Gnedin, N. Y. 1998, MNRAS, 294, 407 [NASA ADS] [CrossRef] [Google Scholar]
- Gunn, J. E., & Gott, III, J. R. 1972, ApJ, 176, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Hasinger, G., Schartel, N., & Komossa, S. 2002, ApJ, 573, L77 [NASA ADS] [CrossRef] [Google Scholar]
- Hayakawa, A., Hoshino, A., Ishida, M., et al. 2006, PASJ, 58, 695 [NASA ADS] [Google Scholar]
- Heath, D., Krause, M., & Alexander, P. 2007, MNRAS, 374, 787 [NASA ADS] [CrossRef] [Google Scholar]
- Iwamoto, K., Brachwitz, F., Nomoto, K., et al. 1999, ApJS, 125, 439 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Kapferer, W., Knapp, A., Schindler, S., Kimeswenger, S., & van Kampen, E. 2005, A&A, 438, 87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kapferer, W., Ferrari, C., Domainko, W., et al. 2006, A&A, 447, 827 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kapferer, W., Kronberger, T., Weratschnig, J., & Schindler, S. 2007a, A&A, 472, 757 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kapferer, W., Kronberger, T., Weratschnig, J., et al. 2007b, A&A, 466, 813 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kapferer, W., Kronberger, T., Ferrari, C., Riser, T., & Schindler, S. 2008, MNRAS, 389, 1405 [NASA ADS] [CrossRef] [Google Scholar]
- Kapferer, W., Sluka, C., Schindler, S., Ferrari, C., & Ziegler, B. 2009, A&A, 499, 87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lovisari, L., Kapferer, W., Schindler, S., & Ferrari, C. 2009, A&A, 508, 191 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Matsushita, K., Ohashi, T., & Makishima, K. 2000, PASJ, 52, 685 [NASA ADS] [Google Scholar]
- Matsushita, K., Finoguenov, A., & Böhringer, H. 2003, A&A, 401, 443 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Matsushita, K., Böhringer, H., Takahashi, I., & Ikebe, Y. 2007a, A&A, 462, 953 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Matsushita, K., Fukazawa, Y., Hughes, J. P., et al. 2007b, PASJ, 59, 327 [NASA ADS] [Google Scholar]
- Mitchell, R. J., Culhane, J. L., Davison, P. J. N., & Ives, J. C. 1976, MNRAS, 175, 29P [NASA ADS] [CrossRef] [Google Scholar]
- Molendi, S., & Gastaldello, F. 2001, A&A, 375, L14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Morrison, R., & McCammon, D. 1983, ApJ, 270, 119 [NASA ADS] [CrossRef] [Google Scholar]
- Mushotzky, R. F., & Loewenstein, M. 1997, ApJ, 481, L63 [NASA ADS] [CrossRef] [Google Scholar]
- Nevalainen, J., Markevitch, M., & Lumb, D. 2005, ApJ, 629, 172 [NASA ADS] [CrossRef] [Google Scholar]
- O’Sullivan, E., Vrtilek, J. M., Kempner, J. C., David, L. P., & Houck, J. C. 2005, MNRAS, 357, 1134 [NASA ADS] [CrossRef] [Google Scholar]
- Pradas, J., & Kerp, J. 2005, A&A, 443, 721 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pratt, G. W., & Arnaud, M. 2002, A&A, 394, 375 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rasia, E., Mazzotta, P., Bourdin, H., et al. 2008, ApJ, 674, 728 [Google Scholar]
- Sanders, J. S., & Fabian, A. C. 2006, MNRAS, 371, 1483 [NASA ADS] [CrossRef] [Google Scholar]
- Sanders, J. S., Fabian, A. C., Allen, S. W., & Schmidt, R. W. 2004, MNRAS, 349, 952 [NASA ADS] [CrossRef] [Google Scholar]
- Sanders, J. S., Fabian, A. C., & Dunn, R. J. H. 2005, MNRAS, 360, 133 [NASA ADS] [CrossRef] [Google Scholar]
- Sato, K., Matsushita, K., & Gastaldello, F. 2009a, PASJ, 61, 365 [NASA ADS] [Google Scholar]
- Sato, K., Yamasaki, N. Y., Ishida, M., et al. 2007, PASJ, 59, 299 [NASA ADS] [Google Scholar]
- Sato, K., Matsushita, K., Ishisaki, Y., et al. 2008, PASJ, 60, 333 [Google Scholar]
- Sato, K., Matsushita, K., Ishisaki, Y., et al. 2009b, PASJ, 61, 353 [Google Scholar]
- Sauvageot, J. L., Belsole, E., & Pratt, G. W. 2005, A&A, 444, 673 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schindler, S., & Diaferio, A. 2008, Space Sci. Rev., 134, 363 [NASA ADS] [CrossRef] [Google Scholar]
- Schmidt, R. W., Fabian, A. C., & Sanders, J. S. 2002, MNRAS, 337, 71 [NASA ADS] [CrossRef] [Google Scholar]
- Simionescu, A., Werner, N., Böhringer, H., et al. 2009, A&A, 493, 409 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Smith, R. K., Brickhouse, N. S., Liedahl, D. A., & Raymond, J. C. 2001, ApJ, 556, L91 [NASA ADS] [CrossRef] [Google Scholar]
- Tamura, T., Kaastra, J. S., den Herder, J. W. A., Bleeker, J. A. M., & Peterson, J. R. 2004, A&A, 420, 135 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tokoi, K., Sato, K., Ishisaki, Y., et al. 2008, PASJ, 60, 317 [Google Scholar]
- Tsujimoto, T., Nomoto, K., Yoshii, Y., et al. 1995, MNRAS, 277, 945 [NASA ADS] [CrossRef] [Google Scholar]
- Werner, N., de Plaa, J., Kaastra, J. S., et al. 2006, A&A, 449, 475 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
Number ratio of SNCC to SN Ia (NII/NIa) and integrated number of SNCC computed using the abundance of O for each considered region.
Best-fit results of the spectral and spatial analysis of the sample of galaxy clusters at an overdensity corresponding to 4500.
All Figures
 |
Fig. 1 Radial profiles of the a) iron, b) oxygen, c) silicon, d) sulfur, and e) argon in solar units, derived from the EPIC spectra. |
| In the text | |
 |
Fig. 2 Radial profiles of the a) O/Fe, b) Si/Fe and c) S/Fe ratio in solar units. |
| In the text | |
 |
Fig. 3 Radial profiles of the relative fraction of SNCC using the O/Fe (red) and Si/Fe (black) ratio. |
| In the text | |
 |
Fig. 4 Left: metallicity maps based on spectra from all three EPIC camera. Right: temperature maps, obtained fitting the spectra with a single temperature model, with the same resolution of the metal maps. The scale for the metallicity and temperature is in solar units and keV, respectively. |
| In the text | |
 |
Fig. 5 Same as Fig. 4. |
| In the text | |
 |
Fig. 6 Significance maps of all the clusters. |
| In the text | |
 |
Fig. 7 Plot of abundance against temperature for each bin. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


