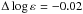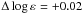| Issue |
A&A
Volume 528, April 2011
|
|
|---|---|---|
| Article Number | A87 | |
| Number of page(s) | 17 | |
| Section | Stellar atmospheres | |
| DOI | https://doi.org/10.1051/0004-6361/201015336 | |
| Published online | 04 March 2011 | |
A non-LTE study of neutral and singly-ionized iron line spectra in 1D models of the Sun and selected late-type stars⋆,⋆⋆
1
Universitäts-Sternwarte München, Scheinerstr. 1, 81679
München,
Germany
e-mail: lyuda@usm.lmu.de
2
Institute of Astronomy, Russian Academy of Sciences,
119017
Moscow,
Russia
e-mail: lima@inasan.ru
3
National Astronomical Observatories, Chinese Academy of Sciences,
A20 Datun Road, Chaoyang
District, Beijing
100012, PR
China
4
Department of Physics and Astronomy, Division of Astronomy and
Space Physics, Uppsala University, Box 516, 75120
Uppsala,
Sweden
5
Max-Planck Institut für Extraterrestrische Physik,
Giessenbachstr.,
85748
Garching,
Germany
Received:
5
July
2010
Accepted:
18
January
2011
Aims. We evaluate non-local thermodynamical equilibrium (non-LTE) line formation for the two ions of iron and check the ionization equilibrium between Fe i and Fe ii in model atmospheres of the cool reference stars based on the best available complete model atom for neutral and singly-ionized iron.
Methods. We present a comprehensive model atom for Fe with more than 3000 measured and predicted energy levels. As a test and first application of the improved model atom, iron abundances are determined for the Sun and five stars with well determined stellar parameters and high-quality observed spectra. The efficiency of inelastic collisions with hydrogen atoms in the statistical equilibrium of iron is empirically estimated from inspection of their different influence on the Fe i and Fe ii lines in the selected stars.
Results. Non-LTE leads to systematically depleted total absorption in the Fe i lines and to positive abundance corrections in agreement with the previous studies, however, the magnitude of such corrections is smaller compared to the earlier results. These non-LTE corrections do not exceed 0.1 dex for the solar metallicity and mildly metal-deficient stars, and they vary within 0.21 dex and 0.35 dex in the very metal-poor stars HD 84937 and HD 122563, respectively, depending on the assumed efficiency of collisions with hydrogen atoms. Based on the analysis of the Fe i/Fe ii ionization equilibrium in these two stars, we recommend to apply the Drawin formalism in non-LTE studies of Fe with a scaling factor of 0.1. For the Fe ii lines non-LTE corrections do not exceed 0.01 dex in absolute value over the whole range of stellar parameters that are considered. This study reveals two problems. The first one is that gf-values available for the Fe i and Fe ii lines are not accurate enough to pursue high-accuracy absolute stellar abundance determinations. For the Sun, the mean non-LTE abundance obtained from 54 Fe i lines is 7.56 ± 0.09 and the mean abundance from 18 Fe ii lines varies between 7.41 ± 0.11 and 7.56 ± 0.05 depending on the source of the gf-values. The second problem is that lines of Fe i give, on average, a 0.1 dex lower abundance compared with those of Fe ii lines for HD 61421 and HD 102870, even when applying a differential line-by-line analysis with regard to the Sun. A disparity between neutral atoms and first ions points to problems of stellar atmosphere modelling or/and effective temperature determination.
Key words: atomic data / atomic processes / line: formation / stars: atmospheres / stars: fundamental parameters
Based on observations collected at the German Spanish Astronomical Center, Calar Alto, Spain and taken from the ESO UVES-POP archive.
Table 5 is only available in electronic form at http://www.aanda.org
© ESO, 2011
1. Introduction
Iron plays an outstanding role in studies of cool stars thanks to the many lines in the visible spectrum, which are easy to detect even in very metal-poor stars. Iron serves as a reference element for all astronomical research related to stellar nucleosynthesis and the chemical evolution of the Galaxy. Iron lines are used to derive basic stellar parameters, i.e. the effective temperature, Teff, from the excitation equilibrium of Fe i and the surface gravity, log g, from the ionization equilibrium between Fe i and Fe ii. In stellar atmospheres with Teff > 4500 K, neutral iron is a minority species, and its statistical equilibrium (SE) can easily deviate from thermodynamic equilibrium owing to deviations of the mean intensity of ionizing radiation from the Planck function. Therefore, since the beginning of the 1970s, a large number of studies attacked the problem of non-local thermodynamic equilibrium (non-LTE) line formation for iron in the atmospheres of the Sun and cool stars. The original model atoms were from Tanaka (1971); Athay & Lites (1972); Boyarchuk et al. (1985); Gigas (1986); Takeda (1991); Gratton et al. (1999); Thévenin & Idiart (1999); Gehren et al. (2001a); Shchukina & Trujillo Bueno (2001), and Collet et al. (2005), and were widely applied in stellar parameter and abundance analyses (see Asplund 2005, for references). It was understood that the main non-LTE mechanism for Fe i is ultra-violet (UV) overionization of the levels with an excitation energy of 1.4 to 4.5 eV. This results in an underpopulation of neutral iron where all Fe i lines are weaker than their LTE strengths, and it leads to positive non-LTE abundance corrections.
The need for a new analysis was motivated by the following problems that were uncovered by the previous non-LTE calculations for iron.
First, the results obtained for the populations of high-excitation levels of Fe i were not always convincing. The highest levels presented in the model atom did not couple thermally to the ground state of Fe ii, which indicates substantial term incompleteness. To force the levels near the continuum into LTE, an upper level thermalization procedure was applied (more details in Gehren et al. 2001a; Korn et al. 2003; Collet et al. 2005).
A second aspect is the treatment of poorly known inelastic collisions with hydrogen atoms. Their role in establishing the statistical equilibrium of atoms in cool stars was debated for decades, from Gehren (1975) to Barklem et al. (2010). Experimental data on H i collision cross-sections are only available for the resonance transition in Na i (Fleck et al. 1991; Belyaev et al. 1999), and detailed quantum mechanical calculations were published for the transitions between the first nine levels in Li i (Belyaev & Barklem 2003; Barklem et al. 2003) and Na i (Belyaev et al. 1999, 2010; Barklem et al. 2010). For all other chemical species, the basic formula used to calculate collisions with H i atoms is the one proposed by Drawin (1968, 1969) as described by Steenbock & Holweger (1984), which suggests that their influence is comparable with electron impacts. The laboratory measurements and quantum mechanical calculations indicate that the Drawin formula overestimates the rate coefficients for optically allowed transitions by one to seven orders of magnitude. Therefore, various approaches were employed in the literature to empirically constrain the efficiency of H i collisions. The studies of stellar Na i lines favor a low efficiency of this type of collisions. For example, Allende Prieto et al. (2004) found that the center-to-limb variation of the solar Na i 6160 Å line is reproduced in the non-LTE calculations with pure electron collisions. Gratton et al. (1999) calibrated H i collisions with sodium using RR Lyr variables and concluded that the Drawin rates should be decreased by two orders of magnitude. Based on their solar Na i line profile analysis, Gehren et al. (2004) and Takeda (1995) recommended to scale the Drawin rates by a factor SH = 0.05 and 0.1, respectively. With a similar value of SH = 0.1, the ionization equilibrium between Ca i and Ca ii in selected metal-poor stars was matched consistently with surface gravities derived from Hipparcos parallaxes (Mashonkina et al. 2007). On the other hand, spectroscopic studies of different chemical species suggested that the H i collision rates might be reasonably well described by Drawin’s formula with SH ≥ 1. For example, empirical estimates by Gratton et al. (1999) resulted in SH = 3 for O i and Mg i and SH = 30 for Fe i. Allende Prieto et al. (2004) and Pereira et al. (2009) inferred SH = 1 from the analysis of the center-to-limb variation of solar O i triplet ~7770 Å lines. The same value of SH = 1 was obtained by Takeda (1995) from solar O i line profile fits. For a review of studies constraining empirically the efficiency of H i collisions, see Lambert (1993); Holweger (1996), and Mashonkina (2009).
As a result of applying incomplete model atoms and a different treatment of collisions with hydrogen atoms, no consensus on the expected magnitude of the non-LTE effects was achieved in the previous studies of iron, and the results were in conflict with each other in some cases. For example, Korn et al. (2003) found a negligible discrepancy between the non-LTE spectroscopic and Hipparcos astrometric distances of the halo star HD 84937, while the non-LTE calculations of Thévenin & Idiart (1999) resulted in a 34% smaller spectroscopic distance of that same star.
This study aims to construct a fairly complete model atom of iron, to be tested on the Sun and selected cool stars with high-quality observed spectra and reliable stellar parameters. Compared with the previous non-LTE analyses of iron, the model atom of Fe i was extended to the high-lying levels that are predicted by the atomic structure calculations of Kurucz (2009), which turned out to be crucial for a correct treatment of the SE of iron in cool star atmospheres. With our improved model atom we tried to empirically constrain the scaling factor SH. We realize that the real temperature dependence of hydrogen collision rates could be very different from that of the classical Drawin formalism, and we may not always achieve consistent SH values from the analysis of different stars. We also realize that the required thermalizing process not involving electrons in the atmospheres of cool metal-poor stars could be very different from inelastic collisions with neutral hydrogen atoms. For example, Barklem et al. (2010; see also Barklem et al. 2003; Belyaev & Barklem 2003; Belyaev et al. 2010) uncovered the importance of the ion-pair production and mutual neutralization process A(nl) + H(1s) ⇌ A+ + H− for the SE of Li and Na. Because no accurate calculations of either inelastic collisions of iron with neutral hydrogen atoms or other type processes are available, we simulate an additional source of thermalization in the atmospheres of cool stars by parametrized H i collisions. Investigating the Sun as a reference star for a subsequent stellar differential line-by-line analysis, we also derive the solar iron absolute abundance and check the solar Fe i/Fe ii ionization equilibrium with an extended list of lines, which can be detected at solar metallicity down to [Fe/H] = −2.5. We find it important to inspect the accuracy of atomic data for various subsamples of iron lines in view of comprehensive abundance studies across the Galaxy targeting stars of very different metallicities.
This paper is organized as follows. The model atom of iron and the adopted atomic data are presented in Sect. 2. There we also discuss how including the bulk of predicted Fe i levels in the model atom affects the SE of iron. In Sect. 3 we study the solar iron spectrum to provide the basis for subsequent differential analyses of stellar spectra. Section 4 describes observations and stellar parameters of our sample of stars, and Sect. 5 investigates which line-formation assumptions lead to consistent element abundances of both ions, Fe i and Fe ii. Uncertainties in the iron non-LTE abundances are estimated in Sect. 6. Our recommendations and conclusions are given in Sect. 7.
2. The method of non-LTE calculations for iron
In this section we describe the model atom of iron and the programs used for computing the level populations and spectral line profiles.
 |
Fig. 1 Atomic structure of Fe i as obtained from laboratory experiments (long lines, black lines in the color online version of the paper) and calculations (short lines, blue lines in the color online version of the paper). See text for the sources of data. |
2.1. Model atom
Energy levels. Iron is almost completely ionized throughout the atmosphere of stars with an effective temperature above 4500 K. For example, the fraction of Fe i nowhere exceeds 10% in the solar atmosphere. Such minority species are particularly sensitive to non-LTE effects because any small change in the ionization rates changes their population by a large amount. To provide close collisional coupling of Fe i to the continuum electron reservoir and consequently establish a realistic ionization balance between the neutral and singly-ionized species, the energy separation of the highest levels in the model atom from the ionization limit must be smaller than the mean kinetic energy of electrons, i.e., 0.5 eV for atmospheres of solar temperature.
In our earlier study (Gehren et al. 2001a, hereafter Paper I), the model atom of Fe i was built up using all the energy levels from the experimental analysis of Nave et al. (1994), in total 846 levels with an excitation energy, Eexc, up to 7.5 eV. The later updates of Schoenfeld et al. (1995) and the measurements of Brown et al. (1988) provided another 112 energy levels for Fe i. All known levels of Fe i are shown in Fig. 1 by long horizontal bars. How complete is this system of levels? In the same figure, the upper energy levels predicted by Kurucz (2009) in his calculations of the Fe i atomic structure are plotted by short bars. As described by Grupp et al. (2009), the new calculations for iron included additional laboratory levels and more configurations than the earlier work of Kurucz (1992). It can be seen from Fig. 1 that the system of measured levels is complete below Eexc ≃ 45 000 cm-1 (5.6 eV), except perhaps for singlets. However, laboratory experiments do not see most of the high-excitation levels with Eexc > 7.1 eV, which should contribute a lot to provide close collisional coupling of Fe i levels to the Fe ii ground state.
 |
Fig. 2 Model atom of Fe i (bottom panel) and Fe ii (top panel). The super-levels are indicated by long lines. The iron spectral lines used in the abundance analysis arise from the transitions shown as continuous lines. |
In our present study, the model atom of Fe i is constructed using not only all the known energy levels, but also the predicted levels with Eexc up to 63 697 cm-1 (7.897 eV), in total 2970 levels. The measured levels belong to 233 terms. Neglecting their multiplet fine structure we obtain 233 levels in the model atom. The predicted and measured levels with common parity and close energies are combined whenever the energy separation is smaller than 150 cm-1 at Eexc < 60 000 cm-1 and smaller than 210 cm-1 at Eexc > 60 000 cm-1. The remaining predicted levels, all above Eexc = 60 000 cm-1, are used to make up six super-levels. For these super-levels we calculated the energy as a g-weighted mean and the total statistical weight amounts from 940 to 2160. Our final model atom of Fe i is shown in Fig. 2.
For Fe ii (Fig. 2) we rely on the reference model atom treated in Paper I and use the levels belonging to 89 terms with Eexc up to 10 eV. The multiplet fine structure is neglected. The ground state of Fe iii completes the system of levels in the model atom.
Radiative bound-bound (b–b) transitions. In total, 11 958 allowed transitions occur in our final model atom of Fe i. Their average-“multiplet” gf-values are calculated using the Nave et al. (1994) compilation for 2649 lines, the Kurucz (2009) calculations for the transitions between the measured levels, in total, for 73 434 lines, and the Kurucz (2009) calculations for the transitions between the measured and predicted and between two predicted levels, in total, for 281 007 lines. The quality of the recent calculations of Kurucz (2009) is estimated by a comparison with the Nave et al. (1994) data. The latter can be referred to as experimental data, even though for a minority of the lines compiled by Nave et al. (1994) the gf-values were derived from solar spectra assuming a solar iron abundance. Taking the experimental sample as reference the theoretical data show a single line scatter of 0.54 dex. Ignoring all lines with deviations above 1 dex (6%), the scatter is reduced to 0.33 dex. The reliability of the calculated gf-values is thus roughly characterized by a factor of 2 statistical accuracy only. It is, however, important that there is no systematic shift between the experimental and calculated data. The mean difference is Δlog gf(calculated-experimental) = −0.04 for the whole sample of lines. For 1525 allowed transitions in Fe ii, gf-values are fully based on the data calculated by Kurucz (1992).
Radiative bound-free (b–f) transitions. Photoionization is the most important process deciding whether the Fe i atom tends to depart from LTE in the atmosphere of a cool star. As in Paper I, our non-LTE calculations rely on the photoionization cross-sections of the IRON project (Bautista 1997). They are available for all levels of Fe i in our model atom with the ionization edge in the UV spectral range, in total, for 149 levels. For the remaining levels of Fe i and all Fe ii levels, the hydrogenic approximation was used. Photoionization weakly affects the SE of Fe ii because Fe iii constitutes only an extremely small fraction of the total iron atoms.
Collisional transitions. All levels in our model atom are coupled via collisional excitation and ionization by electrons and by neutral hydrogen atoms. For Fe i the electron-impact excitations are not yet known with sufficient accuracy, and, as in Paper I, our calculations of collisional rates rely on theoretical approximations. We use the formula of van Regemorter (1962) for the allowed transitions and assume that the effective collision strength Υ = 1 for the forbidden transitions. The latter assumption can be verified for the single forbidden transition of Fe i, 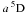 –
–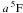 , for which the calculations of Pelan & Berrington (1997) in the IRON Project lead to Υ = 0.98 at T = 4000 K.
, for which the calculations of Pelan & Berrington (1997) in the IRON Project lead to Υ = 0.98 at T = 4000 K.
For the transitions between the Fe ii terms up to 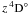 , we employ the data from the close-coupling calculations of Zhang & Pradhan (1995) and Bautista & Pradhan (1996, 1998). The same formulas as for Fe i are applied for the remaining transitions in Fe ii. Ionization by electronic collisions is calculated as in Paper I from the Seaton (1962) classical path approximation with a mean Gaunt factor set equal to
, we employ the data from the close-coupling calculations of Zhang & Pradhan (1995) and Bautista & Pradhan (1996, 1998). The same formulas as for Fe i are applied for the remaining transitions in Fe ii. Ionization by electronic collisions is calculated as in Paper I from the Seaton (1962) classical path approximation with a mean Gaunt factor set equal to 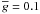 for Fe i and to 0.2 for Fe ii.
for Fe i and to 0.2 for Fe ii.
 |
Fig. 3 Electron (open circles) and hydrogen (filled circles) collision rates of representative transitions in Fe i (left column) and Fe ii (right column) as a function of the transition energy in the model 5780/4.44/0 at a depth point of log τ5000 = −0.5, where T = 5583 K, nH = 0.922 × 1017, and ne = 0.137 × 1014 (top row), and in the model 4600/1.60/−2.50 at a depth point of log τ5000 = −0.5, where T = 4174 K, nH = 0.212 × 1017, and ne = 0.286 × 1011 (bottom row). We assumed SH = 0.1 throughout. |
For collisions with H i atoms, we employ the formula of Steenbock & Holweger (1984) for allowed b − b and b − f transitions and, following Takeda (1994), a simple relation between hydrogen and electron collisional rates, 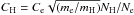 , for forbidden transitions. The efficiency of H i collisions is treated as a free parameter in our attempt to achieve consistent element abundances derived from the two ionization stages, Fe i and Fe ii, in the selected stars. For each object, the calculations were performed with a scaling factor of SH = 0, 0.1, 1, and 2. In Fig. 3 we compare the electron-impact excitation rates with the corresponding H i collision rates for representative transitions in Fe i and Fe ii in the line-forming layers (log τ5000 = −0.5) of the solar-metallicity (Teff/log g/[Fe/H]1 = 5780/4.44/0) and metal-poor (4600/1.60/−2.50) models. At the selected depth point, the electron number density ne in the solar-metallicity model is by a factor of 500 higher than that in the metal-poor and cool atmosphere, while the difference in neutral hydrogen number density nH is much smaller, only a factor of 4. As a consequence, the hydrogen collisions dominate the total collisional rate for most Fe i and Fe ii transitions in the metal-poor model. For solar-metallicity models, the influence of inelastic H i collisions on the SE of iron is expected to be weaker because CH/Ce > 1 is fulfilled only for the Fe i transitions with small energy separation, i.e., smaller than 0.5 eV. For Fe ii, the close-coupling electron-impact excitation rates of Zhang & Pradhan (1995) and Bautista & Pradhan (1996, 1998) are higher compared with the hydrogen collision rates even for small transition energies. A similar relation between CH and Ce also holds outside log τ5000 = −0.5 in the solar-metallicity model. In the metal-poor model, the weakest iron lines form inside log τ5000 = −0.5, where the role of hydrogen collisions is weakened owing to a decreasing nH/ne ratio.
, for forbidden transitions. The efficiency of H i collisions is treated as a free parameter in our attempt to achieve consistent element abundances derived from the two ionization stages, Fe i and Fe ii, in the selected stars. For each object, the calculations were performed with a scaling factor of SH = 0, 0.1, 1, and 2. In Fig. 3 we compare the electron-impact excitation rates with the corresponding H i collision rates for representative transitions in Fe i and Fe ii in the line-forming layers (log τ5000 = −0.5) of the solar-metallicity (Teff/log g/[Fe/H]1 = 5780/4.44/0) and metal-poor (4600/1.60/−2.50) models. At the selected depth point, the electron number density ne in the solar-metallicity model is by a factor of 500 higher than that in the metal-poor and cool atmosphere, while the difference in neutral hydrogen number density nH is much smaller, only a factor of 4. As a consequence, the hydrogen collisions dominate the total collisional rate for most Fe i and Fe ii transitions in the metal-poor model. For solar-metallicity models, the influence of inelastic H i collisions on the SE of iron is expected to be weaker because CH/Ce > 1 is fulfilled only for the Fe i transitions with small energy separation, i.e., smaller than 0.5 eV. For Fe ii, the close-coupling electron-impact excitation rates of Zhang & Pradhan (1995) and Bautista & Pradhan (1996, 1998) are higher compared with the hydrogen collision rates even for small transition energies. A similar relation between CH and Ce also holds outside log τ5000 = −0.5 in the solar-metallicity model. In the metal-poor model, the weakest iron lines form inside log τ5000 = −0.5, where the role of hydrogen collisions is weakened owing to a decreasing nH/ne ratio.
2.2. Programs and model atmospheres
We computed statistical equilibrium populations for Fe i and Fe ii while keeping the atmospheric structure fixed. This is justified by the following considerations. Although iron is an important source of the UV continuous opacity in an atmosphere of close-to-solar metallicity (see Fig. 4, top panel), the variations in its excitation and ionization state between LTE and non-LTE are found to have no significant effect on the emergent fluxes at the stellar parameters with which we are concerned (Fig. 4, bottom panel). Therefore, only minor effects on atmospheric temperature and electron number density distribution are expected.
 |
Fig. 4 Top panel: emergent fluxes calculated using the model of Teff = 5777 K, log g = 4.44, and [M/H] = 0 with iron (log εFe = 7.50, non-LTE with SH = 0.1, continuous curve) and without iron (dotted curve) compared with the solar flux taken from Woods et al. (1996, dashed curve). The observed flux below 1700 Å is contributed by the solar chromosphere. Bottom panel: the ratio between the non-LTE (SH = 0.1) and LTE emergent fluxes in the same model atmosphere with log εFe = 7.50 from the calculations with the final (continuous curve) and reduced (dotted curve, see Sect. 2.3) model atoms. For clearer illustration, the theoretical fluxes were convolved with a Gaussian profile of ΔλD = 2 Å. |
 |
Fig. 5 Departure coefficients, b, for the levels of Fe i and Fe ii as a function of log τ5000 in the model atmospheres 5777/4.44/0 (left column) and 4600/1.60/−2.50 (right column) from the calculations with our final model atom of iron (top row) and the reduced model atom, which ignores the predicted levels of Fe i. Every fifth of the first 60 levels of Fe i is shown. They are quoted in the bottom right part of each panel. All remaining higher levels of Fe i are plotted by dotted curves. For Fe ii we show every fifth of the first 60 levels. They are quoted in the top right part of each panel. The letters z, y, x, ... are used to denote the odd parity terms and a, b, c, ... for the even parity terms. To distinguish Fe i and Fe ii levels, note that b < 1 for each Fe i level outside log τ5000 = 0 in the solar metallicity model and log τ5000 = 0.4 in the metal-poor one. An exception are the highest levels in the layers with log τ5000 around −2.5 in the model 4600/1.60/−2.50. For Fe ii, b ≥ 1 inside log τ5000 = −2 in both model atmospheres. SH = 0.1 throughout. |
The solution of the non-LTE problem with such a comprehensive model atom as treated in this study is only possible, at present, with classical plane-parallel (one-dimensional, 1D) model atmospheres. All calculations were performed with model atmospheres computed with the MAFAGS-OS code (Grupp 2004; Grupp et al. 2009), which is based on up-to-date continuous opacities and includes the effects of line-blanketing by means of opacity sampling.
We used a revised version of the DETAIL program (Butler & Giddings 1985) based on the accelerated lambda iteration (ALI) scheme following the efficient method described by Rybicki & Hummer (1991, 1992) to solve the coupled radiative transfer and statistical equilibrium equations. The opacity package of the DETAIL code was updated by including the quasi-molecular Lyman α satellites following the implementation by Castelli & Kurucz (2001) of the Allard et al. (1998) theory and using the Opacity Project (see Seaton et al. 1994, for a general review) photoionization cross-sections for the calculations of b − f absorption of C i, N i, Mg i, Si i, Al i, and Fe i. In addition to the continuous background opacity, the line opacity introduced by H i and metal lines was taken into account by explicitly including it in solving the radiation transfer. The metal line list was extracted from the Kurucz (1994) compilation and the VALD database (Kupka et al. 1999). It includes about 720 000 atomic and molecular lines between 500 and 300 000 Å. The Fe i and Fe ii lines as well as b − f absorption processes were excluded from the background.
All b − b and b − f transitions of Fe i and Fe ii were explicitly taken into account in the SE calculations. The 57 strongest b − b transitions were treated using Voigt profiles and the remaining transitions using depth-dependent Doppler profiles. Microturbulence was accounted for by inclusion of an additional term in the Doppler width.
The departure coefficients, 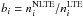 , were then used to compute synthetic line profiles via the siu program (Reetz 1991). Here,
, were then used to compute synthetic line profiles via the siu program (Reetz 1991). Here, 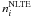 and
and 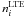 are the statistical equilibrium and thermal (Saha-Boltzmann) number densities, respectively. In this step of the calculations, Voigt profile functions were adopted and the same microturbulence value Vmic as in DETAIL was applied.
are the statistical equilibrium and thermal (Saha-Boltzmann) number densities, respectively. In this step of the calculations, Voigt profile functions were adopted and the same microturbulence value Vmic as in DETAIL was applied.
2.3. Effect of the model atom completeness on the statistical equilibrium of iron
The departure coefficients for selected levels of Fe i and Fe ii in the two model atmospheres 5777/4.44/0 and 4600/1.60/−2.50 are presented in Fig. 5 (top row). Our calculations support the results of the previous non-LTE studies of iron (Athay & Lites 1972; Boyarchuk et al. 1985; Takeda 1991; Gratton et al. 1999; Thévenin & Idiart 1999; Gehren et al. 2001a; Shchukina & Trujillo Bueno 2001; Shchukina et al. 2005; Collet et al. 2005) in the common stellar parameter range in the following aspects.
-
The non-LTE mechanisms for Fe i and Fe ii are independent of effective temperature, surface gravity, and metallicity.
-
All levels of Fe i are underpopulated in the atmospheric layers above log τ5000 = 0. The main non-LTE mechanism is the overionization caused by superthermal radiation of a non-local origin below the thresholds of the levels with excitation energy of 1.4 to 4.5 eV.
-
Fe ii dominates the element number density over all atmospheric depths. Thus, no process seems to affect the Fe ii ground-state and low-excitation-level populations significantly, and they keep their thermodynamic equilibrium values.
To illustrate the difference between the present and previous non-LTE studies, we performed test calculations with the atomic model, where the predicted levels of Fe i are removed. Below we refer to the latter model atom as the reduced model. It includes 233 terms and 10 740 radiative b − b transitios in Fe i and exactly the same levels of Fe ii as in our final model atom. The bottom row panels of Fig. 5 show the departure coefficients computed with the reduced model atom. Evidently (i) the Fe i terms are more underpopulated in the line-formation layers compared to the populations obtained with our final model atom (Fig. 5, top row); (ii) the highest levels do not couple thermally to the ground state of Fe ii; and (iii) the majority of the Fe i terms are close together. The explanation is that the net ionization-recombination rate of the Fe i levels separated by no more than 0.4 eV from the continuum is much lower in the reduced model atom than in the final model atom, for example, by a factor of 1000 and 150 at log τ5000 ≃ −0.6 in the model atmospheres 5777/4.44/0 and 4600/1.60/−2.50, respectively.
We found that emergent fluxes calculated with the MAFAGS-OS solar model atmosphere and using our final model atom well reproduce the observed solar fluxes of Woods et al. (1996) in the 1700–3000 Å spectral range, where neutral iron is an important source of the continuous opacity (Fig. 4, top panel). The observed flux below 1700 Å is contributed by the solar chromosphere. As demonstrated in the bottom panel of Fig. 4, the difference in emergent fluxes between LTE and non-LTE is negligible when employing the final model with SH = 0.1, while the use of the reduced model atom leads to a weaker b − f opacity of neutral iron compared with the LTE value in a way that the change in emergent fluxes is about 20% in the 1600–2900 Å spectral range.
In Sect. 6 we evaluate the difference in solar and stellar non-LTE abundances when using the final and reduced model atoms.
 |
Fig. 6 Best fits (continuous curve) of the solar Fe i 5434 and 6608 Å lines (bold dots in top and bottom panels, respectively) obtained from the non-LTE calculations with SH = 0.1. Fitting parameters are given in Table 5. For Fe i 6608 Å, dotted curves show the effect on the theoretical profile of a ± 0.02 dex variation in the final Fe abundance. The macroturbulence velocity was reduced by 0.3 km s-1 for |
3. Analysis of the solar Fe i and Fe ii lines
In this section, we derive the solar Fe abundance from the Fe i and Fe ii lines. The Sun is used as a reference star for a subsequent stellar abundance analysis. The solar flux observations are taken from the Kitt Peak Solar Atlas (Kurucz et al. 1984). The calculations were performed with the MAFAGS-OS model atmosphere 5777/4.44/0 (Grupp et al. 2009). A depth-independent microturbulence of 0.9 km s-1 was adopted. Throughout this study, the element abundance is determined from line profile fitting. The uncertainty in the fitting procedure was estimated to be less than 0.02 dex for weak and moderate strength lines (see Fig. 6) and less than 0.03 dex for strong lines. Our synthetic flux profiles are convolved with a profile that combines a rotational broadening of 1.8 km s-1 and broadening by macroturbulence with a radial-tangential profile. The most probable macroturbulence velocity Vmac varied mainly between 2.6 and 3.3 km s-1 for different lines of neutral iron and between 3.4 and 3.8 km s-1 for Fe ii lines. For comparison, Gray (1977) found solar macroturbulence velocities varying between 2.9 and 3.8 km s-1 for a small sample of the solar Fe i lines. The Vmac values obtained from the non-LTE (SH = 0.1) fits of individual solar iron lines are indicated in Table 5.
3.1. Line selection and atomic data
The investigated lines were selected according to the following criteria.
-
The lines should be almost free of visible/known blends in the Sun.
-
For each star the spectrum should include lines of various strength to provide an abundance analysis of both close-to-solar metallicity and very metal-poor stars.
-
The list of the Fe i lines should cover a range of excitation energies of the lower level as large as possible to investigate the excitation equilibrium of neutral iron.
 |
Fig. 7 Solar LTE (left column) and non-LTE (SH = 0.1, right column) Fe abundances from the Fe i (open circles) and Fe ii (filled circles) lines plotted as a function of Eexc (top row) and Wobs (bottom row). The mean abundances derived from the Fe i and Fe ii lines along with their standard deviations are quoted in the top row panels. The dotted line indicates the mean abundance derived from the Fe i lines and the shaded grey area its statistical error. In the bottom row panels, the dashed line shows the calculated trend of log εFeI versus Wobs. Everywhere, gf-values indicated in Table 5 were used. |
Despite the existence of many sources of gf-values for neutral iron, there is no single source that provides data for all the selected Fe i lines. We employed experimental gf-values from Bard et al. (1991); Bard & Kock (1994); Blackwell et al. (1979, 1982a,b); Fuhr et al. (1988), and O’Brian et al. (1991). The accuracy of available sets of gf-values for Fe i was discussed by Grevesse & Sauval (1999), and the influence of using various sets of data on the derived solar iron abundance was inspected by Gehren et al. (2001b). Both papers recommended to employ the gf-values published by the Hannover (Bard et al. 1991; Bard & Kock 1994) and Oxford (Blackwell et al. 1979, 1982a,b) groups. Unfortunately, these groups did not provide data for some Fe i lines that are important for the stellar iron spectrum analysis. Five sets of oscillator strengths from Meléndez & Barbuy (2009); Moity (1983); Raassen & Uylings (1998); Schnabel et al. (2004), and the vald database (Kupka et al. 1999) were inspected for Fe ii. We found that the solar mean abundance derived from the Fe ii lines varies between 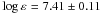 and
and 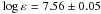 depending on the source of gf-values (Table 1). Hereafter, the statistical error is the dispersion in the single line measurements about the mean:
depending on the source of gf-values (Table 1). Hereafter, the statistical error is the dispersion in the single line measurements about the mean: 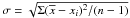 . As reported by Grevesse & Sauval (1999), the data of Raassen & Uylings (1998) for the visible Fe ii lines were underestimated by 0.11 dex, on average, compared with the gf-values obtained using lifetime and branching fraction measurements.
. As reported by Grevesse & Sauval (1999), the data of Raassen & Uylings (1998) for the visible Fe ii lines were underestimated by 0.11 dex, on average, compared with the gf-values obtained using lifetime and branching fraction measurements.
Solar mean iron non-LTE (SH = 0.1) abundances determined using various sources of gf-values.
3.2. Abundance analysis
For each line we determined the element abundance under various line-formation assumptions: non-LTE with SH = 0, 0.1, 1, and 2, and LTE. The quality of the fits is illustrated in Fig. 6 for two Fe i lines. The results are shown in Table 5 and Fig. 7. To present the absolute abundances from the Fe ii lines we used the gf-values from Raassen & Uylings (1998), where available, and Moity (1983), because they provide the mean element abundance consistent with that from the lines of Fe i. Compared with their LTE strength the Fe i lines become weaker and Fe ii lines stronger under non-LTE conditions. The effect is largest for non-LTE with pure electron collisions (SH = 0): the non-LTE abundance correction, ΔNLTE = log εNLTE − log εLTE, ranges between +0.03 and +0.15 dex for various Fe i lines and between 0.00 and −0.02 dex for the Fe ii lines. As expected, the departures from LTE are weaker in the calculations with H i collisions taken into account. For the Fe i lines, ΔNLTE does not exceed 0.09, 0.04, and 0.03 dex, when SH = 0.1, 1, or 2, respectively. For the Fe ii lines, the non-LTE abundance correction is smaller than 0.01 dex in absolute values, independent of the SH value. Our calculations showed that the low-excitation lines of Fe i are subject to stronger deviations from LTE than the higher excitation lines, in agreement with the previous results. For example, with SH = 0.1, ΔNLTE ranges between +0.04 and +0.09 dex for six lines with Eexc < 1 eV, while ΔNLTE = +0.04 dex is the upper limit for the remaining Fe i lines. As a result, an excitation energy gradient of the non-LTE iron abundances was found to be smaller than that for the LTE case. For example, with SH = 0.1, we obtained2 log εFeI = 7.516 + 0.0154 × Eexc(eV).
We see no significant abundance discrepancies between low-excitation and high-excitation lines. However, the abundance scatter is considerably too high for Eexc > 4 eV, independent of the line-formation assumptions used. For example, the difference between the highest (Fe i 5517 Å) and lowest (Fe i 5367 Å) absolute solar abundance is about 0.5 dex in all the cases. The abundance difference between Fe i 5662 Å and Fe i 5367 Å with gf-values from a common source (O’Brian et al. 1991) amounts to about 0.25 dex. There are essentially two explanations for this result: either the gf-values are not reliable or a significant fraction of the iron lines are contaminated by relatively strong (yet undetected) blends or both. Note that with an adopted microturbulence velocity of Vmic = 0.9 km s-1, the trend of log εFeI versus Wobs is completely removed in the non-LTE calculations. The Fe i 5517 Å line is an obvious outlier in the plots of Fig. 7: its abundance is 0.3 dex higher than the mean of the remaining Fe i lines. The solar mean Fe i abundances indicated in Table 3 were computed without Fe i 5517 Å and Fe i 5367 Å taken into account, and the corresponding statistical error is large, σ = 0.09 dex. These results demonstrate how far spectroscopic methods lead us toward accurate and reliable absolute stellar (solar) iron abundance results. Some value around 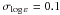 dex seems to denote the current precision limit.
dex seems to denote the current precision limit.
The difference between the solar mean Fe i abundances calculated with SH = 0 and 1 amounts to +0.07 dex. The corresponding value for Fe ii is −0.01 dex. Because the amplitude of the non-LTE effect is smaller than the combined statistical error of the obtained Fe i and Fe ii abundances and smaller than the difference in Fe ii abundances caused by employing various sources of gf-values, we did not endeavor to use the absolute solar Fe abundances determined from two ionization stages to constrain an SH value.
3.3. Comparison with other studies
During the last decade the possibly most advanced approach to solar abundance determinations is based on ab initio 3D, time-dependent, hydrodynamical model atmospheres. We compared our 1D LTE and non-LTE solar Fe abundance determinations with the results of 3D calculations performed independently by three scientific groups. The first 3D solar abundance analysis for Fe was made by Asplund et al. (2000, ANTS2000). For nine common Fe i lines, the difference between their 3D+LTE and our 1D+LTE abundances amounts to, on average, −0.10 ± 0.03 dex. The difference is smaller for the four common Fe ii lines when using the same gf-values, Δ(ANTS2000 – this study) = −0.04 ± 0.01 dex. In their recent 3D determinations, Asplund et al. (2009, AGSS2009) applied gf-values of the Fe ii lines from Meléndez & Barbuy (2009) and 1D non-LTE correction of +0.03 dex for Fe i and got log εFeI = 7.52 ± 0.05 and log εFeII = 7.50 ± 0.04 (here, the error bars are the systematic error added in quadrature with the statistical error calculated as the weighted standard error of the mean). Our 1D non-LTE abundances log εFeI = 7.56 ± 0.09 (Table 3, SH = 0.1) and log εFeII = 7.47 ± 0.05 when using gf-values from Meléndez & Barbuy (2009, Table 1 are consistent within the error bars with the corresponding values of AGSS2009, however, the abundance difference (Fe i – Fe ii) = 0.09 dex is larger compared to the 0.02 dex in AGSS2009. This could be due to the difference between 1D and 3D modeling. Note that updating the method of 3D calculations in AGSS2009 compared with ANTS2000 resulted in the smaller abundance difference (1D – 3D) for Fe i and opposite sign of the 3D effect for Fe ii.
The first non-LTE study for neutral iron that went beyond the 1D analysis was by Shchukina & Trujillo Bueno (2001). Ignoring inelastic collisions with H i atoms in their 1.5D+non-LTE calculations, they found a 0.074 ± 0.03 dex higher solar Fe i based abundance compared to the LTE value. Our 1D+non-LTE analysis with pure electronic collisions gives for the solar Fe i lines a very similar mean non-LTE abundance correction of 0.08 dex. However, the absolute abundance is a 0.11 dex higher compared with log εFeI = 7.50 ± 0.10 obtained by Shchukina & Trujillo Bueno (2001).
Our 1D Fe ii based abundance (the non-LTE effects are negligible) is 0.04 dex lower compared with log εFeII = 7.512 ± 0.062 obtained by Caffau et al. (2011) from their solar 3D analysis when using gf-values from Meléndez & Barbuy (2009) in both studies.
Thus, the difference between our solar iron 1D abundances and the data from the literature based on the 3D calculations does not exceed 0.04 dex when using either the Fe i or Fe ii lines. However, the 3D effect has the opposite sign for the two ions, and this may affect the analysis of the solar Fe i/Fe ii ionization equilibrium.
Characteristics of observed spectra.
Stellar parameters and obtained iron abundances, [Fe/H], for selected stars.
4. Stellar sample, observations, and stellar parameters
Our current sample consists of five stars with the effective temperature and surface gravity determined from methods that are largely independent of the model atmosphere. Two of them, HD 61421 (Procyon) and HD 102870 (β Vir), are close-to-solar metallicity stars. HD 10700 (τ Cet) is a mildly metal-deficient star with [Fe/H] ≃ −0.5. The two remaining stars are very metal-poor (VMP) with [Fe/H] < −2. HD 84937 represents the hot end of the stars that evolve on time scales comparable with the Galaxy lifetime. HD 122563, in contrast, is a cool giant. The selected stars are listed in Table 2.
The spectroscopic observations for three of our program stars were carried out with the fibre-fed échelle spectrograph FOCES at the 2.2 m telescope of the Calar Alto Observatory during a number of observing runs, with a spectral resolving power of R ≃ 60 000 (HD 10700 was also observed at R ≃ 40 000 to get a higher signal-to-noise (S/N) spectrum at λ < 4500 Å). Characteristics of the observed spectra are summarized in Table 2. The S/N ratio is 200 or higher in the spectral range λ > 4500 Å, but lower in the blue. All investigated iron lines lie longward of 4427 Å, and their profile analysis profits from the high spectral resolution and high S/N. For HD 84937 and HD 122563, we used high-quality observed spectra from the ESO UVESPOP survey (Bagnulo et al. 2003).
Procyon, β Vir, and τ Cet are among the very few stars for which the whole set of fundamental stellar parameters except metallicity can be determined from (nearly) model-independent methods. In the most recent study of Bruntt et al. (2010), the angular diameters of these stars were measured using interferometry. The measured bolometric flux, combined with the angular diameter, implied Teff = 5383 ± 47, 6494 ± 48, and 6012 ± 64 K for τ Cet, Procyon, and β Vir, respectively. A surface gravity of log g = 4.54 ± 0.02, 3.98 ± 0.02, and 4.13 ± 0.02, respectively, was computed using the stellar mass and linear radius from Table 2 of Bruntt et al. (2010). Our adopted stellar parameters of these three stars (Table 3) were taken from different studies, but they turned out to be consistent within 1σ with the data of Bruntt et al. (2010). We employed Procyon’s stellar parameters from a careful analysis of Allende Prieto et al. (2002). The interferometric measurements of the angular diameter and the bolometric flux were used by North et al. (2009) to derive Teff and log g of β Vir. For τ Cet the Teff and log g were derived by Di Folco et al. (2004) based on direct interferometric measurements of the angular diameter and stellar evolution calculations.
For HD 84937 the infrared flux method (IRFM) temperatures of Alonso et al. (1996); Meléndez & Ramírez (2004); González Hernández & Bonifacio (2009), and Casagrande et al. (2010), Teff = 6330 K, 6345 K, 6333 K, and 6408 K, respectively, are consistent within 1σ. Our adopted value, Teff = 6350 K, is the average of the four. To determine log g, we used an updated Hipparcos parallax of πHip = 13.74 ± 0.78 mas from van Leeuwen (2007) and a mass of 0.8 M⊙ derived from the tracks of VandenBerg et al. (2000).
For HD 122563 we adopted the Teff(IRFM) = 4600 K recommended by Barbuy et al. (2003) and based on the IRFM determination by Alonso et al. (1999). Using the 2MASS photometric system, González Hernández & Bonifacio (2009) obtained a 200 K higher IRFM temperature of this star. However, they noted that the 2MASS photometric accuracy is very low for bright giant stars. The gravity was calculated with πHip = 4.22 ± 0.35 mas from van Leeuwen (2007) and a mass of 0.8 M⊙ following Barbuy et al. (2003). The gravity errors indicated in Table 3 for HD 84937 and HD 122563 reflect the uncertainty in the trigonometric parallax.
 |
Fig. 8 Non-LTE (SH = 0.1) differential abundances derived from the Fe i (open circles) and Fe ii (filled circles) lines in the selected stars as a function of the observed equivalent width (left column panels) and excitation energy of the lower level (right column panels). In each panel, the dashed line shows the mean iron abundance determined from the Fe i lines. See text for more details. |
5. Fe i versus Fe ii in the reference stars
In this section we derive the Fe i and Fe ii abundances in the selected stars under various line-formation assumptions, i.e., non-LTE with SH = 0, 0.1, 1, and 2 and LTE, and we investigate which of them leads to consistent element abundances from both ionization stages.
5.1. Methodology
To minimize the effect of the uncertainty in gf-values on the final results, we applied a line-by-line differential non-LTE and LTE approach, in the sense that stellar line abundances were compared with individual abundances of their solar counterparts. Our results for Fe abundances are based on a line profile analysis. In order to compare the computed synthetic profiles with observations, they were convolved with a profile that combines instrumental broadening with a Gaussian profile, rotational broadening, and broadening by macroturbulence with a radial-tangential profile. Rotational broadening and broadening by macroturbulence were treated separately only for Procyon and β Vir, with Vsini = 2.6 km s-1 and 2.5 km s-1, respectively (Fuhrmann 1998). We treated the overall effects of rotation and macroturbulence for the remaining stars as radial-tangential macroturbulence. The macroturbulence value Vmac was determined for each star either by Fuhrmann (1998, 2004) or in our previous studies (Korn et al. 2003; Mashonkina et al. 2008) from the analysis of an extended list of lines of various chemical species. For a given star, Vmac was allowed to vary by ± 0.3 km s-1 (1σ).
Microturbulence velocity was determined for each star with the requirement that the iron non-LTE abundance derived from Fe i lines with SH = 0.1 must not depend on the line strength. We note that even for the other line-formation scenarios, the slope of the [Fe/H]I – Wobs plot is also largely removed with the resulting Vmic value.
Figure 8 shows our final non-LTE (SH = 0.1) abundances from individual lines of two ionization stages in each of the investigated stars. The average Fe i and Fe ii abundances obtained in LTE and in non-LTE with SH = 0, 0.1, and 1 are presented in Table 3. Aware of the shortcomings of 1D atmospheric structure modeling, we tend to represent a similar range of the line formation depths for stars of various metallicity. The strongest iron line detected in HD 122563 has Wobs = 123.8 mÅ, while some of the selected iron lines are very strong in Procyon, β Vir, and τ Cet with Wobs up to 250, 305, and 496 mÅ, respectively. Therefore, we used only lines with equivalent widths of less than 125 mÅ in the stellar abundance and microturbulence velocity analyses.
5.2. Non-LTE effects
5.2.1. Absolute abundances from Fe ii lines
In the stellar parameter range with which we are concerned, the non-LTE effects of the investigated Fe ii lines are found to be negligible when H i collisions are taken into account in the SE calculations. For the stars with metal abundances close to solar or mildly deficient, non-LTE with pure electronic collisions leads to a strengthening of the line core for the strongest (W > 40 mÅ) Fe ii lines because the line source function (Slu ≃ bu/bl Bν) drops below the Planck function (Bν) in the uppermost atmospheric layers. Here, bu and bl are the departure coefficients of the upper and lower levels, respectively. The lower levels of the investigated Fe ii lines are all of even parity with Eexc = 2.8–3.9 eV (see Table 5), and they keep their thermodynamic equilibrium populations (bl = 1) throughout the atmosphere. The population of the odd parity quartet and sextet terms with Eexc = 5–6 eV is controlled by the strong transitions to the ground state a6D and low-excitation states a4F, a4D, and a4P. The line center optical depth of these transitions drops below unity at log τ5000 < −2 (Fig. 5), resulting in photon losses in the corresponding lines and underpopulation of the upper levels (bu < 1). For Procyon, β Vir, and τ Cet, the non-LTE abundance correction is negative and does not exceed 0.02 dex in absolute value. The departures from LTE are negligible for the weaker lines. Non-LTE with SH = 0 results in the opposite effect for the VMP stars. This can be understood as follows. In the atmosphere with [Fe/H] = −2.5, the line wing optical depth drops below 1 far inside the atmosphere even for the strongest Fe ii transitions arising from the ground and low-excitation states to the odd parity levels with Eexc = 5–6 eV. As a result, they are pumped by the ultraviolet Jν − Bν(Te) excess radiation and produce enhanced excitation of the odd parity levels in the layers with log τ5000 between +0.3 and −1 (Fig. 5). Here, the term “pumped” (or pumping) is used following Bruls et al. (1992). In the upper layers, log τ5000 < −1, where the line center optical depth of the UV transitions drops below 1, enhanced excitation changes with photon losses resulting in a decrease of the departure coefficients of the odd parity levels. The investigated Fe ii lines are formed in the atmospheres of HD 84937 and HD 122563 inside log τ5000 = −1.4, where for every line the source function exceeds the Planck function, which results in weakening the line relative to its LTE strength. The average non-LTE abundance correction amounts to +0.01 dex and +0.10 dex, respectively.
5.2.2. Absolute abundances from Fe i lines
In all cases, non-LTE leads to a weakening of the Fe i lines. In close-to-solar metallicity models, this is mainly owing to overionization. For each line, the source function is quite similar to the Planck function because most levels behave similarly, as can be seen in Fig. 5 (left top panel). At the other end of the metallicity range, the energy levels become weakly coupled far inside the VMP atmospheres because of deficient collisions (Fig. 5, right top panel). At the depths where the Fe i lines are formed, the upper levels are all depleted to a lesser extent with regard to their LTE populations than are the lower levels. The lines are weaker with regard to their LTE strengths not only because of the general overionization, but also because of bu/bl > 1 resulting in Slu > Bν and the depleted line absorption. The non-LTE effects are the strongest when H i collisions are neglected in the SE calculations. On average, ΔNLTE(SH = 0) = +0.05 dex and +0.06 dex for Procyon and β Vir and increases with decreasing metallicity to +0.13 dex at [Fe/H] = −0.5 (τ Cet), +0.26 dex at [Fe/H] = −2.1 (HD 84937), and +0.43 dex at [Fe/H] = −2.5 (HD 122563). With H i collisions taken into account, the effect on the iron abundance determination is substantially weaker. For example, with SH = 0.1, ΔNLTE = 0.00, +0.04, 0.03, 0.19, and 0.19 dex for the same sequence of stars, respectively.
5.2.3. Differential abundances from Fe i lines
For stellar differential abundances, the non-LTE correction can be introduced as [ΔNLTE] = [Fe/H]NLTE – [Fe/H]LTE. Because the departures from LTE for the solar Fe i lines are small in the calculations with SH ≠ 0, the corresponding [ΔNLTE] and ΔNLTE values turned out to be close together. For example, [ΔNLTE](SH = 0.1) = +0.02, 0.02, 0.00, 0.17, and 0.16 dex for Procyon, β Vir, τ Cet, HD 84937, and HD 122563, respectively. In the SH = 0 case, the non-LTE differential abundance correction is approximately 0.08 dex lower than the corresponding ΔNLTE value.
5.2.4. Fe i excitation equilibrium
For the two VMP stars of our sample, non-LTE leads to the shallower excitation gradient of the Fe i line abundances compared with that obtained under the LTE assumption. For example, with SH = 0.1 (the right column panels of Fig. 8), d[Fe/H]/dEexc = +0.013 dex/eV for HD 84937 and −0.030 dex/eV for HD 122563, while the corresponding LTE values are −0.019 and −0.054 dex/eV, respectively. However, the non-LTE gradient obtained for HD 122563 is still steep compared with other stars of the sample. Our test calculations show that it could be substantially reduced, down to d[Fe/H]/dEexc = −0.008 dex/eV, with an effective temperature revised downward by 80 K (1σ). No significant change in the excitation slope between non-LTE and LTE was found for Procyon, β Vir, and τ Cet, because the departures from LTE for Fe i are small in these stars. The gradient is small, at the level of −0.005 to −0.007 dex/eV, for τ Cet. For Procyon and β Vir, d[Fe/H]/dEexc ≃ 0.02 dex/eV. We caution against determining stellar effective temperatures of metal-poor stars from the Fe i LTE excitation equilibrium.
Uncertainties in the non-LTE analysis of Fe i and Fe ii in selected stars.
5.3. Empirically constraining the efficiency of H i collisions
As can be seen from Table 3, the behavior of the difference between Fe i and Fe ii abundances, Δ(Fe ii – Fe i) = [Fe/H]II – [Fe/H]I, within various line-formation scenarios is different for stars of different metal abundance.
A disparity between the neutral and singly-ionized iron is found in Procyon and in β Vir, independent of either LTE or non-LTE. The least imbalance achieved in non-LTE with SH = 0.1 amounts to 0.06 dex and 0.09 dex, respectively. Very similar results for Fe i/Fe ii in Procyon were obtained earlier by Korn et al. (2003). For the same star, a similar problem was uncovered also for Ca i/Ca ii (Mashonkina et al. 2007). Such a disparity can be caused by the uncertainties either in atmosphere and line-formation modelling or in stellar parameters. The three-dimensional LTE simulations for Procyon (Allende Prieto et al. 2002) showed that weak lines (Wλ ≤ 50 mÅ) of both Fe i and Fe ii are weakened compared to a classical 1D analysis, in a way that the derived Fe abundance of this star increases by 0.05 dex and 0.04 dex, respectively. Thus, LTE+3D modeling does not master Fe i/Fe ii in Procyon. The solution of the non-LTE+3D problem for iron is still a challenge for stellar spectra modeling (see Sect. 6). As discussed by Korn et al. (2003), to remove a discrepancy of 0.07 dex between Fe ii and Fe i in Procyon, one would require either a gravity of log g = 3.81, many standard deviations away from the astrometric result, or a temperature of Teff = 6600 K, almost 2σ higher than the temperature based on bolometric flux. Our test calculations with an 80 K upward revised Teff achieved consistent Fe i and Fe ii abundances of this object (Table 4).
We find that non-LTE with SH ≥ 0.1 is as good as LTE to achieve the ionization equilibrium between Fe i and Fe ii in τ Cet. Yet non-LTE with pure electronic collisions cannot be excluded completely, because an abundance difference of Δ(Fe ii – Fe i, SH = 0) = −0.08 is only by a factor of 1.5 larger than its error bars.
We come to the conclusion that non-LTE is a must when analyzing very metal-poor stellar spectra, whether hot or cool. LTE leads to a discrepancy in abundances between Fe ii and Fe i of 0.09 dex for HD 84937, which is still at the level of 1σ, and 0.21 dex for HD 122563. As can be seen from Table 3, Δ(Fe ii – Fe i) should approach 0 in non-LTE with a SH value of between 0.1 and 1 for HD 84937 and between 0 and 0.1 for HD 122563. With SH = 0.1, Δ(Fe ii – Fe i) = −0.08 dex for the first of them and +0.05 dex for the second one. Most F5 – K0 type stars in the super-solar metallicity down to [Fe/H] = −2.5 domain have stellar parameters Teff and log g in between those for HD 84937 (6350/4.09) and HD 122563 (4600/1.60). Therefore, the uncertainty in the estimated SH value is expected to result in an abundance error of no more than 0.08 dex in the non-LTE calculations for Fe i in this type of stars. Note that this abundance error decreases toward higher metallicity. For comparison, an abundance error caused by using the LTE assumption can be as large as 0.2 dex.
6. Uncertainties in the iron non-LTE abundances
To assess the influence of crucial atomic data and stellar parameters on the accuracy of iron non-LTE abundances, test calculations were performed for Procyon, HD 84937, and HD 122563. For each parameter or atomic model that we varied, we derived stellar Fe abundances from the Fe i and Fe ii lines and then the average values. The results of the tests are summarized in Table 4.
6.1. Hydrogenic collisions
The effect of including hydrogenic collisions in our SE calculations is shown in the first four lines of Table 4. We discussed above how the Fe i and Fe ii abundances vary depending on the SH value. Here, we concentrate on the effect of using the atomic model, where H i collisions were taken into account for the allowed transitions, but were neglected for the forbidden transitions. For a differential analysis of stellar spectra, the calculations were performed with SH = 0, 0.1 and 1 not only for the three tested stars, but also for the Sun. As expected, neglecting hydrogenic collisions for the forbidden transitions leads to substantially stronger departures from LTE for Fe i in the VMP stars. With the modified model atom, no single SH value leading to consistent Fe i and Fe ii abundances in both HD 84937 and HD 122563 was found.
6.2. Completeness of the model atom
For the Sun and the reference stars, calculations were also performed with the reduced atomic model, where all the predicted high-excitation levels of Fe i were removed. As shown in Sect. 2.3, the use of the reduced model atom leads to a stronger overionization of Fe i compared with that calculated with our final model atom. As a result, the Fe i based non-LTE abundances obtained with the reduced model atom are higher than the corresponding values in Table 3. For the Sun, the abundance difference amounts to 0.08 dex with SH = 0.1. The changes in stellar differential abundances are smaller (Table 4). An exception is HD 122563, where the Fe i mean abundance changes by +0.07 dex. We caution against applying an incomplete model atom of neutral iron or any other minority species to a non-LTE analysis of stellar spectra.
6.3. Stellar parameters
We investigated how the uncertainties in stellar parameters influence our choice of the SH scaling factor. For both VMP stars of our sample, the test calculations were performed with a 0.1 dex (more than 1σ) lower gravity and an 80 K (approximately 2σ) revised effective temperature, upward for HD 84937 and downward for HD 122563. The results of these tests can be summarized as follows.
-
The variation in Teff, log g, and Vmic within the error bars does not help to achieve the Fe i/Fe ii ionization equilibrium in HD 84937 and HD 122563 under the LTE assumption.
-
Reducing the gravity by 0.1 dex does not change the excitation gradient of the Fe i-based abundances in each of these two stars. A relatively steep trend of [Fe/H]I versus Eexc obtained in HD 122563 can essentially be removed with a downward revision of the effective temperature by 80 K.
-
The uncertainties in stellar parameters do not influence our conclusion that there is a need for inelastic collisions with hydrogen atoms (or other thermalizing collisional processes not involving electrons) to establish the SE of iron in the atmospheres of metal-poor stars. With the downward revised Teff or log g, HD 122563 favors a low efficiency of H i collisions with SH = 0 and 0.1, respectively. With the higher Teff or the lower gravity of HD 84937, the difference between [Fe/H]I and [Fe/H]II is removed with SH ≃ 1.
6.4. Stellar atmosphere and line formation modeling
Only two non-LTE studies for iron exist in the literature that go beyond the 1D analysis. Shchukina & Trujillo Bueno (2001) and Shchukina et al. (2005) performed 1.5D non-LTE calculations in 3D model atmospheres of the Sun and the metal-poor subgiant HD 140283. They found that the departures from LTE are stronger in 3D than in 1D model and gave a 3D non-LTE abundance correction of Δ3D,NLTE = log ε3D,NLTE − log ε3D,LTE = +0.07 dex for the Sun and about +0.9 dex for HD 140283. Shchukina et al. (2005) have demonstrated that the ionization equilibrium between Fe i and Fe ii in HD 140283 cannot be achieved with Teff = 5700 K, log g = 3.7, and [Fe/H] = −2.5, and they obtained surprisingly large statistical errors of 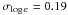 dex and 0.48 dex for the abundances determined from the Fe i and Fe ii lines, respectively. They argued that adopting Teff ≃ 5600 K and [Fe/H] ≃ −2.0 substantially reduces the discrepancies between the two ionization stages. We note that this effective temperature is in conflict with the recently improved IRFM temperature of this star, either Teff = 5755 K (González Hernández & Bonifacio 2009) or Teff = 5777 K (Casagrande et al. 2010). An explanation for this result can be the use of an incomplete model atom of Fe i and ignoring inelastic collisions with H i atoms. The Fe i term diagram applied by Shchukina et al. (2005) is, indeed, complete up to Eexc = 5.72 eV. But at higher energies between Eexc = 5.72 eV and 7.0 eV, it only contains about 50% of the terms identified by Nave et al. (1994). The non-LTE+3D problem for iron still awaits a more satisfactory solution.
dex and 0.48 dex for the abundances determined from the Fe i and Fe ii lines, respectively. They argued that adopting Teff ≃ 5600 K and [Fe/H] ≃ −2.0 substantially reduces the discrepancies between the two ionization stages. We note that this effective temperature is in conflict with the recently improved IRFM temperature of this star, either Teff = 5755 K (González Hernández & Bonifacio 2009) or Teff = 5777 K (Casagrande et al. 2010). An explanation for this result can be the use of an incomplete model atom of Fe i and ignoring inelastic collisions with H i atoms. The Fe i term diagram applied by Shchukina et al. (2005) is, indeed, complete up to Eexc = 5.72 eV. But at higher energies between Eexc = 5.72 eV and 7.0 eV, it only contains about 50% of the terms identified by Nave et al. (1994). The non-LTE+3D problem for iron still awaits a more satisfactory solution.
7. Conclusions
We built a comprehensive model atom for neutral and singly-ionized iron using atomic data for the energy levels and transition probabilities from laboratory measurements and theoretical predictions. With a fairly complete model atom for Fe i, the calculated statistical equilibrium of iron changed substantially by achieving close collisional coupling of the Fe i levels near the continuum to the ground state of Fe ii. There is no need anymore for the enforced upper level thermalization procedure that was applied in the previous non-LTE analyses (Gehren et al. 2001a; Korn et al. 2003; Collet et al. 2005).
Non-LTE line formation for Fe i and Fe ii lines was considered in 1D model atmospheres of the Sun and five reference stars with reliable stellar parameters, which cover a broad range of effective temperatures between 4600 K and 6500 K, gravities between log g = 1.60 and 4.53, and metallicities between [Fe/H] = −2.5 and +0.1. We found that the departures from LTE are negligible for the Fe ii lines over the whole stellar parameter range considered. For Fe i, the non-LTE effects on the abundances are expected to be small for stars with solar-type metallicities such as the Sun, Procyon, and β Vir, and for mildly metal-deficient stars such as τ Cet: a non-LTE correction is at the level of +0.1 dex in non-LTE with pure electronic collisions and of a few hundredths, when inelastic collisions with hydrogen atoms are taken into account in the SE calculations with SH ≥ 0.1.
From a differential line-by-line analysis of stellar spectra we found that the iron ionization equilibrium is not fulfilled in Procyon and β Vir at their fundamental parameters, 6510/3.96 and 6060/4.11, respectively, independent of either LTE or non-LTE. For Procyon, an upward revision of its temperature by 80 K removes the obtained abundance imbalance.
In contrast, consistent iron abundances from both ionization stages were obtained in τ Cet at its given stellar parameters in both non-LTE with SH ≥ 0.1 and in LTE.
Significant departures from LTE for Fe i were found in the two VMP stars of our sample, HD 84937 and HD 122563. Our results indicate the need for a thermalizing process not involving electrons in their atmospheres. Because there are no accurate theoretical considerations of appropriate processes for iron, we simulate an additional source of thermalization in the atmospheres of cool stars by parameterized H i collisions. Close inspection of the ionization equilibrium between Fe i and Fe ii in HD 84937 and HD 122563 leads us to choose a scaling factor of 0.1 to the formula of Steenbock & Holweger (1984) for calculating hydrogenic collisions. The uncertainty in the estimated SH value is expected to result in abundance error of no more than 0.08 dex in the non-LTE calculations for Fe i in the F5 – K0 type stars in the super-solar metallicity down to [Fe/H] = −2.5 domain. However, the situation can be different for extremely and ultra-metal-poor stars. Exactly for these objects the determination of the surface gravity relies in most cases on the analysis of the Fe i/Fe ii ionization equilibrium. Theoretical studies are urgently needed to evaluate the cross-sections of inelastic collisions of Fe i with H i atoms and to search for and evaluate other types of thermalizing processes.
For the Sun, the use of SH = 0.1 leads to an average Fe i non-LTE correction of 0.03 dex and a mean Fe i based abundance of 7.56 ± 0.09. A mean solar abundance derived from Fe ii lines varies between 7.41 ± 0.11 and 7.56 ± 0.05 depending on the source of gf-values. A statistical error of 0.09–0.11 dex is uncomfortably high for the Sun. It is, most probably, caused by the uncertainty in gf-values and, in part, van der Waals damping constants. The problem of oscillator strengths of the Fe lines and their influence on the derived solar iron abundance has been debated for decades (Blackwell et al. 1995; Holweger et al. 1995; Kostik et al. 1996; Caffau et al. 2011). Stellar astrophysics needs accurate atomic data for an extended list of the iron lines, which could be measured in stars of very different metallicities. We therefore call on laboratory atomic spectroscopists for further efforts to improve gf-values of the Fe i and Fe ii lines used in abundance analysis.
Using our carefully calibrated model of iron, cool stars over a broad range of metallicities encountered in the Galaxy can now be analyzed in a homogeneous way to derive their iron abundance and gravity without resorting to trigonometric parallaxes. The dependence of departures from LTE on stellar parameters and an application of the non-LTE technique to the known ultra-metal-poor stars ([Fe/H] < −4.5) will be presented in a forthcoming paper.
Online material
Online material
Line data and iron LTE and non-LTE abundances from an analysis of the solar spectrum.
Acknowledgments
The authors thank Manuel Bautista and Tatyana Ryabchikova for help with collecting the atomic data and Nicolas Grevesse for useful discussion of the accuracy of gf-values for the iron lines. This research was supported by the Russian Foundation for Basic Research (08-02-92203-GFEN-a and 08-02-00469-a), the Russian Federal Agency on Science and Innovation (02.740.11.0247), the Deutsche Forschungsgemeinschaft (GE 490/34.1), and the National Natural Science Foundation of China (No. 10973016). A.J.K. acknowldeges support by the Swedish Reseach Council and the Swedish National Space Board. We also thank the anonymous (second) referee for valuable suggestions and comments. We made use of the NIST, SIMBAD, and VALD databases.
References
- Allard, N. F., Drira, I., Gerbaldi, M., et al. 1998, A&A, 335, 1124 [NASA ADS] [Google Scholar]
- Allende Prieto, C., Asplund, M., Garsia Lopez, R. J., & Lambert, D. 2002, ApJ, 567, 544 [NASA ADS] [CrossRef] [Google Scholar]
- Allende Prieto, C., Asplund, M., & Fabiani Bendicho, P. 2004, A&A, 423, 1109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Alonso, A., Arribas, S., & Martínez-Roger, C. 1996, A&AS, 117, 227 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Alonso, A., Arribas, S., & Martínez-Roger, C. 1999, A&AS, 139, 335 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Anders, E., & Grevesse, N. 1989, Geoch., & Cosmochim Acta, 53, 197 [Google Scholar]
- Anstee, S. D., & O’Mara, B. J. 1995, MNRAS, 276, 859 [NASA ADS] [CrossRef] [Google Scholar]
- Asplund, M. 2005, ARA&A, 43, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Asplund, M., Nordlund, Å., Trampedach, R., & Stein, R. F. 2000, A&A, 359, 743 [NASA ADS] [Google Scholar]
- Athay, R. G., & Lites, B. W. 1972, ApJ, 176, 809 [NASA ADS] [CrossRef] [Google Scholar]
- Bagnulo, S., Jehin, E., Ledoux, C., et al. 2003, ESO Messenger, 114, 10 [Google Scholar]
- Barbuy, B., Meléndez, J., Spite, M., et al. 2003, ApJ, 588, 1072 [NASA ADS] [CrossRef] [Google Scholar]
- Bard, A., & Kock, M. 1994, A&A, 282, 1014 [NASA ADS] [Google Scholar]
- Bard, A., Kock, A., & Kock, M. 1991, A&A, 248, 315 [NASA ADS] [Google Scholar]
- Barklem, P. S., & Aspelund-Johansson, J. 2005, A&A, 435, 373 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Barklem, P. S., & O’Mara, B. J. 1997, MNRAS, 290, 102 [Google Scholar]
- Barklem, P. S., O’Mara, B. J., & Ross, J. E. 1998, MNRAS, 296, 1057 [Google Scholar]
- Barklem, P. S., Belyaev, A. K., & Asplund, M. 2003, A&A, 409, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Barklem, P. S., Belyaev, A. K., Dickinson, A. S., & Gadéa, F. X. 2010, A&A, 519, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bautista, M. A. 1997, A&AS, 122, 167 [Google Scholar]
- Bautista, M. A., & Pradhan, A. K. 1996, A&AS, 115, 551 [NASA ADS] [Google Scholar]
- Bautista, M. A., & Pradhan, A. K. 1998, ApJ, 492, 650 [NASA ADS] [CrossRef] [Google Scholar]
- Belyaev, A. K., & Barklem, P. 2003, Phys. Rev. A, 68, 062703 [NASA ADS] [CrossRef] [Google Scholar]
- Belyaev, A. K., Grosser, J., Hahne, J., & Menzel, T. 1999, Phys. Rev. A, 60, 2151 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Belyaev, A. K., Barklem, P. S., Dickinson, A. S., & Gadéa, F. X. 2010, Phys. Rev. A, 81, 032706 [NASA ADS] [CrossRef] [Google Scholar]
- Blackwell, D. E., Ibbetson, P. A., Petford, A. D., & Shallis, M. J. 1979, MNRAS, 186, 633 [NASA ADS] [CrossRef] [Google Scholar]
- Blackwell, D. E., Petford, A. D., Shallis, M. J., & Simmons, G. J., 1982a, MNRAS, 199, 43 [NASA ADS] [CrossRef] [Google Scholar]
- Blackwell, D. E., Petford, A. D., & Simmons, G. J., 1982b, MNRAS, 201, 595 [NASA ADS] [CrossRef] [Google Scholar]
- Blackwell, D. E., Lynas-Gray, A. E., & Smith, G. 1995, A&A, 296, 217 [NASA ADS] [Google Scholar]
- Boyarchuk, A. A., Lyubimkov, L. S., & Sakhibullin, N. A. 1985, Astrophys., 22, 203 [Google Scholar]
- Brown, C. M., Ginter, M. L., Johansson, S., & Tilford, S. G. 1988, J. Opt. Soc. Am., B5, 2125 [NASA ADS] [Google Scholar]
- Bruls, J. H., Rutten, R. J., & Shchukina, N. 1992, A&A, 265, 237 [NASA ADS] [Google Scholar]
- Bruntt, H., Bedding, T. R., Quirion, P.-O., et al. 2010, MNRAS, 405, 1907 [NASA ADS] [Google Scholar]
- Butler, K., & Giddings, J. 1985, Newsletter on the Analysis of Astronomical Spectra, No. 9, University of London [Google Scholar]
- Caffau, E., Ludwig, H.-G., Steffen, M., et al. 2011, Sol. Phys., 268, 255 [NASA ADS] [CrossRef] [Google Scholar]
- Casagrande, L., Ramírez, I., Meléndez, J., et al. 2010, A&A, 512, 54 [Google Scholar]
- Castelli, F., & Kurucz, R. 2001, A&A, 372, 260 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Collet, R., Asplund, M., & Thévenin, F. 2005, A&A, 442, 643 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
- Christlieb, N., Bessel, M., Beers, T., et al. 2002, Nature, 419, 904 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Di Folco, E., Thévenin, F., Kervella, P., et al. 2004, A&A, 426, 601 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Drawin, H. W. 1968, Z. Physik, 211, 404 [Google Scholar]
- Drawin, H. W. 1969, Z. Physik, 225, 483 [Google Scholar]
- Fleck, I., Grosser, J., Schnecke, A., et al. 1991, J. Phys. B, 24, 4017 [Google Scholar]
- Fuhr, J. R., Martin, G. A., & Wiese, W. L. 1988, J. Phys. Chem. Ref. Data, 17, Suppl. 4 [Google Scholar]
- Fuhrmann, K. 1998, A&A, 338, 161 [NASA ADS] [Google Scholar]
- Fuhrmann, K. 2004, Astron. Nachr., 325, 3 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Gehren, T. 1975, A&A, 38, 289 [Google Scholar]
- Gehren, T., Butler, K., Mashonkina, L., et al., 2001a, A&A, 366, 981 (Paper I) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gehren, T., Korn, A. J., & Shi, J. R., 2001b, A&A, 380, 645 (Paper II) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gehren, T., Liang, Y. C., Shi, J. R., et al. 2004, A&A, 413, 1045 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gigas, D. 1986, A&A, 165, 170 [Google Scholar]
- González Hernández, J. I., & Bonifacio, P. 2009, A&A, 497, 497 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gratton, R. G., Carretta, E., Eriksson, K., & Gustafsson, B. 1999, A&A, 350, 955 [NASA ADS] [Google Scholar]
- Gray, D. F. 1977, ApJ, 218, 530 [NASA ADS] [CrossRef] [Google Scholar]
- Grevesse, N., & Sauval, A. J. 1999, A&A, 347, 348 [NASA ADS] [Google Scholar]
- Grupp, F. 2004, A&A, 420, 289 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Grupp, F., Kurucz, R. L., & Tan, K. 2009, A&A, 503, 177 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Holweger, H. 1996, Phys. Scr., T65, 151 [Google Scholar]
- Holweger, H., Kock, M., & Bard, A. 1995, A&A, 296, 233 [NASA ADS] [Google Scholar]
- Korn, A. J., Shi, J., & Gehren, T. 2003, A&A, 407, 691 (Paper III) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kostik, R. I., Shchukina, N. G., & Rutten, R. J., 1996 A&A, 305, 325 [NASA ADS] [Google Scholar]
- Kupka, F., Piskunov, N., Ryabchikova, T. A., et al. 1999, A&AS, 138, 119 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [PubMed] [Google Scholar]
- Kurucz, R. 2009, http://kurucz.harvard.edu/atoms/2600/ [Google Scholar]
- Kurucz, R. L. 1992, Rev. Mex. Astron. Astrofis., 23, 45 [Google Scholar]
- Kurucz, R. L. 1994, SYNTHE Spectrum Synthesis Programs and Line Data, CD-ROM No. 18, Cambridge, Mass [Google Scholar]
- Kurucz, R. L., Furenlid, I., Brault, J., & Testerman, L. 1984, Solar Flux Atlas from 296 to 1300 nm, Nat. Solar Obs., Sunspot, New Mexico [Google Scholar]
- Lambert, D. L. 1993, Phys. Scr., T47, 186 [CrossRef] [Google Scholar]
- Mashonkina L. 2009, Phys. Scr., T134, 014004 [Google Scholar]
- Mashonkina, L. I., Korn, A. J., & Przybilla, N. 2007, A&A, 461, 261 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mashonkina, L., Zhao, G., Gehren, T., et al. 2008, A&A, 478, 529 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Meléndez, J., & Barbuy, B. 2009, A&A, 497, 611 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Meléndez, J., & Ramírez, I. 2004, ApJ, 615, L33 [NASA ADS] [CrossRef] [Google Scholar]
- Moity, J. 1983, A&AS, 52, 37 [NASA ADS] [Google Scholar]
- Nave, G., Johansson, S., Learner, R. C. M., et al. 1994, ApJS, 94, 221 [NASA ADS] [CrossRef] [Google Scholar]
- North, J. R., Davis, J., Robertson, J. G., et al. 2009, MNRAS, 393, 245 [NASA ADS] [CrossRef] [Google Scholar]
- O’Brian, T. R., Wickliffe, M. E., Lawler, J. E., et al. 1991, J. Opt. Soc. Am. B, 8, 1185 [NASA ADS] [CrossRef] [Google Scholar]
- Pelan, J., & Berrington, K. A. 1997, A&AS, 122, 177 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pereira, T. M. D., Asplund, M., & Kiselman, D. 2009, A&A, 508, 1403 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Raassen, A. J. J., & Uylings, P. H. M. 1998, A&A, 340, 300 [NASA ADS] [Google Scholar]
- Reetz, J. K. 1991, Diploma Thesis, Universität München [Google Scholar]
- Rybicki, G. B., & Hummer, D. G. 1991, A&A, 245, 171 [NASA ADS] [Google Scholar]
- Rybicki, G. B., & Hummer, D. G. 1992, A&A, 262, 209 [NASA ADS] [Google Scholar]
- Seaton, M. J. 1962, in Atomic and Molecular Processes (New York: Academic Press) [Google Scholar]
- Seaton, M. J., Mihalas, D., & Pradhan, A. K. 1994, MNRAS, 266, 805 [NASA ADS] [CrossRef] [Google Scholar]
- Shchukina, N. G., & Trujillo Bueno, J. 2001, ApJ, 550, 970 [NASA ADS] [CrossRef] [Google Scholar]
- Shchukina, N. G., Trujillo Bueno, J., & Asplund, M. 2005, ApJ, 618, 939 [NASA ADS] [CrossRef] [Google Scholar]
- Schnabel, R., Schultz-Johanning, M., & Kock, M. 2004, A&A, 414, 1169 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schoenfeld, W. G., Chang, E. S., Geller, M., et al. 1995, A&A, 301, 593 [NASA ADS] [Google Scholar]
- Steenbock, W., & Holweger, H. 1984, A&A, 130, 319 [NASA ADS] [Google Scholar]
- Takeda, Y. 1991, A&A, 242, 455 [NASA ADS] [Google Scholar]
- Takeda, Y. 1994, PASJ, 46, 53 [NASA ADS] [Google Scholar]
- Takeda, Y. 1995, PASJ, 47, 463 [NASA ADS] [Google Scholar]
- Tanaka, K. 1971, PASJ, 23, 217 [NASA ADS] [Google Scholar]
- Thévenin, F., & Idiart, T. P. 1999, ApJ, 521, 753 [NASA ADS] [CrossRef] [Google Scholar]
- VandenBerg, D. A., Swenson, F. J., Rogers, F. J., et al. 2000, ApJ, 532, 430 [NASA ADS] [CrossRef] [Google Scholar]
- van Leeuwen, F. 2007, A&A, 474, 653 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van Regemorter, H. 1962, ApJ, 136, 906 [NASA ADS] [CrossRef] [Google Scholar]
- Woods, T. N., Prinz, D. K., Rottman, G. J., et al. 1996, J. Geophys. Res., 101, 9541 [Google Scholar]
- Zhang, H. L., & Pradhan, A. K. 1995, A&A, 293, 953 [NASA ADS] [Google Scholar]
All Tables
Solar mean iron non-LTE (SH = 0.1) abundances determined using various sources of gf-values.
Line data and iron LTE and non-LTE abundances from an analysis of the solar spectrum.
All Figures
 |
Fig. 1 Atomic structure of Fe i as obtained from laboratory experiments (long lines, black lines in the color online version of the paper) and calculations (short lines, blue lines in the color online version of the paper). See text for the sources of data. |
| In the text | |
 |
Fig. 2 Model atom of Fe i (bottom panel) and Fe ii (top panel). The super-levels are indicated by long lines. The iron spectral lines used in the abundance analysis arise from the transitions shown as continuous lines. |
| In the text | |
 |
Fig. 3 Electron (open circles) and hydrogen (filled circles) collision rates of representative transitions in Fe i (left column) and Fe ii (right column) as a function of the transition energy in the model 5780/4.44/0 at a depth point of log τ5000 = −0.5, where T = 5583 K, nH = 0.922 × 1017, and ne = 0.137 × 1014 (top row), and in the model 4600/1.60/−2.50 at a depth point of log τ5000 = −0.5, where T = 4174 K, nH = 0.212 × 1017, and ne = 0.286 × 1011 (bottom row). We assumed SH = 0.1 throughout. |
| In the text | |
 |
Fig. 4 Top panel: emergent fluxes calculated using the model of Teff = 5777 K, log g = 4.44, and [M/H] = 0 with iron (log εFe = 7.50, non-LTE with SH = 0.1, continuous curve) and without iron (dotted curve) compared with the solar flux taken from Woods et al. (1996, dashed curve). The observed flux below 1700 Å is contributed by the solar chromosphere. Bottom panel: the ratio between the non-LTE (SH = 0.1) and LTE emergent fluxes in the same model atmosphere with log εFe = 7.50 from the calculations with the final (continuous curve) and reduced (dotted curve, see Sect. 2.3) model atoms. For clearer illustration, the theoretical fluxes were convolved with a Gaussian profile of ΔλD = 2 Å. |
| In the text | |
 |
Fig. 5 Departure coefficients, b, for the levels of Fe i and Fe ii as a function of log τ5000 in the model atmospheres 5777/4.44/0 (left column) and 4600/1.60/−2.50 (right column) from the calculations with our final model atom of iron (top row) and the reduced model atom, which ignores the predicted levels of Fe i. Every fifth of the first 60 levels of Fe i is shown. They are quoted in the bottom right part of each panel. All remaining higher levels of Fe i are plotted by dotted curves. For Fe ii we show every fifth of the first 60 levels. They are quoted in the top right part of each panel. The letters z, y, x, ... are used to denote the odd parity terms and a, b, c, ... for the even parity terms. To distinguish Fe i and Fe ii levels, note that b < 1 for each Fe i level outside log τ5000 = 0 in the solar metallicity model and log τ5000 = 0.4 in the metal-poor one. An exception are the highest levels in the layers with log τ5000 around −2.5 in the model 4600/1.60/−2.50. For Fe ii, b ≥ 1 inside log τ5000 = −2 in both model atmospheres. SH = 0.1 throughout. |
| In the text | |
 |
Fig. 6 Best fits (continuous curve) of the solar Fe i 5434 and 6608 Å lines (bold dots in top and bottom panels, respectively) obtained from the non-LTE calculations with SH = 0.1. Fitting parameters are given in Table 5. For Fe i 6608 Å, dotted curves show the effect on the theoretical profile of a ± 0.02 dex variation in the final Fe abundance. The macroturbulence velocity was reduced by 0.3 km s-1 for |
| In the text | |
 |
Fig. 7 Solar LTE (left column) and non-LTE (SH = 0.1, right column) Fe abundances from the Fe i (open circles) and Fe ii (filled circles) lines plotted as a function of Eexc (top row) and Wobs (bottom row). The mean abundances derived from the Fe i and Fe ii lines along with their standard deviations are quoted in the top row panels. The dotted line indicates the mean abundance derived from the Fe i lines and the shaded grey area its statistical error. In the bottom row panels, the dashed line shows the calculated trend of log εFeI versus Wobs. Everywhere, gf-values indicated in Table 5 were used. |
| In the text | |
 |
Fig. 8 Non-LTE (SH = 0.1) differential abundances derived from the Fe i (open circles) and Fe ii (filled circles) lines in the selected stars as a function of the observed equivalent width (left column panels) and excitation energy of the lower level (right column panels). In each panel, the dashed line shows the mean iron abundance determined from the Fe i lines. See text for more details. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.